Below are the first 10 and last 10 pages of uncorrected machine-read text (when available) of this chapter, followed by the top 30 algorithmically extracted key phrases from the chapter as a whole.
Intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text on the opening pages of each chapter.
Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
Do not use for reproduction, copying, pasting, or reading; exclusively for search engines.
OCR for page 219
Appendix A
Population and Related Projections
Made by the Committee
Gretchen S. Donehower and Carl Boe
This appendix outlines the methods used to generate the population
and labor force projections as well as summary measures and other indica-
tors used in several chapters of this report. The projections were reviewed
for accuracy and consistency by committee members and compared with
results from other such projections. While the committee's projections were
made to 2100, the report primarily discusses results through 2050. Given
the high degree of uncertainty regarding variables such as future rates of
return, productivity growth, international capital flows, and so on, the com-
mittee chose to limit its analysis and discussion to the next four decades.
POPULATION PROJECTIONS BY AGE AND SEX
The population projections used by the committee are based on in-
termediate-cost population projections prepared by the Social Security
Administration (SSA) for its 2011 Trustees Report, with some important
modifications. The committee thanks Felicitie Bell, Office of the Chief
Actuary of the SSA, for her generosity in sharing projection details with
it. The Social Security methods are summarized here briefly, but complete
information on SSA projection methods and assumptions can be found at
http://www.ssa.gov/oact/tr/2011/index.html (accessed June 24, 2011). The
starting population is the 2008 estimated Social Security Area population1
1The Social Security Area population covers the U.S. Census population (residents of all 50
states and Washington, D.C., plus Armed Forces overseas) but adds a small group of potential
Social Security beneficiaries who are not covered by the U.S. Census population. These persons
219
OCR for page 220
220 APPENDIX A
by sex and single year of age. This population is projected forward each
year based on projected rates of fertility, mortality, and net migration. Net
migration is immigrants coming into the population minus emigrants leav-
ing the population.
The age-specific fertility rates used are the same as in the intermediate-
cost SSA projections, with a minor adjustment for the years 2008 and
2009.2 The age distribution of fertility is based on recent historical trends,
while the overall level of fertility is assumed to decline gradually in the
near term and remain constant at just below replacement level. Specifically,
the observed total fertility rate is 2.09 children per woman in 2008 and is
assumed to fall gradually to a constant level of 2.00 children per woman
by 2035.
The main adjustment to the SSA projections is that the mortality rates
used here are lower than those used in the intermediate-cost SSA projection.
As described in Chapter 3, the committee agrees with the Social Security
Advisory Board's Technical Panel on Assumptions and Methods (TPAM)
that there will likely be faster future declines in mortality than reflected
in the intermediate-cost SSA projections. This conclusion is based on an
analysis of potential future trends in smoking and obesity (Technical Panel
on Assumptions and Methods, 2011). The SSA projection assumes that
average life expectancy by 2050 will be 82.2 years, whereas the committee
projection assumes instead an additional 2.3 years of life on average, for a
life expectancy of 84.5 years by 2050. This mirrors the TPAM conclusion.
The corresponding lower age-specific mortality rates are found by searching
for a mortality schedule that is between the SSA intermediate- and high-cost
options and implies a life expectancy in 2050 of 84.5 years. The high-cost
option assumes lower mortality than the intermediate and thus an average
life expectancy of 84.8 years by 2050. The projection used here employs a
mortality schedule that is a weighted average of the two SSA options such
that the desired life expectancy in 2050 of 84.5 years is achieved.
This average is found by first defining a difference term bx,s for age x
and sex s, which is the difference between the death rates mx,s for the high
cost and intermediate cost:
bx,s = ln(mx,shigh) - ln(mx,sintermediate)
are U.S. citizens living abroad, residents of U.S. territories, and noncitizens living abroad who
are insured for future Social Security benefits. They usually comprise around 2 percent of the
U.S. Census population. In the aggregate, the Census and Social Security Area population age
and sex distributions are almost identical.
2Published rates for 2008 were multiplied by 0.99 and for 2009 by 1.01 to match more
closely the predicted birth cohorts of the SSA projections and correct for inconsistencies in-
troduced by interpolation to estimate January 1 populations from July 1 population estimates.
OCR for page 221
APPENDIX A 221
The new death rates that were used for these projections are
mx,s = exp{ln(mx,sintermediate) + kbx,s}
where k, which is the same for both sexes and constant over age, is found
by a search program to achieve the desired average life expectancy of 84.5
years in 2050.
The SSA projection adds net migrants at each projection step based
on a guess about the future trend of migration, legal and illegal combined,
and the age and sex distribution of net migrants from recent history.
The total number of net migrants in the SSA projections begins at only
35,000 in 2008 based on evidence that the recent economic downturn in
the United States has discouraged a great deal of potential immigration
and encouraged some emigration. The projected number of net migrants
quickly rebounds to 1,250,000 by 2015 but then falls slowly but steadily to
1,025,000 by 2085. While the committee's projection uses the same age and
sex distribution of net migration as in the SSA 2011 Trustees Report from
2008 to 2025, its trajectory for future migration is significantly higher than
that of the SSA. As with future mortality, the committee believes that the
future trajectory for net migration developed by the TPAM is more reason-
able than the one currently used in intermediate SSA projections. Thus the
committee adopted the TPAM migration schedule for 2026-2050, which
assumes a constant rate of 3.2 net migrants for every 1,000 residents each
year after 2025.
Given the rates of fertility, mortality, and net migration described
above, the starting Social Security Area population of 2008 is projected
forward in single-year steps of age and time for men and women sepa-
rately using the cohort component method. The projection ends in the
year 2100.3 This projection was the baseline scenario of future change.
Summary measures for fertility, life expectancy, and net migration appear
in Table A-1. For several analyses reported in previous chapters, the rates
of fertility, mortality, and net migration were modified to calculate popula-
tion projections based on alternative scenarios of change. In these cases,
the projections were exactly as described above, except for the alternative
rates described in the scenario.
3The SSA 2011 Trustees Report only published projection results to year 2085 because it is
charged with reporting a 75-year time horizon for Social Security finances. The demographic
projections, however, are estimated internally to 2100.
OCR for page 222
222 APPENDIX A
TABLE A-1 Summary Measures of Demographic Assumptions for
Baseline Projection, Selected Years 2008-2100
Years of Life Expectancy
Total Fertility Rate Net Migrants
Year Men Women Combined (births per woman) (millions)
2008 75.4 80.3 77.8 2.05 0.04
2009 75.6 80.4 77.9 2.04 0.84
2010 75.7 80.5 78.1 2.07 0.82
2015 76.9 81.3 79.0 2.05 1.25
2020 77.9 82.1 79.9 2.04 1.20
2025 78.8 82.9 80.8 2.02 1.14
2030 79.7 83.6 81.6 2.01 1.19
2035 80.5 84.3 82.4 2.00 1.23
2040 81.3 85.0 83.1 2.00 1.27
2045 82.1 85.7 83.8 2.00 1.31
2050 82.8 86.3 84.5 2.00 1.34
2055 83.5 86.9 85.1 2.00 1.38
2060 84.2 87.4 85.8 2.00 1.43
2065 84.8 88.0 86.3 2.00 1.47
2070 85.4 88.5 86.9 2.00 1.52
2075 86.0 89.0 87.4 2.00 1.57
2080 86.5 89.4 88.0 2.00 1.62
2085 87.1 89.9 88.5 2.00 1.67
2090 87.6 90.3 88.9 2.00 1.72
2095 88.1 90.7 89.4 2.00 1.78
2100 88.6 91.1 89.8 2.00 1.84
SOURCE: Committee calculations.
POPULATION PROJECTIONS BY RACE/ETHNIC GROUP
For some of the analyses, population projections by separate groups
defined by race and ethnicity were of interest. The SSA does not take race
or ethnicity into account when it makes projections, so data from the
U.S. Census Bureau were used to break the SSA-based population projec-
tions into race/ethnic groups that are consistent with the main population
projections used in this report. The committee thanks David Waddington,
Ben Bolender, Christine Guarneri, and Donnette Willis of the Population
Projections Branch of the U.S. Census Bureau for sharing data with it for
the project.
Census Bureau projections are done based on the resident population
by age, sex, race, and Hispanic origin. The set of projections published in
2008 was used here and can be found at http://www.census.gov/population/
www/projections/2008projections.html (data first accessed May 31, 2011).
These projections cover the years 2008 to 2050, so the committee extends
the Census 2050 rates to the year 2100 to cover the full period of interest.
OCR for page 223
APPENDIX A 223
While the Census projections define many additional groups, only five
groups were used in this work to avoid small numbers in groups defined
by sex, single years of age, and race/ethnicity. The five race/ethnicity groups
used were (1) Hispanic, (2) non-Hispanic white alone, (3) non-Hispanic
black alone, (4) non-Hispanic Asian alone, and (5) non-Hispanic other. This
last group includes non-Hispanic native Hawaiian and Pacific Islanders,
American Indians and Alaska natives, and multiracial persons.
Census Bureau projected rates based on these five groups do not aggre-
gate to the same rates as in the baseline single-group projection described
in the preceding section. This is due both to the modifications in SSA rates
made by the committee and to the different projection methods used by the
Census Bureau and the SSA. To keep the projection by race/ethnic group
consistent with the single-group projection, it was necessary to use the
race/ethnic projections from Census to disaggregate the baseline projection
rather than using Census rates by race/ethnic groups and projecting them
directly.
This means that the starting population for the race/ethnic projections
is not the starting population of the Census Bureau race/ethnic population
projections. Instead, each age and sex group in the starting population for
the single-group projection is broken down into the five race/ethnic groups
based on the distribution in the Census Bureau population for that age and
sex group.
Then, at each projection step, the total number of vital events (births,
deaths, net migrants) for each age and sex group is estimated for the single-
race projection and broken down into the five race/ethnic groups based on
the distribution that would have occurred given the relative rates (of fertil-
ity, mortality, or net migration) from the Census Bureau race/ethnic popula-
tion projections. In this way, the single-sex and race/ethnic projections are
consistent with each other but the relative changes in the race/ethnic groups
are consistent with the Census Bureau rates by race/ethnic group.
For example, say mortality rates for the single-group projection pre-
dicted 900 deaths to men aged 52 during the year, while the Census mor-
tality rates by race/ethnic group projected 800 deaths across the five race/
ethnic groups. The 900 single-group deaths would be multiplied by the race/
ethnic distribution of the 800 deaths to get the race/ethnic distribution of
the 900 deaths to men aged 52 during the year.
Finally, while the Census Bureau publishes mortality rates by each age/
sex/race/ethnic group, this is not the case for fertility or net migration. Birth
rates are published by race/ethnic group only, not age, so the projection
assumes that the age distribution of fertility for all five race/ethnic groups
is the same as the overall SSA age distribution of fertility. Net migration is
published as counts by sex and race/ethnic group, so the projection assumes
that the age distribution of male net migration is the same as the SSA age
OCR for page 224
224 APPENDIX A
distribution of male net migrants for all five race/ethnic groups. Similarly
for females, the SSA age distribution of female net migrants is used for all
females across race/ethnic groups.
LABOR FORCE PROJECTIONS
The Bureau of Labor Statistics (BLS) usually projects the labor force
only 10 years into the future. Occasionally, though, it extends those near-
term projections to longer periods of time. The labor force projections in
this report are based on labor force participation rates from a longer-term
projection, one first produced in 2006 and later updated to a starting year
of 2008. The method mainly takes historical trends within each age/sex/
race/ethnic group and extrapolates them into the future, but with a logit
transformation so that the future path is nonlinear. During the first part
of the projection period, through 2020, changes in the labor force "are
the result not only of compositional changes in the population, but also of
changes in the detailed labor force participation rates of the various age,
sex, race, and ethnic categories. [These] latter changes are based on the
past labor force behavior of those categories and are often assumed to ap-
proach zero beyond a certain point in the projection horizon. Accordingly,
changes in the aggregate labor force participation rate and in the labor force
between 2020 and 2050 will reflect only changes in the age, sex, race, and
ethnic composition of the population." (Toossi, 2006, p. 22) There is no
economic model involved in the BLS projections, nor is there any attempt
to include the effects of the business cycle.
The BLS data end in 2050, so the 2050 labor force participation rates
were repeated to extend to a 2100 projection horizon. No estimates are
provided for those younger than age 16, so their labor force participation
rate is assumed to be zero. The details of the labor force projections can
be found at http://www.bls.gov/opub/mlr/2006/11/art3full.pdf. (Data with
projections through 2050 were accessed on July 11, 2011, but are no longer
available on the BLS Web site.)
The BLS labor force participation rates are estimated by sex for single
years of time, but for age the groups may span 2 years, 5 years, or more.
To apply these rates to the population schedules by sex and single years
of age, an interpolation method was used. A cubic spline was fitted to the
cumulative counts of population and labor force, generating estimates of
the total population and labor force at each age. The ratio of these produces
labor force participation rates by single years of age that are completely
consistent with the BLS age group rates but provide a smooth single-year-
age schedule. These rates by sex and single year of age and time were then
applied to the population projection described previously to get the total
projected labor force by age and sex.
OCR for page 225
APPENDIX A 225
Note that the BLS labor force participation rates are based on a uni-
verse of the civilian noninstitutional population. They were applied here
to a universe that includes noncivilians and the institutional population to
avoid the need for estimating a further projection of future rates of military
service and institutionalization by age, sex, and race/ethnic group. In the
aggregate, the impact of the different population bases is very small.
The BLS does not include race/ethnicity in its labor force projections,
so data from the March Current Population Survey (CPS) were used to
estimate labor force participation rates by the same five race/ethnic groups
discussed above. The CPS data were accessed through the Integrated Public
Use Microdata Series facility, found at http://cps.ipums.org/cps/. Specifi-
cally, rates for the five groups from 2000 to 2011 were averaged together
to estimate the labor force participation rates of the five groups within each
age and sex group. Five-year age groups were initially estimated to reduce
noise in the estimates, and then the same cumulative spline interpolation
described above was applied to obtain a smooth single-year-of-age schedule.
Then, a single multiplicative adjustment factor for each age-sex-year cell
was computed so that the overall age-sex-year labor force participation rate
was preserved; however, the race/ethnic groups had relative participation
rates in the same ratios as the CPS rates by race/ethnicity for that age and
sex.
SUPPORT RATIO ANALYSES
Calculating a support ratio requires two types of data: counts of popu-
lation by age and per capita estimates of economic activity by age. The com-
mittee refers to the second item, the age schedules of per capita economic
activity, as "age profiles." The National Transfer Accounts project has a
fully developed methodology for estimating age profiles of economic activ-
ity for individuals by age from surveys and administrative data. Details on
the methodology are available at the project Web site, www.ntaccounts.org,
and in Mason and Lee (2011). Examples of age profiles for consumption
and production appear in Figure A-1 for the United States in 2007. Details
on the sources and methods for constructing U.S. age profiles are found in
Lee, Donehower, and Miller (2011).
A support ratio (SR) is the ratio of aggregate age profiles weighted by
population. In mathematical notation, let c(x,t) and yl(x,t) represent the
consumption and labor income profiles, respectively, in Figure A-1 at each
age x at time t. Let n(x,t) be the number of persons age x in the population
at time t. For a support ratio indicating the relative number of producers
to consumers, the calculation is
e yl(x,t) n(x,t) e c(x,t) n(x,t)
SR(t) = x =0 x=0
OCR for page 226
226 APPENDIX A
80,000
70,000
Age Group Average (Current U.S. $)
Consumption
Labor Income
60,000
50,000
40,000
30,000
20,000
10,000
0
0 10 20 30 40 50 60 70 80 90
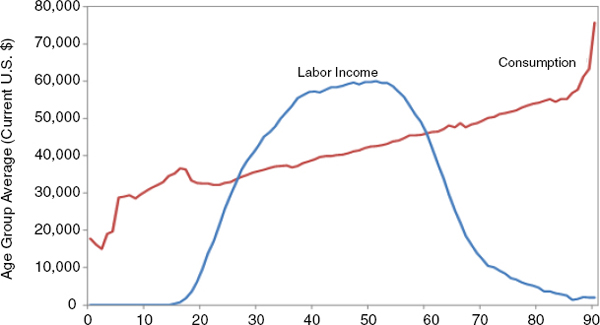
FIGURE A-1 U.S. per capita labor income and consumption, by single year of age,
A-1.eps
2007. SOURCE: Committee calculations.
bitmap with vector type
Similarly, a fiscal SR can be calculated substituting the age profile of taxes
paid for labor income in the numerator and the age profile of government
benefits received for consumption in the denominator.
The SR calculated for one time t in this way gives a snapshot of the
aggregate balance between different pairs of age profiles at time t. If we
combine the age profiles of a fixed time with a population projection, we
can assess what will happen to the balance of age profiles, say labor in-
come and consumption, over time if the age profiles remain fixed but the
demography changes. For example, combining the age profiles shown in
Figure A-1 with the U.S. population projection detailed in the first section
allows generating a time series for t from 2007 to 2100:
e yl(x,2007) n(x,t) e c(x,2007) n(x,t)
SR(t) = x =0 x=0
This analysis was done for other countries with age profiles calculated as
part of the National Transfer Accounts project, using the age profiles cal-
culated for a recent year and combining them with population counts from
the United Nations World Population Prospects database, medium variant
projections (http://esa.un.org/wpp/unpp/panel_population.htm).
Calculating a time series of SRs in this way shows how population ag-
ing affects the ratio of producers to consumers or taxpayers to beneficiaries
over time. It indicates what will happen if age profiles are held constant
and population changes.
OCR for page 227
APPENDIX A 227
Another type of analysis asks how age profiles would have to change
to maintain the level of the SR in the face of population aging. This was
done by taking the labor income curve and extending the peak value for an
additional year of age. For example, using 2007 age profiles for the United
States and the population projection developed for this report, the support
ratio in the United States for 2007 was 0.78. The peak value of average labor
income was about $60,000 for people aged 51. Given population aging, the
SR in the following year fell to just under that in 2007. Instead of allowing
the support ratio to fall in 2008, the committee imagines that the age profile
of labor income stretches at age 51, repeating the $60,000 value for age 52.
The rest of the age profile shifts to the right by 1 year. The old age 52 value
is assigned to age 53, and so on. Then the support ratio for 2008 becomes
0.80. This is above the initial 2007 value, so we proceed to the next year.
The support ratio for 2009 to 2014 with the labor income curve stretched
by 1 year is still above 0.78, so no further adjustment is needed. In 2015,
however, the support ratio with the 1-year labor income extension falls be-
low the 0.78 value, so the labor income curve must be extended again. Now
labor income's $60,000 peak value appears for ages 51, 52, and 53, and the
original value for age 52 is assigned to age 54, for age 53 to age 55, and so
on. Repeating this algorithm for the whole population projection gives an
indication of roughly how many years retirement would have to be delayed
on average to keep the SR from falling below its current level. This type
of calculation can be made for other "thought experiments," such as how
much taxes would have to rise to maintain the current fiscal SR.
A different but more straightforward calculation indicates how much
consumption would have to fall to maintain the current SR if labor income
stayed fixed. That figure is simply the unadjusted SR divided by the SR in
the starting year.
INCOME-WEIGHTED POPULATION
The future impacts of population aging may be conditioned by the
socioeconomic conditions of countries with different future aging trajecto-
ries. To include this variable in the analysis, estimates of future population
age distributions were calculated based not just on counts of population
by age, but also by weighted population counts by age--that is, weighted
by the relative wealth of the country where each projected person resides.
To review the basic population-weighted calculation where each person
counts equally, let n(j,x,t) be the number of persons in country j of age x at
time t. The global population age distribution, or the proportion of people
in the world age q across all j countries at time t, is
Global Population Age Distribution = J e
j=1n(j,q,t) j=1 x=1 n(j,x,t)
J
OCR for page 228
228 APPENDIX A
which is the global number of persons aged q at time t divided by the global
population at time t.
Now we can add a differential weight to each person in the calculation,
based on the per capita gross domestic product (GDP) of each country j at
time t, or GDP(j,t):
GDP-Weighted Global Population Age Distribution =
J e
j=1 GDP(j,t) n(j,q,t) j=1 x=1 GDP(j,t) n(j,x,t)
J
These analyses were done using several different data sources. The
population by age and country were taken from the United Nations World
Population Prospects database, medium variant projections for 2008, avail-
able at http://esa.un.org/wpp/unpp/panel_population.htm. Different GDP
data were used to assess the robustness of the results to different data
sources or scenarios.
One option was to use 2010 per capita GDP data for the entire projec-
tion period. The per capita GDP figures, measured in purchasing power
parity-adjusted international dollars, came from the International Monetary
Fund's (IMF's) World Economic Outlook database, the April 2011 version,
available at http://www.imf.org/external/pubs/ft/weo/2011/01/weodata/
download.aspx (accessed April 28, 2011).
Another option was to use per capita GDP figures for 2010 but mul-
tiply them by projected GDP growth rates to get a projected per capita
GDP for each country. This was done using two different sources for the
projected GDP growth rates. The first was the IMF World Economic Out-
look database mentioned above, which has a projection of average annual
growth from 2010 to 2016. This average annual rate was used to project
each country's GDP out to 2050, which was then divided by its projected
population to get its projected per capita GDP (all adjusted for purchas-
ing power parity). The second source was the consulting firm PriceWa-
terhouseCoopers, which estimates GDP growth using reports on future
economic opportunities. Projected rates from 2010 to 2050 for 22 countries
covering over 80 percent of 2010 global economic output are available at
http://www.pwc.com/en_GX/gx/world-2050/pdf/world-in-2050-jan-2011.
pdf (accessed April 28, 2011). As with the IMF projections, these rates were
used to grow GDP from observed 2010 levels, which were then divided
by projected population to get the per capita figures (also adjusted for
purchasing power parity). For those countries not included in the PriceWa-
terhouseCoopers report, IMF data were used but adjusted by the ratio of
the average PriceWaterhouseCoopers growth estimates to the IMF growth
estimates for the 22 countries with data from both sources.
A few disputed territories or small islands that did not have both popu-
lation and GDP projection data were dropped from the analysis.
OCR for page 229
APPENDIX A 229
TOTAL NET WORTH
If net worth differs by age, then population aging will have an impact on
total net worth and thus the pool of assets available to an economy to fund
growth. To examine this possibility, the committee used data on the aver-
age net worth of families in the United States by the age of the family head.
These data come from the 2007 wave of the Survey of Consumer Finances
(SCF), reported in the Federal Reserve's February 2009 Bulletin (available at
http://www.federalreserve.gov/pubs/bulletin/2009/pdf/scf09.pdf).
Let NW(x,t) be the average net worth of a family with head age x at
time t. In order to apply this family measure to individuals, the commit-
tee assumed that all assets are owned by the head of the family and that
nonheads have no assets. When NW(x,t) is multiplied by the headship rate
h(x,t), or the proportion of persons age x who are family heads at time t,
the product is the average net worth of a person age x at time t.4 The data
on headship come from the 2007 March Supplement of the CPS. The CPS
data were accessed through the Integrated Public Use Microdata Series
facility found at http://cps.ipums.org/cps/.5
Finally, multiplying the average net worth per person in 2007,
NW(x,2007)h(x,2007), by the population schedule n(x,t) gives the total
net worth at time t. Dividing through by the total population gives the per
capita amount:
Per Capita Net Worth (t) =
e
x NW( e
, 2007) h(x, 2007) n(x,t) x
=1 x =1 n(x,t)
As with the other calculations in this report, the committee is interested
in the change brought about by population aging. This formula gives some
indication of that by showing what will happen to per capita net worth in
the future if the age profile of net worth and headship remain constant but
the population continues to age.
4Note that NW(x,t) is the ratio of total net worth of families headed by those age x to the
number of families headed by those age x. The headship rate h(x,t) is the ratio of the number
of families headed by those age x to the number of persons age x. Multiply these two quanti-
ties together and the family terms cancel, leaving a ratio of total net worth of families headed
by those age x to the number of persons age x. This is per capita net worth if we assume that
only family heads own the assets.
5The concept of family in the CPS is not exactly the same as that in the SCF, so the headship
data used from the CPS are the headship rates for households, not families. Across the entire
population, the differences in family and household headship are small, as most households
contain only one family, by both the SCF and CPS definitions.
OCR for page 230
230 APPENDIX A
STOCHASTIC POPULATION PROJECTIONS
Stochastic forecasts of fertility and mortality rates by age and sex,
together with initial population counts and a deterministic migration sched-
ule, allow for the generation of stochastic population trajectories through
time that reflect uncertainty or variation around a long-term trend. The
stochastic population counts (denoted Ns,x,ti, where the indices are sex (s),
age (x), and time (t) and where i indicates a specific trajectory) in turn yield
stochastic support ratios, SRti.
The level of uncertainty is a function of the amount of natural variation
in the historical vital rates and in the forecast uncertainties of mortality and
fertility components. The methodology is that described in Lee and Tul-
japurkar (1994), where the Lee-Carter model is used for both the mortality
and fertility components.
Mortality
Stochastic mortality trajectories were generated following the coher-
ent forecast technique of Li and Lee (2005), which is a Lee-Carter model.
This coherent method lowers forecast uncertainty by grouping forecasts
for 15 low-mortality countries. Inputs to the model are mortality rates for
1950-2007 from the Human Mortality Database (University of California,
Berkeley, and Max Planck Institute for Demographic Research, 2011);
output consists of 1,000 stochastic sex-age-time trajectories Ms,x,ti from
the online LCfit program (available at http://simsoc.demog.berkeley.edu/).
Each projection i is independent from projection j i, and any life table
functional such as e0 may be computed from the set of underlying death
rates by fixing the trajectory number, time, and sex. The median in 2050 of
the 1,000 trajectories for combined-sex e0 is close to 84.5, the target value
from the baseline deterministic mortality projections in Table A-1.
The trajectories Ms,x,ti are "calibrated" so that the median of e0 for each
sex matches up with the baseline values in Table A-1. Specifically, multipli-
ers zs,t near unity are calculated so that
median e0 (zs,t Ms,x,ti) = e0baseline(s,t)
This affects the cloud of trajectories by changing the center while preserving
the density of the cloud about the center.
Fertility
The fertility forecasts consist of simulations from a Lee-Carter model
of age-specific fertility rates (ASFR), using data from the 2011 Trustees Re-
OCR for page 231
APPENDIX A 231
port of the Social Security Administration (http://www.ssa.gov/oact/tr/2011/
index.html) and the small adjustments to data circa 2008 described earlier.
The least-squares fit provided by the singular value decomposition of the
1917-2010 series of ASFR yields i trajectories:
ASFRx,ti = ax + bx Kti
where ax = ASFRx,2010i and |bx| = 1 and Kti is a constrained autoregressive
moving average (1,1) process with autoregressive coefficient 0.9673 and
moving average coefficient 0.5367. The process is constrained so that the
long-run average total fertility rate is 2.0 (see Lee and Tuljapurkar, 1994,
for further details).
Migration
Net migration flows into the population follow the assumptions used
in the deterministic population projections by age and sex (see Table A-1).
Each stochastic trajectory experiences the same migration pattern.
Population
A population trajectory i begins with the initial launch population by
age and sex in 2009, Ns,x,2009i. To bring this population to 2010, losses
from death during the year and additions from new births are determined
using rates Ms,x,2009i and ASFRs,x,2009i applied to the population. Finally,
immigrants are added according to the baseline schedule.
Support Ratio
The SR for the i th trajectory,
e
SRi (t) = x e
=0 yl(x,t) N (x,t) x=0 c(x,t) N (x,t)
i i
is calculated along the trajectory based on the stochastic population counts.
The consumption schedule c(x,t) is normalized so that the support ratio in
2007 is unity.
