The Bureau of Land Management (BLM) asked the committee to address the following questions as part of the discussion of potential rates of horse and burro population growth: Would free-ranging horse and burro populations self-limit if they were not controlled? If so, what indicators (such as rangeland condition, animal condition, and health) would be present at the point of self-limitation? To address those questions, it is necessary to review the factors that limit population growth in an unmanaged population1 and that determine free-ranging horse and burro population growth and dynamics aside from management removals. Population growth and self-limitation are population processes in the sense that they involve a suite of underlying functions that lead to the result. The underlying functions include changes in natality and survival in response to environmental variables that affect forage availability, such as weather and population density.
The committee was also asked to assess whether there is compensatory reproduction as a result of population-size control, such as fertility control or removal from Herd Management Areas (HMAs). Compensatory reproduction is defined as an increase in reproduction as a direct or indirect consequence of management reductions, including removals and contraception. Indirect responses could include increased fertility, foal survival, or adult survival due to reduced competition for forage.
For self-limitation to occur, it is necessary for population processes to respond to population density (Figure 3-1). That is, population processes—such as population growth rates, age-specific survival rates, natality, and age of bearing first offspring (primiparity)—must be density-dependent. As density increases, population growth rate decreases because of increased competition for resources. Population processes are also altered by density-independent factors, particularly climatic conditions and variations. Natality and mortality can be affected by climatic conditions through direct effects on animals. Climatic conditions also affect resource abundance, for example, through effects on forage production.
____________
1 Unmanaged populations of horses and burros are not domestic animals, and they are not fed or given veterinary care. Their numbers are not controlled by removals or contraception.
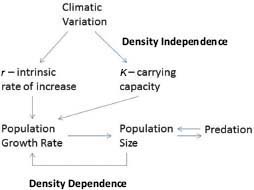
FIGURE 3-1 Population processes, including density-independent and density-dependent controls.
Population size can be reduced by predation, and predator abundance is affected by prey abundance. Population growth can also be affected by dispersal, immigration and emigration, and management factors, such as removal of animals from the range and contraception. This chapter examines the changes in population processes of free-ranging equids due to density-dependent, density-independent, predation, and management factors.
It is a general principle of ecology that populations do not continue to grow indefinitely, but the mechanisms of reduction in growth as densities increase are not always well understood (Flux, 2001). Mechanisms may include competition for resources among members of the same species at high densities (Ginzburg, 1986; Berryman, 2003), complex social behaviors (Wynne-Edwards, 1965), and combinations of physiological responses to social cues (Wolff, 1997).
Density dependence can be seen most easily by examining the S-shaped curve of population size changing over time described by the logistic equation
dN/dt = rN([K – N]/K),
where dN/dt is the instantaneous rate of change in N, N is the size of the population (number of individuals), r is the intrinsic rate of natural increase, and K is the carrying capacity, that is, the maximum population size that the environment can support as affected by resource abundance. The discrete form of the equation defines the population increment over an interval of time, such as a year, and is expressed as
Nt+1 = Nt + R(Nt[K – Nt]/K),
where Nt +1 is the population size in the next year or generation, Nt is the population size in the current year or generation, R is the maximum rate of increase per year or generation, and K is the carrying capacity. The annual or generational increment can be defined as
ΔN = Nt +1 – Nt.
Early in the growth process there is a period in which population grows without limitation because the difference between Nt and K is so large that the density-dependent term ([K - Nt]/K) produces little constraint on ΔN (Figure 3-2A). At the inflection point (point α in Figure 3-2A), ΔN (point β in Figure 3-2A) is maximized, but as Nt approaches K, growth slows; it even becomes negative if Nt is greater than K.
The population trajectory represented by the logistic equation, as portrayed in Figure 3-2A, assumes that R and K do not vary over time. If, however, environmental variation is great and harsh conditions periodically reduce R or K independently of density, the importance of density dependence diminishes. If such variations are great enough, the population will rarely experience density dependence. Population sizes that are strongly affected by such density-independent factors show sawtooth-like increases and decreases and do not come to a steady equilibrium with resources. Density independence is explained further below.
Carrying capacity is a concept that has multiple definitions that depend on the situation. For populations of unmanaged large herbivores, carrying capacity is determined by resource availability, primarily food, so it is sometimes called the food-limited or ecological carrying capacity. Food-limited carrying capacity (K in the logistic model) can be determined empirically by letting a population grow until it comes into quasiequilibrium with the resource base. That idea of carrying capacity is different from the idea of carrying capacity discussed in Chapter 7, in which forage supplies are estimated and combined with an appropriate forage utilization level to set an appropriate management level (AML) in an attempt to preserve a thriving natural ecological balance. That is not to say that a population at or near K cannot result in a thriving natural ecological balance. However, the value of K will most likely be higher than the carrying capacity set in the AML process. Similarly, food-limited carrying capacity will be higher than the stocking rate that maximizes animal or vegetation productivity, which Caughley (1979) referred to as economic carrying capacity. For example, the maximum rate of animal production would be attained at point a in Figure 3-2B, which might be the objective if animals were being produced for sale or for hunting.
Numerous reviews and meta-analyses have shown that density dependence is common in large herbivore populations (Fowler, 1987; Sinclair, 1989; Gaillard et al., 2000). How density dependence affects individual animals and thus life-history traits varies with the ecological context, and effects are stronger in some age-sex classes than in others (Bonenfant et al., 2009). Effects of increased population density on reproduction are manifested through reductions in pregnancy, fecundity, twinning rate, number of offspring per female, percentage of females lactating, and young-to-female ratios and through an increase in age of primiparity, depending on the species, population, and environmental context. Survival rate responses to population density are common, but they vary among ungulate populations.
Effects of Density on Population Processes
Several studies of density dependence have included or focused exclusively on equids. In Kruger National Park, South Africa, adult and juvenile zebra survival rates were adversely affected by density and favorably affected by rainfall (Owen-Smith et al., 2005). Similarly, zebra population dynamics in Kenya were best explained by a model of rainfall-mediated density dependence (Georgiadis et al., 2003) that involved fecundity and survival. An unmanaged horse population in Argentina exhibited density-dependent responses. Reduced fecundity was the primary response to increased density. Adult female survival was also reduced at higher densities, but to a lesser degree (Scorolli and Lopez Cazorla, 2010). In a feral donkey population in Australia, fecundity was high and not related to
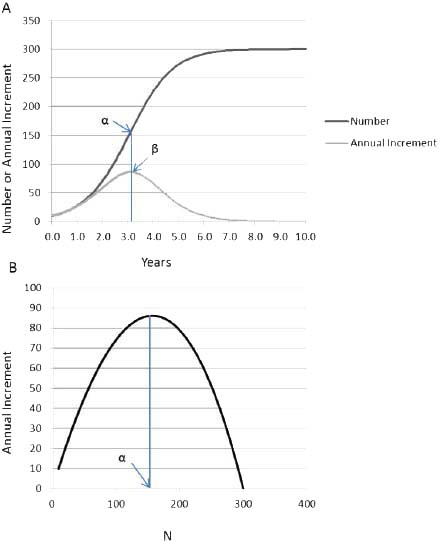
FIGURE 3-2 (A) Example of logistic population growth, with R = 1.18 and K = 300. Population size N and the annual population increment AN are plotted against time. Point a is the inflection point, at which population growth begins to decrease as the population approaches K. The corresponding point (3 shows that annual population increment is maximal at the inflection point. (B) Plot of annual population increment against population size, in which point a is the population size that maximizes the annual increment.
density; however, ages of males at sexual maturity and juvenile mortality increased at higher densities (Freeland and Choquenot, 1990; Choquenot, 1991; also noted in Bonenfant et al., 2009). Pregnancy rates declined at higher densities in horses in the eastern United States (Kirkpatrick and Turner, 1991). In Nevada, it was not uncommon for 2-year-old mares to foal, in contrast to earlier evidence indicating foaling did not begin until the age of 3 (Berger, 1986; Garrott et al., 1991). Garrott et al. (1991) argued that age at first reproduction is more likely to be earlier when forage is more abundant and when competition for forage is reduced. Jenkins (2000) analyzed data from the Granite Range and Pryor Mountain horse herds and reported evidence that population growth rate decreased with increasing population. Roelle et al. (2010) confirmed those findings in the Pryor Mountain horse herd. Thus, density dependence appears to take a variety of forms in equids.
Responses to density are often age-specific. Gaillard et al. (1998) reviewed evidence related to the conceptual model proposed by Eberhardt (1977) in which density effects on population vital rates (e.g., birth and death rates) would occur first in juvenile survival, then in age at first reproduction, then in reproductive rates of prime-aged (most highly reproductive) adults, and finally in adult survival. They noted that Fowler’s (1987) review supported Eberhardt’s model. The Gaillard et al. review provided further support of the model and reported that survival of prime-aged adults is relatively invariant whereas juvenile survival varies considerably from year to year. They reported that the pattern of high, stable adult survival and variable juvenile survival is observed in a wide variety of environments regardless of whether mortality is density-dependent or density-independent. They noted that higher annual variation in juvenile survival as compared to adult survival can arise from multiple causes including increased vulnerability to predation, drought, harsh winters, and factors causing low birth weights and early growth rates. In an unmanaged horse population in Argentina that was approaching carrying capacity, fecundity was affected by density and rainfall, but adult, juvenile, and foal survival rates were not (Scorolli and Lopez Cazorla, 2010). Although juvenile survival varies more than adult survival, population growth rate is highly sensitive to variations in adult survival, less sensitive to changes in juvenile survival, and moderately sensitive to changes in fecundity (Gaillard et al., 2000).
Possible Effects of Domestication
It is possible that domestication has selected for forms of density dependence that are different from those in undomesticated populations. Flux (2001) proposed that the tendency to self-regulate differs between feral and “wild-type” populations. It is believed that domestication of European rabbits by monks for over 600 years has led to feral populations that have been observed at densities of up to 200/ha in Australia and New Zealand (Thompson and King, 1994), whereas “wild” species seldom reach 4/ha. However, it is also likely that introduced rabbit populations in those locations are less affected by predation and disease. Other feral species also reach higher densities than their closest “wild” relatives, such as goats, pigs, cats, and domestic pigeons. Many of those species have been implicated in severely detrimental effects on habitats and native species (Flux, 2001).
Genetic history may contribute to the reproductive response of free-ranging equids to resource scarcity. A population of unmanaged horses in the Camargue (France) declined in body condition because of scarce resources, and this led to reduced foal and mare survival without a concurrent decline in fecundity (Grange et al., 2009). The authors pointed out that that pattern is different from the one in wild, nonferal ungulate populations, in which fecundity decreases well before adult survival as resources become more limiting. Other domesticated species, such as cattle, have shown the same pattern as the Camargue
horses. The authors argued that domestication has selected for reproduction over survival even when resources are scarce. As a result, feral populations are more likely to oscillate strongly, and the tradeoff of decreased adult survival may make them more vulnerable to harsh environmental conditions.
Nutritional and Physiological Mechanisms
Fowler’s (1987) review indicated that food shortage is the primary factor in density dependence. The mechanisms through which food limitation affects population vital rates are most likely effects of poor nutrition, energy balance, and body condition on reproductive processes and survival rates (e.g., Gaidet and Gaillard, 2008). Poor nutritional status may also impair animal feeding and predator avoidance and increase susceptibility to adverse weather. Feral donkey populations in Australia were regulated by food-limited juvenile mortality, which in turn was related to the nutritional status of lactating females (Choquenot, 1991). In an unmanaged population of horses in the Australian Alps, population growth rate declined as numbers increased because of decreased fecundity and decreased adult and juvenile survival (Dawson and Hone, 2012). Those response variables were related to body condition and available food, and mean body condition correlated positively with forage biomass. In the Pryor Mountains, foal survival rate was positively related to precipitation, and this suggests a link to forage production and availability mediated through the condition of the mares (Roelle et al., 2010). The authors cited several other studies, including Garrott and Taylor’s (1990) study of the horse populations in the Pryor Mountains, whose results suggested that forage availability can affect mare condition and thus foaling rates.
In addition to the total quantity of food, the quantity of high-quality food items may be diminished when populations are near carrying capacity. When an Australian donkey population reached carrying capacity, females ingested a diet of low nutritional value, whereas those in a population below carrying capacity were able to ingest a nutrient-rich diet (Freeland and Choquenot, 1990). Low diet quality resulted in low levels of stored nutrients in the females, which impaired their ability to raise offspring.
When resources are scarce, females are induced into anestrus as a result of poor body condition (Ginsberg, 1989). Birth sex ratios may be affected because mares in poorer condition have more female foals (Cameron et al., 1999). The effect of body condition on sex ratio probably occurs at conception. The age at first reproduction and reproductive rates of 2- to 4-year-old horses are affected by competition for forage, which reduces the amount of forage per individual and thus increases the time needed for individuals to attain sexual maturity (Garrott and Taylor, 1990). Saltz et al. (2006) reported that rainfall during the year before conception and drought conditions during gestation were important determinants of reproductive success in Asiatic wild ass. They focused on rainfall before conception because females in poor condition would not go into estrus.
To summarize, the causal pathways underlying density dependence begin with population size (Figure 3-3). Climatic conditions and spatial accessibility determine the availability of forage for herbivores. Population size affects the amount of forage available per animal: as population size increases, forage per animal declines; this results in reduced forage intake and reduced body condition, which affect survival rates and natality.
Behavioral Mechanisms
There are two fundamental mechanisms of behavior-mediated density dependence: increased dispersal at high densities and changes in social interactions that affect reproduction.
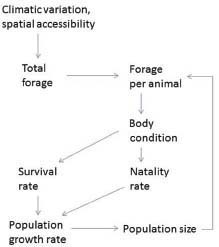
FIGURE 3-3 Nutrition-based mechanisms underlying density dependence and density independence.
The role of dispersal in density dependence remains uncertain because there have been few studies (Bonenfant et al., 2009). Duncan (1992) found no evidence of a social mechanism that regulates equid populations below leverels determined by their food resources. However, others have found that increased social stress at high density may contribute to density dependence (Linklater et al., 2004). Tatin et al. (2009) found that reduced space can slow the growth of a population of a Przewalski’s horse herd before forage becomes limiting. They suggested that reproduction decreased as a result of mare dispersals to avoid incest (Monard and Duncan, 1996).
Where populations are spatially unbounded, dispersal can forestall density-dependent control as long as there are places where populations are small and individuals in crowded locations can disperse (Owen-Smith, 1983; Pulliam, 1988). Such source-sink population complexes where emigration keeps densities low will be common where environmental forces—ranging from physical factors, such as climate, to biological factors involving predators—operate over large areas. But where there are boundaries to dispersal, as on natural islands or habitat islands created by human landscape change, densities can increase to a point at which feedback from crowding lowers fecundity and adult and juvenile survival.
Crowding changes behavior in many ways among horses and burros. In Nevada, high equid densities were associated with increased incidences of confusion, separation, and desertion of foals by mares at water points in the dry season (Boyd, 1979). Berger (1983b) reported that social instability, specifically high rates of turnover among harem males, adversely affect female reproductive success and patterns of age-specific fecundity. He also indicated that increased levels of sexual harassment can lower female body condition and disrupt normal endocrine function. By virtue of their hindgut fermentation system, equids can subsist on low-quality vegetation, and they typically compete by maximizing intake relative to other animals (Rubenstein, 1994). However, when densities increase, individual agonistic interactions increase, and this reduces time available for foraging and thus competitive ability. Equid females rely on male protection to increase time spent in feeding, and
this increases the likelihood that foals will survive to the age of independence (Rubenstein, 1986). Thus, any interference that impinges on a female’s ability to forage can lower body condition and reduce fecundity and survival. Moreover, because band stability increases a female’s long-term reproductive success (Rubenstein and Nuñez, 2009), disturbance that leads to more rapid turnover in the tenure of harem males or increased competition among females that leads to female movements among groups will alter important demographic vital rates.
Including Density Dependence in Models
Density dependence has been considered in a number of models of ungulate population dynamics. The trajectory of an unmanaged population of horses in Argentina was successfully modeled by fitting a simple logistic equation with a best-fit intrinsic rate of increase and carrying capacity (Scorolli and Lopez Cazorla, 2010). Georgiadis et al. (2003) developed a model of zebra populations that included density dependence in the form of a ratio of rainfall (as a surrogate of food availability) to density. The inclusion of that density-dependent term improved model accuracy despite the large fraction of variation that was explained by rainfall alone. Rubenstein (2010) modeled Grevy’s and plains zebra populations. Density dependence was solely through age at first reproduction, inasmuch as population growth rate is very sensitive to the number of 3-year-olds reproducing. Overall fecundity was linked to annual rainfall. Density dependence was statistically significant in models of four horse populations (Eberhardt and Breiwick, 2012): Equus ferus caballus in Argentina (Scorolli and Lopez Cazorla, 2010), the Camargue (Grange et al. 2009), and Oregon (Eberhardt et al., 1982) and Equus ferus przewalskii in a fenced area in France (Tatin et al., 2009).
Density dependence in the population dynamics of Serengeti wildebeest was modeled by Mduma et al. (1999). Density dependence was most strongly exerted through adult mortality, and the primary cause of death was undernutrition. Thus, mortality was modeled as a function of food per capita, and food supply was modeled as a function of rainfall. The model predicted a period of population growth following a period when population size was reduced below food-limited carrying capacity by rinderpest.2 Projected population dynamics varied within a wide range as a result of rainfall and food-supply variation, but the projected population nevertheless reached maximal levels because of density- dependent feedback.
Lubow et al. (2002) fitted a series of alternative population projection models to population data on elk in Rocky Mountain National Park. Logistic regression was used to estimate recruitment (the number of individuals added to a population through births) and survival rates of calves and survival rates of each sex and age segment as functions of population size and seasonal temperatures and precipitation. Because of the effects of population density in the models, populations stabilized at some upper limit, which the authors identified as the carrying capacity. The primary mechanism of density feedback was a nearly linear decline in calf recruitment followed by sharply declining calf survival.
An approach to the modeling of time-varying carrying capacity for Yellowstone elk populations was based on temporal variations in food availability (Wallace et al., 1995, 2004; Coughenour and Singer, 1996b). Food availability was affected by spatial heterogeneity, spatial overlap of elk, and spatially variable food availability. The latter was affected by the distributions of snow depth across the landscape throughout winter, which was affected
____________
2 An often fatal viral disease that affects even-toed ungulates.
by snowfall and temperature, which in turn were related to elevation. The effect of snow depth on forage-intake rate was explicitly represented. An energy-balance model was used to derive temporal changes in elk body condition (fat reserves) on the basis of the balance of energy intake and expenditure. Mean body condition was used to determine the fraction of animals in a normally distributed population that would die because of extremely low body condition—an approach originally developed by Hobbs (1989).
A similar idea was extended into actual population-dynamics modeling. A metaphysiological modeling approach was developed to represent the effects of energy storage on population dynamics (Getz and Owen-Smith, 1999; Owen-Smith, 2002a,b). Because animals and plants can store energy in body tissues, they have a reserve for use in times of food shortage. The approach links animal energy reserves to population dynamics; the reserves alter population dynamics, for example, through an increase in mortality when there are food shortages in the environment.
In an ecosystem modeling approach (Coughenour, 1992, 1999, 2000, 2002; Weisberg et al., 2006), the energy balance of the herbivore population is simulated as an outcome of forage intake and energy expenditure. The energy balance determines storage (fat) reserves, a measure of body condition. Condition in turn affects survival and fecundity. Forage intake depends on forage-biomass density, which establishes a link between population dynamics and forage. This type of model is explained in greater detail in Chapter 6.
Some equid population modelers have avoided considering density dependence and food-limited carrying capacity because populations are limited by other factors. Saltz and Rubenstein (1995) modeled Asiatic wild ass populations with a Leslie matrix, but because the populations were so small relative to the expansive area available, it was unlikely that density dependence was important, so it was not included in the model. Although the WinEquus model that is used by BLM has the capability to consider K (carrying capacity), it is rarely invoked in most BLM applications of the model because populations are always held below food-limited capacity by management removals (see Chapter 6). Gross (2000) ignored food limitations and carrying capacity in his individual-based model of the Pryor Mountain herd. He presumed that horse populations will be managed below food-limited carrying capacity and therefore not allowed to self-regulate. Linklater et al. (2004) also did not attempt to consider density dependence in their model, although it was useful for estimating population growth rates below carrying capacity.
The assumption that most BLM-managed populations are below food-limited carrying capacity and thus unaffected by density dependence appears to be reasonable given that management has heretofore aimed to ensure the prevention of rangeland deterioration, largely interpreted as preventing overuse of the forage and habitat (see Chapter 7). However, an outcome of this situation is that few data or modeling studies have provided information on outcomes of density dependence in horse or burro populations on lands under the purview of BLM. Although density dependence has not been a concern in BLM-managed HMAs and models, it will be necessary to include it in any model that addresses the question posed to the committee regarding self-limitation.
DENSITY-INDEPENDENT POPULATION CONTROLS
Large herbivore population dynamics are generally influenced by a combination of stochastic environmental variation and population density (Saether, 1997). Unmanaged or minimally managed populations should be expected to fluctuate about some mean tendency in quasiequilibrium, and the degree of fluctuation will depend on the degree of climatic variability. The dynamics of more intensively managed populations can also
be expected to vary in response to density-independent factors, inasmuch as density-independent effects are in play irrespective of whether populations are managed to levels below which density dependence takes effect.
Density independence is often incorporated into predictive models of equid population dynamics. Saltz et al. (2006) applied a Leslie matrix model with demographic and environmental stochasticity to an Asiatic wild ass population in Israel. Annual precipitation during the year before conception, drought conditions during gestation, and population size determined reproductive success. They reported that increased rainfall variability in global climate-change scenarios increased extinction probability by a factor of nearly 10. The widely used WinEquus population model (see Chapter 6) incorporates density independence as stochastic variation in recruitment and survival. At the other end of the model-complexity spectrum, the ecosystem modeling approach described in Chapter 6 represents density independence by simulating climatically driven variations in forage production and effects of snow cover on forage availability.
Effects of Climatic Variability
Variable precipitation and winter weather conditions can have marked effects on horse and burro population dynamics. Precipitation affects equids indirectly through its effect on total forage biomass production and the length of time that forage remains green and more highly nutritious (Figure 3-3). Winter weather can act directly on horses and burros through thermal stress, but more often it acts indirectly as snow cover affects forage availability.
A stage-structured model of an elk population in Yellowstone that included calf, cow, and bull elk classes modeled recruitment and mortality of each class by using the best equations determined from forward, stepwise multiple regression analyses and using precipitation amounts and elk number as the independent variables (Coughenour and Singer, 1996a). Winter precipitation was a surrogate for snow cover and later forage availability. The model revealed that expected population trajectories should exhibit wide variation in response to this density-independent regulation. Although a population equilibrium could be predicted and could be interpreted as one measure of food-limited carrying capacity, there was considerable variation above and below the equilibrium value. A series of mild winters, for example, could result in population sizes above mean K, and the converse would be true in a series of severe winters.
Precipitation appears to have a substantial influence on equid populations. Berger (1986) could find little evidence of density dependence in his data on the Granite Range HMA and suggested that responses to weather variations were overriding and confounding. Roelle et al. (2010) reported that foal survival rate in the Pryor Mountain Wild Horse Range was positively related to precipitation, probably because of the effects of variable forage production on mare condition. They noted that other investigators had suggested that forage availability can affect foaling rates in this manner (Green and Green, 1977; Nelson, 1978; Berger, 1986; Siniff et al., 1986; Garrott and Taylor, 1990). Horse populations in Australia possibly increased by a factor of 4 during good rainfall years in the 1970s (Berman, 1991), and dry conditions and more intense management reduced the population by 70 to 80 percent in the central part of the country. A 10- to 20-percent birth rate is probably realistic in poor years, and a 25- to 30-percent birth rate in good years (Berman, 1991). Joubert (1974) observed lower recruitment rates in a zebra population in dry years and a large dieoff during a drought. Owen-Smith et al. (2005) reported that juvenile survival was sensitive to rainfall variability in most of 10 African ungulate species, and there was no evidence of density dependence. Rainfall also affected adult survival in several declining species.
Density-independent mortality was documented by Berger (1983a) in the Granite Range of Nevada. Two horse groups perished as a result of severe winter snowstorms. High-altitude, snow-induced mortality may be common. He concluded that unpredictably heavy snow accumulation is a principal mortality agent in the Granite Range, as it may be elsewhere in the Great Basin. Berger (1983a) referred to the winter of 1977, when an estimated 300 horses (50 percent of the population) died in the Buffalo Hills near the Granite Range. Berger (1986) reported a pattern of low mortality in most years but markedly higher mortality in occasional years of bad weather. In Wyoming’s Red Desert, abortions and stillbirths after a severe winter reduced natality by one-third (Boyd, 1979).
Reduction in Equilibrial Tendencies by Density Independence
In climatically variable environments, the importance of density-independent population dynamics increases. The implication of strong density independence is that, in climatically variable environments, herbivore populations should not be expected to reach a steady state in which population density is in stable equilibrium with forage production. Climatic variations include severe winters and droughts. When the coefficient of variation of annual rainfall, and presumably food availability, exceeds 30 percent, population size is less likely to be determined by mean food-limited carrying capacity (Caughley, 1987; see also the section “Understanding Ecosystem Dynamics” in Chapter 7). Saether (1997) also theorized that lags in the responses of populations to environmental variations, in the absence of predation, will make a stable equilibrium between ungulates and their food resources unlikely. As a result, horse populations may not necessarily decline rapidly during moderate droughts despite reductions in plant growth, and the grazing pressure, expressed as a percentage offtake, may periodically increase above average values.
Ellis and Swift (1988) proposed that plant-herbivore systems in climatically variable environments are unlikely to be equilibrial and that traditional concepts of food-limited carrying capacity have relatively little value in predicting herbivore population sizes and dynamics in such environments. They proposed that a herbivore population in an environment subject to periodic droughts is periodically reduced to a low level independently of density. The population then recovers slowly until the next drought causes another reduction. As a result, the population is kept below food-limited carrying capacity—it is unable to use available food resources fully because of low density. That idea was supported by a model of zebra population dynamics (Georgiadis et al., 2003) that provided realistic predictions for 2 decades (Georgiadis et al., 2007). The model captured the fundamental mechanism of rapid population decline during dry periods and slow increase during wet periods. The greater the variability in rainfall, the greater the proportion of time that the population spends below carrying capacity.
The Ellis and Swift (1988) study generated controversy: some interpreted it to suggest that plant-herbivore systems would be generally nonequilibrial and herbivore populations would naturally be held below food-limited carrying capacity and thus below sizes that would cause overgrazing and degradation. The conclusions of Ellis and Swift, however, were limited to environments that had a high degree of climatic variability, and the implication was that such systems have nonequilibrial tendencies, not that they are absolutely nonequilibrial. Illius and O’Connor (1999, 2000) showed that herbivore populations in drought-prone environments would be “disequilibrial,” still in quasiequilibrium with critical food supplies during dry periods. Thus, plant resources should appear to be lightly used during wet periods, and on the average a small fraction of plant growth should be used. Illius and O’Connor recognized the importance of key resource areas on the
landscape, such as natural dry-season grazing reserves that define the dry-season bottlenecks and thus limit herbivore populations to a particular density. Density dependence therefore exists, but it is temporally variable inasmuch as food-limited carrying capacity varies with precipitation and, in seasonally cold environments, with snow cover.
Predators prey on wild equids; predation on onagers and zebras has been reported in Asia (Solomatin, 1973) and Africa (Kruuk, 1972; Schaller, 1972), respectively. In Africa, predation may limit some zebra populations (Sinclair and Norton-Griffiths, 1982; Mills et al., 1995). Zebras and other ungulates were not limited by food in Namibia but most likely by predation or disease (Gasaway et al., 1996). Zebra maintained excellent body condition during dry seasons and after droughts. Recruitment rates continued to be high, corresponding to those of a growing population. Such recruitment rates could be balanced only by high rates of yearling and adult mortality, which would presumably be caused by predation or disease. Predation was suspected of being a major population control in a collection of ungulate populations in Kruger National Park (Owen-Smith et al., 2005). Adult zebra survival was strongly related to increasing density, but the steepness of the response indicated that it was strongly affected by prey-switching by lions in response to decreased availability of alternative prey species. Mills et al. (1995) reported that zebra populations in Kruger were influenced by predation but to a smaller extent than wildebeest or buffalo. However, rainfall was the primary determinant of zebra population dynamics. In Serengeti National Park, Tanzania, zebra populations have remained roughly constant for decades, despite large changes in wildebeest and other bovid numbers caused by a rinderpest epidemic (Sinclair and Norton-Griffiths, 1982; Grange et al., 2004). Very low first-year survival limits the zebra population in the Serengeti, according to Grange et al. (2004), who found evidence that rates of predation on zebras were high and hypothesized that predation potentially holds the population in a “predator pit.” The principal predators, lion and spotted hyena, feed mainly on adult zebra, so it was not clear what the main sources of foal mortality were. Using data from 23 near-natural ecosystems in Africa, Grange and Duncan (2006) reported that zebra abundance relative to that of bovids is lower in ecosystems that have high lion densities and that zebra abundance is not as affected by forage abundance as bovid abundance; this suggests that zebras are more sensitive to predation than are bovids. Rubenstein (2010) reported that 73 percent of lion dung samples contained Grevy’s zebra and 53 percent contained plains zebra hair. One wildlife conservancy had high rates of lion predation on zebra.
Wolves are quite capable of preying on equids. In southern Europe, equids constituted 6.2 percent of wolf diets (range, 0-24 percent) (Meriggi and Lovari, 1996). In Abruzzo National Park, Italy, horses constituted 70 percent of wolf diets; however, unguarded horses are commonly hobbled in that area to prevent long-range movements (Patalano and Lovari, 1993, cited in Meriggi and Lovari, 1996). In northwestern Spain, a population of free-ranging ponies is heavily preyed on by wolves (Lagos and Barcena, 2012). Foal survival rate was very low (0.41), and 76 percent of foal carcasses found were killed by wolves. Van Duyne et al. (2009) reported that wild Przewalski’s horse foals were killed by wolves in Hustai National Park, Mongolia, and cautioned that predation could influence translocation efforts. However, those horses are sufficiently vigilant to survive and reproduce, so perhaps they have not lost essential skills (King and Gurnell, 2012). Wolves in a multiprey system have been reported to prey on feral horses in Alberta, Canada. Webb (2009) reported that one of 36 kills by wolves included a feral horse. Webb (2009) located 192 ungulates that had
been killed by wolves in 11 packs from 2003 to 2006. Some 7 percent were feral horses, and they made up 12 percent of the total biomass consumed (0.01 ± 0.02 feral horse/pack per day). Despite evidence that wolves prey on equids elsewhere, the committee was unable to identify any examples of wolf predation on free-ranging equids in the United States.
Most predation on free-ranging equids in North America has been attributed to mountain lions. That has been reported by Robinette et al. (1959) and Ashman et al. (1983). Berger (1983c) cited an unpublished report of 21 cases of mountain lion predation on free-ranging horses in the Great Basin; those deaths spanned more than 20 years and had negligible effects on population growth. Feral (but not free-ranging) horses constituted 11 percent of mountain lion diets in Alberta (Knopff and Boyce, 2009). Horses constituted 10-13 percent of adult male lion diets, but female lion diets were almost devoid of horses (Knopff et al., 2010). Overall, mountain lion predation on free-ranging equids in North America is, with few exceptions, considered uncommon (Berger, 1986).
One of the exceptions is the free-ranging horse population on the central California-Nevada border. Turner et al. (1992) examined foal survival rates in the area (the Montgomery Pass Wild Horse Territory managed by the U.S. Forest Service) because there was a ban on mountain lion hunting in California and low hunting pressure in Nevada that led to a high density of mountain lions. The study was conducted from May 1986 to July 1991 by examining the horse and mountain lion populations and documenting deaths of horses. The average annual cohort of foals over the 5 years was 32. The annual survival rates were calculated for foals (0.27), yearlings (0.95), and adults (0.96). From 1987 to 1990, 48 foals were lost; 58 percent were located as carcasses and 82 percent of those were killed by mountain lions. The authors concluded that mountain lion predation had a substantial effect on the demography of that free-ranging horse population. The study was continued, and Turner and Morrison (2001) used 11 years of data (1987-1997) to examine again the influence of mountain lions on the horse population in Montgomery Pass Wild Horse Territory. Their results supported the earlier work of Turner et al. (1992): mountain lions were responsible for the deaths of 45 percent of the foals that were born. Mountain lion predation was also hypothesized as a major factor in limiting horse population growth in an area of southern Nevada where they use high-elevation forested habitats in summer (Greger and Romney, 1999). Those habitats are excellent for mountain lions because of their broken topography.
By and large, research that has addressed the question of predation on free-ranging equids in North America has been limited to anecdotal observations and a few published papers, but at the time of the committee’s review, studies at the University of Nevada, Reno, that should provide more quantitative data were under way. The work in several mountain ranges of western Nevada was examining predation by mountain lions in multi prey systems in which free-ranging horses had various densities. Diet data were being obtained by using information from GPS-collared mountain lions to investigate predation events; more than 700 predation events had been investigated as of June 2012. Ten of 13 collared mountain lions that had access to free-ranging horses regularly consumed horses as prey. Horses were documented to have been consumed as prey by collared mountain lions in eight mountain ranges throughout the study area in western Nevada (Virginia, Pah Rah, Fox, Lake, Wassuk, and Excelsior ranges and Virginia and Smoke Creek Mountains). Preliminary data suggest that in that study area, where free-ranging horses are available as prey, more than 50 percent of the diet of collared mountain lions is made up of horses when diet data on individual mountain lions are pooled. Preliminary results suggest that mountain lions in that multiprey system are generalists at the population level but that some diet specialization occurs at the individual level: some lions select for deer where horses are more abundant, and some select for horses to the near exclusion of other prey items where
mule deer, bighorn sheep, and domestic animals are present. There is also some evidence that the magnitude of predation on horses by mountain lions may be related to the density of free-ranging horses, greater predation on horses occurring where densities of horses are higher (Andreasen, 2012).
The potential for mountain lions to affect the sizes of populations of free-ranging horses in North America is limited by the fact that most HMAs are in areas that have few mountain lions. The ranges of mountain lions tend to be concentrated in forested areas and at higher elevations (Kertson et al., 2011) and in areas that have mountainous or otherwise broken topography with limited viewsheds. In contrast, many horse populations favor habitats that have more extensive viewsheds. Mountain lions are ambush predators and require habitats that provide opportunities for stalking or finding prey without being seen. Other predators, such as wolves, are more cursorial—capable of pursuing prey across open habitats.
That a large predator, when abundant, can substantially influence the dynamics of free-ranging horses is not surprising inasmuch as black bears (Zager and Beecham, 2006), mountain lions (Wehausen, 1996), and other predators (Ballard et al., 2001; Boertje et al., 2010) have exerted strong influences on ungulate populations. However, the influence of predation on horses in the western United States is considerably limited by a lack of habitat overlap both with mountain lions and with wolves. Another constraint is that among free-ranging horse populations, foals are the usual prey, and predation on adults has rarely been documented until the recent studies in Nevada. Population size is not affected as much by foal survival as it is by adult survival (Eberhardt et al., 1982), and foal survival is strongly affected by other variables (such as weather).
CONSEQUENCES AND INDICATORS OF SELF-LIMITATION
If a population of herbivores were to self-limit, effects on the ecosystem would be expected. This section reviews the theory, expectations, and case-study examples of free-ranging horses in self-limiting circumstances.
Theory
Riney (1964) and Caughley (1970, 1976) proposed that, on introduction of a large herbivore into an ecosystem not previously occupied, there would be an initial irruption of the population that would lead to a decline in vegetation conditions, which would in turn lead to a decline in the herbivore population and allow partial vegetation recovery (Figure 3-4). The herbivore-vegetation system would then reach a new equilibrium between plant productivity and herbivore population density in which vegetation productivity and cover may be less than that in a system that does not have herbivores or in a system that is managed for maximal herbivore productivity. The resulting plant-herbivore system may be less productive, have less standing herbaceous biomass, and have a different plant species composition, but it may nevertheless be functional and sustainable. That conceptual model assumes that the vegetation-soil system has the capacity to persist in some form through and beyond the initial period after an introduction, in which it has been heavily used and reduced in function. It also assumes that surviving vegetation components would be adapted to withstand recurrent herbivory and would increase in relative abundance to form a plant community that is more adapted to withstand herbivory. As noted in Chapter 7, under some conditions, productivity of herbivory-adapted plant species may not be reduced by herbivory.
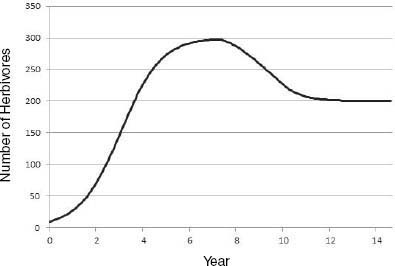
FIGURE 3-4 Large-herbivore population trajectory after an introduction. Herbivory causes a decline in plant production and thus in K. Here, K in the underlying logistic model declines linearly from 300 to 200 individuals from year 7 to year 10, and this results in a decline in herbivore population size.
General Expectations
There is no doubt that large herbivores have numerous effects on their environments that result from grazing, browsing, trampling, and behavioral and competitive interactions with other species (see Chapter 7). When the population is food-limited and population growth rate decreases to zero, the forage resource base will most likely be heavily grazed. Horses and burros have the ability to graze plants down to the ground. They can kill plants through uprooting and trampling, create areas of low vegetation cover, and change plant species composition to favor less desirable or exotic species. At some point, reduced vegetation cover can lead to accelerated soil erosion and decreased vegetation productivity and rangeland health (NRC, 1994; Pellant et al., 2005). If resulting feedbacks to equid population growth are ineffective or if they have been disrupted by human activities, rangeland ecosystems can be pushed across thresholds into degraded states from which recovery is difficult or impossible (see Chapter 7).
Grazing pressures can be expected to be spatially heterogeneous. In expansive habitats, it is simplistic to think of a mean grazing pressure uniformly distributed across the landscape; a variety of factors affect animal distributions beside forage. It is more realistic to expect that some areas will be heavily, perhaps “excessively,” grazed while other areas are little used and may serve as refugia for plant species that are more sensitive to grazing by large herbivores. The heavily used, disturbed areas are, however, also refugia for disturbance-adapted plant species. One example is the existence of increased levels of disturbance near water sources. Such areas have sometimes been referred to as sacrifice areas
because they are an inevitable outcome of the presence of large herbivores, their requirements for water, and the fact that water is distributed at point locations.
It can be expected—on the basis of logic, experience, and modeling studies cited above—that because horses or burros left to “self-limit” will be food-limited, they will also have poorer body condition on the average. If animals are in poorer condition, mortality will be greater, particularly in times of food shortage resulting from drought or severe winter weather. Indeed, when population growth rate is zero, mortality must balance natality. Whether that is acceptable to managers or the public is beyond the purview of the committee, but it is a biological reality.
It is difficult to generalize about whether these are natural and expected outcomes in unmanaged large-herbivore or, more specifically, free-ranging equid ecosystems. On the basis of evidence presented above, many large-herbivore populations are regulated through food limitation as a natural process. The evidence reviewed above also indicates that predation is a factor in some large-herbivore populations and some equid populations. Most horse and burro populations in North America appear to be little affected by predation because predators are absent or present at low densities, possibly because they have been extirpated or simply because habitats are not suitable for them. The degree of naturalness is also affected by other human activities, such as restrictions on dispersal and other movements, the presence of livestock, and water development.
Case Studies
The only way to know the consequences of self-limitation for the vegetation, horses and burros, and the ecosystem is to observe the consequences where self-limitation has been allowed to occur. As pointed out above, there are few cases in which free-ranging horse populations have not been managed and have been left to self-regulate and in which simultaneous scientific studies of the vegetation and of the equids have been carried out. But there are probably many cases in North America in which equid populations have gone unmanaged, or have been minimally managed, for a number of years. In some cases, the equids have been studied but their effects on habitats have not (e.g., Berger, 1986). In other cases, the equids and their effects on landscapes have not been studied. Some unmanaged populations on tribal lands have received little or no scientific study.3
The responses of equids to a situation of self-limitation have been discussed above with regard to density dependence. As noted, density dependence results from food limitation, a decline in animal nutritional condition, and consequent decreased recruitment and survival rates. Many examples of equid ecosystems around the world were given. Chapter 7 reviews the numerous effects that horses have on their habitats and on other species and examines the concepts of thriving natural ecological balance and AMLs. Horses will have some effects on their habitats at the point of food limitation, and these could be pronounced. On the basis of studies of systems that have high densities of horses, although not necessarily at the point of food limitation, reasonably well-informed hypotheses can be developed about the expected state of vegetation and other species when the equid population reaches the point of self-limitation. However, whether such a system can be self-sustaining (or perhaps even “thriving”) over the long term cannot be known without experimentation.
____________
3 For example, Yakama Nation in Washington, available online at http://www.ynwildlife.org/.
New Zealand
Free-ranging horses in New Zealand are derived from animals introduced from various sources in the 19th and 20th centuries (Rogers, 1991). They once ranged over much of the central North Island but have diminished since the 1950s. The only remaining population survives in the Kaimanawa Mountains because of restricted public access on military lands. The Kaimanawa unmanaged population was continuing to increase and had not reached food limitation as of 1990 (Rogers, 1991). However, in the southern portion of the area, horses were expanding their ranges in response to increased density. The most important habitats for horses included wide basins with areas of volcanic ash supporting tall red tussock and short hard tussock grasslands. Grazing by domestic sheep, cattle, and horses and burning since the 1890s converted tall red tussock to short tussock grasslands.
A 20-m x 20-m grazing exclosure in degraded short tussock grassland resulted in changed plant species composition. The dominant intertussock grass species increased while 12 low-stature species and total species diversity decreased as the hard tussock species increased in stature and shaded them. Adventive (introduced) species also expanded. It is notable that the tall red tussock grass decreased. The exclosure also showed that grazing was not reducing the recruitment of hard tussock. Thus, cessation of horse grazing did not restore the original red tussock species, so the vegetation might have been converted to an “alternate stable state” as explained in the section “Understanding Ecosystem Dynamics” in Chapter 7. Furthermore, cessation of grazing resulted in adverse changes in species composition toward the adventive species, and this indicates that a moderate level of grazing would maintain the more desirable hard tussock grassland physiognomy (appearance) and species composition.
Vegetation responses to horses varied from north to south. In the north, where horse numbers were low, in the most prevalent habitats, red tussock appeared to be slowly recovering from the degradation resulting from early European livestock. In some habitats in the north, particularly mesic sites, horse grazing continued to have substantial adverse effects on biodiversity. In contrast, in the south, the landscape was more resilient to horse grazing because of the changes in species composition that had resulted from prior European livestock grazing. Thus, it might be concluded that exposure to grazing in the south had changed the plant community to one that is more resilient, and thus adapted, to further grazing by free-ranging horses. Moreover, the persistence of the hard tussock physiognomy (appearance) depends on continued moderate grazing.
Balancing free-ranging horses with the conservation of biodiversity across the landscape depends on the recognition of spatial heterogeneity between the north and south. In the south, Rogers (1991) concluded that horse preserves could be recognized where their numbers could be manipulated for the benefit of the horses and indigenous landscapes. In the north, however, he concluded that horse grazing compromises nature conservation values, so their numbers may have to be controlled.
It should be noted that no mammalian herbivores were present in New Zealand before the introduction of domesticated livestock by European settlers. Consequently, the responses of vegetation in New Zealand to introduced mammalian herbivores could differ from responses of vegetation that has coevolved with mammalian herbivores.
Central Australia
Berman (1991) studied populations of feral horses in central Australia. Aerial surveys in 1981 and 1984 indicated that there were about 206,000 animals. Populations may have
quadrupled during a period of good rains in the 1970s, but drier conditions, decreased rangeland availability, and management more recently have reduced the population by 70-80 percent. That suggests that horse populations increased and then decreased in response to forage availability; horses might have been above food-limited carrying capacity in dry conditions. Berman observed that variations in vegetation, wildlife, and soil erosion corresponded with changes in grazing intensity. High densities were associated with denudation, low densities of kangaroos, water holes with horse carcasses, and increased gully erosion. Horse and cattle dung density and gully erosion decreased with distance from water while plant cover and kangaroo dung increased with distance from water. Feral horses were able to affect almost all rangeland areas in central Australia because they are able to walk up to 50 km from water and traverse hills, which are barriers to cattle. Berman noted that many examples of soil erosion exist in parts of central Australia; although these have often been attributed to overgrazing by horses and cattle, it is difficult to prove that horses and cattle cause a substantial amount of erosion because erosion also takes place without them in these environments. Horse and cattle diets and habitats overlap, so it was not possible to differentiate vegetation and soil responses that were due to horses rather than cattle.
Argentina
In the Pampean grasslands of Ernesto Tornquist Provincial Park, Argentina, an unmanaged population of horses increased according to a logistic curve and was beginning to show signs of density dependence, as noted above (Scorolli and Lopez Cazorla, 2010). Although density had no effects on survival, it affected fecundity. The authors hypothesized that fecundity was reduced at higher densities because of reduced pregnancy in mares that had low body condition. De Villalobos and Zalba (2010) and de Villalobos et al. (2011) reported that the horses reduced herbaceous cover and facilitated establishment of an invasive pine species. They suggested that grazing had caused reduced plant diversity and species evenness and altered the composition of communities. Other native and exotic ungulate species had declined as a result of competition with the horses.
Shackleford Banks
Shackleford Banks, a barrier island off the coast of North Carolina, supports a population of free-ranging horses that has experienced increases and decreases in population numbers in response to changes in carrying capacity resulting from management practices. Before the National Park Service (NPS) acquired the island and incorporated it into the Cape Lookout National Seashore, free-ranging horses shared the island with domestic livestock, including cattle, sheep, and goats (Rubenstein, 1981). After NPS removed all domestic stock from the island in the late 1980s, free-ranging horse numbers more than doubled from a competitively determined, food-limited carrying capacity of 104 animals to a new level, without competition from livestock, slightly over 220. That provided an opportunity to witness changes in behavior and vital rates when density-dependent effects were removed and reappeared as the population expanded. At first, body-condition scores increased from 3.5 to over 4 (on a 1-5 scale, with a score of 1 representing a horse in poor condition) as food previously consumed by livestock was now being eaten by horses. Fecundity also increased slightly, the interbirth interval declined from about 3 years to slightly more than 2 years and mortality in adult and juvenile males and females dropped 15 percent (Rubenstein and Dobson, 1996). However, as the population reached the new carrying capacity, those patterns reversed, and vital rates returned to their previous equilibrium levels.
Observable declines in body condition and increases in mortality, especially after hurricanes and winter storms, prompted the development of a plan for population control (Rubenstein and Dobson, 1996). As the population climbed to its new peak of 225 animals, rates of aggression increased among males and normally peaceful females, the variety of social systems changed as territorial harems gave way to harems that had large overlapping ranges, and many harems became populated by more than one male. Although those changes helped to mediate some of the consequences of crowding while the population was in transition, in the end a new carrying capacity was reached and was accompanied by changes in behavior and vital rates. One of the biggest changes was a reduction in the stability of the harem. Pressure from increasing numbers of bachelor and harem males lowered female feeding rates, increased the percentage of females that changed groups each year from just under 11 percent to just over 25 percent, and increased the skew in reproductive success (a nonequitable distribution of reproduction among individuals) of males and females. Once NPS started managing the population to cycle around 125, average body condition and vital rates improved and the reproductive skew of both sexes was reduced, and this improved the genetic health of the population (Rubenstein and Nuñez, 2009).
Horses on Shackleford Banks decreased the abundance of Spartina grasses (Wood et al., 1987; Hay and Wells, 1991). Grazed habitats had less vegetation, a higher diversity of foraging birds, higher densities of crabs, and lower species richness of fishes (Levin et al., 2002). Horses altered habitats indirectly in many ways.
Oostervaardersplassen, the Netherlands
In the Oostvaardersplassen Reserve in the Netherlands, Heck cattle, red deer, and Konik horses have been left unmanaged since the 1980s and have reached high densities (Vulink, 2001). It is a relatively moist ecosystem, having been reclaimed from the sea and having high annual precipitation. The management objective is to allow natural processes to operate to the greatest extent possible although the reserve is fenced. The management is informed by an appreciation of the natural, expected, and even desirable effects of large herbivores on other components of the ecosystem and the possibility of natural regulation through density dependence. Herbivores were originally introduced to keep the vegetation in a more open state because there was considerable woody encroachment. The herbivore species are close analogues of the native herbivores that would have been present hundreds of years ago. Large predators are absent. The Konik horses have shown a higher intrinsic rate of population increase than Heck cattle (Vulink, 2001) and have outnumbered the cattle, which apparently are regulated by food shortage in winter. If current trends continue, the horses and red deer will probably outcompete the cattle and displace them (ICMO2, 2010).
Because the reserve is small and most of it is easily visible to the public, animals that die of starvation or old age can be seen, and this leads to dilemmas with respect to the ethical treatment of animals (ICMO, 2006; ICMO2, 2010). Large dieoffs during severe winters are periodic. On ethical grounds, animals that are suffering and dying are culled (shot) to prevent further suffering. That is also justified as a replacement for predators and as a moral responsibility of humans because of the creation of artificial barriers to movements out of the reserve (fences).
The following responses have been observed:
- The number of animals culled in response to weather conditions is highly variable.
- The number of animals culled has increased over the last decade because populations have reached ecological (food-limited) carrying capacity.
- The average body condition of animals has declined over the last decade.
- Mortality has increased with annual variability in mortality. Mortality is expected to balance recruitment in the near future.
- Plant productivity and the number of animals that the area can support will possibly decline somewhat because of depletion of soil nutrients.
- Grazing promotes short swards and prevents woody regeneration.
- Grazing increases plant diversity on the small scale but not the large scale. (ICMO2, 2010)
Pryor Mountain Wild Horse Range
A population of horses descended from Andalusian Spanish mustangs has inhabited the Pryor Mountains possibly since the 1700s (BLM, 1984). The earliest record of their presence is a photograph of a roundup of 101 horses in 1910. Although the horses have inhabited the Pryor Mountains since then, they were never counted until 1970. Horse traps were built by ranchers in the 1930s and 1940s, but the numbers removed were never recorded. When BLM announced plans to remove the horses in 1964, they appeared to be in good shape despite the condition of the range. Local ranchers commented that the range was not overgrazed, that horse birth rates were low, and that the horses were in no worse condition than they were 50 years before (Ryden, 1990). Notably, considerable numbers of domestic livestock were permitted to use the range from 1907 to 1930. Half as many livestock units were permitted after 1930. In 1970, when a census of the horses occurred, there were 270 horses (Feist and McCullough, 1975). Horse reductions began with roundups in 1971 and 1973 and reduced the herd to 120-130. The horses have since been managed through removals to about 85-120. Most recently, the U.S. Department of Agriculture’s Natural Resources Conservation Service carried out an assessment (Ricketts et al., 2004), which recommended an AML of 45-142 and noted the following:
- Over the last half-century, the conditions of the horse range were described as very poor to fair in a number of BLM assessments.
- The condition of the range is getting worse on the basis of low proportions of preferred plant species and evidence of soil erosion.
- In 2004, the health of the rangeland at six sites was rated at 2.0-3.75 (average, 2.75) on a scale of 0-5. A score of 4 or more is considered healthy relative to the historical potential climax vegetation. A score of 2.5 or less is considered unhealthy and to have a strong possibility of nonrecovery in the absence of external energy inputs (such as mechanical seeding). (Ricketts et al., 2004)
Apparently, although horses have been managed since 1973 at much lower numbers than were present initially and despite reductions in livestock numbers in the 1930s, unhealthy range conditions have persisted. However, Singer et al. (2000) noted that former managers who visited the range in 1997 remarked on an overall improvement in plant condition.
In an ecosystem modeling assessment (see Chapter 7) of the Pryor Mountain Wild Horse Range, it was possible to examine vegetation and animal responses to various horse densities, including the number present in 1970 (Coughenour, 1999, 2000, 2002). It was also possible to determine food-limited carrying capacity by letting the model run with no horse removals until it came into quasiequilibrium with vegetation productivity. With horse numbers held constant at 270, the model simulated markedly reduced herbaceous biomass compared with what happened with no horses. Forb biomass proportion increased while
grass proportion decreased. Root biomass was also decreased. In the simulation in which horse populations were allowed to grow freely, plant responses were not much different from those with the number fixed at 270.
Grazing was predicted to be heterogeneously distributed. When 1971-1996 observed horse numbers (87-250 horses; mean, 157) were used, 40-70 percent of the landscape was predicted to be lightly grazed, 5-20 percent grazed less than 80 percent, and 5-15 percent grazed to 50- to 80-percent offtake. The model predicted that with historical horse densities, some parts of the landscape would experience substantial decreases in herbaceous biomass. With no culling, the fraction of the landscape that would be heavily grazed would increase markedly. The model simulated that horse numbers would initially increase to over 300, level off, plunge dramatically in response to a drought, and then gradually increase and level off at a mean of 270, the food-limited carrying capacity. In both the fixed number and the freely varying simulations, horse body condition declined to low levels, particularly in dry years or years with severe winters. In separate simulations comparing horse body conditions with no culling versus actual densities in 1970-1995, horse body condition was markedly lower with no culling. At food-limited carrying capacity, plant cover would be lower than what exists on the range, and the fraction of the landscape receiving extremely heavy use would increase (see Chapter 7). In the heavily used areas, herbaceous cover would be reduced to less than 20 percent of potential, and soil erosion rates in those areas would probably also be higher. Horses would be in poorer body condition, and horse mortality would be higher.
Management itself alters horse and burro population growth rates through a variety of mechanisms aside from the simple direct effects of removals or reduced fertility due to contraception. The indirect effects of management are considerable. One likely response is compensatory population growth as a result of reductions in numbers. Horse and burro populations are seldom limited by density because they are kept below food-limited carrying capacity through removals and to some extent through treatment with the contraceptive porcine zona pellucida (PZP; discussed in Chapter 4). Indeed, AMLs are usually set in such a way that considerable forage material is uneaten; this is the very purpose of the allowable use level (see Chapter 7). That leaves horses and burros in a position for compensatory population growth because they are below food-limited carrying capacity. If there were no intervention, herds would reach food-limited carrying capacity, body condition would decline, natality and survival rates would decline, and more animals would die of starvation. Removals are likely to keep the population at a size that maximizes population growth rate (see Figure 3-2B), which in turn maximizes the number of animals that must be removed and processed through holding facilities. Management may also alter population growth by affecting dispersal, particularly through fencing but also by permitting conflicting land uses that alter habitats for horses and burros. Impaired dispersal would decrease population growth because of increased competition for forage. Water provision, in contrast, could increase population growth rate by increasing the area of habitat that has water and thus total available forage. Horses in arid Australia were reported to range as far as 50 km from water (Berman, 1991), but maximum distances would probably be considerably less in rugged topography or where there are other impediments to movement.
Compensatory Reproduction
Compensatory reproduction in response to gathers is likely in any population that exhibits density dependence. To the extent that a population is being regulated by food supply, decreased density will provide more forage per individual, increasing body condition, reproduction, and survival and thus population growth rate. Choquenot (1991), in a study of feral donkeys in Australia, reported that population growth was regulated by food-related juvenile mortality. Dawson and Hone (2012) advised that compensatory responses in survival, fecundity, and age at first reproduction in the population should be considered in any management program. In particular, they were referring to the fact that their data showed that survival and fecundity were increased and age at first reproduction decreased at lower densities, so it is likely that reductions in density due to culling will have the same effect.
The response of population growth rate to increased density must be known in order to predict the degree of compensatory growth that can be expected at a given population density. If the population size is above the theoretical inflection point of the logistic growth trajectory (point α in Figure 3-2A), reductions will increase the annual population growth increment. However, if the population size is below the theoretical inflection point, reductions will decrease the annual growth increment. Various models of density dependence, as discussed above, could be used to predict the degree of compensatory growth resulting from animal removals in relation to the population size and the rate of removal.
Gathering has also been shown to have varied indirect effects on reproductive success. In Idaho and Wyoming, foaling success rates were higher among gathered horses than among horses that were not gathered (Hansen and Mosley, 2000). Foaling success rates in Idaho were 29 percent, 31 percent, and 43 percent for mares not gathered, mares gathered and adopted, and mares gathered but released, respectively. In Wyoming, foaling success rates were 29 percent, 42 percent, and 48 percent in those groups. There were no statistically significant differences among groups, however, most likely because samples were small in relation to high variance. Effects of gathers on body condition, lactation status, and pregnancy were not reported. It is important to note that such results, if real, would most likely be attributable to forage limitation and lower body condition among ungathered than among gathered mares. In contrast, in another study, foaling was lower among gathered horses. Pregnant mares that were gathered and removed had substantially lower reproductive success than ungathered mares at one site, and gathered and released mares had less reproductive success than ungathered mares at a second site (Ashley and Holcombe, 2001). The authors speculated that that was a result of loss of fetuses due to the stress of being gathered and handled for a long period. Animals that were removed were transported 246 km to a holding facility, where they were held for 21 days before adoption. A number of miscarriages were observed at the holding facility.
Kirkpatrick and Turner (1991) compared a population managed with annual foal removals on Chincoteague Island, Virginia, with an unmanaged population on Assateague Island, Maryland. Management-level applications of PZP did not begin on Assateague Island until 1994, after the 1989 study (Turner and Kirkpatrick, 2002.) They hypothesized that there would be greater fetal losses in the unmanaged population because of the concurrent physiological stresses of lactation and pregnancy (weaning rarely occurs before 1 year and it commonly occurs at 2 years). They estimated pregnancy and foaling rates of 40 free-ranging mares on Assateague Island and 48 managed mares on Chincoteague Island and found a higher foaling rate in the Chincoteague population because a greater percentage of mares foaled annually (80 percent). The hypothesis of greater fetal loss was not supported: there
was no difference between the two populations. However, pregnancy and foaling rates in the Chincoteague population were nearly double those in the Assateague population. The authors suggested that the greater pregnancy and foaling rates were due to cessation of lactational anestrus and that the cessation of lactation in mares that had their foals removed resulted in these animals going back into estrus. However, the authors provided no evidence that lactating mares were not cycling. Another possible cause of increased pregnancy and foaling in the managed population is reduced energetic demands due to cessation of lactation. In contrast, Wolfe et al. (1989) used plasma progesterone measurement to examine pregnancy rates in 553 free- ranging mares. They found no difference in pregnancy rate between lactating and nonlactating mares. Kirkpatrick and Turner (1991) suggested that the reason that no difference was found was that the method for detecting pregnancy—measurement of plasma progesterone—can be inaccurate. Although the method is widely used for detecting pregnancy in other species, it is not reliable for equids. It is also known that although lactational anestrus does occur, it is very uncommon, and most mares resume cycling 5-9 days after foaling. In summary, it is possible that population management via foal removals may result in increased fecundity, but evidence of a lactational anestrus mechanism is lacking. It is also possible that pregnancy and foaling rates are reduced in lactating mares because of the lower body condition that results from the energetic demands of lactation. Because horse populations on BLM lands are not managed through foal removals, this form of compensatory reproduction probably has little relevance.
The effects of PZP on population growth, longevity, and body condition were studied over a 10-year period on Assateague Island (Turner and Kirkpatrick, 2002). PZP clearly reduced foaling rates among contracepted animals. However, mortality in mares and foals decreased, and two older age classes appeared (21-25 years and over 25 years), which indicated an increase in longevity. Body-condition scores of nonlactating mares increased substantially but those of lactating mares did not change. The cause of the decrease in foal mortality was unclear, but it could have been due to increased body condition of the mares. Body condition of untreated mares, or of treated mares in which the treatment has lost effectiveness, could increase because of reduced competition for forage. In treated mares, contraception reduces the energetic costs of reproduction, and this also results in increased body condition and longer life span (Gray and Cameron, 2010). Nuñez et al. (2010) also found that treated mares had better body condition than untreated mares; this could result in an extended breeding season and increased chance of conception in animals that have low PZP antibody levels. Thus, the favorable effects of increases in body condition, longevity, foal survival, and length of breeding season on population growth rate could offset to some extent the adverse effects of contraception on reproduction and population growth rate. That might be termed compensatory population growth; however, it is unlikely that the degree of compensation would be sufficient to overcome the degree to which contraception reduces reproduction and population growth.
Effects Related to Ability of Animals to Disperse
Ecologically adaptive movement patterns are still exhibited by many extant horse populations. Free-ranging horses in Nevada move from low to high altitudes in spring or early summer after the wave of vegetation green-up, and they move to low elevations in fall (Berger, 1986). However, changes in land ownership and allocations of lands for livestock use may interfere with traditional movement patterns and may preclude the re-establishment of natural movements, ones that presumably exist in truly wild and free-ranging equid populations.
The importance of movement for coping with drought is illustrated by observations in Namibia (Gasaway et al., 1996). Ungulates, including zebra, maintained near average mortality during severe drought because they could move over large areas and find food reserves in areas not regularly grazed. Low ungulate densities and clumped distributions were responsible for the existence of infrequently used areas that served as drought reserves. Such dry-season food reserves were also important in keeping mortality low in Kruger National Park during a drought in 1982-1983 (Walker et al., 1987). In contrast, populations in two other reserves, which were near their food-limited carrying capacity before the drought, lacked such lightly grazed food reserves and suffered high mortality (Walker et al., 1987, as noted by Gasaway et al., 1996).
An important question is the extent to which horse (and cattle) grazing can be managed to compensate for losses in natural movement patterns, which presumably were important determinants of the grazing regimes experienced by plant species that evolved during or before the Pleistocene in the presence of large herbivores. The mix of private, tribal, and public ownership often fragments landscapes that might have been more natural, expansive grazing areas. Differences between agency policies may exacerbate the fragmentation. Fencing can interfere with movement to other areas when forage is depleted and cause heavier intensities and frequencies of herbivory than would occur otherwise.
Confinement or restrictions on migration or dispersal movements will probably result in a plant-herbivore system that has different dynamics from one that does not have such constraints. In general, the smaller the area that a population is limited to, the greater the potential for a self-regulating system with undesirable qualities, such as population crashes and population oscillations. Spatial constraints can lead to reductions in vegetation cover to lower levels than would be seen otherwise, followed perhaps by vegetation recovery after horse populations decline in response to food shortages. However, there is also an increased likelihood of irreversible shifts in vegetation communities, in accordance with recent theory and observations of alternate stable states, to communities dominated by invasive plant species, by shrubs, or by bare ground with little or no seed bank to support recovery (see the section “Understanding Ecosystem Dynamics” in Chapter 7).
In contrast, such generalizations as “confinement will result in range degradation” are also unwarranted. The degree of confinement, the areas that are inaccessible, the availability and dispersion of water, climate, and vegetation productive potential can all modify the response. Confinement may have little or no consequences or great consequences, depending on those factors.
Additional challenges arise from migration and dispersal across HMA boundaries. A designated HMA may constitute the core range of a herd or population, but dispersal movements outside the HMA are possible. Dispersing animals may move onto areas that are subject to conflicting land uses or management objectives. Conversely, movements of animals into an HMA from surrounding areas that are under different management jurisdictions can work at cross purposes to the management objectives of an HMA. Where such cross-jurisdictional movements occur, it is necessary to establish co-operative relationships among adjacent landowners.
Large herbivore populations are influenced by density dependence, density-independent factors, and predation. Most large herbivore populations show some degree of density-dependent limitation, particularly when predation is low. Likewise, many wild equid populations exhibit density dependence. Density dependence has operated in some
free-ranging horse and burro populations in the western United States and elsewhere. The primary way that populations self-regulate or self-limit is through increased competition for forage at higher densities, which results in smaller quantities of forage per animal, poorer body condition, and decreased natality and survival rates. Behavioral mechanisms can also contribute to density dependence, particularly increased dispersal, and increased agonistic interactions and decreased band stability may interfere with foraging and reproductive success.
Clearly, it is possible to incorporate density dependence into models as a population process. Although it has been omitted from some models because populations were believed to be held below food-limited carrying capacity by management or other factors, it was found necessary to include in others when it was an important component of population dynamics, particularly in wild, unmanaged populations of equids. There are basically two approaches to modeling density dependence. One is through the inclusion of a direct effect of density, often in relation to an assumed or derived food-limited carrying capacity (K), which must be empirically determined for the system in question. Although total forage biomass may be estimated through vegetation sampling (see Chapter 7), there is still a need to demonstrate how population variables respond to diminished forage biomass; thus, there is a need for empirical studies. The other approach is through mechanistic modeling of competition for limited forage at higher densities and its effects on survival and reproduction. The first approach is more site-specific, but in either case, there is a need to assign values to parameters based on data from case studies of populations that are allowed to reach levels at which density dependence takes effect. However, there are few such case studies. The committee suggests that existing situations of self-limited populations be studied or that an experiment be conducted to enhance understanding of such systems.
Density-independent variation is also an important consideration. Most equids under BLM purview inhabit arid and semiarid environments characterized by high variability in annual precipitation and thus forage. In some environments, variable snow cover is also an issue. When climatic variation is high, plant-herbivore systems become increasingly disequilibrial. In such environments, density dependence may be relatively weak, and population dynamics may be driven largely by density independence, with resulting large variability in survival and recruitment. Populations may also be driven below any theoretical food-limited carrying capacity that is based on mean forage biomass.
Predation can be important in controlling the sizes of some populations of wild equids, but the degree of control is highly variable. In intact equid ecosystems in Africa, zebra populations are probably limited to some extent by predators, but climatically influenced variations are strong in comparison, so it is difficult to establish the effect of predation quantitatively. In some North American free-ranging horse populations, there clearly is predation by mountain lions. However, the degree of limitation has not been established. More problematic is the fact that mountain lion ranges are not widespread throughout the principal habitats of the horses under BLM purview. The limitation of the range is not necessarily due to human hunting or extirpation, inasmuch as these habitats may simply be poor habitats for mountain lions. Mountain lions are ambush predators, requiring habitats with broken topography and tree cover, whereas horses tend to use areas that have extensive viewsheds. Wolves are cursorial and capable of chasing prey across open, flat topography. They have a great impact on a few populations on other continents and certain areas in Canada, but their distribution in the western United States has been severely reduced by humans, and very few, if any, free-ranging horse habitats are occupied by wolves.
Several case studies have demonstrated the potential outcomes of a self-limited equid population. Equids invariably have some effect on vegetation abundance and composition
(see Chapter 7). Vegetation cover is usually reduced, and often there are shifts in species composition. There is limited evidence that erosion rates are increased. However, none of the case studies included scientific experimentation that showed that the changed vegetation cannot persist over a long period of time or that complete loss of vegetation cover is inevitable. Case studies have also reported increased competition with other wildlife species and adverse effects on habitats of some species. In some cases, vegetation changes were probably due in part to historical livestock grazing. In other cases, horse population reductions were not shown to reverse vegetation changes.
The results of the case studies are consistent with theoretical predictions that when a herbivore population is introduced, vegetation cover will initially change and productivity will often be reduced by herbivory. In some environments, however, moderate levels of herbivory have little effect or even beneficial effects on plant production (see Chapter 7). Vegetation production may decline, but it may stabilize at a lower level as herbivore populations come into quasiequilibrium with the altered vegetation cover. The reduction in plant cover may be great enough to cause accelerated soil erosion, an important indicator of reduced rangeland health. If erosion reduces soil water-holding capacity and soil fertility, the productive capacity of the vegetation and of the forage base will decline and the resulting feedback effects on equid population growth might reduce grazing pressure and further erosion. Whether unmanaged, quasiequilibrial soil-plant-equid ecosystems can persist over a long term on rangelands administered by BLM is unknown, but there are pertinent examples of unmanaged equids in Africa that have persisted for millennia, in some cases despite weak or no evidence of predator limitation. Feedbacks from the plant-soil system to equid population growth must have enough functionality for long-term ecosystem persistence. Such feedbacks may be disrupted by various human activities. Thus, there is a need to be able to predict equid population responses to decreased forage productivity concurrently with vegetation productivity declines in response to erosion in landscape ecosystems that are affected by human activities, such as habitat fragmentation.
The literature clearly demonstrates that density dependence due to food limitation will reduce population growth rates in equids and other large herbivores through reduced fecundity and survival. The total annual population increment will decline at higher densities (Figure 3-2A). Some of the reduction in annual population increment at high densities will probably be due to reduced fertility, and much of the reduction can also be expected to be due to increased mortality. The literature and the case studies show that although density dependence can regulate population sizes, responses will probably include increased numbers of animals in poor body condition and high numbers of animals dying from starvation. Those may be unacceptable outcomes for some stakeholders, particularly those who perceive that they result from human interference with natural processes of dispersal, access to key forage resources, or predation. If so, it could be argued that humans are potentially responsible for the starvation and mortality.
The committee was charged with addressing the question of compensatory reproduction in response to population controls. As discussed above, it is quite likely that there would be compensatory increases in recruitment and decreases in mortality in response to lower animal numbers, whether because of removals or contraception, because of decreased competition for forage, and or because of improved body condition. Mares in better body condition can be expected to have higher fertility rates, and foal survival can also be higher. An increased foaling rate has been observed in one population that was managed through foal removals, but the likelihood of observing that response generally is questionable, and, because horse populations on BLM lands are not managed by foal removals, this possibility is irrelevant in any event. Finally, there is no evidence that contraception
stimulates reproduction through physiological mechanisms. On the contrary, the purpose of contraception is to decrease fertility.
A managerially important finding was that free-ranging horse populations are often limited by removals to levels below food-limited carrying capacity, so population growth rate could be increased by the removals through compensatory population growth related to decreased competition for forage. Thus, the number of animals that must be processed through holding facilities is probably increased by management.
Andreasen, A. 2012. Predation on Feral Horses by Mountain Lions in Nevada. Presentation to the National Academy of Sciences’ Committee to Review the Bureau of Land Management Wild Horse and Burro Management Program, May 14, Washington, DC.
Ashley, M. and D. Holcombe. 2001. Effect of stress induced by gathers and removals on reproductive success of feral horses. Wildlife Society Bulletin 29:248-254.
Ashman, D.L., G.C. Christensen, M.L. Hess, G.K. Tsukamoto, and M.S. Wickersham. 1983. The Mountain Lion in Nevada. Reno: Nevada Department of Wildlife. 75 pp.
Ballard, W.B., D. Lutz, T.W. Keegan, L.H. Carpenter, and J.C. DeVos, Jr. 2001. Deer-predator relationships: A review of recent North American studies with emphasis on mule and black-tailed deer. Wildlife Society Bulletin 29:99-115.
Berger, J. 1983a. Ecology and catastrophic mortality in wild horses: Implications for interpreting fossil assemblages. Science 220:1403-1404.
Berger, J. 1983b. Induced abortion and social factors in wild horses. Nature 303:59-61.
Berger, J. 1983c. Predation, sex ratios, and male competition in equids (Mammalia: Persiodactyla). Journal of Zoology (London) 201:205-216.
Berger, J. 1986. Wild Horses of the Great Basin: Social Competition and Population Size. Chicago: University of Chicago Press.
Berman, D.M. 1991. The Ecology of Feral Horses in Central Australia. Ph.D. dissertation. University of New England, Australia.
Berryman, A.A. 2003. On principles, laws and theory in population ecology. Oikos 103:695-701.
BLM (Bureau of Land Management). 1984. Herd Management Area Plan Pryor Mountain Wild Horse Range. Billings, MT: U.S. Department of the Interior.
Boertje, R.D., M.A. Keech, and T.F. Paragi. 2010. Science and values influencing predator control for Alaska moose management. Journal of Wildlife Management 74:917-928.
Bonenfant, C., J.M. Gaillard, T. Coulson, M. Festa-Bianchet, A. Loison, M. Garel, L.E. Loe, P. Blanchard, N. Pettorelli, N. Owen-Smith, J. du Toit, and P. Duncan. 2009. Empirical evidences of density-dependence in populations of large herbivores. Advances in Ecological Research 41:313-357.
Boyd, L. 1979. The mare-foal demography of feral horses in Wyoming’s Red Desert. Pp. 185-204 in Proceedings of the Symposium on the Ecology and Behavior of Wild and Feral Equids, R.H. Denniston, ed. Laramie: University of Wyoming.
Cameron, E.Z., W.L. Linklater, K.J. Stafford, and C.J. Veltman. 1999. Birth sex ratios relate to mare condition at conception in Kaimanawa horses. Behavioral Ecology 10:472-475.
Caughley, G. 1970. Eruption of ungulate populations with emphasis on Himalayan thar in New Zealand. Ecology 51:53-72.
Caughley, G. 1976. Wildlife management and the dynamics of ungulate populations. Pp. 183-246 in Applied Biology, Vol. 1, T.H. Coaker, ed. New York: Academic Press.
Caughley, G. 1979. What is this thing called carrying capacity? Pp. 2-8 in North American Elk: Ecology, Behaviour and Management, M.S. Boyce and L.D. Hayden-Wing, eds. Laramie: University of Wyoming.
Caughley, G. 1987. Ecological relationships. Pp. 158-187 in Kangaroos: Their Ecology and Management in Sheep Rangelands of Australia, G. Caughley, N. Shepard, and J. Short, eds. Cambridge, UK: Cambridge University Press.
Choquenot, D. 1991. Density-dependent growth, body condition and demography in feral donkeys: Testing the food hypothesis. Ecology 72:805-813.
Coughenour, M.B. 1992. Spatial modeling and landscape characterization of an African pastoral ecosystem: A prototype model and its potential use for monitoring drought. Pp. 787-810 in Ecological Indicators, D.H. McKenzie, D.E. Hyatt, and V.J. McDonald, eds. London and New York: Elsevier Applied Science.
Coughenour, M.B. 1999. Ecosystem Modeling of the Pryor Mountain Wild Horse Range. Final Report to U.S. Geological Survey Biological Resources Division, U.S. National Park Service, and U.S. Bureau of Land Management. Fort Collins, CO: Natural Resource Ecology Laboratory.
Coughenour, M.B. 2000. Ecosystem modeling of the Pryor Mountain Wild Horse Range: Executive summary. Pp. 125-131 in Managers’ Summary—Ecological Studies of the Pryor Mountain Wild Horse Range, 1992-1997, F.J. Singer and K.A. Schoenecker, compilers. Fort Collins, CO: U.S. Geological Survey.
Coughenour, M.B. 2002. Ecosystem modeling in support of the conservation of wild equids: The example of the Pryor Mountain Wild Horse Range. Pp. 154-162 in Equids: Zebras, Asses and Horses: Status Survey and Conservation Action Plan, P.D. Moehlman, ed. Gland, Switzerland: International Union for Conservation of Nature.
Coughenour, M.B. and F.J. Singer. 1996a. Elk population processes in Yellowstone National Park under the policy of natural regulation. Ecological Applications 6:573-593.
Coughenour, M.B. and F.J. Singer. 1996b. Yellowstone elk population responses to fire: A comparison of landscape carrying capacity and spatial-dynamic ecosystem modeling approaches. Pp. 169-180 in The Ecological Implications of Fire in Greater Yellowstone, J. Greenlee, ed. Fairfield, WA: International Association of Wildland Fire.
Dawson, M.J. and J. Hone. 2012. Demography and dynamics of three wild horse populations in the Australian Alps. Austral Ecology 37:97-102.
de Villalobos, A.E. and S.M. Zalba. 2010. Continuous feral horse grazing and grazing exclusion in mountain pampean grasslands in Argentina. Acta Oecologica 36:514-519.
de Villalobos, A.E., S.M. Zalba, and D.V. Pelaez. 2011. Pinus halepensis invasion in mountain pampean grassland: Effects of feral horses grazing on seeding establishment. Environmental Research 111: 953-959.
Duncan, P. 1992. Horses and Grasses: The Nutritional Ecology of Equids and Their Impact on the Camargue. Ecological Studies 87. New York: Springer-Verlag.
Eberhardt, L.L. 1977. Optimal management policies for marine mammals. Wildlife Society Bulletin 5:162-169.
Eberhardt, L.L. and J.M. Breiwick. 2012. A scheme for evaluating feral horse management strategies. International Journal of Ecology, Article ID 491858, 5 pp.
Eberhardt, L.L., A.K. Majorowicz, and J.A. Wilcox. 1982. Apparent rates of increase for two feral horse herds. Journal of Wildlife Management 46:367-374.
Ellis, J.E. and D.M. Swift. 1988. Stability of African pastoral ecosystems: Alternate paradigms and implications for development. Journal of Range Management 41:450-459.
Feist, J.D. and D. McCullough. 1975. Reproduction in feral horses. Journal of Reproduction and Fertility Supplement 23:13-18.
Flux, J.E.C. 2001. Evidence of self-limitation in wild vertebrate populations. Oikos 92:555-557.
Fowler, C.W. 1987. A review of density dependence in populations of large mammals. Pp. 401-441 in Current Mammalogy, H.H. Genoways, ed. New York: Plenum.
Freeland, W.J. and D. Choquenot. 1990. Determinants of herbivore carrying capacity: Plants, nutrients, and Equus asinus in northern Australia. Ecology 71:589-597.
Gaidet, N. and J.M. Gaillard. 2008. Density-dependent body condition and recruitment in a tropical ungulate. Canadian Journal of Zoology-Revue Canadienne De Zoologie 86:24-32.
Gaillard, J.M., R. Andersen, D. Delorme, and D.C. Linnell. 1998. Family effects on growth and survival of juvenile roe deer. Ecology 79:2878-2889.
Gaillard, J.M., M. Festa-Bianchet, N.G. Yoccoz, A. Loison, and C. Toïgo. 2000. Temporal variation in fitness components and population dynamics of large herbivores. Annual Review of Ecology and Systematics 31:367-393.
Garrott, R.A. and L. Taylor. 1990. Dynamics of a feral horse population in Montana. Journal of Wildlife Management 54:603-612.
Garrott, R.A., T.C. Eagle, and E.D. Plotka. 1991. Age-specific reproduction in feral horses. Canadian Journal of Zoology-Revue Canadienne De Zoologie 69:738-743.
Gasaway, W.C., K.T. Gasaway, and H.H. Berry. 1996. Persistent low densities of plains ungulates in the Etosha National Park, Namibia: Testing the food-regulation hypothesis. Canadian Journal of Zoology-Revue Canadienne De Zoologie 74:1556-1572.
Georgiadis, N., M. Hack, and K. Turpin. 2003. The influence of rainfall on zebra population dynamics: Implications for management. Journal of Applied Ecology 40:125-136.
Georgiadis, N., J.G.N. Olwero, G. Ojwang, and S.S. Romanach. 2007. Savanna herbivore dynamics in a livestock-dominated landscape: I. Dependence on land use, rainfall, density, and time. Biological Conservation 137:461-472.
Getz, W.M. and N. Owen-Smith. 1999. A metaphysiological population model of storage in variable environments. Natural Resource Modeling 12:197-230.
Ginsberg, J.R. 1989. The ecology of female behavior and male reproductive success in Grevy’s zebra, Equus grevyi. Symposia of the Zoological Society of London 61:89-110.
Ginzburg, L.R. 1986. The theory of population dynamics: I. Back to first principles. Journal of Theoretical Biology 122:385-389.
Grange, S. and P. Duncan. 2006. Bottom-up and top-down processes in African ungulate communities: Resources and predation acting on the relative abundance of zebra and grazing bovids. Ecography 29:899-907.
Grange, S., P. Duncan, J-M. Gaillard, A.R.E. Sinclair, P.J.P. Gogan, C. Packer, H. Hofer, and M. East. 2004. What limits the Serengeti zebra population? Oecologia 140:523-532.
Grange, S., P. Duncan, and J.M. Gaillard. 2009. Poor horse traders: Large mammals trade survival for reproduction during the process of feralization. Proceedings of the Royal Society of London Series B 276:1911-1919.
Gray, M.E. and E.Z. Cameron. 2010. Does contraceptive treatment in wildlife result in side effects? A review of quantitative and anecdotal evidence. Reproduction 139:45-55.
Green, N.F. and H.D. Green. 1977. The wild horse population of Stone Cabin Valley: A preliminary report. Pp. 59-65 in Proceedings of the National Wild Horse Forum. Reno: University of Nevada, Cooperative Extension Service.
Greger, P.D. and E.M. Romney. 1999. High foal mortality limits growth of a desert feral horse population in Nevada. Great Basin Naturalist 59:374-379.
Gross, J.E. 2000. A dynamic simulation model for evaluating effects of removal and contraception on genetic variation and demography of Pryor Mountain wild horses. Biological Conservation 96:319-330.
Hansen, K.V. and J.C. Mosley. 2000. Effects of roundups on behavior and reproduction of feral horses. Journal of Range Management 53:479-482.
Hay, M.E. and J.T. Wells. 1991. Effects of Feral Horses on the Production, Distribution, Abundance, and Stability of Salt-Marsh Plants. Final Report. Washington, DC: National Oceanic and Atmospheric Administration.
Hobbs, N.T. 1989. Linking energy balance to survival in mule deer: Development and test of a simulation model. Wildlife Monographs 101:3-39.
ICMO (International Commission on Management of the Oostvaardersplassen). 2006. Reconciling Nature and Human Interests. The Hague/Wageningen, The Netherlands: ICMO.
ICMO2 (International Commission on Management of the Oostvaardersplassen 2). 2010. Natural Processes, Animal Welfare, Moral Aspects and Management of the Oostvaardersplassen. The Hague/Wageningen, The Netherlands: ICMO2.
Illius, A.W. and T.G. O’Connor. 1999. On the relevance of nonequilibrium concepts to semi-arid grazing systems. Ecological Applications 9:798-813.
Illius, A.W. and T.G. O’Connor. 2000. Resource heterogeneity and ungulate population dynamics. Oikos 89:283-294.
Jenkins, S.H. 2000. Density dependence in population dynamics of feral horses. Bureau of Land Management Resource Notes, No. 26, 2 pp.
Joubert, E. 1974. Composition and limiting factors of a Khomas Hochland population of Hartmann’s zebra (Equus zebra hartmannae). Madoqua 1:49-50.
Kertson, B.N., R.D. Spencer, J.M. Marzluff, J. Hepenstall-Cymerman, and C.E. Gure. 2011. Cougar space use and movements in the wildland-urban landscape of western Washington. Ecological Applications 21:2866-2881.
King, S.R.B. and J. Gurnell. 2012. Vigilance and its links to social cohesion in a reintroduced equid. Presentation at International Wild Equid Conference, September 18-22, Vienna, Austria.
Kirkpatrick, J.F. and J.W. Turner. 1991. Compensatory reproduction in feral horses. Journal of Wildlife Management 55:649-652.
Knopff, K.H. and M.S. Boyce. 2009. Prey specialization by individual cougars in multiprey systems. Transactions of the 74th North American Wildlife and Natural Resources Conference 72:195-210.
Knopff, K.H., A.A. Knopff, A. Kortello, and M.S. Boyce. 2010. Cougar kill rate and prey composition in a multiprey system. Journal of Wildlife Management 74:1435-1447.
Kruuk, H. 1972. The Spotted Hyena. Chicago: University of Chicago Press.
Lagos, L. and F. Bárcena. 2012. Foal survival and wolf predation in a population of Galician wild ponies (Equus ferus sp.). Presentation at International Wild Equid Conference, September 18-22, Vienna, Austria.
Levin, P.S., J. Ellis, R. Petrik, and M.E. Hay. 2002. Indirect effects of feral horses on estuarine communities. Conservation Biology 16:1364-1371.
Linklater, W.L., E.Z. Cameron, E.O. Minot, and K.J. Stafford. 2004. Feral horse demography and population growth in the Kaimanawa Ranges, New Zealand. Wildlife Research 31:119-128.
Lubow, B.C., F.J. Singer, T.L. Johnson, and D.C. Bowden. 2002. Dynamics of interacting elk populations within and adjacent to Rocky Mountain National Park. Journal of Wildlife Management 66:757-775.
Mduma, S.A.R., A.R.E. Sinclair, and R. Hilborn. 1999. Food regulates the Serengeti wildebeest: A 40-year record. Journal of Animal Ecology 68:1101-1122.
Meriggi, A. and S. Lovari. 1996. A review of wolf predation in Southern Europe: Does the wolf prefer wild prey to livestock? Journal of Applied Ecology 33:1561-1571.
Mills, M.G.L., H.C. Biggs, and I.J. Whyte. 1995. The relationship between rainfall, lion predation and population trends in African herbivores. Wildlife Research 22:75-88.
Monard, A.M. and P. Duncan. 1996. Consequences of natal dispersal in female horses. Animal Behaviour 52:565-579.
Nelson, K.J. 1978. On the Question of Male-Limited Population Growth in Feral Horses (Equus caballus). M.S. thesis. New Mexico State University, Las Cruces.
NRC (National Research Council). 1994. Rangeland Health: New Methods to Classify, Inventory, and Monitor Rangelands. Washington, DC: National Academy Press.
Nuñez, C.M., J.S. Adelman, and D.I. Rubenstein. 2010. Immunocontraception in wild horses (Equus caballus) extends reproductive cycling beyond the normal breeding season. PLoS One 5:e13635.
Owen-Smith, R.N. 1983. Dispersal and the dynamics of large herbivore populations in enclosed areas: Implications for management. Pp. 127-143 in Management of Large Mammals in African Conservation Areas, R.N. Owen-Smith, ed. Pretoria: Haum.
Owen-Smith, R.N. 2002a. Adaptive Herbivore Ecology: From Resources to Populations in Variable Environments. Cambridge, UK: Cambridge University Press.
Owen-Smith, N. 2002b. A metaphysiological modeling approach to stability in herbivore-vegetation systems. Ecological Modelling 149:153-178.
Owen-Smith, N., D.R. Mason, and J.O. Ogutu. 2005. Correlates of survival rates for 10 African ungulate populations: Density, rainfall and predation. Journal of Animal Ecology 74:774-788.
Patalano, M. and S. Lovari. 1993. Food habits and trophic niche overlap of the wolf Canis lupus, L., 1758, and the red fox Vulpes vulpes (L., 1758) in a Mediterranean mountain area. Revue d’Ecologie (La Terre et la Vie) 48:23-38.
Pellant, M., P. Shaver, D.A. Pyke, and J.E. Herrick. 2005. Interpreting Indicators of Rangeland Health, Version 4: Technical Reference 1734-6. Denver, CO: U.S. Department of the Interior.
Pulliam, H.R. 1988. Sources, sinks, and population regulation. American Naturalist 132:652-661.
Ricketts, M.J., R.S. Noggles, and B. Landgraf-Gibbons. 2004. Pryor Mountain Wild Horse Range Survey and Assessment. Bozeman, MT: U.S. Department of Agriculture, Natural Resources Conservation Service.
Riney, T. 1964. The impact of introductions of large herbivores on the tropical environment. IUCN Publications New Series 4:261-273.
Robinette, W.L., J.S. Gashwiler, and O.W. Morris. 1959. Food habits of the cougar in Utah and Nevada. Journal of Wildlife Management 23:261-273.
Roelle, J.E., F.J. Singer, L.C. Zeigenfuss, J.I. Ransom, L. Coates-Markle, and K.A. Schoenecker. 2010. Demography of the Pryor Mountain Wild Horses, 1993-2007. U.S. Geological Survey Scientific Investigations Report 2010-5125. Reston, VA: U.S. Geological Survey.
Rogers, G.M. 1991. Kaimanawa feral horses and their environmental impacts. New Zealand Journal of Ecology 15:49-64.
Rubenstein, D.I. 1981. Behavioural ecology of island feral horses. Equine Veterinary Journal 13:27-34.
Rubenstein, D.I. 1986. Ecology and sociality in horses and zebras. Pp. 282-302 in Ecological Aspects of Social Evolution, D.I. Rubenstein and L.W. Wrangham, eds. Princeton, NJ: Princeton University Press.
Rubenstein, D.I. 1994. The ecology of female social behaviour in horses, zebras and asses. Pp. 13-28 in Animal Societies, Individuals, Interactions, and Organization, P.J. Jarman and A. Rossiter, eds. Kyoto, Japan: Kyoto University Press.
Rubenstein, D.I. 2010. Ecology, social behavior, and conservation in zebras. Advances in the Study of Behavior 42:231-258.
Rubenstein, D.I. and A. Dobson. 1996. Demographic and Genetic Dynamics of Island Feral Horses: Implications for Fertility Control. Report to the National Park Service, Washington, DC.
Rubenstein, D.I. and C. Nuñez. 2009. Sociality and reproductive skew in horses and zebras. Pp. 196-226 in Reproductive Skew in Vertebrates: Proximate and Ultimate Causes, R. Hager and C.B. Jones, eds. Cambridge, UK: Cambridge University Press.
Ryden, H. 1990. America’s Last Wild Horses, Revised and Updated. New York: E.P. Dutton & Co.
Saether, B-E. 1997. Environmental stochasicity and population dynamics of large herbivores: A search for mechanisms. Trends in Ecology and Evolution 12:143-149.
Saltz, D. and D. Rubenstein. 1995. Population dynamics of a reintroduced Asiatic wild ass (Equus hemious) herd. Ecological Applications 5:327-335.
Saltz, D., D.I. Rubenstein, and G.C. White. 2006. The impact of increased environmental stochasticity due to climate change on the dynamics of Asiatic wild ass. Conservation Biology 20:1402-1409.
Scorolli, A.L. and A.C. Lopez Cazorla. 2010. Demography of feral horses (Equus caballus): A long-term study in Tornquist Park, Argentina. Wildlife Research 37:207-214.
Schaller, G.B. 1972. The Serengeti Lion. Chicago: University of Chicago Press.
Sinclair, A.R.E. 1989. Population regulation in animals. Pp. 197-241 in Ecological Concepts: The Contribution of Ecology to an Understanding of the Natural World, J.M. Cherrett and A.D. Bradshaw, eds. Oxford: Blackwell Scientific.
Sinclair, A.R.E. and M. Norton-Griffiths. 1982. Does competition or facilitation regulate migrant ungulate populations in the Serengeti? A test of hypotheses. Oecologia (Berlin) 53:364-369.
Singer, F.J., L. Zeigenfuss, L. Coates-Markle, and F. Schwieger. 2000. A demographic analysis, group dynamics, and genetic effective number in the Pryor Mountain wild horse population, 1992-1997. Pp. 73-89 in Managers’ Summary—Ecological Studies of the Pryor Mountain Wild Horse Range, 1992-1997, F.J. Singer and K.A. Schoenecker, compilers. Fort Collins, CO: U.S. Geological Survey.
Siniff, D.B., J.R. Tester, and G.L. McMahon. 1986. Foaling rate and survival of feral horses in western Nevada. Journal of Range Management 39:296-297.
Solomatin, A.O. 1973. The Kulan. Pp. 249-276 in Wild Ungulates (in Russian), A.A. Kaletsky, ed. Moscow, Russia: Lesnaya Promyschlenost.
Tatin, L., S.R.B. King, B. Munkhtuya, A.J.M. Hewison, and C. Feh. 2009. Demography of a socially natural herd of Przewalski’s horses: An example of a small, closed population. Journal of Zoology 277:134-140.
Thompson, H.V. and C.M. King. 1994. The European Rabbit. The History and Biology of a Successful Colonizer. Oxford: Oxford University Press.
Turner, A. and J.F. Kirkpatrick. 2002. Effects of immunocontraception on population, longevity and body condition in wild mares (Equus caballus). Reproduction Supplement 60:187-195.
Turner, J.W., Jr., M.L. Wolfe, and J.F. Kirkpatrick. 1992. Seasonal mountain lion predation on a feral horse population. Canadian Journal of Zoology 70:929-934.
Turner, J.W., Jr. and M.L. Morrison. 2001. Influence of predation by mountain lions on numbers and survivorship of a feral horse population. Southwestern Naturalist 46:183-190.
Van Duyne, C., E. Ras, A.E.W. De Vos, W.F. De Boer, R.J.H.G. Henkens, and D. Usukhjargal. 2009. Wolf predation among reintroduced Przewalski horses in Hustai National Park, Mongolia. Journal of Wildlife Management 73:836-843.
Vulink, J.T. 2001. Hungry Herds: Management of Temperate Lowland Wetlands by Grazing. Ph.D. dissertation. University of Groningen, The Netherlands.
Walker, B.H., R.H. Emslie, R.N. Owen-Smith, and R.J. Scholes. 1987. To cull or not to cull: Lessons from a southern African drought. Journal of Applied Ecology 24:381-401.
Wallace, L.L., M.G. Turner, W.H. Romme, R.V. O’Neil, and Y. Wu. 1995. Scale of heterogeneity and winter foraging by elk and bison. Landscape Ecology 10:75-83.
Wallace, L.L., M.B. Coughenour, M.G. Turner, and W.H. Romme. 2004. Fire patterns and ungulate survival in Northern Yellowstone Park: The results of two separate models. Pp. 299-317 in After the Fires: The Ecology of Change in Yellowstone National Park, L.L. Wallace, ed. New Haven, CT: Yale University Press.
Webb, N. 2009. Density, Demography, and Functional Response of a Harvested Wolf Population in West-Central Alberta, Canada. Ph.D. dissertation. University of Alberta, Canada.
Wehausen, J.D. 1996. Effects of mountain lion predation on bighorn sheep in the Sierra Nevada and Granite Mountains of California. Wildlife Society Bulletin 24:471-479.
Weisberg, P., M. Coughenour, and H. Bugmann. 2006. Modelling of large herbivore—vegetation interactions in a landscape context. Pp. 348-382 in Large Herbivore Ecology and Ecosystem Dynamics, K. Danell, R. Bergstrom, P. Duncan, and J. Pastor, eds. Cambridge, UK: Cambridge University Press.
Wolff, J.O. 1997. Population regulation in mammals: An evolutionary perspective. Journal of Animal Ecology 66:1-13.
Wolfe, M.L., L.C. Ellis, and R. MacMullen. 1989. Reproductive rates of feral horses and burros. Journal of Wildlife Management 53:916-924.
Wood, G.W., M.T. Mengak, and M. Murphy. 1987. Ecological importance of feral ungulates at Shackleford Banks, North Carolina. American Midland Naturalist 118:236-244.
Wynne-Edwards, V.C. 1965. Self-regulating systems in populations of animals. Science 147:1543-1548.
Zager, P. and J. Beecham. 2006. The role of black bears and brown bears as predators on ungulates in North America. Ursus 17:95-108.
































