













Below is the uncorrected machine-read text of this chapter, intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text of each book. Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
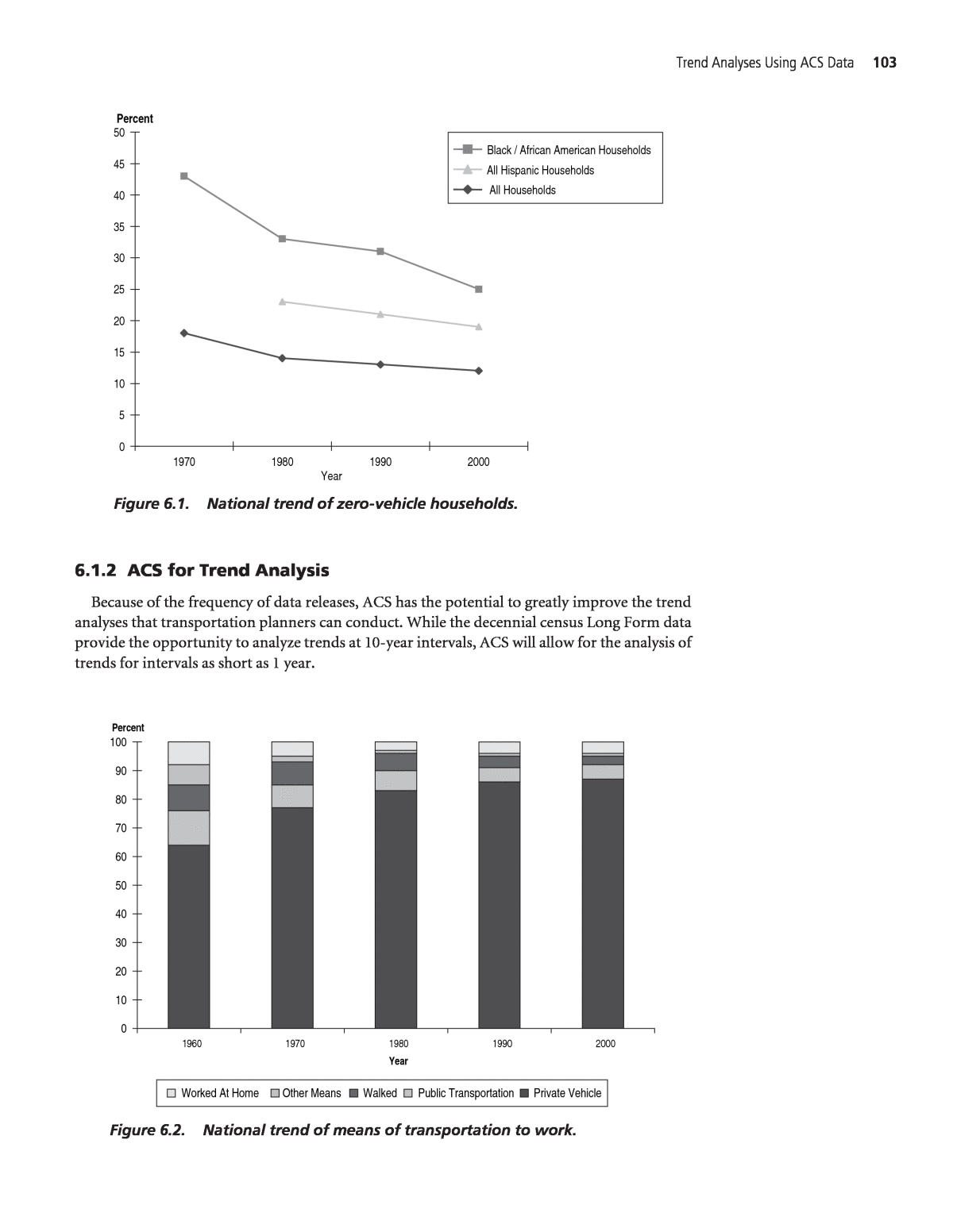
This section describes trend analysis as a common application of census data. It is organized as follows. Section 6.1 defines trend analysis and its uses, and provides some examples of how analysts use census data for these purposes. A detailed list of specific examples of uses of census data for this purpose is provided at the end of the section. Section 6.2 describes some benefits and limitations of shifting from census to ACS data related to trend analysis. Finally, Section 6.3 is a case study showing how to do trend analysis using ACS data. 6.1 Trend Analysis Trend analysis is a common application of census data that consists of examining the change in a given characteristic over time to understand future needs and guide policy planning. Trend analysis requires the availability of data for multiple time periods and consistency of the question and response categories over the time period considered. The decennial census, with its standard questions, relatively consistent data collection procedures, and comprehensive coverage, has been a good tool for performing trend analysis. Transportation planners have often used decennial census data to consistently monitor changes in population growth rates, population composition, and work trip behavior in a given area. Trend analysis is normally performed to ⢠Evaluate the overall pattern of change (magnitude and direction) in a characteristic over time; ⢠Compare the levels of a characteristic between particular time periods, such as before and after an event; ⢠Compare geographic areas across time; ⢠Compare different populations across time to evaluate absolute and relative changes in a characteristic; and ⢠Examine data over time to help in forecasting future conditions. 6.1.1 Examples of Use Census data have been used by transportation planners and others for analyzing a variety of demographic and journey to work trends. Figures 6.1 and 6.2 show examples of how trend analyses using decennial census data have been presented. Figure 6.1 shows a national trend of zero-vehicle households,51 and Figure 6.2 shows a national trend of means of transportation to work.52 A list of specific examples of using census data to do trend analysis also is provided at the end of this section. 102 C H A P T E R 6 Trend Analyses Using ACS Data 51 Murakami, E., 2003, âHouseholds without Vehicles, 2000.â See www.fhwa.dot.gov/ctpp/sr0103.htm. 52 N. Srinivasan, 2002, âJourney to Work Trends.â See www.fhwa.dot.gov/ctpp/sr0902.htm.
Trend Analyses Using ACS Data 103 0 5 10 15 20 25 30 35 40 45 50 1970 1980 1990 2000 Year Percent All Households Black / African American Households All Hispanic Households Figure 6.1. National trend of zero-vehicle households. 0 10 20 30 40 50 60 70 80 90 100 1960 1970 1980 1990 2000 Year Percent Worked At Home Other Means Walked Public Transportation Private Vehicle Figure 6.2. National trend of means of transportation to work. 6.1.2 ACS for Trend Analysis Because of the frequency of data releases, ACS has the potential to greatly improve the trend analyses that transportation planners can conduct. While the decennial census Long Form data provide the opportunity to analyze trends at 10-year intervals, ACS will allow for the analysis of trends for intervals as short as 1 year.
104 A Guidebook for Using American Community Survey Data for Transportation Planning 6.2 Benefits and Limitations of ACS for Trend Analysis This section summarizes the perceived benefits and limitations of using ACS data for trend analysis. In our discussions with transportation planners, the following potential benefits of ACS were identified: ⢠The availability of regularly updated ACS data may allow for more data points for trend analysis, especially to identify a steady trend or a sudden jump or drop in a trend variable like trip distribution by time. â Another application identified by users is to use the more frequently reported data to validate and enhance demographic projections for use in travel demand models.53 ⢠Given the lower sample sizes in ACS and the need to examine corresponding confidence inter- vals, however, users need to be wary of the following new issues: â ACS data come with a lot of variability and standard errors for each yearly estimate. â Because several potential data releases are possible for a particular year, (e.g.: one-year estimate, three- and five-year average), planners must pay more attention and may need to examine several numbers instead of one.54 This issue is further illustrated in the case study included in this section. ⢠The time-series component of ACS may help improve the relationship between means and medians of key trend variables and the percentages of households falling into different categories. The following ACS issues were identified as potential problems for trend analysis: ⢠ACS estimates will need to be based on moving averages of the trend variables. It can be problematic to evaluate year-to-year changes by using multiyear moving average estimates because some of the data are from overlapping time periods and are consequently identical. In comparing these overlapping estimates, the variances of the estimates of change will be underestimated incor- rectly. Moving averages also present similar problems when used as dependent variables in statis- tical models (such as time-series models) and regression models, since the statistical properties of the data (such as autocorrelations) would be affected by the overlaps in the moving averages. ⢠The potential advantage of ACS possibly providing insights into seasonality issues will not be realized, because information by month and quarter will not be provided. In addition, the weighting of estimates to the July 1 reference date in the annual population estimates will make the analysis of data for areas with highly seasonal populations more difficult to interpret. 6.3 Trend Analysis Case Study This section presents a case study that demonstrates how ACS estimates might be used for performing trend analyses. It shows how to analyze the change in a characteristic over recent years and whether the estimates indicate that a meaningful change has taken place. Section 3 of this guidebook has detailed instructions on downloading ACS data. Assume that you are a transportation analyst working in a hypothetical MPO in the autumn of 2007. Your manager has asked you to examine how the percentage of workers in the central county of your region (called Central County) that use public transportation (bus or trolley bus, streetcar or trolley car, subway or elevated, railroad) to work has been changing over the period 1996-2006. 53 C. Alexander, 2002, âA Discussion of the Quality of Estimates from the American Community Survey for Small Population Groups,â Personal correspondence with Caliper Corporation, David Hartgen, and Vermont Agency of Transportation. 54 See, for example, C. Taeuber, 2004, âThe American Community Survey: Challenges and Opportunities.â See http://rnyi.cornell.edu/Overview%205-14-04.ppt.
Although aggregate ridership data are available, transit on-board survey data that provide infor- mation on ridersâ trip purposes and other details are only available for snapshots in time over the past decade, so it is difficult to make conclusions about how commuter ridership has changed. This section describes some options for presenting the analysis results to policymakers. A use- ful way to analyze trends is to plot the indicator of interest versus time. This helps in visualizing the magnitude and direction of change in the indicator of interest, helps identify outliers, and provides insight into subsequent analysis strategies that could be used. Presentation options for two types of analysis are described. First, the trend at the county level is analyzed. Second, the county-level trend is compared to the city-level trend. Figure 6.3 shows the percentage of workers in Central County using public transportation to work, using the annual estimates. For each year, the lower bound, upper bound, and midpoint of the 90 percent confidence interval are shown. The following conclusions can be drawn from this analysis: ⢠There is no real noticeable trend in the percentage of workers using public transportation to work over the years 1996-2006; and ⢠The change is statistically not significant except for the change between 1996-1997, 1997-1998, and 1999-2000 (see âAnalysis Stepsâ section). One can alternatively show the actual percentages for each year, the difference in percentages, the confidence interval of the difference, and whether the difference is statistically significant (see, for example, Table 6.7). Figure 6.4 shows a comparison of the trends for Central County and a smaller city in the county, called Fairview City, using the five-year moving average data for both geographies to maintain consistency of comparison. The following conclusions can be drawn from this analysis: ⢠The confidence intervals at the city level are larger than at the county level, as expected, because of smaller sample sizes at smaller geographies; and ⢠Overall, the percentage of workers using public transportation to work is smaller in Fairview City than in Central County as a whole. 6.3.1 Available Data For areas with population over 65,000, the Census Bureau will release annual ACS estimates as well as three- and five-year moving averages. Since the total population of the county in Trend Analyses Using ACS Data 105 Percent 0 2 4 6 8 10 12 14 1996 1997 1998 1999 2000 2001 2002 2003 2004 2005 2006 Figure 6.3. Percentage of workers in Central County using public transportation to work, using annual ACS estimates.
106 A Guidebook for Using American Community Survey Data for Transportation Planning Year Total Workers Lower Bound Upper Bound Workers by Public Transportation Lower Bound Upper Bound 1996 305,713 303,259 308,167 32,133 31,052 33,214 1997 309,411 303,548 315,274 38,427 36,119 40,735 1998 312,609 305,785 319,433 33,883 31,365 36,401 1999 316,423 312,417 320,429 34,027 31,691 36,363 2000 330,828 327,614 334,042 39,289 36,977 41,601 2001 326,542 323,206 329,878 38,222 35,934 40,510 2002 319,537 313,896 325,178 36,333 33,076 39,590 2003 318,607 313,050 324,164 36,297 33,179 39,415 2004 318,000 312,423 323,577 35,616 32,453 38,779 2005 318,500 312,940 324,060 35,258 32,017 38,499 2006 319,000 313,407 324,593 34,580 31,314 37,845 Table 6.1. Annual ACS data for Central County,1996-2006. question is greater than 65,000 in each of the years 1996-2006, all three types of ACS data are available for use. Table 6.1 shows the number of workers using public transportation to work and the total number of workers in Central County. This table uses annual ACS data for the years 1996 through 2006. You can find the annual ACS data at the county level available online at the Census Bureau ACS website. Every estimate is associated with a lower bound and an upper bound cor- responding to the 90 percent confidence interval. The 90 percent confidence interval means that 90 times out of 100 the true value of the characteristic for that area falls between the lower and upper bounds of an estimate derived from a sample like the one taken. Tables 6.2 and 6.3 show the three-year and five-year moving averages, respectively, of the number of workers using public transportation and the total number of workers. Since the first 1996-2000 1997-2001 1998-2002 1999-2003 2000-2004 2001-2005 2002-2006 Percent Central County Fairview City 0 2 4 6 8 10 12 14 Figure 6.4. Percentage of workers in Central County and Fairview City using public transportation to work, using the five-year moving average ACS estimates.
Trend Analyses Using ACS Data 107 Year Total Workers Lower Bound Upper Bound Workers by Public Transportation Lower Bound Upper Bound 1996-1998 309,244 306,136 312,353 34,814 33,620 36,009 1997-1999 312,814 309,532 316,097 35,446 34,066 36,825 1998-2000 319,953 317,106 322,800 35,733 34,353 37,113 1999-2001 324,598 322,556 326,639 37,179 35,844 38,514 2000-2002 325,636 323,203 328,069 37,948 36,414 39,482 2001-2003 321,562 318,698 324,426 36,951 35,265 38,636 2002-2004 318,715 315,486 321,943 36,082 34,246 37,918 2003-2005 318,369 315,156 321,582 35,724 33,891 37,556 2004-2006 318,500 315,280 321,720 35,151 33,290 37,012 Table 6.2. Three-year moving average data for Central County, 1996-2006. Year Total Workers Lower Bound Upper Bound Workers by Public Transportation Lower Bound Upper Bound 1996-2000 314,997 312,868 317,126 35,552 34,579 36,524 1997-2001 319,163 316,986 321,339 36,770 35,717 37,822 1998-2002 321,188 319,035 323,341 36,351 35,202 37,499 1999-2003 322,387 320,385 324,389 36,834 35,627 38,040 2000-2004 322,703 320,556 324,850 37,151 35,872 38,431 2001-2005 320,237 317,906 322,568 36,345 34,988 37,703 2002-2006 318,729 316,231 321,227 35,617 34,181 37,052 Table 6.3. Five-Year moving average data for Central County, 1996-2006. year of data collection is 1996, the first three-year moving average is available in 1999. Initially, the Census Bureau calculated the three-year average estimates as (1996 Estimate + 1997 Estimate + 1998 Estimate)/3 However, for the full ACS data release beginning with 2005 data, the three-year averages will be calculated as the weighted averages of the data collected over the three-year period. Thus, the three-year average estimates are calculated in the same way as the single-year estimates, but over the course of three years. The same method is employed for five-year estimates. Since the 1996 to 2003 data are based on the ACS demonstration phase, the three- and five- year moving average estimates and their lower and upper bounds would not be available online. Therefore, these estimates have been synthesized for this case study. All computation methods are described in the next section. 6.3.2 Analysis Steps For this case study, two types of analyses are conducted. First, the percentage of workers using public transportation to work and its 90 percent confidence interval is computed for all three types of estimates: annual data, three-year moving average data, and five-year moving average data. Then, the difference in the percentage of workers using public transportation to work between any given two years and the statistical significance of the difference is computed. The formulas used in the analyses are based on documents released by the Census Bureau on the
108 A Guidebook for Using American Community Survey Data for Transportation Planning accuracy of ACS data, the three-year averages, and the change profiles.55 The formulas are pre- sented in Section 4 of this guidebook, and also are used in the Section 5 case studies. Annual Data In any given year, you could compute an estimate of the proportion of work- ers who used public transportation to work, as given in Equation 5.1. For example, using the 1996 data, the proportion of workers who used public transportation to work is equal to To compute the confidence interval of the percentage of workers who used public transporta- tion to work, you need to know its standard error. The steps needed to compute the standard error are similar to what is described in Sections 4 and 5. For example, using Equation 5.3, the standard error of the number of workers who used public transportation to work in 1996 is equal to Similarly, the standard error of the total number of workers in 1996 is equal to Using Equation 5.4, the standard error of the proportion of workers who used public trans- portation to work in 1996 is equal to Finally, using Equations 5.6, 5.7, and 5.8 (page81), the lower and upper bounds of the 90 per- cent confidence interval for the percentage of workers who used public transportation to work in 1996 are given by Similar computed values for all years from 1996-2006 are shown in Table 6.4. Three-Year Moving Average Data Given the lower and upper bounds of the confidence intervals for the three-year average total number of workers and the number of workers using public transportation to work, the other computations of the percentage of workers using pub- lic transportation to work and its confidence interval would be the same as those described for the annual data case. As mentioned earlier, the three-year moving average data were not avail- able for the 1996-2003 data and, therefore, are synthesized for this case study. The lower bounds and upper bounds of the 90 percent confidence interval for the three-year moving average estimates are derived in the same way as for the single-year estimates, and were shown in Table 6.2. The computed values are summarized in Table 6.5. UB PË . . . . .1996 0 1051 1 645 0 0021 0 1085 10 85( ) = + Ã = = % LB PË . . . . .1996 0 1051 1 645 0 0021 0 1017 10 17( ) = â Ã = = % SE PË , , , ,1996 2 2 2 1 305 713 657 32 133 305 713 1( ) = [ ] â 492 0 0021 0 212[ ] = =. . % SE YË , , . ,1996 305 713 303 259 1 645 1 492( ) = â = SE XË , , . 1996 32 133 31 052 1 645 657( ) = â = Ë , , . . %P1996 32 133 305 713 0 1051 10 51= = = 55 See âChange Estimates,â at www.census.gov/acs/www/Downloads/ACS/accuracy2002change.pdf, âAccuracy of the Data (2003),â at www.census.gov/acs/www/Downloads/ACS/accuracy2003.pdf, and âThree-Year Aver- ages,â at www.census.gov/acs/www/Downloads/ACS/ThreeYrAvg.pdf.
Five-Year Moving Average Data The computed values for the five-year moving average data are similar to those for the three-year moving average data, and are shown in Table 6.6. Computing Differences in Percentages The next step in the analysis is to compute the difference in the percentage of workers using public transportation to work between any two consecutive years and the statistical significance of the differences. It is important to note that statistically valid annual estimates of change cannot be computed from the difference of two moving averages if the two moving averages are based on overlapping data. Table 6.7 summarizes the three-year estimates that can be validly compared with each other. For the series involving data from 11 years (1996 to 2006), a maximum of three time peri- ods (assuming three-year moving averages) that do not include overlapping years should be sta- tistically compared to each other. For example, moving averages of 1996-1998, 1999-2001, and 2002-2004 can all be compared to each other without the effects of the overlapping data. Using five-year moving averages, a maximum of two time periods that do not include overlapping years can be compared to each other (e.g., moving averages of 1996-2000, 2001-2005). Trend Analyses Using ACS Data 109 Total Workers Number of Workers by Public Transportation Percentage of Workers by Public Transportation Year Estimate SE Estimate SE Estimate SE LB UB 1996 305,713 1,492 32,133 657 10.51 0.21 10.17 10.85 1997 309,411 3,564 38,427 1,403 12.42 0.43 11.71 13.13 1998 312,609 4,148 33,883 1,531 10.84 0.47 10.07 11.61 1999 316,423 2,435 34,027 1,420 10.75 0.44 10.03 11.48 2000 330,828 1,954 39,289 1,406 11.88 0.42 11.19 12.57 2001 326,542 2,028 38,222 1,391 11.71 0.42 11.01 12.40 2002 319,537 3,429 36,333 1,980 11.37 0.61 10.37 12.37 2003 318,607 3,378 36,297 1,895 11.39 0.58 10.43 12.35 2004 318,000 3,390 35,616 1,923 11.20 0.59 10.22 12.18 2005 318,500 3,380 35,258 1,970 11.07 0.61 10.07 12.07 2006 319,000 3,400 34,580 1,985 10.84 0.61 9.83 11.85 Table 6.4. Annual data computation worksheet for the percentage of workers who used public transportation to work with 90 percent confidence interval. Total Workers Number of Workers by Public Transportation Percentage of Workers by Public Transportation Year Estimate SE Estimate SE Estimate SE LB UB 1996-1998 309,244 1,890 34,814 726 11.26 0.22 10.89 11.63 1997-1999 312,814 1,996 35,446 839 11.33 0.26 10.91 11.76 1998-2000 319,953 1,731 35,733 839 11.17 0.26 10.75 11.59 1999-2001 324,598 1,241 37,179 812 11.45 0.25 11.05 11.86 2000-2002 325,636 1,479 37,948 933 11.65 0.28 11.19 12.12 2001-2003 321,562 1,741 36,951 1,025 11.49 0.31 10.98 12.01 2002-2004 318,715 1,963 36,082 1,116 11.32 0.34 10.76 11.89 2003-2005 318,369 1,953 35,724 1,114 11.22 0.34 10.66 11.79 2004-2006 318,500 1,957 35,151 1,131 11.04 0.35 10.46 11.61 Table 6.5. Three-Year moving average data computation worksheet for the percentage of workers who used public transportation to work with 90 percent confidence interval.
110 A Guidebook for Using American Community Survey Data for Transportation Planning The difference in the percentage of workers using public transportation to work between two years is given by Equation 5.2. For example, this difference between 1996 and 1997 is The steps needed to compute the statistical significance of this difference are similar to what was described in Section 5. The standard error of the difference in the percentage of workers who used public transportation to work between 1996 and 1997 is given by Equation 5.5 and is equal to The 90 percent margin of error of the difference in the percentage of workers who used public transportation to work between 1996 and 1997 is given by Equation 5.6 and is equal to: The lower and upper bounds of the 90 percent confidence interval of the 1996-1997 differ- ence in percentages are given by Equations 5.7 and 5.8, respectively, and are equal to LB DIFF1996 1997 1 91 0 79 1 12â( ) = â =. . . % ME DIFF1996 1997 1 645 0 48 0 79â( ) = à =. . . % = à [ ] +[ ] =100 0 0043 0 0021 0 482 2% . . . % SE DIFF SE P SE P1996 1997 1997 1100â( ) = à ( )â¡â£ â¤â¦ +% Ë Ë 996( )â¡â£ â¤â¦ DIFF P P1996 1997 1997 1996100 100 0 1â = à â( ) = Ã% Ë Ë % . 242 0 1051 1 91â( ) =. . % Total Workers Number of Workers by Public Transportation Percentage of Workers by Public Transportation Year Estimate SE Estimate SE Estimate SE LB UB 1996-2000 1997-2001 1998-2002 1999-2003 2000-2004 2001-2005 2002-2006 314,997 319,163 321,188 322,387 322,703 320,237 318,729 1,294 1,323 1,309 1,217 1,305 1,417 1,519 35,552 36,770 36,351 36,834 37,151 36,345 35,617 591 640 698 733 778 825 872 11.29 11.52 11.32 11.43 11.51 11.35 11.17 0.18 0.19 0.21 0.22 0.24 0.25 0.27 10.99 11.20 10.97 11.06 11.12 10.93 10.73 11.59 11.84 11.67 11.79 11.90 11.77 11.62 Table 6.6. Five-Year moving average data computation worksheet for the percentage of workers who used public transportation to work with 90 percent confidence interval. Year 1996-1998 1997-1999 1998-2000 1999-2001 2000-2002 2001-2003 2002-2004 2003-2005 2004-2006 1996-1998 1997-1999 1998-2000 1999-2001 2000-2002 2001-2003 2002-2004 2003-2005 2004-2006 Table 6.7. Valid comparisons of ACS three-year average estimates.
Finally, the statistical significance of the difference in percentages is determined according to the rules described in Section 5. For example, since both the lower and upper bounds of the 90 percent confidence interval of the difference in percentage of workers who used public transportation to work between 1996 and 1997 are positive, it can be concluded with 90 percent certainty that this difference is statistically significant. Similar computed values for the years 1996 through 2006 are shown in Table 6.8. 6.4 Conclusions from the Case Study As described, one can plot the trend versus time. Figures 6.5 and 6.6 show these plots for the three- and five-year moving average data. Similar to the conclusions drawn from the analysis of annual estimates, Figures 6.5 and 6.6 indicate that the change in the percentage of workers using public transportation to work was minimal; the plots of the three- and five-year moving averages are almost flat. This also illustrates that estimates based on the moving averages tend to smooth out any sudden changes in the indi- cator of interest. For example, even though there is a significant increase (around 2 percent) in the percentage of workers using public transportation to work between years 1996 and 1997 in the annual data plot, the increase occurs at a slower rate using the three- and five-year moving average data analysis. The drop in the rate in 1998 dampens the effect of the one-year variation. Even if there were a more pronounced increase from one year to the next, the multiyear esti- mates would have shown the increase at a slower rate. The dampening is desirable in the case of year-to-year minor fluctuations (noise), but means that trends that occur for smaller geographic areas will not be detectable for some time. The confidence intervals become narrower (i.e., more stable estimates) for the three-year moving average data than for the annual data, and narrower for the five-year moving average data than for the three-year moving average data. This reflects the larger sample sizes, but the seemingly increased precision comes at the cost of the more difficult interpretation of the multiyear averages. For the second analysis comparing the trends at the county level and at the city level for Fairview City, only five-year moving average data would be available for Fairview City, a small UB DIFF1996 1997 1 91 0 79 2 70â( ) = + =. . . % Trend Analyses Using ACS Data 111 Percentage of Workers Using Public Transportation to Work Year Estimate SE (Estimate) Difference SE (Diff) ME (Diff) LB (Diff) UB (Diff) Significant? 1996 10.51 0.21 1997 12.42 0.43 1.91 0.48 0.79 1.12 2.70 Yes 1998 10.84 0.47 -1.58 0.64 1.05 -2.63 -0.53 Yes 1999 10.75 0.44 -0.09 0.64 1.06 -1.14 0.97 No 2000 11.88 0.42 1.12 0.61 1.00 0.12 2.12 Yes 2001 11.71 0.42 -0.17 0.59 0.98 -1.15 0.80 No 2002 11.37 0.61 -0.33 0.74 1.21 -1.55 0.88 No 2003 11.39 0.58 0.02 0.84 1.38 -1.36 1.41 No 2004 11.20 0.59 -0.19 0.83 1.37 -1.56 1.17 No 2005 11.07 0.61 -0.13 0.85 1.40 -1.53 1.27 No 2006 10.84 0.61 -0.23 0.86 1.42 -1.65 1.19 No Table 6.8. Difference in percentages of workers using public transportation to work using annual ACS data.
112 A Guidebook for Using American Community Survey Data for Transportation Planning area with population less than 20,000. Therefore, for comparison purposes, since only the five- year data are available for the small area, the five-year average estimates for the county also should be used. The confidence intervals at each of the two geographic levels can then be plot- ted, as was shown in Figure 6.4. The confidence intervals at the city level are larger than at the county level, as expected, because of smaller sample sizes at smaller geographies. For any given time period, one can then compare the two moving average estimates (county and city levels) using the difference calculations described in Sections 4 and 5. Often, when the confidence intervals for the areas being compared are significantly different and not overlapping, an analyst will know that the difference is statisti- cally significant without calculating the standard errors of the differences. For example, the confi- dence interval at the city level corresponding to the 2001-2005 moving average does not overlap with the confidence interval at the county level. The upper bound of the confidence interval at the city level is smaller than the lower bound of the confidence interval at the county level. Therefore, one can be pretty certain that the percentage of workers using public transportation to work is smaller in Fairview City than in Central County as a whole. To determine the statistical significance of the difference, an analyst could apply the differences analysis described in Section 5. 0 2 4 6 8 10 12 14 1996-1998 1997-1999 1998-2000 1999-2001 2000-2002 2001-2003 2002-2004 2003-2005 2004-2006 Percent Figure 6.5. Percentage of workers in Central County using public transportation to work, using three-year moving average data. Percent 1996-2000 1997-2001 1998-2002 1999-2003 2000-2004 2001-2005 2002-2006 0 2 4 6 8 10 12 14 Figure 6.6. Percentage of workers in Central County using public transportation to work, using five-year moving average data.
This case study has shown how some elements of trend analysis can be accomplished using ACS data. Some of the issues that data users should be aware of when analyzing ACS data for the purpose of trend analysis are summarized below. 6.4.1 When to Use Each Type of Estimate When more than one type of estimate is available (either in the form of annual and moving average estimates or in the form of moving average estimates of different lengths), as in the case of geographic areas with 65,000+ population, the choice of estimate to use depends on the pur- pose of the analysis. Consistency If the characteristics of two populations in areas of similar geographic scales (e.g., populations of two counties or two states) are compared over time, it is important to use the same type of estimate to ensure consistency. For example, if County A has a 65,000+ popu- lation and County B has a population less than 65,000, then it is recommended to use the moving average estimate from County A (rather than the single-year estimate, which is available) to compare it to the moving average estimate from County B (where annual estimates are unavailable). Reduction in Lag Time If the timeliness of the data is important for the analysis, and if the single-year estimates are deemed reliable (e.g., with reasonable standard errors and without too many fluctuations), the analyst could use the single-year estimates rather than the moving aver- age estimates to reduce the lag time between the analysis year and data collection year. Reliability If the trend analysis focuses on a certain sub-population for whom three- and five-year moving averages are available, and if greater reliability is desired, the five-year moving averages would be more stable to use. Reducing Correlations As was discussed in the example above, moving averages that include overlapping years are correlated. Therefore, when modeling a trend using ordinary least squares regression or Poisson regression (see below), or testing for the significance of an annual rate of change, it is recommended that annual estimates be used rather than moving average esti- mates that include overlapping years. 6.4.2 Correlation between Moving Average Data When three- or five-year moving average data are used for computing differences in estimates between different years, users should be aware of the correlation between these estimates. For example, annual estimates of change cannot be computed from the difference of two mov- ing averages if the two moving averages are based on data from overlapping years (e.g., a mov- ing average of years 1996-1998 and a moving average of years 1997-1999). This is because when standard statistical procedures are used to test for significant differences between estimates over time, it is assumed that the two estimates are drawn from independent samples, an assumption that is violated in the case of two consecutive moving averages. One can, for example, compare a moving average of data from years 1996-1998 with a moving average of data from years 1999 and beyond, because these two intervals do not include overlapping years. 6.4.3 Modeling the Trend In addition to visually observing the pattern of change in the percentage of workers using pub- lic transportation to work and computing differences in percent distributions, statistical meth- Trend Analyses Using ACS Data 113
114 A Guidebook for Using American Community Survey Data for Transportation Planning ods can be used to model the trend and help in forecasting future values. Regression analysis (e.g., ordinary least squares [OLS] regression) is one such tool that also allows for the inclusion of other variables that could affect the indicator of interest. When using a regression to model a trend, it is preferable to use the actual annual rates rather than the moving averages because of the high correlations between moving averages from over- lapping years. The dependent variable can be the actual percentage of workers using public trans- portation, as in the following model: Percentage of workers using public transportation t = Intercept + Slope * Yeart where Yeart has the values 1 to N (number of years for which annual data are available). Alternatively, the dependent variable can be the natural logarithm of the percentage of work- ers using public transportation to work. A log transformation of the data does not change the overall direction of the trend, but it flattens the percentages and might give more realistic results. For example, applying a decreasing linear trend that uses the actual percentages, the percentage of workers using public transportation will equal zero in some future year. With a logarithmic transformation, however, it approaches zero but does not exactly equal zero. The logarithmic regression is of the following form: Ln(Percentage of workers using public transportation t) = Intercept + Slope * Yeart The regression equations can then be used to predict the percentage of workers using public transportation in any given future year. In this case study, the trends are not modeled because the number of datapoints available for estimation is very small. Other statistical techniques that can be used to model trends are Poisson regressions and time series analyses, which require more specialized software packages than those that perform OLS regression. Also, note that time series models allow for correlation in the error terms of the mod- eled observations, unlike OLS or Poisson regressions, which assume that the error terms are independent. 6.5 Specific Uses of Census Data for Trend Analyses 6.5.1 Demographic Trends Transportation planners and demographers need to monitor how a regionâs population has changed over time to better understand how the regionâs transportation system has evolved in order to inform forecasts of future regional growth. Some examples include ⢠Use of census data to understand demographic and economic growth in Lake, Porter, and LaPorte counties in Northwestern Indiana (Northwestern Indiana Regional Planning Commission).56 ⢠Development of growth and regional change projections by TAZ for the Johnson City (Ten- nessee) MPO Long-Range Transportation Plan.57 ⢠Use of census data by several counties in preparation of their comprehensive plans to under- stand trends and project these trends into the future. For example, Broward County, Florida, uses census data for economic and population modeling. 56 See www.nirpc.org/Census-DemoIntro.html. Last accessed November 8, 2004. 57 Johnson City MPO Long-Range Transportation Plan, âSection 2: Growth and Regional Change.â See www.jcmpo.org/lrtp/chap2.pdf (August 15, 2001).
⢠Use of CTPP 2000 data by the Maryland State Data Center to create a CD-ROM containing selected items from Part 1 and Part 2 for mapping via ArcView. Place-of-work data were used as part of an analysis of 10 military bases in Maryland in preparation for base realignment and closure, 2005.58 ⢠Use of census data to examine the aging of population and racial diversity, determine future transportation needs, evaluate travel behavior based on age and/or race groups, develop high- way projects to add capacity, develop and support policies (e.g., access control on identified cor- ridors in anticipated high-growth areas), and support public involvement/outreach purposes.59 ⢠Use of census data to develop population growth factors and demographic forecasts for trans- portation planning development work and modeling efforts.60 ⢠Use of 150 years of census data to study trends in the race and ethnicity history of Utah (espe- cially focusing on minority groups) and construct a historical county-level race/ethnicity data- base for Utah spanning 1850 through 2000. 61 6.5.2 Journey-to-Work Trends Trends of intercounty commuting are being classified at three levels: at the national level, for long-distance commuting, and for metropolitan commuting. Cervera and Hartgen,62 and Soot, DiJohn, and Christopher63 provide examples of recent efforts to review journey-to-work trends. Additional examples of published reports on journey-to-work trends include the following: ⢠FHWAâs Journey-to-Work Trends Report64 that describes commuting trends at the national level, as well as for large metropolitan areas, using data from 1960 to 2000. ⢠North Jersey Transportation Planning Authorityâs (NJTPA) use of county-to-county com- muter flow data from 1980 to 2000 to depict commute patterns for residents in Northern New Jersey.65 The report analyzed changes in trip mode shares to work, travel times, and vehicle availability from 1990 to 2000 at the county level in Northern New Jersey. ⢠Metropolitan Council of Twin Citiesâ use of county-to-county commuter flows to analyze regional changes in commute behavior in the Minneapolis-St. Paul Region.66 ⢠Puget Sound Regional Councilâs analysis of trends in the Central Puget Sound Region using 1980, 1990, and 2000 Census data.67 ⢠Northwest Michigan Council of Governmentâs use of census data to map trends in popula- tion, employment, and commute for the 10 counties constituting Northwest Michigan.68 Trend Analyses Using ACS Data 115 58 Personal correspondence with Jane Traynham, Maryland State Data Center. For an example of the applica- tion, see www.mdp.state.md.us/msdc/military/military_site.htm. November 10, 2004. 59 Personal correspondence with Minnesota DOT, Indiana DOT, Pioneer Valley Regional Planning Commis- sion, Tulare County Association of Governments. 60 Personal correspondence with Nebraska Department of Roads, Denver Regional Council of Governments (DRCOG), Southeast AR Regional Planning Commission (Arkansas). 61 P.S. Perlich, Utah Minorities: The Story Told by 150 Years of Census Data. University of Utah, 2002. 62 E.D. Cervera and D.T. Hartgen, âTrends in North Carolinaâs Inter-County and Intra-County Commuting, 1990- 2000,â Submitted to the Transportation Research Board, National Research Council, Washington, D.C., 2003. 63 Siim Soot, Joseph DiJohn, and Ed Christopher, 2003, âChicago-Area Commuting Patterns and Emerging Trends,â Urban Transportation Center, March 28, 2003. See www.berwyned.com/papers/co2cochgo.pdf. 64 N. McGuckin and N. Srinivasan, âJourney to Work Trends in the United States and its Major Metropolitan Areas, 1960-2000.â Federal Highway Administration, 2003. 65 North Jersey Transportation Planning Authority, âJourney-to-Work Data: Census 2000 County-to-County Worker Flow Data for the NJTPA Region,â November 2003. See www.njtpa.org/planning/census2000/ 2000JTWAnalysis2.pdf. 66 Robert Paddock, âCounty-County Commute Flow in the Minneapolis-St. Paul Regionâ CTPP 2000 Status Report, May 2003. See www.trbcensus.com/newsltr/sr0503.pdf. 67 Puget Sound Regional Council, âPuget Trends,â No. T1, April 2003. 68 Northwest Michigan Council of Governments, âTransportation to Work Characteristics and Trends for Northwest Michigan,â August 2002.
116 A Guidebook for Using American Community Survey Data for Transportation Planning ⢠Commuting patterns in Utah and county trends for 1980, 1990, and 2000.69 ⢠Trends in 1970 through 1990 county-to-county commuter flows by means of transportation, âdesire lineâ maps, reverse commuting, and interregional commuting in the Philadelphia region.70 ⢠Analysis of commuting to downtown in the San Francisco Bay Area.71 ⢠San Francisco Bay Area MTCâs study of county-to-county commuters from 1960 to 1990 and the change in household vehicle availability since 1960.72 ⢠Other reports by the Chicago Area Transportation Study,73 the San Diego Association of Gov- ernments, the Puget Sound Regional Council in the Seattle region, the Maryland Department of Transportation.74 In addition, through interviews and personal correspondence with transportation planners at state departments of transportation and metropolitan planning organizations, it was evident that journey-to-work trends analysis (e.g., modal split, households without vehicles, locality-to-locality commute flows, average commute) is a common application of the decennial census data (e.g., at Minnesota DOT, Indiana DOT, Mass Highway, Hampton Roads Planning District Commission, Yakima Valley Conference of Governments, Denver Regional Transit District). For example, at Indi- ana DOT, available census employment data were compared to previous data in order to identify changes in employment type, primary industry, and occupation. Identified trends were used to fore- cast travel demand, evaluate access to jobs, study the movement of goods, and develop/evaluate transportation projects or policies designed to encourage future economic expansion. 69 P. Perlich, âCommuting Patterns in Utah: County Trends for 1980, 1990, and 2000.â Utah Economic and Busi- ness Review, 2003. 70 Delaware Valley Regional Planning Commission, âJourney to Work Trends in the Delaware Valley Region, 1970-1990.â Direction 2020 Report 5, Philadelphia, June 1993. 71 C. Purvis, 2004, âCommuting to Downtown.â See www.mtc.ca.gov/datamart/census/ctpp2000/ (May 6, 2004). 72 C. Purvis, 1994, âThe Decennial Census and Transportation Planning: Planning for Large Metropolitan Areas,â Transportation Research Board, Decennial Census Data for Transportation Planning, Conference Proceedings 4, Irvine, California, March 13-16, 1994. 73 Ed Christopher, 1996, âCensus Data Use in Illinois by a Large Metropolitan Planning Organization,â Trans- portation Research Board, Decennial Census Data for Transportation Planning, Case Studies and Strategies for 2000, Conference Proceedings 13, April 28-May 1, 1996. 74 TCRP Report 28: Transit Markets of the Future: The Challenge of Change, Transportation Research Board, National Research Council, Washington, D.C., 1998. See http://gulliver.trb.org/publications/tcrp/tcrp_rpt_28- a.pdf.
