

































































Below is the uncorrected machine-read text of this chapter, intended to provide our own search engines and external engines with highly rich, chapter-representative searchable text of each book. Because it is UNCORRECTED material, please consider the following text as a useful but insufficient proxy for the authoritative book pages.
30 3.1 Safety Data Analysis Aspects Introduction This research segment covers the work done for the safety data analysis aspects of the project. Throughout this report the words âcollisionâ and âcrashâ are used interchangeably. The broad objectives of this project required an analysis of WVCs and road environment data from state DOT sources. Specifically, the planned purpose of the safety analysis was to produce results that would assist with the development of guidelines on: ⢠Methods for identifying WVC problem locations, ⢠The evaluation of the safety effectiveness of crossing miti- gation measures, ⢠The establishment of a monitoring program to facilitate the identification of collision-prone locations and the evaluation of crossing mitigation measures, and ⢠Cost-benefit and cost-effectiveness considerations. The following sections document efforts towards developing these guidelines. The two aspects to the safety research, although linked, are summarized separately: ⢠Aspect 1: The application of reported WVC data typically available in state DOT databases and ⢠Aspect 2: An investigation of how the application of two databases, reported WVCs and carcass removals, can lead to different roadway improvement decisions Aspect 1: Application of Reported WildlifeâVehicle Collision Data The general objectives of the research undertaken for this aspect are consistent with those of SafetyAnalyst (www. safetyanalyst.org), a safety management guide being devel- oped by the FHWA for use by DOTs. SafetyAnalyst is envisioned as a set of software guides used by state and local highway agencies for safety management and to improve their programming of site-specific safety improvements. SafetyAnalyst incorporates state-of-the-art safety manage- ment approaches into computer-based analytical guides to aid the decision-making process to identify safety improvement needs and develop a systemwide program of site-specific improvement projects. The general objectives of this research address three general aims: 1. Identify collision-prone locations for existing or proposed roads for all collision types combined or for specific target collision types; 2. Aid in the evaluation, selection, and prioritization of potential mitigation measures; and 3. Evaluate the effectiveness of mitigation measures already implemented. Meeting these objectives requires the use of state-of-the-art statistical methods (e.g., predictive negative binomial models and empirical Bayes procedures) to produce a widely accepted and usable guide that can be readily applied by DOTs in their completion of items 1 and 2 for animalâvehicle collisions and to provide initial insights as part of a framework for future research to make additional progress on item 3 with respect to wildlife crossings. It is expected that results of this research project, specifically the predictive models developed, can be applied within SafetyAnalyst in undertaking tasks 1, 2, and 3 above with respect to wildlifeâvehicle collisions. Aspect 2: Comparison of WildlifeâVehicle Collision and Carcass Removal Data Reported WVC data may represent only a small portion of the large number of WVCs that occur61,201. A second type of data, obtained from records of carcass removals, has also been used to describe the WVC problem and determine the need C H A P T E R 3 Phase 2 Segments
31 for and impacts of WVC countermeasures. This aspect of NCHRP 25-27 was conducted to investigate the hypothesis that roadside carcass removal data not only indicate a different magnitude for the WVC problem, but may also show differ- ent spatial patterns than reported WVC data. The choice of the database (collisions or carcasses) used to evaluate the WVC problem, therefore, may lead to the identification of different hotspot locations and ultimately different counter- measure improvements. Patterns were examined visually by GIS plots, and by the development of comparable negative binomial WVC and deer carcass removal models. WVC and deer carcass removal data were obtained from the Iowa Department of Transportation (IaDOT). The creation and analysis of GIS-based data that include the attributes and location of roadway segment cross sections, reported WVCs, and deer carcass removals can be used to an- swer a number of questions: ⢠Is the number of reported deer carcass removals different than the reported number of WVCs statewide and along individual roadway segments? ⢠Are different âhigh collisionâ segments identified when reported WVCs and deer carcass removal data are used for the safety analysis of individual roadway segments? In other words, do they have different occurrence patterns? ⢠Are there any apparent relationships between traffic flow, roadway cross section characteristics, and reported WVCs? Are these relationships, if they exist, similar for deer carcass removal data? The activities completed as part of this aspect of NCHRP 25- 27 (e.g., plots, summary measures, and models) were used to investigate and compare the patterns of two databases (i.e., reported WVCs and deer carcass removals) that have been used to define and mitigate the WVC problem. Research Approach: Methods and Data The research approach emerged from a review of the exist- ing literature, specifically from a consideration of the gaps in existing knowledge. Methods Aspect 1: Application of reported wildlifeâvehicle colli- sion data. Predictive models for wildlifeâvehicle collisions (commonly called âsafety performance functionsâ [SPFs]) are crucial to state-of-the-art methods for filling safety analy- sis gaps and developing the requisite guidelines for mitigat- ing these collisions. These models are derived from historical data and relate collision frequency to physical roadway and roadside characteristics and to measures of exposure. They were developed for, and apply to, reported large-animal WVCs (as distinguished from data reported only as carcass removal) and, with a view to the application of the models, for use only with those variables for which data are readily available within the typical DOT safety databases. Because animal exposure data (a measure of the numbers of animals involved in WVC that are near the road, and the amount of time they spend near the road over the course of a specific measured time unit) are not among these readily available variables, this approach will result in some unexplained variation in the dependent variable. The safety model inputs are limited to roadway (between shoulder edges) variables because few DOT databases include roadside information (e.g., guardrail, roadside sight distance) or adjacent landscape (off right-of-way) characteristics. Even so, it is still necessary to estimate models for lower levels of data availability that may exist in some jurisdictions. The result is three funda- mental levels of SPFs: ⢠Level 1: These SPFs include only the length and annual average daily traffic volume (AADT) of a segment. ⢠Level 2: These SPFs require that segments be classified as flat, rolling, or mountainous terrain and also use the length and AADT of a segment. ⢠Level 3: These SPFs include additional roadway variables such as average lane width in addition to the Level 2 variables. The SPFs can be used in a number of applications: ⢠Application A: SPFs can be used with caution to identify roadway factors associated with a high propensity for wildlifeâvehicle collisions. These cautions pertain to possibly counterintuitive inferences that may result from omitted, in- correctly specified, or correlated factors. This application can be useful in roadway design and planning decisions that have implications for wildlifeâvehicle collisions. ⢠Application B: SPFs can be used in the identification of roadway segments that may be good candidates for wildlifeâ vehicle collision countermeasures. ⢠Application C: SPFs can be used in estimating the effec- tiveness of potential countermeasures that are considered for candidate segments. ⢠Application D: SPFs can be used in evaluating the effective- ness of implemented countermeasures using state-of-the-art methods for observational before-after studies.114 For the last three applications, which are key elements in this project, collision history often is used as a predictor. However, it is now well recognized as a poor predictor be- cause collision history tends to be short term (<3 years) rather than long term (â¥3 years) and therefore subject to random fluctuation and associated vagaries of regression to the mean.
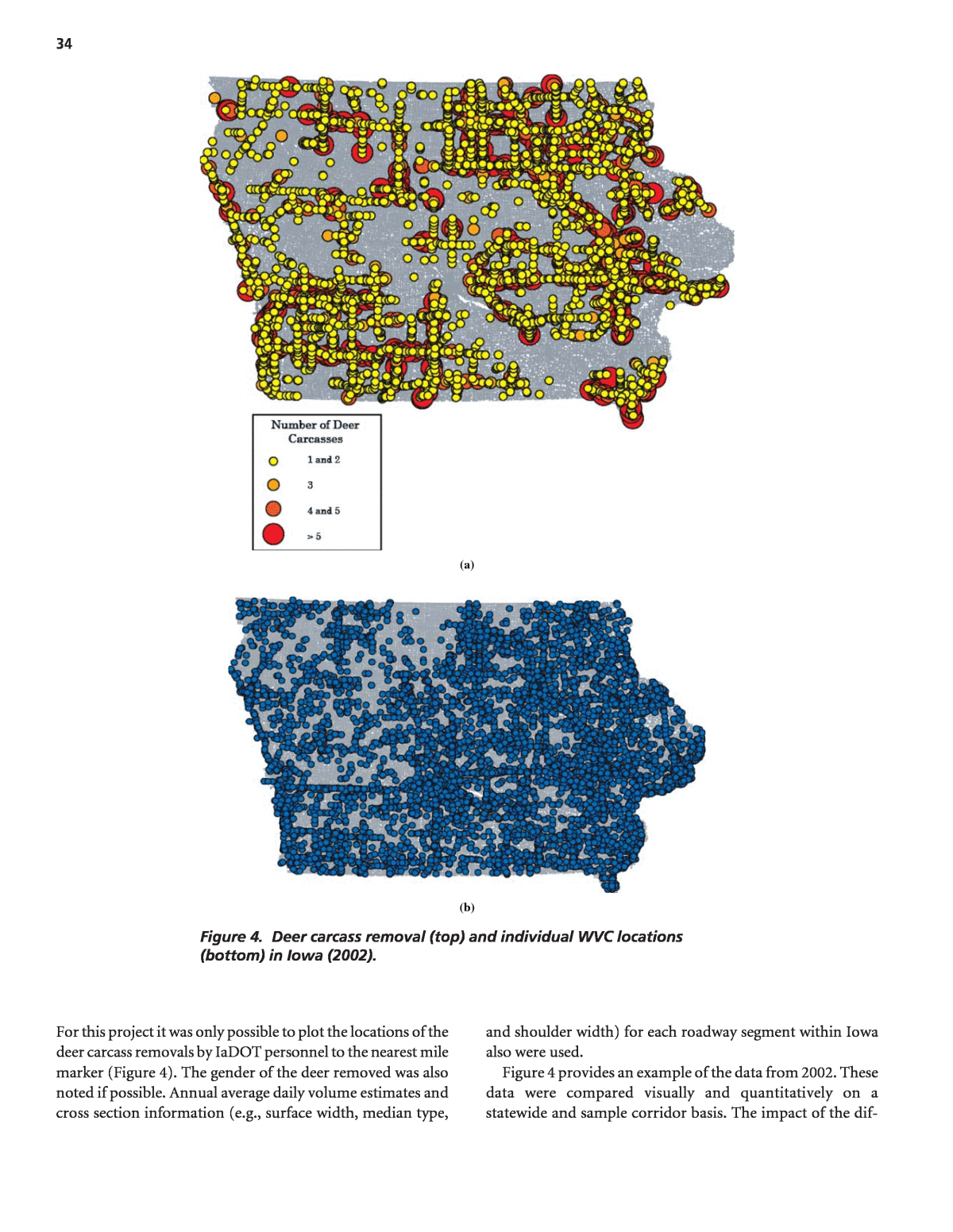
32 The result is that for Application A, resources are often wasted on safer sites that are wrongly identified and good candidates may be ignored. As a result, the countermeasure effectiveness estimates for Applications C and D can be exag- gerated. The regression to the mean problem cannot be overemphasized and so is illustrated in Appendix D. While the SPF can provide less biased predictions than the collision count for Applications B, C, and D, estimates ob- tained from these models can have a high variance because of the inability to include potentially important explanatory variables in them. In recognition of this difficulty and the problems with estimates from collision counts, an empirical Bayes (EB) procedure has been used.177 This procedure in essence takes a weighted average of the two estimates, recog- nizing that both provide important clues as to a locationâs safety. In effect, by using the collision counts to refine the SPF prediction, the EB procedure accounts for factors, such as off right-of-way characteristics and animal exposure, that affect wildlifeâvehicle collision frequency but are not in the model. For example, a location that has more animal movements than the âaverageâ location, but that is similar in the charac- teristics of the prediction model, will tend to have more col- lisions than the âaverageâ location. With EB refinement comes higher collision prediction accuracy. The EB proce- dure is illustrated by way of example applications, in the âIn- terpretation, Appraisals, and Applicationsâ section. The development of the SPFs involved determination of which explanatory variables should be used, if and how vari- ables should be grouped, and how variables should enter into the model (i.e., the best model form). Consistent with the com- mon research practice in developing these models, generalized linear modeling was used to estimate model coefficients, assuming a negative binomial error distribution. In specifying a negative binomial error structure, the dispersion parameter k, which relates the mean and variance of the regression esti- mate, is estimated from the model and the data. The value of k is such that, the smaller its value, the better a model is for the set of data (See Appendix B). Conveniently, the dispersion parameter estimated in the SPF calibration is used to derive the weights for the two sets of information used in the EB procedure. Aspect 2: Comparison of wildlifeâvehicle collision and carcass removal data. The tasks completed for this research were done to evaluate the value of collecting and plotting WVC and deer carcass removal data by location, and to test the straw hypothesis that these two datasets may also identify different roadway locations for potential WVC countermea- sures. The magnitude and patterns of location-based WVC reports and deer carcass removal datasets in Iowa were com- pared qualitatively through visual GIS plots and quantita- tively (e.g., WVC frequency per mile). The GIS plots and summary tables from these comparison activities are sum- marized in the âFindings and Resultsâ section. Similar to As- pect 1, negative binomial prediction models were also used. WVC and deer carcass removal prediction models (or SPFs) that considered traffic flow and roadway cross section ele- ments as potential input variables were created and com- pared. The results of these activities are also described in the âFindings and Resultsâ section. Several types of computer software were used to overlay, present, and summarize the WVC and deer carcass removal data within the GIS platform. Microsoft® Excel⢠and True- Basic⢠were used to manage the deer carcass removal data. The ArcGIS 9.1⢠platform was used to present and analyze the collision and carcass datasets spatially. ArcCatalog⢠was used as a file management program and applied specifically for organizing spatial data. Most of the mapping activities took place in ArcMapâ¢. ArcGuidebox⢠was used for some of the more complicated spatial analysis, and the large size of the roadway inventory database files required the use of FileMakerâ¢. The modeling of the WVC and deer carcass removal information was completed with SAS⢠statistical software. Data Aspect 1: Application of reported wildlifeâvehicle collision data. The models for predicting the frequency of reported wildlifeâvehicle collisions were developed for rural two-lane and rural multilane roadways using Highway Safety Informa- tion System (HSIS) data from California, North Carolina, Utah, and Washington and for rural freeway roadways with data from California, Utah, and Washington. These are the typical classifications used by DOTs in other aspects of safety management. Tables 6 through 9 summarize the data used. Aspect 2: Comparison of wildlifeâvehicle collision and carcass removal data. Three different databases were used to compare the magnitude and patterns of WVCs and deer carcass removals in Iowa. First, 10 years of police-reported WVC information in a GIS-acceptable format were acquired from the IaDOT. The data included the location of the WVCs and information provided on the police reports (e.g., sever- ity, surface conditions, time of day, and age of driver). A large majority of the reported WVCs involved white-tailed deer (Odocoileus virginianus). The reported WVCs in 2001, 2002, and 2003 were used in this analysis. The individual WVC locations were provided by the IaDOT and plotted by latitude and longitude coordinates. For example, the 2002 WVC locations plotted on a roadway map of Iowa within a GIS platform are shown in Figure 4. The two other datasets that were used included informa- tion about deer carcass removals and roadway cross sections.
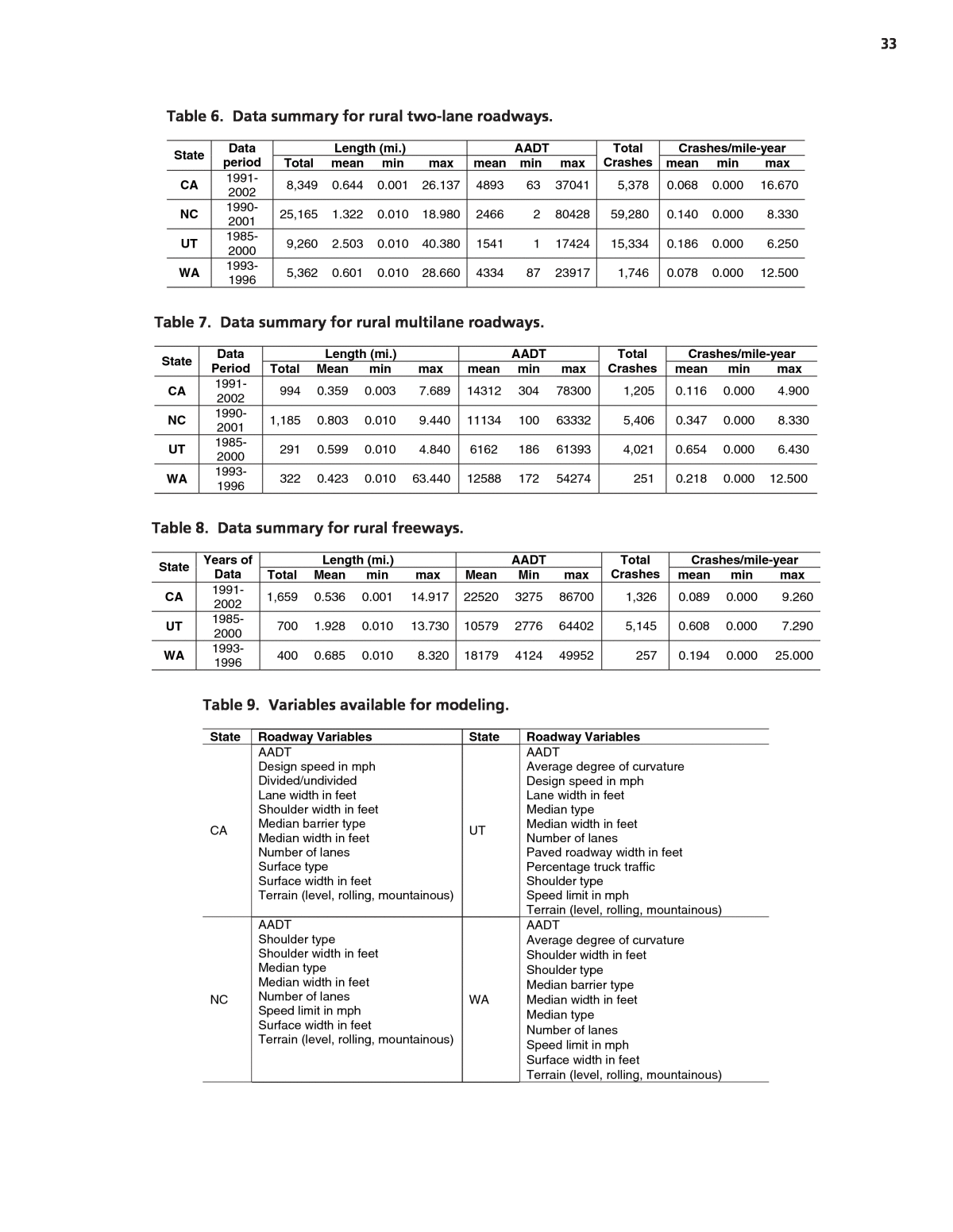
33 Length (mi.) AADT Crashes/mile-year State Dataperiod Total mean min max mean min max Total Crashes mean min max CA 1991-2002 8,349 0.644 0.001 26.137 4893 63 37041 5,378 0.068 0.000 16.670 NC 1990-2001 25,165 1.322 0.010 18.980 2466 2 80428 59,280 0.140 0.000 8.330 UT 1985-2000 9,260 2.503 0.010 40.380 1541 1 17424 15,334 0.186 0.000 6.250 WA 1993-1996 5,362 0.601 0.010 28.660 4334 87 23917 1,746 0.078 0.000 12.500 Table 6. Data summary for rural two-lane roadways. Length (mi.) AADT Crashes/mile-year State DataPeriod Total Mean min max mean min max Total Crashes mean min max CA 1991-2002 994 0.359 0.003 7.689 14312 304 78300 1,205 0.116 0.000 4.900 NC 1990-2001 1,185 0.803 0.010 9.440 11134 100 63332 5,406 0.347 0.000 8.330 UT 1985-2000 291 0.599 0.010 4.840 6162 186 61393 4,021 0.654 0.000 6.430 WA 1993-1996 322 0.423 0.010 63.440 12588 172 54274 251 0.218 0.000 12.500 Table 7. Data summary for rural multilane roadways. Length (mi.) AADT Crashes/mile-year State Years of Data Total Mean min max Mean Min max Total Crashes mean min max CA 1991-2002 1,659 0.536 0.001 14.917 22520 3275 86700 1,326 0.089 0.000 9.260 UT 1985-2000 700 1.928 0.010 13.730 10579 2776 64402 5,145 0.608 0.000 7.290 WA 1993-1996 400 0.685 0.010 8.320 18179 4124 49952 257 0.194 0.000 25.000 Table 8. Data summary for rural freeways. State Roadway Variables State Roadway Variables CA AADT Design speed in mph Divided/undivided Lane width in feet Shoulder width in feet Median barrier type Median width in feet Number of lanes Surface type Surface width in feet Terrain (level, rolling, mountainous) UT AADT Average degree of curvature Design speed in mph Lane width in feet Median type Median width in feet Number of lanes Paved roadway width in feet Percentage truck traffic Shoulder type Speed limit in mph Terrain (level, rolling, mountainous) NC AADT Shoulder type Shoulder width in feet Median type Median width in feet Number of lanes Speed limit in mph Surface width in feet Terrain (level, rolling, mountainous) WA AADT Average degree of curvature Shoulder width in feet Shoulder type Median barrier type Median width in feet Median type Number of lanes Speed limit in mph Surface width in feet Terrain (level, rolling, mountainous) Table 9. Variables available for modeling.
34 (a) (b) Figure 4. Deer carcass removal (top) and individual WVC locations (bottom) in Iowa (2002). For this project it was only possible to plot the locations of the deer carcass removals by IaDOT personnel to the nearest mile marker (Figure 4). The gender of the deer removed was also noted if possible. Annual average daily volume estimates and cross section information (e.g., surface width, median type, and shoulder width) for each roadway segment within Iowa also were used. Figure 4 provides an example of the data from 2002. These data were compared visually and quantitatively on a statewide and sample corridor basis. The impact of the dif-
35 Number and Percentage of Roadway Milesa Number and Percentage of WildlifeâVehicle Collisions Number and Percentage of Deer Carcass Removals Roadway System Interstate 1,020.46(0.9%) 1,892 (8.2%) 6,382 (25.3%) U.S. Highway 3,635.25(3.2%) 6,042 (26.2%) 10,205 (40.4%) Iowa State Route 5,039.19(4.4%) 5,722 (24.8%) 8,075 (32.0%) Farm to Market Route 30,843.84(27.3%) 6,826 (29.6%) 119 (0.4%) Area Type Rural 97,885.5(86.6%) 20,222 (87.6%) 22,155 (87.7%) Urban 15,172.75(13.4%) 2,872 (12.4%) 3,103 (12.3%) Number of Lanesb Two 109,471.10(96.8%) 16,429 (71.1%) 13,393 (53.0%) Four 2,033.43(1.8%) 4,898 (21.2%) 9,650 (38.2%) a Roadway mileage changes each year. Number and percentage of roadway miles in table represents average annual mileage that existed from 2001 to 2003. b Number includes through, turn, and two-way left-turn lanes. Table 10. Total WVC and deer carcass removals by roadway characteristic (2001â2003). ferent spatial accuracies of the data and the plots on the re- sults of this work are noted where appropriate. Table 10 shows the number and percentage of Iowa roadway mileage, reported WVCs, and deer carcass removals along roadways with varying characteristics. The traffic volume and cross section attribute data collected were also used with the WVC and deer carcass removal data to develop prediction models. Descriptive statistics for the 2001 to 2003 roadway length, AADT, WVC, and deer carcass removal data used in the model development are summarized in Table 11. The length of the segments evaluated and modeled was pri- marily defined by the changes in roadway cross section design (e.g., number of lanes). Only those rural roadway segments with a length of <_ 0.1 mi were used in the development of the model. Findings and Results Aspect 1: Application of Reported WildlifeâVehicle Collision Data Tables 12 through 14 provide details of the SPFs. For each of the four states, three levels of SPFs were developed with varying Two-Lane Rural Roadway Multilane Rural Roadway Roadway Category Total Mean Min Max Total Mean Min Max Length (Miles) 6,529 0.49 0.10 1.78 1,317 0.35 0.10 1.39 Average Annual Daily Traffic (AADT) NAa 2,433 103 13,000 NA1 12,659 180 77,433 WildlifeâVehicle Collisions/ Mile-Year 6,721 0.39 0.00 16.32 3,438 0.87 0.00 14.23 Carcass Removals/ Mile-Year 11,640 0.64 0.00 75.85 8,288 1.97 0.00 93.33 a NA = Not Applicable Table 11. Modeling database summary (rural segments > 0.1 mi).
36 Model Form: Total wildlifeâvehicle collisions/mile-year = LANEWIDSPEEDHISURFWIDAADT 5432exp1State/ Model Terrain ln (s.e.) 1 (s.e.) 2 (s.e.) 3 (s.e.) 4 (s.e.) 5 (s.e.) Dispersion parameter CA 1 All -7.8290(0.1868) 0.6123 (0.225) 1.6098 Flat -8.7034(0.2005) Rolling -8.1810(0.1930)CA 2 Mountainous -8.0343(0.1989) 0.6636 (0.0228) 1.4831 Flat -8.5357(0.2046) Rolling -7.9275(0.1968)CA 3 Mountainous -7.7157(0.2029) 0.6518 (0.0230) Design 55 -0.3310 (0.0449) Else = 0 1.4493 NC 1 All -4.5625(0.0576) 0.3743 (0.0078) 0.9222 Flat Rolling -4.3984 (0.0745)NC 2 Mountainous -5.5363(0.0653) 0.3637 (0.0077) 0.8142 Flat Rolling -4.3805 (0.0773) NC 3 Mountainous -5.7195(0.0685) 0.4447 (0.0087) -0.0122 (0.0022) Posted < 55 -0.7165 (0.0248) Else = 0 0.7353 UT 1 All -9.1135(0.1423) 1.0237 (0.0205) 1.7610 Flat -9.3123(0.3385) Rolling -9.0528(0.3393)UT 2 Mountainous -8.7728(0.3006) 1.0092 (0.0410) 1.6123 Flat -12.987(0.9608) Rolling -12.803(0.9613)UT 3 Mountainous -12.408(0.9485) 0.8073 (0.0455) Posted 55 -0.6646 (0.1344) Else = 0 0.4751 (0.0838) 1.3985 WA 1 All -8.6850(0.3020) 0.7802 (0.0367) 1.3825 WA 2 All -8.5319(0.3552) 0.8034 (0.0426) -0.0584 (0.0117) 1.0237 WA 3 All -8.5161(0.3493) 0.7622 (0.0426) -0.0696 (0.0124) Posted 55 0.4358 (0.0964) Else = 0 0.9528 Table 12. SPFs for rural two-lane roadways. data requirements. The first level required only the length and AADT of a segment. The second level included the requirement that segments be classified as flat, rolling, or mountainous ter- rain. The third level of SPFs added additional roadway variables such as average lane width. All variables were from state HSIS data. Segments were defined as sections of roads, generally be- tween significant intersections and having essentially common geometric characteristics. Illustration of the application of the SPFs developed is a key component of this aspect of the safety research. These applications are illustrated in the âInterpreta- tion, Appraisals, and Applicationsâ section. In general, the calibrated SPFs make good intuitive sense in that the sign, and to some extent the magnitude, of the esti- mated coefficients and exponents accord with expectations. Surprisingly, the exponent of the AADT term, although rea- sonably consistent for the three levels of models in a state, varied considerably across states. This exponent varied significantly across facility types, reflecting differences in traffic operating
37 Model Form: Total wildlifeâvehicle collisions/mile-year = SPEEDHIMEDWIDAADT 432exp1State/Model Terrain ln (s.e.) 1 (s.e.) 2 (s.e.) 3 (s.e.) CA 1 All -5.2576(0.4397) 0.3290 (0.0470) Flat -6.4592(0.4523) Rolling -5.7615(0.4398)CA 2 Mountainous -5.5220(0.4498) 0.3926 (0.0464) Flat -6.4885(0.4485) Rolling -5.8372(0.4360)CA 3 Mountainous -5.6577(0.4462) 0.4145 (0.0464) -0.0057 (0.0015) NC 1 All -3.3660(0.6314) 0.2501 (0.0684) Flat Rolling -2.5310 (0.6063)NC 2 Mountainous -4.1844(0.5934) 0.1736 (0.0641) Flat Rolling -2.4303 (0.5871)NC 3 Mountainous -4.0785(0.5741) 0.1858 (0.0621) UT 1 All -4.1217(0.6231) 0.4414 (0.0742) Flat -4.4878(1.5295) RollingUT 2 Mountainous -3.4508 (1.5013) 0.3900 (0.1754) WA 1 All -12.7417(1.9219) 1.2066 (0.2028) Flat -12.9945(1.9091) RollingWA 2 Mountainous -11.8326 (1.8894) 1.1398 (0.1987) Flat -14.1608(2.1029) RollingWA 3 Mountainous -13.2591 (2.0800) 1.2721 (0.2153) 0.1244 (0.0775) Table 13. SPFs for rural multilane roadways. conditions. The variables found to be significant at the 10% level varied by state were: AADT: Annual average daily traffic SURFWID: Total surface width (feet) LANEWID: Average lane width (feet) HI: Average degree of curvature SPEED: Posted speed in North Carolina & design speed in California (mph) MEDWID: Median width (feet) MEDTYPE: Positive barrier or unprotected For application in another state, or even for application in the same four states for different years from those in the calibration data, the models should be recalibrated to re- flect differences across time and space in factors such as collision reporting practices, weather, driver demograph- ics, and wildlife movements. In essence, recalibration involves using a multiplier, which is estimated to reflect these differences by first using the models to predict the number of collisions for a sample of sites for the new state or time period. The sum of the collisions for those sites is divided by the sum of the model predictions to derive the
38 Model Form: Total wildlifeâvehicle collisions/mile-year = MEDTYPESURFWIDHIMEDWIDAADT 5432exp1State/Model Terrain ln (s.e.) 1 (s.e.) 2 (s.e.) 3 (s.e.) 4 (s.e.) 5 (s.e.) Dispersion parameter Flat -6.2814(0.7166) RollingCA 1 Mountainous -4.7526 (0.7098) 0.2810 (0.0726) 1.5885 Flat -5.6746(0.6925) RollingCA 2 Mountainous -4.3198 (0.6857) 0.3050 (0.0700) -0.0126 (0.0014) 1.3543 UT 1 All -4.3930(1.4121) 0.4356 (0.1550) 1.9966 Flat -7.8707(1.4831) Rolling -6.9760(1.4811)UT 2 Mountainous -6.0374(1.4516) 0.7272 (0.1632) 1.5641 Flat 8.0592(1.4808) Rolling -7.1234(1.4773) UT 3 Mountainous -6.0651(1.4465) 0.7472 (0.1630) Median Type Positive barrier -1.0633 (0.4623) Unprotected 0.0000 1.5277 WA 1 All -15.5153(1.7866) 1.3969 (0.1809) 0.8816 Flat -16.8612(1.7977) Rolling -15.8572(1.7634)WA 2 Mountainous -15.4443(1.7846) 1.4355 (0.1784) 0.7807 Flat -9.9014(3.9034) Rolling -8.8909(3.8877)WA 3 Mountainous -8.4610(3.8975) 1.4507 (0.1793) -0.1483 (0.0765) 0.7867 Table 14. SPFs for rural freeways. multiplier. Further details of this procedure are provided in Appendix B. In deciding which among available competing models is best to adopt for another state for which a similar model may not be available, goodness-of-fit tests must be conducted. Choosing the most appropriate model is especially important because the exponents for AADT, by far the most dominant variable, differ so much between states. A discussion of these tests is provided in a recent FHWA report.241 A summary is presented as part of Appendix B. Aspect 2: Comparison of WildlifeâVehicle Collision and Carcass Removal Data The findings from this aspect of the safety analysis focused on the challenges related to combining WVC and deer carcass removal data on a roadway network within a GIS platform. This information is useful because it helps define where the WVC and deer carcass removal data were reported or collected, and whether the occurrence of either is actually over- or under-represented along roadways with particular charac- teristics. In addition, the results of visual and quantitative WVCs, and deer carcass removal comparisons (statewide, example corridor, and model content) are described. In general, the amount of two-lane roadway mileage used in the modeling was almost 5 times greater than the multilane roadway mileage (See Table 11). Two-lane roadways with medians were not included. The multilane database included all State Routes, U.S. Highways, or Interstate highways with more than two through lanes. Overall, despite the propor- tions of roadway mileage in the database, approximately two WVCs were reported along the two-lane roadways for every
39 WVC reported along the multilane roadways. Similarly, the number of deer carcasses removed from two-lane roadways was about 1.4 times that removed from the multilane road- ways. The mean number of WVCs and carcass removals per mile-year, however, along the multilane roadways in the database are much greater than those along the two-lane roadways. Additionally, the AADT along the multilane rural roadways was also greater than the two-lane roadways. WVC and deer carcass removal GIS activities. There are a number of advantages when information is incorporated into a GIS platform, including an increased ability to organ- ize and integrate spatial data, the relatively easy presentation of the data, and the capability to quickly analyze and/or com- pare one or more datasets. Visual patterns are also easier to discern, and data can be assembled from multiple sources and formats to produce broader and more rigorous evaluation ac- tivities. The GIS process in a safety data project is typically composed of three steps: (1) data acquisition and importa- tion, (2) data management, and (3) spatial analysis. The first steps are often the most difficult. The general objective of the GIS activities in this aspect of the safety data analysis was to combine and document spatial rep- resentations of the WVC and deer carcass removal locations. Deer carcass removal data and locations are not normally avail- able in any consistent manner across jurisdictions. In this study, the carcass reports included route and milepost to reference locations of deer carcasses to the road network. To geo-code these records, the research team obtained the location of the mileposts from the Iowa State University Center for Trans- portation and Education (CTRE). This information was devel- oped from different DOT data sources and combined with a GIS data set. The WVC data were relatively easy to incorporate into the GIS platform because latitude and longitude coordinate positions for each incident were available. The spatial accuracy of the carcass removal locations was different; they were esti- mated to the nearest 0.1 milepost. In addition, the individual whole milepost locations (e.g., 1.0, 2.0, etc.) on the Iowa road- way GIS map were the only spatial data connection that would allow the plotting of the deer carcass removal locations. For schedule and budget reasons, therefore, the estimated locations of the deer carcass removals were rounded to the nearest milepost, summed, and plotted. The total number of deer carcass removals in 2002 is plot- ted in Figure 4 at each milepost (with scaled and shaded circles to represent the different number at each location). This spatial modification was considered appropriate given the accuracy of the datasets provided, the objective of this work (i.e., a comparison of data as they might be available to a decision maker), and the WVC and carcass removal data likely to be available within other states. The impact of this spatial alteration on the results of the comparisons and modeling activities in this research are noted below. The statistics in Table 10 might also be used for gross compari- son purposes to roadway segments of interest with similar characteristics. A review of the percentages by roadway sys- tem reveals that the deer carcass removal data are primarily from the interstates, U.S. Highways, and State Routes. This trend is not surprising because the data provided was from the IaDOT. About 80% of the WVC reported, on the other hand, occurred on U.S. Highways, State Routes, and farm to market roadways. The percentage of WVCs and carcasses removed along interstates, U.S. Highways, and State Routes are much greater than their statewide roadway mileage would suggest. For every reported WVC along the interstate, there were more than three carcasses collected. Table 10 shows that the percentage of urban and rural roadway mileage is essentially the same as the percentage of WVCs and deer carcass removals in these areas. From a roadway mileage point of view, the number of WVCs and deer carcass removals also appears to be over-represented along four- lane roadways. More than 90% of the WVCs and deer carcass removals from 2001 to 2003 occurred along two- and four- lane roadways. Statewide and sample corridor comparisons. The avail- ability of WVC and deer carcass removal data in Iowa within a GIS platform that contains information about the Iowa roadway network allowed a relatively easy comparison and calculation of various safety measures related to each dataset. Statewide WVC and deer carcass removal frequencies and rates are shown in Table 15 for the 3-year analysis time period as are the combined number of deer carcasses removed by the IaDOT and those sal- vaged through the Iowa Department of National Resources (IaDNR). About 34% of roadside deer carcasses are salvaged under permit from the state. Sixty-six percent of the roadside deer carcasses are removed by IaDOT and their location noted (these are the removals plotted in Figures 4 and 5). According to the IaDNR, the roadway locations for the deer carcasses it permits for salvage are not consistently collected and should therefore not be used for analysis. The numbers in Table 15 are general statewide measures and when recalculated for individual roadway segments are often different (Table 16). The data in Table 15 illustrate three statewide databases that provide different values for the WVC data in Iowa. The number of deer carcasses removed by IaDOT, for example, is approximately 1.09 times greater than the number of WVCs reported to the police. The number of salvaged and unsalvaged deer carcasses, on the other hand, is approximately 1.66 times greater. The other safety measures show a similar trend. However, only the WVCs and deer car- cass removals in Table 15 are related to roadway location in Iowa, and typically the location of the latter is not known. The plots in Figures 4 and 5 show that the spatial patterns of the
40 Metricsa WVC CarcassRemovalsb Salvaged and Unsalvaged Deer Carcassesc Total 23,094 25,258 38,283 Rate per Year 7,698 8,419 12,761 Rate per Roadway Mile 0.20 0.22 0.34 Rate per Hundred Million Vehicle-Miles-of-Travel 25.3 27.6 41.9 a Statewide roadway mileage and vehicle-miles-of-travel used in all calculations. b Deer carcass removals are those recorded and summarized by the Iowa DOT by location. c Salvaged and unsalvaged deer carcasses are summarized by the Iowa Department of National Resources. The Department of Transportation deer carcass removals are a portion of this total, but they are the only removals for which roadway location is known. Table 15. Statewide wildlifeâvehicle collision and deer carcass removal metrics (2001 to 2003). Figure 5. Deer carcass removal and WVC locations along segments of Interstate 80 and U.S. Highway 18 (2002). WVC and deer carcass removal data are also different. It is not likely that this conclusion will change if the data were plotted differently. The use of different databases could lead to different statewide policy and corridor-level decisions related to WVCs. In addition, the choice of the database used could lead to different conclusions. Figure 5 shows the reported WVCs and deer carcass removals for sample roadway segments along Interstate 80 and U.S. Highway 18 in Iowa. Note that no WVCs were reported along this segment of U.S. Highway 18 in 2002. A more detailed summary of the WVCs and deer carcass removals along these two segments is shown in Table 16. These measures could be compared to the statewide results in Table 15 and/or those calculated for roadways with similar characteristics (See Table 10). The results of this type of general comparison can be used as a filter to determine whether a particular roadway segment needs more detailed consideration. Figures 4 and 5 generally show that reported WVCs and deer carcass removal data (as available) likely have different spatial patterns. This lack of similarity could lead to the implementation of countermea- sures along different roadway segments. Table 16 summarizes the WVC and deer carcass removal data from 2001 to 2003 for the roadway segments shown in Figure 5. The differences in the magnitude of the WVCs and deer carcass removals that occur along these roadway segments are clear. Overall, the number of carcasses removed along the Interstate 80 segment was 8.6 times greater than the number of WVCs reported. The number of carcasses collected along U.S. Highway 18, on the other hand, was 3.8 times greater than the number of re- ported WVCs. More than 90% of the Interstate 80 segment length sum- marized in Table 14 (and shown in Figure 5) was classified as a four-lane rural freeway. The frequencies and rates in Table 16 are all generally greater than the statewide measures for a roadway with these characteristics. Only the use of a WVC rate
41 Variable Rates I-80 Wildlifeâ Vehicle Collisions (8.4 Mi) I-80 Deer Carcass Removals (8.4 Mi) U.S. Hwy 18 Wildlifeâ Vehicle Collisions (9.9 Mi) U.S. Hwy 18 Deer Carcass Removals (9.9 Mi) Total Number 19.0 163.0 5.0 19.0 Rate / Year 6.3 54.3 1.7 6.3 Rate / Roadway Mile 2.3 19.3 0.51 1.9 Rate / Hundred Million Vehicle-Miles-of-Travel 10.4 89.6 17.2 65.4 Note: See Figure 5 for plots of 2002 wildlifeâvehicle collisions and deer carcass removals along these segments in Iowa. Table 16. Comparison of roadway segment WVC and deer carcass removal measures (2001 to 2003). might lead to the conclusion that this segment has a typical WVC data level. The U.S. Highway 18 segment in Figure 5 is primarily a two-lane rural roadway. Mixed conclusions result when the WVC and deer carcass removal measures for this roadway (See Table 16) are compared to relevant statewide measures. The WVCs and deer carcasses removals per mile along the segment are larger than the statewide measures, but the rates (based on volume) are both smaller than those cal- culated for the entire state. Clearly, the choice of the data (WVCs or deer carcass removals) and the measures (e.g., per mile or rate) that are used impacts whether a particular road- way segment might be identified for closer consideration. The comparisons described above consider average values, but more critical WVC frequency or rate data could be used as an initial step to identify hotspot roadway segments. WVC and deer carcass removal model development and comparison. Prediction models using WVC, deer carcass re- moval, and roadway cross section data from Iowa were developed to assist in the identification of potential hotspot roadway segments and are described next. They can be applied in a manner similar to those described previously in this report. This section of the safety analysis report focuses on the differ- ences between the models developed with the WVC and deer carcass removal data and the potential impact of those differ- ences. A site visit to each potential âhighâ collision or carcass segment is necessary for confirmation purposes and the iden- tification of specific countermeasure installation locations. The combination of WVC, deer carcass removal, and road- way location data in a GIS platform allowed the production of prediction models to describe the relationships between the oc- currence of a WVC or carcass removal and several roadway cross section characteristics typically available through DOT databases. These analyses applied to rural paved two-lane and multilane roadways in Iowa with a State Route, U.S. Highway, or Interstate designation. They can be applied within an empirical Bayesian approach. The negative binomial models or SPFs were created from 2001, 2002, and 2003 data to predict WVCs or deer carcass removals per mile-year. Details of the rural two-lane and multilane models are shown in Tables 17 and 18. Prediction (not causal) models with only AADT are provided later in this section. Volume-only models were developed for comparison and application purposes. The vari- ables considered for use in each of the models were selected from the Iowa roadway cross section database (which included more than 90 factors). The following variables, which came from the IaDOT database, were considered: AADT: Annual average daily traffic on roadway (vehicles per day in both directions) AVGSHLD: Average of left- and right-shoulder widths on two-lane roadways CRASHES: Number of police-reported animal-vehicle collisions (used in one model for deer carcass removal prediction) LANES: Total number of through lanes present LSHDWID: Width of the left side or inside shoulder (nearest foot) MEDTYPE: Classified as zero (0) if unprotected or 1 if a positive barrier MEDWID: Width of the median between the edges of traffic lanes (nearest foot) RSHDWID: Width of the right side or outside shoulder (nearest foot) SPEED: Posted speed in miles per hour SURFWID: Surface width of roadway measured from edge of pavement to edge of pavement (feet) The form and content of the WVC and deer carcass re- moval prediction models developed for rural two-lane road- ways in Iowa are shown in Table 17. Two models were devel- oped for both WVCs and deer carcass removals with different sets of independent variables. Both models are provided be- cause they produce similar results, but have different input variables, which may make them useful to different practi- tioners. The variables in the models include AADT, SPEED, and AVGSHLD; for one deer carcass removal model, the num-
42 Model Form: Total WVCs or deer carcass removals per mile-year = CRASHESSPEEDAVGSHLDAADT 432exp1ModelDependent Variable ln( )a (s.e.) 1 (s.e.) 2 (s.e.) 3 (s.e.) 4 (s.e.) Dispersion Parameter WVCs/ Mile-Year -5.9203 (0.2088) 0.6164 (0.0283) 0.0193 (0.0067) 1.0179 WVCs/ Mile-Year -6.4968 (0.3807) 0.6429 (0.0268) 0.0095 (0.0059) 1.0196 Deer Carcass Removals/ Mile-Year -5.4332 (0.2957) 0.5784 (0.0403) 0.0677 (0.0096) 5.2702 Deer Carcass Removals/ Mile-Year -4.9635 (0.2954) 0.4890 (0.0405) 0.0701 (0.0096) 0.2714 (0.0225) 5.0062 a These symbols represent the parameters estimated in the modeling process and that measure the impact of each independent variable on the expected crash frequency. Table 17. Models for rural two-lane roadways (segments > 0.1 mi) in Iowa. Model Form: Total WVCs or deer carcass removals per mile-year = CRASHESMEDTYPEMEDWIDAVGSHLDAADT 5432exp1Model Dependent Variable ln( ) (s.e.) 1(s.e.) 2(s.e.) 3 (s.e.) 4 (s.e.) 5 (s.e.) Dispersion Parameter WVCs/ Mile-Year -0.9021 (0.3905) 0.0527 (0.0391) 0.0390 (0.0205) With Median Barrier: -0.2471 (0.0851) Unprotected: 0.0000 0.6360 Deer Carcass Removals/ Mile-Year -4.6677 (0.5972) 0.5616 (0.0660) 0.0017 (0.0011) 7.8601 Deer Carcass Removals/ Mile-Year -4.3118 (0.5851) 0.4871 (0.0637) 0.3314 (0.0385) 7.2680 Table 18. Models for rural multilane roadways (segments >_ 0.1 mi) in Iowa. ber of reported WVCs was included. The model coefficients for all models are shown in Table 17 along with their standard error and the model dispersion parameter. The impact of the variables in each model is somewhat different, and the ex- planatory value of the WVC model appears to be greater than the deer carcass removal model. The large dispersion parame- ter of the deer carcass removal model is high, which should be considered if it is applied. Given that most jurisdictions do not have deer carcass removal data by location, it is encouraging that the CRASHES data may be used as a predictor of carcasses. Thus, if carcass data could be collected even for a subset of the roadways in a jurisdiction, a model that included reported col- lisions to predict carcasses could be recalibrated and applied. The differences in these models further support the conclusion that the use of WVC or deer carcass removal data can result in the identification of different roadway segments for potential countermeasure implementation. Of course, some of the dif- ferences shown in Table 17 are due to the differences in the spa- tial accuracy of the information provided for the two databases and ultimately plotted in the GIS platform. These accuracies, however, are typical. Similar WVC and deer carcass removal prediction models were also developed for rural multilane roadways in Iowa. The model coefficients for these models are shown in Table 18 as are their standard errors and the model dispersion parame- ters. There are more differences in these models than those produced for the two-lane rural roadways. The models in Table 18 contain different variables. The models include one or more of the AADT, AVGSHLD, MEDTYPE, and MEDWID predictor variables. As with the two-lane models, the number of WVCs could also prove to be a useful predic- tor of deer carcass removal frequency. The results of this
43 Model Form: Total wildlifeâvehicle collisions or deer carcass removals per mile-year = 1AADTModel Dependent Variable ln( ) (s.e.) 1 (s.e.) Dispersion Parameter Rural Two-Lane Roadway WVCs/ Mile-Year -5.9894 (0.2077) 0.6439 (0.0268) 1.0204 Deer Carcass Removals/ Mile-Year -5.5973 (0.2952) 0.6662 (0.0384) 5.3432 Rural Multilane Roadways WVCs/ Mile-Year -1.2494 (0.2985) 0.1199 (0.0321) 0.6381 Deer Carcass Removals/ Mile-Year -4.8520 (0.5923) 0.5919 (0.0640) 7.8791 Table 19. Volume-only models (segments > 0.1 mi) in Iowa. 0.00 0.50 1.00 1.50 2.00 2.50 0 2000 4000 6000 8000 10000 12000 14000 Average Annual Daily Traffic W VC s or D ee r C ar ca ss R em ov al s Pe r M ile -Y ea r WVCs Deer Carcass Removals Figure 6. Two-lane rural roadway volume-only model results. model development activity further support the importance of choosing the appropriate database to evaluate collision problem locations. The dispersion parameter of the deer car- cass removal model is high, which should be considered in the application of this model. Finally, WVC and deer carcass removal models, with AADT as the only input variable, were also developed. These models are shown in Table 19. They were created for applica- tion if the data for the roadway cross section variables in the previous models were not available. In addition, the volume- only models were compared to the other models to investi- gate the additional explanatory value offered by the addition of more road cross section variables. A comparison of the dis- persion parameters with those in Tables 17 and 18 reveals that the inclusion of other roadway cross section variables in the models adds little to the predictive strength of the WVC and deer carcass removal models. In other words, the AADT measure contains most of the explanatory value of these models. Overall, the explanatory value of the WVC models with only AADT is still better than those developed with deer carcass removal data. Some of this difference, as previously stated, is due to the inconsistency in the location accuracy of the two datasets. The high dispersion parameters of the deer carcass removal models in Table 19 should be noted. Figures 6 and 7 plot the AADT (volume-only) deer car- cass removal and WVC models in Table 19 for two-lane and multilane rural roadways, respectively. Because AADT is the only independent variable, a simple comparison shows that the models diverge as AADT increases, dramat- ically so for multilane roadways. These plots illustrate that the deer carcass removal and WVC frequencies predicted are different and not strictly linearly correlated. The avail- ability of WVC data throughout the United States led the research team to ask whether the volume-only WVC mod- els might be recalibrated to predict deer carcass removals. To do so, the volume-only WVC models were applied to the deer carcass removal database. The sum of the observed deer carcass removals was then divided by the sum of the predictions from the WVC model. This factor was applied as a multiplier to the WVC volume-only model and the deer carcass removal predictions were recalculated and compared (See Figure 6 and Figure 7). This comparison was completed separately for the two-lane and multilane rural roadway data.
44 WVCs Deer Carcass Removals 0.00 1.00 2.00 3.00 4.00 5.00 6.00 7.00 0 20000 40000 60000 80000 100000 Average Annual Daily Traffic W VC s or D ee r C ar ca ss Re m ov al s pe r M ile -Y ea r Figure 7. Multilane rural roadway volume-only model results. -400.00 -300.00 -200.00 -100.00 0.00 100.00 200.00 300.00 400.00 0 40002000 6000 8000 12000 1400010000 Average Annual Daily Traffic Cu m ul at iv e De er C ar ca ss R em ov al R es id ua ls WVC Recalc. Minus 2 Std. Dev. Plus 2 Std. Dev. Figure 8. Cumulative residuals for two-lane rural roadway volume-only WVC model recalibrated and applied to deer carcass removals. Cumulative residual (CURE) plots were used to assess how well the models (SPFs) performed for all values of AADT. To construct a CURE plot the data are sorted in ascending order of the variable of interest and the cumulative residuals (observed minus predicted frequencies) are plotted on the y-axis with the x-axis being the values of the variable of inter- est. Also plotted are the ±2Ï standard deviation limits. These limits are calculated based on the assumption that the sum of residuals for the model is approximately normally distributed with the mean equal to 0. If the plot of cumulative residuals is outside these limits then the SPF can be concluded to be pre- dicting poorly within that range of the independent variable. Figure 8 indicates that for rural two-lane roadways the volume-only WVC model performed reasonably well for predicting the mean deer carcass removal frequency if it can be recalibrated. The cumulative residual plotted is generally between the two standard deviation curves. For site-specific estimates, it is still important to have a record of the number of deer carcass removals to combine with the prediction in the EB framework to provide good estimates of the long-term expected deer carcass removal frequency. The dispersion parameters of the deer carcass removal models show that these data are much more overdispersed than the WVC data. This difference rein- forces the need for deer carcass removal data at the site level. Figure 9, on the other hand, shows that for multilane rural road- ways, the recalibrated volume-only WVC model does not perform well. The cumulative residuals show that the model overpredicts for AADT less than approximately 15,000 vehicles per day and then underpredicts for higher AADT. The CURE plot deviates well outside two standard deviations. Interpretation, Appraisal, and Applications Aspect 1: Application of Reported WildlifeâVehicle Collision Data As they stand, the primary application of the models is for the safety management of existing roads as opposed to design or planning applications for new or newly built roads. For existing
45 Annual Average Daily Traffic Cu m ul at iv e De er C ar ca ss R em ov al R es id ua ls -1600.00 -1400.00 -1200.00 -1000.00 -800.00 -600.00 -400.00 -200.00 0.00 200.00 400.00 0 10000 20000 30000 40000 50000 60000 70000 80000 90000 WVC Recalc. Minus 2 Std. Dev. Plus 2 Std. Dev. Figure 9. Cumulative residuals for multilane rural roadway volume-only WVC model recalibrated and applied to deer carcass removals. roads, WVC data are available and used, along with the model predictions in an empirical Bayes procedure to estimate the ex- pected long-term mean collision frequency of a specific roadway segment. The following three types of model applications, which would be most relevant to the development of the desired guide- lines, are summarized and illustrated in the sections to follow: ⢠Network screening to identify roadway segments that may be good candidates for WVC countermeasures, ⢠Evaluation of the effectiveness of implemented counter- measures, and ⢠Estimation of the cost effectiveness of potential counter- measures. Network screening to identify roadway segments that may be good candidates for wildlifeâvehicle collision coun- termeasures. Two fundamental methodologies are pre- sented and illustrated for this application: ⢠Identifying and ranking sites based on a high expected frequency of WVCs, and ⢠Identifying and ranking sites based on a high proportion of WVCs SPFs are used in the first application. The second applies for situations where an SPF may not be available or applicable. Identifying and ranking sites based on a high long-term fre- quency of wildlifeâvehicle collisions. As noted earlier, the short- term collision count at a location is not a good estimate of its safety. Thus, identifying and ranking collision-prone locations based on short-term counts will be inaccurate. Longer term collision frequency data are now recognized as the best basis for identifying and ranking these locations. The long-term frequency of WVC data at a site is obtained by using the EB methodology that combines the siteâs WVC frequency with the frequency expected by applying the SPFs described earlier. In this approach, overlapping segments of equal length should be considered in what is often termed a âsliding windowâ approach. A brief overview of the method is provided with an example calculation. When the SafetyAn- alyst (www.safetyanalyst.org) software becomes available, there will be a facility to consider segments of different length using a sophisticated âpeak searchingâ algorithm. In the EB procedure, the SPF is used to first estimate the number of collisions that would be expected at locations with traffic volumes and other characteristics similar to the ones being analyzed. The estimate (P) is then combined with the count of collisions (x) observed to obtain an estimate of the expected number of collisions (m). This estimate of m is: m = w1(x) = w2(P), where the weights (w1 and w2) are estimated from the mean and variance of the SPF estimate as: w1 = P/(P + 1/k) w2 = 1/k/(P + 1/k), and where k is the dispersion parameter for a given model and is estimated from the SPF calibration process with the use of a maximum likelihood procedure. In this process, a negative binomial distributed error structure is assumed with k being the dispersion parameter of the distribution. For network screening purposes, each segment is then ranked in descend- ing order by the expected number of collisions (m). As an illustration, suppose that the two-lane rural roads in Utah are divided into 1-mi WVC segments that may or may not overlap. Consider one such segment for which the fol- lowing information applies: ⢠Length = 1 mi (1.6 km) ⢠Years of data = 16
46 Site Rank by EB Method Rank by Proportions Method 11430 1 9 10194 2 6 9463 3 3 10336 4 48 11546 5 11 9947 6 4 9154 7 2 10177 8 5 6749 9 1 6716 10 35 11545 11 19 11554 12 12 10195 13 7 10197 14 8 11432 15 47 6697 16 28 9477 17 920 10673 18 18 6752 19 80 6694 20 86 Table 20. Comparison of alternative ranking methods. ⢠WVCs observed = 40 ⢠Average AADT = 2,066 First, the UT 1 model from Table 12 is used for this example to calculate the regression estimate (P). Next, the weights (w1 and w2) are calculated. w1 = 4.36/(4.36 + 1/1.7610) = 0.88 w2 = 1/1.7610/(4.36 + 1/1.7610) = 0.12 Last, the regression estimate (P) and the observed collision count (x) are combined. m = 0.88(40) + 0.12(4.36) = 35.72 The EB estimate of the expected number of collisions dur- ing the 16-year period is 35.72, lower than the observed count of 40. This EB estimate is used in ranking this location rela- tive to the other 1-mi segments. Identifying and ranking sites based on a high proportion of wildlifeâvehicle collisions. Where traffic volume and other characteristics necessary to estimate the expected colli- sion frequency at a site are unavailable, identifying sites with a high proportion of WVCs might be appropriate. This method uses the observed counts for WVCs and all collisions at a site but adjusts for the ânoiseâ in each of these counts. For example, one is more certain that the proportion is high for a site with 20 WVCs out of 30 collisions than for a site with 2 WVCs out of 3 collisions. The theory behind this method is described in Appendix C. Of particular note is that the method only requires the counts of WVCs and all collisions at sites to be screened (i.e., SPFs are not required). This method is also being implemented in SafetyAnalyst. By way of illustration, the Utah two-lane rural roadway dataset is used. The data were manipulated into 1-mi long segments, although any desired length could be considered. All sites were ranked by the two methods. The top 20 sites ranked using the EB estimate of mean WVC frequency out- lined earlier are presented in Table 20. The same segments were also screened based on the prob- ability that their proportion of WVCs is greater than 20.7%, the mean proportion for all segments. The rankings from this âproportionsâ method are shown in the last column of Table 20. As seen, seven of the top ten segments identified by the EB method were also in the top ten ranked by the proportions method. Thirteen of the top twenty seg- ments identified by the EB method were also in the top twenty ranked by the proportions method. It appears that ranking by a high proportion of WVCs may be a reasonable P = â =( )( )exp( . )( , ) ..16 1 9 1135 2 066 4 361 0237 P = ( )( ) ( )years length AADTα β1 alternative to ranking by the EB estimate of WVCs if the required data or resources are not available for developing or applying SPFs. Evaluation of the safety effectiveness of implemented countermeasures, specifically the installation of animal crossings. The methodology for the conduct of a proper observational before-after study is well documented in a landmark book by Hauer.114 The statistically defendable before-after analysis methodology proposed overcomes the difficulties associated with simple before-after comparisons of collision counts. The proposed methodology: ⢠Properly accounts for regression-to-the-mean, ⢠Overcomes the difficulties of using collision rates in nor- malizing for traffic volume differences between the before and after periods, ⢠Reduces the level of uncertainty in the estimates of safety effects, ⢠Provides a foundation for developing guidelines for esti- mating the likely safety consequences of installing a cross- ing and fencing, and ⢠Properly accounts for differences in collision experience and reporting practice in amalgamating data and results from diverse jurisdictions. The task is to estimate what was the effect on safety of installing wildlife crossing measures. In this, âsafetyâ is the expected number of WVCs per unit of time for a road seg- ment of interest. This estimate requires three steps:
47 1. Predict what safety would have been during the âafterâ pe- riod, had the status quo been maintained, 2. Estimate what safety was during the after period with crossing measures in place, and 3. Compare the two. The following approach to Step 1 (predicting what safety would have been during the after period had the status quo been maintained) is suggested: ⢠Account explicitly for the effect of changes in traffic flow by using an SPF; ⢠Account for the effect of weather, demography, and other variables by using a comparison group to recalibrate the SPFs to be used; and ⢠Account for possible selection bias (regression-to-the-mean effects) and improve estimation accuracy by the EB method using the best available methodology.114 In the EB approach, the change in safety for a given colli- sion type is given by: λâÏ where λ is the expected number of collisions that would have occurred during the after period without the crossing measures and Ï is the number of reported collisions during the after period. In estimating λ, the effects of regression to the mean and changes in traffic volume are explicitly accounted for by using SPFs relating collisions of different types and severities to traffic flow and other relevant factors for each jurisdiction based on locations without crossing measures. The exposure of animals to the roadway is not accounted for. In the EB procedure, the SPF is used to first estimate the number of collisions that would be expected during the before period at locations with traffic volumes and other characteristics similar to the one being analyzed. The esti- mate (P) is then combined with the count of collisions (x) during the before period at a treatment site to obtain an es- timate of the expected number of collisions (m) before the crossing measures were installed. This process is identical to that presented earlier, but is repeated here for completeness. This estimate of m is: m = w1(x) + w2(P) where the weights (w1 and w2) are estimated from the mean and variance of the SPF estimate as: w1 = P/(P + 1/k) w2 = 1/k/(P + 1/k) and where k is the dispersion parameter for a given model and is estimated from the SPF calibration process with the use of a maximum likelihood procedure. In that process, a negative bi- nomial distributed error structure is assumed with k being the dispersion parameter of this distribution. The variance of the estimate (m) is: Var(m) = ((x + 1/k)P2)/(1/k + P)2 A factor f is then applied to m to account for the length of the after period and differences in traffic volumes between the before and after periods. This factor is the value of the SPF prediction for the after period divided by P: f = sum of SPF predictions post treatment/P The result, after applying this factor, is an estimate of λ. The procedure also produces an estimate of the variance of λ. Var(λ) = (f/P)2Var(m) The estimate of λ is then summed over all locations in a treat- ment group of interest (to obtain λsum) and compared with the count of collisions during the after period in that group (Ïsum). The variance of λ is also summed over all sections in the treatment group. The Index of Effectiveness (θ) is estimated as: θ = (Ïsum/λsum) / {1 +[Var(λsum)/(λsum2]} The standard deviation of θ is given by: Stddev(θ) = [θ2{[Var(Ïsum)/Ïsum2] + [Var(λsum)/(λsum2]}/[1 + Var(λsum)/λsum2]2]0.5 The percent change in collisions is in fact 100(1 â θ); thus, a value of θ = 0.7 with a standard deviation of 0.12 indicates a 30% reduction in collisions with a standard deviation of 12%. As an illustration of the method, Table 21 presents the re- sults of an analysis for two sites located in Utah (U.S. Hwy 40 between mileposts 4.0 and 8.0, and Utah Route 248 between mileposts 3.3 and 13.5). Each site involved the construction of one or more at-grade wildlife crossings and continuous exclusion fencing that extended beyond the limits of the crossings themselves. Note that the roadway inventory data has divided these sections of the road into multiple subseg- ments due to differences in number of lanes, AADT, and other variables. The results for the demonstrative case indicate a WVC reduction of: (1 â 0.702) * 100 = 29.8% with a standard error of 9.1% Note that this result is based on only two sites in one state and thus should not be used as conclusive evidence of the safety benefits of installing wildlife crossings and fencing. Estimation of the cost effectiveness of a potential coun- termeasure, such as a crossing. The objective is to pro- vide designers and planners with a guide to estimate the change in WVC frequency expected with the installation of
48 Site No. of Lanes Length Years Before Years After AADT Before AADT After Crashes Before (x) Crashes After ( ) Sum of SPF Predictions After k w1 w2 m Var (m) Var ( ) 1 4 2.04 9 6 7654 13227 39 18 18.85 1.53 0.97 0.03 38.52 32.69 37.42 26.96 1 4 1.96 9 6 7450 13227 45 47 18.11 1.53 0.97 0.03 44.28 38.04 42.96 31.69 2 2 0.05 4 6 2630 7493 1 1 0.36 1.76 0.13 0.87 0.20 0.87 0.03 0.48 2 2 0.19 4 6 2630 7493 0 0 1.37 1.76 0.36 0.64 0.20 0.88 0.07 1.38 2 2 0.58 4 6 2630 7493 2 5 4.19 1.76 0.63 0.37 1.61 7.06 1.01 19.39 2 3 0.18 4 6 2630 7493 0 2 1.30 1.76 0.34 0.66 0.19 0.85 0.07 1.28 2 4 0.21 4 6 2630 7493 3 2 1.24 1.53 0.44 0.56 1.62 3.86 0.72 4.07 2 4 0.12 4 6 2553 7493 3 2 0.71 1.53 0.31 0.69 1.13 2.73 0.35 2.04 2 4 1.40 4 6 1707 3375 3 6 5.80 1.53 0.81 0.19 2.97 6.03 2.42 9.95 2 4 0.07 4 6 1707 3375 0 0 0.29 1.53 0.18 0.82 0.12 0.24 0.02 0.09 2 4 0.42 4 6 1707 3375 4 2 1.74 1.53 0.57 0.43 2.64 5.36 1.50 6.17 2 3 2.70 4 6 1707 3375 16 17 8.62 1.76 0.83 0.17 13.82 41.66 11.53 104.77 2 4 0.34 4 6 1707 3375 8 2 1.41 1.53 0.52 0.48 4.47 9.05 2.30 9.46 2 4 0.08 4 6 1707 3375 0 1 0.33 1.53 0.20 0.80 0.13 0.26 0.03 0.11 2 3 3.09 4 6 1707 3375 10 21 9.86 1.76 0.85 0.15 9.00 27.14 7.67 69.71 2 2 0.77 4 6 1707 3375 0 0 2.46 1.76 0.59 0.41 0.33 1.01 0.20 1.79 SUM 126 121.26 177.74 289.36 0.702 VAR( ) 0.008 S.E.( ) 0.091 Table 21. Illustration of EB before-after study for U.S. Highway 40 and Utah Route 248 in Utah.
49 wildlife crossings and fencing at a segment of roadway under consideration. For the approach, an SPF representative of the existing road segment is required. Therefore, an SPF must already exist for the jurisdiction or data must be available to enable a recalibration of a model calibrated for another jurisdiction. The SPF would be used, along with the segmentâs collision history, in the EB procedure to estimate the expected collision frequency with the status quo in place; that estimate of colli- sion frequency would then be compared to the expected frequency if a crossing and fencing were constructed in order to estimate their benefits. This model application requires four steps: 1. Assemble data and collision prediction models for road segments: a. Obtain the count of WVCs; b. For each year, obtain or estimate the average AADT; and c. Estimate the AADT that would prevail for the period immediately after construction. 2. Use the EB procedure documented earlier, with the data from Step 1, and the road segment model to estimate the ex- pected annual number of WVCs that would occur without construction of the crossing and fencing. 3. Apply a Collision Modification Factor (CMF) to the ex- pected collision frequency with the status quo in place to get the expected benefit in terms of the number of annual WVC expected to be reduced. A CMF is an adjustment to the estimate based on the expected reduction in WVCs. Until a reliable CMF can be determined from properly conducted before-after studies, an interim CMF could be developed through an expert panel as has been done for other roadway safety countermeasures. 113 4. Compare against the cost, considering other impacts if desired, and using conventional economic analysis guides. The results of the analysis above may indicate that crossings are justified based on a consideration of safety benefits. This justification should not be taken to mean that crossings should be constructed, because: a. Other measures may have higher priority in terms of cost effectiveness, b. The safety benefits may need to be assessed in the light of other impacts, and c. Other locations may be more deserving of a crossing. In other words, the results of the above analysis should be fed into the safety resource allocation process. As an illustration, suppose a 2-mi long section of road, with data from 1998 to 2002, is being considered for the con- struction of a wildlife crossing and fencing along the entire section. This section experienced 18 WVCs during this time period. The average AADT was observed to be 5,000 and is assumed to increase by 5% following the proposed construc- tion, although this anticipated increase in traffic is not related to the contemplated construction. The SPF to be used is: Use the EB procedure to estimate the expected annual num- ber of WVCs that would occur without construction of the crossing and fencing. w1 = 6.74/(6.74 + 1/1.6098) = 0.92 w2 = 1/1.6098/(6.74 + 1/1.6098) = 0.08 Last, the regression estimate (P) and the observed collision count (x) are combined. m = 0.92(18) + 0.08(6.74) = 17.1, or 3.4/year The combination of a high dispersion parameter (k) and rel- atively long length of the segment leads to a relatively high weight being given to the SPF estimate (P). Because traffic is expected to increase 5% in the period after the contemplated construction the estimate (m) is adjusted by the ratio of the AADT term in the model: m* = 3.4*(5000 * 1.05)1.0237/(5000)1.0237 = 3.57/year An appropriate CMF is applied to the estimate (m* ) to esti- mate the expected benefit in terms of the number of annual WVCs expected to be reduced. For this illustration assume that the expected reduction is 20% (i.e., that the CMF is (100-20)/100 = 0.8). Annual Benefit = 0.20(3.57) = 0.71 wildlifeâvehicle collisions Apply the estimated cost per collision to the previously esti- mated annual WVC benefit to estimate the dollar value benefit per year. Compare this benefit against the annualized cost of construction, maintenance, and other relevant considerations. Aspect 2: Comparison of WildlifeâVehicle Collision and Carcass Removal Data The primary objective of this aspect of the safety data analy- sis was to investigate the hypothesis that the choice and appli- cation of reported WVC and carcass removal data (as they might exist and could be plotted at a DOT) could result in varying policies or WVC countermeasure-related roadway de- velopment decisions. One or both of these two databases have been used in the past to describe the magnitude of the WVC problem and to propose and evaluate the effectiveness of WVC countermeasures. Overall, the visual and quantitative findings of the reported WVC and deer carcass removal com- parison activities revealed that both their magnitudes and P = â =( )( )exp( . )( , ) ..5 2 9 1135 5 000 6 741 0237 P k= â( )( )exp( . )( ) ;.years length AADT9 1135 1 0237 = 1 6098.
50 patterns are different. This fact is important when choosing a database for public information purposes, future research ac- tivities, and countermeasure implementation/evaluation choices. The objectives of the activities and the validity of the databases available need to be considered. The GIS figures, summary data, and models developed as part of this research could be useful to the IaDOT, but require recalculation and/or recalibration for application in other states. For example, the statewide tallies and rates in Tables 15 and 16 can be used for an initial or gross comparison to the WVC or deer carcass removal experience along particular roadway segments. Potential hotspot locations for WVCs or deer carcass removals might be defined initially for further ex- amination. In the following discussion, the focus is on the im- pact of the reported WVCs and deer carcass removal compar- ison results rather than the direct application of the plots, measures, and models calculated. Some of the challenges related to combining and presenting these data in a GIS platform are also discussed. WVC and carcass removal GIS activities. The combi- nation of collision and carcass data within a GIS platform, if available by location, can be difficult. The importation of dif- ferent datasets into a GIS platform requires the definition and compatibility of the systems used to locate these data. In this project, the objective was to have WVC and deer carcass removal information in the same GIS platform for compar- ison and modeling purposes. The locations of the WVCs were available in latitude and longitude for the 3 years con- sidered, however, the deer carcass removal locations were es- timated to the nearest 0.1 milepost and, because of project constraints, could only be summed, plotted, and modeled to the nearest milepost. The deer carcass removals were plotted as proportional circles to represent the different number of removals at one location (rather than stacked), but the reported WVCs (located by latitude and longitude) were plotted individually. As noted throughout this report, these differences in accuracy and data collection did have an im- pact on the comparison results, but were not considered atypical. It is also unlikely the conclusions of this research would change if the spatial accuracy and/or plotting were more similar. However, a similar accuracy and consistency in the collection of both types of data would be desirable, but is not currently typical at DOTs. The availability of WVCs, deer carcass removals, and roadway cross section informa- tion within a GIS platform did, however, allow a relatively easy summary, comparison, and modeling of the Iowa data. Statewide, example corridor, and model comparisons. The statewide and sample transportation corridor reported WVC and deer carcass removal patterns in the GIS plots of this re- port are clearly different (Figure 4 and 5). The difference becomes more obvious along the shorter roadway segments (Figure 5). The plots and safety measures calculated as part of this project also indicate that the two databases define the mag- nitude of the animal collision problem differently. In addition, the prediction models developed for reported WVCs and deer carcass removals had different coefficients and/or input variables. The use of any of these guides to set WVC-related policies or determine potential locations for WVC counter- measures will likely produce different and possibly less efficient and effective results. The choice of safety measures (e.g., WVCs per year) may also impact the results of any comparison. It is important to understand the basis and defining criteria of the database(s) being considered. Some of the difference in the reported WVC and deer carcass removal GIS plot patterns, safety measures, and mod- els are the result of different data collection patterns and approaches (e.g., spatial accuracy and consistency). Another portion of the difference is likely because often more carcasses are removed than WVCs reported to the police (i.e., the dataset size is different). For example, WVCs that result only in prop- erty damage are reported only if an estimated minimum dollar amount of vehicle damage results (e.g., ⥠$1,000). Therefore, reported WVC data might best describe the more serious WVC events, and carcass removal data might best describe the overall number of conflicts between vehicles and animals. Unfortu- nately, the reporting of WVCs (even if the minimum property damage requirement is met) appears to vary widely from state to state and carcass removal locations are not typically collected in any consistent manner. Whether one or both datasets can or should be used within a particular state needs to be decided on a case-by-case basis. As indicated earlier, similar accuracy and consistency in the collection of both types of data are also desirable. This similarity allows the proper visual or quantita- tive combination and comparison of the databases. Conclusions and Suggested Research Ambitious objectives were set out in defining a plan of work for the safety data analysis for this project. These objectives were complementary to the overall project objectives to pro- vide guidance in the form of clearly written guidelines for the selection of crossing types, their configuration, their appro- priate location, monitoring and evaluation of crossing effec- tiveness, and maintenance. The significant progress that has been made in achieving these safety data analysis objectives is summarized as bulleted conclusions for this part of the proj- ect. Yet, further effort and consideration are needed because of limitations in data currently available to effectively address all of the objectives set out and because of the implications of some of the findings. Recommendations for further work and considerations are identified in a separate subsection.
51 Conclusions Aspect 1: Application of reported wildlifeâvehicle colli- sion data. This aspect of the work involved the develop- ment of safety performance functions and illustrated their potential applications related to the objectives of the project, rather than investigative research. Nevertheless, a few con- clusions may be drawn: ⢠Safety performance functions were successfully calibrated for four states (in addition to that calibrated for Aspect 2) to relate police-reported wildlifeâvehicle collisions to variables normally available in state DOT databases. For these func- tions, AADT was the dominant variable, with additional sig- nificant variables, such as speed, lane and shoulder width, and median type, making relatively small contributions to the explanatory power of the SPFs. ⢠The SPFs varied considerably across states in terms of the effect of the key AADT variable. ⢠The empirical Bayes procedure can be used to combine SPF predictions with WVC history to better estimate a lo- cationâs safety in accounting for key factors such as animal movements not in the SPFs. ⢠The empirical Bayes estimate can be used for screening the road network to identify candidate locations for WVC countermeasures. However, for situations where SPFs, or the resources required to calibrate them, are not available, a method that ranks locations according to their propor- tion of WVCs can produce reasonable results. An illustration was presented of the application of SPFs in an empirical Bayes before-after study of safety effective- ness of a wildlife crossing installation. Sufficient installation data were not available to enable the formal study that was envisaged. Aspect 2: Comparison of wildlifeâvehicle collision and carcass removal data. The following conclusions are based on the data combination, comparison, and analysis activities previously described. The general objective of these activities was to visually and quantitatively determine whether the use of WVC and deer carcass removal data might lead to the identification of different roadway segments for potential countermeasure implementation. ⢠Police-reported WVC and/or deerâvehicle collision (DVC) data by roadway location are available throughout the United States, but animal or deer carcass removal data by location are rarely collected and/or summarized. Carcass removal data may sometimes be available for short periods of time and/or for specific roadway seg- ments, but is not typically collected consistently through- out a state for many years. Both of these databases can be used to define the WVC problem, but the results will often differ. ⢠The WVC and deer carcass removal data used in this research was obtained from the IaDOT. These two datasets were collected with different methods and at different lev- els of accuracy. This situation is not surprising, but it did lead to some challenges related to their combination and comparison in a GIS platform. The WVC data from 2001 to 2003 was available by latitude and longitude, but the deer carcass removal locations were adjusted to the closest milepost and summed. The impacts of modifying the deer carcass removal locations on the results of this research are noted where appropriate. ⢠A quantitative summary of the 2001 to 2003 WVC and deer carcass removal data used in this research confirmed that there is a difference in their magnitude. There are more deer carcasses removed than WVCs reported. In addition, and not surprisingly, the WVC and deer carcass removal data are collected from different types of roadways. IaDOT primarily removes deer carcasses from interstates and U.S. Highways. A greater percentage of the police-reported WVCs occur on farm to market routes and local roadways. ⢠A visual comparison of statewide and regional WVC and deer carcass removal plots support the hypothesis that the data from these two databases may result in the identifica- tion of different roadway segments as potential locations of concern. A similar comparison along example segments of Interstate 80 and U.S. Highway 18 resulted in the same conclusion. A quantitative comparison of the WVC and deer carcass removal safety measures along these segments to relevant statewide calculations also supported the con- clusion that the choice of dataset (e.g., WVC or deer carcass removal) does matter. In addition, and not surprisingly, the choice of the safety measure used in the comparison also has an impact. The data used, type of safety measure calculated, and the analysis approach applied all impact how âhighâ collision locations are iden- tified. Some of the differences observed in the data and the models developed are caused by the dissimilarity in the ac- curacy and plotting approach of the WVC and deer carcass removal data used. ⢠WVC and deer carcass removal regression models were created for rural two-lane and multilane roadways. The rural two-lane and multilane roadway WVC and deer carcass removal models have different coefficients and/or variables. The results of these WVC and deer car- cass removal prediction models would be different for the same roadway segment. This difference could impact decisions related to countermeasure implementation. Overall, the WVC models generally had better explana- tory value than the deer carcass removal models, and the deer carcass removal models should be used with caution
52 due to their high overdispersion parameters. The WVC and deer carcass removal models that included only AADT did not appear to be dramatically different in their predictive capability than the models that included additional cross section variables. The proper use and calibration of these models is explained in other sections of this report. ⢠There is some potential to the use of WVC prediction models for the estimation of deer carcass removals along a roadway segment, but a suitable database of deer carcass removals needs to be available for recalibrating the WVC model. More research is needed on the value of this type of application. Recommendations Aspect 1: Application of reported wildlifeâvehicle colli- sion data. ⢠Empirical Bayes procedures, using the safety performance functions presented and police-reported WVCs (where accurate carcass removal data are unavailable), can be used for several tasks related to the project objectives: â Network screening to identify candidate roadway segments for WVC countermeasures; â Evaluation of the safety effectiveness of wildlife crossing installation and other WVC countermeasures; and â Estimation of the cost effectiveness, specifically the safety benefits, of a contemplated wildlife crossing or other WVC countermeasure. ⢠Sufficient data should be collected to enable a full study of the safety effectiveness of crossings installed, using the methodology illustrated in previous sections. A minimum of 20 installations should provide useful results. ⢠An expert panel, similar to panels conducted recently for traffic engineering countermeasures under NCHRP 17-25, should be convened to develop collision modification fac- tors for WVC countermeasures. These factors are used to estimate the safety benefits of a contemplated wildlife crossing or other WVC countermeasure. ⢠For application in states other than those for which SPFs are presented, it is most desirable to develop SPFs for that stateâs data. Where such development is not possible, an SPF from one of the four states for which SPFs are presented can be applied, but it should be recalibrated to reflect differences across time and space in factors such as collision reporting practices, weather, driver demograph- ics, and off-roadway variables such as wildlife movements. A procedure for doing this recalibration is presented in Appendix A. To determine which of the four models is best to adopt for another state, some goodness-of-fit tests will need to be conducted. A summary of these tests is presented as part of Appendix B. Aspect 2: Comparison of wildlifeâvehicle collision and carcass removal data. ⢠The use of police-reported WVCs to identify potential countermeasure locations may only define a portion of a statewide or corridor-specific wildlife collision problem. The locations identified as âhighâ reported WVC locations may not be the same as those identified as âhighâ wildlife or deer carcass removal locations. ⢠Currently, some type of police-reported animalâvehicle/ deerâvehicle collision (AVC/DVC) data is typically avail- able at every state transportation agency. The total number and location of deer carcass removals, on the other hand, are rarely collected consistently statewide. For this type of situation, the research team recommends that reported AVC/DVC data should be used if safety improvements are the primary objective, and deer or animal carcass removal data (if not available by roadway location) should be used for public education and to describe the magnitude of the animal collision problem from an ecological point of view. However, when the following recommendation is accom- plished, a more well-defined application of both databases would be desirable. ⢠The collection of statewide or corridor-specific WVCs or DVCs and large-animal carcass removal locations is rec- ommended to define the magnitude and patterns of the safety concerns related to this issue. The consistent collec- tion and plotting of both types of data with the same spa- tial accuracy is desirable. ⢠When feasible and available, both WVCs or DVCs and large-animal carcass removal locations are recommended for use in combination to help define the magnitude and patterns of this safety concern both statewide and along specific corridors. However, the double counting of animalâvehicle collisions should be avoided; e.g., deer car- cass removals should be ignored that occur at the same time and location as a reported WVC or DVC. In this case, the attributes collected with the animal or deer removal (e.g., gender, estimated age, and species) might be trans- ferred, if possible, to the reported WVC database. ⢠The models developed in this research are recommended for use only after they are appropriately calibrated and the users understand the limitations of the models. The results of these models should be appropriately applied within an em- pirical Bayesian approach. The empirical Bayesian approach and model calibration of these types of models are explained within several sections and appendices of this report. The development of AVC/DVC models with more reported and carcass removal data is also recommended. Models that ad- just for the severity (e.g., property-damage-only, injury, and fatality) of the large-animalâ or deerâvehicle collisions may also be useful (if there is enough variability in this collision characteristic). In general, it might be assumed that deer or
53 animal carcass removals that were not the result of a re- ported WVC or DVC were likely the outcome of a property- damage-only collision whose value did not require it to be reported. 3.2 Limiting Effects of Roadkill Reporting Data Due to Spatial Inaccuracy Introduction Wildlifeâvehicle collisions do not occur randomly along roads but are spatially clustered190,124,51,134 because wildlife movements tend to be associated with specific habitats, terrain, and adjacent land-use types. Thus, landscape spatial patterns would be expected to play an important role in determining locations where the probability of being involved in a wildlifeâvehicle collision is higher compared to other loca- tions.95 Explanatory factors of wildlife roadkill locations and rates vary widely among species and taxa. To properly mitigate road impacts for wildlife and increase motorist safety, transportation departments need to be able to identify where particular individuals, species, taxa, and vertebrate com- munities are susceptible to high roadkill rates along roads. Quality field data documenting locations and frequencies of wildlifeâvehicle collisions can offer empirical insights to help address this challenging safety and ecological issue. As part of maintaining state and provincial highway sys- tems, transportation departments often collect information on the location of wildlifeâvehicle collisions. Typically, maintenance personnel do not conduct routine surveys of animal roadkilled carcasses, but instead collect this infor- mation opportunistically while carrying out their daily work. Occasionally the information may be referenced to wildlife species and specific geographical landmarks such as 1.0-mile-markers or 0.1-mile-markers; however, oppor- tunistically collected roadkill data are usually not spatially accurate. One study has shown that errors in roadkill reporting may be 500 m or greater.53 The inherent spatial error in most agency datasets limits the types of applications for which the data are useful in transportation planning and mitigation efforts. This report demonstrates how wildlifeâvehicle collision carcass data can be analyzed to guide transportation manage- ment decision making and mitigation planning for wildlife crossings. The research team investigated the relative impor- tance of factors associated with wildlife roadkills using two dif- ferent datasets: one with highly accurate (high-resolution) GPS location data (<_ 10 m error) representing an ideal situa- tion and another lower resolution dataset with high spatial error (<_ 0.5 mi or 800 m = low resolution), which is referred to as âmile-markerâ data and is more characteristic of the datasets available from most transportation agencies. This report illustrates how spatial accuracy of the data affects the process of identifying variables that contribute to wildlifeâ vehicle collisions. Based on these outcomes, the research team makes recommendations for collecting roadkill data more systematically and accurately, emphasizing the value of spatial accuracy in identifying and prioritizing problematic areas for highway mitigation projects. The intent of this effort is to provide an overview of considerations regarding the quality and application of wildlifeâvehicle collision carcass data to aid in assessing and mitigating wildlifeâvehicle collisions. This study was conducted in the Central Canadian Rocky Mountains approximately 150 km west of Calgary, straddling the Continental Divide in southwestern Alberta and south- eastern British Columbia (Figure 10). The study area encom- passes 11,400 km2 of mountain landscapes in Banff, Kootenay, and Yoho national parks, and adjacent Alberta provincial lands. This region has a continental climate characterized by long winters and short summers.121 Vegetation consists of open forests dominated by lodgepole pine (Pinus contorta), Douglas fir (Pseudotsuga menziesii), white spruce (Picea glauca), Engle- mann spruce (Picea englemannii), quaking aspen (Populus tremuloides), and natural grasslands. Geology influences the geographic orientation of the major drainages in the region, characterized by valleys running north to south and delineated by steep shale mountains. On a regional scale, east-west movements of animals across and between these valleys are considered vital for long-term sus- tainability of healthy wildlife populations in the region. The transportation corridors associated with the major water- sheds influence the distribution and movement of wildlife in the region. As the most prominent drainage, the Bow Valley accommodates the Trans-Canada Highway (TCH), one of the most important and, therefore, heavily traveled trans- portation corridors in the region. Highways in the study area traverse montane and subalpine ecoregions through four major watersheds in the region (Figure 10). Table 22 describes the location and gen- eral characteristics of the five segments of highways that were included in this study. Research Approach: Methods and Data Data Collection Spatially accurate dataset. In August 1997, efforts were initiated to maximize data collection from carcasses resulting from WVCs and to improve the spatial accuracy (resolution) of reported locations of WVCs occurring on the highways in the study area. The research team worked with the agencies and highway maintenance contractors that were responsible for collecting and reporting wildlife carcasses, primarily elk.
54 Banff National Park Kootenay National Park Kananaskis Valley Yoho National Park Province Figure 10. Location of Canadian study area. a 2005 annual average daily traffic volume. Data from Parks Canada; Banff National Park; and Alberta Transportation, Edmonton, Alberta. b 1999 summer average daily traffic volume. Data from Alberta Transportation, Edmonton, Alberta. Highway Watershed Province Road Length (km) Traffic Volume (ADT) Posted Vehicle Speed (km/h) Trans-Canada Highway Bow River Alberta, East of Banff National Park 37 16,960 a 110 Trans-Canada Highway Bow River Banff National Park, Alberta 33 8,000 a 90 Trans-Canada Highway Kicking Horse River Yoho National Park, British Columbia 44 4,600 a 90 Highway 93 South Kootenay River Kootenay National Park, British Columbia 101 2,000 a 90 Highway 40 Kananaskis River Alberta 50 3,075b 90 Table 22. Characteristics of the major highways in the Canadian study area. The agencies consisted of Parks Canada (Banff, Kootenay, and Yoho National Parks), Alberta Sustainable Resource De- velopment (Bow Valley Wildland Park, and Kananaskis Country) and Volker-Stevin, maintenance contractor for the Trans-Canada Highway east of Banff National Park in the province of Alberta. This collaborative effort included na- tional park wardens, provincial park rangers, and mainte- nance crews of Volker-Stevin. The research team provided colored pin-flags to mark the sites in the right-of-way where roadkilled wildlife were
55 observed and collected. After placing a pin-flag, collaborators were asked to report to the research team via telephone, fax, or email. Most wildlife carcasses were pin-flagged and re- ported within 48 hours. The collaborators recorded the location of wildlife car- casses by describing the location with reference to a nearby landmark (e.g., 0.3 km west of Banff National Park east en- trance gate). Each reported WVC carcass site was re-located and confirmed by measuring the odometer distance from the reported landmark to the pin-flagged site. Once the location was confirmed, researchers recorded the actual location in Universal Transverse Mercator (UTM) grid coordinates using a differentially correctable GPS unit (Trimble Naviga- tion Ltd., Sunnyvale, California, USA) with high spatial ac- curacy (<_ 10 m). The UTM coordinates were recorded in a database along with the original date of each reported road- kill and information regarding the species, sex, age, and num- ber of individuals involved. For this study, the research team used only ungulate car- cass data (UVC), because ungulate species composed 76% of the total wildlife mortalities. In addition, these species are often the greatest safety concern to transportation agencies given their size and relatively common occurrence in rural and mountain landscapes. Ungulate species included white- tailed and mule deer (Odocoileus virginianus and Odocoileus hemionus, respectively), unidentified deer (Odocoileus sp.), elk (Cervus elaphus), moose (Alces alces), and bighorn sheep (Ovis canadensis). The UVC data obtained from the methods described in the previous paragraphs are hereafter referred to as the âspatially accurate,â âhigh-resolution,â or âGPSâ dataset and serve as a benchmark for the analysis. Mile-marker dataset. To investigate the influence that spatial accuracy and scale may have on the results and inter- pretation of the data, the research team created a mile-marker dataset using the spatially accurate dataset, but shifting each UVC location to the nearest hypothetical mile-marker. To do this, each of the five highways in the study area was divided into 1.0-mile-marker segments using ArcView 3.3.77 All spatially ac- curate UVC data were plotted onto the road network and then moved to the nearest mile-marker reference point. Each ob- served data point was moved an average distance of 400.2 m ± 218.8 m (min. 7.3, max. 793.9) to its nearest mile-marker. The research team recorded the UTM coordinates of each mile- marker location and summed the number of UVCs in that mile-marker segment, defined as 800 m (0.5 mi) up and down the road of the given mile-marker. The UVC data adjusted to the closest mile-marker are hereafter referred to as the âspa- tially inaccurate,â âlow-resolution,â or âmile-markerâ data. High- and low-kill locations. The mean number of road- kills per mile were calculated for each highway and rounded to the nearest whole number. Buffers of 800 m (0.5 mi) radius were generated around each mile-marker sampling site and each highway segment within the buffer was categorized as a high-kill or low-kill zone. This categorization was determined by comparing the total number of UVCs associated with a segment to the mean number of UVCs per mile for the same stretch of road for each of the five highways in the study area. If the summed number of UVCs associated with a single mile- marker segment was higher than the average calculated per mile for the same highway, that mile-marker segment was considered a high-kill zone. Similarly, if the summed number of UVCs within a mile-marker segment was lower than the av- erage for that highway, the mile-marker segment was defined as a low-kill zone. Each spatially accurate UVC location was classified as a high-kill or low-kill zone according to which mile-marker segment it fell within. For example, a mile- marker segment with greater than or equal to 2 roadkills on Highway 40 in Kananaskis was a high-kill zone, while a segment with less than 2 roadkills was a low-kill zone. Variables and Models Site-specific variables. The research team measured site- specific variables at 499 sites from the GPS data and 120 sites from the mile-marker dataset between April 2003 and July 2005. Only 499 UVC locations were used; 47 UVC reports from Kootenay Highway 93 South were excluded because they occurred prior to the clearing of roadside vegetation along a 24 km stretch of the Kootenay Highway 93 South. Using a differentially correctable GPS unit to locate each sam- pling site, the research team measured 14 variables to be used as possible factors explaining UVC occurrence (Table 23). A range finder (Yardage Pro® 1000, Bushnell® Denver, CO) measured distance to nearest vegetative cover, and the inline and angular visibility measurements. Vegetative cover, habi- tat, topography, and slope were all estimated visually. Field visibility variables estimated the extent to which a motorist could see ungulates on the highway right-of-way, or con- versely, how far away an oncoming vehicle could be seen from the side of the highway. Field visibility was measured via a rangefinder as the distance that an observer, standing at one of three positions (edge of the pavement, 5 m from pavement edge, or 10 m from pavement edge), lost sight of a passing vehicle. This measurement represents the distance that an ap- proaching driver might be able to see an animal from the road. Because in most cases it could not be determined from what side a vehicle struck an animal, or in which direction the vehicle was traveling, four visibility measurements were taken at each position (two facing each direction of traffic on both sides of the highway). These four measurements were aver- aged to provide mean values estimating visibility at the edge of the road, 5 m away from the edge of the road, and 10 m
56 Variable Name Definition Field variables Habitat class* Dominant habitat within a 100 m radius on both sides of the highway measured as open (O): meadows, barren ground; water (W): wetland, lake, stream; rock (R); deciduous forest (DF); coniferous forest (CF); open forest mix (OFM) Topography* Landscape scale terrain measured as flat (1), raised (2), buried-raised (3), buried (4), partially buried (5), partially raised (6) Forest cover Mean percentage (%) of continuous forest cover (trees > 1 m height) in a 100 m transect line perpendicular to the highway, taken from both sides of the road Shrub cover Mean percentage (%) of shrub cover (trees and shrubs < 1 m high) in a 100 m transect line perpendicular to the highway, taken from both sides of the road Barren ground Mean percentage (%) of area devoid of vegetation (rock, gravel, water, pavement, etc.) in a 100 m transect line perpendicular to the highway, taken from both sides of the road Vegetative cover Mean distance (m) to vegetative cover (trees and shrubs > 1 m high) taken from both sides of the road Roadside slope Mean slope ( ) of the land 0â5 m perpendicular to the pavement edge taken from both sides of the road Verge slope Mean slope ( ) of the land 5â10 m perpendicular to the pavement edge taken from both sides of the road Adjacent land slope Mean slope ( ) of the land 10â30 m perpendicular to the pavement edge taken from both sides of the road Elevation GPS height (m) Road width Distance (m) from one side of the highway pavement to the other In-line visibility field* Mean distance at which an observer standing at the pavement edge could no longer see passing vehicles; taken from each direction on both sides of the highway Angular visibility 1 Mean distance at which an observer standing 5 m from the pavement edge could no longer see passing vehicles; taken from each direction on both sides of the highway Angular visibility 2 Mean distance at which an observer standing 10 m from the pavement edge could no longer see passing vehicles; taken from each direction on both sides of the highway Distance-to-landscape features Drainage Distance (m) to the nearest waterway (river, stream, or creek) that crossed the road Human use Distance (m) to the nearest human use feature along the highway Barrier-guardrail Distance (m) to the nearest Jersey barrier or guardrail GIS-generated buffer variables Road curvature Length (m) of each highway segment within each buffer Open water Area (km2) of open water within each buffer Human use Area (m2) of human use features within each buffer River length The length (m) of all rivers within each buffer Barrier length The length (m) of all Jersey barriers and guardrails in each buffer * Variable measure obtained from field measurement (1) flat (2) raised (3) buried-raised (4) buried (5) partially buried (6) partially raised Table 23. Definition and description of variables used. from the edge of the road. These positions are defined as âin- line visibility,â âangular visibility 1,â and âangular visibility 2,â respectively, as referred to in Table 23. Spatial and elevation data were collected along each high- way approximately every 25 m, by driving at 50 km/h and recording a GPS location every second. Elevation was ob- tained on site from a GPS unit for the spatially accurate data locations, whereas elevation for the mile-marker points was extracted from the GPS-created highway layer. GIS-generated variables. Measurements for most vari- ables were obtained in the field; some were obtained using Ar- cView 3.3 GIS.77 Distance from each sampling site to landscape features (Table 23) was calculated using GIS. The research team generated 800 m (0.5 mi) radius buffers around each spa- tially accurate and mile-marker sampling site and calculated the area or length of each landscape feature within each buffer. The road network was used to calculate the length of each high- way segment within each buffer to measure curvature of the highway (Table 23). Data Analysis The research team tested whether the spatially accurate UVCs were distributed randomly by comparing the spatial pattern of collisions with that expected by chance, in which
57 case the likelihood of collisions for each road section would show a Poisson distribution.32 For each of the four water- sheds, the research team classed the highways into segments 100 m long and recorded presence (1) or absence (0) of the observed UVC points in each segment. A Kolmogorov- Smirnov one-sample test was used to determine whether the empirical distribution differed from a Poisson distribution. Also a Ï2 test based on overall highway length was used to determine if an obvious UVC aggregation was significant along the cleared section or low valley bottom of Kootenay Highway 93 South. Finally, the research team determined the aggregation of UVCs along each highway (i.e., whether kills were evenly spread or clumped) by determining the percent- age of mile-markers associated with a UVC location. Univariate analyses were used to identify which of the continuous variables (unpaired t-tests) and categorical vari- ables (Ï2 contingency tests) differed significantly (P < 0.05) between high- and low-kill sites within the spatially accurate and mile-marker datasets. The significance of each differen- tiated class within the categorical variables was evaluated using Baileyâs confidence intervals.48 Logistic regression analyses were used to identify which of the significant parameters best predicted the likelihood of UVC occurrence within the spatially accurate and mile-marker datasets.123 Stepwise (backward) regression procedures were used to remove variables from the equation until each result- ing model was not significantly more informative than the previous one. The log-likelihood ratio test123 was used to de- termine the ability of each model to discriminate between high- and low-kill zones based on location attributes. Signifi- cance of explanatory variable coefficients was based on the Ï2 of the Wald statistic.123 Standardized estimate coefficients were calculated by multiplying logistic regression coefficients (B) by the standard deviation of the respective variables. With this, the research team assessed the relative importance of the explana- tory variables within the model. Odds ratios were examined to assess the contribution that a unit increase in the predictor variable made to the probability of a UVC occurring.229 Hosmer-Lemeshow goodness-of-fit test statistics were in- cluded to see how well the model predicted the dependent vari- able. To validate the high-resolution and mile-marker models, the research team generated cross-validation classification ac- curacies for each model. Both the high- and low-resolution models were validated with a random subset of 20% of the data not included in their development. Prior to performing the regression analysis, the research team tested potential explanatory variables for multicollinear- ity.167 Where variables correlated (r > 0.7), the research team removed one of the two variables from the analysis. Final models and variable coefficients with a P-value less than or equal to 0.1 were considered significant. The research team used the SPSS statistical package version 11.0 for all statistical analyses220, and Microsoft Excel and ArcView GIS 3.377 for all other analyses. Findings and Results Summary of UngulateâVehicle Collision Data A total of 546 UVC observations were recorded between August 1997 and November 2003 on all highways in the study area. Deer (mule deer, white-tailed deer, and unidentified deer) were most frequently involved in collisions and com- posed 58% of the kills, followed by elk (27%), moose (7%) bighorn sheep (3%) and other ungulates, including moun- tain goats and unidentified species (5%). The majority of UVCs occurred on the TCH east of Banff National Park in the province of Alberta (46%), followed by Highway 93 South in Kootenay National Park (22%), High- way 40 in Kananaskis Country (12%), the TCH in Yoho Na- tional Park (10%), and the TCH in Banff National Park (10%). Calculating the average number of kills per mile for each highway in the study area showed that the majority of UVCs occurred on the TCH in the province of Alberta (13.6 kills/mi), followed by the TCH in Banff National Park (2.6 kills/mi), the TCH in Yoho National Park (2.1 kills/mi), Highway 40 in Kananaskis (2.1 kills/mi), and Highway 93 South in Kootenay National Park (1.8 kills/mi). These UVC rates followed traffic volume trends, which were highest on the TCH east of Banff National Park in the province of Al- berta, followed by the TCH in Banff National Park, TCH in Yoho National Park, Highway 40 in Kananaskis Country, and Highway 93 South in Kootenay National Park. Spatial Distribution of Roadkills The accuracy of the location where site-related variables were measured for the spatially accurate locations was approximately less than or equal to 10 m. The UVC distributions from the spa- tially accurate dataset differed significantly from random distri- butions along all five highways in the study area (Kolmogorov- Smirnov one-sample test: TCHâBow River Valley, d = 0.715; Highway 93 South in Kootenay, d = 0.940; TCHâYoho, d = 0.892; Highway 40 in Kananaskis, d = 0.874; all P < 0.01). The distribution of UVCs on Highway 93 South in Kootenay showed a significant aggregated distribution where the highway traversed the low valley bottom with 60% of the kills occurring along a 24 km (23%) stretch of road (Ï2 = 63.9, P < 0.0001). The TCH in Alberta had the majority of mile markers associated with a roadkill (89%), followed by the TCH in Banff National Park (86%), followed by Highway 40 (84%), followed by High- way 93 South in Kootenay National Park (61%), and the TCH in Yoho National Park (57%). Because of the non-random pat- tern and aggregation of UVCs, the research team explored
58 Spatially Accurate Mile-Marker Variable High Low P-value High Low P-value Field variables Habitat Rock Coniferous forest Open forest mix 2 144 112 11 177 54 <0.0001 Topography Flat Buried-raised 241 32 172 71 <0.0001 24 12 0.0035 Forest cover 46.7 53.3 0.0256 Openness 47.3 41.6 0.0496 Adjacent land slope 11.4 15.9 0.0059 Road width 34.1 24.8 0.0001 19.51 15.2 0.0300 Distance-to-landscape features Drainages 2389.9 3068.9 0.0003 Barrier-guardrail 627.0 1052.2 0.0003 GIS-generated buffer variables Barrier length 272.7 353.2 0.0182 336.51 548.4 0.0036 Open water 49.2 109.8 0.0001 This table shows a comparison using a spatially accurate dataset (n = 499; 391 high- and 108 low-density points) and mile-marker dataset (n = 120; 63 high- and 57 low-density points). Mean values are shown for quantitative variables, and frequencies for each differentiated type are shown for categorical variables, along with their associated P-values. Only those values that were significant at P < 0.05 are displayed. Table 24. Univariate comparison of factors contributing to UVCs. which landscape and road-related factors may be contributing to the distribution of collisions in the study area. Models Univariate tests. Table 24 shows the results of the uni- variate tests comparing high- and low-kill locations for each environmental variable contributing to the probability of UVCs in each dataset. Each dataset had variables in each group that were significant in detecting differences between UVC high- and low-kill zones, however only three of ten vari- ables were significant in the mile-marker dataset. Within the spatially accurate dataset, Table 24 shows that six of the field-based variables were significant: habitat class, topography, forest cover, openness, adjacent land slope, and road width. Only two of the field variables (road width and topography) were significant from the mile-marker dataset. In both datasets, more UVCs occurred when the topography was flat and the roads were wide. In the spatially accurate dataset, more UVCs occurred than expected in open forest habitat and fewer UVCs occurred than expected in conifer- ous forest and rocky areas. Within the landscape feature variables, distance to drainage and barrier-guardrail were significant (negatively correlated) in the spatially accurate dataset. More UVCs occurred than ex- pected closer to drainages perpendicular to the roadway and closer to barriers-guardrails (including Jersey barriers). No distance-to-landscape features were significantly correlated to the high- and low-kill zones in the mile-marker dataset. Within the GIS-derived variables, areas of open water showed a significant negative correlation to the dependent variable in the spatially accurate dataset, while only the meas- ure of barrier length gave a significant negative correlation in both datasets. Less open water and shorter lengths of barriers were associated with high-kill zones. To reduce intercorrelation between the variables,252 the re- search team omitted the percentage of forest cover from fur- ther analyses because it was highly correlated (r > 0.70) with percentage of cleared ground. Logistic regression analysis. Both models ranked differ- ently in their ability to predict the observed likelihood for UVCs (Table 25). The variables used in each model could col- lectively be used to predict where a UVC would occur for the spatially accurate model (P < 0.0001) but not for the mile- marker model (P = 0.584) as determined from the log likeli- hood ratio test. For the spatially accurate model, the Hosmer- Lemeshow statistic was higher than the mile-marker model. The predictive capabilities of the GPS model correctly classi- fied 81.8%, while the mile-marker model correctly classified only 64.4% of the selected UVC data. Model validation accu- racies were 76.9% for the GPS model and 63.3% for the mile- marker model. Type of habitat was the most important vari- able in explaining UVCs in the GPS dataset. Ungulateâvehicle collisions were less likely to occur near open water, deciduous forest, closed coniferous forest, and open forest mix relative to open habitat. Kills were 2.7 times less likely to occur in water- dominated habitats (lakes, wetlands) relative to open habitat
59 Variable Spatially Accurate Mile-Marker Habitat Water 1â Coniferous forest 4â Deciduous forest 5â Open forest mix 2â Distance to drainage 3â Barrier-guardrail N/A+ Road width N/A+ Barrier length N/Aâ 1â Open water N/Aâ HosmerâLemeshow test 0.764 0.512 Model development & validation accuracies (%) 81.8 76.9 64.4 63.3 N/A = standard deviation in the logistic regression output was equal to 0 Table 25. Logistic regression analyses for modeling factors contributing to UVCs. areas (dry meadows, clearings). Further, distance to drainage had a significant negative correlation with the occurrence of UVCs in the GPS model. The distance to barrier-guardrail and the length of the barriers within the buffer both showed a negative correlation with UVCs. In the mile-marker model, barrier length showed a significant negative correlation with UVCs. In Table 25, results are presented from the logistic regression analyses for modeling the factors contributing to UVCs using two datasets. They include a spatially accurate dataset (n = 499 locations; 391 high- and 108 low-density points) and a mile- marker dataset (n = 120; 63 high- and 57 low-density points). Also shown are their associated ranking of significant (P < 0.10) standardized estimate coefficients and their sign. Num- bers indicate the rank of importance of the variable. The sign indicates the influence the variable or variable level has on the probability of a roadkill occurring [(â) negative correlation or (+) positive correlation]. Hosmer-Lemeshow goodness-of-fit test and overall cross-validation accuracies are included; the term N/A means that the standard deviation in the logistic regression output was equal to 0. Interpretation, Appraisal, and Applications Summary of UVC Data For this analysis, the research team used the largest data- base of its kind with spatially accurate information on the occurrence and specific carcass location of WVCs. The traf- fic mortality database is also unique in that it spans a relatively short time period (1999â2005), whereas other databases, regardless of their spatial accuracy, often contain roadkill information from a decade or more. The short time span used in this analysis is important because over long time periods, environmental variables may change (e.g., roadside vegetation and motorist visibility, habitat quality), as can road-related variables (e.g., guardrail and Jersey barrier installation, road widening and improvements, lighting), thus confounding analysis and resulting in possi- ble spurious results. Previous explanations for the clustering of WVCs included parameters such as animal distribution, abundance, and dis- persal and road-related factors including local topography, vegetation, vehicle speed, and fence location or type.190,4,47 Few studies have demonstrated that WVCs were correlated with traffic volume.160,4,47,124 The majority of WVCs in the analysis took place in the provincial section of the TCH followed by Highway 93 South in Kootenay National Park. However, when the roadkill frequencies were standardized by highway length in the study area, the rate of roadkill was found to correlate positively with traffic volume. Factors in addition to traffic volume may influence colli- sion rates, but may be masked if a more detailed and rigor- ous analysis is not conducted. Previous research in the same Canadian study area found that elkâvehicle collision rates were significantly different between road types and declined over time on the TCH in Banff and Yoho National Parks, and Highway 93 South.53 In this analysis, when the effects of traffic volume and elk abundance on elkâvehicle collision rates were isolated, the latter was particularly important.53 Significant interactions indicated that road type influenced these effects and greater elk abundance led to increased elkâvehicle collisions. For this analysis, the research team did not include elk abundance as an independent variable because the elk abundance data available for analysis was not at the same spatial resolution as the site-specific loca- tions in the accurate UVC model. Of the five highways in- cluded in this study, the relative abundance of ungulates is highest in the provincial section of the TCH and Kootenay River Valley along Highway 93 South. The other highways (TCH-Banff, TCH-Yoho, and Highway 40) are situated at higher elevations and have lower ungulate densities. Few studies investigating factors influencing WVCs have included data on animal abundance.20,190,53
60 Models of UngulateâVehicle Collisions Spatial distribution and aggregation. The spatial distribu- tion of UVCs on all five highways in the study area was not random. The most notable aggregation was along the 24 km stretch of highway on 93 South. This segment of highway bi- sects key ungulate ranges in the valley bottoms of the mon- tane region, with elevation less than 1240 m.188 Several environmental and road-related variables had high explanatory power in describing UVCs on all highways, and these variables were dependent on the spatial accuracy of the dataset. Results of the univariate analysis demonstrated that the GPS dataset had substantially more significant variables (n = 10 variables) explaining the factors associated with UVCs than the mile-marker dataset (n = 3 variables). Predictive ability of datasets. Univariate tests and logis- tic regression analysis were used to determine the predictive ability of the two datasets. Univariate tests. Among the field-based variables, only two were identified in the mile-marker dataset as being sig- nificant in detecting differences between high- and low-kill UVC zones. The same variables were also identified among the six significant variables in the GPS dataset. Two of the variables from the distance-to-landscape features and GIS- generated buffer variables were significant from the spatially accurate dataset, whereas the mile-marker dataset had none. Univariate tests are often used as a preliminary step to identify one or more variables that are most likely good pre- dictors of responses to include in an a priori logistic regres- sion analysis.123 The results of the univariate tests of signifi- cance provide an interesting comparison of how well each dataset is able to describe the relationship between predictor variables and the location of UVCs. Of the 22 variables used in the initial univariate test to identify variables that differed significantly between high- and low-kill UVC zones, 10 (roughly half) of the spatially accurate variables compared to only 3 (< 10%) of the mile-marker variables were statistically significant (see Table 24). Logistic regression analysis. Results of the logistic re- gression analysis to predict the likelihood of UVCs for the two datasets analyzed in this study showed the GPS model was statistically significant, however, the mile-marker model was not. Further, both of the models differed considerably in how well they predicted the likelihood of UVCs. Strong support of the predictive ability of the GPS model compared to the mile- marker model was found with the higher cross-validation scores. These results provide strong evidence that the GPS- collected data is more likely to be informative in explaining WVCs than the mile-marker data. Factors that explain collisions. The spatially accurate model indicated that adjacent habitat type was the most im- portant variable in explaining UVCs. The proximity to open habitat increased the likelihood of UVCs as opposed to habi- tats characterized by open water, deciduous forest, closed coniferous forest, and open forest mix. Gunther et al.109 re- ported that elk were involved in collisions significantly more often than expected in non-forested cover types. Many deerâvehicle collisions in Pennsylvania were concentrated around woodland-field interfaces in predominantly open habitat.15 On the other hand, some studies have not found this association between habitat type and UVCs.4,25 Wildlife tends to be associated with specific habitats that provide resources and environmental conditions that promote occu- pancy and survival.176 Thus, the spatial distribution of habi- tat types adjacent to or bisected by a highway transportation corridor would likely influence the extent, severity, and loca- tions of vehicle collisions with wildlife. Landscape variables other than habitat and topography may also be important attributes determining UVCs. For example, distance to nearest drainage was significantly and negatively correlated with the occurrence of UVCs in the spatially accu- rate model. Ungulates had a greater tendency to be involved in traffic collisions close to drainage systems. Drainage systems are known travel routes for wildlife, particularly in narrow glacial valleys such as Banffâs Bow Valley.51 Furthermore, research has shown that topography, particularly road align- ment with major drainages, strongly influences the movement of ungulates toward roadways and across them.20,45,159,86 The proximity to potential barriers such as Jersey barriers and guardrails was an important predictor of UVCs in the study area. The same result was found when measuring the length of Jersey barrier or guardrail within the 800 m buffer in high- and low-kill UVC zones. UVCs were found to occur nearer to Jersey barriers and guardrails, which may be because animals are funneled to the ends of the barriers and cross the highway at this point. Furthermore, fewer animals were killed when the length of barriers within the 800 m buffer decreased. These results suggest that the barrier is obstructing animal movement and funneling animals to barrier ends, or particu- lar features in the landscape associated with barriers such as lakes and steep topography are deterring animals from ap- proaching the highway at these locations. Barnum 14 found that animals crossed more frequently at culverts, bridges, and at-grade crossings with no guardrail or median barrier. The only study modeling AVCs that included guardrails in the analysis also found that animals tended to avoid highway sections with these potential barriers; i.e., collisions were less likely to occur where barriers were present.158 The results have important ecological implications because they suggest that median barriers and guardrails may obstruct animal movement across highways. Further, the results have
61 important management implications because state trans- portation agencies are constructing highway median barriers with virtually no information on how they affect wildlife movement and mortality. Despite these potential impacts, the 2003 AASHTO Roadside Design Guide does not address the impact of median barrier installation. Resource managers and transportation biologists have identified this lack as a severe shortcoming that needs immediate attention. A recent Transportation Research Board report highlighted the urgent need to better understand how wildlife respond to and are potentially impacted by highway barriers.233 Spatial accuracy and interpretation of results. In the mile-marker dataset, few landscape variables were significant. For example, level or gentle topography due to flat terrain is bisected by the TCH in the province of Alberta. Further, road width was a significant explanatory variable due to the width and number of lanes of traffic on the TCH in the province of Alberta. Both of these variables are not as dependent on spatial accuracy, because they were broad-scale measurements with low variability occurring on large sections of the highway. None of the distance-to-feature variables showed signifi- cance in the mile-marker dataset. These types of variables are strongly dependent on spatial accuracy of reporting UVCs. For example, if a UVC location has an error up to 800 m, it will be evident in the measurement of these variables. The GIS-generated buffer variables could be used to meas- ure factors associated with UVCs in a mile-marker dataset.158 The buffer encompasses the entire area in which the UVCs would have occurred, thus the factors associated with that roadkill are incorporated into the measurement of the variables. Barrier length was a significant explanatory variable in both datasets and area of open water was marginally signif- icant in the mile-marker dataset. These variables would have to be a broad-scale landscape feature such as the area of a feature within the entire buffer. Dataset comparison. The primary result of the analyses was that the GPS UVC model identified more factors that may contribute to UVCs than the mile-marker model. This result lends strong support to a categorical distinction between high- kill versus low-kill UVC zones (or where they are less likely to occur) when modeling is performed with high-resolution spatially accurate UVC data. Animalâvehicle collisions have been modeled at a range of spatial scales, from local to state and nationwide analy- ses.124,183,158,206,192 Previous studies have used readily available data (carcass or collision statistics) to identify variables that in- fluence the risk of animalâvehicle collisions and have recommended measures to reduce the number of fatalities. These studies have largely relied on referencing collision data several ways: (1) accepting and using location data (point data) or highway segments with animalâvehicle collisions (hotspots) without knowledge of the inherent spatial error,20,15,89,25,208 (2) referencing to a highway mile-marker system,124 (3) refer- encing to a 0.1-mile-marker (or 0.1-km) system,190,158,206,125 or (4) using spatially accurate UTM locations (<_ 10 m error) ob- tained by a GPS unit at the collision location.53,192,193 The previous review of published studies illustrates that many studies that modeled animalâvehicle collisions typically have used data with a significant amount of spatial error, in- troduced by relying on a mile-marker system or an equally flawed approach of not being able to verify the degree of spa- tial error associated with the collision data. One study that rigorously measured the reporting error in the Canadian Rocky Mountain parks using GPS locations found the error was on average 516 ± 808 m, and ranged from 332 ± 446 m to 618 ± 993m.53 Plotting animalâvehicle collisions on maps using grid co- ordinates may not improve spatial accuracy in reporting. In the previously mentioned study, the average distance report- ing error associated with roadkill records (based on occur- rence reports and mortality cards from the mountain national parks) was 969 ± 1,322 m.53 The work presented in this report is the first to the research teamâs knowledge to test the value of low-resolution spatial data by comparing model performance results with a high-resolution spatially accurate dataset. Besides learning about the parameters that con- tribute to UVCs in the study area, the research team discov- ered that spatially accurate data does make a difference in the ability of models to provide not just statistically significant re- sults, but more important, biologically meaningful results for transportation and resource managers responsible for reduc- ing UVCs and improving motorist safety. These results have important implications for transporta- tion agencies that may be analyzing data that is referenced to a mile-marker system and is spatially inaccurate. These impli- cations are equally important for statewide analyses or even smaller districts. Spatially inaccurate data would be suitable for coarse-scale analysis to identify UVC hotspots, but for fine-scale needs (project or district level), greater accuracy in data will be essential for a rigorous analysis and development of sound mitigation recommendations. A joint U.S.âCanada-wide standard for the recording of animalâvehicle collisions would not only stimulate transporta- tion departments and other organizations to collect more spa- tially accurate roadkill data, but it would also allow for better in- tegration and analyses of the data. Some transportation agencies are also beginning to use personal data assistants (PDAs) in combination with a GPS for routine highway maintenance ac- tivities (e.g., Washington State).126 These two initiatives can help agencies collect more spatially accurate and standardized data that will eventually lead to more informed analyses for trans- portation decision making.
62 Landscape vs. road-related variables. Wildlife tends to be associated with specific habitats, terrain, and adjacent land use types. Thus, landscape spatial patterns would be expected to play an important role in determining roadkill locations and rates.95 Explanatory factors of wildlife roadkills vary widely between species, often explained by habitat prefer- ences and species abundance patterns.52,192 Increasingly, stud- ies are beginning to look at the types of variables that explain wildlifeâvehicle collisions, whether they are associated with landscape and habitat characteristics, or physical parameters related to the road environment.208,206 In this study, 22 vari- ables were evaluated, 11 associated with landscape or habitat attributes and 9 associated with the road environment. In the univariate analysis, 10 variables were significant in explaining UVCs; 8 were related to landscape, while only 2 were associ- ated with the road environment. In the logistic regression analysis, three explanatory variables were significant; two were landscape based and one was from the road environ- ment. These results demonstrate the importance of ecologi- cal attributes in the analysis and suggest that analyses that fail to adequately consider ecological variables in UVC analyses along with road-related variables may be appropriate for safety considerations but are likely to provide unreliable re- sults when wildlife population viability is a concern. Summary. This study is the first of which the research team is aware that tested the value of low-resolution spatial data accurate to the mile-marker with a high-resolution GPS dataset accurate to within a few meters. High-resolution data were found to make a significant difference in the ability of models to provide biologically meaningful predictions of the variables responsible for UVCs. The analyses used the largest database of its kind with spatially accurate information on the occurrence and specific carcass location of UVCs. The data- base covered the period from August 1997 to November 2003. Most noteworthy was the significant difference in pre- dictive ability between the models. The high-resolution UVC model had higher predictive power in identifying factors that contributed to collisions when compared to a lower resolu- tion dataset based on mile-marker references. Additionally, the high-resolution models were more robust than models from the low-resolution mile-marker dataset. UVCs were clustered on all highways in the study area. The high-resolution model had substantially more significant variables explaining the factors associated with UVCs than the mile-marker model. Adjacent habitat type was the most important variable in explaining UVCs in the high-resolution model. Distance to nearest drainage also was significant and negatively correlated with the occurrence of UVCs. There was a greater tendency for traffic collisions close to drainages sys- tems and close to barriers such as Jersey barriers and guardrails. These findings lend support for the development of a U.S.âCanadian standard for recording WVCs and suggest that further research into new technologies that will enable transportation agencies to collect WVC data of appropriate spatial resolution is needed. Conclusions and Suggested Research The primary result of this analysis was that a UVC model developed with high-resolution location data had high predictive power in identifying factors that contribute to collisions. The location of where high-kill versus low-kill UVC zones are likely to occur is highly dependent on the resolution of the models used. Plotting animal-vehicle collisions on maps using grid coor- dinates may not improve spatial accuracy. In this study, the average distance reporting error associated with roadkill records using UTM grid coordinate references on occurrence reports and mortality cards from the mountain national parks was 969 m ± 1322 m.53 The research team found that model- ing collision-related parameters with low-resolution location data did not produce models with high predictability. As a consequence, the models could not be expected to produce properly directed or applied mitigation of WVCs. These results have important implications for transporta- tion agencies that may be analyzing data that has been refer- enced to a mile-marker system or that is, unknown to them, spatially inaccurate. These implications are equally important for state-wide analyses or even the smaller districts. Low- resolution data or data that is spatially accurate to the mile- marker may be used for coarse-scale analysis to identify UVC hotspots. However, for finer scale needs (project or district level), higher resolution spatial data appear essential for a rig- orous analysis and development of sound mitigation recom- mendations. A U.S.âCanadian standard for recording WVCs not only would stimulate transportation departments and other organizations to collect more spatially accurate roadkill data, but also would allow for a better integration and analyses of the data. These two initiatives, spatially accurate (higher res- olution) data and standardized data collection, can help agen- cies to collect data that will eventually lead to more informed analyses for transportation decision making. 3.3 Hotspots Modeling Introduction Wildlifeâvehicle collisions are a significant problem in North America, particularly in rural or suburban areas where people rank them as a major safety concern. A recent survey of motorists in Montana, Idaho, and Wyoming ranked ani- mals on the roadway as one of the top three safety issues.82 A survey of northern California and rural Oregon stakehold- ers reported similar concerns. In much of the western United
63 States, road networks are extensive and motor vehicle use has sharply increased as wild lands are progressively developed and suburbanized.21,110 Human population growth and its as- sociated infrastructure expansion, as well as increasing wildlife populations in some areas, have led to greater safety concerns and the need to develop effective countermeasures to mitigate WVCs. In 2002, an estimated 1.5 million WVCs resulted in 150 fatalities and $1.1 billion in vehicle damage in the United States.116 Studies have demonstrated that WVCs are not random occurrences but are spatially clustered.190,124,51,134 However, few studies specifically probe the nature of WVC hotspots or their use and application in transportation planning148,136 and few have been spatially explicit. Most have utilized only one method of determining hotspot locations. Many of the studies characterizing WVCs have appeared in scientific and management-focused journals, and often include different conclusions or recommendations for managers to consider in designing wildlife-friendly highways.190,124,183,158 However, lack- ing are best management practices for identifying WVC hotspots based on current knowledge and technology to help guide planning and decision making. Because WVCs represent a distribution of points, clustering techniques can be used to identify hotspots. Simple plotting of WVC location points can be done in a variety of GIS formats, for example, ArcView® or ArcGIS®77,78 currently being used by many transportation agencies. Simple plotting does not require statistical algorithms or metrics but is based on visual groupings of roadkill clusters and decision-based rules of defining hotspots. Clustering of WVCs has been correlated to animal distributions, abundances, and dispersal habits and road-related factors including local topography, vegetation, vehicle volume and speed, and fence location or type.190,4,47,51 In this report, the research team investigates various WVC hotspot identification clustering techniques that can be used in a variety of landscapes, taking into account different scales of application and transportation management concerns (e.g., motorist safety, endangered species management). Using WVC carcass datasets from two locations in North America with varying wildlife communities, landscapes, and transportation planning issues, the research team demon- strates how this information can be used to identify WVC hotspots at different scales of application (from project level to state level analysis). The model-based clustering tech- niques that are demonstrated include a linear nearest neigh- bor analysis used initially to measure if the WVC locations were random and then Ripleyâs K statistic, nearest-neighbor measurements, and density measures to identify hotspots. An overview of software applications that facilitate these types of analyses is provided. The information presented in this report is intended to advance understanding of the considerations that should be taken into account when analyzing WVC datasets of varying qualities and scales. Results from this ef- fort are intended to help agencies assess the efficacy of their current WVC data collection and analytical techniques. The work complements the growing body of research on mitigat- ing road impacts for wildlife and improving highway safety. Finally, it provides practitioners and managers with methods that can be quickly applied to available information and ultimately streamline the delivery of transportation projects in areas where WVCs are a major concern to agencies and stakeholders. Research Approach: Methods and Data Mapping Techniques The objective of this research was to investigate different mapping techniques that can be used to identify WVC hotspots. The techniques can be categorized as (1) simple graphic, visual mapping exercises and (2) modeling of analyt- ical techniques used to identify non-random clusters or aggregations of WVCs. The simple plotting of WVCs can be done in a variety of GIS formats, for example ArcView® or ArcGIS®, which currently are being used by many transporta- tion agencies. Simple plotting does not require statistical algorithms or metrics but is based on visual groupings of road- kill clusters and decision-based rules of defining hotspots. Modeling WVCs using clustering mapping techniques is more complicated. The research team evaluated the mapping techniques in the context of different scales of application (project-level to state-level analysis) and transportation man- agement concerns (e.g., motorist safety, endangered species management). Different mapping techniques are described using one dataset, WVCs in the Canadian Rocky Mountains, to demonstrate how this readily available information can be used by transportation agencies to identify collision hotspots at different scales of application. Then one clustering tech- nique (CrimeStat®) was selected and hotspot analyses run using two different datasets: UVC carcass data from the Canadian Rocky Mountains and California Department of Transportation (Caltrans) deer carcass data (DVC) from Northern California. The following sections describe the hotspot patterns/configurations and examine how they may differ by species and the two landscape types. Study Area Canadian Rocky Mountains. This study took place in the central Canadian Rocky Mountains in western Alberta approximately 100 km west of Calgary (see Figure 10 in Section 3.2). The area encompasses the Bow River watershed and includes mountain landscapes in Banff National Park and adjacent Alberta Provincial lands in Kananaskis Country.
64 Highway Watershed Province Road Length (km) Traffic Volume (ADT) Posted Vehicle Speed (km/h) Trans-Canada Highway Bow River Alberta, East of Banff National Park 37 16,960 a 110 Trans-Canada Highway Bow River Banff National Park, Alberta 33 8,000 a 90 Trans-Canada Highway Kicking Horse River Yoho National Park, British Columbia 44 4,600 a 90 Highway 93 South Kootenay River Kootenay National Park, British Columbia 101 2,000 a 90 Highway 40 Kananaskis River Alberta 50 3,075b 90 a 2005 annual average daily traffic volume. Data from Parks Canada; Banff National Park; and Alberta Transportation, Edmonton, Alberta. b 1999 summer average daily traffic volume. Data from Alberta Transportation, Edmonton, Alberta. Table 26. Characteristics of the major highways in the study area. Topography is mountainous; elevations range from 1,300 m to over 3,400 m; and valley floor width varies from 2 to 5 km. Highways in the study area traverse montane and subalpine ecoregions through four major watersheds in the region. Table 26 describes the location and general characteristics of the five segments of highways that were included in this study. Vegetation consisted of open forests dominated by Douglas fir (Pseudotsuga menziesii), white spruce (Picea glauca), lodgepole pine (Pinus contorta), Englemann spruce (P. englemannii), aspen (Populus tremuloides) and natural grasslands. The research team obtained the UTM coordinates using a GPS unit for over 500 spatially accurate carcass loca- tions (< 3 m error) of WVCs between 1997 and 2004 in the Canadian Rocky Mountains. The research team used the UTM Nad 83 location to plot all of the WVC data within ArcGIS 9.0 on the highway network. The hillshade raster dataset was derived from the digital elevation model (DEM: Parks Canada, GIS data management) and used as a backdrop layer for visual interpretation. Northern California. This study took place in Sierra County, California, in the Sierra Nevada Mountains (Figure 11). California State Route (SR) 89 runs along the east side of the Sierra Nevada Mountains from the towns of Truckee to Sierraville. The highway is a two-lane undivided highway with an AADT of 2,250, peaking at 3,300 in the summer months. Elevation ranged from 6,150 ft (â¼ 1,875 m) surrounding the southern most section of the highway (mile-marker 11.0) to 5,081 ft (â¼ 1,549 m) in the northern section. The dominant vegetation was ponderosa pine (Pinus ponderosa), bitterbrush (Purshia tridentata), and sagebrush (Artemisia tridentata). The area is located in a rainshadow and receives relatively less precipitation than more westerly locations. Snowfall can accumulate 2 to 3 ft (â¼ 0.6 to 0.9 m) during winter (Sandy Jacobson, personal communication). SR 89 bisects an impor- tant migration route for the Loyalton-Truckee mule deer (Odocoileus hemionus) herd, which travels across the highway during seasonal migrations. The highway also bisects the home ranges of numerous resident deer and is used by forest carnivores and amphibians. Caltrans has consistently col- lected deer carcass data on this highway from June 1979 to October 2005. The research team used 849 deer carcass loca- tions collected along 33 mi of SR 89. The data were collected by maintenance supervisors and vary in spatial accuracy (1.0-mi, 0.1-mi, and 0.001-mi). Findings and Results Hotspot Identification and Patterns for One Species and Landscape Simple graphic techniques, one dataset. A total of 546 WVC observations were recorded between August 1997 and November 2003 on all five highways in the study area. Deer composed 58% of the kills, followed by elk (27%), moose (7%), Rocky Mountain bighorn sheep (3%), and other un- gulate species (5%). The majority of WVCs occurred on the TCH east of Banff National Park in the province of Alberta (46%), followed by Highway 93 South in Kootenay National Park (22%), Highway 40 in Kananaskis Country (12%), the TCH in Yoho National Park (10%), and the TCH in Banff National Park (10%). A simple visual analysis of the WVC locations is shown in Figure 12. A simple plotting of all WVC locations along high- ways does not clearly identify key areas where WVCs occurred or areas where higher than average densities of collisions occurredâat least in this type of mountainous landscape that characterized the study area. Simple plotting resulted in carcass locations being tightly packed together, in some cases directly overlapping with neighboring carcass locations, thus making it difficult to identify distinct clusters, i.e., where the real high-risk collision areas occurred. The use
65 Figure 11. Location of study area in northern California in Sierra County, CA. of a DEM and/or land cover map overlay does provide read- ily available information on the juxtaposition of WVCs to ter- rain features (e.g., lowlands, lakes, steep terrain, vegetation cover types). A visual analysis can provide some cursory conclusions about why and where WVCs tend to occur most. However, a more rigorous spatial analysis can be carried out to summarize or test statistically the âwhy and whereâ questions. Terrain and habitat are often key factors influencing where WVCs occur (see Section 3.2).52,15,158,25 Type of terrain and the nature of the landscape mosaic likely influence WVC hotspot clustering pat- terns. For example, landscapes with homogeneous cover types and with little topographic relief (i.e., flat terrain) would likely result in a more random pattern of movement across a high- way, and thus a more dispersed pattern of collision locations on a given stretch of highway. Contrarily, a highly heteroge- neous landscape with dissected topography is more likely to re- sult in more clearly defined crossing locations and collision hotspots. The factors that contribute to these collisions will be different in both landscapes. More simplistic models with fewer explanatory variables could possibly be used to charac- terize the level, more homogeneous landscape, but more com- plex models with numerous variables may work better in the more diverse landscape. Landscape diversity may well influ- ence the causes and spatial distribution of WVCs. Analytical techniques, one dataset. The research team used a linear nearest neighbor analysis, cluster analysis, Rip- leyâs K analysis, and density measures to identify collision hotspots at different scales of application. Linear nearest neighbor analysis. All WVCs were plotted for each highway on the highway network layer in ArcGIS 9.0. The research team used the Hawthâs Analysis Guides24 exten- sion to generate the same number of ârandom WVCsâ as there were actually observed on each highway. A first order linear nearest neighbor index (NNI) was then used to evalu- ate if the distribution of the observed WVCs in each region of the Canadian Rocky Mountains differed from a random distribution. The NNI is a ratio between the mean nearest dis- tance to each WVC [d(nn)] and the mean nearest distance that would be expected by chance [d(ran)]. Hawthâs Analysis Guides were used to calculate d(nn) and d(ran). NNI = d(nn)/d(ran) If the observed mean distance is smaller than the random mean distance, then the WVCs occur closer together than ex- pected by chance and NNI < 1. Once tabulated, the data were imported into Microsoft Excel and a Z-statistic adapted from Clark and Evans50 was calculated to test if there were signifi- cant differences between random and observed distances.
66 Figure 12. Spatially accurate locations of WVC locations on each road in each of the watersheds.
67 Region No. clusters Mean cluster length ± SD (km) No. high-kill zones Mean high-kill zone aggregation length ± SD (km) Cluster overlap indexa TCH-Yoho (YNP) 6 1.00 ± 0.32 7 2.80 ± 1.33 1.00 TCH-Banff (BNP) 6 0.92 ± 0.38 11 4.40 ± 3.98 0.64 TCH-Alberta (AB) 7 1.32 ± 0.14 12 3.84 ± 1.63 0.90 Hwy 40-Kananaskis 6 0.96 ± 0.42 13 4.16 ± 3.29 0.85 Hwy 93-Kootenay (KNP) 17 0.86 ± 0.39 19 3.49 ± 2.34 0.56 a (cluster lengthhigh kill zone /cluster length) Table 27. Descriptive statistics of the nearest neighbor clusters and high-kill zone aggregations. The nearest neighbor index showed clustering (NNI < 1) for all highway regions except for the TCH in Yoho, which showed evidence of dispersion (Table 27). The Z-statistic was significant (P < 0.05) for the TCH in Alberta and marginally significant (P = 0.066) for Highway 93 South. The NNI used in this analysis is only an indicator of first order spatial ran- domness; a K-order nearest neighbor distance (e.g., second or third order) would likely better describe the overall spatial distribution of WVCs.145 Sample sizes were small on the TCH in Yoho and Banff, and on Highway 40 in Alberta (n < 100), making overall spatial distributions of WVCs in these regions difficult to describe. The linear NNI is a quick and easy statistical test of spatial distribution of WVCs to initially determine whether colli- sions are distributed randomly across a stretch of highway or larger highway network (e.g., a DOT district or region). If the test indicates WVC clustering (NNI < 1.0), then the subse- quent step would be to identify where the clusters occur using a GIS-based spatial analysis. Some spatial analysis techniques include cluster analyses using a GIS-based NNI,25 mapping roadkill densities using a âmoving windowâ analysis,213 or a road segment approach to mapping roadkill densities.89,136 One approach that has great promise and is user-friendly is the CrimeStat program developed by Levine.146 Cluster analysis: nearest neighbor hierarchical technique. The research team used CrimeStat version III146 to determine the location of high-kill zones or WVC hotspots within each of the five highways of the Canadian Rocky Mountains study area. CrimeStat is a nearest neighbor hierarchical technique, which identified a series of points that are spatially close based on a predefined set of criteria.146 The clustering is repeated until either all points (WVCs) are grouped into a single clus- ter or else the clustering criterion fails. A fixed threshold dis- tance (800 m) was used for the search radius to determine the inclusion of a WVC in a cluster. This threshold distance (800 m) is the same radius used in the mile-marker density analysis (see âDensity measures: WVCs per mile segmentâ below). The criterion for the minimum number of points required to define a cluster was the mean number of WVCs per mile for each highway region, the same criterion used to determine whether a 1-mi buffer was a high- or low-kill zone (see âDensity measures: WVCs per mile segmentâ below). A convex hull was used as the cluster output; it draws a polygon around the WVCs in the cluster. Because roadkills occur in a one dimensional plane, a line was drawn from the two outer- most points along the road within the convex hull for visual display and to calculate the length of each WVC cluster. The nearest neighbor CrimeStat analysis produced a total of 42 WVC clusters along 41 km of highway in the study area (Figure 13). Compared to the simple visual analysis of WVCs, the CrimeStat modeling technique effectively reduced the blurring of WVC hotspots on long stretches of highway. As mentioned earlier, simple plotting of WVC lo- cations tends to result in tight groupings of collision points that often overlap with other WVC locations, making it a challenge to identify where the really high-risk collision areas actually occur. The location and number of WVC hotspots generated by the CrimeStat technique are clearly defined and can be identified with associated landscape or road-related features in each highway area. Ripleyâs K analysis. Ripleyâs K statistic describes the dis- persion of data over a range of spatial scales.200,67 Ripleyâs K statistic was calculated for all WVC mortalities in each region. The research team used the K statistic as defined by Levine,145 but modified it for points distributed in one dimension (e.g., along a line or road network). The result- ing algorithm was coded in Avenue⢠and run in ArcView GIS.77 The algorithm counted the number of neighboring WVCs within a specified scale distance (t) of each WVC, and these counts were summed over all WVCs. The research team standardized the WVC totals by sample size (N) and highway length (RL) to allow for comparison between each highway region. The process was repeated for incrementally larger scale distances up to RL for all five highways. The K statistic (adapted from Levine and OâDriscoll)77,185 was defined as: K RL N I 2 ( ) ( )distance dobs ij j N i i j N = == â ââ 11
68 Figure 13. Clusters or hotspots derived from CrimeStat III software on each road in each of the watersheds in Alberta, Canada.
69 A) TCH in Yoho NP -8 -6 -4 -2 0 2 4 6 0 10 20 30 40 50 B) TCH in Banff NP -3 -2 -1 0 1 2 3 4 5 6 0 10 20 30 40 C) TCH in Alberta -3 -2 -1 0 1 2 3 4 5 0 10 20 30 D) Highway 40 Alberta -4 -3 -2 -1 0 1 2 3 4 5 6 7 0 10 20 30 40 50 E) Highway 93 South Kootenay NP -5 0 5 10 15 20 25 30 0 20 40 60 80 100 120 Scale Distance t (km) Figure 14. Plotted values of L statistic for the Ripleyâs K statistic of WVCs from five highways in Canadian Rocky Mountain study area. Ordinate axis is L(distance) for all 5 graphs. where dij is the distance from WVC i to WVC j and I(dij) is an indicator function that returns 1 if dij <_ distance and returns 0 if otherwise.185 A distance increment of 280 m was used for all five highway regions to allow for a minimum of 100 ds bins on the shortest section of highway (i.e., the TCH in Alberta). To assess the significance of K-values, the research team ran 50 simulations of the above equation based on random distri- butions of points for each of the five categories. Figure 14 displays the results as plots of L versus distance, where L is the difference between the observed K-value and the mean of the K-values for the 50 simulations.185 Positive values of L indicate crowding and negative values indicate dispersion. Figure 14 also presents the 95% confidence limits, calculated as the upper or lower 95th percentile of the random simulations minus the mean of the random simulations.185 The research team defined significant crowding as any value of L above the upper confidence limit and significant dispersion as any value of L below the lower confidence limit. The distribution of WVCs was heterogeneous and signif- icantly more clustered or dispersed than would be expected by chance over a wide range of scales (P < 0.05, Figure 14). In all highway regions there was significant clustering of WVCs and some significant dispersion. The TCH in Yoho had a small degree of clustering from 1 to 2 km at an inten- sity of 0.3 km, and significant dispersion at spatial scales from 3 to 12 km and 18 to 45 km. This dispersion peaked at an intensity of 7 km. Neighbor K statistics are well suited for the description of one-dimensional spatial distribu- tions.200,104,192 The range of scales over which clustering appears significant is dependent on the intensity of the dis- tribution of roadkills.52,192 Peaks in L(t) (i.e., the intensity of clustering) occurred between km 4 and 5 for the TCH in Alberta and the TCH in Banff, which means there was an average of 4 to 5 extra neighbors within the scale distance of 0 to 10 km on the TCH in Banff and 0 to 12 km on the TCH in Alberta. Both these aggregations can be seen in Figure 14.
70 In Banff they correspond with the section of the TCH that bi- sects a North-South aligned major drainage. At large scale distances, the TCH in Banff National Park and Alberta show a random distribution with small scales of dispersions. On Highway 93 South there is a large peak (27 extra neighbors) in WVC clustering at a scale distance of 0 to 80 km. This peak corresponds to the bulk of the WVCs that occurred at the southernmost section of Highway 93 in low-elevation mon- tane habitat. Further, the highway bisects a key ungulate movement corridor in this area. The Ripleyâs K analysis clearly shows the spatial distribu- tion of WVCs along each segment of highway. The large- scale aggregation evident on Highway 93 South in Kootenay shows the importance of broad-scale landscape variables such as elevation and valley bottoms in a mountain envi- ronment. The scale extent of WVC aggregations in each study area can be used to help determine the scale extent and type of variables to be used in explaining the occurrence of road mortality of wildlife. Further, the locations of high- intensity roadkill clustering within each area can help to focus or prioritize the placement of mitigation activities, such as wildlife crossings or other countermeasures, on each highway segment. Density measures: WVCs per mile segment. For the next two analyses, the mile-marker data generated from the study described in Section 3.2 was used. The research team divided each of the five highways in the Canadian Rocky Mountain study area into 1.0-mile-marker segments and plotted all spa- tially accurate WVC carcass data onto each road network. The research team then moved each carcass location point to the nearest mile-marker reference point. The research team recorded the UTM coordinates of each mile-marker location and summed the number of WVCs in that mile-marker seg- ment, defined as 800 m (~ 0.5 mi) on either side of the given mile-marker location. For the first analysis, termed the graduated or weighted mile kill, the research team weighted each mile-marker by the summed number of WVCs associated with it and used grad- uated symbols in ArcView 3.3 to display WVCs along each highway region. A 1:50,000 DEM with a pixel size of 30 m à 30 m was used to derive the hillshade (GIS database manage- ment, Banff National Park) for the highways in the study area and used as a backdrop for visualization. Figure 15 effectively shows where the WVCs occurred in relation to the valleys and rugged terrain of the Rocky Mountain landscape. The black arrows in the figures indicate where there was a large cluster- ing of WVCs, which generally was where the highway bisected a valley bottom. The TCH in Alberta has a consistent stretch of WVCs (14 to 24 roadkills at each mile-marker) from the Banff National Park east boundary to just west of Highway 40. The first westernmost gap in mortality numbers (indicated by the star symbol) is due to the presence of 4.5 km of fenced highway with one underpass, while the second gap in WVCs is due to a large lake and river system on the north side of the TCH. For the second analysis, termed high kill and low kill, the re- search team categorized each mile-marker segment as a high- kill or low-kill zone by comparing the summed number of WVCs associated with a single mile-marker segment to the av- erage number of WVCs per mile for the same stretch of road, for each of the five highways in the study area. If the summed number of WVCs associated with a single mile-marker seg- ment was higher than the average calculated per mile for the same highway, that mile-marker segment was considered a high-kill zone. Similarly, if the summed number of WVCs within a mile-marker segment was lower than the average for that highway, the mile-marker segment was listed as a low-kill zone. Each low- and high-kill zone (buffer) was color-coded and displayed on each highway segment along with the asso- ciated lakes layer. Other features in the landscape, such as human use and rivers, were not displayed because they were not available at the correct scale resolution. The lakes layer was digitized from 1:50,000 topographic maps and only displayed with an 800 m buffer around each highway in each region. To compare the level of aggregation of high-kill zones between highway regions, the research team measured the mean length of each high-kill aggregation. A high-kill aggregation was de- fined as a high-kill zone (buffer) with at least one neighboring high-kill zone. When standardized for roadway length, the majority of WVCs occurred on the TCH in Alberta (13.5 roadkills/mi), followed by the TCH in Banff (2.6 roadkills/mi), the TCH in Yoho (2.1 roadkills/mi), Highway 40 (2.1 roadkills/mi), and Highway 93 South (1.8 roadkills/mi). These rates of WVC were used to determine high- and low-kill segments in each highway region. This analysis produced 97.6 km of high-kill zones on all highways in the study area (Figure 16). In 52% of the cases, a high-kill zone had a neighboring high- kill zone. Highway 93 South had the most high-kill zones; however, the TCH in Banff had the highest mean length of aggregated high-kill zones, while the TCH in Yoho had the lowest mean length of high-kill zones (Table 27). The stan- dard deviations on TCH-BNP were high, indicating that the size of aggregations fluctuated highly. Figure 16 shows one main aggregation and a few single high zones on the TCH in Banff. In both the mile-marker visualizations (Figures 15 and 16), the DEM backdrops clearly show that high-kill zones are associated with valleys moving perpendicular to the direction of the highway. For example, there is a large aggregation (~13 km) of high-kill zones on Highway 93 South in Kootenay National Park that bisects key ungulate ranges in the valley bottoms of the montane region, at an elevation less than 1,240 m.
71 Figure 15. Weighted mile-markers derived from summed collisions by mile-marker on each road in each of the watersheds. Comparison of Hotspot Identification Techniques Visual analysis and observation versus analytical techniques. The pros and cons of the simple visual analysis of WVC versus more complex or analytical methods were discussed earlier (âSimple graphic techniques, one datasetâ). Essentially, with simple plotting of WVCs there is a tendency for roadkill points to overlap and visually mask the impor- tance of segments of highway that have a high density of WVCs. Modeling or analytical techniques permit a more de- tailed assessment of where WVCs occur, their intensity, and the means to begin prioritizing highway segments for poten- tial mitigation applications. Last, the identification and de- lineation of WVC clusters, which often vary widely in length
72 Figure 16. Density of kills at each mile marker on each road in each of the watersheds. depending on distribution and intensity of collisions, facili- tates between-year or multiyear analyses of the stability or dynamics of WVC hotspot locations. CrimeStat versus density-based techniques. Using the nearest neighbor CrimeStat analysis, 42 WVC clusters were produced and together occupied a total of 41 km (15%) of highway in the study area. The nearest neighbor CrimeStat technique was more conservative compared to the mile-marker density analysis; it identified less length of highway as a WVC hotspot. Additionally, the average length of WVC clusters was shorter than the density-based high-kill aggregations; however
73 Figure 17. Spatially accurate locations of carcasses from deerâvehicle collisions on State Route 89 in Sierra County, California. the CrimeStat analysis produced clusters that were not con- tinuous (Table 27). If the research team had selected a larger search radius for inclusion of roadkill points, fewer clusters would have been identified. CrimeStat also consistently pro- duced fewer clusters of WVCs than the mile-marker density analysis. Use of either technique for identifying WVC or roadkill hotspots may depend on the management objective. The CrimeStat approach is useful for identifying key hotspot areas on highways with many roadkills because it filters the road- kill data to extract where the most problematic areas lay. The mile-marker density analysis results in identifying more hotspot clusters on longer sections of highway. Although this approach appears to be less useful to management, it may be a preferred option where managers are interested in taking a broader, more comprehensive view of wildlifeâvehicle con- flicts within a given area. This broader view may be necessary not only to prioritize areas of conflicts but also to plan a suite of mitigation measures. The location of the larger clusters produced by the density analysis could be tracked each year to determine how stable they are or whether there is a notable amount of shifting between years or over longer time periods. This type of information will be of value to managers in ad- dressing the type of mitigation and intended duration (e.g., short-term vs. long-term applications). The nearest neighbor CrimeStat clusters followed a spatial distribution similar to the mile-marker high-kill zones (Fig- ure 13). The degree of overlap between the two techniques was high for three of the five highways. For example all the clusters on the TCH in Yoho fell within high-kill zone aggre- gations (Table 27). Similar patterns of overlap were found for the TCH in Alberta and Highway 40 in Kananaskis Country. Less overlap of clusters defined by the two techniques was found for Highway 93 South and the TCH in Banff. These results pose the questions: What mechanisms influence the spatial patterns of clusters derived by both techniques? Why is cluster overlap high in some areas, but low in others? Both techniques coincided perfectly on the TCH in Yoho (100% overlap), whereas they were most divergent on Highway 93 South in Kootenay National Park (roughly 50% overlap). The overlap of clusters on the other three highways was aligned with either one of the two endpoints above. From inspection of the WVC data on all five highways, the research team suggests that the amount of WVC cluster overlap from the two techniques is likely influenced by the density and distri- bution pattern of WVCs. High overlap was found on the TCH inYoho, where steep terrain dictates more or less where animals can cross the highway. There are few suitable loca- tions where wildlife can cross the TCH; thus, roadkills occur in clearly defined sections. Clusters will naturally overlap or be in proximity because collisions rarely occur outside the key highway crossing areas. On highways that have less topo- graphic constraints and more dispersed wildlife habitat, WVCs will tend to be greater in number and more uniformly distributed than on the Yoho highway. Cluster definition will tend to diverge, and clusters from the two approaches will be- come spatially isolated. The reason is that the density-based method has a tendency to accommodate outlying or marginal WVCs that normally would not cluster using CrimeStat. Hotspot Identification and Patterns for Different Species and Landscapes For this analysis, the research team selected one clustering technique (CrimeStat) and conducted a hotspot analysis for two different datasets: WVC carcass data from Canadian Rocky Mountains and Caltrans DVC carcass data for North- ern California. The data for Northern California was described previously in the âStudy Areaâ section and shown in Figure 17. CrimeStat version III 146 was used to determine the location of DVC carcass hotspots along SR 89 in Sierra County, California, and the five highways in the Canadian Rocky Mountains. For visual comparisons, the research team plotted all DVC data along SR 89 in Sierra County, Califor- nia. The following paragraphs describe the hotspot patterns and configurations, and examine how they may differ by species and the two landscape types. The mean number of DVCs along California SR 89 was 25.7 kills/mi for the 26-year period and equates to roughly 1 kill recorded per mile per year. The simple plotting of carcass
74 Highway Number of clusters Mean cluster length ± SD (km) Route 89 9 1.34 ± 0.26 Table 28. Descriptive statistics of the CrimeStat clusters delineating deerâ vehicle collision hotspot clusters on State Route 89, Sierra County, California. locations on SR 89 shows a high degree of overlap of DVC points. As was the case with the simple plots made of WVCs in the Canadian Rocky Mountains, identification of the actual hotspot location was difficult. The excessive overlap and what appears to be continuous clustering of DVC points was most likely a result of the high number and density of DVCs for the relatively short stretch of highway. Note that the California DVC data were obtained from a 26-year period along 53 km (~33 mi) of highway, compared to more than 500 points from the Canadian study area obtained from more than 250 km (~155 mi) of highway during a 7-year period. Nine CrimeStat clusters with a mean length of 1.34 ± 0.26 km (Table 28) were created on California SR 89 and occupied more than half of the 18 km section. Hotspots were associated with a variety of terrain types, but largely with mountainous terrain. Some of the hotspot clusters appear to be associated with valley bottom habitats, but a substantial amount can be linked with river courses in rugged terrain. Given the large number of hotspots identified along SR 89, management would need to prioritize which ones represented real safety and wildlife conservation concerns. The large 26-year dataset clouds the picture by having numerous DVCs on one stretch of highway. A sequential analysis of DVC hotspots in 5-year increments would help identify trends and patterns in hotspot distribution and bring to light the more problematic sections of highway. Interpretation, Appraisal, and Applications GIS Linkages to Hotspot Data The collection of wildlifeâvehicle collision carcass data is important for many reasons, but serves as important baseline information to guide the planning and management of road- way safety. Wildlifeâvehicle collision data can be used to quickly identify coarse-scale problematic areas on roads, as demonstrated with the techniques just discussed, and help guide efficient planning and decision making if transporta- tion improvement plans encompass WVC hotspots. This re- port has explored ways GIS-based information can be linked to hotspot data and their applications. With the hotspot data collected and stored in a database format, the next logi- cal step is to look at the types of GIS data that can be used to perform analyses for transportation management. These in- clude coarse-scale or preliminary analyses that can be used in rapid assessments to identify wildlifeâtransportation conflicts or to streamline planning and implementation of wildlife and safety needs. They are preliminary by nature, but are useful in initial examinations of the relationships between wildlifeâ vehicle collisions and the natural and man-made environ- ment around them. The type of data needed to identify the location of hotspots for wildlifeâvehicle collisions need not be spatially accurate, because mitigation measures usually address problematic areas that cover several miles of highway. For this reason, data accurate to the 1.0 mile-marker is suffi- cient. Existing agency carcass data are sufficient. Bridge rebuilding and retrofits are excellent examples where hotspot information can be utilized to identify areas where highway improvement projects can improve motorist safety and habitat connectivity for wildlife. The periodic reconstruc- tion of highway bridges that span waterways are excellent opportunities to benefit from structural work projects to im- prove wildlife and fish passage along riparian corridors by widening bridge spans or habitat enhancement.98 Today, state transportation planning exercises such as STIP (Statewide Transportation Improvement Program) are identi- fying key areas for transportation infrastructure investments. At the same time, state natural resource agencies have been mandated by Congress to develop comprehensive wildlife con- servation plans that address a full array of wildlife and habitat conservation issues.98 Coordination of both network plans in a timely and integrated fashion would be a significant contribu- tion to streamlining environmental concerns in transportation planning. A recent example of integrating agency roadkill information with standard GIS data for sustainable trans- portation planning took place in Vermont.9 The transportation department (VTrans) developed a centralized database of roadkilled wildlife carcass, wildlife road crossing, and related habitat data for individual species throughout the state. To expand and improve wildlife carcass reporting data, a partner- ship and recording procedures were developed with VTrans field and district staff enabling them to record a new array of wildlife carcass information. With their wildlife carcass infor- mation they performed a GIS-based wildlife linkage habitat analysis using landscape-scale data to identify or predict the lo- cation of potentially significant Wildlife Linkage Habitats (WLHs) associated with state roads throughout Vermont. The project relied on readily available GIS data including (1) land use and land cover data, (2) data on developed or built areas, and (3) contiguous or âcoreâ habitat data obtained from the University of Vermont. The components that composed the overall GIS data layers were then ranked in accordance with their relative significance to creating potential WLH. The analysis, in conjunction with the newly updated wildlife carcass data, provided a science-based planning guide that will aid VTrans in understanding, addressing, and mitigating the
75 effects of roads on wildlife movement, mortality, and habitat and public safety early in the design process for transportation projects. There are a variety of GIS modeling approaches today, from simple to more complex models requiring high-resolution and spatially explicit data. Most GIS modeling used for trans- portation planning purposes tends to be coarse scale and does not require specially developed GIS data layers.13,65,212 Like GIS-based data on animal movements, hotspot information can be used to identify problematic areas and thus integrate mitigation where highway improvement capital will be invested. Hotspot areas that are associated with existing below-grade crossings (e.g., drainage culverts and bridges) can be identified by linking GIS data, allowing structural and land planning recommendations to be made to improve perme- ability at unsuitable passages. In another example, WVC carcass data were used along Interstate 90 in Washington to evaluate the relationship be- tween hotspot clusters and important landscape characteris- tics.214 Carcass density was mapped using the approach described earlier, classifying segments as high, moderate, or low ungulate-kill density. A classification tree analysis (using S-Plus 2000) was used to determine the importance of 10 landscape- scale variables (GIS layers comprising road and landscape fea- tures) in the study area. Classification tree analysis is well suited for analysis of GIS spatial data. Being a non-parametric tech- nique, it involves no assumptions of normal distribution, works well with categorical data, and is robust to the relatively subjec- tively determined sample sizes inherent with GIS raster data. Further, linking these coarse-scale hotspots with environmen- tal data (e.g., terrain, habitat suitability, zones of animal move- ment) can provide a relatively quick and reliable project-level or district-level assessment of how to prioritize mitigation activities directed at wildlifeâvehicle collisions. Conclusions In this section the research team suggests guidelines for hotspot application. Data on hotspots of WVCs can help transportation managers increase motorist safety and habitat connectivity for wildlife by providing safe passage for wildlife across busy roadways. Knowledge of the geographic location and severity of WVCs is a prerequisite for devising mitigation schemes that can be incorporated into future infrastructure projects such as bridge reconstruction and highway expan- sion. Hotspots in proximity to existing below-grade wildlife passages can help inform construction of structural retrofits that can help keep wildlife off roadways and increase habitat connectivity. The WVC data that transportation departments currently possess are suitable for meeting the primary objective of identifying hotspot locations at a range of geographic scales, from project-level (< 50 km of highway) to larger district- level or state-wide assessments on larger highway network systems. The spatial accuracy of WVCs is not of critical importance for the relatively coarse-scale analysis of where hotspots are located. To determine site-specific factors that contribute to WVCs, more spatially accurate data are required. Thus, WVCs referenced to a mile-marker system will be sufficient for transportation agencies to identify the location of problematic areas for motorists and wildlife. WVC data with greater spatial accuracy are equally useful in determining the location of hotspots; however, they are not essential to begin examining highwayâwildlife conflict areas. The research team has outlined and described various tech- niques available that can help delineate WVC hotspots. Sim- ple plotting of collision points is a relatively straightforward means of identifying problematic areas; however, as sample sizes increase, the tendency for roadkilled carcasses to overlap (hide other points) increases. The length of highway exam- ined, the number of animals killed, and time period of data collection all influence the density of collision points. Other factors such as terrain, wildlife abundance, and wildlife habitat quality adjacent to the highway will further affect the spatial distribution (random/continuous or non-random/clustered) of WVCs on a given highway. Modeling or analytical tech- niques permit a more rigorous assessment of where WVCs are likely to occur, their intensity, and the means to begin priori- tizing highway sections for mitigative actions. The nearest neighbor CrimeStat method essentially pinpoints the location of WVC hotspots, whereby the segmental analyses of WVC densities provide a more comprehensive evaluation of mitiga- tion options and prioritization of mitigation schemes based on cost-benefit, scheduling of transportation projects, or severity of motorist safety concerns. Collection of WVC data (both reported vehicle collision and carcass collection data) by transportation departments will be increasingly beneficial, especially if the collection procedures are more systematic. Currently, in many state agencies, WVC data collection is not consistent and varies from district to district. The research team is not aware of many state transportation departments that have consis- tently used WVC hotspot data for decision making in transportation projects or strategic planning with future infrastructure plans such as STIP in mind. Systematic data collection and protocols will allow for cost-effective use of the data and greater management benefits by providing important baseline information for planning environmen- tal mitigation in projects. Further, properly collected pre-mitigation data provide a critical reference point for ultimately assessing the performance of mitigation meas- ures that are adopted. See Appendix E for a literature review of papers that have addressed hotspot identification.
76 3.4 Influence of Roads on Small Mammals Introduction Highways have the potential to affect the abundance and distribution of small mammals. Differences in the density of many small mammals have been reported when road verges have been compared to the habitats beyond them.2,1,19 This density difference may be due to structural or vegetative dif- ferences in habitat, water runoff, or the additional impact of noise, vibration, deposition of road salt or other chemicals, or differential rates of predation between the verge and adjacent land. Highways may also act as barriers or partial barriers to movement.186,143,153,103,49,107,170,36 Such barriers may indirectly lead to population impacts due to the reduced probability of genetic flow and demographic ârescueâ (inflow of animals to counter local extirpations caused by random events) for small populations. Direct mortality of small mammals on the high- way surface186 appears to have variable effects on population density2 as well as demographic changes such as the dispro- portionate loss of sex or age classes that tend to disperse. While highways have been well established as contributing to such impacts,186,143,153,103,49,107,170,36 to what extent is not entirely clear. Questions remain as to what impact highways, includ- ing traffic volume, have on the diversity and density of species found in the dry forested ecosystems typical of much of the mountainous region of western North America, to what ex- tent the effects extend beyond the highway, and if the impacts are due to the highway specifically or to the presence of a dis- turbed ROW generally. Both direct effects (animal mortality) and indirect effects influence animal response to the roaded landscape. Direct ef- fects such as actual road kills, impact all species, but collisions with larger wildlife species (deer, elk, moose, caribou, and large carnivores) pose the most risk to driver safety and result in higher automobile damage and human injury. Knapp (www.deercrash.com/states/data.htm) showed that for the five-state Upper Midwest (Illinois, Iowa, Michigan, Wisconsin, and Minnesota), 121,584 deer-vehicle collisions caused over $206.6 million in vehicle damages, but more important, re- sulted in 35 human deaths and 4,666 injuries from 2003 to 2004. Direct effects are on the rise, and so are the costs to cit- izens. Indirect effects of roads on wildlife putatively are as im- portant to ecological communities as are direct effects such as mortality. The most commonly reported indirect effects in- clude (1) loss of habitat, (2) reduction of habitat quality, (3) fragmentation of once âmore continuousâ habitat with asso- ciated increases in edge density and edge buffer effects, (4) habitat disconnectedness, and (5) barrier effects. One com- plication is that the landscape consequences from indirect effects are interrelated suggesting that parsing out the contri- bution of each effect will take a long-term experimental approach. Such an approach is not possible or feasible in the time available for this project. However, permeability can be assessed and species responses to roaded landscapes can be measured. The null hypothesis that the research team tested is that indirect effects, taken as a whole, have little significant effect on animal population response. Significant was defined as greater than 10% deviation, after background variation has been taken into account. The first level predicted responses were an expected speciesâ presence or absence, composition, and relative abundance to change at increasing distances from the road if habitat quality was reduced, if habitat frag- mentation was increased, if there were edge buffer effects, if there was habitat disconnectedness, and if there were barrier effects. Assessment of causality to a specific indirect effect was not possible or practical within the time schedule and funding available. The summation of the effects, however, was simple to document. Animal response near roads could be compared with a control response to a non-roaded area. The term âre- sponseâ means the difference in the number of small mam- mal species diversity and their relative abundance. Jaeger et al.133 explained that roads and traffic can affect the persis- tence of animal populations in four distinct ways: (1) a de- crease in habitat amount and quality, (2) increased mortal- ity, (3) barrier effects that prevent animals from accessing resources across the road, resulting in (4) fragmented and subdivided populations. The small-mammal research in Utah and British Colum- bia allowed the impact of roads on habitat quality for small mammals to be assessed at varying distances from the road. If habitat quality declined due to road traffic, the research team expected a decline in the numbers and relative abun- dance of small-mammal species nearer to roads. To investi- gate this question, the research team compared the relative abundance of small mammals at varying distances from a major interstate highway in Utah and a two-lane highway and high-voltage transmission-line ROW in British Columbia. These locations allowed the research team to compare the ef- fects of two very different types of roads while simultaneously addressing the effect of distance from the ROWs. For this field effort, the research team selected sites in west- ern British Columbia and in the Intermountain Region of Utah to determine if any general response of small, terrestrial vertebrates exists for arid and mesic sites. There is tremen- dous variation across the North American continent in terms of vegetation cover, topography, levels of urban develop- ment, land use practices, road density, and traffic volume, as well as differences in the typical species diversity, richness, and abundance in local areas. Yet, it was impossible to cap- ture that entire variation in one study. Nevertheless, this is the case with most ecological studies, and there is an impera- tive to capture the basic ecological responses and apply those
77 fundamental principles to mitigation and management. The approach for this study was to develop ecological principles that have conceptual generality and that can be applied broadly. The caveat of course is the necessity for gathering local, empirical data that will inform the programming, plan- ning, design, and construction phases of building, upgrading, and maintaining roads. For this effort, sites characterized by natural vegetation located next to roads were selected and compared to sites distant from the road. Indirect effects have been suggested to operate within 100 m of a road; however, as a precaution, we designed our sampling protocol to detect changes that may occur up to 600 m or more from the road. Small mammals have relatively small home ranges and limited mobility, and the research team expected that results should be evident within 600 m from the road. The research team measured small-mammal speciesâ presence or absence, composition, and relative abundance through trapping periods in the sum- mer months of 2004 and 2005. In both Utah and British Columbia, the research team sampled at increasing distances from the road to address these putative effects: ⢠If habitat quality is reduced near the roadway, the presence or absence, composition, and relative abundance of species is expected to change at increasing distances from the road. ⢠If there are edge buffer effects along the road, there is ex- pected to be a zone close to the road where the presence, abundance, and composition of species will be dramati- cally influenced. Research Approach: Methods and Data The work for this segment was conducted in Utah and British Columbia in two very different habitats. Utah is lo- cated in the Intermountain West of the United States. The study site was composed mainly of sagebrush (Artemisia spp.) habitat, and the road verge (ROW) is largely non-vegetated. Conversely, the British Columbia site in Canada is heavily forested with a densely vegetated road verge. The research team adapted its sampling scheme to maximize capture of small mammals for these very different sites. The following paragraphs describe how the field work was conducted in each site. The research team began work in Utah in 2004 as part of an ongoing study and continued in 2005. In British Columbia, the research team conducted the field work dur- ing summer 2005. Utah Permeability and small-mammal trapping. This study was conducted in the high-elevation desert region of the Great Basin of western Utah near Beaver, Utah (latitude 38°16â² N and longitude 112°37â² W), adjacent to Interstate 15 (I-15), a four-lane divided highway with an average of 16,015 vehicles/day. Elevation ranged from 1,700 to 1,900 m (5,500 to 6,300 ft). Vegetation cover was dominated by big sage- brush (Artemisia tridentata) with an occasional inclusion of pinyon pine (Pinus edulis) and juniper (Juniperus osteosperma) trees. The road verge included sagebrush and grassy vegetation or was completely non-vegetated. The weather was characterized by below-freezing temperatures and snow cover during the winter and high temperatures during the summer. Maximum temperatures occasionally exceeded 38°C (100°F) and minimum temperatures were usually above â23°C (â10°F), with annual mean temperature of 8.6°C (47.4°F). Annual precipitation (in the form of rain and snow) was less than 305 mm (12 in.), and came prima- rily during winter, early spring, and late summer. Relative humidity was very low and evaporation potential was high. Prolonged periods of drought are frequent in the region. The soil on the trapping sites was composed mainly of fine sand deposits with occasional volcanic rocky areas. Study sites were established in sagebrush-steppe vegetation along 20 mi (~32.2 km) of Interstate 15, centered on UTM (NAD27) X = 354471 Y = 4248267. Small-mammal sampling was con- ducted exclusively in sagebrush habitat on both sides of the road (Figure 18). Because changes in sagebrush habitat were detected along the road, the research team designated the dif- fering habitats A, B, and C. Small mammals were live and lethal trapped from 30 May to 14 August in 2004 and from 17 June to 18 August in 2005. The trapping design was altered between the 2004 and 2005 field seasons to maximize the useful information gleaned. In 2004, trapping webs were used to assess road influence on small-mammal communities. In 2005, the research team used trapping lines to compare the Utah results with the British Co- lumbia trapping scheme. During summer 2004, 12 transects were completed with 2 trapping webs per transect, for a total of 24 webs. The first trapping web was placed at 50 m (close) and the second at 400 m (distant) from the road (Figure 19). Each web was composed of eight segments extending 50 m outwards from a central point. Each segment had six trapping stations of two traps each, located 5, 10, 20, 30, 40, and 50 m from center, with one trapping station located at the center of the web for a total of 98 traps [half lethal (snap) and half live (non-lethal)] per web and a total of 2,352 traps for the 24 webs. During summer 2005, 3 trapping lines were placed par- allel to the road along each of 5 transects (Figure 19) for a total of 15 trapping lines. Lines were placed at increasing distances from the exclusion fence: at 0 m (close), 200 m (mid), and 600 m (distant). Each line was 150 m in length and contained 30 traps total, for a total of 450 traps for the 15 trapping lines. The research team completed a total of 8,406 trap-nights. For
78 Figure 18. Sagebrush habitat in southwestern Utah where small-mammal trapping was conducted. Close Close Mid Distant Distant 2004 2005 Figure 19. Schematic representation of sampling schemes in 2004 and 2005. safety reasons, the ROW verge between the road edge and the 2.4 m deer exclusion fence was not sampled because of very high traffic volume. All traps in both sampling schemes were baited with a mix- ture of horse grain and peanut butter, and checked on three consecutive mornings and afternoons (lethal traps only). Upon capture, all animals were identified, sex determined, measured, marked, and released. Dead animals were removed from the study site. Data analyses. Web-based data analysis for 2004 em- ployed a distance method described by Anderson et al.5 that utilizes first capture locations for each individual and distance to the center of the web plot. The software program Distance 4.140,41 was used to calculate densities and variance estimates. For analysis, capture data was pooled in âclose websâ and âdis- tant websâ because of the low number of animals sampled in each web. Estimation was only possible for the most abundant species (i.e., > 30 captured individuals per pooled database) or for all small mammals combined. Density estimations in Dis- tance were obtained by every possible combination of models (uniform, half-normal, hazard, and negative exponential) and adjustment terms (cosine, simple polynomial, and Hermite polynomial). See Appendix F. Final model selection was based on Akaikeâs Information Criterion (AIC) value and on model performance. Each dataset was used in its entirety without truncation. Intervals used in Distance (0.0, 7.5, 15, 25, 35, and 45 m) were the midpoints between trap-stations. Resulting densities in close and distant webs were tested for significant differences using Wald test.
79 Analysis for trapping line data in 2005 was conducted using a closed population mark-recapture method in Pro- gram MARK 4.3.243 Closure was assumed given that trapping occurred in a sufficiently brief interval, and the removals were known and accounted for in the analysis.246 A Huggins Closed Capture estimator was applied to obtain abundance estimates and the respective confidence intervals. Capture data was pooled in three groups representing increasing distances from the road (close, mid and distant). Estimates were ob- tained for the null and other models to represent variability in capture and recapture probabilities. Models that did not converge were discarded. Remaining models were selected based on AIC value and averaged to obtain final estimates of abundance. Differences in abundance estimates were tested using Wald test. The ShannonâWiener diversity index (H) was used to compare community diversity at different distances from the road.17 The index was calculated for each web or trapping line in all transects and tested for distance-related differences by the Wilcoxon paired-sample test for 2004 data and by Friedmanâs test for 2005 data.250 The least significance differ- ence (LSD) multiple-comparison test was used with 2005 data to determine if any pair of distances (close vs. mid; close vs. distant; mid vs. distant) was significantly different.218 British Columbia Permeability and small-mammal trapping. Field sites were located in the Rocky Mountain Trench of southeastern British Columbia at elevations of 830 to 1000 m, centered on 50.1° N by 115.8° W. Eight study sites were selected for each of two treatments (Figure 20): along a 30 km stretch of Highway 93/95 (mean total ROW width 57 ± 9 m SD, including 12 m wide highway), and along 40 km of a high-voltage transmission line (mean ROW width 62 ± 8 m SD). The transmission-line ROW was composed of a rough track, but no developed road (Figure 20, right panel). Highway and transmission-line sam- pling was equally distributed within the trapping period. The most recent data for highway traffic volume was recorded in 2001, approximately 25 km south of the southernmost high- way site. Traffic volume averaged 1,791vehicles/day annually, including a peak of 2,043 vehicles/day during July and August (S. Daniels, Ministry of Transportation, Cranbrook, British Columbia, unpublished data). Traffic volume along the trans- mission line was essentially nil (estimated 1 to 5 vehicles/day average on an annual basis; the research team saw <1 vehi- cle/site/day of trapping or baiting). Traps were placed on three transects: at 50 m, 300 m, and 500 m distant from and paralleling the road. The research team consistently set the 50 m transect 20 m into the forest to standardize its distance from a change in habitat type. This placement resulted in an average distance of 49 m from the highway centerline, or 51 m from the transmission line cen- terline. Sites were not randomly selected. Rather, the research team used 1:20,000 orthophotos and field inspections to locate all points along the transmission line. The study area had pre- dominantly mesic soils; continuous or nearly continuous for- est cover; and no minimal or major roads, large cut-blocks, significant habitat shifts, or other sampling sites within 600 m radius on at least one side of the ROW. An equal number of highway sites fitting the same criteria were selected. Each transect was 150 m long and oriented parallel to the ROW (326° to 360°). The research team established 16 trap stations per transect (10 m intervals), with two snap traps (Snap-E Mousetrap, Kness Mfg. Co., Inc., Albia, Iowa) occu- pying each trap station (Figure 21). The research team used a grease gun to bait traps with a mix of peanut butter and rolled oats, placed them unopened for 1 week, replaced the bait, and left them unopened for an additional week (i.e., a 2-week pre- bait). Then the traps were baited again, set for 2 nights, and Figure 20. Right-of-way types: Highway 93/95 (left) and high-voltage transmission line (right).
80 Figure 21. Schematic of site layout for a highway site. checked each morning. Animals trapped were removed, tentatively identified to species and bagged, then positively identified, sexed, weighed, and measured later on the day of capture. The research team completed all capture work from 14 through 18 June and 4 through 8 July 2005. The study site was within the Interior Douglas-Fir biogeo- climatic zone (IDF) in the provinceâs dry climatic region.35 Within the IDF, six âsite seriesâ (descriptors of potential cli- max vegetation and soil moisture) have been described. The research team judged the forested portion of all sites to be composed historically of the same predominant site series: Douglas-fir (Pseudotsuga menziesii), lodgepole pine, (Pinus contorta), pinegrass (Calamogrostis rubescens), and twinflower (Linnaea borealis). However, because of topographic variabil- ity, past wildfires, and partial-cut logging, study sites were mid-seral mixes of Douglas-fir, lodgepole pine, western larch (Larix occidentalis), and ponderosa pine (P. ponderosa), with a minor component of trembling aspen (Populus tremuloides) and paper birch (Betula papyrifera). The research team did not measure habitat variables, but did record general habitat con- ditions subjectively. Crown closure was typically 40% to 60%, with portions of some sites ranging from about 10% to 80%. At all sites, the dominant understory plant was pinegrass with roughly 5% to 20% cover, but up to approximately 50% cover in some small openings of past disturbance. Other common understory species in all sites included soopolallie (Shepherdia canadensis), birch-leaved spirea (Spiraea betulifolia), common snowberry (Symphoricarpos albus), saskatoon (Amelanchier alnifolia), Douglas-fir saplings, and heart-leaved arnica (Ar- nica cordifolia). Tall Oregon grape (Mahonia aquifolium), showy aster (Aster conspicuus), twinflower, wild strawberry (Fragaria virginiana), and a variety of mosses contributed to the greater ground cover in moister microhabitats or cool aspects. Bluebunch wheatgrass (Agropyron spicatum), june- grass (Koeleria macrantha), arrow-leaved balsamroot (Bal- samorhiza sagittata), and kinnikinnick (Arctostaphylos uva- ursi) were more commonly present in drier locations with a sparse understory and less pinegrass. Small patches under dense Douglas-fir cover had essentially no understory. While downed woody debris was sporadically present, there was typ- ically little of this because of the relatively young forest age and its history of past disturbance. All ROWs were predominantly vegetated by wild and/or agronomic grasses and wild straw- berry, with variable cover of other forbs, no trees or downed woody debris, and minimal shrub cover. Data analyses. The research team compared the number of species trapped (and abundance of each) among transects and among treatments. Where sample sizes permitted, the re- search team also compared weights of adult males, weights of adult females, sex ratios and juvenile:adult ratios among tran- sects and treatments using t-tests and Ï2 tests as appropriate using the program JMP IN (SAS Institute, Inc., Cary, North Carolina). Findings and Results Utah In 2004, a total of 11 species were captured; two species were captured exclusively in areas close to the road (rock squirrel [Spermophilus variegates] and sagebrush vole [Lem- miscus curtatus]), and two species were captured exclusively distant from the road (piñon mouse [Peromyscus truei] and
81 No. individuals captured Genus species Common name Close (50 m) Distant (400 m) Peromyscus maniculatus Deer Mouse 124 120 Perognathus parvus Great Basin Pocket Mouse 39 54 Tamias minimus Least Chipmunk 27 18 Dipodomys microps Chisel-Toothed Kangaroo Rat 5 1 Rethrodontomys megalotis Western Harvest Mouse 4 3 Peromyscus boylii Brush Mouse 3 11 Neotoma lepida Desert Woodrat 2 1 Lemmiscus curtatus Sagebrush Vole 1 0 Spermophilus variegatus Rock Squirrel 1 0 Ammospermophilus leucurus White-Tailed Antelope Squirrel 0 4 Peromyscus truei Piñon Mouse 0 2 Table 29. Species detected at different distances from Interstate 15 in 2004. No. individuals captured Genus species Common name Close (0 m) Mid (200 m) Distant (600 m) Perognathus parvus Great Basin Pocket Mouse 12 4 2 Peromyscus maniculatus Deer Mouse 10 1 1 Dipodomys microps Chisel-Toothed Kangaroo Rat 8 11 2 Tamias minimus Least Chipmunk 2 1 0 Sylvilagus audubonii Desert Cottontail 2 0 0 Lepus californicus Jackrabbit 1 0 0 0 Neotoma lepidaDesert Woodrat 1 0 Table 30. Species detected at different distances from Interstate 15 in 2005. white-tailed antelope squirrel [Ammospermophilus leucurus]). The remaining seven species were captured at both distance classes from the road (Table 29). During 2005, a total of seven species was captured (Table 30) with three species caught exclusively close to the road (desert cottontail [Sylvilagus audubonii], jackrabbit [Lepus californicus], and desert woodrat [Neotoma lepida]). Results from density and abundance comparisons between different distances from the road indicate that, in most cases, small sample sizes prevented a precise estimation to discern clear trends. Despite the lack of statistical significance, in 2004 deer mice (Peromyscus maniculatus) had lower densities closer to the road (Figure 22) while Great Basin pocket mice (Perog- nathus parvus) exhibited the opposite trend (Figure 23). Re- sults of ShannonâWiener diversity index (H) analysis revealed there were variations in diversity trends in different years. Dur- ing 2004, the ShannonâWiener diversity index (Table 31) was significantly higher in areas distant from the road (Wilcoxon Z = â2.224, P = 0.026) as compared to results in 2005 (Table 32) in which diversity peaked close to the road (Friedman test Ï2 = 6, P = 0.05; LSD Hclose > Hmid and Hclose > Hdistant, P < 0.05). For all species in 2004, the overall trend was increased density with increasing distance from the road (Figure 24); however, the result was not statistically significant (Wald test Z = â0.49, P = 0.63). However, the transects were established along about 20 mi (â¼32.2 km) of habitat adjacent to Interstate 15, and the research team noticed changes in sagebrush habi- tat, especially in Area B, an area geographically between Areas A and C. Area B had a noticeably different habitat (a distinct sagebrush habitat type), so the research team conducted the same analysis for all species but segregated the data by three distinct geographic areas. Different trends were found in dif- ferent areas (Figure 25). Densities recorded in Area B were sig- nificantly greater than in Area A for both close (Wald test Z = â2.15, P = 0.03) and distant webs (Wald test Z = â3.07, P = 0.002), and both were significantly higher than in Area C for close (Wald test Z = â2.84, P = 0.004) and distant webs (Wald test Z = â2.97, P = 0.003). For 2005, there was a statistically sig- nificant trend toward higher abundance near the road (Wald test Z = 3.99, P < 0.001) than distant from it (Figure 26). British Columbia The research team trapped 401 individuals, including nine species of rodents and two species of shrews. The three most commonly trapped species (Table 33) were deer mice
82 Diversity Index Transect Hclose Hdistant 1 0 0 2 0.8 1.27 3 0.8 1.01 4 0 0.3 5 0.35 0.56 6 0.35 1.04 7 1.17 1.3 8 0.43 0.6 9 0.6 0.67 10 0 0.5 11 0.14 0 12 0.99 0.81 Table 31. Values of ShannonâWiener diversity index (H) estimated for 2004 by transect in close and distant webs in Utah. Diversity Index Transect Hclose Hmid Hdistant 1 0.67 0.69 0 2 0.64 0 0 3 1.31 0 0.64 4 1.35 1 0 5 1.04 0.45 0 Table 32. Values of ShannonâWiener diversity index (H) estimated for 2005 by transect in close, mid, and distant trapping lines in Utah. D en si ty E st im at es (P . p ar vu s) close distant Distance from Road 29.6 20.2 0 10 20 30 40 50 60 70 Figure 23. Density estimates of Perognathus parvus in 2004 at different distances from the road. (Peromyscus maniculatus), southern red-backed voles (Clethrionomys gapperi), and yellow-pine chipmunks (Tamias amoenus). True trapping effort was slightly uneven among treatments, sites, and transects because of various trapping impediments that are inherent to field work in which environmental variables are not always controllable (Table 33). Trapping problems included several brief but heavy rains that snapped traps, larger animals stepping on traps or otherwise snapping them, non-functional traps, usually due to soil thrown up by the impact of raindrops, and a few captures of songbirds which prevented the capture of small mammals. As a result, realized trapping effort was 78% of attempted trapping effort. Capture rates, adjusted for realized trapping effort (Table 33), were low and un- evenly distributed spatially for most species. Total capture rates were 9.8 and 12.6 captures per 100 trap-nights, in re- lation to attempted and realized trapping effort respectively. Six species were more abundant at highway sites, while five were more abundant at transmission-line sites. Five species were present at more highway than transmission-line sites and four were present at more transmission-line than high- way sites. The low sample sizes and clumpy, among-site dis- tribution of captures prevented within-species comparisons of spatial distribution in relation to transect, with the ex- ception of deer mice (Figure 27). For this species, there was no difference in capture rate among transects for highway sites (Ï2 P = 0.93) but a difference was realized for trans- mission-line sites (P = 0.04). Comparing highway to trans- mission-line sites for each transect, a marginally significant 83.9 168.3 0 50 100 150 200 250 300 350 400 450 close distant Distance from Road D en si ty E st im at es (P . m an icu lat us ) Figure 22. Density estimates of Peromyscus manicu- latus in 2004 at different distances from the road.
83 difference was evident for deer mice between treatments only for the 600 m transect (ROW P = 0.32, 50m P = 0.47, 300m P = 0.83, 600m P = 0.05). For both male and female deer mice, animal weights did not differ among transects for highway or transmission-line sites (ANOVA P > 0.44 for all comparisons; Figure 28). Com- paring highway to transmission-line sites for each sex and transect, no differences in weight were evident (t-test P > 0.24 for all comparisons) with the possible exception of males on the 600 m transect (P = 0.06). There was no difference in sex ratio among transects for highway sites (Ï2 P = 0.88), but there was some evidence of a difference among transects for transmission-line sites (P = 0.07; Figure 29). Comparing highway to transmission-line sites for each transect, there was weak evidence of a difference between treatments only for the 600 m transect (ROW P = 0.92, 50 m P = 0.79, 300 m P = 0.32, 600 m P = 0.09). Juvenile:adult ratios did not vary significantly among tran- sects for either treatment, or among transect for any treatment (Ï2 P > 0.17 for all comparisons except highway vs. transmis- sion line for ROW transect, for which P = 0.08; Figure 30). Sample sizes were relatively low, likely due to a combination of a low realized trapping effort, some periods of inclement weather that may have limited animal activity and survivor- ship, and the timing of sampling effort. The field season oc- curred in early June and July when recovery from the annual winter population decline would have been incomplete for some species.225 Combining all transects per site, similar pat- terns of diversity and abundance were evident between trans- mission-line and highway sites, although distribution was clumpy for most species. With the exception of deer mice and yellow-pine chipmunks, each species occurred at fewer than half of the sites, despite being common at some of those sites. For any given transect distance, only deer mice were trapped at more than half of the sites. This clumping suggests that within the forest, microhabitat or some other localized effect was stronger than any influence of distance to the highway. Species diversity was lowest in ROW transects than any other transect. However, there is no strong evidence to suggest that this observation was related to anything beyond a shift from native forest at 50, 300, and 600 m transects, to the less complex structure and vegetation of the disturbed habitat in the ROW. For example, optimal habitat for yellow-pine chip- munks appears to be open forest with abundant woody debris; southern red-backed voles are most common in mature forests with abundant shrub and ground cover; heather voles are associated with a dense shrub layer and abundant woody debris; and in the dry interior of British Columbia where this study area was located, long-tailed voles are associated with shrub thickets.178 Thus, ROWs with no forest or downed woody debris and few shrubs would be expected to have fewer of these species, independent of the presence of a highway nearby. The only species trapped more often on ROW tran- sects was the western jumping mouse, consistent with its 0 50 100 150 200 250 300 350 close distant Distance from Road D en si ty E st im at es (S ma ll M am ma ls) 115.4 148.8 Figure 24. Density estimates of small mammals in 2004 at different distances from the road. 81.3 36.2 272.5 593.6 31.7 53.50 200 400 600 800 1000 1200 close distantclose close distantdistant Area A Area B Area C Distance from Road (per geographic areas) D en si ty E st im at es Figure 25. Density estimates of small mammals in 2004 at different distances from the road in three distinct geographic areas.
84 preferred habitats, which are more typically associated with ROWs than forest (i.e., rich meadows with abundant forbs).178 Had there been a strong effect of highway proximity, differ- ences between the highway and transmission-line sites should have been found for the ROW transects. In fact, no species were more common in the transmission-line ROW than in the highway ROW with the exception of the aforementioned western jumping mice, which were found at only two sites sep- arated by 1.5 km. Interestingly, no presence was detected at a site between the two, which appeared to be largely identical 57.35 59.05 7.270 20 40 60 80 100 120 140 160 180 close mid distant Distance from Road Es tim at ed A bu nd an ce (N ) Figure 26. Density estimates of small mammals in 2005 at different distances from the road. Note: Blanks indicate no captures for that species. Highw ay (no. animals/no. sites) Transmission Line (no. animals/no. sites ) Species In ROW 50 m Out 300 m Out 600 m Out Hwy Total In RO W 50 m Out 300 m Out 600 m Out Tr Ln Total Gran d Total Sorex cinereus Common Shrew 1/ 1 1/ 1 1/1 1/1 2/2 3/ 3 Sorex monticolus Dusky Shrew 0/ 0 2/2 2/2 2/ 2 Glaucomys sabrinus Northern Flying Squirrel 1/ 1 1/ 1 0/0 1/ 1 Tamias amoenus Yellow-pine Chipmunk 1/ 1 9/ 4 3/ 3 4/ 2 17/ 6 3/3 3/1 3/2 9/4 26/10 Clethrionomys gapperi Southern Red- Backed Vole 16/ 2 8/ 2 9/ 3 33/ 3 1/1 10/2 11/3 44/ 6 Microtus longicaudus Long-Tailed Vole 1/ 1 1/ 1 3/2 1/1 2/2 6/3 7/ 4 Microtus pennsylvanicus Meadow Vole 1/ 1 1/ 1 3/ 2 5/ 3 1/1 1/1 2/1 7/ 4 Phenacomys intermedius Heather Vole 1/ 1 2/ 2 6/ 5 9/ 5 2/2 1/1 3/2 12/ 7 Mus musculus House Mouse 1/ 1 1/ 1 0/0 1/ 1 Peromyscus maniculatus Deer Mouse 28/ 8 29/ 6 34/ 8 35/ 8 126/ 8 41/8 29/8 34/7 57/8 161/ 8 287/16 Zapus princeps Western Jumping Mouse 0/ 0 7/2 2/1 2/1 11/2 11/ 2 Table 33. Small-mammal species trapped in British Columbia on transects within high- way and transmission-line rights-of-way (ROWs) or at varying distances from the ROW centerlines.
85 0 10 20 30 40 ROW 50 600300 Transect Pe rc en t o f C ap tu re s highway n=126 powerline n=161 Note: Data adjusted for realized trap effort and non-availability of traps due to the capture of other species. Figure 27. Distribution of deer mouse captures among transects for each treatment. habitat. This observation suggests a strongly uneven distribu- tion, and the likelihood that the greater abundance at the transmission-line sites was a chance effect. Deer mice provide a better opportunity to compare trans- mission-line ROW to highway ROW transects, given this species employs very broad habitat-use patterns and distribu- tion.178 It was also typically abundant in the samples for this study. There were no observed differences between transmis- sion-line and highway ROW samples for deer mouse abun- dance, sex ratio, and male weight or female weight. There was, however, a weak suggestion of a greater proportion of juveniles in the sample on the highway site. The latter observation could be taken to be indicative of a highway effect, with juveniles perhaps being displaced to lower quality habitat or alterna- tively having higher survivorship. Still, there was evidence of differences among treatments at the 600 m transect for deer mouse abundance, as well as male weight and sex ratio. It would be extremely unlikely that a highway effect would be evident at the 600 m transect without being obvious at the 300 m, 50 m, and ROW transects. This observation suggests a high likelihood of any differences between treatments in deer mouse variables being related at least as much to chance, microhabi- tat, or other localized effects as to the presence of the highway. Adams and Geis2 conducted similar research in the south- eastern, midwestern, and northwestern United States. Their results also suggest that the effect of road proximity differs by species. When the percentage composition they report for deer mice is converted to absolute numbers, abundance was consistently higher near interstate than county highways. Whether this phenomenon was related to the larger area of grassy habitat along interstate highways is not clear, but it does suggest that large highway size and volume did not have an overwhelmingly negative effect on deer mice. In keeping with that observation, the research team found no consistent regional patterns of deer mouse abundance in relation to dis- tance from highway. The only other species reported by Adams and Geis2 that had more than one capture in the British Columbia study area was the meadow vole, for which there was a general tendency to be more common closer to roads, but no consistent pattern with respect to highway size. Geographically closer to the British Columbia study area was the field site of Mills and Conrey170 in northwestern Montana. In forested habitat adjacent to the ROW of two 2-lane high- ways, southern red-backed vole abundance was greater on a trapping grid close to the highway at one site but greater on a grid distant from the highway at the other site. Deer mice and chipmunks (combining yellow-pine chipmunks and red- tailed chipmunks [Tamias ruficaudis]) appeared to be mar- ginally more abundant on the grids nearest to the highways. At a site along a four-lane highway, rodent abundance on a trapping grid straddling the ROW-forest boundary was com- pared to a second grid farther from the highway and entirely in the forest. In that case, deer mice were more abundant near the highway, whereas red-backed voles and chipmunks were most abundant farther from the highway. Those results are consistent with a simple preference for open habitats by deer mice and for forest by red-backed voles and chipmunks, which is consistent with the results of this study. Interpretation, Appraisal, and Applications In Utah, the research team recorded higher abundance and density further from the road in 2004, and higher diversity and 0 5 10 15 20 25 ROW 50 600300 Females Transect Transect A du lt M ea n W ei gh t ( g) highway n=46 powerline n=53 0 5 10 15 20 25 ROW 50 600300 Males A du lt M ea n W ei gh t ( g) highway n=36 powerline n=57 Figure 28. Weights of adult deer mice, compared among transects for each treatment.
86 abundance closer to the road in 2005. These conflicting trends suggest that roads per se do not have a direct effect on small mammal distribution. Other factors clearly have a more decisive influence. Abundance and density seem to be primarily influenced by the presence of suitable habitat and resource availability. Desert habitat quality is very often dependent on precipitation levels, which were very different in 2004 (wet) and 2005 (dry). In 2004, the general habitat quality appeared to be good throughout the range. In contrast, during a drier year such as 2005, green vegetation and suitable habitat appeared to be limited to areas adjacent to the road, which may have acted as a water collector and perhaps was responsible for the higher con- centration of individuals and species near the road. Similarly in British Columbia, there were no consistent pat- terns to indicate small mammal abundance or densities changed consistently within the forest as distance from the ROW increased. If there were demonstrated demographic ef- fects caused by this relatively low-volume, two-lane highway other than those due to the simple shift in habitat type from forest to graminoid (grass) cover in the ROW, they were less evident than were the effects of site or microhabitat conditions in the ROW. Similarly, the 60 m wide highway or transmission- line ROWs that dissected mesic coniferous forest appeared to be negative for most species and potentially neutral to positive for others, with total species diversity lower in the ROW than forest. This is not to suggest that impacts due to the highway itself may not exist for some species, but that large samples, highly consistent habitat conditions, and correctly focused transplant experiments may be required to detect them. Conclusions Jaeger et al.133 suggested four ways that roads might influ- ence the persistence of animal populations. One important parameter includes a decrease in habitat amount and quality near roads. If habitat quality decreases, the animals that in- habit areas near roads would be expected to decrease in di- versity, density, and/or abundance. The results from the dry, arid Intermountain West sagebrush country of Utah and the mesic, coniferous forests of southern British Columbia found no consistent patterns to suggest that habitat quality differed beyond the ROW verge. The research team found no consis- tent pattern that small mammals were impacted close to the road and conclude that, at least on these study sites, roads did not impact habitat quality beyond the ROW. The research team suggests other factors may be responsible for the differ- ences in small mammal species diversity, density, and abun- dance that were documented. 3.5 Restoring Habitat Networks with Allometrically Scaled Wildlife Crossings Introduction The placement of crossings has been a relatively hit-or-miss proposition lacking solid ecological theory to underpin the decision, in part because the idea of landscape permeability has not been traditionally viewed from an animal perspective. Permeability refers specifically to the ability of species of all kinds to move relatively freely across the roaded landscape. By this definition, landscape permeability differs from the term connectivity. Connectivity refers to the human perception of how connected the landscape matrix is, irrespective of organ- ism scaling. Permeability implies free movement by organisms across the landscape. Stevens et al.âs224 use of the term âfunc- tional connectivityâ (i.e., the ability of an animal to cross a landscape) is roughly equivalent to this definition of perme- ability, but relies on the concept of relative resistance of matrix habitat separating habitat patches. Relative resistance refers to the degree to which boundary conditions between habitats as well as habitat physical structure allow or impede animal movement. Animal vagility (i.e., the capacity or tendency of an organism or a species to move about or disperse in a given environment) differs from species to species, and with age and sex class in many species. An animalâs movement capabilities define in large part its abilities to find resources necessary for survival. The development of allometric equations that relate the home range sizes of species to movement ability allows the calculation of scaling properties for individual species. Allom- etry is a fundamental concept in biology. It began with considerations of the relation between the size of an organism and the size of any of its parts; for example, between brain size highway n=126 powerline n=161 0.0 0.5 1.0 1.5 2.0 ROW 50 600300 Transect M al es : F em al es Figure 29. Sex ratios of deer mice, compared among transects for each treatment. 0 10 20 30 40 50 60 % S am pl e Ju v en ile s highway n=126 powerline n=161 ROW 50 600300 Transect Figure 30. Juveniles as a percentage of total deer mouse sample, compared among tran- sects for each treatment.
87 and body size, where animals with bigger bodies have bigger brains. Here the relationships between home range size and dif- ferent measures of movement ability (namely, Median Dispersal Distance [MedDD] and linear home range distance [LHRD]) are referred to as allometric because movement ability changes in proportion to home range size, which is re- lated to the size of organisms; i.e., there are consistent scaling properties that can be expressed by equations. Scaling prop- erties can be translated into movement distances characteris- tic of a species. Movements of animals over time can be referred to as their ecological neighborhood, i.e., a region de- fined by an animalâs movement pattern. Ecological neigh- borhoods for any individual species vary depending upon which process is involved. For example, while foraging move- ment distances typically are relatively short, migratory move- ments involve larger ecological neighborhoods. Animals of similar size tend to have similarly sized home ranges and eco- logical neighborhoods. When this is so, it is possible to estab- lish scaling domains that include a few to many species. For the purposes of this report, a scale domain refers to a range of species movement distances that are similar, so that several species can be considered to belong to that particular domain. Domains range from small to large, typically with more sedentary animals belonging to a domain characterized by short movement distances and highly vagile animals belong to a domain characterized by longer movement distances. To the extent that species belonging to a specific domain move similarly, the placement of wildlife crossings of appropriate type and configuration at appropriate (allometric) distances will promote landscape permeability. Less vagile animals need crossings placed closer together, while for more vagile animals wildlife crossings can be spaced further apart. The advantage of domains is that often, a single crossing can be used by many different types of species. There are obvious ad- vantages for both population viability and driver safety when species use crossings and stay off the road surface. Mitigation to decrease the effects of the roaded landscape includes, among other things, the construction of crossings of two general types; those that promote wildlife crossing over the road, and those that provide passage underneath. The num- ber, type, configuration, and placement of crossings will determine whether permeability is restored to the roaded landscape. The relevant hypothesis is that landscape perme- ability can be improved by the placement of crossings allo- metrically scaled to organism movement characteristics. Research Approach: Methods and Data The roaded landscape has both direct (e.g., roadkill) and in- direct (e.g., habitat loss, reduced habitat quality, fragmenta- tion, loss of connectivity and reduced permeability, and barrier effects) effects on wildlife populations and on ecological patterns and processes.26,30 In particular, animal movement is hindered as road density and traffic volume increase. Spatial linkage, accomplished by animal movement, is critical because the arrays of resources that are essential to population viability are usually distributed heterogeneously across the habitat net- work.168 Animal movement can be seasonal migrations120 that tend to be cyclic, dispersal events227 that are usually unidirec- tional,180 or ranging behavior144,228,216 characterized by shorter exploratory movement within a home range or territory. Re- gardless, the ability of animals to move has profound impacts on ecological phenomena and processes, including individual fitness, population structure, life history strategies, foraging dy- namics, and species diversity.3,33 Generically, dispersal has been defined as the movement of organisms, their propagules, or their genes away from the source.223,234,59,179,38 Although this study explores the patterns of dispersal distances to understand the placement of wildlife crossings, clearly the processes involved in dispersal underpin our ecological understanding. The phenomena of immigration and emigration, collectively termed dispersal, are two of four (births and deaths being the other two) processes that are the least understood in the fields of population ecology and life history evolution,75 and repre- sent one of the most significant gaps in how ecologists under- stand animal ecology.22 Wiens246 has argued that dispersal is a complex process that involves more than just patterns of where animals settle. According to Doerr and Doerr75 a more com- prehensive view of dispersal is emerging. Clobert et al.59 have argued recently that at least three components are involved in dispersal: (1) a decision to leave the natal area, (2) a middle phase where new areas are searched and evaluated, and (3) a final phase that involves choosing a place to settle. This view suggests that dispersal distances result from this integrated se- ries of decisions and processes and are influenced by environ- mental and physiological factors, as well as stochastic events.75 Perhaps most critical to our understanding is a dearth of data regarding these processes. For this report, dispersal is consid- ered to be at the level of individuals and populations. Although barrier effects are not similar across roads, the effects of road geometrics (e.g., road type, width, presence of fences) present significant problems to animals, resulting in fragmented habitats, disconnected networks, non-permeable or semi- permeable landscapes26 and often isolated populations.43,240,137 A Brief History of Allometric Scaling in Ecology Allometric scaling in ecology has had a long history. The fol- lowing summary is intended not to cover the history exhaustively, but only to indicate the line of logic that led to these analyses. As early as 1909, Seaton209 recognized that animal size corresponded roughly with home range size. Mohr174 dis- cussed the same relationship specifically for mammalian species.
88 Kleiber141 looked at the scaling relationships between basal metabolic rate (BMR) and body mass and found that BMR = aM0.75, where M is body mass, a is the allometric coefficient (y intercept), and 0.75 is the allometric scaling exponent. The general form of the allometric (power law) scaling equation is: Y = aXb where Y is the response variable, X is the explanatory variable, a is a scaling constant or coefficient (y intercept), and b is the scaling exponent equal to the regression slope.141,147 McNab165 showed that among mammals, an almost identical power law (scaling exponent) existed between home range size and body weight, although Harestad and Bunnell112 found scaling expo- nent values near 1.0 or greater when they looked at different trophic levels. They concluded that differences in weight alone accounted for a large proportion of the differences between male and female or subadult and adult home range sizes. They suggested that inter-trophic (namely, herbivores vs. carnivores vs. omnivores) scaling functions differed significantly from each other. Damuth68 and Brown37 have suggested that the dif- ference between the scaling exponents of 0.75 for energy re- quirements and approximately 1.0 for home range size may be explained by per capita resource requirements and greater over- lap in home ranges for larger mammals. However, more recent work by Kelt and Van Vuren,139 working from a large data base of over 700 publications, found that the scaling relations of inter-trophic home ranges did not differ and scaled with a slope of 1.13, greater than either the results of McNab165 or Harestad and Bunnell112. Kelt and Van Vuren139 (p. 637) admit however that the relationship between home range size and body mass âhas been perhaps the most difficult to understand.â Recently, Wolff248 and Sutherland et al.227 demonstrated that body size of mammals is linearly related to dispersal distance when both variables were expressed on a log10 scale. However, as Bowman et al.33 point out, both of these relationships are limited because: (1) some species disperse much further than expected from body size, and (2) some mammals have larger or smaller home ranges than predicted for a given body size. Given these results, one expects that home range size and dispersal distance should co-vary across mammalian species and this is the argument that Bowman et al.33 expand upon. They argue that the residual vari- ance in the body size versus home range, and the body size ver- sus dispersal distance relationships represent real differences in vagility independent of body size and therefore the relationship between dispersal distance and home range size should co-vary across mammal species after the effects of body size are removed. The Dispersal Distance Connection Dispersal is a fundamental element of demography,7 col- onization,117 and gene flow182 but dispersal movements are perhaps the least well understood of ecological phenom- ena.227 Bowman et al.33 showed that dispersal distance is ac- tually more closely related to home range size (R2 = 0.74) than to body size (R2 = 0.60), where R2 is the proportion of the variance explained by home range size and body size, re- spectively. This discovery is significant because dispersal dis- tances, as well as ranging and migratory behavior, represent animal movement across the landscape. Bowman et al.33 found that when body size effects were removed, the slope of the relationship of the residuals of dispersal distance re- gressed against the residuals of home range size was not sig- nificantly different from 0.50 (F = 31.6, df = 1, 32, P = 3.2 x 10â6, S.E.E. = 0.54), a result with very important ramifica- tions. The significance is this: Dispersal distance is a linear measure, while home range area is a squared linear measure. Because X0.05 is equal to the square root of X, and because X in the scaling equation is equal to home range area, taking the square root of the home range area yields a linear di- mension of home range, allowing dispersal distance to be re- lated to home range size by a single constant value. Bowman et al.33 found that maximum dispersal distance (MaxDD) was related to home range size (HR) by the equation: MaxDD = 40 (linear dimension of HR) and median dispersal distance (MedDD) was related to home range size by the equation: MedDD = 7 (linear dimension of HR) Because home range size is easy to measure and is readily available in published literature, appropriate scaling functions for deciding the general ecological neighborhood of species would appear to be easy to obtain. If so, they provide the next step to inform the placement of wildlife crossings. What is an Ecological Neighborhood? The concept of ecological neighborhoods is defined by three properties: (1) an ecological process (e.g., inter-patch movement), (2) a time scale relevant to the process, and (3) an organismâs activity during that time period.3 Additionally, no single temporal or spatial scale is appropriate to represent the mix of processes that influence individual and species re- sponses through time and space; hence, several ecological neighborhoods exist, depending upon what process is involved (e.g., foraging, territory defense, migration). Char- acteristically, for mobile organisms, the ecological neighbor- hood for a given process is the region within which that organism is active, definable by its movement patterns. In- deed, Addicott et al.3 (p. 343) suggest that âfor neighbor- hoods. . . . the most appropriate indicator of activity may be a measure of net movement of individuals . . . . One [such in- dicator] is the direct measurement of dispersal distances.â
89 Source: Redrawn from Addicott et al.3 0 B A 50 95 0 50 95 N1 N2 Na Nb inter-patch movement spatial unit (distance) foraging % c um ul at iv e di st rib ut io n of m ov em en t Figure 31. Theoretical relation- ship between the cumulative distribution of organism move- ment and spatial scale, i.e., eco- logical neighborhood. Figure 31 shows the theoretical relationship between movement and two ecological neighborhoods where N1 and N2 represent two different spatial units related to two distinct animal activities. The horizontal and vertical dashed lines in- dicate different âneighborhood sizesâ for the two different ac- tivities (dotted lines, Figure 31A). In general, thinking about landscape permeability involves larger spatial units. In this example, foraging involves a smaller ecological neighborhood (N1), but inter-patch movements, which might include find- ing mates or additional resources, typically involves larger spatial areas (N2), i.e., larger ecological neighborhoods, and may be equated with some measure of dispersal. When roads cross the landscape, the larger ecological neighborhoods that animals use (e.g., related to inter-patch movement) may be intersected. When such intersection oc- curs, barrier effects become apparent. In Figure 31, both inter- patch interactions involving movement over large distances and the movements related to the shorter foraging activities are defined by a cumulative distribution of distances moved. Each line in Figure 31B represents a cumulative distribution of movements with an associated neighborhood size (N1, N2) for foraging and inter-patch movements. The decision crite- rion is 95% of all movements related to either process,3 but is arbitrary; it could easily be different. Given the results from Bowman et al.,33 the problem of deciding an appropriate spac- ing for wildlife crossings is now somewhat easier because plan- ners can relate ecological neighborhoods of activity required by animals to survive to a distance measure. Usually, ecologi- cal neighborhoods are defined for each individual species. However, it is unreasonable from a management perspective to attempt to place crossings allometrically for each individ- ual species. Some grouping of species is desirable, especially if their home range sizes are similar in size and have small among versus between group differences. Domains of Scale To the extent that (1) similarities in home range sizes exist for groups or guilds of species and (2) there are recognizable differences between groups, it should be possible to deter- mine a few effective scale domains that characterize the movements of each group. Theoretically, boundaries of scale domains should be recognized where the differences (e.g., in dispersal distances) increase as transitions between domains are approached. If possible, then the recognition of a few groups or guilds composed of similarly sized species with similar home range domains is an important first step in determining the spatial location for effective crossings for most species. The assumption is that similarly sized animals will use similar types and similarly spaced crossings. However, there may be inter-trophic differences (i.e., carni- vores, herbivores, and omnivores may scale differently). If so, consideration should be given when deciding on the type and placement of wildlife crossing. The calculation of guild- specific movement domains is an important step in allomet- rically placing wildlife crossings. To the extent that these arguments hold, the placement of appropriate types of cross- ings can be accomplished in a scale-informed and sensitive manner, resulting in a more permeable roaded landscape that effectively restores the broader habitat network. Wildlife Crossings and Inter-Patch Movements The intent, of course, of establishing allometrically scaled wildlife road crossings is to enhance inter-patch movements. Most if not all organisms live in discontinuous habitat patches of suitable habitat within a matrix of less suitable habitat that is embedded in larger, naturally heterogeneous landscapes,34 and the presence of roads generally increases patch isolation. Ecologically, animal vagility and movement ability determine if populations are isolated in a naturally heterogeneous land- scape.3,34 Although important, inter-patch movement has not been extensively studied and few empirical estimates of move- ment rates or effects on populations have been derived.34 It is unclear what amount of inter-patch movement is needed to influence the dynamics of populations divided by roads. While real problems exist in gathering inter-patch movement data,34 Bowne and Bowers34 conducted a database search to determine the extent that documented rates were available. From a review of 415 published articles, they found that for 89 species-system combinations, roughly 15% of all individ- uals in a population moved between habitat patches each
90 generation. More importantly, population rates (i.e., birth rates, death rates, recruitment, survival) were either positive (n = 28) or neutral (n = 14) over 95% of the time, but nega- tive in only two instances (<5%). This finding underscores the necessity of restoring functional connectivity to the roaded landscape. Inter-patch movements may involve relative short distances or long-distance dispersal. Shorter movements are more frequent, while longer dispersal distances are typically rare.232 Description of Methods Bowman et al.33 developed their home range dispersal re- lationships for mammals from data given in Harestad and Bunnel.112 For this study, the Harestad and Bunnell112 data was augmented with the species home range list given in Holling122 Appendix 7 to amass a total of 103 mammalian species from around the world (Appendix G). Other sources of home range information are available, but the Harestad and Bunnell112 data are well known, are accepted by ecolo- gists, and have been used to advance the allometric scaling of mammals.139 The Holling122 paper increased the number of species for which reliable home range data are available. Only data for species with at least five replicates were used in the Holling paper. Some species do not occur in North America, but were included because (1) their home range area infor- mation was reliable and (2) they provided a reasonable sample size from which to develop reliable dispersal distance domains. Elimination of duplicate entries left 103 species. A caveat is necessary here. Home range size varies over time for individuals and for populations. The values used in this study are the best representative values available for the species. Individual home ranges will no doubt vary around these mean values. The Bowman et al.33 equations were then used to calculate MedDD (i.e., 7* âHR) and LHRD (i.e., âHR) from these home range data and from data in 10 papers that listed daily move- ment distances (DMD) to explore if a consistent relationship existed between DMD and the MedDD. If a consistent rela- tionship exists, then three different scaling domains could be developed to inform the placement of crossings. All three transformations (MedDD, LHRD, and DMD) represent different ecological neighborhoods for individual species. After the distance conversions were calculated, the research team applied a hierarchical monothetic agglomerative cluster- ing technique using Wardâs linkage method with a Euclidean distance measure as the sorting strategy162 to detect natural breaks in the data. Monothetic refers to the clustering of one variable (i.e., the measure of home range); agglomerative refers to the procedure of clustering groups of species and means such that each group starts as a single species and is clustered (agglomerated) by some linkage method. Euclidean distance was used because it is one of the simplest measures and is roughly equivalent to the linear distance between any two measures. The shorter the distance, the more similar the meas- ures and the more likely the species involved will be included in a group. Wardâs method is based on minimizing the sum of the squares of distances from each individual species to the centroid of its group.161 The method produces a clustering matrix and a dendrogram of the species groups. The research team chose to represent the data to the sixth cluster (i.e., to the 0.16-mi level). After the natural breaks were detected, frequency distribu- tions for the species home range areas that had been converted to the median dispersal distances and to the linear home range distances were calculated. The frequency distributions are equivalent to scale domains that represent similar scaling by groups of species. The research team also compared trophic level (i.e., carnivore, herbivore, and omnivore) median disper- sal distances to determine if differences existed. The research team looked at a sample of 10 papers that provided daily move- ment data and examined if a consistent relationship existed between daily movement distances and median dispersal dis- tance. Because median dispersal distance and linear home range distances are derived from home range area, if there was a relationship, it should apply to any of these measures. Finally, the research team compared the options for spac- ing wildlife crossings and presented the most feasible scaling domains for large mammals that are most likely to be in- volved in serious animalâvehicle collisions. Findings and Results Mammalian Species Scaling: Median Dispersal Distance When the median dispersal distance equation (7 * â Home Range) was used, mammalian species dispersal distances ranged from 0.06 mi for the northern pocket gopher (Tho- momys talpoides) to 168.46 mi for the wolverine (Gulo gulo). Of 103 species, 50% scaled to less than 4 mi (Figure 32, Table 34). More than 70% of species had median dispersal distances of 8 mi or less. When median dispersal distances were grouped by a hierarchical polythetic agglomerative clustering technique,162 55.4% scaled longer than 3.05 mi (Figure 33). Not all trophic levels (i.e., carnivores, herbivores, and om- nivores) scale similarly. One expects that carnivores, whose prey is the herbivore component of the community, would travel greater distances and have larger home ranges. Simi- larly, herbivores, whose primary food resource includes plants, would be expected to scale differently and indeed that is the case. Indeed, MedDD for omnivores ranged from 0.39 to 50.05 mi, herbivores ranged from 0.06 to 16.47 mi, and carnivores from 0.14 to 168.46 mi (Figures 34 and 35). It is
91 MedDD (mi)* 0.5 1.0 2.0 3.0 4.0 6.0 8.0 20.0 35.0 >35.0 Cumulative% 28.2 35.0 40.8 44.7 50.5 63.2 70.9 85.4 90.3 100 *mile value given is upper limit for that distance domain Table 34. Cumulative percentage of mammalian species that scale at distances from 0.5 to more than 35 mi. 0 0.0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 20 40 60 80 MEDIAN DISPERSAL DISTANCE (miles) CU M UL AT IV E PE RC EN T SP EC IE S 100 1.00 0.900.85 0.45 0.35 0.23 0.41 0.73 0.53 0.50 120 140 160 MEDIAN DISPERSAL DISTANCE DOMAINS Figure 32. Median dispersal distances of 103 mammalian species with no clustering. MEDIAN DISPERSAL DOMAINS BY SPECIES GROUPS FOR 103 MAMMALIAN SPECIES 7.8 28.2 8.7 23.3 4.9 27.2 0.0 5.0 10.0 15.0 20.0 25.0 30.0 0.16 1.07 3.05 7.15 10.71 >11.00 MEDIAL DISPERSAL DISTANCE (miles) PE R CE NT O F SP EC IE S Note: X-axis values represent the upper boundary of the particular domain. Figure 33. Median dispersal (7 * Home Range) domains for 103 mammalian species based on a hierarchical polythetic agglomerative clustering.
92 COMPARISON OF TROPHIC MEDIAN DISPERSAL DISTANCES 4.9 7.3 12.2 24.4 7.3 43.9 14.6 53.7 4.9 12.2 2.4 12.2 0.0 19.0 9.5 42.9 4.8 23.8 7.8 28.2 8.7 23.3 4.9 27.2 CARNIVORES HERBIVORES OMNIVORES TOTAL SPECIES 0.00 10.00 20.00 30.00 40.00 50.00 60.00 0.16 1.07 3.05 7.15 10.71 >11 DISTANCE (miles) PE R CE NT O F SP EC IE S Figure 35. Comparison of the median dispersal distance domains of carnivores, herbivores, and omnivores. Figure 34. Carnivores, herbivores, and omnivores show different median dispersal distances. clear that wildlife crossings placed 6 mi or more apart will not provide either permeability or adequate crossing opportuni- ties for approximately 63% of the mammalian species likely to be found on the landscape. Clearly median dispersal distances provide only the extreme limit and by themselves cannot fully inform the placement of wildlife crossings. Mammalian Species Scaling: Linear Dimension Distance At the other end of the spectrum, the linear dimension of the home range (âHR) provides a scaling that more closely ap- proximates the majority of movements made by mammalian species, which typically move within their home range for most of the year. During spring and fall of course, juvenile an- imalsusually make longer migratory movements.227 When lin- ear movement domains were used to place multiple wildlife crossings according to a mile-marker spacing, approximately 12% of species would be likely to cross at a distance of 7 mi, approximately 30% at 3.0 mi, and approximately 64% at crossing distances of 1 mi. All species would likely cross at a spacing distance of 0.16 mi (Figure 36). Consequently, maxi- mum landscape permeability is more likely when placing wildlife crossings based on the linear scale domains. Mammalian Species Scaling: Daily Movement Distance It is possible that daily dispersal distances may provide an alternative scenario for placing wildlife crossings; however, daily movement distances are difficult to collect and often not uniformly collected. For example, Krausman et al. (unpub- lished data) collected movement data on 46 mule deer (Odocoileus hemionus) whose movements were followed
93 HIERARCHICAL MONOTHETIC AGGLOMERATIVE CLUSTERING 35.92 33.98 17.48 6.80 3.88 1.94 0 5 10 15 20 25 30 35 40 0.16 1.07 3.05 7.15 10.71 >11 LINEAR DISTANCE DOMAINS (mi) PE R CE NT S PE CI ES Figure 36. Linear ( Home Range) dispersal domains for 103 mammalian species using hierarchical monothetic agglomerative clustering. using radio telemetry from 1999 to 2003 (Figure 37). Record- ing of the relocations occurred at about 24-hour intervals. The data indicate that the majority of individual daily move- ments were short with 85.1% being 1,000 meters or less. Certainly deer moved greater distances; however, recording only two locations, one at the beginning of the period and one at the end, essentially straightens what is a much more tortu- ous movement pathway. This movement oversimplification is the major problem of using daily movement data. The most accurate method for assessing daily movement distances would measure the trajectory of the animalâs pathway at short intervals for several 24-hour periods using GPS collars set to record locations frequently, and then take a mean value. Sea- sonality affects daily movement patterns, so an adequate sam- ple is needed. Typical methods for collecting daily movement distance data include following the trajectory for a few hours and then extrapolating daily movement distance, or taking only a few (often as few as two) telemetry relocations over a 24-hour period and then measuring the straight-line distance between relocations. This method seriously underestimates daily movement distances. However, if there is a consistent relationship between daily movement distances and median dispersal distance, with prop- erly collected data (e.g., by using continuously monitoring GPS radio transmitting collars), a conversion factor can be developed for daily movement distance domains that might help inform wildlife crossing distance. The research team initially found 10 species for which daily movement data were available (Table 35). Each individual movement represents the straight-line distance between two relocations taken approximately 24 hours apart. The relationship between median dispersal distance and daily movement distance for all 10 species is quite loose, with a mean of 61.95, S.D. = 83.62, P = 0.05. Mean values for carnivores alone = 42.66, S.D. = 84.45, P = 0.05, and for herbivores, mean = 96.4, S.D. = 93.27, P = 0.05. The variation of the ratios between the median dispersal and daily movement distances is too large to give a realistic and reasonable conversion factor. With a larger sample, the results might be different. Alternatively, when accu- rate multiple daily movement distance estimates become avail- able for those large species that account for the greatest safety risk when WVCs occur, then a proper daily movement distance scal- ing can be developed for individual species. Additional work will be necessary to see if those data exist. Interpretation, Appraisal, and Applications There are at least three potential options in spacing wildlife crossings using allometric distance domains. All involve scaling to home range area and are (1) the median dispersal distance , (2) a linear dimension of home range ( HR), and (3) a scaling measure related to daily dispersal distance. Using the linear dimension of the species home range to develop scale domains is most conservative and places crossings closest together. The implication is that crossings are no further apart than the linear dimension of the largest home range in the scale domain. Using the square root of the home range to establish scal- ing domains to inform the placement of wildlife crossings is most reasonable because shorter dispersal distances by juve- niles are more frequent.227 Additionally, animal fidelity to 7 * HR( )
94 Species TLa MedDDb (m) DMDc (m) Ratio Swift fox (Vulpes velox)d C 19,712 18,500 1.07 European marten (Martes martes)e C 8,573 5,100 1.68 Eurasian lynx (Lynx lynx)f C 30,128 3,800 7.93 Polecat (Mustela putorius)g C 9,899 1,097 9.02 Wolverine (Gulo gulo)h C 271,109 1,400 193.60 Lemming (Dicrostonyx groenlandicus)i H 213 15 14.08 Mule deer (Odocoileus hemionus)j H 11,823 311 38.02 Moose (Alces alces)k H 24,400 220 111.90 Cotton rat (Sigmodon hispidus)l H 4,670 21 221.60 Wild boar (Sus scrofa)m O 274,485 13,280 20.67 atrophic level: C = carnivore, H = herbivore, O = omnivore; bmedian dispersal distance; cdaily movement distance; dCovell et al.64; eZalewski et al.250; fMoa et al.173; gBrzezinski et al.39; hRenzhu et al.198; iSchmidt et al.207; jKrausman, unpublished data; kCourtois et al.63; lSulok et al.226; mSpitz and Janeau218. Table 35. Daily movement distances for 10 mammalian species. Figure 37. Distribution of daily movement distances of 46 telemetered mule deer from 1999 to 2003. home range areas suggests that shorter individual movement distances predominate among all sexes and ages. Thus, the linear scale approach would appear to promote greatest permeability (Figure 38, Table 36). A less conservative approach uses the median dispersal distance,33 i.e., seven times the linear dimension of home range, as the criteria for developing the scale domains. Longer distance dispersal does occur less frequently but is important for recolonizing areas as well as gene flow.227 An intermediate approach might use daily movement distances to develop distance domains. Typ- ically, one might expect that mammals would travel signifi- cantly longer distances in their search for resources. To the extent that daily movement data are available for species, al- lometric domains can be developed to inform the placement of wildlife crossings. The sample given in Table 35, however, suggests that a large sample will be needed to extract the rela- tionship, if it exists. Conclusions Placing Crossings for Large Mammals The involvement of large terrestrial mammals in wildlifeâvehicle collisions tends to result in greater vehicle damage and greater potential for human injury and death than the involvement of smaller body-sized animals. Large-
95 Figure 38. Degree of landscape permeability for mammalian species is dependent upon which distance domain (linear home range distance, daily movement or median dispersal distance) is used to develop the scaling domains, and hence the spacing between wildlife crossings. Species HR (mi2) HR (mi) MedDD (mi) White-tailed deer (Odocoileus virginianus) 0.8 0.9 6.1 Mule deer (Odocoileus hemionus) 1.1 1.1 7.4 Pronghorn antelope (Antilocapra americana) 4.1 2.0 14.2 Moose (Alces alces) 5.0 2.2 15.2 Elk (Cervus canadensis) 5.0 2.2 15.6 Bighorn sheep (Ovis canadensis) 5.5 2.4 16.5 Black bear (Ursus americanus) 9.3 3.1 21.4 Grizzly bear (Ursus arctos) 35.8 6.0 41.9 Table 36. Home range of large mammals and derived scaling domains for wildlife crossing placement. bodied animals are a greater safety risk on the road. It appears that to achieve the kind of landscape permeability that will help ensure the health of large-mammal popula- tions (i.e., deer, moose, elk, and bear) and to minimize WVCs, placement of wildlife crossings in areas where pop- ulations of these animals exist will entail at least a multistep decision process. The first involves deciding which allo- metric scaling domain is appropriate and feasible. Highest permeability will be obtained when crossings of appropri- ate type and design are placed using the LHRD (the âHR (mi) column in Table 36). Crossings placed according to the MedDD domains are clearly too far apart to create high permeability of the landscape. However, placing wildlife crossings using the LHRD domain for white-tailed deer and mule deer at about 1 mi (1.6 km) apart in areas where these animals cross the road frequently, and are often hit by vehicles, would certainly improve highway safety and help ensure ease of movement, improving landscape permeabil- ity for these animals. Using the MedDD values of 6.1 to 7.4 mi to space the crossings for these deer species clearly is in- appropriate and will do little to reduce WVCs or facilitate movement. Similar arguments are appropriate for the other species listed in Table 36 and for all species in general. However, using scaling domains represents only the first step in ensuring landscape permeability and improving highway safety. Local information about migration path- ways, areas of local animal movement across roads, hotspots of WVCs, and carcass data on the road provides essential additional information to inform the location of wildlife crossings. Caveats Clustering techniques, such as the hierarchical mono- thetic agglomerative clustering method, make no considera- tion for topography, land form, or landscape structure. They simply group similar clusters of animals based on specified criteria. When the clusters are used to group species by allo- metric distances, one implicit assumption is that all species use all parts of the landscape in a homogeneous manner. This clearly is not the case. Additionally, all measurements are derived ultimately from published home range areas. The home range of an animal is an area traversed by the individ- ual in its normal activities of food gathering, mating, and caring for young.171 Home range area is a measure that implicitly assumes that the animal uses all parts of its range. Although there are some home range measurement tech- niques (i.e., the center of activityâkernel method249 and the non-parametric method, e.g., area determination by GPS Cartesian coordinates and analyzed with map software) that measure not only the extent of the area used by the animal but also concentrations of activity within the home range, the oldest and most commonly used method is the mini- mum convex polygon home range estimator175 that estimates only area of use. A clearer and more concise measure of resource use can be obtained by following an animalâs move- ment trajectory and assessing what resources it is using, but this method is seldom done and large datasets are unavail- able. An advantage of following animal trajectories is that daily movement distances could be estimated. In summary, using home range area to establish allometric distance domains can be problematic; however, other consis- tently collected and reliable data are not widely available. A clear need is the gathering of a sufficient sample of accurate home range information. The use of the linear home range dimension, coupled with local knowledge of animal move- ments across the road and with animal crash and carcass data, provides an ecologically sound approach to inform the place- ment of animal crossings.
96 3.6 Interpretation of Research Results The sections on the Phase 2 research studies (safety [3.1], ac- curacy modeling [3.2], hotspot analysis [3.3], small mammals and putative habitat degradation effects [3.4], allometric plac- ing of wildlife crossings [3.5]) contain important information and suggestions for implementation. In particular, Sections 3.1, 3.2, and 3.3 address different ways to achieve similar purposes and therefore potentially may be confusing for the reader. For example, Section 3.1 involves analyses of WVCs and road envi- ronment data from state DOT sources. Section 3.2 involves an investigation into the relative importance of factors associated with wildlife killed on the road using two different datasets: one based on high-resolution, spatially accurate location data (<3 m error) representing an ideal situation and a second dataset created from the first that was characterized by lower resolution data (<_ 0.5 mi or 800 m, i.e., mile-marker data) and likely typi- cal of most transportation agency data. Section 3.3 investigates several wildlife kill hotspot identification clustering techniques within a GIS framework that can be used in a variety of land- scapes. This section on the interpretation of the research results will guide the reader in understanding these sections. The safety research (Section 3.1) is most effectively used when the purpose is to assess if a specific mitigation has been successful in reducing WVCs to improve public safety. It employs the use of SPFs, predictive models for AVCs. SPFs typically relate the response variables (AVC data and/or roadside carcass collection data) to the explanatory variables (physical roadway and roadside characteristics; often referred to as road geometrics). Other explanatory variables that animals respond to (e.g., topography, vegetative cover, and other off-road variables) are not among these variables that are readily available within the typical DOT safety data- bases. Hence, this approach will result in some unexplained variation, because the safety approach limits the explanatory variables to road geometrics. Regardless, this approach is valuable because only these lower levels of data availability may exist in some jurisdictions. The SPF approach is statistically correct and accounts for âregression to the meanâ problems. It makes use of three dif- ferent levels of road data commonly available. The first level re- quires data on (1) road length and (2) ADDT. The second level adds the requirement that road segments be classified as flat, rolling, or mountainous terrain. The third level incorporates the data used in levels 1 and 2, but includes additional roadway variables such as average lane width. The safety approach has several applications and can be used to: ⢠Identify collision-prone locations for existing or proposed roads for all collision types combined or for specific target collision types ⢠Aid in the evaluation, selection, and prioritization of po- tential mitigation measures; and ⢠Evaluate the effectiveness of mitigation measures already implemented. An important caveat is that the safety approach does not address any aspect of wildlife population response. As the models stand, their primary application is for the safety man- agement of existing roads as opposed to design or planning applications for new or newly built roads. Significantly, the before-after analysis may be judged as successful from a road safety perspective, while at the same time the wildlife popu- lation concerned may be significantly reduced. A second aspect of the safety effort was to investigate the hypothesis that roadside carcass removal data not only indi- cate a different magnitude for the WVC problem, but may also show different spatial patterns than reported WVC data, and lead to the identification of different roadway locations for potential WVC countermeasures. The magnitude and patterns of location-based WVC reports and deer carcass re- moval datasets from Iowa were compared qualitatively through visual GIS plots and quantitatively (e.g., frequency per mile). Police-reported WVC information, deer carcass removals, and deer salvage data were evaluated. Results showed that the number of deer carcasses removed from the road was approximately 1.09 times greater than the number of WVCs reported to the police. The number of salvaged and unsalvaged deer carcasses, on the other hand, was approxi- mately 1.66 times greater. Clearly, the choice of the database impacts whether a particular roadway segment might be identified for closer consideration. The message here is that the choice of the database used to define and evaluate the WVC problem and its potential countermeasures requires careful consideration. Recommendations are provided in this report about how the databases might be used appropriately and how the data can be most profitably collected. To understand the important variables that account for WVCs, then environmental variables must be considered that are not normally included in datasets available from DOTs. The safety research recognized that variables other than road- related variables might be important. In the accuracy model- ing (Section 3.2), the research team used 14 ecological field variables, 3 distance-to-landscape-feature variables, and 5 GIS- generated buffer variables as explanatory variables to assess their relative importance in explaining where ungulates were killed on the road. Further, the research team assessed whether the spatial accuracy of these datasets was important in identi- fying the significant explanatory variables. Spatially accurate data were discovered to make a difference in the ability of models to provide not just statistically significant results but more importantly, biologically meaningful results for trans- portation and resource managers responsible for reducing
97 WVCs and improving motorist safety. Hence, these models are especially applicable when it is important to locate hotspot areas of WVCs and hence wildlife crossings during the design and planning of new roads. The hotspot analysis (Section 3.3) investigated WVC hotspot identification techniques, taking into account differ- ent scales of application and transportation management concerns. Studies of WVCs have demonstrated that they are not random occurrences but are spatially clustered. Data on hotspots of WVCs can aid transportation managers in in- creasing motorist safety and habitat connectivity for wildlife. Knowledge of the geographic location and severity of WVCs is a prerequisite for devising mitigation schemes that can be incorporated into future infrastructure projects (e.g., bridge reconstruction, highway expansion). Many of the studies characterizing WVCs have appeared in scientific and management-focused journals and often include different conclusions or recommendations for managers to consider in designing wildlife-friendly highways. However, lacking are best management practices for identifying WVC hotspots based on current knowledge and technology to help guide planning and decision making. Few studies specifically address the nature of WVC hotspots or their use and appli- cation in transportation planning. Because WVCs represent a distribution of points, recently developed and refined clus- tering techniques can be used to identify hotspots. As an initial step, the researchers used the linear nearest neighbor index (a simple plotting technique) to assess whether the location of dead ungulates found on roads as a result of WVCs was random. The results, however, are only an indicator of first order spatial randomness, i.e., an indi- cator to what extent the animal kill locations may be clumped. Simple plotting most often results in collision points being tightly packed together, in some cases directly overlapping with neighboring WVC carcass locations, thus making it difficult to identify distinct clusters, i.e., where the real high-risk collision areas occurred. Modeling or analyt- ical techniques permit a more detailed assessment of where WVCs occur, their intensity, and the means to begin prioritizing highway segments for potential mitigation applications. Hence, more definitive analytical clustering techniques are needed. The research team used Ripleyâs K statistic of roadkills, near- est neighbor measurements (using CrimeStat software), and density measures to more formally identify WVC hotspot locations, once roadkill locations were found to be unevenly dispersed. The Ripleyâs K analysis clearly shows the spatial distribution of WVCs and the importance of broad-scale landscape variables (such as elevation and valley bottoms in a mountain environment). Further, the locations of high- intensity roadkill clustering within each area can help to focus or prioritize the placement of mitigation activities, such as wildlife crossings or other countermeasures, on each highway segment. The research team found that the nearest neighbor (CrimeStat) approach was useful for identifying key hotspot areas on highways with many roadkills because it, in essence, filters through the roadkill data to extract where the most prob- lematic areas lay. The density analysis approach identified more hotspot clusters on longer sections of highway. Although the density analysis approach appears to be less useful to man- agement, it may be a preferred option where managers are interested in taking a broader, more comprehensive view of wildlifeâvehicle conflicts within a given area. Such a broader view may be necessary not only to prioritize areas of conflicts but also to plan a suite of mitigation measures. The location of the larger clusters produced by the density analysis could be tracked each year to determine how stable they are or whether there is a notable amount of shifting between years or over longer time periods. This type of information will be of value to managers in addressing the type of mitigation and intended duration (e.g., short-term vs. long-term applications). The identification and delineation of WVC clusters, which often vary widely in length depending on distribution and intensity of collisions, facilitates between-year or multiyear analyses of the stability or dynamics of WVC hotspot loca- tions. The WVC data that transportation departments currently possess are suitable for meeting the primary objec- tive of identifying hotspot locations at a range of geographic scales, from project-level (<50 km of highway) to larger district-level or state-wide assessments on larger highway network systems. The spatial accuracy of WVCs is not of crit- ical importance for the relatively coarse-scale analysis of where hotspots are located. Any of the analytical clustering tech- niques can be used when more detailed information is needed.
