Mechanical Aspects of Soft Contact Lenses
James T. Jenkins
My colleagues and I at Cornell University are interested in the physical principles that govern how a soft lens stays positioned on the eye, how it is moved from this centered position by the action of the blink, and how it returns to a centered position following a blink (e.g., Jenkins and Shimbo, 1984; Knoll and Conway, 1987). We are also concerned with the orientational positioning of the lens; this involves the match between the back surface of the lens and the corneal topography.
One of the things we are interested in predicting is the thickness of the tear film behind the contact lens. This tear film is important both to the mechanical behavior of the lens and to the health of the eye.
ELASTOHYDRODYNAMICS
The lid provides the overwhelming force in the problem of lens positioning (Miller, 1967). Roughly every 5 seconds it comes crashing down on this delicate structure. Surprisingly, it does not have too great an influence on it, largely because the tear film behind a soft contact lens is so thin.
In any case, following a blink the lens is deformed and displaced slightly; it then recovers its original position in the period between blinks. The way it recovers this centered position is essentially by balancing the forces associated with the elastic deformation against the viscous resistance of the fluid in the tear film behind it. It is this process that we would like to understand better.
The parameters that characterize the mechanics of the lens include the profile of the lens thickness. So we suppose that we know how the thickness varies from the center to the edge, and, when we are dealing with a toric lens, we suppose that we know how the thickness varies as we move around
any circle at a fixed radius. The mechanical property of the lens material that we employ is its resistance to stretching. In engineering terminology this is Young's modulus of the material.
The name of the interaction is elastohydrodynamics. This is a term that indicates there is a deformable body (the lens) that is interacting with a viscous fluid (the tear film beneath it).
It must be pointed out that there is a difference between the mechanical behavior of a soft lens and that of a hard lens. The hard lens is essentially rigid. The forces that maintain its adherence and drive its centering are associated with the curvature of the tear film at its edge. These forces, in conjunction with the action of the lid, permit a tear film of greater thickness behind the lens; consequently, there is much more movement of the hard lens on the eye.
In modeling the soft lens, the central portion is taken to be an elastic sheet that resists stretching, and the region near the edge is considered to be an elastic shell that resists bending. Usually there is no need to worry about the bending resistance unless we are trying to change the curvature of the lens rather dramatically, but that is exactly what is happening at the edge of the lens.
AN ILLUSTRATION
Now I would like to illustrate the way these mechanical principles are used in an effort to solve perhaps the simplest problem that could be formulated for this lens-cornea system—that is, simply to predict the shape of the lens centered on an axisymmetric cornea with a given negative pressure behind it.
We start out with a standard lens and a standard cornea (Figure 1). I do not think anyone would argue with this picture of the cornea and a spherical lens sitting with its edge on the sclera.
Imagine that this lens is gradually drawn down on the eye with a negative pressure applied to its back. What we would like to do is to predict the evolution of the shape of the lens with the change in the negative pressure behind it.
What happens as the pressure is gradually decreased? First, the lens begins to translate toward the cornea. The edge of the lens begins to move away from the center, and, near the edge, the lens rotates about the line of contact. Eventually, the slope of the lens at the edge becomes equal to that of the sclera. Then, with further decrease in pressure, the point at which edge contact begins moves toward the center. Throughout, the central portion of the lens has been approaching the cornea. At some value of the pressure the center of the lens touches the center of the cornea, and, with further decreases, the point at which central contact is made moves toward the edge.
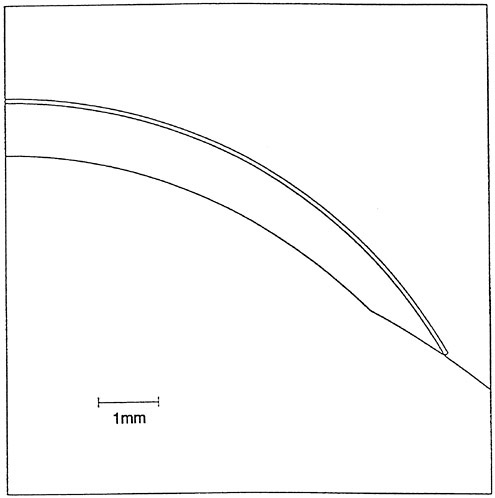
FIGURE 1 Soft lens on the eye. The central radius of curvature of the cornea is 0.78 cm, its diamter is 1.20 cm, and its shape factor is 0.6. The sclera is a sphere of radius 1.30 cm. The lens is spherical with a back radius of 0.84 cm, a diameter of 1.45 cm, and a uniform thickness of 0.07 cm; its Young's modulus E is equal to 4 × 106 dynes/cm2.
I should say that this is not just a story I have made up. This is the scenario that evolves as we determine solutions to the differential equations that describe the balance of forces within the lens (Askari and Jenkins, 1989). So this is a solution to a mathematical problem resulting from our model for the mechanical behavior of the lens.
Figure 2 shows the evolution of shape as the pressure decreases. This is a prediction based typical lens material and a realistic thickness. Figure 3 shows the corresponding evolution of the pressure on the back of the lens as the regions of contact develop.
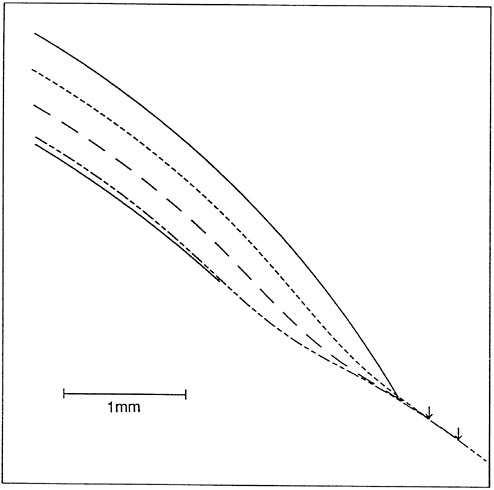
FIGURE 2 Deformed configurations of the soft lens of Figure 1 Shown with the undeformed shape are successively more deformed configurations corresponding to decreasing tear film pressure P. Values of (P/E) × 104 are equal to 0 (undeformed), −0.12 (edge tangent to sclera), −0.40 (edge rolling in), and −0.77 (lens touches center of cornea).
We have predicted the deformed configuration of the soft lens, the pressure distribution applied to its back, and the tear film thickness beneath it. In addition, the levels of pressure agree with those observed in experiments (Martin and Holden, 1986). However, there is an embarrassment of riches, because for every value of the negative pressure there is a distorted configuration. The lens is like a suction cup. When we push down on a suction cup and ask what the equilibrium configuration is, there are any number of them, depending on how hard we push down.
The question is: Does the system seek a solution that is in one sense or
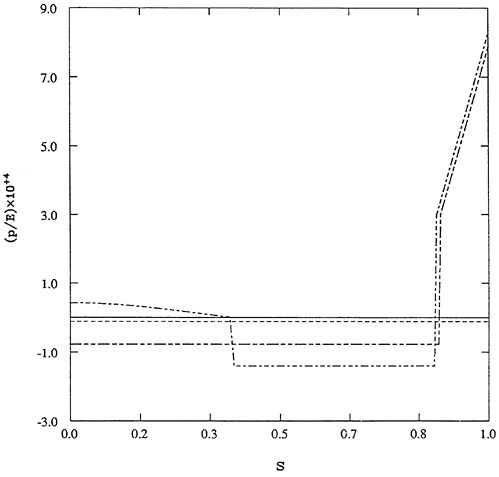
FIGURE 3 Distribution of pressure p on the back of the soft lens for several values of the tear film pressure P. Graphed is (p/E) × 104 versus the fraction s of arc length along the lens for (P/E) × 104 equal to 0, −0.12, −0.77, and −1.40.
another more natural? The way this question is phrased in a mechanical context is in terms of the total energy of the system—that is, the energy stored in the lens as a result of its being stretched and bent and the energy that we have invested in drawing the lens toward the cornea. Plot that as a function of pressure, and, if that shows a minimum, we will say that the configuration at that value is the one the lens seeks on the eye. The results are plotted in Figure 4
My hope had been that, once the lens was in contact with the cornea, this curve would start to go up. This would be the case if there were a minimum of energy. Unfortunately, as the lens contacts the cornea on the center line and this central contact begins to spread, the energy decreases further. The
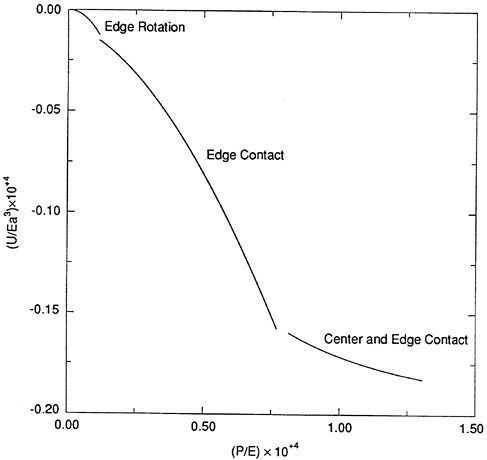
FIGURE 4 Total energy U, normalized by the cube of the central radius a of the lens and Young's modulus versus the normalized tear film pressure.
purely mechanical analysis predicts that the configuration with the least energy is that with the lens in complete conformity with the eye. This is unrealistic; it indicates that the model is too simple.
What must be taken into account, and this is crucial, is that other aspects of the system are involved in determining the tear film thickness behind the lens. For example, when this lens is on the eye, there is a constant exchange of water between the lens, the atmosphere, the tear film, and the cornea. This probably determines the volume of tear film available.
These aspects of the system aren't mechanical but chemical. The water moves through the system in response not only to changes in water but also to changes in oxygen, lactic acid, salt, or other chemical constituents.
This chemical component must be included in order to place the me-
chanical system in its proper context. So, at the moment, we are using a simple model for transport of water and salt across the cornea (Klyce and Russell, 1979), the tear film, and the contact lens (Yasuda et al., 1971), with evaporation into the atmosphere (Hamano et al., 1980), in order to understand how the interaction between the mechanical part of the system and the chemical and evaporative parts of the system serve to determine the volume of tear film behind the lens.
In terms of the importance for the task at hand, I think this indicates that extremes of humidity can have a profound influence on the mechanical behavior of this system. Next we hope to be able to quantify this and to be able to predict the natural configuration of a soft lens on an eye over a range of atmospheric humidities.
REFERENCES
Askari, E., and J.T. Jenkins 1989 Equilibrium configurations of the soft contact lens upon the eye. (in preparation)
Hamano, H., M. Hori, and S. Mitsunaga 1980 Application of an evaporimeter to the field of ophthalmology (in Japanese). Journal of the Japanese Contact Lens Society 22(2):101–107.
Jenkins, J.T, and M. Shimbo 1984 The distribution of pressure behind a soft contact lens. Journal of Biomechanical Engineering 106:62–65.
Klyce, S.D., and S.R. Russell 1979 Numerical solutions of coupled transport equations applied to corneal hydration dynamics. Journal of Physiology 292:107–134.
Knoll, H.A., and H.D. Conway 1987 Analysis of blink-induced vertical motion of contact lenses. American Journal of Optometry and Physiological Optics 64(2):153–155.
Martin, D.K., and B.A. Holden 1986 Forces developed beneath hydrogel contact lenses due to squeeze pressure. Physics in Medicine and Biology 30(6):635–649.
Miller, C. 1967 Pressure of the lid on the eye. Archives of Ophthalmology 78:328–330
Yasuda, H. C. E. Lamaze and A. Peterlin 1971 Diffusive and hydraulic permeabilities of water in water-swollen polymer membranes. Journal of Polymer Science: Part A-2 9:117–131.







