2 KEY AMERICAN INDUSTRIES
In this chapter's review of the positions of five American industries, the following questions are addressed: What is their competitive position? To what extent do they utilize advanced technology? What use do they make of quantitative reasoning and computational and mathematical modeling?
A thorough study of the correlation between competitiveness and technology would require further analysis, which is beyond the scope of this report. The industries surveyed here all depend very strongly on technology. With the partial exception of the automotive industry, the mathematical sciences have a long and deep history of involvement with the technological bases of these industries. The automotive industry and the petroleum industry are the largest contributors to the U.S. trade deficit. The U.S. petroleum industry is resource-limited and is strongly competitive in its international operations. Telecommunications is the only service industry analyzed in this chapter. It is noteworthy among service industries for its continually improved products at decreasing costs, achieved through the successful use of technology. This success of telecommunications is not unique within the service sector. Other service industries that have achieved success through organizational innovation and technology include the airline and financial services industries.
The United States is part of a global economy. In order to purchase goods and services on the global market, we must also sell them. We sell a wide range of products, from lumber to jet airliners. Lumber is an example of a ''low-tech'' industry. Many countries have trees to sell on the world market. The prices that can be charged for them are constrained by this competition, and wages in the U.S. lumber industry
are not high by U.S. standards. Aircraft is an example of a "high-tech" industry. Wages tend to be higher in the aircraft industry and other high-tech industries than in lumber and other low-tech industries. Much of our country's future economic well-being, then, depends on our ability to establish and maintain competitive positions in industries in which the value added by our labor is high.
The extent of the problem of competitiveness for U.S. industry can be indicated by the following statistics [3].
In 1989 the service sector generated a $20 billion trade surplus while manufacturing trade produced a $115 billion trade deficit. Petroleum imports produced a $50 billion trade deficit, while agriculture produced a moderate surplus. Current accounts were settled in part through the $72 billion worth of companies and real estate that were purchased by foreign investors in the same year. To paraphrase the discussion of Made in America [4], it will not be possible to close the trade gap through growth in the service sector. On the other hand, Quinn [5] argues that in the service sector high-technology capital investment has been rising rapidly since the mid-1960s. In fact, the service sector depends on manufacturing for its vitality, and cannot be expected to remain healthy while manufacturing continues to lose ground. Figures 2.1–2.4 show a consistent loss of U.S. market share for U.S. manufacturing across many industries over the last decade.
Several conclusions can be drawn from the analysis in this chapter. The historic record of economic success for the United States cannot be taken for granted in the future. Technology is an important aspect of economic success. The mathematical sciences are nearly always an integral part of that technology, both on the basis of computational simulation1 and on the basis of quantitative reasoning and modeling. Technology applies to all phases of the product cycle and is not simply a research and development activity. It is most effective when the interrelations among these phases are considered, such as the relations among
product design, cost, and quality. In fact, simultaneous attention to production efficiency, production quality, and consumer requirements seems to be necessary for competitive success in a manufacturing industry.
The MIT Commission on Industrial Productivity, in its study [4], cites six contributing factors present in many of the areas where the U.S. competitive position has been weakened.
-
Outdated strategies
-
Short time horizons
-
Technological weaknesses in development and production
-
Neglect of human resources
-
Failure of cooperation
-
Government and industry at cross-purposes
Several of these factors are discussed in this report; technological weakness is the central concern. Technical training and education are a major means of maximizing human resources. The mathematical sciences community is making a substantial effort to improve mathematics education and training. Problems with technology transfer are a major aspect of the failure of cooperation. Short time horizons result in a systematic undervaluation of research and development. There is a possible technical basis for this undervaluation, in the neglect of the option value in decision making, as is discussed in §3.1. Research and development are important largely because of their option value. One aspect of outdated strategies is the promotion of standardized products for mass markets. As markets become more fragmented to serve individualized customer tastes and needs, flexible manufacturing and inventory control become important technical issues, which are being addressed through mathematical modeling.
2.1 Aircraft
Commercial aircraft manufacture enjoys a strong positive balance of payments. This is true despite the fact that U.S. dominance of the
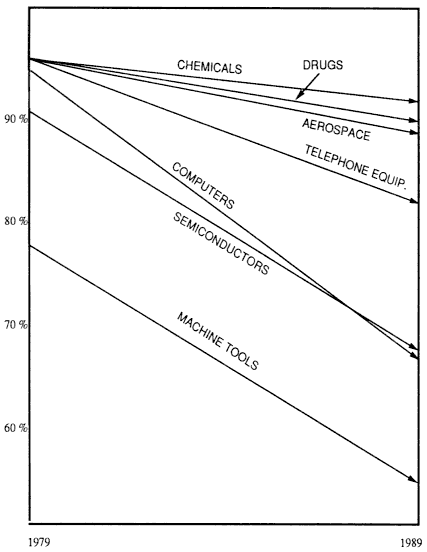
FIGURE 2.1 U.S. factories' share of U.S. market: high-tech industries. Over the past decade, the loss by U.S. factories of domestic market share in high-technology industries averaged 0.9 percentage points per year on a dollar weighted basis. The total market loss was $45 billion from a total market of $518 billion. Total U.S. manufacturing employment in these industries decreased from 1.66 million to 1.39 million, or 1.7 percentage points per year. Adapted, by permission, from [3]. Copyright ©1990 by the Time Magazine Co.
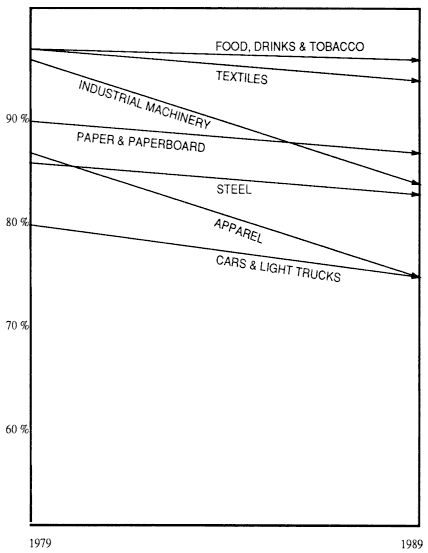
FIGURE 2.2 U.S. factories' share of U.S. market: other industries I. U.S. factories in major industries with a combined annual market value of $728 billion and manufacturing employment of 3.82 million have lost domestic market share at an average rate of 0.4 percentage points per year over the past decade. The total market loss was $28.5 billion. Over the past decade, the total U.S. manufacturing employment in these industries decreased from 4.23 million to 3.41 million, or 2.1 percentage points per year. Adapted, by permission, from [3]. Copyright ©1990 by the Time Magazine Co.

FIGURE 2.3 U.S. factories' share of U.S. market: Other industries II. Additional major industries with a combined market value of $66 billion annually and manufacturing employment of 0.58 million show a similar pattern of decrease in domestic market share and total employment. Adapted, by permission, from [3]. Copyright ©1990 by the Time Magazine Co.
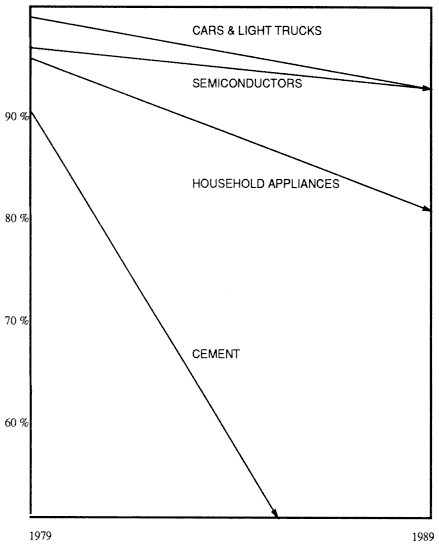
FIGURE 2.4 U.S-owned share of U.S. production capacity. A significant decrease in the U.S.owned share of U.S. production capacity occurred in a number of industries over the past decade. Adapted, by permission, from [3]. Copyright ©1990 by the Time Magazine Co.
marketplace is now challenged by Airbus, a heavily subsidized competitor from Europe. In the United States, a high degree of cooperation in this area exists among industry, government, and academia. NASA has sponsored studies of aircraft design, while military procurement has aided the development of commercial manufacturing facilities. However, owing to the divergence of military and commercial aircraft technologies, the commercial aircraft industry may receive less benefit from these sources in the future. For these reasons, the continued competitive position of the domestic aircraft manufacturing industry cannot be taken for granted.
The importance of the mathematical sciences to the competitive position of the aircraft industry is developed in §3.2 and again in §3.11. A brief summary of those sections follows. In aircraft design, fuel efficiency and speed are key factors that influence sales. The design of aircraft is based to a very large extent on computation, which is necessary to solve equations that describe the flow field around the wing and the complete airframe. Numerical analysis is a critical technology in the development of the computer codes needed for the design work. Included here is the algorithm development for fluid flow, grid generation, and structural analysis. Structural analysis, flutter, and vibration are studied by finite element methods. Stability of control elements has been analyzed by control theory. Engineering design and manufacturing depend on computer-aided design (CAD) and computer-aided manufacturing (CAM), which depend on mathematical tools for their theoretical bases. Computational fluid dynamics (CFD) helps in the design of new aircraft and defines the most important wind tunnel tests. CFD favorably affects the time available for the aeronautical engineers when a particular airplane configuration must be "frozen" in order to begin with the design of the manufacturing process. Repair protocols used in aircraft maintenance facilities have been strongly influenced by operational analysis.
2.2 Semiconductors and Computers
The transistor and the computer are American inventions. Until the 1980s, the U.S. industry was dominant worldwide. In the last decade, Japanese corporations have dominated the semiconductor industry, with a 50 percent market share, and a much higher share for
memory chips. These companies have. established an increasingly competitive position in computers. Various explanations have been advanced for the loss of the U.S. competitive position, including dumping and restrictive trade practices by Japan, fragmentation of the U.S. semiconductor industry into a multitude of start-up firms, and the differences in interest rates and planning time horizons, both favoring Japanese companies. However, these explanations are peripheral in comparison to the absolute dominance of Japanese firms in manufacturing. Their superiority is evident in speed, quality, and especially in the incremental introduction of New technology. The computer industry is at the heart of most high-technology developments, and so its strategic value is enormous, both in terms of projected future markets and in its influence on the rest of the economy. For this reason, a number of studies have been directed to the question of how to support this industry and to prevent further erosion of its competitive position. (See A Strategic Industry at Risk [6], cited in Appendix A.9.)
Computation and mathematical modeling are essential tools for the design of various computer components. The importance of these methods is likely to increase as the technology advances and as forces of economic competitiveness require shorter development times from the conception of a technology to its introduction in the marketplace. The design and fabrication of today's chip necessitate many computational tools. To predict the electrical characteristics of semiconductor devices, designers have to solve differential equations that govern the flow of the holes and the electrons. The rapid change of electrical properties within these devices (at gate edges) leads to stiff differential equations, for which numerical methods have been developed. The layout of gates and devices on a chip is a complex problem, which has been addressed by discrete optimization methods and by simulated annealing. Computation and modeling are used in preparing the masks that are used to fabricate the chips. The testing of the manufactured chip to ensure that its millions of parts function as designed poses a difficult computational problem, for which several combinatorial and statistical methods have been developed. And finally, the structural properties of the packaging have to be simulated to predict heat-induced stresses.
The design of magnetic discs is equally demanding of computational simulation tools. The magnetic field generated, the micro-magnetic
forces within the disc head, the air flow around the head, and the mechanical properties of the disc head subassembly are all important for the design and development of modern discs. Computational methods are indispensable to the engineer who is engaged in disc design, replacing the expensive and time-consuming construction of physical prototypes. Mathematics has played an important role in the development of the codes used to store the information on magnetic discs. Symbolic dynamics provided a methodology for encoding information with maximal efficiency.
Computation and mathematical modeling are important aspects of the technical support for sales, through modeling of customers' technical problems. Software development and methods of numerical computation are areas of competitive strength for the United States. The computer industry maintains a substantial in-house effort in the mathematical sciences and has strong academic ties to support the development of numerical methods.
2.3 Petroleum
The petroleum industry originated and first reached prominence in the United States. Today, although the U.S. industry is highly competitive in international exploration and production, its domestic operations are limited by the availability of natural resources. Most of the remaining domestic reserves are located in high-cost, marginal, or economically depleted fields. As a consequence, the industry is one of the two largest contributors to the U.S. balance of payments deficit. The deficit associated with imported petroleum in 1989 was $50 billion [3]. Moreover, the trade deficit owing to the amount of imported petroleum is likely to increase and has the potential to increase at a significant rate, as one can see from the rate of decline of U.S. oil production in the years preceding the Alaskan North Slope discoveries. A structural problem of this industry is the need to prevent or delay the abandonment of marginal fields, while awaiting the development of cost-effective enhanced oil recovery methods or some future increase in petroleum prices that would justify production of the residual oil. It is commonly estimated that after conventional production, about two-thirds of the original oil remains in place. Therefore the marginal or economically depleted fields are important as a potential
future resource. In addition to the major producers, there are many independent operators. The technical level of the independents varies, but it is fair to say that it is totally impossible for them to match the technical expertise of the major producers. Technology support and transfer therefore become very important issues.
Two critical technologies that address the problems of the domestic petroleum industry are the characterization of reservoir geology and the prediction of fluid flow patterns through this geology. Characterization is needed to identify classes of reservoirs most at risk of abandonment that also have the largest potential for future production. It is also needed as a preliminary step in the prediction of fluid flow patterns and in the design of enhanced oil recovery projects. The fluid flow patterns are needed to guide future development, for example, to set the location of additional wells.
In order to model the flow of oil through porous media, it is important to have a true representation of the geological strata and their properties that characterize the behavior of the flow. Figure 2.5 represents a model geology used to test the validity of the method. Figure 2.6 shows the structure that was derived from measurements of the reflected signals at many different recording stations. Such ''synthetic'' models are important for estimating the accuracy of the method chosen for the signal analysis.
Reservoir characterization depends on geostatistics, random fields, signal processing, Fourier analysis, and the solution of the wave and elasticity equations for the interpretation of seismic signals. It depends on the solution of an inverse problem known as history matching to reconstruct reservoir geology from oil production records and requires sophisticated modeling of well-logging tools. Reservoir characterization makes extensive use of computations. Fluid flow patterns in reservoirs are the central concern in petroleum reservoir engineering. They are studied computationally and depend on finite element, finite difference, and adaptive mesh refinement methods; fast Fourier transforms; free boundary problems; and nonlinear conservation laws. In the future, parallel computing will play a large role. Mathematical scientists have been involved in most or all phases of these studies (see Figure 2.7).
Many other technologies dependent on the mathematical sciences have been and are being used in the petroleum industry. Scheduling theories and mathematical programming are used to assign destinations
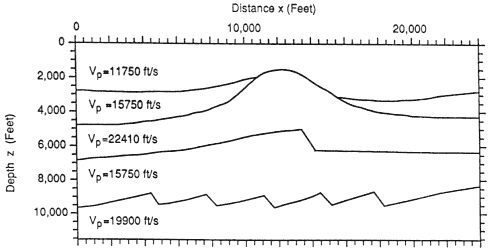
FIGURE 2.5 Marathon model geology for seismic simulation study. Velocity of sound is assumed to be constant in layers separated by curved surfaces. Courtesy of Dong et al. [7], Figure 4.
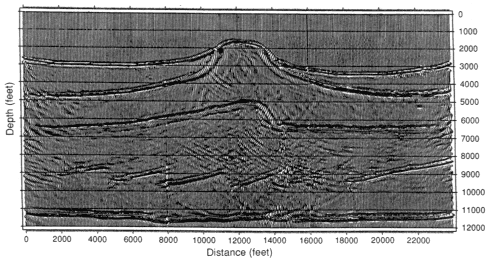
FIGURE 2.6 Reconstruction of geology from seismic inversion, using simulated seismic signals and the model geology shown in Figure 2.5. Courtesy of Dong et al. [7], Figure 8.

FIGURE 2.7 Flow pattern in a small portion of an idealized reservoir, with a well for production of petroleum at the upper right corner and a well for the injection of a displacing fluid (e.g., water) at the lower left corner. Shown here is the position of an interface between the two fluids, at four distinct times in the displacement process. The reservoir is heterogeneous, which causes fluid instabilities in the form of fingers. The fingers lead to bypassing of oil and thus reduce total oil recovery. Courtesy of F. Pereira, State University of New York at Stony Brook.
and cargoes to oil tankers. Refinery design and control depend on differential equations and control theory. The cleanup of oil spills can be monitored using fluid flow computations. Novel technologies, such as the use of microbes to degrade hydrocarbons in situ, are understood by computational modeling, before extensive and time-consuming field tests are initiated. Modeling of geological basins depends on computational and mathematical models and is important in the selection of potential sites for exploratory drilling.
2.4 Automobiles
The mass production and assembly line methods on which the automobile industry depends were first invented and developed in the United States. Nonetheless, the industry has been in decline in this country for three decades. The U.S. automobile industry moved from a position of world dominance and a strong export surplus in the 1950s to a weak competitive position in the 1980s. This industry is one of the two largest contributors to our present trade deficit, with a 1987 negative trade balance of nearly $ 60 billion (see [4]). Several factors have been advanced as critical in the decline of this industry. Various commentators have blamed labor, management, or government, or the hostile relations among these sectors. Changes in consumer taste have occurred more rapidly than changes in the industry's product offerings. The primary technical weaknesses concern quality, cost, reliability, and the time required to initiate a new model or design. Automation has been less successful in the United States than in Japan, and important innovations, for example, just-in-time (JIT) inventory control, were first introduced abroad. Recent developments have moderated these negative trends. The quality of U.S. automobiles is now getting closer to that of Japanese cars and is ahead of the European imports.2 The last year has seen a 2.6 percent increase in market
|
2 |
In its annual ratings of automobiles, Consumer Reports uses a five-level scale, ranging from much-better-than-average to much-worse-than-average. An analysis of one-and two-year-old domestic and imported automobiles for which data were available in 1988, 1989, and 1990 shows an average net improvement of one-fifth of a rating step for domestic cars, while the imports slipped by one-third of a step on average. This measure differs from the rating used by J.D. Powers Associates, which is based on surveys of customer satisfaction during the first three months of ownership (see [8]), according to which U.S. automobiles are nearly equal in quality to that of Japanese cars. |
share for U.S.-manufactured automobiles, representing a shift from imports to U.S.-built Japanese-brand automobiles. Competition for market share remains intense and is shifting to design questions. Here the competitive advantage of the Japanese companies lies in the speed of their design cycle, which at four years is reported to be well below the U.S. design time. Japan's market share is strongest among younger owners and so has a built-in growth advantage.
Design, engineering, and manufacturing have changed enormously under the influence of the computer. In almost all cases, the computer requires mathematical theories for its successful employment. Starting from an artist's rendering, detailed shape functions are generated by computer-aided design. This construction is based on the theory of splines, which is a polynomial interpolation method whose fundamental theory and applications were developed by mathematical scientists. Shapes are transformed into structural elements through computer-aided engineering (CAE). Here, a complete finite element model of the structure is developed and optimized to produce lighter weight, control vibrations, and assure strength (see Figure 2.8). Many components have their own detailed models. The combustion process in the engine has been modeled computationally to achieve better fuel efficiency and emission control. Computer-aided manufacturing involves the construction of dies and stamps for metal formation, the computer control of lathes and machining equipment, and control of automation for the manufacturing process. It also involves scheduling and routing of work in progress from one station to another and to the design of the factory floor layout. Mathematical methods have served as an input to important aspects of the CAD/CAE/CAM process.
Mathematical ideas and tools are used to solve a broad spectrum of automotive industry problems. Strategic economic planning has been improved to include the option value of decision choices. Since the future value of research is almost exclusively an option value (i.e., it allows but does not require future decisions to be made or options to be exercised), the need for these methods in the evaluation of research is evident. Operations research was used to solve market strategy problems, such as the fleet mix problem, to achieve the best mix of different vehicles to be produced that met given miles/gallon requirements.
The importance of advanced technology is captured in the following

FIGURE 2.8 The complex functional geometry of this automobile inner panel was designed and represented using new feature-based surface design methods developed at the General Motors Research Laboratories. The triangular mesh shown on the surface was computed automatically by relying on the same feature information used to design the part. Thus the feature-based surface representation can serve as a link between the design and analysis of the part. Figure courtesy of General Motors Research Laboratories.
question and its answer. Which country will be a strong competitor in the world auto market? The one that best succeeds in shortening the design process, improving manufacturing, and meeting customers' needs (see [9]).
2.5 Telecommunications
Telecommunications is a noteworthy example of an economically successful service industry. Major accomplishments have been to pioneer new technologies, lower unit costs, and expand service offerings consistently over a period of decades. Major research achievements basic to the growth of this industry include the invention of the transistor, developmental work in computers and operating systems, and work on fiber optics. The industry has been very successful in the design of semiconductor devices, which are required for telephone switching networks. Queuing theory, information theory, and coding theory for signal compression were developed within the telecommunications industry, as were marketing models for fair pricing of products. This industry has been a leader in the development and use of statistical quality control methods. The telecommunications industry moved rapidly to exploit a major breakthrough in the design of interior point methods for linear programming, applying them to the design of optimal switching networks. These methods are broadly applicable to a wide range of problems and have been adopted, e.g., by the airline industry, for the solution of scheduling problems. This industry is also a leader in the development of statistical and mathematical models of speech. It has been a leader in the early development of mathematical models of the physiology of the human ear. The mathematical sciences have been strongly represented in the telecommunications industry, which maintains close relations with academic mathematical scientists who have also investigated many of the above topics.
The 1980s saw the implementation of the first telephone network management scheme, which looks at the entire nationwide network as one sharable resource and replaces the previous hierarchical schemes, which divided the country into regions and imposed restrictions on sharing. The concepts and design for this nonhierarchical network are rooted in mathematics (queues, stochastic networks, teletraffic, and mathematical programming) and were developed at AT&T Bell Labo-

FIGURE 2.9 This figure shows the traffic calling pattern in the AT&T network 30 minutes after the 1989 California earthquake. The shaded lines indicate increases in call volumes above normal. The network is designed and maintained using a linear programming formulation for normal traffic patterns. Following the earthquake, outbound traffic was given priority through dynamic network management controls, and extra capacity was allocated for outbound traffic by an adaptive routing algorithm. Figure courtesy of AT&T.
ratories over the past decade.
Another significant innovation, real-time state-dependent routing, is currently being implemented. Under this scheme, the state of congestion existing at the time of an individual call is used to determine the call's route. The scheme relies on new technology and new conceptual understanding of network behavior, which in turn is derived from mathematics and simulations (see Figure 2.9).


















