3 THE PRODUCT CYCLE
The mathematical sciences have played key roles in virtually every aspect of the product cycle, from strategic economic planning to maintenance, repair, and (in the case of hazardous waste) disposal. Inventory, schedule, and transport route planning are all based on mathematical theories. Engineering design is based on the solution of differential equations, often by computational means. Markets are studied by examining statistical samples, allowing optimal choices of product mix to be determined. Optimal strategies are determined by operations research methods. Complex systems are described in terms of probability models. These same methods, including methods of statistical quality control, apply to the manufacturing process as well. This chapter draws on case studies to consider specific approaches, based on the mathematical sciences, to specific economic functions in specific industries.
3.1 Economic Planning
Decision makers involved in financial analysis generally rely on conventional capital budgeting techniques to quantify the dollar value of an investment. These techniques consist of traditional discounted cash flow (DCF) calculations. DCF methods provide a good conceptual framework for evaluating several types of investments. But in many cases, the assumptions required by DCF methods prohibit evaluation of important investment characteristics. For example, future opportunities created by today's investments are often treated as intangibles. Consequently, investments to develop new manufacturing technologies, to achieve differentiation through quality, or to establish operating flexibility may appear too risky, and DCF calculations may indicate that
they have negative present values. As a result, investment opportunities in those areas are systematically undervalued, with detrimental consequences for future competitiveness.
To overcome this capital budgeting shortcoming, finance theory has recently provided some very powerful extensions to the traditional methodology. Those extensions are based on what is known as option pricing theory (OPT), or contingent claim analysis. The seminal contributions to OPT were made at MIT in the late 1960s and early 1970s. OPT had a direct and significant impact in practice through its applications in financial markets (pricing of traded "call" and "put" options). Following that success, the possibility of extending OPT to real capital investment decisions was soon realized. As a result, a significant volume of research has been carried out on this topic. By now, it has been well established that option-like characteristics permeate virtually every aspect of the complex investment decisions facing an industrial firm. It is also perceived today that OPT provides the best and most economically consistent set of quantitative tools for capturing complex interactions of time and uncertainty inherent in investment decisions.
Significant industrial applications of OPT cover a very broad range of subjects. They include the evaluation of research and development projects, natural resource exploration, flexible production facilities, and optimal timing and abandonment decisions, to cite just a few. The analytical techniques involved in OPT require the use of stochastic calculus and general equilibrium pricing methods of financial economics. A continuous lognormal diffusion process, sometimes superimposed on a Poisson or jump process, is commonly used to model uncertainty.
At General Motors (GM), OPT has been successfully applied to capital investment decisions involving new manufacturing technologies, new product introduction, and flexible plant capacity. More specifically, it has been used as a financial tool to evaluate developmental activities for new technologies that would require sequential capital investments. Investment at each stage was modeled as buying an option to invest in the next stage. Implementing this approach explicitly takes into account the value of the upside potential of a new product or technology. In addition, OPT was instrumental in generating significant insights about investment in flexible plant capacity. It helped
calculate the dollar value of the flexibility to quickly accommodate demand levels for different products exceeding the dedicated capacity of a manufacturing facility. It also helped to compute the dollar value of the flexibility to increase the volume of a product that turns out to be more profitable than originally expected. An important result from the application of OPT at GM has been the realization that there is an optimal level of product-mix flexibility, beyond which any additional benefits are marginal. Consequently, only a certain percentage of total capacity has to support flexible manufacturing. Recent extensions of the technique provide significant assistance in evaluating international projects by explicitly taking into account the impact of exchange rate volatility.
Financial executives in industry have indicated the importance of using OPT to evaluate their most complex investment decisions. Other companies, such as Merck and Company, GTE Laboratories, and Mc-Kinsey and Company, have also used OPT in their planning. (See [10], [11], and [12].)
There is a great need today to translate business strategies into consistent capital allocation decisions. OPT provides the quantitative background that can, in principle, fulfill this need. The analytical tools that result from continuing research in this area would significantly contribute to making more informed investment decisions (see Figure 3.1.)
3.2 Simulation and Design—Aircraft
The design of aircraft is unusual as an engineering discipline in several respects. The degree of dominance of computational and mathematical modeling in the design process is rare. The importance of successful design to the competitive viability of the product is unusual, as is the rate of technical progress and innovation. The high degree of cooperation among industry, government, and academia is no doubt important for the rate of progress; so is the level of governmental support for the development of the fundamental science. The computationally intensive aspect of the design process probably increased the rate of technical innovation as well.
The importance of design is easy to understand. The rate of fuel consumption is largely independent of speed through much of the tran-
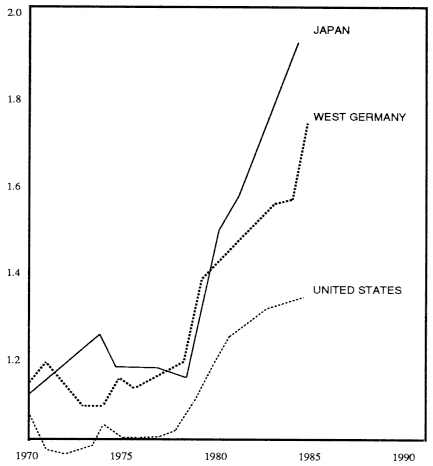
FIGURE 3.1 Industrial-funded R&D as a percentage of gross domestic product. Surveys reveal that high priority is attached to return on investment for U.S. managers, and to market share for Japanese managers. Cost accounting, which neglects the option value of investments, leads to systematic undervaluation of research and to short time horizons. Whether for these or other reasons, the results of the last decade show a consistently lower rate of investment in R&D by U.S. managers than by their Japanese and German counterparts. Reprinted, by permission, from [4]. Copyright ©1989 by MIT Press.
sonic range. The design goal is to fly subsonic, but only slightly so, and the design problem is to find the wing and total aircraft shapes that are efficient at these speeds. For example, an increase in speed of 10 percent allows a decrease in fuel costs of 10 percent, but through better utilization of the fleet of aircraft, a reduction of all operating and capital costs by about 10 percent is achieved as well. These reduced costs, in turn, determine the competitive viability of the aircraft, and averaged over the useful life of the fleet to which the design applies, far outweigh any conceivable level of design costs.
Early successful computer design algorithms were developed in collaboration between mathematicians and aeronautical engineers, and for reasons given above, considerable effort has gone into improving the computations and the modeling since then. Computations have replaced a large fraction of the expensive and time-consuming tests done in wind tunnels. More importantly, based on computational fluid dynamics, far greater ranges of tests can now be carried out in wind tunnels. Manufacturers of commercial aircraft use computer modeling to obtain certificates of airworthiness for new aircraft designs more quickly than would otherwise be possible. Because of their efficiency and lower cost, computations allow consideration of an increased range of design alternatives and thus lead to an increased quality of design. The computational approach also shortens the duration of the design cycle, an important aspect of economic competitiveness. Because the most important part of the fluid flow field is near the wing, the computations are arranged to consider this region more carefully, through the use of adaptive grids. A substantial effort goes into the construction of grids alone. Another large effort has been mounted to improve the computational algorithms that describe the fluid dynamics. Turbulence modeling is important because even the fastest computers do not resolve all the physically important phenomena, especially in the boundary layer near the wing surface. Thus, approximate descriptions of the phenomena are required. Flame chemistry and combustion are important within the jet turbine. The turbulent flow behind the wing is a safety hazard for closely following aircraft since the trailing vortex remains stable for relatively long times. That fact has to be considered in determining the safe spacing of aircraft—not only for takeoffs and landings, but in the air traffic corridors as well. Vortex methods have
been applied to this problem; they produce very highly resolved portraits of the flow field. All of the above areas are currently undergoing active research; the results of this research will be needed for the next aircraft design cycle (see Figure 3.2).
Structural strength and stability are modeled through the use of finite element codes, while wing flutter analysis is an eigenvalue problem. Composite materials are used in aircraft design, for example, to produce strong but flexible helicopter blades. Mathematical theories of homogenization are used to describe the material strength of such composites. The significance of control for aircraft lies in the fact that there are more mechanical degrees of freedom available to the designer than can be used effectively by the pilot. Control theory allows selection of optimal control parameters, for the pilot's use. Fluid dynamic simulation codes can predict the effect of control surfaces on the flight response, and thus apply not only to cruise conditions, but also to the transient conditions of takeoff and landing. One aspect of pilot training, and therefore public safety, is the pilot's ability to respond to emergency conditions. The operation of an aircraft in adverse conditions can obviously be studied only by computer simulation. Pilot training in unusual conditions (landing with some engines not working, for example) can then be obtained in a computer-operated flight simulator. The flight simulator, of necessity, is instructed by the computational simulation of fluid dynamics.
3.3 Design and Control of Complex Systems
The mathematical sciences have played a major role in the development of the engineering capabilities required to design and control high-performance systems. Mathematical models have become a standard part of the preliminary design process for building such systems. They are the building blocks on which virtually all computer-aided design (CAD) software is based. These models are significantly less expensive to build and run, in terms of both time and money, than more traditional physical prototypes. Mathematical models are especially useful either when a proposed design is to be tested for feasibility or when the number of degrees of freedom is so large that guidance is necessary to reduce the range of design or control choices. In a semiconductor wafer fabrication facility, for instance, the manufacturing process may
consist of hundreds of steps, each of which can be modified somewhat in order to improve the yield in high-quality chips. An engineer using mathematical modeling quickly gains an understanding of the basic qualitative behavior of the system (e.g., how the system responds to an increase in the load on some subsystem). This deeper insight into system behavior can have an important impact on the ultimate quality of the design produced. Finally, the development of real-time control strategies for these systems inherently relies on mathematical and computational tools and representations, since the system typically must respond without human intervention.
The engineering systems being designed and built today involve systems issues of a complexity that would have been difficult to imagine even two decades ago. This point is perhaps best illustrated with examples.
-
With the advent of computer-integrated manufacturing, the hardware capabilities of modern manufacturing systems are constantly increasing. However, it frequently turns out that a significant bottleneck to full utilization of these sophisticated resources can be linked to the complex interactions among the various machines that make up the system. For example, it is well known that the manner in which orders are released through a multi-product manufacturing facility can have a major impact on the throughput of the system. Machine interference can occur when orders are improperly scheduled, which can significantly affect the productivity of the facility.
The ''intelligence'' of modern manufacturing systems, in which mathematical theory augments conventional engineering, creates new opportunities for system control that were not present in the previous technologies. The information gathering and processing capability of current systems permits the facility to monitor quality problems in real time and to deal with local bottlenecks by rescheduling orders appropriately.
-
Consider the nation's long-distance telephone network as it exists today. The overwhelming amount of traffic carried by the nation's long-distance telephone network is voice. The traffic is digitized and carried in a communication mode called circuit-switching. For circuit-switching, the call is given its circuits at set-up time for its exclusive use; i.e., no sharing or buffering is involved. An alternative approach,
-
called packet-switching, is built on the premise that buffering (in units called packets) leads to more efficient use of bandwidth, especially for sporadic traffic with bursts of high volume. Data traffic generated by computers and terminals has such characteristics, and data networks and services are being used increasingly. A great deal of research, much of it mathematical, is being focused on the design of wide-area data networks operating at very high speeds, i.e., at gigabits per second. The National Research and Educational Network, with its goal of linking 3,000 campuses, represents a milestone in national networking.
Modeling these systems as networks of queues abstracts mathematically the basic structure present in these examples. Each resource (e.g., the node-to-node "links" in the long-distance network, the input-output devices in a computer system, the work centers in a manufacturing facility) in the system is modeled as a queue with a waiting room and an associated set of servers. Customers (e.g., packets in the network setting, requests to a data base, orders in a manufacturing facility) move from queue to queue as service is received from each facility along a customer's path. Congestion occurs in the model when large numbers of customers contend for limited resources. The degree of congestion has an important impact on the performance of the system. As a consequence, systems designers often use these models to determine the "choke points" of their systems. The system can then be reconfigured by the designer to mitigate the impact of these "choke points.''
The arrival and service time patterns of customers in these models are unpredictable, and therefore, probability theory and statistics play a large role. If certain special assumptions are made about the nature of the patterns of unpredictability, then key performance measures can be calculated in terms of the solution of a (very large) system of simultaneous linear equations. Thus, significant effort has been expended in recent years to develop computational algorithms capable of solving these large systems of equations.
Frequently, the system of linear equations is so large that conventional numerical techniques are inapplicable. Fortunately, a large class of queuing networks has a product-form structure. The product-form structure permits one to calculate the performance measures of interest by solving a much smaller system of linear equations. The development,
analysis, and extension of the product-form queuing network theory have had a significant impact on the performance of complex engineering systems. Similar product-form equations arise in mathematical models of human physiology. Software packages that make significant use of these modeling ideas are fundamentally altering the culture of the engineering community. They offer design engineers rapid preliminary analysis and feasibility studies for systems of a complexity that would be difficult, if not impossible, to attack using other techniques.
The mathematical sciences have also made decisive contributions to the study of the real-time control issues associated with these complex systems. Based on an interplay between exact solutions of simple models and educated guesses for realistic situations checked by performance analysis, effective decision rules can be found. This approach to developing control rules for real-time applications has met with success in manufacturing contexts (e.g., reducing the scrap rate when using computer-controlled lathes to cut metal), as well as telecommunications settings (e.g., dynamic routing of packets in digital networks).
Simulations are used in situations in which analysis is too difficult to be tractable or enlightening. Discrete-event simulation is a methodology that mathematical scientists have played a leading role in developing. The discrete events are, for example, customers propagating from one station to another in a queuing network, with states that change discretely (rather than continuously). The computer simulation approach offers the system designer an opportunity to visualize the actual operation of the system over time (e.g., in a manufacturing setting, one can watch parts being assembled as they travel through the facility). As a consequence, many commercially available simulation packages have extensive graphical interfacing capabilities. A disadvantage of simulation, relative to the more limited tools described above, is that building simulation models typically requires considerably more development effort on the part of the systems designer (in part because a simulation usually models the system at a higher level of detail). A research topic of great interest is the design of algorithms for discrete-event simulations that harness the power of large numbers of processors (several thousand in the Connection Machine) in massively parallel computers.
3.4 Machine Tools for Manufacturing
According to reliable estimates, the United States spends over $100 billion each year in machining operations. Industrial efforts to reduce these costs involve development of new and improved materials for cutting tools. The most advanced tools are made of ceramic composites. Knowledge concerning the characteristics of these composites, such as their extreme hardness, corrosion and wear resistance, strength at elevated temperatures, and electrical properties, comes from physical experiments. These experiments are very complex because they involve a large number of intricately linked variables, and the interrelations among the variables may not be known. The experiments are subject to the sensitivity of the processes, to uncontrollable processing variations, and to unavoidable variations in raw materials. The techniques of statistically planned experiments that have been developed over the last 50 years are particularly useful to address such situations. Such techniques were applied to the problem of ceramic composites processing research, in a collaboration involving materials scientists, statisticians, and an industrial ceramics developer.
The focus of the collaboration was processing of silicon carbide whisker reinforced alumina matrix composites used as advanced cutting tools. The object of the experiment was to study the cause-and-effect relationships among processing conditions (whisker characteristics and amount, time, temperature, and pressure), microstructures (density, alumina grain size, and homogeneity), mechanical properties (flexural strength, hardness, and fracture toughness), and machining performance (flank and nose wear). The results of a set of experiments indicated that hardness and strength are strong indicators of machining performance, and mean density is a strong predictor of hardness and strength. In addition, robust processing conditions applicable to the kind of equipment used were identified. The fractional factorial experiment approach used in this study reduced the cost of conducting the experiment by a factor of four without sacrificing any relevant information. The key idea is to consider the multidimensional space defined by the input factors and to focus on evaluating only the linear effects (main effects) and pairwise interaction effects of the input factors on the output responses. The benefits of such collaborative research accrue when efficient strategies, based on factorial experiments and other
designs, are routinely used by experimental scientists and engineers in the design and optimization of the materials processing conditions.
3.5 Simulation and Production—Petroleum
The mathematical sciences play a central role in many aspects of the development of our energy potential from hydrocarbons. The same techniques are applicable to other problems of national interest. Applications to groundwater flow, contaminant transport, cleanup of hazardous waste, and nuclear waste disposal all require the same mathematical and computational techniques. Applied mathematicians, numerical analysts, and computational scientists are becoming essential components of groups addressing such problems in many applications.
Mathematical models are important in exploration for petroleum, in characterizing the reservoirs, geologically and geochemically, and in developing production strategies to optimize recovery. The following physical problems have been studied systematically by mathematical scientists: building correct mathematical models from physical principles; understanding the mathematical properties of the models, such as existence, uniqueness, regularity, and continuous dependence of the solution upon data; developing discretization methods in a stable and accurate fashion; and producing computational algorithms, which take advantage of the emerging computer architectures for efficient solution.
Exploration via seismic inverse techniques leads to an extremely difficult mathematical problem. This is the inverse problem, in which a portion of the solution is given (the source signal and the reflected signal at sensor locations on the earth's surface), and the problem is to find the equation generating the solution, i.e., the reflection and transmission coefficients of the deeply buried geological layers. The direct problem is linear, but the inverse problem is highly nonlinear. Since uniqueness and continuous dependence of the solution (i.e., the geology) on data (i.e., the seismic signal) are properties that are almost impossible to attain, there is a need to quantify the degree of nonuniqueness, to deal with noisy data, and to identify new data collection locations and techniques to decrease the ill-posedness of the problem. Analysis of shear waves and elastic response has recently been included in seismic interpretation. Accurate interface conditions, absorbing boundary conditions, and grid refinement techniques are sorely needed for three-
dimensional applications. Finally, efficient solution algorithms, which take advantage of the new parallel and vector computer architectures, must be developed for full three-dimensional seismic problems.
Large-scale models of basin evolution provide a more global approach to locating oil deposits and discovering properties of petroleum reservoirs. The basin models describe thermal maturation, geochemical diagenesis, and local fluid flow effects over geological time periods. These models incorporate descriptions of processes from macroscopic plate tectonics to microscopic pore and throat development and geochemical changes. Large, coupled systems of nonlinear partial differential equations describe these complex geological, geochemical, and geothermal processes. These techniques, coupled with sedimentary and depositional theories, are essential in the location of subtle stratigraphic traps. They also form the basis of reservoir characterization in general. Advancement in these areas is being seriously impeded by the need for mathematics at all levels—from existence/uniqueness theorems to large-scale algorithm development. Geostatistics and length-scale averaging via homogenization techniques are also very important for dealing with uncertainty in the data.
Since primary and secondary recovery techniques leave up to 70 percent of the original oil in place, improved oil recovery methods are necessary so that we may use this major domestic source of energy. Large-scale reservoir simulation is essential as a predictive mechanism to help understand the fluid, physical, and chemical processes and use them to optimize hydrocarbon production. Present simulation techniques cause a serious loss of detail of the flow description and thus give limited, but still valuable, information. Compositional paths and Riemann problems have been studied by both engineers and mathematicians to provide insight into nonlinear wave and frontal interactions. A recent analysis of three-phase flow equations has revealed nonphysical features in commonly used equations, leading to a revision of the equations used in large-scale simulations. There is a need for better numerical techniques in large-scale simulation to resolve complex local physical phenomena.
Reservoir fluid flow should be studied in collaboration with geologists, geochemists, and geostatisticians to develop better reservoir characterizations and to incorporate data on different length scales in the
simulators. For fractured reservoirs, a dual system of equations exists: for flow in the fracture cracks and for flow in the rock matrix between the cracks. The coupling between these systems depends on the spacing between the cracks as well as the detailed properties of the rock matrix. This coupling has been studied recently, using homogenization theory. Interface methods follow the fluid interfaces, and adaptive grid refinement methods resolve the local physics of the complex chemical and physical fluid interactions. The nonlinear fingering process must be understood in the context of reservoir heterogeneities. Also, the global effects of the fingering process must be modeled on a reservoir scale, since this phenomenon will often dominate the flooding process. Usually this modeling is done by homogenization methods. The highly nonlinear, coupled systems of partial differential equations required in the models of enhanced oil recovery processes must be analyzed to obtain their major properties. Extremely difficult, large-scale inverse problems are necessary for history matching to obtain the unknown reservoir and flow properties in situ. Mixed finite-element methods, characteristic methods, and upwind methods give improved discretization techniques for the accurate treatment of nonlinear, transport-dominated flows. Due to the enormous size of the problems for field-scale applications, efficiency is the key to success, and algorithm development must use the newly emerging capabilities of supercomputers. Preliminary indications are that parallel computing will succeed in resolving the reservoir simulation problem.
3.6 Statistical Quality Control and Improvement
Statistics has very widespread applications and is among the leaders of the mathematical sciences in this regard. Statistics gains its importance in the physical and engineering sciences through the interpretation of measurements and the analysis of statistical significance and of errors in field and laboratory data. The use of statistics is well established in the biological sciences and medicine. In the social sciences, statistics is fundamental. Often statistics is the first of the mathematical sciences used in the analysis of data, and the first to be actively involved in the mathematical formulation of new science or technology, as the necessary precursor to its quantitative evolution.
The use of statistics for quality control originated from the need
to control complex manufacturing operations. In order to meet this demand, a number of new statistical ideas were formed and developed. Sequential sampling provides a notable example of the far-reaching effects that resulted. Sequential sampling has been used in the conduct and analysis of drug studies and clinical trials. At the same time, the emphasis on collecting data and applying basic and standard statistical techniques was highly successful in improving quality and reducing costs.
Statistically planned experiments were, in the main, developed within the context of agricultural experimentation. These methods have had phenomenal success in increasing crop yields and animal production. The ability of these strategies to extract vital information from comparatively few experiments is of great value, especially in manufacturing.
It is now commonplace to have mechanical design questions treated through carefully planned experiments. Influenced largely by the design engineer G. Taguchi, the focus of many experiments is on the reduction of variability of the performance of a product—now recognized as a key component of quality. Traditional statistical approaches were not clearly appropriate for such a goal. New statistical problems were formulated, leading to new experimental strategies and analyses. This is an area of ongoing research.
The following two case studies describe applications of statistical quality control (SQC) to problems in AT&T manufacturing units. These examples illustrate that substantial quality improvements (and consistent cost savings) result from the application of SQC to manufacturing processes.
In one example of a new automatic assembly, an operation comprising two assembly machines was plagued by low productivity: one machine was operating at 50 percent of its design capacity whereas the other was operating at only 25 percent of its design capacity. Despite numerous problems, no data had been collected.
The first activity of the SQC investigation was to collect data to identify the failure modes. Using standard techniques, the SQC team identified the principal problem: too great a variability in the dimensions of plastic parts used in the assembly. A related problem was excess bowing and warping in these parts caused by excessive vari-
ability in the melting point of the plastic from one batch to another owing to overly generous specifications. The machines were simply insufficiently robust to tolerate such variability. The solution was (1) to reduce variability in the dimensions of the plastic components and (2) to increase the robustness of the machines.
A secondary problem was excessive variability of the solder coating of certain metal components used in the process: on occasion, the coating was too thick and the component jammed. On investigation, it was discovered that the variability of the coating was within design specifications, but the latter were, again, overly generous. The problem was solved by adjusting the machine to permit greater variability and by tightening the specification.
After a year's work, the productivity increased by 121 percent, the labor hours were cut by 61 percent, and the yield (proportion of usable products) increased from 90 percent to 98 percent.
A second example concerned serious problems in the manufacture of an electronic component: the yield was only 84 percent, and only 50 percent of the scheduled delivery dates were met. A major difficulty was excess variability of the various characteristics of the component assembly. Variability occurred particularly in the automatically controlled acid bath used in the manufacture. SQC techniques identified the problem: the machinery that determined the pH value of the acid and corrected any discrepancies was overcompensating, causing excess variability. Reducing this variability by recalibration increased the yield to 95 percent. Additional problems caused by excess variability in constituent parts were also corrected by imposing tighter controls.
In the first year of operation after these corrections, $12 million was saved and the proportion of delivery dates met increased to 95 percent.
3.7 Manufacturing Process Control
Continuous production control is vital in the metals, glass, and chemical industries, among others. Process control in these applications typically involves 20 to 200 control variables and 10 to 100 quality (response) variables. The objective of the control is to monitor and adjust the process to ensure that the quality measures of the products meet the specifications of the customers. A basic difficulty in such control problems is that the information available for relating control and
quality variables is typically obtained during product manufacture, and thus is observational in character. Designed experiments are extremely difficult to carry out, owing to the very large number of control variables and the practical difficulties of perturbing a large-scale industrial process.
Process improvement calls for (1) sophisticated methods of variable selection to discover the most influential control variables and (2) high-dimensional nonlinear modeling to approximate their effect on the quality measures. These procedures can require massive computational resources, multivariate methods for time series data, and graphical representation and modeling of high-dimensional data.
Major management goals in the control of manufacturing processes include the discovery of better methods of process diagnosis and the development of effective procedures for quality improvement. The first goal requires the identification of quality variables specifically sensitive to particular steps in the process or particular pieces of equipment that may be drifting out of control. The second goal requires the development of a high-dimensional model, presumably nonlinear, that quantifies the effect of changes in the values of the control variables on the quality variables.
The large number of control variables means that the statistical analysis is operating at the very edge of what is currently possible and requires the development of new experimental procedures. Fortunately, there is some prior information that can be used to sharpen the analysis. Industry engineers have scientific grounds for believing that the response surface will be relatively flat with respect to most of the control variables and most interactions. Also, again on physical grounds, there is often an understanding of the functional form of the relationship between some of the control and quality variables.
A manufacturing process vital to U.S. economic competitiveness is the fabrication of very large scale integrated (VLSI) circuits or computer chips. This specific example illustrates some of the points made above. The process is extremely complex and is becoming much more so as the density of devices on the chips continues to increase dramatically. As this density increases, the process tolerances are decreased, and process control becomes more sensitive, so that statistical methods are of ever increasing importance. The development of statistical
methods to understand this process better, to diagnose equipment malfunctions, to increase yield, and to reduce process variability represents a major technical challenge.
The VLSI fabrication process consists of several steps performed on silicon wafers. The steps include oxidation, photolithography, plasma etching, and so on. Some of these steps are repeated many times over the course of the fabrication process. Determination of whether an integrated circuit (IC) produced by this process will be acceptable depends on several characteristics measured at the completion of the process (e.g., zero state threshold voltage, VT0). If a characteristic is not acceptable, the defect may have occurred at any one of several early steps in the process. Unfortunately, one cannot measure characteristics such as VT0 until fabrication is completed. The proportion of unacceptable ICs is often quite high for a new product, until the processes involved are stabilized.
It would be useful to model the steps in the VLSI fabrication process, statistically, in order to be able to monitor and adjust the quality of ICs as they are being produced, and to detect equipment malfunctions at the end of a process step rather than at the end of the entire fabrication process.
3.8 Sensor-Based Manufacturing
Modern control theory has shown in the aerospace industry that dramatic improvements can be achieved by using all available sensors. The United States is the world leader in the areas of control and signal processing (e.g., Kalman filtering, adaptive filtering, unsupervised learning, iterative deconvolution) required for optimal extraction of information from sensor data. Much of this work has been carried out by mathematically inclined engineers, drawing on a broad range of mathematical disciplines. Preliminary investigation has demonstrated that application of these ideas to the field of semiconductor fabrication can have a significant impact on process performance. Furthermore, with a projected cost of $1 billion for an IC fabrication line in the year 2000, a reduction in start-up time and defect percentages can have a tremendous financial impact.
Lithography is a key process in IC manufacturing: it involves the generation of masks, and the attendant problems in their use. A com-
mon estimate is that nearly three-fourths of the manufacturing costs of semiconductor chips can be attributed to the lithography stage. Among the problems in lithography are the methods for measuring critical dimensions (e.g., linewidths) rapidly and noninvasively. Recently neural network classification strategies have been applied to edge detection of wafer patterns using digitized images. Successful results have been confirmed in several test cases by careful comparison to time-consuming measurements obtained by use of a scanning electron microscope. The neural network algorithms are noninvasive and rapid, and they have low noise sensitivity because of an adaptation mechanism. Furthermore, the unsupervised neural network device requires only normally available a priori information and can also be applied to solve the problem of mask-wafer alignment. More generally, a number of digital image processing techniques that have been used so successfully for satellite and space-probe images could be used in lithography; the barriers between fields are such that lithographers have focused more on direct physical measurement as opposed to indirect measurement followed by signal processing.
A recent application in this direction has been to new methods for temperature measurement of wafers being processed in very hot (1000°C) rapid thermal processing ovens. Pyrometers are relatively inexpensive temperature measuring devices but their accuracy is poor. Therefore, there is a considerable research effort to devise sensors based on other principles. However, by using appropriate signal processing techniques (in particular, a type of extended Kalman filtering technique), it appears that the pyrometer measurements can be processed to yield accurate temperature measurements and to track their variation with time.
Such temperature measurements are currently used by semiconductor specialists to gauge the progress of various reactions and processes. However, they are also essential in the application of modern multivariate control strategies, which when given the measurements of a reasonable number of sensor variables and given a reasonable number of control parameters, can give significantly better control than that achievable with single variable controls. Through the use of computers and signal processing strategies, the mathematical models on which the control is based can be updated with the acquisition of new data,
to optimize manufacturing operations or paths to improve quality and throughput.
3.9 Manufacturing Standards
The highly competitive IC industry has a never-ending demand for submicrometer feature sizes on ICs and for metrological techniques for measuring and characterizing these features. Early on, the IC industry became aware that there was a problem in obtaining agreement of linewidth measurements among the mask suppliers and IC manufacturers. The National Institute of Standards and Technology (NIST), an agency in the U.S. Department of Commerce, was asked by a commercial standards maker to check its linewidth measurement standards. The absence of standards at the required dimensions had led to a proliferation of industrial in-house standards with no agreement among them.
The fundamental problem was identified as the measurement of the width of the lines on the IC photomask. A decision was made to create a new measurement reference, an artifact that mimicked the photomasks used in industry. A measurement system was developed, interactions between the measurement instrument and the specimen were studied, procedures for properly using the photomask in the field were developed, and theoretical models were developed to explain how an optical microscope would respond to light diffracting around the edges of a line on the photomask.
Establishing control in manufacturing across numerous industrial suppliers and consumers requires a process metrology that is consistent across all users. Such a process metrology is based on modeling and experimentation found in modern statistical theory and practice. Two elements of this modeling and experimentation stand out: (1) so-called round-robin experiments across industrial sites to establish precise measures of variation from site to site and (2) individual measurement control systems at a site that enable the continuous improvement of measurement quality. Mathematical techniques of efficient experimentation and measurement process control are fundamental to establishing these elements.
The round-robin experiment required a high-precision test specimen, which was developed by NIST. The round-robin, involving 10
companies (IC manufacturers, photomask makers, and instrument makers), clearly demonstrated that there was a measurement problem in the industry. Following this experiment, NIST developed its first linewidth standard. A procedure was developed by NIST statisticians to ensure measurement process control for the certification of each standard reference material (SRM) issued for sale to the IC industry. These certified standards were immediately in great demand. Linewidth standards are now available for a number of materials. An automated measurement system and sophisticated statistical process control procedures are used to certify the linewidths on these photomasks. These standards are in demand and many manufacturing firms have adopted this technology.
This example illustrates the use of SRMs. These are well-characterized, homogeneous, stable materials with specific properties that are measured and certified by a national reference laboratory. An extensive campaign of measurements and tests is undertaken during the process of developing and certifying SRMs, and collaboration of statisticians with the physical scientists who actually make the measurements plays an essential role. The composition of 90 percent of the steel produced in the United States is controlled by measurements based on SRMs. SRMs serve nearly all sectors of manufacturing, including electronics, instruments, computer instrumentation, ferrous and nonferrous metals, mining, glass, rubber, plastics, primary chemicals, nuclear power, and transportation.
3.10 Production, Inventories, and Marketing
Equipment acquisition and purchased subassemblies account for more than 90 percent of the manufacturing costs of some high-technology products. Many companies avoid corresponding increases in the costs of capital by more carefully coordinating their production, inventories, and product distribution. Their efforts combine statistical data analysis and operations research methods.
Pfizer, Inc., one of the country's major pharmaceutical manufacturers, reduced its U.S. inventories by $24 million during a three-year period, improved its customer service by reducing its back orders by 95 percent, and sharply improved overall management control. Five years of production and sales history were statistically analyzed to develop mathematical models for production lot sizes and target inven-
tory levels. The models were optimized with a combination of dynamic programming and artificial intelligence techniques.
Net interest expenses for Blue Bell, Inc., one of the world's largest apparel manufacturers, had increased 20-fold. Financing inventory had dramatically pushed up the company's cost of doing business. A new production planning process, designed with operations research techniques and statistical data analysis, was tested and implemented. In less than two years, inventories were reduced by $115 million with neither a decrease in sales or customer service, nor an increase in other manufacturing costs.
Bethlehem Steel is the second largest U.S. steel producer. It faced the challenge of efficiently operating a new ingot mold stripping facility against strong competition. The competing process had the disadvantage of higher capital costs, but the advantage of improved yield, productivity, and product quality. Optimization of the ingot-based plant utilized combinatorial mathematics and mathematical programming to select ingot mold sizes. The resulting annual savings exceeded $8 million.
The cost of financing working capital at CITGO, the nation's largest independent refiner and marketer of petroleum products, had increased more than 30-fold while gross margins had decreased. An optimization-based decision support system for planning supply, distribution, and marketing (called the SDM system) was developed and implemented. The system, based in large part on statistics and mathematical programming, integrates CITGO's key economic and physical SDM characteristics over a short-term (11-week) planning horizon. Management uses the system for many types of decision making—pricing; where to buy, sell, or trade products; how much inventory to maintain; and how much product to ship by which method. Major benefits accruing from the SDM model included reduction in product inventory and improved operational decision making. Annual interest savings of $14 million were realized after an inventory reduction of $116 million. Improvements in decision making are estimated to be worth another $25 million yearly.
3.11 Maintenance and Repair
Mathematical and statistical modeling and simulation are vital steps
in the process of planning viable repair and maintenance facilities, especially if the facilities are complex, involving multiple work stations, sources of supplies, and so on. The same considerations apply as well to the design of manufacturing facilities. The initial consideration is feasibility: will the proposed facility function well, in terms of costs, inventory, and production cycle time? Once feasibility is established, simulations provide invaluable information regarding facility design, deployment, and use of machinery, parts, and personnel. After an optimally designed facility has been built, further simulations allow final adjustment of operating procedures to achieve optimal performance.
Consider the case of United Airlines, faced with the problem of turbine blade repair. Although the general image of aircraft repair may be one of mechanics swarming over planes, in what constitutes a job shop approach, in actuality there may be significant cost savings in establishing specialized facilities to ''remanufacture'' certain standard parts. United decided to establish such a dedicated facility to remanufacture turbine blades. The facility was expected to cost $15 million. An initial feasibility study was undertaken to determine whether the dedicated facility would function better than the job shop in terms of costs, inventory, and repair cycle time. The simulations were based on probability models for distributions of demand for repaired blades, supplies of defective blades, and the progression of repair through the remanufacturing stages of the facility. Once feasibility was established, simulations allowed optimal balance of all production and repair machinery. After the construction of this optimally designed facility, the actual operation gave rise to additional data in terms of revised probability measures in the simulation model, which allowed further simulations, to achieve improved performance.
The economic leverage of these simulations is considerable, as a small investment in simulation can save many hundreds of thousands of dollars on a project of the size discussed above.
























