6
Aerosols in Homes and Mines
The measurement methods used to determine the effective size of the radon progeny in air are generally based on the use of diffusional deposition in the sampler to remove some of the airborne activity in a well-defined manner. By making a series of such measurements and knowing the theoretical rates at which the deposition should occur, the size distribution of the radioactive aerosol can be inferred. Thus, to understand the experimental methods used for activity-weighted size distribution and/or unattached fraction measurements, it is necessary to present the theoretical considerations upon which the measurement instruments are based. In the next sections, the relationship between size and diffusivity will be presented along with the theory of diffusive deposition of particles on the inside surfaces of cylinders and on strands of wire mesh screen.
RELATIONSHIP BETWEEN PARTICLE SIZE AND DIFFUSION COEFFICIENT
The particle diffusion coefficient, D, for aerosols is commonly estimated by the equation,
where k is the Boltzmann constant (1.38 × 10-16 erg°K-1), T is the temperature in degrees Kelvin (293 K at 20°C and 1 atm), dp is the particle diameter in centimeters, μ is the gas viscosity (1.83 × 10-4 g cm/s for air), and C is the Cunningham correction factor given by Friedlander (1977),
where λ is the mean free path of the gas (0.65 × 10-5 cm for air at 20°C and 1 arm of pressure).
Equation 6-2 was empirically derived to fit the entire range of values of dp/λ from the continuum to the free molecular regimes (Davies, 1945). However, Equations 6-1 and 6-2 overestimate the particle diffusion coefficient in the 0.5-1.75-nm particle diameter range. To illustrate this overestimation, consider the diffusion coefficient for a radon-222 (222Rn) atom whose atomic diameter is estimated to be 0.46 nm. This diffusion coefficient was measured by Hirst and Harrison (1939) to be 0.12 cm2/s. Equations 6-1 and 6-2 predict a diffusion coefficient of 0.20 cm2/s for a 0.5-nm-diameter cluster. This result is further evident from a comparison (Figure 6-1) with the diffusion coefficient calculated by using the kinetic theory of gases (Loeb, 1961; Porstendörfer, 1968; Raabe, 1969). The kinetic theory equation for the diffusion coefficient of molecular clusters in a gas is
where Vr is the root mean square velocity of the gas (5.02 × 104 cm/s for air at 20°C), N is the number concentration of gas molecules (2.51 × 1019 cm3 for air at 760 mm Hg and 20°C), s is the sum of the radii of the gas molecules (0.155 × 10-7 cm for air) and of the cluster, M is the molecular weight of the cluster, and m is that of the gas (28.9 for air).
In order to use a single equation for the particle diffusion coefficient over the entire size range for dp > 0.5 nm, the Einstein-Cunningham Equations 6-1 and 6-2 may be fitted to the kinetic theory Equation 6-3 in the 0.5-1.75-nm size range in a manner that yields the original Einstein-Cunningham Equations 6-1 and 6-2 for dp > 1.75 nm. This result may be obtained by the substitution of
for dp (in centimeters) in Equation 6-2 for the Cunningham constant C. The molecular weight-cluster size relationship for polonium-218 (218Po)-H2O clusters was used for the molecular weight factor [(M + m)/M]1/2 in the kinetic theory equation (Equation 6-3) and to obtain the fitting parameter d* in Equation 6-4. Figure 6-1 is a plot of the corrected and uncorrected Einstein-Cunningham equations and the kinetic theory diffusion coefficient equation versus particle diameter (the kinetic theory equation is plotted without the [(M + m)/M]1/2 factor, which rapidly approaches unity).
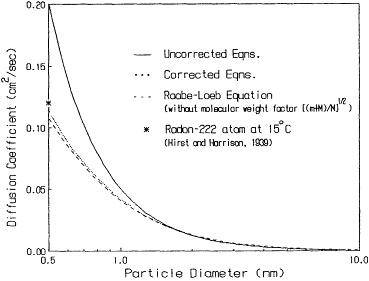
Figure 6-1 Diffusion coefficient for particles 0.5-10 nm in diameter.
Penetration of Aerosols Through a Tube
Theoretical equations for diffusional deposition in circular tubes are well documented in the literature (e.g., Gormley and Kennedy, 1949; Fuchs, 1964). Of particular interest when sampling highly diffusive ultrafine cluster aerosols are tube penetration equations for the prediction of diffusional deposition or wall losses in the entrances of sampling tubes. Typically, the ''wall loss'' lengths L in these situations are smaller than the tube length required for the development of a laminar flow profile ("entrance length"). This entrance length z beyond which a parabolic flow field is established is (Fuchs, 1964),
where R is the radius of the tube, and Ret = 2UρR/μ is the Reynolds number of the tube. Within this entrance distance, z, a developing flow exists and could enhance diffusional deposition. Theoretical studies by Tan (1969) and Chen and Comparin (1976) suggest that for highly diffusive aerosols with small Schmidt numbers (Sc= v/D) and penetration parameter, μ* = DL/R2U < 0.05 (small entrance length L and high flow velocity U), assuming a uniform flow profile may be a suitable first-order approximation for the prediction of diffusional deposition losses.
Ingham (1975) developed an analytical, matched-asymptote solution for uniform flow penetration through a circular tube, Pt, given by,
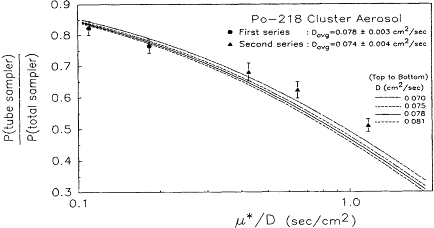
Figure 6-2 Assessment of penetration of radioactive particles into a cylindrical tube compared to the theoretical predictions of Ingham (1975).
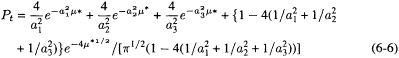
The parameters ![]() (=5.783186),
(=5.783186), ![]() (=30.471262),
(=30.471262), ![]() (=74.887007) are the zeros of the zero-order Bessel function of the first kind, J0(an) = 0 (Tan, 1969). Equation 6-6 is valid for tube Reynolds number Ret < 1,200 and tube Peclet number (Pet = RU/D) > 100.
(=74.887007) are the zeros of the zero-order Bessel function of the first kind, J0(an) = 0 (Tan, 1969). Equation 6-6 is valid for tube Reynolds number Ret < 1,200 and tube Peclet number (Pet = RU/D) > 100.
Thomas (1955) attempted to verify the laminar flow tube penetration theory equations using gas molecules and reported agreement to within 20-30%. The discrepancies were attributed to experimental difficulties and possible entrance effects. Scheibel and Porstendörfer (1984) attempted a verification of tube penetration theory using monodisperse particles (dp > 4 nm). They reported good agreement with the laminar flow theory (Gormley and Kennedy, 1949) for particle sizes greater than 15 nm and large deviations for particle sizes below 5 nm. The discrepancies were resolved by including terms for uniform flow deposition in the entrance of the tube and for deposition on the front face of the tubes. Recent studies by Ramamurthi et al. (in press) have found that tube penetration theory accurately predicts the deposition behavior of highly diffusive radioactive particles if the value ![]() . For μ* > 0.05, Equation 6-6 systematically underpredicts the penetration of particles through the tube. Figure 6-2 shows the results of this test of penetration of a single tube as a function of the diffusion parameter, μ*/D.
. For μ* > 0.05, Equation 6-6 systematically underpredicts the penetration of particles through the tube. Figure 6-2 shows the results of this test of penetration of a single tube as a function of the diffusion parameter, μ*/D.
Deposition of Ultrafine Particles onto Wire Screens
An equation of penetration through wire screens based on the theory of fibrous filtration was derived by Cheng and Yeh (1980) and Cheng et al. (1980). The penetration equation for a wire screen, with wire diameter df, thickness w, volume fraction α, and sampling face velocity U, for ultrafine particles, dp < 0.1 μm, is given by,
where
and D is the particle diffusion coefficient. Equation 6-7 is valid for wire Reynolds numbers (Ref = Uρdf/μ, where ρ is the density of air) less than 1 (Emi et al., 1982). The fan model filtration theory has been applied to wire screens and experimentally verified for particle sizes dp > 15 nm (0.015 μm) (Cheng and Yeh, 1980). Scheibel and Porstendörfer (1984) have further verified the fan model for particle sizes ![]() nm. Recent work with charged and uncharged 218Po clusters in the 0.5-1.5-nm size range has also indicated general agreement with the wire screen fan model penetration Equation 6-7 (Holub and Knutson, 1987; Ramamurthi et al., in press), although calibration studies remain necessary for dp < 4 nm. The penetration characteristics for a wire screen operating in the 0.5-100 nm size range can thus be determined from Equations 6-7, 6-8, and 6-9. Typical penetration curves are shown in Figure 6-3.
nm. Recent work with charged and uncharged 218Po clusters in the 0.5-1.5-nm size range has also indicated general agreement with the wire screen fan model penetration Equation 6-7 (Holub and Knutson, 1987; Ramamurthi et al., in press), although calibration studies remain necessary for dp < 4 nm. The penetration characteristics for a wire screen operating in the 0.5-100 nm size range can thus be determined from Equations 6-7, 6-8, and 6-9. Typical penetration curves are shown in Figure 6-3.
Further, each screen-velocity combination can be conveniently parameterized by its dp(50%) (Ramamurthi and Hopke, 1989), the particle diameter for 50% collection efficiency, because of the form of the penetration in Equation 6-7. This parameter can be determined (using a log-linear diffusion coefficient approximation) as,
for 0.001 < KVF < 0.325. These dp(50%) values are a convenient way of characterizing the particular screen parameters and face velocity of the sampling flow. However, as can be seen by the curves in Figure 6-3, there is a distinct difference between the relatively slowly changing penetration-versus-diameter behavior of screens and the sharp cutoffs that are observed with inertial collections systems such as impactors or cyclones.
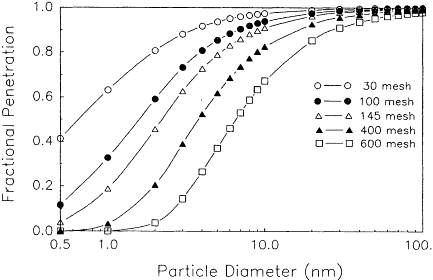
Figure 6-3 Fractional penetration through various mesh screens at a face velocity of 10 cm s-1.
MEASUREMENT METHODS FOR UNATTACHED FRACTION
Diffusion Sampler
Most of the early work on "unattached" fraction measurements was carried out in uranium mines. In the earliest studies, including the work of Chamberlain and Dyson (1956), the unattached fraction was determined by measurement of the penetration of the activity through a right circular cylinder. Using the tube penetration theory of Gormley and Kennedy (1949), the fractional penetration can be related to πDL/2Q, where D is the diffusion coefficient of the radioisotope, L is the length of the tube, and Q is the volumetric flow rate through the tube. Details of the theory of penetration of particles through a tube are given in the previous section. The diffusion coefficients of the radon decay products are assumed to have a single, very much larger value than the diffusion coefficients of the condensation nuclei to which the radon progeny become attached. Thus, by comparing the amount of activity penetrating through a tube of given dimensions at a given flow rate with the total airborne decay product activity, the fraction of unattached activities could be estimated.
The amount of unattached radioactivity has been measured in this manner by a number of investigators (Craft et al., 1966; Fusamura et al., 1967; Duggan and Howell, 1969). A problem that tends to confuse the literature of unattached fraction measurements is the number of ways in which the unattached radioactivity is reported. The International Commission on Radiological Protection
(ICRP) has defined the unattached fraction as the fraction of the equilibrium number of 218Po ions that are unattached to particles (ICRP, 1959). However, the method used to measure the attached fraction readily yields the fraction of unattached 218Po atoms to the total number of 218Po atoms actually present. Chamberlain and Dyson (1956) made the first report of unattached fraction to be 0.1 using what became the ICRP definition (ICRP, 1959). It is important to carefully determine in each case what the investigator means by "unattached" fraction in order to compare results.
Wire Screen Samplers
The diffusion samplers were fairly cumbersome devices to use, and therefore a simpler and more portable system was developed based on the collection of the activity on wire mesh screens. Wire mesh screens have become the most commonly used method for estimating unattached radon daughter fractions. The early development of these systems was described by James et al. (1972), Thomas and Hinchliffe (1972), and George (1972). These systems were much easier to use, although initially they suffered from the lack of a well-developed theory to relate the screen properties to their collection efficiency. The collection efficiency of wire screens for unattached 218Po was therefore determined empirically from calibration experiments with fresh 218Po in the absence of ambient aerosols as a function of screen parameters and face velocity. Compared with the currently accepted theory described below, the equation of Thomas and Hinchliffe (1972) overestimates wire screen collection efficiencies for particle diameters dp < 1.0 to 2.0 nm and dp > 5.0 to 7.0 nm for most screen-velocity combinations.
George (1972) developed a standard method for measuring unattached 218Po fractions: a 60-mesh stainless steel screen is sampled simultaneously with a parallel filter, followed by counting of the alpha particles on both the screen and filter; 218Po data are extracted from both the screen and the filter by the modified Tsivoglou technique, and the unattached fraction is calculated as the ratio of twice the activity on one face of the screen to the activity on the filter. This method has been widely used to obtain estimates of the unattached fraction in a variety of different environments.
The wire screen penetration theories developed by Cheng and Yeh (1980), Cheng et al. (1980), and Yeh et al. (1982) are presented earlier, along with a semi-empirically corrected diffusion coefficient equation in the molecular cluster size range to characterize unattached fraction measurements reported in earlier studies, Equations 6-1 and 6-2.
A number of wire screen measurement studies of the unattached 218Po fraction are reported in the literature (George, 1972; James et al., 1972; Raghavayya and Jones, 1974; Bigu and Kirk, 1980; Stranden and Berteig, 1982; Bigu, 1985; Reineking et al., 1985). Table 6-1 provides a compilation
TABLE 6-1 Wire Screen Parameters and Face Velocities Used in Previously Published Wire Screen "Unattached" Fraction Measurements
of the wire screen parameters and face velocities used in these studies. Each screen-velocity combination is characterized by its dp(50%) parameter obtained from Equation 6-1. Nominal values for commonly undocumented parameters such as w and α were taken from wire screen manufacturers' catalogs for screens with the appropriate combination of mesh number and wire diameter reported in the studies.
Figure 6-4 shows the calculated particle collection efficiency characteristics for each of the studies listed in Table 6-1, as determined by the theory of Cheng and Yeh (1980) discussed above. The collection efficiencies for the 60-mesh screens used by George (1972) and the 150-mesh screens used by Bigu (1985) axe also plotted, although the wire Reynolds numbers are greater than 1. Wire screens with collection efficiencies that differ only slightly are plotted together for comparison purposes. The collection efficiencies of the screens are between 70 and 90% and 6 and 12%, respectively, for 1-and 10-nm-diameter particles and decrease rapidly in the 1-to 3-nm size range.
The concept of an unattached fraction measurement is to have a system that will collect all of the highly diffusive activity without collecting any activity attached to particles. The separation of aerosol size distributions into well-defined modes has been used to great advantage in studying the much larger sized modes ![]() in the ambient aerosol. However, such measurements
in the ambient aerosol. However, such measurements
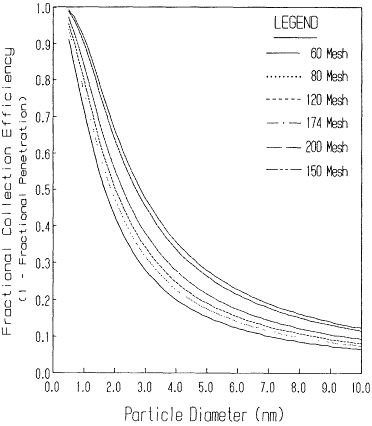
FIGURE 6-4 Collection characteristics for the wire mesh screen systems used in a number of the reported "unattached" fraction measurements.
are possible because the separation of large particles is based on their inertial properties. In this case, devices with sharp cutoff points such as cyclones or impactors can be designed (Lodge and Chan, 1986). However, because of the stochastic nature of diffusional deposition, the collection curves for wire screens or tubes are much more gradual functions of particle size. To illustrate the problem with using a single screen for making such a dichotomous measurement, Figure 6-5 shows the collection efficiency curves with dp(50%) along with the characteristics of a log-normally distributed aerosol size distribution with a median diameter of 1.0 nm and a geometric standard deviation of 1.5 in the range suggested by Reineking and Porstendörfer (1986). Nominal values for w and α were obtained from screen manufacturers' catalogs (see Hopke et al. [in press] for details and references).
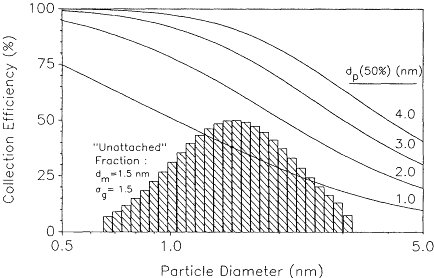
Figure 6-5 Collection efficiency curves for "typical" wire screens characterized by dp(50%) values of 1, 2, 3, and 4 nm and presentation of a log-normal size distribution characteristic of the "unattached" fraction.
It can be seen that the use of wire screens underestimates the unattached fraction if it indeed consists of an ultrafine cluster mode in the 0.5-to 3-nm size range (Reineking and Porstendörfer, 1986). The cumulative collection of activity as a function of size is presented in Figure 6-6. The underestimation of the unattached cluster mode in each of the studies is presented in Table 6-1. The wire screens used in these studies would underestimate such an unattached cluster mode by 14 to 48%, depending on the dp(50%) parameter for the particular screen-velocity combination. The choice of a single, optimized screen dp(50%) parameter that maximizes the collection of the unattached mode while minimizing the collection of attached activity may hence be beneficial for single-screen unattached fraction measurements.
To facilitate the appropriate choice of this parameter, the collection efficiency of a log-normally distributed aerosol particle mode was determined as a function of the wire screen dp(50%), as shown in Figure 6-6. From the data in Figure 6-6 it appears that a wire screen dp(50%) is an optimal choice yielding about 90% collection of the unattached mode (dm = 1 nm, σg = 1.5, 0.5 < dp < 3 nm), while minimizing the collection of activity in the second aerosol mode (dm = 25 nm, σg = 1.75, 10 < dp < 60 nm) to less than 8%. Activity in the latter size range may be significant in indoor air following cooking, as reported by Tu and Knutson (1988a). The collection of activity attached to the larger aerosol particle mode (dm = 125 nm, σg = 2.0, 40 < dp < 400 nm) is minimal for a dp(50%) of <10 nm, and is about 1% for a dp(50%) of 4 nm. This
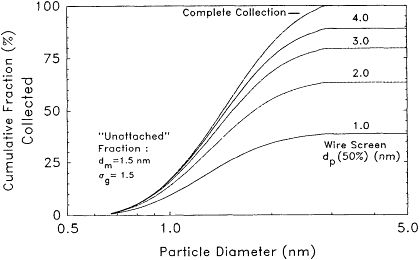
Figure 6-6 Cumulative collection fraction of an ultrafine activity mode.
result is consistent with the calculations by Van der Vooren et al. (1982) for the collection of attached activity in this size range by wire screens sampling the unattached mode. In the sampling of dusty atmospheres with particle sizes of a dp of >0.5 μm (500 nm), collection by impaction and interception may become significant; but for wire screens with a df of >100 μm, an α of <0.3 and a U of <10.0 cm/s the wire screen collection efficiency for a 5-μm-diameter particle is less than 5%. More recent work by Reineking and Porstendörfer (1990) suggests that there can be errors in unattached fraction measurements caused by inertial collection of radioactivity-carrying particles of >100 nm in diameter.
Another consideration of wire screen systems is the activity measurements. Measurement of the activity collected by a wire screen is complicated by the deposition of activity on the front and back faces of the screen as well as alpha absorption losses in the screen weaves. The ratio of activity collected on the front and back faces of a wire screen has been found to be clearly dependent on both the screen parameters and the activity distribution sampled by the screen (Holub and Knutson, 1987). For single wire screen samplers, analysis of total or reference filter (At) and wire screen backup filter (Abf) activities would yield more reliable estimates of the unattached fraction and would help to circumvent the problems associated with analyzing the wire screens themselves for collected activity. However, depending on the amount of activity that attaches to the screen, such a procedure may lead to low statistical precision in the activity determination on the screen backup filter.
REVIEW OF PAST UNATTACHED FRACTION MEASUREMENTS IN MINE ATMOSPHERES
Diffusion Sampler Measurements
Craft et al. (1966) used a diffusion sampler and an assumed diffusion coefficient of 0.045 cm2/s, to find a wide range of fractions of 0 to 0.73. However, they defined their fraction as the ratio of unattached radon daughter alpha-energy concentration to the total radon decay product alpha-energy concentration. They concluded that there is so much variability from location to location and mine to mine that it is not possible to select any particular value of unattached activity as being representative of actual mine conditions. They observed that in the presence of diesel smoke, the unattached fractions were low.
Fusamura et al. (1967) also used a tube diffusion sampler. They assumed a diffusion coefficient of 0.054 cm2/s and found fractions of 218Po from 0.06 to 0.13 in active areas of mines where dust-producing activities were in progress and from 0.09 to 0.25 in inactive areas of mines according to the ICRP definition. They found that drilling operations produced substantial oil mists to which the radon progeny attached. In areas where pneumatic loaders or picks were used, the unattached fractions were in the 0.09 to 0.13 range. It was anecdotally reported that in areas where no work was being done, the unattached fraction was as high as 0.5, but no specific number was reported related to their measurements in particular locations in several mines.
George and Hinchliffe (1972) and George et al. (1975, 1977) of the Health and Safety Laboratory (HASL; now the Environmental Measurements Laboratory) described an extensive series of measurements in active uranium mines in the Grants mineral belt of New Mexico. In those studies, they used a diffusion sampler that was based on the studies of deposition of unattached radon progeny in an impactor stage (Mercer and Stowe, 1969). The collection efficiency as a function of sample flow rate is given in Figure 6-7.
However, Subba Ramu (1980) built a similar device and suggests that the device is about 90% efficient at 1 liter/min. Subba Ramu claims that the difference in efficiencies between the HASL devices described by George and Hinchliffe (1972) and his sampler were due to his "extreme precautions to minimize the presence of attached radon daughter products, which interfere with accurate calibration." Thus, there exists some uncertainty in the earlier measurements, and they may underpredict the unattached fractions.
The results of the series of measurements are summarized in Figures 6-8 and 6-9. Figure 6-9 shows the unattached fractions of 218Po, fa, as defined by the ratio of the total 218Po activity collected in the sampler divided by the collection efficiency times the total airborne 218Po activity as measured on an open face filter. Figure 6-8 shows the unattached fraction as defined by ICRP (1959).
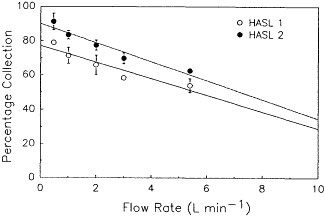
Figure 6-7 Collection efficiency of the HASL diffusion samplers for 218Po as a function of flow rate redrawn from data in George and Hinchliffe (1972). The lines are simple first-order regression lines drawn through each set of points.
These values were obtained by multiplying the fa values by the ratio of the total airborne 218Po activity concentration (picocuries [pCi]/liter) to the radon concentration (pCi/liter). It should be noted that the ICRP unattached fraction values are substantially lower than the fraction of 218Po that is unattached.
Cooper et al. (1973) also used a Mercer and Stowe (1969) diffusion sampler to measure unattached fractions in mines. They examined a mine in the Uravan Belt area of Colorado (mine A) and a mine in Ambrosia Lake, New Mexico (Grants mineral belt) (mine B). The results of these studies also included detailed analyses of the collected inorganic and organic particulate matter. Only 13 unattached fraction measurements are reported: 10 in mine A and 3 in mine B. The results of Cooper et al. (1973) are summarized in Figure 6-10. Unattached 218Po compared with total 218Po was determined to be 0.49 ± 0.14; for 214Pb it was 0.067 ± 0.019, and for 214Bi it was 0.032 ± 0.009. The unattached fraction of the potential alpha-energy concentration was 0.12, with a range of 0.09 to 0.14.
Wire Screen Measurements
Raghavayya and Jones (1974) made measurements of radon, decay product concentrations, unattached fractions of each decay product, and condensation nuclei concentration in three mines in Colorado and New Mexico. They used the approach of Thomas and Hinchliffe (1972) to calculate collection efficiency. However, since they calculated that they would obtain 92.59% collection for D of 0.06 cm2/s activity, they assumed that there is 100% unattached activity and
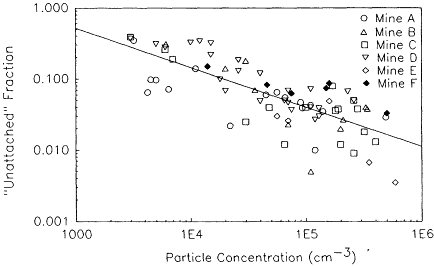
Figure 6-8 ''Unattached" fraction of 218Po as defined by ICRP (1959) measured in New Mexico uranium mines as a function of particle concentration. Data for this plot were taken from George and Hinchliffe (1972) and George et al. (1977).
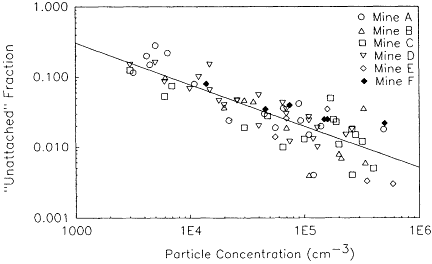
Figure 6-9 "Unattached" fraction of 218Po as defined relative to total 218Po measured in New Mexico uranium mines as a function of particle concentration. Data for this plot were taken from George and Hinchliffe (1972) and George et al. (1977).
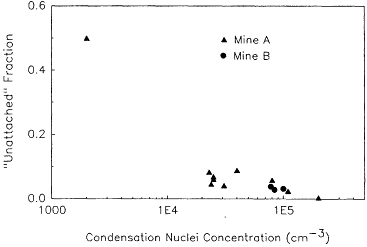
Figure 6-10 "Unattached" fraction measurements of Cooper et al. (1973). All of the results are the fraction of 218Po activity that is "unattached."
no attached collected activity in the high-particle-concentration atmospheres in the mines. They counted the wire screens and had difficulties getting the total activity measured with a separate filter to match the sum of the activity on the screen plus that on the backup filter. They developed an empirical correction factor to obtain the values they present as the fraction of activity for each decay product that is unattached and activity for a total unattached fraction relative to the activity of radon.
Mercer (1975) noted that their correction factor produces a minimum value of the unattached fraction. He provided an alternative analysis of the calibration data and a new set of f values. However, other problems have been noted in Mercer's results. Kotrappa and Mayya (1976) examined the equations used to calculate the 218Po, 214Pb, and 214Bi concentrations and found errors in the equations of Raghavayya and Jones (1974). Kotrappa and Mayya (1976) have recalculated the concentrations of the decay products, working levels, and a revised set of total unattached fractions that they incorrectly described as following the ICRP (1959) definition. The corrected total unattached fractions are presented as a function of the condensation nuclei concentration in Figure 6-11.
In general, the 218Po results show the largest unattached fraction compared with the results for longer-lived 214Pb and 214Bi. The ranges of the fractions of unattached atoms to atoms present are as follows:
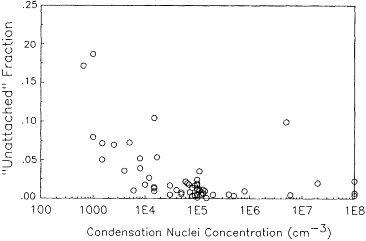
Figure 6-11 Total "unattached" fraction, ft, as measured by Raghavayya and Jones (1974) with corrected values of Kotrappa and Mayya (1976).
Further examination of the results of Raghavayya and Jones (1974) still suggest problems in their measurements. For example, it would be expected that as the condensation nuclei count (c) increases, there should also be an increase in the equilibrium fraction (F), as defined by
The equilibrium fraction as a function of the condensation nuclei concentration is presented in Figure 6-12. It can be seen that there is no clear trend in the data. From prior measurements of attachment coefficients (Raabe, 1969; Porstendörfer and Mercer, 1979), it would be anticipated that there should be a substantial increase in the equilibrium factor with increasing particle concentrations. These results thus suggest a substantial problem in either the radon progeny measurements or the field measurements of the number of condensation nuclei.
Bigu and Kirk (1980) measured unattached fractions in two Canadian mines using both a diffusion sampler and a wire screen system. The collection efficiencies of the diffusion and wire screen samplers were reported to be 53 and 95%, respectively, when operated at 2 liters/min. Their unattached 218Po fraction results are presented in Table 6-2. In general, there is reasonable agreement between the two measurements. Unfortunately, there are only limited condensation nuclei measurements, and no radon measurements were reported. Thus, the ICRP F values cannot be calculated, nor can the equilibrium fraction
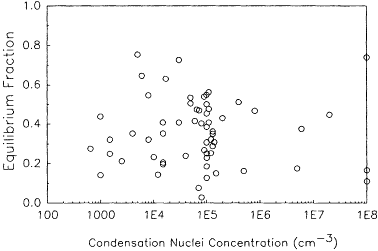
Figure 6-12 Equilibrium fraction, calculated from the data of Raghavayya and Jones (1974) as corrected by Kotrappa and Mayya (1976), as a function of the condensation nuclei count.
be determined. The values are similar to the other values reported for active working areas of mines.
Other measurements were performed in one Canadian mine by Busigin et al. (1981). They used parallel plate diffusion batteries. Their measurements were in active mining areas with high particle concentrations (approximately 106 nuclei/cm3). Under these conditions, they found no distinct unattached fractions, with an upper limit of 1 to 2%. Subsequently, the same group made more extensive measurements in two mines using a wire screen sampler (Khan et al., 1987). Although that report followed publication of the detailed theory of wire screen collection in the early 1980s, this group continued to use the collection efficiency curve of Thomas and Hinchliffe (1972). Thus, the penetration efficiencies have some error and lead to an underestimation of the unattached fraction by approximately 10 to 15%. In subsequent measurements, Bigu (1985) also found very small values of unattached progeny (<0.01) with aerosol concentrations in excess of 105/cm3.
Stranden and Berteig (1982) made a series of 33 measurements in an iron ore mine in Norway. They also used the collection efficiency curve of Thomas and Hinchliffe (1972) and reported the fractions of unattached 218Po, 214Pb, and 214Bi and the fraction of unattached potential alpha energy concentration (PAEC). The unattached PAEC is obtained from the individual concentrations as follows:
TABLE 6-2 ''Unattached" Fraction Measurements Reported by Bigu and Kirk (1980)
|
|
|
"Unattached" Fraction |
Condensation Mining |
|
||
|
Mine |
Test No.a |
D.S.b |
W.S.c |
Nuclei (cm-1) |
Operation |
Area of Mine |
|
A |
1 |
.09 |
.07 |
2.5 × 105 |
Drilling and slushing |
Non-Diesel |
|
B |
2 |
.064 |
— |
3.0 × 105 |
Drilling |
Non-Diesel |
|
A |
3 |
.058 |
— |
— |
Drilling |
Non-Diesel |
|
A |
4 |
.014 |
.025 |
— |
Roof bolting |
Non-Diesel |
|
A |
5 |
.0047 |
.0047 |
— |
Mucking |
Diesel |
|
A |
6 |
.006 |
.0025 |
— |
Mucking and drilling |
Diesel |
|
A |
7 |
.0067 |
.007 |
— |
Mucking, drilling, and roof bolting |
Diesel |
|
a Each test represents one day during which a number of measurements were made. b Diffusion sampler measurements. c Wire screen measurements. |
||||||
The distribution of values for these four variables are presented in Figure 6-13. In this case, condensation nuclei concentrations were not measured. However, they did obtain very reasonable relationships for fa and fp, with the respirable dust concentration (particles of <7 μm) in mg/m3. Their results are summarized in Table 6-3.
Summary of Mining Exposure
From the limited number of measurements of activity-size distributions made in active mines, it is necessary to estimate the typical exposure conditions in the mine. In this review, an attempt has been made to estimate the conditions both in the areas where active drilling, slushing, and other activities could produce substantial airborne particle concentrations, in the haulage drifts where the material was being transported from the active mine sites to the sites where it could be conveyed to the surface, and in areas where nonmining activities were being conducted (workshops, lunchrooms, etc.). In the report of Cooper et al.
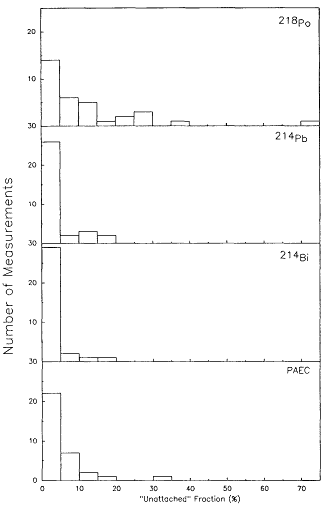
Figure 6-13 Distributions of the "unattached" fractions of the three radon decay products and the potential alpha-energy concentration (PAEC) measured in an iron ore mine. Redrawn from the graph in Stranden and Berteig (1982).
(1973), very detailed descriptions of the sampling locations are provided. They found AMD values between 0.20 and 0.36 μm in locations near active mining sites with an average value around 0.25 μm. Bigu and Kirk (1980) provide airborne respirable dust concentrations, AMAD and unattached fraction values specifically in working locations such as "Slusher position 1." They found very low unattached fractions and AMAD values also of the size of 0.25 μm. Thus, because of the very clear descriptions of locations and corresponding activity,
TABLE 6-3 Values for the Mean and Median "Unattached" Fractions as Measured in a Norwegian Iron Ore Mine by Stranden and Berteig (1982)
|
Species |
Mean |
Median |
|
218Po |
0.123 |
0.063 |
|
214Pb |
0.057 |
0.032 |
|
214Bi |
0.032 |
0.018 |
|
PAEC |
0.059 |
0.038 |
these results were given high weight in concluding the results for the active mining area. For the haulage drifts, the extensive values of George (1972) and George et al. (1975, 1977), particularly as reevaluated by Knutson and George (1990) were given the most credence and their average AMAD value of 0.15 μm was used for the average size in the open areas of the mine away from the actual mining activities. The values for the nonmining enclosed spaces were estimated from the indoor results presented in the next section.
INDOOR ATMOSPHERES
Diffusion Sampler Measurements
Duggan and Howell (1969) first attempted to use electrostatic collection of the decay products to determine the unattached fractions. However, as is now known (Hopke, 1989a,b), neutralization of the decay products is sufficiently rapid in normal air that only a small fraction of the highly diffusive fraction of the activity is charged. Duggan and Howell then used a rectangular channel diffusion battery to remove the unattached activity. The battery had 28 channels with cross-sections of 0.07 by 5 cm and operated at a flow rate of 80 liters/min. They measured the unattached fraction in outdoor and laboratory air at quite low radon concentrations (0.04 to 0.39 pCi/liter). In the approximately 50 measurements that were made, they obtained values in the range of 0.07 to 0.40 with no discernible relationship between the unattached fraction and the radon concentration. No measurements of the condensation nuclei concentrations were reported, nor was there any apparent attempt to obtain size distribution results from the measurements. Thus, it is difficult to use these values to assess the exposure to unattached progeny in either the ambient atmosphere or indoor air.
Shimo and Ikebe (1984) and Shimo et al. (1985) presented results of unattached fraction measurements in an underground tunnel of the Mikawa Crustal Movement Observatory of Nagoya University (Nagoya, Japan) using a
diffusion tube. They then used the tube as the body of a proportional counter and followed the decay of the alpha activity in order to extract the concentrations of the three decay products. The total activity of each decay product was determined by using the Thomas-modified Tsivoglou method (Thomas, 1970). Radon concentrations were in the range of 73.5 to 251 pCi/liters. The aerosol concentrations were measured with a Pollak-type condensation nuclei counter and were found to be in the range of 2,000 to 10,000/cm.
Wire Screen Measurements
Only a limited number of measurements of unattached fractions in single-family homes, apartments, offices, and other nonmine locations have been performed. Porstendörfer and coworkers (Reineking et al., 1985; Reineking and Porstendörfer, 1986; Porstendörfer, 1987; Reineking and Porstendörfer, 1990) have made measurements of both unattached fractions and the total activity size distributions for a series of rooms in unoccupied houses. In those studies, they varied the ventilation rate and added aerosol sources to the room. From the results of the measurements on the radon progeny, radon, and particle concentrations, they then calculated the unattached fractions of 218Po, 214Pb, and potential alpha energy and the equilibrium fractions. The results of the unattached fraction of PAEC as a function of condensation nuclei concentration in five rooms with and without aerosol sources are shown in Figure 6-14. Figure 6-15 presents the equilibrium factor as a function of particle concentration for these same rooms. In a later report (Porstendörfer, 1987), three additional rooms were characterized with similar results. In their most recent report, Reineking and Porstendörfer (1990) also provide some results for a limited number of measurements in the ambient atmosphere. These results are presented in Table 6-4.
Vanmarcke et al. (1985, 1987, 1989) used a screen diffusion battery with a characteristic dp(50%) of 4 nm for "unattached" fraction measurements in indoor air. In addition aerosol size distributions were made with an automated aerosol spectrometer system (Raes et al., 1984). They measured the unattached fraction of PAEC and reported that their results indicate "that the fraction of unattached radon daughters is higher than assumed in earlier studies." A sequence of unattached fraction measurements made in a single Belgian house is shown in Figure 6-16 (Vanmarcke et al., 1985). Additional studies made in the same house and in several other locations including the authors' laboratory and a railroad station as well as a second room of the house. Figure 6-17 summarizes the equilibrium and unattached fraction measurements plotted as a function of the attachment rate inferred from the aerosol size distribution. Unfortunately, none of the reports by that group provided actual values of these variables, nor summary statistics of their measurements.
The Ghent, Belgium, group (Vanmarcke and coworkers) intercompared
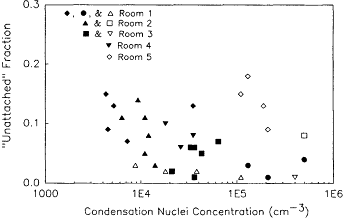
Figure 6-14 "Unattached" fraction of potential alpha-energy concentration, fp, as a function of the condensation nuclei concentration. Data taken from Porstendörfer (1987).
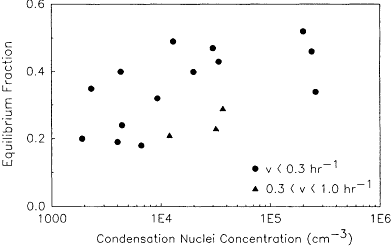
Figure 6-15 Equilibrium factor as a function of condensation nuclei concentration. Data taken from Porstendörfer (1987).
their measurement methodologies with those of the group from Göttingen, Germany, (Reineking and Porstendörfer). The results of this intercomparison study have been presented by Vanmarcke et al. (1988). The results of the intercomparison of radon and radon decay product concentrations are presented in Figure 6-18. It should be noted that Ghent values for 218Po were consistently higher than the Göttingen values, although the radon concentrations varied
TABLE 6-4 Concentrations of Radon, "Attached" and "Unattached" Activities, fp, F Values, and Particles (N) Measured in the Ambient Atmosphere near Göttingen (1 m Above the Ground During Daylight) by Reineking and Porstendörfer (1990)
|
Period |
222Rn (Bq m-3) |
218Po (Bq m-3) |
218Po (Bq m-3) |
214Pb (Bq m-3) |
214Pb (Bq m-3) |
214Bi (Bq m-3) |
N (103 cm-3) |
fp |
F |
No. of Values |
|
February 1986 |
14.6 (4.2-37.7) |
6.8 (1.4-21.5) |
0.8 (0.0-3.0) |
7.5 (1.9-24.1) |
0.1 (0.0-1.6) |
8.1 (2.0-22.4) |
41 (14-71) |
0.012 (0-0.098) |
(0.37-0.67) 0.51 |
8 |
|
October 1986 |
11.3 (2.0-23.6) |
7.8 (0.8-18.2) |
1.5 (0.0-5.6) |
8.4 (1.1-17.6) |
0.2 (0.0-1.7) |
9.1 (0.8-20.6) |
41 (7.5-89) |
0.031 (0-0.180) |
0.79 (0.51-1.15) |
13 |
|
July 1988 |
6.9 (1.0-17.2) |
3.9 (0.4-19.7) |
0.6 (0.0-1.9) |
4.3 (0.6-20.6) |
0.1 (0.0-2.0) |
4.6 (0.6-20.1) |
23 (7.7-93) |
0.014 (0-0.216) |
0.64 (0.23-1.19) |
15 |
|
Mean |
10.2 (1.0-37.7) |
6.0 (0.4-21.5) |
1.0 (0.0-5.6) |
6.5 (0.6-24.1) |
0.1 (0.0.-2.0) |
7.0 (0.6-22.4) |
34 (7.5-93) |
0.020 (0-0.216) |
0.67 (0.23-1.19) |
36 |
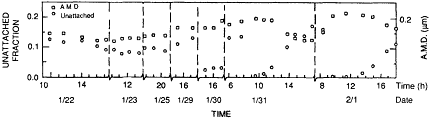
Figure 6-16 Time sequence of measurements in a Belgian house. Figure taken from Vanmarcke et al. (1985) and used with permission.
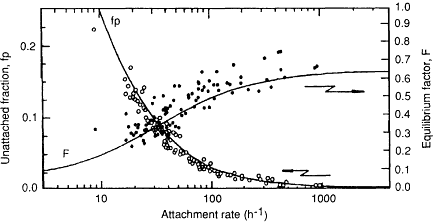
Figure 6-17 Equilibrium factor and the "unattached" fraction of potential alpha-energy concentration as a function of the estimated attachment rate based on measured aerosol size distributions.
between the higher and lower values. There thus appears to be a consistent measurement problem that leads to high 218Po results and systematically high fp values as shown in Figure 6-19. It can be seen that the Ghent values are generally higher than the Göttingen values, particularly in the absence of an additional aerosol source. The Göttingen unattached fraction values are generally in good agreement with those observed in other studies. Thus, although there is excellent agreement for the equilibrium fraction results, it appears that the fp values of Vanmarcke et al. (1988) are high and may overestimate the true value by more than 50%.
Stranden and Strand (1986) measured the unattached fraction and the equilibrium factor in occupied dwellings and an underground hydroelectric generating station and compared these results with their underground mining results. There were no descriptions of the housing units, the locations in
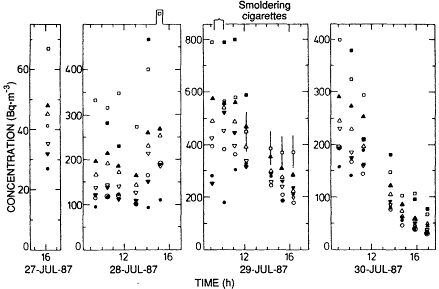
Figure 6-18 Radon and radon decay product concentrations measured during the Ghent-Göttingen intercomparison study. Filled symbols are Ghent; open symbols are Göttingen. Figure taken from Vanmarcke et al. (1988) and used with permission.
which sampling occurred, nor the "normal activities" that were ongoing in the dwellings and the generating station. They fit their data to an equation of the form
where a and b are empirical coefficients. They linearized the equation using a logarithmic transformation and performed least-squares fits to the data. Such a process produces biased results because the uncertainties are not uniform and do not propagate linearly through a logarithmic transformation. They obtained the following results:
If the same analysis is applied to the data obtained by Reineking and coworkers (1985, 1990), an equation of the form fp = 0.0177 F-2.50 with a correlation coefficient of 0.80 is obtained. Thus, close agreement of unattached and equilibrium fractions has been obtained for aerosols in these different indoor
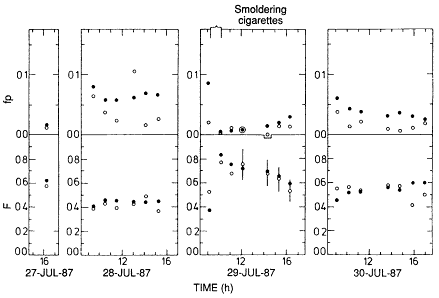
Figure 6-19 Evolution of the ''unattached" and equilibrium fractions as measured in the Ghent-Göttingen intercomparison study. Figure taken from Vanmarcke et al. (1988) and used with permission.
spaces. These results indicate that the size distribution of the indoor aerosol must be similar in these houses, although the concentration may vary.
Kojima and Abe (1988) developed an automated tape sampler for the "alpha-energy" spectroscopic measurement of the time sequence of unattached fraction in Japanese houses. They used a 500-mesh screen at a face velocity of 29.7 cm/s. They also used the calibration curve of Thomas and Hinchliffe (1972) to estimate a collection efficiency of 99%. They calibrated the counting efficiency of activity on the screen. The correction factor for undetectable activity on the back of the screen was determined to be 0.79 ± 0.21. As in the other measurements of the front-to-back ratio (Holub and Knutson, 1987), the amount of activity on the back side of the filter is dependent on the actual size of the unattached mode. There was also a loss of activity in the sampler's inlet. The correction factor for the sampler head loss is 0.82 ± 0.10. They were able to measure 2 Bq of 218Po per m3 and 0.3 Bq of 214Pb per m3 with a relative standard deviation of 50%.
The instrument was then deployed in a detached, two-story concrete house used in the typical Japanese life-style. Figure 6-20 provides the diurnal variations of the unattached fractions of each of the three decay products and the aerosol concentration. A summary of the unattached fraction measurements made over 7 months (November 1986 to May 1987) is presented in Table 6-5.
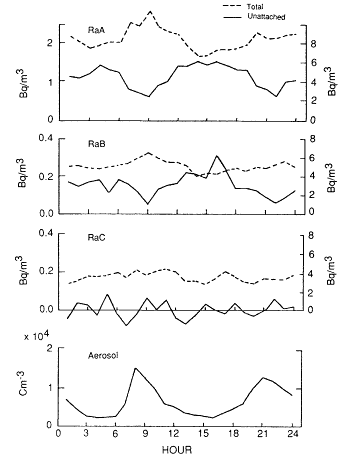
Figure 6-20 Diurnal variation of the "unattached" fractions of each of the radon decay products and the aerosol concentration. Left axis for unattached; right axis for total. Figure taken from Kojima and Abe (1988) and used with permission.
It should be noted that during this 7-month period the total 218Po concentration dropped from 11.1 Bq/m3 in November to 3.9 Bq/m3 in May. Thus, concentrations in this house are very low; it should be noted that Japanese construction and life-style are quite different from those in the United States.
Unattached fraction wire screen measurements must be tempered with the recognition that (1) the unattached fraction is, in reality, an ultrafine cluster mode in the 0.5-to 3-rim size range, (2) the collection efficiency versus particle diameter characteristics for wire screens do not allow a distinct separation of the unattached and attached fractions, and (3) there can be collections of
TABLE 6-5 Summary Results of the "Unattached" Fractions Measured in a Single Japanese House (Kojima and Abe, 1988)
|
|
|
"Unattached" |
"Unattached" |
|
|
Period |
No. of Values |
218Po |
214Pb |
PAEC |
|
November 1986 |
142 |
0.12 |
0.025 |
0.032 |
|
December |
168 |
0.11 |
0.028 |
0.034 |
|
January 1987 |
144 |
0.12 |
0.035 |
0.043 |
|
February |
240 |
0.078 |
0.024 |
0.031 |
|
March |
200 |
0.13 |
0.029 |
0.045 |
|
April |
190 |
0.19 |
0.041 |
0.055 |
|
May |
227 |
0.21 |
0.040 |
0.064 |
large particles (> 100 nm) on screens through inertial impaction (Reineking and Porstendörfer, 1990). Through appropriate choice of screen operating parameters, efficient collection of the 0.5-to 3-nm activity fraction may be obtained, while minimizing the collection of attached activity. Because unattached fraction measurements are inexact representations of the particle size information needed to utilize the dosimetric model developed and presented elsewhere in this report, the next section will review the more recent measurements that have been developed and employed to characterize the indoor radioactive aerosol.
ACTIVITY-WEIGHTED SIZE DISTRIBUTIONS
Recently, methods have been developed by which the entire radioactive aerosol size distribution can be deduced from data regarding the collection of activity on or its penetration through a series of screens. From these distributions, that portion of the size range that is to be defined as "unattached" can be calculated. Early measurements of the activity-weighted size distributions were made with conventional aerosol sampling systems such as tube or screen diffusion batteries (George and Breslin, 1980). Since condensation nuclei counters are commonly used as the particle detector for the corresponding number distributions, their rapid decrease in counting efficiency below 10 nm limits their utility to particle diameters >5 nm. Thus, these systems were typically designed with a minimum-size "particle" of 10 nm in mind.
The first activity-size measurements in indoor and ambient air were made by Sinclair et al. (1977) using a specially designed high-volume flow diffusion battery. They observed bimodal distributions with activity mode diameters of 7.5 and 150 nm in indoor atmospheres and 30 and 500 nm outdoors in New York City. Similar results were reported by George and Breslin (1980). Becker et al. (1984) only observed the larger mode using a modified impactor method with a minimum detectable size of 10 nm. Their measurements were made
in Göttingen, Germany. More extensive measurements in New York City by the group at the Environmental Measurements Laboratory (EML) have been reported by Knutson et al. (1984) using several different types of diffusion batteries as well as cascade impactors. They again observed modes around 10 nm and 130 nm in the PAEC-weighted size distribution measured with a low-volume screen diffusion battery. Four samples taken with a medium-volume (25-liter min-1) screen diffusion battery showed a major mode at 80 to 110 nm and a minor mode containing 8 to 9% of the PAEC with a diameter <5 nm. Finally, the same group made measurements at Socorro, N. Mex. (George et al., 1984). They reported that the major mode was only slightly different from that found in New York, but the minor mode was always < 5 nm, distinctly smaller than the New York distributions.
One of the problems with the extension of screen diffusion batteries to smaller particle sizes is the substantial collection efficiency of the high-mesh-number screens typically used in diffusion batteries designed to cover the range of particle sizes from 5 to 500 nm. At normally used flow rates, a single 635-mesh screen has greater than 90% efficiency for collecting 1-nm particles, the size of "unattached" 218Po having a diffusion coefficient of the order of 0.05 cm2 s-1. Thus, once the Yeh-Cheng screen penetration theory had been validated to 4 nm by Scheibel and Porstendörfer (1984) and the limitations of high-mesh-number screens were recognized, it was then possible to begin to examine alternative diffusion battery designs that could be extended to smaller particle diameters.
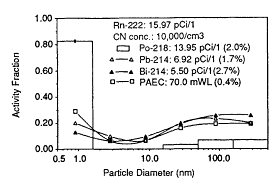
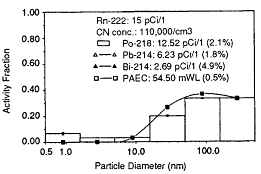
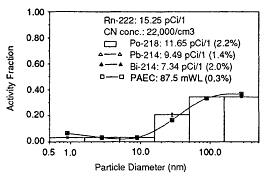
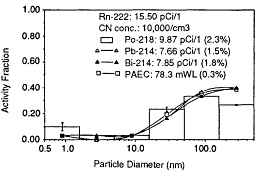
Reineking et al. (1985), Reineking and Porstendörfer (1986), and Reineking et al. (1988) used the high-volume-flow diffusion batteries described by Reineking and Porstendörfer (1986) to obtain activity-size distributions. They obtained their size distributions by fitting log-normal distributions using a SIMPLEX algorithm. Size distributions of indoor air in rooms without and with additional aerosol sources are presented in Figures 6-21 and 6-22, respectively. From these results, it can be surmised that the unattached fraction is the mode with a median diameter of 1.2 nm and geometric standard deviation of 1.5 nm.
Holub and Knutson (1987) reported the development of low-flow diffusion batteries with low-mesh-number screens and extension of the EML batteries to smaller sizes. Tu and Knutson (1988a,b) used 25-liter/min screen diffusion batteries to measure the 218Po-weighted size distributions in the presence of several specific aerosol sources. The results of these measurements are presented in Figures 6-23 and 6-24. The presence of a mode around 10 nm is again observed in curve 1 in Figure 6-23 . Only in curve 1 (no active aerosol sources) in Figure 6-24 was a mode at 1 nm observed. In all of the other cases, the activity was attached to the aerosol present in the house. The attachment was confirmed by independently measuring the aerosol size distributions by using an electrical aerosol analyzer (Liu and Pui, 1975) and the attachment coefficients
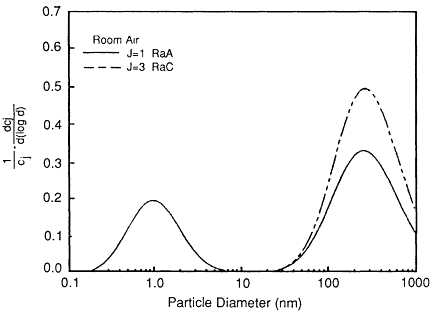
Figure 6-21 Activity-weighted size distribution of the indoor aerosol in a closed room without additional aerosol sources. Figure taken from Reineking and Porstendörfer (1986) and used with permission.
recommended by Porstendörfer et al. (1979). The agreement between the measured and calculated activity-weighted size distributions was excellent.
Several other groups, including the National Radiation Protection Board (NRPB) of the United Kingdom and the Australian Radiation Laboratory (ARL), have also developed these graded screen diffusion batteries for activity-size distribution measurements. An intercomparison between these three groups (EML, NRPB, and ARL) has been performed (Knutson et al., 1988). This initial comparison found difficulties for particles with sizes of >500 nm and <20 nm. For the large particles, the problem arises from impaction on the screen, and thus, there is an apparently excessive collection of activity in the ultrafine size range. For the smaller particle size range, there were several unexplainable discrepancies among the measurements.
Further tests of the single-screen methods were performed by Holub et al. (1988) in which EML, ARL, and the U.S. Bureau of Mines (BuMines) made measurements in a chamber at ARL. The results agreed well as to the size of the unattached progeny. There were differences of about a factor of 2 in the measured amounts of airborne activity, but these differences were attributed to differences in sampling location rather than difficulties with the various screen configurations. The single-screen measurements showed significant differences
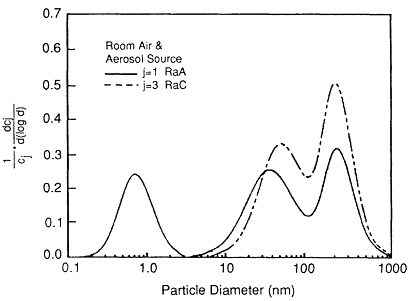
Figure 6-22 Activity-weighted size distribution of the indoor aerosol in a closed room with an additional aerosol source. Figure taken from Reineking and Porstendörfer (1986) and used with permission.
from the conventional screen diffusion battery measurements for the unattached fraction size, but were in good agreement for the attached mode sizes. These results can be anticipated because of the lack of resolution for the diffusion battery below 5 nm.
Several more recent intercomparison studies involving these three groups, the U.S. Bureau of Mines, Denver Research Center (BuMines), P. K. Hopke's group (then at the University of Illinois, Urbana), and the Inhalation Toxicology Research Institute (ITRI) at Albuquerque, N. Mex., found excellent agreement among the various activity-weighted size measurements as well as with the size distributions inferred from measurements of the particle size distributions by using a differential mobility analyzer (Ramamurthi et al., 1989). Thus, the results of these studies suggest that it is now possible to measure activity-weighted size distributions from 0.5 to 500 nm.
Several automated systems that make use of this methodology have been developed. Strong (1988) developed a system with six sampling heads containing 0, 1, 3, 7, 18, and 45 stainless steel, 400-mesh wire screens. He measured the size distributions in several rooms in two houses at two times of the year. The size distributions observed in the kitchen are presented in Figure 6-25. These results are summarized in Table 6-6. It should be noted that in the kitchen curve in Figure 6-25, a trimodal distribution is observed: a true unattached fraction
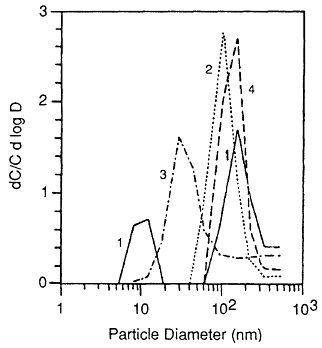
Figure 6-23 218Po-weighted size distributions measured in house I. 1. cooking (5 min); 2. frying food; 3. cooking soup; 4. cigarette smoldering. Figure taken from Tu and Knutson (1988a) and used with permission.
at 1 nm, a nuclei mode at 10 nm, and an accumulation mode at 100 to 130 nm. In Table 6-6, the unattached fractions presented are the integrated values from the size distributions. A problem then arises as to what unattached means since Strong integrated the distribution up to >10 nm to obtain that fraction that he attributes as being unattached. For the distribution in the kitchen with cooking, the activity median diameter for the unattached fraction was given as 11 nm. Such attribution is a clear departure from the original purpose for defining an unattached fraction. The advent of these measurement systems requires a more precise definition of the meaning of the unattached fraction.
Subsequent to these original measurements, Strong (1989) modified his system by changing the screens to 1,200-mesh screens and 1, 4, 14, and 45 400-mesh screens as well as the open channel. This modification provides a stage such that there is better resolution at the smallest-sized particles and the range of the system can be extended to 0.5 nm. The effective resolution cutoff of the original battery was about 2 nm. With the new battery, trimodal distributions were clearly observed (Figure 6-26). Although these measurements were made in the living room, the kitchen was adjacent to the living room, and
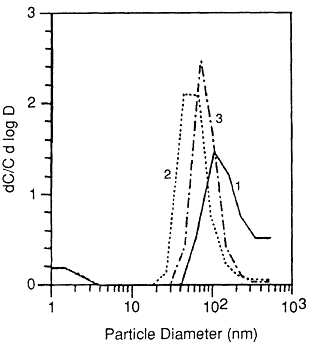
Figure 6-24 218Po-weighted size distributions measured in house II after a kerosene heater was operated for: 1. 0 min; 2. 80 min; 3. 200 min. Figure taken from Tu and Knutson (1988a) and used with permission.
cooking with a gas stove was being performed at the time these measurements were made. These results show the advantage of being able to measure the size distribution and determine the actual exposure of individuals to airborne radon progeny activity.
A similar system has been developed at the Australian Radiation Laboratory by Solomon (personal communication, 1989). It was designed for measurements in the particle size range of 2 to 600 nm. The measurements were extended to a smaller size range (0.5 to 100 nm) by using a manual, serial, single-screen array sampling at 1 to 6 liters/min and to lower concentrations in the same size range by using larger screens (9.5-cm diameter) and a 100-liter/min flow rate. Solomon examined both the Twomey (1975) and expectation-maximization (Maher and Laird, 1985) algorithms for deconvoluting the size distributions from the screen penetration data. In both cases, Solomon has developed a Monte Carlo method for determining the stability of the inferred size distributions. New input values for the concentrations found on each stage were chosen from a normal distribution by using the measured radon decay product activity as the mean value and the measured uncertainty as the standard deviation of the distribution.
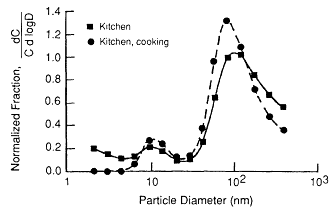
Figure 6-25 Activity-size distributions measured in a rural house kitchen by Strong (1988). Used with permission.
TABLE 6-6 Summary of Activity-Size Measurements Made by Strong (1988) in Two Houses in the United Kingdom
|
|
Ambient Aerosol |
Attached |
Unattached |
||||
|
Site |
Median (nm) |
GSDaN |
(cm-3) |
AMD (nm) |
GSD |
fp (%) |
AMD (nm) |
|
Rural (summer) |
|||||||
|
Bedroom |
42 |
2.0 |
5,000 |
130 |
2.4 |
17 |
2.0 |
|
Living room |
30 |
2.0 |
5,100 |
150 |
2.1 |
17 |
2.0 |
|
Kitchen |
33 |
1.7 |
11,000 |
130 |
2.0 |
18 |
6.0 |
|
Kitchen (cooking) |
30 |
1.7 |
470,000 |
110 |
1.9 |
11 |
11.0 |
|
Rural (winter) |
|||||||
|
Living room |
32 |
1.7 |
4,700 |
130 |
2.1 |
20 |
2.0 |
|
Urban (winter) |
|||||||
|
Living room |
30 |
2.1 |
15,000 |
110 |
2.1 |
20 |
3.5 |
|
Mean (all sites) |
33 |
2.0 |
8,200 |
130 |
2.1 |
18 |
3.1 |
|
a GSD = Geometric standard deviation. |
|||||||
This process can be repeated a number of times to provide a measure of the precision and robustness of the estimated size distributions.
A semicontinuous automated system has been developed at the University of Illinois by Ramamurthi and Hopke (1991). This system consists of six sampling heads with various combinations of screens, described in Table 6-7 along
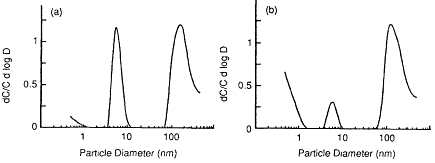
Figure 6-26 Trimodal activity-size distribution measured by Strong (1989) under conditions of (a) F = 0.36, CN = 10,000 cm-3; (b) F = 0.26, CN = 5,000 cm-3.
with their corresponding dp(50%) values. Activity-size distributions were determined in a single house by using this system. The measurements were conducted in a three-level residence in Princeton, N.J. The house (PU-22) is instrumented by the Center for Energy and Environmental Studies, Princeton University, for continuous measurements of the radon concentration, temperature, humidity, and differential pressures. Activity-size distributions were measured in the basement and first floor of the house over a 1-week period (September 13 to 20, 1989). Grab samples for decay product activity concentrations were taken intermittently and analyzed by the gross alpha-photomultiplier tube method for comparison with the total concentration estimates from the automated system. The detectable particle number concentration in the sampling environment was continuously monitored by an Environment One model 100 condensation nuclei counter (CNC).
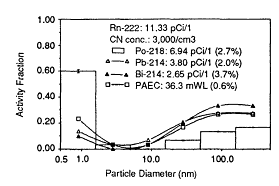
Initial activity-size distribution measurements were made in the basement of the house. Number concentrations of particles in the basement varied between 2,000 and 8,000/cm3 as detected by the CNC. The lack of windows or other major openings to the outside was thought to be responsible for the low concentrations. Radon concentrations varied between 5 and 500 pCi/liter during the 7-day period with the time period for fluctuations being much longer than the 15-min sampling interval. A total of 15 measurements were made during the 7-day period, with a remarkable degree of consistency in the shape of the measured activity-size distributions. Figure 6-27 shows the typical 218Po, 214Pb, and 214Bi distributions observed in the basement of the house at a radon concentration of 55 pCi/liter and a particle number concentration of 3,000/cm3. The 218Po distribution in Figure 6-27 is plotted as a histogram to illustrate the nature of the distribution, whereas the 214Pb and 214Bi distributions are shown by curves connecting the midpoint diameter values.
The 218Po distribution showed that ![]() of the 218Po activity was in the
of the 218Po activity was in the
TABLE 6-7 Characteristics of the Stages in the Graded Screen Array System of Ramamurthi and Hopke (1990)
|
|
Sampler |
|||
|
Unit |
Slit Width (cm) |
Diameter (cm) |
Wire Screen Mesh × Turnsa |
dp(50%) (0.5-350-nm range) |
|
1 |
0.5 |
5.3 |
— |
— |
|
2 |
0.5 |
5.3 |
145 |
1.0 |
|
3 |
0.5 |
5.3 |
145 × 3 |
3.5 |
|
4 |
0.5 |
5.3 |
400 × 12 |
13.5 |
|
5 |
1.0 |
12.5 |
635 × 7 |
40.0 |
|
6 |
1.0 |
12.5 |
635 × 20 |
98.0 |
|
a Wire screen parameters given by Yeh et al. (1982). NOTE: Sampling flow rate = 15 liters/min (each unit). Detector-Filter separation |
||||
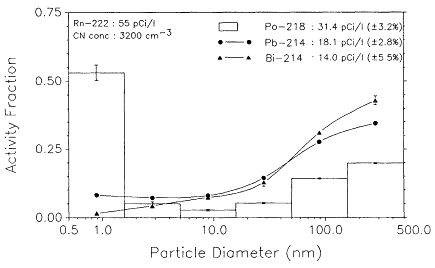
Figure 6-27 Typical Po-218, Pb-214, and Bi-214 activity-size distributions observed in a house basement in Princeton, N.J.
smallest inferred size interval, with a midpoint diameter of ≈0.9 nm (diffusion coefficient, ![]() ). This fraction closely resembles the classical, highly diffusive unattached fraction. The magnitude of the cluster fraction agreed well with theoretical predictions from attachment rate calculations at the observed particle number concentration (Porstendörfer et al., 1979). Very little of the 218Po activity existed in the range from 1.6 to 16 nm, with the remainder of
). This fraction closely resembles the classical, highly diffusive unattached fraction. The magnitude of the cluster fraction agreed well with theoretical predictions from attachment rate calculations at the observed particle number concentration (Porstendörfer et al., 1979). Very little of the 218Po activity existed in the range from 1.6 to 16 nm, with the remainder of
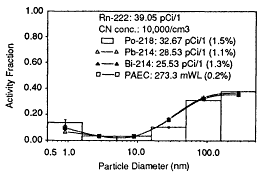
the activity attached to the larger ambient aerosol particles (diameter, >50 nm). The corresponding 214Pb and 214Bi distributions showed much smaller activity fractions in the 0.9-nm size range. The longer lifetime of these decay products permits a greater fraction of activity to become attached to the ambient aerosol. For all three distributions, the attached mode peaked in the 160-500-nm size range. However, this measurement system cannot be used to determine particle sizes greater than 500 nm in diameter. The activity distributions obtained are in general agreement, with respect to both the 218Po cluster fraction and the size range of attached activity, with the distributions measured by Tu et al. (1989) in the basement of this house under similar conditions at an earlier date.
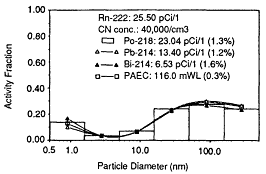
Several measurements of activity-size distributions were also made in the kitchen on the first level of the house. The initial measurements were performed under typical conditions of 20,000 particles/cm3 and a radon concentration of ![]() . The results of the measurement are shown in Figure 6-28. The 218Po size distribution showed a large fraction of the 218Po activity
. The results of the measurement are shown in Figure 6-28. The 218Po size distribution showed a large fraction of the 218Po activity ![]() with a diffusivity similar to that of the classical unattached fraction. However, a significant fraction
with a diffusivity similar to that of the classical unattached fraction. However, a significant fraction ![]() was in the 1.6-5.0-nm size interval. The corresponding 214Pb and 214Bi distributions indicate insignificant activity fractions in the 0.5-1.6-nm size interval, but a significant mode between 1.6 and 5.0 nm. The differences in the size distributions obtained in the basement and in the kitchen area related primarily to the 1.6-to 5.0-nm size interval, with the attached activity modes remaining in the 160-to 500-nm size range. This result suggests the presence of condensable constituents leading to the formation of particles in the 1.6-to 5.0-nm size interval or a source of very fine primary particles. This process may then allow the radon decay products to become associated with the 1.6-to 5.0-nm size mode in varying fractions depending upon the relative lifetimes. The presence of six large gas range pilot lights may be related to the formation of this mode, and similar effects are believed to have been observed by Tu et al. (1989) in other houses.
was in the 1.6-5.0-nm size interval. The corresponding 214Pb and 214Bi distributions indicate insignificant activity fractions in the 0.5-1.6-nm size interval, but a significant mode between 1.6 and 5.0 nm. The differences in the size distributions obtained in the basement and in the kitchen area related primarily to the 1.6-to 5.0-nm size interval, with the attached activity modes remaining in the 160-to 500-nm size range. This result suggests the presence of condensable constituents leading to the formation of particles in the 1.6-to 5.0-nm size interval or a source of very fine primary particles. This process may then allow the radon decay products to become associated with the 1.6-to 5.0-nm size mode in varying fractions depending upon the relative lifetimes. The presence of six large gas range pilot lights may be related to the formation of this mode, and similar effects are believed to have been observed by Tu et al. (1989) in other houses.
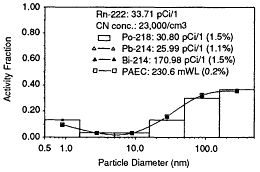
In a final experiment, activity-size distributions were measured following the continuous addition of aerosols generated in the kitchen from lighting the gas stove burners of the kitchen range. Figure 6-29 shows the distributions measured with particle number concentrations of ![]() and a radon concentration of
and a radon concentration of ![]() . The large concentrations of particles generated could be presumed to be rapidly coagulating soot cluster aggregates. The 218Po and 214Pb activity distributions measured under these conditions (Figure 6-29) were dramatically different from those measured in the basement and background kitchen conditions. The 218Po distribution revealed very little activity in the 0.5-to 1.6-nm size interval (unattached fraction), with most of the activity spread out over the size interval range from 1.6 to 50 nm. The fraction of 218Po attached to particles of > 100 nm in diameter was reduced to a negligible level, probably because of the very large number of smaller particles produced by the gas burners. The distribution of 214Pb revealed that the activity
. The large concentrations of particles generated could be presumed to be rapidly coagulating soot cluster aggregates. The 218Po and 214Pb activity distributions measured under these conditions (Figure 6-29) were dramatically different from those measured in the basement and background kitchen conditions. The 218Po distribution revealed very little activity in the 0.5-to 1.6-nm size interval (unattached fraction), with most of the activity spread out over the size interval range from 1.6 to 50 nm. The fraction of 218Po attached to particles of > 100 nm in diameter was reduced to a negligible level, probably because of the very large number of smaller particles produced by the gas burners. The distribution of 214Pb revealed that the activity
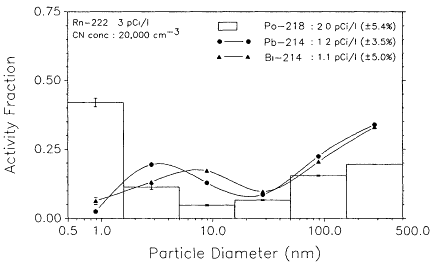
Figure 6-28 Po-218, Pb-214, and Bi-214 activity-size distributions measured under typical conditions in the kitchen of the test house.
was spread out over the size spectrum dp > 1.6 nm, while the 214Bi distribution remained similar to those measured prior to the addition of external aerosols. However, these latter results may be due to the timing of the sampling interval, which was between 20 and 35 min after the start of continuous addition of the external aerosols. Consequently, steady-state 214Pb and 214Bi distributions may not have been attained.
A stability analysis was performed for each of the size distributions shown in Figures 6-27, 6-28, and 6-29. This analysis provides an estimate of the stability of the inferred solutions with respect to errors in the input penetration data, and the results are represented by the error bars indicated in the figures. The size distributions obtained in the experiments were found to be stable and relatively insensitive to perturbations in the input data of the order of the associated measurement errors. The errors in the size interval fractions estimated from this procedure are too small to be seen in these figures and thus were not included.
Additional measurements were made in another one-story residence with living room, dining room, kitchen, two bedrooms, a study room, two bathrooms, and basement in the Princeton, N.J., area (Li, 1990; Hopke et al., 1990a,b). Activity-size distributions were measured in the living room and one of the bedrooms over a 2-week period (January 16 to 31, 1990). A total of about 10 measurements were made in the living room, and more than 100 measurements were made in the bedroom with different types of particle generation. Aerosols were generated from candle burning, cigarette smoking, vacuuming (electric
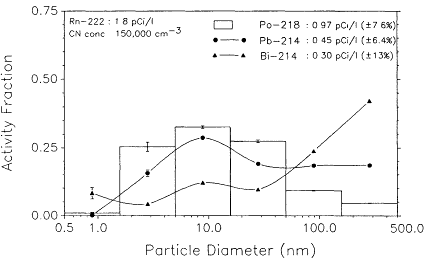
Figure 6-29 Po-218, Pb-214, and Bi-214 activity-size distributions measured during the continuous generation of aerosols from the kitchen gas stove burners.
motor), cooking, and opening doors from normal activities in the domestic environments. The particle concentrations were measured by using a Gardner manual condensation nucleus counter. The concentration and size distribution of radon progeny were determined by a semicontinuous graded screen array system. A sequence (0-15, 15-35, 35-75 min) with 75-min sampling was chosen because the radon concentration was in the range of 5 to 50 pCi/liter.
The influence of cigarette smoking (20 min) on the radon progeny size distributions in a closed bedroom are shown in Figure 6-30. The measurements were made 5 min after lighting the cigarette (5-20 min), 80 min later (80-95 min), and 155 min later (155-170 min). The fraction of 218Po in the 0.9-nm size range changed from 60 to 8%. The fraction of 214Pb and 214Bi in the 0.9-nm size range was about 10% and essentially became zero. The fraction of three distributions in the 1.5-to 15-nm size range stayed the same. There was a large increase (from 40 to 80%) of 218Po in the attached mode (50-to 500-nm size range), with insignificant changes (from 35 to 40%) in 214Pb and 214Bi fractions in this mode.
The influence of cooking on the radon progeny size distributions with an open bedroom door is shown in Figure 6-31. A steak was pan fried for 20 min (0-20 min) by using a gas stove burner in the kitchen. The measurements were made 5 min later (5-20 min), 80 min later (80-95 min), and 155 min later (155-170 min). The fraction of 218Po in the 0.9-nm size range changed from 60 to 15%. The fractions of 214Pb and 214Bi in the 0.9-nm size range changed from 15 to 10%. There was a very low fraction of activity in the 1.5-to 15-nm
size range for background, and it increased to 10% because of cooking. A large increase (from 35 to 70%) of 218Po was observed in the attached mode and peaked at the 50-to 500-nm size range, with only small changes (from 40 to 50%) in 214Pb and 214Bi distributions.
Because of the large number of particles generated by normal activities in the domestic environment, the working level increases for a period of time, while the unattached fraction decreases. The particles generated from cigarette smoke and cooking dramatically shifted almost all of the radon progeny to the attached fraction and remained for a long period of time. The particles produced from candle burning and vacuuming were much smaller, with an average attachment diameter around 15 nm. The candle and vacuuming particles did decrease the unattached fraction, but returned to the original background distributions about 150 min later.
Summary of Indoor Exposure
In evaluating the information on the aerodynamic size of the particles carrying the radioactivity in the indoor environment, the results of Reineking and Porstendörfer (1986, 1990), Tu and Knutson (1988a,b), Ramamurthi and Hopke (1990), Li (1990), and Hopke et al. (1990a,b) were reviewed. From these results, the unattached activity appears to have a diffusion equivalent diameter of 0.0011 µm and typically represents about 8% of the airborne alpha activity energy. The typical indoor radioactive aerosol has a mode with an AMD of 0.15 µm with a geometric standard deviation of 2.0. The presence of sidestream cigarette smoke provides a substantial number of larger sized particles so that the AMD increases to 0.25 µm with a geometric standard deviation of 2.5. During periods of active smoking, the unattached fraction diminishes to 0.1, and on average, the unattached activity represents about 3% of the total activity in houses with smokers.
Other activities can produce particles with small diameters so that during vacuuming or cooking, an additional mode in the activity-size distribution with an average diameter of 0.02 µm and containing 15% of the airborne alpha energy can be observed. Because of the high mobility of these particles, this mode is quite transient and will disappear in a few hours time.
Finally, there are times in closed rooms such as bedrooms with relatively low air exchange rates that the particle concentration can be sufficiently low that a much higher fraction of the activity is in the unattached mode. It is estimated that a typical value for the unattached fraction under these circumstances is 16%.
REFERENCES
Becker, K. H., A. Reineking, H. G. Scheibel, and J. Porstendörfer. 1984. Radon daughter activity size distributions. Radiat. Prot. Dosim. 7:147-150.
Bigu, J. 1985. Radon daughter and thoron daughter deposition velocity and unattached fraction under laboratory conditions in underground uranium mines. J. Aerosol Sci. 16:157-165.
Bigu, J, and B. Kirk. 1980. Determination of the unattached radon daughter fractions in some uranium mines . Presented at the Workshop on Attachment of Radon Daughters, Measurement Techniques and Related Topics, October 30, 1980, University of Toronto. (Report available from CANMET, P.O. Box 100, Elliot Lake, Ontario, Canada.)
Busigin, A., A. W. Van der Vooren, and C. R. Phillips. 1981. Measurement of the total and radioactive aerosol size distributions in a Canadian uranium mine. Am. Ind. Hyg. Assoc. J. 42:310-314.
Chamberlain, A. C., and E. D. Dyson. 1956. The dose to the trachea and bronchi from the decay products of radon and thoron. Br. J. Radiol. 29:317-325.
Chen, R. Y., and R. A. Comparin. 1976. Deposition of aerosols in the entrance of a tube. J. Aerosol Sci. 7:335-341.
Cheng, Y. S. 1989. Deposition of thoron daughters in human head airways. Technical Exchange Meeting, Grand Junction, Colo., September 18-19, CONF 8909190. NTIS.
Cheng, Y. S., and H. C. Yeh. 1980. Theory of screen type diffusion battery. J. Aerosol Sci. 11:313-319.
Cheng, Y. S., J. A. Keating, and G. M. Kanapilly. 1980. Theory and calibration of a screen-type diffusion battery. J. Aerosol Sci. 11:549-556.
Cooper, J. A., P. O. Jackson, J. C. Langford, M. R. Petersen, and B. O. Stuart. 1973. Characteristics of Attached Radon-222 Daughters under both Laboratory and Field Conditions with Particular Emphasis upon Underground Mine Environments. Report to the U.S. Bureau of Mines, contract H0220029. Richland, Wash.: Battelle Pacific Northwest Laboratories.
Craft, B. F., J. L. Oser, and E W. Norris. 1966. A method for determining relative amounts of combined and uncombined radon daughter activity in underground uranium mines. Am. Ind. Hyg. Assoc. J. 27:154-159.
Davies, C. N. 1945. Definitive equations for the fluid resistance of spheres. Proc. Phys. Soc. 57:259-270.
Duggan, M. J., and D. M. Howell. 1969. The measurement of the unattached fraction of airborne RaA. Health Phys. 17:423-427.
Emi, H., C. Kanaoka, and Y. Kuhabara. 1982. The diffusion collection efficiency of fibers for aerosol over a wide range of Reynolds numbers. J. Aerosol Sci. 13:403-413.
Friedlander, S. K. 1977. Smoke, Dust and Haze. New York: John Wiley & Sons .
Fuchs, N. A. 1964. The Mechanics of Aerosols. New York: MacMillan Press.
Fusamura, N, R. Kurosawa, and M. Maruyama. 1967. Determination of f-value in uranium mine air. Pp. 213-227 in Symposium on Instruments and Techniques for the Assessment of Airborne Radioactivity in Nuclear Operations. Vienna: International Atomic Energy Agency.
George A. C. 1972. Measurement of the uncombined fraction of radon daughters with wire screens. Health Phys. 23:390-392.
George, A. C., and A. J. Breslin. 1980. The Distribution of Ambient Radon and Radon Daughters in Residential Buildings in the New Jersey-New York Area, National Radiation Environment III, Vol. 2. CONF-780422. Oak Ridge, Tenn.: Technical Information Center, U.S. Department of Energy.
George, A. C., and L. Hinchliffe. 1972. Measurements of uncombined radon daughters in uranium mines. Health Phys. 23:791-803.
George, A. C., L. Hinchliffe, and R. Sladowski. 1975. Size distribution of radon daughter particles in uranium mine atmospheres. Am. Ind. Hyg. Assoc. J. 36:484-490.
George, A. C., L. Hinchliffe, and R. Sladowski. 1977. Size Distribution of Radon Daughter Particles in Uranium Mine Atmospheres. HASL-326. New York: Health and Safety Laboratory.
George, A. C., M. H. Wilkening, E. O. Knutson, D. Sinclair, and L. Andrews. 1984. Measurements of radon and radon daughter aerosols in Socorro, New Mexico. Aerosol Sci. Technol. 3:277-281.
Gormley, P., and M. Kennedy. 1949. Diffusion for a stream flowing through a cylindrical tube. Proc. R. Irish Acad. 52A:163-167.
Hirst, B. W., and G. E. Harrison. 1939. The diffusion of Rn gas mixtures. Proc. R. Soc. Lond. Ser. A 169:573-586.
Holub, R. F., and E. O. Knutson. 1987. Measuring polonium-218 diffusion-coefficient spectra using multiple wire screens. Pp. 340-356 in Radon and Its Decay Products: Occurrence, Properties and Health Effects, P. K. Hopke, ed. Symposium Series 331. Washington D.C.: American Chemical Society.
Holub, R. F., E. O. Knutson, and S. Solomon. 1988. Tests of the graded wire screen technique for measuring the amount and size distribution of unattached radon progeny. Radiat. Prot. Dosim. 24:265-268.
Hopke, P. K. 1989a. Use of electrostatic collection of 218Po for measuring Rn. Health Phys. 57:39-42.
Hopke, P. K. 1989b. The initial behavior of 218Po in indoor air. Environ. Int. 15:299-308.
Hopke, P. K., M. Ramamurthi, and C. S. Li. 1990a. Measurements of the size distributions of radon progeny in indoor air. In Aerosols: Science, Industry, Health, and Environment, Vol. 2, S. Masuda and K. Takahashi, eds. Oxford: Pergamon Press.
Hopke, P. K., M. Ramamurthi, and C. S. Li. 1990b. Measurements of size distributions of indoor radioactive aerosol. Presented at the 29th Hanford Symposium on Health and the Environment. Richland, Washington, October 1990.
Hopke, P. K., M. Ramamurthi, and E. O. Knutson. In press. A measurement system for Rn decay product lung deposition based on respiratory models. Health Phys.
Ingham, D. B. 1975. Diffusion of aerosols for a stream flowing through a cylindrical tube. J. Aerosol Sci. 6:125-132.
International Commission on Radiological Protection (ICRP). 1959. Report of Committee II on Permissible Dose for Internal Radiation, ICRP Publication 2. Oxford: Pergamon Press.
James A. C., G. F. Bradford and D. M. Howell. 1972. Collection of unattached RaA atoms using wire gauze. J. Aerosol Sci. 3:243-254.
Khan, A., C. R. Phillips, and P. Duport. 1987. Analysis of errors in the measurement of unattached fractions of radon and thoron progeny in a Canadian uranium mine using wire screen methods. Radiat. Prot. Dosim. 18:197-208.
Knutson, E. O., A. C. George, R. H. Knuth, and B. R. Koh. 1984. Measurements of radon daughter particle size. Radiat. Prot. Dosim. 7:121-125.
Knutson, E. O., K. W. Tu, S. B. Solomon, and J. Strong. 1988. Intercomparison of three diffusion batteries for the measurement of radon decay product particle size distributions. Radiat. Prot. Dosim. 24:261-264.
Kojima, H., and S. Abe. 1988. Measurement of the total and unattached radon daughters in a house. Radiat. Prot. Dosim. 24:241-244.
Kotrappa, P., and Y. S. Mayya. 1976. Revision of Raghavayya and Jones' data on the radon decay in mine air. Health Phys. 31:380-382.
Li, C. S. 1990. Field Evaluation and Health Assessment of Air Cleaners in Removing Radon Decay Products in Domestic Environments. Ph.D. thesis. University of Illinois, Urbana, Ill. Department of Energy Report DOE ER61029-2.
Liu, B. Y. H., and D. Y. H. Pui. 1975. On the performance of the electrical aerosol analyzer. J. Aerosol Sci. 6:249-264.
Lodge, J. P., Jr., and T. Chan. 1986. Cascade Impactor: Sampling and Data Analysis. Akron, Ohio: American Industrial Hygiene Association,
Loeb, L. B. 1961. The Kinetic Theory of Gases, 3rd ed. New York: Dover Publications.
Maher, E. F., and N. M. Laird. 1985. Algorithm reconstruction of particle size distribution from diffusion battery data. J. Aerosol Sci. 16:557-570.
Mercer, T. T. 1975. Unattached radon decay products in mine air. Health Phys. 28:158-161.
Mercer, T. T., and W. A. Stowe. 1969. Deposition of unattached radon decay products in an impactor stage. Health Phys. 17:259-264.
Porstendörfer, J. 1968. Die Diffusionkoeffizienten und mittleren freien Weglangen der Geladenen und neutral radon-folge Produkte in Luft. Z. Physik. 213:384-396.
Porstendörfer, J. 1987. Free-fractions, attachment rates, and plate-out rates of radon daughters in houses. Pp. 285-300 in Radon and Its Decay Products: Occurrence, Properties and Health Effects, P. K. Hopke, ed. Symposium Series 331. Washington D.C.: American Chemical Society.
Porstendörfer, J., and T. T. Mercer. 1979. Influence of electric charge and humidity upon the diffusion coefficient of radon decay products. Health Phys. 15:191-199.
Porstendörfer, J., G. Röbig, and A. Ahmed. 1979. Experimental determination of the attachment coefficients of atoms and ions on monodisperse particles. J. Aerosol Sci. 10:21-28.
Raabe, O. G. 1969. Concerning the interactions that occur between radon decay products and aerosols. Health Phys. 17:177-185.
Raes, F., A. Janssens, A. DeClercq, and H. Vanmarcke. 1984. Investigation of the indoor aerosol and its effect on the attachment of radon daughters. Radiat. Prot. Dosim. 7:127-131.
Raghavayya, M., and J. H. Jones. 1974. A wire screen-filter paper combination for the measurement of fractions of unattached daughter atoms in uranium mines. Health Phys. 26:417-430.
Ramamurthi, M., and P. K. Hopke. 1989. On improving the validity of wire screen ''unattached'' fraction Rn daughter measurements. Health Phys. 56:189-194.
Ramamurthi, M., and P. K. Hopke. 1990. Simulation studies of reconstruction algorithms for the determination of optimum operating parameters and resolution of graded screen array systems (non-conventional diffusion batteries). Aerosol Sci. Technol. 12:700-710.
Ramamurthi, M., and P. K. Hopke. 1991. An automated, semi-continuous system for measuring indoor radon progeny activity-weighted size distributions, dp: 0.5-500 nm. Aerosol Sci. Technol. 14:82-92.
Ramamurthi, M., P. K. Hopke, R. Strydom, K. W. Tu, E. O. Knutson, R. F. Holub, W. Winklmayr, W. Marlow, and S. C. Yoon. 1989. Radon decay product activity size distribution measurement methods—A laboratory intercomparison. Presented at the American Association for Aerosol Research Meeting, Reno, Nev., October 1989.
Ramamurthi, M., R. Strydom, and P. K. Hopke. In press. Assessment of wire and tube penetration theories using a 218PoOx cluster aerosol. J. Aerosol Sci.
Reineking, A., and J. Porstendörfer. 1986. High-volume screen diffusion batteries and a-spectroscopy for measurement of the radon daughter activity size distributions in the environment. J. Aerosol Sci. 17:873-879.
Reineking, A., and J. Porstendörfer. 1990. "Unattached" fraction of short-lived decay products in the indoor and outdoor environment: An improved single screen method and results. Health Phys. 58:717-727.
Reineking, A., K. H. Becker, and J. Porstendörfer. 1985. Measurements of the unattached fractions of radon daughters in houses. Sci. Total Environ. 45:261-270.
Reineking, A., K. H. Becker, and J. Porstendörfer. 1988. Measurement of activity size distributions of the short-lived radon daughters in the indoor and outdoor environment. Radiat. Prot. Dosim. 24:245-250.
Scheibel, H. G., and J. Porstendörfer. 1984. Penetration measurements for tube and screen type diffusion batteries in the ultrafine particle size range. J. Aerosol Sci. 15:673-682.
Shimo, M., and Y. Ikebe. 1984. Measurements of radon and its short-lived decay products and unattached fraction in air. Radiat. Prot. Dosim. 8:209-214.
Shimo, M., Y. Yoshihiro, K. Hayashi, and Y. Ikebe. 1985. On some properties of 222Rn short-lived decay products in air. Health Phys. 48:75-86.
Sinclair, D., A. C. George, and E. O. Knutson. 1977. Application of diffusion batteries to measurement of submicron radioactive aerosols. Pp. 103-114 in Airborne Radioactivity. La Grange Park, Ill.: American Nuclear Society.
Stranden, E., and L. Berteig. 1982. Radon daughter equilibrium and unattached fraction in mine atmospheres. Health Phys. 42:479-487.
Stranden, E., and T. Strand. 1986. A dosimetric discussion based on measurements of radon daughter equilibrium and unattached fraction in different atmospheres. Rad. Prot. Dosim. 16:313-318.
Strong, J. C. 1988. The size of attached and unattached radon daughters in room air. J. Aerosol Sci. 19:1327-1330.
Strong, J. C. 1989. Design of the NRPB activity size measurement system and results. Presented at the Workshop on "Unattached" Fraction Measurements, University of Illinois, Urbana, Ill., April 1989.
Subba Ramu, M. C. 1980. Calibration of a diffusion sampler used for the measurement of unattached radon daughter products. Atmosph. Environ. 14:145-147.
Tan, C. W. 1969. Diffusion of disintegration products of inert gases in cylindrical tubes. Int. J. Heat Mass Trans. 12:471-478.
Thomas, J. W. 1955. The diffusion battery method for aerosol particle size determination. J. Colloid Sci. 10:246-255.
Thomas, J. W. 1970. Modification of the Tsivoglou method for radon daughters in air. Health Phys. 19:691-693.
Thomas, J. W., and L. E. Hinchliffe. 1972. Filtration of 0.001 µm particles with wire screens. J. Aerosol Sci. 3:387-393.
Tu, K. W., and E. O. Knutson. 1988a. Indoor radon progeny particle size distribution measurements made with two different methods. Radiat. Prot. Dosim. 24:251-255.
Tu, K. W, and E. O. Knutson. 1988b. Indoor outdoor aerosol measurements for two residential buildings in New Jersey. Aerosol Sci. Technol. 9:71-82.
Tu, K. W., A. C. George, and E. O. Knutson. 1989. Summary of results of radon progeny particle size in indoor air. Presented at the American Association for Aerosol Research Meeting, Reno, Nev., October 1989.
Twomey, S. 1975. Comparison of constrained linear inversion and an iterative nonlinear algorithm applied to the indirect estimation of the particle size distribution. J. Comp. Phys. 18:188-200.
Van der Vooren, A. W., A. Busigin, and C. R. Phillips. 1982. An evaluation of unattached radon (and thoron) daughter measurement techniques. Health Phys. 42:801-808.
Vanmarcke, H., A. Janssens, and F. Raes. 1985. The equilibrium of attached and unattached radon daughters in the domestic environment. Sci. Tot. Environ. 45:251-260.
Vanmarcke, H., A. Janssens, F. Raes, A. Poffijn, P. Perkvens, and R. Van Dingenen. 1987. The behavior of radon daughters in the domestic environment. Pp. 301-323 in Radon and Its Decay Products: Occurrence, Properties and Health Effects, P. K. Hopke, ed. Symposium Series 331. Washington, D.C.: American Chemical Society.
Vanmarcke, H., A. Reineking, J. Porstendörfer, and F. Raes. 1988. Comparison of two methods for investigating indoor radon daughters. Radiat. Prot. Dosim. 24:281-284.
Vanmarcke, H., P. Berkvens, and A. Poffijn. 1989. Radon versus Rn daughters. Health Phys. 56:229-231.
Yeh, H. C., Y. S. Cheng, and M. M. Orman. 1982. Evaluation of various types of wire screens as diffusion battery cells. J. Colloid Interface Sci. 86:12-16.