The committee has recommended that the National Flood Insurance Program (NFIP) adopt and implement a modern approach to the analysis of flood risks that will serve as input to the assessment of flood insurance and provide a sound foundation for transitioning to risk-informed floodplain management. The approach recommended is founded on decades of risk analysis experience in the natural hazards and civil infrastructure arena and environmental health and life safety. This experience has evolved in the private and public sectors (USACE, 1996, 2006; USNRC, 2011; AIR, 2012; RMS, 2012; EPA, n.d.) and specifically in the levee-flood risk areas as evidenced by recent studies in Dallas, Texas, New Orleans, Louisiana, Sacramento, California, and in California’s Sacramento-San Joaquin Bay Delta (URS/JBA, 2008; IPET, 2009; CA DWR, 2012; USACE, 2012). This appendix provides further background and support for the modern risk analysis recommended in Chapter 3, including continued discussion of elements of a modern flood risk analysis.
NEW CAPACITY ENABLING A RISK-BASED ANALYSIS
At the initiation of the NFIP in the 1970s, simplified analysis was necessary and appropriate. Hydraulic modeling capabilities were limited. Much of the hydraulic analysis for floodplain delineation, for example, was completed with computer program HEC-2 (USACE, 1991), a one-dimensional (1-D) steady-flow open-channel flow analysis application that was executed on large mainframe computers and for which the channel system was described on IBM punch cards, and the channel system description, which includes the channel cross-section geometry, often was derived from U.S. Geological Survey 7.5-minute quadrangle topographic maps; maps with contour intervals of 10 feet that are accurate to ±5 feet (1.5 meters) of the actual elevation. Furthermore, at the onset of the NFIP, knowledge of performance of levees was limited, and the notion of evaluating the potential for levee failure and describing performance in terms of the probability of failure with a fragility curve had not found its way into flood and floodplain analysis. Although a fundamental description of economic consequences and an associated probability of occurrence did play a limited role in flood insurance rate setting and management planning (e.g., in the computation of expected inundation reduction benefit attributable to a flood management project), a detailed understanding and description of risk were not widespread in the floodplain management community, and procedures and tools for risk analysis were not readily available.
Technological advances in the past 40 years now make risk analyses of large insurance portfolios possible within the context of the NFIP. For example, the NRC (2007) notes that Lidar (light detection and ranging) technol-
ogy has matured to the point that it “is capable of producing a bare-earth elevation model with 2-foot equivalent contour accuracy in model terrain and land-cover types.” With geographic information system tools, overland flow on floodplains can be more accurately modeled from these data in a systematic, automated manner, with minimum human processing and few errors. Further, the state of practice of hydraulic modeling has advanced greatly since the early days of the NFIP, with two-dimensional (2-D) unsteady open channel and overland flow models now widely used. In fact, FEMA’s list of acceptable models for hydraulic analysis includes five such models.1 Data for estimation of consequence of inundation, particularly estimation of inundation damage, are readily available. These include, for example, property values, property type categorization, and property elevation data in FEMA’s Hazards-United States (Hazus) databases.2
The technical capability now exists for implementing and applying risk analysis as proposed in this report. In fact, other state and federal agencies with responsibilities for flood risk management have recognized the need for complete risk analyses to support their decision making, and have incorporated those analyses in their programs. To varying degrees, those analyses:
• Account for the full range of hazard, going beyond the one percent chance event, considering events as common as the 50 percent chance event and as rare as the 0.1 percent or 0.01 percent chance event.
• Include an explicit assessment of the consequences of inundation. Most analyses consider economic consequences, some life safety, and few environmental consequences.
• Evaluate all potential mechanisms for flooding areas that are protected by a flood protection system, including overtopping (without levee or structural failure), misoperation, breaching, and ponding. In addition, damages that may be caused by breaching itself, such as might be caused by the scour that occurs during the breach process, can be evaluated.
• Account for the performance of flood protection systems throughout the range of possible hazards. The analyses consider, for example, that a levee designed for the 10 percent chance event may reduce adverse economic consequence due to the one percent chance event, even though it will not eliminate all damage due to that event. They also represent the possibility, though unlikely, of failure of a FEMA “certified” levee during events that are smaller or larger than the one percent chance event.
• Acknowledge and evaluate the uncertainties about the various inputs to the analysis, including natural variability and lack of perfect understanding and ability to model the natural processes.
For example, all flood damage reduction studies conducted by the U.S. Army Corps of Engineers are required to analyze risk (USACE, 2006). The requirement applies to USACE studies that lead to feasibility reports, general design memorandums, and general re-evaluation reports. The regulation specifically prohibits traditional deterministic approaches—such as inclusion of freeboard to account for what are described as “hydrologic, hydraulic, and geotechnical uncertainties.” Instead, USACE analyses must use technical procedures presented in Engineering Manual 1110-2-1619 (USACE, 1996), Engineering Technical Letter 110-2-556, and companion documents.
In addition to the foregoing public-sector applications, private companies have developed flood risk analysis tools for evaluating insurance portfolios (AIR, 2012; RMS, 2012).
EXAMPLES OF CURRENT USE OF A RISK ANALYSIS TO EVALUATE FLOOD RISKS
As discussed in Chapter 3, the use of risk analysis methods to evaluate flood risks and specifically to consider the performance of levees has been ongoing and improving for more than a decade. This includes the development of a probabilistic approach by USACE in the 1990s (USACE, 1996). More recently, after the events of Hurricane Katrina, there has been considerable development and application of risk analysis methods to evaluate the flood
_______________
1 See http://www.fema.gov/national-flood-insurance-program-flood-hazard-mapping/numerical-models-meeting-minimum-requirement-0.
risks and the performance of levees and flood protection systems in general. As a response to the damage caused by Katrina and the levee failures, the USACE formed a team to conduct a detailed risk and reliability analysis of the New Orleans hurricane protection system, including an assessment of economic consequences as part of the Interagency Performance Evaluation Task Force study (IPET, 2009). During the same period and partly in response to Hurricane Katrina, the California Department of Water Resources carried out a comprehensive risk analysis on the more than 1,200 miles of levees in the Sacramento-San Joaquin Delta (URS/JBA, 2008). This analysis evaluated flood and seismic risks to Delta levees (which are more like dams because they have water against them year round) and the economic risks to the state. Following the Delta risk study, California DWR is conducting flood risk studies in the Central Valley, including the extensive development of levee fragility curves. As part of the California Central Valley Flood Protection Plan, engineers have developed levee fragility curves at approximately 300 locations in approximately 1 year, following an extensive data collection effort (CA DWR, 2012). Similarly, USACE has developed levee fragility curves for use in ongoing planning studies, all of which now employ complete risk analysis (USACE, 2006).
The events of Hurricane Katrina led to significant changes at USACE in terms of their use of risk analysis methods in its levee and dam safety programs. In fact, the IPET evaluation led to USACE making a major paradigm shift, transforming USACE to a risk-informed agency (USACE, 2008). Whereas USACE had been using risk analysis in limited ways prior to Katrina, the impact of failure of USACE-designed structures led to a wholesale move to implementation of risk analysis for the management of the nation’s flood risk. As part of these changes, USACE is advancing its risk analysis methods for levees and developing new tools to improve the assessment of flood protection systems (USACE, 2008).
DETAILED DICUSSION OF A MODERN RISK-BASED ANALYSIS
As described in the report, there are a number of key elements to conducting a modern risk analysis. These include:
• the requirement that uncertainties, specifically epistemic uncertainties, be identified and evaluated as an integral part of the analysis;
• modeling and considering the performance of flood protection systems, including the potential for failure and breaching, misoperation, overtopping, and flooding of areas protected by these systems, in the assessment of the potential for flooding and damage; and
• a systems-based approach for the modeling of the hydrologic and hydraulic systems and the flood protection systems that provide protection to a community.
As it pertains to the NFIP, the purpose of a risk-based approach to the analysis of flood risks, including the performance of flood protection systems, is multifold. It is intended to provide a quantitative measure of the flood damages associated with flood hazards that can be used to support the NFIP determination of flood insurance rates. This assessment needs to consider the performance of levee systems and, given the language in 44 CFR §65.10, all elements of flood protection systems and their role in the potential for flooding. In addition to insurance-motivated needs of the NFIP, the risk analysis and, more specifically, the products of the risk analysis will support other floodplain management aspects of the program (risk communication, planning, etc.).
The analysis of flood risks is a multidisciplinary evaluation that is made on the basis of available information. As such, the recognition and evaluation of these epistemic uncertainties is a key concept in modern risk analysis. As a starting point for the development of an NFIP risk analysis methodology, it is important that a clear definition of uncertainty and risk be established. Furthermore, as procedures for the implementation of an NFIP risk analysis method are developed, clear definitions of the responsibilities of the professionals involved in the study, the evaluations they are expected to perform, and the results they generate are critical. Experience suggests that in complex, multidisciplinary evaluations it is important that responsibilities are clearly defined and the technical interface between different parts of the analysis are laid out.
Characterizing Aleatory and Epistemic Uncertainty
As noted above and in Chapter 3, uncertainties are an integral part of the modern risk-based analysis. To evaluate and model aleatory and epistemic uncertainties, a characterization can be made in terms of their effect on models and estimates of model parameters (Table I-1). Modeling epistemic uncertainty represents differences between a physical process (hurricane surge, embankment failure) and prediction models. Modeling epistemic uncertainty can be estimated by comparing model predictions to observed events/performance. Parameter uncertainty is the epistemic uncertainty associated with the estimates of model parameters as derived from available data. Parametric uncertainty is quantified by observing the variation in parameters inferred (either in a direct or an indirect manner).
The distinction between aleatory and epistemic uncertainty is not intuitive and can be difficult to ascertain. Furthermore, the assessment of these uncertainties is model dependent. For example, a simple engineering model of an event (levee performance during a flood) may have higher model aleatory variability than a more complex model that addresses more details of the physical process of a levee dealing with the loads it is exposed to during the flood (i.e., increased hydrostatic loading, wave action, seepage forces, etc.). At the same time, the more complex model may have larger parametric epistemic uncertainty; there are more parameters to estimate and there may be limited data to estimate them. Thus, the characterization of uncertainties is model dependent, making the distinction between different types of uncertainty difficult. Nonetheless, making a distinction between the sources of uncertainty in a logical manner helps ensure that all uncertainties are identified and quantified. In principle, epistemic uncertainties are reducible with the collection of additional data or the use/development of improved models.
A Conceptual Framework for Flood Risk Analysis
As described in the main report, a starting point for the development of an NFIP flood risk analysis is a conceptual framework for flood risk analysis that can be defined as:
![]()
where risk (R) is a function of flood hazard (H), vulnerability (V), and consequence (C). In this context, risk is a function of the flood hazard a community is exposed to, the vulnerability of flood protection systems and the potential that their failure will contribute to flooding, and the consequences associated with system failures and the damage to a community exposed to flooding, including economic impact and life safety.
As noted in Chapter 3, this framework can be extended to include the concepts of uncertainty. This extension
TABLE I-1 Characterization of Aleatory and Epistemic Uncertainty on Models and Model Parameters
| Element | Type of Uncertainty | |
| Epistemic | Aleatory | |
| Modeling | Uncertainty about a model and the degree to which it can predict events or outcomes (e.g., levee performance), that is, to what extent a model has a tendency to over- or underpredict observations | Aleatory modeling uncertainty is the variability that is not explained by a model. For instance, this variability is attributed to elements of the physical process that are not modeled and therefore represents a variability (random differences) between model predictions and observations. |
| Parametric | Uncertainty associated with the estimates of model parameters, given available data, indirect measurements, etc. | This uncertainty is similar to aleatory modeling uncertainty. This is a variability that may be due to systematic, but random, variations associated with parameters of a model. |
SOURCES: Abrahamson et al. (1990), USR/JBA (2008), IPET (2009).
provides a quantitative definition of risk (Kaplan and Garrick, 1981; ASME/ANS, 2009; IPET 2009) in probabilistic terms:
![]()
where v = frequency of occurrence or exceedance, and is a measure of the aleatory uncertainty (the randomness of events); ρ = probability as a measure of the confidence to which an estimate of v is the true value, or the epistemic uncertainty in the estimate of v. For purposes of a flood risk analysis, the consequences of flooding are measured in terms of the economic damages. Typically, results of risk analysis would be expressed in terms of a frequency distribution on economic damages (dollars). This is denoted
![]()
where n() = frequency of occurrence per year; and c = consequences measured in dollars.
Another risk metric is the expected annual losses, which can be estimated by
![]()
The estimate of flood consequences and their frequency of occurrence are uncertain, that is v(c) cannot be determined with certainty; there is epistemic in estimating the frequency and magnitude of floods, uncertainty in the performance of flood protection systems, and the magnitude of consequences. There is therefore a distribution on the estimate of v(c). A formal analysis of the uncertainties in the components of a risk analysis (h, v, and C) produces a probability distribution on the estimate of v(c), the estimate of risk. This probability distribution that quantifies the uncertainty in the estimate of v(c) can be thought of as a distribution from which confidence intervals on the estimate of risk can be derived.3 Kaplan and Garrick (1981) provide a quantitative definition of risk that includes the quantification of aleatory and epistemic uncertainties and the estimate of consequences:
![]()
or, in terms of the risk example above, equation (I-5) can be written,
![]()
where, v = frequency of occurrence or exceedence, as is a measure of the aleatory uncertainty; C = a consequence metric (e.g., economic impact, public safety); ρ = probability as a measure of epistemic uncertainty in the estimate; and where,
![]()
The frequency of occurrence is a measure of the aleatory uncertainty of events or outcomes (consequences), their randomness or stochastic character. An example of aleatory uncertainty is the occurrence of flood events in a watershed, or the performance of a levee for a given flood level. Equation (I-6) defines a discrete probability mass function on the frequency distribution of consequences, where probability is a measure of epistemic uncertainty in the estimate of v.
_______________
3 The notion of confidence intervals is a useful concept for purposes of illustrating the measure of uncertainty in the risk analysis results. In fact, however the assessment of uncertainties is not same as a statistical analysis of a dataset from which confidence intervals on parameter estimates are derived.
Risk Analysis Methodology
A primary product of a risk analysis for the NFIP is an assessment of the frequency of economic consequences that can occur as a result of flood-related events. For a unit of exposure (a particular property) or for an entire portfolio, the risk analysis will evaluate the potential that a unit may experience flooding and the damage (loss) that will occur as a result of the flooding. For a property behind a levee, the mechanisms that may lead to flooding are
• levee breach, prior to a levee being overtopped;
• inflow to the protected area (behind the levee) due to overtopping that does not result in breaching of the levee;
• flooding that occurs due to failure to close gates or other closures;
• levee breaching as a result of overtopping;
• flooding behind the levee that occurs due to intense rainfall, storm drains getting backed up, etc. that result in flooding/ponding in the protected area behind the levee.
The loss that occurs will vary, depending on
• depth and velocity of flooding associated with the different flooding mechanisms (see above); and
• proximity to the location of the levee breach. For instance, when a levee breaches, the depth of flooding behind the levee might end up at 2 feet above the first-floor elevation. However, a property that is located at or near a breach may be completely destroyed as a result of the depth of water, the high velocities of flow that will occur, and/or the fact the unit is located in the scour zone of the breach which undermines the foundation of the unit, etc.
A primary product of the risk analysis for an individual insured property or for an entire portfolio is an assessment of the frequency of economic consequences, which will vary in scale depending on the size of the flood events and the flooding mechanisms that can occur. This result, repeated from above, can be denoted,
![]()
where λ() is the frequency of exceedance of the economic consequences and ρi is the probability associated with an estimate of the flood risk, λ(C > c)i.
To estimate the result in equation (I-8), there are two fundamental components to the risk model. The first can be referred to as the aleatory flood risk model, which estimates the frequency of occurrence (or exceedance as shown in equation (I-8)) of flood damages. For an individual property, this can generally be denoted
![]()
where
v(ej) = frequency of occurrence of flood event i;
P(LPSj > Fi) = probability of levee system performance state j, given flood event, Fi;
P(eijk | LPSj) = probability of flood elevation k due to flood event, Fi and levee system performance state, LPSj; and
P(C > c | ej) = probability that consequences of flooding will exceed a level c, given the occurrence of a flood elevation ej.
The summations are carried out over (1) the range and type of flood events, (2) the number of different levee system performance states, and (3) the range of flood elevations that may occur given the flood events that may occur and the different levee performance states. The summation over flood events applies to all events that could lead to flooding. These could include local precipitation that might lead to ponding/flooding behind levees in the
protected area, larger precipitation events that result in high river flows, ice jamming events, etc. The levee performance states can vary considerably depending on the number or type of structures and components that form the levee system. These may include levee breaching at different locations and at different flood elevations (pre- and post-overtopping), failure to close flood gates, structural or stability failure of floodwalls, etc. The performance of the levee system determines the different flooding mechanisms that may occur.
Regarding equation (I-9), first, the use of flood elevation as a metric for the characterization of the flood hazard can be considered a surrogate for the flood threat which may be multidimensional. As noted above, the level of damage that occurs may be a function of the depth and velocity of flooding. It also may be a function of debris content, the scour that may occur near a breach, etc. Second, the flooding that occurs is a function of the occurrence of different flooding mechanisms, some of which may involve levee failures, others of which do not. For purposes of this discussion, the characterization of the hazard is stated in terms of elevation as a surrogate. Equation (I-9) represents the aleatory model for estimating the random chance that flooding will occur and cause property damage.
The second element of the flood risk model is the “model of epistemic uncertainties.” If all of the models and parameters that are required to implement equation (I-9) were known with certainty, a single estimate of (C > c) could be determined. This of course is not the case, because there are numerous sources of uncertainty in the assessment of flood hazards, in the estimate of the fragility of levee systems, and in the estimate of the flood damages. As a result, there is uncertainty in the estimate of (C > c). Therefore, as part of the flood risk analysis, an epistemic uncertainty model needs to be developed for the flood hazard analysis, the fragility analysis, and the flood damage model. In addition, a method to propagate these uncertainties to derive the uncertainty in the flood risk needs to be implemented.
Typically, simulation methods are used to carry out this analysis (e.g., Monte Carlo or Latin Hypercube simulation). Other approaches include the use of logic trees to enumerate all of the possible combinations of uncertain models and parameters. Conceptually, the estimate of the uncertainty in the flood risk analysis can be illustrated in a logic tree, as shown in Figure I-1. Across the top of the logic tree are the uncertainty elements of the flood risk model (again, shown here in conceptual form). For elements in the logic tree, there are a series of branches that represent alternative, discrete models are parameter estimates. Collectively, these discrete estimates model the uncertainty in that component of the risk model (e.g., flood hazard model). Associated with each branch is a probability weight, derived from the uncertainty analysis for that part of the flood risk model. The weight corresponds to the degree-of-belief that a particular model or parameter estimate is the true state of nature. Each path through the logic tree represents one, alternative (but uncertain) estimate of the flood risk, based on the uncertain inputs defined along the path and the basis for the risk calculation (equation (I-9).
COMPONENTS OF THE MODERN RISK-BASED ANALYSIS
The modern risk analysis recommended for NFIP insurance, mitigation, and communication programs requires a complete description of the flood hazard. In Chapter 3, a summary description of the modern risk-based analysis is provided which includes a flood hazard analysis, levee and other hydraulic structure and component and fragility analysis, systems analysis, inundation analysis, consequence assessment, and risk and uncertainty quantification. The discussion of these components is expanded, when relevant, here. Also, new components are discussed.
Flood Hazard Analysis
In the context of the committee’s recommendation, a description of the flood hazard includes a specification of the magnitude (e.g., peak flood elevation) and its frequency of occurrence (or, more commonly, frequency of exceedance). Hazard at a given location in a floodplain is described with a discharge (flow)-frequency or elevation-frequency distribution. For analysis of riverine flood risk, the latter commonly is derived from the former. For coastal risk analysis, the elevation-frequency function is developed directly.
Methods of development of discharge-frequency functions for rivers are well known and well documented. If an adequate record of unregulated discharge at a site is available, an analytical frequency distribution can be
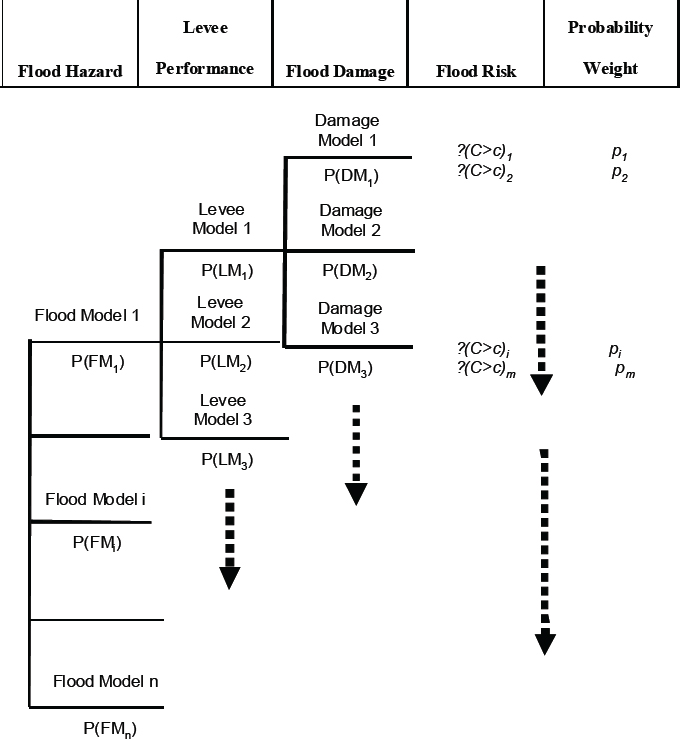
Figure I-1 Illustration of a logic tree, showing the uncertainty in different components of risk analysis.
fitted to the data. FEMA generally follows the standard of practice for this distribution fitting with historical flow observations. In cases for which data available are inadequate for distribution fitting, FEMA guidance suggests regional methods, transfer methods, empirical equations, and watershed modeling methods for estimating discharge of specified probability.4 While certain refinements to both distribution fitting and alternative methods
_______________
4 See http://training.fema.gov/EMIWeb/edu/docs/fmc/Chapter%204%20-%20Flood%20Risk%20Assessment.pdf.
will be necessary for the comprehensive risk analysis proposed herein—notably enhancements to evaluating the epistemic uncertainty about the frequency curves—the hazard description required for risk analysis proposed herein is fundamentally the same as that currently required for FEMA studies. The assessment of epistemic uncertainties in hydrologic modeling, frequency analysis, and estimation of flood elevations is an important element of a comprehensive risk analysis and in the stability of the results (climate change and other physical changes aside). The assessment of epistemic uncertainties must consider the parametric uncertainties associated with limited data, correlation of model parameters, and modeling uncertainties which may include alternative modeling interpretations of the analysts (Yankee Atomic, 1984; IPET, 2009). Thus the same hydrologic engineering methods can be used, with enhancements, and the existing technical knowledge base and experience of analysts will be useful and usable for comprehensive risk analysis.
A key to success of the risk analysis proposed herein is the capability to model the behavior of the riverine, coastal, or floodplain system with sufficient detail and sufficient accuracy to predict water surface elevations and velocities throughout the area of interest, given the discharge values estimated with frequency fitting or alternative methods. Capabilities for such modeling are readily available and well understood in the engineering and floodplain management community.
For flood studies such as those conducted by FEMA, channel flow (or flow contained by the levees) is described well in many cases with a 1-D hydraulic model. Such a model predicts the water surface elevation and velocity in the channel for specified flow rates by solving equations that represent the conservation of mass and momentum in the channel as the water moves downstream. In some cases, a 1-D model is not adequate for representing channel flow, because the inherent assumption that flow is predominately in a single direction is violated. In that case, a 2-D model would be used. The products of application are similar, but with variations both longitudinally and laterally in the channel represented.
Software applications with 1-D and 2-D models currently accepted by FEMA for NFIP studies are usable for the risk analysis proposed herein.5 Again, certain enhancements are necessary to adequately describe the uncertainty about predicted elevations, but the analysis applications and the knowledge and experience of users are directly usable.
Flood Protection System Performance
The subject of this study and the issues the NFIP is facing are centered around levees, because they are a major component of flood protection systems. However, 44 CFR §65.10 discusses more broadly the fact that flood protection systems that a community relies on are often a composite of many different elements. These include:
• structures of various types, including levees, floodwalls, gates, buildings, etc.;
• natural structures (levee foundations, old streambeds);
• interior drainage systems; pumping systems (pumps, pumphouse), drainage ditches and canals, power supplies, control systems, fuel supplies, etc.; and
• operational requirements for pump system operation, gate closure, etc.
As such, the flood protection that is provided to a community relies on the ability of a “system” to perform as intended during flood events. One of the significant lessons from Hurricane Katrina was the recognition and admission by the Corps of Engineers that the New Orleans Hurricane Protection System (HPS) was a system in name only (IPET, 2009). The post-event evaluations made it clear the HPS was not designed, operated, or maintained as a system and as such did not perform as one during Katrina (IPET, 2009).
Section 65.10 dictates the requirements for elements of the flood protection system, such as an operational plan for the levee system, the installation of gates or other closures, etc. The residual risk in protected areas is a function of the reliability of the flood protection system as a whole, not just of the individual system elements. The
_______________
5 See http://www.fema.gov/national-flood-insurance-program-flood-hazard-mapping/numerical-models-meeting-minimum-requirement-0 and http://www.fema.gov/national-flood-insurance-program-flood-hazard-mapping/numerical-models-meeting-minimum-requirement-3.
assessment of flood risks requires a system-level analysis where the system includes the watershed (the hydrologic system), the hydraulic system (river channels, floodplain), and the flood protection system.
As part of a risk analysis, a systems modeling approach that considers the physical and operational elements of a flood protection system that are required to prevent flooding needs to be used. The system performance (system reliability) over a wide range of flood events is considered in order to estimate the risk in the floodplain, in the protected as well nonprotected, waterside areas of the system. The performance of the system of structures and other components that make up the system is integral to the hydraulic response - whether the protection system is breached or not.
Structure, Component, and Operational Reliability
A key element of the risk analysis is the assessment of the reliability of structures as well as other elements of the flood protection system to perform their intended function. This includes the integrity of the structures (levees, floodwalls, interface between structures, etc.) and operational reliability (actions of personnel) to close gates or other closures, operation drainage systems, etc. For purposes of the risk analysis, the reliability of structures is characterized in terms of the conditional probability of failure expressed as a function of an appropriate metric of the flood hazard (i.e., peak flood elevation) (USACE, 1996; URS/JBA, 2008; IPET, 2009; Schultz et al., 2010) (see Figure I-2). In addition to the assessment of fragility for structures in which the reliability depends on the loading level, there are other elements of the flood protection system whose reliability is independent of the level of flooding. Examples include the reliability of mechanical and electrical equipment (e.g., pump systems), actions of personnel (installation of closures, pump system operations, etc.).
A critical part of the reliability assessment is the collection of information about the various system components so that an understanding of system interactions, potential modes of failure (see Figure I-3 for a view of different levee failure modes) and performance can be developed. With respect to the assessment of fragility curves for structures (levees, floodwalls, etc.), various methods are available (URS/JBA, 2008; IPET, 2009; Schultz et al.,
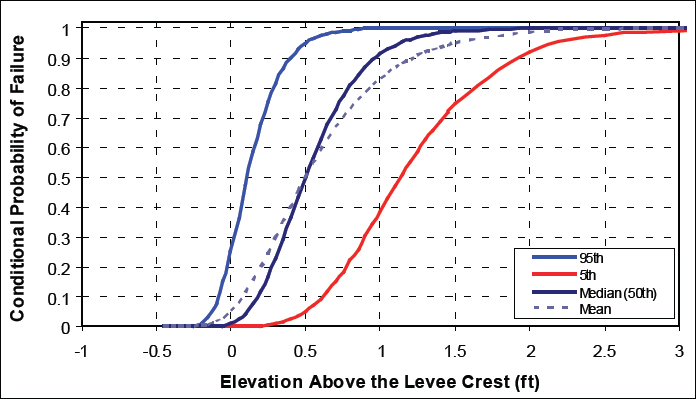
FIGURE I-2 Levee fragility curve.
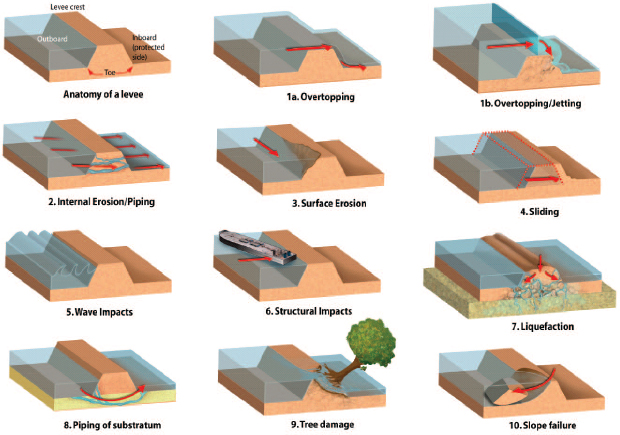
FIGURE I-3 Earthen levees are subject to a suite of potential failure modes. Not all failure modes are correlated to river stage. and this are excluded from consideration of levee fragility curves based on a function between river stage and system probability of failure. For example, dredging immediately adjacent to an earthen levee changes the capacity of that system to resist underseepage and piping (failure mode number 8). This activity, however, would not be captured and communicated to the system managers/operators through levee fragility curves defined by river stage.
SOURCE: Courtesy of Zina Deretsky, National Science Foundation.
2010). These range from judgmental approaches that rely on expert evaluations, often in cases where there is limited data, to empirical, and analytical methods (URS/JBA, 2008; IPET, 2009; Schultz et al., 2010). Empirical methods take advantage of observational data documenting the performance of structures under a variety of loads. Observations may be obtained systematically through controlled experiments or may be collected in an opportunistic fashion from flood events. Analytical methods that can be used to develop fragility curves are based on structural models that evaluate the likelihood that performance limits of the structure are exceeded. These methods have the advantage that they are based on physical models, or at least explicit physical relationships between capacity and demand. A limitation of analytical and empirical methods is that there are potential failure modes that may not be readily addressed by either approach. As a consequence, fragility assessments are often a hybrid of different methods, depending on the information that is available to perform the analysis.
There can be considerable epistemic uncertainty in the estimate of the fragility for structures (Figure I-4). A particularly vexing aspect of levees is the uncertainty associated with foundation conditions. The conditions along a levee can be complex and dynamic (Saucier, 1994). These changing subsurface conditions tend to promote preferential seepage beneath levees, often along buried or abandoned channels, as shown in Figure I-5. Underseepage tends to be “spotty,” or inconsistent in some areas, and fairly predictable in other areas, depending on the underlying geology (Kolb, 1976). Underseepage can also be exacerbated by infiltration in riverside borrow pits, excavated to construct the adjacent levees (Mansur and Kaufman, 1957). The quantification of uncertainties and
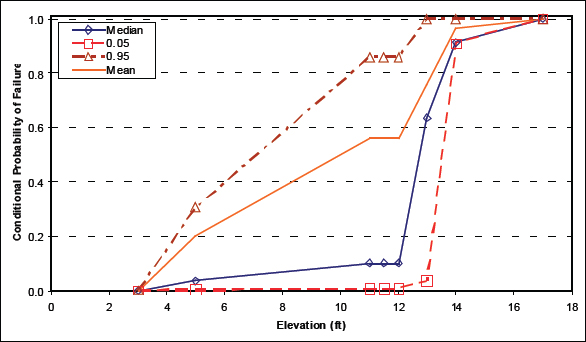
FIGURE I-4 Uncertainty in the estimate of levee fragility for a levee in New Orleans. Dashed lines correspond to the 0.05 and 0.95 uncertainty levels in the estimate of the conditional probability of failure.
SOURCE: IPET (2009).
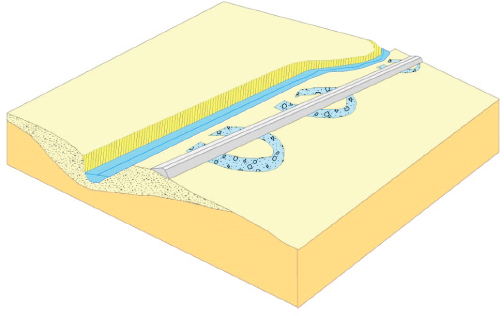
FIGURE I-5 Levees are commonly placed on floodplains adjacent to the present course of the river channels. These embankments are usually underlain by older channel deposits, such as the oxbows sketched above. These dynamic conditions often promote the paths or preferential seepage and hasten differential settlement of the levee embankment.
SOURCE: Rogers (2012).
their potential impact on levee performance will be one of the most challenging aspects of developing fragility curves over the coming decade.
Inundation Analysis Including Levee Breach and Inundation
If the flow rate in a leveed channel increases, the water surface elevation will increase. At a certain flow rate, the water-surface elevation will exceed the top of levee elevation, and water will flow onto the “protected” floodplain—the interior area on the landside of the levee. This floodplain flow may be simulated with a 1-D or 2-D model. Figure I-6 illustrates conceptually such an integrated model of channel and floodplain flow, as would be required for a complete risk analysis as proposed herein. A 1-D model represents the channel flow regime, and a water-surface elevation is computed for a specified exceedence probability. If that water-surface elevation is greater than the elevation of the top of the levee (which is represented in the figure with the heavy line), water spills from the channel. That process is simulated with an appropriate 1-D or 2-D model for the risk analysis proposed. In the illustration, a 2-D model is illustrated. This uses a fixed grid, with elevation and flow resistance parameters described for each cell of the grid. The equations of fluid motion are solved to account for the flow from each cell to all adjacent cells, thus estimating the depth of inundation for each cell. The 1-D and 2-D models are “coupled” at locations where water spills from the channel onto the floodplain and vice versa, as illustrated by the arrows in the figure.
A levee between the channel and floodplain limits the exchange of water between the channel and floodplain, with flow onto the floodplain occurring only when the channel capacity is exceeded if the levee performs as designed. However, the levee may breach prior to (or after) overtopping. In that case, water flows from the channel through the levee breach and onto the floodplain. Shown in Figure I-7, flow onto the protected floodplain is simulated, again, with an appropriate model. As before, model results include water surface elevations and velocity
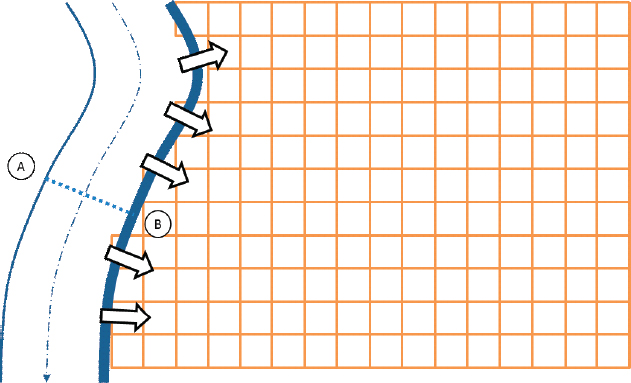
FIGURE I-6 A one-dimensional model commonly is used to represent channel flow (Left). The A-B transect illustrates a cross section of the channel in the 1-D model of flow that typically would be used to simulate behavior of the river. A two-dimensional model may be used to represent more complex flow patterns on the adjacent floodplain (Right).
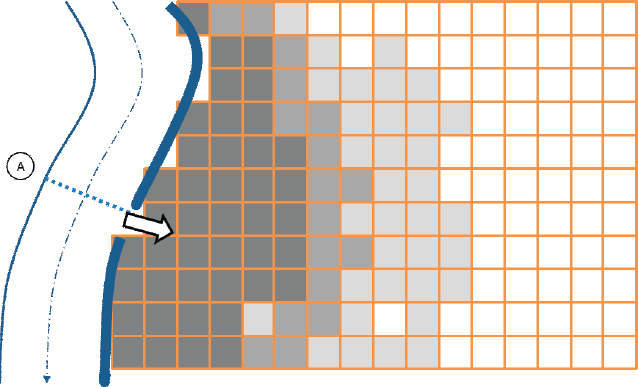
FIGURE I-7 A one-dimensional model of flow in the channel (Left) can be coupled with a two-dimensional model of flow on the floodplain (Right), with flow moving from the channel onto the floodplain through the levee at the breach. The heavy line represents the levee, and the arrow shows the location of the breach or overflow section through which water flows.
for each cell, in this case with water delivered to the floodplain from the channel through the levee. The floodplain elevations may be mapped, as illustrated, with shading to represent depth. Such analysis can be completed for any flow condition in the channel, including the one percent chance event and larger or smaller events.
For risk analysis, properties of the levee breach are described for modeling the breach. The properties are determined from empirical data, or application of geotechnical engineering analyses and standards of practice, as described earlier in this report.
Consequence Assessment
A modern risk analysis requires the estimation of consequence of inundation for the entire range of hydrologic events and the various states of and levee system performance. This consequence evaluation is commonly accomplished with a model that describes in a quantitative manner the consequences of flooding, given the consequences of the flooding (i.e., depth and velocity of flow), and properties of the exposed floodplain assets (i.e., construction type and material, foundation type and elevation, and content type and value).
A simple elevation-damage function, such as that illustrated by Figure I-8, is typical of models used to characterize the consequence of flooding of the exposed inventory in a floodplain. Such a function may represent economic loss for a single element of the inventory—such as a single residence and its contents—or the function may represent the aggregated loss for groups of items. The function may represent tangible (direct and/or indirect) loss and/or intangible loss. The tangible consequence of flooding may include a broad range of deleterious effects and associated costs, including (a) economic damage to buildings and contents; (b) damage to outbuildings, landscaping, vehicles, boats, and other inventory not within buildings; (c) damage to infrastructure, including transportation facilities, utilities, communications facilities, and so on; (d) damage to vegetation, including crops; (e) emergency response, management, and recovery costs, including flood-fighting costs; security, evacuation,
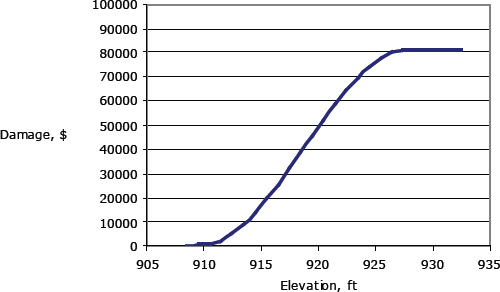
FIGURE I-8 Example of an elevation-damage model prediction of consequence (damage), given flood properties (water-surface elevation).
search and rescue costs, debris removal, and others; and (f) other economic impacts, such as displacement costs for temporary quarters, disruption time for affected people, economic impacts of loss of service of transportation and utility functions, loss of business income, loss of public services, and others.
Consequences considered in a flood risk analysis need not be restricted to economic loss. Thus, the elevation-damage function may be interpreted broadly to represent any undesired consequences that can be predicted from knowledge of flood properties.
FEMA has developed consequence models for various structure types, content of structures, infrastructure, vehicles, and other relevant categories. These models, derived from information gathered from insurance claims, are included in FEMA’s Hazus software application. With similar analysis of historical inundation damage data, augmented with analysis of building methods, USACE has developed, published, and used generic elevation-damage models (USACE, 2000, 2003). For flood situations or structures not well represented by these readily available models, site-specific models are required. Those are developed from (a) empirical analysis of post-flood damage surveys; (b) detailed engineering analysis of cost of repair, considering various flood depths at a property and using cost estimates from, for example, Marshall & Swift’s Residential and Commercial Estimator, Means Square Foot Costs, and the BNI Home Builder’s Costbook (2013); or (c) expert elicitation, using professional judgment offered by knowledgeable economists and engineers.
Risk analyses may be completed independently for each property within the floodplain. This will provide the economic information needed for insurance rate setting for individual properties. In addition, or as an alternative, economic values can be aggregated by political boundary, by structure type, and so on as appropriate for decision making for mitigation or for risk communication.
Risk Quantification
The final step in the risk analysis is the probabilistic combination of the different parts of the risk analysis to estimate the frequency of flooding, performance of the flood protection systems, and flood damages. The quantification also includes the propagation of epistemic uncertainties in the flood hazard, levee system performance and economic damage assessment, to derive the uncertainty in the risk analysis results. With current analytical and computational capabilities the estimation of flood risks can be carried out at the individual property level, the community level, and for the NFIP portfolio. These capabilities make it possible for a modern NFIP risk analysis
to provide comprehensive support to all aspects of the program: insurance, flood risk communication, floodplain management, etc.
REFERENCES
Abrahamson, N. A., P. G. Somerville, and C. A. Cornell. 1990. Uncertainty in numerical strong ground motion predictions. Pp 407-416 in Proceedings of the Fourth U.S. National Conference on Earthquake Engineering: May 20-24, 1990, Palm Springs, California, Vol. 1. Oakland, CA: Earthquake Engineering Research Institute.
AIR (American Institutes for Research). 2012. AIR Models Overview. Available online at http://www.air-worldwide.com/Models/Overview/. Accessed November 28, 2012.
ASME/ANS (American Society of Mechanical Engineers and American Nuclear Society). 2009. Standard for Level 1/Large Early Release Frequency Probabilistic Risk Assessment for Nuclear Power Plant Applications, Addenda to ASME/ANS RA-S-2009. LaGrange Park, IL: ANS.
CA DWR (California Department of Water Resources). 2012. 2012 Central Valley Flood Protection Plan: A Path for Improving Public Safety, Environmental Stewardship, and Long-Term Economic Stability. Available online at: http://www.cvfpb.ca.gov/CVFPP/index.cfm.
EPA (U.S. Environmental Protection Agency). n.d. Risk Analysis Guidelines and Tools, Available online at http://www.epa.gov/riskassessment/guidance.htm. Accessed December 10, 2012.
IPET (Interagency Performance Evaluation Task Force). 2009. Performance Evaluation of the New Orleans and Southeast Louisiana Hurricane Protection System: Final Report.. Available online at https://ipet.wes.army.mil/. Accessed December 4, 2012.
Kaplan, S., and B. J. Garrick. 1981. On the quantitative definition of risk. Risk Analysis 1(1): 11-27.
Kolb, C. R. 1976. Geologic control of sand boils along Mississippi River levees. Chapter 6 in Geomorphology and Engineering, D. R. Coates, ed. Stroudsburg, PA: Dowden, Hutchinson and Ross.
Mansur, C. I., and R. I. Kaufman. 1957. Underseepage, Mississippi River Levees, St. Louis District. ASCE Transactions 122: 985-1008.
NRC. 2007. Elevation Data for Floodplain Mapping. Washington, DC. The National Academies Press.
RMS (Risk Management Solutions). 2012. RMS Models. Available online at http://www.rms.com/models/. Accessed November 28, 2012.
Rogers, J. D. 2012. Evolution and Development of Flood Control Engineering. GE 301 Lectures. Available online at http://web.mst.edu/~rogersda/umrcourses/ge301/. Accessed November 15, 2012.
Saucier, R. T. 1994. Geomorphology and Quaternary Geological History of the Lower Mississippi Valley. Vicksburg, MS: USACE.
Schultz, M. T., B. P. Gouldby, J. D. Simm, and J. L. Wibowo. 2010. Beyond the Factor of Safety: Developing Fragility Curves to Characterize System Reliability. Washington, DC: USACE.
USACE (U.S. Army Corps of Engineers) 1991. HEC-2 Water Surface Profiles: User’s Manual. Davis, CA: Hydrologic Engineering Center.
USACE. 1996. Risk-Based Analysis for Flood Damage Reduction Studies. EM 1110-2-1619. Washington, DC: USACE.
USACE. 2000. Generic Depth Damage Relationships: Economic Guidance Memorandum EGM 01-03. Washington, DC: USACE.
USACE. 2003. Generic Depth Damage Relationships for Residential Structures with Basements: Economic Guidance Memorandum EGM 04-01. Washington, DC: USACE.
USACE. 2006. Risk Analysis for Flood Damage Reduction Studies. ER 1105-2-101. Washington, DC: USACE.
USACE. 2008. Improving Public Safety—From Federal Protection to Shared Risk Reduction. Memo to Honorable Jim Nussle, Director, Office of Management and Budget. Washington, DC: USACE
USACE. 2012. Risk Assessment: Trinity River Corridor, Dallas Floodway Near Dallas, TX. Washington, DC: USACE.
USNRC (U.S. Nuclear Regulatory Commission). 2011. Practical Implementation Guidelines for SSHAC Level 3 and 4 Hazard Studies. NUREG-2117. Rockville, MD: USNRC.
URS/JBA (URS Corporation/Jack R. Benjamin & Associates, Inc.). 2008. Delta Risk Management Strategy (DRMS), Phase 1, Risk Analysis Report (Draft). Sacramento: California Department of Water Resources.
Yankee Atomic Electric Company. 1984. Probability of Extreme Rainfalls. YAEC-1405. Dallas, TX: Yankee Atomic Energy.
















