As discussed in Chapter 1, pesticides are designed to have biological activity and are “intended for preventing, destroying, repelling or mitigating any pest” [7 U.S.C. § 136 (u)(1)]. Pesticides might cause a variety of effects on nontarget organisms, including listed species, and effects on individuals might ultimately affect a population. Determining the potential for and possible magnitude of effects is a process known as effects analysis, and various aspects of that process are addressed in this chapter.
First, the committee discusses characterization and evaluation of sublethal, indirect, and cumulative effects. Next, it describes the models that are used to estimate effects of a pesticide at the individual and population levels, clarifies the relationship between the models at these two levels, and evaluates major assumptions used in the modeling approaches.
Because there are many sources of uncertainty in effects analysis, the final three sections of this chapter address various aspects of uncertainty. As described in Chapter 3, pesticides are typically mixtures (formulations) of active ingredients and other materials (inerts), are often mixed with other pesticides and other chemicals (adjuvants) in the field, and are applied to areas that already contain mixtures of chemicals. What is evaluated becomes a complicated question and is often viewed as a substantial source of uncertainty. Accordingly, the committee discusses the state of the science of mixtures assessment and provides some guidelines on assessing the hazard posed by a pesticide active ingredient in light of all the other components in the formulation, tank mixture, and environment. It then addresses the uncertainty surrounding interspecies extrapolations and the use of surrogate species and the quantitative characterization of uncertainty.
Throughout this chapter, the committee provides suggestions on how to incorporate the information presented into the approaches used by the US Environmental Protection Agency (EPA) to determine whether a pesticide “may affect” (Step 1, Figure 2-1) or is “likely to adversely affect” a listed species (Step 2, Figure 2-1) and into the approaches used by the US Fish and Wildlife Service
(FWS) and the National Marine Fisheries Service (NMFS)—collectively referred to as the Services—to make jeopardy determinations (Step 3, Figure 2-1).
SUBLETHAL, INDIRECT, AND CUMULATIVE EFFECTS
Pesticides can kill organisms that are closely or distantly related to their intended targets, and they can cause sublethal changes that can affect reproduction, shorten lifespans, or make the organisms unable to compete. The following sections discuss how to incorporate sublethal effects into ecological risk assessments, how effects on one organism might indirectly affect others, and how pesticide effects might be modified by exposure to other environmental stressors.
Sublethal Effects
Pesticides can have sublethal effects at multiple levels of biological organization: molecular, cellular, tissue, organism, population, and community. Only when compensatory or adaptive mechanisms at one level of biological organization begin to fail do deleterious effects become apparent at higher levels. The committee considered how to assess objectively the degree to which observed effects of pesticides on organisms are adverse. Defining that concept is essential for ecological risk assessment because even if an effect is reliably observed, that alone might not be sufficient to conclude that the effect is adverse. The committee concluded that the only reasonable way to determine whether an effect is adverse and how adverse it might be is to assess the degree to which it affects the organism’s survival and reproductive success. It then is possible to extrapolate from changes in an individual organism’s survival or reproductive success to estimate population effects. If an adverse effect is large enough, it might lead to extinction of the species. EPA reached a similar conclusion in its overview of the ecological risk-assessment process (EPA 2004, p. 31): “If the effects on the survival and reproduction of individuals are limited, it is assumed that the risk at the population level from such effects will be of minor consequence. However, as the risk of reductions in survival and/or reproduction rates increase, the greater the potential risk to populations.”
EPA and the Services agree on the inclusion of sublethal effects in the risk-assessment process but disagree on the extent to which such effects should be included. For example, in its responses to committee questions, EPA explained that its focus is “on how to relate the relevance of sublethal data to an assessment of the risks to fitness of listed species,” with fitness defined as “an individual’s ability to survive and reproduce” (EPA 2012a, p. 2). Furthermore, EPA considers that incorporation of sublethal effects into an ecological risk assessment must be accompanied by an explicit relationship that defines the contribution of the sublethal effect to an individual organism’s fitness in terms of the end points of “survival, growth and reproduction” (EPA 2012a, p. 20). EPA
stated that it “does not believe that all sub-lethal effects or that all levels of a sub-lethal effect on an individual constitute a compromise of individual fitness” (EPA 2012a, p. 3).
EPA’s approach differs from the Services’ approach. For example, FWS “casts a wide net for each potentially affected species to ensure that the most sensitive endpoints are captured and evaluated” (FWS 2012, p. 2). It contends that “at present, data describing ‘sub-lethal’ effects are acknowledged but then set aside and not used by EPA in making effects determinations or characterizing the potential effects of the action, unless other data or studies are available that would enable EPA to quantify a relationship between the ‘sub-lethal’ effect and EPA’s traditional endpoints, survival, growth, or reproduction.” FWS (2012, pp. 2-3) continued that “in contrast, when characterizing the ‘Effects of the Action’ pursuant to the ESA [Endangered Species Act], the FWS does not limit itself to using only those data that quantify changes in survival, growth, or reproduction.”
As discussed in the section on effects models below, assessing the effects of pesticides on listed species requires quantifying the effect of a pesticide on survival and reproduction of a species in the wild. Any effect that results in a change in one component is relevant to the assessment. In contrast, any effect that does not change either component is irrelevant with respect to a quantitative assessment of population effects. The relevance of any particular sublethal effect is likely to depend on the species. Growth, for example, might be a relevant effect in some species but not in others. In mammalian species, retarded growth might increase age of first reproduction but not affect reproductive output thereafter. In many fish species, size of the individual organism is directly related to reproductive output throughout the lifespan. Many plant species do not need to achieve a particular size for maximal reproductive output. Therefore, the committee recommends that EPA in Step 2 (see Figure 2-1) cast a wide net and identify information about sublethal effects of a chemical. If possible, EPA’s assessment should include information about responses at various chemical concentrations (a concentration-response curve) and, at a minimum, include a qualitative assessment of the relationship between sublethal effects and survival and reproduction. In Step 3 (see Figure 2-1), the Services should show how such effects change demographic measures (survival or reproduction) of a listed species and incorporate such information into the population viability analyses or should state that such relationships are unknown but possible and include a qualitative discussion in the uncertainty section of the biological opinion (BiOp). The Services face the greatest challenge in Step 3 in determining whether an observed sublethal effect will change survival or reproduction in the natural population and, if so, the magnitude of such a change in relation to the predicted exposure.
Relationships between sublethal effects and changes in population growth rates span a continuum of uncertainty that depends on the ability to quantify the
link. At one extreme, the relationship between a sublethal effect and survival or reproduction has not been quantified empirically, and the available mechanistic information is not sufficient to model the causal chain quantitatively. For example, markers of oxidative stress—such as glutathione or superoxide dismutase—indicate a physiological response to a chemical, but the relationship of the response to survival or reproduction is not known. Such a response could not be easily quantified with respect to population assessment if the observed response were the only pertinent information.
At the other extreme, the link between sublethal effects and population persistence might be clear, quantifiable, and well documented in the literature. For example, the singing ability of some male birds directly affects the probability of their establishing and holding a territory and forming pair bonds with mates (Spencer et al. 2003). Impaired singing ability could directly affect reproductive success during the breeding season if the male song did not attract a female mate. Similarly, impaired growth of juvenile salmon might result in a reduction in size of individual salmon as they migrate to sea and could reduce survival. Specifically, Baldwin et al. (2009) modeled the relationship between sublethal effects on acetylcholinesterase activity and feeding behavior of juvenile Chinook salmon and reductions in growth after short-term exposure to environmentally realistic concentrations of organophosphate and carbamate pesticides. Reductions in growth correlated with reduced size at ocean entry and with later survival. Mebane and Arthaud (2010) modeled the effects of sublethal effects of low concentrations of copper on growth of juvenile Chinook salmon and projected potential effects on population size, recovery rates, and extinction risks.
Many sublethal effects might have a link to population viability, but that link has not yet been quantified. An example is altered olfactory ability, which has been shown to increase predation risk in some species of salmon because of an inability to detect chemical cues that signal the presence of a predator or because of a loss of homing ability (Scholz et al. 2000). Whether altered olfactory ability affects survival will depend on the degree of its expression in the natural environment, the presence of predators during the time that olfaction is lost, and whether it occurs in fish whose size makes them susceptible to predation. Impaired immune function is another example in which an organism is affected, but the effect on population viability is unclear. A working immune system is critical for survival, but an alteration of some aspect of immune function and its effect on disease resistance are often less clear—for example, Does a given reduction in circulating leukocytes affect susceptibility to disease? Furthermore, the effect of an impaired immune system on disease susceptibility hinges partly on the presence of a pathogen. The committee notes that exposure to pesticides in some species might actually increase defense responses to predation. For example, Barry (1998) observed increased helmet formation—a defense response that deters predation efficiency—in daphnia exposed to low concentrations of endosulfan.
Uncertainties in concentration-response relationships or differences between laboratory and field responses, particularly behavioral responses, further complicate the quantification of changes in survival and reproductive success in response to sublethal toxicity. Assessment of sublethal effects, as well as cumulative and indirect effects, is even more complicated in species that have complex life cycles and population structures, such as Pacific salmon (see Box 4-1 for further discussion).
The committee concludes that survival and reproduction are the principal effects in determining population viability. The inability to quantify the relationship between sublethal effects and survival or reproductive success does not negate the potential importance of such effects for population persistence. However, the relationship remains a hypothesis that can be described only qualitatively with reference to the scientific literature for why such a hypothesis is tenable. Implications for risk characterization can be discussed qualitatively, not quantitatively, as an additional uncertainty beyond uncertainties that are propagated in a formal quantitative manner. The narrative can be considered by a decision-maker according to the applicable policy constraints regarding risk tolerance. However, such a separation of important risk components and uncertainty into quantitative and qualitative portions that cannot formally be combined makes it difficult to integrate and interpret the results of a risk assessment. Integration can be improved by quantifying better the relationships that are viewed as critical for understanding the risks posed by a pesticide to a listed species. One way to facilitate integration of the hypothetical relationship into the formal risk assessment is to conduct extensive reviews of comparative data or empirical case studies or to conduct targeted new studies that could help to derive defensible scientific quantification of the links between sublethal effects and survival or reproduction.
Indirect Effects
The Services have defined indirect effects as “those that are caused by the proposed action and are later in time, but still are reasonably certain to occur” (50 C.F.R. 402.02). Thus, their definition from a regulatory standpoint characterizes indirect effects as simply delayed effects. Depending on how one interprets that definition, it could be quite restrictive and different from most ecologists’ understanding of indirect effects, which typically include effects on prey, competitors, or predators of a listed species or on other aspects of the species’ ecological milieu but not direct effects on the species. On the basis of the documents reviewed by the committee, it appears that the restrictive definition is not used by the agencies; therefore, this section discusses indirect effects as including those normally understood by the term.
Pacific salmon and trout (Oncorhynchus spp.) are the basis of valuable commercial and recreational fisheries; part of the economy, ceremony, and subsistence of American Indians; components of complex ecosystems to which they contribute great quantities of nutrients; symbols of clean water and healthy rivers; and a host of other attributes related to human and natural systems (NRC 1996). Many factors have contributed to declines in salmon and trout, which are, in some cases, protected under the US Endangered Species Act (Gustafson et al. 2007). Protection of the listed distinct population segments (DPSs) has ramifications for a wide variety of human activities, including application of chemicals to control animals and plants that are considered crop pests and weeds.
There are five species of Pacific salmon in North America: Chinook, O. tshawytscha; coho, O. kisutch; sockeye, O. nerka; chum, O. keta; and pink, O. gorbuscha. There are also two trout species of the same genus: rainbow/steelhead trout, O. mykiss, and cutthroat trout, O. clarkii. Both trout species are quite variable phenotypically and have several subspecies (Behnke 1992). All Pacific salmon are spawned in freshwater, and most migrate to sea and return to freshwater at maturity to spawn (that is, they are anadromous); however, resident populations of sockeye salmon (kokanee) are well known and a few individuals of other salmon species (such as Chinook salmon) do not migrate to sea but mature to a small size in streams. All trout are spawned in freshwater, but may be exclusively nonanadromous or resident (that is, they spend their whole lives in freshwater), a mix of anadromous and resident, or virtually all anadromous. Each salmon and trout species is structured into discrete breeding populations because the adults return to their natal site to spawn (Quinn 2005). Therefore, the population, rather than the species, is the fundamental unit of conservation, and this is why DPSs of Pacific salmon and trout have been listed.
As a consequence of the complex population structure of Pacific salmon, some breeding populations can be highly endangered whereas other populations of the same species are abundant and able to sustain substantial exploitation from fisheries—for example, sockeye salmon in the Stanley Basin of Idaho vs those in Alaska’s Bristol Bay (Hilborn et al. 2003; Gustafson et al. 2007). Pacific salmon and trout populations also vary considerably in life-history patterns, including the timing of a series of key events: the return migration by adults from the ocean to freshwater, the spawning season, the emergence of juveniles from gravel nests, the duration of residence in freshwater, and migration to sea (Quinn 2005). Therefore, depending on the species and populations in question, fish might be present in one river at vulnerable times of their lives and absent from another river at the same time of that year, and these variations in life-history traits could affect how salmonids are exposed to pesticides. For example, some juvenile Chinook salmon migrate from their natal streams to the ocean in their first summer of life whereas
other juveniles of the same species spend a full year in the river system before migrating to sea (Taylor 1990; Healey 1991). The committee notes that the variation in spatial and temporal distribution of juvenile salmon residing in and migrating from river systems is further complicated by the substantial numbers of hatchery-produced juveniles, whose differences from wild fish in size, growth rate, and release timing can all affect migration patterns (Giorgi et al. 1997; Beckman et al. 1998).
Sublethal effects on sensory capacity, reaction, swimming ability, buoyancy control, or other aspects of performance might increase mortality. For example, chlorpyrifos, a common organophosphate insecticide, inhibited acetylcholinesterase in the brain and muscle of salmonids and affected spontaneous swimming and feeding behaviors of juvenile coho salmon in a concentration-dependent manner in the laboratory (Sandahl et al. 2005). Whether and to what degree sublethal effects affect survival in natural conditions is not clear. Laboratory exposure of cutthroat trout to carbaryl, an insecticide applied to oyster beds in some estuaries, affected swimming performance and predator avoidance (Labenia et al. 2007). It is certainly plausible (and perhaps even parsimonious) to conclude that there will be effects on survival in natural settings if environmental concentrations and exposure durations are comparable with those in the laboratory experiments, but the magnitude of the effects in relation to other sources of mortality is difficult to measure or model. Another complication in modeling the effects of pesticide exposure is that salmonids often prey on other salmonids (Duffy and Beauchamp 2008).
Moreover, if the population as a whole is stressed by factors that increase mortality over natural levels—such as water diversions that reduce flows, dams that alter sediment transport patterns, shoreline development in rivers or estuaries, or predation by nonnative species—the cumulative effects of the many stressors might be sufficient to put populations in jeopardy even though any single stressor, such as pesticide exposure, could have been sustained. Chemicals can also have indirect effects on individual organisms and the population. For example, most of the diet of juvenile salmon and trout in streams consists of insects, both larval stages of aquatic insects and terrestrial insects that fall on the stream surface (Nielsen 1992). Reductions in the prey base by pesticides might affect growth rate and life-history transitions that depend on growth (Mangel and Satterthwaite 1998) and have subtle but profound effects on fitness. Analogously, shifts in the insect community and changes in fish behavior associated with fine sediment in the stream bottom might reduce growth and survival of juvenile steelhead (Suttle et al. 2004).
Finally, the variation in life-history traits, between and even within species and subspecies, reinforces the importance of knowing the ecology of the particular species and population of concern for ecological risk assessment. It also highlights the difficulty of identifying a reliable surrogate species for testing and analysis, in particular a species whose life history is similar to that of the species of interest. For example, pink salmon generally migrate the short distance to the sea as soon as they emerge as free-swimming fry whereas juvenile Chinook salmon usually remain in freshwater for months to a year
and coho for more than a year. Pink salmon usually spawn within a few kilometers or tens of kilometers of the sea whereas Chinook salmon can migrate 1,500 km upstream or more to spawn, so their juveniles have to migrate the same distance to return to the sea. The different species also have different preferences for spawning substrate, stream sizes, and spawning seasons, all of which vary among their geographic distributions. Thus, the choice of a surrogate species for analysis and testing is challenging and complex at best. Even more challenging are the intraspecific variations in behavior, physiology, and distribution. For example, stream-type and ocean-type Chinook salmon differ in many attributes (Quinn 2005) that could affect exposure and vulnerability to pesticides. All the variation further emphasizes the need to assess the suitability of the surrogates and the applicability of the laboratory tests carefully when making decisions about likely effects of pesticides and other chemicals on listed species (Macneale et al. 2010).
Pesticides can indirectly affect a given species via effects on other species in the community. Indirect-effects analysis examines how a pesticide affects the habitat of a species. Because the indirect effects of pesticides on the species of concern can be favorable or unfavorable, it is more appropriately described as effects analysis than as hazard analysis. For example, the prey of the species of interest might be reduced in abundance or eliminated by the pesticide, perhaps because the prey is the target pest species or is affected along with the species of interest. Alternatively, populations of its predator or competitor might be reduced and the abundance of the species of interest thereby increased.
Because some indirect effects can be quantified, the committee recommends that they be incorporated into effects analysis. For example, for a situation in which food is the limiting factor and the major indirect effect is a 50% reduction in the food resource of the species of interest, the indirect effect can be incorporated into the population model by a 50% reduction in carrying capacity (maximum population size that can be supported by a specified area). In most cases, determining and quantifying such effects are more challenging and might require a conceptual model that incorporates the major components and linkages of the species’ habitat that would respond to pesticide applications (see section “Effects Models” below). The modeling would entail an understanding of the ecology of all the species that might be at risk from pesticide exposure that live in the same area as and use resources similar to those of the listed species. There might be multiple nodes and links between affected species and the species in question, which might result in a fairly complex community dynamics model.
There are many candidate models and associated computer software for simulating community and ecosystem interactions (see, for example, Verhoef and Morin 2010). The primary hurdle in their use in decision-making applications is the large number of parameters that are poorly known, which
results in substantial implicit uncertainty. Because of the uncertainty, it is important when using such modeling tools to strive to estimate component uncertainties quantitatively in a realistic and scientifically defensible way and to propagate all the component uncertainties through the community-level analysis formally and explicitly. Such methods as Bayesian networks and Monte Carlo approaches for quantifying uncertainty in analyses were discussed in Chapter 2. If quantitative information about community relationships is lacking, a qualitative modeling approach could be considered, such as signed digraphs, loop analysis, and matrix analysis (Puccia and Levins 1991). Those types of modeling can help to determine which variables should be included in a community or ecosystem model and can provide insight into which ones should be measured to provide the greatest reduction in uncertainty.
As in the different approaches used to evaluate sublethal effects, EPA and the Services appear to differ (on the basis of their responses to committee questions) in the extent to which they consider indirect effects. EPA (2012a, p. 22) stated that “if the best available biological information for a listed species does not establish a relationship between the affected taxa and the listed species, EPA believes that a no effect conclusion is warranted.” That approach is logical, but relationship is not defined. FWS (2012, p. 5) stated that EPA does not consider potentially important “tertiary” effects and that “community-level effects are not considered.” FWS (2012, p. 5) continued that EPA “only considers potential direct effects to those resources immediately relevant to the listed species.” Likewise, NMFS (2012, p. 4) stated that “aspects such as prey dynamics (e.g., how quickly prey availability returns to background levels) and trophic consequences of herbicide applications are not considered” by EPA.
EPA uses a chemocentric approach to the assessment and begins with what is known about a chemical and its potential to affect various attributes of species’ habitat. The Services take a species-centric approach and describe what is known about the life history of the species of concern, from which they infer the potential for pesticide-related effects. The different approaches seem to follow the same pattern as those used to evaluate sublethal effects, in which EPA takes a more quantitative approach and the Services a more qualitative approach. However, both quantitative information and qualitative information are necessary for comprehensive ecological assessments of the interactions of xenobiotic chemicals with the critical features of a species’ habitat. Development of a species-specific conceptual model during the problem-formulation phase of the ecological risk assessment includes a specific enumeration of the important habitat components, which can then be addressed quantitatively or qualitatively—depending on the available information—during the effects analysis. The FIFRA Endangered Species Task Force has already begun to gather information on habitat and niche requirements of endangered species into an electronic database accessible to EPA and the Services (FESTF 2012).
Cumulative Effects
In the context of the ESA, cumulative effects are defined as “those effects of future State or private activities, not involving Federal activities that are reasonably certain to occur within the action area of the Federal action subject to consultation” (50 CFR 402.02). As is the case with indirect effects, that definition is not the common definition used by many ecologists who tend to use the definition promulgated by the Council on Environmental Quality (CEQ) under the National Environmental Policy Act (40 CFR Parts 1500-1508, 1978) in which a cumulative effect is “the incremental [effect] of [an] action when added to other past, present, and reasonably foreseeable future actions.” In other words, cumulative effects are ones that “interact or accumulate over time and space, either through repetition or in combination with other effects” (NRC 2003, p. 2). However, the regulatory definition in 50 CFR 402.02 becomes much more like the CEQ definition if one incorporates the “environmental baseline,” which includes past and present conditions. The committee could not determine a scientific basis for excluding other federal actions from the consideration of cumulative effects. Present and past federal actions are included in the environmental baseline. Therefore, in the following discussion, the committee’s understanding of cumulative effects incorporates the environmental baseline. The committee notes that cumulative effects are related to aggregate effects—effects that result from exposure through multiple pathways. However, such effects would also be captured by considering or incorporating baseline conditions
Species live in variable environments and are constantly subjected to a variety of stressors. Some stressors, such as extreme weather, are stochastic (random and inherently unpredictable in magnitude and frequency) and might act on populations in a non-density-dependent fashion. In other words, the effects will be the same regardless of how many organisms are present. Other stressors, such as parasitism and predation, are more predictable and are density-dependent (they depend on the number of organisms present). Exposure to pesticides is one of many exogenous stressors that might influence the type and degree of response of species (Coors and De Meester 2008). Rohr et al. (2006) proposed using concepts in community ecology and evolutionary theory to provide insights about cumulative effects of pesticides and other anthropogenic or natural stressors. Their approach encompasses the use of direct and indirect effects of pesticide applications to assess the sensitivity of various communities and to identify which stressors will have the greatest effect.
The stressors that currently affect listed species are considered part of the environmental baseline conditions. Therefore, the interaction of existing stressors with the pesticides under consideration is within the purview of the Services and appropriately part of a BiOp. EPA, as the action agency, is responsible for providing the Services with any information that is known about how toxicity of a pesticide is modified by environmental factors (for example, effects of cold
stress on pesticide toxicity). The responses to multiple stressors that are likely to have an effect (or have an increased effect) in the future are the cumulative effects. The committee has concluded that population models (see section “Effects Models at the Population Level” below) provide an objective, quantitative, and practical framework for incorporating baseline conditions and projected future cumulative effects into the ecological risk assessment in a way that is relevant to the requirements of the ESA. For example, a population model can represent the direct effects estimated from concentration-response relationships as reductions from baseline in survival and reproductive success and also can include effects on survival and reproduction of current and future habitat loss (as decreasing carrying capacity), habitat fragmentation (as changes in the spatial structure of the model), and climate change (for example, as increases in temporal variability of survival and fecundity to simulate the effect of an increase in frequency of extreme weather events). Such an approach will necessarily be chemocentric because the pesticide is the additive stress, but the approach also takes into account species-environment interactions and includes the effects of stressors other than the pesticide on a species.
In some cases, the pesticide being assessed has been in use for a long time, and the baseline population model already includes pesticide-induced reductions in survival and fecundity. Therefore, the calculated reductions in survival and fecundity are added to the baseline model's survival and fecundity (thus increasing their values) to obtain a model that simulates the dynamics of a population that is not exposed to the pesticide. The difference between the projections of that model and of the baseline model is an estimate of the degree to which current use and past use of the pesticide are contributing to the risks faced by a listed species or preventing its recovery. Thus, the risk assessor uses the information (risks with and without the pesticide) to inform the reregistration decision. The procedure described here does not require any more data than the case in which the baseline data are coming from populations that are not exposed to a pesticide.
Effects models are used to characterize the effects of a pesticide at the individual level (effects on survival and reproduction) and at the population level (effects on population viability and recovery). EPA and NMFS use different models to evaluate the potential effects of a pesticide active ingredient on listed species and critical habitat. As described in its overview of ecological risk assessments for listed species (EPA 2004), EPA does not use effects models in its assessments. It assesses direct effects associated with different pesticide concentrations by using a risk-quotient (RQ) model that involves dividing an estimated exposure concentration by an effect concentration based on various prescribed toxicity tests and on published data. The derived RQ is compared with various levels of concern (LOCs) to determine whether a direct effect is likely. During
its Step 2 assessments, EPA might also use direct-effect LOCs to draw inferences about the potential for indirect effects on listed species that rely on nonendangered organisms as critical food or shelter resources. The indirect-effects analysis also serves as the basis for analyzing potential effects on designated critical habitat. Population effects are addressed simply as an extension of individual effects; if survival or reproduction is affected, EPA assumes population-level consequences and makes a “likely to adversely affect” determination, which requires formal consultation with the Services (Step 3, see Figure 2-1). See Chapter 5 for further discussion of the RQ approach.
NMFS uses population models as one of several lines of evidence to address the question of population persistence explicitly. The BiOp on the effect of three pesticides on salmonids (NMFS 2008) served as an example of the NMFS modeling approach for the committee. In that BiOp, NMFS assessed risk by examining the overlap in the estimated environmental concentration (EEC) and effect concentration ranges, using a literature survey of effects observed in the field, and using a weight-of-evidence analysis for multiple lines of evidence applicable to a number of risk hypotheses. NMFS also evaluated potential effects of pesticides on populations with two models: a life-history population model that estimated changes in a population’s rate of growth (lambda) on the basis of reduced individual survival after a 4-day exposure to acutely lethal concentrations and an individual-based growth and life-history population model that also estimated changes in lambda on the basis of reductions in growth of juveniles due to acetylcholinesterase inhibition and reduced prey abundances. That modeling was not done for a specific EEC but for a range of possible environmental concentrations that could be related to an EEC.
The committee was asked to consider the various approaches for evaluating pesticide effects, and it interpreted its specific task concerning models to be an assessment of modeling approaches at the individual and population levels, a clarification of the relationship between models at these two levels, and an evaluation of the major assumptions of the models. The following sections address those topics.
Effects Models at the Individual Level
All chemicals affect organisms through interactions at the cellular level—for example, binding to cell receptors and inducing or blocking normal responses, inhibiting or stimulating enzymes, causing cell death, or disrupting normal DNA replication. Some cellular changes result in measurable responses that might affect an organism’s ability to survive and reproduce. Because organisms have redundant systems to maintain homeostasis and various mechanisms to detoxify and eliminate chemicals, there are exposures below which no organismal (individual) effects occur. However, individual organisms differ in their ability to tolerate chemical exposure, and this results in variability around the effects threshold. Variability throughout the toxic range is illustrated by a standard con-
centration-response curve (also known as a dose-response or exposure-response curve), which is essentially a cumulative distribution function of the percentage of animals in a test population that exhibit a given response at each exposure concentration.
Superimposed on the interindividual (intraspecies) biological variability is variability from different sources, including interspecies variability, and uncertainty resulting from measurement imprecision and from extrapolation of experimental concentrations. Those types of uncertainty and approaches to incorporating them in individual-level models are discussed below in the section “Interspecies Extrapolations and Surrogate Species.” The combined effects of those types of uncertainty can be expressed as confidence intervals around values on the concentration-response curve.
To evaluate potential effects on a species correctly, direct effects of pesticides on survival and reproduction must be estimated, and these estimates must correspond to the conditions expected in nature. The range of concentrations needs to include all plausible values that might result from the fate and transport models (see Chapter 3) for the populations that are being assessed. Because the values vary in space and time, the predicted effects on survival and reproduction also vary. The temporal and spatial variability in direct effects must then be incorporated into the population model to estimate population-level effects. An important source of uncertainty in this process is the measurement of direct effects on individual survival and reproduction under laboratory conditions, where demographic rates might be higher than in the natural environment of the species. Thus, the results of laboratory experiments need to be scaled to values expected in nature. There are two aspects of that scaling. First, the effects measured in the laboratory must be used to estimate the toxicant’s effects in nature by taking into account the relative periods of exposure in the laboratory experiments (Pe) and in the wild (Pw). That step is not necessary if the two exposure periods are about the same. However, if there is a substantial difference, an adjustment might be necessary. For example, if the experimental mortality (Me) is measured over a 4-day period, but the exposure in the wild is estimated from exposure models to be, for example, 8 days, the overall mortality in the wild (Mw) might be higher than in the laboratory. How much higher depends on assumptions about how the pesticide affects individual organisms. An extreme assumption would be that all organisms that are highly responsive to the pesticide die in the first 4 days and that the mortality over 4-day and 8-day periods would be the same (Mw = Me). Another assumption could be that mortality in the wild is the same during each 4-day period. Thus, pesticide mortality in the wild would be calculated as Mw = 1 - (1 - Me)Pw/Pe. Second, the estimated toxicant mortality must be combined with the natural mortality. For example, if pesticide mortality and natural mortality are independent, the survival rate in the natural environment of the species can be calculated as (1 - Mw)(S), where S is the survival rate in nature without any pesticide effects. In some cases, the calculated mortality is expected to be in the baseline model because the pesticide has been in use and the model parameters are based on a population exposed to
the pesticide (see the section “Cumulative Effects” above). In that case, the survival rate in the model (S) already includes the calculated pesticide mortality (Mw). To obtain a model that simulates the dynamics of a population that is not exposed to the pesticide, the survival rate would be calculated as S/(1 - Mw), again assuming that pesticide mortality and natural mortality are independent. Although the examples in this section are given only for mortality effects, similar calculations also need to be done for the reproductive component of the effects data.
The committee notes that the effects end point is often summarized as a single point on the concentration-response curve, such as the concentration that kills 50% of the test population (LC50). However, for the purposes of population modeling as discussed below, the effects must be estimated at a range of concentrations that includes all values that the populations that are being assessed might plausibly experience. Therefore, the committee concludes that test results expressed only as threshold values or point estimates—for example, the no-observed-adverse-effect level, the lowest observed-adverse-effect level, or the LC50—provide insufficient information for a population-level risk assessment.
Effects Models at the Population Level
The results of the effects model (the changes in survival and reproductive success as a function of pesticide exposure) are used in population models to assess effects on listed species. Population models are used to estimate population-level end points—such as population growth rate, probability of population survival (population viability), and probability of population recovery—on the basis of individual-level effects. Because the ESA is concerned with species or listed units within named species, the effects of pesticides must be expressed at the population and species levels. Therefore, the committee concludes that population models are necessary to quantify the effects of pesticides on populations of listed species.
The need for effects analyses to be conducted at the population level has been emphasized for at least the last 2 decades (see, for example, Cairns and Pratt 1993; Baird et al.1996; Ferson et al. 1996; Munns et al. 1997; Forbes and Calow 1999) and has been covered in several recent books (see, for example, Pastorok et al. 2002; Akçakaya et al. 2008; Barnthouse et al. 2007; Stark 2012). The applications of population models for effects analyses are too many to list comprehensively; some examples are Munns et al. (1997), Kuhn et al. (2000), Topping et al. (2005), Duchet et al. (2010), Willson et al. (2012).
Other types of models that have been used to assess ecological risks posed by pesticides and other toxic chemicals include models of individual organisms, bioenergetics models, and community and ecosystem models. As noted, the focus on population models in this report is necessitated by the specific requirement of predicting effects on listed species (for example, the risk of extinction) under the ESA. Other modeling types are appropriate for estimating other types
of ecological effects; however, for calculating the probability of extinction or decline of a listed species, demographic population models are the most practical and relevant tools available.
Using a population model requires three inputs. Two of the inputs are the outputs of the exposure and effects models described previously. Effects models describe the change in population-model parameters (survival and reproduction) as a function of pesticide concentration, and exposure models provide estimates of pesticide concentration over time and space. The third input is demographic and life-history information, such as age at first reproduction, age-specific (or stage-specific) survival and fecundity rates over time and space in natural populations, and mechanisms and magnitude of density-dependent processes.
There is a large variety of population models, from deterministic, exponential models of a single population to stochastic, age-structured or stage-structured, spatially explicit metapopulation models with complex forms of density dependence (see introductions and reviews in Burgman et al. 1993; Akçakaya et al. 1999, 2008; Quinn and Deriso 1999; Caswell 2001; Morris and Doak 2002; Pastorok et al. 2002 for topics covered in the sections that follow). The appropriate models for purposes of pesticide-effects modeling are complex, species-specific models that incorporate all the relevant demographic parameters and spatial structure required to predict extinction risk. Some species, such as North American Pacific and Atlantic salmon, have been carefully studied and probably have sufficient data to assign values to parameters in such models. However, many listed species have been studied in only a cursory manner, and modelers have only enough information to characterize the life history of a group of species and are only able to use simple, generic, deterministic models that predict lambda, the finite rate of increase in the population. The committee concludes that in the absence of detailed demographic information, it is appropriate to use such models to characterize the baseline condition of a listed species, provided that the analyst incorporates estimates of uncertainty—for example, by using reasonable “high” and “low” demographic inputs—to bound the range of probable lambdas and includes a discussion in the final risk assessment about the magnitude of the uncertainty resulting from this lack of knowledge.
The sections that follow discuss important issues related to various components of population models that are especially relevant to assessing the risks posed by pesticide exposure.
Temporal Scale
The temporal scale of an assessment has two components: the time step of the model and the time horizon (duration) of the assessment. For most species in temperate ecosystems with generation times of 1 year or longer, an annual time step is appropriate. Except for the simplest models, whose main result consists of asymptotic measures of population performance (such as lambda), models that estimate population viability require specification of a time horizon. There
is a tradeoff between relatively short time horizons, which allow more reliable projections but might not be relevant for the conservation of the species (because the goal is long-term existence of the species), and relatively long time horizons, which are more relevant but result in more uncertain projections of population viability. Even if the effect at the individual level occurs for only a few years, population-level effects might be observed longer because of changes in the age structure of the population. To account for such transitory effects, an assessment can use a time horizon of several generations of the species or the period during which a pesticide is expected to affect the population, whichever is longer.
Spatial Scale
The spatial scale of an assessment has two components: resolution and extent. For most population models, the spatial resolution should coincide with the typical sizes of the areas (or ranges of sizes) occupied by populations or subpopulations of the species. That might require a translation of the results of the exposure model to reduce the spatial resolution to a level that is appropriate for the species. In other words, the results of exposure modeling at very fine resolution (for example, 30-m grid cells for a species with a 1-ha home range and populations occupying areas of several square kilometers) can be translated into effects at the population level by calculating an overall reduction in survival and reproduction in each population on the basis of the average EEC to which the population will be exposed. The average EEC would be estimated with errors by the exposure model, and the errors would be incorporated by using joint probability distributions (see Chapter 5).
Ideally, the spatial extent of the models would include all areas in which a modeled species is exposed to the pesticide being evaluated. Both the spatial distribution of the species and the distribution of pesticide in the landscape might be heterogeneous. As a result, different populations of the species might be exposed to different concentrations of the pesticide, and even individual organisms in a population might have different exposures. In some cases, spatial variability of exposure can lead to source-sink dynamics in a metapopulation (Palmqvist and Forbes 2008).1 That is, populations that are exposed to the pesticide might become sink populations2 and thus deplete the populations that are not exposed; conversely, exposed populations might remain extant despite exposure because of dispersal from the unexposed populations in the same metapopulation (Spromberg and Johnson 2008). Accordingly, if there is dispersal between populations, exposure of one population can cause a reduction in an-
______________________
1A metapopulation is a set of populations of the same species in the same general geographic area that might exchange individual organisms through dispersal.
2A sink population has more deaths than births and remains extant only because there are more immigrants than emigrants.
other, unexposed population. Depending on the spatial separation of the areas, separate assessments can be performed for each area or a single assessment can be performed with a metapopulation model that represents each area as one or more populations.
The spatial variability of exposure would be estimated on the basis of spatially explicit projections of the exposure models, and the spatial variability in the species distribution would be based on the projections of a species-distribution model (an ecological-niche model or habitat-suitability model) that might be based on geospatial data (see the section “Characterization and Delineation of Habitat” in Chapter 3). The committee concludes that in the absence of spatial data, it is appropriate to use generic, single-population models with no spatial structure that include average exposure and environmental conditions expected in the exposed area of the species’ range and to incorporate errors estimated with exposure modeling.
Temporal Variability
Variability (or stochasticity) refers to parameters of a population model that vary randomly, such as survival rates or fecundities in different age classes. Temporal variability means that models cannot predict the population size in the future precisely. Instead, they can project statistical distributions of future population sizes. The distributions are often used to calculate risks, such as risk of species extinction, risk of population extirpation, or risk of population decline to a predetermined level. Incorporating temporal variability results in a more realistic model that has more relevant end points, such as extinction risk. The committee concludes that population models that incorporate temporal variability and focus on probabilistic results are needed for assessing risks at the population level and that deterministic models are insufficient for this task. However, in the absence of such information, deterministic models with such end points as lambda (the finite rate of increase) can be used as the initial step of risk assessment. In such cases, every effort should be made to obtain the data necessary to estimate temporal variability, and the uncertainties in the end points reported should be clearly described in the assessment with the recognition that a deterministic baseline model might bias the assessment. Notwithstanding the use of a deterministic baseline model, uncertainties in the exposure analysis and the dose-response analysis should be incorporated into a risk assessment, for example, by using joint probability distributions (see Chapter 5).
Density Dependence
Density dependence (most commonly, the reduction in fecundity and survival that occurs as population size increases and that results from competition for food, breeding habitat, or other critical resources) is an important aspect of the dynamics of many populations and their responses to toxicants (Forbes et al.
2001, 2003). In the absence of data on effects of density on population growth and for screening-level assessments, it is reasonable to use density-independent models. Such models often use population growth rate as the main result, although if the models are stochastic, they can also be used to estimate population viability (the probability of population decline or extinction over a specified period). Although density-independent models make a number of assumptions and leave out important aspects of population dynamics, their results are more relevant for assessing pesticide effects on species than the results of models that assess pesticide effects only on individual organisms.
If there is evidence that survival or reproduction changes as a function of population density, it is important to incorporate density dependence into a model. That a species is rare or has been in decline does not necessarily mean that its dynamics are not density-dependent. For example, if the species has been declining because of habitat loss, its dynamics are probably density-dependent. In addition, species that have declined to very low abundances might be subject to depensation or inverse density dependence, which is the reduction in survival or fecundity that occurs at low density and accelerates the species’ decline and which is commonly referred to as Allee effects (Courchamp et al. 2008).
Incorporating density dependence into a model of a population whose vital rates (survival or fecundity) might be affected by pesticide exposure presents challenges (Moe 2007). For example, the pesticide exposure might reduce the growth rate of the population by the same amount regardless of population size. Those conditions would make the density-dependence functions of baseline and effects models (population models with and without pesticide exposure) have the same shape (Figure 4-1A). In other cases, the pesticide effects on the growth rate of the population might be stronger in large populations (Figure 4-1B) and result in more-than-additive (synergistic) effects, or the pesticide effects might be stronger in small populations (Figure 4-1C) and result in less-than-additive (antagonistic) effects (see, for example, Forbes et al. 2001; Moe 2007). Thus, pesticide exposure might reduce the carrying capacity (or equilibrium population size) directly (by reducing survival and fecundity at all densities) or indirectly (by, for example, reducing abundance of species on which the species of interest preys). Whether the effect will be additive, synergistic, or antagonistic depends on several factors, including which life-history stages are affected by toxicity and density dependence (Forbes et al. 2001). The committee concludes that it is not accurate to assume that mortality due to pesticide exposure will be compensated for by density dependence; it is likely that such exposure will decrease the growth rate of a population at all densities and generally depress the population growth-density curve as depicted in Figure 4-1.
Effects analysis requires knowledge or judgment of the adverse effects associated with individual chemicals or chemical combinations at concentrations
predicted to occur in the exposure environment. The toxicity of a chemical mixture probably will not be known, and it is not feasible to measure the toxicity of all pesticide formulations, tank mixtures, and environmental mixtures. Therefore, combined effects must be predicted on the basis of models that reflect known principles of the combined toxic action of chemicals (El-Masri et al. 1997). This section discusses the state of the science of mixture toxicity, raises practical issues associated with mixture assessments, and provides a case study of the application of information in the context of assessing risks to listed species posed by pesticides.
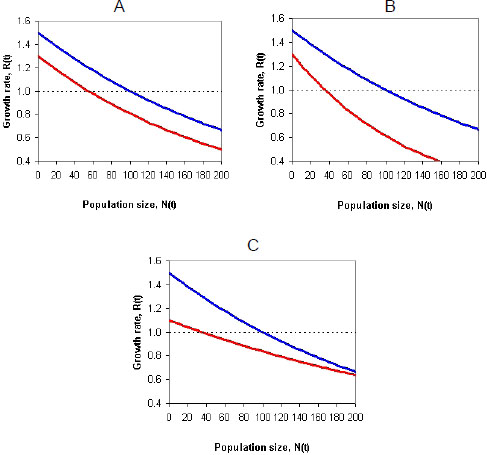
FIGURE 4-1 The effect of pesticide exposure on a density-dependence function. In all three graphs, the top curve shows the baseline model, and the bottom curve shows the effect model. Each curve shows the effect of density on population growth rate. Pesticide effects might decrease population growth equally at all densities (A), more at higher densities (B), or more at lower densities (C). Source: RAMAS 2011®. Reprinted with permission; copyright 2011, RAMAS®. RAMAS is a registered trademark of Applied Biomathematics. See also Forbes et al. (2001) and Moe (2007).
Additivity and Interactions
The term additivity is used to designate forms of joint action in which the response to a mixture can be modeled on the basis of the expected responses to the mixture components in the absence of any toxic interactions. Two forms of additivity—concentration addition and response addition—are generally considered.3 Concentration addition assumes that the components of the mixture act by the same mechanism4 and that the components differ from each other only in their potency. Response addition assumes that the response to the mixture can be predicted on the basis of the expected responses to the individual components of the mixture. Toxic interactions are cases in which the joint toxic action of mixture constituents cannot be adequately described on the basis of additivity alone. Interactions are generally classified as synergistic (greater than additive) or antagonistic (less than additive). The frequency with which pesticide mixtures are found in surface waters is often cited as rationale for exploring the toxicity of pesticide mixtures (Scholz et al. 2006; Belden et al. 2007a; Laetz et al. 2009).
Concentration Addition
The central mechanistic assumption of concentration addition is that chemicals act by the same mechanism and differ from each other only in relative potency, with potency defined as the ratio of equitoxic doses. If the concentration of Chemical 1 associated with a given response rate is twice that of Chemical 2, Chemical 1 has half the potency of Chemical 2. Thus, relative potency can be used to convert an effective concentration of one chemical to a toxicologically equivalent concentration of another chemical.
Implicit in the application of concentration addition is the assumption that the slopes of the concentration-response curves for all mixture components are identical. The assumption of equal slopes follows directly from the assumption of functionally identical mechanisms of action. The slope of the concentration-response function is essentially a measure of the variability of individual tolerances in a population. Under the assumption that all chemicals in a mixture have the same mechanism of action, it follows that the distribution of individual tolerances and hence the shapes of the concentration-response curves will be the
______________________
3Concentration addition is also referred to in the literature as dose addition, simple similar action, or similar joint action. Response addition is also referred to in the literature as independent joint action or dissimilar joint action (see, for example, Bliss 1939; Finney 1971; EPA 2000). For consistency and simplicity, only the terms concentration addition and response addition are used in this discussion; it is recognized that dose addition is preferable to concentration addition when exposures are expressed as doses.
4Mechanism is defined in this context as the molecular interaction between a pesticide active ingredient and a biological target (for example, an enzyme or ion channel) that is responsible for the response being measured.
same for each chemical; hence, the slopes of the concentration-response functions of all the chemicals will be identical.
In practice, the slopes of the concentration-response functions will seldom be identical even for chemicals that have the same mechanism of action. Similarly, because of random variability, repeated bioassays of the same chemical on the same species by the same investigators will seldom have identical slopes. In such cases, methods are available for testing the significance of the differences between slopes and for constraining slopes to be parallel (Finney 1971). If the slopes of the concentration-response curves are identical (or can be constrained to be so without a significant lack of fit), the selection of the reference chemical for defining relative potency is incidental. That is, changing the reference chemical will change the relative potency values but will have no effect on the estimate of the concentration-response curve for the mixture.
In some cases, chemicals with the same mechanism of action at the receptor level can differ from each other in other ways (for example, differences in metabolic pathways) that can lead to differences in slopes in whole-animal studies. If the slopes of chemicals that act (or presumably act) similarly do differ, relative potency will vary with the magnitude of the response, and the application of concentration addition will be inappropriate.
Concentration addition is attractive because it is mathematically simple and is often viewed as a conservative assumption. As discussed below, concentration addition will typically predict a response rate that is equal to or higher than any form of response addition; it is conservative in this sense. Some groups have recommended concentration-addition as a general default method for mixture risk assessment, particularly for screening-level assessments (IPCS 2009; Kortenkamp et al. 2012). The EPA guidance for mixture risk assessment, however, recommends that concentration addition be applied only to groups of similarly acting chemicals (EPA 2000, p. 11). The committee concludes that the utility of concentration addition as a predictive and unbiased model for assessing joint action depends heavily on the underlying assumptions of concentration addition—similar mechanisms of action and parallel slopes. If those conditions are met, relative potency will be constant for all concentrations, so relative potency can be used to convert the concentration of one chemical into an equivalent concentration of another chemical. That conversion can be used to add concentrations correctly. If the underlying assumptions of concentration addition are violated, however, there is no reason to expect its application to be predictive. Application of concentration addition in those cases might lead to substantial errors that underestimate or overestimate the actual risk. Therefore, although the concentration-addition model has been demonstrated to predict the toxicity of pesticide active-ingredient mixtures more accurately when the pesticide active ingredients have the same mechanism of action (Belden et al. 2007a), caution should be exercised in using concentration-addition modeling as a default approach.
Response Addition
Response addition is a form of noninteractive joint action in which the response to a mixture is estimated on the basis of the responses (rather than the concentrations) that would be expected from the components of the mixture. Response addition does not assume that the components of a mixture act by the same or even a similar mechanism and does not assume anything about the slopes of the concentration-response curves. The slopes of the concentration-response curves for chemicals that have different mechanisms of action might or might not differ significantly. The only requirement is that the chemicals produce the same effect. In most practical applications of response addition, the end point is mortality; however, response addition can be applied to any quantal response. Response addition can take various forms, depending on assumptions about the correlation of tolerances in the population.
A review of the literature on pesticide-mixture toxicity revealed that the response-addition model provided somewhat more accurate predictions of toxicity than the concentration-addition model when the pesticide active ingredients had different mechanisms of action (Belden et al. 2007b). Response addition also has been shown to provide more accurate estimates of toxicity of mixtures that consist of dissimilarly acting pesticide and nonpesticide chemicals (Walter et al. 2002; Backhaus et al. 2004).
Synergy
Arguably, the greatest concern in evaluating hazards and risks to listed species posed by chemical mixtures that contain pesticides is whether constituents of the mixtures act to enhance the toxicity of the pesticide active ingredient. Indeed, pesticide synergists are often included in pesticide formulations (Jones 1998) and can enhance the toxicity of an active ingredient to nontarget organisms by a factor of 100 (Sahay and Agarwal 1997). The activity of some pesticide active ingredients also is substantially enhanced when they are administered in combination with other pesticides. Finally, chemicals to which coexposure occurs might increase the toxicity of a pesticide active ingredient by increasing its bioavailability or potency in the environment of the exposed organism.
Pesticide Formulation Synergists
Pesticide formulation synergists typically function by inhibiting cytochrome P450-mediated inactivation of the active ingredient (Hodgson and Levi 2001). They can enhance the effects of some pyrethroids, organophosphates, carbamates, and rotenone. Formulation synergists include bucarpolate, dietholate, iprobenfos, jiajizengxiaolin, MGK 264, octachlorodipropyl ether, piperonyl butoxide (PBO), piperonyl cyclonene, piprotal, propyl isome, sesamex, sesamolin, sulfoxide, and zengxiaoan. PBO is among the most potent and widely
used formulation synergist (EPA 2005). Because formulation synergists are specifically used to increase the potency of pesticide active ingredients, they are most likely to produce the greatest enhancement of pesticide toxicity.
Toxicity evaluations that used the amphipod Hyalella azteca revealed that coexposure to PBO caused up to about a sevenfold increase in the toxicity of permethrin (Amweg et al. 2006). The synergistic potency of PBO increased as exposure concentration increased with a threshold concentration of 2.3 ìg/L in water. The threshold concentration for synergy to occur stands in contrast to PBO surface-water concentrations, which are typically less than 80 ng/L even after direct application to surface water for mosquito abatement (Orlando et al. 2003, 2004; LeBlanc et al. 2004; Amweg et al. 2006). Given that H. azteca is considered sensitive to pyrethroids (Werner et al. 2010), that PBO is considered the most potent of formulation synergists, and that PBO concentrations in surface water after application tend to be below concentrations necessary to elicit synergism, there is a low probability that synergists associated with pesticide formulations enhance the toxicity of pesticide active ingredients. The greatest probability of synergistic effects might be when synergist-containing pesticide formulations are applied directly to aquatic systems or when there is direct contact between the formulation and a species.
Synergistic Interactions among Active Ingredients
As discussed in Chapter 3, pesticide active ingredients have the potential to coexist in tank mixtures or as environmental mixtures. In some cases, the toxicity of pesticide active-ingredient combinations has been shown to be greater than additive. The synergy has been exploited in recommended tank formulations to treat pests. With respect to nontarget species, the synergy has been recognized as a potential source of enhanced ecological threat. The following are examples of known synergistic interactions between pesticide active ingredients.
Organophosphates and Carbamates. Organophosphates and carbamates share a mechanism of action: inhibition of the enzyme acetylcholinesterase. Accordingly, the joint toxicity of organophosphates and carbamates should conform to a concentration-addition model. Indeed, the in vitro inhibition of acetylcholinesterase activity in salmon brains by combinations of organophosphates and carbamates showed that to be the case (Scholz et al. 2006). However, in vivo exposure of salmon to binary combinations of organophosphates, carbamates, or a combination of organophosphate and carbamate resulted in greater inhibition of brain acetylcholinesterase activity than would be predicted by concentration addition (Laetz et al. 2009). Serine esterases are important in the metabolic detoxification of organophosphates and carbamates (Cashman et al. 1996). Studies have shown that those esterases can be selectively inhibited by binding of one substrate, which results in increased toxicity of another because of its reduced detoxification (Murphy et al. 1959; Clement 1984).
Pyrethroids and Organophosphates. Studies in rodents (Ortiz et al. 1995) and insects (Martin et al. 2003) have shown that combinations of pyrethroids and organophosphates can synergize to produce greater than additive toxicity. Pyrethroids also are metabolized by serine esterases (Cashman et al. 1996), and it is reasonable to assume that various combinations of pyrethroids, organophosphates, and carbamates would have the potential to elicit greater than additive toxicity through the inhibition of serine esterases and perhaps other detoxification enzymes (Bielza et al. 2007).
Ergosterol Biosynthesis-Inhibiting Fungicides and Pyrethroids. Ergosterol biosynthesis-inhibiting (EBI) fungicides are potent inhibitors of some cytochrome P450 enzymes, and this inhibition is responsible for their mode of toxicity to fungi (Thompson 1996). Some EBI fungicides are imidazoles (for example, prochloraz and clotrimazole), triazoles (for example, propiconazole and tebuconazole), and morpholines (for example, fenpropimorph and aldimorph). Coexposure to some EBI fungicides and pyrethroids has been shown to result in greater than additive toxicity, presumably because of the inhibition of P450-mediated detoxification of the pyrethroids. The synergistic effect of EBI fungicides has been detected in a wide array of terrestrial and aquatic organisms (Norgaard and Cedergreen 2010; Bjergager et al. 2012) and reviewed in Cedergreen et al. (2006).
Synergy at High Laboratory Concentrations
Demonstrations of synergistic toxicity under controlled laboratory conditions often are performed at high chemical concentrations that are toxic even in the absence of synergy (see, for example, Anderson and Zhu 2004; Laetz et al. 2009). However, such synergy is of little use in identifying and quantifying synergy at low, environmentally relevant concentrations.
Many of the toxic mechanisms by which interactions might occur are saturable processes (such as rates of absorption, metabolism, and excretion), and many are governed by Michaelis-Menten or similar kinetics. In such processes, there are probably interaction thresholds—concentrations below which interactions are not likely to occur or, if they occur, will be minimal and probably not detectable (Figure 4-2). Toxic interaction thresholds have been described in terrestrial mammals (Dobrev et al. 2001; Yang and Dennison 2007; El-Masri 2010) and in aquatic organisms (Mu and LeBlanc 2004; Rider and LeBlanc 2005). Although the assessment of interaction thresholds is evolving, the current view, informed by empirical data, is that they are in the range of toxicity thresholds of the individual components of the mixtures (Yang and Dennison 2007). Similar observations were made much earlier and before the formal discussion of interaction thresholds (see, for example, Feron et al. 1995). Interaction thresholds make sense in the context of the underlying kinetics and might be useful in assessing whether concerns about potential toxic interactions are important in exposures to specific mixtures.
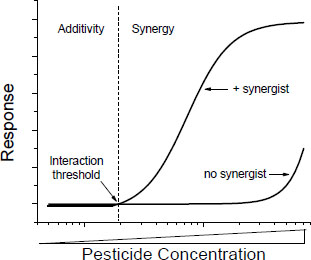
FIGURE 4-2 Concentration-response curve of a chemical in the presence and absence of a synergist. Toxicity of the chemicals is consistent with additivity below the interaction threshold and with synergy above the interaction threshold.
The existence of interaction thresholds does not necessarily reduce the probability of additive responses to mixtures of chemicals in which each chemical is below its own toxic threshold. In such cases, an additivity model might suggest the potential for a toxic response. The concept of interaction thresholds simply indicates that the probability of toxic interactions (as opposed to some form of additive joint action) is reduced if the total exposure does not exceed a threshold based on an assumption of additivity. A difficulty in the application of the concept of interaction thresholds is quantification of the threshold, which is difficult in the risk assessment of single chemicals and mixtures.
Uncertainty Factor to Account for Synergism
A specific charge to the committee was to “consider the selection and use of uncertainty factors to account for the lack of data on…synergy [and] additivity.” The committee concludes that there is no scientific basis for applying a generic uncertainty factor under the presumption of a synergistic interaction. Doing so would introduce a bias into the risk assessment.
As an alternative to generic uncertainty factors, EPA’s supplemental guidance for mixture risk assessment outlines a weight-of-evidence approach for incorporating quantitative consideration of interactions by using numerical binary weight-of-evidence scores that are based largely on qualitative information on potential interactions and any information on the magnitude of interactions of mixture components (EPA 2000, Section 4.3.1.1, pp. 90-103). That method was developed in the context of human-health risk assessment, and no examples of
its application to ecological risk assessment could be found. Furthermore, no studies or analyses that address the accuracy of the method in predicting responses to mixtures could be found.
Antagonism
Antagonism occurs when components of a mixture interact in a manner that results in toxicity that is less than would be predicted under an assumption of additivity. Antagonistic interactions that are most likely to affect pesticide toxicity occur when two components of a mixture are competing for the same target site of toxicity and the less toxic component competitively displaces the more toxic component or when a component of the mixture inhibits the metabolic conversion of a pesticide to a more toxic derivative. The former situation has been well described with binary combinations of pesticide active ingredients that share a mechanism of action. For example, exposure of the Asian catfish Mystus vittatus to the acetylcholinesterase inhibitors dichlorvos and thiotox or dichlorvos and carbofuran resulted in less toxicity than would be predicted on the basis of additivity (Verma et al. 1980). In both cases, exposure to the less toxic component at the maximum tolerated concentration reduced the toxicity of the more toxic constituent, presumably because of competitive displacement of the more toxic component from the target enzyme. Similar antagonistic effects have been observed with pairs of pyrethroid insecticides (Schleier and Peterson 2012).
Although PBO is typically used as a pesticide synergist by inhibiting cytochrome P450 activity, it and other cytochrome P450 inhibitors can decrease the toxicity of pesticides that are enzymatically converted to more toxic oxidative metabolites. For example, malathion and parathion are metabolically converted to their more toxic oxon derivatives by the actions of cytochrome P450s. Exposure of daphnids to either insecticide and PBO significantly reduced toxicity of the insecticides (Rider and LeBlanc 2005). Similar antagonism was observed with PBO and chlorpyrifos, which also is metabolically converted to the more toxic oxon derivative (Ankley and Collyard 1995; El-Merhibi et al. 2004).
The committee emphasizes that for a mixture component to antagonize (reduce) the toxicity of a pesticide active ingredient, the pesticide active ingredient must be present at a concentration that actually elicits toxicity. Given that circumstance, the committee concludes that ecological risk assessment should focus on the pesticide active ingredient alone and avoid the added uncertainties associated with estimating the reduction in risk due to the presence of an antagonist.
Complex Mixtures
Many environmental mixtures are highly complex, that is, contain a large number of components. That can complicate the exposure and effects analyses of the mixtures. As discussed at some length in EPA’s supplemental guidance
on mixture risk assessment (EPA 2000), confidence in the application of component-based methods diminishes as the number of components of a mixture increases. For some highly complex mixtures, such as petroleum distillates and surfactants, component-based methods might be impossible because the components are not well characterized and toxicity data on them are lacking.
For complex mixtures, the preferred assessment method is to use data on the whole mixture, termed the mixture of concern. The toxicity of the mixture is assessed with a bioassay. A problem with the mixture-of-concern approach, however, is that the composition of many complex mixtures is variable. Often, toxicity data are not available on the mixture of concern but are available on similar mixtures. Addressing those types of situations involves an assessment of sufficient similarity, that is, determining which, if any, of the mixtures on which data are available can be used to assess the toxicity of the mixture of concern reliably. EPA (2000, p. 38) offers only brief and general guidance on assessing sufficient similarity:
In determining whether a mixture is sufficiently similar, consideration should be given to any available information on the components that differ or are contained in markedly different proportions from the mixture of concern. In addition, if information exists on differences in environmental fate, uptake and pharmacokinetics, bioavailability, or toxicological effects for either of these mixtures or their components, it should be considered in deciding on a risk assessment approach.
EPA (2000) also notes that the comparative-potency method might be useful in assessing toxicity of complex mixtures. Essentially, that method involves using toxicity data on complex mixtures for which two toxicity end points—for example, an LC50 and a reproductive no-observed-effect concentration (NOEC)—are known to estimate a toxicity value (say, a reproductive NOEC) for a mixture for which only the other end point (an LC50) is known.
Simply because a mixture is complex does not indicate that the joint action of the mixture is complex. It is highly relevant to examine the frequency at which environmentally relevant chemical mixtures elicit cumulative toxicity. Olmstead and LeBlanc (2005a) evaluated the toxicity of a mixture of nine chemicals, including pesticides, at the median concentration in US surface waters as measured by Kolpin et al. (2002) and dilutions and fortifications thereof. The mixture elicited concentration-dependent toxicity at exposure concentrations between the median and 10 times the median concentrations of the chemicals, and the investigators were able to predict the toxicity of the mixture accurately with a model that combined concentration addition and response addition. However, further analyses revealed that the toxicity of the mixture could be explained largely by a single constituent, chlorpyrifos. The experiment was repeated without chlorpyrifos in the mixture. Toxicity was not eliminated by the removal of chlorpyrifos; rather, the remaining chemical mixture elicited toxicity at a higher concentration. Again, analyses of the responses to the individual
chemicals in the mixtures revealed that toxicity of the new chemical mixture was due to the actions of a single constituent in the mixture, diazinon. Thus, the chemical mixtures, at environmentally relevant constituent ratios, produced toxicity, but toxicity could be attributed primarily to a single constituent.
Adam et al. (2009) evaluated the aggregate toxicity to the amphipod Gammarus pulex of four pesticides—propiconazole, tebuconazole, 3-iodo-2-propinyl butyl carbamate, and cypermethrin—at concentration ratios typically found in commercial formulations. Toxicity of the mixture could be explained by the concentration of cypermethrin. Studies of environmental samples that contain chemical mixtures have typically shown that toxicity of the mixture can be attributed to one or a few constituents (Amweg et al. 2006; Belden et al. 2007a).
Although mixtures of pesticides and other chemicals clearly exist in the environment, the presence of a mixture does not necessarily imply toxicity. Furthermore, on the basis of mixture modeling theory discussed above, the presence of dissimilarly acting chemicals, each present at a concentration that elicits no toxicity, would not be predicted to elicit toxicity in a mixture in the absence of synergy. The presence of chemicals that have the same mechanism of action, each at a concentration that elicits no toxicity, would be predicted to elicit toxicity only if the combined, potency-normalized concentrations of the chemicals exceed the threshold concentration for a response.
Practical Issues in Assessing Effects of Pesticide Mixtures
Assessment of the effects of pesticide mixtures is associated with many practical aspects. This section first describes the positions taken and approaches used by EPA and the Services, then discusses various issues associated with pesticide formulations, and finally provides a perspective on the magnitude of interactions.
Agency Positions and Approaches
Approaches to addressing risks associated with exposures to mixtures are clearly a major source of disagreement between EPA and the Services, although the discord is not based on any fundamental disagreement about methods. The BiOps prepared by NMFS (2008, 2009, 2010, 2011) suggest that general guidelines used by EPA have been adopted by NMFS inasmuch as they reference EPA methods for ecological risk assessment (EPA 1998a, 2004). In specific and quantitative considerations of mixture exposures (for example, NMFS 2010, p. 465ff), the Services adopt concentration addition for mixtures of similarly acting pesticides, and this approach is consistent with the methods recommended by EPA (EPA 1986, 1989, 1998a, 2000, 2002).
Although EPA and the Services appear to accept the same basic methods in mixture risk assessment, their implementations of the methods differ substan-
tially. Each BiOp developed by NMFS expresses substantial concern for mixture exposures and the potential for synergistic effects. As discussed further below, similar concerns are also expressed by FWS. Although EPA guidelines (EPA 1998a, 2004) certainly recognize and appreciate the potential importance of exposure to mixtures, ecological risk assessments prepared by EPA focus on single active ingredients in the generic risk assessments (EPA 2004). The Services, in contrast, note a need to address exposures to all active ingredients and inerts that might affect populations of species (for example, FWS 2009).
Although diametrically opposed, the positions of the Services and EPA both have merit. EPA may elect to look at only single agents in most of its risk assessments, but agency-wide guidelines for mixture risk assessment, particularly EPA’s Supplementary Guidance for Conducting Health Risk Assessment of Chemical Mixtures (EPA 2000), provide quantitative approaches for incorporating any available information on potential chemical interactions into a risk assessment. The approaches, however, are extremely labor-intensive, are accompanied by substantial uncertainties that are not readily quantified, and are best suited to site-specific analyses in which exposures to specific chemicals can be estimated with confidence. Thus, EPA takes the position that practical and unavoidable limitations in resources and data preclude a detailed quantitative assessment of chemical interactions, and the Services take the position that a quantitative assessment of interactions should be done. The committee concludes that quantitative assessment of chemical joint action is warranted if adequate data are available on the exposures to and toxicities of the chemicals. Approaches for such analyses are detailed further in the final section of this chapter, “Conclusions and Recommendations.”
Formulation Toxicity
Several practical issues arise in the determination and use of data on pesticide formulations. There is the issue of availability of toxicity data on the inerts and the formulations themselves. There are also issues of the applicability of formulation data, particularly in considering long-term or chronic effects, and the applicability of formulation data that are extrapolated from other formulations. Those issues and others are discussed below.
Toxicity Data on Inerts
As discussed by Levine (1996), the original testing requirements for inerts in pesticide formulations were developed by the Food and Drug Administration, and these requirements were less rigorous than the testing requirements for the pesticides (that is, the active ingredients). In 2006, the EPA Inert Ingredient Assessment Branch completed a series of inert-ingredient tolerance-reassessment decision documents; however, documents covering all approved inerts do not appear to be available (EPA 2012b). One explanation is that tolerances are de-
veloped only for chemicals that are approved for use on food crops. List 1 inerts (toxic inerts) cannot be used on food crops and therefore do not have tolerance-reassessment documents. EPA has prepared guidance documents for companies involved in the development of new food-use inerts (EPA 20120c), new nonfood-use inerts (EPA 2012d), and low-risk polymer inerts (EPA 2012e); additional guidance is provided in EPA’s Pesticide Registration Manual (EPA 2012f). Although the documents do not contain an explicit list of required tests, they suggest that EPA could require the same types of tests as are required for active ingredients. With the exception of the guidance document on low-risk polymers, all the inerts guidance documents refer to the Office of Prevention, Pesticides, and Toxic Substances Harmonized Test Guidelines, which are used in the registration of pesticide active ingredients (EPA 2013). The committee found neither a specific list nor examples of the tests required for a new inert under EPA’s guidance documents for developing new pesticide inerts.
Related to the availability of toxicity data and testing requirements for pesticide inerts is the determination of whether additional data are needed on them. EPA noted that it will often rely on acute toxicity studies of formulations in mammals to determine whether acute toxicity studies of formulations should be required in fish and invertebrate species (E. Odenkirchen, EPA, personal commun., April 4, 2012). Specifically, the agency referred to a series of standard studies often referred to collectively as the mammalian six-pack: acute oral toxicity (EPA 1998b), acute dermal toxicity (EPA 1996), acute inhalation toxicity (EPA 1998c), acute eye irritation (EPA 1998d), acute dermal irritation (EPA 1998e), and skin sensitization (EPA 2003). The extent to which those acute studies in mammals will be reliable in assessing the potential of inerts to enhance toxicity of pesticide active ingredients to fish and aquatic invertebrates is not clear. The committee identified no explicit analyses that support the use of mammalian six-pack studies of active ingredients and formulations to assess the potential of inerts to enhance toxicity to fish and aquatic invertebrates.
Toxicity Data on Formulations
Pesticide formulations are not tested as extensively as active ingredients. However, if data are available on both an active ingredient and a formulation, the contribution of inerts to the toxicity of the formulation can be at least crudely assessed. All pesticide formulations must identify the percentages of their active ingredients. If πa.i. is the proportion of an active ingredient in a formulation and ζF is the toxicity value for the formulation, such as the LC50, the toxicity value of the active ingredient (ζa.i.) is the product of those two terms. ζa.i. can then be compared with experimentally determined toxicity values of the active ingredient alone. If, for example, the LC50 of the active ingredient as part of the formulation is substantially lower than the LC50 of the active ingredient alone, it suggests that some components of the formulation might be contributing substantially to the toxicity of the formulation. Conversely, if the LC50 of the
active ingredient as part of the formulation is substantially higher than the measured LC50 of the active ingredient alone, it suggests that some components of the formulation might be reducing the toxicity of the active ingredient. That type of comparison often yields the only type of quantitative information that can be used to assess the toxicological importance of inerts in a formulated product.
Chronic toxicity studies are not generally conducted on pesticide formulations and are not available on most inerts. In cases in which a chronic toxicity value is available for an active ingredient (Cha.i.) and acute toxicity values are available for the active ingredient alone (Aca.i.) and the active ingredient as part of the formulation (AcForm), a chronic toxicity value for the formulation (ChForm) could be estimated by using the following formula:
![]()
where all toxicity values are expressed in units of active ingredient.
The above approach raises important issues. A major assumption is that acute toxic potency and chronic toxic potency will be the same or at least closely related. Acute toxicity end points, such as mortality, will often bear little relationship to chronic end points, such as growth and reproductive capacity, and there will be little or no basis for assuming that the underlying mechanisms of action in producing acute and chronic effects are comparable. The approach becomes more palatable when the same mechanism-based end point is used for acute and chronic toxicity evaluations. For example, cholinesterase inhibition might be considered for assessing responses to acute and chronic exposures to an organophosphate or carbamate insecticide. Again, the major impediment to the use of the approach is the general lack of mechanism-based data on effects after chronic exposure.
Environmental Partitioning and Applicability of Formulation Studies
A major reservation in the use of formulation studies concerns environmental transport. Unless an active ingredient and inerts in a formulation have similar chemical-fate and environmental-fate properties—this is seldom the case—the active ingredient and the other components of the formulation will partition at different rates in various environmental compartments (see Chapter 3). If the partitioning is substantial, as is often the case, there is little rationale for asserting that differences in acute toxic potency will have any relationship to differences in effects of chronic exposures, a relationship that is assumed in the approach described above.
Considerations of environmental partitioning also affect the usefulness of chronic studies of formulated products. Although longer-term studies can be conducted on pesticide formulations, such studies typically involve designs in
which partitioning processes do not occur. The studies can provide useful information on the long-term effects of a formulation as it is applied, but these exposures probably have little relevance to exposures that occur in the environment as environmental partitioning occurs.
In some cases—for example, the Roundup formulations of glyphosate (EPA 2008)—detailed information is available on the toxicity of an active ingredient, the toxicity of specific inerts, and the toxicity of a formulation. In such cases, more detailed assessments can be conducted on the basis of analyses of toxic interactions or available data on the mixture of concern.
Data-Bridging
Another problem that arises in using formulation studies to assess the toxicity of inerts in pesticide formulations concerns “data-bridging.” Although EPA generally requires at least acute toxicity data on pesticide formulations, it will often allow toxicity studies on one formulation to support the registration of another. That general approach is sometimes referred to as bridging registration (EPA 2012f). Data-bridging is used in the United States (EPA 2002, 2012f) and member nations of the Organisation for Economic Co-operation and Development (OECD 2001). Although data-bridging is motivated by economic factors (reducing the costs associated with pesticide registration) and ethical factors (reducing the number of animals that must be used in toxicity studies), the process of data-bridging must be supported by similarities between the two formulations to be scientifically credible.
The committee concurs that data-bridging is sensible if two formulations are identical (the same formulation marketed under different names). If two formulations are substantially different, however, formulation-specific data are required. Recently, EPA (2012g) released relatively detailed guidance for waiving mammalian acute toxicity studies. Although the document is titled Guidance for Waiving or Bridging of Mammalian Acute Toxicity Tests for Pesticides and Pesticide Products, the main focus concerns the criteria for waiving acute toxicity studies rather than for bridging data among formulations. The OECD guidelines (OECD 2001, p. 89ff) articulate bridging principles that are generally consistent with EPA’s approach to assessing sufficient similarity. However, formulation-bridging is not transparent. In the absence of information, uncertainty can lead to assumptions that are not justified.
Foreign Formulations
Information is sometimes available on the toxicity of pesticide formulations used outside the United States. If comparable information is available on the US and foreign formulations, the information on the US formulation should take precedence because it will be the most applicable. If information is not available on the US formulation, the relevance and utility of the information on
the foreign formulation will be difficult to assess. For example, EPA’s ecological risk assessment of glyphosate (EPA 2008) concludes that the probability that glyphosate will affect reproduction of mammals and birds is minimal, and similar conclusions have been drawn in several other risk assessments of glyphosate (WHO 1994; Giesy et al. 2000; Williams et al. 2000). One study in the South American literature, however, indicates that exposure to a South American formulation of Roundup, which contains glyphosate and proprietary surfactants, reduces testosterone concentrations in rats (Dallegrave et al. 2007). Similar reductions were observed in mallards after exposure to a South American formulation of Roundup (Oliveira et al. 2007). As part of the public comments on the registration review of glyphosate, it has been suggested that EPA use the data on the South American formulations to assess the risks to birds and mammals associated with exposures to US formulations (BeyondPesticides 2009); that is, the information on the foreign formulations should essentially be bridged to US formulations. Although pesticide manufacturers are required to disclose information on the composition of pesticide formulations registered in the United States to EPA, the requirement does not extend to pesticide formulations used only outside the United States. Therefore, EPA and the Services probably do not have access to information that would be useful in assessing the similarities or dissimilarities between US and foreign formulations. In the absence of that information, the merits of including data from studies of foreign formulations cannot be determined.
Magnitude of Interactions
EPA seldom addresses interactions quantitatively in ecological risk assessments of pesticides. In three BiOps, NMFS (2008, 2009, 2010) does address information on joint action and relies primarily on the publication by Laetz et al. (2009), which assayed acetylcholinesterase inhibition in Pacific salmon (Oncorhynchus kisutch) for all binary combinations of three organophosphates (diazinon, malathion, and chlorpyrifos) and two carbamates (carbaryl and carbofuran). The study by Laetz et al. (2009) notes interactions that range from additivity to synergism with an increasing prevalence of synergism as the exposures increased. The latter observation is consistent with the concept of interaction thresholds described above. The BiOps, however, do not attempt to use the information from Laetz et al. (2009) to adjust estimates of expected biological responses to mixtures quantitatively. NMFS (2009, p.266) noted that “we are unable to create a predictive model of synergistic toxicity as dose response relationships with multiple ratios of pesticides are not available and the mechanism remains to be determined.” Other BiOps contain similar language and express concerns about mixtures.
EPA’s agency-wide supplementary guidance for mixture risk assessment (EPA 2000) discusses methods for quantitatively addressing toxic interactions, but the methods are cumbersome to apply, and experiments that would be useful
in assessing the predictive value of the methods seem not to have been conducted. The guidance document, however, reviews studies of the acute toxicity of all possible binary combinations of more than 50 industrial chemicals in rats (Smyth et al. 1969) and notes that deviations from the assumption of additivity span a factor of about 5 (expected to observed ratios of LD50 values of binary mixtures range from about 0.2 to 5). More recently, Boobis et al. (2011) searched publications on mammalian toxicology from 1990 to 2008 for studies reporting synergy at low sublethal doses. They discerned a maximum magnitude of synergy of about 3.5. The studies suggest that chemical interactions can modify toxicity, typically by less than a factor of 10. Exceptions do exist. PBO was shown to decrease the toxicity of malathion to daphnids (Daphnia magna) by as much as a factor of 100 (Rider and LeBlanc 2005), and the pesticide synergist N-octyl bicycloheptene dicarboximide increased the toxicity of deltamethrin to a snail (Lymnaea acuminate) by as much as a factor of 300 (Sahay and Agarwal 1997).
A Case Study: Assessing Pesticide-Containing Mixtures
Conventional approaches to assessing the risks posed by exposure to chemical mixtures first determine EECs of the mixture components and then estimate the hazard associated with those exposures. The approach is most appropriate for estimating whether the margin of safety for exposed listed species is sufficient. Table 4-1 provides a hypothetical dataset to exemplify how hazard from exposure to a pesticide in combination with other chemicals in the environment could be assessed by using established approaches discussed in this report. The listed species of concern in this exercise is sockeye salmon (Oncorhynchus nerka), and the pesticide of concern is cypermethrin, a pyrethroid. The cypermethrin is in a formulation that also contains the synergist PBO. The formulation will be added to a tank mixture that contains another pyrethroid insecticide, deltamethrin; a surfactant, Polysorbate-20; and a stabilizer, Epoxisoy. Contents of the tank mixture will be used for insect-pest control according to label specifications. And, several chemicals—nonylphenol, ethinyl estradiol, caffeine, acetaminophen, PBO, and cypermethrin—are known or predicted to be present in the exposure environment at measurable concentrations. Thus, the salmon might be exposed simultaneously to nine chemicals that originate from various sources. At issue is whether exposure to the chemical mixture poses a risk to the salmon.
Columns 2, 3, and 4 in Table 4-1 depict the sources of the chemicals and their concentrations in the different sources. Exposure of salmon to the mixture constituents can be estimated from those data. For example, cypermethrin is present in the formulation at a concentration of 0.05%. Once in the tank mixture, cypermethrin is diluted to a concentration of 250 mg/L (ppm), and the predicted concentration in the environment is 0.01 ìg/L (ppb). The concentration of cypermethrin in the formulation can be derived from the label, the concentration in
the tank mixture is calculated on the basis of the dilution to which the formulation is subjected, and the environmental concentration would be determined from modeling using, for example, PRZM2/EXAMS II.
Column 5 of Table 4-1 presents the final environmental exposure chemical concentrations, which are the sums of the concentrations of the individual chemicals in Column 4 (environmental exposure concentration). Most of the values are the same as presented in the previous column unless the chemical appears twice. For example, cypermethrin was present in the formulation to be applied with a residual amount (0.005 ppb) already present in the environment; thus, the final concentration of cypermethrin in the exposure environment is the sum of the two concentrations. The exposure analysis concerning the mixture of chemicals present in the environment is arguably the most challenging aspect of the mixture risk assessment owing to the high degree of uncertainty about the identity of chemicals and their environmental concentrations. Column 6 of Table 4-1 identifies chemicals expected to elicit toxicity by the same mechanism of action: chemicals that act similarly are assigned the same letter. Thus, cypermethrin and deltamethrin are both expected to elicit toxicity through the disruption of axonal sodium channels and are both assigned the letter a. Nonylphenol and polysorbate 20 have the ability to mobilize the pesticide and are identified with the letter b. Nonylphenol and ethinyl estradiol elicit estrogenic activity and are therefore identified with the letter c.
It is necessary at this stage to identify the adverse response of the listed species that is deemed most relevant to the pesticide of concern. In this exercise, disruption of axonal sodium channels is assumed to be the mechanism of action, and immobilization and loss of equilibrium are identified as the relevant responses because these sublethal responses are considered indicative of impending lethality or reproductive impairment. The other eight chemicals are considered only in their potential capacity to modify that response to cypermethrin. Thus, reproductive impairment associated with the combined estrogenicity of nonylphenol and ethinyl estradiol would not be considered relevant to the assessment of cypermethrin and would not be integrated into the toxicity assessment. If one or more components of the environmental mixture were predicted to elicit toxicity independently of cypermethrin, risk assessments of those components might be warranted.
Column 7 (K values) of Table 4-1 identifies chemicals that have the potential to enhance the toxicity of cypermethrin and the similarly acting chemical deltamethrin in a nonadditive manner. That would include synergists, PBO in this exercise. The modifying effect of the synergist PBO on the response to cypermethrin and deltamethrin is defined by a coefficient of interaction (K) (Mu and LeBlanc 2004; Rider and LeBlanc 2005; TenBrook et al. 2010), which can be viewed as a special case of the coefficient of synergism (ê) as described by Finney (1942). K values are typically determined experimentally by assessing the effect of increasing concentrations of a synergist on a specific response to a pesticide—such as an estimate of the effective concentration at which 50% of
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| Chemical | Formulation (%) | Tank (ppm) | Environment (ppb) | Final Exposure Concentration (ppb) | Similar-Actinga | K Values | EC50 (ppb) | Slope |
| Formulationb | ||||||||
| Cypermethrin | 0.05 | 250 | 0.01 | 0.015 | a | 5.0 | 14 | |
| PBO | 1.0 | 5,000 | 0.2 | 0.205 | Cyper: 1.0c Delta: 1.0c | 10,000 | 5.0 | |
| Tank | ||||||||
| Deltamethrin | 100 | 0.004 | 0.004 | a | 3.1 | 15 | ||
| Polysorbate 20 | 10,000 | 0.40 | 0.40 | b | 25,000 | 2.3 | ||
| Epoxisoy | 5,000 | 0.20 | 0.20 | 75,000 | 3.3 | |||
| Environment | ||||||||
| Nonylphenol | 0.001 | 0.001 | b,c | 1,500 | 5.7 | |||
| Ethinyl estradiol | 0.05 | 0.05 | c | 1,400 | 6.1 | |||
| Caffeine | 500 | 500 | 33,000 | 3.9 | ||||
| Acetaminophen | 0.01 | 0.01 | 100 | 6.3 | ||||
| PBO | 0.005 | |||||||
| Cypermethrin | 0.005 | |||||||
aChemicals that act similarly are assigned the same letter.
bFormulations can be evaluated for the potential contribution of inerts as described in the section “Formulation Toxicity.”
cK values of 1.0 were assigned to the synergist PBO because the environmental exposure concentration of PBO in this exercise was considered to be below the interaction threshold.
the population exhibits a defined response (an EC50)—in a surrogate species (Figure 4-3). Thus a K value of 2.0 would indicate that the corresponding concentration of synergist in the exposure environment would be expected to increase the toxicity of a pesticide by a factor of two (Figure 4-3). Alternatively, K values can be estimated on the basis of the available literature on the modifying effect of a synergist on the toxicity of a pesticide. K values also can be derived for factors that affect the environmental availability of a chemical (for example, enhanced mobility or dissolution because of a surfactant). However, those modifying effects would be more appropriately addressed when modeling environmental exposures.
Columns 8 (EC50) and 9 (Slope) of Table 4-1 define the toxicity of each chemical with respect to the response of concern (immobilization or loss of equilibrium in this exercise). The concentration-response curve is used to define the EC50 and the slope (or power) of the relationship. Those values are required for later mixture modeling. Typically, the data are determined experimentally by using a surrogate species after an appropriate exposure duration. EC50 data are often available from the literature, and EC50 and slope values are required for FIFRA guideline studies.
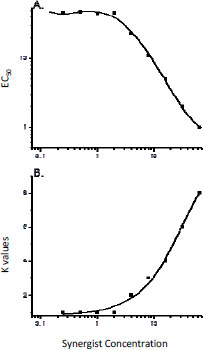
FIGURE 4-3 Example derivations used to determine K values. (A) Measured effect of the synergist on the EC50 of the chemical of interest. (B) K values at various concentrations of the synergist, calculated as the ratio of the EC50 of the targeted chemical in the absence of the synergist to the EC50 in the presence of a defined concentration of the synergist.
The response of the salmon to the toxicity of cypermethrin and the chemical mixture at the exposure site can be calculated from the data. First, the response to cypermethrin and deltamethrin at the exposure site is calculated with a concentration-addition model. Several concentration-addition model formats have been developed (Niederlehner et al. 1998; Safe 1998; Altenburger et al. 2000; Cleuvers 2003; Olmstead and LeBlanc 2005b) that are derivations of the original model presented by Finney (1942). Next, the responses (immobilization and loss of equilibrium) to each chemical, or groups of similarly acting chemicals, in the mixture are calculated with a response-addition model. The model originally described by Bliss (1939) remains the model of choice for calculating the joint action of dissimilarly acting chemicals (Backhaus et al. 2000; Walter et al. 2002; Olmstead and LeBlanc 2005b). Individual responses are then multiplied by appropriate K values to account for synergistic interactions. In this exercise, the K values of PBO are both 1.0; this indicates that the PBO concentration in the environment is not expected to modify the toxicity of cypermethrin or deltamethrin. Finally, the adjusted individual responses are summed to provide an estimate of the predicted response to the chemical mixture.
Data requirements and logistical considerations often temper efforts to assess the toxicity of chemical mixtures. Decisions on which chemicals in a mixture have the highest probability of toxic interaction with the pesticide active ingredient must be made and used to focus the assessment. Guidance for that decision-making is summarized in the section “Conclusions and Recommendations” of this chapter. Ultimately, some judgment must be made as to whether the possible adverse consequences associated with ignoring mixture effects outweigh the uncertainty associated with using nonempirical approaches to fill data gaps and to estimate the effects of mixture constituents on pesticide toxicity.
INTERSPECIES EXTRAPOLATIONS AND SURROGATE SPECIES
Different species often respond differently to chemical exposures because of differences in, for example, metabolic rates and pathways, the presence of functional genes, and different enzyme systems. Those differences can result in large differences in sensitivity; for example, adult guinea pigs (Cavia porcellus) are up to 5,000 times more sensitive to dioxins than are hamsters (Mesocricetus auratus) (Kociba and Schwetz 1982). Therefore, there is concern about how to extrapolate toxicity information from tested species to species of concern. Although the idea of finding a scientifically credible surrogate species might be appealing, the committee finds this approach difficult for two reasons.
First, it is not always straightforward to select a scientifically credible surrogate for a listed species. For example, rainbow trout are often used as surrogates for endangered Pacific salmon species because they are in the same genus, but they might respond differently to chemicals and other environmental stressors (Buhl and Hamilton 1991; EPA 2007). Moreover, there are seasonal differences in timing of breeding and larval development among species—generally,
trout in the spring and salmon in the fall (Quinn 2005)—and differences among species in sensitivity during development, juveniles being more sensitive than larval fish (Buhl and Hamilton 1991). Consequently, exposure at a given place and time will have different effects among species because of their inherent vulnerability and differences in timing of development (see Box 4-1). There are many other physiological and ecological differences among species that will also affect their vulnerability to stressors, such as temperature and disease, so the overall effect of exposure to contaminants at a given time of the year can vary considerably.
Second, not all species are amenable to the degree of domestication required to conduct laboratory experiments, and the use of some might lead to public objections if they are suggested for such studies, for example, dogs as wolf surrogates or cats as jaguar or ocelot surrogates. It is also hard to imagine an appropriate surrogate for many species, such as polar or grizzly bears. Therefore, a scientifically credible alternative approach is to define a range of sensitivities within which the sensitivity of a species of concern could reasonably be expected to occur or a range that could be used to make reasoned extrapolations from species that have been tested by using inferences based on other chemicals. Life histories would need to be considered. If different life histories lead two related species that have similar toxicological sensitivities to a chemical to occupy different locations at different times, their susceptibility to a chemical could be quite different.
Listed species are not inherently more sensitive to chemicals than species that are not listed (Sappington et al. 2001; Besser et al. 2005; Dwyer et al. 2005), so similar methods of cross-species extrapolations can be used for any ecological risk assessment. Those methods include interspecies correlation analyses or interspecies correlation estimation (ICE) (Dyer 2006; Raimondo et al. 2010) and species sensitivity distributions (SSDs) (Posthuma et al. 2001). ICE models use the initial toxicity estimate for one species to estimate toxicity values for other species. The toxicity values can then be used either directly (if the species whose values are predicted is the species of concern) or in the development of SSDs. Knowledge about the mechanism of action of a chemical and the physiological similarity between test species and species of concern can provide empirical evidence to use in interpreting the theoretical relationships derived with the ICE model. Dyer et al. (2006) showed that using estimated values in an SSD in addition to or instead of measured values results in identification of threshold concentrations within an order of magnitude of those derived from distributions based only on empirical data. If a small dataset is available, bootstrapping or a Monte Carlo analysis may also be used to generate a response distribution (Warren-Hicks and Hart 2010). Bayesian approaches, which use all the information underlying the concentration-response data and result in presentation of the entire range of values that could be encountered beyond those of the tested species, have also been used to generate the end-point values for use in an SSD (Moore et al. 2010).
An SSD is a statistical distribution of the various concentrations at which different species have the same response to a chemical (Posthuma et al. 2001). Figure 4-4 provides an example of an SSD. The simplest approach is to display the SSD as a cumulative distribution function in much the same way that interindividual variability is displayed as an exposure-response function. An SSD can be based on any outcome—such as mortality, growth, or enzyme activity—for any group of species (such as all aquatic species, fishes, or plants) for any metric, such as EC50, NOEC, or LC50. Generally, a lognormal distribution is assumed, although Newman et al. (2000) point out that such an assumption is not always valid and that when sufficient data are available a data-specific distribution should be used. At the very least, the model’s goodness of fit should be evaluated or acknowledged (Farrar et al. 2010). Furthermore, the data points used to generate the SSD have associated uncertainty that should be carried forward in generating the distribution. That uncertainty can be used to put confidence limits around the hazard concentration (HC) at the selected percentile and to determine the number of data points needed to define the HC with a desired amount of precision. Generally, the 5th percentile of the distribution is accepted as a matter of policy as the concentration that would maintain the viability of most species (HC5), and preference is given to using the lower confidence limit of the HC5. The HC5s from SSDs of multiple chemicals for aquatic organisms—whether based on tested species or on extrapolations from ICE models—have been shown to be significantly lower than concentrations derived by using safety factors of 10 and 97% lower than the LC50s of all endangered species (Raimondo et al. 2008).
A reasonable alternative to the use of SSD models is to use concentration-response models (or single-point estimates) available for each species to assign values to parameters in the population model with a Monte Carlo approach. For example, the percentage of the population that survives an estimated exposure can be randomly selected from all the species tested. At the exposure concentration of interest, survival might be 50% for a population of quail, 75% for a songbird, and 30% for a duck. One of those values would be randomly selected, and the population model would be run to determine the population-level end point (for example, lambda or risk of extinction or decline); that process would be repeated 1,000 times to generate a distribution of the population-level end points that reflects the range of possible survival rates of the nontested species at the estimated exposure concentrations. That approach assumes that the species of interest has an unknown survival rate that is encompassed by the range of survival rates of all other measured species. The latter species could be constrained to ones that are similar taxonomically (or physiologically) to the species of concern, or all species could be included to make the resulting analysis as robust as possible. All types of population-level end-point values (such as median, mean, and upper or lower bounds) are carried forward to the risk characterization. The process outlined here would be conducted simultaneously for reproduction.
FIGURE 4-4 Species sensitivity distributions for 2, 2’-dipyridyldisulfide derived by using a Bayesian statistical model. Source: Mochida et al. 2012. Reprinted with permission; copyright 2012, Aquatic Toxicology.
The committee concludes that the procedures outlined above, which result in a range of sensitivities, are good alternatives to the use of a single surrogate species. The use of a single surrogate species is often difficult to justify, but the use of a set of species would give a good idea of the range of possible organismal responses to a pesticide. As noted, life-history variations would need to be considered.
OTHER UNCERTAINTIES IN EFFECTS ANALYSIS
An effects analysis describes how a species of concern or a biological component of its habitat responds when exposed to a stressor, in this case a pesticide formulation, including the active ingredient and other constituent chemicals. It also includes an analysis of how the pesticide interacts with other environmental stressors, either increasing or decreasing the toxic response. However, all such estimates are uncertain, because of either measurement error or lack of knowledge. As stated in Chapter 2, the uncertainty should be clearly defined and propagated through the risk assessment. Currently, EPA and the Services do not quantitatively incorporate uncertainty in the effects analysis. Although they all report confidence intervals around most of the effects end points, they ultimately use only deterministic approaches (single point estimates of the magnitude of effect at a particular exposure concentration) or qualitative descriptions (particularly for behavioral and sublethal effects other than quantifiable reproduction responses). And they do not explain their selection of particular effects concentrations when selecting toxicity thresholds (for example, the choice of an EC25 instead of an EC10, or vice versa). Therefore, much quantitative information that
could explain the possible range of effects at single or multiple exposure concentrations is not used. General statements about “uncertainty” or “considerable uncertainty” are made, and these provide little or no guidance to a decision-maker because the terms are vague and open to multiple interpretations.
The committee recommends that all parties use quantitative uncertainty analyses whenever sufficient data are available. Selection of a particular approach depends on the amount of data available, the timeframe for conducting an assessment, and the preference of the risk assessors. Nearly all toxicity studies provide some information about concentration-response relationships, including measures of variability; and many measured environmental-response variables, such as productivity rates, also have time-dependent variability estimates. Therefore, quantified uncertainty estimates about effects values can be developed and used in the risk assessments. There are many well-documented methods for quantifying uncertainty in chemical toxicity assessments and in population models that are supported by user-friendly commercial software, including probability bounds, confidence intervals, Monte Carlo analysis, and Bayesian techniques (Spear 1997; Borsuk et al. 2004; Solomon et al. 2008; Link and Barker 2010; Warren-Hicks and Hart 2010; McLaughlin and Jain 2011). If quantitative effects data are insufficient for input into a quantified risk assessment or a quantitative uncertainty analysis, a qualitative statement about the risk potential and degree of uncertainty (such as low, medium, or high) can be used instead provided that they are accompanied by some bounding definitions (such as different by orders of magnitude). In cases in which some effects have quantifiable uncertainty and others do not, the committee recommends that the formal risk assessment focus on end points that are quantifiable and include quantitative measures of variability. The “others” should be described qualitatively and used as supplemental information after qualitative uncertainty categories or lines of evidence that might be useful are clearly defined.
CONCLUSIONS AND RECOMMENDATIONS
Sublethal, Indirect, and Cumulative Effects
• An adverse effect should be defined by the degree to which an organism’s survival or reproduction is affected; thus, assessing the effects of a pesticide on a listed species requires quantifying the effect of the pesticide on survival and reproduction of the species in the wild. Any effect that results in a change in survival or reproduction is relevant to the assessment, and any effect that does not change either outcome is irrelevant with respect to a quantitative assessment of population effects.
• To determine whether a pesticide is “likely to adversely affect” a listed species, a broad search should be conducted to identify information on sublethal effects of the pesticide and possible concentration-response relationships.
• To provide information to support a jeopardy determination, the Services should either (a) show how sublethal effects change survival or reproduction and incorporate such information into the population viability analysis or (b) state that such relationships are unknown but possible and include a qualitative discussion of uncertainty in the BiOp.
• When indirect effects can be quantified, they should be incorporated into the effects analysis.
• Population models provide an appropriate framework for incorporating baseline conditions and projected future cumulative effects into the assessment. Evaluation of those effects is within the purview of the Services and an appropriate part of the BiOp.
Effects Models
• Because the ESA is concerned with species or listed units within named species, the effects of pesticides must be expressed at the population level. Accordingly, population models that incorporate temporal variability and focus on probabilistic results are needed for assessing population risks. Although deterministic projection models are insufficient for that task, they can be used in the absence of information on temporal variability in the elements of the baseline model provided that the risk assessment recognizes the potential bias that might result from using them.
• Spatial structure and density dependence might have important effects on population dynamics and must be incorporated into population models when data are available. However, in the absence of such data, it is appropriate to use generic, single-population models that characterize the life history of a group of species to estimate the effects of a pesticide on a given species.
• The assumption that mortality due to pesticide exposure will always be compensated for by density dependence is not scientifically valid because such exposure will likely decrease the growth rate of the population at all densities and generally depress the population growth-density curve.
• For the purposes of population modeling, effects need to be estimated at a range of concentrations that includes all values that the population might reasonably encounter. Test results expressed only as threshold values or point estimates—such as the no-observed-adverse-effects level, the lowest observed-adverse-effects level, and the LC50—do not provide enough information for a population-level risk assessment.
Mixtures
• A quantitative mixture risk assessment requires extensive data, including data on the identity, concentration, and toxicity of mixture components. Challenges in assessing risk to listed species from pesticide-containing mixtures
arise largely because of the lack of such data and the lack of understanding of the potential for interactions among mixture components.
• In the absence of such quantitative data, the possible contribution of specific mixture components to the toxicity of a pesticide active ingredient cannot be incorporated into a quantitative risk assessment. However, the risk assessor should describe the possible effects of mixture components on the risk estimate to the decision-maker.
• The committee emphasizes that the complexity of assessing the risk posed by chemical mixtures should not paralyze the process. The following guidelines provide a tool for helping to determine when and how to consider components other than the pesticide active ingredient in a risk assessment:
1. The toxicity of the pesticide active ingredient is central to the assessment. Other chemicals are relevant only if they modify the toxicity of the pesticide active ingredient or the susceptibility of the species of concern to the active ingredient.
2. The toxicity end point most relevant to the species of concern must be determined before initiation of the effects analysis.
3. Mixture components that do not elicit the relevant response in the species of concern do not need to be considered in the effects analysis. Mixture components that do elicit the relevant response need to be considered in the effects analysis.
4. In the absence of any data that would support the hypothesis of a synergistic interaction between the pesticide active ingredient and other mixture components, the effects analysis should proceed on the assumption that the components have additive effects.
5. For chemicals that have common mechanisms of action and parallel slopes in the concentration-response curves, concentration addition is a reasonable approach for modeling additive effects. However, caution should be exercised in using concentration-addition modeling as a default approach when no mechanistic data or concentration-response data are available.
6. For chemicals that have different mechanisms of action, response addition (with a zero correlation of individual tolerances) is a reasonable approach for modeling additive effects. For this case, mixture components will contribute to the response only when present in the environment at concentrations that elicit the relevant response. That is, such components do not need to be considered when present at concentrations below their toxic thresholds.
7. Potential synergistic interactions need be considered only when a synergist is present in the environment above its interaction threshold concentration. In the case of synergism, it is probably prudent to generate information on toxic interactions to ensure accurate evaluation of potential responses of the species of concern.
8. In the case of antagonism, uncertainties associated with both exposures and toxic interactions will seldom justify a quantitative modification of the effects analysis.
9. The use of uncertainty factors to compensate for the absence of information on potential interactions of mixture components is not recommended. When data are available, quantitative methods can be used to evaluate the interactions.
Interspecies Extrapolation, Surrogate Species, and Other Uncertainties
• Many difficulties are associated with the use of surrogate species to estimate risk to a species on which data are not available or cannot easily be obtained.
• An alternative approach to using a single surrogate species is to define a range of sensitivities within which the sensitivity of the species of concern could reasonably be expected to occur or a range of sensitivities that could be used to make reasoned extrapolations from species that have been tested by using inferences based on other chemicals.
• Because listed species are not inherently more sensitive to chemicals than species that are not listed, similar methods of cross-species extrapolations can be used for any ecological risk assessment and include interspecies correlation analysis and species sensitivity distributions.
• Life histories need to be considered whether one is identifying a single surrogate species or using an alternative approach. For example, if two related species have similar toxic sensitivities to a chemical but have different life histories that lead them to occupy different locations at different times, their susceptibility to the chemical could be different.
• In all cases and for all methods, quantitative uncertainty analyses should be used whenever sufficient data are available.
Adam, O., P.M. Badot, F. Degiorgi, and G. Crini. 2009. Mixture toxicity assessment of wood preservative pesticides in the fresh water amphipod Gammarus pulex (L). Ecotoxicol. Environ. Saf. 72(4):441-449.
Akçakaya, H.R., M.A. Burgman, and L. Ginzburg. 1999. Applied Population Ecology Principles and Computer Exercises using RAMAS EcoLab 2.0, 2nd Ed. Sunderland, MA: Sinauer Associates.
Akçakaya, H.R., J.D. Stark, and T.S. Bridges, eds. 2008. Demographic Toxicity: Methods in Ecological Risk Assessment. New York: Oxford University Press.
Altenburger, R., T. Backhaus, W. Boedeker, M. Faust, M. Scholze, and L.H. Grimme. 2000. Predictability of the toxicity of multiple chemical mixtures to Vibrio fisch-eri: Mixtures composed of similarly acting chemicals. Environ. Toxicol. Chem. 19(9):2341-2347.
Amweg, E.L., D.P. Weston, J. You, and M.J. Lydy. 2006. Pyrethroid insecticides and sediment toxicity in urban creeks from California and Tennessee. Environ. Sci. Technol. 40(5):1700-1706.
Anderson, T.D., and K.Y. Zhu. 2004. Synergistic and antagonistic effects of atrazine on the toxicity of organophosphorodithioate and organophosphorothioate insecticides to Chironomus tentans (Diptera: Chironomidae). Pestic. Biochem. Physiol. 80(1):64-64.
Ankley, G.T., and S.A. Collyard. 1995. Influence of piperonyl butoxide on the toxicity of organophosphate insecticides to three species of freshwater benthic invertebrates. Comp. Biochem. Physiol. C Pharmacol. Toxicol. Endocrinol. 110(2):149-155.
Backhaus, T., R. Altenburger, W. Boedeker, M. Faust, M. Scholze, and L.H. Grimme. 2000. Predictability of the toxicity of a multiple mixture of dissimilarly acting chemicals to Vibrio fischeri. Environ. Toxicol. Chem. 19(9):2348-2356.
Backhaus, T., A. Arrhenius, and H. Blanck. 2004. Toxicity of a mixture of dissimilarly acting substances to natural algal communities: Predictive power and limitations of independent action and concentration addition. Environ. Sci. Technol. 38(23): 6363-6370.
Baird, D.J., L. Maltby, P.W. Greig-Smith, and P.E.T. Douben. 1996. ECOtoxicology: Ecological Dimensions. London: Chapman & Hall.
Baldwin, D.H., J.A. Spromberg, T.K. Collier, and N.L. Scholz. 2009. A fish of many scales: Extrapolating sublethal pesticide exposures to the productivity of wild salmon populations. Ecol. Appl. 19(8):2004-2015.
Barnthouse, L.W., W.R. Munns, and M.T. Sorensen. 2007. Population-Level Ecological Risk Assessment. Pensacola, FL: CRC Press.
Barry, M.J. 1998. Endosulfan-enhanced crest induction in Daphnia longicephala: Evidence for cholinergic innervation of kairomone receptors. J. Plankton Res. 20(7):1219-1231.
Beckman, B.R., D.A. Larsen, B. Lee-Pawlak, and W.W. Dickhoff. 1998. Relation of fish size and growth rate to migration of spring chinook salmon smolts. N. Am. J. Fish. Manage. 18(3):537-546.
Behnke, R.J. 1992. Native Trout of Western North America. American Fisheries Society Monograph 6. December 1992.
Belden, J.B., R.J. Gilliom, J.B. Martin, and M.J. Lydy. 2007a. Relative toxicity and occurrence patterns of pesticide mixtures in streams draining agricultural watersheds dominated by corn and soybean production. Integr. Environ. Assess. Manag. 3(1): 90-100.
Belden, J.B., R.J. Gilliom, and M.J. Lydy. 2007b. How well can we predict the toxicity of pesticide mixtures to aquatic life? Integr. Environ. Assess. Manag. 3(3):364-372.
Besser, J.M., N. Wang, F.J. Dwyer, F.L. Mayer, Jr., and C.G. Ingersoll. 2005. Assessing contaminant sensitivity of endangered and threatened aquatic species, Part II. Chronic toxicity of copper and pentachlorophenol to two endangered species and two surrogate species. Arch. Environ. Contam. Toxicol. 48(2):155-165.
Beyond Pesticides. 2009. Re: Registration Review; Glyphosate Docket Opened for Review and Comment. Docket Number: EPA-HQ-OPP-2009-0361 [online]. Available: http://www.beyondpesticides.org/documents/glyphosate-final9-21-1.pdf [accessed Nov. 16, 2012].
Bielza, P., P.J. Espinosa, V. Quinto, J. Abellán, and J. Contreras. 2007. Synergism studies with binary mixtures of pyrethroid, carbamate and organophosphate insecticides on Frankliniella occidentalis (Pergande). Pest. Manag. Sci. 63(1):84-89.
Bjergager, M.B., M.L. Hanson, K.R. Solomon, and N. Cedergreen. 2012. Synergy between prochloraz and esfenvalerate in Daphnia magna from acute and subchronic exposures in the laboratory and microcosms. Aquat. Toxicol. 110-111:17-24.
Bliss, C.I. 1939. The toxicity of poisons applied jointly. Ann. Appl. Biol. 26(3):585-615.
Boobis, A., R. Budinsky, S. Collie, K. Crofton, M. Embry, S. Felter, R. Hertzberg, D. Kopp, G. Mihlan, M. Mumtaz, P. Price, K. Solomon, L. Teuschler, R. Yang, and R. Zaleski. 2011. Critical analysis of literature on low-dose synergy for use in screening chemical mixtures for risk assessment. Crit. Rev. Toxicol. 41(5):369-383.
Borsuk, M.E., C.H. Stow, and K.H. Reckhow. 2004. A Bayesian network of eutrophication models for synthesis, prediction, and uncertainty analysis. Ecol. Model. 173(2-3):219-239.
Buhl, K.J., and S.J. Hamilton. 1991. Relative sensitivity of early life stages of arctic grayling, coho salmon, and rainbow trout to nine inorganics. Ecotox. Environ. Safe 22(2): 184-197.
Burgman, M.A., S. Ferson, and H.R. Akçakaya. 1993. Risk Assessment in Conservation Biology. London: Chapman and Hall.
Cairns Jr., J., and J. Pratt. 1993. Trends in ecotoxicology. Sci. Total Environ. 134(suppl. 1):7-22.
Cashman, J.R., B.Y. Perotti, C.E. Berkman, and J. Lin. 1996. Pharmacokinetics and molecular detoxication. Environ. Health Perspect. 104(Suppl. 1):23-40.
Caswell, H. 2001. Matrix Population Models: Construction, Analysis, and Interpretation, 2nd Ed. Sunderland, MA: Sinauer Associates.
Cedergreen, N., A. Kamper, and J.C. Streibig. 2006. Is prochloraz a potent synergist across aquatic species? A study on bacteria, daphnia, algae and higher plants. Aquat. Toxicol. 78(3):243-252.
Clement, J.G. 1984. Role of aliesterase in organophosphate poisoning. Fundam. Appl. Toxicol. 4(2 Pt. 2):S96-S105.
Cleuvers, M. 2003. Aquatic ecotoxicity of pharmaceuticals including the assessment of combination effects. Toxicol. Lett. 142(3):185-194.
Coors, A., and L. De Meester. 2008. Synergistic, antagonistic and additive effects of multiple stressors: Predation threat, parasitism, and pesticide exposure in Daphnia magna. J. Appl. Ecol. 45(6):1820-1828.
Courchamp, F., J. Berec, and J. Gascoigne. 2008. Allee Effects in Ecology and Conservation. New York: Oxford University Press.
Dallegrave, E., F.D. Mantese, R.T. Oliveira, A.J. Andrade, P.R. Dalsenter, and A. Langeloh. 2007. Pre- and postnatal toxicity of the commercial glyphosate formulation in Wistar rats. Arch. Toxicol. 81(9):665-673.
Dobrev, I.D., M.E. Andersen, and R.S. Yang. 2001. Assessing interaction thresholds for trichloroethylene in combination with tetrachloroethylene and 1, 1, 1-trichloroethane using gas uptake studies and PBPK modeling. Arch. Toxicol. 75(3):134-144.
Duchet, C., M.A. Coutellec, E. Franquet, C. Lagneau, and L. Lagadic. 2010. Populationlevel effects of spinosad and Bacillus thuringiensis israelensis in Daphnia pulex and Daphnia magna: Comparison of laboratory and field microcosm exposure conditions. Ecotoxicology 19(7):1224-1237.
Duffy, E.J., and D.A. Beauchamp. 2008. Seasonal patterns of predation on juvenile Pacific salmon by anadromous cutthroat trout in Puget Sound. T. Am. Fish. Soc. 137(1):165-181.
Dwyer, F.J., F.L. Mayer, L.C. Sappington, D.R. Buckler, C.M. Bridges, I.E. Greer, D.K. Hardesty, C.E. Henke, C.G. Ingersoll, J.L. Kunz, D.W. Whites, T. Augspurger, D.R. Mount, K. Hattala, and G.N. Neuderfer. 2005. Assessing contaminant sensi-
tivity of endangered and threatened aquatic species: Part I. Acute toxicity of five chemicals. Arch. Environ. Contam. Toxicol. 48(2):143-154.
Dyer, S.D., D.J. Versteeg, S.E. Belanger, J.G. Chaney, and F.L. Mayer. 2006. Interspecies correlation estimates predict protective environmental concentrations. Environ. Sci. Technol. 40(9):3102-3131.
El-Masri, H. 2010. Toxicological interaction thresholds of chemical mixtures. Pp. 207-214 in Principles and Practice of Mixtures Toxicology, M. Mumtaz, ed. Weinheim: Wiley-VCH.
El-Masri, H.A., K.F. Reardon, and R.S. Yang. 1997. Integrated approaches for the analysis of toxicologic interactions of chemicals mixtures. Crit. Rev. Toxicol. 27(2):175-197.
El-Merhibi, A., A. Kumar, and T. Smeaton. 2004. Role of piperonyl butoxide in the toxicity of chlorpyrifos to Ceriodaphnia dubia and Xenopus laevis. Ecotoxicol. Environ. Saf. 57(2):202-212.
EPA (U.S. Environmental Protection Agency). 1986. Guidelines for the Health Risk Assessment of Chemical Mixtures. EPA/630/R-98/002. Risk Assessment Forum, U.S. Environmental Protection Agency, Washington, DC. September 1986 [online]. Available: http://www.epa.gov/raf/publications/pdfs/CHEMMIX_1986.pdf [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 1989. Interim Procedures for Estimating Risks Associated with Exposures to Mixtures of Chlorinated Dibenzo-p-Dioxins and Dibenzofurans (CDDs and CDFs) and 1989 Update. EPA/625/3-89/016. NTIS PB90145756. Risk Assessment Forum, U.S. Environmental Protection Agency, Washington, DC.
EPA (U.S. Environmental Protection Agency). 1996. Health Effects Test Guidelines OPPTS 870.1200 Acute Dermal Toxicity. EPA 712-C-96-192. Office for Prevention, Pesticides and Toxic Substances, U.S. Environmental Protection Agency. June 1996 [online]. Available: http://iccvam.niehs.nih.gov/SuppDocs/FedDocs/EPA/EPA-870-1200.pdf [accessed Nov. 20, 2012].
EPA (U.S. Environmental Protection Agency). 1998a. Guidelines for Ecological Risk Assessment. EPA/630/R-95/002F. Risk Assessment Forum, U.S. Environmental Protection Agency, Washington, DC. April 1998 [online]. Available: http://www.epa.gov/raf/publications/pdfs/ECOTXTBX.PDF [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 1998b. Health Effects Test Guidelines OPPTS 870.1100 Acute Oral Toxicity. EPA 712-C-98-190. Office for Prevention, Pesticides and Toxic Substances, U.S. Environmental Protection Agency.
August 1998 [online]. Available: http://iccvam.niehs.nih.gov/methods/acutetox/invidocs/EPA_870_1100.pdf [accessed Nov. 2012].
EPA (U.S. Environmental Protection Agency). 1998c. Health Effects Test Guidelines OPPTS 870.1300 Acute Inhalation Toxicity. EPA 712-C-98-193. Office for Prevention, Pesticides and Toxic Substances, U.S. Environmental Protection Agency. August 1998 [online]. Available: http://iccvam.niehs.nih.gov/SuppDocs/FedDocs/EPA/EPA-870-1300.pdf [accessed Nov. 20, 2012].
EPA (U.S. Environmental Protection Agency). 1998d. Health Effects Test Guidelines OPPTS 870.2400 Acute Eye Irritation. EPA 712-C-98-195. Office for Prevention, Pesticides and Toxic Substances, U.S. Environmental Protection Agency. August 1998 [online]. Available: http://iccvam.niehs.nih.gov/SuppDocs/FedDocs/EPA/EPA_870_2400.pdf [accessed Nov. 20, 2012].
EPA (U.S. Environmental Protection Agency). 1998e. Health Effects Test Guidelines OPPTS 870.2500 Acute Dermal Irritation. EPA 712-C-98-196. Office for Prevention, Pesticides and Toxic Substances, U.S. Environmental Protection Agency. August 1998 [online]. Available: http://iccvam.niehs.nih.gov/SuppDocs/FedDocs/EPA/EPA_870_2500.pdf [accessed Nov. 20, 2012].
EPA (U.S. Environmental Protection Agency). 2000. Supplementary Guidance for Conducting Health Risk Assessment of Chemical Mixtures. EPA/630/R-00/002. Risk Assessment Forum Technical Panel, U.S. Environmental Protection Agency, Washington, DC. August 2000 [online]. Available: http://www.epa.gov/raf/publications/pdfs/CHEM_MIX_08_2001.PDF [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 2002. Guidance on Cumulative Risk Assessment of Pesticide Chemicals That Have a Common Mechanism of Toxicity. Office of Pesticide Programs, U.S. Environmental Protection Agency, Washington, DC. January 14, 2002 [online]. Available: http://www.epa.gov/oppfead1/trac/science/cumulative_guidance.pdf [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 2003. Health Effects Test Guidelines OPPTS 870.2600 Skin Sensitization. EPA 712-C-03-197. Office for Prevention, Pesticides and Toxic Substances, U.S. Environmental Protection Agency. March 2003 [online]. Available: http://www.regulations.gov/#!documentDetail;D=EPA-HQ-OPPT-2009-0156-0008 [accessed Nov. 20, 2012].
EPA (U.S. Environmental Protection Agency). 2004. Overview of the Ecological Risk Assessment Process in the Office of Pesticide Programs, U.S. Environmental Protection Agency: Endangered and Threatened Species Effects Determinations. Office of Prevention, Pesticides and Toxic Substances, Office of Pesticide Programs, U.S. Environmental Protection Agency, Washington DC. January 23, 2004 [online]. Available: http://www.epa.gov/oppfead1/endanger/consultation/ecorisk-overview.pdf [accessed Aug. 29, 2012].
EPA (U.S. Environmental Protection Agency). 2005. Overview of the Piperonyl Butoxide Risk Assessments. Docket ID EPA-HQ-OPP-2005-0042. Pesticides: Reregistration, U.S. Environmental Protection Agency [online]. Available: http://www.epa.gov/opp00001/reregistration/piperonyl/ [accessed Feb. 19, 2013].
EPA (U.S. Environmental Protection Agency). 2007. Aquatic Life Ambient Freshwater Quality Criteria – Copper, 2007 Revision. EPA-822-R-07-001. Office of Water, Office of Science and Technology, U.S. Environmental Protection Agency, Washington, DC. February 2007 [online]. Available: http://water.epa.gov/scitech/swguidance/standards/criteria/aqlife/copper/upload/2009_04_27_criteria_copper_2007_criteria-full.pdf [accessed Feb. 19, 2013].
EPA (U.S. Environmental Protection Agency). 2008. Risks of Glyphosate Use to Federally Threatened California Red-legged Frog (Rana aurora draytonii). Pesticide Effects Determination. Environmental Fate and Effects Division, Office of Pesticide Programs, Washington, DC. October 17, 2008 [online]. Available: http://www.epa.gov/espp/litstatus/effects/redleg-frog/glyphosate/determination.pdf [accessed on Feb. 26, 2012].
EPA (U.S. Environmental Protection Agency). 2012a. EPA Response to NAS Questions, March 28, 2012 [online]. Available: http://www.thecre.com/forum1/wp-content/uploads/2012/04/ESAEPAATRAZINE.pdf [accessed Nov. 15, 2012].
EPA (U.S. Environmental Protection Agency). 2012b. Inert Ingredients in Pesticide Products-Reassessment Decision Documents. U.S. Environmental Protection Agency [online]. Available: http://www.epa.gov/opprd001/inerts/decisiondoc_a2k.html [accessed Mar. 26, 2012].
EPA (U.S. Environmental Protection Agency). 2012c. General Guidance for Petitioning the Agency for the Establishment of a New/Amended Food Use Inert Ingredient Tolerance or Tolerance Exemption. Office of Chemical Safety and Pollution Prevention, Office of Pesticide Programs, Registration Division, U.S. Environmental Protection Agency. September 12, 2012 [online]. Available: www.epa.gov/opprd001/inerts/inertpetition.pdf [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 2012d. General Guidance for Requesting a New Nonfood Use Inert Ingredient. Office of Chemical Safety and Pollution Prevention, Office of Pesticide Programs, Registration Division, U.S. Environmental Protection Agency. September 13, 2012. [online]. Available: http://www.epa.gov/opprd001/inerts/nonfood_inert.pdf [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 2012e. Guidance to Petitioners for Low Risk Polymer Submissions. Office of Chemical Safety and Pollution Prevention, Office of Pesticide Programs, Registration Division, U.S. Environmental Protection Agency. September 12, 2012 [online]. Available: http://www.epa.gov/opprd001/inerts/lowriskpolymer.pdf [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 2012f. Pesticide Registration Manual, Chapter 2: Registering a Pesticide Product. May 2012 [online]. Available: http://www.epa.gov/opprd001/registrationmanual/chapter2.html#metoo [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 2012g. Guidance for Waiving or Bridging of Mammalian Acute Toxicity Tests for Pesticides and Pesticide Products (Acute Oral, Acute Dermal, Acute Inhalation, Primary Eye, Primary Dermal, and Dermal Sensitization). Office of Pesticide Programs. Available: http://www.epa.gov/opp00001/science/acute-data-waiver-guidance.pdf [accessed Nov. 19, 2012].
EPA (U.S. Environmental Protection Agency). 2013. Harmonized Test Guidelines. U.S. Environmental Protection Agency [online]. Available: http://www.epa.gov/ocspp/pubs/frs/home/guidelin.htm [accessed Mar. 26, 2013].
Farrar, D., T. Barry, P. Hendley, M. Crane, P. Mineau, M.H. Russell, and E.W. Odenkirchen. 2010. Issues underlying the selection of distributions. Pp. 31-52 in Application of Uncertainty Analysis to Ecological Risks of Pesticides, W.J. Warren-Hicks, and A. Hart, eds. Pensacola, FL: SETAC Press.
Feron, V.J., J.P. Groten, D. Jonker, F.R. Cassee, and P.J. van Bladeren. 1995. Toxicology of chemical mixtures: Challenges for today and the future. Toxicology 105(2-3): 415-427.
Ferson, S., L.R. Ginzburg, and R.A. Goldstein. 1996. Inferring ecological risk from toxicity bioassays. Water Air Soil Poll. 90(1-2):71-82.
FESTF (FIFRA Endangered Species Task Force). 2012. FIFRA Endangered Species Task Force Data Use in the Assessment of the Risk of FIFRA-Regulated Pesticides to Species Regulated by the ESA. A background document prepared by the FIFRA Endangered Species Task Force for the NAS Panel on Ecological Risk Assessment under FIFRA and ESA, January 25, 2012.
Finney, D.J. 1942. The analysis of toxicity tests on mixtures of poisons. Ann. Appl. Biol. 29(1):82-94.
Finney, D.J. 1971. Probit Analysis, 3rd Ed. Cambridge: Cambridge University Press.
Forbes, V.E., and P. Calow. 1999. Is the per capita rate of increase a good measure of population-level effects in ecotoxicology? Environ. Toxicol. Chem. 18(7):1544-1556.
Forbes, V.E., R.M. Sibly, and P. Calow. 2001. Toxicant impacts on density-limited populations: A critical review of theory, practice, and results. Ecol. Appl. 11(4):1249-1257.
Forbes, V.E., R.M. Sibly, and I. Linke-Gamenick. 2003. Joint effects of population density and toxicant exposure on population dynamics of Capitella sp. I. Ecol. Appl. 13(4):1094-1103.
FWS (U.S. Fish and Wildlife Service). 2009. Informal Consultation on the Effects of Diazinon and Racemic Metolachlor Reregistration on the Endangered Barton Springs Salamander. Letter to Arthur-Jean B. Williams, Environmental Fate and Effects Division, Office of Pesticide Programs, U.S. Environmental Protection Agency, from M.A. Nelson, Division of Consultation, Habitat Conservation Planning, Recovery and State Grants, U.S. Fish and Wildlife Service, Washington, DC. January 14, 2009.
FWS (U.S. Fish and Wildlife). 2012. Response to Committee Questions for Agency and Services, from Rick Sayers, Chief, Division of Consultation, HCPs, Recovery, and State Grants, U.S. Fish and Wildlife Service Endangered Species Program. March 28, 2012 [online]. Available: http://www.thecre.com/forum1/wp-content/uploads/2012/04/esafwsatrazine1.pdf [accessed Nov. 19, 2012].
Giesy, J.P., S. Dobson, and K.R. Solomon. 2000. Ecotoxicological risk assessment for Roundup herbicide. Rev. Environ. Contamin. Toxicol. 167:35-120.
Giorgi, A.E., T.W. Hillman, J.R. Stevenson, S.G. Hays, and C.M. Peven. 1997. Factors that influence the downstream migration rates of juvenile salmon and steelhead through the hydroelectric system in the mid-Columbia River basin. N. Am. J. Fish. Manage. 17(2):268-282.
Gustafson, R.G., R.S. Waples, J.M. Myers, L.A. Weitkamp, G.J. Bryant, O.W. Johnson, and J.J. Hard. 2007. Pacific salmon extinctions: Quantifying lost and remaining diversity. Conserv. Biol. 21(4):1009-1020.
Healey, M.C. 1991. Life history of chinook salmon (Oncorhynchus tshawytscha). Pp. 311-393 in Pacific Salmon Life Histories, C. Groot, and L. Margolis, eds. Vancouver: University of British Columbia Press.
Hilborn, R., T.P. Quinn, D.E. Schindler, and D.E. Rogers. 2003. Biocomplexity and fisheries sustainability. Proc. Natl. Acad. Sci. USA 100(11):6564-6568.
Hodgson, E., and P.E. Levi. 2001. Metabolism of pesticides. Pp. 531-562 in Handbook of Pesticide Toxicology, 2nd Ed., R.I. Krieger, ed. London: Academic Press.
IPCS (International Programme on Chemical Safety). 2009. Assessment of Combined Exposures to Multiple Chemicals: Report of a WHO/IPCS International Workshop on Aggregate/Cumulative Risk Assessment. Harmonization Project Document No. 7. Geneva: World Health Organization [online]. Available: http://www.who.int/ipcs/methods/harmonization/areas/workshopreportdocument7.pdf [accessed Mar. 26, 2013].
Jones, D.G. 1998. Piperonyl Butoxide: The Insecticide Synergist. New York: Academic Press.
Kociba, R.J., and B.A. Schwetz. 1982. Toxicity of 2, 3, 7, 8-Tetrachlorodibenzo-p-dioxin (TCDD). Drug Metab. Rev. 13(3): 387-406.
Kolpin, D.W., D.T. Furlong, M.T. Meyer, E.M. Thurman, S.D. Zaugg, L.B. Barber, and H.T. Buxton. 2002. Pharmaceuticals, hormones, and other organic wastewater contaminants in U.S. streams, 1999-2000: A national reconnaissance. Environ. Sci. Technol. 36(6):1202-1211.
Kortenkamp, A., R. Evans, M. Faust, F. Kalberlah, M. Scholze, and U. Schuhmacher-Wolz. 2012. Investigation of the State of the Science on Combined Actions of Chemicals in Food through Dissimilar Modes of Action and Proposal for Science-based Approach for Performing Related Cumulative Risk Assessment. European Food Safety Authority, January 31, 2012 [online]. Available: http://www.efsa.europa.eu/en/supporting/doc/232e.pdf [accessed Mar. 26, 2013].
Kuhn, A., W.R. Munns, S. Poucher, D. Champlin, and S. Lussier. 2000. Prediction of population-level response from mysid toxicity test data using population modeling techniques. Environ. Toxicol. Chem. 19(9):2364-2371.
Labenia, J.S., D.H. Baldwin, B. L. French, J.W. Davis, and N.L. Scholz. 2007. Behavioral impairment and increased predation mortality in cutthroat trout exposed to carbaryl. Mar. Ecol. Prog. Ser. 329:1-11.
Laetz, C.A., D.H. Baldwin, T.K. Collier, V. Hebert, J.D. Stark, and N.L. Scholz. 2009. The synergistic toxicity of pesticide mixtures: Implications for risk assessment and the conservation of endangered Pacific salmon. Environ. Health Perspect. 117(3):348-353.
LeBlanc, L.A., J.L. Orlando, and K.M. Kuivila. 2004. Pesticide Concentrations in Water and in Suspended and Bottom Sediments in the New and Alamo Rivers, Salton Sea Watershed, California, April 2003. Data Series 104. U.S. Geological Survey, Reston, VA [online]. Available: http://swrcb2.swrcb.ca.gov/water_issues/programs/?swamp/docs/reglrpts/rb7_pesticide_saltonseaws.pdf [accessed Nov. 19, 2012].
Levine, T.E. 1996. The regulation of inert ingredients in the United States. Pp. 1-11 in Pesticide Formulation and Adjuvant Technology, C.L. Foy, and D.W. Pritchard, eds. Boca Raton, FL: CRC Press.
Link, W.A., and R.J. Barker. 2010. Bayesian Inference: With Ecological Applications. New York: Academic Press.
Macneale, K.H., P.M. Kiffney, and N.L Scholz. 2010. Pesticides, aquatic food webs, and the conservation of Pacific salmon. Front. Ecol. Environ. 8(9):475-482.
Mangel, M., and W.H. Satterthwaite. 2008. Combining proximate and ultimate approaches to understand life history variation in salmonids with application to fisheries, conservation, and aquaculture. Bull. Mar. Sci. 83(1):107-130.
Martin, T., O.G. Ochou, M. Vaissayre, and D. Fournier. 2003. Organophosphorus insecticides synergize pyrethroids in the resistant strain of cotton bollworm, Helicoverpa armigera (Hubner) (Lepidoptera: Noctuidae) from West Africa. J. Econ. Entomol. 96(2):468-474.
McLaughlin, D.B., and V. Jain. 2011. Using Monte Carlo analysis to characterize the uncertainty in final acute values derived from aquatic toxicity data. Int. Environ. Assess. Manag. 7(2):269-279.
Mebane, C.A., and D.L. Arthaud. 2010. Extrapolating growth reductions in fish to changes in population extinction risks: Copper and Chinook salmon. Hum. Ecol. Risk Assess. 16(5):1026-1065.
Mochida, K., H. Amano, K. Ito, M. Ito, T. Onduka, H. Ichihashi, A. Kakuno, H. Harino, and K. Fujii. 2012. Species sensitivity distribution approach to primary risk analysis of the metal pyrithione photodegradation product, 2, 2’-dipyridyldisulfide in the Inland Sea and induction of notochord undulation in fish embryos. Aqua. Toxicol. 118-119:152-163.
Moe, S.J. 2007. Density dependence in ecological risk assessment. Pp. 69-92 in Population-Level Ecological Risk Assessment, L.W. Barnthouse, W.R. Munns, and M.T. Sorensen, eds. Boca Raton: CRC Press.
Moore, D.R.J., W.J. Warren-Hicks, S. Qian, A. Fairbrother, T. Aldenberg, T. Barry, R. Luttik, and H.T. Ratte. 2010. Uncertainty analysis using classical and Bayesian hierarchical models. Pp. 123-141 in Application of Uncertainty Analysis to Ecological Risks of Pesticides, W.J. Warren-Hicks, and A. Hart, eds. Pensacola, FL: SETAC Press.
Morris, W.F., and D.F. Doak. 2002. Quantitative Conservation Biology: Theory and Practice of Population Viability Analysis. Sunderland, MA: Sinauer Associates.
Mu, X., and G.A. LeBlanc. 2004. Synergistic interaction of endocrine disrupting chemicals: Model development using an ecdysone receptor antagonist and a hormone synthesis inhibitor. Environ. Toxicol. Chem. 23(4):1085-1091.
Munns, W.R., D.E. Black, T.R. Gleason, K. Salomon, D. Bengtson, and R. Gutjahr-Gobell. 1997. Evaluation of the effects of dioxin and PCBs on Fundulus heteroclitus populations using a modeling approach. Environ. Toxicol. Chem. 16(5):1074-1081.
Murphy, S.D., R.L. Anderson, and K.P. DuBois. 1959. Potentiation of toxicity of malathion by triorthotolyl phosphate. Proc. Soc. Exp. Biol. Med. 100(3):483-487.
Newman, M.C., D.R. Ownby, L.C.A. Mézin, D.C. Powell, T.R.L. Christensen, S.B. Lerberg, and B.A. Anderson. 2000. Applying species-sensitivity distributions in ecological risk assessment: Assumptions of distribution type and sufficient numbers of species. Environ. Toxicol. Chem. 19 (2):508-515.
Niederlehner, B.R., J. Cairns, Jr., and E.P. Smith. 1998. Modeling acute and chronic toxicity of nonpolar narcotic chemicals and mixtures to Ceriodaphnia dubia. Ecotoxicol. Environ. Saf. 39(2):136-146.
Nielsen, J.L. 1992. Microhabitat-specific foraging behavior, diet, and growth of juvenile coho salmon. T. Am. Fish. Soc. 121(5):617-634.
NMFS (National Marine Fisheries Service). 2008. Biological Opinion, Environmental Protection Agency Registration of Pesticides Containing Chlorpyrifos, Diazinon, and Malathion. National Marine Fisheries Service, Silver Spring, MD. November 18, 2008 [online]. Available: http://www.nmfs.noaa.gov/pr/pdfs/pesticide_biop.pdf [accessed Nov. 13, 2012].
NMFS (National Marine Fisheries Service). 2009. Biological Opinion, Endangered Species Act Section 7 Consultation, Environmental Protection Agency Registration of Pesticides Containing Carbaryl, Carbofuran, and Methomyl. National Marine Fisheries Service, Silver Spring, MD. April 20, 2009 [online]. Available: http://www.nmfs.noaa.gov/pr/pdfs/carbamate.pdf [accessed Nov. 12, 2012].
NMFS (National Marine Fisheries Service). 2010. Biological Opinion, Endangered Species Act Section 7 Consultation, Environmental Protection Agency Registration of Pesticides Containing Azinphos methyl, Bensulide, Dimethoate, Disulfoton, Ethoprop, Fenamiphos, Naled, Methamidophos, Methidathion, Methyl parathion, Phorate and Phosmet. National Marine Fisheries Service, Silver Spring, MD. August 31, 2010 [online]. Available: http://www.nmfs.noaa.gov/pr/pdfs/final_batch_3_opinion.pdf [accessed Nov. 13, 2012].
NMFS (National Marine Fisheries Service). 2011. Biological Opinion, Endangered Species Act Section 7 Consultation, Environmental Protection Agency Registration of Pesticides 2, 4-D, Triclopyr BEE, Diuron, Linuron, Captan, and Chlorothalonil. National Marine Fisheries Service, Silver Spring, MD. June 30, 2011[online]. Available: http://www.nmfs.noaa.gov/pr/pdfs/consultations/pesticide_opinion4.pdf [accessed Nov. 13, 2012].
NMFS (National Marine Fishers Service). 2012. NOAA Fisheries (NMFS) Response to Questions from the Committee on Ecological Risk Assessment under FIFRA and ESA, from Scott Hecht, NOAA, to David Policansky, March 30, 2012 [online]. Available: http://www.thecre.com/forum1/wp-content/uploads/2012/04/esanmfsatrazine.pdf [accessed Nov. 19, 2012].
Norgaard, K.B., and N. Cedergreen. 2010. Pesticide cocktails can interact synergistically on aquatic crustaceans. Environ. Sci. Pollut. Res. 17(4):957-967.
NRC (National Research Council). 1996. Upstream: Salmon and Society and Pacific Northwest. Washington, DC: National Academy Press.
NRC (National Research Council). 2003. Cumulative Environmental Effects of Oil and Gas Activities on Alaska’s North Slope. Washington, DC: National Academies Press.
OECD (Organisation for Economic Co-operation and Development). 2001. Harmonized Integrated Classification System for Human Health and Environmental Hazards of Chemical Substances and Mixtures. ENV/JM/MONO(2001)6. OECD Series on Testing and Assessment Number 33. OECD [online]. Available: http://iccvam.niehs.nih.gov/SuppDocs/FedDocs/OECD/OECD_hclfinaw.pdf [accessed Nov. 19, 2012].
Oliveira, A.G., L.F. Telles, R.A. Hess, G.A. Mahecha, and C.A. Oliveira. 2007. Effects of the herbicide Roundup on the epididymal region of drakes, Anas platyrhynchos. Reprod. Toxicol. 23(2):182-191.
Olmstead, A.W., and G.A. LeBlanc. 2005a. Toxicity assessment of environmentally-relevant pollutant mixtures using a heuristic model. Integr. Environ. Assessm. Manag. 1(2):114-122.
Olmstead, A.W., and G.A. LeBlanc. 2005b. Joint action of polycyclic aromatic hydrocarbons: Predictive modeling of sublethal toxicity. Aquat. Toxicol. 75(3):253-262.
Orlando, J.L., K.M. Kuivila, and A. Whitehead. 2003. Dissolved Pesticide Concentrations Detected in Storm-water Runoff at Selected Sites in the San Joaquin River Basin, California, 2000-2001. Open-File Report 03-101. U.S. Geological Survey, Reston, VA [online]. Available: http://pubs.usgs.gov/of/2003/ofr03101/pdf/ofr03101.pdf [accessed Nov. 19, 2012].
Orlando, J.L., L.A. Jacobson, and K.M. Kuivila. 2004. Dissolved Pesticide and Organic Carbon Concentrations Detected in Surface Waters, Northern Central Valley, California, 2001-2002. Open File Report 2004-1214. U.S. Geological Survey, Reston, VA [online]. Available: http://pubs.usgs.gov/of/2004/1214/ofr2004-1214.pdf [accessed Nov. 19, 2012].
Ortiz, D., L. Yanez, H. Gomez, J.A. Martinez-Salazar, and F. Diaz-Barriga. 1995. Acute toxicological effects in rats treated with a mixture of commercially formulated products containing methyl parathion and permethrin. Ecotoxicol. Environ. Saf. 32(2):154-158.
Palmqvist, A., and V.E. Forbes. 2008. Demographic effects of the polycyclic aromatic hydrocarbon, fluoranthene, on two sibling species of the Polychaete Capitella cap-itata. Pp. 200-212 in Demographic Toxicity: Methods in Ecological Risk Assessment, H.R. Akçakaya, J.D. Stark, and T.S. Bridges, eds. New York: Oxford University Press.
Pastorok, R.A., S.M. Bartell, S. Ferson, and L.R. Ginzburg, eds. 2002. Ecological Modeling in Risk Assessment: Chemical Effects on Populations, Ecosystems, and Landscapes. Boca Raton, FL: CRC Press.
Posthuma, L., G.W. Suter, and T.P. Traas, eds. 2001. Species Sensitivity Distributions in Ecotoxicology. Boca Raton, FL: CRC Press.
Puccia, C.J., and R. Levins. 1991. Qualitative modeling in ecology: Loop analysis, signed digraphs, and time averaging. Pp. 119-143 in Qualitative Simulation Modeling and Analysis, P.A. Fishwick, and P.A. Luker, eds. New York: Springer.
Quinn, T.P. 2005. The Behavior and Ecology of Pacific Salmon and Trout. Seattle: University of Washington Press.
Quinn, T.J., II, and R.B. Deriso. 1999. Quantitative Fish Dynamics. New York: Oxford University Press.
Raimondo, S., D.N. Vivian, C. Delos, and M.G. Barron. 2008. Protectiveness of species sensitivity distribution hazard concentrations for acute toxicity used in endangered species risk assessment. Environ. Toxicol. Chem. 27(12):2599-2607.
Raimondo, S., C.R. Jackson, and M.G. Barron. 2010. Influence of taxonomic relatedness and chemical mode of action in acute interspecies estimation models for aquatic species. Environ. Sci. Technol. 44(19):7711-7716.
RAMAS. 2011. Incorrectly modeling impact under density dependence. Avoiding Mistakes in Population Modeling: Density Dependence [online]. Available: http://www.ramas.com/CMdd.htm#ddimpact [accessed Apr. 18, 2013].
Rider, C.V., and G.A. LeBlanc. 2005. An integrated addition and interaction model for assessing toxicity of chemical mixtures. Toxicol. Sci. 87(2):520-528.
Rohr, J.R., J.L. Kerby, and A. Sih. 2006. Community ecology as a framework for predicting contaminant effects. Trends Ecol. Evol. 21(11):606-613.
Safe, S. 1998. Hazard and risk assessment of chemical mixtures using the toxic equivalency factor approach. Environ. Health Perspect. 106(suppl. 4):1051-1058.
Sahay, N., and R.A. Agarwal. 1997. MGK-264-Pyrethroid synergism against Lymnaea acuminata. Chemosphere 35(5):1011-1021.
Sandahl, J.F., D.H. Baldwin, J.J. Jenkins, and N.L. Scholz. 2005. Comparative thresholds for acetylcholinesterase inhibition and behavioral impairment in coho salmon exposed to chlorpyrifos. Environ. Toxicol. Chem. 25(1):136-145.
Sappington, L.C., F.L. Mayer, F.J. Dwyer, D.R. Buckler, J.R. Jones, and M.R. Ellersieck. 2001. Contaminant sensitivity of threatened and endangered fishes compared to standard surrogate species. Environ. Toxicol. Chem. 20(12):2869-2876.
Schleier, J.J., and R.K. Peterson. 2012. The joint toxicity of type I, II, and nonester pyrethroid insecticides. J. Econ. Entomol. 105(1):85-91.
Scholz, N.L., N.K. Truelove, B.L. French, B.A. Berejikian, T.P. Quinn, E. Casillas, and T.K. Collier. 2000. Diazinon disrupts antipredator and homing behavior in chinook salmon (Oncorhynchus tshawytscha). Can. J. Fish. Aquat. Sci. 57(9):1911-1918.
Scholz, N.L., N.K. Truelove, J.S. Labenia, D.H. Baldwin, and T.K. Collier. 2006. Dose-additive inhibition of chinook salmon acetylcholinesterase activity by mixtures of organophosphate and carbamate insecticides. Environ. Toxicol. Chem. 25(5):1200-1207.
Smyth, H.F., C.S. Weil, J.S. West, and C.P. Carpenter. 1969. An exploration of joint toxic action: Twenty-seven industrial chemicals intubated in rats in all possible pairs. Toxicol. Appl. Pharmacol. 14(2):340-347.
Solomon, K.R., T.C.M. Brock, D. de Zwart, S.D. Dyer, L. Posthuma, S.M. Richards, H. Sanderson, P.K. Sibley, and P.J. van den Brink. 2008. Extrapolation Practice for Ecotoxicological Effect Characterization of Chemicals. Pensacola, FL: SETAC Press. 380pp.
Spear, R.C. 1997. Large simulation models: Calibration, uniqueness and goodness of fit. Environ. Modell. Softw. 12(2-3):219-228.
Spencer, K.A., K.L. Buchanan, A.R. Goldsmith, and C.K. Catchpole. 2003. Song as an honest signal of developmental stress in zebra finch (Taeniopygia guttata). Horm. Behav. 44(2):132-139.
Spromberg, J.A., and L.L. Johnson. 2008. Potential effects of freshwater and estuarine contaminant exposure on lower Columbia River Chinook salmon (Oncorhynchus tshawytscha) populations. Pp. 123-142 in Demographic Toxicity: Methods in Ecological Risk Assessment, H.R. Akçakaya, J.D. Stark, and T.S. Bridges, eds. New York: Oxford University Press.
Stark, J.D. 2012. Demography and modeling to improve pesticide risk assessment of endangered species. Pp. 259-270 in Pesticide Regulation and the Endangered Species Act, K.D. Racke, B.D. McGaughey, J.L. Cowles, A.T. Hall, S.H. Jackson, J.J. Jenkins, J.J. Johnston, eds. ACS Symposium Series 111. Washington, DC: American Chemical Society.
Suttle, K.B., M.E. Power, J.M. Levine, and C. McNeely. 2004. How fine sediment in riverbeds impairs growth and survival of juvenile salmonids. Ecol. Appl. 14(4):969-974.
Taylor, E.B. 1990. Environmental correlates of life-history variation in juvenile chinook salmon, Oncorhynchus tshawytscha (Walbaum). J. Fish Biol. 37(1):1-17.
TenBrook, P.L., A.J. Palumbo, T.L. Fojut, P. Hann, J. Karkoski, and R.S. Tjeerdema. 2010. The University of California-Davis methodology for deriving aquatic life pesticide water quality criteria. Rev. Environ. Contam. Toxicol. 209:1-155.
Thompson, H.M. 1996. Interactions between pesticides: A review of reported effects and their implications for wildlife risk assessment. Ecotoxicology 5(2):59-81.
Topping, C.J., R.M. Sibly, H.R. Akçakaya, G.C. Smith, and D.R. Crocker. 2005. Risk assessment of UK skylark populations using life-history and individual-based landscape models. Ecotoxicology 14(8):925-936.
Verhoef, H.A., and P.J. Morin. 2010. Community Ecology: Processes, Models, and Applications. New York: Oxford University Press. 247pp.
Verma, S.R., S. Rani, S.K. Bansal, and R.C. Dalela. 1980. Effects of the pesticides thiotox, dichlorvos and carbofuran on the test fish Mystus vittatus. Water Air Soil Pollut. 13(2):229-234.
Walter, H., F. Consolaro, P. Gramatica, M. Scholze, and R. Altenburger. 2002. Mixture toxicity of priority pollutants at No Observed Effect Concentrations (NOECs). Ecotoxicology 11(5):299-310.
Warren-Hicks, W.J., and A Hart, eds. 2010. Application of Uncertainty Analysis to Ecological Risks of Pesticides. Pensacola, FL: SETAC Press.
Werner, I., L.A. Deanovic, D. Markiewicz, M. Khamphanh, C.K. Reece, M. Stillway, and C. Reece. 2010. Monitoring acute and chronic water column toxicity in the northern Sacramento-San Joaquin estuary, California, USA, using the euryhaline amphipod, Hyalella azteca: 2006 to 2007. Environ. Toxicol. Chem. 29(10):2190-2199.
WHO (World Health Organization). 1994. Glyphosate. Environmental Health Criteria 159. Geneva: World Health Organization [online]. Available: http://www.inchem.org/documents/ehc/ehc/ehc159.htm [accessed Feb. 19, 2013].
Williams, G.M., R. Kroes, and I.C. Munro. 2000. Safety evaluation and risk assessment of the herbicide Roundup and its active ingredient, glyphosate, for humans. Regul. Toxicol. Pharmacol. 31(2 Pt 1):117-165.
Willson, J.D., W.A. Hopkins, C.M. Bergeron, and B.D. Todd. 2012. Making leaps in amphibian ecotoxicology: Translating individual-level effects of contaminants to population viability. Ecol. Appl. 22(6):1791-1802.

























































