Science Drivers—Condensed Matter and Materials Physics
Most applications of high magnetic fields to the study of condensed matter systems have been concerned with “hard” condensed matter systems—typically, rigid solids or structures fabricated from such solids. These would include the surfaces of solids and interfaces between solids, small particles of a solid, wires with nanometer-scale diameters, and two-dimensional materials such as graphene, which is regular and practically rigid even though it is just a single layer of carbon atoms.
The properties of hard condensed matter systems are determined by the Coulomb forces between electrons and the constituent ions and by the constant motion of the electrons, dictated by the microscopic laws of quantum mechanics. Scientific research seeks to understand how these fundamental laws lead to huge diversity in the macroscopic behavior of different materials, nanostructures, and devices. With increased understanding comes the ability to design and optimize materials to attain desired technological goals and, on occasion, to conceive of radically new technologies that can have a profound effect on our lives.
Magnetic field studies have been a very important tool for exploring the electronic structure of condensed matter systems. Although applied magnetic fields in many cases have a relatively small effect on the overall electronic structure, they enable experimental techniques that can reveal properties of the underlying electronic structure that would be otherwise inaccessible. In other cases, magnetic field effects can be strong enough to drastically change the nature of the electronic state
itself. In either situation, access to higher magnetic fields is important to allow the study of new materials and new phenomena.
Magnetic fields couple most strongly to the electrons in a material, either by acting on electrical currents generated by the electrons’ quantum mechanical motion, or by coupling to the magnetic moments arising from the electrons’ intrinsic spin. These coupling mechanisms are indeed the basis for the majority of experiments using high magnetic fields to study the electronic structure of materials. However, the much weaker coupling of magnetic fields to the magnetic moments of nuclear spins is also important, as it is the physical basis for nuclear magnetic resonance (NMR) techniques. Although NMR techniques are most widely used in studies of chemical and biological systems, which will be discussed in Chapters 3 and 4, NMR techniques can also be used to extract information about the electrons in condensed matter systems by measuring changes in the nuclear response that arise from magnetic interactions between the nuclei and the electrons. For example, NMR measurements have played a key role in elucidating the fundamental properties of electrons in superconductors, two-dimensional electron systems, and antiferromagnets.
The electronic structures of condensed matter systems can vary in many ways. Materials may be either electrical conductors or insulators, whose conductivities may differ by many orders of magnitude, even at room temperature. At low temperatures, some materials are superconductors, which can carry currents with no resistance at all. In many systems, both insulators and conductors, electrons on individual atoms can develop magnetic moments, which may order at low temperatures in a variety of ways. In other cases, instabilities in the electron system can lead to spatially periodic oscillations in the charge density and/or to displacements in atomic positions that change the symmetry of the crystal, and may lead to macroscopic electric dipole moments (ferroelectricity). In some cases, magnetic moments and atomic displacements are coupled, and magnetic fields can be used to influence electric polarizations. Of particular interest are systems that may change from one form of order to another as a function of temperature, pressure, or alloy composition; such materials may have very peculiar properties close to their phase transitions. Magnetic fields may provide a way for studying such phase transitions, and in some cases they may be strong enough to directly influence these transitions.
Crystalline materials are typically characterized by an electronic band structure, which specifies a discrete set of allowed electron energies for each possible electron momentum. Metals, which are good conductors of electricity, will typically have a surface in momentum space, known as the Fermi surface, separating occupied electron states, whose energies lie below a cutoff (the Fermi energy), from empty states, whose energies lie above the cutoff. Electrons close to the Fermi surface are of particular interest because they play a dominant role in electrical transport and many other properties of the material. Strong magnetic fields can lead to
oscillations in transport and other electronic properties, whose periods depend on the precise size and shape of the Fermi surface. The ability to extract information about the Fermi surface through measurement of these oscillations is one reason magnetic fields are such an important tool for studying conducting materials.
Magnetic fields are particularly vital in the study of superconducting materials. Typically, superconductors will expel magnetic fields up to a certain field strength, denoted the lower critical field, Hc1. Above Hc1, magnetic fields will enter, but the material retains superconducting properties up to an upper critical field, Hc2. Measurement of the critical fields, as a function of temperature and orientation of the sample, gives important information about the underlying parameters of the superconductor. Superconductors with very large values of Hc2 are of special interest, because it is precisely those superconductors that have potential for use in the construction of high-field superconducting magnets.
A relatively new direction of high magnetic field research is in the area of soft condensed matter, which encompasses a variety of physical systems that are soft in the sense that they can be easily deformed by mechanical or thermal stress or electric and magnetic fields. Such systems include polymers, gels, colloids, membranes, and biological cells or organisms. The binding between molecules in these mostly organic or biological materials (hydrogen bonding, van der Waals, or π-π bonding) is much weaker than in normal solids. High magnetic fields can be used to assemble and align functional, organic or inorganic, nano- and microstructures and to probe their structures, properties, and dynamics, with potential applications in drug delivery, optics, sensors, and nanoelectronics. Applications of high magnetic fields in these experiments make use of the torque exerted by a magnetic field on an object with an anisotropic diamagnetic susceptibility or the force exerted on any object by a strong gradient in field strength.
In the remainder of this chapter, a number of examples are discussed where high magnetic fields play a critical role in condensed matter research.
All systems are disordered if the temperature is large enough, with no discernible correlations or patterns in time or space for the configurations of the particles that make up the system. In most solid materials, the particles of interest are the electrons, which carry both a charge and a magnetic moment. Interactions among these electrons can lead to instabilities in their overall energy that are resolved in most cases by the establishment of some type of order. Some compounds order magnetically, when the magnetic moments of individual atoms spontaneously take on long-lived and spatially periodic patterns that create internal magnetic fields as the temperature is reduced. In some cases, materials are transformed from metals, where electrons are free to move and carry current, to insulators, where
they become spatially localized and thus incapable of carrying electrical current. Some metals can become superconducting, where a condensed state is formed that consists of electron pairs with opposite moments and opposite momenta, capable of carrying electrical current without dissipating energy. Order is overwhelmingly favored as the temperature is lowered toward absolute zero, where the system is said to enter its lowest energy, or ground, state. Most systems become ordered at nonzero transition temperatures, but in some cases this order can be suppressed to progressively lower temperatures by varying a parameter such as pressure or the electric or magnetic field, or simply by changing the composition of the material in question. An extremal ordered state occurs when the transition temperature is continuously suppressed to zero temperature, forming a quantum critical point (QCP). Here the system is poised just on the verge of becoming ordered, and in the absence of this order it fluctuates wildly and unpredictably among configurations where order is only present on short length scales and for short times (Hertz, 1976; Millis, 1993; Sachdev, 1999; Sachdev, 2008).
Much of the functionality that we demand of modern materials depends on the presence of these collective electronic instabilities, as they lead to different and competing ground states: superconductivity, and full or partial charge, orbital, and magnetic order. Controlling the relative stabilities of these ground states by means of external parameters such as electric or magnetic field, chemical variation, pressure, or temperature lends these materials their technological value as novel sensors, or as active elements in electrical or mechanical systems. Indeed, the greatest sensitivity to external variables, and the most complex interplay of energy scales, is generically found near QCPs. It is widely believed that materials with the most extremized functionality require the near balance of competing ground states, and examples of families hosting these QCPs have been documented in virtually every class of material where strong electronic correlations are possible. The most celebrated example is the emergence of superconductivity with the extinguishing of magnetic order in f-electron-based heavy fermion compounds (Mathur et al., 1998), as well as in the iron-pnictide and cuprate superconductors. One of the earliest QCPs studied involves the interplay of superconductivity and charge density wave instabilities in layered chalcogenides (Morosan et al., 2006), in conductors formed from organic molecules (Jaccard et al., 2001), and even in the A-15 family that hosts the most widely used conventional superconductors Nb3Sn and NbTi (Bilbro and McMillan, 1976). Of particular interest for applications is the symbiosis of ferroelectricity and magnetic order present in multiferroic compounds (Rowley et al., 2010; Kim et al., 2009).
Quantum criticality, when ordering is prohibited at any nonzero temperature and occurs only at zero temperature, is increasingly believed to be a central feature of the phase behaviors of virtually every class of correlated electron system from the f-electron-based heavy fermions (Gegenwart, 2008; Von Lohneysen and
Wolfle, 2008), to complex oxides that include cuprates (Broun, 2008), as well as low-dimensional conductors (Jaccard, 2001), and three-dimensional-based metals with magnetism such as the Fe pnictides and chalcogenides (Dai et al., 2009). Very few compounds form with magnetic order possible only at zero temperature, and in most cases it is necessary to use pressures, compositions, or magnetic fields to tune the ordering temperature to zero degrees to form a QCP if magnetic order is continuous, or a quantum end point (QEP) if the magnetic transition becomes discontinuous or first order. Quantum critical (QC) compounds can be exquisitely sensitive to disorder, making compositional tuning problematic. Pressure tuning has an appealing simplicity, although the bulky equipment needed for high-pressure measurements may limit experimental access, particularly for thermodynamic measurements, which are of particular value for understanding how cooperative phases are stabilized at the lowest temperatures. For all these reasons, magnetic field B tuning is increasingly attractive, particularly if it is paired with low temperatures T to span an extended range of B/T. Since ordering temperatures are emergent scales, the fields required to suppress order may be very small, as in YbRh2Si2, where only 0.6 T is required to drive the 0.065 K Neel temperature to zero degrees (Custers et al., 2003), or very large, as in SrCu2(BO3)2, where 20 T is required to induce magnetic order via the Bose-Einstein condensation of dimer triplets (Kageyama et al., 1999).
Systems where QCPs dominate have remarkable properties that challenge our understanding of such apparently simple concepts as metallic conduction. When magnetic fields suppress magnetic order in heavy fermions, or superconductivity in YBCO (Sebastian et al., 2010) to expose bare QCPs, the electrical resistivity ñ becomes linear in temperature, although the quadratic temperature dependence of a normal metal is regained when the system is tuned sufficiently far from the QCP (Custers et al., 2003). The violation of the Wiedemann-Franz law in CeCoIn5 near the field-tuned QCP (Tanatar et al., 2007) implies that the entities that carry charge and heat are very different from the familiar conduction electrons found in normal metals. Indeed, the familiar idea that electrical current is carried by individual electrons, or quasiparticles, must itself fail when the strong QC fluctuations limit their lifetime to be less than ħ/E, given by the Uncertainty Principle (Smith et al., 2008). It is not yet known how universal these observations are, and we have yet to even scratch the surface on how we might exploit these unusual metals to manipulate charge, spin, and heat to provide novel functionalities. These unconventional metals prove to have novel ground states, once the more familiar magnetic order is suppressed (Julian, 1996). Of most interest is the unconventional superconductivity that often is revealed when pressure or composition is used to suppress magnetic or charge order to a temperature of zero degrees. Indeed, this idea has become close to a prescription for finding new families of superconductors (Basov and Chubokov, 2011). Surely the discovery of field-induced superconductivity in ferromagnetic
UGe2 and URhGe represents the most exotic realization of the expectation that unconventional superconductors are stabilized by the plethora of low-energy excitations that proximity to QCPs can afford (Lévy et al., 2005).
Superconductivity is not the only instability that is found when magnetic order becomes impossible beyond its QCP. One option, found in systems as diverse as Sr3Ru2O7, Co-doped BaFe2As2, and possibly cuprates, is partial or nematic electronic order where there is a spontaneously broken rotation symmetry that does not involve the breaking of translational symmetry (Fradkin et al., 2010). High magnetic fields have been instrumental for delineating the full phase behaviors for these systems, most notably in URu2Si2 (Figure 2.1). Here, the nature of the “hidden” order parameter remains uncertain (Kim et al., 2003; Mydosh and Oppeneer, 2011), although it has recently been proposed to be an electronic nematic as well (Okazaki et al., 2011). It seems likely that new types of order will emerge as higher fields and more sophisticated measurement techniques become available.
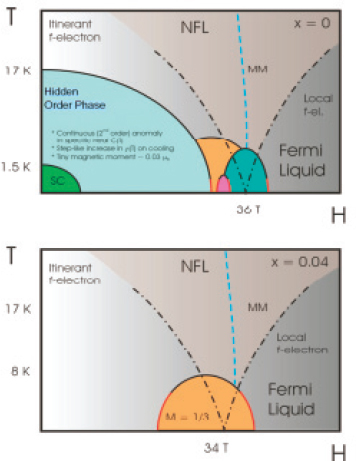
FIGURE 2.1 Sketch of the high magnetic field T-H phase diagrams for URu2Si2 and U(Ru0.96Rh0.04)2Si2. MM, metamagnetic transitions; NFL, non-Fermi liquid; and phase II is colored in orange. SOURCE: Reprinted figure with permission from J.A. Mydosh and P.M. Oppeneer, 2011, Colloquium: Hidden order, superconductivity, and magnetism: The unsolved case of URu2Si2, Reviews of Modern Physics 83: 1301-1322, Figure 12. Copyright 2011 by the American Physical Society.
The electronic states of the system itself may also be in transition at the QCP, where the system may fluctuate between very different states such as a localized moment antiferromagnet and a nonmagnetic metal, where order persists only in the form of strong electronic correlations with limited range and lifetime (Figure 2.2). This dual role for the QCP as an electronic delocalization transition implies that there is an associated Fermi surface volume change. Indeed, Hall effect measurements on YbRh2Si2 (Paschen et al., 2004) and quantum oscillation studies of CeIn3 (Harrison et al., 2007) and CeRhIn5 (Shishido et al., 2005) have provided evidence for this quantum critical breakdown of the Fermi surface. It is clear that quantum oscillation measurements like the ones carried out on f-electron-based heavy fermions have been instrumental for establishing the link between QC and electronic delocalization, and the application of these ideas to other types of QC systems is an important area of future effort. High fields and low temperatures are particularly needed to resolve the heavy mass parts of the Fermi surface, which seem to be most strongly impacted by proximity to the QCP (McCollam et al., 2005).
Our understanding of quantum critical matter is driven forward by the continuous discovery of new materials with new and remarkable properties. The exploration of the phase behaviors of these new compounds is crucial, and there is an underlying expectation that there is an overarching phase diagram, with individual compounds representing various regimes of this master phase diagram. Magnetic fields, especially if they can be combined with other variables like pressure, are important not only for tuning the strength of order but also as a thermodynamically relevant scaling variable. There is every reason to believe that the availability of high fields will lead to the discovery of new types of QCPs and ordered phases, both in existing materials and in those that are yet to be discovered.
Innovations in high-field measurement techniques over the past decade have greatly accelerated progress. It is not enough to use high fields to access a novel ordered phase. Also needed is an experimental description of the thermodynamic and transport properties of this new phase. New techniques for carrying out measurements of the specific heat (Jaime et al., 2000), magnetocaloric effect (Kohama et al., 2010), and magnetostriction (Jaime et al., 2012) in pulsed fields have greatly increased the types of basic information available about these high-field phases, enabling a full thermodynamic analysis. Many of these innovations have been made possible by the availability of long-pulse magnets. In this vein, the availability of higher field magnets for neutron scattering experiments can similarly be expected to be transformative.
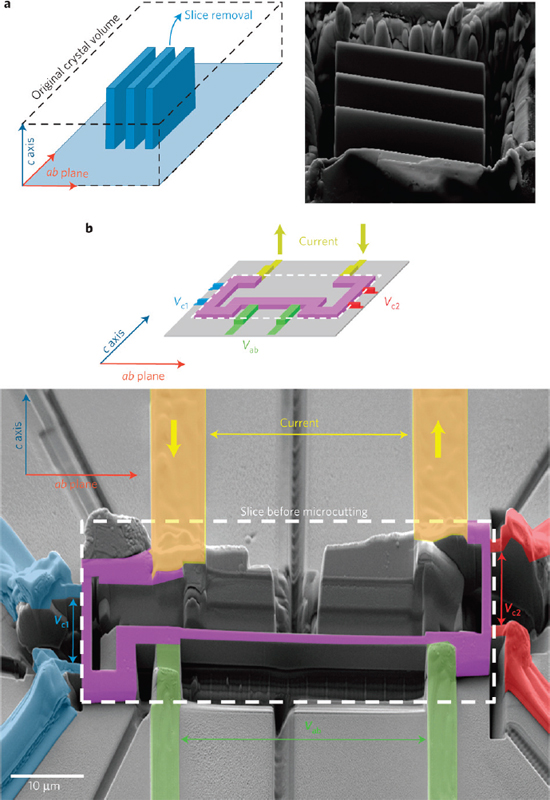
One of the most significant technical advances in pulsed field measurement techniques has been the application of focused ion beams (FIB) for shaping single crystals (Moll et al., 2010). Electrical resistivity measurements have been limited in the past by eddy current heating, while low signal-to-noise ratios made measurements on good conductors problematic. Both of these problems can be largely
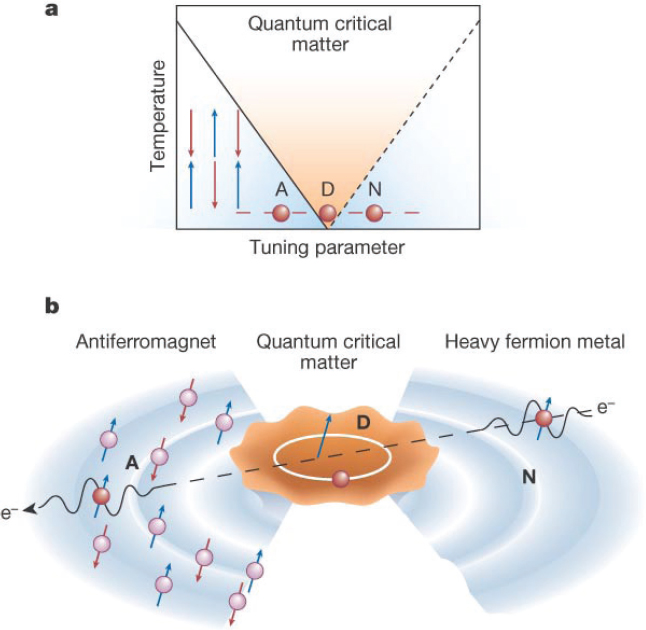
FIGURE 2.2 (Below) Schematic phase diagram near a QCP. QCPs distort the fabric of the phase diagrams creating a V-shaped phase of quantum critical matter fanning out to finite temperatures from the quantum critical point. As matter is tuned to quantum criticality, ever-larger droplets of nascent order develop. On length-scales greater than these droplets, electrons propagate as waves. Inside the droplet, the intense fluctuations radically modify the motion of the electron and may lead to its breaking up into its constituent spin and charge components. (Above) Physics inside the V-shaped region of the phase diagram probes the interior of the QCPs (D), whereas the physics in the normal metal (N) or antiferromagnet (A) reflects their exterior. If, as we suspect, quantum critical matter is universal, then no information about the microscopic nature of the material penetrates into the droplets. Making an analogy with a black hole, the passage from noncritical to critical quantum matter involves crossing a “material event horizon.” Experiments that tune a material from the normal metal past a QCP force electrons through the “horizon” in the phase diagram into the interior of the quantum critical matter, from which they ultimately reemerge through a second horizon on the other side into a new universe of magnetically ordered matter. SOURCE: Reprinted by permission from Macmillan Publishers Ltd.: Nature. P. Coleman and A.J. .Schofield, 2005, Quantum criticality, Nature 433: 226-229. Copyright 2005.
overcome using FIB to shape single crystal samples to have small cross sections, and by tailoring the sample dimensions and current to target the needed voltage levels for a successful measurement (Figure 2.3). FIB processing also allows the deposition of high-conductivity contacts, avoiding surface oxidation issues. It is possible that FIB processing of samples will also make high-pressure resistance measurements less challenging, possibly opening the door to the more routine use of high pressures and high dc fields for the exploration of QC matter. A range of new experimental applications can be contemplated, including quantum oscillation measurements (Sebastian et al., 2012), the implementation of devices where the sample charge and spin transport can be modified independently of the magnetic field, and even the simultaneous measurement of electrical transport with other quantities such as thermal conductivity or specific heat. One of the main constraints on pulsed magnets has been the need to provide slow rise times to avoid eddy current heating and similar experimental considerations. FIB has the potential to provide better control over these parameters, making experiments in magnets with faster rise times and thus higher peak fields feasible. It is generally believed that the next generation of higher field pulsed magnets for user science would require new innovations in the development of high strength/high conductivity materials for the magnet conductors. Implementation of FIB processing may mean that much higher pulsed fields could be available for user science soon, with the promise of expansion to even higher fields as improved magnet conductors become available.
FIGURE 2.3 Four-probe resistance bars for simultaneous c-axis and ab-plane resistivity measurements carved out of a SmFeAsO0.7F0.25 single crystal using the FIB. (Top) A crystal is positioned on a substrate with the c axis pointing perpendicular to the plane. The dashed volume indicates the original crystal that is removed during FIB cutting, leaving only the lamellar standing. (Bottom) The lamella is transferred to another substrate and flipped, so that its c axis is now aligned in the plane (short edge). Most of this lamella (dashed line) is again removed, leaving only the small current path standing (violet). Eight platinum leads are deposited onto the crystal edges (all other colors) that are connected to the resistance bars by narrow (~800 nm for c axis) crystal bridges. The common current is injected through the yellow contacts and traverses two c-axis resistance bars (blue and red voltage contacts) and one along the ab plane (green and violet contacts). Dimensions of resistance bars: length ~35 μm (ab plane), ~5 μm (c axis), cross section ~1.5 μm2. SOURCE: Reprinted by permission from Macmillan Publishers Ltd.: Nature Materials. P.J.W. Moll, R. Puzniak, F. Balakirev, K. Rogacki, J. Karpinski, N.D. Zhigadlo, and B. Batlogg, 2010, High magnetic-field scales and critical currents in SmFeAs(O,F) crystals, Nature Materials 9:628-633. Copyright 2010.
HIGH MAGNETIC FIELD STUDIES OF LOW-DIMENSIONAL, FRUSTRATED, AND QUANTUM MAGNETS
In conventional magnetic materials, such as ferromagnets and antiferromagnets, a quantity of immediate interest is the temperature at which there is an onset of long-range order among the atomic moments, or spins. Above this “critical” temperature, Tc, the spins are disordered in space and fluctuate randomly in time as a result of thermal fluctuations. Below Tc, the spins freeze into a static pattern with long-range order, wherein the identification of the orientation of a spin anywhere in the sample defines the orientation of all others. The simplest theory for predicting Tc is the so-called “mean field theory.” In mean field theory, the magnitude of Tc is proportional to the interaction energy between neighboring spins and to the number of neighbors. An applied magnetic field will also change Tc in different ways depending on the type of long-range order and depending on the magnitude of the applied field. In order to assess whether a field is high enough to affect a change in Tc, one converts field strength to temperature by considering the energy difference between a spin that is aligned and one that is antialigned with the field. This energy is given by gμBH, where g ~ 2, μB is the Bohr magneton (atomic unit of magnetism), and H the applied field. For H equal to 1 tesla, this energy is equivalent to a thermal energy of 1.3 K. Thus, in order to substantially affect a long-range ordered state, a field with strength equivalent to Tc must be applied. For most single investigators using helium-cooled superconducting solenoids, a field strength of 10 tesla is readily obtainable, thus allowing the modification of materials with Tc up to only ~13 K. In this section the committee considers classes of magnets where Tc is suppressed compared to predictions based on mean field theory. In some cases, this is accompanied by a smaller field scale, required to alter the ordered state.
The effects of low-dimensionality, frustration, and quantum zero point motion all conspire to suppress the mean field Tc in magnets by promoting fluctuations that destabilize the order. Such factors not only reduce Tc but can also give rise to new, previously unexpected states of matter as well as exotic excitations. Low dimensionality, frustration, and quantum zero point motion are all fixed by the material’s composition and crystal structure so that their effects in suppressing long-range order can only be inferred from intermaterials comparisons. Applied magnetic fields offer a way to tune these effects, either by stabilizing them (as for ferromagnetic fluctuations) or destabilizing them (as for antiferromagnetic fluctuations). Thus, magnetic fields are essential tools for studying new phases of magnetic matter, and the committee discusses the role of high magnetic fields in understanding exotic states.
The crystal structures allowed in our three-dimensional Euclidean space demonstrate a variety of low-dimensional substructures. For example, materials with a micaceous crystal structure can provide an effective two-dimensional (2D) space in which magnetic ions within a layer interact more strongly with one another than with ions in other layers. Structures also exist that promote 1D interactions along chains of ions. The most prominent difference between such quasi-1D or quasi-2D systems and 3D materials is a reduction of the critical temperature, Tc, at which long-range order appears. A decrease in Tc is expected from mean field theory since Tc varies with the number of nearest neighbors as well as the interaction energy between neighboring ions. In a simple 3D cubic lattice, every ion has six neighbors, whereas this number is four for a square 2D lattice and two for a chain 1D lattice. Theories that go beyond mean field theory and take into account fluctuations of ionic spins show that these fluctuations further reduce Tc. For instance, the Ising model of 1D magnets shows that Tc for a chain system is not just less than its 3D counterpart by a factor of three, rather it is zero, reflecting the fact that only one spin that is pointing in the wrong direction can destroy the ordered state, which is not too surprising since in 1D there is only one path to communicate the ordering information. In quasi-2D magnets, fluctuations that prevent traditional long-rage order can lead to exotic types of order, such as the Kosterlitz-Thouless state of quasi-long-range order, where the correlations among spins are not long range but decay as a power of their separation. Such low-dimensional systems also exhibit unusual excitations from the ground state that are not observed in 3D. One example in 1D is that of the sine-Gordon soliton, an excitation that travels without losing its shape—that is, it is dispersionless due to the mathematics of nonlinear fields in one dimension. Such excitations were observed 30 years ago in the quasi-1D system CsNiF3, as distinct signatures in the magnetic field behavior of the thermodynamics of the Ni-centered spin. In quasi-2D systems, such as the BaNi2(PO4)2, vortex excitations of a Kosterlitz-Thouless state are strongly implied by inelastic neutron scattering studies. In both materials, the Ni spins are constrained by microscopic electric fields to lie in a plane, a feature that stabilizes the topological soliton and vortex excitations for a reason similar to the reason one can lasso a zucchini but not an orange (see Figure 2.4).
Another example of the importance for high-field studies of quasi-1D magnets is given by the work of Oshikawa et al. (1997). They showed that for 1D spin chains with strong quantum fluctuations, the magnetization is topologically quantized as a function of magnetic field, a phenomenon that bears similarity to the quantum Hall effect observed in 2D electron metals in a magnetic field. A physical realization of this theory is found in the azurite structure compound Cu3(CO3)2(OH)2, shown in Figure 2.5. Here, the s = ½ Cu ions form a linear chain with alternating numbers
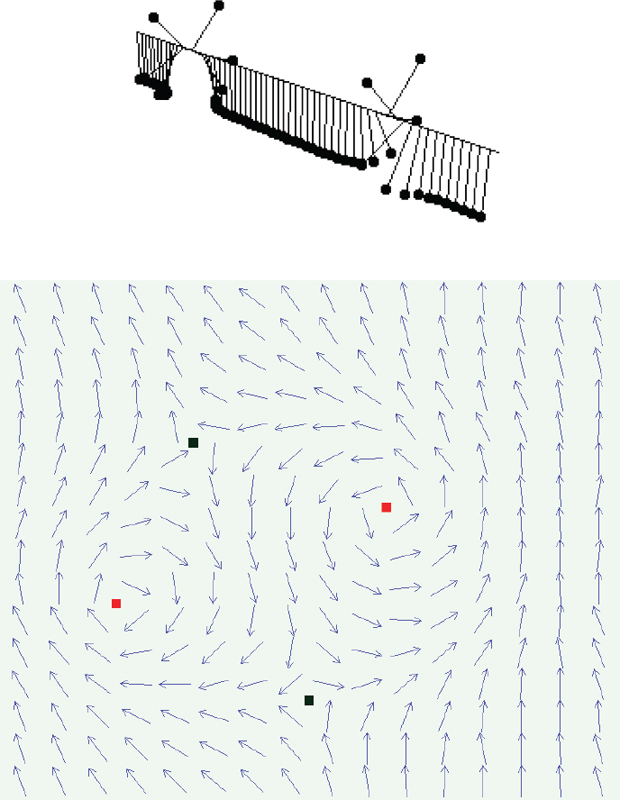
FIGURE 2.4 (Top) A pair of solitons of opposite sign in a 1D chain, where the pendula represents spins. (Bottom) Vortices on a 2D spin system. SOURCE: (Top) Courtesy of Kanehisa Takasaki, Kyoto University. (Bottom) Courtesy of Evgeny Demidov, Institute for Physics of Microstructures, Russian Academy of Sciences.
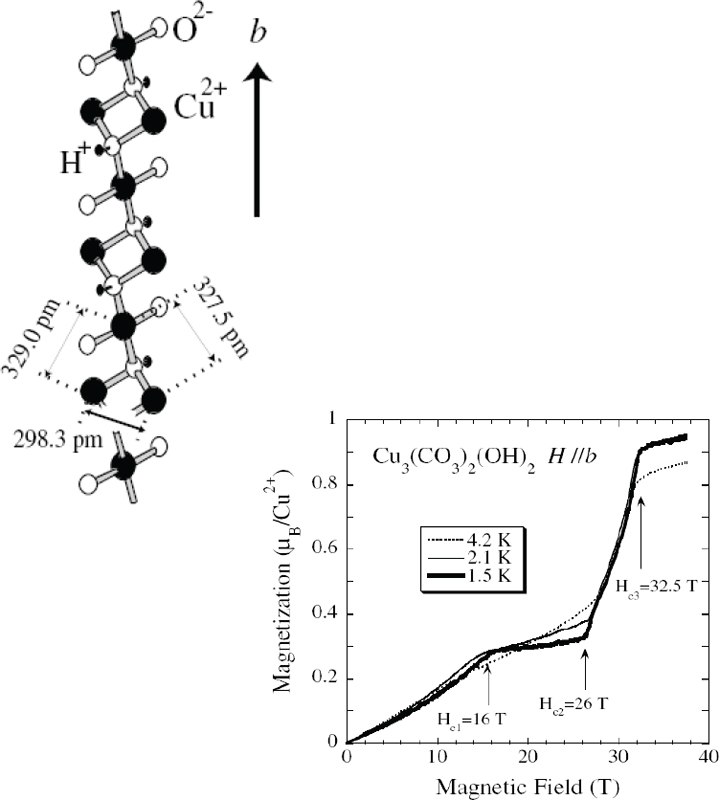
FIGURE 2.5 (Left) Schematic view of the crystal structure of the azurite Cu3(CO3)2(OH)2 along the b axis. (Right) The high-field magnetization of Cu3(CO3)2(OH)2 measured below 4.2 K. SOURCE: (Left) Reprinted figure with permission from H. Kikuchi, Y. Fujii, M. Chiba, S. Mitsudo, T. Idehara, T. Tonegawa, K. Okamoto, T. Sakai, T. Kuwai, and H. Ohta, 2005, Experimental observation of the ⅓ magnetization plateau in the diamond-chain compound Cu3(CO3)2(OH)2, Physical Review Letters 94:227201, Figure 1(b). Copyright 2005 by the American Physical Society. (Right) Reprinted figure with permission from the same source, Figure 2(a).
of nearest neighbors on the chain, the so-called “diamond spin chain.” The figure shows this structure and the magnetization, which demonstrates a field-induced state having ~ ⅓ of the saturation magnetization. In the Oshikawa et al. picture, this plateau is associated with a periodic modulation of the local magnetization along the chain. This is one example of how magnetic fields can create exotic states of matter.
Another example of the importance of high magnetic fields for quasi-1D magnets is the spin chain system CoNb2O6. In this compound, the cobalt spins are of the Ising type, meaning that the spin direction is constrained by local atomic forces to point along a single direction, the Ising axis. For a spin ½ ion, such as divalent Co, such constraint leads to two distinct quantum states, aligned and anti-aligned when the magnetic field is applied along the Ising axis. When a magnetic field is applied perpendicular to this direction, however, the system’s eigenstates are a combination of the two original states. While the dominant interactions in CoNb2O6 are along the chain, weak interchain interactions induce antiferromagnetic 3D ordering below 2.95 K in zero field. This order can also be destroyed by applying a transverse magnetic field greater than 5.5 tesla near 0 K. At this quantum critical transverse field of the Ising chain, a degenerate spectrum of eight quasiparticles has been theoretically predicted. In order to observe these quasiparticles, a small additional field was applied along the Ising direction and inelastic neutron scattering was performed. As shown in Figure 2.6, left, peaks corresponding to the energy loss of the neutron beam are observed at well-defined energies. The ratio between the energies of these first two peaks is shown to the right, where it is seen that, as the transverse field approaches the critical value of 5.5 tesla, this ratio approaches the golden mean, as predicted by the theory. The emergence of a field theory with eight massive particles arising only from an Ising chain system in a magnetic field is a spectacular example of how complex states of matter can arise from a set of simple ingredients.
Organic molecules are the basis for a large number of molecular magnets. These molecules tend to be flat—C60 being a well-known exception—and thus the resulting crystal structures typically resemble stacks of molecules. In these structures, the shortest van der Waals bond between stack edges defines the dimensionality of charge transport or dominant magnetic order, and this dimensionality is often quasi-1D or quasi-2D. The prevalence of 1D interactions among organics makes them ideal systems in which to study Fermi-surface instabilities such as Peierls or spin-Peierls transitions. Also, due to the large effective distance between molecules containing a transition metal ion, the mean field energy scale for magnetism can be low and therefore easily destroyed by magnetic field. The interplay
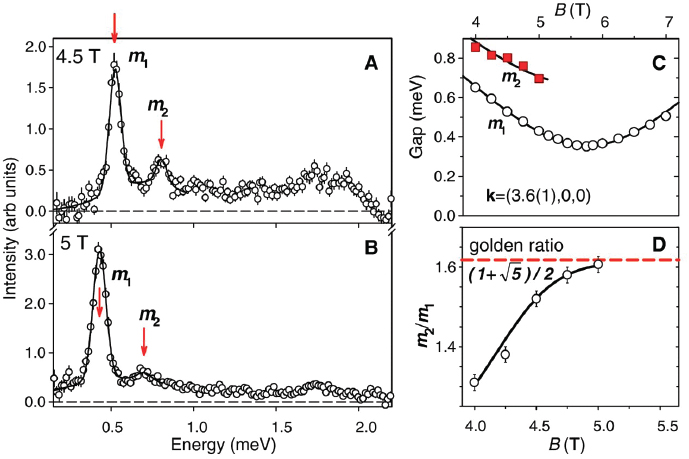
FIGURE 2.6 (A and B) Energy scans at the zone center at 4.5 and 5 tesla (T) showing two peaks, m1 and m2, at low energies. (C) softening of the two energy gaps near the critical field (above ~5 T the m2 peak could no longer be resolved). The incomplete gap softening is attributed to the interchain couplings as described in the text. (D) The ratio m2/m1 approaches the golden ratio (dashed line) just below the critical field. SOURCE: From R. Coldea, D.A. Tennant, E.M. Wheeler, E. Wawrzynska, D. Prabhakaran, M. Telling, K. Habicht, P. Smeibidl, and K. Kiefer, 2010, Quantum criticality in an Ising chain: Experimental evidence for emergent E8 symmetry, Science 327:177-180. Reprinted with permission from AAAS.
between such magnetism and charge transport is demonstrated in the compound λ-(BETS)2FeCl4, which possesses a low-field antiferromagnetic state with BETS standing for bis(ethylenedithio)-tetraselenafulvalene. Near fields of 18 tesla, the antiferromagnetic state is destroyed and a superconducting state appears, eventually being destroyed itself at 41 T.
Organic crystalline systems are also well-suited to study magnetic quantum effects in low dimensions due to the commonality of free radicals, which have an unpaired electron, which often leads to a spin-½ moment on the molecule. In the quasi-2D organic system κ-(BEDT-TTF)2Cu2(CN)3 (BEDT-TTF stands for bis(ethylenedithio)tetrathiafulvalene), the presence of this spin-½ moment has led to the observation of quantum spin liquid behavior, related to the frustrating effects of a triangular lattice in this compound. The interplay of magnetism and
superconductivity demonstrated in λ-(BETS)2FeCl4, mentioned above, suggests a compelling motivation for the continued study of organic compounds in high magnetic fields. The molecular nature of organics allows, in principle, the decoupling of the pairing excitation from the lattice, the so-called Little mechanism for superconductivity. This mechanism has never been confirmed as originally envisioned, although superconductivity in alkali-doped C60, which is mediated by intra-molecular vibrations, bears some similarity. It is conceivable that ordinary magnetism in organics is a common mask for a superconducting state that is revealed only in very high magnetic fields. Superconductors uncovered in this manner would provide intriguing examples motivating possible synthetic routes for new superconductors in low fields.
The concept of frustration in magnetic materials is relatively simple. A conventional unfrustrated long-range-ordered antiferromagnetic state is depicted in the left hand side of Figure 2.7. Here, each arrow represents an ionic spin in a 2D Ising magnet, as would be realized in the low-temperature state of CoCs3Br5, for example. In such systems, the magnetic (antiferromagnetic) interaction is compatible with the lattice in the sense that there exists an ordered state in which each magnetic bond can minimize its energy. To the right is shown a counterexample, illustrating the basic conundrum behind geometrical frustration. Symmetry incompatibility between the magnetic interactions and the geometry of the triangle-based lattice implies that there exists no state in which each bond can minimize its energy. In
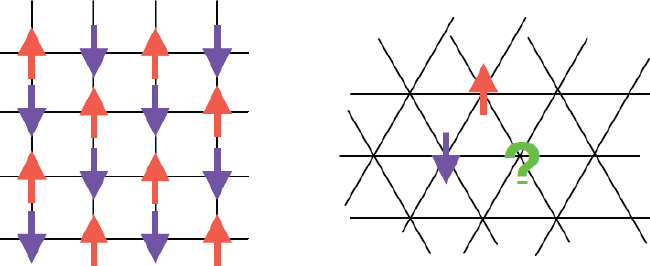
FIGURE 2.7 (Left) Unfrustrated antiferromagnetic structure on a square 2D lattice. (Right) Frustrating structure of the 2D triangular lattice for Ising spins.
the limit where a solid is built up from such triangles, the lowest energy state contains a nonzero fraction of high energy bonds. More importantly, as can be seen in Figure 2.7, for the triangle, there are three ways to achieve a spin configuration with one high energy bond. These multiple, or degenerate, states at the atomic level eventually lead to low energy states for the bulk solid that are different from the traditional long-range-ordered states. These frustrated states fall into one of two generic classes, depending on whether the spin can point continuously in any direction or point only along a given (Ising) axis defined by the other ions in the crystal. In the first case, the continuity of spin direction, combined with the degeneracy of available states, leads to “spin-liquid”-like behavior. In the second case, the high energy bond is in a different position from triangle to triangle and the resulting disorder is frozen in at low temperatures. This is a so-called “spin ice” state, by analogy with the disordered hydrogen positions in water ice.
Fortunately, there exist many crystal structures that provide a triangular atomic building block. Indeed the large mineral families of the pyrochlores, the spinels, and the delafossites contain several model compounds for the behavior implied above and the study of its interaction with magnetic field.
One example is found in the spinel compound ZnCr2O4, shown in Figure 2.8. This compound can be viewed as a 3D structure containing corner-sharing tetrahedra of trivalent Cr ions with spin ⅔. The tetrahedron is the three-dimensional analogue of the triangle used above—namely, a frustrating unit out of which a lattice can be constructed, as shown in Figure 2.8 for the B-sites of the spinel lattice.
Measurements of the magnetic susceptibility of ZnCr2O4 in the temperature range 50-300 K can be described by mean field theory and suggest that antiferromagnetic ordering should have occurred at Tc = 390 K. Instead, antiferromagnetic order in ZnCr2O4 sets in at Tc = 12 K. Here, the magnetic interactions are so strong that ordering is accompanied by changes in the lattice constant and sound velocity. Despite possessing Tcs that are much lower than the mean field prediction, frustrated magnets are affected by magnetic fields on the scale of the spin-spin interactions, reflecting the local nature of the frustration phenomenon. For example, even though ZnCr2O4 orders at 12 K, suggesting that fields of order 10 tesla would be able to modulate Tc, such fields have almost no effect. In order to explore whether higher fields could affect ZnCr2O4, an experiment was performed using a field compression technique, and the magnetization probed using Faraday rotation, shown in Figure 2.9. At a temperature of 6 K, ZnCr2O4 exhibits a sharp increase in magnetization at about 130 T in the [111] direction with several smaller anomalies at higher fields, as shown. The anomalies at 240 T, 290 T, and 350 T correspond to ⅔, ¾, and 5/6 of the full moment, and while a theoretical understanding is not yet fully developed, the underlying kagome structure in the [111] direction suggests dimensional reduction might take place, leading to topological phases.
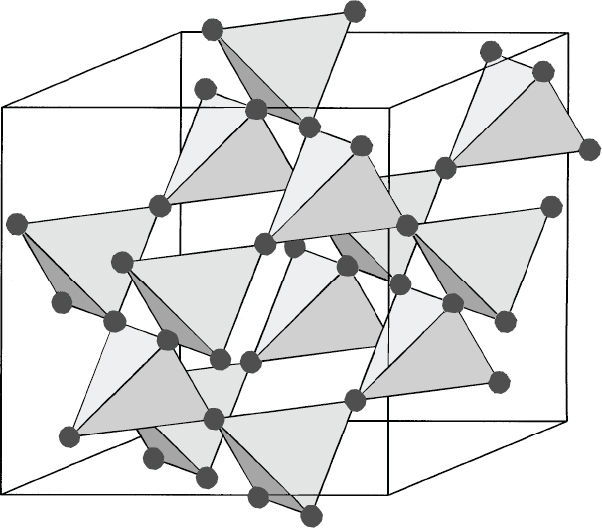
FIGURE 2.8 Lattice structure of the magnetic (A) sites in the pyrochlore compound A2B2O7 or the B sites in the spinel compound AB2O4. SOURCE: S.T. Bramwell and M.J. Harris, 1998, Frustration in Ising-type spin models on the pyrochlore lattice, Journal of Physics: Condensed Matter 10:L215-L220. © IOP Publishing. Reproduced by permission of IOP Publishing. All rights reserved.
High Fields for Frustrated Multifunctional Materials
Researchers are presently searching for new materials that simultaneously possess the properties of ferromagnetism and ferroelectricity. The former property is used in information storage and the latter is used in sensors and actuators. The search for materials that not only possess both properties but where one property controls the other is motivated by applications such as electrically controlled information storage or electrodes on spintronics devices. These materials searches are uncovering a wealth of complex new phases, one example of which is Ni2V3O8. Originally identified as a possible frustrated magnet due to its “kagome staircase” structure, it was soon discovered to exhibit a ferroelectric phase at low fields, as shown in the phase diagram in Figure 2.10 as the C phase. Subsequent measurements above 20 tesla revealed a complex high-field phase diagram, with magnetization plateaus corresponding to ⅔, ¾, and 8/9 of the saturation magnetization.
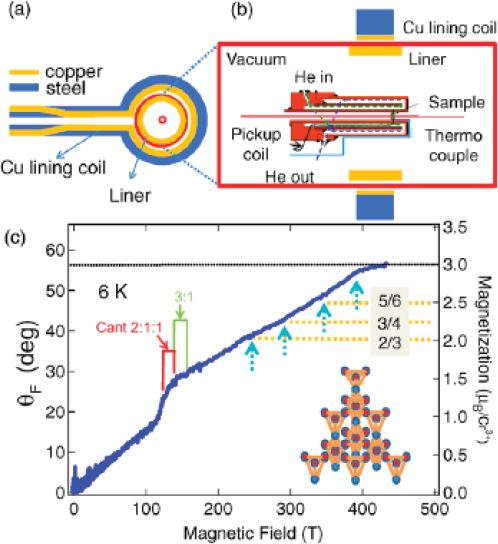
FIGURE 2.9 (a) Primary coil for the electromagnetic flux compression; (b) handmade optical cryostat made of “stycast” resin; (c) magnetization of ZnCr2O4 measured by the Faraday rotation method at 6 K under ultrahigh magnetic fields generated by the flux compression. Arrows show the phase transitions above the plateau phase. SOURCE: With kind permission from Springer Science and Business Media: E. Kojima et al., 2010, Magnetic orders of highly frustrated spinel, ZnCr2O4 in magnetic fields up to 400 T, Journal of Low Temperature Physics 159:3-6, Figure 1.
Quantum Matter Probed by High Magnetic Fields
In the example described earlier of high-field studies of the quasi 1D Ising system CoNb2O6, the effect of the magnetic field was to offset the effect of the mean ordering field. Since the energy between the ground state doublet and the next excited quartet state is about 300 cm-1, the effect of the transverse applied field is to mix the Ising eigenstates en route to polarizing the spins at high field. This mixing involves quantum fluctuations, which ultimately destabilize the 3D order at a critical field of ~ 5 T. Another example of the balance between quantum fluctuations and long-range order induced by exchange interactions is found in
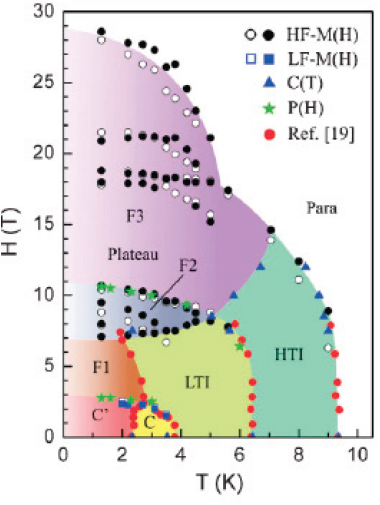
FIGURE 2.10 H-T phase diagram for Ni3V2O8 for H ![]() a, determined from magnetization (M), electric polarization (P), and specific heat (C) measurements. Open (closed) symbols are for increasing (decreasing) field. The phases are as follows: HTI, high temperature incommensurate; LTI, low temperature incommensurate; C and C’ are two different commensurate phases; F1, F2, and F3 are phases the nature of which is unknown at present. SOURCE: Reprinted figure with permission from J. Wang, M. Tokunaga, Z.Z. He, J.I. Yamaura, A. Matsuo, and K. Kindo, 2011, High magnetic field induced phases and half-magnetization plateau in the S=1 kagome compound Ni3V2O8, Physical Review B 84:220407(R), Figure 3. Copyright 2011 by the American Physical Society.
a, determined from magnetization (M), electric polarization (P), and specific heat (C) measurements. Open (closed) symbols are for increasing (decreasing) field. The phases are as follows: HTI, high temperature incommensurate; LTI, low temperature incommensurate; C and C’ are two different commensurate phases; F1, F2, and F3 are phases the nature of which is unknown at present. SOURCE: Reprinted figure with permission from J. Wang, M. Tokunaga, Z.Z. He, J.I. Yamaura, A. Matsuo, and K. Kindo, 2011, High magnetic field induced phases and half-magnetization plateau in the S=1 kagome compound Ni3V2O8, Physical Review B 84:220407(R), Figure 3. Copyright 2011 by the American Physical Society.
LiCuVO4. LiCuVO4 possesses an inverse spinel structure with an orthorhombic distortion where the Cu2+ (s = ½) ions form chains separated by the nonmagnetic Li, V, and O ions. An antiferromagnetic phase with an incommensurate spiral spin structure sets in at 2.3 K. Zhitomirsky and Tsunetsugu predicted this structure to exhibit a quantum spin nematic phase at high fields by a magnetic analogy to the orientational ordering of needlelike molecules in liquid crystals. Figure 2.11 shows the magnetization of LiCuVO4 using a pulsed-field technique. The kink at Hc3 is interpreted as evidence for the appearance of the quantum spin nematic phase. Confirmation of this new state of magnetism will require neutron-scattering studies, but the fields required are beyond those presently available in neutron-scattering facilities.
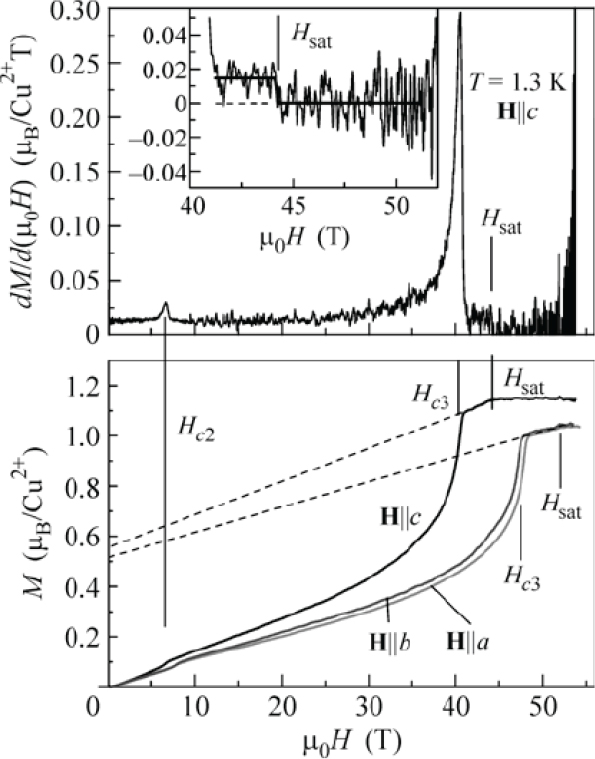
FIGURE 2.11 (Upper panel) dM/dH of LiCuVO4 measured using a pulsed-field technique. The inset shows dM/dH near Hsat. The solid line is a fit to a step function. (Lower panel) M(H) at T = 1.3 K, obtained by integration for H ![]() a, b, c. The solid lines correspond to the magnetization for the fielddescending process. The straight dashed lines are linear fits in the range Hc3 < H < Hsat and extrapolations to these fits to zero field. SOURCE: With kind permission from Springer Science and Business Media: L.E. Svistov, T. Fujita, H. Yamaguchi, S. Kimura, K. Omura, A. Prokofiev, A.I. Smirnov, Z. Honda, and M. Hagiwara, 2011, New high magnetic field phase of the frustrated S=1/2 chain compound LiCuVO4, JETP Letters 93:21, Figure 2.
a, b, c. The solid lines correspond to the magnetization for the fielddescending process. The straight dashed lines are linear fits in the range Hc3 < H < Hsat and extrapolations to these fits to zero field. SOURCE: With kind permission from Springer Science and Business Media: L.E. Svistov, T. Fujita, H. Yamaguchi, S. Kimura, K. Omura, A. Prokofiev, A.I. Smirnov, Z. Honda, and M. Hagiwara, 2011, New high magnetic field phase of the frustrated S=1/2 chain compound LiCuVO4, JETP Letters 93:21, Figure 2.
The above examples illustrate the uniqueness of magnetic systems for studying phase transitions in condensed matter systems. With the variety of magnetic ions, effective dimensionalities, and reasonably precise knowledge of the spin-spin interactions, magnets are used to model generic problems in statistical physics. The ability to create magnetic fields over a wide range of energies allows us to continuously challenge and expand our understanding of matter.
SUPERCONDUCTORS IN HIGH MAGNETIC FIELDS: AN EXPANDING FRONTIER
Early in the history of superconductivity (see Box 2.1), its relation to magnetic field became the object of enduring fascination. The Meissner effect, the full expulsion of the external magnetic field from a bulk superconductor below a certain maximum field strength, provided an early clue to the microscopic origin
BOX 2.1
Superconductors:
Low-Tc and High-Tc, Conventional and Unconventional
Superconductivity at critical temperature Tc = 4.2 K was discovered in 1911 in mercury. Numerous elemental metals (Pb, Al, Nb, and others) become superconducting at Tc < 10 K. The transition temperature of metallic alloys and compounds (e.g., Nb3Sn) can exceed 15-20 K. The microscopic mechanism of superconductivity in these materials is understood within the Bardeen-Cooper-Schrieffer (BCS) theory epitomizing the key role of the electron-phonon interaction in superconducting pairing. The discovery of superconductivity in copper oxides (cuprates) in 1986 has revolutionized this field of research and all of condensed matter physics. Not only is the transition temperature of the cuprates high (the record is 160 K), but many electronic and magnetic properties of the cuprates reveal radical departures from the BCS scheme. Thus, cuprates are commonly referred to as high-Tc superconductors and also as unconventional superconductors. However, not all cuprates have high transition temperatures. For example, the Re2-xCexCuO4 family has Tc < 25 K (Re, rare earth elements). And yet these particular cuprates are as unconventional as some of their counterparts with much higher Tc. Likewise, several other classes of low-Tc materials (organic compounds and heavy-fermion systems) possess exotic properties and are regarded as prototypical examples of unconventional superconductivity despite their low Tc in the range of 0.1-10 K. Iron-based superconducting pnictides and chalcogenides (Tc < 60 K) appear to have much in common with cuprates and other superconducting systems where magnetism is likely to be involved in a major way with superconductivity. It is therefore tempting to classify these two classes as unconventional superconductors. Other materials, including MgB2 (Tc = 40 K) and A3C60 (Tc < 40 K), show relatively high transition temperatures. However, because the electron-phonon interaction is believed to be responsible for superconductivity in both MgB2 and A3C60, these systems are usually referred to as conventional superconductors (Choi et al., 2002, Gunnarsson, 1997).
of superconductivity as a state exhibiting coherent quantum behavior “over miles of dirty lead wire,” in John Bardeen’s words.
A new dimension of interplay between superconductivity and magnetic fields became apparent with the discovery of the so-called “type II” superconductors, which stand in contrast to the elemental type I superconductors. In the latter, the magnetic field is expelled until it completely suppresses superconductivity at a critical field Hc. On the contrary, in the case of the type II materials, above a lower critical field Hc1, the magnetic field intrudes into the superconductor in the form of quantized flux lines, each carrying a unit of fundamental flux quantum Hc/2e. This flux quantization signals the crucial role played in superconductivity by pairs of electrons of charge 2e (Cooper pairs) and is recognized as yet another universal property of type II superconductors, alongside the Meissner effect. Superconductivity is suppressed only when one reaches an upper critical field Hc2. In the region between the Hc1 and Hc2, the fluxes are anchored to the locations of topological defects in the complex superconducting order parameter (i.e., vortices) and organize themselves into an ordered array, the Abrikosov lattice. Thus the field-temperature (H-T) phase diagram of conventional type II superconductors was completed (Figure 2.12) and became understood rather well (Tinkham, 1996; de Bruyn Ouboter, 1997). Because of their ability to carry electrical current with vanishing resistance, even in high magnetic fields, type II superconductors are the materials of choice for construction of high-field magnets for research, and also for a wide array of applications, including medical MRI.
High-Temperature Superconductivity in Copper Oxides
The discovery of high-temperature superconductivity (HTS) in copper oxides (Bednorz and Mueller, 1986) with Tc reaching 160 K, inaugurated the new era of extreme type II superconductivity (Figure 2.12). The main characteristic of these extreme type II superconductors is that Hc2 is orders of magnitude larger than Hc1, often reaching into tens or even hundreds of tesla. Consequently, the ability to perform measurements in very high magnetic fields is an essential component of frontier research in HTS. In effect, the “mixed” state between Hc1 and Hc2, where superconductivity coexists with magnetic field, became the dominant region in the phase diagram, while the Meissner state is found in only a tiny sliver at very low fields, below Hc1. Notably, Tc in HTS systems is comparable to the characteristic electronic energies, including the Fermi energy EF. This is significant since Tc << EF is the key condition for the validity of the conventional BCS theory, perhaps the most successful “mean-field” theory in all of physics.
With Tc in cuprates routinely around 100 K, reaching fields of tens or even 100 T became both an experimental challenge and imperative. A worldwide effort
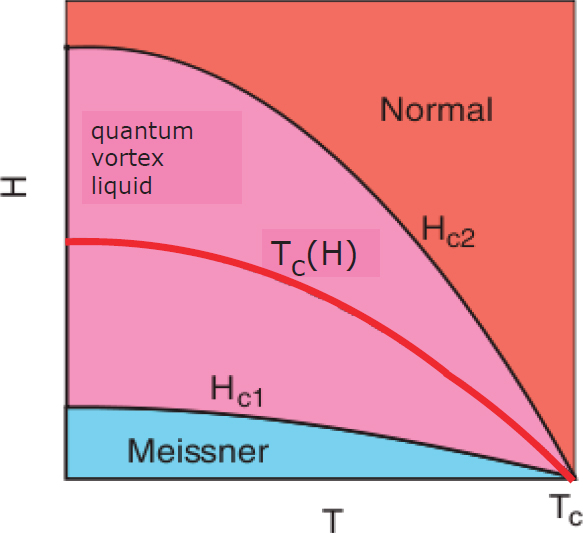
FIGURE 2.12 Phase diagram of extreme type II superconductors: In conventional type II superconductors, the magnetic field-temperature (H-T) phase diagram is marked by the upper and lower critical fields, Hc1 and Hc2, respectively. For visual clarity, the size of Hc1 relative to Hc2 in extreme type II systems, routinely less than 1 percent, is intentionally exaggerated. At Hc1 the magnetic field penetrates into a superconductor in the form of quantized fluxes, while at Hc2 the Abrikosov lattice of such fluxes disappears along with the superconductivity itself. In extreme type II HTS these lines morph into gradual crossovers as strong thermal and quantum fluctuations erase the mean-field BCS features and replace them with phase transitions of an entirely different kind. For example, the true superconducting transition Tc(H) is now the line where fluctuating vortices, already present in the normal state, turn from a liquidlike correlated state into some kind of a frozen arrangement, the precise nature of which involves an elaborate interplay among interactions, disorder, and materials features (the symmetry of the underlying crystal lattice, the symmetry of Cooper pairs, the presence or absence of gapless quasiparticles, etc.). The exploration of the vast regime between Tc(H) and Hc2(T), relying on magnetic fields as high as tens or even hundreds of tesla, has been one of the richest and intellectually most rewarding areas of research in physics during the past 10 to 15 years and is bound to remain so in the coming decade.
in studies of the interplay of superconductivity with high magnetic fields in the cuprates is at the cutting edge of research in condensed matter physics. Among the outcomes of this research is a refined understanding of superconducting fluctuations, phase transitions in vortex arrays, and quantum oscillations in superconductors. These efforts continue, recently reenergized by the discovery of HTS in iron pnictides and chalcogenides, multiband and less anisotropic relatives of cuprates, opening yet another window from which to view the fundamental phase diagram of Figure 2.12.
The cuprate high-Tc materials are a striking example of unconventional superconductors. Unlike conventional BCS superconductors, where the Cooper pairing of electrons is due to attractive interactions mediated by lattice vibrations, the Cooper pairing in these new materials is likely the product of repulsion. While there may not be a clear-cut experiment that would establish this directly beyond reasonable doubt, this point of view is strongly supported by the unconventional d-wave nature of Cooper pairs in cuprates, which has been explicitly demonstrated. Within the BCS theory, superconducting pairing impacts only a small fraction of electrons residing in the immediate vicinity of the Fermi surface: a surface of constant energy in the momentum space which separates empty and filled electron levels in the normal metallic state. In conventional BCS superconductors the Cooper pairs form in an s-wave state, which leads to a superconducting energy gap that is more or less uniform all around the Fermi surface. In the cuprates, however, the low-energy fermionic excitations are gapless at certain points or lines on the Fermi surface. These excitations lead to dramatic differences in thermodynamic and transport properties compared to the prescriptions of BCS theory.
Very importantly, as one looks for deviations from the mean-field BCS description, these low-energy quasiparticles and their interactions with superconducting vortices, through thermal and quantum fluctuations, become a fundamental problem in reconstructing the phase diagram of HTS. Various elements of this problem are the subject of intense ongoing research, much of which involves very high magnetic fields (some recent examples are in Riggs et al., 2011; Sebastian et al., 2008; Wu et al., 2011). Magnetic fields are crucial since, by weakening superconductivity, they usher in strong fluctuations.
Not only is the superconductivity of the cuprates unconventional, but their normal state properties are equally exotic. Common metals are described by the Fermi liquid theory establishing that, despite their high density in a metal, electrons behave as noninteracting quasiparticles. In the high-Tc cuprates, there are very strong correlations among the electrons even in the normal state, which render inapplicable existing approaches developed for weakly or noninteracting electronic systems. The strong correlations result from the fact that the superconducting cuprates are materials where a modest density of either electrons or holes have been introduced in the CuO2 planes of an insulating antiferromagnetic
(AF) host. The high-Tc phenomenon involves a delicate balance of competing effects, including superconducting pairing, electronic correlations, and spin and/or charge order. These latter factors are at least partially responsible for anomalous sensitivity of HTS cuprates to external perturbations, including magnetic fields, as well as extreme dependence of observables upon composition and/or disorder. A remarkable property of many cuprates is a pseudogap, a partial gap dominating the excitation spectrum of underdoped materials. It is universally recognized that understanding the pseudogap physics is an imperative step toward uncovering the mystery of high-Tc superconductivity (Norman et al., 2005).
High magnetic fields are uniquely suited to address and resolve some of the most pressing issues in the field of cuprate superconductivity. Specifically, fields above the upper critical field suppress superconductivity and thus provide experimental access to the T → 0 normal state properties in the absence of superconductivity. Data by Ando et al. (1995) obtained in pulsed magnetic fields in the mid-1990s indicated that, in some materials, the normal state transport at T < Tc has a resemblance to insulators and is in stark contrast to that of ordinary metals (Ando et al., 1995). More recent high-field experiments performed for less disordered cuprate compounds have uncovered quantum oscillations, a phenomenon that is a hallmark of the well-defined Fermi surface (Doiron-Leyraud, 2007).
High magnetic fields will continue to play an essential role in superconductivity research. High fields allow access to the low-temperature regime of cuprates and pnictides, where quantum fluctuations away from the BCS theory dominate. Thus, entirely new quantum states of matter, not just uncovered by but induced by high magnetic fields, become a realistic possibility. One example of such a novel field-induced state is the formation of unidirectional charge- and/or spin-ordered regions in the cuprates, commonly referred to as stripes (Lake et al., 2002). This and other discoveries show that magnetic field research in cuprates is of high intellectual impact. Furthermore, this work is of unparalleled technological significance since in the background of the purely scientific quest, there is always the key issue of practical uses of extreme type II superconductors in energy generation, transmission, and storage, as well as numerous other applications from superfast trains to powerful particle accelerators. In particular, as detailed in Chapter 7 of this report, cuprate high-Tc material is the only viable material system for the development of all-superconducting magnets at 30 T and above.
High-Temperature Superconductivity in Iron Pnictides and Chalcogenides
Iron-based HTS burst onto the scene in 2008. This was a major serendipitous discovery that occurred subsequent to the 2005 NRC study on Opportunities in High Magnetic Field Science. As the first HTS materials that are not copper-based (Kamihara et al., 2008), iron-based superconductors have engendered a tsunami
of activity. The iron-based systems continue to be a vibrant and rapidly evolving area, adding new facets to the field of unconventional high-Tc superconductivity. This much is known: these are multiband HTS, with a Fermi surface consisting of several distinct “pockets.” The superconducting gap appears to have opposite signs on these pockets, suggesting that the interelectron repulsion is again a likely culprit behind the HTS mechanism. The cuprate and pnictide families appear to share a number of characteristics (Basov and Chubukov, 2011). Specifically, the normal state properties of both families of materials are dominated by strong correlations in the electronic system. Both cuprates and pnictides reveal quantum oscillations in high magnetic fields (Shishido et al., 2010). However, pnictides are less anisotropic than cuprates, bringing the full phase diagram of Figure 2.12 into the range reachable by available or soon-to-be-available magnetic fields. The pnictides show great promise for high-field applications, because their relatively high Tc, large critical fields, and weaker anisotropies are appealing virtues for such applications (Larbarestier et al., 2001).
Organic superconductors were an early domain for high magnetic field research in superconductivity. While these materials nominally are not HTS, they are extreme type II systems, and their special anisotropic properties allow one to use high magnetic fields to enter into regimes that relate to the most interesting issues in cuprates and pnictides. In particular, the competition of superconductivity with spin and charge density-waves, quantum oscillations in the superconducting state indicating gapless excitations, along with other phenomena was first observed in these materials. This is still a very active subject of research, with high magnetic fields playing a key role (Lebed, 2008).
Recently, there has been much excitement about a new distinct class of superconductors, said to exhibit topological superconductivity. Topological superconductors are expected to have a number of very peculiar properties, which could have unique applications. Further discussion of this subject, which is still in its infancy, may be found in the section Topological Phases.
The Next Ten Years for High-Temperature Superconductors
Here, the committee highlights some of the most promising research directions that it anticipates for the next decade:
• Transport experiments on unconventional superconductors in ultrahigh magnetic fields are likely to produce groundbreaking discoveries. With broader availability of intense magnetic fields, transport measurements can be performed in the regime where the applied magnetic field is comparable to the depairing (upper critical) field Hc2, even in the case of high-temperature superconductors. Transport studies in this regime are challenging but still much easier to carry out than often more informative but much more technically involved spectroscopic measurements.
• Correlated HTS such as cuprates and pnictides are among the most promising systems exhibiting fundamental departures from the mean-field, weak-coupling BCS theory. This is one of the looming intellectual challenges in condensed matter physics. Quantum and thermal fluctuations of vortices, their dynamics, and interactions with gapless quasi-particles will continue to be among the most active areas of inquiry. High magnetic field experiments are unique in their proven capacity to tune in to these phenomena— a direction that is likely to lead to vibrant new developments.
• The connection between topological insulators and superconductivity will surely be vigorously explored in the near future. In particular, possible Majorana fermion states in Tl-superconductor systems or in vortex cores of topological superconductors are bound to be a major new arena for high magnetic field research.
• Progress in the general area of unconventional superconductivity will be determined by close coordination of research at magnet facilities (dc and pulsed) and by material scientists. In this context, it may be an important question to ask why quantum oscillations in the cuprates were discovered by a Canadian-French collaborative group and not by a U.S. group, despite the fact that the National High Magnetic Field Laboratory (NHMFL) had worked on magnetotransport of YBCO in high fields before the competition. The answer will be familiar to many readers of this report: The Canadian-French team had unrestricted access to absolutely top-quality single crystals. This is an example of the United States lagging behind in integrating top new materials expertise into leading university physics programs.
• The vortex state is the electromagnetic face of superconductivity. Progress in this field will critically depend on spectroscopy and (nano)imaging techniques that will enable new insights into vortex dynamics.
• The problem of unconventional superconductivity is perhaps the most remarkable but not the only example of phase transitions in correlated metals. Ultrahigh magnetic fields will aid deeper understanding of these phase transitions, provided it becomes possible to apply spectroscopic
methods to tackle the problem. Unfortunately, one of the most informative spectroscopies in condensed matter physics, angular-resolved photoemission spectroscopy, is impossible in high magnetic fields. Therefore, one will need to rely on future advances of scanning tunneling microscopes and photon- and/or neutron-based spectroscopies.
• Unconventional superconductors are prone to phase separation on diverse length scales. Various imaging methods from atomic to meso-scale in ultrahigh magnetic fields are likely to make a decisive impact on the understanding of these phase separations.
• Advances in state-of-the-art characterization techniques compatible with ultrahigh magnetic fields will help to revolutionize materials for magnet technology.
Magnetic fields can have a particularly large effect in materials with a low density of charge carriers. In these systems, Planck’s constant times the cyclotron frequency induced by a strong magnetic field can become comparable to the Fermi energies arising from quantum mechanical motion of the carriers, or to the energy scale of Coulomb interactions between the carriers. As a result, strong magnetic fields have long been used as a powerful tool for studying semimetals and semiconductors.
Semimetals are materials that would be insulating except for a small overlap between the energies of their valence and conduction bands, which causes a small number of electrons to be transferred from the valence band to the conduction band. Consequently, a semimetal has a small density of electron-like carriers arising from filled states in the conduction band and an equal number of holelike carriers due to empty states in the valence band. In semiconductors, the valence and conduction bands do not overlap, but carriers may be introduced by impurities or defects, whose concentration can be made very low in carefully grown material. A low-dimensional electron gas may be produced near the surface of a bulk semiconductor, or in other low-dimensional geometries, by a surface treatment or by application of an electrostatic potential via an external gate.
Low-Dimensional Semiconductor or Semimetal Systems
A general area that has remained at the frontier of physics research for the past three decades is that of low-dimensional systems. Spatial confinement of electrons to a plane, a line, or a small dot often dramatically alters the material’s properties and gives rise to novel phenomena with no counterparts in bulk materials. In some cases, interactions among electrons can become dominant over their kinetic
energies and can lead to exotic phases that are quite different from the phases encountered in bulk materials. Even in systems with weakly interacting electrons, confinement in a low-dimensional geometry can lead to striking differences from the behavior of the bulk material. Beyond its scientific interest, investigation of such low-dimensional systems also has tremendous practical implications: As the feature size of transistors becomes smaller and smaller, quantum phenomena are not only relevant, they are ubiquitous. High magnetic fields have been used both as a tool for studying new materials and structures, in order to elucidate the nature of the electronic structure that would be present in the absence of a field, and as an instrument for inducing behavior that is completely different from the behavior in zero field.
A low-dimensional system of particular interest is the two-dimensional electron system (2DES). Traditionally, such a system is achieved in semiconductor heterostructures—that is, by confining the charge carriers to the interface of two semiconductors that have different band gaps. More recently, new materials, such as graphene and the surface states of a topological insulator, have emerged as new 2D systems with novel properties that are promising for both understanding fundamental physics and exploring technological applications.
The prototypical 2D phenomena are the quantum Hall effects (QHE),1 a collection of peculiar phenomena that occur in 2D electron systems, at low temperatures, in strong magnetic fields. Under these conditions, electrons’ orbitals coalesce into Landau levels (LLs), which may give rise to the integer and fractional quantized Hall effects (IQHE and FQHE), where the Hall conductance is quantized at integer or fractional values of the conductance quantum e2/h = (25.9 kΩ)-1, with e being the electron charge and h being Planck’s constant. Other peculiar phenomena observed under these conditions include the unquantized QHE, where electrons in a strong magnetic field show properties similar to a Fermi liquid in zero magnetic field, highly anisotropic phases associated with formation of charge-density waves, and formation of collective states in bilayer systems where counter-propagating currents in the two layers can flow with zero resistance. FQHE states give rise to new types of collective excitations, including particles with charges that are a fraction of the charge of an electron and have quantum properties intermediate between fermions and bosons. In addition, certain FQHE states are believed to have particles with nonlocal hidden degrees of freedom, which lead to a phenomenon termed “non-abelian statistics,” and which might be exploited for quantum computation. Owing to its precise quantization, the IQHE is now used as the standard of electrical resistance. The various QHE are signatures of novel states of matter, whose understanding has posed a major challenge to researchers over the past three decades.
________________
1 For a review, see R.E. Prange and S.M. Girvin, eds., 1987, The Quantum Hall Effect, 1st ed., Graduate Texts in Contemporary Physics, Springer.
A very important parameter in the description of quantum Hall systems is the Landau level filling factor, f = n Φ0/B, where n is the two-dimensional electron density and Φ0 = h/e is the quantum of magnetic flux. For example, the integer QHE is found when f is close to an integer, and the fractional QHE is seen, under appropriate conditions, when f is close to certain rational fractions, such as ⅓, ⅔ or 2/5. The magnetic field necessary to achieve a given filling factor is therefore proportional to the electron density in the sample.
In order to observe quantized Hall effects, the electron mobility must be sufficiently high. For the integer QHE, the criterion is roughly B < ~ μ-1, where B is the magnetic field in tesla and μ is the mobility in m2/Vs. For the fractional QHE, the required mobility is generally higher. Typically, the mobility in a given material increases with increasing electron density. With improved techniques of sample preparation, however, the density required to achieve a given mobility may be decreased. Due to these improvements, most experiments on quantized Hall effects in semiconductors are currently done in local laboratories, using commercial magnets with fields below 15 T. Much of this work is done using GaAs structures, where mobilities as high as 3,000 m2/Vs have been achieved, at electron densities such that even f = ⅓ occurs below 15 T. However, higher magnetic fields become necessary if one wants to explore QHE in materials with lower mobility.
One specialized facility that has played a significant role in exploring aspects of the QHE is the NHMFL high B/T facility at the University of Florida. This facility enables one to reach extremely low temperatures, down 1 mK, using a nuclear demagnetization stage, in contrast to the base temperatures of 10-15 mK generally achievable with a dilution refrigerator.
An area of recent study where very high fields have been crucial is in the observation of QHE in graphene. Graphene is a single layer of graphite, and thus is truly 2D, as it is precisely one atomic layer thick.2 It is a unique material, whose many amazing material properties include some that are seldom found in the same material, such as high mechanical strength and elasticity, extraordinary electrical conductivity and 98 percent optical transparency, extremely high current-carrying capacity, chemical stability, and thermal conductivity. It is also nature’s thinnest elastic membrane that is both transparent and conducting, which makes it perfect for applications as transparent electrodes and flexible electronics. Since its experimental isolation on insulating substrates in 2004 (Novoselov et al., 2004), graphene
________________
2 For a review, see A.K. Geim and K.S. Novoselov, 2007, The rise of graphene, Nature Materials 6:183; M.S. Fuhrer, C.N. Lau, and A.H. MacDonald, 2010, Graphene: Materially better carbon, MRS Bulletin 35:289.
has quickly emerged as a most promising candidate for post-silicon electronic material, with a wide range of applications in electronics, sensors, displays, solar cells, miniaturized actuators, coatings, and composites (Novoselov et al., 2012).
In addition to its technological applications, graphene has a unique electronic band structure (Castro Neto et al., 2009; Das Sarma et al., 2011). The honeycomb lattice of carbon atoms gives rise to a peculiar energy-momentum dispersion: Instead of the parabolic bands normally found in semiconductors, metals, and insulators, the dispersion in graphene is linear, with the conduction and valence bands touching at two isolated points (the so-called Dirac points) in a plot of energy versus the x and y components of electron momentum (see Figure 2.13). Thus, graphene is either a zero band gap semiconductor or a zero-overlap semimetal, depending on one’s perspective. Electron motions in graphene are described by Dirac’s equation for zero-rest mass particles, E(k) = ħvFk, with an effective “speed of light” vF, where vF ~ 106 m/s is the Fermi velocity. These massless electrons in graphene also have chirality or “handedness,” much akin to that of neutrinos, which is not found in standard 2D electron gas (2DEG). Moreover, unlike standard 2DEG, which are buried below a surface, graphene is all-surface, enabling experiments that cannot be otherwise performed, such as optical spectroscopy, scanning tunneling microscopy, and mechanical manipulation. The 2010 Nobel prize in physics was awarded to André Geim and Kostya Novoselov for their groundbreaking experiments on graphene.
The first generation of graphene experiments was performed on Si/SiO2 substrates, with a typical mobility of between ~ 0.1 and 1 m2/Vs. Thus, compared to traditional 2DEG, higher magnetic fields were required to measure the Landau level gaps, break the fourfold degeneracy of the lowest Landau levels, and demonstrate the quantum Hall ferromagnetic state in graphene. Interestingly, the energetic separation between graphene’s lowest Landau levels is unusually large, enabling
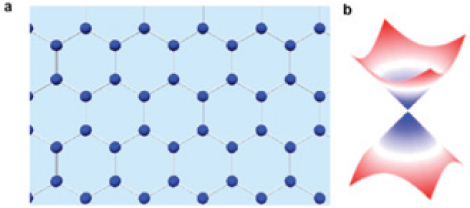
FIGURE 2.13 Atomic lattice and a portion of the electronic band structure of graphene. SOURCE: Reprinted from C.N. Lau, W. Bao, and J. Velasco, Jr., 2012, Properties of suspended graphene membranes, Materials Today 15:238, Copyright 2012, with permission from Elsevier.
the first observation of QHE at room temperature (performed at B = 30-45 T) (Novoselov, 2007). More recently, sample mobility has been improved to 10-100 m2/Vs by either suspending graphene or using hexagonal boron nitride as the substrate, so that IQHE and FQHE have been observed using lower electron densities, at fields available in commercial magnets.
The knowledge and insights gained from the early quantum Hall measurements on graphene have been invaluable in elucidating the peculiar properties of that material, and high field studies of graphene continue to be indispensible today. The current outstanding questions include the nature of the QH states at f = 0, or zero charge density, which have diverging Hall and longitudinal resistance in both single-layer and bilayer graphene; quantum phase transitions among the symmetry-broken QH states; topologically nontrivial phases; presence of sky-rmions (spin textures); Wigner crystals (electron solid); and FQHE with unusual fractions or sequence due to the approximate SU(4) symmetry of the electron states in graphene (see Figure 2.14). These questions can be answered only with transport
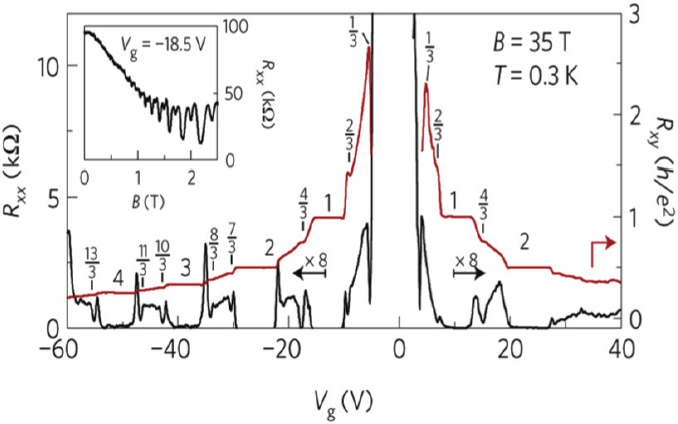
FIGURE 2.14 Longitudinal resistance (left axis) and Hall resistance (right axis) of a graphene sample versus gate voltage, which changes the carrier density, measured at B = 35 tesla. Quantized Hall conductance values are indicated. SOURCE: Reprinted by permission from Macmillan Publishers Ltd.: Nature Physics. C.R. Dean, A.F. Young, P. Cadden-Zimansky, L. Wang, H. Ren, K. Watanabe, T. Taniguchi, P. Kim, J. Hone, and K.L. Shepard, 2011, Multicomponent fractional quantum Hall effect in graphene, Nature Physics 7:693-696. Copyright 2011.
and/or optical measurements in dc and pulsed high magnetic fields with varying field angles and temperature.
A rather unique direction of graphene research is strain-based engineering of its electrical properties, which takes advantage of the “softer” side of graphene. Being both an excellent electrical conductor and an elastic membrane that can sustain more than 25 percent strain, graphene’s electrical properties can be strongly affected by strain and morphology. Moreover, inhomogeneous strains in graphene affect the electronic motion in a similar way to an applied magnetic field. In fact, electrons in highly strained graphene have been observed to experience pseudomagnetic fields greater than 300 T (Levy et al., 2010). Thus, one can tailor graphene’s electronic properties via careful design of strains. Interplay of such enormous pseudomagnetic field with the real magnetic field will be an exciting frontier and a step toward strain-based graphene electronics.
A closely related allotrope of graphene is carbon nanotubes (Smalley et al., 2001), which can be visualized as seamless cylinders of graphene, with diameters ~1 nm for single-walled carbon nantoubes and up to hundreds of nanometers for multiwalled carbon nanotubes. Depending on the orientation of the cylinder axis relative to the atomic honeycomb lattice, a carbon nanotube can be either a one-dimensional metal or semiconductor. High magnetic fields have been employed to probe the spin-orbit interactions, to close band gaps in semiconducting nanotubes, and to induce spin polarization and Aharonov-Bohm quantum interference effects. These high field studies are expected to continue to yield important information on fundamental interactions in 1D wires.
One of the most interesting semimetal materials is bismuth, which has an unusual band structure consisting of one hole and three electron pockets. The electrons are massless, similar to graphene, except that here the degenerate Dirac point occurs slightly below the Fermi energy of the pure material. The density of electrons and holes in bismuth is exceptionally low. Consequently, the so-called “quantum limit,” where all the charge carriers are confined to the lowest Landau level, can be achieved at relatively modest magnetic field ~ 10 T, above which electrical properties were expected to be featureless. Surprisingly, recent experiments at magnetic fields up to 31 T reveal striking oscillations and sharp rises in measurements of the Nernst effect, resistivity, and magnetization, as well as signatures for first-order phase transition induced by magnetic fields (Behnia et al., 2007; Li et al., 2008). Theoretical investigation (Alicea and Balents, 2009) suggests that the
quantum limit is suppressed by an unusual spin-orbit induced Zeeman effect, and electron interactions at high magnetic fields may give rise to distinct phases such as Wigner crystals and charge density waves. Further investigation in high fields will be warranted to ascertain these behaviors and to uncover new phenomena in bismuth and other semimetals.
During the last few years, a new class of materials, “topological phases,” has emerged as an exciting frontier of science. These materials have a number of remarkable properties that were not previously envisaged, and strong magnetic fields have played an important role in their exploration.
Topological insulators and topological superconductors are materials that have an energy gap for electronic excitations in their interior, but of necessity have low-energy excitations located at their boundaries. Transport properties, such as electrical conduction, may be dominated by these surface excitations.
The quantum mechanical ground states of these materials are characterized by “topological quantum numbers,” which cannot change their values as one continuously varies an external parameter such as the pressure applied to the system, unless the system undergoes a phase transition in which the energy gap closes and reopens again. Topological phases have quantum numbers that are different from those of ordinary, nontopological phases, so they represent a conceptually distinct state of matter. Mathematically, the topological quantum numbers characterize the way the ground state evolves if one changes certain parameters in the Hamiltonian, which affect its explicit form but do not affect the ground state energy. The set of such ground states forms a surface in the quantum-mechanical Hilbert space, and surfaces corresponding to different topological phases are distinguished from each other in much the same way as the surface of a sphere is topologically distinct from the surface of a donut—the surfaces cannot be deformed into each other without tearing and re-stitching.
The earliest known examples of topological insulators were in fact the quantized Hall states of 2D electron systems at low temperatures, and in a strong magnetic field. It was shown in the 1980s that the quantized Hall conductance of these systems is related to a winding number, which describes the way in which the ground-state wave function evolves when one varies the boundary conditions of the system. This winding number is an integer that, in principle, may be positive or negative and arbitrarily large.
By contrast, for the topological insulators of greatest current interest, the topological numbers have only two possible values, typically equal to 1 in the topological phase and 0 in the trivial non-topological phase. (Such numbers are often denoted Z2 numbers, in contrast to the case of arbitrary integers, which are denoted
Z numbers.) These topological phases are strictly defined only in systems which preserve time-reversal symmetry—that is, systems in the absence of an external magnetic field, which do not have frozen local magnetic moments. Nevertheless, application of strong magnetic fields can be a strong tool for manipulating or probing these systems.
Originally it was thought that topological insulators could exist only in two-dimensional systems or in systems that were essentially a stack of weakly connected layers. However, we now know that there are different kinds of topological insulator that can exist in genuinely 3D systems. In fact, topological insulators can exist, mathematically, in any dimension, with appropriate classes of symmetry restrictions, and a complete classification of these phases has been developed, at least for models of weakly interacting electrons in a periodic potential.
Concrete examples of Z2 topological insulators have been realized in both 2D and 3D. All these materials share a common trait—that is, a strong spin-orbit coupling, which causes band inversion and flips the parity of the valence band. Coincidentally, the nature of the edge/surface state of a topological insulator is dictated by the spin-orbit coupling, so that for a given momentum direction, only one direction is allowed for the electron spin. This type of spin polarization is often called “helical,” although the spin direction is typically perpendicular to the direction of motion, in contrast to the case of a helical massless particle in high-energy physics, such as a neutrino. An interesting consequence of the helical spin polarization is the existence of dissipationless spin current at the edge/surface of a topological insulator. This property could have important implications for applications in spintronics. Also interesting is the fact that the edge/surface state consists of massless Dirac fermions, whose existence is guaranteed by the time-reversal symmetry. This aspect gives the two-dimensional surface states of a 3D topological insulator a close relation to graphene, but in topological insulators there is neither valley nor spin degeneracy, reducing the number degrees of freedom of the Dirac fermions to one quarter of those in graphene.
Transport studies of helically spin-polarized surface Dirac fermions inhabiting the surface of 3D topological insulators are a promising research frontier. One would expect various novel physics, including dissipationless spin current and topological protection from backscattering, to show up in transport properties of topological surface states. However, transport studies of the surface states have proved a challenge because of the coexistence of bulk transport channels due to doping by defects in available topological insulator samples. Nevertheless, experiments on thin samples in high magnetic fields, carried out at NHFML, were able to distinguish the surface from the bulk contributions. Surface quantum oscillations have been successfully observed, and the Dirac nature of the surface states has already been elucidated. Recent improvements in materials preparation have also contributed to a separation of bulk and surface contributions. More recently,
the discovery of an intrinsically bulk-insulating material, Bi2Te2Se, gave a big boost to the surface transport studies. Furthermore, by improving the bulk-insulating properties of Bi2Te2Se in a Bi2-xSbxTe2-ySey solid-solution system, researchers have already succeeded in preparing bulk single crystals showing surface-dominated transport (see Figure 2.15). Also, MBE growth of strained HgTe thick films has successfully provided 3D topological insulator samples showing surface-dominated transport. Using those samples, we may anticipate that novel quantum transport phenomena, including the fractional quantum Hall effect in topological surface states, will become an exciting realm of high magnetic field science.
The Dirac nature of the surface states of topological insulators has also been observed in STM and optical experiments involving high magnetic fields. In the next 10 years, those new types of high magnetic field experiments will become increasingly more important for the exploration of novel physics associated with nondegenerate Dirac fermions.
Intriguingly, it has been shown that the quantum field theory of topological insulators resembles that of a hypothetical particle in high-energy physics, called the “axion,” and this theory leads to various interesting predictions such as the quantization of the magnetoelectric effect, the appearance of an image magnetic monopole, and the half-integer quantum Hall effect. All those phenomena are yet
FIGURE 2.15 (Left) Basic crystal structure of a most promising topological-insulator material, the tetradymite Bi2-xSbxTe2-ySey system. This material exhibits a highly bulk-insulating character and a tunable surface Dirac fermions. (Center) Since the surface transport is significant in this material, the apparent resistivity at cryogenic temperatures decreases when the sample thickness is reduced; the thickness dependence shown here suggests that the transport is 70 percent due to surface in the 8-μm thick crystal. (Right) Shubnikov-de Haas oscillations in high magnetic fields up to 45 tesla observed in this material reveal the Dirac nature of the surface state. SOURCE: (Left and center) reprinted figures with permission from A.A. Taskin, Z. Ren, S. Sasaki, K. Segawa, and Y. Ando, 2011, Observation of Dirac holes and electrons in a topological insulator, Physical Review Letters 107:016801, Figure 1(a) and Figure 4. Copyright 2011 by the American Physical Society. (Right) Courtesy of N. Phaun, Princeton University, adapted from J. Xiong, Y. Luo, Y. Khoo, S. Jia, R.J. Cava, and N.P. Ong, 2012, High-field Shubnikov–de Haas oscillations in the topological insulator Bi2Te2Se, Physical Review B 86:045314.
to be experimentally discovered, and an important prerequisite to the realization of those phenomena is to open a gap in the surface state. It has been proposed that high magnetic fields will be useful for this purpose, and the higher the field, the larger the gap, the easier the observation. This provides excellent opportunities for high magnetic field science to play a major role in the discovery of fundamentally new physics.
In a topological superconductor, the energy gap that protects the topological phase is actually the superconducting gap. The low-energy excitations at the boundary of a topological superconductor are exotic quasi-particles called Majorana fermions, which are their own antiparticles, and which should have a number of unusual properties. Notably, it has been proposed that, in appropriate situations, where Majorana excitations can be localized and kept well separated from each other, they could be useful for fault-tolerant quantum computing.
A promising way to materialize a topological superconductor is to induce electron pairing in the edge/surface state of a topological insulator via proximity effect of a conventional superconductor. One might also use a strongly spin-orbit-coupled semiconductor like InSb or InAs instead of topological insulators, but in this case a magnetic field is required to quench the spin degrees of freedom without suppressing the superconducting state. Recently there have been encouraging developments in realizing analogous topological superconductivity in 1D hybrid structures, where a nanowire of InSb or InAs is proximity coupled to a bulk superconductor.
Topological superconductivity may also be found in natural bulk superconductors when the superconducting order parameter is parity odd. For example, Sr2RuO4 is likely to have a time-reversal breaking, quasi-2D topological superconducting state, which would host Majorana fermions in the half-quantized vortices in magnetic fields. Also, CuxBi2Se3 was recently shown to be a time-reversal-invariant 3D topological superconductor, which hosts intriguing helical Majorana fermions on the surface. It is expected that more topological superconductors will be discovered in natural compounds or in artificially constructed hybrid systems. Considering the important roles that high magnetic fields have played in superconductivity research, we may expect that topological superconductors will naturally provide new exciting opportunities for high magnetic field science.
HIGH MAGNETIC FIELDS IN SOFT MATTER RESEARCH
As was mentioned in the overview to this chapter, applications of high magnetic fields to soft condensed matter research take advantage of the torques and forces on materials that can be exerted by a magnetic field. These may be used to align molecules or other small objects while they are being studied by one or
another experimental probe, or they can be used to control materials preparation, such as crystal growth, in a desired way.
The main interaction with magnetic fields is caused by diamagnetism, the appearance of a weak magnetic moment in a material in opposition to an external magnetic field. This phenomenon is present in all materials and arises from the deformation of the electron orbits in atoms and molecules by the Lorentz force. To magnetically manipulate nanostructures, one takes advantage of the anisotropy of a material’s diamagnetic response, which grows rapidly with size. For example, the increase in the magnetic energy by an object with N atoms or molecules is
Δ E = N χ B2 / 2μ0
where μ0 is the free space permeability and χ the susceptibility tensor per molecule. This energy may vary considerably depending on the relative orientation between the molecule and the magnetic field. Typically, for a single molecule, ![]() χ
χ![]() is miniscule (<10-7) for all orientations, hence even at B = 100 T, the difference in energy between different orientations is negligible. However, for a benzene aggregate with 105 molecules (but which is still only ~ 5 nm in size), it becomes energetically favorable at room temperature to align to the direction of the magnetic field at B = 20 T. Similarly, nanoscale chemical aggregates or biological cells can be oriented using high magnetic fields and studied in situ or ex situ. Since the orientational torque is quadratic in B, high magnetic fields are required to study nanometer-sized aggregates (Maret and Dransfield, 1985).
is miniscule (<10-7) for all orientations, hence even at B = 100 T, the difference in energy between different orientations is negligible. However, for a benzene aggregate with 105 molecules (but which is still only ~ 5 nm in size), it becomes energetically favorable at room temperature to align to the direction of the magnetic field at B = 20 T. Similarly, nanoscale chemical aggregates or biological cells can be oriented using high magnetic fields and studied in situ or ex situ. Since the orientational torque is quadratic in B, high magnetic fields are required to study nanometer-sized aggregates (Maret and Dransfield, 1985).
In supramolecular chemistry and liquid crystals, relatively weak van der Waals forces or π-π bonding are involved in the process of self-assembly of targeted molecular building blocks into larger structures, like vesicles, dendrites, fibers, wires, etc. Magnetic fields may be used to probe these intermolecular interactions by determining the internal structure that is important for their properties. For instance, dye molecules can aggregate in solution in different geometries like stacked or herringbone structures, and their optical response strongly depends on the stacking. One type of aggregate shifts optical absorption or emission to the red while the other shifts it to the blue. Therefore it is possible to tune the absorption in a desired way. The stacking occurs usually in a liquid environment, and it is important to determine the structure under these conditions, which makes standard microscopy or light-scattering techniques hard to use. In a magnetic field the aggregates orient in a specific way with respect to the field while at the same time, optically, the light polarization with respect to this direction can be varied. In this way, the optical absorption along different axes can be determined in an in situ
experiment. Molecular materials are considered as a possible element in photovoltaic devices, and it is important to match their optical properties to the optical spectrum of the sun, which makes a detailed knowledge of their structure necessary.
Another example is the study of optical properties of nanotubes in solution. A magnetic field readily aligns these tubes along the field axis and allows the study of their properties. In this way it has been possible to observe B-periodic Aharonov Bohm oscillations in the optical absorption of large-diameter carbon nanotubes as a function of magnetic field whenever an integer number of flux quanta fit in the cross section of the tube (Zaric et al., 2004).
It is also possible to use the magnetic forces to deform aggregate shapes like spheres or dendrites, and the deformation can be determined through optical experiments. In this way molecular forces on a nanometer scale can be quantitatively determined in a noninvasive manner. It is important to be aware of these diamagnetic forces. For example, molecular alignment in high fields produces observable effects in NMR spectra, which in principle can be used as constraints on the structures of macromolecules such as proteins.
It is of particular interest that the magnetic field experienced by a nano-object is practically identical to the applied field. Although it is easily possible to deform many objects with an electric field, the large values of typical dielectric constants mean that the local electric field may be very different from the externally applied field, which renders any quantitative analysis very difficult in that case.
Apart from aligning aggregates in solution with magnetic fields and studying them in situ, one may also use the fields to order matter in solution and then fix it in some way and study the ordered material ex situ afterwards. In general all collective states of soft matter like liquid crystals are very easily affected by magnetic orientation since domains in liquid crystalline material contain many molecules. Cooling liquid crystals in a field through the nematic phase transition leads to perfectly oriented materials since the first nuclei at the transition temperature can easily rotate in the magnetic field and aggregate after alignment. The cooled liquid crystalline film is fully transparent, free from domain boundaries, and shows a very high degree of birefringence. Strongly polarizing optically transparent films are useful optical components. Another example is that superior conducting polymers can be made from cylindrical stacks of coronene molecules that aggregate in solution and are then deposited on a substrate by evaporating the solution in a field. The resulting perfectly aligned stacks show a conductivity two orders of magnitude higher than the nonaligned stack, not aligned in a field. Such an increased mobility is very important for organic transistors (Shklyarevsky et al., 2005).
A very different application of diamagnetism is magnetic levitation. Since diamagnetic materials gain energy in a magnetic field, they experience a force F (per unit volume) toward the lower field region, given by
F = (χ/2μ0) grad B2
which is proportional to the gradient of the square of the field strength. In a magnet with a vertical bore, this force acts against gravity and enables complete levitation of most diamagnetic organic materials for B ~ 16-20 T and gradients ~ 100 T/m (Beaugnon and Tournier, 1991). Such levitation, apart from being a striking demonstration of diamagnetism of living organisms, also allows study of materials under microgravity or artificially variable gravity, such as crystal growth under weightless conditions or fluid dynamical problems as a function of gravitational acceleration (Berry and Geim, 1997). An example of fluid dynamics is the study of cryogenic liquids like the ones used as rocket fuel. Understanding the behavior of these liquids in weightless conditions is important in rocket design, and such studies can easily be done with magnetic levitation.
Finally, many experiments have been done in microgravity in an attempt to improve the crystal quality of, in particular, protein crystals. High-quality protein crystals are essential for protein structure determination, which is an essential tool for the pharmaceutical application, for example. The idea is that in weightless conditions the convection plume occurring around the growing crystals is suppressed. This plume arises because the solution near the growing crystal has a different density since it is depleted because of the molecules that are deposited on the surface. The reduction of the growth velocity is known to lead to higher crystal quality. It is possible to suppress the growth plume also in high magnetic fields under the condition that the grad B2 value suppresses the buoyancy of the depleted solution. This condition often requires much higher fields than the usual levitation condition (see Figure 2.16).
In summary, there are many as yet unexplored areas in research on soft matter in high magnetic fields since it is not widely recognized that at high magnetic fields diamagnetic energies may become important. Since these forces increase with B2, higher fields will rapidly make them even more important and opportunities for unexpected results will be even greater. This area of application is interdisciplinary par excellence since it requires physicists, chemists, and possibly even biologists to work together.

FIGURE 2.16 An image of the growth plume of growing lysozyme protein crystals at effective gravity G = 1 (normal gravity) and in a very high magnetic field gradient, showing that with field-induced effectively zero gravity (G = 0) convection can be suppressed and that gravity can even be inverted (G = 0.08). SOURCE: Reprinted with permission from M.C.R. Heijna, P.W.G. Poodt, K. Tsukamoto, W.J. de Grip, P.C.M. Christianen, J.C. Maan, J.L.A. Hendrix, W.J.P. Van Enckevort, and E. Vlieg, 2007, Magnetically controlled gravity for protein crystal growth, Applied Physics Letters 90:264105. Copyright 2007, American Institute of Physics.
High magnetic fields are a critical research tool in many areas of condensed matter and materials physics. Of the many examples of research in high magnetic fields cited in this chapter, a large fraction were carried out at facilities run by NHFML. The experiments were carried out by users from a large variety of universities and research institutions based in the United States and in other countries around the world. Those users may have brought with them samples, and in some cases measuring devices, prepared at their home institutions. In addition to magnet time, NHFML would have supplied technical support, as well as measurement instruments and cryogenic facilities for much of this work. The availability of higher magnetic fields, in both dc and pulsed modes, will be very important for continued progress in this area. (Specific magnet recommendations relevant to this research will be discussed in Chapter 7.) The use of high magnetic fields in soft matter research (biological cells, molecular aggregates, vesicles, polymers, some of them discussed in Chapter 3) has great promise but is largely underexploited. A close collaboration between the large facility and strongly interested chemists and biologists is necessary to fulfil these promises.
Materials Near Quantum Critical Matter
Basov, D.N., and A.V. Chubukov. 2011. Manifesto for a higher Tc. Nature Physics 7:272.
Bilbro, G., and W.L. McMillan. 1976. Theoretical model of superconductivity and the martensitic transformation in A15 compounds. Physical Review B 14:1887.
Broun, D. 2008. What lies beneath the dome? Nature Physics 4:170.
Custers, J., P. Gegenwart, H. Wilhelm, K. Neumaier, Y. Tokiwa, O. Trovarelli, C. Geibel, F. Steglich, C. Pépin, and P. Coleman. 2003. The break-up of heavy electrons at a quantum critical point. Nature 424:524.
Dai, J., Q. Si, J.-X. Zhu, and E. Abrahams. 2009. Iron pnictides as a new setting for quantum criticality. Proceedings of the National Academy of Sciences U.S.A. 106:4118.
Fradkin, E., S.A. Kivelson, M.J. Lawler, J.P. Eisenstein, and A.P. Mackenzie. 2010. Nematic fermi fluids in condensed matter physics. Annual Review of Condensed Matter Physics 1:153.
Gegenwart, P., Q. Si, and F. Steglich. 2008. Quantum criticality in heavy-fermion metals. Nature Physics 4:186.
Harrison, N., S.E. Sebastian, C.H. Mielke, A. Paris, M.J. Gordon, C.A. Swenson, D.G. Rickel, M.D. Pacheco, P.F. Ruminer, J.B. Schillig, J.R. Sims, A.H. Lacerda, et al. 2007. Fermi surface of CeIn3 above the Néel critical field. Physical Review Letters 99:056401.
Hertz, J. 1976. Quantum critical phenomena. Physical Review B 14:1165.
Jaccard, D., H. Wilhelm, D. Jérome, J. Moser, C. Carcel, and J.M. Fabre. 2001. From spin-Peierls to superconductivity: (TMTTF)2PF6 under high pressure. Journal of Physics: Condensed Matter 13:L89.
Jaime, M., R. Movshovich, G.R. Stewart, W.P. Beyermann, M.G. Berisso, M.F. Hundley, P.C. Canfield, and J.L. Sarrao. 2000. Closing the spin gap in the Kondo insulator Ce3Bi4Pt3 at high magnetic fields. Nature 405:160.
Jaime, M., R. Daou, S.A. Crooker, F. Weickert, A. Uchida, A.E. Feiguin, C.D. Batista, H.A. Dabkowska, and B.D. Gaulin. 2012. Magnetostriction and magnetic texture to 100.75 Tesla in frustrated SrCu2(BO3)2. Proceedings of the National Academy of Sciences U.S.A. 109:12404.
Julian, S.R., C. Pfleiderer, F.M. Grosche, N.D. Mathur, G.J. McMullan, A.J. Diver, I.R. Walker, and G.G. Lonzarich. 1996. The normal states of magnetic d and f transition metals. Journal of Physics: Condensed Matter 8:9675-9688.
Kageyama, H., K. Yoshimura, R. Stern, N.V. Mushnikov, K. Onizuka, M. Kato, K. Kosuge, C.P. Slichter, T. Goto, and Y. Ueda. 1999. Exact dimer ground state and quantized magnetization plateaus in the two-dimensional spin system SrCu2(BO3)2. Physical Review Letters 82:3168.
Kim, J.W., S.Y. Haam, Y.S. Oh, S. Park, S.-W. Cheong, P.A. Sharma, M. Jaime, N. Harrison, J.H. Han, G.-S. Jeon, P. Coleman, and K.H. Kim. 2009. Observation of a multiferroic critical end point. Proceedings of the National Academy of Sciences U.S.A. 106: 15573.
Kim, K.H., N. Harrison, M. Jaime, G.S. Beobeinger, and J.A. Mydosh. 2003. Magnetic-field-induced quantum critical point and competing order parameters in URu2Si2. Physical Review Letters 91:256401.
Kohama, Y., Y.C. Marcenat, T. Klein, and M. Jaime. 2010. AC measurement of heat capacity and magnetocaloric effect for pulsed magnetic fields. Review of Scientific Instruments 81:104902.
Lévy, F., I. Sheikin, B. Grenier, and A.D. Huxley. 2005. Magnetic field-induced superconductivity in the ferromagnet URhGe. Science 309:1343.
Mathur, N.D., F.M. Grosche, S.R. Julian, I.R. Walker, D.M. Freye, R.K.W. Haselwimmer, and G.G. Lonzarich. 1998. Magnetically mediated superconductivity in heavy fermion compounds. Nature 394:39.
McCollam, A., R. Daou, S.R. Julian, C. Bergemann, J. Flouquet, and D. Aoki. 2005. Spin-dependent masses and field-induced quantum critical points. Physica B: Condensed Matter 359-360:1.
Millis, A.J. 1993. Effect of a nonzero temperature on quantum critical points in itinerant fermion systems. Physical Review B 48:7183.
Moll, P., R. Puzniak, F. Balakirev, K. Rogacki, J. Karpinski, N.D. Zhigadlo, and B. Batlogg. 2010. High magnetic-field scales and critical currents in SmFeAs(O, F) crystals. Nature Materials 9:628.
Morosan, E., H.W. Zandbergen, B.S. Dennis, J.W.G. Bos, Y. Onose, T. Klimczuk, A.P. Ramirez, N.P. Ong, and R.J. Cava. 2006. Superconductivity in CuxTiSe2. Nature Physics 2:544.
Mydosh, J., and P.M. Oppeneer. 2011. Colloquium: Hidden order, superconductivity, and magnetism: The unsolved case of URu2Si2. Reviews of Modern Physics 83:1301.
Okazaki, R., T. Shibauchi, H.J. Shi, Y. Haga, T.D. Matsuda, E. Yamamoto, Y. Onuki, H. Ikeda, and Y. Matsuda. 2011. Rotational symmetry breaking in the hidden-order phase of URu2Si2. Science 331:439.
Paschen, S., T. Luhmann, S. Wirth, P. Gegenwart, O. Trovarelli, C. Geibel, F. Steglich, P. Coleman, and Q. Si. 2004. Hall-effect evolution across a heavy-fermion quantum critical point. Nature 432:881.
Rowley, S., R. Smith, M. Dean, L. Spalek, M. Sutherland, M. Saxena, P. Alireza, C. Ko, C. Liu, E. Pugh, S. Sebastian, and G. Lonzarich. 2010. Ferromagnetic and ferroelectric quantum phase transitions. Physica Status Solidi B 247:469.
Sachdev, S. 1999. Quantum Phase Transitions. Cambridge University Press, New York, N.Y.
Sachdev, S. 2008. Quantum magnetism and criticality. Nature Physics 4:173.
Sebastian, S.E., N. Harrison, M.M. Altarawneh, C.H. Mielke, R. Liang, D.A. Bonn, W.N. Hardy, and G.G. Lonzaricha. 2010. Metal-insulator quantum critical point beneath the high Tc superconducting dome. Proceedings of the National Academy of Sciences U.S.A. 107:6175.
Sebastian, S.E., N. Harrison, R.X. Liang, et al. 2012. Quantum oscillations from nodal bilayer magnetic breakdown in the underdoped high temperature superconductor YBa2Cu3O6+x. Physical Review Letters 108:196403.
Shishido, H., R. Settai, H. Harima, and Y. Onuki. 2005. A drastic change of the Fermi surface at a critical pressure in CeRhIn5: dHvA study under pressure. Journal of the Physical Society of Japan 74:1103.
Smith, R.P., M. Sutherland, G.G. Lonzarich, S.S. Saxena, N. Kimura, S. Takashima, M. Nohara, and H. Takagi. 2008. Marginal breakdown of the Fermi-liquid state on the border of metallic ferromagnetism. Nature 455:1220.
Tanatar, M.A., J. Paglione, C. Petrovic, and L. Taillefer. 2007. Anisotropic violation of the Wiedemann-Franz Law at a quantum critical point. Science 316:1320.
Von Lohneysen, H., and P. Wolfle. 2008. CP1014 Lectures on the Physics of Strongly Correlated Systems XII: Twelfth Training Course (A. Avella and F. Mancini, eds.). American Institute of Physics, College Park, Md.
Superconductors in High Magnetic Fields
Ando, Y., G.S. Boebinger, A. Passner, T. Kimura, and K. Kishio. 1995. Logarithmic divergence of both in-plane and out-of-plane normal-state resistivities of superconducting La2-xSrxCuO4 in the zero-temperature limit. Physical Review Letters 75:4662.
Basov, D.N., and A.V. Chubukov. 2011. Manifesto for higher Tc. Nature Physics 7:272.
Bednorz, J.G., and K.A. Müller. 1986. Possible high Tc superconductivity in the Ba-La-Cu-O system. Zeitschrift für Physik B Condensed Matter 64:189.
de Bruyn Ouboter, R. 1997. Heike Kamerlingh Onnes’s discovery of superconductivity. Scientific American 276:98.
Doiron-Leyraud, N., C. Proust, D. LeBoeuf, J. Levallois, J.-B. Bonnemaison, R. Liang, D.A. Bonn, W.N. Hardy, and L. Taillefer. 2007. Quantum oscillations and the Fermi surface in an underdoped high-Tc superconductor. Nature 447:565.
Kamihara, Y., T. Watanabe, M. Hirano, and H. Hoson. 2008. Iron-based layered superconductor La[O1-xFx]FeAs (x = 0.05-0.12) with Tc = 26 K. Journal of the American Chemical Society 130:3296.
Lake, B., H.M. Rønnow, N.B. Christensen, G. Aeppli, K. Lefmann, D.F. McMorrow, P. Vorderwisch, P. Meibidl, N. Mangkorntong, T. Sasagawa, M. Nohara, H. Takagi, and T.E. Mason. 2002. Antiferromagnetic order induced by an applied magnetic field in a high-temperature superconductor. Nature 415:29901.
Larbalestier, D., A. Gurevich, D.M. Feldmann, and A. Polyanskii. 2001. High-Tc superconducting materials for electric power applications. Nature 414:368.
Lebed, A., ed. 2008. The Physics of Organic Superconductors and Conductors. Springer Series in Materials Science, Volume 110. Springer-Verlag, Berlin, Heidelberg, New York.
Norman, M.R., D. Pines, and C. Kallin. 2005. The pseudogap: Friend or foe of high T-c?“ Advances in Physics 54:715.
Riggs, R.C., O. Vafek, J.B. Kemper, J.B. Betts, A. Migliori, F.F. Balakirev, W.N. Hardy, R. Liang, D.A. Bonn, and G.S. Boebinger. 2011. Heat capacity through the magnetic-field-induced resistive transition in an underdoped high-temperature superconductor. Nature Physics 7:332.
Sebastian, S.E., N. Harrison, E. Palm, T.P. Murphy, C.H. Mielke2 R. Liang, D.A. Bonn, W.N. Hardy, and G.G. Lonzarich. 2008. A multi-component Fermi surface in the vortex state of an underdoped high-Tc superconductor. Nature 454:200.
Shishido, H., A.F. Bangura, A.I. Coldea, S. Tonegawa, K. Hashimoto, S. Kasahara, P.M.C. Rourke, H. Ikeda, T. Terashima, R. Settai, Y. Ōnuki, et al. 2010. Evolution of the Fermi surface of BaFe2(As1-xPx)2 on entering the superconducting dome. Physical Review Letters 104:057008.
Tinkham, M. 1996. Introduction to Superconductivity, 2nd ed. McGraw Hill, New York, New York.
Wu, T., H. Mayaffre, S. Krämer, M. Horvatić, C. Berthier, W.N. Hardy, R. Liang, D.A. Bonn, and M.-H. Julien. 2011. Magnetic-field-induced charge-stripe order in the high-temperature superconductor YBa2Cu3Oy. Nature 477:191.
Semiconductors and Semimetals
Alicea, J., and L. Balents. 2009. Bismuth in strong magnetic fields: Unconventional Zeeman coupling and correlation effects. Physical Review B 79:241101.
Behnia, K., L. Balicas, and Y. Kopelevich. 2007. Signatures of electron fractionalization in ultraquantum bismuth. Science 317:1729.
Castro Neto, A.H., F. Guinea, N.M.R. Peres, K.S. Novoselov, and A.K. Geim. 2009. The electronic properties of graphene. Review of Modern Physics 81:109.
Das Sarma, S., S. Adam, E.H. Hwang, and E. Rossi. 2011. Electronic transport in two dimensional graphene. Review of Modern Physics 83:407.
Levy, N., S.A. Burke, K.L. Meaker, M. Panlasigui, A. Zettl, F. Guinea, A.H.C. Neto, and M.F. Crommie. 2010. Strain-induced pseudo-magnetic fields greater than 300 Tesla in graphene nanobubbles. Science 329:544.
Li, L., J.G. Checkelsky, Y.S. Hor, C. Uher, A.F. Hebard, R.J. Cava, and N.P. Ong. 2008. Phase transitions of Dirac electrons in bismuth. Science 321:547.
Novoselov, K.S., V.I. Fal’ko, L. Colombo, P.R. Gellert, M.G. Schwab, and K. Kim. 2012. A roadmap for graphene. Nature 490:192.
Novoselov, K.S., A.K. Geim, S.V. Morozov, D. Jiang, Y. Zhang, S.V. Dubonos, I.V. Grigorieva, and A.A. Firsov. 2004. Electric field effect in atomically thin carbon films. Science 306:666.
Novoselov, K.S., Z. Jiang, Y. Zhang, S.V. Morozov, H.L. Stormer, U. Zeitler, J.C. Maan, G.S. Boebinger, P. Kim, and A.K. Geim. 2007. Room-temperature quantum hall effect in graphene. Science 315:1379.
Smalley, R.E., M.S. Dresselhaus, G. Dresselhaus, and P. Avouris, eds. 2001. Carbon Nanotubes: Synthesis, Structure, Properties and Applications. 1st ed. Springer-Verlag, Berlin, Heidelberg, New York.
High Magnetic Fields in Soft Matter Research
Beaugnon, E., and R. Tournier. 1991. Levitation of organic materials. Nature 349:470.
Berry, M.V., and A.K. Geim. 1997. Of flying frogs and levitrons. European Journal of Physics 18:307.
Maret, G., and K. Dransfeld. 1985. Biomolecules and polymers in high steady magnetic fields. Topics in Applied Physics 57:143.
Shklyarevsky, I.O., P. Jonkheijm, N. Stutzmann, D. Wasserberg, H.J. Wondergem, P.C.M. Christianen, A.P.H.J. Schenning, D.M. de Leeuw, J. Wu, K. Müllen, and J.C. Maan. 2005. High anisotropy of the field-effect transistor mobility in magnetically aligned ciscotic liquid-crystalline semiconductors. Journal of the American Chemical Society 127:16233.
Oshikawa, M., M. Yamanaka, and I. Affleck. 1997. Magnetization plateaus in spin chains: “Haldane Gap” for half-integer spins. Physical Review Letters 78:1984.
Zaric, S., G.N. Ostojic, J. Kono, J. Shaver, V.C. Moore, M.S. Strano, R.H. Hauge, R.E. Smalley, and X. Wei. 2004. Optical signatures of the Aharonov-Bohm phase in single-walled carbon nanotubes. Science 304:1129.