Land Change Modeling Approaches
To move land change modeling forward, it is critical that a common language is established to differentiate modeling approaches according to their theoretical and empirical bases. The diversity of approaches to land change modeling, along with differences in definitions between practitioners from different disciplines, does not lend itself to a discrete classification system. Agarwal et al. (2002) described models in terms of how they handle spatial, temporal and decision making complexity. While this approach provided useful distinctions at the time that review was completed, significant progress in developing all modeling approaches has blurred even some of those distinctions.
The committee has identified six generally recognized groups of approaches to land change models (LCMs), the first five of which are arrayed roughly in order from least to most structurally oriented (i.e., focused on process): (1) machine learning and statistical, (2) cellular, (3) sector-based economic, (4) spatially disaggregated economic, (5) agent-based, and (6) hybrid approaches. While we mention statistical approaches in the first category explicitly, statistical methods are used in some way within most of the approaches. There are overlaps in the degree and type of process orientation among the approaches that depend on the details of the specific model representing these approaches. We include the sixth type to acknowledge the importance of studies and applications that combine the different approaches into a single model or modeling framework. The following sections outline the theoretical and empirical bases as well as technical, research, and data challenges for each approach. Examples of each approach are also provided. Because of similarities in the approaches, we address both forms of economic models in a combined section. Following the discussion of
each approach, we compare the key assumptions, data requirements, and recommended uses of each modeling approach.
MACHINE LEARNING AND STATISTICAL
Theoretical and Empirical Basis
Machine learning and statistical methods in LCMs involve approaches to represent relationships between inputs (i.e., driving variables) and outputs (i.e., land use or cover changes). The data are used to generate maps of transition potentials that give an empirically based measure of the possibility of particular land transitions. Together with traditional parametric approaches, usually in the form of logistic regression (Millington et al. 2007), generalized linear modeling, or generalized additive modeling (Brown et al. 2002), several different kinds of Bayesian and machine learning algorithms have been used in influential LCMs. For example, the Dinamica model offers the option of logistic regression or a weights-of-evidence approach, which estimates a statistical model similar to logistic regression, but does so within a Bayesian framework (Carlson et al. 2012).
Neural networks play a central role in both the Land Transformation Model (Pijanowski et al., 2002; Ray and Pijanowski, 2010; Tayyebi et al., in press) and Idrisi’s Land Change Modeler (Eastman, 2007; see Box 2.1). Neural networks represent relationships between land transitions and their explanatory variables through a network of weighted relationships that the algorithm adjusts iteratively. Genetic algorithms (GAs) have been used to optimize the rule set for cellular automaton models, by iteratively adjusting the parameter string that defines weights on variables (Jenerette and Wu, 2001). The SLEUTH model (Clarke, 2008) uses an input-assisted incremental approach to calibrate a cellular automata model, but attempts have been made to use genetic algorithms for this purpose (Goldstein 2004). Classification and regression trees are data mining tools that use a sequential partitioning process and have been used to model the probabilities of landscape change (McDonald and Urban, 2006). A comparison across approaches that included logistic regression, Bayesian analysis, weights of evidence, and a neural network showed a case-study site where the neural network produced a more accurate prediction during a validation interval as measured by the area under the relative operating characteristic (ROC) curve and a Pierce skill score (Eastman et al., 2005). Although we do not review all of the individual methods in detail, we describe the strengths and weaknesses of this overall approach relative to the other modeling approaches covered in this study.
Modeling approaches that employ a machine learning or statistical approaches typically receive input in the form of two types of maps: (1) maps of land cover at time points that bound the calibration interval, and (2) maps of explanatory variables, such as topographic slope, distance to roads, etc. After the algorithm
finds this relationship for the calibration interval, the relationship is then typically used to extrapolate the same relationship into a subsequent validation interval during which the predictive power can be tested. Machine learning algorithms can be appropriate for situations where data concerning pattern are available and theory concerning process is scant. There are many cases where it is possible to obtain land cover maps from more than one time point along with explanatory variables for a study site where the investigator is partially ignorant concerning the detailed processes of land transformation. A machine learning algorithm attempts to learn the mathematical or logical relationships among the patterns of land cover and the patterns of the explanatory variables. The machine learning algorithm focuses exclusively on encoding and extrapolating the pattern of the land change, as opposed to the process of change. If the approach is used for prediction, then the prediction assumes stationarity in the land change pattern from the calibration interval to the subsequent time interval. Machine learning algorithms are used to predict by extrapolating historic patterns and can perform the extrapolation in a manner that does not require theory concerning detailed processes of change.
Machine learning algorithms are not designed to simulate feedbacks and nonstationary processes in coupled natural and human systems, nor are they designed to evaluate the effects of policies that attempt to modify processes so that future patterns will be different than the past patterns. Machine learning algorithms are not designed to simulate the mechanisms of human decision making, because machine learning algorithms lack theory concerning the behavior of decision making.
Statistical regression methods assume a fixed mathematical form with coefficients that an algorithm estimates to produce an optimal fit, where optimal is defined by a mathematical criterion, i.e., a maximum-likelihood criterion. The maximum-likelihood criterion leads to a mathematical formula to estimate the regression’s coefficients. For example, the regression equation could assume a monotonic sigmoidal relationship between land cover change and topographic slope. Then the maximum-likelihood algorithm estimates the equation’s coefficients so the regression curve fits as closely as possible to the data, given the form of the monotonic sigmoidal relationship. The coefficients indicate whether the assumed monotonic relationships are increasing or decreasing, and at what rate. The logistic regression might also include interactions among the explanatory variables. Diagnostic measurements help to interpret the fitted coefficients of the regression equation.
In comparison with logistic regression, machine learning algorithms do not require strong assumptions concerning a particular form of a mathematical equation to express a relationship between the land cover map(s) and the map(s) of explanatory variable(s). Machine learning algorithms attempt to mimic biological learning systems through predictive artificial intelligence tools. They fit a relationship between the land change variable and the explanatory variable(s)
BOX 2.1
The Multi-Layer Perceptron
The Multi-Layer Perceptron (MLP) is a machine learning algorithm that is available as an option in the Land Change Modeler within the Idrisi GIS software. MLP is a neural network that receives maps of explanatory variables and land transitions for a calibration time interval and then produces a map of transition potential for temporal extrapolation beyond the calibration time interval. The transition potential is an index on a scale from 0 to 1, where higher numbers indicate pixels that have a combination of explanatory values that are more similar to places where the particular transition occurred during the calibration interval compared to places where the transition did not occur.
The maps in this box illustrate validation information using Idrisi’s tutorial data concerning the gain of disturbed land in Chiquitania, Bolivia. The MLP produced the transition potential map based on the gain of disturbance during a calibration interval (1986-1994) and explanatory variables including slope, elevation, and distance from streams, roads, urban areas, and previous disturbances. The validation interval is 1994-2000; thus, the disturbed pixels of 1994 are masked from the analysis because they are not candidates for post-1994 gain of disturbance. Map A shows the validation data, where black patches show a gain of disturbance. Map B is the output from the MLP, where darker shades indicate relatively higher transition potentials. Map C is a transition potential map that is based exclusively on proximity to disturbed pixels of 1994, where relatively higher transition potentials are assigned to pixels that are closer to disturbance of 1994. The proximity model is included because it is best practice to compare the map from a relatively naïve model to the output from a more complex model.
in a manner that is more flexible than regression concerning the mathematical structure of the fitted relationship and can be designed to be more robust to errors in the data (Bishop, 1995). The algorithm uses an iterative process to fit a relationship between the patterns in the land cover maps and the explanatory variables. Over repeated iterations, the algorithm adjusts the model parameters until the algorithm satisfies a stopping criterion. The stopping criterion signals that the algorithm either has generated a particular degree of fit for the relationship between the land cover maps and the explanatory variables, or a particular amount of stability in the fit from iteration to iteration.
Machine learning algorithms do not necessarily assume sigmoidal or monotonic relationships between the likelihood of land change and explanatory variable(s). The machine learning algorithms can also fit interactions among variables, just as regressions can. Machine learning algorithms are similar to common statistical approaches, in the respect that theory concerning processes
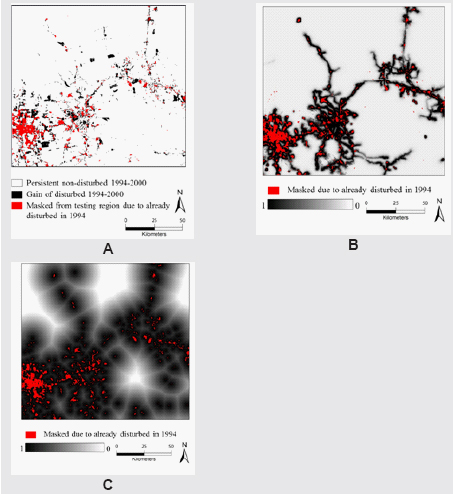
FIGURE (A) Gain of disturbance during validation interval, (B) transition potential from Idrisi’s Multi-Layer Perceptron, and (C) transition potential from a naïve proximity model.
of land change is expressed through the selection of explanatory variables to include and their expected relationships and functional forms, though the theory does not necessarily need to be rich. Many models base selection of variables on the von Thünen idea of land rents, which relates land use, cover, and change to location relative to markets and transportation as well as land suitability through variables like soil quality and slope. This theoretical basis is shared with many cellular models, and is described in more detail in that section.
Machine learning and statistical approaches can be appropriate for situations where data concerning pattern are available and theory concerning process is scant. In terms of short-term PP uses of models, machine learning approaches can be used to make useful predictions. There are many cases where it is possible to obtain land cover maps from more than one time point along with explanatory variables for a study site where the investigator is partially ignorant concerning the detailed processes of land transformation. A machine learning algorithm can
be used to first identify and represent patterns in data, relating inputs (predictor variables) and outputs (a land or land change variable) then generalize those relationships to other data sets. As more data become available for LCM applications, the ability of machine learning algorithms, in particular, to represent and generalize relationships in those data offers significant potential for dealing efficiently with large data volumes.
Technical, Research and Data Challenges
Because the methods and resulting modeled relationships involved in both machine learning and statistical approaches are developed inductively on the basis of the inputted data, the models are particularly sensitive to the inputs. For example, statistical or machine learning models can be applied to model either land use or land cover, and the categories used in the classification will determine the resulting model form. The meaning of the model is determined by the definitions of these categories. Therefore, model suitability for a given purpose will be dependent on the categories in the input map. For these reasons, and because land cover data are more plentiful than land use data, statistical and machine learning approaches are suitable for modeling land cover changes directly, even though these changes may come about through human choices about land use. While machine learning methods have been developed in ways that make them less sensitive to random errors in the input data than statistical methods, systematic biases in data will always affect the resulting models.
Used in a predictive mode, both machine learning and statistical approaches generally assume stationarity in the relationship between predictor and land change variables, i.e., that the model fitted during the calibration interval can be applied to the subsequent time interval without modification. The advantage is that these approaches can be used to predict by extrapolating historic patterns, and can perform the extrapolation in a manner that does not require theory concerning detailed processes of change. Additionally, any variables included as predictors in the model can be modified to generate scenarios of future change. For example, if distance to roads is a predictor variable it is a relatively simple task to simulate the effect of introducing a new road by recalculating distance to the nearest road. The disadvantage is that variables that are not included in the model, but that might change over time, cannot be accounted for in the projections or scenarios. What this often means is that scenarios involving changes to the economic penalties or incentives or other behaviorally related variables or constraints cannot be simulated. However, we address reduced-form econometric approaches in the section on Economic models, in which statistical methods can be used to estimate and evaluate behaviorally oriented scenarios.
Statistical and machine learning approaches differ in the degree of a priori structure imposed by the modeler, such that machine learning algorithms can more easily represent a variety of complex relationships but there exists a
greater risk of overfitting. Overfitting can occur when an algorithm produces a mathematical or logical relationship between observed land change and a set of explanatory variables that fits the details of a particular calibration data set but does not apply to a broader set of applications. This can happen when the relationship fits the details of the calibration data in such a way that the model fails to represent the general principles that extend to other times or places. Spatial or temporal nonstationarity in the land change process can mean that a good fit at one time or place will not generalize well to other times or places. For example, a machine learning algorithm might be able to fit a tight relationship between land cover maps and explanatory variables for a given time interval but do a relatively poor job of matching observations when the relationship is extrapolated to time points beyond the calibration interval, for example because the market or policy conditions differ between the two time periods.
If the model is overfit during the calibration stage, then the investigator can be lured into a false sense of trust that the model can predict accurately the patterns in data for which the model was not calibrated. Overfitting can occur in nearly any modeling approach, especially approaches that calibrate a model based on a single case study. Thus, an important research topic concerns methods to measure and to address overfitting. Because this is a well-known problem in machine learning algorithms, a variety of techniques have been developed to reduce the risks of overfitting, and generalization outside the calibration data has been demonstrated for LCMs (Pijanowski et al. 2005). One approach that has not yet been tried with LCMs is to generate 100s or 1000s of models based on the stochastic elements of machine learning that can serve as a model ensemble and characterize a range of possible models for a given data set.
Interpretation of output can be challenging because many algorithms produce a map of “transition potential” for each land transition, where the transition potential indicates whether the apparent conditions are such that the chances of land change are relatively high versus low. The transition potentials are typically real values on the interval from 0 to 1, and have meaning in terms of their relative ranking, but are not necessarily probabilities of change because they are based on the time interval of change from the data on which they are based. A separate algorithm typically selects pixels with the highest-ranking transition potentials to make a hard classification of future change, where the number of selected pixels is based on an anticipated quantity of land change over some specified time interval. This situation makes it challenging to compare two or more maps of transition potential, since a map that has a higher average transition potential does not necessarily imply a higher anticipated quantity of change compared to a map that has a lower average transition potential. Even if two maps have the same average transition potential, it is not clear how to compare maps when they have differences in the distribution of the transition potentials, for example, when one distribution has a single mode but the other distribution does not. A transition potential can be interpreted as a probability when it indicates the chance
that a particular categorical transition will occur in the pixel during a specific time interval. It is possible to convert some types of transition potentials to probabilities by scaling the transition potentials using a projected quantity of each categorical transition during a specific time interval (Hsieh, 2009). If transition potentials are probabilities, then they have an implied quantity of change for the specified time interval.
Compared to statistical methods, for which a large body of theory exists to facilitate diagnosing and interpreting the structure of a given model, machine learning approaches are often criticized as a ‘black box’ for which interpretation of the model structure and performance is a challenge. This is a well-known challenge for machine learning approaches, and a variety of methods have been developed to understand how the predictor variables relate to the outcome (e.g., to open the black box). For example, a simple approach to understanding the relative contribution of different variables to a machine learning model is to leave out each of the variables one at a time and re-calibrate the model (Pijanowski et al. 2002). Additionally, in terms of measuring how well the relative ranks from the model represent the spatial allocation of the observed transitions, The Relative Operating Characteristic (ROC) is frequently used because it is designed to measure the degree to which higher ranks are concentrated on the feature of interest (i.e., change). ROC has been criticized because many modelers use only a single summary statistic of the area under the ROC curve (AUC) to indicate association (Lobo et al., 2008). The AUC fails to expose the rich information that proper interpretation of the full ROC curve can reveal. Another criticism is that, like other metrics of predictive ability, the AUC can be large due to correctly predicted persistence, not correctly predicted change. This problem can be mitigated through careful selection of the study extent and by proper use and interpretation of the full ROC curve.
Modifications and alternatives to the ROC type of analysis can better express the manner in which a transition potential map fits the empirically observed land change. Proper selection of the measurement is important because the apparent performance of the algorithm can be sensitive to the selection of the measurement. For example, if the machine learning algorithm attempts to maximize the percentage of pixels that agree between the simulated map of land cover types and the reference map for the same time point, then the algorithm might generate output that systematically underestimates the quantity of change. This can occur because a simulation of land change is likely to generate allocation errors when it simulates change; thus, it can reduce the number of those allocation errors by simply predicting very little change. If instead the algorithm seeks to maximize a different measurement, such as the figure of merit (Pontius et al., 2008, 2011), then the algorithm has an incentive to simulate a more accurate quantity of change, because one must simulate an accurate quantity of change in order to have the possibility to generate a high figure of merit.
Cellular land change models use discrete spatial units as the basic units of simulation. Such spatial units can be regularly shaped pixels, parcels, or other land units and are usually arrayed in a tessellation. Cellular models use a variety of input information to simulate the conversions of land cover or land use in these land units based on a rule set or algorithm that is applied synchronously to all spatial units and that represents the modeler’s understanding of the land change process. The algorithm represents decision making that is, implicitly, assumed to take place at the level of the spatial units of simulation, with a one-to-one correspondence assumed between the spatial units and decision maker. Often, the same decision algorithm is applied to all spatial units in a study area, or to large regions within the study area. Variation in decision making can, therefore, solely arise from the attributes of the spatial unit, rather than from the differences in decision making of the actors managing the spatial units.
Theoretical and Empirical Basis
A wide variety of cellular models has emerged over the past two decades, differing in their specification and underlying theoretical and empirical basis. Differences between cellular model types relate to differences in the algorithms and the underlying assumptions that govern the decision rules at the level of spatial units. Another difference between groups of cellular models relates to the way the quantity of change is determined, as distinct from the locations of change. Modelers generally choose between either constraining the total areas of land change at the regional level or determining the regional level of land change simply as the aggregate of the changes at the level of individual spatial units (Figure 2.1). In this section we first look at the theoretical and empirical basis of the decision models. This is followed by a discussion of the top-down versus bottom-up guidance in determining the regional quantities of allocated land change.
An assortment of conversion rules have been applied within cellular models. However, the underlying assumptions can be categorized in three different groups based on the underlying theoretical basis of the models (Schrojenstein Lantman et al., 2011): (1) a continuation of historical trends and patterns, (2) allocation based on suitability of the land, and (3) allocation based on neighborhood interactions.
Continuation of historical trends and patterns
The premise behind the use of historical trends to project future trends is that future land use is assumed to follow patterns of change corresponding to recent or historical changes. The use of this assumption may vary from simple application of transition probabilities from observed historic changes to the use of observed land changes over a past period to empirically estimate relationships between land change and location characteristics. This latter case is similar to
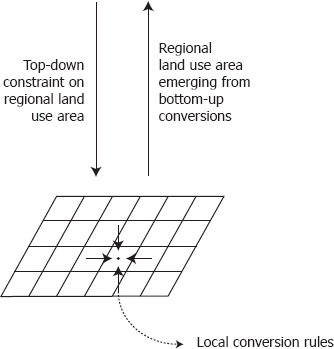
Figure 2.1 Different modeling approaches: Spatial allocation is constrained by a top-down demand or fully determined by local conversion rules.
the application of machine learning methods outlined in the previous section and is elaborated below in the discussion of land suitability. As an example, this may mean that if agricultural land use was found close to cities in the past, it is assumed that future predictions of agricultural land will be allocated close to cities. Implicitly, this assumes stationarity in the underlying decision making of the actors of land change. Often times this assumption is appropriate, but a better understanding of the specific model elements for which and conditions under which stationarity is a reasonable assumption would help with structural evaluation of models, a topic we revisit in Chapter 3.
The most well-known approach to constructing models based on continuation of historical trends is the use of Markov chains. In its basic application to land change, spatial data are used to calculate a transition matrix over an historic time period and then used to derive transition probabilities for the different types of conversions. These probabilities are used to calculate land areas of different land types in the future in a nonspatial manner. Burnham (1973) was one of the first to propose using Markov chain analyses for modeling land use change, but they were later applied by others (Muller and Middleton 1994; Fearnside; Turner 1987). Because of its simplicity, Markovian analysis was very popular during the early phase of development of land change models. However, the approach has a number of limitations. The primary limitations of Markov transition probability-
based models for land use and land cover change analyses are (1) the assumption of stationarity in the transition matrix, that is, that it is constant in both time and space; (2) the assumption of spatial independence of transitions; and (3) the difficulty of ascribing causality within the model, that is, that transition probabilities are often derived empirically from multitemporal maps with no description of the process (Baker, 1989; Brown et al., 2000).
Several authors have tried to overcome some of these limitations by merging the Markovian concepts with other simulation rules and concepts; (Goigel and Turner, 1988; Guan et al., 2011. These hybrid models often use Markovian models to determine future quantities of change while the spatial patterns are simulated by another type of cellular model. Though many models have developed approaches other than Markov chains to describe future changes, the assumption of stationarity is common in other model types. Many statistical and econometric models of relations between land use and location factors assume that such relations remain valid for the period of simulation.
Suitability of land
Many cellular models use, in one way or another, an assessment of the suitability of the spatial units for alternative land uses as a determinant of the conversion rules. The land suitability in cellular models is underpinned by the theoretical work of von Thünen (1966) and Alonso (1964), which explained land use allocation patterns based on the spatial variations in land rent for different land uses. Following on the premise that land users aim to maximize profit, each parcel is converted to the use with the highest land rent at that location. While land suitability is often represented only in a relative terms, these suitability models provide a basis for understanding where different land uses or covers are most likely to be found. Whether or not land rents are calculated in absolute or relative terms often depends on data availability, and relative land rents are commonly used for models of land cover, where there may not be a good theoretical link between economic rent and cover type. In the original specification of the von Thünen model, land rent differs by location and land use due to differences in transportation cost and distance to the market. Elaborations of these premises accounted for differences in soil quality and infrastructure (Alonso, 1964), while Walker and others (Walker, 2004;Walker and Solecki, 2004) extended the underlying bid-rent model to account for development and agency.
The suitability of the land is determined in different ways. In some models land suitability is directly derived from the physical suitability for alternative uses based on agroecological zoning assessments; in other instances this is represented by the potential crop yield that may be obtained (Schaldach et al., 2011). Other approaches also include infrastructural and socioeconomic location characteristics in the determination of the suitability for a particular use. The importance of different location factors as determinant of the suitability can be based on expert knowledge captured in multicriteria evaluation procedures (Schaldach et al.,
2011), a statistical or machine learning approach (as described above), or econometric estimation based on current land use patterns, described below in the section on economic approaches (Chomitz and Gray, 1996; Nelson and Geoghegan, 2002; Verburg et al., 2004a). Multi-criteria evaluation methods do not make strict use of the rent-based framework of von Thünen, but provide a means of evaluating how changes in policy goals or preferences affect desired land allocations in a planning context (Eastman et al. 1995; Klosterman 1999). It is important to note that econometrically derived suitability maps include factors related to both physical suitability and the accessibility of locations and population pressure.
The implementation of suitability maps and their role in allocating land change differs between models. Differences mainly depend on the number of land use and land cover types addressed and the level of competition assumed among the categories. In its simplest form land change between two classes is simulated (e.g., urban vs. nonurban or forested vs. deforested area). Land changes in such binary cases are simply calculated by applying a cutoff to the suitability surface assigning the land use to the highest part of the suitability surface. The cutoff value can be determined such that the regional-level quantity of each land use type that needs to be allocated is matched (Pontius et al., 2001). In case of multiple land cover or land use types these may be allocated hierarchically based on their presumed competitive strengths. Often urban land uses are allocated first, after which agricultural land uses are allocated according to the suitabilities of the locations not yet occupied by urban land use (Letourneau et al., 2012; van Delden et al., 2007). (Semi)natural land uses often occupy the remaining locations.
In other models a more dynamic simulation of the competition between land uses or covers is implemented. This is done, for example, by accounting for the relative differences in suitability for different land uses and the overall demand for those land uses at the regional level or through the dynamic calculation of a shadow price for land (Verburg and Overmars, 2009).
Neighborhood interactions
Neighborhood interactions in cellular models are based on the presumption that the possibility of transition from one use of land to another is dependent on the land use of the locations in the neighborhood. The theoretical underpinning for neighborhood effects was provided by Fujita et al. (1999) and Krugman (1991, 1999). Arthur (1994) used this concept to explain path dependence in the development of cities. In agricultural land use models a rationale for neighborhood interactions is provided by the process of imitation of crop choice and agricultural management between neighboring farmers or within their social network. Empirical evidence, however, has shown that such relations are not always observed as clearly as theory would suggest (Schmit and Rounsevell, 2006).
The best-known implementation of neighborhood interactions in land change models is in the form of cellular automata (CA). Made famous by Gardner (1970), John Conway’s game of life is the best-known example of a cellular automaton
to date. Hägerstrand (1967) and Tobler (1970) first introduced cellular automata in geography, but they were further developed by Couclelis (1985), Batty and Xie (1994), and White et al. (1997). The basic principle of CA is that land use change can be explained by the current state of a cell and changes in those of its neighbors. CA comprises four elements: (1) cell space, (2) cell states, (3) time steps, and (4) transition rules (White and Engelen, 2000). Transition rules specify what land changes will (be likely to) happen based on the nearby land cover types and can be specified based on expert opinion or derived from different types of statistical analysis to inform the specification of the neighborhood rules (Verburg et al., 2004b). However, often expert-based rules for neighborhood interaction are calibrated based on observed transitions to ensure that the algorithm reproduces the observed land cover or -use patterns.
Neighborhood interactions can also be captured in land change models by including them as part of the determinants of the local suitability, for example, by including a variable in the suitability model that represents the number of occurrences of same land use type in the neighborhood. This may be achieved by including an autoregressive term in the econometric model (Lin et al., 2010) or a neighborhood variable in the statistical and machine learning models described in the section above. Neighborhoods can vary between simple neighborhoods of surrounding cells to more complex neighborhoods based on network analysis or predefined regions.
An important consequence of including neighborhood interactions is the emergence of complex spatial patterns from relatively straightforward decision rules as result of the path dependence of the simulation. This allows representation of a number of typical characteristics of land change, such as the emergence of cities (Arthur, 1994). Given their ability to represent characteristics of complex system, CA models are sometimes described as a type of agent-based model. The key difference is that, for cellular models, spatial entities are the basic units of simulation and the topology (or connection) between those units remains fixed, whereas agent-based models (described below) represent decision making units that have a flexible and dynamic relationship with land units. The fixed structure of the cellular models is least limiting in systems where the land characteristics are reasonable indicators of the actor characteristics (e.g., farmers on agricultural land are different from residents of urban land) and where movement of actors of different types among locations is not a significant aspect of system dynamics.
Top-down or bottom-up determination of aggregate land change
Amounts of land use and land cover change are determined in a top-down fashion when observations or projections of the aggregate rate of change are available for the region as a whole. These land use—change estimates are used as to bound an allocation procedure to identify the locations of land use or land cover changes. Models using a top-down structure are constrained cellular automata models such as Environment Explorer (de Nijs et al., 2004; White and
Engelen, 2000) and models like CLUE-s (Verburg et al., 2002) and the Land Transformation Model (Pijanowski et al., 2002).
Bottom-up procedures typically begin calculations at the level of the individual land units. Examples of such models using a bottom-up structure are pure cellular automata models that calculate transitions purely based on the state of the neighboring cells. Also the well-known SLEUTH model, in its original form, uses a bottom-up approach (Clarke and Gaydos, 1998). Both the top-down and the bottom-up approaches have comparative advantages. Whereas the top-down approach explicitly incorporates drivers at a higher aggregation level, in addition to local drivers that determine spatial allocation patterns, the bottom-up approach gives much more weight to local drivers as determinants of aggregate changes at higher levels. While some models are exclusively top down or bottom up in nature, some combine these approaches in a hybrid. Verburg and Overmars (2009), for example, present a hybrid approach in which the dynamics of urban and agricultural land are constrained in a top-down manner, by the trade and regional demand, while the dynamics between (semi)natural land use types is determined solely by the local dynamics originating from the site-specific conditions and land use history. This hybrid demonstration illustrated that the appropriate choice of a top-down or bottom-up approach depends on the dominant processes that influence the dynamics of a specific land use or land cover type.
Technical, Research, and Data Challenges
Cellular approaches have been extremely successful if measured in terms of the number of applications. A wide range of cellular models have been developed over the past two decades, mostly based on variations of the implementation of the concepts described above. A number of the earlier cellular models, for example, SLEUTH (Clarke and Gaydos, 1998), GEOMOD (Pontius et al., 2001), and CLUE-s (Verburg et al., 2002), have been very widely applied across case studies (see Box 2.2). Another indication of success has been the application of this modeling approach in decision support. These models have been used not only in local stakeholder dialogues on land use planning (Van Berkel and Verburg, 2012) and regional assessments (Claggett et al., 2004), but in national to global scale decision-support (Uthes et al., 2010; van Delden et al., 2011; Verburg et al., 2008).
The success of cellular models can be attributed to their relative simplicity in structure and application. The cellular data format matches very well the format of land cover data derived from remote sensing and allows a straightforward processing. Also, the underlying concepts of trend projection, location suitability, and neighborhood interactions are intuitive and can be parameterized by empirical analysis of time-series data or more advanced econometric and calibration methods. The structure of models become much more complex when parcels or other spatial units are used instead of rectangular pixels (Lazrak et al., 2010).
Cellular models are widely available, even included as part of some commercial GIS packages. Because of their availability and simplicity, these models are sometimes selected for these reasons and not because the underlying concept fits well with the case-study specifics. Operation of cellular models is tied to the spatial data layers on which they rely, not only land cover data but also the potential location factors that determine the likelihood of finding a particular land cover type at a specific location. Often, model applications are based on a rich set of physical factors describing terrain, soil, and climate conditions. Spatial variations in socioeconomic conditions, including land tenure, are generally identified as important considerations for land change, but they are sometimes ignored in model applications due to the limited availability of spatially explicit socioeconomic data (Verburg et al., 2011). However, they are included in a number of model applications through inclusion of, for example, census data, polygons representing parks or other public land, and zoning maps.
In spite of their many advantages, cellular models also have clear drawbacks. These are mainly related to the lack of clear theoretical link between the conversion rules and the actual agents of decision making. By defining the transition rules for spatial entities, like pixels, the validity of the conversion rules is largely restricted to the specific spatial extent and resolution for which the rules are defined or empirically estimated. Though heterogeneity of the land surface is represented through variables measuring land suitability and access, heterogeneity of the actors, for example residential homebuyers with different preferences cannot be represented directly. Furthermore, interactions in cellular models are almost exclusively represented by spatial neighborhoods, mostly ignoring interactions through social and other networks. Finally, scale dependency in spatial models (Veldkamp et al., 2001; Walsh et al., 1999) is an issue that makes it difficult to transfer model parameterizations across case studies and scales.
Many cellular models provide reasonable projections of land cover changes over relatively short time frames (e.g., up to 20 years). However, in cellular models run over large extents and used to inform climate change assessments, the simulations are extended to periods of up to one century and over such longer time scales, feedbacks in socioecological systems become increasingly important. Scarcity of land resources, perception of environmental impact, the functioning of the global economic system, as well as policy responses may lead to a modification of conversion rules as a result of preceding land changes and changing decision-making strategies by agents (Meyfroidt, 2013). Cellular models that include neighborhood interactions in the transition rules include feedbacks more explicitly as the neighborhood state is updated during each simulation step. However, the model rules generally use the same algorithm (with different inputs) over space and time, limiting the representation of endogenous adjustments to feedbacks, leading to greater potential for significant divergence between projections and actual outcomes over longer time frames. In principle, cellular models
BOX 2.2
Modeling Land Change Under Alternative Policy Scenarios In Europe
The CLUE (Conversion of Land Use and its Effects) model is one of the most frequently used land use models worldwide. Although the original model was published in 1996 it has been frequently updated and improved to take stock of the recent advances in land science and developments in environmental modeling. Different versions of the CLUE model, especially Dyna-CLUE and CLUE-scanner, have been frequently used in European applications to support policy discussion and ex ante evaluations (UNEP, 2007; Verburg et al., 2008). Currently an operational version of the model is used by the European Commission Joint Research Centre for routine assessments. The CLUE model is a cellular model that uses a top-down allocation of land use demands calculated by nonspatial models. Its allocation is based on suitability maps that are estimated using current-day relations between land use and location factors. Neighborhood interactions are included for urban land uses in a manner similar to cellular automata models to represent agglomeration effects.
For the European application, CLUE operates on a 1 km2 spatial resolution and yearly time steps. This resolution makes it possible to account for specific spatial policies and location-specific driving factors. In the case of adaptation and mitigation measures, such regional specificity is important to capture the feedbacks of local conditions and governance to macroscale patterns of land change. The spatial detail is needed to make sufficiently accurate assessments of land change effects on emissions and other ecosystem services (Kienast et al., 2009). This is especially true for the determination of land change effects on emissions of carbon and other greenhouse gases, where the location of land change is of prime importance. Tailor-made and scale-specific impact assessment modules, documented in peer-reviewed literature, are available for assessment of impacts of land change on carbon, hydrology, ecosystem services, and biodiversity.
are capable of implementing feedbacks into the rules and model structure, but examples of their implementation are rare (Claessens et al., 2009).
SECTOR-BASED AND SPATIALLY DISAGGREGATED ECONOMIC
Theoretical and Empirical Basis
Economic models of land change begin with a structural model of underlying microeconomic behavior (e.g., utility or profit maximization) that determines demand and supply relationships and generates aggregate outcomes of prices and land use patterns. Focused on the economic behavior of human actors, economic models tend to focus on land use, as opposed to land cover, though they can be included within integrated models that also produce land cover outputs. Fundamental to economic models is the price mechanism, which both determines
individual choices and is determined by the cumulative choices of all individuals within a given market area. The concept of equilibrium is used to ensure that individual choices and aggregate outcomes are consistent with each other. Although equilibrium may be defined in various ways, the condition of market clearing, meaning that prices adjust such that markets clear (i.e., excess demand and excess supply are zero in all factor and output markets), is standard in these models. Equilibrium may be static, in which case agents are myopic and prices and land use patterns are unchanging, or dynamic, in which case agents are typically forward looking and prices and land uses are changing over time subject to a constant market-clearing condition. For example, the basic economic land use model posits a landowner’s land use decision as a profit-maximizing decision in which the landowner chooses the productive use of the land that maximizes the landowner’s net returns. Whereas a model with static expectations considers only net returns in the current period, a model with dynamic expectations accounts for the forward-looking expectations of landowners over future costs and returns, which influences the land use decision today. Economists typically use the word dynamics to mean forward-looking behavior while others use it to mean changes in state variables over time without specific regard to expectations (Irwin and Wrenn, 2013). Both types of dynamics are important in the context of land use modeling. Forward-looking behavior is a critical element of many economic land use models—for example, farmers that make current planting decisions based on anticipated future prices of agricultural commodities. Accounting for changes in land use over time is an equally important modeling goal, particularly for policy scenarios.
Structural economic models are specified based on a number of maintained assumptions (e.g., of agents’ behaviors, market structure, and functional form) and the parameter values are often estimated using econometric methods. In other cases parameter values may be guided by theory, taken from previous studies reported in the literature, or a range of values may be explored to examine the sensitivity of the model to specific parameter assumptions. A fully specified structural model can be simulated to generate predictions of prices and land use outcomes under baseline and alternative conditions. The advantage of a structural approach is that, by modeling the underlying processes explicitly, it is possible to account for aggregate-level feedbacks from market interactions (e.g., a change in the price of a substitute good) or nonmarket feedbacks (e.g., congestion externalities) that influence the equilibrium. A structural modeling approach is necessary when the goal is to evaluate the impacts of a nonmarginal change, including policy changes, on land use outcomes or to generate projections of future land use changes under alternative scenarios. This is particularly important when modeling complex processes like land use, in which nonmarginal feedbacks can arise from interactions within and between the socioeconomic and biophysical systems. Because the structural models explicitly describe economic processes and interactions, their reliance on the stationarity assumption is less
limiting than for the statistical, machine learning, and cellular models. Structural models may represent only one or several interdependent sectors of the economy (partial equilibrium) or may include all input and output markets of the economy (general equilibrium). Because of their added complexity, general equilibrium models are defined at more aggregate spatial units (e.g., at the scale of a county, region, or nation), whereas partial equilibrium models can be defined either at the scale that is commensurate with the individual agent or at more aggregate scales. Although structural models rely on a number of maintained assumptions related to the equilibrium, the agent behavior, and market structure, the specification of these structural characteristics improve the fidelity of these model over statistical, machine learning, and cellular approaches to the economic processes leading to land use change. Their data requirements, however, are quite different. Remotely sensed land cover data is less useful than data on the determinants of the supply (e.g., land quality distribution) and demand (e.g., economic activity) for different land uses.
In other cases, the goal of the research is not to explicitly model the underlying structural processes of demand and supply, but rather to identify a causal relationship between one or more explanatory variables and the dependent land use variable. In such cases, a reduced-form econometric model is estimated instead. A reduced-form model can be derived by expressing the outcome variable of interest (e.g., land use, land change, or land value) as a function of explanatory variables that are hypothesized to influence profits, utility, or other primitives of the structural model. Continuing the example from above, the revenues and costs associated with a parcel’s land use are posited to be a function of parcel-specific variables, including the parcel’s physical land characteristics and its location relative to input and output markets. Because the focus of reduced-form modeling is on causal identification and estimating effects, a central empirical challenge is to address problems of endogeneity that arise when an explanatory variable is correlated with the error term. Such endogeneity may arise, for example, from a simultaneous relationship between the dependent and explanatory variables, omitted variables, or through a systematic, but unobserved, process that determines selection among the set of land parcels or locations that are observed. Addressing such identification challenges is the principal focus of reduced-form econometric modeling. However, because neither price formation nor any other market or nonmarket feedbacks are explicitly modeled, these models cannot be used for analysis of nonmarginal changes that would cause the system to equilibrate. For this reason, use of reduced-form econometric models for projection or prediction, like the statistical models discussed above, generally relies on the assumption of temporal stationarity. Because they are derived from an underlying economic model of behavior, reduced-form econometric models are better suited for modeling land use rather than land cover outcomes. However, when land use data are not available, remotely sensed land cover data can be used as a reason-
able proxy when the relationship between land use and land cover is relatively direct, for example, deforestation resulting from agricultural expansion (Nelson and Hellerstein 1997; Pfaff et al. 2007). This is no longer the case when land cover is not a direct outcome of the underlying land use decision. For example, low density exurban development is a residential land use that is comprised mostly of vegetative (non-urban) land cover. While econometric techniques may still be used for identification, the model results reveal causality related to land cover not land use and would be misleading if interpreted in terms of land use. In the absence of a clear identification strategy, reduced-form models estimated with data on land cover provide only a pattern-based correlation analysis similar to the statistical models discussed above.
Economists have used both structural and reduced-form models defined at varying spatial scales and geographic extents to model land change processes. At the most aggregate scale, sector-based models represent global input and output markets that are distinguished by just a few homogeneous regions. At the most disaggregate scale, spatial models of individual land use decisions are estimated using spatial data on land parcels with a geographic extent of a single county. In what follows, we first discuss sector-based models, which vary in their spatial scale and extent, but are aggregate structural economic models of one or more sectors of the economy. We then consider spatially disaggregate models, which use data at the field, parcel, or neighborhood levels to model individual land use or location decisions. These models may be either structural or reduced form, depending on the research question and available data, and are defined by one or more equilibrium assumptions. These models can incorporate site-specific characteristics, such as soil quality; location attributes, such as distance to the nearest town and neighborhood quality; and individual agent characteristics. Space may enter as a source of exogenous heterogeneity or as an endogenous factor that is jointly determined with spatial equilibrium prices and land use outcomes. Examples of the latter include congestion externalities, agglomeration effects, and income sorting. Here we provide only a brief overview of these various modeling approaches. More detailed reviews of sector-based models are available from André et al. (2010), Hertel et al. (2009), Palatnik and Roson (2009), van der Werf and Peterson (2009), and van Tongeren et al. (2001). For more discussion of spatially disaggregate models see Brady and Irwin (2011), Irwin et al. (2009), and the chapters by Irwin and Wrenn (2013), Klaiber and Kuminoff (2013), and Plantinga and Lewis (2013) in The Oxford Handbook of Land Economics (Duke and Wu, 2013).
Sector-Based Models
Sector-based models are structural models of one or more sectors of the economy that model the flows of inputs (labor, capital) and outputs (commodities) across regions or countries in which land is a fixed factor of production.
Models are distinguished by the scope of the economic system that is represented: general equilibrium models represent the global economy and the interactions and feedbacks between different sectors (markets), partial equilibrium (PE) models consider detailed description of a specific sector or sectors (e.g., agriculture, forestry production, and/or fuel production system) as a closed system without linkages with the rest of the economy. PE models determine prices, production, and the proportions (or shares) of land within a geographical region (usually a country or region) used as inputs in the agricultural, forestry, and/or fuel sectors. These models assume that economic conditions in the rest of the world remain unchanged.
Computable general equilibrium (CGE) models operationalize the general equilibrium structure by using computational methods to solve for the supply, demand, and price levels that support equilibrium across interconnected markets of an open economy (Wing, 2004). CGE models are able to capture macroeconomic processes and international feedback effects through changes in relative prices of inputs and outputs. While broad in geographic and sectorial scope, CGE models have limited spatial resolution and usually partition the world into a few large homogeneous regions. Each region has a regional representative household that allocates resources domestically and production sectors that produce goods and services using consumer-owned endowments as primary inputs. Each region interacts with other regions through trade. Consumers maximize utility, while producers maximize profits in a perfectly competitive market setting, leading to endogenously determined prices and quantities of goods and factors of production (Khanna and Crago, 2012). This representation means that heterogeneity among consumers and producers within a sector, for example in terms of risk tolerance or access to capital, are not accounted for in these models.
PE and CGE models explain the amount of land allocated to different uses by demand-supply structures of the land-intensive sectors under certain exogenously defined constraints. In addition to data tables of input and output of all included commodities, the most important inputs are elasticities, which describe, for example, the sensitivity of consumer demand to price changes and of producers’ output decisions to input price changes.
Examples
Examples of PE models, which consider only the agricultural sector, are the ASMGHG model (McCarl and Schneider, 2001; Schneider, 2000), IMPACT (Rosegrant et al., 2002), and the model of De Cara et al. (2005). An example of a PE model describing the forestry sector is the Global Timber Market Model (Sohngen et al., 1999). The following models include both the agricultural and forestry sectors: AgLU (Sands and Edmonds, 2005; Sands and Leimbach, 2003), FASOM (Adams et al., 2005), and GLOBIOM (Havlik et al., 2008) (see Box 2.3).
Examples of CGE models analyzing the effect of land cover and land use change include FARM (Wong and Alavalapati, 2003), the Global Trade Analysis
Project (GTAP) model (Hertel et al., 2009), the Emissions Prediction and Policy Analysis (EPPA) model (Babiker et al., 2008), and the IMAGE (Alcamo et al., 1998). These models are similar in that they are global in scope and are multiregion, multisector, and multifactor models.
Technical research and data challenges
PE models are able to provide initial assessment of the costs and potentials of emission reductions for a local or regional policy option. A key limitation of PE models is that demand for a land use sector is exogenously given. If there is a shock to the system, equilibrium prices change, but it does not change incomes of consumers and producers and affects demand curves endogenously. Nevertheless, the higher level of detail that comes with a lower level of regional aggregation comes as an advantage. As the scale of the policy and the region under study becomes larger, CGE models that focus on these effects may have an advantage. However, the first generation of CGE models was overly simplistic and did not capture many important characteristics of land use economics. Over the past one and a half decades, different attempts have been made to extend CGE models to allow for detailed analyses of the land use sector. Each modeling approach has its own advantages and drawbacks in terms of data requirements, computational practices, and accuracy of representation.
There can be gains from coupling the CGE model with models of other disciplines or narrower or broader scope, for example when studying linkages
BOX 2.3
The Agriculture and Land Use (AgLU) Sector-Based Economic Model
The Agriculture and Land Use (AgLU) model simulates land use change globally and carbon emissions resulting from land use policies. The model was developed as an extension of the Edmonds-Reilly-Barns (ERB) model of energy consumption and carbon emissions (Edmonds et al.,1996) which utilizes oil, gas, coal, and commercial biomass global markets (Sands and Kim, 2009).
The three primary drivers of land use change are population growth, income growth, and autonomous increases in future crop yields. Currently efforts are under way to develop the Integrated Earth System Model (iESM) by merging the GCAM model with the National Center for Atmospheric Research’s Community Earth System Model to advance the science of human and Earth system interactions, including studies of land use, future bioenergy systems, hydrology, climate adaptation, and mitigation. One trade-off, however, is computational intensity for the near-limitless options in human systems and decision making. Accordingly, iESM is expected to advance a new class of human-Earth systems understanding and analytic capabilities while working in tandem with other established modeling capabilities.
between climate policy and land use. A few efforts have coupled equilibrium models with detailed biophysical models. For example, the PE model IMPACT allows for the combined analysis of water and food supply and demand. Based on a loose coupling with global hydrologic models, climate change impacts on water and food can be analyzed using IMPACT (Zhu et al., 2008). IMAGE is a biophysically based global CGE model of agriculture and land use (Alcamo et al., 1998) that provides an interlinked system of atmosphere, economy, land, and ocean. IMAGE is the first model to have considered the feedback between land use change and climate change in both directions. Like IMAGE, MIT’s EPPA model is a forward-looking (Babiker et al., 2008) CGE model that is part of MIT’s integrated assessment model, the Integrated Global System Model, which links a set of coupled human activity and Earth system models (Sokolov et al., 2005). However, the EPPA model focuses on fossil-fuel emissions from energy production and includes agriculture as an aggregate sector only, with land as an input that is imperfectly substitutable with the energy materials composite. Another example of a coupled modeling system is KLUM-GTAP (Ronneberger et al., 2009), where the static global CGE model GTAP is coupled to the land use model KLUM (Ronneberger et al., 2005). The biophysical aspects of land are included indirectly, as area-specific yields differ for each unit of land.
Spatially Disaggregated Models
Spatially disaggregated economic models are based on the assumption of an underlying behavior of profits or utility maximization or cost minimization, all of which are continuous variables. However, land use is typically measured as a categorical variable at the individual parcel or decision-maker level, requiring a discrete choice framework to model an individual’s optimal land use decision (Bockstael, 1996). Dynamic discrete choice models that account for both the evolution of the model’s state variables and how agents form expectations over future values of these variables are computationally difficult, and estimation with more than a few state variables becomes intractable. For this reason, most spatially disaggregated models model land use change over time but assume static expectations (Plantinga and Lewis, 2013) (see Box 2.4).
Structural models are distinguished from reduced-form models by explicitly representing the underlying microeconomic behavioral process (e.g., profit maximization or cost minimization) and the mechanism by which these individual decisions aggregate up to market-level outcomes. Although the basic concept of equilibrium is used to solve this aggregation problem, models differ in how equilibrium is defined in the relevant input and output markets. Models may treat prices as exogenous if the market extent is large relative to the geographic extent of the study. For example, agricultural and forest commodity prices that are determined by large regional markets and global market competition are exogenous to individual farm or forest operators (e.g., Antle et al., 2001). On the
other hand, if the modeling goal is to simulate policies that may induce large-scale land use shifts, then the price-feedback effects must be accounted for by specifying market-equilibrium conditions (e.g., Lubowski et al., 2006). While most models assume frictionless markets, equilibrium conditions may also reflect market frictions that would constrain the equilibrium, such as information costs, credit constraints, or moving costs (e.g., Bayer et al., 2009). If space is important, then prices will depend not only to the quantity of land in alternative uses but also on its spatial distribution. In turn, the spatial distribution of land use depends on price and its spatial variation. Equilibrium is determined by appealing to the concept of spatial equilibrium. In a model with homogeneous agents, such as the urban bid-rent model, spatial equilibrium is characterized by equal utility or profits across space since any advantage or disadvantage of a location is capitalized into its price. On the other hand, models that account for heterogeneity in preferences or income, such as the equilibrium-locational models, characterize spatial equilibrium as a Nash equilibrium in which each individual makes an optimal decision given the location or land use decisions of all other agents (Kuminoff et al., 2010). In each case, price is the equilibrating mechanism that determines the quantity and pattern of land use and land change.
Because data on revenues and costs associated with spatially disaggregated land use choices are often not available, spatially disaggregate models are often reduced form. In many cases, the model may not be fully reduced to only exogenous variables; that is, the model may include one or more endogenous explanatory variables that are determined by the same equilibrium process as the dependent variable. For example, in the case of open-space spillovers that influence the amenity value of a location, the spatial distribution of open space is endogenous to the land market and thus the spatial pattern of residential and open space are jointly determined. In a reduced-form model, in which these structural relationships are not explicitly represented, problems of endogeneity, for example, that arise from simultaneity or unobserved correlation, violate the statistical assumptions of the model. A variety of econometric methods have been developed to address these identification problems. If properly dealt with, the estimated reduced-form model yields consistent and unbiased estimates of the net effects of the explanatory variables on the modeled land use outcome. Because of their focus on causal identification, reduced-form models are often preferred when the research goal is to test one or more specific hypotheses by identifying key parameters. For example, this is the case with reduced-form models used in quasiexperimental designs in which the goal is often to evaluate the effect of a specific policy or policy change on land use outcomes (Towe and Lynch, 2013). Reduced-form models can also be used to simulate land use change in response to a change in a policy or other variable of the model. However, because these models are limited by the assumption of a constant equilibrium, they can only be used to simulate the effect of marginal changes on land change outcomes.
In order to predict the effects of a policy or other change on two-dimensional
BOX 2.4
Spatially Disaggregated Economic Model
Lewis et al. (2011) developed a spatially disaggregated integrated assessment model to examine the impacts of incentive-based policies on land change and biodiversity conservation. Similar to Nelson et al. (2008), the land change model starts with an econometric model of land use decision making that uses a random sample of plot-level, repeat observations from the National Resources Inventory taken at multiple points in time (1982, 1987, 1992, 1997). The authors take advantage of the panel structure of their data by estimating a random-parameters logit model that controls for unobserved spatial heterogeneity and temporal correlations, which is important for obtaining consistent and unbiased estimates of the land change model parameters. Predicted net returns for each plot are generated using county-level average net revenue estimates from Lubowski et al. (2006) and plot-level data on land quality and other characteristics. The inclusion of economic returns in the model is significant because it provides the mechanism for simulating landscape outcomes under alternative policies on payment for ecosystem services. Using predicted net revenues for each land use for each parcel, the authors calculate the landowner’s minimum willingness-to-accept bid, which is the necessary payment that is needed to compensate the landowner for taking land out of production and putting it into conservation.
Because biodiversity is dependent on spatially disaggregated patterns of land use, a random sample of plot-level data is insufficient for predicting the policy impacts on biodiversity outcomes. The authors solve this problem by applying the parameter estimates from the plot-level econometric model to a complete set of cropland and pasture parcels that are contained within the 2.93
land use patterns using a spatial disaggregated economic model, some kind of a spatial simulation approach needs to be used in addition to the statistical estimation. A challenge arises in applying the results of discrete-choice models, which are probabilistic in nature, to spatial simulation models. Although some researchers form deterministic rules from these probabilistic transition estimates, this ignores the stochastic nature of the model results. An alternative is to generate a large number of different landscapes conforming to the underlying probabilistic rules (Plantinga and Lewis, 2013). The challenge is then to summarize this information in a way that conveys the distribution of potential landscape pattern outcomes and is useful for policy evaluation. Any simulation of alternative policy scenarios or future conditions based on an econometric model necessarily relies on a stationarity assumption, that the conditions under which the simulations are made are identical to those under which model was fit. The less structural detail in the model, i.e., the less the processes are endogenous, the stronger is the stationarity assumption.
million hectares of their study region. Willingness-to-accept bids and transition probabilities for each parcel starting in cropland or pasture and ending in one of four land uses (cropland, pasture, forest, or urban) are calculated. A range of conservation payment policies are considered that differ in terms of the total budget and the subset of landowners who are considered eligible. Simulations of the predicted landscape that would exist 50 years after the policy is enacted are generated 500 times for each policy. The result is a prediction of the spatial distribution of land in conservation and agricultural production for each policy.
The authors provide a normative assessment of the policies by computing a biodiversity score for each of the simulated landscapes. This integration of positive land change and ecosystem models with a normative analysis of the economic and ecological trade-offs is something that relatively few studies have attempted, but yet is critical for policy guidance (Polasky and Segerson, 2009). The authors evaluate the efficiency of the predicted outcomes under each policy by comparing the biodiversity score of each policy at each of the budget levels to the maximum biodiversity score that is theoretically possible for each budget level. They find that simple incentive-based policies that do not account for the spatial pattern of conserved lands are highly inefficient. This inefficiency arises from the benefits of conserving large spatially contiguous areas and the inability of the regulator to spatially coordinate payments to landowners since the willingness-to-accept bids are private information and therefore the regulator cannot anticipate ex ante the resulting spatial landscape of conservation under a given policy and budget. The authors conclude that an auction mechanism to elicit landowners’ willingness-to-accept bids and some means to provide incentives for enrollment of spatially contiguous lands are likely necessary to achieve real efficiency gains.
Examples
The early spatially disaggregated models were reduced-form binary or multinomial discrete-choice models of discrete land use or land cover categories (e.g., Bockstael, 1996; Chomitz and Gray, 1995; Nelson and Hellerstein, 1997). These were very similar in form to the statistical approaches described above. Subsequent innovations in modeling came with the application of duration models to account for time (and nonstationarity) and time-varying variables in the land conversion process (Irwin and Bockstael, 2002; Newburn and Berck, 2011; Towe et al., 2008) and with price data that provide a means to impute net returns at an individual level (Antle et al., 2001; Lubowski et al., 2006; Wu et al., 2004). Most recently researchers have developed econometric models that incorporate both the discrete and the continuous change aspects of land use (Lewis, 2010; Lewis et al., 2009; Wrenn and Irwin, 2012) (see Box 2.4). This is an important innovation given that both outcomes—the discrete land use change and the intensity with which the land is used—have important impacts on many issues directly related to land use and its spatial configuration including ecosystem fragmentation, loss of farmland, and urban decentralization.
Landscape simulation models differ in their research goals. In some cases, the question centers on local spatial effects and how they influence the spatial structure of markets or land use. For example, Irwin and Bockstael (2002, 2004) used estimates from reduced-form duration models to simulate the influence of local spatial interactions from neighboring developments on residential development patterns. Wu and Plantinga (2003) simulated a spatial equilibrium model based on the urban bid-rent model to examine the influence of public open space on the spatial structure of urban land rents and land use. Caruso et al. (2007) used a similar model to consider the influence of endogenous green amenities and congestion effects on the resulting urban land use pattern. Newburn and Berck (2011) developed a spatial simulation model based on the urban growth model of Capozza and Helsley (1989) to examine the influence of preference heterogeneity and differences in suburban versus exurban development costs on leapfrog development patterns.
In other cases, parcel-level econometric models have been usefully integrated with ecosystem models to examine the influence of land management policies on private landowners’ land use decisions that in turn affect climate change, species conservation, water quality, or other ecosystem services. For example, Nelson et al. (2008) used National Resources Inventory plot-level data for the United States over several time periods to estimate an econometric model of a landowner’s decision to allocate land to one of six uses (crops, pasture, forest, urban, range, and land enrolled in the Conservation Reserve Program). Decisions are posited to be a function of their current land use, land quality of the plot, specific landowner characteristics, and economic net returns for each land use, which are predicted at the plot level by interacting an estimate of average county-level net returns with a plot-level measure of land quality. The empirical model yields transition probabilities expressed as functions of net returns and the starting land use, which allows for the simulation of incentive-based policies by modifying net returns and using the model estimates to predict the effect on landowners’ land use choices. The estimates are used to generate predicted transition probabilities for land parcels located in a western U.S. region under several different conservation payment policies. Uncertainty is accounted for by running many simulations for each policy scenario and examining the distribution of land use patterns for each scenario. Predicted land use patterns are then used as inputs into models that predict the provision of carbon sequestration and biodiversity conservation. The results show that there are trade-offs between these two ecosystem services and that policies aimed at increasing the provision of carbon sequestration do not necessarily increase species conservation.
A recent innovation in structural modeling is the application of equilibrium-locational-choice models to simulate the effects of various land use policies on housing markets and land use allocations at a neighborhood scale. Using the observed outcomes of the household sorting process and house prices across neighborhoods, it is possible to estimate structural econometric models of house-
hold location that are consistent with a spatial equilibrium. Because the model estimates reflect the underlying preference structure and how households respond to market feedbacks (e.g., a price change) and nonmarket feedbacks (e.g., open-space patterns), the model can be used to predict household location choices under future scenarios in which nonmarginal changes may cause households to resort. Walsh (2007), for example, examines how an open-space policy affects household re-sorting by changing the spatial equilibrium distribution of private and public open space across neighborhoods within a metropolitan region. He finds the surprising result that a policy to provide additional public open space can result in less overall open space as demand for these locations increases and households substitute away from private open space.
Technical research and data challenges
The primary advantages of structural models of land change are twofold. First, they account for the fundamental role of prices (e.g., costs and revenues) in explaining individual land use decisions in ways that most machine learning and cellular models do not. This permits simulations of incentive-based economic policies such as payments for ecosystem services. Recent econometric models of land change have incorporated spatially disaggregated predictions of net revenues and in so doing accomplish this important goal (e.g., Lewis et al., 2011; Lubowski et al., 2006; Nelson et al., 2008). Second, models in which price is endogenous are able to capture the feedback effects of predicted land use changes on prices and thus can be used to predict the outcomes of policies that induce nonmarginal changes and cause the system to reequilibrate. Equilibrium locational-choice models provide the best example of this approach to date (e.g., Klaiber and Phaneuf, 2010; Walsh, 2007). Combining these two approaches by developing an econometric structural model of land use at the parcel level, in which the parameters of the market equilibrium are jointly estimated, is a much more difficult task and one that has not been achieved. The model by Lubowski et al. (2006) provides an alternative approach that combines econometric-based predictions of policy-induced land use changes with a policy simulation model that uses demand elasticities from previous studies to account for the subsequent changes in the prices of agricultural and forest commodities. This analysis is carried out at a national level. Accounting for market feedbacks in a spatially disaggregated land use simulation model may not be necessary for some output markets (e.g., if commodity markets are global), but assumptions regarding spatial equilibrium in more localized markets, including land and housing markets, are necessary to capture spatially disaggregated market and nonmarket feedbacks. Despite the modeling challenges, developing a spatially disaggregated LCM that accounts for such feedbacks is critical for developing spatially disaggregated, dynamic land change models and coupling land change and ecosystem models over longer periods of time.
Although structural models are necessary for nonmarginal land change pre-
diction and policy scenarios, they also face a number of challenges. All structural models require maintained assumptions about agent behavior, market structure, and functional form. In addition, econometric structural models require a number of identifying assumptions about the error processes. Spatial simulation models, on the other hand, require assumptions about parameter values. Many of these assumptions are difficult to test empirically and therefore additional data and analysis are needed to better justify these assumptions. In some cases, structural models are also limited in the spatial dimension. Equilibrium locational-choice models, for example, are limited to a neighborhood scale of analysis. In most cases this neighborhood scale may be sufficient, but smaller-scale analysis of feedbacks and land use change may be necessary for certain research questions, for example, questions related to land fragmentation and the impact of land use change on ecosystems. Other challenges include incorporation of dynamics, both in terms of accounting for agents’ expectations over the future evolution of equilibrium prices, as well as modeling the evolution of prices and land uses over time. So-called dynamic equilibrium models that represent changes in equilibrium prices, quantities, and other economic variables over time are well known in economics but are difficult to implement in a spatially explicit setting. Some progress has been made in urban economics (Desmet and Rosi-Hansberg, 2010) and resource economics (Brock and Xepapadeas, 2010; Smith et al., 2009). More work is needed to develop spatial dynamic models of land change and to specify these models empirically to make them useful for policy simulations. Finally, structural models are limited by their data requirements, given that data on revenues and costs are often difficult to obtain and that it takes a long time to develop them. Satellites are unlikely to provide much of the required data. These models require a minimum of several years to gather data, implement the model, and generate policy simulations.
Like structural models, reduced-form models have a number of strengths and limitations. The primary strength of reduced-form models is their focus on causal identification. By making explicit assumptions regarding the data generating process, the variables that are observed and unobserved, and the structure of the error process, these models go beyond simple correlation analysis, as generally employed in the statistical modeling approach described above, to identification of causal effects. This is essential to testing hypotheses and developing predictive models that can be used for policy. In addition, while assumptions are still necessary for identification and interpretation of the results, these models typically impose fewer assumptions on the data than do structural models. Finally, provided data are available, these models can be implemented in a reasonable time frame and, because the parameters reflect the causal relationships between the observed variables and equilibrium outcomes that are based on underlying microeconomic behavior, they can be usefully applied to policy scenarios.
A primary limitation of reduced-form models is their lack of a structural representation of the underlying demand and supply processes that generate the
observed land use outcomes. Any application of reduced-form estimates to a simulation model implicitly assumes that the underlying equilibrium relationships, including prices, remain unchanged (i.e., are stationary). This is a reasonable assumption for marginal changes in the system, but not for scenarios of nonmarginal changes, such as the introduction of a new policy or a change in an existing policy that would induce large-scale shifts in land use allocations or prices. For this same reason, their usefulness for simulating landscape changes over longer periods of time is also limited.
Agent-based models (ABMs) represent, in computer code, systems that are composed of multiple heterogeneous and interacting actors (i.e., agents; Brown, 2006). These systems are often referred to as “multi-agent systems” (Wooldridge, 2002) and describe intelligent agents, their interactions, and their natural environment. The term “individual-based models” is commonly used in the ecology literature to describe models of this sort in applications to ecological systems (DeAngelis and Gross, 1992). In the context of land change, agents can include land owners, households, farmers, development firms, collectives, migrants, management agencies, or policy-making bodies, that is, any actor that makes decisions or takes actions that affect land use or land-cover patterns and processes (Parker et al., 2003). Agents are discrete entities that are characterized by both their attributes and their behaviors. The attributes of agents can be continuous measures, like the amount of available capital, or discrete categories, like “has children” or “belongs to a cooperative.” Agents can interact with each other and with the environment in which they live to collect information or carry out actions that modify their context. Though not all agent-based models are spatially explicit, those used in land change research nearly always are, meaning that the agents and/or their actions are referenced to particular locations on the Earth’s surface. Because ABMs instantiate a conceptual model that specifies the agents, the attributes, actions, and interactions, they are structural models that represent the processes of land change explicitly.
Theoretical and Empirical Basis
ABMs belong to a category of models known as discrete-event simulations (Zeigler et al., 2000), which run with some set of starting conditions over some period of time, allowing the programmed agents to carry out their actions until some specified stopping criterion is satisfied, usually indicated by either a certain amount of time or a specified system state. By simulating the individual actions of many diverse actors, and measuring the resulting system behavior and outcomes over time (e.g., the changes in patterns of land cover), ABMs can be useful tools for studying the effects of land change processes that operate at multiple scales
and organizational levels. Measured at some time in the future, these system outcomes can also be used to evaluate projections of land use, land cover, or other state variables. Because agents can adapt their behavior to changing conditions, the stationarity assumption can be somewhat relaxed in ABMs. To the degree that ABMs rely on input data from some period of time to establish parameter values or fix decision processes that do not adapt in other ways (e.g., through learning mechanisms) to changing contexts, projections into the future will necessarily require the assumption of stationarity parameters and decision processes. So, while ABMs can be constructed in ways that relax the assumption of constancy in relationships (i.e., stationarity), they are not always constructed in that way. Because of this ability to relax assumptions, however, ABMs are well suited to representing complexity in land systems.
ABMs have been used for a wide range of applications, from explaining spatial patterns of land use or settlement and testing social science concepts, often using exploratory-theoretical models, to policy analysis and planning, more often using empirical-predictive models (Matthews et al., 2007). Models and applications toward the exploratory-theoretical end of this continuum tend to resemble a range of complex systems models that are often mathematical or analytical in nature (LUCC, 2002), including some cellular automata models. Applications of ABMs that aim to test concepts or explain patterns are often compared with analytical models of the same system to demonstrate how the ABM (e.g., because of heterogeneity and interaction) produces results that deviate from a simpler mathematical model. For example, an ABM used to evaluate the relationship between the width and location of a greenbelt and patterns of urban sprawl was able to recreate results from a simple one-dimensional analytical model, but it also demonstrated the sensitivity of results in that model to assumptions about homogeneity in agent preferences and in the landscape, and to feedbacks between agent preferences their location relative to the greenbelt (Brown et al., 2004).
Models and applications toward the empirical-predictive end of the model-application continuum require increasing support from empirical observations to orient the models toward more realistic representations of real systems. Land change applications of ABMs have incorporated a variety of empirical data types into the description of agents, thereby providing some empirical support for the types, characteristics, beliefs, and knowledge of agents (Robinson et al., 2007; Smajgl et al., 2011). These data inputs have been derived from social surveys (Berger and Schreinemachers, 2006), participant observation and ethnographic methods (Huigen et al., 2006), field and laboratory experiments (Castillo and Saysel, 2005; Evans et al., 2006), a “companion modeling” approach that uses participatory methods to engage agents in the construction of their model (LePage et al., 2012), and Geographic Information System (GIS)-based spatial data (Irwin and Bockstael, 2002). Additionally, a variety of approaches has been employed to evaluate the outcomes of models, often through evaluation of predictive accuracy (e.g., Brown et al., 2005). An approach to evaluating model outcomes, referred
to by Grimm et al. (2005) as pattern-oriented modeling, identifies primary and secondary patterns that a model can produce and that can be compared with observed patterns in data. When outcomes of interest involve spatial patterns on land, a common method is to use satellite or aerial imagery to construct maps of land categories at multiple points in time and to compare maps generated by the models to these observations and to employ statistical descriptions of the degree of match. ABMs can be used to model land use, land cover, or both. If land cover, the decisions that affect land cover and land management need to be represented explicitly, and the theoretical basis for modeling these land cover or management decisions is not as fully developed across different systems as is land use theory. When they represent land cover patterns, ABMs benefit from Earth observation data, but data to inform agents attributes, their social interactions and decision processes is more commonly required for these models.
Issues of multi-finality and equifinality, due to exogenous control, path dependence and multiequilibria, affect the predictability of these complex systems and, therefore, the usefulness of traditional measures of predictive accuracy of these models. The pattern-oriented modeling approach can use a wider range of patterns, or “stylized facts” (Janssen and Ostrom, 2006), to validate the model. For example, a model of rubber crop adoption in Laos (see Box 2.5) was evaluated in terms of the amount of land area planted in rubber, the rate of adoption in the study area, and the income inequality among the farmers of the region (Evans et al., 2011). In application, ABMs are then commonly used to generate alternative future scenarios that can be compared in terms of how the patterns respond to changes in model inputs, parameters, or structures, rather than making point predictions.
The most important strength of agent-based models is the ability to explicitly represent agent behavior while providing a range of options for representing that behavior (An, 2012). Many economic land use models derive from assumptions of profit or utility maximization that are assumed to fully determine actors’ land use or location decisions. In addition to these behavioral assumptions, these models typically consider only limited sources of agent or spatial heterogeneity. Finally, even when uncertainty enters the model, agents are assumed to form rational expectations based on a known distribution of the stochastic process (e.g., Capozza and Helsley, 1990). Research in behavioral and decision modeling (An, 2012; NRC, 2008b) has produced a range of alternative behavioral models that incorporate cognitive processes and uncertainty to explain human decision making and that can be implemented and evaluated with agent-based models. For example, (a) land use actors can exhibit heterogeneity in their attributes, preferences, or decision-making strategies (Robinson, 2006); (b) the amount of information available to agents and effort agents use to search for and/or evaluate alternatives can limit, or bound, their level of rationality (Manson, 2006; Simon, 1997); (c) alternatives to utility maximization include, for example, using satisficing behavior, in which agents select alternatives that are “good enough” using
BOX 2.5
Agent-Based Model of Rubber Adoption in a Laos Village
Montane mainland Southeast Asia is a region of great biological and cultural diversity that has seen the conversion from traditional agricultural systems to more permanent cash crops driven by regional and global markets (Fox and Vogler, 2005). This conversion has primarily been from traditional agriculture to commercial rubber production and is driven by decisions at the household level in which small land holders to convert their land.
An agent-based model was used to investigate the transition from shifting cultivation to rubber production for a study area in northern Laos PDR to assess changes in household-level inequalities with the transition from shifting cultivation to rubber adoption (Evans et al., 2011). Parameters on household-level land use preference and risk tolerance in the model were fit so that the model reproduced historical land cover patterns (see map below) and household allocations of land to rubber versus upland crops developed from field interviews. The interviews indicated that households with different assets, experience, and risk tolerance had different approaches to this new opportunity resulting in heterogeneity of land use and income.
The model calculated a dramatic change in income inequality through the 1984-2006 simulation period (see Figure 2). The model demonstrates several pulses of rubber adoption and that labor is not the constraining factor as some households continue to allocate a majority of their labor to upland crop production through the model simulation.
The model produces a pattern of early adopters and late adopters that fits well with theories regarding the diffusion of innovation. This approach provides insight on the impact of agricultural innovation on inequality.
heuristics to determine agent choices (Gotts et al., 2003); (d) agents can learn from and adapt to their environment and, therefore, evolve their approaches to accessing information, their preferences, and their decision strategies (Magliocca et al., 2011); (e) the influence of updated social networks, which can have variable and dynamic structures, can have powerful influences on decisions by affecting availability of information and resources (Entwisle et al., 2008); and (f) uncertainty and variability in environmental conditions, information availability, or decision outcomes can affect agent behaviors (Zellner, 2008).
By explicitly representing heterogeneous agents and the interactions among agents and between agents and their environment, ABMs are particularly useful for modeling the formation of outcome patterns, like bilateral prices formed through a series of transactions (e.g., Filatova et al., 2009), or patterns on a landscape (e.g., Jepsen et al., 2006), which result from a system that lacks centralized
FIGURE 1 Simulated land cover 2006 (Evans et al., 2011).
FIGURE 2 Simulated land cover areas (ha) and Gini coefficient (Evans et al., 2011).
control. This is particularly important where the combination of interactions at the agent level and heterogeneity among agents produces nonlinear dynamics at the aggregate level and renders aggregate or representative-agent models inadequate. For example, a model that included a skewed distribution of risk preferences, as observed in survey data, produced patterns of land rights and development that better matched the observed situation near the Dutch coast than did a model that included agents with homogenous risk preferences (Filatova et al., 2011). Decentralized systems of heterogeneous and interacting agents can exhibit path dependence, such that different equilibria are reached depending on the starting point or the order in which actions are taken (Brown et al., 2005). For example, the size distribution of farms and their productivity in a region after a period of time can be dependent on the average farm size for the first period, with implications for approaches to regional structural change.
Because behavior is represented explicitly in ABMs as a decision-making process carried out by heterogeneous agents, the models align with conceptual models of land use systems involving the interactions of multiple types of actors. Because the actions and outcomes of individual agents can be tracked within a model, it is easier to communicate the structure and function of an ABM to stakeholders than a model that represents agent-level decisions and actions in a stylized or aggregate manner through mathematical or statistical functions. This alignment has facilitated a number of applications in which ABMs are used alongside role-playing games to facilitate participatory modeling and learning about resource management problems (Barrateau et al., 2001; d’Aquino et al., 2003; Dumrongrojwatthana et al., 2011). This approach has been referred to as “companion modeling” and has been most vigorously pursued by the developers of Cormas, based in France (LePage et al., 2012). As models become more complicated, with more detail that provides for greater fidelity with real-world systems, however, this communication advantage can be lost. An intuitive understanding of even a moderately complex model can be challenging, and often requires both an understanding of the underlying code and experience with sensitivity analysis through running the model interactively by changing parameter values.
Agent-based models are being coupled with models’ natural processes. to understand dynamics in coupled natural and human systems. Though this has often involved mainly loose coupling to date, that is, passing output from one model to another, ABMs of land change are increasingly being tightly coupled with environmental models of various sorts. For example, by coupling an ABM that represented demographic and economic processes of households with models of forest growth and panda habitat, An et al. (2005) were able to demonstrate the effects of energy and internal-migration policy in China on panda habitat. Coupling models in this way offers promise for exploring dynamics of coupled natural and human systems, and for understanding the role of feedbacks in land system dynamics (Liu et al., 2007).
Technical, Research, and Data Challenges
Many of the challenges related to the use of ABMs stem from their resource-intensive nature relative to model design, implementation, parameterization, calibration, and execution. Because models are usually designed with specific questions in mind and can require significant investments in data about both agent-level characteristics and aggregate outcomes to apply in specific settings, a given model may not be generalizable across other situations or scientific and research applications. For these reasons, problems that are simpler (i.e., can be explained with simpler analytical models) or focused on prediction rather than structural explanations may not need ABMs and the effort involved. Also, because the range of potential systems that can be represented in ABMs is quite
large, it is quite reasonable to expect that the theory and data needed to build a model may not be fully developed in any given instance. In these cases, development and analysis of an ABM might usefully contribute to the development of theory or the identification of data collection requirements.
The computational and empirical resources required to implement and apply ABMs have limited their application in land change science to local-scale questions and applications. Efforts have been made recently to develop probabilistic (Valbuena et al., 2010), aggregation (Rounsevell et al., 2012), and metasimulation (Zou et al., 2012) schemes for generating and applying the insights of ABMs to regional and even global scales. Challenges remain in broadly applying and comparing these schemes and evaluating them through formal calibration and validation activities. Furthermore, approaches of this sort can be used to provide structures by which insights from multiple case studies conducted at local scales can be aggregated for understanding and integration at regional and global scales and to identify how to make compromises between spatial extent and agent complexity (e.g., larger spatial extents may require fewer or simpler agents due to computational constraints).
The following additional challenges were identified by participants in our workshop:
• Economic models of behavior commonly incorporate processes of expectations formation and forward-looking behavior. These processes are not often well developed in many agent-based models, and best practices for doing so need to be developed.
• More modeling work is needed to bridge the gap between spatial economic models and ABMs, building on the strengths of each approach. Because agent-based models do not enforce an equilibrium or spatial equilibrium condition, models that represent market processes employ ad hoc assumptions to specify the bidding and market interaction processes. In the absence of one or more closing conditions that establish an equilibrium, there is no way of ensuring that these individual behaviors will generate land prices consistent with a market equilibrium (Chen et al., 2011). In addition, because of data requirements, these assumptions of bidding behavior and market interactions are difficult to test. Comparisons are needed between spatial equilibrium models that incorporate agent heterogeneity, but rely on a static spatial equilibrium assumption to derive market prices, and agent-based models that incorporate heterogeneity, alternative types of behaviors, and dynamics over time, but that use ad hoc approaches to derive market prices.
• There is need to develop methods to standardize and improve efficiency of parameterizing agent decision models. For example, links between statistical and agent-based modeling could be better developed, such that methods for calibrating preference and decision functions for use in ABMs can be developed using econometric, experimental, and participatory approaches.
• Increasing call for use of ABMs in predictive settings will require better methods for assimilating data and updating models on the fly. For example, operational models will need to be able to be updated when an exogenous shock occurs.
• Agent-based modeling efforts benefit from the availability of a wide range of data types. These include survey data that are spatially referenced to parameterize decision functions; data on land management, use, value, and ownership to complement land cover data; and longitudinal versions of all of these data types. Efforts to collect, make accessible, and integrate these data will enhance these modeling activities.
• Additional work is needed on methods to integrate data across disparate sources. For instance, data developed using different functional unit definitions, spatial extents, different levels of aggregation, and by different agencies might need to be integrated within a single ABM and could be harmonized through a variety of interpolation, down-scaling, or up-scaling approaches. Currently researchers often recreate data because they are not able to access and/or integrate existing data.
• The structural validity of the rules and algorithms used to represent agent actions and their interactions in these models has been challenging to demonstrate. For ABMs, the validation of agent dynamics is often more important than the validation of the model outcomes that are the most common validation targets for LCMs.
• Because agent-based models can frequently generate multiple outputs, due to stochasticity of parameters or inputs, it is important to evaluate the diversity of models outcomes that can result from them. This is especially important when combined with evaluation of multiple scenarios, defined by alterations in model settings to reflect alternative possible futures or policy interventions. Stronger norms for full exploration of the space of model outcomes is needed in land change modeling. This goal might benefit from cross-fertilization of methods from other modeling communities to learn how to synthesize many runs (Monte Carlo–type approaches).
• Development of new, dynamic, and multidimensional methods of analysis and visualization is needed to help better understand relationships between model parameters and model outputs. These methods can further be used to convey to stakeholders what a model is actually doing and can be used to display behaviors of individual model components (like agents or locations).
• There is a general need for standards and norms for documenting and sharing agent-based models. A National Science Foundation–funded effort to coordinate research, dissemination, and documentation of agent-based models has produced a web-based portal for model sharing (i.e., openabm.org), and the ongoing research on the standards of evidence and communication regarding use of models in science is crucial to further uptake and credibility of these modeling activities.
Many LCMs are not easily classified into one of the categories discussed in the preceding sections. Here we address the fact the conceptual and methodological approaches described above are quite often used in combination to represent various aspects of land change patterns and processes. For example, machine learning and statistical approaches are often used to develop suitability maps that then serve as one of the inputs to a cellular model that incorporates land suitability with neighborhood effects to project future land use (Almeida et al. 2008; Li and Yeh 2002) or land cover (Hilbert and Ostendorf 2001) patterns. Similarly, sector-based economic models have been integrated with spatial allocation models to downscale land areas determined in large-scale general equilibrium and integrated assessment models for large world regions to individual pixels. The Global Land Model (Hurtt et al., 2011;Hurtt et al., 2006) uses a relatively simple expert-based ranking of relative suitabilities in combination with an assumed hierarchical ordering of allocation. Other allocation mechanisms are possible, building on the statistical, machine learning, and cellular approaches described above. As a final example of hybrid models, coupled representations of land use and land cover dynamics, as a means of representing the dynamics of both the natural and the human processes involved in land change, have been developed by combining the statistical, cellular and agent-based approaches described above. For example, An et al. (2005) were able to successfully represent interactions between human demography and fuel use, and availability and quality of panda habitat by representing dynamics in the human communities with agents and the forest dynamics and habitat characteristics with cellular models that incorporated algorithms for forest growth and habitat suitability, some of which had been developed using statistical models for determination of suitabilities.
Theoretical and Empirical Basis
Land change is the result of multiple human-environment interactions operating across different scales ranging from global trade of food and energy to local management of land resources at the farm and landscape level. It is represented in data ranging from satellite observations of land cover to surveys of human attitudes, perceptions, and behaviors, with many other types of data in between. So far, researchers have not succeeded in defining an all-compassing theory of land change, and the feasibility of formulating such theory is not evident. Additionally, we have not yet reached the point where we have all the data we need to characterize the various land use and land cover changes that are occurring in various systems throughout the world. Therefore, it is reasonable to expect that some hybridization of the above approaches, accounting for the heterogeneous theories and data environments confronting models that incorporate land use and
land cover change dynamics, is necessary to serve contemporary scientific and management purposes.
Theories from multiple disciplines, such as economics, geography, demography, ecology, and anthropology, contribute to the explanation of land change. Often, these theories are related to specific land conversion processes or sectors, for example, ecological succession (Cushman et al. 2010), Boserupian theory concerning the effects of population on land use sustainability (Boserup, 1965; Turner and Fischer-Kowalski, 2010), the induced-intensification thesis (Turner and Ali, 1996), neo-Thünen theory about moving frontiers and urban markets (Walker, 2004;Walker and Solecki, 2004), and the theories of Fujita and Krugman about urban development (Fujita et al., 1999a,b), as notable examples. Most theories cannot adequately explain the complexity of land use decision making, nor address the processes driving both land use and land cover change.
It is well understood that decision making processes about land change, as well as many of the ecological and disturbance processes affecting land cover change, are context dependent and one or multiple theories may provide a proper representation for a specific case study or land change process. Therefore, the choice of theory and model concept may depend on the specific scale of analysis, the processes studied, the availability of data, and the case-study characteristics. As an example, in a mature land market, models based on economic theory may best be able to capture the dominant processes. In a deforestation frontier the land market may not be functioning at all and models driven by geographic or institutional factors may be more useful.
At the same time, land change may be influenced by several types of processes synchronously that require different modeling concepts: for example, although land decision makers may be oriented towards optimizing benefits of land use, these benefits are often influenced by land change in the neighborhood, creating scaling effects. Because land change modeling often involves representation of cross-scale interactions, interactions among different land types or sectors, and determination of both the amount and spatial pattern of land cover types, there are multiple procedural opportunities for including different modeling approaches. While some opportunities for hybridization (e.g., for representing different land sectors) are driven by differences in the theoretical basis for such models, others (e.g., for crossing scales) are driven by the relative efficiency of different algorithmic approaches to linking across scales and processes, and still others, e.g., linking models of land use and land cover, are driven by multiple concerns that also include data availability. Hybrid modeling approaches therefore can combine different underlying conceptual frameworks, theories, and empirical observations into a system representation and allow the modeler to choose appropriate procedure for modeling depending on the practical needs of modeling across the range of representation in land systems.
Hybrid approaches can involve:
1. a combination of approaches to more fully represent decision making, for example, agent-based decision making that includes a cellular neighborhood model to account for neighborhood interactions in the decision making, or a machine learning model to represent human cognition (e.g., Manson 2005);
2. the use of different approaches for different scales to capture the dominant processes at the scale addressed, for example, economic models for aggregate land shares that constrain cellular spatial-allocation models (e.g., Sohl et al., 2012);
3. the use of different modeling concepts for different land change types considered, for example, using a cellular automata (neighborhood-based) model for urban land use with an econometric approach for other land cover types (Verburg and Overmars, 2009); or
4. the use of one approach to parameterize a model using a different approach, for example, machine learning to parameterize a cellular model (Pijanowski et al., 2005; Sangermano et al., 2010).
5. the conceptual integration of modeling frameworks, for example, the development of a common language to refer to automata with fixed (i.e., cellular) versus flexible (i.e., agent-based) topologies (Torrens and Benenson, 2005).
Strengths and Weaknesses
Hybrid modeling approaches take advantage of the strengths of the individual approaches and reduce some of their inherent limitations. The lack of overarching theory or systems description in some cases, and data or both in others, makes it necessary to carefully match existing theories and modeling concepts to the conditions and empirical contexts under which they are valid. Hybrid approaches allow such flexibility. At the same time, hybridization of modeling concepts allows the development of novel approaches can better represent the complexity of reality.
Hybridization also involves risks. Often the combination of multiple concepts leads to an increased complexity reducing the ease of interpretation of simulated changes and hampering causal tracing of emergent land changes. For this reason, model calibration and validation across the multiple hybridized components can be challenging. Separate components of a hybrid model might be calibrated in different ways, according to the empirical demands of each approach, but there is often little theoretical guidance on how the combination of components should be parameterized. As with any modeling approach, the ways the combination of model types represents reality and to what extent the model is able to answer the questions of the stakeholders of the modeling effort will determine its success.
A COMPARISON OF LAND CHANGE MODELING APPROACHES
Ultimately, the aims of land change modeling are to advance the science of land change, to improve our understanding of interactions between land change and various environmental processes, and to provide capacity to support decision making around problems involving land change. For these purposes, the various modeling approaches reviewed here provide capabilities to explain and learn (EL) about land system dynamics, as well as to project and predict (PP) future states of land systems. The ability to evaluate the impacts of environmental and social changes on the land system, especially through the use of scenarios, and to provide input to other models is also an important use to which models have been put.
We have arranged the five main modeling approaches in our assessment roughly in order from those most focused on modeling pattern (beginning to Machine Learning and Statistical Approaches) to more structural models that focus more on the processes of land change (including Economic and Agent-Based Approaches) (Table 2.1). While an evaluation of the validity of any given model or approach for any given purpose is beyond the scope of this assessment, we were able to identify some of the implications of these broad differences for how models based on these approaches can be used. In general terms, models that have a more explicit representation of a given process, like those that represent land use decision making with structural Economic or Agent-Based approaches, are more flexible to different types of changes in context that can be evaluated through model scenarios, including for example changes in credit availability, the level of enforcement for illegal activities, or the amount of information available about alternative choices. Paradoxically, perhaps, models with a greater degree of explicitness in representing process, while useful for predicting the consequences of alternative scenarios qualitatively, often perform less well making quantitative projections or predictions about specific outcomes at specific places or times. This can result from their inclusion of processes for which parameter values are unavailable empirically or are highly uncertain, feedback processes that can create path dependent outcomes with multiple equilibria, thereby raising the level of uncertainty in predictions, or processes that produce outcomes for which semantically compatible observations are unavailable. The key example of this latter point is the challenge, especially over large extents, of obtaining spatially explicit land use information. The need for land use data, due to its relative incompatibility with satellite measurements, is a mismatch with which the LCM community consistently struggles. For these reasons, approaches that are focused on fitting observed patterns (like Statistical and Machine Learning approaches) and extrapolating them into the future can both satisfy the users for which making near-term predictions is an important goal and make efficient use of the extensive record of spatially explicit land cover and other remotely sensed observations. As we have discussed in Chapter 1, these models are not limited by data so much
as they are by a lack of representation of the theory behind our understanding of land change processes. Machine Learning approaches can represent well the relationships between, for example, land cover changes that are observable in multiple Landsat images over time and a variety of biophysical, location, and other variables, and used these relationships for extrapolation to estimate where future changes might be expected to occur. As long as the structural elements of the system remain unchanged (i.e., are stationary), projections can provide useful information about near-term changes. Because of their thinner theoretical and process grounding, however, models that focus on observed patterns are limited in their ability to support evaluations of scenarios involving structural change. While no single modeling approach can serve all purposes equally well, each of the modeling approaches we describe has been adapted within a wide variety of settings, often to move them along this pattern-process continuum, and the hybrid modeling approaches that combine specific approaches provide particular flexibility in developing models that address particular challenges.
The relative strengths of the approaches with respect to representing patterns and processes, then, further affect their appropriateness within policy-and decision-making contexts. The committee considered the roles that LCMs can play within the context of the cycle of policy and decision making presented in Chapter 1(adapted from Verdung, 1997), and developed an approximate mapping of modeling approaches to stages in that cycle (Figure 2.2). Within this mapping, we identify the suitability of machine learning and cellular models in the problem identification step, because of their assumptions of stationarity and lack the richer structural detail about process needed to evaluate the effects of changes in policy structure. Projections of future trends can be useful to identify situations in which significant problems may arise if action is not taken, for example in managing total maximum daily loads in an area experiencing significant urban growth. These modeling approaches can also be useful at later stages, where, for example, policies or decisions that involve changing or constraining land changes spatially (e.g., through creation of protected areas) or where baselines based on extrapolating past trends are needed for ex ante assessment, but their comparative advantage is in problem identification.
To consider interventions that affect agent behaviors or might generate market feedbacks that have spillover effects on other components or locations in the land system, the richer behavioral specificity of agent-based and structural economic models provides a basis for exploring the structure of the land system and the interactions inherent in it, and exploring dynamics that might benefit from intervention. For example, links between household inequality and environmental outcomes can be explored to identify the reasons for and opportunities to improve both. The process specificity of these modeling approaches is usually needed to weigh the effects of alternative interventions.
In moving to a decision about some policy or other action, structural economic models, including both sector-based and spatially disaggregate as well as
Table 2.1 Generalized characteristics of modeling approaches.
| Modeling Approach | Pattern-Process | Land cover, Land use | Key Assumptions | Typical Data Requirements | Recommended Uses |
| Machine Learning and Statistical | Pattern |
Land cover | Strong stationarity | Land cover maps from at least two time points Some number of maps of predictor variable(s) | Make forecasts of land cover patterns under stationarity Extrapolating past patterns |
| Cellular | Land cover, land use | Stationarity Strong spatial control and/or interaction No market interactions | A land cover map at some point in time Some number of maps of predictor variable(s) | Forecast land cover patterns Evaluate changes in spatial controls without market feedbacks | |
| Spatially Disaggregated Economic Models | Land use | Utility or profit maximization Price and/or spatial equilibrium Heterogeneous agents sometimes specified | Data on land use or land cover at one or more point(s) in time Economic and biophysical variables that influence land demand and supply Any other required instrumental variables | Reduced-form models: Identify the causal effect of key variables on land change outcomes Structural models: Simulate effects of policy changes on land market outcomes, including changes in prices and land use patterns | |
| Modeling Approach | Pattern-Process | Land cover, Land use | Key Assumptions | Typical Data Requirements | Recommended Uses |
| Sector-Based Economic Models | |
Land use | Utility or profit maximization Price and/or spatial equilibrium Heterogeneous agents sometimes specified Utility or profit maximization Price equilibrium Representative agents | Economic variables that influence aggregate demand and supply, including prices of commodities and values of trade at a regional or country scale | Forecast aggregate land changes under a variety of market-based changes that can affect demand and supply |
| Agent-Based Models | Process | Land cover, Land use | Usually heterogeneous agents Variable interactions among agents | Data describing characteristics of agents Qualitative or quantitative data on decision processes Data on land use or land cover at some point(s) in time | Explore land change processes, often under stylized conditions Explore effects of exogenous change on a system, where it has not happened Explore future scenarios where past patterns may be poor indicators of future outcomes |
NOTE: Column 2 indicates the arrangement of approaches along a continuum of focus on pattern vs. process. Column 3 addresses the types of outcomes (land use, land cover, or both) for which each approach has tended to be applied. Column 4 lists key assumptions that characterize how the approach handles data. Column 5 describes the input data requirements and Column 5 lists key recommended uses.
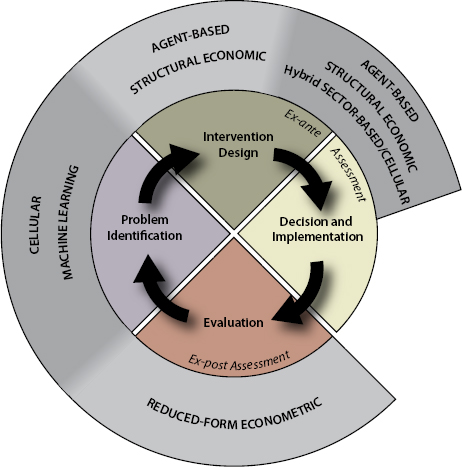
Figure 2.2 Land change modeling approaches (outer circle) placed within the context of the policy-and decision-making cycle (inner circle). SOURCE: modified from Verdung, 1997.
agent-based models, and hybrid models provide capabilities that can be exploited for assessing the possible effects of the policy, ex ante. For example, the GTAP model (Hertel, 1997), which is a static multi-region, multi-sector, CGE model, was used to evaluate the implications of biofuel mandates for land use demand both within the United States and internationally through the possible effects on the prices of food commodities (Keeney and Hertel, 2009).
Once policies or decisions have been implemented, the need for evaluating the effects of these implementations, ex post, is often quite effectively met through use of reduced-form economic models that estimate the magnitude of the effect of the intervention, usually by comparing observable outcomes either before and after the intervention or in an intervention area and some comparable
location. For example, Andam et al. (2008) used reduced-form econometric methods to evaluate the effectiveness of protected areas in reducing deforestation globally by estimating the effects of the protected areas on deforestation rates in comparison with those found in areas in close proximity to protected areas.
Understanding the underlying structures, assumptions, and data requirements of different modeling approaches is critical to understanding their applicability for various scientific and decision-making purposes. This review provides a framework for comparison of multiple modeling approaches in relation to specific objectives. The next section of this report outlines opportunities and needs for advances that will improve modeling capabilities into the future.














































