TONY JEBARA
Columbia University
Many real-world social networks involve topological connectivity information such as a set of edges between pairs of nodes that indicate a relationship between the individuals represented by the nodes. Furthermore, social networks also involve attributes associated with each node, such as a vector of demographic information describing the individual. Such networks are formed from the vast social data, mobile data, and location data being generated by large populations of users. Although most network growth models are based on incremental link analysis (Adamic and Adar 2003), it is also informative to consider how users’ data profiles alone (after censoring the connectivity information) can be used to accurately predict the connectivity information. For example, in a class of incoming freshmen students with no known friendship connections, is it possible to predict which pairs will become friends at the end of the year using only their demographic profile information? Similarly, can colocation be used to predict communication—that is, using only the location history of a population of mobile phone users, can an observer predict which pairs of users are likely to communicate with each other?
To algorithmically reconstruct these networks, two methods—structure-preserving metric learning (SPML) (Shaw and Jebara 2009; Shaw et al. 2011) and degree-distributional metric learning (DDML) (Huang et al. 2011)—have been proposed. Both automatically recover a Mahalanobis distance metric from network and profile information. The simpler method, SPML, ensures that a connectivity algorithm (such as k-nearest neighbors or b-matching; Huang and Jebara 2007) yields the correct connectivity when applied on the distances computed using the learned Mahalanobis distance metric. The more sophisticated method, DDML, also estimates the degree of each node in addition to the Malahanobis distance metric.
The SPML approach begins with a known network and known attributes for the nodes, such as a friendship network of n students as they graduate from college. Figure 1 depicts such a network in the box on the left side. Nodes are adjacent to each other when the people they correspond to are friends (in other words, an edge links the two nodes). On the right side of Figure 1 is a representation of this connectivity information represented as an adjacency matrix A containing n rows and n columns of binary entries. For each individual in the network, it is also possible to observe static demographic attributes (e.g., age, height, weight, hometown, income bracket, favorite music, dorm room assignment), represented by a matrix X containing d rows and n columns of real entries as shown in the right side of Figure 1. Assume that A and X are training data to be used to determine the distance metric.
After training, the goal is to predict the adjacency matrix for a new set of incoming students on their first day of college by observing only their demographic attributes (X’). This prediction should closely match the true A’ adjacency matrix that would be formed at the time of graduation for this new set of students. More specifically, A and X permit the estimation of an appropriate distance metric that can then be used to compute the distance between user i’s demographic vector xi and user j’s demographic vector xi. This distance metric helps quantify how various attributes compete in the formation of friendship links, for example, how much does an age difference matter relative to a height difference when computing the affinity or distance between a pair of users? Given a good distance metric that balances all the multivariate demographic attributes, it eventually becomes
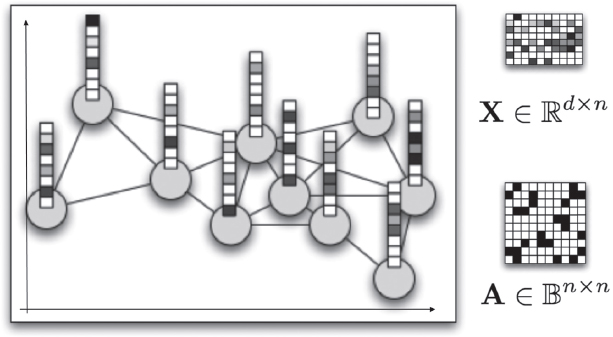
FIGURE 1 A social network with connectivity information (A) and attributes (X) to be used as training data for recovering a distance metric.
possible to reliably reconstruct A from X alone. To then test how well this method performs and generalizes, one uses the learned distance metric to reconstruct an unseen network A’ from only new X’ demographic data.
To evaluate the performance of such a framework, it is standard to use the area under the receiver operating characteristic curve. In a variety of synthetic and real-world experiments, SPML was capable of predicting links and edges from node attributes more accurately than standard techniques (Huang et al. 2011; Shaw et al. 2011). In particular, the approach outperforms simple naïve distance metrics (like Euclidean distance), relational topic models (Chang and Blei 2010), and support vector machine classifiers (Boser et al. 1992).
Furthermore, the SPML approach is efficient and quickly processes large network datasets. Computationally, it performs the optimization of a cost function using stochastic gradient descent. This conveniently eliminates the running-time dependency on the size of the network and makes it possible to scale to networks with hundreds of thousands of nodes and millions of edges. SPML has been used to reconstruct networks from Facebook data, Wikipedia data, FourSquare data, and mobile phone call detail records. Figure 2 shows the results of reconstructing Facebook data (Traud et al. 2011). Some interesting interpretable findings emerge. For instance, through Facebook social networks it appears that when students form friendships, those at Harvard are relatively more attentive to differences in relationship status, those at Stanford and Columbia are relatively more sensitive to differences in graduation year, and for those at MIT differences in dorm assignments are most important. Thus, social network structure helps tease apart demographic attributes and determine which are more or less relevant.
Like Facebook data, mobile phone data is also well suited for the SPML framework. Using a large dataset of location-augmented call detail records (CDRs) from a mobile phone carrier, it is possible to use phone calls and text messages between pairs of users to establish the existence of a friendship. Let the attributes of each user be their individual location history (the places they visited as measured by GPS or tower triangulation of the user’s mobile device). One broad goal is to estimate distance metrics that reveal the colocations or meeting places that are most likely to correlate with (or predict) friendship (or communication) in the calling network. Are people more likely to be friends if they spend time together in high- or low-population-density regions? If they colocate in a coffee shop or at a subway station? The findings from this study are currently under review in a forthcoming article.
Finally, once a network is reconstructed (for instance using SPML), it is straightforward to do a variety of interesting things with it, such as visualize the network (Shaw and Jebara 2009) or predict missing attributes for some users (e.g., marital status, income) (Jebara et al. 2009 and Wang et al. 2013).
In conclusion, the graph topology of a social network helps define metrics of similarity and dissimilarity and reshapes the axes of demographic attributes. Novel algorithms such as SPML can be used to predict which networks could
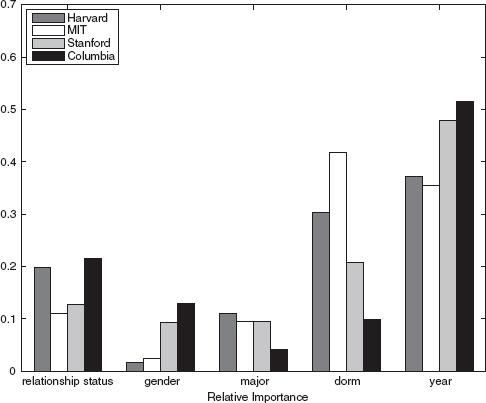
FIGURE 2 The relative importance of various demographic attributes (on the y-axis) for reconstructing friendship edges. Note that the relative importance of the demographic attributes varies across the four different universities in the study.
likely form between new users and elucidate which specific aspects of user profiles and demographics are predictive of communication and social interaction (Lazer et al. 2009; Newman 2003).
REFERENCES
Adamic LA, Adar E. 2003. Friends and neighbors on the Web. Social Networks 25:211–230.
Boser BE, Guyon IM, Vapnik VN. 1992. A training algorithm for optimal margin classifiers. Proceedings of the 5th Annual ACM Workshop on Computational Learning Theory.
Chang J, Blei D. 2010. Hierarchical relational models for document networks. Annals of Applied Statistics 4:124–150.
Huang B, Jebara T. 2007. Loopy belief propagation for bipartite maximum weight b-matching. Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics (AISTATs), San Juan, Puerto Rico, March.
Huang B, Shaw B, Jebara T. 2011. Learning a degree-augmented distance metric from a network. Proceedings of a Neural Information Processing Systems (NIPS) workshop, Beyond Mahalanobis: Supervised Large-Scale Learning of Similarity, Sierra Nevada, December.
Jebara T, Wang J, Chang SF. 2009. Graph construction and b-matching for semi-supervised learning. Proceedings of the International Conference on Machine Learning (ICML), Montreal, June.
Lazer D, Pentland A, Adamic L, Aral S, Barabasi AL, Brewer D, Christakis D, Contractor N, Fowler J, Gutmann M, Jebara T, King G, Macy M, Roy D, Van Alstyne M. 2009. Computational social science. Science 323(5915):721–723.
Newman M. 2003. The structure and function of complex networks. SIAM Review 45:167–256.
Shaw B, Jebara T. 2009. Structure preserving embedding. Proceedings of the International Conference on Machine Learning (ICML), Montreal, June.
Shaw B, Huang B, Jebara T. 2011. Learning a distance metric from a network. Proceedings of a Neural Information Processing Systems (NIPS) workshop, Beyond Mahalanobis: Supervised Large-Scale Learning of Similarity, Sierra Nevada, December.
Traud A, Mucha P, Porter M. 2011. Social structure of Facebook networks. arXiv 1102.2166 [cs.SI].
Wang J, Jebara T, Chang SF. 2013. Semi-supervised learning using greedy max-cut. Journal of Machine Learning Research (JMLR) 14(Mar):771–800.
This page intentionally left blank.






