7
Computation
Beyond Theory and Experiment: Seeing the World Through Scientific Computation
Certain sciences—particle physics, for example—lend themselves to controlled experimentation, and others, like astrophysics, to observation of natural phenomena. Many modern sciences have been able to aggressively pursue both, as technology has provided ever more powerful instruments, precisely designed and engineered materials, and suitably controlled environments. But in all fields the data gathered in these inquiries contribute to theories that describe, explain, and—in most cases—predict. These theories are then subjected to subsequent experimentation or observation—to be confirmed, refined, or eventually overturned—and the process evolves to more explanatory and definitive theories, often based on what are called natural laws, more specifically, the laws of physics.
Larry Smarr, a professor in the physics and astronomy departments at the University of Illinois at Champaign-Urbana, has traveled along the paths of both theory and experimentation. He organized the Frontiers symposium's session on computation, which illustrated the premise that computational science is not merely a new field or discipline or tool, but rather an altogether new and distinct methodology that has had a transforming effect on modern science: first, to permanently alter how scientists work, experiment, and theorize; and second, to expand their reach beyond the inherent limitations of the two other venerable approaches (Box 7.1).
Modern supercomputers, explained Smarr, ''are making this alternative approach quite practical (Box 7.2). The result is a revolu-
|
BOX 7.1 COMPUTATION The new terrain to be explored by computation is not a recent discovery, but rather comes from a recognition of the limits of calculus as the definitive language of science. Ever since the publication of Newton's Philosophiae naturalis principia mathematica in 1687, "calculus has been instrumental in the discovery of the laws of electromagnetism, gas and fluid dynamics, statistical mechanics, and general relativity. These classical laws of nature have been described," Smarr has written, by using calculus to solve partial differential equations (PDEs) for a continuum field (Smarr, 1985, p. 403). The power and also the limitation of these solutions, however, are the same: the approach is analytic. Where the equations are linear and separable, they can be reduced to the ordinary differential realm, and calculus and other techniques (like the Fourier transform), continued Smarr, "can give all solutions for the equations. However, progress in solving the nonlinear PDEs that govern a great portion of the phenomena of nature has been less rapid" (Smarr, 1985, p. 403). Scientists refer to the results of their analysis as the solution space. Calculus approaches the solution of nonlinear or coupled differential equations analytically and also uses perturbation methods. These approaches have generally served the experimenter's purpose in focusing on a practical approximation to the full solution that—depending on the demands of the experiment—was usually satisfactory. But mathematicians down through history (Leonhard Euler, Joseph Lagrange, George Stokes, Georg Riemann, and Jules Henri Poincaré, to name only the most prominent) have not been as concerned with the practicalities of laboratory experiments as with the manifold complexity of nature. Smarr invoked mathematician Garrett Birkhoff's roll call of these men as predecessors to mathematician and computational pioneer John von Neumann, whose "main point was that mathematicians had nearly exhausted analytical methods, which apply mainly to linear differential equations and special geometries" (Smarr, 1985, p. 403). Smarr believes von Neumann "occupies a position similar to that of Newton" in the history of science because he realized the profound potential of computation to expand science's power to explore the full solution space; as Birkhoff put it, "to substitute numerical for analytical methods, tackling nonlinear problems in general geometries" (p. 403). These distinctions are not mere mathematical niceties of scant concern to working scientists. The recognition that a vaster solution space may contain phenomena of crucial relevance to working physicists—and that computers are the only tools to explore it—has revitalized the science of dynamical systems and brought the word chaos into the scientific lexicon. Smarr quoted another mathematician, James Glimm, on their significance: "Computers will affect science and technology at least as profoundly as did the invention of calculus. The reasons are the same. As with calculus, computers have increased and will increase enormously the range of solvable problems'" (Smarr, 1985, p. 403). |
|
BOX 7.2 THE RIGHT HAND OF THE MODERN SCIENTIST Since the late 1940s, Smarr noted, "computers have emerged as universal devices for aiding scientific inquiry. They are used to control laboratory experiments, write scientific papers, solve equations, and store data." But "the supercomputer has been achieving something much more profound; it has been transforming the basic methods of scientific inquiry themselves" (Smarr, 1992, p. 155). "Supercomputer," Smarr explained, is a generic term, referring always to "the fastest, largest-memory machines made at a given time. Thus, the definition is a relative one. In 1990, to rate as a supercomputer, a machine needed to have about 1 billion bytes of directly addressable memory, and had to be capable of sustaining computations in excess of a billion floating point operations per second" (p. 155). These fairly common measures for rating computer power refer to an information unit (a byte contains eight of the basic binary units, 1 or 0, called bits) and the speed with which additions, subtractions, multiplications, or divisions of decimal numbers can be accomplished. These machines had between 100 and 1000 times the power of the personal computers commonly in use, and might cost in the neighborhood of $30 million. As he surveyed the growth of computational science, however, Smarr predicted that the "rapidly increasing speed and connectivity of networks will contribute to altering how humans work with supercomputers" (p. 162). He envisions that scientists and others working from personal and desktop machines will enjoy almost instantaneous access to a number of supercomputers around the country at once, with various parts of their programs running on each. He foresees that "the development of new software will make it seem as if they were occurring on one computer. In this sense the national network of computers will appear to be one giant 'metacomputer' that is as easy to use as today's most user-friendly personal machines'' (p. 163). Smarr credited von Neumann with the recognition, in the 1940s, that the technology of electronic digital computers "could be used to compute realistically complex solutions to the laws of physics and then to interrogate these solutions by changing some of the variables, as if one were performing actual experiments on physical reality" (p. 158). The American government's experience in World War II uncovered a number of practical applications of this principle and other uses for the computer's speed, "to aid in nuclear weapons design, code breaking, and other tasks of national security" (p. 157), reported Smarr. This effort developed in the succeeding decades into government centers with major laboratories—as reliant on their computers as on the electricity that powered them—at Los Alamos, New Mexico, and Livermore, California. "From the efforts of the large teams of scientists, engineers, and programmers who worked on the |
|
earlier generations of supercomputers, a methodology arose that is now termed computational science and engineering," according to Smarr (p. 157). It was their early high cost and the fact that only a few centers were feasible that made the government the primary purchaser of computers in the early years. But "throughout the 1980s, their use spread rapidly to the aerospace, energy, chemical, electronics, and pharmaceutical industries," summarized Smarr, "and by the end of the decade, more than 200 supercomputers were serving corporations" (p. 159). Academic researchers and scientists joined this parade in ever greater legions during the 1980s, and support by the National Science Foundation led to the creation of five major supercomputer centers. Smarr, the director of the National Center for Supercomputing Applications (NCSA) at the University of Illinois, explained that the information infrastructure—built both of the machines themselves and the networks that connect them—is evolving to make "it possible for researchers to tap the power of supercomputers remotely from desktop computers in their own offices and labs" (p. 160). The national system called Internet, for example, has "encompassed all research universities and many four-year colleges, federal agencies and laboratories," and, Smarr reported, has been estimated to involve "more than a million users, working on hundreds of thousands of desktop computers," communicating with each other (p. 160). SOURCE: Smarr (1992). |
tion our understanding of the complexity and variety inherent in the laws of nature" (Smarr, 1985, p. 403). Perhaps even more revolutionary, suggested Smarr, is what scientists can do with this new understanding: how they can use these more realistic solutions to engage in "a more constructive interplay between theory and experiment or observation than has heretofore been possible" (p. 403). The increasing power and economy of individual PCs or scientific work-stations and their access through networks like Internet to supercomputers, predicted Smarr, will lead to a new way of doing daily science.
Imaging is one of the fundamental cornerstones of this new way of doing science. "A single color image," said Smarr, can represent "hundreds of thousands to millions of individual numbers" (Smarr, 1992, p. 161). Today's typical desktop computers "can even run animations directly on the screen. This capability, called scientific visu-
alization, is radically altering the relationship between humans and the supercomputer" (p. 161). Indeed, the value of such pictures cannot be overestimated. Not only do they allow the compression of millions of data points into a coherent image, but that image is also a summary that appeals to the way the human brain processes information, because it establishes a picture and also moves that coherent picture through time, providing insight into the dynamics of a system or experiment that might well be obscured by a simple ream of numbers.
Among the participants in the session on computation, William Press, an astrophysicist at Harvard University, noted that starting several years ago, interdisciplinary conferences began to be awash with "beautiful movies" constructed to model and to help investigators visualize basic phenomena. "What is striking today," Press commented, "is that computer visualization has joined the mainstream of science. People show computer movies simply because you really cannot see what is going on without them." In fact Press believes strongly that computer modeling and visualization have become "an integral part of the science lying underneath."
The computation session's participants—also including Alan Huang of AT&T Bell Laboratories, Stephen Wolfram of Wolfram Research, and Jean Taylor from the Department of Mathematics at Rutgers University, discussed scientific computation from several diverse points of view. They talked about hardware and software, and about how both are evolving to enhance scientists' power to express their algorithms and to explore realms of data and modeling hitherto unmanageable.
THE MACHINERY OF THE COMPUTER
Digital Electronics
In the 1850s British mathematician George Boole laid the foundation for what was to become digital electronics by developing a system of symbolic logic that reduces virtually any problem to a series of true or false propositions. Since the output of his system was so elemental, he rejected the base 10 system used by most of the civilized world for centuries (most likely derived from ancient peoples counting on their fingers). The base 2 system requires a longer string of only two distinct symbols to represent a number (110101, for example, instead of 53). Since there are but two possible outcomes at each step of Boole's system, the currency of binary systems is a perfect match: an output of 1 signifies truth; a 0 means false. When
translated into a circuit, as conceptualized by Massachusetts Institute of Technology graduate student Claude Shannon in his seminal paper ''A Symbolic Analysis of Relay and Switching Circuits" (Shannon, 1938), this either/or structure can refer to the position of an electrical switch: either on or off.
As implemented in the computer, Boolean logic poses questions that can be answered by applying a series of logical constructs or steps called operators. The three operators found in digital computers are referred to by circuit designers as logic gates. These gates are physically laid down on boards and become part of the system's architecture. The computer's input is then moved through these gates as a series of bits. When a pair of bits encounters a gate, the system's elementary analysis occurs. The AND gate outputs 1 when both elements are 1, meaning, "It is true that the concept of and applies to the truth of both elements of the set"; conversely, the AND gate produces 0 as an output, meaning false, if either (or both) of the two elements in question is false; the OR gate outputs a 1, meaning true, if either element (or both) is a 1; with the NOT gate, the output is simply the reverse of whichever symbol (1 or 0) is presented.
Thus the physical structure of the basic elements of a circuit—including its gate design—becomes integral to analyzing the relationship of any pair of bits presented to it. When the results of this analysis occurring throughout the circuit are strung together, the final outcome is as simple as the outcome of any of its individual steps—on or off, 1 or 0, true or false—but that outcome could represent the answer to a complex question that had been reduced to a series of steps predicated on classical logic and using the three fundamental operators.
What is gained by reducing the constituent elements of the system to this simplest of all currencies—1 or 0, on or off—is sacrificed, however, in computational efficiency. Even the most straightforward of problems, when translated into Boolean logic and the appropriate series of logic gates, requires a great many such logical steps. As the computer age enters its fifth generation in as many decades, the elegant simplicity of having just two elemental outcomes strung together in logic chains begins to bump up against the inherent limitation of its conceptual framework. The history of computer programs designed to compete with human chess players is illustrative: as long as the computer must limit its "conceptual vision" to considering all of the alternatives in a straightforward fashion without the perspectives of judgment and context that human brains use, the chess landscape is just too immense, and the computer cannot keep up with expert players. Nonetheless, the serial computer will always have a
role, and a major one, in addressing problems that are reducible to such a logical analysis. But for designers of serial digital electronics, the only way to improve is to run through the myriad sequences of simple operations faster. This effort turns out to reveal another inherent limitation, the physical properties of the materials used to construct the circuits themselves.
The Physical Character of Computer Circuitry
Integrated circuits (ICs), now basic to all computers, grew in response to the same generic challenges—moving more data faster and more efficiently—that are impelling scientists like Huang "to try to build a computer based on optics rather than electronics." By today's sophisticated standards, first-generation electronic computers were mastodons: prodigious in size and weight, and hungry for vast amounts of electricity—first to power their cumbersome and fragile vacuum tubes and then to cool and dissipate the excess heat they generated. The transistor in 1947 and the silicon chip on which integrated circuits were built about a decade later enabled development of the second-and third-generation machines. Transistors and other components were miniaturized and mounted on small boards that were then plugged into place, reducing complex wiring schemes and conserving space.
By the 1970s engineers were refining the IC to such a level of sophistication that, although no fundamental change in power and circuitry was seen, an entirely new and profound fourth generation of computers was built. ICs that once contained 100 or fewer components had grown through medium-and large-scale sizes to the very large-scale integrated (VLSI) circuit with as at least 10,000 components on a single chip, although some have been built with 4 million or more components. The physics involved in these small but complex circuits revolves around the silicon semiconductor.
The electrical conductivity of semiconductors falls between that of insulators like glass, which do not conduct electricity at all, and copper, which conducts it very well. In the period just after World War II, John Bardeen, Walter Brattain, and William Shockley were studying the properties of semiconductors. At that time, the only easy way to control the flow of electricity electronically (to switch it on or off, for example) was with vacuum tubes. But vacuum tube switches were bulky, not very fast, and required a filament that was heated to a high temperature in order to emit electrons that carried a current through the vacuum. The filament generated a great deal of heat and consumed large amounts of power. Early computers based
on vacuum tubes were huge and required massive refrigeration systems to keep them from melting down. The Bardeen-Brattain-Shockley team's goal was to make a solid-state semiconductor device that could replace vacuum tubes. They hoped that it would be very small, operate at room temperature, and would have no power-hungry filament. They succeeded, and the result was dubbed the transistor. All modern computers are based on fast transistor switches. A decade later, the team was awarded a Nobel Prize for their accomplishment, which was to transform modern society.
How to build a chip containing an IC with hundreds of thousands of transistors (the switches), resistors (the brakes), and capacitors (the electricity storage tanks) wired together into a physical space about one-seventh the size of a dime was the question; photolithography was the answer. Literally "writing with light on stone," this process allowed engineers to construct semiconductors with ever finer precision. Successive layers of circuitry can now be laid down in a sort of insulated sandwich that may be over a dozen layers thick.
As astounding as this advance might seem to Shannon, Shockley, and others who pioneered the computer only half a lifetime ago, modern physicists and communications engineers continue to press the speed envelope. Huang views traditional computers as fundamentally "constrained by inherent communication limits. The fastest transistors switch in 5 picoseconds, whereas the fastest computer runs with a 5 nanosecond clock." This difference of three orders of magnitude beckons, suggesting that yet another generation of computers could be aborning. Ablinking, actually: in optical computers a beam of light switched on represents a 1, or true, signal; switching it off represents a 0, or false, signal.
NEW DIRECTIONS IN HARDWARE FOR COMPUTATION
Computing with Light
The major application of optics technology thus far has been the fiber-optic telecommunications network girding the globe. Light rays turn out to be superior in sending telephone signals great distances because, as Huang described it, with electronic communication, "the farther you go, the greater the energy required, whereas photons, once launched, will travel a great distance with no additional energy input. You get the distance for free. Present engineering has encountered a crossover point at about 200 microns, below which distance it is more efficient to communicate with electrons rather than photons. This critical limit at first deflected computer designers'
interest in optics, since rarely do computer signals travel such a distance in order to accomplish their goal." To designers of telecommunications networks, however, who were transmitting signals on the order of kilometers, the "extra distance for free" incentive was compelling. The situation has now changed with the advent of parallel processing, since a large portion of the information must move more than 200 microns. Energy is not the only consideration, however. As the physical constraints inherent in electronic transmission put a cap on the speed at which the circuitry can connect, optical digital computing presents a natural alternative. "The next challenge for advanced optics,'' predicted Huang, "is in the realm of making connections between computer chips, and between individual gates. This accomplished, computers will then be as worthy of the designation optical as they are electronic."
Huang was cautious, however, about glib categorical distinctions between the two realms of optics and electronics. "How do you know when you really have an optical computer?" he asked. "If you took out all the wires and replaced them with optical connections, you would still have merely an optical version of an electronic computer. Nothing would really have been redesigned in any fundamental or creative way." He reminded the audience at the Frontiers symposium of the physical resemblance of the early cars built at the turn of the century to the horse-drawn carriages they were in the process of displacing and then continued, "Suppose I had been around then and come up with a jet engine? Would the result have been a jet-powered buggy? If you manage to come up with a jet engine, you're better off putting wings on it and flying it than trying to adapt it to the horse and buggy." A pitfall in trying to retrofit one technology onto another, he suggested, is that "it doesn't work"—it is necessary instead to redesign "from conceptual scratch.'' But the process is a long and involved one. The current state of the art of fully optical machines, he remarked wryly, is represented by one that "is almost smart enough to control a washing machine but is a funky-looking thing that will no doubt one day be regarded as a relic alongside the early mechanical computers with their heavy gears and levers and hand-cranks" (Figure 7.1).
The Optical Environment
Optics is more than just a faster pitch of the same basic signal, although it can be indisputably more powerful by several orders of magnitude. Huang surveyed what might be called the evolution of optical logic:

Figure 7.1 The digital optical processor. Although currently only about as powerful as a silicon chip that controls a home appliance such as a dish-washer, the optical processor may eventually enable computers to operate 1000 times faster than their electronic counterparts. It demonstrates the viability of digital optical processing technology. (Courtesy of A. Huang.)
I believe electronics—in terms of trying to get the basic stuff of transmission in and out of the chips—will reach an inherent speed limit at about 1 gigahertz. The next stage will involve subdividing the chip differently to use more optical modulators or microlasers. A clever rearrangement of the design should enable getting the systems to work at about 10 gigahertz, constrained only by the limits inherent to the integrated circuit wiring on the chip itself. Surmounting this limit will require building logic gates to connect one array to another, with each logic gate using an optical modulator. Such an architecture should enable pushing up to the limits of the semiconductor, or about 100 gigahertz.
Not only a pioneer in trying to develop this new optical species of computer, Huang has also been cited with teaching awards for his thoughtful communicative style in describing it. He worries that the obsession with measuring speed will obscure the truly revolutionary nature of optical computing—the process, after all, is inherently constrained not only by the physics of electronic transmission, but also by a greater limit, as Einstein proved, the speed of light. But photons
of light moving through a fiber tunnel—in addition to being several orders of magnitude faster than electrons moving through a wire on a chip—possess two other inherent advantages that far outweigh their increased speed: higher bandwidth and greater connectivity.
In order to convey the significance of higher bandwidth and greater connectivity, Huang presented his "island of Manhattan" metaphor:
Everybody knows that traffic in and out of Manhattan is really bottlenecked. There are only a limited number of tunnels and bridges, and each of them has only a limited number of lanes. Suppose we use the traffic to represent information. The number of bridges and tunnels would then represent the connectivity, and the number of traffic lanes would represent the bandwidth.
The use of an optical fiber to carry the information would correspond to building a tunnel with a hundred times more lanes. Transmitting the entire Encyclopedia Britannica through a wire would take 10 minutes, while it would take only about a second with optical fiber.
Instead of using just an optical fiber, the systems we are working on use lenses. Such an approach greatly increases the connectivity since each lens can carry the equivalent of hundreds of optical fibers. This would correspond to adding hundreds of more tunnels and bridges to Manhattan.
This great increase in bandwidth and connectivity would greatly ease the flow of traffic or information. Try to imagine all the telephone wires in the world strung together in one giant cable. All of the telephone calls can be carried by a series of lenses.
The connectivity of optics is one reason that optical computers may one day relegate their electronic predecessors to the historical junkyard (Figure 7.2). Virtually all computing these days is serial;
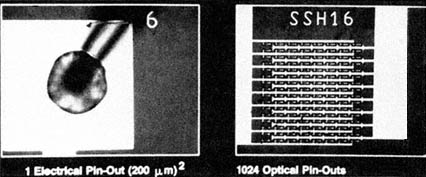
Figure 7.2 Optical vs. electrical pin-outs. The greater connectivity of optics is indicated in this comparison of a VLSI bonding pad with an array of SEED optical logic gates in the equivalent amount of area. (Courtesy of A. Huang.)
the task is really to produce one output, and the path through the machine's circuitry is essentially predetermined, a function of how to get from input to output in a linear fashion along the path of the logic inherent to, and determined by, the question. Parallel computing—carried out with a fundamentally different machine architecture that allows many distinct or related computations to be run simultaneously—turns this structure on its ear, suggesting the possibility of many outputs, and also the difficult but revolutionary concept of physically modifying the path as the question is pursued in the machine. The science of artificial intelligence has moved in this direction, inspired by the manifest success of massively parallel "wiring" in human and animal brains.
With the connectivity advantage outlined, Huang extended his traffic metaphor: "Imagine if, in addition to sending so many more cars through, say, the Holland Tunnel, the cars could actually pass physically right through one another. There would be no need for stoplights, and the present nightmare of traffic control would become trivial." With the pure laser light generally used in optics, beams can pass through one another with no interference, regardless of their wavelength. By contrast, Huang pointed out, "In electronics, you're always watching out for interference. You can't send two electronic signals through each other."
Although the medium of laser light offers many advantages, the physical problems of manipulating it and moving it through the logic gates of ever smaller optical architectures present other challenges. In responding to them, engineers and designers have developed a remarkable technique, molecular beam epitaxy (MBE), which Huang has used to construct an optical chip of logic gates, lenses, and mirrors atom by atom, and then layer by layer (Box 7.3; Figure 7.3). It is possible, he explained, to "literally specify . . . 14 atoms of this, 37 of that, and so on, for a few thousand layers." Because of the precision of components designed at the atomic level, the light itself can be purified into a very precise laser beam that will travel through a hologram of a lens as predictably as it would travel through the lens itself. This notion brings Huang full circle back to his emphasis on deflecting simple distinctions between electronics and optics: "With MBE technology, we can really blur the distinction between what is optical, what is electronic, and what is solid-state physics. We can actually crunch them all together, and integrate things on the atomic level." He summarized, "All optical communication is really photonic, using electromagnetic waves to propagate the signal, and all interaction is really electronic, since electrons are always involved at
|
BOX 7.3 BUILDING THE OPTICAL LENS While the medium of laser light offers so many advantages, the physical problem of manipulating and moving it through the logic gates of ever smaller optical architecture presents challenges. "In optical systems, the basic pipeline architecture to move the data consists of various lens arrangements, then a plane of optical logic gates, another array of lenses, another array of logic gates," up to the demands of the designer, said Alan Huang. "We discovered that the mechanics of fabrication—trying to shrink the size of the pipeline—poses a real problem," he continued, "prompting us to search for a new way to build optics. We've arrived at the point where we grow most of our own devices with molecular beam epitaxy (MBE)." Designers and engineers using MBE technology start with gallium arsenide as a conductor for the optical chip because electrons move through it faster than through silicon and it is inherently more capable of generating and detecting light. The process involves actually fabricating layer after layer of atomic material onto the surface of the wafer. Elements of aluminum, gallium, and other fabricating materials are superheated, and then a shutter for a particular element is opened onto the vacuum chamber in which the wafer has been placed. The heated atoms migrate into the vacuum, and by what Huang described as "the popcorn effect" eventually settle down on the surface in a one-atom-thick lattice, with their electrons bonding in the usual way. "So you just build the lattice, atom by atom, and then layer by layer. What's remarkable about it is, in a 2-inch crystal, you can see plus or minus one atomic layer of precision: I can literally specify—give me 14 atoms of this, 37 thick of that, for a few thousand layers," Huang explained. But there is an even more astounding benefit to the optical lens, involving lasers. The MBE process permits such precision that a virtual laser-generating hologram of the lens will work as well as the lens itself. Thus, though Huang may pay an outside "grower" $4000 to build a gallium arsenide chip with lenses on it, from that one chip 10 million lasers can then be stamped out by photolithography. Normal, physical lenses are generally required to filter the many wavelengths and impurities in white light. With pure laser light of a precise frequency, the single requirement of deflecting the beam a certain angle can be accomplished by building a quantum well sensitive to that frequency, and then collapsing the whole structure into something physicists call a Fresnel zone plate. The prospect of this profusion of lasers, Huang suggested, should surprise no student of the history of technology: "You now probably have more computers in your house than electric motors. Soon, you will have more lasers than computers. It kind of sneaks up on you." |

Figure 7.3 The extraordinary precision of this molecular beam epitaxy machine allows scientists to build semiconductor chips atomic layer by atomic layer. (Courtesy of A. Huang.)
some level." Extraordinary advances in engineering thus permit scientists to reexamine some of their basic assumptions.
THE COMPUTER'S PROGRAMS-ALGORITHMS AND SOFTWARE
Algorithms—the term and the concept—have been an important part of working science for centuries, but as the computer's role grows, the algorithm assumes the status of a vital methodology on which much of the science of computation depends (Harel, 1987). Referring to the crucial currency of computation, speed, Press stated that "there have been at least several orders of magnitude of computing speed gained in many fields due to the development of new algorithms."
An algorithm is a program compiled for people, whereas software is a program compiled for computers. The distinction is sometimes meaningless, sometimes vital. In each case, the goal of solving a particular problem drives the form of the program's instructions. A successful algorithm in mathematics or applied science provides definitive instructions for an unknown colleague to accomplish a particular task, self-sufficiently and without confusion or error. When that al-
gorithm involves a computer solution, it must be translated through the appropriate program and software. But when around 300 B.C. Euclid created the first nontrivial algorithm to describe how to find the greatest common divisor of two positive integers, he was providing for all time a definitive recipe for solving a generic problem. Given the nature of numbers, Euclid's algorithm is eternal and will continue to be translated into the appropriate human language for mathematicians forever.
Not all algorithms have such an eternal life, for the problems whose solutions they provide may themselves evolve into a new form, and new tools, concepts, and machinery may be developed to address them. Press compiled a short catalog of recent "hot" algorithms in science and asked the symposium audience to refer to their own working experience to decide whether the list represented a "great edifice or a junkpile." Included were fractals and chaos, simulated annealing, Walsh functions, the Hartley and fast Fourier transforms, fuzzy sets, and catastrophe theory. The most recent among these, which Press speculated could eventually rival the fast Fourier transform (FFT) as a vital working tool of science, is the concept of wavelets.
Over the last two decades, the Fourier transform (FT) has reduced by hundreds of thousands of hours the computation time working scientists would otherwise have required for their analyses. Although it was elucidated by French mathematician J.B.J. Fourier "200 years ago," said Press, "at the dawn of the computer age it was impractical for people to use it in trying to do numerical work" until J.W. Cooley and J.W. Tukey devised the FFT algorithm in the 1960s. Simply stated, the FFT makes readily possible computations that are a factor of 106 more complicated than would be computable without it. Like any transform process in mathematics, the FT is used to simplify or speed up the solution of a particular problem. Presented with a mathematical object X, which usually in the world of experimental science is a time series of data points, the FT first changes, or transforms, X into a different but related mathematical object X'.
The purpose of the translation is to render the desired (or a related) computation more efficient to accomplish. The FT has been found useful for a vast range of problems. Press is one of the authors of Numerical Recipes: the Art of Scientific Computing (Press et al., 1989), a text on numerical computation that explains that "a physical process can be described either in the time domain, or else in the frequency domain. For many purposes it is useful to think of these as being two different representations of the same function. One goes back and forth between these two representations by means of the Fourier transform
equations" (p. 381). The FT, by applying selective time and frequency analyses to an enormous amount of raw data, extracts the essential waveform information into a smaller data set that nevertheless has sufficient information for the experimenter's purposes.
Wavelets
The data signals presented to the computer from certain phenomena reflect sharp irregularities when sudden or dramatic transitions occur; the mathematical power of the FT, which relies on the creation and manipulation of trigonometric sines and cosines, does not work well at these critical transition points. For curves resulting from mathematical functions that are very complex and that display these striking discontinuities, the wavelet transform provides a more penetrating analytic tool than does the FT or any other mathematical operation. "Sine waves have no localization," explained Press, and thus do not bunch up or show a higher concentration at data points where the signal is particularly rich with detail and change. The power of wavelets comes in part from their variability of scale, which permits the user to select a wavelet family whose inherent power to resolve fine details matches the target data.
The fundamental operation involves establishing a banded matrix for the given wavelet family chosen. These families are predicated on the application of a specific set of coefficient numbers—which were named for Ingrid Daubechies, a French mathematician whose contributions to the theory have been seminal—and are called Daub 4 or Daub 12 (or Daub X), with a greater number of coefficients reflecting finer desired resolution. Press demonstrated to the symposium's audience how the Daub 4 set evolves, and he ran through a quick summary of how a mathematician actually computes the wavelet transform. The four special coefficients for Daub 4 are as follows:
The banded matrix is established as follows: install the numbers c0 through c3 at the upper left corner in the first row, followed by zeros to complete the row; the next row has the same four numbers directly below those on the first row, but with their order reversed and the c2 and c0 terms negative; the next row again registers the numbers in their regular sequence, but displaced two positions to the right, and so on, with zero occupying all other positions. At the end of a row of the matrix, the sequence wraps around in a circulant.
The mathematical character that confers on the wavelet transform its penetrating power of discrimination comes from two properties: first, the inverse of the matrix is found by transposing it—that is, the matrix is what mathematicians call orthogonal; second, when the fairly simple process of applying the matrix and creating a table of sums and differences is performed on a data set, a great many vanishing moments result—contributions so small that they can be ignored with little consequence. In practical terms, a mathematical lens seeks out smooth sectors of the data, and confers small numbers on them to reduce their significance relative to that of rough sectors, where larger numbers indicate greater intricacy or sudden transition. Press summarized, "The whole procedure is numerically stable and very fast, faster than the fast Fourier transform. What is really interesting is that the procedure is hierarchical in scale, and thus the power of wavelets is that smaller components can be neglected; you can just throw them out and compress the information in the function. That's the trick."
Press dramatically demonstrated the process by applying the wavelet transform to a photograph that had been scanned and digitized for the computer (Figure 7.4). "I feel a little like an ax murderer," he commented, "but I analyzed this poor woman into wavelets, and I'm taking her apart by deleting those wavelets with the smallest coefficients." This procedure he characterized as fairly rough: a sophisticated signal processor would actually run another level of analysis and assign a bit code to the coefficient numbers. But with Press simply deleting the smallest coefficients, the results were striking. With 77 percent of the numbers removed, the resulting photograph was almost indistinguishable from the original. He went to the extreme of removing 95 percent of the signal's content using the wavelets to retain "the information where the contrast is large," and still reconstructed a photograph unmistakably comparable to the original. ''By doing good signal processing and assigning bits rather than just deleting the smallest ones, it is possible to make the 5 percent picture look about as good as the original photograph," Press explained.
Press pointed out that early insights into the wavelet phenomenon came from work on quadrature filter mirrors, and it is even conceivable that they may help to better resolve the compromised pictures coming back from the Hubble Space Telescope. And while image enhancement and compression may be the most accessible applications right now, wavelets could have other powerful signal-processing uses wherever data come by way of irregular waveforms, such as for speech recognition, in processing of the sound waves used in geological explorations, in the storage of graphic images, and

Figure 7.4 Application of a wavelet transform to a photograph scanned and digitized for the computer. (A) Original photograph. (B) Reconstructed using only the most significant 23 percent of wavelets. (C) Reconstructed using only the most significant 5 percent of wavelets, that is, discarding 95 percent of the original image. (Courtesy of W. Press.)
in faster magnetic resonance imaging and other scanners. Work is even being done on a device that would monitor the operating sounds of complex equipment, such as jet engines or nuclear reactors, for telltale changes that might indicate an imminent failure. These and many other problems are limited by the apparent intractability of the data. Transforming the data into a more pliable and revelatory form is crucial, said Press, who continued, ''A very large range of problems—linear problems that are currently not feasible—may employ the numerical algebra of wavelet basis matrices and be resolved into sparse matrix problems, solutions for which are then feasible."
Experimental Mathematics
The work of Jean Taylor, a mathematician from Rutgers University, illustrates another example of the computer's potential to both support research in pure mathematics and also to promote more general understanding. Taylor studies the shapes of surfaces that are stationary, or that evolve in time, looking for insights into how energies control shapes; the fruits of her work could have very direct applications for materials scientists. But the level at which she approaches these problems is highly theoretical, very complex, and specialized. She sees it as an outgrowth of work done by mathematician Jesse Douglas, who won one of the first Fields medals for his work on minimal surfaces. She illustrated one value of the computer by explaining to the symposium the dilemma she often faces when trying to respond to queries about what she does. She may begin to talk about minimal surfaces at their extremes, which turn into polyhedral problems; this suggests to her listeners that she does discrete and computational geometry, which, she says, as it is normally defined does not describe her approach. Work on minimal surfaces is usually classified as differential geometry, but her work seems to fall more into the nondifferential realm. Even trained geometers often resort to categorizing her in not-quite-accurate pigeonholes. "It is much easier to show them, visually," said Taylor, who did just that for the symposium's audience with a pair of videos rich with graphical computer models of her work, and the theory behind it.
"Why do I compute?" asked Taylor. "I have developed an interaction with the program that makes it an instrumental part of my work. I can prove to others—but mainly to myself—that I really understand a construction by being able to program it." She is in the business of developing theorems about the equilibrium and growth shapes of crystals. The surfaces she studies often become "singular, producing situations where the more classical motion by curvature breaks down,'' she emphasized. No highly mathematical theory alone can render such visual phenomena with the power and cogency of a picture made from evolving the shape with her original computer model (Figure 7.5).
This sophisticated dialectic between theory and computer simulation also "suggests other theorems about other surface tension functions," continued Taylor, who clearly is a theoretical mathematician running experiments on her computer, and whose results often go far beyond merely confirming her conjectures.
Stephen Wolfram is ideally positioned to evaluate this trend. "In the past," he told symposium participants, "it was typically the case
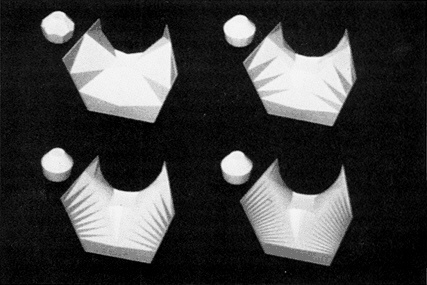
Figure 7.5 Four surfaces computed by Taylor, each having the same eight line segments (which lie on the edges of a cube) as a boundary, but with a different surface energy function for each. Each surface energy function is specified by the equilibrium single-crystal shape (the analog of a single soap-bubble) at the upper left of its surface. Computations such as this provide not only the raw material for making conjectures but also a potential method for proving such conjectures, once the appropriate convergence theorems are proved. (Courtesy of J. Taylor.)
that almost all mathematicians were theoreticians, but during the last few years there has arisen a significant cohort of mathematicians who are not theoreticians but instead are experimentalists. As in every other area of present day science, I believe that before too many years have passed, mathematics will actually have more experimentalists than theorists."
In his incisive survey of the computer and the changing face of science, The Dreams of Reason, physicist Heinz Pagels listed the rise of experimental mathematics among the central themes in what he considered "a new synthesis of knowledge based in some general way on the notion of complexity. . . . The material force behind this change is the computer" (Pagels, 1988, p. 36). Pagels maintained that the evolution concerns the very order of knowledge. Before the rise of empirical science, he said, the "architectonic of the natural sciences
(natural philosophy), in accord with Aristotelian canons, was established by the logical relation of one science or another" (p. 39). In the next era, the instrumentation (such as the microscope) on which empirical science relied, promoted reductionism: "the properties of the small things determined the behavior of the larger things," according to Pagels (p. 40), who asserted that with the computer's arrival "we may begin to see the relation between various sciences in entirely new dimensions'' (p. 40). Pagels believed that the common tool of the computer, and the novel perspective it provides on the world, are provoking a horizontal integration among the sciences, necessary in order to "restructure our picture of reality" (p. 42).
Implementing Software for Scientists
One of those providing a spotlight on this new picture of scientific reality is Wolfram, who runs Wolfram Research, Inc., and founded the Center for Complex Systems at the Urbana campus of the University of Illinois. Wolfram early realized the potential value of the computer to his work but found no adequate programming language that would fully utilize its power. He began working with a language called SMP and has since created and continued to refine a language of his own, which his company now markets as the software package Mathematica , used by some 200,000 scientists all over the world. He surveyed the Frontiers audience and found half of its members among his users.
Mathematica is a general system for doing mathematical computation and other applications that Press called "a startlingly good tool." As such, it facilitates both numerical and symbolic computation, develops elaborate sound and graphics to demonstrate its results, and provides "a way of specifying algorithms" with a programming language that Wolfram hopes may one day be accepted as a primary new language in the scientific world, although he pointed out how slowly such conventions are established and adopted (Fortran from the 1960s and C from the early 1970s being those most widely used now). Wolfram expressed his excitement about the prospects to "use that sort of high-level programming language to represent models and ideas in science. With such high-level languages, it becomes much more realistic to represent an increasing collection of the sorts of models that one has, not in terms of traditional algebraic formulae but instead in terms of algorithms, for which Mathematica provides a nice compact notation."
Similarly, noted Wolfram, "One of the things that has happened as a consequence of Mathematica is a change in the way that at least some people teach calculus. It doesn't make a lot of sense anymore
to focus a calculus course around the evaluation of particular integrals because the machine can do it quite well." One of the mathematicians in the audience, Steven Krantz from the session on dynamical systems, was wary of this trend, stating his belief that "the techniques of integration are among the basic moves of a mathematician—and of a scientist. He has got to know these things." From his point of view, Wolfram sees things differently. "I don't think the mechanics of understanding how to do integration are really relevant or important to the intellectual activity of science," he stated. He has found that, in certain curricula, Mathematica has allowed teachers who grasp it a freedom from the mechanics to focus more on the underlying ideas.
THE SCIENCES OF COMPLEXITY
Cellular Automata
Wolfram, according to Pagels, "has also been at the forefront of the sciences of complexity" (Pagels, 1988, p. 99). Wolfram is careful to distinguish the various themes and developments embraced by Pagels' term—which "somehow relate to complex systems"—from a truly coherent science of complexity, which he concedes at present is only "under construction." At work on a book that may establish the basis for such a coherent view, Wolfram is a pioneer in one of the most intriguing applications of computation, the study of cellular automata. ''Computation is emerging as a major new approach to science, supplementing the long-standing methodologies of theory and experiment," said Wolfram. Cellular automata, "cells'' only in the sense that they are unitary and independent, constitute the mathematical building blocks of systems whose behavior may yield crucial insights about form, complexity, structure, and evolution. But they are not "real," they have no qualities except the pattern they grow into, and their profundities can be translated only through the process that created them: computer experimentation.
The concept of cellular automata was devised to explore the hypothesis that "there is a set of mathematical mechanisms common to many systems that give rise to complicated behavior," Wolfram has explained, suggesting that the evolution of such chaotic or complex behavior "can best be studied in systems whose construction is as simple as possible" (Wolfram, 1984, p. 194). Cellular automata are nothing more than abstract entities arranged in one or two (conceivably and occasionally more) dimensions in a computer model, each one possessing "a value chosen from a small set of possibilities, often just 0 and 1. The values of all cells in the cellular automaton are
simultaneously updated at each 'tick' of a clock according to a definite rule. The rule specifies the value of a cell, given its previous value and the values of its nearest neighbors or some other nearby set of cells" (p. 194).
What may seem at first glance an abstract and insular game turns out to generate remarkably prescient simulations that serve, according to Wolfram, "as explicit models for a wide variety of physical systems" (Wolfram, 1984, p. 194). The formation of snowflakes is one example. Beginning with a single cell, and with the rules set so that one state represents frozen and the other state water vapor, it can be shown that a given cell changes from a vapor state to a frozen state only when enough of its neighbors are vaporous and will not thereby inhibit the dissipation of enough heat to freeze. These rules conform to what we know about the physics of water at critical temperatures, and the resulting simulation based on these simple rules grows remarkably snowflake-like automata (Figure 7.6).
Cellular automata involve much more than an alternative to running complicated differential equations as a way of exploring snowflake and other natural structures that grow systematically; they may be viewed as analogous to the digital computer itself. "Most of [their] properties have in fact been conjectured on the basis of patterns generated in computer experiments" (Wolfram, 1984, p. 194). But their real power may come if they happen to fit the definition of a universal computer, a machine that can solve all computable problems. A computable problem is one "that can be solved in a finite time by following definite algorithms" (p. 197). Since the basic operation of a computer involves a myriad of simple binary changes, cellular automata—if the rules that govern their evolution are chosen appropriately—can be computers. And "since any physical process can be represented as a computational process, they can mimic the action of any physical system as well" (p. 198).
Resonant with the fundamental principles discussed in the session on dynamical systems, Wolfram's comments clarified the significance of these points: "Differential equations give adequate models for the overall properties of physical processes," such as chemical reactions, where the goal is to describe changes in the total concentration of molecules. But he reminded the audience that what they are really seeing, when the roughness of the equations is fully acknowledged, is actually an average change in molecular concentration based on countless, immeasurable random walks of individual molecules. But the old science works. At least the results produced a close enough fit, for many systems and the models based on differential equations that described them. "However," Wolfram continued,

Figure 7.6 Computer-generated cellular automaton pattern. The simulated snowflake grows outward in stages, with new cells added according to a simple mathematical rule. Hexagonal rule = 1010102. (Reprinted with permission from Norman H. Packard and Stephen Wolfram. Copyright © 1984 by Norman H. Packard and Stephen Wolfram.)
"there are many physical processes for which no such average description seems possible. In such cases differential equations are not available and one must resort to direct simulation. The only feasible way to carry out such simulations is by computer experiment: essentially no analysis of the systems for which analysis is necessary could be made without the computer."
The Electronic Future Arrives
The face of science is changing. Traditional barriers between fields, based on specialized knowledge and turf battles, are falling. "The material force behind this change is the computer," emphasized Pagels (Pagels, 1988, p. 36), who demonstrated convincingly how the computer's role was so much more than that of mere implement.
Science still has the same mission, but the vision of scientists in this new age has been refined. Formerly, faced with clear evidence of complexity throughout the natural world, scientists had to limit the range of vision, or accept uneasy and compromised descriptions. Now, the computer—in Pagels' words the ultimate "instrument of complexity"—makes possible direct examination and experimentation by way of computation, the practice of which he believed might deserve to be classed as a distinct branch of science, alongside the theoretical and the experimental. When colleagues object that computer runs are not real experiments, the people that Pagels wrote about, and others among the participants in the Frontiers symposium, might reply that, in many experimental situations, computation is the only legitimate way to simulate and capture what is really happening.
Wolfram's prophecy may bear repetition: "As in every other area of present day science, I believe that before too many years have passed mathematics will actually have more experimentalists than theorists." One of the reasons for this must be that no other route to knowledge and understanding offers such promise, not just in mathematics but in many of the physical sciences as well. Pagels called it "the rise of the computational viewpoint of physical processes," reminding us that the world is full of dynamical systems that are, in essence, computers themselves: "The brain, the weather, the solar system, even quantum particles are all computers. They don't look like computers, of course, but what they are computing are the consequences of the laws of nature" (Pagels, 1988, p. 45). Press talked about the power of traditional algorithms to capture underlying laws; Pagels expressed a belief that ''the laws of nature are algorithms that control the development of the system in time, just like real programs do for computers. For example, the planets, in moving around the sun, are doing analogue computations of the laws of Newton" (p. 45).
Indisputably, the computer provides a new way of seeing and modeling the natural world, which is what scientists do, in their efforts to figure out and explain its laws and principles. Computational science, believes Smarr, stands on the verge of a "golden age," where the exponential growth in computer speed and memory will not only continue (Box 7.4), but together with other innovations achieve something of a critical mass in fusing a new scientific world: "What is happening with most sciences is the transformation of science to a digital form. In the 1990s, a national information infrastructure to support digital science will arise, which will hook together supercomputers, massive data archives, observational and experimental instruments, and millions of desktop computers." We are well on the way, he believes, to "becoming an electronic scientific community" (Smarr, 1991, p. 101).
|
BOX 7.4 PARALLEL COMPUTING Whether serial or parallel, explained neuroscientist James Bower from the California Institute of Technology, all computers "consist of three basic components: processors, memory, and communication channels," which provide a way to distinguish and compare them. Up until the 1970s, said Larry L. Smarr of the National Center for Supercomputing Applications (NCSA), computer designers intent on increasing the speed and power of their serial machines concentrated on "improving the microelectronics" of the single central processing unit (CPU) where most of the computation takes place, but they were operating with a fundamental constraint. The serial CPUs are scalar uniprocessors, which means that they operate—no matter how fast—on but one number at a time. Smarr noted that Seymour Cray, called "the preeminent supercomputer designer of recent decades, successfully incorporated a [fundamental] improvement called vector processing," where long rows of numbers called vectors could be operated on at once. The Cray-1 model increased the speed of computing by an order of magnitude and displaced earlier IBM and Control Data Corporation versions (that had previously dominated the market in the 1960s and 1970s) as the primary supercomputer used for scientific and advanced applications. To capitalize on this design, Cray Research, Inc., developed succeeding versions, first the X-MP with four, and then the Y-MP with eight powerful, sophisticated vector processors able to "work in parallel," said Smarr. "They can either run different jobs at the same time or work on parts of a single job simultaneously." Such machines with relatively few, but more powerful, processors are classified as coarse-grained. They ''are able to store individual programs at each node," and usually allow for very flexible approaches to a problem because ''they operate in the Multiple-Instruction Multiple-Data (MIMD) mode," explained Bower. By contrast, another example of parallel processing put to increasing use in the scientific environment is the Connection Machine, designed by W. Daniel Hillis, and manufactured by Thinking Machines Corporation. Like the biological brains that Hillis readily admits inspired its design, the Connection Machine's parallelism is classified as fine-grained. In contrast to the more powerful Cray machines, it has a large number of relatively simple processors (nodes), and operates on data stored locally at each node, in the Single-Instruction Multiple-Data (SIMD) mode. Hillis and his colleagues realized that human brains were able to dramatically outperform the most sophisticated serial computers in visual processing tasks. They believed this superiority was inherent in the fine-grained design of the brain's circuitry. Instead of relying |
|
on one powerful central processing unit to search through all of the separate addresses where a bit memory might be stored in a serial computer, the Connection Machine employs up to 65,536 simpler processors (in its present incarnation), each with a small memory of its own. Any one processor can be assigned a distinct task—for example, to attend to a distinct point or pixel in an image—and they can all function at once, independently. And of particular value, any one processor can communicate with any other and modify its own information and task pursuant to such a communication. The pattern of their connections also facilitates much shorter information routes: tasks proceed through the machine essentially analyzing the best route as they proceed. The comparatively "blind" logic of serial machines possesses no such adaptable plasticity. "Each processor is much less powerful than a typical personal computer, but working in tandem they can execute several billion instructions per second, a rate that makes the Connection Machine one of the fastest computers ever constructed," wrote Hillis (1987, p. 108). Speed, cost per component, and cost per calculation have been the currencies by which computers have been evaluated almost from their inception, and each successive generation has marked exponential improvement in all three standards. Nonetheless, Smarr believes the industry is approaching a new level of supercomputing unlike anything that has gone before: "By the end of the 20th century, price drops should enable the creation of massively parallel supercomputers capable of executing 10 trillion floating-point operations per second, 10,000 times the speed of 1990 supercomputers," This astounding change derives from the massively parallel architecture, which "relies on the mass market for ordinary microprocessors (used in everything from automobiles to personal computers to toasters) to drive down the price and increase the speed of general-design chips. Supercomputers in this new era will not be confined to a single piece of expensive hardware located in one spot, but rather will be built up by linking "hundreds to thousands of such chips together with a high-efficiency network," explained Smarr. |
BIBLIOGRAPHY
Harel, David. 1987. Algorithmics: The Spirit of Computing. Addison-Wesley, Reading, Mass.
Hillis, W. Daniel. 1987. The connection machine. Scientific American 256(June):108–115.
Pagels, Heinz R. 1988. The Dreams of Reason: The Computer and the Rise of the Sciences of Complexity. Simon and Schuster, New York.
Press, William, Brian P. Flannery, Saul A. Teukolsky, and William T. Vetterling. 1989. Numerical Recipes: The Art of Scientific Computing. Cambridge University Press, New York.
Shannon, Claude E. 1938. A symbolic analysis of relay switching and controls. Transactions of the American Institute of Electrical Engineers 57:713–723.
Smarr, Larry L. 1985. An approach to complexity: Numerical computations. Science 228(4698):403–408.
Smarr, Larry L. 1991. Extraterrestrial computing: Exploring the universe with a supercomputer. Chapter 8 in Very Large Scale Computation in the 21st Century. Jill P. Mesirov (ed.). Society for Industrial and Applied Mathematics, Philadelphia.
Smarr, Larry L. 1992. How supercomputers are transforming science. Yearbook of Science and the Future. Encyclopedia Britannica, Inc., Chicago.
Wolfram, Stephen. 1984. Computer software in science and mathematics. Scientific American 251 (September): 188–203.
Wolfram, Stephen. 1991. Mathematica: A System for Doing Mathematics by Computer. Second edition. Addison-Wesley, New York.































