10
Physics
Quasicrystals and Superconductors: Advances in Condensed Matter Physics
by EDWARD EDELSON
The physics session of the 1990 Frontiers of Science symposium was devoted to two separate and unusual topics in condensed matter physics (the physics of solid and liquid objects), which the chairman, Daniel Fisher of Harvard University, described as including everything "that is much bigger than a molecule, much smaller than a mountain, and not too hot"—a range diverse enough to occupy almost half of all physicists. Both topics—high-temperature superconductivity and quasicrystals—concerned fields that "seemed to be, if not dead, at least not so active in the 1970s and the early 1980s" but suddenly came to life as the result of major, surprising discoveries, Fisher said.
High-temperature superconductivity, which has received wide coverage in the popular press, has become the focus of intensive effort among applied and theoretical physicists and materials scientists. The discovery in 1986 by J. Georg Bednorz and Karl Alex Mueller of the IBM Research Laboratories in Zurich, Switzerland, of a new class of materials that lose all electrical resistance at unprecedentedly high temperatures has captured professional interest as well as public attention. Visions of levitated trains, new energy sources, and ultra-accurate scientific instruments have energized a field in which incremental advances had been the norm for decades. The discovery also transformed superconductivity from "the most well-understood problem in solid-state physics," in the words of Alex Zettl of the University of California, Berkeley, to a field where a thousand theo-
retical flowers have bloomed in efforts to explain why the newly discovered materials are capable of high-temperature superconductivity.
The other development discussed in the physics session, although less publicized in the lay press, has had an equally revolutionary effect on the field of crystallography. It is the discovery of a class of materials that violate the rigorous, long-established rules about crystals—solids that consist of regular, repeating, three-dimensional units. Theory had held that certain structures were forbidden by nature. Now structures have been found to exist that are neither glasses nor crystals. They are not composed of the repeating, three-dimensional units of crystals, and they exhibit symmetries found neither in crystals nor in glasses. These quasicrystals, as they are called, are a fundamentally new, ordered state of matter.
The unusual nature of a quasicrystal is best explained by a two-dimensional analogy, the tiling of a floor or other surface. We customarily cover a floor with square tiles, which can be said to have fourfold symmetry because they have four equal sides. A surface can also be covered with triangular tiles, which have threefold symmetry, and with tiles that have sixfold symmetry. But it cannot be covered completely by pentagons, which have fivefold symmetry. No matter how cleverly we lay pentagonal tiles, gaps are left that cannot be filled using those tiles. In the same way, a three-dimensional space can be filled periodically with crystal units that have fourfold or sixfold symmetry but not, according to theory, by crystal units with fivefold symmetry. That theory now has been upset by the discovery of crystal units that have fivefold symmetry and fill space completely. As in the case of superconductivity, this discovery has excited the interest of physicists, who are studying the properties of quasicrystals and how they are made in nature, as well as of theorists, who are exploring the mathematical and physical implications of the existence of quasicrystals.
SUPERCONDUCTIVITY
A Brief History
The phenomenon of superconductivity was discovered in 1911 by a Dutch physicist, H. Kamerlingh Onnes, who found that the electrical resistance of mercury vanished suddenly when the metal was cooled to a temperature of about 4 kelvin (K), which is 4 degrees Celsius above absolute zero (Table 10.1). If an electrical current is established in a ring of frozen mercury that is maintained at that
temperature, the current will persist indefinitely. By contrast, such a current dies away quickly in an ordinary conducting material such as copper.
In the 1930s, another characteristic of superconducting materials was described. If an ordinary metal is placed in a magnetic field, the magnetic field permeates the material. Superconducting materials act differently. Some of them expel the magnetic field completely; others allow only partial penetration. This Meissner effect, as it is called, is responsible for the ability of permanent magnets to be levitated above a superconductor. In expelling the field of the magnet, the superconductor generates its own magnetic field, which pushes the magnet away and allows the magnet to float over the superconducting sample.
A full microscopic theory of superconductivity was achieved in the 1950s by three physicists, John Bardeen, Leon N. Cooper, and J. Robert Schrieffer. The Bardeen-Cooper-Schrieffer (BCS) theory starts with the picture of a normally conducting metal whose atoms are arranged in a three-dimensional crystal structure. Some of the loose-
TABLE 10.1 Developments in Superconductivity
|
Theory |
Date |
Experiment |
|
No theory |
1911 |
Superconductivity discovered Tc = 4.2 K |
|
London equations |
1930 |
Meissner effect |
|
BCS theory |
1950 |
Isotope effect |
|
Superconductivity: "Most well-understood problem in solid-state physics |
1960 |
Type II materials, Josephson effects |
|
1970 |
Tc = 23 K |
|
|
High-Tc theory? |
1986 |
Tc = 30 K |
|
|
1987 |
Tc = 90 K |
|
|
1988 |
Tc = 125 K Copper oxides |
|
SOURCE: Courtesy of A. Zettl. |
||
ly held outer electrons drift away from the metal atoms in the crystal, forming an electron gas that flows freely through the crystal lattice. The flow of these electrons is the electrical current that runs through the metal. These electrons do not have limitless freedom, however. Some of them interact with impurities in the metal and with the vibrations of the atoms that form the crystal lattice. The interaction of the electrons with the atomic vibrations causes the electrical resistance found in metals at ordinary temperatures.
Electrons, which have a negative charge, ordinarily repel each other. The essence of the BCS theory is that under some circumstances they can have a net attractive interaction and thus form pairs. The BCS theory pictures an electron traveling through a lattice of metal ions, which are positively charged because they have lost some of their electrons. The negatively charged electron may be attracted to another negatively charged electron by way of the oscillations of the metal ions. The two electrons form a pair—a Cooper pair, in the language of the BCS theory. All the Cooper pairs act together as a unified quantum system. Circulating currents made up of Cooper pairs do not decay in the ordinary manner of currents composed of single electrons.
One useful way to picture the interaction is to say that one negatively charged electron attracts the positively charged ions around it, causing a slight distortion in the lattice. The distortion produces a polarization, an area of increased positive charge. A second electron is attracted by this pocket of positive charge; it thus becomes coupled to the first electron, following it through the lattice.
Another description of the same phenomenon is that the electrons are coupled by the interchange of a virtual particle, the phonon. Phonons represent the vibrations of the lattice. In either picture, the electron-phonon coupling allows the electrons to pair and then to flow unhindered through the lattice. Anything that destroys the Cooper pairs—for example, heat that increases the lattice vibrations above a certain limit—destroys superconductivity.
Among other things, the BCS theory explains why superconductivity occurs in metals only at very low temperatures. At higher temperatures, thermal motion begins to break Cooper pairs apart. Above a given transition temperature, all the pairs are broken and superconductivity vanishes. BCS theory also explains why metals that are good conductors at room temperature may not be superconductors at low temperatures: they do not have a large enough phonon-electron interaction to allow Cooper pairs to form.
In the BCS theory, a material's transition temperature, the temperature at which it becomes superconducting, depends only on three
factors: the phonon frequency in the lattice, the density of states (energy levels that electrons can occupy) near the Fermi energy (the highest electron energy occupied in the material at low temperature), and the strength of the electron-phonon coupling energy.
Another feature of superconducting materials is the isotope effect. If an atom of one element in a superconducting material is replaced by an isotope of greater mass, the transition temperature of the material generally goes down. This so-called isotope effect occurs because transition temperature is approximately proportional to the frequency of the lattice vibrations, and isotopes of greater mass have lower vibration frequencies. The isotope effect, first demonstrated in mercury in 1950, was fundamental to the development of the BCS theory, because it strongly implied that phonons were the glue that held Cooper pairs together.
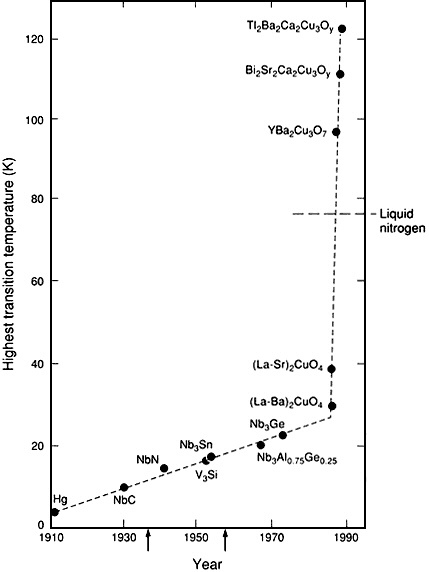
The success of the BCS theory came against a background of slow, dogged advances in superconducting materials research. Starting from the 4.15-K transition temperature of mercury described by Onnes in 1911, physicists discovered a series of materials with progressively higher transition temperatures. By the mid-1970s, the record transition temperature was 23 K, in a niobium-germanium compound.
For practical purposes, characteristics other than transition temperature are also important. Superconductivity can be destroyed by a high current density or a strong magnetic field. Technologically, the most desirable superconducting material has a high transition temperature and a high critical current and remains superconducting in a strong magnetic field. One such material that combines these qualities is a niobium-titanium compound that is used in superconducting magnets such as those found in medical magnetic resonance imaging devices and those being built for the Superconducting Super Collider, the world's largest particle accelerator.
Another property of superconductors, described by Brian Josephson in the early 1960s, is the Josephson effect. If two samples of superconducting material are separated by a thin barrier, some of the Cooper-paired electrons will tunnel through. This tunneling is explained by quantum theory, in which subatomic particles are described equally well as wave packets. It is the wave aspect of electrons that allows tunneling to occur. The electron as a particle cannot pass through a barrier; as a wave, it can. The Josephson effect has led to the development of high-accuracy superconducting electronic instruments, such as ultrasensitive magnetometers, that use the tunneling effect.
By the late 1980s, therefore, superconductivity was a well-understood if hardly dynamic field. BCS theory explained the phenome-
non but provided no help in finding more useful superconductors. Magnet makers had mastered the skill of working with the available superconductors but were chafing under the necessity of cooling the materials to a few degrees above absolute zero. Those temperatures could be achieved only by the use of liquid helium as the coolant in extremely expensive refrigeration systems. The quest taken up in superconductivity research was to find a material that would be superconducting at a temperature above 77 K, which would allow use of inexpensive refrigeration systems with nitrogen (which becomes liquid at 77 K) as the coolant. But such an advance was nowhere in sight. The highest known transition temperature had increased by an average of 0.3 K per year for several decades. Extrapolation of a line through points on a graph representing new highs in transition temperature indicated that liquid nitrogen temperatures would be reached late in the 21st century. Occasionally, one laboratory or another would make a preliminary report of a material with extremely high transition temperatures, but none of those reports stood up under scrutiny.
Start of a New Era
Thus there was great excitement when Bednorz and Mueller reported in 1986 an apparent transition temperature of 30 K in a material completely different from the known superconductors, a ceramic made up of copper, oxygen, barium, and lanthanum. This time the claim was verified, and the world of superconductivity entered a new era. Within a matter of months, Paul Chu at the University of Houston and Maw-Kuen Wu at the University of Alabama reported that a copper oxide ceramic containing yttrium and barium had a transition temperature well above 90 K, easily in liquid nitrogen territory. The record now is a transition temperature of 125 K, in a copper oxide that contains thallium, barium, and calcium (Figure 10.1).
Challenges Posed by High-temperature Superconducters
These high-temperature superconductors pose a number of challenges. One is the practical matter of making devices from these materials. Since the new materials are ceramics, they are not easily made into wires for magnets. In addition, although their transition temperatures are high, their critical currents are not; they can carry only a small fraction of the current that can flow through an ordinary copper wire without losing their superconductivity. A substantial
effort in academic and industrial laboratories has started to solve some of these problems.
Physicists have also been challenged to provide a theory for high-temperature superconductivity. The atomic structure of the new superconductors is quite different from that of the known materials. The outstanding feature of the new high-temperature materials is that they are oxides, most of which are electrical insulators. They have planes consisting of atoms of copper and oxygen, with two copper atoms for each oxygen. The other atoms, such as barium and yttrium, are between the copper-oxygen planes. In the language of physics, these materials are highly anisotropic: the two-dimensional planes of atoms dominate the structure. One assumption of many physicists was that the mechanism of superconductivity for these new materials might be closely related to this structural anisotropy.
The implication was that high-temperature superconductivity might well not be explained by the BCS theory—an implication strengthened by the belief that the theory could not accommodate such high transition temperatures. Investigations to see whether BCS theory or some variation on it could explain the new superconductivity began, and are still continuing.
A first approach to the issue was to determine whether the electrons in the new materials formed pairs during the superconducting phase. As Zettl explained, there are two standard ways to make this determination. One is to make a ring of the material. The magnetic flux through the ring is quantized, and measurements of the quantum of flux can determine whether the unit of charge that produces the magnetic flux is the charge on one electron, e, or two electrons, 2e. If the charge is e, the electrons are not paired; if it is 2e, they are.
A second method is to make a Josephson junction, allow electron tunneling to occur, and shine microwaves of a known frequency on the junction. The interference between this frequency and an internal frequency generated by the tunneling electrons indicates whether the charge is e or 2e.
Both experiments were done within months, and both indicated an effective charge of 2e: electrons in high-temperature superconductors are paired. ''It is pretty clear that we have a pairing mechanism, and the question then becomes what mechanism is holding these pairs together,'' Zettl said.
The BCS theory makes some specific predictions about the properties of electron pairs. Calculations done by Marvin Cohen and co-workers indicated that the BCS theory could accommodate a transition temperature as high as 100 K.
However, experiments done by Zettl and others to measure the
isotope effect in the new materials produced results that complicated the issue. In these experiments, the oxygen-16 atoms in the material were replaced by oxygen-18 isotopes. The predicted result given by the BCS theory was a 5-K reduction in the transition temperature. The actual reduction was a small fraction of 1 K. Further calculations showed that the BCS theory could be consistent with a small or non-existent isotope effect under certain circumstances. And other calculations showed that the quasi-two-dimensional system of the new materials could also suppress the isotope effect. But it is almost impossible to accommodate both the observed high transition temperatures and the small isotope effect within BCS theory, Zettl said—one of the many unresolved issues about the new materials.
The issue of dimensionality has become very important. Several experimental programs have examined whether the superconducting current flows only along the planes of the materials or if it is three-dimensional. Some experiments tried to determine whether the new materials behaved as a collection of weakly coupled slabs, with all the action associated with superconductivity limited to the copper-oxygen slabs. In one group of experiments designed to test this idea, layers of nonsuperconducting copper oxide were inserted between the copper-oxygen layers of a superconducting compound. The material remained a superconductor even when the insulating layers became very thick, but the transition temperature of the superconducting material went down. In another experiment, Zettl and his collaborators intercalated iodine and other atomic species between the copper-oxygen layers, steadily increasing the distance between the layers of a superconducting ceramic. Even with a 23 percent expansion of the vertical distance of the material, the transition temperature scarcely changed. "This is evidence that the superconductivity does not strongly rely on three-dimensional coupling between superconducting sheets, with obvious implications for two-dimensional mechanisms," Zettl said.
Another question concerned what is called the energy gap in these materials. The energy gap consists of a range of energies that electrons in the material cannot achieve; measurement of the energy gap can give the binding energy and coherence length (the distance between electrons) of the electron pairs. The existence of a gap, and its magnitude if it does exist, are important theoretically. One class of proposed theories about the new materials is based on high binding energy for the electron pairs, the so-called strong-coupling limit, while another class is based on low binding energy, the so-called weak-coupling limit.
One measurement used to describe a superconducting material is
a dimensionless number derived by multiplying the energy gap by 2 and dividing it by the Boltzmann constant times the transition temperature. In the classic BCS theory, in the weak-coupling limit, the value of this expression is about 3.5. A number larger than 3.5 indicates strong electron coupling and hence a large gap.
Values for this number can be derived in several ways. One is to use nuclear magnetic resonance (NMR) to examine a material. A sample is placed in a magnetic field and radio waves of appropriate frequency are beamed in. The relaxation time of nuclei as they give up the absorbed energy gives information about the properties of the sample. NMR data give values for the yttrium-barium-copper oxide in the range of 8 to 11. Another method is to study the absorption of infrared light by the material. Using this method of infrared spectroscopy, experimenters have obtained values between 3.5 and 8.
A third method is tunneling, in which a voltage is applied to a metal tip in contact with the superconducting material. If the voltage is sufficient to break the Cooper pairs, electrons will tunnel through. The applied voltage is thus a measure of the superconducting gap. "From such tunneling measurements on the superconducting oxide bismuth-strontium-calcium-copper-oxygen, two distinct values for the energy gap have been determined: 3.5 and 7," Zettl said. "The two values refer to different crystallographic orientations. The smaller value is consistent with BCS theory, while the larger value is not."
The issue of strong binding versus weak binding of the electron pairs thus remains confusing, said Duncan Haldane of Princeton University, another speaker at the symposium, who focused on the theoretical issues.
One critical factor in trying to develop a theory to explain the new materials, Haldane said, is their odd behavior in terms of electrical resistance above the transition temperature. When a metal such as copper is cooled, its resistance decreases linearly at high temperatures and then undergoes a very rapid decrease at lower temperatures. In the new materials, the resistance decreases linearly to much lower temperatures than expected, disappearing suddenly at the transition temperature. "This linear resistance above the superconducting transition is difficult to explain within the usual pictures of conductivity in metals," Haldane said.
Development of New Theories
The new theories can be grouped into two classes. One group assumes weak coupling, whereas a second assumes strong coupling. Most of the theories assume that polarization causes electron pairing.
In the electron-phonon interaction of the BCS theory, the electron polarizes the lattice. Two other things can be polarized, charge or spin. A huge variety of exotic polarizing mechanisms—excitons, plasmons, spin fluctuations—have been proposed.
A theory based on charge polarization postulates the excitonic mechanism, first outlined by Vitaly Ginzburg of the Soviet Union and independently by William Little of Stanford University and later developed by Bardeen, David Allender, and James Bray at the University of Illinois. It pictures electrons as being paired by exchange of a virtual particle, the exciton, that comes into existence when an electron moves to a higher energy state, creating a hole, and then drops back to the lower energy state. It can be put in another way: the electron creates a polarization cloud by pushing nearby electrons away because of the Coulomb repulsion between similarly charged particles. A second electron has its energy lowered because of the polarization cloud and forms a pair with the first. One problem with the excitonic mechanism is that it predicts transition temperatures that are too high—by hundreds or even thousands of kelvins. In addition, the requisite excitations have not been observed.
A spin-polarization theory first developed by P.-G. de Gennes assumes the production of virtual particles called magnons. It starts with a nonsuperconducting material in the antiferromagnetic state, in which neighboring electrons have spins of opposite orientation. When the material is doped by the addition of another element, holes are created that also carry a spin. Each hole wants to spin antiparallel to the electrons, but it also wants to delocalize—spread its wave function to other sites. But it sees antiferromagnetic electrons whose spins are aligned parallel with it at these other sites. Its spin is tilted, so that the electron can delocalize to some degree and still have a favorable alignment of its spin with the antiferromagnetic electrons. This causes a spin polarization cloud to form, attracting a second electron and forming a pair. The interaction is mediated by polarizing spin degrees of freedom.
The charge-polarization and spin-polarization theories are based on two sharply different pictures of the electron structure of the material. BCS theory assumes that the conduction electrons that form a Cooper pair are delocalized and move relatively independently. Charge-polarization theories also are based on this structure. Many spin-polarization theories assume a strikingly different structure, called the Mott-Hubbard insulator.
As described by Sir Nevill Mott, a British Nobel laureate in physics, and John Hubbard, a Briton who was with IBM before his death, the Mott-Hubbard insulator picture assumes that the electrons are in
an ordered, strongly correlated structure. The atoms in the lattice have outer electron shells that are almost exactly half-filled, so that there is one conduction electron per atom and the material is an insulator. Doping the material produces mobile holes. The collective behavior responsible for the transition to superconductivity occurs through correlations of the electron spins.
Another spin-polarization theory based on the Hubbard model pictures strong coupling of the electrons based on antiferromagnetic spin fluctuations. The charge carriers are holes—missing electrons—that are created as barium is added to lanthanum copper oxide. Cooper pairing occurs as a result of interactions between the spins of the holes and neighboring electrons.
One theory that aroused enthusiasm for a while was based on exotic particles called anyons or semions, which are neither bosons nor fermions, Haldane said. A pair of fermions can form a boson; so can a pair of bosons, he explained. In a two-dimensional system, there is a third possibility: Two semions can pair to form a boson, too. The anyon theory is that the boson sea of a high-temperature superconductor is formed by as-yet-undetected particles whose properties are halfway between those of fermions and bosons. The anyon theory requires time-reversal breaking—a violation of the rule that a movie made of a particle interaction would show the exact reverse of that interaction when run backward. Experiments done at Bell Laboratories in 1990 indicated that time reversal was violated in the new superconductors, a finding that gave prominence to the anyon theory. Interest has faded as other laboratories have failed to replicate the broken time-reversal studies, Haldane said.
Yet another theory assumes the existence of "soft" phonons associated with what is called a breathing mode, in which oxygen atoms that are around copper ions in the lattice move in and out regularly. As temperature drops, the breathing mode should soften—that is, oscillate at lower and lower frequencies. Below a given temperature, the oscillation stops. The resulting "frozen phonons" allow strong electron coupling that permits high transition temperatures.
Another theory posits interactions mediated by bipolarons. A polaron is an electron that sits in a pocket of positive charge in a lattice; a bipolaron is a pair of such electrons. Bipolarons can undergo a Bose condensation if the electron structure of a material meets certain conditions that can occur in layered materials such as the oxide superconductors.
Philip W. Anderson of Princeton University has proposed a resonance valence bond (RVB) theory that assumes no polarization of any kind. It postulates a spin liquid, in which electrons can be described
as being in a kind of square dance, with overall order maintained even as dancers constantly change partners. RVB theory holds that electron pairs can exist in material that is not superconducting. Superconductivity occurs when the material is doped to create holes, which form pairs and undergo Bose condensation.
None of the theories has won general acceptance, Haldane said, nor is any resolution of the issue in sight.
Progress Toward Practical Applications
But just as was true of the low-temperature superconductors, progress toward practical applications of the new materials is being made, said Zettl and Peter Gammel of Bell Laboratories, another speaker at the Frontiers symposium. Both spoke about the issue of preserving superconductivity in strong magnetic fields, which is essential for making superconducting magnets.
The copper oxide superconductors, like the low-temperature superconductors now used in large magnets, do not expel magnetic fields completely. Instead, the magnetic field penetrates the material in some areas, forming vortices that are not superconducting; the rest of the material remains superconducting. At sufficiently high magnetic fields, the vortices can pervade the sample, and superconductivity vanishes. Current flowing through the material can cause the vortices to move, which likewise destroys superconductivity. The critical current is that which causes the vortices to move enough to destroy the zero-resistance state.
A new theory and its experimental verification have provided an explanation for this behavior of the high-temperature superconductors. In low-temperature superconductors, the problem has been solved by introducing defects into the material. The defects "pin" the magnetic field lines, thus preventing them from interfering with superconductivity.
The anisotropy of the new superconductors makes this method much less effective. Their layered structure means that a magnetic line that is pinned by a defect in one layer may not be pinned by a corresponding defect in other layers. As a result, the transition to superconductivity in these materials does not occur in a narrow range of temperatures. Instead, resistivity tends to decrease gradually; in some cases, the material never loses all resistance in a strong magnetic field. This phenomenon appeared to present a major barrier to use of the high-temperature superconductors in magnets, one of the major applications of superconducting materials.
A theory proposed by Matthew Fisher of IBM offered a way out
of this dilemma, at least for yttrium-based superconductors. Fisher started with the standard picture of magnetic field lines going through the superconductor in bundles, or vortices. It is these vortices that are pinned by defects in low-temperature superconductors. Fisher proposed that in the new material, interactions between the vortices can cause them to freeze in place at low temperatures, in a sudden transition that allows the material to be a true superconductor. According to this theory, the phenomenon is analogous to the freezing of water, which is liquid until the temperature is lowered sufficiently. A high-temperature superconductor thus would be a "vortex glass," because the vortices would be frozen at a transition temperature.
Others elaborated on the theory, producing precise predictions that could be tested experimentally. One such prediction was that the superconductor would undergo a sharp phase transition, losing all resistivity, at a given temperature; it would be the transition to the vortex glass state. Other predictions about the transition to the vortex state could be made, but they were difficult to measure because experiments required a degree of precision that was at the boundary of existing instrumentation.
Recently, Gammel and others have done confirmatory experiments on yttrium-containing superconductors. The results were in agreement with the predictions of the vortex glass theory. Experiments on other high-temperature superconductors are ongoing.
Verification of the vortex glass theory has important implications for physicists working on industrial uses of the new superconductors. For example, the theory might help researchers introduce defects into superconducting materials in a way designed to make the transition to the vortex glass state, and thus to superconductivity, occur at higher temperatures. In this case, fundamental theory has had a direct impact on practical applications of a promising new technology.
The greatest progress has been made in the field of miniature electronic instruments using thin films of high-temperature superconductors, Zettl said: "Our electronics industry is based on thin-film techniques, and these materials lend themselves rather well to thin-film fabrication."
QUASICRYSTALS
Solid materials have traditionally been divided into two broad classes, based on atomic order. One class consists of the glasses. These are solids whose atoms are in a random, close-packed arrangement. A glass can be regarded as a liquid whose flow is immeasurably slow.
The second class consists of the crystals, whose atoms are or
dered in a regular, periodically repeating three-dimensional pattern. Crystals can be decomposed into clusters of atoms called unit cells. A crystal consists of a large number of close-packed, identical unit cells—in theory, an infinite number—which extend in all directions and fill space completely. One property of a crystal is that all the unit cells have the same orientation in space. Consequently, a crystal can overlie itself only when it is rotated by specific angles through specific points. A unit cell that has twofold symmetry must be rotated by 180 or 360 degrees to overlie itself; if it has threefold symmetry, it must be rotated by 120, 240, and 360 degrees. Only twofold, threefold, fourfold, and sixfold rotational symmetries are possible in crystals, because only unit cells with these symmetries can fill three-dimensional space completely. Fivefold symmetry is strictly forbidden.
As mentioned previously, there is a close analogy between crystals and two-dimensional tilings. A surface can be covered completely by rectangles, which have twofold symmetry; by square tiles, which have fourfold symmetry; by triangular tiles, which have threefold symmetry; or by hexagonal tiles, which have sixfold symmetry. It cannot be covered completely by pentagonal tiles, which have five-fold symmetry.
But physicists now have discovered a class of solid materials that are neither glasses nor crystals; they have been named quasicrystals. Peter Bancel, a physicist then at the IBM Watson Research Center in Yorktown Heights, N.Y. (and now at the Center for the Studies of Chemical Metallurgy in Paris), who spoke at the symposium, described quasicrystals as "ordered atomic solids that possess long-range quasiperiodic positional order and a long-range non-crystallographic orientational order." In other words, they fill space completely without having the symmetry and order of classic crystals. Their atomic arrangements exhibit overall symmetries, such as fivefold, eightfold and tenfold symmetries, that have never before been observed. "The breakthrough raises the possibility of a whole class of materials with surprising electronic, vibrational, and thermal properties," said Paul J. Steinhardt of the University of Pennsylvania, a participant in the symposium and a leading figure in the story of quasicrystals.
The first quasicrystal was discovered in 1982 by Dany Shechtman, an Israeli physicist working at the National Bureau of Standards (now the National Institute of Standards and Technology) outside Washington, D.C. Schechtman was studying the properties of alloys formed by very rapid cooling. When he quenched a liquid mixture of aluminum and a small amount of manganese, he produced a solid composed of micron-sized grains with feathery arms. The unusual nature of the material became apparent when it was
viewed by electron diffraction, a procedure in which a beam of electrons is directed through a solid. The patterns resulting from the scattered, or diffracted, electrons in the material can be interpreted to indicate the atomic structure and symmetry of the solid.
The diffraction pattern of the aluminum-manganese alloy consisted of sharp spots arranged with fivefold symmetry; coincidence could thus be achieved by rotations of 72 degrees. The diffraction pattern indicated that the material consisted of a space-filling atomic structure with the symmetry of an icosahedron. (An icosahedron is a regular polyhedron with 20 identical triangular faces and six fivefold symmetry axes.) The observation of this icosahedrally symmetric pattern was startling precisely because an icosahedron, rotated about one of its axes, has the fivefold rotational symmetry that conventional crystallography held to be impossible for a crystal. At about the time that Shechtman made his discovery, Paul Steinhardt and his graduate student, Dov Levine, had been trying to understand the properties of glassy solids. Earlier, Steinhardt had been running computer simulations of rapid cooling of a liquid made of idealized spherical atoms. The readout showed a glass that included some clusters of symmetrical, icosahedral atomic structures. Steinhardt and Levine then proposed the theoretical possibility that quasicrystals with five-fold symmetry could exist. As the story developed, this theoretical model incorporated many of the features actually seen in the new alloys, and it has emerged as the leading explanation for them.
Steinhardt had started from a consideration of two-dimensional nonperiodic tilings. It was then known that a surface can be covered by a tiling with two or more tile types in which the tile order is quasiperiodic: the tiles repeat in a sequence made up of subsequences whose periods are in an irrational ratio. (An irrational number is one that cannot be expressed as the ratio of two integers. Pi is an irrational number, as is the square root of 2.) The overall sequence never quite repeats perfectly, but the surface is nonetheless covered completely.
The study of these nonperiodic two-dimensional tilings had been going on since the 1960s. In 1966, Robert Berger of Harvard University showed that a surface could be covered completely by a nonperiodic tiling. Berger described two solutions, one with more than 20,000 types of tile and one with 104 types.
The British mathematical physicist Roger Penrose of Oxford University ultimately found a solution with just two tile types. He showed how two types of four-sided tiles, both rhombi (a rhombus is a parallelogram with all sides of equal length), a fat and thin diamond, could cover a surface nonperiodically. The two fundamental shapes in a "Penrose tiling" are arranged in a pattern with fivefold orientational order.
Steinhardt and Levine extended Penrose's tiling to three dimensions, working out a way to fill space quasiperiodically with rhombohedra, solids that are the three-dimensional equivalents of Penrose's diamond-shaped tiles. The two researchers ran computer simulations of such nonperiodic structures, showing the diffraction pattern that they would produce. The computer-generated diffraction patterns proved to be nearly identical to that of Shechtman's aluminum-manganese alloy.
That work provided important theoretical underpinning for Shechtman, who initially did not have an easy time convincing the scientific community that his discovery was the real thing. The quasiperiodic order in his diffraction pattern did not extend indefinitely. In fact, it extended for only a few hundred angstroms. One explanation immediately invoked by doubters was that the material was not a truly quasiperiodic crystal, but merely a set of crystallites arranged in an icosahedrally symmetric cluster, a phenomenon called twinning.
A growing crystal sometimes starts reproducing itself in one direction, producing a twin of itself. Shechtman's observations could potentially be explained away by assuming that twinning had created twins, which would deceptively appear to have the observed symmetry. It was not until 1984 that convincing arguments and further observations showed that the twinning model failed. Shechtman published his results, and shortly afterward, Steinhardt and Levine published their theory. Shechtman's experimental work and the Steinhardt-Levine theory supported each other well, however, and condensed matter physicists began to explore the realm of quasicrystals.
There followed a major burst of activity that led to the discovery and description of many more quasicrystalline materials. More than 100 quasicrystal alloys have now been identified. Each is made up of at least two different atomic species, with aluminum being one component in most cases. Most of these quasicrystals display icosahedral symmetry, but other symmetries have also been observed.
The first known quasicrystals were metastable. They were formed by rapid quenching of a liquid alloy, and if they were heated, their atoms were rearranged to form conventional metallic crystal structures. Later, alloys with stable quasicrystalline structures were discovered. The first example was an alloy of aluminum, lithium, and copper. These stable quasicrystals are valuable for research. Unlike the unstable materials, they can be solidified slowly from the liquid state, so that larger perfect quasicrystals can be formed, some of them centimeters in size. These quasicrystals make possible the measurement of physical properties such as thermal and electronic behavior.
Some doubts based on experimental evidence still remained, however.
Electron diffraction patterns showed the sharp Bragg peaks that indicate crystalline order. Diffraction patterns made with x rays or neutrons, however, had some fuzzy peaks, which could be interpreted as showing that quasicrystals did not fill space completely over very long ranges and that gaps would be found sooner or later if quasicrystals were made large enough. Two developments, one experimental and one theoretical, settled the issue in favor of quasicrystals.
The experimental evidence came from a Japanese research team that reported an alloy of aluminum, copper, and iron that had better icosahedral symmetry over longer distances than anything previously seen when examined by all methods of crystallography.
''When we looked at the new material, we found that we were getting Bragg peaks that were sharp and limited to the resolution of our high-resolution x-ray scattering apparatus, and these Bragg peaks were indexing exactly to an icosahedral reciprocal lattice,'' Bancel said. "This then was immediate evidence that we really had a quasiperiodic crystal and that these other models that had been brought forth could not be used to describe the aluminum-copper-iron phases," he explained.
Only a year earlier, there appeared to have been convincing arguments that it was impossible to grow such a perfect quasicrystal: to cover a surface with Penrose tiles, the tiles must be placed carefully in the precise order needed to ensure complete coverage; a slight error produces an incomplete configuration, with gaps in the coverage. Because of the long-range nature of the quasiperiodic order, critics expressed doubts that atoms could come together to grow perfect quasicrystals. An atom would have to sense the positions of other atoms at arbitrarily large distances to maintain the quasiperiodic order, and that seemed highly unphysical, the critics said. What in nature occurs that allows the three-dimensional analogs of Penrose tiles to fit together in a space-filling array?
A key turning point came in 1987, when it was realized that the argument based on Penrose tilings was fallacious, Steinhardt said. "Most importantly, it turned out that by making slightly longer-range rules than Penrose's matching rules you could avoid making mistakes altogether," he said. The new rules constrain the way in which two tiles are allowed to join not only along an edge but also around a vertex.
Penrose's rules required the tiles to fit together in specific ways based on matching faces, or sides, of the diamonds. Those rules, however, did not guarantee complete coverage of a surface. Someone who followed the rules could find a gap in the coverage after laying only a few tiles. In 1987, George Y. Onoda, a physicist at the
IBM Thomas J. Watson Research Center, working with Steinhardt and with David P. DiVincenzo of IBM and Joshua E.S. Socolar of Harvard University, developed a set of rules that led to a complete tiling scheme requiring only short-range interactions.
The original Penrose rules were based on marking edges of the two kinds of diamonds with different arrows pointing in different directions. A complete tiling under those rules required adjacent tiles to have matching arrow types and directions along shared edges. The new rules added two requirements, based on matching both edges and vertices of the Penrose tiles. The rules defined a "forced vertex" as one that was not completely surrounded by other tiles and had an edge that could be matched in only one way by another tile. One rule said that such new "forced tiles" should be added to a forced vertex until no forced vertices were left. The second rule said that in the absence of forced vertices, a fat diamond should be added to any corner of the array.
In computer simulations, the new rules produced infinitely large Penrose tilings, removing most of the theoretical objections. "The results provide new insights as to how materials with only short-range atomic interactions can grow large, nearly perfect quasicrystal grains," reported Onoda et al. (1988, p. 2653).
It is plausible that nature follows such rules. When a conventional crystal is grown from a seed, some sites of the crystal seed are "stickier" than others, encouraging atoms or molecules to attach there rather than at "nonsticky" sites. The same is true of quasicrystal seeds, Steinhardt said, with the sticky sites determined by a three-dimensional version of the Onoda et al. growth rules.
Assume a seed is immersed in a liquid containing atoms that will join the seed. In the case of a crystal, atoms join the seed at a regular rate, building layer after layer to form a large crystal over time. In the case of a perfect quasicrystal growing according to the rules of Onoda et al., the structure grows quickly at first, as atoms attach at the highly sticky forced sites. Occasionally, however, the cluster grows out to a surface that has no forced sites. Then, after some time, an atom eventually attaches at the less sticky corner sites. A quasicrystal thus displays "a herky-jerky growth process, every now and then waiting for the low-probability sticking sites to fill in when there are no high-sticking probability sites left," Steinhardt said. At the symposium, he showed a film of a computer simulation of a seed cluster of quasiperiodic tiles, representing atoms, in a liquid where it was bombarded constantly by other tiles. The film showed a stop-and-start growth process, with waits for a low-probability sticky site to be filled when all high-probability sticky sites were occupied. "This
shows that if you allow me to choose the range of sticking probabilities, I can grow a quasicrystal to arbitrarily large finite size without making even one mistake," Steinhardt said. But the time needed to reach that size grows exponentially as the size increases, due to the less sticky sites, he added.
There is an important exception to that observation, however. One of the computer simulations run by Steinhardt started with a seed that had a specific defect, one that was discovered in the course of investigation. The defective seed looks like a ring of tiles with a hole in the center (Figure 10.2). The hole cannot be filled consistent with Penrose's rules, but the Penrose rules can be used to tile the outside of the ring and beyond. With this deliberately defective seed, growth never stops, because growth sites for the addition of atoms to the quasicrystal are always available. Steinhardt calls the defect that allows this quasicrystal growth a decapod because it has 10-fold symmetry.

Figure 10.2 Beginning from the ring of tiles shown in the center, a Penrose tiling can be rapidly grown by attaching tiles only at highly sticky "force" sites. The ring of tiles that form the seed has a defect in the middle–the center cannot be tiled according to the proper Penrose matching rules. However, the outside can be tiled and grown without ever reaching a dead surface. (Courtesy of P. Steinhardt.)
Quasicrystals have provided a field day for mathematicians, who are familiar with quasiperiodic functions, which are the sum of periodic functions with periods of irrational ratio. A well-known example of a quasiperiodic function that relates to the new field of quasicrystals is the Fibonacci sequence, named for a 12th-century Italian mathematician. The Fibonacci sequence begins with 1, and each subsequent value is derived by taking the sum of the two preceding numbers; the first terms of the sequence are thus 1, 1, 2, 3, 5, 8, 13, 21, 34. . . . The ratio of two consecutive numbers approaches an irrational ratio called the golden ratio.
If the Penrose tiles are marked with specially chosen line segments, the segments join across tile edges to form five sets of infinite, parallel lines that are pentagonally oriented (Figure 10.3). Some of
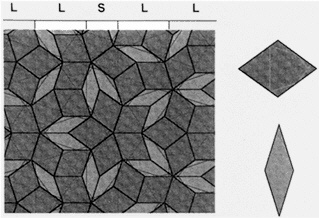
Figure 10.3 Penrose tiling showing the Ammann line decoration. The tiling consists of two types of tiles. Penrose discovered a set of matching rules that constrain the way two tiles can join together such that the only way to fill the plane consistent with those rules is by the Penrose tiling pattern above. Although there are many ways of choosing the tiles and matching rules, one way is to choose fat and skinny rhombus shapes and then to decorate each with the line segments shown on the right. (The lines are called Ammann lines because R. Ammann first suggested them.) The matching rule is that two tiles are allowed to join only if the segments join continuously across the interface. The segments join up to form a Fibonacci se quence of long and short intervals. (Courtesy of P. Steihardt.)
the spaces between lines are short and some are long. The long-range spacing of short and long lines in each set of Ammann lines forms a Fibonacci sequence in which the ratio of long to short spacings approaches the golden ratio.
"It is not periodic, but it is ordered and predictable," Steinhardt said. "You can have both ordering and nonperiodicity."
Quasicrystals may have practical applications. There are indications that they may be highly resistant to deformation, which would make them valuable for use in heavy-duty bearings. The task of exploring their physical, as well as their mathematical, properties is just beginning.
"We're in the same boat as physicists were with crystals a hundred years ago," Steinhardt said: "We have the structure of quasicrystals. Now we must predict their electronic and physical properties. This is a mathematical challenge, because the mathematics for crystals doesn't work for quasicrystals."
BIBLIOGRAPHY
Onoda, George Y., Paul J. Steinhardt, David P. DiVincenzo, and Joshua E.S. Socolar. 1988. Growing perfect quasicrystals. Physical Review Letters 60:2653–2656.
RECOMMENDED READING
Asimov, Isaac. 1988. Understanding Physics. Dorset Press Reprint Series. Hippocrene Books, New York.
DiVincenzo, D., and P.J. Steinhardt (eds.). 1991. Quasicrystals: The State of the Art. World Scientific Publishing Company, Singapore.
Steinhardt, P.J. 1990. Quasicrystals: A New Form of Matter. Endeavour 14(3):112–116.
Steinhardt, P.J., and S. Ostlund (eds.). 1987. The Physics of Quasicrystals. World Scientific Publishing Company, Singapore.