3
Dynamical Systems
When the Simple Is Complex: New Mathematical Approaches to Learning About the Universe
The science of dynamical systems, which studies systems that evolve over time according to specific rules, is leading to surprising discoveries that are changing our understanding of the world. The essential discovery has been that systems that evolve according to simple, deterministic laws can exhibit behavior so complex that it not only appears to be random, but also in a very real sense cannot be distinguished from random behavior.
Dynamical systems is actually an old field, because since ancient times we have tried to understand changes in the world around us; it remains a formidable task. Understanding systems that change linearly (if you double the displacement, you double the force), is not so difficult, and linear models are adequate for many practical tasks, such as building a bridge to support a given load without the bridge vibrating so hard that it shakes itself apart.
But most dynamical systems—including all the really interesting problems, from guidance of satellites and the turbulence of boiling water to the dynamics of Earth's atmosphere and the electrical activity of the brain—involve nonlinear processes and are far harder to understand.
Mathematician John Hubbard of Cornell University, lead speaker in the dynamical systems session of the Frontiers symposium, sees the classification into linear and nonlinear as "a bit like classifying
NOTE: Addison Greenwood collaborated on this chapter with Barbara A. Burke.
people into friends and strangers.'' Linear systems are friends, "occasionally quirky [but] essentially understandable." Nonlinear systems are strangers, presenting "quite a different problem. They are strange and mysterious, and there is no reliable technique for dealing with them" (Hubbard and West, 1991, p. 1).
In particular, many of these nonlinear systems have been found to exhibit a surprising mix of order and disorder. In the 1970s, mathematician James Yorke from the University of Maryland's Institute for Physical Science and Technology used the word chaos to describe the apparently random behavior of a certain class of nonlinear systems (York and Li, 1975). The word can be misleading: it refers not to a complete lack of order but to apparently random behavior with nonetheless decipherable pattern. But the colorful term captured the popular imagination, and today chaos is often used to refer to the entire nonlinear realm, where randomness and order commingle.
Now that scientists are sensitive to the existence of chaos, they see it everywhere, from strictly mathematical creations to the turbulence in a running brook and the irregular motions of celestial bodies. Nonrigorous but compelling evidence of chaotic behavior in a wide array of natural systems has been cited: among others, the waiting state of neuronal firing in the brain, epidemiologic patterns reflecting the spread of disease, the pulsations of certain stars, and the seasonal flux of animal populations. Chaotic behavior has even been cited in economics and the sociology of political behavior.
To what extent the recognition of chaos in such different fields will lead to scientific insights or real-world applications is an open question, but many believe it to be a fundamental tool for the emerging science of complexity.
Certainly the discovery of "chaos" in dynamical systems—and the development of mathematical tools for exploring it—is forcing physicists, engineers, chemists, and others studying nonlinear processes to rethink their approach. In the past, they tended to use linear approximations and hope for the best; over the past two or three decades they have come to see that this hope was misplaced. It is now understood that it is simply wrong to think that an approximate model of such a system will tell you more or less what is going on, or more or less what is about to happen: a slight change or perturbation in such a system may land you somewhere else entirely.
Such behavior strikes at the central premise of determinism, that given knowledge of the present state of a system, it is possible to project its past or future. In his presentation Hubbard described how the mathematics underlying dynamical systems relegates this deterministic view of the world to a limited domain, by destroying confi-
dence in the predictive value of Newton's laws of motion. The laws are not wrong, but they have less predictive power than scientists had assumed.
On a smaller scale, dynamical systems has caused some upheavals and soul-searching among mathematicians about how mathematics is done, taught, and communicated to the public at large. (All participants in the session were mathematicians: William Thurston from Princeton University, who organized it; Robert Devaney of Boston University; Hubbard; Steven Krantz of Washington University in St. Louis; and Curt McMullen from Princeton, currently at the University of California, Berkeley.)
Mathematicians laid the foundations for chaos and dynamical systems; their continuing involvement in such a highly visible field has raised questions about the use of computers as an experimental tool for mathematics and about whether there is a conflict between mathematicians' traditional dedication to rigor and proof, and enticing color pictures on the computer screen or in a coffee-table book.
"Traditionally mathematics tends to be a low-budget and low-tech and nonslick field," Thurston commented in introducing the session. In chaos, "you don't necessarily hear the theorems as much as see the pretty pictures," he continued, "and so, it is the subject of a lot of controversy among mathematicians.''
THE MATHEMATICS OF DYNAMICAL SYSTEMS
Historical Insights—Implications of Complexity
The science of dynamical systems really began with Newton, who first realized, in Hubbard's words, "that the forces are simpler than the motions." The motions of the planets are complex and individual; the forces behind those motions are simple and universally applicable. This realization, along with Newton's invention of differential equations and calculus, gave scientists a way to make sense of the world around them. But they often had to resort to simplifications, because the real-world problems studied were so complex, and solving the equations was so difficult—particularly in the days before computers!
One problem that interested many scientists and mathematicians—and still does today—is the famous "three-body" problem. The effect of two orbiting bodies on each other can be calculated precisely. But what happens when a third body is considered? How does this perturbation affect the system?
In the late 1880s the king of Sweden offered a prize for solving
this problem, which was awarded to French mathematician and physicist Henri Poincaré (1854–1912), a brilliant scientist and graceful writer with an instinct for delving beneath the surface of scientific problems.
In fact, Poincaré did not solve the three-body problem, and some of his ideas were later found to be wrong. But in grappling with it, he conceived many major insights into dynamical systems. Among these was the crucial realization that the three-body problem was in an essential way unsolvable, that it was far more complex and tangled than anyone had imagined. He also recognized the fruitfulness of studying complex dynamics qualitatively, using geometry, not just formulas.
The significance of Poincaré's ideas was not fully appreciated at the time, and it is said that even Poincaré himself came to doubt their implications. But a number of mathematicians followed up the many leads he developed. In France immediately after World War I, Pierre Fatou (1878–1929) and Gaston Julia (1893–1978) discovered and explored what is now known as Julia sets, seen today as characteristic examples of chaotic behavior. In the United States George Birkhoff developed many fundamental techniques; in 1913 he gave the first correct proof of one of Poincaré's major conjectures.
Although dynamical systems was not in the mainstream of mathematical research in the United States until relatively recently, work continued in the Soviet Union. A major step was taken in the 1950s, by the Russian Andrei Kolmogorov, followed by his compatriot Vladimir Arnold and German mathematician Jürgen Moser, who proved what is known as the KAM (Kolmogorov-Arnold-Moser) theorem.
They found that systems of bodies orbiting in space are often astonishingly stable and ordered. In a book on the topic, Moser wrote that Poincaré and Birkhoff had already found that there are "solutions which do not experience collisions and do not escape," even given infinite time (Moser, 1973, p. 4). "But are these solutions exceptional?" he asked. The KAM theorem says that they are not.
In answering that question, the subtle and complicated KAM theorem has a great deal to say about when such systems are stable and when they are not. Roughly, when the periods, or years, of two bodies orbiting a sun can be expressed as a simple ratio of whole numbers, such as 2/5 or 3—or by a number close to such a number—then they will be potentially unstable: resonance can upset the balance of gravitational forces. When the periods cannot be expressed as such a ratio, the system will be stable.
This is far from the whole story, however. The periods of Saturn and Jupiter have the ratio 2/5; those of Uranus and Neptune have a
ratio close to 2. (In fact, some researchers in the 19th century, suspecting that rationality was associated with instability, speculated that a slight change in the distance between Saturn and Jupiter would be enough to send Saturn shooting out of our solar system.)
But the KAM theorem, combined with Birkhoff's earlier work, showed that there are little windows of stability within the ''unstable zones" associated with rationality; such a window of stability could account for the planets' apparent stability. (The theorem also answers questions about the orbit of Saturn's moon Hyperion, the gaps in Saturn's rings, and the distribution of asteroids; it is used extensively to understand the stability of particles in accelerators.)
In the years following the KAM theorem the emphasis in dynamical systems was on stability, for example in the work in the 1960s by topologist Stephen Smale and his group at the University of California, Berkeley. But more and more, researchers in the field have come to focus on instabilities as the key to understanding dynamical systems, and hence the world around us.
A key role in this shift was played by the computer, which has shown mathematicians how intermingled order and disorder are: systems assumed to be stable may actually be unstable, and apparently chaotic systems may have their roots in simple rules. Perhaps the first to see evidence of this, thanks to a computer, was not a mathematician but a meteorologist, Edward Lorenz, in 1961 (Lorenz, 1963). The story as told by James Gleick is that Lorenz was modeling Earth's atmosphere, using differential equations to estimate the impact of changes in temperature, wind, air pressure, and the like. One day he took what he thought was a harmless shortcut: he repeated a particular sequence but started halfway through, typing in the midpoint output from the previous printout—but only to the three decimal places displayed on his printout, not the six decimals calculated by the program. He then went for a cup of coffee and returned to find a totally new and dramatically altered outcome. The small change in initial conditions—figures to three decimal places, not six—produced an entirely different answer.
Sensitivity to Initial Conditions
Sensitivity to initial conditions is what chaos is all about: a chaotic system is one that is sensitive to initial conditions. In his talk McMullen described a mathematical example, "the simplest dynamical system in the quadratic family that one can study," iteration of the polynomial x2 + c when c = 0.
To iterate a polynomial or other function, one starts with a num-
ber, or seed, x0, and performs the operation. The result (called x1) is used as the new input as the operation is repeated. The new result (called x2) is used as the input for the next operation, and so on. Each time the output becomes the next input. In mathematical terminology,
x1 = f (x0), x2 = f (x1 ), x3 = f (x2), . . .
In the case of x2 + c when c = 0 (in others words, x2), the first operation produces x02, the second produces (x02)2, and so on. For x = 1, the procedure always results in 1, since 12 equals 1. So 1 is called a fixed point, which does not move under iteration. Similarly,-1 jumps to 1 when squared and then stays there.
What about numbers between-1 and 1? Successive iterations of any number in that range will move toward 0, called an "attracting fixed point." It does not matter where one begins; successive iterations of any number in that range will follow the same general path as its nearby neighbors. These "orbits" are defined as stable; it does not matter if the initial input is changed slightly. Similarly, common sense suggests, and a calculator will confirm, that any number outside the range-1 < x < 1 will iterate to infinity.
The situation is very different for numbers clustered around 1 itself. For example, the number 0.9999999 goes to 0 under iteration, whereas the number 1.0000001 goes to infinity. One can get arbitrarily close to 1; two numbers, almost equal, one infinitesimally smaller than 1 and the other infinitesimally larger, have completely different destinies under iteration.
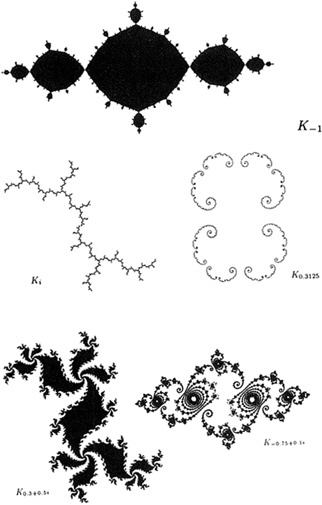
If one now studies the iteration of x2 + c, this time allowing x and c to be complex numbers, one will obtain the Julia set (Figure 3.1), discovered by Fatou and Julia in the early 20th century, and first explored with computers by Hubbard in the 1970s (Box 3.1). (To emphasize that we are now discussing complex numbers, we will write z2 + c, z being standard notation for complex numbers.)
"One way to think of the Julia set is as the boundary between those values of z that iterate to infinity, and those that do not," said McMullen. The Julia set for the simple quadratic polynomial z2 + c when c = 0, is the unit circle, the circle with radius 1: values of z outside the circle iterate to infinity; values inside go to 0.
Thus points arbitrarily close to each other on opposite sides of the unit circle will have, McMullen said, "very different future trajectories." In a sense, the Julia set is a kind of continental divide (Box 3.2).
Clearly, to extrapolate to real-world systems, it behooves scientists to be aware of such possible instabilities. If in modeling a sys-
|
BOX 3.1 COMPLEX NUMBERS To define the Julia set of the polynomial x2 + c (the Julia set being the boundary between those values of x that iterate to infinity under the polynomial, and those that do not), one must allow x to be a complex number. Ordinary, real numbers can be thought of as points on a number line; as one moves further to the right on the line, the numbers get bigger. A complex number can be thought of as a point in the plane, specified by two numbers, one to say how far left or right the complex number is, the other to say how far up or down it is. Thus we can write a complex number z as z = x + iy, where x and y are real numbers, and i is an imaginary number, the square root of-1. Traditionally the horizontal axis represents the real numbers, and so the number x tells how far right or left z is. The vertical axis represents imaginary numbers, so the number y tells how far up or down z is. To plot the complex number 2 + 3i, for example, one would move two to the right (along the real axis) and up three. (Of course, real numbers are also complex numbers: the real number 2 is the complex number 2 + 0i.) Using this notation and the fact that i2 =-1, complex numbers can be added, subtracted, multiplied, and so on. But the easiest way to visualize multiplying complex numbers is to use a different notation. A complex number can be specified by its radius (its distance from the origin) and its polar angle (the angle a line from the point to the origin forms with the horizontal axis.) The radius and angle are known as polar coordinates. Squaring a complex number squares the radius and doubles the angle. To return now to the polynomial z2 + c when c = 0, we can see that if we take any point on the unit circle as the beginning value of z, squaring it repeatedly will cause it to jump around the circle (the radius, 1, will remain 1 on squaring, and the angle will keep doubling). Any point outside the unit circle has radius greater than 1, and repeatedly squaring it will cause it to go to infinity. Thus the Julia set for z2 + c when c = 0 is the unit circle. |
|
BOX 3.2 THE FEIGENBAUM-CVITANOVIC CASCADE Another viewpoint on chaos is given by the Feigenbaum-Cvitanovic cascade of period doublings, which, in McMullen's words, "in some sense heralds the onset of chaos." It shows what happens to certain points inside Julia sets. While by definition points outside the Julia set always go to infinity on iteration, points inside may have very complicated trajectories. In the simplest case of z2 + c, when c = 0, the points inside all go to 0, but nothing so simple is true for all Julia sets. Figure 3.2 shows what happens in the long run as you iterate x2 + c for-2 < c < 0.25 and x real. To draw it, you iterate each function f(x) = x2 + c, starting at x = 0. The first iterate is 02 + c = c, so that on iteration c is used for the next x value, giving c2 + c, which is used for the next x value, and so on. For each value of c from 0.25 to-2 perform, say, 100 iterations without marking anything, and then compute another 50 or so, this time marking the value you get after each iteration (using one axis to represent values of x and the other for values of c). The picture that emerges is the cascade of period doublings. First, a single line descends in a curve, then it splits into two curves, then—sooner this time—those two curves each split into two more, and—sooner yet—these four split into eight, and so on. Finally, at about c =-1.41 you have a chaotic mess of points (with little windows of order that look just like miniature cascades). What does the picture represent? The single line at the top is formed of points that are attracting fixed points for the polynomials x2 + c: one such fixed point for each value of c. Where the line splits, the values produced by iteration bounce between two points (called an attractive cycle of period two); where they split again they bounce between four points (an attractive cycle of period four), and so on. Cascades of period doublings have been observed in nature, said McMullen. Moreover, a remarkable feature is that the pace at which the period doublings occur, first slowly, then picking up speed, as they come closer and closer together, can be represented by a number that is the same whatever system one is studying. "This is a universal constant of nature," McMullen said. "It is a phenomenon that may have remarkable implications for the physical sciences." |
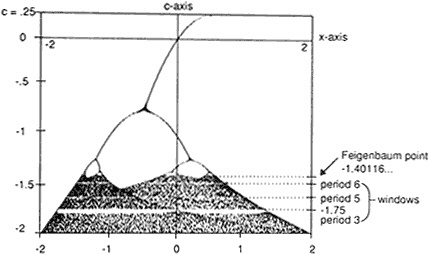
Figure 3.2 The cascade of period doublings, heralding the onset of chaos. It is produced by iterating x2 + c, for each value of c. The single line at the top is formed of points that are attracting fixed points. Where the line splits, the values produced by iteration bounce between two points; where they split again they bounce between four points, and so on. (Reprinted with permission from Hubbard and West, 1991. Copyright © 1991 by Springer-Verlag New York Inc.)
tem one is in the equivalent of the stable range, then approximate models work. If one is, so to speak, close to the Julia set, then a small change in initial conditions, or a small error in measurement, can change the output totally (Figure 3.2).
CHAOS, DETERMINISM, AND INFORMATION
Instabilities and Real-world Systems
In his talk, "Chaos, Determinism, and Information," Hubbard argued that this is a very real concern whose ramifications for science and philosophy have not been fully appreciated. He began by asking, "Given the limits of scientific knowledge about a dynamical system in its present state, can we predict its behavior precisely?" The answer, he said, is no, because "instabilities in such systems amplify the inevitable errors."
Discussing ideas he developed along with his French colleague Adrien Douady of the University of Paris-XI (a joint article has been
published in the Encyclopedia Universalis), Hubbard asked participants whether they thought it conceivable that a butterfly fluttering its wings someplace in Japan might in an essential way influence the weather in Ithaca, New York, a few weeks later. "Most people I approach with this question tell me, 'Obviously it is not true,'" Hubbard explained, "but I am going to try to make a serious case that you can't dismiss the reality of the butterfly effect so lightly, that it has to be taken seriously."
Hubbard began by asking his audience to consider a more easily studied system, a pencil stood on its point. Imagine, he said, a pencil balanced as perfectly as possible—to within Planck's constant, so that only atomic fluctuations disturb its balance. Within a bit more than a tenth of a second the initial disturbance will have doubled, and within about 4 seconds—25 "doubling times"—it will be magnified so greatly that the pencil will fall over.
As it turns out, he continued, the ratio of the mass of a butterfly to the mass of the atmosphere is about the same as the ratio of the mass of a single atom to the mass of a pencil. (It is this calculation, Hubbard added, that for the first time gave him "an idea of what Planck's constant really meant. . . . to determine the position of your pencil to within Planck's constant is like determining the state of the atmosphere to within the flutterings of one butterfly.")
The next question is, how long does it take for the impact of one butterfly on the atmosphere to be doubled?
In trying to understand what the doubling time should be for equations determining the weather, I took the best mathematical models that I could find, at the Institute for Atmospheric Studies in Paris. In their model, the doubling time is approximately 3 days. Thus, roughly speaking, if you have completely lost control of your system after 25 doubling times, then it is very realistic to think that the fluttering of the wings of a butterfly can have an absolutely determining effect on the weather 75 days later.
"This is not the kind of thing that one can prove to a mathematician's satisfaction," he added. "But," he continued, "it is not something that can just be dismissed out of hand." And if, as he believes, it is correct, clearly "any hope of long-term weather prediction is absurd."
From the weather Hubbard proceeded to a larger question. Classical science, since Galileo, Newton, and Laplace, has been predicated on deterministic laws, which can be used to predict the future or deduce the past. This notion of determinism, however, appears incompatible with the idea of free will. The contradiction is "deeply disturbing," Hubbard said. "Wars were fought over that issue!"
The lesson of a mathematical theorem known as the shadowing lemma is that, at least for a certain class of dynamical systems and possibly for all chaotic systems, it is impossible to determine who is right, a believer in free will or a believer in deterministic, materialistic laws.
In such systems, known as hyperbolic dynamical systems, uncertainties double at a steady rate until the cumulative unknowns destroy all specific information about the system. "Any time you have a system that doubles uncertainties, the shadowing lemma of mathematics applies," Hubbard said. "It says that you cannot tell whether a given system is deterministic or randomly perturbed at a particular scale, if you can only observe it at that scale."
The simplest example of such a system, he said, is angle doubling. Start with a circle with its center at 0, and take a point on that circle, measuring the angle that the radius to that point forms with the x-axis. Now double the angle, double it again and again and again. You know the starting point exactly and you know the rules, and so of course you can predict where you will be after, say, 50 doublings.
But now imagine that each time you double the angle you jiggle it "by some unmeasurably small amount," such as 10 to 15 (chosen because that is the limit of accuracy for most computers: they cut off numbers after 15 decimal digits). Now "the system has become completely random in the sense that there is nothing you could measure at time zero that still gives you any information whatsoever after 50 moves."
What is unsettling—and this is the message of the shadowing lemma—is that if you were presented with an arbitrarily long list of figures (each to 15 decimals) produced by an angle-doubling system, you could not tell whether you were looking at a randomly perturbed system or an unperturbed (deterministic) one. The data would be consistent with both explanations, because the shadowing lemma tells us that (again, assuming you can measure the angles only to within 10 to 15 degrees) there always is a starting point that, under an unperturbed system, will produce the same data as that produced by a randomly perturbed system. Of course it will not be the same starting point, but since you do not know the starting point, you will not be able to choose between starting point a and a deterministic system, and some unknowable starting point b and a random one.
"That there is no way of telling one from the other is very puzzling to me, and moreover there is a wide class of dynamical systems to which this shadowing lemma applies," Hubbard said. Scientists modeling such physical systems may choose between the determinis-
tic differential equation approach, or a probabilistic model; ''the facts are consistent with either approach."
"It is something like the Heisenberg-Schrödinger pictures of the universe" in quantum mechanics, he added. "In the Heisenberg picture you think that the situation of the universe is given for all time. . . . You are just discovering more and more about it as time goes on. The Schrödinger picture is that the world is really moving and changing, and you are part of the world changing."
"It has long been known that in quantum mechanics these attitudes are equivalent: they predict exactly the same results for any experiment. Now, with the shadowing lemma, we find this same conclusion in chaotic systems," Hubbard summed up.
Implications for Biology?
If the "butterfly effect" is a striking symbol of our inability to predict the workings of the universe, Hubbard believes that another famous symbol of dynamical systems, the Mandelbrot set, suggests a way of thinking about two complex and vital questions: how a human being develops from a fertilized egg, and how evolution works.
He used a video to demonstrate the set, named after Benoit Mandelbrot, who recognized the importance of the property known as self-similarity in the study of natural objects, founding the field of fractal geometry (Box 3.3).
The largest view of the Mandelbrot set looks like a symmetric beetle or gingerbread man, with nodes or balls attached (Figure 3.3); looked at more closely, these balls or nodes turn out to be miniature copies of the "parent" Mandelbrot set, each in a different and complex setting (Figure 3.4). In between these nodes, a stunning array of geometrical shapes emerges: beautiful, sweeping, intricate curves and arcs and swirls and scrolls and curlicues, shapes that evoke marching elephants, prancing seahorses, slithering insects, and coiled snakes, lightning flashes and showers of stars and fireworks, all emanating from the depths of the screen.
For Hubbard, what is astounding about the Mandelbrot set is that its infinite complexity is set in motion by such a simple formula; the computer program to create the Mandelbrot set is only about 10 lines long. "If someone had come forth 40 years ago with a portfolio of a few hundred of these pictures and had just handed them out to the scientific community, what would have happened?" he asked. "They would presumably have been classified according to curlicues and this and that sticking out and so forth. No one would ever have dreamed that there was a 10-line program that created all of them."
|
BOX 3.3 JULIA SETS AND THE MANDELBROT SET The Julia set and the Mandelbrot set, key mathematical objects of dynamical systems, are intimately related. The Julia set is a way to describe the sensitivity of a mathematical function to initial conditions: to show where it is chaotic. The Mandelbrot set summarizes the information of a great many Julia sets. For there is not just one Julia set. Each quadratic polynomial (z2 + c, c being a constant), has its own Julia set—one for each value of c. The same is true for cubic polynomials, sines, exponentials, and other functions. All Julia sets are in the complex plane. As we have seen, the Julia set for the simple quadratic polynomial z2 + c, c = 0, is the unit circle: values of z outside the circle go to infinity on iteration; values inside go to 0. But let c be some small number, and the Julia set becomes a fractal, McMullen said. In this case it is "a simple closed curve with dimension greater than 1." The curve is crinkly, "and this crinkliness persists at every scale." That is, if you were to magnify it, you would find that it was just as crinkly as before; it is self-similar. Other Julia sets—also fractals—form more intricate shapes yet, from swirls to clusters of tiny birds to crinkly lines suggestive of ice breaking on a pond. The Mandelbrot set—some mathematicians prefer the term quadratic bifurcation locus—summarizes all the Julia sets for quadratic polynomials. Julia sets can be roughly divided into those that are connected and those that are not. (A set is disconnected if it is possible to divide it into two or more parts by drawing lines around the different parts.) The Mandelbrot set is formed of all the values of c for which the corresponding quadratic Julia set is connected. |
Thus the Mandelbrot set is a prime example of a data-compressible system, that is, one created by a program containing far less information than it exhibits itself. It is, although complex, far from random, a random system being one that cannot be specified by a computer program or algorithm that contains less information than the system itself.
Hubbard suggested that the concept of data compressibility (sometimes known as low information density), a notion borrowed from computer science, could be useful in biology. "It is, I am almost sure, one of the really fundamental notions that we are all going to have to come to terms with."
"The real shock comes when you realize that biological objects
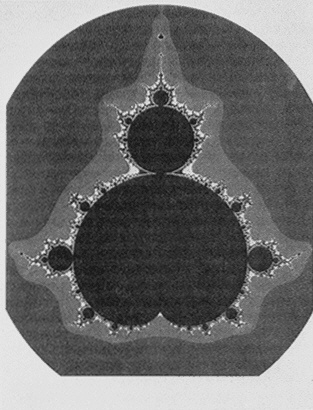
Figure 3.3 Mandelbrot set. Using computers as an experimental tool, mathematicians have found that simple rules can lead to surprisingly complicated structures. The computer program that creates the Mandelbrot set is only about 10 lines long, but the set is infinitely complex: the greater the magnification, the more detail one sees. (Courtesy of J.H. Hubbard.)
are specified by DNA, and that DNA is unbelievably short,'' he said. The "computer program" that creates a human being—the DNA in the genome—contains about 4 billion bits (units of information). This may sound big, but it produces far more than 100 trillion cells, and "each cell itself is not a simple thing." This suggests that an adult human being is far more data compressible—by a factor of 10,000, perhaps 100,000—than the Mandelbrot set, which itself is extraordinarily compressible.

Figure 3.4 Blowup of the Mandelbrot set. A small Mandelbrot set appears deep with the Mandelbrot set. (Courtesy of J.H. Hubbard.)
Hubbard sees the relatively tiny amount of information in the human gene as "a marvelous message of hope. . . . A large part of why I did not become a biologist was precisely because I felt that although clearly it was the most interesting subject in the world, there was almost no hope of ever understanding anything in any adequate sense. Now it seems at least feasible that we could understand it."
It also makes evolution more credible, he said: "Instead of thinking about the elaboration of the eye, you can think in terms of getting one bit every 10 years. Well, one bit every 10 years doesn't sound so unreasonable, whereas evolving an eye, that doesn't really sound possible."
THE ROLE OF COMPUTERS AND COMPUTER GRAPHICS
Since chaotic systems abound, why did scientists not see them before? A simple but not misleading answer is that they needed the
right lens through which to examine the data. Hubbard recounted a conversation he had with Lars Ahlfors, the first recipient of the Fields Medal, the mathematical equivalent of the Nobel Prize. "Ahlfors is a great mathematician; no one could possibly doubt his stature. In fact, he proved many of the fundamental theorems that go into the subject. He tells me," Hubbard said,
that as a young man, just when the memoirs of Fatou and Julia were being published, he was made to read them as—of course—you had to when you were a young man studying mathematics. That was what was going on. And further, in his opinion, at that moment in history and in his education they represented (to put it as he did) the pits of complex analysis. I am quoting exactly. He admits that he never understood what it was that they were trying to talk about until he saw the pictures that Mandelbrot and I were showing him around 1980. So, that is my answer to the question of the significance of the computer to mathematics. You cannot communicate the subject—even to the highest-level mathematician—without the pictures.
McMullen expressed a similar view: "The computer is a fantastic vehicle for transforming mathematical reality, for revealing something that was hitherto just suspended within the consciousness of a single person. I find it indispensable. I think many mathematicians do today."
Moreover, computer pictures of chaos and dynamical systems have succeeded—perhaps for the first time since Newton's ideas were argued in the salons of Paris—in interesting the public in mathematics. The pictures have been featured prominently in probably every major science magazine in the country and appear on tote bags, postcards, and teeshirts. Mandelbrot's 1975 book, Les objets fractals: forme, hasard et dimension (an English translation, Fractals: Form, Chance and Dimension, was published in 1977), which maintained that a great many shapes and forms in the world are self-similar, repeating their pattern at ever-diminishing scales, attracted widespread attention, and James Gleick's Chaos: Making a New Science was a surprise best-seller.
To some extent this attention is very welcome. Mathematicians have long deplored the public's unawareness that mathematics is an active field. Indeed, according to Krantz, the most likely explanation why no Nobel Prize exists for mathematics is not the well-known story that the mathematician Mittag-Leffler had an affair with Nobel's wife (Nobel had no wife) but simply that "Nobel was completely unaware that mathematicians exist or even if they exist that they do anything."
The mathematicians at the Frontiers symposium have tried to combat this ignorance. Hubbard, who believes strongly that research and education are inseparable, teaches dynamical systems to undergraduates at Cornell University and has written a textbook that uses computer programs to teach differential equations. Devaney has written not only a college-level text on dynamical systems, but also a much more accessible version, designed to entice high school students into learning about dynamical systems with personal computers. Thurst-on has developed a "math for poets" course at Princeton—"Geometry and the Imagination"—and following the symposium taught it to bright high school students in Minnesota.
"The fact that this mathematics is on the one hand so beautiful and on the other hand so accessible means that it is a tremendous boon for those of us in mathematics," Devaney said. "All of you in the natural sciences, the atmospheric sciences, astrophysicists, you all have these incredibly beautiful pictures that you can show your students. We in mathematics only had the quadratic formula and the Pythagorean theorem. . . . The big application of all of this big revolution will be in mathematics education, and God knows we can use it."
One of the scientists in the audience questioned this use of pictures, arguing that "the problem with science is not exciting people about science. . . . [It] is providing access. The reason that people are not interested in science is because they don't do science, and that is what has to be done, not showing pretty pictures." Devaney responded:
You say that you have worked with elementary school students, and there is no need to excite them about science. That is probably true. That indicates that—as natural scientists—you have won the battle. In mathematics, however, this is far from the case. I run projects for high school students and high school teachers, and they are not excited about mathematics. They know nothing about the mathematical enterprise. They continually say to us, "What can you do with mathematics but teach?" There is no awareness of the mathematical enterprise or even of what a mathematician does.
But the popularity of the chaotic dynamical systems field, accompanied by what mathematicians at the session termed "hype," has also led to concerns and uneasiness. "I think chaos as a new science is given to a tremendous amount of exaggeration and overstatement," Devaney said. "People who make statements suggesting that chaos is the third great revolution in 20th-century science, following quantum mechanics and relativity, are quite easy targets for a comeback—
'Yes, I see. Something like the three great developments in 20th-century engineering: namely, the computer, the airplane, and the poptop aluminum can.'"
Some mathematicians, Krantz among them, feel that the public visibility of chaos is skewing funding decisions, diverting money from equally important, but less visible, mathematics. They also fear that standards of rigor and proof may be compromised. After all, the heart of mathematics is proof: theorems, not theories.
In his talk, Hubbard had related a telling conversation with physicist Mitchell Feigenbaum: "Feigenbaum told me that as far as he was concerned, when he thought he really understood how things were working, he was done. What really struck me is that as far as I was concerned, when I thought I really understood what was going on, that was where my work started. I mean once I really think I understand it, then I can sit down and try to prove it."
Part of the difficulty, Devaney suggested, is the very availability of the computer as an experimental tool, with which mathematicians can play, varying parameters and seeing what happens.
"With the computer now—finally—mathematics has its own essentially experimental component," Devaney told fellow scientists at the symposium. "You in biology and physics have had that for years and have had to wrestle with the questions of method and the like that arise. We mathematicians have never had the experimental component until the 1980s, and that is causing a few adjustment problems."
Krantz—who does not himself work in dynamical systems—has served as something of a lightning rod for this controversy following publication in The Mathematical Intelligencer of his critique of fractal geometry (Krantz, 1989). (He originally wrote the article as a review of two books on fractals for the Bulletin of the American Mathematical Society . The book reviews editor first accepted, and then rejected, the review. The article in The Mathematical Intelligencer was followed by a rebuttal by Mandelbrot.)
In that article, he said that the work of Douady, Hubbard, and other researchers on dynamical systems and iterative processes "is some of the very best mathematics being done today. But these mathematicians don't study fractals—they prove beautiful theorems." In contrast, he said, "fractal geometry has not solved any problems. It is not even clear that it has created any new ones."
At the symposium, Krantz said that mathematicians "have never had this kind of attention before," and questioned "if this is the kind of attention we want."
"It seems to me that mathematical method, scientific method, is
something that has been hard won over a period of many hundreds, indeed thousands, of years. In mathematics, the only way that you know something is absolutely true is by coming up with a proof. In science, it seems to me the only way you know something is true is by the standard experimental method. You first become educated. You develop hypotheses. You very carefully design an experiment. You perform the experiment, and you analyze it and you try to draw some conclusions."
"Now, I believe absolutely in approximation, but successful approximation should have an error estimate and should lead to some conclusion. One does not typically see this in fractal geometry. Mandelbrot himself says that typically what one does is one draws pictures."
Indeed, Devaney remarked, "many of the lectures one hears are just a bunch of pretty pictures without the mathematical content. In my view, that is tremendously unfortunate because there is a tremendous amount of beautiful mathematics. Beyond that there is a tremendous amount of accessible mathematics."
Yet these concerns seem relatively minor compared to the insights that have been achieved. It may well distress mathematicians that claims for chaos have been exaggerated, that the field has inspired some less than rigorous work, and that the public may marvel at the superficial beauty of the pictures while ignoring the more profound, intrinsic beauty of their mathematical meaning, or the beauty of other, less easily illustrated, mathematics.
But this does not detract from the accomplishments of the field. The fundamental realization that nonlinear processes are sensitive to initial conditions—that one uses linear approximations at one's peril—has enormous ramifications for all of science. In providing that insight, and the tools to explore it further, dynamical systems is also helping to return mathematics to its historical position, which mathematician Morris Kline has described as "man's finest creation for the investigation of nature" (Kline, 1959, p. vii).
Historically, there was no clear division between physics and mathematics. "In every department of physical science there is only so much science . . . as there is mathematics," wrote Immanuel Kant (Kline, 1959, p. vii), and the great mathematicians of the past, such as Newton, Gauss, and Euler, frequently worked on real problems, celestial mechanics being a prime example. But early in this century the subjects diverged. At one extreme, some mathematicians affected a fastidious aversion to getting their hands dirty with real problems. Mathematicians "may be justified in rejoicing that there is one science at any rate, and that their own, whose very remoteness from
ordinary human activities should keep it gentle and clean," wrote G.H. Hardy (1877–1947) in A Mathematician's Apology (Hardy, 1967, p. 121). For their part, physicists often assumed that once they had learned some rough-and-dirty techniques for using such mathematics as calculus and differential equations, mathematics had nothing further to teach them.
Over the past couple of decades, work in dynamical systems (and in other fields, such as gauge theory and string theory) has resulted in a rapprochement between science and mathematics and has blurred the once-clear line between pure and applied mathematics. Scientists are seeing that mathematics is not just a dead language useful in scientific computation: it is a tool for thinking and learning about the world. Mathematicians are seeing that it is exciting, not demeaning, when the abstract creations of their imagination turn out to be relevant to understanding the real world. They both stand to gain, as do we all.
BIBLOGRAPHY
Hardy, G.H. 1967. A Mathematician's Apology. Cambridge University Press, Cambridge.
Hubbard, John H., and Beverly H. West. 1991. Differential Equations: A Dynamical Systems Approach. Part I: Ordinary Differential Equations. Springer-Verlag, New York.
Kline, Morris. 1959. Mathematics and the Physical World. Thomas Y. Crowell, New York.
Krantz, Steven. 1989. The Mathematical Intelligencer 11(4):12–16.
Lorenz, E.N. 1963. Deterministic non-periodic flows. Journal of Atmospheric Science 20:130–141.
Moser, Jürgen. 1973. Stable and Random Motions in Dynamical Systems. Princeton University Press, Princeton, N.J.