9
The Management of Human Resources
In previous chapters we have described JPM Project results showing that job performance can be measured and that it can be predicted, with varying degrees of success, by entrance tests of cognitive ability. The second major goal of the JPM Project is to develop models for setting military enlistment standards (the minimum test scores required for entry into military service) based on the information now available about the job performance that can be anticipated for given ASVAB scores.1 Some might think that the validity correlations of tests with performance reported in Chapter 8 show that the link between entrance standards and job performance has been established, and so the work is done. But the management problem does not stop with a correlation, because higher-aptitude personnel cost more to recruit. There is a tension between the Services ' desire to recruit the most highly qualified men and women possible and the equally felt need of Congress to contain costs by holding down recruiting budgets. This is a quandary familiar to private-sector employers who must balance the productivity gains from hiring highly skilled workers against the costs of positioning themselves at the high end of the labor market.
The second phase of the JPM Project is concentrating on the development of analytical tools that will illuminate for policy makers the effects of
|
1 |
See Green et al. (1988) for a lengthier discussion by committee members, military researchers, and consultants of the issues involved in providing an empirical basis for military enlistment standards. |
alternative decisions on performance and costs. There is no single discipline that has the analytical tools in hand to answer the questions of quality and costs fully. In personnel work, the traditional approach has been to rank applicants in order of their predicted performance. Since higher test scores indicate a probability of better performance on the job, the simple answer offered by psychological measurement is that more is better. From this point of view, performance is the essential consideration, and the costs of increased performance are not calculated.
Management specialists tend to use the econometric approach to questions of selection standards. In the military context, some interesting models for setting enlistment standards were developed in the 1970s and 1980s. These models were designed to locate the most cost-effective cutoff score; they do not help answer the question of how much performance is sufficient in some absolute sense, but rather set enlistment standards in order to minimize personnel costs per unit of productivity. From this point of view, cost is the essential consideration.
Neither the psychometric nor the econometric approach alone is satisfactory. If the military is to fulfill its mission to provide for the national defense, enlistment standards must be set at a level that will produce a first-term corps that as a group can master all of the enlisted jobs and that can also provide the next generation of leaders. Hence, in the committee's view, costs should not be allowed to drive the analysis. At the same time, a simple more-is-better policy is untenable, particularly in these times of fiscal retrenchment. Military and civilian policy makers need analytical tools that will provide a deeper understanding of the distribution of recruit quality needed to maintain adequate levels of job performance. And the policy process would benefit from better modeling of the trade-offs between costs and performance.
Phase II of the JPM Project provides an interesting opportunity to apply a fairly rich body of job performance data to the development of techniques for modeling the policy maker's need to balance performance requirements and personnel costs. Although the research is still under way and will have to be reported elsewhere, we take the opportunity here to discuss the general outlines of the problem of balancing quality and costs as it relates to setting military enlistment standards —and in the process to review some of the earlier work that provides the intellectual heritage of the Phase II efforts.
Although it draws on the JPM Project, the discussion is not limited by the design decisions made in this instance. The chapter examines, for example, how a competency approach to performance measurement could contribute important information to the setting of enlistment standards even though the JPM performance data cannot be readily interpreted along a competency scale. And because of the status of Phase II, the chapter necessarily raises more questions than it has answers to report.
The chapter begins with a brief review of personnel selection and placement procedures in the U.S. Armed Services including a discussion of current military job allocation procedures and the role of job performance information in implementing those procedures. Next it examines the notion of competency or job mastery and how this approach to measuring job performance might be pertinent to modeling cost/performance trade-offs. The discussion then focuses on existing applications of cost-benefit analysis to questions of employee selection and allocation. The last major section of this chapter addresses the problems associated with setting standards for several jobs at the same time—in the discussion, we examine the competition among jobs for the available talent and review several approaches for comparing the utility of performance across jobs.
PERSONNEL ACCESSION AND JOB ALLOCATION
Although the numbers will decline substantially in this period of military downsizing, during the 1980s the Services selected approximately 300,000 persons annually from over 1 million applicants across the country. The enlistment standards that new recruits must meet to gain entry into the Services, and to specific jobs within a Service, have evolved over many years. They are based on accumulated experience in employing and training young people, many of whom are entering their first full-time job. As described earlier, the Services base their first enlistment decision on the Armed Forces Qualification Test (AFQT), a composite of several subtests in the Armed Services Vocational Aptitude Battery (ASVAB). The minimum acceptable ASVAB scores vary by high school graduation status; they have at times also varied by gender. Additional requirements are set for the applicant 's medical status and moral character as manifested in the main by record of previous illegal activities. (For details, see Eitelberg, 1988; Waters et al., 1987.) In what follows, we emphasize the assessment of skills and abilities rather than physical condition or past experiences, although the discussion applies generally to any valid predictor.
Jobs in the Services are varied and in many cases involve the performance of complex or hazardous tasks. In order to develop a cadre of well-qualified recruits, the military personnel accession system must attract a substantial number of applicants, collect information about their capabilities, and, using that information, decide who to enlist and how to allocate across jobs those that do enlist. Because applicants have the option of refusing employment, or enlistment, the system must also decide how aggressively to court applicants and how far to go in accommodating their preferences as to job, duty station, and length of service.
Large employers like the military generally have openings in a great many jobs; in such cases, it is often efficient to consider job assignment as
a second decision, to be made after the primary decision to employ (or the applicant's decision to accept employment). Each job has its own minimum applicant requirements—some are at the same level as those used for employment decisions themselves, and others are higher than the first-stage requirements for employment. In the private sector, labor laws and union restrictions must also be taken into consideration.
Minimum standards are especially vital when employment decisions must be made at different times by decentralized staff for each individual, independent from others who might also be applying. Moreover, it may be prudent to hire and place prospects as they apply, rather than postpone decisions until a large pool of applicants is available, from which the best can be selected. By that time, the pool may have evaporated, as applicants find alternative opportunities. Job standards and job specifications take on added importance in such dynamic day-to-day hiring environments. The Services have introduced the added complication of the delayed entry program, whereby good prospects can be signed up immediately for entry into the military at a later time when they have completed personal commitments (e.g., high school) or when a desired position—a “training school seat”—becomes available.
JOB ALLOCATION AND MULTIPLE STANDARDS
Before considering methods for setting entrance standards, it is important to consider the practical context for such standards. In the Services, extensive computer-based systems are used for allocating recruits in ways that control for competition among the jobs in each Service.
Each Service has local recruiting stations staffed with enlisted personnel who contact prospects and try to convince them to apply. Recruiters are given quotas specifying how many of what kind of qualified recruits are needed. Upper limits are often placed on the number of non–high school graduates and the number of persons with below-average AFQT scores who may be recruited. The applicant's qualifications are evaluated in greater detail at one of the 68 Military Entrance Processing Stations (MEPS). If the applicant qualifies for entry, the Service classifier then helps the applicant to select one of the job options that the Service's computer-based allocation system presents.
Each Service uses a somewhat different system for classifying recruits. The Air Force uses its Procurement Management System (PROMIS) to assign a proportion of its recruits—some 50 percent in the mid 1980s, about 35 percent in 1991—to specific specialties before they enlist. The remainder are guaranteed an assignment in one of four general categories of jobs; the specific assignment is made early in Basic Military Training, via the Processing and Classification of Enlistees (PACE) system (Peña, 1988).
The Navy classifies recruits with its system, Classification and Assignment within Pride (CLASP) (Kroeker and Rafacz, 1983), which is very similar to the Air Force PROMIS system. The Marine Corps ' Recruit Distribution Model is designed to assign recruits to the most complex specialty for which they are qualified. The Army is currently using a system called REQUEST, but it is developing a more sophisticated system, the Enlisted Personnel Assignment System, or EPAS (Schmitz, 1988).
The main function of these allocation systems is to predict the applicant 's performance on each of the available jobs, determine which jobs the applicant is qualified for, and from among those select the person-job assignments that would be most beneficial to the Service. Obtaining the best performance on each job must be assessed in terms of the requirements for all jobs. For example, if one job has much higher entrance standards than the others, the recruits with superior talents may all be assigned to that job, leaving the less talented recruits for the other jobs. Such a solution would not be acceptable. Military manpower experts all stress the importance of having some superior workers assigned to each job. Such workers are said to be the best source of supervisors as well as instructors for future recruits. The relative value of these considerations is not easily quantified, but the military manpower systems start with the assumption that an adequate distribution of performance is essential in every job.
The Services' allocation algorithms have different ways of effecting an efficient distribution of talent among jobs. The Air Force and the Navy use a nonlinear aptitude/difficulty component, whereas the Army uses explicit quality goals for each job, stated in terms of proportions of incumbents in various AFQT categories. As the quality goals are or are not met, changes are made in the job priorities in the system. Minimum standards set lower bounds on talent for each specialty and have indirect effects on the talent mix.
The current military personnel accession system appears to work adequately, but many of its procedures lack a formal basis. It is reasonable to expect that the system would improve with a stronger empirical basis. Methods for measuring job performance are now well developed, and standard methods for relating entrance test scores to performance criteria are well known. But setting entrance standards, allocating applicants to jobs, and budgeting recruiting resources make up a complex and interdependent set of policy functions that could be clarified with the aid of computer-based models. With the above background concerning the military personnel accession system in mind, we now turn to some approaches to the development of the needed methods.
COMPETENCY SCALES
If performance scores are to be useful in setting entrance standards, the interpretation of the scores must be clear. The interpretive framework that
would be most useful for balancing costs and performance requirements would be a competency scale indicating level of job mastery. The traditional approach of personnel psychologists to measurement is to compare people with each other. Most tests, like the aptitude tests used for Service entry, are designed to be interpreted comparatively. The scores can be interpreted only by reference to norms. In fact, the primary entry qualifier, the AFQT, reports scores on a percentile scale, which emphasizes its comparative nature: a person who scores 70 has a general aptitude that is better than about 70 percent of the people in the 1980 reference population. The score does not, however, indicate that the person is 70 percent as good as needed to do a good job.
There is another approach to measurement, one that gained vogue in education circles in the 1970s under the name of criterion-referenced testing. Such tests are designed to measure individual performance against a standard of desired performance. The measurement of job proficiency lends itself to this approach, and performance tests can be constructed in a way that permits interpreting proficiency on an absolute scale. This approach seems particularly salient to the policy question of how much quality is enough. One would like to be able to say, for example, that a person can do a job at 70 percent of the level of someone who has mastered the job, and that this represents journeyman-level performance. A scale that measures proficiency in this manner has been called a competency scale. The idea is familiar to the general public, and to teachers, who often have more trouble appreciating the strictly comparative scale of aptitude tests. But a performance scale with an external, fixed referent rather than a comparative norm is not usually encountered in personnel work, and thus it needs explication.
The term competency as used here denotes a way of interpreting scores on a performance scale. It follows that there are degrees of competency. The term has often been used in related contexts to signify a simple dichotomy that separates the competent from the incompetent. Such a dichotomy is often encountered, as in deciding whether someone has passed or failed a course of study, or deciding whether a high school student has or has not developed enough competence to be awarded a diploma. But in the job performance context, any dichotomy would be artificial and unnecessary. In selection systems, cutoffs are placed on entrance tests, not on performance measures—on the input, not on the output. Setting a particular input standard results in a consequent output distribution of job performance scores—some low, some intermediate, some high. Policy makers must decide if the resulting distribution of performance scores is acceptable.
It cannot be expected that all incumbents will become experts. All that can be expected is that a reasonable proportion of each skill level will be available. Also, because the predictor tests are imperfectly related to performance, selecting the higher scorers does not guarantee eventual high-level
job performance. The minimum standard for job entry will have only an indirect effect on the distribution of job competence. Raising the minimum cutoff will raise the mean and reduce the variance of the distribution of competence, but a considerable spread will remain. Setting entrance standards must ultimately depend on a judgment about the acceptability of the resultant distribution of competence.
Consider an oversimplified illustration of the effects of setting entrance standards. The scores on the entrance test used to predict performance have a distribution. Some people will score high, others will score lower. Likewise, there is a distribution of performance; inevitably, some incumbents will not perform as well as others. Technical training schools cannot be expected to turn out only experts. A more realistic expectation is that job incumbents will develop and improve on the job. There is always a flow of personnel through a job. As some incumbents become experts, others are being promoted or released, and still others are just entering the job. There will always be some novices, some apprentice-level job incumbents, many journeymen, some masters, and a few experts. Managers of human resources would find it desirable to establish an expected or realistically acceptable distribution of proficiency in each job cadre.
Figure 9-1 shows, for a large group of applicants, predictor scores and performance scores that are related in the usual psychometric fashion, assuming a moderate validity correlation and roughly normal distributions of both scores. For purposes of discussion, we assume the availability of performance scores for people who will not be selected and therefore will have no chance to actually perform. Each person is, in principle, represented by a point on the diagram, and the entire population by a swarm of points roughly elliptical in shape. The figure indicates by an ellipse the distribution of scores on both predictor and criterion for the total population, and it shows the effect of three alternative standards on the predictor. Each standard cuts off a group of predictor scores and leads to a skewed distribution of performance scores for those exceeding the predictor cutoff.
Two major points are clear from this schematic view of the selection process. First, setting a cutoff on the predictor composite does not entail setting a corresponding cutoff on the performance measure. Second, evaluating the result of a particular predictor cutoff requires evaluating the resulting distribution of performance scores. Whether a given cutoff is acceptable depends on whether the resulting performance distribution is acceptable, as well as on the additional considerations of cost, personnel needs, and so on. Deciding whether a performance distribution is acceptable would be greatly aided if performance scores could be interpreted as competency. The interpretation of a performance test score refers to the inferences about job performance that can legitimately be drawn from criterion test performance. To the extent that a criterion measure is representative of the work
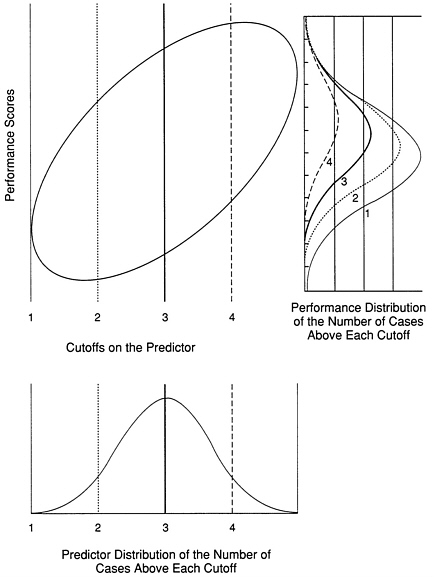
FIGURE 9-1 Schematic scatterplot of predictor and performance scores.
required on the job, some kind of inference is warranted from the test to the job domain.
Establishing a scale of competency is not straightforward by any means. The job domain must first be delineated in terms of the job 's constituent tasks or in some other units. Moreover, some tasks may be more important, or more critical, than others. An incumbent who can do 70 percent of the job tasks may not be able, in some sense, to do 70 percent of the job. Green and Wigdor (Vol. II) discuss this issue in further detail.
There are many levels of proficiency and, at any point in time, any job will have some incumbents at each level. There is merit in having some sort of interpretive scale anchors making it possible to establish various levels, associated with such terms as novice, apprentice, journeyman, master, expert. They might be strongly related to the various pay grades of enlisted personnel or to the already-established skill levels associated with military jobs.
A slightly different approach would be to establish a minimum competency score on a job performance measure and to establish some acceptable proportion of incumbents who are at or above that level. Bentley (1986) reported an approach to this problem for one Air Force specialty; it involved setting minimum acceptable levels of performance on each task in a walk-through performance test. Hutchins (1986) used a similar approach, with judgments obtained through a Delphi technique, for a Navy rating. Arabian and Hanser (1986) discussed the general problem in the Army context. And Mayberry (1987) reported a systematic approach to developing a competency scale for Marine infantrymen.
SETTING MINIMUM STANDARDS FOR A SINGLE JOB
The next step in the development of methods for managing accessions is to find a rationale for setting a minimum entrance standard for a single job. Such methods are of limited practical use, since jobs usually do not exist in isolation. Still, it is wise to understand the details of a model for setting one standard before attempting to develop a method for many jobs at once.
Every job has certain minimum qualifications. Employers want to avoid hiring typists who cannot type or chauffeurs who cannot drive. Although most jobs require additional training, some initial level of knowledge, skill, and ability is needed as a starting point. Some jobs are so demanding that relatively few people can be trained to do them. Other jobs could be filled by many people if they were given very extensive training, but such training is too expensive; more highly qualified applicants are needed to keep the time and expense of training within reasonable limits. Some jobs are so critical that a poorly skilled person in the job is worse than useless and may actually be dangerous. Sometimes poor performance is merely embarrassing; sometimes it is even expected and tolerated, as when a mess hall worker cooks poorly or a sergeant types poorly. In other cases, poor performance can cost lives and in such cases misallocation is intolerable.
Determining the validity of a selection test normally does not include setting a minimum standard. Rather, it assumes that a large group of applicants is tested, all at once, and that a single decision is made to select a certain number of the top scorers. The concept of a job-success ratio refers to the proportion of accepted applicants who can be expected to achieve at some acceptable level and thus be called successful. The famous Taylor
and Russell (1939) tables display, for a normal bivariate distribution, the success ratio as a function of the proportion of applicants who are accepted. It is tacitly assumed that applicants are accepted from the top scorers, that the selected applicants all have predicted performance levels well above an acceptable minimum, and that all who are offered the job will accept. Since predictions are usually far from perfect, not all those who are selected are expected to succeed. For any given score on the predictor, there is a corresponding distribution of performance. In a stable environment, this experience will recur, yielding the same “hit” rate. If the selection tests are useful, the proportion of expected successes will be higher as the selection ratio is reduced, and fewer applicants will be accepted.
In practice, an appropriate minimum standard is often critical. Some people are so unskilled that they should not be hired, no matter how severe the need. The minimum standard must be set high enough to reject most of these people. By contrast, highly talented applicants will have the choice of several jobs (or schools or other alternatives), they may not accept a job that is offered, and they will be more expensive to attract and retain. Thus, the minimum must be set low enough to ensure an adequate number of acceptances while avoiding overinvesting in applicant talent. If standards are raised, more recruiting effort—and expense—will be required to obtain adequate numbers of recruits; if standards are lowered significantly, training time will increase, and attrition may also increase (which in turn implies that a larger group of recruits will have to be trained so that an adequate number remain after the expected attrition).
In the past, the cost-benefit trade-off has been evaluated subjectively, and equilibrium has been reached by judgment, negotiation, and compromise. Not inappropriately, entrance standards have changed according to the supply and quality of recruits. They have responded to pressures to economize in lean times and pressures toward risk aversion in better times.
This system has two striking weaknesses. First, it provides little evidence as to how much additional investment in recruitment is warranted, or how much saving could be achieved as the recruit mix changes. Second, it leaves policy makers with less evidence than they would like as to the competence of the force they have recruited. With objective measures of job performance in hand, there is now a realistic possibility of developing better-informed methods for setting entrance standards, based on econometric models that pit costs against performance. Although cost-performance trade-off models are still in the development stage, they are sufficiently promising to interest policy makers and might provide attractive alternatives to the traditional method of setting standards and assessing the manpower quality of the force.
Two methods have been proposed for objectively setting a minimum entry standard for a single job. Both methods are premised on partial-equi-
librium rather than general-equilibrium models. That is, they involve models that take into consideration the various competing forces of costs and performance for a particular job, but they do not consider the possible impact on other related jobs, each of which also has its own cost and performance needs. The first method, the utility difference approach, has its roots in psychometric work in personnel decision making. The other method is based on the so-called Rand model, a well-known econometric analysis. Both approaches are concerned with a cost-benefit analysis of the problem that seeks to determine the best trade-off between costs and resulting performance.
The Utility Difference Approach
Brogden (1949) suggested an approach to the cost-benefit analysis of personnel selection, which was further developed by Cronbach and Gleser (1965) and more recently extended by Cascio and Ramos (1986). The model is widely used in industrial and organizational psychology, and it is the basis for a well-known economic evaluation by Hunter and Schmidt (1982) of the U.S. Employment Service's widespread use of the General Aptitude Test Battery, GATB (see Hartigan and Wigdor, 1989).
The main purpose of the analysis is to justify the cost of applicant aptitude testing by comparing the cost of testing with the resulting increases in the value of employee performance. The increased value is taken to be the difference between the performance utility of the selected workers and the performance utility that would have been experienced if selection had been at random. The utility of performance is assumed to be a linear function of the criterion used for validating the entrance tests. The criterion is formulated as a monetary scale of performance worth. Since test scores are imperfectly related to job performance, the potential utility of a prospective employee is given by his or her predicted performance, which is derived from a linear regression function relating job performance to scores on the predictors. The model states that the marginal productivity gain due to using the selection procedure is the difference between the cost of that testing and the mean marginal gain in performance realized by selecting applicants with a valid predictor test.
The simplest version of the model has only one predictor. In this version, the mean marginal performance gain is the product of three factors: the validity correlation of the predictor, the average standard predictor score for the selected applicants, and the standard deviation of the performance measure, in dollars. The first two factors can be readily calculated, but establishing the dollar-valued standard deviation of performance is a challenge. It would seem that expensive cost accounting methods would be needed to estimate this parameter, but Cascio (1987) claims that behavioral
methods are just as accurate and are cheaper and quicker to accomplish. He reviews several methods for estimating the standard deviation of performance, which specifies the unit of the scale. The simplest approach is to estimate it as 40 percent of the average salary paid to the employees in a job class (Schmidt and Hunter, 1983). This figure represents the lower bound of the 95 percent confidence interval, based on the cumulative results of studies that actually measured the dollar value of job performance of individual employees.
Such salary-based estimates of the performance scale may not be appropriate for the JPM Project because the metric of salary dollars may not be very relevant in a military context. One alternative is the Superior Equivalents Technique (SET), which was developed by Eaton et al. (1985) specifically for use in situations in which individual salary is only a small percentage of the value of performance to the organization or of the cost of the equipment operated (e.g., a jet engine mechanic or a nuclear power technician). The standard deviation is first expressed in performance units and then converted to dollar units. A subject matter expert judges how many soldiers performing at the 85th percentile would be equivalent to a fixed number of soldiers performing at the 50th percentile. Then, by assuming the value of the 85th percentile is one standard deviation higher than the value at the 50th, the standard deviation in monetary units can be obtained readily.
Several aspects of the utility difference analysis are worth noting. First, better test scores mean higher predicted performance and therefore better yield. Utility is assumed to be a linear function of test scores. A candidate with an outstanding test score is worth more than a candidate with a mediocre score. As discussed below, a linear function may not always be appropriate, however.
Second, nothing in the formulation precludes negative utilities. Since the model adds the utilities of all the incumbents, it implies that utilities differ only in degree, but in some cases, negative utilities would seem to differ in kind. Sometimes work that is detrimental to a mission can be offset by the performance of others, but sometimes it cannot. Some jobs are better not done at all than if done by someone who does harm—for example, jobs involving very delicate and costly machinery or possible endangerment of human life. Perhaps this just means that the utility scale needs changing, but in general the model is easier to accept if poor performance has low but still positive value.
Third, the economic benefit of testing is calculated as the difference between the total utility realized from those hired, minus the cost of testing all applicants. If few are hired, their combined value has to be relatively high to offset the cost of testing, whereas if many are hired even a small validity has positive value. This conclusion depends on the assumption that those with the highest test scores are hired. In the simple version of the
model, no allowance is made for applicants not accepting offered employment or for rejection of applicants on other grounds, such as a significant criminal record. Such allowances can of course be made (Hogarth and Einhorn, 1976; Boudreau, 1988).
Cascio proposes extending the cost-benefit analysis to cover the setting of minimum standards. The costs of training and recruiting would have to be included with testing costs. The cutoff would be set at the point at which benefits (utility) equal cost. To our knowledge, however, this calculation has actually been done only in the private sector. A thorough review of the model in the military context is given by Zeidner and Johnson (1989).
The Rand Approach
Much of the recent military work on models for standard setting stems from seminal work done at the Rand Corporation. The basic Rand model, as described by Armor et al. (1982)was designed to set the enlistment standard for the Army occupation of infantryman as a single cutoff score on the combat aptitude (CO) composite of the ASVAB. The data base used included about 14,000 infantrymen who entered the Army during fiscal 1977.
The Rand group based its measure of performance on the Skill Qualification Test (SQT), an assessment device administered annually by the Army 's Training and Doctrine Command to soldiers in the field. This work preceded the JPM Project and the Army's Project A. During the time of this study, the SQT had three components, a written test of job knowledge, a hands-on test of some job-specific tasks, and a set of supervisory ratings; Armor et al. (1982) noted that the written component was responsible for most of the variance in the test scores. (In later years, the hands-on test and the supervisor's ratings were dropped from the SQT.) Scores on the SQT ranged from 0 to 100 percent. The Army had established 60 percent as the minimum passing score, and this operational definition was accepted by Armor et al. to identify persons who had “qualified” by passing the SQT.
The Rand group then modified the performance criterion for their econometric analysis by incorporating a temporal component as well. The resulting criterion was called the Qualified Man Month (QMM) and was defined as a “month of post-training duty time contributed by a person who can pass the SQT at a minimum standard” (Armor et al., 1982:14). To contribute a QMM, a soldier had to pass basic training, pass advanced training, stay in the service long enough to take the SQT, pass the SQT by obtaining a score of at least 60, and stay in the service one month. For each additional month in the Army, this soldier would contribute an additional QMM. Soldiers who develop skills quickly, passing the SQT early in their career, are more productive and contribute more QMMs. For example, a soldier who stays in the Army for two and a half years after passing the SQT contributes 30
QMMs. In addition to rewarding early achievement, the index also incorporates retention—a soldier who leaves the Army before his or her tour of duty is up stops adding QMMs.
In the Rand analysis the criterion (QMM) was based on SQT qualification and attrition; the predictors were the AFQT, the CO (combat aptitude) composite on the ASVAB, and high school diploma status. The relation between the criterion and the predictors was established empirically through the 1977 data base of 14,000 infantrymen. The Rand group used a categorical regression system in place of traditional psychometric methods. The soldiers were cross-classified by AFQT category (7 categories), CO composite score category (10 categories), high school diploma status (2 categories), and length of time in service (5 categories). Because of the high correlations among some of the variables, some cells in the cross-classification were empty. For each cell, the proportion of soldiers retained was determined as a function of time in service. SQT scores were regressed on AFQT score, CO composite score, high school diploma status, and time in service at the individual level using a logistic regression2 to derive coefficients for each predictor. (The regression was based on one administration of the SQT.) These coefficients were then used to derive predicted performance levels for a group with a given ability mix (e.g., AFQT CAT IIIA, CO 90-100, HSG, TIS 2-2.5 years), using the midpoint of that group's scores on the predictor variables for convenience. Except for the SQT regression, which represents a specific functional form, all relationships were unconstrained and could be nonlinear, or indeed nonmonotonic, if that is what the data indicated. In fact, the results were generally monotonic, but often nonlinear.
Having established the QMM as an index of the quality of soldier performance, and having determined its relation to the predictors, the next analytic step was to develop an expression for the various costs. The cost components of the Rand equation are the variable costs (i.e., those that vary with the number of soldiers) involved in recruiting, basic training, advanced training, and retention. Fixed costs, such as maintaining recruiting stations and training centers and paying a base number of recruiters and trainers, are not included, because they would not vary with different entrance standards. The various temporal stages were separated because they apply to different numbers of soldiers. Only those applicants who become recruits require basic training, only those recruits who get through basic training go on to
|
2 |
A logistic regression of a categorical variable on continuous variables is a model relating the category proportions, p, to the variables x1, x2, x3, . . . , through the equation (Fienberg, 1977): |
advanced training, and only those who finish training and become combat infantrymen have retention costs.
The variable costs of training were taken to be the costs of soldier pay and materials. The variable costs of retention were the costs of salary and benefits from the end of training through the first tour of service. Determining the costs of recruiting was more complex. First, it was assumed that only high-quality enlistees (AFQT Categories I-IIIA, who are high school graduates) generate variable recruiting costs. Lower-quality recruits were assumed to be available with no additional cost. Second, Armor et al. proposed two alternatives for obtaining more high-quality recruits, either paying bonuses to enlistees or increasing the number of recruiters. As it turned out, both alternatives led to the same conclusion about the optimal enlistment standard, but increasing the number of recruiters was more expensive.
Armor et al. decided to fix end strength, that is, to hold constant the number of soldiers completing their first tour, and to find the entrance standard that minimized the variable cost per QMM. This can be done by calculating both cost and average QMM, and their ratio, for each possible cutoff, or enlistment standard, on the predictor, which in this case was the ASVAB's CO composite. Thus, the optimal enlistment standard was the value of the CO composite for which the ratio of cost to performance was lowest. One effect of a raised enlistment standard would be that some incumbents would not have been accepted for enlistment—it was assumed that they would have been replaced by enlistees with qualifications similar to those in the remaining eligible categories. In the analysis, the numbers of individuals in each of the remaining cells was simply increased proportionally. A similar assumption was made for lowered standards.
The optimal enlistment standard determined by the model for the base year was a score of 87 on the CO composite, which was close to the then-current (fiscal 1982) operational requirement of 85, but higher than the operational level of the base year, fiscal 1977. The optimal level would vary from year to year according to the demographics of the recruit population, the economic climate, the number of positions to be filled, and so on. The optimal level would have cost more to implement in fiscal 1977 than would the actual fiscal 1977 level, but more QMMs would have been obtained. The authors stated that the increased costs would add only a small percentage amount to the total budget for recruiting and maintaining the force. The higher standards would lead to having more recruits who could do the job, that is, to having more months of qualified performance at a lower cost per month.
The authors also concluded that high school graduates in AFQT Category IV were less cost-effective (fewer QMMs per unit cost) than nongraduates in AFQT Categories I-IIIA, because low-ability graduates are less likely to pass basic training, advanced training, or the SQT. Recall that the cost
equation of the model assumed that neither group required any marginal recruiting cost.
Because Armor et al. thought that their assumptions about recruiting costs were tenuous, they recomputed their model for several alternative assumptions about those costs. The resulting value of the index cost per QMM changed considerably, but the minimum was realized somewhere between a score of 80 and 90 on the ASVAB composite for combat infantrymen, for all assumptions examined, thus lending confidence to the original conclusions.
Evaluating the Models
The Rand model and the utility difference model provide important early steps toward rationalizing the standard-setting process. Each model leaves out some factors, as any model must if it is to be sufficiently understandable to be useful.
Both models maximize performance for a fixed force size and both contain the implication that fewer excellent soldiers are equivalent to a larger number of more mediocre performers, but neither model explicitly considers whether better selection could result in smaller personnel needs. Indeed, the quality-quantity trade-off implied by both models might not be realistic. This is especially true when one considers that in wartime attrition increases because of casualties. And this, in turn, affects decisions about the size and character of a peacetime force.
One technical difference between the two models should be noted. The utility difference model is a cost-benefit analysis, which has the significant disadvantage of requiring both utility and cost to be measured on the same scale—monetary utility in this case. Many find the expression of utility in dollar terms simplistic, although the monetary scale does have the advantage, at least in principle, of providing the same metric across jobs. (If the money and the utility are equivalent across different jobs, the multiple job case is simplified.) The Rand model is a cost-efficiency analysis, which uses a ratio as an index of the cost-benefit trade-off. When the difference is replaced by a ratio, such as utility per unit cost, utility and cost can each be measured on its own scale, and the only important assumption is that the utilities of the personnel can be aggregated by addition, an assumption that many find problematic as well.
Another significant technical difference between the two models is that the Rand model dichotomizes performance—one QMM is as good as another and one month served without qualifying on the SQT is as bad as another. That is surely a simplification. For example, those who passed the SQT were presumably more valuable in the preceding month than those who did not pass. (By contrast, the utility difference model views utility as
improving linearly with performance, an assumption that can also be questioned.) However, for a cost-benefit analysis along the lines of the Rand model such assumptions might not be critical. Armor has performed analyses with the Rand model, using a continuous criterion. He replaced a proportion of QMMs in each cell, with the expected (i.e., average) performance of the individuals in that cell. The general nature of the results is unchanged—the location of the minimum cutoff was very similar to that found with the dichotomous criterion.
Both models are focused on setting a minimum entrance standard, or cutoff score, on a predictor. Neither considers the more complicated question of the distribution of quality above the minimum level. Setting a minimum standard does not necessarily ensure an adequate distribution of recruit quality, because there is nothing to prevent a job's being filled by people who are all just at or just above the minimum. Although this is not likely to occur, it could happen; for example, if one job has a minimum below that established for any other job, it will get all the lowest-level qualifiers, since they can qualify only for that job. Although neither model expects this, neither model prevents it. The utility difference model assumes a normal distribution of applicants and assumes that all who are offered employment will accept, in which case the distribution above the minimum would be realized. The Rand model bases its results on empirical data from individuals actually on the job, which is certainly more realistic, but it assumes that if the cutoff is raised the distribution of those remaining would be altered proportionately—not by the addition of people just at the new minimum. Although it is difficult to see how to improve on these assumptions, the lack of explicit attention to the distribution of talent remains a concern.
Mayberry (1988) and May (1986) consider the effect of minimum entrance standards on the entire distribution of performance, rather than simply the number of QMMs. They show that a low entrance standard has the effect of lowering the relative number of incumbents who perform at superior levels. They do not, however, propose any selection mechanisms other than a minimum standard that might be used to influence the distribution of performance.
SETTING STANDARDS FOR SEVERAL JOBS
The various models for setting standards for a military job are, in many respects, very sophisticated, yet models that apply to only a single job miss the major manpower problem of how to allocate scarce resources. Plainly, making personnel decisions in a multijob environment requires not only comparing one recruit with the others, but also comparing one job with other jobs. How this is done will critically affect the conclusions reached
and will probably affect the minimum entry standards set for the various jobs.
A main shortcoming of an analysis of only one job is the problem of partial equilibrium. When treating only one job in isolation, it is natural to assume that, with a few exceptions, every applicant who scores above the selection cutoff will accept employment in that job. That is almost certainly never the case in a multijob system. Models must be expanded to consider not only the possibility that the applicant might reject the offered job, but also the distinct possibility that the organization might p` place the applicant in a different job. In the military situation, an applicant who is qualified for one job is generally qualified for, and may have a desire for, many jobs. Yet at best he or she can accept only one. Any position in which he or she is placed will have opportunity costs, and those costs will be highest when the applicant's qualification is highest. To determine where the applicant should optimally be placed requires a general-equilibrium approach.
At this stage of the analysis, differential prediction is assumed to be possible with the available predictors. If the same predictor measure (e.g., the AFQT) is used for every job and only a single dimension of skill or ability is involved, the problem of allocating talent to jobs becomes much easier than if different predictors are used or if jobs vary in types of abilities and level of difficulty. Indeed, for jobs at the same level of difficulty, job vacancies and applicant interest may play decisive roles.
There is controversy within the profession of industrial and organizational psychology about the value or even the possibility of differential predictions. Nevertheless, all the Services use different composites of ASVAB tests for predicting performance in different types of jobs.
With differential predictions and with jobs of varying difficulty, there are complex interactions among the minimum standards set for each job. Moreover, minimum standards alone do not guarantee that the allocation algorithms will provide a range of talent for each job. The interactions of the standards for different jobs and their mutual but competing need for a distribution of talent are not well understood, but it is certainly widely recognized that revising the standards for one job has immediate effects on other jobs. To study the interactions, models for standard setting must be extended.
Revisiting the Rand and Utility Difference Models
The Rand model was extended modestly by Fernandez and Garfinkle (1985) to a situation involving four jobs. The same criterion of QMMs and roughly the same evaluations of variable costs were used, although the variable recruiting costs were limited to bonuses for AFQT Categories I
IIIA high school graduates (whereas Armor et al., 1982 had also considered increasing the number of recruiters). The main change in the extended Rand model was in the constraints on optimization. Fernandez and Garfinkle argued that since part of their multijob problem was where to assign recruits, holding numbers of incumbents constant was not reasonable in their study. Instead, they held QMMs constant and then determined cost per QMM for various levels of job entry standards. Armor et al., for their part, held force size constant and minimized cost per QMM, on the assumption that the Army planned for a force of a certain size and that quality cannot be exchanged for quantity.
An important consequence of holding the number of QMMs constant in the four jobs under study was that the status quo was thereby accepted as the relative requirements of the four jobs. The system goal was taken to be each job's actual number of QMMs during the years under study. In a sense, this sidesteps the issue of how to allocate quality by simply accepting the status quo rather than facing the complex problem of comparing the relative values of the jobs. It confines studies of personnel allocation to studies of the means while ignoring the ends.
The utility difference approach of Brogden (1949), Cronbach and Gleser (1965), and their followers can also be extended to the multijob case. With its linear evaluation of utility, the utility difference model meshes well with linear programming models of the classification problem (Charnes et al., 1953), the name given to the personnel allocation problem in the operations research literature. Such models can easily handle any number of jobs, but they are designed for batch assignment, with everyone in the batch being assigned at the same time. Assigning applicants one at a time, as they apply, is called the secretary problem, and adds considerable complexity to the linear programming approaches. However, the particular side conditions of allocation —every person must get exactly one job, and every job opening must be filled—permits use of efficient network algorithms (Schmitz and Nord, 1987).
A model for standard setting in a total system with many jobs should include some way of controlling the distribution of talent among jobs. Nord and White (1988), in their design of the Army's EPAS system, considered quality goals to be boundary conditions or constraints on their system; they explicitly studied the effect of including or not including those constraints. They found, not surprisingly, that the effect of distributing talent across jobs to match quality goals results in substantially reduced overall utility of the job assignments than when no such constraints exist.
Nord and White also pointed out a number of technical problems that have not yet been dealt with adequately. One is the effect of different validities for different jobs. If two jobs have equal importance and require equal numbers of recruits, but performance can be predicted more accu
rately for one job than for the other, the more predictable job will get the better recruits, because the predicted performance will be better for that job—by regressing predictions toward the mean as the degree of predictability decreases. As a result, the jobs that are not well predicted will suffer. This effect is more apparent in the utility difference model, in which utility is assumed to increase linearly with predicted performance, but it is also present in the Rand model, as pointed out by Armor et al.
Comparing Jobs
Comparing jobs is a critical part of deciding how to allocate personnel across multiple jobs most effectively. In making their job comparisons, Fernandez and Garfinkle assumed that equal performance levels could be considered equally valuable in all jobs—that is, they treated all QMMs as equivalent and optimized on the total number. In lieu of such an arbitrary assumption, a direct comparison of job value is needed. One likely candidate is to place job performance for every job on a single overall scale of utility. Sadacca et al. (1988) took an empirical approach to determining utility—they devised an elaborate procedure in which Army officers were asked to make comparative judgments of utility for various levels of performance in each of several military occupational specialties. Nord and White (1988) used the resulting utilities to compare two methods of job allocation based on different models for utility aggregation. The model in which only average group utilities were maximized led to higher utility than a model concerned with individual utilities.
Competency scales are also useful ingredients in making comparisons among jobs. With an absolute scale of competency, the same score indicates roughly the same level of performance across jobs. Placing jobs on a single scale—whether of performance utility, job difficulty, importance, or some other dimension—allows comparative judgments to be made objectively. Experts could be asked to make absolute judgments about the acceptability of a performance distribution and the possible negative value of very poor performance. This would avoid some of the pitfalls faced by Sadacca et al., who asked their experts how a soldier at the 70th percentile among motor mechanics compared in utility with a soldier at the 30th percentile among cannon crewmen. A percentile is a purely relative scale of performance, and it may misrepresent the quality of the performance. In principle, most of the motor mechanics could be no better than journeymen, whereas most of the cannon crewmen could be masters or experts. In practice, such an occurrence is very unlikely, and in fact the judges may have had an idealized distribution of performance in mind, but to some extent the known quality of the job incumbents could bias the comparisons.
Alley (1988) described an imaginative alternative to comparing jobs with
respect to utility. He proposed instead that jobs be compared in terms of how difficult they are to learn. A scale of learning difficulty implies that the more time and effort needed to learn a job, the higher the abilities needed in the assigned recruits. All military jobs require intense specialized training, so a comparison of learning difficulty can be quite objective. Even though learning difficulty provides a dimension along which different jobs can be rated, the question remains: Is learning the right dimension? The fact that two such different concepts as performance value and learning difficulty might each provide a useful common scale for comparing jobs suggests that there may be other dimensions worth considering. For the present, the question must be left unanswered.
Generalizing Across Jobs
A practical hurdle to be overcome in any multiple job allocation systems is the need to consider all jobs. If job performance information is only available on a subset of jobs, as is the case in the JPM Project, some means must be found for generalizing that information to the remaining jobs. One possibility is to combine military occupations into a few large clusters of similar jobs and then to generalize from one or two jobs in a cluster to other similar jobs. Hunter and Schmidt's validity generalization model (Hunter, 1980) is a well-known approach to this problem.
Most of the work on validity generalization is concerned only with the validity correlations, including the degree of relationship between predictors and criteria. A central question is how far to generalize —to all jobs, as Hunter and Schmidt often claim, or to only closely related jobs? Sackett (Vol. II) pointed out that different types and levels of descriptors can produce very different groupings. For example, job similarity can be based on a comparison of job analyses, which in turn can focus on specific behaviors, general behaviors, or needed abilities, each providing a different basis for job clustering. Pearlman (1980) reviewed and analyzed several approaches and selected ability requirements as the best job descriptors when clustering jobs for validity purposes.
For setting standards, validity correlations alone are not enough. One has to be able to generalize performance score distributions, including means and standard deviations, or at least to generalize minimum requirements across jobs. That is, one must know not only which aptitudes are predictive of performance, but also what level of performance is predicted from a given level of aptitude.
Sackett (Vol. II) discussed three methodologies that can be used to generalize both validity and cutoff scores. One method uses job components from McCormick's Position Analysis Questionnaire (PAQ) —which would permit predictions of mean test scores as well as estimations of validity
correlations. Judges would have to identify those PAQ dimensions most likely to be indicative of good performance in a given job. A second method employs an item-level analysis of the judged importance of the test item for predicting performance. This type of analysis, although useful in high school competency tests, is largely irrelevant in connecting aptitude tests with job performance. A third method scales jobs on needed ability by using paired comparisons. In all of these methodologies, the processes of judgment are fundamental, as are the sources of such judgments.
Generalizing the research on validity relationships usually assumes that predictors and criteria remain constant. Within groups of similar jobs, the Services generally use the same predictive ASVAB composites. However, an important feature of the JPM Project is the use of different types of criterion measures, including hands-on performance tests, walk-through performance tests, simulations, job knowledge tests, and ratings. These measures are more or less costly to obtain. More important, however, they measure different aspects of performance, possibly limiting the extent of validity generalization.
Another approach to generalizing is the synthetic validity project recently described by Wise et al. (1988). The research project uses a variety of job characteristics in determining how far to generalize validity and how to estimate the validity relationship. The project has the unique opportunity for extensive independent evaluation of the methodology, because the projected validities can be compared with actual validity correlations in the same and related jobs. The project plans to collect judgmental data relevant to the validity and standards issues and to connect this new data base whenever and wherever possible with the extensive criterion-related validation data base developed by the Army. The results of this project will be very useful in understanding the extent and limitations of validity generalization.
SUMMARY
Although the problem of linking entrance standards and quality goals to job performance is complex, the main outlines are now understood and much of the basic methodology seems to be in hand. There is reason to expect that important advances can be made in developing objective, empirically based methods of demonstrating the levels of quality needed in the recruit population to ensure adequate staffing of a range of first-term military jobs and to seed the next generation of leaders. Some of the work reported in this chapter also encourages optimism that cost-performance trade-off models for setting enlistment standards can be designed to handle more sophisticated performance information and a larger number of jobs.
The process of setting minimum entry standards and using job performance data must be understood in the larger setting of allocating personnel
to various jobs within the military. Indeed, the modeling of optimal entrance standards must take account of the details of the algorithms themselves. In some systems, filling technical school training seats is the highest priority, leaving little room for the decision rules for estimated job performance to come into play beyond the exclusion of those below the entrance standards. But the development of multijob models for setting standards could provide a blueprint for reweighting the factors considered in allocation decisions to emphasize job performance over and above the management of the training flow. In effect, one might suggest a model in which a single minimum standard would be replaced by a set of standards keyed to the performance distribution needed to supply each job with its required mix of abilities.
Of special interest with regard to the problem of maximizing performance within a given pool of enlistees is the picture presented by Nord and White (1988) of the way in which minimum entrance standards would interact in an assignment model with the mechanisms (e.g., quality goals) used to maintain an acceptable distribution of recruit quality in all Army jobs. Clearly, any method for setting minimum entrance standards must take account of these mechanisms as side conditions on the optimization. The model cannot be given free rein to assign applicants only to optimize their aggregate individual value to the Service.
To be useful for setting standards in a complete personnel system, existing models must be extended to the situation with many jobs. When performance has not been measured for all jobs, various means are available for generalizing the validity correlations and cutoff scores from the measured jobs to other jobs.
The central problem, however, is not how to extend the models, but how to compare jobs. Not only must average performance on one job be valued relative to average performance on other jobs, but each level of performance must be comparatively valued. Performance utility and learning difficulty offer possible scales on which jobs can be ranged, and other dimensions might also be viable alternatives.























