Range Restriction Adjustments in the Prediction of Military Job Performance
Stephen B. Dunbar and Robert L. Linn
INTRODUCTION
Common practice in establishing the criterion-related validity of a test or battery of tests to be used for selection or classification involves performing a linear regression of a relevant measure of performance on the test battery and reporting various descriptive statistics that assess the magnitude of the linear relationship between predictor(s) and the criterion. Although alternatives to the familiar correlation coefficient and perhaps less familiar regression slopes and intercept exist, these alternatives make the task of characterizing criterion-related validity of the battery more cumbersome. The correlation coefficient, in particular, allows for ready comparisons of predictive validity across occupational categories as well as across different predictor and criterion measures, so that its widespread use is not surprising. In the context of military performance assessment, correlations allow for comparisons of predictive validity over time and across Services. Such comparisons are important components in the validation of selection composites that are used for prediction in a wide variety of occupational categories such as military training programs.
Whatever appeal correlations have for these and other reasons must be weighed against certain limitations, several of which are especially relevant in the context of criterion-related validity studies. When a correlation coefficient is used to make inferences about the predictive validity of a test
battery for a population of applicants or enlistees, its values should ideally be estimated from a random sample of the applicant population. In most settings where predictive validity needs to be established, the only sample available for estimating the desired population values is one containing individuals, selected in part on the basis of scores on the predictor(s) in question, who have remained with a program long enough for criterion scores to be obtained. Besides the difficulties presented by the use of nonrandom samples in calculating correlations, the well-known sensitivity of correlations, slopes, and intercepts to linearity and homoscedasticity in the joint distribution of predictors and criteria is an area of concern. This concern can be magnified by selection effects.
This paper provides an overview of standard procedures used to adjust correlations and regression parameters for the effects of selection, commonly referred to as corrections for range restriction. Technical issues related to the accuracy of these adjustments are considered, especially where they are likely to have implications for the types of adjustment procedures appropriate for large-scale predictive validity studies of an aptitude battery like the Armed Services Vocational Aptitude Battery (ASVAB). The paper concludes with a discussion of issues related to the implementation of a set of adjustment procedures for validation studies in the military, where the choice of the reference population, choice of selection variables for making adjustments, and choice of an analytical procedure all have important consequences for the assessment of the predictive validity of present and future versions of the ASVAB.
SELECTION EFFECTS IN CORRELATION AND REGRESSION
Although the effects of various types of nonrandom selection on correlation coefficients, slopes, and intercepts are well-documented in the psychometric literature (cf. Thorndike, 1949; Gulliksen, 1950; Lord and Novick, 1968), a brief review of these effects will establish the context for technical issues related to their use in studies of criterion-related validity. Figure 1, Figure 2, Figure 3 and Figure 4 illustrate the effects of the usual types of selection on the bivariate scatterplot of a selection test (X) and a performance criterion (Y). In Figure 1, the scatterplot of a sample of 5,000 observations from a bivariate normal population is shown, along with the least-squares regression line of Y on X. The correlation between X and Y in this population is .60. Figure 2 and Figure 3 demonstrate the effects of explicit selection on X and Y, respectively—explicit selection in these examples involves actual truncation of the marginal distribution of the selection variable and is clearly visible by inspection of the scatterplot. When selection is explicit on X, the Y on X least-squares regression line is unaltered because of assumed linearity. However, estimates of the correlation between X and Y are altered because of the reduced
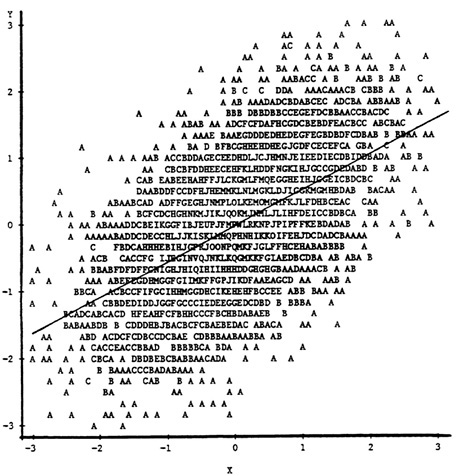
FIGURE 1 Scatterplot of a criterion (Y) and a predictor (X) in an unselected sample (N = 5,000, ρXY = .60).
variance of X in the selected sample. In Figure 2, with only the upper 50 percent of the observations on X included, the resulting correlation of .398 underestimates the population correlation by a substantial amount. When selection is explicit on Y, both the terms in the Y on X least-squares regression and the correlation coefficient are affected. In Figure 3, with only the upper 50 percent of scores on Y included, the regression line (depicted by the broken line) has a smaller slope and larger intercept, while the correlation between X and Y of .412 again underestimates the population value.
While explicit selection can occur, particularly when X is a screening device like an admissions test, a more likely situation would depict X as one of several measures used to select individuals. In such a situation one might imagine a third variable, Z, as the explicit selection variable—Z can be
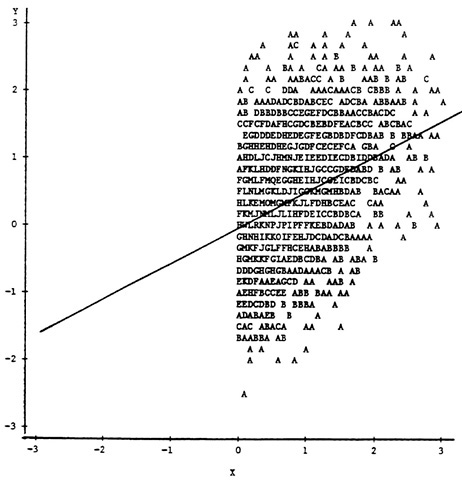
FIGURE 2 Explicit selection on X.
thought of as a kind of composite measure that includes such factors as self or administrative selection as well as scores on other predictors and is positively correlated with X and Y under typical circumstances. That Z can be thought of as a composite measure is reflected in its designation as an ideal discriminant function separating selected and nonselected groups (Cronbach et al., 1977) or as a latent variable underlying the true selection process (Muthén and Jöreskog, 1983). In this case, both X and Y are referred to as incidental selection variables because the selection effects on the bivariate distribution of X and Y are indirect. This type of selection effect also exists when interest focuses on the predictive value of an alternative set of variables imperfectly correlated with the explicit selection variable. In such a situation, the alternative predictors represent incidental selection variables.
The more subtle effects of explicit selection on Z are illustrated in Figure 4. The XY scatterplot in this figure is based on a trivariate normal popula-
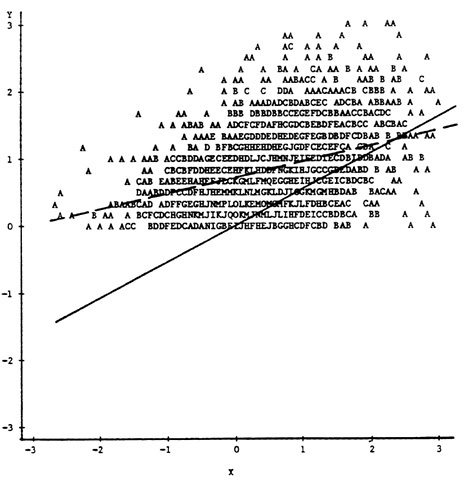
FIGURE 3 Explicit selection on Y.
tion distribution of X, Y, and Z in which the correlation between Y and each of X and Z is .60 and the correlation between X and Z is .90. The scatterplot contains only the upper 50 percent of the observations on Z, and, as can be seen in the figure, the only evidence for this being a selected sample is a reduction in the variability of the marginal distributions of X and Y. Even when X and the true selection variable are as highly correlated as in this example, the effects of incidental selection yield a least-squares regression line (again depicted by the broken line) with reduced slope and a correlation between X and Y (.414) that underestimates the population correlation substantially.
Although the plots in Figure 1, Figure 2, Figure 3 and Figure 4 do provide an indication of the types of selection effects that can occur in practice, they do not show how differential selectivity can complicate the interpretation of correlations based on selected samples. Table 1 illustrates the effects of different degrees of range
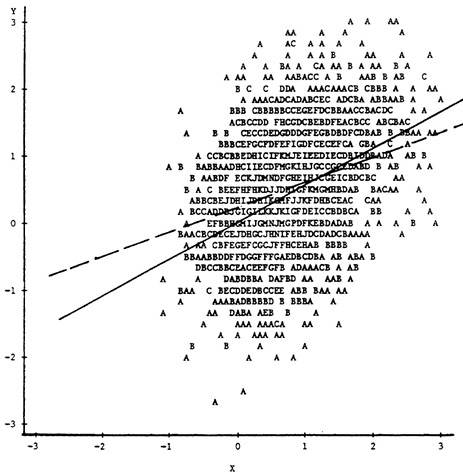
FIGURE 4 Explicit selection on Z.
restriction on the correlations of two measures with a criterion; one of the two measures represents the explicit selection variable (Z in the above discussion), while the other represents an incidental selection variable (X). The statistics in the table are based on a trivariate normal population in which the correlations between the criterion, Y, and Z and X are .50 and .45, respectively, and the correlation between Z and X is .50. The selection ratio indicates the proportion of the total sample that is selected into the validation sample on the basis of scores on the explicit selection variable Z. The standard deviation of Z is given in the second column of the table and the correlations between the predictor variables and the criterion in the third and fourth columns.
With no selection on Z, the correlations shown in the table are equal to the population values of .50 and .45. However, as the selection ratio de-
TABLE 1 Illustration of the Effects of Range Restriction for Z on the Correlation of Z and X with a Criterion Measure Y
|
Selection Ration |
Standard Deviation of Z |
Correlation with Y |
|
|
Z |
X |
||
|
1.0 |
1.000 |
.50 |
.45 |
|
.7 |
.701 |
.38 |
.37 |
|
.6 |
.649 |
.35 |
.36 |
|
.5 |
.603 |
.33 |
.35 |
|
.4 |
.559 |
.31 |
.34 |
|
.3 |
.515 |
.29 |
.33 |
|
.2 |
.468 |
.26 |
.32 |
|
.1 |
.411 |
.23 |
.31 |
|
.05 |
.371 |
.21 |
.30 |
creases and the proportion of individuals excluded from the validation sample increases, the correlations between the predictors and the criterion steadily decrease. For example, if only individuals in the top 70 percent of scores on Z are selected (selection ratio of .7) and hence available for a validation study, the estimates of the correlations of Z and X with the criterion would be expected to decrease to .38 and .37, respectively. When only the upper 30 percent are selected, the corresponding correlations become .29 and .33, while for selection of the upper 5 percent they become .21 and .30. The effects of explicit and incidental selection shown in Table 1 clearly lead to a steady decrease in the assessed predictive values of Z and X when product-moment correlations are used to describe the degree of association with the criterion. However, the table also shows this decrease to be more dramatic for the explicit selection variable, Z, than it is for X. In spite of the fact that the population correlations indicate Z to be the better predictor, the effects of explicit selection on Z lead to a misleading indication that X is the better predictor once the selection ratio drops below .6. The degree by which one is misled clearly increases as the degree of selectivity increases. Examples such as these provide a clear indication that understanding of selection effects is crucial to the interpretation of results from criterionrelated validity studies. Without risk of hyperbole, one could say that the predictive validity of a selection instrument cannot be accurately characterized unless the possible effects of sample selection are accounted for to some extent.
Coping With the Effects of Selection
The subtle ways in which biases introduced by sample selection affect estimates of correlations in an entire applicant pool are difficult to account for in any exhaustive way; however, it is possible to obtain useful assessments of the degree of association between a set of predictors and a criterion even with selected samples. Although no method of adjusting for selection effects is without limitations, it is often possible to obtain a less biased indication of predictive validity either by employing an adjustment procedure or by examining alternatives to the validity coefficient.
Allred (in this volume) provides an excellent review of alternatives to the validity coefficient for describing the results of a predictive validity study, many of which are less sensitive to the effects of selection. The scatterplots shown previously are the most straightforward example of an alternative approach. They provide a very detailed representation of the relationship between a predictor and a criterion measure. Such detail can be important for detecting specific characteristics of the relationship—ceiling and floor effects, marked departures from linearity, changes in the degree of criterion variability depending on predictor score (heteroscedasticity), and outliers can all be discerned from careful inspection of a scatterplot. In addition to the scatterplot, Allred shows how graphical displays of the criterion distribution at fixed levels of the predictor can offer a more concise evaluation of potential nonlinearity and heteroscedasticity than the scatterplot. The various types of expectancy tables discussed by Allred provide estimates of the criterion performance expected for any prespecified level of performance on the predictor(s) and are also useful indicators of the predictor-criterion relationship. General measures of association used in the analysis of contingency tables (cf. Bishop et al., 1975) could conceivably be applied to such expectancy tables in order to provide a numerical index analogous to the correlation coefficient—but the tables are also valuable in their own right.
When scatterplots or plots of conditional distributions indicate that the relationship between predictor and criterion is approximately linear and homoscedastic, the use of the familiar summary statistics from correlation and regression is most meaningful. Although a bivariate, or in the case of multiple predictors multivariate, normal distribution of predictor(s) and criterion is not strictly required for these conditions to hold, normality is the basis for the significance tests and confidence intervals used for inferences about population correlations and regression parameters. The obvious difficulty for formal statistical inference in the context of a criterion-related validity study lies in the fact that the random sampling scheme required, given that normality conditions are satisfied, can seldom be attained in practice. The estimates of the unknown population values are biased by nonrandom sample selection—the adjustment procedures reviewed below
attempt to remove at least a portion of this bias by incorporating specific assumptions about the selection process into estimates of correlations and regression parameters.
Corrections for Sample Selection Bias
The most common procedures for adjusting correlations for the effects of sample selection were first introduced by Pearson (1903) for the bivariate case and later extended by Lawley (1943-1944) to the case of multiple predictors and criteria. These procedures are sometimes referred to as the Pearson-Lawley corrections and have been used extensively in validation research in certain Services for a number of years. As discussed by Lord and Novick (1968), Lawley's extension of Pearson's two- and three-variable corrections describes the relationships between complete sets of explicit and incidental selection variables based on two assumptions: (1) the regression of each incidental selection variable on any combination of the explicit selection variables is linear, and (2) the errors of estimate incurred in regressing incidental on explicit selection variables are constant (i.e., they are homoscedastic). When these conditions are satisfied, the covariances among the incidental selection variables can be expressed as
where C represents the variance-covariance matrix of the variables indicated by subscripts x and z, which refer to incidental and explicit selection variables, respectively. An asterisk is used to distinguish matrices based on the selected sample from those based on the unselected population.
As can be seen from the above expression, it is the relationship among explicit selection variables in the unselected population versus selected sample (Czz vs. ![]() ) that determines the size of the adjustment made by the Lawley correction procedure. For the case of no selection, Czz and
) that determines the size of the adjustment made by the Lawley correction procedure. For the case of no selection, Czz and ![]() are identical and the term in parentheses vanishes, yielding Cxx =
are identical and the term in parentheses vanishes, yielding Cxx = ![]() . As selection affects the elements of
. As selection affects the elements of ![]() , the elements of
, the elements of ![]() are adjusted accordingly.
are adjusted accordingly.
For the special case illustrated earlier, in which Z was the lone explicit selection variable and X and Y were incidental selection variables of substantive interest, the Pearson-Lawley expression for the correlation between X and Y in the unselected population is given by
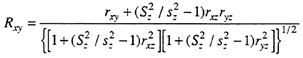
where upper-case R and S designate correlations and standard deviations in the unselected population, respectively, and lower-case r and s designate corresponding quantities in the selected sample. If the explicit selection variable, Z, were known, its standard deviation in the unselected population or applicant pool is all that would be necessary in addition to selected sample statistics in order to estimate the XY correlation. Thus, the expression given above would be applicable in a situation where, for example, selection was explicit on a composite variable, but interest in the correlations between individual elements of the composite and the criterion existed. Where a number of explicit selection variables are known, the Lawley extension of the above three-variable formula would provide the appropriate adjustment under assumptions (1) and (2).
Inspection of the above formula provides some insight into the concepts underlying this and other corrections for range restriction. The numerator of this formula shows that the sample rxy is being incremented by a factor related to the selection ratio and the magnitudes of the correlations between the explicit selection variable and the variables of substantive interest. As selectivity increases, the ratio of standard deviations in the unselected to selected groups becomes larger and the correction factor increases. Similarly, when the explicit selection variable is highly correlated with the variables of substantive interest, the correction factor can be quite large. In either case, the similarity of the above formula to the one used for calculating partial correlations makes clear that the adjustment for explicit selection on Z “undoes” precisely what partial correlation is designed to do. That is, instead of factoring out variance that is not considered related to the correlation between X and Y, the above equation factors in variance that is considered related to that correlation.
If X itself happens to be the explicit selection variable, the Pearson twovariable correction formula yielding Rxy can be obtained by simply substituting x for z in the subscripts of the above formula and simplifying the resulting expression, yielding
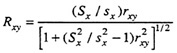
where upper- and lower-case quantities are defined as before. Because Z, conceived as a true selection variable, is not likely to be observed in practice, the above two-variable correction formula has been widely used, even when selection is not, strictly speaking, explicit on X.
The application of these formulas is quite simple and can be illustrated by again considering the scatterplots in Figure 2 and Figure 4. Recall that these plots depicted explicit selection on X and Z, respectively. When selection is
explicit on X, the two-variable selection formula gives a corrected estimate of .577 for the correlation between X and Y in contrast to the observed rxy of .398 in the selected sample. Similarly, when selection is explicit on Z, the three-variable formula gives a corrected estimate of .590 for Rxy in contrast to the rxy of .414 in the selected sample. As expected, the corrected values in these two instances are quite close to the population correlation of .60 in that assumptions (1) and (2) are perfectly satisfied and the correct explicit selection variable is available. Perhaps a more realistic example would depict X as the only available proxy for the unobserved true selection variable and treat it as explicit even though it is incidental. When the two-variable formula is thus used in the setting depicted in Figure 4, the corrected estimate of Rxy is .540, still smaller than the population correlation. As suggested below, this undercorrection is likely to be a common occurrence when the Pearson-Lawley procedures are used in practice.
Technical Considerations and the Accuracy of Pearson-Lawley Corrections
The principal technical issues that have implications for the value of corrections for range restriction in practice relate to their accuracy in the presence of violated assumptions and their degree of sampling error. With regard to the former area of concern, studies by Rydberg (1963), Linn (1968), Novick and Thayer (1969), Brewer and Hills (1969), Greener and Osburn (1979, 1980), Linn et al. (1981), Dunbar (1982), Gross and Fleischmann (1983), and Booth-Kewley (1985) have addressed the general issue of bias in results of range restriction adjustments when either regression or selection assumptions are not satisfied. Gullickson and Hopkins (1976), Forsyth (1971), Bobko and Rieck (1980), Dunbar (1982), Gross and Kagen (1983), Brandt et al. (1984), and Allen and Dunbar (1990) have provided descriptions of the sampling behavior of estimates of correlations and regression parameters that have been corrected for range restriction. The principal findings of some of these studies are reviewed below.
The concern regarding the effects of nonlinearity and/or heteroscedasticity in the criterion-predictor relationship is aptly expressed by Lord and Novick (1968), who argue that the Pearson-Lawley corrections can give overly optimistic indications of predictive validity when assumptions are not met. In spite of a common observation that departures from linearity and homoscedasticity are likely to occur at the same time in applied settings, most studies of the behavior of the Pearson-Lawley corrections under violated assumptions have examined nonlinearity and heteroscedasticity separately. Results of studies using both real and simulated data suggest that the effects of violated assumptions on the accuracy of the Pearson-Lawley corrections depend on the nature of the violation. Greener and Osburn
(1979, 1980), for example, found nonlinearity to be a more serious concern than heteroscedasticity for low to moderate degrees of selectivity when using Pearson's two-variable correction for explicit selection. These authors found a strong tendency toward undercorrection when the slope of the regression line was smaller in the extreme portions of the predictor scale than it was in the middle. Moreover, the magnitude of the undercorrection increased as the degree of selectivity increased. Dunbar (1982) obtained a similar result with simulated data, but also found that overcorrections could occur when the slope was higher in the extremes of the predictor scale than in the middle.
Although the effects of nonlinearity can be quite severe, it was a concern for heteroscedasticity in the joint predictor-criterion distribution that led Lord and Novick (1968) to their words of caution. Test scores in particular, they argued, tend to have distributional forms such that variation about a regression line is apt to be smallest in the tails. When only the upper 10 or 20 percent of an applicant group is selected, an inflated estimate of the population correlation can result. Novick and Thayer (1969) documented this effect for the case of explicit selection in an empirical study of the accuracy of the Pearson-Lawley correction formulas. Using real data sets truncated from the left to represent various degrees of range restriction, they found corrections to have uncertain precision for extreme degrees of selection and a preponderance of overcorrections in sets of data where the principal violation was the presence of heteroscedasticity. Greener and Osburn (1980) extended this finding through a more systematic set of simulated bivariate distributions in which the scatter around the regression line was reduced at the extremes of the predictor score distribution. They too found overcorrections to predominate when the selected sample represented less than half of the unselected population.
Booth-Kewley (1985) investigated the accuracy of univariate and multivariate corrections using ASVAB test scores and criterion data from seven Navy technical training schools. Time, expressed as number of days that a student took to complete the training course, served as the criterion variable. Validity coefficients of ASVAB tests for all students completing courses were used as unrestricted “population ” values for each course. Restricted samples with selection ratios of .10 through .90 in steps of .10 were created by truncation on the selection composite for each school. Multivariate corrections were generally closer to the unrestricted validities than were the univariate corrections, and the latter were still generally better than the uncorrected values. Overcorrections were common for both the univariate and multivariate procedures, however, perhaps because of the distributions of the criterion variable, time till completion.
Results that suggest the Pearson-Lawley correction formulas might lead to systematic overestimation of the predictor-criterion correlation are espe-
cially disturbing when one considers their practical application in educational or training programs in which the exact character of the joint predictor-criterion distributions cannot be determined. In such settings, however, it is likely that selection is not explicitly made on the basis of an available predictor or set of predictors, but is based on some kind of composite measure that is not perfectly correlated with available selection tests. If the selection tests are truly incidental selection variables, then in evaluating the above tendencies toward overcorrections under particular circumstances, one must consider the dual effect of violated assumptions regarding the selection process as well as the regressions of explicit on incidental selection variables. Linn and colleagues (Linn, 1968; Linn et al., 1981) have illustrated how substituting an incidental selection variable for an explicit selection variable in Pearson's two-variable formula results in a consistent bias toward undercorrection when other assumptions are satisfied and the correlation between the available and true selection variables is at least moderately positive. Whether or not this bias is sufficient to overshadow the potential for overcorrection in the situations noted above was examined by Dunbar (1982) and Gross and Fleischmann (1983). An example from the former illustrates some typical findings with regard to this question.
Dunbar's (1982) examination of the Pearson-Lawley corrections focused on the combined effects of violated assumptions and incompletely specified selection rules (i.e., selection rules where one or more factors involved in sample selection was ignored in the application of a correction formula). While selection was always based on a third variable, it was modeled by both a step function (as in explicit selection on Z) and a smooth probability function (as when an unknown factor like self-selection enters the selection process, making Z itself an incidental selection variable). Table 2 provides a summary of results from applying Pearson's two- and three-variable formulas to selected samples from four types of distributions of X, Y, and Z, such that
-
All regressions are linear and homoscedastic.
-
The regression of Y on Z and X has reduced slope at extreme predictor scores.
-
The regression of Y on Z and X has reduced scatter about the regression line at extreme predictor scores.
-
The regression of Y on Z and X has both reduced slope and scatter at extreme scores.
Case (2) was intended to provide a situation where undercorrection was likely, case (3) where overcorrection was likely, and case (4) where either under- or overcorrection could occur depending on how the effects of nonlinearity and heteroscedasticity interacted. Entries in the table, except where noted, represent average differences over 80 replications between sample correla-
TABLE 2 Average Differences Between Corrected and Population Correlations in Fisher's Z Equivalents
|
Selection |
Type of Y on X Regression |
||||
|
Rule |
Ratio |
(1) |
(2) |
(3) |
(4) |
|
Two–Variable Corrections |
|||||
|
Step |
.90 |
−.028 |
−.029 |
−.044 |
−.036 |
|
Function |
.50 |
−.118 |
−.124 |
−.122 |
−.130 |
|
.10 |
−.148 |
−.190 |
−.107 |
−.170 |
|
|
Smooth |
.49 |
−.048 |
−.048 |
−.050 |
−.051 |
|
Curve |
.37 |
−.112 |
−.123 |
−.113 |
−.127 |
|
.09 |
−.142 |
−.191 |
−.104 |
−.171 |
|
|
Three–Variable Corrections |
|||||
|
Step |
.90 |
−.001 |
.006 |
−.006 |
.000 |
|
Function |
.50 |
.001 |
−.018 |
.002 |
−.020 |
|
.10 |
−.006 |
−.124 |
.043 |
−.093 |
|
|
Smooth |
.49 |
.001 |
−.002 |
.001 |
−.004 |
|
Curve |
.37 |
.000 |
−.026 |
.004 |
−.025 |
|
.09 |
.008 |
−.127 |
.042 |
−.094 |
|
|
NOTE: Averages are over 80 replications except where selection ratios are .10 or .09, in which case 62 and 61 replications were performed, respectively. Type of Y on X regressions are: (1) linear and homoscedastic, (2) nonlinear, with reduced slope at extreme X scores, (3) heteroscedastic, with reduced scatter at extreme X scores, and (4) nonlinear and heteroscedastic, with reduced slope and scatter at extreme X scores. SOURCE: Based on Dunbar (1982). |
|||||
tions corrected for range restriction and population correlations, expressed as Fisher's Z equivalents.
Several striking patterns in the behavior of the Pearson-Lawley corrections can be discerned from the results in the table. First of all, when the two-variable correction was used in the absence of information concerning Z, undercorrections occurred regardless of the degree to which assumptions were satisfied. The bias toward undercorrection was larger for case (2); however, the dominant pattern is one of increasing negative bias as the selection ratio gets smaller. Of particular note in this regard was that for the heteroscedastic case (3), Dunbar's results indicated that the negative bias introduced by using the two-variable formula outweighed any positive bias introduced by reduced scatter about the regression line.
A second result that is noteworthy involved the interaction between nonlinearity and heteroscedasticity. When these assumptions were violated at the same time, the reduced slope at extreme X scores appeared to have a greater
effect on the accuracy of the corrected values than did reduced scatter, making undercorrections common even when the correct three-variable adjustment procedure was used. The dominant influence of nonlinearity was also noted by Gross and Fleischmann (1983), who also provide an important illustration of large overcorrections when the slope of the Y-on-X regression increased and the scatter about the regression line decreased with increasing predictor scores. However, Dunbar's results suggest that, to the extent reduced slopes at extreme predictor scores are more common in practice, the tendency toward underestimating the validity of a test considered to be only part of a selection decision is stronger than any tendency toward overestimation using the Pearson-Lawley corrections. This is not to say that overestimation will not occur, but rather that it is a bias less likely to occur in typical settings where predictive validity studies are conducted. Because some types of violations can lead to serious overcorrections, standard practice should include investigations of the plausibility of assumptions and the likely nature of any departures from linearity and homoscedasticity. Scatterplots, plots of conditional distributions of the criterion, and plots of residuals, such as those described by Allred (in this volume), can be useful in this regard.
The sampling behavior of correlation coefficients corrected for restriction of range is a second major area of concern in applications of the PearsonLawley adjustment procedures. As with any statistical procedure whose use involves some degree of uncertainty, that uncertainty clouds the precision of the resulting statistic as an estimate of a population parameter. As mentioned previously, the sampling error of adjusted correlations has been investigated both empirically (Forsyth, 1971; Gullickson and Hopkins, 1976; Dunbar, 1982; Gross and Kagen, 1983; Brandt et al., 1984 , and Allen and Dunbar, 1990) and analytically (Kelley, 1923; Cohen, 1955; Bobko and Rieck, 1980; Allen and Dunbar, 1990), with results in general agreement that standard errors of corrected correlations can be quite large under conditions of extreme selectivity.
Bobko and Rieck (1980) present an expression discussed by Kelley (1923) for the large-sample standard errors of correlation coefficients corrected for explicit selection. In the case of explicit selection on the predictor, the approximate standard error of the corrected correlation under bivariate normality is a function of the ratio of the standard deviation in the unselected population to that in the selected sample, the magnitude of the correlation in the selected sample, and the sample size. Table 3 illustrates the relative magnitudes of the standard errors of uncorrected, SE(r), and corrected, SE(R), correlations for situations in which the corrected correlation is equal to .5, the size of the sample is 100, and the variables follow a bivariate normal distribution. Given in the columns of the table are values of the ratios of standard deviations, uncorrected and corrected correlations, and their estimated standard errors. In addition, the last two columns of the table indi-
TABLE 3 Illustrative Values of Standard Errors of Correlations Equal to .5 after Correcting for Explicit Selection on the Predictor
|
K |
r |
SE(r) |
R |
SE(R) |
W |
N' |
|
1.0 |
.500 |
.075 |
.500 |
.075 |
1.000 |
00 |
|
1.2 |
.434 |
.081 |
.500 |
.086 |
1.065 |
14 |
|
1.4 |
.381 |
.085 |
.500 |
.098 |
1.151 |
35 |
|
1.6 |
.339 |
.088 |
.500 |
.110 |
1.249 |
58 |
|
1.8 |
.305 |
.091 |
.500 |
.123 |
1.354 |
83 |
|
2.0 |
.277 |
.092 |
.500 |
.135 |
1.465 |
117 |
|
2.2 |
.254 |
.094 |
.500 |
.148 |
1.579 |
147 |
|
2.4 |
.234 |
.095 |
.500 |
.160 |
1.696 |
185 |
|
2.6 |
.217 |
.095 |
.500 |
.173 |
1.815 |
232 |
|
2.8 |
.202 |
.096 |
.500 |
.186 |
1.936 |
275 |
|
3.0 |
.189 |
.096 |
.500 |
.198 |
2.058 |
328 |
|
NOTE: A sample of 100 in the selected group is assumed for all SE 's. The following notation is used for column headings: K is the ratio of the standard deviation in the unselected population to the standard deviation in the selected group. r is the correlation in the selected group. SE(r) is the estimated standard error of r. R is the correlation corrected for explicit selection on the predictor. SE(R) is the approximate standard error of the corrected correlation. W is the factor by which the standard error of the observed correlation is increased due to correction for explicit selection. N' is the number of additional cases required for the SE(R) to equal SE(r) when the latter is based on 100 cases. |
||||||
cate, respectively, the factor by which correcting for range restriction increases the standard error and the number of observations represented by the loss in precision as a result of correcting. The last column, in other words, gives the approximate number of additional observations required for the corrected estimate to be as precise an estimate of the population correlation as the uncorrected estimate is with a sample size of 100.
As can be seen from the entries in the table, under conditions of minimal selection, the loss in precision incurred by correcting for range restriction is relatively minor. When the ratio of standard deviations, K, is slightly greater than 1, the standard error of the corrected correlation, SE(R), is only 1.065 times larger than the corresponding value for the uncorrected correlation, SE(r). However, when the standard deviation in the unselected population is twice as large as it is in the selected sample (K = 2.0), SE(R) is nearly half again as large as its uncorrected counterpart. In this case, the loss in precision translates into a need for about 117 additional observations in order for a corrected estimate under this degree of selectivity to have as much preci-
sion as has the uncorrected estimate from a sample of 100. When the standard deviation is three times as large in the unselected group, the loss in precision represents a need for 328 additional observations.
Clearly, for situations of extreme degrees of explicit selection on the predictor, the gain in terms of reduced bias via adjusting for selection effects can be completely undermined in terms of increased uncertainty associated with the resulting point estimate (Gross and Kagen, 1983). Moreover, empirical results suggest that this increased uncertainty can have even more deleterious effects under conditions of violated assumptions (Dunbar, 1982). The illustrations in Table 3 reflect approximate sampling fluctuations when specific distributional assumptions are satisfied exactly. If uncertainty also exists with respect to specification of explicit selection variables, the efficiency of a corrected correlation can be expected to decrease even further. This added uncertainty should be kept in mind when interpreting correlations that have been corrected for restrictions of range. Allen and Dunbar (1990) provide more recent results on the sampling behavior of correlations corrected for incidental selection.
Alternative Adjustment Procedures
Recently, the Pearson-Lawley correction formulas have been given a richer conceptual framework by the selection modeling approach to dealing with nonrandom sampling. Although the substantive concerns of researchers using selection modeling techniques are often in the area of evaluation of educational and social programs (e.g. Heckman, 1974; Hausman and Wise, 1976; Cronbach, 1982) with nonequivalent control group designs, their techniques are closely related in intent to the Pearson-Lawley procedures, in that they seek less biased estimates of treatment effects associated with independent variables. As will be seen in the review presented below, many selection modeling approaches derive flexibility in adjusting for sample selection bias at the expense of more stringent assumptions about the nature of the selection process. Some methods also require more complex procedures for the estimation of parameters and larger sample sizes for acceptable degrees of efficiency in parameter estimation. In spite of these difficulties in implementation, a more complete understanding of the validation problems described at the outset of this paper can be gained from a brief review of this general approach.
Muthén and Jöreskog (1983) provide an overview of some basic selection modeling procedures. The bias in rxy, bo, and bx when X and Y are incidental selection variables provides a relatively simple case for purposes of illustration. If Z is assumed to be the only explicit selection variable, then the selection process is described by a threshold value, t, such that observations exist in the selected sample only when Z > t; in other words, t
is a cut score that truncates the distribution of Z in the selected sample. The regression or conditional expectation of the criterion given values on the predictor of substantive interest then becomes
E(Y\X, Z > t) = bo + bxX + E(e\Z > t).
The final term in the above expression conveys the notion that predictions of one incidental selection variable from another are not unbiased. Here the bias is reflected in a conditional expectation of prediction error that is nonzero. Muthén and Jöreskog (1983) show that E(e\Z > t) depends on the shape of the distribution of Z, the explicit selection variable. When a particular distributional form is specified for Z (or, for that matter, an entire set of Zs), maximum likelihood estimates for parameters in the above equation can be developed giving consistent estimates for the regression parameters and correlation coefficient (cf. Goldberger, 1980). Although particular procedures for accomplishing this have been introduced by Tobin (1958), Heckman (1979), and Muthén and Jöreskog (1983), to mention a few, for the special case of multivariate normality among all variables (explicit and incidental) it also appears that maximum likelihood estimates can be obtained directly from the Pearson and Lawley formulas (Cohen, 1955; Muthén and Jöreskog, 1983). Methods that are based on other distributional forms can require complex iterative procedures for estimating parameters for which convergence to a proper solution is not always guaranteed. Application of these procedures during the normal course of validation activities may not be feasible, given the present state of their development.
In addition to the complete maximum likelihood approaches mentioned above, methods for modeling the selection process as a kind of two-stage procedure have been used with some success (see, for example, Heckman, 1979). In these approaches, the information usually assumed to be available consists of scores on selection variables for all individuals, a binary variable equal to 1 if an individual is selected and 0 otherwise, and a criterion measure for all individuals selected. For multivariate normal selection variables, Heckman's (1979) two-stage approach to adjusting for selection effects involves:
-
estimating the nonzero conditional expectation of prediction error for individuals via probit regression of the binary variable on the selection variables and
-
entering this estimate (the selection term) along with the predictors of substantive interest in an ordinary least-squares regression, using criterion data from the selected sample.
The first step in this approach provides an indication, loosely speaking, of the chance that a given individual will be lost due to sample selection;
adding this as a term in the regression equation provides an adjustment for the fact that sample selection is not random. Heckman (1979) showed that this two-stage procedure provides consistent estimates of slopes and intercepts in the regression equation for the selected sample. In validation studies where interest focuses on predicted criterion scores for individuals, as in many studies of differential prediction, the Heckman adjustment can provide less biased assessments of expected performance over a range of predictor scores. This may be relevant to certain types of group comparisons in the Joint-Service context, where a common criterion variable exists. The general approach can also be adapted to provide an alternate means of correcting correlation coefficients, albeit at the expense of distributional assumptions about the selection variables that are not required by the PearsonLawley procedures.
A simple example of the effects of the Heckman adjustment illustrates its potential use in criterion-related validity studies. Table 4 shows the results of Heckman's two-stage procedure applied to data from the simulated trivariate normal distribution referred to previously in the context of Figure 4. Recall that the population correlations between Y and each of Z and X were .60, the correlation between Z and X was .90, and the variables were standardized so that the intercept and slope of the Y-on-X regression were 0 and .6, respectively. The table contains adjusted and unadjusted estimates of this intercept and slope for samples selected from either the upper 10 or 50 percent of the population distribution of the selection variable, Z. Also given are the intercept and slope in the sample of 5,000 cases from which the selected samples were actually drawn. Below each parameter estimate the corresponding standard error is given in parentheses.
Entries in Table 4 show the same bias for parameter estimates in the regression equation that was discussed with respect to correlation coefficients. When the selection ratio is .50, the adjustment made by the Heckman procedure is small but provides very accurate point estimates; moreover, the weight assigned to the selection term estimated in the probit stage is moderate. On the other hand, the standard errors of the adjusted values are noticeably larger than those of their unadjusted counterparts, indeed sufficiently larger that the adjusted point estimate of both intercept and slope is within two standard errors of the unadjusted sample value. This phenomenon is exacerbated when the selection ratio drops to .10, with less encouraging results concerning the point estimates themselves. Here the slope is overestimated, the intercept is underestimated, and a band extending two standard errors to either side of the adjusted value encompasses the entire width of the same band around the unadjusted value. Note also that the weights assigned to the selection terms for both selection situations are close enough to zero in standard error units to allow one to incorrectly conclude that selectivity is negligible in each case.
The above results illustrate one feature of the two-stage procedures that
TABLE 4 Illustration of the Heckman Adjustment Under Two Degrees of Selection on Z
|
Population Correlation |
X |
1.0 |
||
|
Matrix |
Y |
.6 |
1.0 |
|
|
Z |
.9 |
.6 |
1.0 |
|
|
Regression Equation in Sample of 5,000 |
Y = −.013 + .596(X) |
|||
|
Selection Ratio |
||||
|
.50 |
.10 |
|||
|
Parameter |
Uncorrected |
Corrected |
Uncorrected |
Corrected |
|
Intercept |
.089 |
−.007 |
.396 |
−.340 |
|
(.023) |
(.069) |
(.108) |
(.546) |
|
|
Slope for X |
.529 |
.597 |
.407 |
.720 |
|
(.023) |
(.053) |
(.065) |
(.239) |
|
|
Selection Term |
— |
.129 |
— |
.314 |
|
(.085) |
(.226) |
|||
|
NOTE: Standard errors are given in parentheses. |
||||
may limit their utility in the context of test validation. As withany selection modeling approach, the accuracy obtained is contingent on correct specification of the selection process and inclusion of all relevant variables in the probit stage. As noted by Cronbach (1982), if important variables are omitted during estimation of the term representing the probability of selection, then the adjustment will only remove a portion of the bias due to sample selection. This situation parallels the use of Pearson's two-variable correction when selection is actually incidental. However, as more variables are used to describe the selection process accurately, overlap between independent variables in the probit and least-squares stages of the procedure is likely to increase, leading to a selection term that tends to be highly correlated with other predictors in the least-squares model. The resulting collinearity contributes an added degree of instability in the adjusted parameter estimates beyond the instability to be expected simply because adjusted estimates are being employed. In the example, the large standard errors are due in part to the high correlation between Z and X and to the fact that both variables were included in the probit regression analysis. The problem this poses for criterion-related validity studies lies in the fact that most potential selection variables are precisely those variables whose use as predictors is being validated. Under these circumstances, one might expect the standard errors of the adjusted estimates to be too large to allow for useful inferences
about population correlation coefficients and regression parameters when selection is severe. In other situations, either where selection is moderate or reasonable values for variances in the unselected group are difficult to determine, the two-stage procedure may have some promise.
Some of the technical limitations of the Heckman approach alluded to in the above example have been studied in greater detail, with concern again centering on violated assumptions regarding the distribution of selection variables and on sampling fluctuations of the adjusted estimates. Goldberger (1980) addressed the problem of bias in the adjustment when the selection variables are not normally distributed, suggesting that it can be quite large with only modest departures from normality. When the specific departure is such that the regression of Y on X has a reduced slope in the upper range of the X scores, the two-stage adjustment tends to be conservative, just as did the Pearson-Lawley corrections in this situation (Dunbar, 1982). Unfortunately, this and other selection modeling approaches have seen limited use in empirical studies of criterion-related validity; as a consequence, there is presently little basis for judging how they might perform if used in largescale validation studies.
Sampling fluctuations and the efficiency of estimates obtained in the selection modeling approaches have also received attention recently, particularly in Nelson's (1984) examination of the behavior of the Heckman two-step method, Olsen's (1980) least-squares version of the method, and a full maximum likelihood version with respect to the degree of collinearity introduced by overlap between variables describing the selection process and variables to be evaluated as predictors. Nelson's results confirm the general suspicions aroused concerning the two-step methods by the example given previously: adjustments for selection bias are most needed precisely when the two-step methods for making them are ineffectual. That is, the high degree of collinearity expected when the selection process is completely specified resulted in unacceptable sampling errors in the parameter estimates from the Heckman and Olsen procedures. Nelson's results showed the full maximum likelihood method to perform better under most circumstances in his simulation study—to the extent that this method is related in spirit to the Pearson-Lawley corrections, some preference for the latter might be inferred from these results. In any case, it appears that a more careful evaluation of some of the alternative approaches to dealing with range restriction problems needs to be made in the context of test validation research before such methods can be used with much confidence on a large scale. Some of the Services are currently engaged in such efforts—results from such studies can have direct implications regarding the expected accuracy of selection modeling approaches in the Joint-Service context (see Rossmeissl and Brandt, 1985; Dunbar, 1986).
A final note on alternative procedures concerns the potential application
of certain Bayesian approaches to handling the missing data problem caused by selection. Rubin (1977), for example, developed a method for assessing the influence of nonrespondents on the results of sample surveys based on subjective notions about the characteristics of nonrespondents. These notions are formalized in terms of the parameters of prior distributions for observations in the nonrespondent population.
In a test validation context, one might consider unselected examinees as analogous to the nonrespondents that Rubin's methods are designed to handle, nonrespondents with particular characteristics because of administrative as well as self selection. Herzog and Rubin (1983) and Glynn, et al. (1986) provide extended discussions and examples of how repeated imputations of missing observations based on a variety of prior distributions can be used together with available data to estimate the desired parameters of a combined population of selected and unselected examinees. The combination of such “mixture models ” with repeated imputations from a range of reasonable prior distributions can make explicit the amount of uncertainty that exists regarding the predictive validity of a test. As noted by Rubin (1977), these methods, and perhaps any method for handling selection bias, are best considered as ways of formalizing the possible effects of missing observations on outcome measures rather than as substitutes for random samples normally required for valid inferences about the characteristics of a population.
IMPLICATIONS FOR PREDICTIVE VALIDITY IN A JOINT-SERVICE CONTEXT
The problem of range restriction is not new to anyone concerned with establishing the criterion-related validity of selection and classification tests in the Services, although the methods for coping with it have been far from uniform over the years. Some Services have used either the Pearson or Lawley corrections routinely in reporting the results of validity studies for the ASVAB and its predecessors, while others have questioned this use, especially when validation is conducted within particular occupational categories (cf. Sims and Hiatt, 1981; and Air Force Human Resources Laboratory, 1982, for an instance of this contrast of viewpoints). Because many things can affect the magnitudes of correction factors, comparison of corrected correlations across Services is not a simple task. The choice of analytical procedures, base or reference populations to which the corrected estimates are intended to generalize, and the variables that are to serve as explicit selection measures can all influence the magnitudes of corrected estimates of predictive validity. These issues are discussed in what follows as they relate to the use of adjustment procedures for validating the ASVAB against measures of performance in current use for military jobs, and for
validating alternative measures of job proficiency (surrogate criteria) against on-site evaluations of job performance (benchmark measures).
Analytical Procedure
The demands on a procedure for dealing with selection effects in the Joint-Service context for military performance assessment are not typical of many settings in which test validation studies are conducted. One purpose behind Service-wide efforts in this regard is the achievement of a degree of comparability in characterizations of predictive validity
-
across Services,
-
across jobs of a similar nature within and between Services, and
-
across jobs that involve different tasks and hence different combinations of ASVAB subtests for selection.
Moreover, a concern exists for examining the consistency of predictions of performance criteria for groups of military trainees distinguished by sex, race or ethnicity, and level of education. Comparisons of this kind, which make the cooperative venture especially useful, can be hopelessly confounded by varying degrees of range restriction in the groups involved. This problem is duly noted with respect to comparisons across occupations in the work of Schmidt and Hunter (1977) on validity generalization, and with respect to comparisons across demographic groups in the work of Linn (1983a, 1983b) on differential prediction. An important observation regarding the purpose of corrections for range restriction with such comparisons in mind is that they are as much needed to obtain comparability as they are to provide precise estimates of population values. Because they are also to be used with a variety of criterion measures (surrogate as well as benchmark measures of job performance), their limitations need to be fully understood and appreciated.
As indicated at various points in the preceding review, the standard PearsonLawley correction procedures are familiar to most personnel psychologists and appear to have been carefully evaluated in both analytical and empirical studies, many of the latter being performed with the specific problems of criterion-related validity in mind. The limitations of these procedures and the conditions under which they are likely to give misleading indications of predictive validity are well documented. In contrast to these conventional techniques, the procedures based on selection modeling are in comparative infancy. Their relationship to the conventional procedures is only partially understood and their use in the context of predictive validity studies has been all but nonexistent. In addition, the sample size requirements of the more sophisticated estimation methods accompanying some of the selection
modeling procedures may not be met by many military job classifications for which validity checks are desired. Thus, it is probably premature to endorse these newer methods in the context of ASVAB validation. Regarding their use on a routine basis, more caution is probably warranted due to the multiplicity of alternate methods and to problems in the technical implementation of some. It is also premature, however, to dismiss these methods as inappropriate for criterion-related validity studies in general—further investigations of these techniques with military performance data is to be encouraged.
Reference Population
Results from the application of any adjustment procedure necessarily reflect the characteristics of the group from which information about the unselected population is obtained. In cases where the Pearson-Lawley corrections are used, the source of estimates of the variances and covariances of selection variables in the unrestricted group, in addition to the selection process itself, determines the magnitude of any correction factor. Variations in these estimates, such as those caused by preexisting differences between potential enlistees opting for one Service over the others, result in correction factors of varying magnitudes and make the corrected values difficult to interpret. For these reasons, when comparison across Services is important, using the entire accession populations within Services in a given year as reference groups would be counterproductive. The corrected predictive validities for selection composites would differ from Service to Service as well as from year to year. Clearly, a reference population common to all Services reporting predictive validities for the ASVAB is desirable.
Recent versions of the ASVAB have been anchored to a nationally representative sample of men and women drawn as part of the National Longitudinal Survey (NLS) of Youth Labor Force Behavior, sponsored by the Departments of Labor and Defense and usually referred to as the 1980 Youth Population (U.S. Department of Defense, 1982). Although the 1980 Youth Population does not precisely reflect current applicant pools for each Service, it does provide a frame of reference that would allow corrected correlations to be directly comparable across Services. Moreover, it does not constitute a group about which concerns over self-selection phenomena would arise, as would be the case for an accession population.
In spite of the fact that the 1980 Youth Population is the closest example of any kind of normative group for dealing with the effects of range restriction, there are some limitations in using it. As a representative sample of the nation's youth, this group contains individuals who would be judged ineligible for military service on the basis of ASVAB scores used in the initial screening of enlistees and is thus atypical of a projected mobilization
population in the wider range of talent represented. With this wide range of talent, one could expect correction factors to be quite large in some cases, certainly larger than expected when interest is focused on the predictive validity of ASVAB composites for only those recruits who have passed an initial screening. In view of the fact that corrections based on the total 1980 Youth Population might be artifactually large, some portion of this group might be best chosen to meet the need of adjusting validity coefficients for comparability across Services. The effects of suggested restrictions of the Youth Population on the magnitudes of correction factors are illustrated in the example presented below.
In order to provide an idea of the kinds of results to be expected when using the Pearson-Lawley correction procedures in connection with the 1980 Youth Population, an example is given in Table 5 based on training data from nine Marine Corps clerical specialties. Given in Table 5 are uncorrected and corrected correlations between the ASVAB clerical composite from Forms 8/9/10 used by the Marine Corps and final course grades in training. The Lawley corrections given in the table assume the 10 individual subtests to be explicit selection variables, and the composite and course grades to be incidental selection variables. The adjusted values given in column A were obtained by using the variances and covariances of subtest standard scores for the total Youth Population (U.S. Department of Defense, 1982). To approximate the situation in which only that portion of the Youth Population eligible for military service is used, subtest standard deviations from the total sample were adjusted for four degrees of truncation under the assumption that each subtest followed a normal distribution. The resulting reduced standard deviations were used along with the original correlations from the total sample in obtaining a variance-covariance matrix among explicit selection measures that would provide a rough indication of how much smaller correction factors might be with ineligible examinees deleted from the reference group. This procedure probably underestimates the amount by which correction factors would change if, for example, the bottom 10 percent of the AFQT distribution (the actual screening composite) were deleted from the reference group since only the standard deviations were altered in the calculations.
As can be seen from the entries in Table 5, the Lawley corrections suggest that the amount of range restriction in these groups is substantial in nearly all cases. For the specialties with reasonably large sample sizes, the smallest difference between corrected and unconnected validity coefficients is .19 in the second administrative group. For other training courses, the corrections in column A based on the entire Youth Population are quite large. The range restriction phenomenon is further illustrated in the lower portion of Table 5, which contains subtest standard deviations for each training cohort and for the entire Youth Population. Inspection of these
TABLE 5 Corrected Predictive Validities of the Marine Corps Clerical Composite in Nine Clerical Training Programs Based on 1980 Youth Population and Subtest Standard Deviations in Selected and Unselected Groups
|
Panel (a) |
|||||||
|
Corrected Validities |
|||||||
|
Training Program |
N |
Uncorrected Validity |
A |
B |
C |
D |
E |
|
Administrative 1 |
632 |
.32 |
.56 |
.52 |
.50 |
.48 |
.46 |
|
Administrative 2 |
620 |
.25 |
.44 |
.41 |
.39 |
.37 |
.36 |
|
Communications center |
332 |
.19 |
.56 |
.52 |
.50 |
.48 |
.47 |
|
Supply stock |
653 |
.47 |
.69 |
.65 |
.63 |
.62 |
.60 |
|
Aviation supply |
379 |
.30 |
.55 |
.51 |
.49 |
.47 |
.45 |
|
Finance records |
227 |
.20 |
.65 |
.62 |
.60 |
.58 |
.57 |
|
Basic preservation |
51 |
.28 |
.36 |
.34 |
.33 |
.32 |
.31 |
|
Subsistence supply |
66 |
.11 |
.59 |
.56 |
.54 |
.52 |
.51 |
|
Aviation operations |
87 |
.36 |
.66 |
.63 |
.61 |
.59 |
.57 |
values shows the varying degrees of selectivity across groups. Generally speaking, the standard deviations in the training cohorts are one-half to two-thirds the size of the corresponding values in the proposed reference population.
The effects of removing ineligible individuals from the Youth Population prior to adjusting the predictive validities of the clerical composite for se-
lection effects are shown in columns B through E in the upper portion of Table 5. Even after deleting lower scoring individuals, it appears that corrected values remain likely to be substantially larger than the uncorrected ones in some cases—extreme selection in some occupational specialties, such as the financial records clerk group in this instance, makes this result unavoidable. However, the relative magnitudes of the corrected validity coefficients across training programs remain the same regardless of the proportion of the reference group that is deleted.
It should be noted that the regular pattern of steadily decreasing estimates of predictive validity for increasing degrees of truncation in the proposed reference population is to be expected when the selection variables (here ASVAB subtests) have symmetric distributions, as assumed in this illustration. ASVAB subtests are well known to have nonsymmetric distributions. This is likely to influence the pattern of decreasing estimates of validity when the reference population is truncated on AFQT. Indeed, Maier (1985) has shown that the effects of truncation on the multivariate corrections are more complex than the example here would indicate, in part because of skewness in the distributions of selection variables and in part because of the effects of truncation on the covariances of selection variables. Neither factor is considered in the example presented above.
Selection Variables
In the above example, individual ASVAB subtests served as explicit selection variables. In practice, most job training programs in the military make use of one or more composite measures in selecting recruits for training. Typically, cut scores for selection are established on the composite scale separately for high school graduates and nongraduates, making high school graduation an additional selection variable. This custom poses several problems for the usual correction procedures in the Joint-Service context. First of all, ASVAB selection composites are not uniform from Service to Service, so that using the actual selection measure would again militate against the goal of comparability in the resulting values. Here, comparability is in direct conflict with accurate specification of the selection process. If using the subtests instead of the composite measures means that the selection mechanism is incompletely specified, the Pearson-Lawley corrections might likely give conservative indications of the predictive validity of the composites. Second, the inclusion of graduation status as a dichotomous selection variable in the Pearson-Lawley formulation is reasonable in principle, but complicated by the fact that certain job training programs admit only recipients of high school diplomas. No variability in the selected sample for such groups represents a kind of limiting case for the Pearson-Lawley procedure, in which no simple correction for range restriction is feasible. It would therefore seem appropriate to consider ASVAB subtests as the only avail-
able measures that are both closely related to the selection process and common to all Services. Any systematic errors incurred as a result of this choice are likely to result in corrected validities that are smaller than they might otherwise be with more detailed specification of the selection mechanisms operating for individual training and occupational cohorts.
In considering the choice of variables used in correcting for range restriction, the properties of criterion measures should not be overlooked. Selection effects are likely to increase when surrogate and benchmark measures are used as criteria. General attrition can be expected to alter the distribution of both types of measures relative to the distribution of final grades in training, and the logistic problems of collecting systematic on-site evaluations of performance could have unknown effects on the range of talent represented in the distributions of benchmark variables. If selectivity is augmented by factors such as these, both the bias error and sampling error of corrected correlations will be affected and the degree of uncertainty regarding the resulting values magnified. The possible presence of additional sources of unreliability in alternative performance measures is another area of concern. While it may be the case that all of these factors (i.e., added selectivity and measurement error) suggest an increased tendency for the Pearson-Lawley corrections to be conservative, their exact influence in individual cases is difficult to determine. To the extent that unreliability may effect corrections that are overly conservative, additional corrections for attenuation might be appropriate. These would of course increase the sampling errors of observed values even further.
CONCLUDING REMARKS
The effects of selection on correlation coefficients and regression parameters place the personnel psychologist on the horns of a classic statistical dilemma. To retain observed values gives an extremely misleading view of the relationship between predictor and criterion variables, but to correct observed values places one at the mercy of assumptions that will not be strictly satisfied in practice and of an added degree of uncertainty in estimating population values. While there is no inherent magic in any procedure for dealing with the effects of selection bias, neither is there an inherent sorcery. Rather, a balanced indication of the quality of a given predictor can be achieved by reporting both uncorrected and corrected validity coefficients and by careful documentation of the methods used to obtain the corrected estimates. The tenability of assumptions can be examined in individual cases through the use of graphical techniques described elsewhere, and in some cases reasonable speculation about the influence of violated assumptions can be entertained. The review of analytical techniques suggested the use of the standard Pearson-Lawley correction formulas in vali-
dation studies involving Service-wide applications. A common reference population and set of explicit selection variables also seem desirable for any degree of comparability to be achieved through corrections for restriction of range. When a summary statistic is needed to describe the predictive validity of a selection instrument in a variety of settings, these approaches can provide a more complete assessment of the relationship between that instrument and the relevant measures of on-the-job performance.
REFERENCES
Air Force Human Resources Laboratory 1982 Aptitude Index Validation of the Armed Services Vocational Aptitude Battery (ASVAB) Forms 5, 6, and 7. Air Force Human Resources Laboratory, Personnel Research Division Lackland Air Force Base, Tex.
Allen, N.L., and S.B. Dunbar 1990 Standard error of correlations adjusted for incidental selection. Applied Psychological Measurement, 14:83-94.
Bishop, Y.M.M., S.E. Fienberg, and P.W. Holland 1975 Discrete Multivariate Analysis: Theory and Practice. Cambridge, Mass.: MIT Press.
Bobko, P., and A. Rieck 1980 Large sample estimators for standard errors of functions of correlation coefficients. Applied Psychological Measurement 4:385-398.
Booth-Kewley, S. 1985 An Empirical Comparison of the Accuracy of Univariate and Multivariate Corrections for Range Restriction. TR-85-19. Navy Personnel Research and Development Center, San Diego, Calif.
Brandt, D., D. McLaughlin, L. Wise, and P. Rossmeissl 1984 Complex Cross-Validation of the Validity of a Predictor Battery. Paper presented at the annual meeting of the American Psychological Association, Toronto.
Brewer, J., and J.R. Hills 1969 Univariate selection: the effects of size of correlation, degree of skew, and degree of restriction. Psychometrika 34:347-361.
Cohen, A.C. 1955 Restriction and selection in samples from bivariate normal distributions Journal of the American Statistical Association 50:884-893.
Cronbach, L.J. 1982 Designing Evaluations of Educational and Social Programs. San Francisco: JosseyBass.
Cronbach, L.J., D.R. Rogosa, R.E. Floden, and G.G. Price 1977 Analysis of Covariance in Non-Randomized Experiments: Parameters Affecting Bias. Occasional paper, Stanford Evaluation Consortium, Stanford University.
Dunbar, S.B. 1982 Corrections for Sample Selection Bias. Unpublished doctoral dissertation, Department of Educational Psychology, University of Illinois at Urbana-Champaign.
1986 Comparing Regression Equations Across Training Programs: An Empirical Study of Prior Selection Effects and Alternative Predictive Composites ONR Technical Report 86-1: Measurement Research Group, Iowa City, Iowa.
Forsyth, R.A. 1971 An empirical note on correlation coefficients corrected for restriction of range. Educational and Psychological Measurement 31:115-123.
Glynn, R.J., N.M. Laird, and D.B. Rubin 1986 Selection modeling versus mixture modeling with non-ignorable nonresponse In H. Wainer, ed., Drawing Inferences from Self-Selected Samples. New York: SpringerVerlag.
Goldberger, A.S. 1980 Abnormal Selection Bias. Workshop Paper 8006. Social Systems Research Institute, University of Wisconsin-Madison.
Greener, J.M., and H.G. Osburn 1979 An empirical study of the accuracy of corrections for restriction in range due to explicit selection. Applied Psychological Measurement 3:31-41.
1980 Accuracy of corrections for restriction in range due to explicit selection in heteroscedastic and non-linear distributions. Educational and Psychological Measurement 40:337346.
Greenlees, J.S., W.S. Reece, and K.D. Zieschang 1982 Imputation of missing values when the probability of response depends on the variable being imputed. Journal of the American Statistical Association 77:251-261.
Gross, A.L., and L. Fleischmann 1983 Restriction of range corrections when both distribution and selection assumptions are violated. Applied Psychological Measurement 7:227-237.
Gross, A.L., and E. Kagen 1983 Not correcting for restriction of range can be advantageous. Educational and Psychological Measurement 43:389-396.
Gullickson, A., and K. Hopkins 1976 Interval estimation of correlation coefficients corrected for restriction of range. Educational and Psychological Measurement 36:9-25.
Gulliksen, H. 1950 Theory of Mental Tests. New York: John Wiley & Sons. Hausman, J.A., and D.A. Wise 1976 The evaluation of results from truncated samples: the New Jersey income maintenance experiment. Annals of Economic and Social Measurement 5:421-445.
Heckman, J.J. 1974 Shadow prices, market wages, and labor supply. Econometrica 42:679-694.
1979 Sample selection bias as a specification error. Econometrica 47:153-161.
Herzog, T.N., and D.B. Rubin 1983 Using multiple imputations to handle nonresponse in sample surveys In W.G. Madow, I. Olkin, and D.B. Rubin, eds., Incomplete Data in Sample Surveys, Volume 2. Theory and Bibliographies. New York: Academic Press.
Kelley, T.L. 1923 Statistical Method. New York: MacMillan & Co.
Lawley, D. 1943–1944 A note on Karl Pearson's selection formulae. Royal Society of Edinburgh: Proceedings, Section A 62:28-30.
Linn, R.L. 1968 Range restriction problems in the use of self-selected groups for test validation. Psychological Bulletin 69:69-73.
1983a The Pearson correction formulas: implications for studies of predictive bias and estimates of educational effects in selected samples. Journal of Educational Measurement 20:1-15.
1983b Predictive bias as an artifact of selection procedures. In H. Wainer and S. Messick, eds., Principals of Modern Psychological Measurement: A Festschrift for Frederic M. Lord. Hillsdale, N.J.: Lawrence Erlbaum Associates.
Linn, R.L., D.L. Harnisch, and S.B. Dunbar 1981 Corrections for range restriction: an empirical investigation of conditions resulting in conservative corrections. Journal of Applied Psychology 66:655-663.
Lord, F.M., and M.R. Novick 1968 Statistical Theories of Mental Test Scores. Reading, Mass.: Addison-Wesley.
Maier, M.H. 1985 Effects of Truncating a Reference Population on Corrections of Validity Coefficients for Range Restriction. Research Memorandum 85-40. Center for Naval Analyses, Alexandria, Va.
Muthén, B., and K.G. Jöreskog 1983 Selectivity problems in quasi-experimental studies. Evaluation Review 7:139-174.
Nelson, F.D. 1984 Efficiency of the two-step estimator for models with endogenous sample selection. Journal of Econometrics 24:181-196.
Novick, M.R., and D.T. Thayer 1969 An Investigation of the Accuracy of the Pearson Correction Formulas . Research Memorandum 69-22. Princeton, N.J.: Educational Testing Service.
Olsen, R.J. 1980 A least-squares correction for selectivity bias. Econometrica 48:1815-1820.
Pearson, K. 1903 Mathematical contributions to the theory of evolution—XI: On the influence of natural selection on the variability and correlation of organs. Philosophical Transactions of the Royal Society, London, Series A 200:1-66.
Rossmeissl, P., and D. Brandt 1985 Modeling the Selection Process to Adjust for Restriction in Range Paper presented at the annual meeting of the American Psychological Association, Los Angeles.
Rubin, D.B. 1977 Formalizing subjective notions about the effects of nonrespondents in sample surveys. Journal of the American Statistical Association 72:538-543.
Rydberg, S. 1963 Bias in Selection. Stockholm: Almquist and Wiksell.
Schmidt, F.L., and J.E. Hunter 1977 Development of a general solution to the problem of validity generalization Journal of Applied Psychology 62:529-540.
Sims, W.H., and C.M. Hiatt 1981 Validation of the Armed Services Vocational Aptitude Battery (ASVAB) Forms 6 and 7 with Applications to ASVAB Forms 8, 9 and 10. Report 1160. Center for Naval Analyses, Alexandria, Va.
Thorndike, R.L. 1949 Personnel Selection. New York: John Wiley and Sons.
Tobin, J. 1958 Estimation of relationships for limited dependent variables. Econometrica 26:24-36.
U.S. Department of Defense 1982 Profile of American Youth: 1980 Nationwide Administration of the Armed Services Vocational Aptitude Battery. Office of the Assistant Secretary of Defense (Manpower, Reserve Affairs and Logistics), Washington, D.C.































