Alternatives to the Validity Coefficient for Reporting the Test-Criterion Relationship
Linda J. Allred
Test scores are widely used as the basis for personnel decisions such as selection and placement. Applicants for clerical positions must pass a typing test, colleges require some minimum score on the Scholastic Aptitude Test, and government employees take the Civil Service examinations. Even preschoolers must meet minimum standards on intelligence tests for admission to many private kindergartens. These testing programs provide an objective method of screening individuals to find those best qualified for the job in question. (The use of the word job in this sense refers to any employment, training, or academic situation in which a testing program is used.)
The effectiveness of a testing program in selecting appropriate individuals depends on how well the test scores correspond with some objective measure of actual performance. The relationship of test scores to an objective performance measure is called predictive validity.
The assessment of validity requires first of all a performance measure to serve as the criterion against which the test is validated. The criterion might be simply success or failure, or retention or dismissal, but a more precise measure of achievement or performance allows a better validation. Here, a suitable measure of performance is presumed to exist. In addition, for purposes of this discussion, it is assumed that a group of persons is tested and then hired, selected, or appointed without regard to the test, so that the full potential effect of the test can be examined.
The relationship between test scores and performance is often expressed
as a validity coefficient (r), a number between 0 and 1.0 that indicates how well the performance measure, or criterion, is predicted by the test. The validity coefficient indicates the overall strength of the test-criterion relationship for the group being studied, but its meaning is obscure to a nontechnical audience. Nor does it help much to say that r2(the squared validity coefficient) indicates the proportion of performance variance accounted for by the test. Other more direct means are needed for displaying the meaning of a validity correlation coefficient. Moreover, the coefficient does not provide full information about this relationship.
Various methods are available for displaying detailed information about the test-criterion relationship. These methods range from a full plot of test and performance score data to ways of grouping test scores into intervals and then providing detailed information about the distribution of performance scores for groups of individuals in each test score interval.
Several sets of hypothetical data are shown here to illustrate these display methods. Each data set includes a test score and a performance score for 1,000 individuals. To simplify the interpretation of these data sets, both the test and the performance measure range from a minimum of 0 to a maximum of 50.
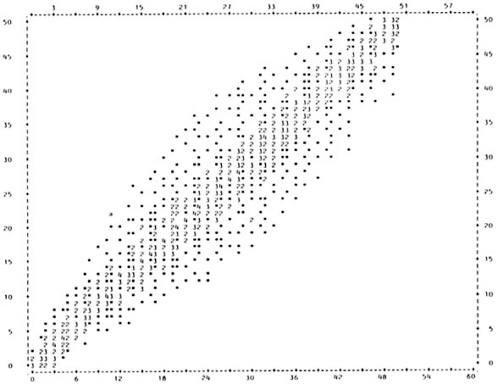
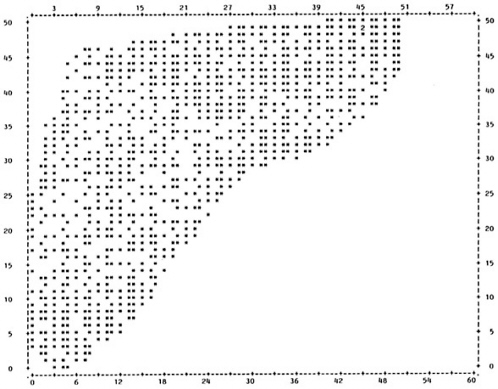
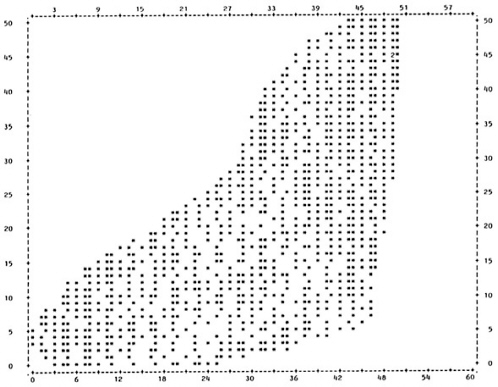
The simplest method of displaying the test-criterion relationship is the scatter plot. This is a graph showing each individual's scores on the test and the performance measure. The test score is normally listed on the horizontal axis and performance is listed on the vertical axis. Figure 1a shows the scatter plot for data set A (all figures in this chapter are located at the end of the text). Each * represents a single individual, and a number indicates that more than one individual had that test and performance score. For example, point a represents an individual with a test score of 11 and a performance score of 22. This data set illustrates a very strong relationship between test score and performance. The individuals in this group who score high on the test also score high on the performance measure, and vice versa. The validity coefficient for this data set is .96.
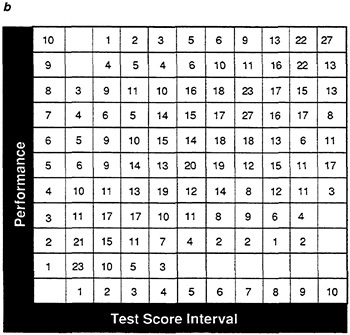
The difference between a strong and a moderate relationship is apparent if Figure 1a is compared to Figure 1b, which shows the scatter plot for data set B. In this example, there is still a tendency for the highest test scores to be associated with high performance scores and vice versa, but there is much more variation than was seen with data set A in Figure 1a. The validity coefficient for data set B is .52.
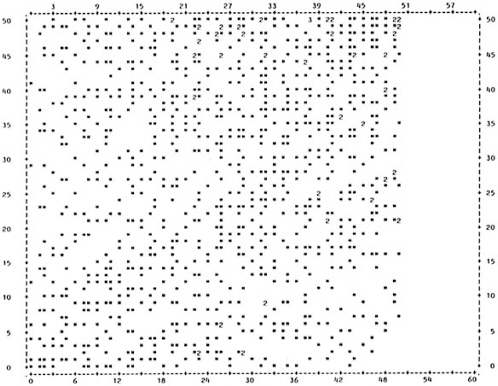
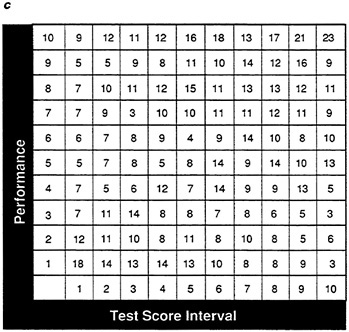
Figure 1c shows a very weak relationship. There is a wide range of scores on the performance measure for each possible test score. For example, individuals who have a test score of 3 have performance scores ranging from 0-50, while those with a test score of 43 also range from 0-50 on the performance measure. Thus, there is relatively little difference in performance at high and low test scores. The validity coefficient for this data set is only .19.
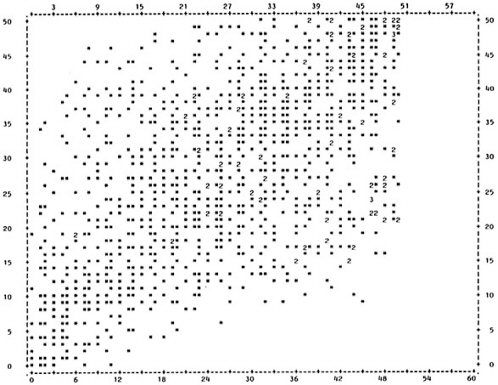
Comparison of these three scatter plots gives an indication of the differences in data distribution for tests with different validities. In addition, the scatter plot is useful for detecting differences in distribution among tests with the same validity. Figure 1d and Figure 1e show scatter plots for two distributions, both with a validity coefficient of .65. Although the tests have the same validity, it is apparent from comparison of the scatter plots that the two distributions are very different. Reporting the validity coefficient alone for either of these data sets would not reveal the abnormality of the distribution.
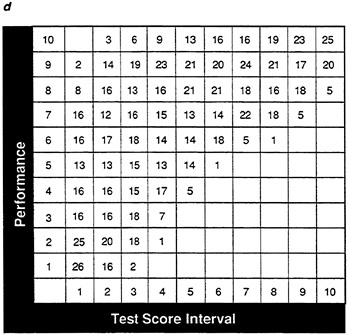
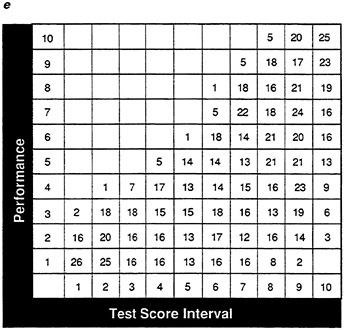
Data sets D and E illustrate a special kind of validity problem that exists when the predictive ability of the test is not equal at all levels of the test. In Figure 1d (data set D), high test scores are associated with only high performance scores, yet low test scores are associated with the full range of performance scores. In Figure 1e (data set E) the opposite is true, with less variability in performance scores at lower test score levels. This type of situation can occur for a number of reasons. Aptitude tests, for example, may measure prior experience with the subject matter, rather than ability; individuals with prior experience do well on the test and on the performance measure. However, some individuals who do poorly on the test will gain experience on the job and also do well on the performance measure. Similar problems are common in diagnostic testing when a positive test result confirms the presence of a condition but a negative result does not rule out the condition, or vice versa.
The scatter plot is an important tool in evaluating test validity, but its usefulness tends to be limited to giving the evaluator a general idea of the regularity of the distribution. In order to get more specific information about the test-criterion relationship, it is important to look at some measure of representative criterion performance at various test score levels. The most obvious way to do this is to plot an average performance score for each test score interval.
The purpose of testing is to predict performance from a test score. Without the test, the best prediction of performance that can be made is the average performance score for the entire group. For example, if we know only that the average grade point average for college freshmen is 2.5, and we know nothing else about a particular high school senior, then the only prediction we can make about that senior 's performance the following year is the group average, or 2.5. However, we will be making the same prediction for all students, so predicted performance will not allow us to distinguish between students who will do well and those who will fail. On the other hand, if we know that this student has a score of 98 on a college entrance examination and that the average grade point average for students who score between 95 and 100 on that entrance exam is 3.5, then we can feel more confident that this particular student will do well in college.
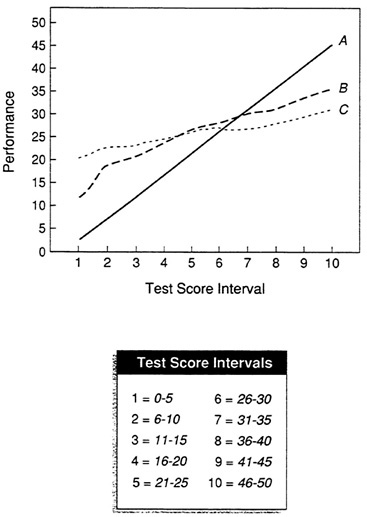
In Figure 2, average performance is plotted at 5-point intervals of test
score for data sets A, B, and C. (In this particular example, the steepest line also represents the most valid test, but this is not always true. The steepness of the line depends on the scale of both test and criterion. Relative steepness indicates relative validity only when comparing test scores and criterion measures of similar scale.) For data set A, the predicted performance score for individuals with test scores in the 0-5 interval would be 3.3, while the prediction for individuals in the 46-50 interval would be 46.5. For the least valid test, data set C, there is relatively little difference in predicted performance score between test score intervals. However, displaying only the arithmetic average, or mean criterion score, disregards the variability of these performance scores about the mean.
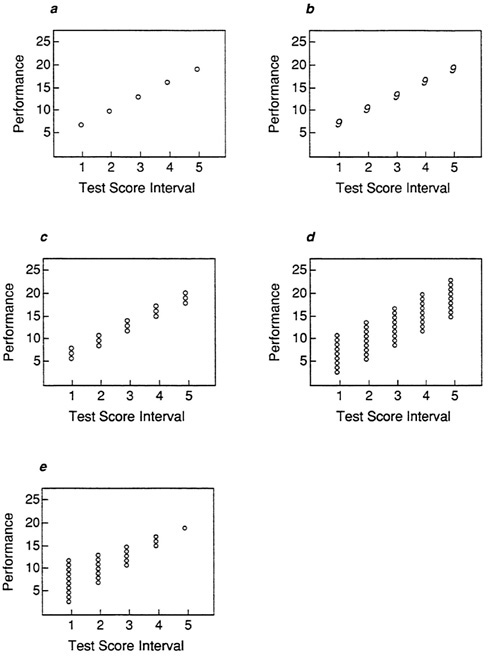
For example, Figure 3a shows a simple plot of mean performance score for five intervals of a test score. This plot could represent any one of the situations in Figure 3b, Figure 3c, Figure 3d and Figure 3e. In Figure 3b, there is a perfect relationship between test score and performance; knowing an individual's test score would permit a perfectly accurate prediction of performance. In Figure 3c, there is a small amount of variability around the mean performance score, so that the prediction of performance from a test score will not always be perfect, but it will be very nearly so. Figure 3d shows substantial variability; performance scores at one test score interval considerably overlap those at adjacent intervals. Prediction of performance scores at each test score interval will involve much error. The distribution in Figure 3e shows much variability at lower test score intervals, decreasing to no variability at the highest interval (similar to the situation in Figure 1e). Predicted performance at high test score intervals will be very accurate, but there will be error in prediction at lower intervals.
The implications for personnel decisions based on the plot in Figure 3a would vary widely depending on which distribution is involved. Unless some indication of variability is also included, however, it would be impossible to tell which distribution is represented. For this reason, the plot of means alone may be misleading.
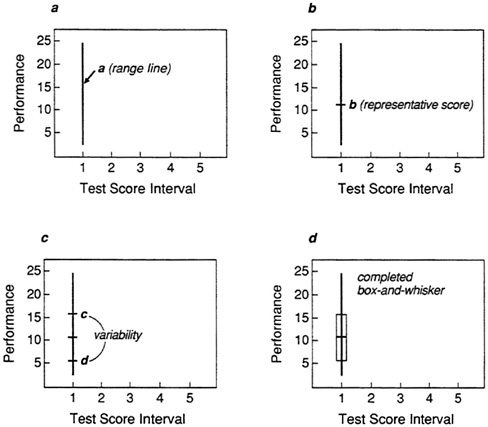
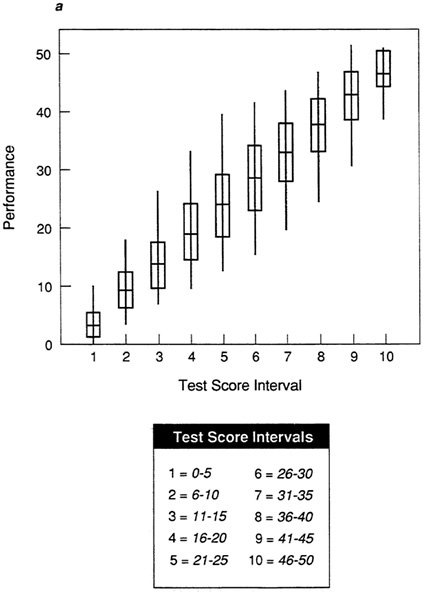
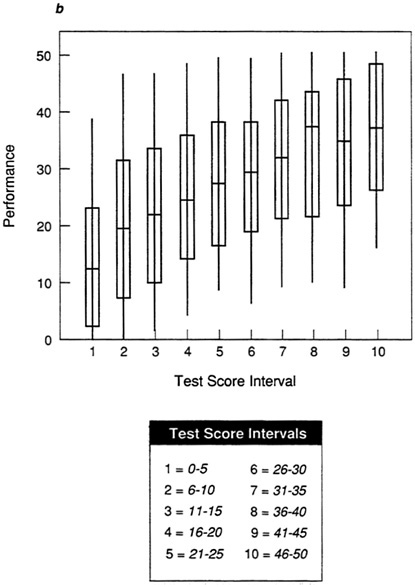
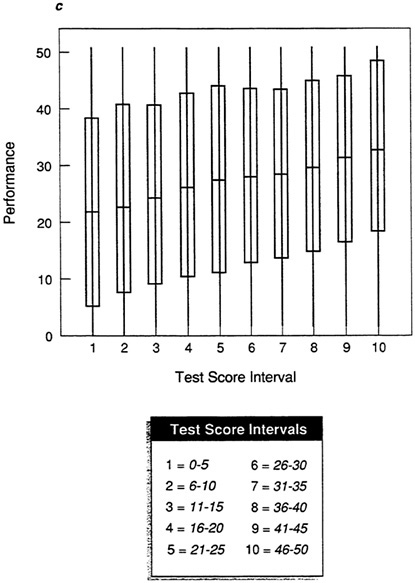
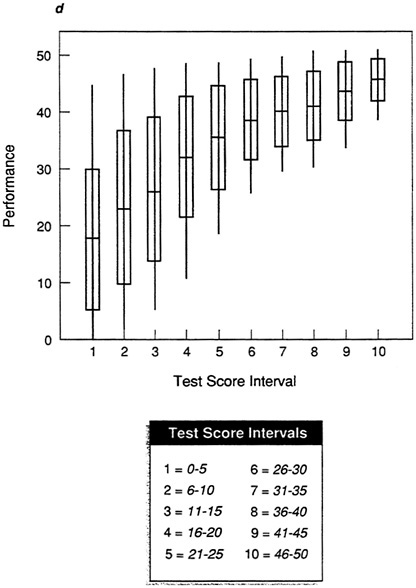
The box-and-whisker plot in Figure 4 provides a method of displaying both a measure of representative performance and variability about that measure. For each interval of test score, a line (a) is drawn between the lowest and highest values of performance. This is the “whisker” and represents range. The “box” is formed by placing a short line (b) perpendicular to the range line at the point of representative performance and two lines (c and d) on either side of that line to indicate variability. The lines are then connected, forming a box. Two types of box-and-whisker plot are generally used. In the first, the measure of representative performance is the arithmetic average, or mean. Variability is the standard deviation, which is an index of the differences between individual scores and the mean. In a normal, symmetrical distribution, 68 percent of the individual scores will be
within one standard deviation above and below the mean. Since the validity coefficient is based on the mean and standard deviation, this method provides a direct display of the information contained in the validity coefficient.
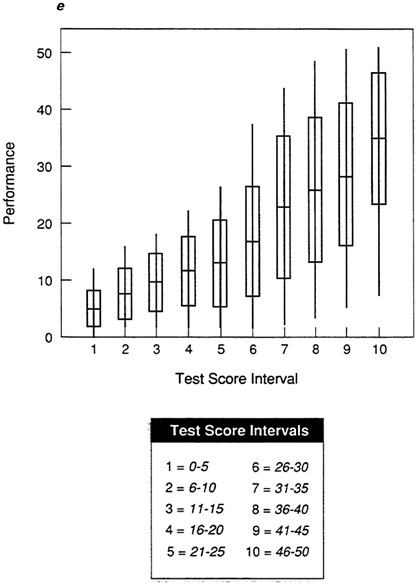
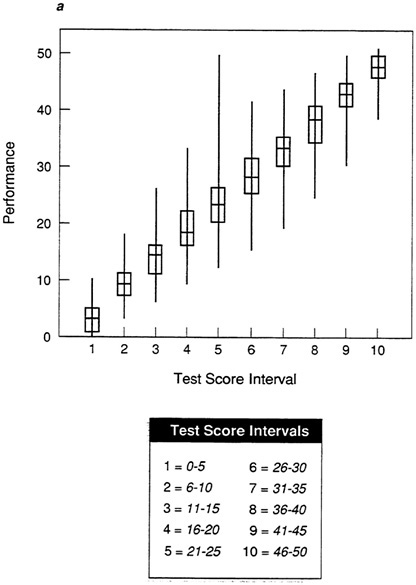
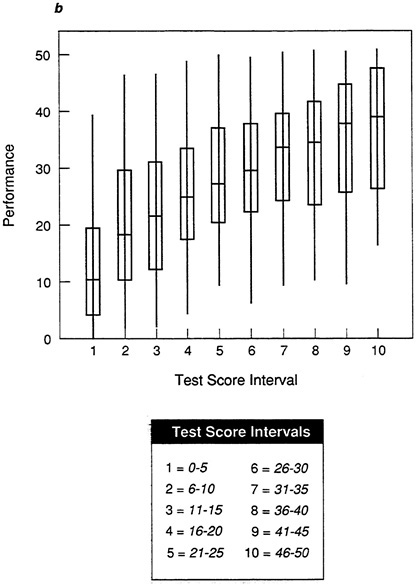
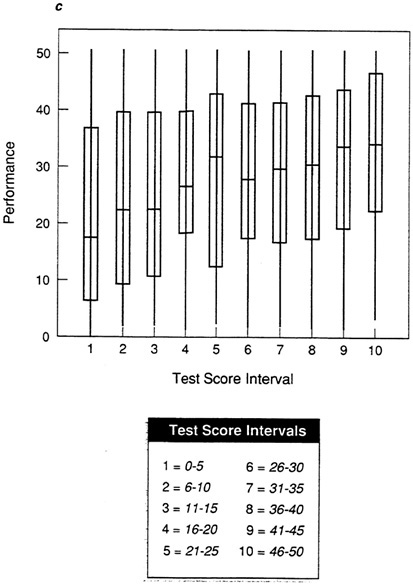
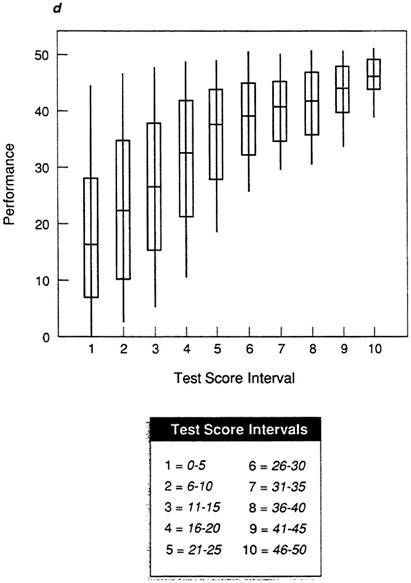
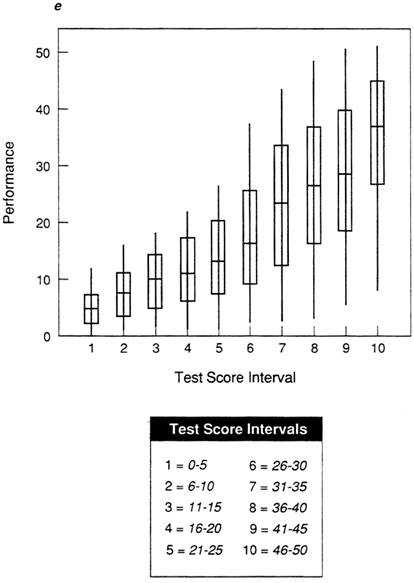
Figure 5a, Figure 5b, Figure 5c, Figure 5d and Figure 5e show box-and-whisker plots for data sets A-E using the mean and standard deviation. By comparing each plot to the corresponding scatter plot in Figure 1, it is possible to see that the box-and-whisker plot provides a convenient summarization of the information in the scatter plot. For an individual in any given test score interval, the best prediction of performance is the most representative score, in this case the mean. The size of the box indicates how tightly clustered performance scores are about the mean. When the range is narrow and the box is small, as in the test score intervals in Figure 5a (data set A), then the prediction of performance will be very accurate.
In Figure 5b, the moderate validity coefficient is reflected in the longer whiskers and boxes in the plot. Performance scores are less tightly clustered about the mean in each test score interval, so there is more vertical overlap among intervals, and the range differs less among intervals than with the plot of data set A in Figure 5a. As a result, there will be more inaccuracy in the prediction of performance score from test score (so the validity coefficient is lower). Figure 5c shows the weak test-criterion relationship for data set C. If the box-and-whisker plot is compared to the scatter plot for this data set in Figure 1c, it is apparent that the box-and-whisker plot is much clearer. At almost every test interval, the full range of performance scores is represented and the boxes are very long, indicating that performance scores are distributed broadly about the mean. If the best prediction, the mean, is used, there will be considerable error in predicted performance.
The abnormalities in the distributions for data sets D and E are clear in the box-and-whisker plots in Figure 5d and Figure 5e. It is now easy to see the areas of the distributions in which there will be the greatest prediction error. For data set D (Figure 5d), prediction will be fairly accurate at high test score intervals, but there will be significant error in the prediction of performance for those with lower test scores. For data set E, prediction will be more accurate at lower test scores, with many errors at the upper test score intervals.
For specific types of personnel decisions, this information is critically important. If the cost of poor performance is very high, then a selection test needs to be very accurate in selecting applicants who will not perform poorly. The test in data set D will permit selection of only those applicants who will do well, while the test in data set E would not. For data set E, at any test score interval many individuals will be selected who will perform poorly. The box-and-whisker plot makes it possible to see exactly where the most prediction error will occur with the test in question.
In addition to the mean and standard deviation, percentiles can be used as the measures of representative performance and variability in the boxand-whisker plot. Because percentiles are more readily acceptable to the nonstatistician, this method may often be preferable. The 50th percentile, or median, is used instead of the mean, and the 25th and 75th percentiles are used instead of the standard deviation to form the box. The whisker still indicates the range from the 1st to the 100th percentiles.
Figure 6a, Figure 6b, Figure 6c, Figure 6d and Figure 6e show box-and-whisker plots based on percentiles for data sets A-E. In the first interval of data set A (Figure 6a), the 50th percentile is 3. Twenty-five percent had performance scores higher than 5 (the 75th percentile), and 25 percent were at 1 or below. As can readily be seen by comparing these figures to Figure 5a, Figure 5b, Figure 5c, Figure 5d and Figure 5e, the information is very similar but is presented in terms more commonly understood. In addition, unlike the mean and standard deviation, percentiles are less affected by outliers—single individuals who score much higher or lower than others in the group.
In the examples above, test scores were divided into 10 five-point intervals. By using equal intervals, the general shape of the original distribution is maintained. However, it is possible to use other methods of dividing the test scores. Percentiles can be used as the basis for dividing test scores, so that the first interval is composed of the lowest 10 percent of test scores, the second interval is the next 10 percent, etc. This will result in approximately equal numbers of individuals in each interval, although the shape of the distribution may be somewhat distorted. In addition, standard scores, such as T-scores, may be used for determining the intervals, but these standard scores often require some degree of expertise to interpret.
In many test-criterion situations, some minimal level of acceptable performance is present. For example, most colleges have a minimum grade point average that must be maintained for an individual to remain enrolled. Performance scores above the minimum or cutoff are considered successes, while those below are considered failures. In this situation, an important validity issue is not the prediction of a performance score per se, but rather the prediction of success or failure. The expectancy chart displays information about successes or failures at different test score intervals. In general, test score intervals are listed in the left column, and bars are used to represent the proportion of successes or failures in each interval. As with the box-and-whiskers plot, test score intervals may be defined as equal intervals of raw test scores, as percentiles, or as standard scores.
The expectancy chart provides a simple method of evaluating the utility of a test. In most test-criterion situations, test users must consider the numbers of successful and failing individuals in economic terms, i.e., the relative cost of success and failure must be considered. The strategy used in implementing a test will depend on the test user's needs. In some cases, a specific number of individuals need to be selected. If the cost of failure is
high, then the test user will need to minimize the number of applicants selected who fail. On the other hand, if the cost of failure is low, then many applicants can be selected. The expectancy chart can be used to evaluate the efficiency of different test score cutoffs to best serve the test user's specific needs.
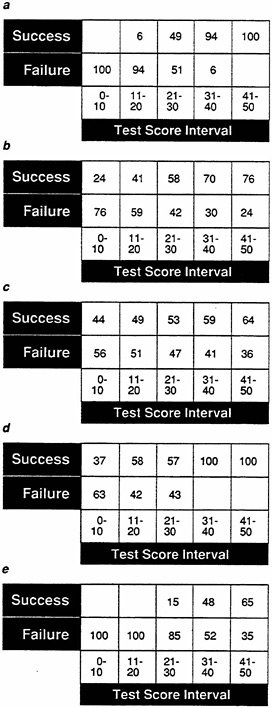
To illustrate the expectancy chart in Figure 7a, Figure 7b, Figure 7c, Figure 7d and Figure 7e, an arbitrary criterion cutoff of 25 has been applied to samples A-E. Success is thus defined as a performance score greater than 25, and failure is a score of 25 or below. The proportions of successful individuals are given at five-point test score intervals for these data sets. For data set A (Figure 7a), 100 percent of the individuals with test scores in the 46-50 interval succeed, dropping to 0 percent at the 6-10 score interval. It would be possible with this test to establish a test score cutoff so that no individuals who are selected fail. With a test of high validity, the proportion of individuals who succeed should be very high at the upper intervals, dropping abruptly to zero as the performance cutoff is reached.
By comparison, for data set B (Figure 7b), 79 percent of the highest test score group and 14 percent of the lowest test score group succeed. At any test score cutoff, some individuals will fail, although the proportion will be much lower if the test score cutoff is relatively high. For data set C (Figure 7c), test efficiency is clearly low. The proportion of individuals who will succeed if selected is only 67 percent at the highest test score interval and drops only to 41 percent at the lowest interval. Thus, for any test score interval, there will be almost equal numbers of successes and failures.
The differences between the distributions for data sets D and E are also apparent in the expectancy charts for these data sets (Figure 7d and Figure 7e). Although these distributions have the same validity coefficient, the greater efficiency of the test in data set D for selecting successful individuals is apparent in Figure 7d. One hundred percent of the individuals in each of the upper four test score intervals succeed, while the proportions of successes at the upper intervals in Figure 7e are much lower.
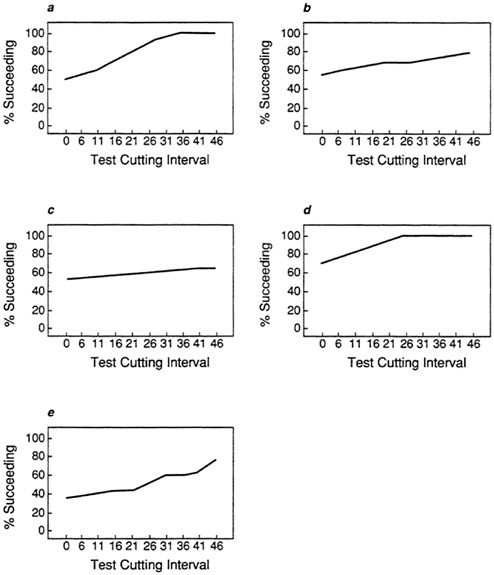
In addition to reporting either the proportion of successes or failures within each test score interval, it is possible to use the expectancy chart to display the proportion of total individuals selected who would succeed at various test score cutoffs. This type of expectancy chart is useful for determining what cutting score would best serve the test user's needs. Figure 8a, Figure 8b, Figure 8c, Figure 8d and Figure 8e show the proportion of total individuals selected who would succeed at test score cutoffs in steps of five. The efficiency of tests with different validities is evident when the expectancy charts for data sets A-C are compared.
With data set A, (Figure 8a) at a cutoff score of 36 on the test 100 percent of the individuals selected will succeed, dropping to only 51 percent if no cutting score is used. For B, (Figure 8b) at any cutting score the
proportion of successes is lower, ranging from 78 percent at the highest cutting score to 55 percent if no cut is used. With C, ( Figure 8c) the maximum proportion of successes is only 67 percent. Once again, the relative efficiency of the tests in samples D and E is clear (Figure 8d and Figure 8e).
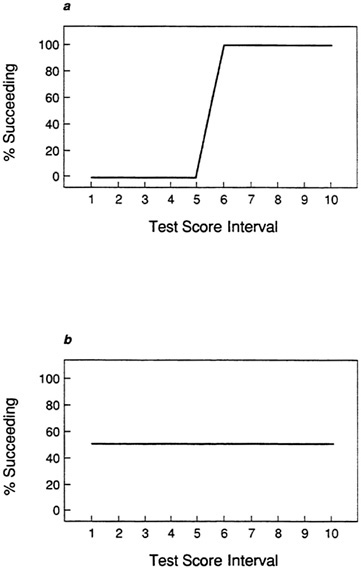
The information in the expectancy chart can also be demonstrated by plotting the proportion of successes in each test score interval or at each cutting score. In the expectancy plot, the proportion of successes in each interval gives a clear indication of how well a test discriminates among individuals. If a test is a perfect predictor of performance, then it is possible to find a test score above which all individuals succeed and below which all individuals fail. The plot of such a test is shown in Figure 9a. At the five lowest test score intervals, all individuals fail, while all individuals in the upper five test score intervals succeed. In contrast, Figure 9b shows a test that does not discriminate among individuals. At each test score interval, the proportion of successes is 50 percent.
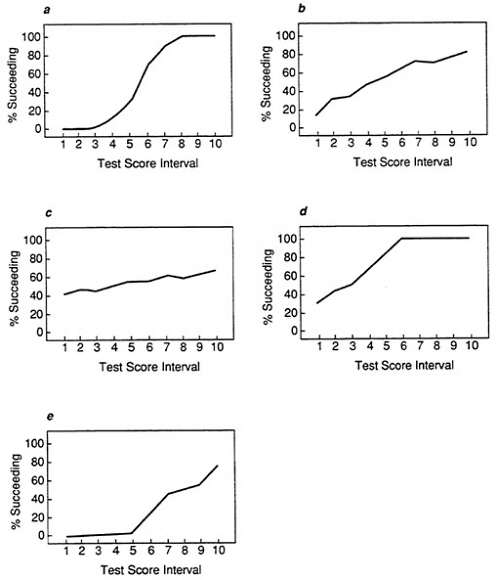
In Figure 10a, Figure 10b, Figure 10c, Figure 10d and Figure 10e, the proportion of successes is plotted at 10 five-point test score intervals for the sample data sets. By comparing these plots to the plots in Figure 9a and Figure 9b, it is apparent that the test in sample provides the best overall discrimination between successes and failures. This type of plot is particularly useful for comparing different tests for use with the same performance measure.
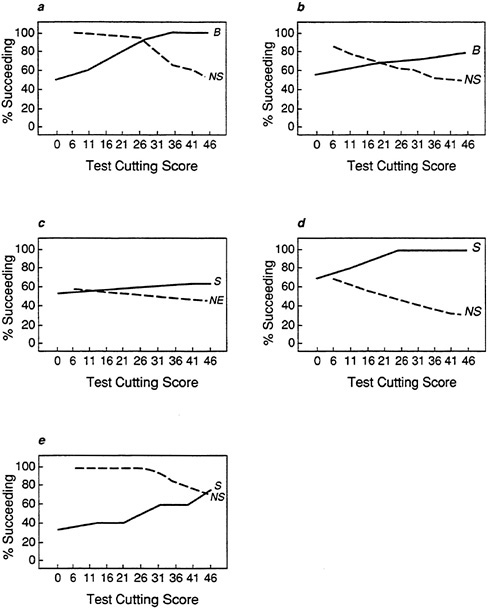
In addition, it is often important to determine how much improvement in the proportion of successes occurs at different cutting scores on the test. When no cutting score is used, that is, when the test is not used, the proportion of individuals who succeed is called the base rate. By plotting the proportion of successes at each cutting score, it is possible to evaluate the use of a test compared to the base rate alone. Figure 11a, Figure 11b, Figure 11c, Figure 11d and Figure 11e show the proportion of successes at ten cutting scores for the five sample data sets. The relative efficiency of the test in data set A (Figure 11a) is displayed by the fairly sharp climb from the base rate (51 percent successes) to 100 percent. With the moderate validity in data set B (Figure 11b) the climb is less steep and 100 percent is not reached, while with the low validity in data set C there is little improvement in the proportion of successes across all cutting scores.
An important issue in many testing situations is not only how many individuals selected by the test succeed but also how many of those rejected would not have succeeded. In Figure 12 the proportions of individuals not selected who would have failed is superimposed on the plots of proportions of successful individuals from Figure 11. This type of plot is useful for determining the most efficient cutting score. For example, in Figure 12a (for data set A), at a cutting score of about 26 on the test, over 90 percent of those selected would succeed, while over 90 percent of those not selected would have failed. The abnormal distributions in data sets D and E are
reflected in the plots in Figure 12d and Figure 12e. For data set D, at the higher cutting scores all of those selected succeed, but many individuals not selected would have succeeded also.
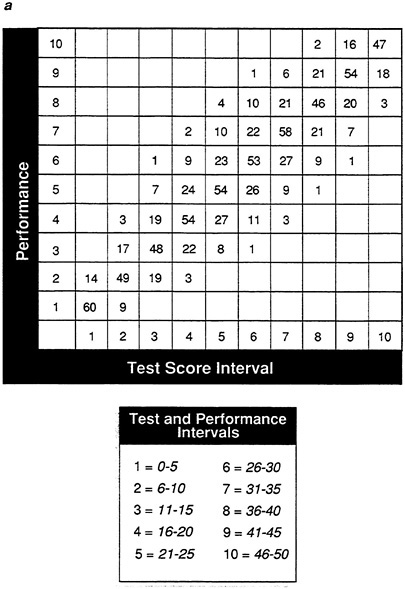
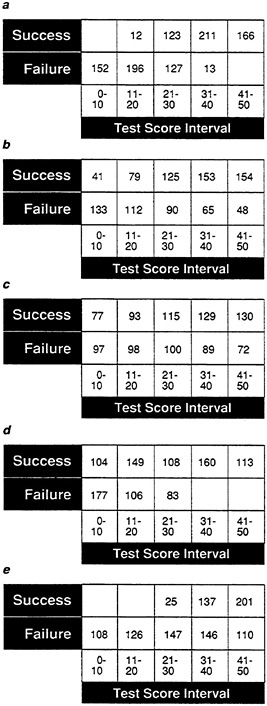
The expectancy table also provides a method of displaying information about the proportion of individuals at various test and criterion levels. It is possible to examine the proportion of individuals in each test score interval who perform at various criterion levels. Figure 13 shows the proportion of individuals in five 10-point test score intervals with performance scores in each of five 10-point intervals. In sample A (Figure 13a), 87 percent of the 152 individuals with test scores of 10 or below also have performance scores of 10 or below, and 13 percent have performance scores of 11-20. In the highest test score interval (41-50), 81 percent of the 166 individuals are in the top performance score interval, 18 percent in the next highest interval, and 1 percent in the middle interval.
In Figure 14, a performance score cutoff is applied, defining success, as before, as a performance score over 25. As with the expectancy chart, the expectancy table can provide an easy method of displaying the proportion of successes at various test intervals. Once again, both the different validities of samples A-C (Figure 14a, Figure 14b and Figure 14c) and the abnormal distributions in samples D and E (Figure 14d and Figure 14e) are apparent.
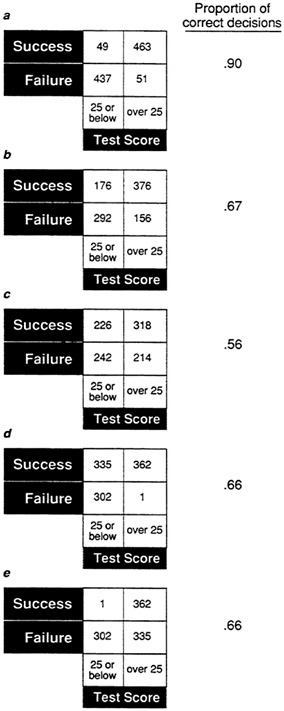
A simple 2 × 2 expectancy table provides a quick indication of the proportion of successes when a cutoff test score is used. In Figure 15a, Figure 15b, Figure 15c, Figure 15d and Figure 15e, a test score cutoff of 25 is applied to each of the five sample data sets. For data set A (Figure 15a), 90 percent of the individuals who would be accepted would succeed, while for data set C (Figure 15c) only 60 percent of those accepted would succeed.
With the expectancy methods discussed above, the proportion of successes is evaluated. However, frequently it may be useful to look at the actual number of individuals at various test and performance score intervals. The frequency table is also a method of displaying information about the success or failure of individuals at various test score intervals. In the frequency table, both the test score and the performance measure are grouped into intervals and the numbers of individuals who fall into each interval are listed. The frequency table, in essence, provides a summary of the information in the scatter plot. Figure 16a, Figure 16b, Figure 16c, Figure 16d and Figure 16e show frequency tables using 10 fivepoint intervals for both test score and the performance measure for data sets A-E. As with other display methods, the relative validities of data sets A-C are apparent if Figure 16a, Figure 16b and Figure 16c are compared, and the abnormalities in data sets D and E are visible in Figure 16d and Figure 16e.
In Figure 17, successful performance has been defined again as a performance score over 25, and the test score intervals have been reduced to five 10-point intervals.
The frequency table provides an excellent method for evaluating the cost
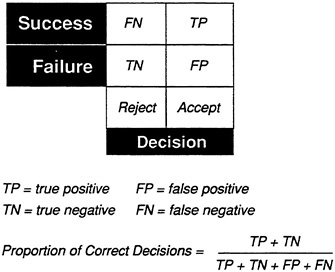
or utility of a test score cutoff. Once the cutoff has been determined, a simple 2 × 2 table can be used to display the number of successes and failures in the select and reject groups. With this method, it is simple to determine the number of correct decisions made about individuals. Accepting an individual who succeeds and rejecting an individual who would fail are correct decisions. These are called, respectively, true positives (TP) and true negatives (TN). Accepting an individual who fails is a false positive (FP) (the test incorrectly predicts success), and rejecting an individual who would succeed is a false negative (FN). The proportion of correct decisions is the total of true positives and true negatives divided by the total number of individuals (n):
(TP + TN)/(TP + TN + FP + FN)
or
(TP + TN)/n.
The general form of the 2 × 2 table is shown in Figure 18. True positives are entered in the upper right quadrant and true negatives in the lower left quadrant. Figure 19a, Figure 19b, Figure 19c, Figure 19d and Figure 19e show 2 × 2 tables for the sample data sets. The proportions of correct decisions range from .90 for sample A to .56 for C. The different types of errors for samples D and E are clear. For sample D (Figure 19d), there are virtually no false positives, but many false negatives. For sample E (Figure 19e), there are many false positives but no false negatives. Although the proportions of correct decisions are the same for the two distributions, the tests would have very different implications. If the cost of failure is high, data set D would be excellent for minimizing the number of individuals accepted who would fail. On the other hand, if the cost of failure is minimal but the payoff for success is high, the relationship in data set E would be preferable.
Display methods such as those described above are useful tools for describing test validity to the nonstatistician. In addition, however, these methods have a major advantage over the validity coefficient. The validity coefficient is extremely sensitive to changes in the range of test or performance scores. In many validity studies the individuals being measured have already been selected on some basis (often the test itself), so they do not represent the full range of abilities. It is very difficult to get performance measures on individuals at the lower levels because test users (employers, school administrators, etc.) are reluctant to admit every applicant just to evaluate test validity. As a result, it is only possible to estimate the validity coefficient from the preselected individuals available. This truncation of the range of test and performance scores artificially reduces the validity coefficient of the test.
For example, Figure 20 shows the results of preselection on data set A at
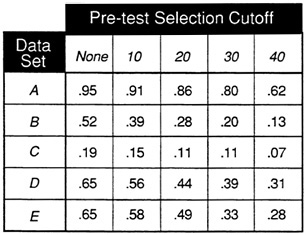
various test score cutoffs. Even at a cutting score of 20, the general trend in the distribution is present. However, Figure 21 shows the results of preselection on validity coefficients for the sample data sets by imposing test-score cutoffs at the 10, 20, 30, and 40 test- score levels. The effect of preselection is most dramatic for the moderate validity sample (B), in which the validity coefficient drops from .52 to .39 if the lowest cutoff score is applied. Although the coefficient of .52 for data set B would represent a respectable validity, if the range is further restricted by preselection, the validity coefficient plummets to .28 for a test-score cutoff of 20. Mathematical methods exist for correcting the validity coefficient for restriction of range and should be applied when this situation exists.
Examination of the scatter plot and box-and-whisker plots can indicate the presence of restriction of range due to preselection, as there will be very few individuals at the lower intervals. In addition, display methods are generally less dependent on range. Although restriction of range will be apparent, these methods look at performance as a function of test score intervals. As a result, the efficiency of a test is often detectable in these display methods when the validity coefficient is artificially reduced. For example, the trends in the relationships in all of the sample data sets are still apparent if the lowest two test-score intervals are deleted in all of the ten-interval test score figures presented here.
In summary, while the validity coefficient is an important part of test evaluation, alternative methods exist for displaying the test-criterion relationship. The scatter plot and the box-and-whisker plot are particularly useful in the identification of distribution abnormalities. In addition, the box-and-whisker plot provides an indication of the levels at which there is the most (or least) prediction error. Expectancy methods (chart, table, and plot) are essential in the evaluation of the prediction of two-level criteria (e.g., success versus failure), especially in terms of cost-benefit analysis. The frequency table also permits determination of the proportion of correct decisions.
Many of the methods presented here were originally developed for use in personnel testing. However, these methods are easily extended to any testcriterion situation. The final choice of display methods should depend on both test user needs and level of psychometric expertise.

FIGURE 7a Expectancy chart for data set A: proportiion of successful individuals in each test score interval.
NOTE: Success is defined as a performance score greater than 25.
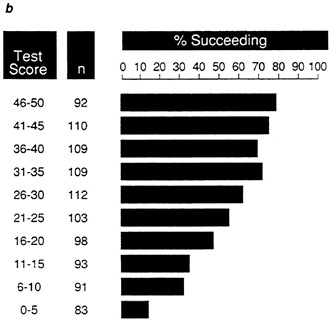
FIGURE 7b Expectancy chart for data set B: proportion of successful individuals in each test score interval.
NOTE: Success is defined as a performance score greater than 25.
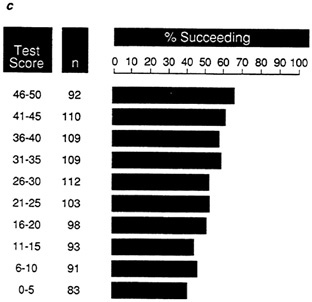
FIGURE 7c Expectancy chart for data set C: proportion of successful individuals in each test score interval.
NOTE: Success is defined as a performance score greater than 25.
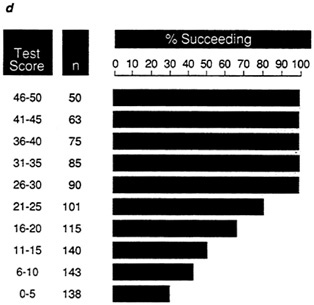
FIGURE 7d Expectancy chart for data set D: proportion of successful individuals in each test score interval.
NOTE: Success is defined as a performance score greater than 25.
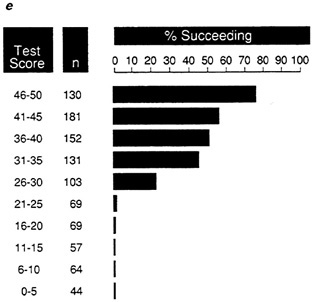
FIGURE 7e Expectancy chart for data set E: proportion of successful individuals in each test score interval.
NOTE: Success is defined as a performance score greater than 25.
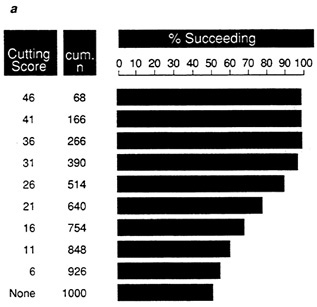
FIGURE 8a Expectancy chart for data set A: proportion of successful individuals at each cutting score.
NOTE: Success is defined as a performance score greater than 25.
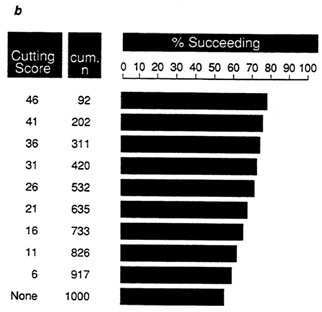
FIGURE 8b Expectancy chart for data set B: proportion of successful individuals at each cutting score.
NOTE: Success is defined as a performance score greater than 25.

FIGURE 8c Expectancy chart for data set C: proportion of successful individuals at each cutting score.
NOTE: Success is defined as a performance score greater than 25.
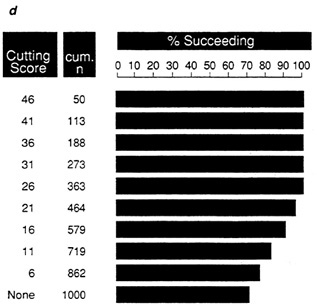
FIGURE 8d Expectancy chart for data set D: proportion of successful individuals at each cutting score.
NOTE: Success is defined as a performance score greater than 25.
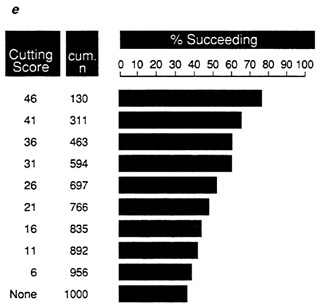
FIGURE 8e Expectancy chart for data set E: proportion of successful individuals at each cutting score.
NOTE: Success is defined as a performance score greater than 25.
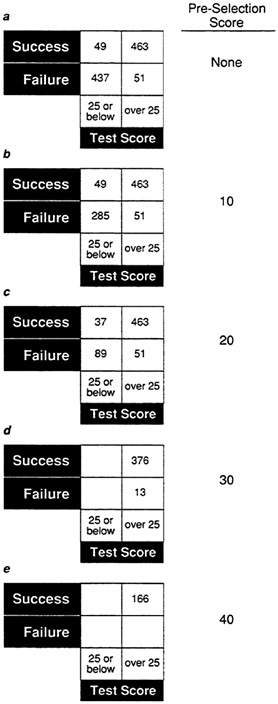
FIGURE 20 Frequency tables showing effect of preselection of frequency table in Figure 19 for data set A.
NOTES: Success is defined as a performance score greater than 25. Test cutoff score of 25 determines levels of test score.