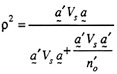Generalizability Theory and Military Performance Measurements: I. Individual Performance
Richard J. Shavelson
INTRODUCTION
This paper sketches a statistical theory of the multifaceted sources of error in a behavioral measurement. The theory, generalizability (G) theory (Cronbach et al., 1972), models traditional measurements such as aptitude and achievement tests. It provides estimates of the stability of a measurement (“testretest” reliability in classical test theory), the consistency of responses to parallel forms of a test (“equivalent-forms ” reliability), and the consistency of responses to test items (“internal-consistency” reliability). Each type of classical reliability coefficient defines measurement error somewhat differently. One of G theory's major achievements is that it simultaneously estimates the magnitude of the errors influencing all three classical reliabilities. Hence, we speak of G theory as a theory of the multifaceted sources of error.
Performance measurements may contain the same sources of error as traditional pencil-and-paper measurements: instability of responses from one occasion to the next, nonequivalence of supposedly parallel forms of a performance measurement, and heterogeneous subtask responses. And more. Two additional, pernicious sources of error are inaccuracies due to scoring, where observers typically score performance in real time, and inaccuracies
The author gratefully acknowledges helpful and provocative comments provided by Lee Cronbach and the graduate students in his seminar on generalizability theory. The author alone is responsible for the contents of this paper.
due to unstandardized testing conditions, where performance testing is typically carried out under widely varying laboratory and field conditions.1 G theory's ability to estimate the magnitude of each of these sources of error, individually and in combinations, enables this theory to model human performance measurement better than any other.
The next section provides an example of how generalizability theory can be applied to military job performance measurements, using hypothetical data. The third section presents G theory formally, but with a minimum of technical detail. Key features of the theory are illustrated with concrete numerical examples. The fourth section presents applications of the theory. These applications were chosen to highlight the theory 's flexibility in modeling a wide range of measurements. The fifth section concludes the paper by discussing some limitations of the theory.
APPLICATION OF GENERALIZABILITY THEORY TO THE MEASUREMENT OF MILITARY PERFORMANCE
Background
Military decision makers, ideally, seek perfectly reliable measures of individuals' performance in their military occupational specialities. 2 Even with imperfect measures, the decision maker typically treats as interchangeable measures of an individual's performance on one or another representative sample of military occupational specialty tasks (and subtasks) that were carried out at any one of many test stations, on any of a wide range of occasions, as scored by any of a large number of observers. Because he wants to know what the person 's performance is like, rather than what he did on one particular moment of observation, he is forced to generalize from a limited sample of behavior to an extremely large universe: the individual's job performance across time, tasks, observers, and settings. This inference is sizable. Generalizability theory provides the statistical apparatus for answering the question: Just how dependable is this measurement-based inference?
To estimate dependability, an individual's performance needs to be observed on a sample of tasks/subtasks, on different occasions, at different stations, with different observers. A generalizability study (G study), then, might randomly sample five E-2s,3 who would perform a set of tasks (and subtasks) on two different occasions, at two different stations, with four
|
1 |
By design, traditional pencil-and-paper tests control for scoring errors by using a multiplechoice format with one correct answer, and testing conditions are standardized by controlling day, time of day, instructions, etc. |
|
2 |
“Military occupational specialty” is used generically and applies to Air Force specialties and Navy ratings as well as to Army and Marine Corps military occupational specialties. |
|
3 |
Large samples should be used. For illustrative purposes, small samples are more instructive. |
observers scoring their performance. An individual would be observed under all possible combinations of these conditions or a total of 16 times (2 occasions × 2 stations × 4 observers) on the set of tasks/subtasks.
If performance is consistent across tasks, occasions, stations, and observers—i.e., if these characteristics of the measurement do not introduce systematic or unsystematic variation in the measurement —the measurement is dependable and the decision maker's ideal has been met. More realistically, however, if the individual 's score depends on the particular sample of tasks to which he was assigned, on the particular occasion or station at which the measurement was taken, and/or on the particular observer scoring the performance, the measurement is less than ideally dependable. In this case, interest attaches to determining how to minimize the impact of different sources of measurement error.
Performance Measurement: Operate and Maintain Caliber .38 Revolver
To make this general discussion concrete, an example is in order. One of the Army's military occupational specialty-specific performance measures involves operating and maintaining a caliber .38 revolver. The soldier is told that this task covers the ability to load, reduce a stoppage in, unload, and clean the caliber .38 revolver, and that this will be timed. The score sheet for this measurement is presented in Table 1. Note that there are two measurements taken: time and accuracy.
In the G study, suppose that each of five soldiers performed the revolver test four times: on two different occasions (e.g., week 1 and week 2) at two different test stations.4 The soldiers' performance on each of the three tasks and subtasks (see Table 1) was independently scored by four observers. Also, each task as a whole is independently timed. Hypothetical results of this study are presented in Table 2 for the time measure. Note that time is recorded for each of three tasks and not for individual subtasks (Table 1); hence, subtasks are not shown in Table 2.
Classical Theory Approach
With all the information provided in Table 2, how might classical reliability be calculated? With identical performance measurements taken on
|
4 |
There is good reason to worry about an order effect. This is why “tuning” subjects before they are tested is strongly recommended (e.g., Shavelson, 1985). “Tuning” is familiarizing subjects with the task before they are tested. (If a subject can “fake” the task in a performance test, this means that she can perform it.) Nevertheless, soldiers would be counterbalanced such that half would start at station 1 and half at station 2. Finally, as will be seen, an alternative design with occasions nested within stations might be used. |
TABLE 1 Caliber .38 Revolver Operation and Maintenance Task
|
Score |
|||
|
Task |
Subtask |
Go |
No Go |
|
Load the weapona |
(1) Held the revolver forward and down |
— |
— |
|
(2) Pressed thumb latch and pushed cylinder out |
— |
— |
|
|
(3) Inserted a cartridge into each chamber of the cylinder |
— |
— |
|
|
(4) Closed the cylinder |
— |
— |
|
|
(5) Performed steps 1-4 in sequence |
— |
— |
|
|
Time to load the weapon |
_______________ |
||
|
Reduce a stoppageb |
(6) Recocked weapon |
— |
— |
|
(7) Attempted to fire weapon |
— |
— |
|
|
(8) Performed steps 6-7 in sequence |
— |
— |
|
|
Time to reduce stoppage |
_______________ |
||
|
Unload and clear the weaponc |
(9) Held the revolver with muzzle pointed down |
— |
— |
|
(10) Pressed thumb latch and pushed cylinder out |
— |
— |
|
|
(11) Ejected cartridges |
— |
— |
|
|
(12) Inspected cylinder to ensure each chamber is clear |
|||
|
(13) Performed steps 6-9 in sequence |
— |
— |
|
|
Time to unload and clear the weapon |
_______________ |
||
|
NOTES: Instructions to soldier: aThis task covers your ability to load the revolver; we will time you. Begin loading the weapon. bYou must now apply immediate action to reduce a stoppage. Assume that the revolver fails to fire. The hammer is cocked. Begin. cYou must now begin unloading the weapon. |
|||
TABLE 2 Caliber .38 Revolver Operation and Maintenance Task: Time to Complete Tasks
|
Observer |
||||||
|
Station |
Occasion |
Task |
1 |
2 |
3 |
4 |
|
1 |
84 |
85 |
86 |
87 |
||
|
82 |
84 |
85 |
85 |
|||
|
1 |
91 |
92 |
92 |
94 |
||
|
83 |
82 |
84 |
85 |
|||
|
75 |
76 |
78 |
78 |
|||
|
76 |
76 |
77 |
77 |
|||
|
75 |
84 |
75 |
76 |
|||
|
1 |
2 |
83 |
81 |
83 |
81 |
|
|
77 |
78 |
76 |
77 |
|||
|
69 |
70 |
70 |
70 |
|||
|
94 |
95 |
96 |
97 |
|||
|
91 |
92 |
93 |
94 |
|||
|
3 |
99 |
99 |
99 |
99 |
||
|
93 |
94 |
94 |
95 |
|||
|
83 |
83 |
84 |
85 |
|||
|
* * * |
||||||
|
2 |
80 |
81 |
81 |
82 |
||
|
78 |
78 |
81 |
80 |
|||
|
1 |
84 |
84 |
84 |
85 |
||
|
80 |
81 |
80 |
82 |
|||
|
73 |
74 |
74 |
75 |
|||
|
73 |
73 |
74 |
76 |
|||
|
74 |
73 |
74 |
75 |
|||
|
2 |
2 |
77 |
75 |
76 |
75 |
|
|
73 |
74 |
72 |
77 |
|||
|
69 |
70 |
70 |
71 |
|||
|
90 |
89 |
90 |
92 |
|||
|
90 |
89 |
90 |
91 |
|||
|
3 |
89 |
91 |
93 |
93 |
||
|
87 |
87 |
89 |
89 |
|||
|
83 |
84 |
85 |
84 |
|||
two occasions, a test-retest reliability can be calculated. By recognizing that tasks are analogous to items on traditional tests, an internal consistency reliability coefficient can be calculated.
A test-retest coefficient is calculated by correlating the soldiers ' scores at occasion 1 and occasion 2, after summing over all other information in Table 2. The correlation between scores at the two points in time is .97. If soldiers' performance times are averaged over two occasions to provide a performance time measure, the reliability is .99, following the SpearmanBrown prophecy formula.
An internal-consistency coefficient is calculated by averaging, for each task, soldiers' performance times across stations, occasions, and observers. The soldiers' average task performance times would then be intercorrelated: r(task 1,task 2), r(task 1,task 3), and r(task 2,task 3). The average of the three correlations would provide the reliability for a single task, and the Spearman-Brown formula could be used to determine the reliability for performance times averaged over the three tasks. The reliability of performance-time measures obtained on a single task is .99, and the reliability of scores averaged across the three tasks is .99.
Generalizability Theory Approach
Two limitations of classical theory are readily apparent. The first limitation is that a lot of information in Table 2 is ignored (i.e., “averaged over”). This information might contain measurement error that classical theory assumes away. This could lead to false confidence in the dependability of the performance measure. The second limitation is that separate reliabilities are provided; which is the “right one”? G theory overcomes both limitations. The theory uses all of the information obtained in the G study, and it provides a coefficient that includes a definition of error arising from each of the sources of error in the measurement. Finally, G theory estimates each source of variation in the measurement separately so that improvements can be made by pinpointing which characteristics of the performance measurement gave rise to the greatest error.
Generalizability theory uses the analysis of variance (ANOVA) to accomplish this task. A measurement study (called a generalizability study) is designed to sample potential sources of measurement error (e.g., raters, occasions, tasks) so that their effects on soldiers ' performance can be examined. Thus soldiers and each source of error can be considered factors in an ANOVA. The ANOVA, then, can be used to estimate the effects of soldiers (systematic, “true-score” variation), each source of error, and their interactions. More specifically, the ANOVA is used to estimate the variance components associated with each effect in the design (“main effects” and “interactions”). As Rubin (1974:1050) noted, G theory concentrates on mixed models analysis
of variance designs, that is, designs in which factors are crossed or nested and fixed or random. Emphasis is given to the estimation of variance components and ratios of variance components, rather than the estimation and testing of effects for fixed factors as would be appropriate for designs based on randomized experiments.
Variance Components
The statistical machinery for analyzing the results of a G study is the analysis of variance. The ANOVA partitions the multiple sources of variation into separate components (“factors” in ANOVA terminology) corresponding to their individual main effects (soldiers, stations, occasions, tasks, and judges) and their combinations or interactions. The total variation in performance times (shown in Table 2) is partitioned into no less than 31 separate components—five individual components and all their possible combinations (Cartesian products)—accounting for the total variation in the performance-time data (see Table 3).
Of the 30 sources of variation, 1 accounts for performance consistency: the soldier (or P for person) effect represents systematic differences in the speed of performance among the five soldiers (variance component for soldiers in Table 3). By averaging the time measure across observers, tasks, occasions, and stations, we find that soldier 5 performed the task the fastest and soldier 3 performed the task the slowest. The other three soldiers fell in between. This variation in mean performance can be used to determine systematic differences among soldiers, called true-score variance in classical test theory and universe-score variance in generalizability theory. This universe-score variance—variance component for P = 14.10 (Table 3)—is the signal sought through the noise created by error. It is the “stuff” that the military decision maker would like to know as inexpensively and as feasibly as possible.
The 29 other sources of variation represent potential measurement error. The first four sources of variation are attributable to each source of error considered singly (“main effects” in ANOVA terminology). The station effect (variance component for station in Table 3) shows whether mean performance times, averaged over all other factors, systematically vary as to the location at which the measurement was taken. Apparently performance time did not differ according to station (variance component for station = 0). This is not surprising; unlike many other performance measurements, the revolver task appears self-contained. The occasion effect shows whether performance times, averaged over all other factors, change from one occasion to the next. Relative to other variance components, performance appears stable over occasions. The task effect shows whether performance times differed over tasks 1-3. Since task 2 contained fewer subtasks (three)
TABLE 3 Generalizability Study for a Soldier (P) × Station (S) × Occasion (O) × Task (T) × Judge (J) Design
|
Source of Variation |
df |
Mean Squares |
Variance Components |
|
Soldiers (P) |
4 |
1020.80 |
14.10 |
|
Stations (S) |
1 |
1.00 |
0.00 |
|
Occasions (O) |
1 |
1273.00 |
7.40 |
|
Tasks (T) |
2 |
1659.80 |
20.00 |
|
Judges (J) |
3 |
349.80 |
2.45 |
|
PS |
4 |
1.00 |
0.00 |
|
PO |
4 |
239.00 |
9.55 |
|
PT |
8 |
9.80 |
0.00 |
|
PJ |
12 |
106.80 |
8.75 |
|
SO |
1 |
1.00 |
0.00 |
|
ST |
2 |
1.00 |
0.00 |
|
SJ |
3 |
1.00 |
0.00 |
|
OT |
2 |
59.80 |
1.25 |
|
OJ |
3 |
97.80 |
3.20 |
|
TJ |
6 |
1.80 |
0.00 |
|
PSO |
4 |
1.00 |
0.00 |
|
PST |
8 |
1.00 |
0.00 |
|
PSJ |
12 |
1.00 |
0.00 |
|
POT |
8 |
9.80 |
1.00 |
|
POJ |
12 |
1.80 |
0.00 |
|
PTJ |
24 |
1.80 |
0.00 |
|
SOT |
2 |
1.00 |
0.00 |
|
SOJ |
3 |
1.00 |
0.00 |
|
STJ |
6 |
1.00 |
0.00 |
|
OTJ |
6 |
1.80 |
0.00 |
|
PSOT |
8 |
1.00 |
0.00 |
|
PSOJ |
12 |
1.00 |
0.00 |
|
PSTJ |
24 |
1.80 |
0.00 |
|
SOTJ |
6 |
1.00 |
0.00 |
|
PSOTJ (residual) |
24 |
1.00 |
1.00 |
than tasks 1 and 3 (five each), performance time on task 2, averaged over all other sources of variation, should be shorter. The task effect reflects this characteristic of the performance measurement (variance component for task = 20). And variation across judges shows whether observers are using the same criterion when timing performance. From a measurement point of view, main-effect sources of error influence absolute decisions about the
speed of performance (regardless of how other soldiers performed; called “absolute decisions ”). The soldiers' performance times will depend on whether they are observed by a “fast” or “slow” timer, at a “fast” or “slow” station, and so on.
The remaining sources of variation in Table 3 reflect combinations or “statistical interactions” among the factors. Interactions between persons and other sources of error variation represent unique, unpredictable effects; the particular performance times assigned to soldiers have one or more components of unpredictability (error) in them. As a consequence, different tasks, observers, or occasions might rank order soldiers differently and unpredictably.5 The soldier × judge effect (variance component = 8.75), for example, indicates that observers did not agree on the times they assigned to each soldier. If observer 1, for example, were used in the performance measurement, soldier 1 might be timed as faster than soldier 4. If observer 4 were used, the rank ordering would be reversed. The soldier × task interaction indicates that soldiers who performed quickly on task 1 also performed quickly on the other tasks, compared to their peers. The rank ordering of soldiers apparently does not depend on the task they performed. This is why the internal consistency coefficient, based on classical theory, was so high (.99). The soldier × occasion × judge interaction indicates judges disagreed on performance times they assigned each soldier, and the nature of this disagreement changed from one occasion to the next (negligible, Table 3). The most complex interaction, soldiers × stations × occasions × tasks × observers, reflects the effect of an extremely complex combination of error sources and other unmeasured and random error sources. It is the residual that accounts for the remaining variation in all performance times.
The remainder of the interactions do not involve persons. As a consequence, they do not affect the rank ordering of soldiers. However, they do affect the absolute performance-time score received by each soldier. For example, a sizable occasion × judge interaction would indicate that the performance times received by soldiers depend both on who observes them and on what occasion that observation occurs. A sizable task × judge interaction would indicate that the performance times received by soldiers depends on the particular task and observer. In doing task 1, for example, the soldiers would want judge 3 because she assigns the fastest times on this task while, in performing task 3, they might want judge 1 because he assigns the fastest times on that task.
|
5 |
Technically, an interaction could also occur when soldiers have identical rank orders across, say, occasions and the distance between soldiers' performance times on each occasion is different (an ordinal interaction). An interaction with reversals in rank order (a disordinal interaction) is more dramatic and, for simplicity, is used to describe interpretations of interactions in this paper. |
Improvement of Performance Measurement
Just as the Spearman-Brown prophecy formula can be used to determine the number of items needed on a test to achieve a certain level of reliability, the magnitudes of the sources of error variation can also be used to determine the number of occasions, observers, and so on that are needed to obtain some desired level of generalizability (reliability). For example, the effects involving judges (soldier × judge, judge × task, judge × task × occasion, etc.) can be used to determine whether several judges are needed and whether different judges can be used to score the performance of different soldiers, or whether the same judges must rate all soldiers due to disagreements among them. The analysis of the performance-time data in Table 3 suggests, based on the pattern of the variance component magnitudes, that several judges are needed and that the same set of judges should time all soldiers (e.g., variance components for PJ and OJ).
Generalizability of the Performance Measurement
Generalizability theory provides a summary index representing the consistency or dependability of a measurement. This coefficient, the “generalizability coefficient,” is analogous to the reliability coefficient in classical theory. The coefficient for relative decisions reflects the accuracy with which soldiers have been rank ordered by the performance measurement, and is defined as:
where n′ is the number of times each source of error is sampled in an application of the measurement. For the data in Table 3, with n = 1 station, occasion, task, and judge:
The G coefficient for absolute decisions is defined as:
where n′ is the number of times each source of error is sampled in an application of the measurement. For the data in Table 3, with n = 1 station, occasion, task, and judge:
Regardless of whether relative or absolute decisions are to be made on the basis of the performance measurement, the dependability of the measure based on the G theory analysis is considerably different than the analysis based on classical theory. In these examples, it is especially important to sample occasions and judges extensively for relative decisions and to sample tasks extensively as well for absolute measurements.
Summary: Revolver Test With Accuracy Scores
Recall that both time and accuracy were recorded by four observers judging soldiers' performance in the caliber .38 revolver performance test. By way of reviewing the application of G theory to performance measurements, hypothetical data on accuracy is presented. This is not merely a repeat of what has gone before. The accuracy data call for a somewhat different analysis than the performance-time data.
Design of the Revolver Test Using Accuracy Scores
In the generalizability study, each of five soldiers performed the revolver test four times: on two different occasions (O) at two different test stations. The soldiers' (P) performance on each of the three tasks (T) and subtasks (S) (see Table 1) was independently judged by four observers (J). Hypothetical accuracy scores for this G-study design are presented in Table 4. The data in Table 4 have been collapsed over stations. This seemed justifiable. Because of the nature of the revolver task, stations did not introduce significant measurement error. Further, to simplify the analysis, only two of the three tasks were selected: loading and unloading/cleaning the revolver. Including the stoppage removal task would have created an “unbalanced” design, with five subtasks for tasks 1 and 3 each and only three subtasks for task 2. (See the later discussion of unbalanced designs.)
The data in Table 4 represent a soldiers × occasion × task × subtask:task × observer (P × O × T × S:T × J) design. Notice that each of the two tasks—loading and unloading—contain somewhat different subtasks. So identical subtasks do not appear with each task and we say that subtasks are nested within tasks (cf. a nested analysis of variance design). The consequence of nesting can be seen in Table 5, where not all possible combinations of P, O, T, S:T, and J appear in the source table as was the case in Table 3. This is because all terms that include interactions of T and S:T together cannot be estimated due to the nesting (see the later discussion of nesting).
TABLE 4 Caliber .38 Revolver Operation and Maintenance Task: Accuracy
|
Observer |
|||||||
|
Occasion |
Task |
Subtask |
1 |
2 |
3 |
4 |
|
|
1 |
0 |
0 |
1 |
1 |
|||
|
0 |
0 |
1 |
1 |
||||
|
1 |
0 |
0 |
0 |
1 |
|||
|
1 |
1 |
1 |
0 |
||||
|
1 |
1 |
1 |
0 |
||||
|
0 |
0 |
1 |
1 |
||||
|
0 |
1 |
1 |
1 |
||||
|
2 |
1 |
1 |
1 |
1 |
|||
|
1 |
1 |
1 |
0 |
||||
|
1 |
1 |
1 |
0 |
||||
|
0 |
0 |
0 |
1 |
||||
|
0 |
0 |
1 |
1 |
||||
|
1 |
3 |
0 |
1 |
1 |
1 |
||
|
0 |
1 |
1 |
1 |
||||
|
1 |
1 |
1 |
0 |
||||
|
0 |
0 |
0 |
1 |
||||
|
0 |
0 |
1 |
1 |
||||
|
4 |
0 |
0 |
1 |
1 |
|||
|
0 |
0 |
1 |
1 |
||||
|
0 |
1 |
1 |
1 |
||||
|
0 |
0 |
0 |
1 |
||||
|
0 |
0 |
0 |
1 |
||||
|
5 |
0 |
0 |
1 |
1 |
|||
|
0 |
1 |
1 |
1 |
||||
|
0 |
1 |
1 |
1 |
||||
|
* * * |
|||||||
|
2 |
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
1 |
||||
|
1 |
1 |
0 |
0 |
0 |
|||
|
0 |
0 |
1 |
1 |
||||
|
0 |
1 |
1 |
1 |
||||
|
1 |
0 |
1 |
0 |
||||
|
0 |
1 |
1 |
1 |
||||
|
2 |
0 |
1 |
0 |
1 |
|||
|
1 |
1 |
1 |
1 |
||||
|
1 |
1 |
1 |
0 |
||||
|
1 |
0 |
1 |
1 |
|||
|
0 |
0 |
1 |
1 |
|||
|
2 |
3 |
1 |
1 |
0 |
1 |
|
|
1 |
1 |
1 |
0 |
|||
|
1 |
1 |
1 |
1 |
|||
|
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
1 |
|||
|
4 |
0 |
0 |
0 |
1 |
||
|
1 |
1 |
0 |
0 |
|||
|
0 |
1 |
1 |
1 |
|||
|
0 |
0 |
0 |
0 |
|||
|
0 |
0 |
0 |
0 |
|||
|
5 |
0 |
0 |
0 |
1 |
||
|
1 |
0 |
1 |
0 |
|||
|
1 |
1 |
1 |
1 |
|||
Variance Components and G Coefficients
In G theory, interest attaches to the estimated variance components. 6 In Table 5, the variance component for soldiers, ![]() = .03, reflects universescore variance—systematic differences among soldiers that decision makers want to know about.
= .03, reflects universescore variance—systematic differences among soldiers that decision makers want to know about.
The remaining 22 terms in the table represent potential sources of measurement error. Relative to other components, variance components PJ, PJS:T, and POJS:T are sizable. Notice that in each component soldiers (P) and observers (J) are involved. Observers apparently do not agree with one another in scoring individual soldiers' performance, and this disagreement among observers changes with subtask and occasion. As a result, the G coefficient for a measurement made with one observer on one occasion is: .12 for relative decisions and .10 for absolute decisions.
TABLE 5 Generalizability Study for a Soldier (P) × Occasion (O) × Task (T) × Subtask:Task (S:T) × Observer (J) Design
|
Source of Variation |
df |
Mean Squares |
Variance Components |
|
Soldiers (P) |
4 |
3.140 |
.030 |
|
Occasions (O) |
1 |
0.010 |
.000 |
|
Tasks (T) |
1 |
0.810 |
.000 |
|
Subtasks:Tasks (S:T) |
8 |
0.881 |
.013 |
|
Observers (J) |
3 |
2.093 |
.005 |
|
PO |
4 |
0.123 |
.000 |
|
PT |
4 |
0.135 |
.000 |
|
PS:T |
32 |
0.153 |
.000 |
|
PJ |
12 |
0.885 |
.025 |
|
OT |
1 |
0.000 |
.000 |
|
OS:T |
8 |
0.036 |
.000 |
|
OJ |
3 |
0.837 |
.012 |
|
TJ |
3 |
0.330 |
.000 |
|
JS:T |
24 |
0.376 |
.014 |
|
POT |
4 |
0.013 |
.000 |
|
POS:T |
32 |
0.036 |
.000 |
|
POJ |
12 |
0.224 |
.013 |
|
PTJ |
12 |
0.230 |
.000 |
|
PJS:T |
96 |
0.248 |
.074 |
|
OTJ |
3 |
0.067 |
.000 |
|
OJS:T |
24 |
0.091 |
.000 |
|
POTJ |
12 |
0.071 |
.000 |
|
POJS:T |
96 |
0.100 |
.100 |
Modifications for Future Decision Studies
This pattern of findings suggests one or some combination of modifications to the performance test:
-
Modify procedures so that observers are not also test administrators —lapses in attention may give rise to inconsistencies.
-
Train observers more extensively and maintain training checks over the period of performance testing.
-
Increase the number of observers judging performance.
Only the last recommended change can be evaluated with the hypothetical data. By using four observers, the G coefficients are .36 and .29 for relative and absolute decisions, respectively. Clearly, modifications in test-
ing procedures, training procedures, or both may be needed to increase generalizability within practical manpower and cost limits.
SKETCH OF GENERALIZABILITY THEORY
Background
Generalizability theory evolved out of the recognition that the concept of undifferentiated error in classical test theory provided too gross a characterization of the multiple sources of variation in a measurement. The multifaceted nature of error was portrayed in the last section using a hypothetical performance measurement: operating and maintaining a caliber .38 revolver. For example, a soldier might be observed by one of many observers, on one of many possible occasions, performing one of many tasks. G theory assesses each source of error—observers, occasions, tasks in this example—to characterize the dependability of the measurement and improve the job performance test design.
G theory views a behavioral measurement as a sample from a universe of admissible observations. The universe is characterized by one or more sources of error variation or “facets” (e.g., observers, occasions, tasks). This universe is typically defined as all combinations of the levels (called conditions in G theory) of the facets. In the last section's example, the universe for performance-time measurement was characterized by four facets: stations, occasions, tasks, and observers. The universe of admissible observations consisted of performance-times measured by all combinations of stations, occasions, tasks, and observers. The soldier's performance times—obtained from four observers on two tasks performed at two stations on two occasions—represented a sample from the universe of admissible observations. The decision maker intended to generalize these performance measurements to the entire universe of admissible observations.
Since different measurements may represent different universes of admissible observations, G theory speaks of the ideal datum as universe scores, rather than true scores as does classical theory, acknowledging that there are different universes to which decision makers may wish to generalize. Likewise, the theory speaks of generalizability coefficients rather than the reliability coefficient, realizing that the computed value of the coefficient may change as the definition of the universe changes.
Variance Components
In G theory, a measurement is decomposed into a component for the universe score (analogous to the true score in classical theory) and one or more error components (facets). To illustrate this decomposition, a two-
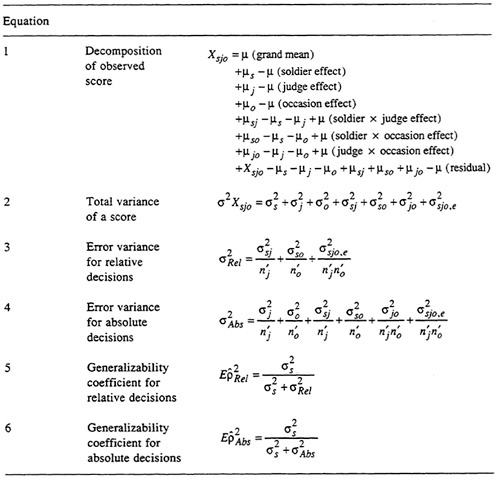
facet design is used for simplicity: soldiers × judges × occasions. The object of measurement, soldiers, is not a source of error and, therefore, is not a facet. (The argument presented here readily extends to more complex designs such as those described in the previous section.)
The score Xsjo assigned to a particular soldier's (s) performance by a particular judge (j) on a particular occasion (o) can be decomposed into eight components as shown in equation 1 in Table 6. The single observed score Xsjo and each component other than mu (μ) in equation 1 has a distribution. For all soldiers in the universe of judges and occasions, the distribution of μs − μ has a mean of 0 and a variance denoted by ![]() (called the universescore variance). Similarly, there are variances associated with each of the
(called the universescore variance). Similarly, there are variances associated with each of the
error components: they are called variance components. For example, the variance of μo − μ is denoted by ![]() . The variance of the collection of Xsjo for all soldiers, judges, and occasions included in the universe, then, is the sum of all of the variance components in equation 2 (see Table 6). In words, the variance of the scores can be partitioned into independent sources of variation due to differences between soldiers, judges, occasions, and their interactions.
. The variance of the collection of Xsjo for all soldiers, judges, and occasions included in the universe, then, is the sum of all of the variance components in equation 2 (see Table 6). In words, the variance of the scores can be partitioned into independent sources of variation due to differences between soldiers, judges, occasions, and their interactions.
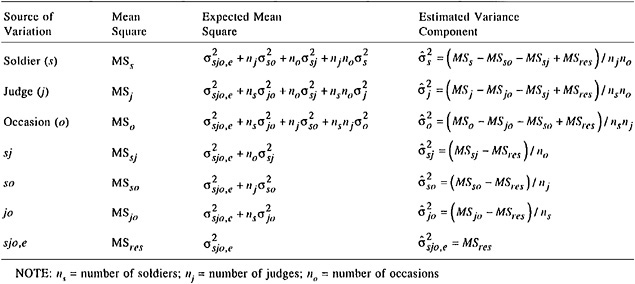
Numerical estimates of the variance components can be obtained from an analysis of variance (ANOVA) by setting the expected mean squares for each component equal to the observed mean squares and solving the set of simultaneous equations as shown in Table 7. (This is how the numerical values of the components of variance in Table 3 were obtained.) The variance component for soldiers (![]() ) represents universe-score variance, and the remaining components represent error variance. G theory focuses on the variance components. The relative magnitudes of the components provide information about particular sources of error in scores assigned to the soldiers' performance.
) represents universe-score variance, and the remaining components represent error variance. G theory focuses on the variance components. The relative magnitudes of the components provide information about particular sources of error in scores assigned to the soldiers' performance.
As an example, the performance-time data reported in Table 2 were pooled over stations and tasks to produce data in the form of a soldier × judge × occasion G study. The results of the analysis of these hypothetical data are presented in Table 8. The observed score variance is partitioned into its sources in the first column of the table. The variance components in the last column are obtained by setting the mean squares in the table equal to their expectations and solving the equations shown in Table 7. For example,
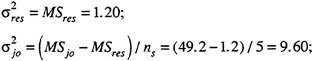
and so on.
The variance component for soldiers in Table 8 represents systematic (universe-score) variation in performance times among soldiers—it is the signal the decision maker is looking for. The variance component for occasions is sizable; it represents mean differences in the times on occasions 1 and 2. Soldiers were slower on one occasion than on the other. The small variance component for judges indicates that the judges were very close in reporting average time to complete the revolver exercise. The sizable SJ interaction component indicates that judges disagree as to which soldiers were faster than others. The large SO interaction component indicates that the difference among soldiers ' performance times changes from one occasion to the next; i.e., some soldiers perform faster, others slower, and this ordering changes over occasions. The relatively small OJ variance component indicates that judges are reasonably consistent in the mean performance
TABLE 8 Analysis of Hypothetical Data from the Soldier × Occasion × Judge Design
|
Source of Variation |
df |
Mean Squares |
Estimated Variance Components |
|
Soldiers (S) |
4 |
506.20 |
42.30 |
|
Occasions (O) |
1 |
607.40 |
22.20 |
|
Judges (J) |
3 |
175.40 |
7.35 |
|
SO |
4 |
116.00 |
28.65 |
|
SJ |
12 |
53.70 |
26.25 |
|
OJ |
3 |
49.20 |
9.60 |
|
SOJ,e (residual) |
12 |
1.20 |
1.20 |
|
SOURCE: Based on hypothetical data in Table 2. |
|||
times they record on the two occasions. And the small residual component indicates that other unidentified sources of error have little influence on the measurement.
Generalizability and Decision Studies
Typically enlistees are tested on only one occasion and their performance is scored by a single judge who is also responsible for administering the test. This procedure is dictated in large part by cost and convenience, and perhaps also by lack of information on the consequences this procedure has for the reliability of the performance measurement. Generalizability theory provides a method for estimating measurement error due to inconsistencies arising from one occasion to another, or from one judge to another. Once the important source of error has been identified, reliability can be forecast for alternative performance-measurement procedures. That is, with some front-end cost and inconvenience, a performance measurement program can be designed to minimize cost and inconvenience for a given level of reliability.
G theory recognizes that certain studies (G studies) are associated with the development of a measurement procedure, for example, to determine the relative influence of the sources of measurement error (judges and occasions in our example) on the dependability of a performance measurement. This information enables the test developer to recommend the number of times each potential measurement facet needs to be sampled to obtain a dependable measurement for decision making purposes. The universe of admissible observations in the G study is defined as broadly as possible within practical and theoretical constraints to estimate as many variance
components as possible. To this end, Cronbach et al. (1972) recommended using a crossed G study design so that all of the possible variance components can be estimated. By doing so, the findings will have wide applicability to as many practical measurement settings as possible.
Other studies, decision (D) studies, then apply the procedure; decisions are made, at least in part, on the basis of the measurement. For example, military policy makers might examine some aspects of readiness by measuring individual and unit performance. Or they might revise enlistment standards based on the correlation between performance and measures of these standards.
The results of the G study provide information for optimizing the design of the D study. If the G study showed that one (or more) source of error variation was very small, the decision maker could reduce the number of conditions of the facet, select (and thereby control) one level of the facet, or ignore the facet altogether. This permits a smaller—and presumably less costly—design for the decision study than that used in the G study. If, however, soldiers' performances varied by occasion, as was the case in the example G study (Table 8), soldiers should be observed on multiple occasions, and the average of their scores (performance times) should be used in further analyses (such as correlating enlistment attributes with job performance measures).
In an important sense, a D study reflects the results of applying a SpearmanBrown-like prophecy formula (in classical theory) to determine how many judges and occasions are needed for the performance measurement to meet minimal reliability (generalizability) standards. For example, the generalizability of the performance measurement in the S × O × J study can be increased by decreasing error associated with inconsistency across occasions—variances associated with occasions and the interactions: soldier × occasion, judge × occasion, and residual. This error variance can be reduced by taking the average of the occasion scores. This tack has the effect of reducing all variance components involving occasions by 1/no′, where no′ is the number of occasions to be sampled in the D study. For example, suppose to reduce measurement errors due to inconsistencies among occasions, a D study were planned to take the average of three occasions ' performance times on the revolver test. To determine what the variance component for occasions would be in the D study, we divide the variance component for occasions in Table 8 by three, with the result that ![]() = 2.45. The SO variance component would be reduced to 28.65/3 = 9.55, and the residual variance component would be .40. Similarly, error variance due to judges could be decreased by averaging scores over judges. The variance components reflecting variation over judges would correspondingly be divided by nj′, the number of judges to be sampled in the D study, and the residual component would be divided by the product of no′ and nj′.
= 2.45. The SO variance component would be reduced to 28.65/3 = 9.55, and the residual variance component would be .40. Similarly, error variance due to judges could be decreased by averaging scores over judges. The variance components reflecting variation over judges would correspondingly be divided by nj′, the number of judges to be sampled in the D study, and the residual component would be divided by the product of no′ and nj′.
Relative and Absolute Decisions
G theory recognizes that decision makers may use the same measurement in different ways. Some interpretations may focus on individual differences among soldiers. For example, determining the relation between enlistment attributes and military job performance depends only on the rank-ordering of soldiers on enlistment variables and on job performance variables. The decision maker, then, is concerned mainly with the generalizability of the rank ordering of soldiers over the facets of the measurement (judges and occasions in our example). We speak of relative decisions in this case.
Other interpretations may focus on the level of performance itself, without reference to other soldiers' performance. The written examination for a driver's license is an example—pass or fail is determined by the number of incorrect answers, not by how others performed on the examination. Likewise, decisions about military readiness might depend on absolute standards, not on how other units did. In both cases, decision makers are interested in absolute levels of performance and hence are concerned with the generalizability of absolute decisions.
Of course, decision makers can be and are interested in both kinds of decisions. The important point is that the distinction between relative and absolute decisions has important implications for the definition of measurement error and, as a consequence, the dependability of a performance measurement.
Measurement Error for Relative Decisions
For relative decisions, the error variance consists of all variance components that affect the rank-ordering of soldiers; all variance components representing interactions of the facets with the object of measurement—soldiers in our example. The error variance for relative decisions is shown in equation 3 of Table 6. The error variance for relative decisions reflects disagreements among judges and inconsistencies over occasions about the ordering of soldiers' performance. These disagreements and inconsistencies are considered error because they do not reflect systematic differences in soldiers' performance, yet they change, in unpredictable ways, measures of soldiers' performance.
Notice that the remaining score components in an observed score (see equation 1 in Table 6) are constant for all soldiers. Consequently, they do not influence the rank ordering of performance and are not defined as relative error.
Measurement Error for Absolute Decisions
For absolute decisions, the error variance consists of all variance compo-
nents except that for universe scores (see equation 4 in Table 6). The error variance for absolute decisions reflects differences in mean ratings of soldiers across judges and occasions, as well as disagreements about the ranking of soldiers' performance. When the decision maker is concerned with the absolute level of performance, the variance components associated with effects of judges and occasions (![]() ,
, ![]() , and
, and ![]() ) are defined as error variance. The leniency of one judge as compared to another will influence a soldier's score as might, for example, the soldier's mental and physical condition on the particular day on which the test is given. That is, perceptions of particular judges who observe a soldier and the events occurring during the particular occasion will influence the observed score and, hence, the decision maker's estimate of the soldier's universe score. Thus, it may be important to obtain measures of soldiers' performance on several occasions using several judges so that these influences will be averaged out.
) are defined as error variance. The leniency of one judge as compared to another will influence a soldier's score as might, for example, the soldier's mental and physical condition on the particular day on which the test is given. That is, perceptions of particular judges who observe a soldier and the events occurring during the particular occasion will influence the observed score and, hence, the decision maker's estimate of the soldier's universe score. Thus, it may be important to obtain measures of soldiers' performance on several occasions using several judges so that these influences will be averaged out.
Generalizability Coefficients for Relative and Absolute Decisions
While stressing the importance of the variance component, G theory also provides a coefficient analogous to the reliability coefficient in classical theory. The generalizability coefficient for relative decisions is given in equation 5 (Table 6). In the equation, the symbol ![]() , indicates the expected value of the squared correlation between observed scores and universe scores. An analogous coefficient can be defined for absolute decisions as in equation 6 of the same table.
, indicates the expected value of the squared correlation between observed scores and universe scores. An analogous coefficient can be defined for absolute decisions as in equation 6 of the same table.
The generalizability coefficient, ![]() , indicates the proportion of observedscore variance (
, indicates the proportion of observedscore variance (![]() +
+ ![]() ) or (
) or (![]() +
+ ![]() ) that is due to universe-score variance (
) that is due to universe-score variance (![]() ). In this respect, it is a ratio of signal to [signal + noise]. It ranges from 0 to 1.00 and, like the reliability coefficient in classical theory, its magnitude is influenced by variation among soldiers' scores and the number of observations made. The number of observations is taken into account in much the same way as in the Spearman-Brown formula in classical theory (see the discussion on D studies above). Using the Spearman-Brown formula, one can estimate the reliability of a test of any length from the reliability of the original test. Analogously, in equations 3 and 4 (Table 6), the denominator indicates the number of observations to be made in the D study (number of judges and occasions). As the number of observations increases, the error variance (
). In this respect, it is a ratio of signal to [signal + noise]. It ranges from 0 to 1.00 and, like the reliability coefficient in classical theory, its magnitude is influenced by variation among soldiers' scores and the number of observations made. The number of observations is taken into account in much the same way as in the Spearman-Brown formula in classical theory (see the discussion on D studies above). Using the Spearman-Brown formula, one can estimate the reliability of a test of any length from the reliability of the original test. Analogously, in equations 3 and 4 (Table 6), the denominator indicates the number of observations to be made in the D study (number of judges and occasions). As the number of observations increases, the error variance (![]() ) or (
) or (![]() ) decreases and the generalizability coefficient,
) decreases and the generalizability coefficient, ![]() , increases.
, increases.
A major contribution of generalizability theory is that it allows the researcher to pinpoint the sources of measurement error (e.g., judge, occasion, or both) and to increase the appropriate number of observations so that error “averages out.” The researcher can estimate how many conditions of each facet are needed to obtain a certain level of generalizability. If, for example, variation due to occasions is large relative to variation due to soldiers, and
variation due to judges is small, increasing the number of occasions would produce a lower estimate of error variation and consequently a higher generalizability coefficient (see equation 4, Table 6), whereas increasing the number of judges would have little effect on the estimates of error variation and generalizability. (See Shavelson and Webb, 1981, for details on optimizing generalizability coefficients by selecting conditions of two facets.)
Random and Fixed Facets
To this point, the presentation of G theory has assumed that the conditions of the measurement have been randomly sampled from an indefinitely large universe.7 In the hypothetical S × J × O design, we assumed that the four judges were sampled randomly from a universe of judges, and that the two occasions were sampled randomly from a universe of admissible occasions. In the previous section, a more comprehensive design was described: soldiers × stations × occasions × tasks × observers. The analysis assumed that the two stations were a random sample from an indefinitely large universe, that the two occasions were a random sample, that the three tasks were a random sample from a large universe of tasks, and that the observers were sampled randomly.
Generalizability theory, then, can model the military decision maker 's ideal performance measurement. This is a measurement that generalizes over all possible stations at which the test might be given, over all possible occasions on which the test might be given, over all possible tasks in a military occupational specialty, and over all possible observers who might time and score soldiers' performance.
The assumption of random facets is more an ideal than an actuality in performance measurement. The truth be known, in most performance measurement studies stations are not randomly sampled, occasions are not randomly sampled, tasks are not randomly sampled, and judges are not randomly sampled. Indeed, soldiers may not be randomly sampled. This fact is made clear in reports from all four Services [Office of the Assistant Secretary of Defense (Manpower, Reserve Affairs, and Logistics), 1983]:
-
It is simply not feasible to develop a measure of performance for every task performed by a soldier in an MOS. . . . The variables considered important in selecting tasks for testing were frequency, criticality, and variability of performance (p. 25).
-
These tests will be developed for tasks or part tasks that are (1) routinely done by at least 90% of first-term sailors . . , (2) feasible to test in a
|
7 |
Variance component estimates for restricted universes are readily available (see Brennan, 1983; Cardinet and Allal, 1983). |
-
hands-on mode on actual equipment, and (3) not severely affected by limited operational constraints (i.e., equipment only partially operable) (p. 58).
-
From occupational survey data, [AF] critical specialty and job-type specific tasks will be identified. Subject matter experts (SMEs) will aid the developers in dichotomizing the tasks into those which can be economically observed and those which must be measured by interview. The SME's will then develop procedures for observing task performance . . . (p. 45)
-
[Marine Corps] test administrators will be trained in how to give and score hands-on tests . . . . The administrators will be assigned full-time to the research project (p. 73).
Generalizability theory handles sampling issues in two ways. The first way is to assume that the conditions of a measurement facet are exchangeable with other potential conditions (see Shavelson and Webb, 1981, for details). Thus, if the test administrators (observers or judges) are considered exchangeable for other observers who might have been used, or if the test occasions are considered exchangeable for other occasions, these facets might legitimately be considered random. In this case, G theory treats these facets as random and proceeds with an analysis like that presented in Table 8.
A second way G theory treats these sampling issues is to recognize that either (1) decision makers are not interested in generalizing beyond the conditions of the facet, or (2) the conditions of the facet exhaust the universe of possible conditions (cf. a fixed factor in the ANOVA). Hence, the sample of tasks, n(tasks), equals the universe of tasks, N(tasks). For example, the three tasks comprising the caliber .38 revolver operation and maintenance test—loading, reducing a stoppage, and unloading/clearing the weapon—might exhaust the universe of tasks over which decision makers might wish to generalize. In this case, the task facet would be considered a “fixed facet.”
Statistically, G theory treats fixed facets by averaging over the conditions of a fixed facet and examining the generalizability of these averages over the random facets (Cronbach et al., 1972:60; see Erlich and Shavelson, 1976, for a proof). This tack is justified because by averaging over the conditions of a fixed facet the average is over the entire universe. Averaging provides the best score for an individual because it represents the individual's universe score over the conditions of the fixed facet. The statistical analysis of data from G studies with a fixed facet proceeds by carrying out an ANOVA on scores averaged over the conditions of the fixed facet.
Consider a modification of the hypothetical S × J × O generalizability study (Table 8). Suppose that the judges observed the speed of the soldiers' performances on three tasks—loading, reducing a stoppage, and unloading—and that these three tasks exhausted the universe of possible revolver tasks. This modification produces a three-facet G study with two random
facets (occasions and judges) and one fixed facet (tasks). Each soldier 's performance-time data would be averaged over the three tasks for each judge and each occasion. An S × J × O ANOVA would be used to analyze these averages.
An analysis of hypothetical performance-time data from the S × J × O × T* generalizability study (where T* denotes a fixed facet) is provided in Table 9. Two things about the table are noteworthy. First, the results in part (a) are similar to those reported in the previous section for the soldier × station × judge × occasion × task—completely random design, since the variance components are (virtually) uncorrelated and, anyway, the effects of the station facet and its interactions with all other facets were 0.
Second, the data were analyzed as a completely random design and mean squares and variance components were recomputed for the restricted universe of generalization—to occasions and judges, weighted for the number of tasks (Table 9, part b). All of the components involving task variation (e.g., T, ST, OT, JT, SOT)—the within-T components—go to 0 because scores are averaged over facet T (see Cronbach et al., 1972:115). This is the same result that would have been obtained if a S × J × O design had been run on performance times averaged over tasks.
Incidentally, the generalizability coefficients for relative decisions are the same for the two models (Table 9, part c). This happened because, in the S × O × J × T (random) model, the person × task and higher-order person × task × (etc.) variance components are 0 except in the case where ![]() = 1.00. Compared to the other sources of relative error (e.g., SO and SJ), the person × task interactions have no appreciable effect on the relative G coefficient (with “real” data, there is no a priori reason to expect soldier × task variance components to be 0).
= 1.00. Compared to the other sources of relative error (e.g., SO and SJ), the person × task interactions have no appreciable effect on the relative G coefficient (with “real” data, there is no a priori reason to expect soldier × task variance components to be 0).
This is not the case for the absolute G coefficient where the variance component for task enters into the definition of measurement error in the random model and is sizable (20). Even after dividing it by the number of tasks sampled (3), it is still sizable (6.67).
Finally, the results of the S × O × J × T* G study reported in Table 9 are identical to those in Table 8 that reported the data from a S × J × O design. In both analyses, the task facet is ignored (averaged over) as is the station facet.
Before leaving the topic of fixed facets, we should note that the definition of a fixed facet that leads one to “average over” its conditions might be misleading in certain circumstances (see Shavelson and Webb, 1981). In a teaching context, for example, it might not make sense to average over elementary teachers' performance in teaching mathematics and English. Teachers do different things in teaching the two subject matters, and to ignore these differences by averaging over them would lead to misconceptions and loss of information. A redefinition of the fixed facet that recognizes such differences,
TABLE 9 Analysis of Data from a S × O × T × J* Design Where T* is a Fixed Facet
|
Source of Variation |
df |
Mean Square |
Variance Componentsa |
|
(a) Random Model |
|||
|
Soldier (S) |
4 |
1020.80 |
14.10 |
|
Occasion (O) |
1 |
1273.00 |
7.40 |
|
Task (T) |
2 |
1659.00 |
20.00 |
|
Judge (J) |
3 |
349.80 |
2.45 |
|
SO |
4 |
239.00 |
9.55 |
|
ST |
8 |
9.80 |
0.00 |
|
SJ |
12 |
106.80 |
8.75 |
|
OT |
2 |
59.80 |
1.25 |
|
OJ |
3 |
97.80 |
3.20 |
|
TJ |
6 |
1.80 |
0.00 |
|
SOT |
8 |
9.80 |
1.00 |
|
SOJ |
12 |
1.80 |
0.00 |
|
STJ |
24 |
1.80 |
0.00 |
|
OTJ |
6 |
1.80 |
0.00 |
|
SOTJ,e (residual) |
24 |
0.40 |
0.40 |
|
(b) Mixed Model with Task Fixed |
|||
|
S |
4 |
506.20 |
42.30 |
|
O |
1 |
607.40 |
22.20 |
|
J |
3 |
175.40 |
7.35 |
|
SO |
4 |
116.00 |
28.65 |
|
SJ |
12 |
53.70 |
26.25 |
|
OJ |
3 |
49.20 |
9.60 |
|
SOJ,e (residual) |
12 |
1.20 |
1.20 |
|
(c) Generalizability Coefficientsb |
|||
|
Random Model |
Mixed Model (T* Fixed) |
||
|
|
|
||
|
|
|
||
then, might be appropriate. There may be analogous situations in military performance testing, such as distinguishing between daytime and nighttime performance. If there is any doubt, the analysis of the fixed facet would proceed in two stages. In the first stage, a G-study analysis would be carried out treating all facets as random to assess the variability among conditions of the (candidate) fixed facet. Large variance components associated with the candidate facet would suggest that performance differs across conditions; a large person by candidate-facet interaction would indicate that individuals' performances are not ordered the same under different conditions of the candidate facet. If this is the case, a second stage might be to conduct G-study analyses for each condition of the candidate facet separately.
G and D Studies With Crossed and Nested Facets
In the previous examples, crossed designs have been used to illustrate generalizability theory. In a crossed design, the levels of each variable are combined with the levels of all other variables. In the example G study (Table 8), all soldiers were observed by all judges on both testing occasions. We denoted this crossed design by the notation, S × J × O, indicating there are ns × no × nj (= 5 × 2 × 4) = 40 combinations of conditions in the design.
There are cases where not all conditions of one facet can be combined
with all conditions of one or more other facets. One example is the G study design in which soldiers' performance was scored on two occasions by four judges on the subtasks of loading and unloading/checking a caliber .38 revolver (see Table 4). The subtasks involved in loading the revolver are not exactly the same as those involved in unloading the revolver. That is, the subtasks are unique to the particular task performed. We say that subtasks are nested within tasks and write the design symbolically to represent this nesting: P × O × J × T × S:T where S:T is read, “subtasks are nested within tasks,” and P refers to soldiers (mnemonically, persons).
Nesting also arises in traditional achievement testing, where the first 10 items might deal with reading comprehension and the next 10 items might examine science knowledge. We say that items (“subtasks ”) are nested within subject-matter topics (tasks). A design in which 100 students (S) take an achievement test with multiple topics (T) and each topic contains a different set of items (i) would be designated as follows: S × T × I:T.
A third example, common with performance measurements, is when judges A and B score the performance of soldier 1, observers C and D score the performance of soldier 2, and so on. In this case, we say that judges (J) are nested within soldiers (S). This design would be represented as: S × J:S. More generally, the conditions of facet A are said to be nested in the conditions of facet B when, for each condition of facet B, there is more than one condition of facet A, and the conditions of facet A are different for each condition of facet B.
The major consequence of nesting is that not all variance components can be estimated. In the P × O × J × T × S:T design, variance components for the following interactions cannot be estimated: TS:T, PTS:T, OTS:T, JTS:T, POTS:T, PJT:ST, and OJTS:T (see Table 4). In the S × T × I:T design, variance components for TI:T and STI:T cannot be estimated. And finally, the variance component for SJ:S cannot be estimated in the S × J:S design. In general, interaction components of variance cannot be estimated for interactions containing the nested variable and the variable in which it is nested.
Since nested designs do not provide variance components for all sources of measurement error, Cronbach et al. (1972) recommended that G studies employ crossed designs. Only when many conditions need to be sampled are nested G studies recommended.
The crossed-design recommendation, however, does not extend to D studies. At the time a D study is conducted, sources of measurement error should have already been pinpointed. The aim of the D study is to obtain large samples of conditions for errorsome facets. To this end, nesting is a boon. The hypothetical S × J × O generalizability study with two occasions and four judges had revealed large variance components for occasions and the interaction of soldiers and occasions (Table 8). A D study should use as many occasions as possible, but three per soldier seems like the limit. So,
the following nested D-study design might be used: S × J:P × O where soldiers are crossed with judges and occasions are nested within each soldier. In this example, the variance component for occasions would be sampled np × no = 5 × 3 = 15 times, not just 2 times as in the G study. And the variance component for the JO:P interaction, for example, would be sampled nj × (np × no) = 60 times!
Multivariate Generalizability Theory
Performance measurements often describe performance with more than one score. In an example used in this section, two judges timed and scored the performance of five soldiers on three tasks—loading, reducing a stoppage, and clearing a revolver—on each of two occasions. Two different sets of scores may be of concern to the decision maker. The first is a profile or composite consisting of performance time and accuracy. The second is a profile or composite of performance times across the three tasks, or a profile or composite of accuracy scores across the tasks.
In assessing the reliability or generalizability of profiles or composites, most studies take a univariate approach. Tasks, for example, would be treated as a facet—source of error—in the measurement and a univariate G analysis would be conducted as has been done in the examples up to this point. Or the time and accuracy measures, for example, would be treated separately in univariate G studies, producing two different sets of findings and, perhaps, conflicting D-study recommendations. In short, the univariate approach does not assess sources of error covariation (correlation) among the multiple scores. Such information is important for designing an optimal decision study and for permitting a decision maker to determine the composite (across tasks or across time and accuracy) with maximum generalizability.
Generalizability theory provides a method for taking into account the covariances among performance-measurement scores. Just as univariate generalizability theory stresses interpretations of the pattern of variance components, multivariate G theory stresses interpretation of variance and covariance components (see Webb et al., 1983, for a concise, elementary presentation of the theory). It also provides a summary index for a composite of scores, a multivariate generalizability coefficient analogous to the univariate coefficient.
To make the presentation of multivariate G theory concrete, let's simplify the design of the revolver operation and maintenance measure to a soldier × occasion design. Three measures are obtained: scores on time to (1) load, (2) remove a stoppage from, and (3) unload the revolver. This design may be described as a S × O design with a set of three scores (or dependent variables).
Perhaps the easiest way to explain the multivariate version is by analogy
to the univariate case. In the univariate case, we treat the data from the S × O design with three task scores as a S × O × T design with one performance score per cell of the design. An observed score (e.g., time) is decomposed into the universe score and error scores corresponding to occasions, tasks, their interactions with each other and with soldiers. An estimate of each component of variation in the observed scores is obtained. For this twofacet, univariate design, ![]() is the estimated universe-score variance. For relative decisions, the estimate of the multifaceted error variance is:
is the estimated universe-score variance. For relative decisions, the estimate of the multifaceted error variance is:
where no′ and nt′ are the numbers of conditions of the facets in the decision study, and the generalizability coefficient is:
In extending the notion of multifaceted error variance to multivariate designs, we treat tasks not as a facet but as three dependent variables: time to load (lXso), time to remove a stoppage (rXso), and time to unload (uXso). For each measure, the components of the observed score variance reflect variation between soldiers ![]() and a residual, which is the interaction of students with occasions confounded with error (
and a residual, which is the interaction of students with occasions confounded with error (![]() ):
):
σ2(lXso) = σ2(ls) + σ2(lso,e)
σ2(rXso) = σ2(rs) + σ2(lso,e)
σ2(uXso) = σ2(us) + σ2(uso,e)
where
l is the loading task
r is the removing task
u is the unloading task
X is an observed score
s is soldiers
o is occasions.
So, σ2(lXso) is the observed score variance on the loading task and σ2(uso,e) is the residual variance on the unloading task. Moreover, the components of
one score (e.g., (lXso) can be related to (covary or correlate with) the components of the other scores (e.g., (lXso). For a composite of the three scores, the expected observed-score variance (the universe-score variance plus the residual variance) depends on the components of covariance as well as on the components of variance. The observed-score variance of this composite can be expressed as the variance-covariance matrix shown in part (a) of Table 10.
In univariate G theory, the expected observed-score variance can be decomposed into components for universe-score variance and error variances. In multivariate G theory, the expected observed-score variance-covariance matrix can also be decomposed. For relative decisions, the decomposition is given in part (b) of Table 10.
Just as the analysis of variance can be used to obtain estimated components of variance, Multivariate ANalysis Of VAriance (MANOVA) provides a computational procedure for obtaining estimated components of variance and covariance. While ANOVA provides scalar values for the sums of squares and mean squares, MANOVA provides matrices of sums of squares and crossproducts and mean squares and crossproducts.
Estimates of components of covariance are obtained by setting the expected mean product (MP) equations equal to the observed mean products and solving the set of simultaneous equations. (As in the univariate case, estimated variance components are obtained by setting the expected mean square equations equal to the observed means squares and solving the set of simultaneous equations.) The equations in part (c) of Table 10 relate mean products to their expectations such that components of variance and covariance for the universe score matrix (Table 10, part (b)) can be obtained. The first three equations in part (c) reflect the univariate case, in which each subtest is examined separately, whereas all six equations represent the multivariate case.
The results of a multivariate analysis—the variance and covariance components for persons, occasions, and residual—are given in Table 11 using hypothetical data. Part (1) contains components of universe-score variance and covariance. Universe-score variance components are found along the main diagonal, and covariance components are given off the diagonal. The high covariance components among the universe scores across the three tasks, relative to the residual covariance components, indicate that soldiers who load the revolver quickly also remove the stoppage and unload the revolver quickly. That is, there is an underlying speed component in tasks that involve operating and maintaining a caliber .38 revolver. The one high residual component of covariance suggests that unexplained factors undermine the consistency of performance times and that the loading and unloading task scores tend to fluctuate together.
The multivariate G coefficient is an analog to the univariate G coefficient
TABLE 10 Decomposition of a Composite of Scores on Three Performance Tasks —Loading, Removing a Stoppage from, and Unloading a Revolver
TABLE 11 Estimated Variance and Covariance Components Underlying the Expected Observed-Score Variance in the Soldier × Occasion Multivariate G Study of Performance on Three Revolver Tasks no = 1
|
Task |
|||
|
Source of Variation |
(1) Loading |
(2) Removing |
(3) Unloading |
|
Soldiers (S) |
|||
|
Loading |
4.27 |
||
|
Removing |
1.07 |
4.05 |
|
|
Unloading |
2.08 |
1.14 |
5.84 |
|
Residual (SO,e) |
|||
|
Loading |
2.34 |
||
|
Removing |
0.00 |
0.78 |
|
|
Unloading |
0.84 |
0.18 |
1.10 |
(Table 10, part (d); see Shavelson and Webb, 1981; Webb et al., 1983). From a random effects MANOVA, the canonical variates (weights applied to the three task times) are determined to maximize the ratio of universe score variation to universe score plus error variation. By definition, the first composite that emerges from the analysis is the most reliable. In our hypothetical example, the multivariate generalizability of a composite composed of the three tasks with performance times obtained at one occasion is .73 for the first canonical variate.
In forming the composite to optimize the multivariate G coefficient, time to remove a stoppage was given the greatest weight (.37), while the other two tasks received considerably less weight (time to load, .11; and time to unload, .07). This weighting might not fit with what experts consider to be the correct weighting, because the composite is formed solely on statistical grounds, not on conceptual or practical ground.
A composite can be formed on conceptual or practical grounds simply by having the decision maker supply weights for the three tasks, and then by (1) taking the weighted sum of the three scores for each soldier, and (2) running an S × O univariate G analysis on the composite. The resulting univariate G coefficient for this composite can be compared with the statistically optimum multivariate coefficient to determine the precision lost to achieve conceptual or practical validity.
Symmetry in Behavioral Measurements
Typically, most behavioral measurement have been used to differentiate individuals. Hence, national achievement tests are designed to spread out individuals' scores by including difficult items. Military performance tests have been or will be designed to selectively sample tasks that differentiate individuals' military occupational specialty performance. The work of Cardinet, Tourneur, and Allal (Cardinet et al., 1976a, 1976b, 1981; Cardinet and Allal, 1983; Cardinet and Tourneur, 1974, 1977; Tourneur, 1978; Tourneur and Cardinet, 1979; for a different perspective, see Wittman, 1985) recognized, however, that the focus of measurement may change, depending on a particular decision maker 's purpose. For example, the decision maker might want to know whether there are systematic differences in the behavior of different subgroups of people in a population or whether the population can be considered homogeneous. Or, the decision maker might be interested in performance scores on a set of tasks (e.g., task difficulty) and not in the differentiation of individuals' performance on the set of tasks. Hence, the task, and not the individual, becomes the object of measurement. Variation among individuals' performance on the task becomes a source of measurement error.
The principle of symmetry of behavioral measurements states that each of the facets of a factorial design can be selected as the object of study; individuals are not necessarily the sole object of measurement. This principle led Cardinet and his colleagues to distinguish among four stages of a measurement study:
-
Observation design—choice of facets and their conditions, and the computation of mean squares;
-
Estimation—decisions about whether the facets are finite or infinite, random or fixed, and the estimation of variance components;
-
Measurement—specification of the facet (or combination of facets) that is the focus of measurement, and specification of the sources of error; and
-
D-study designs.
The notion that symmetry leads to the possibility of multifaceted populations is something not considered in classical theory. This is particularly germane to military performance testing because individuals are parts of small units (e.g., crews) which are parts of larger units (e.g., platoons), which are parts of still larger units (e.g., companies), and so on. The level and consistency of an individual 's performance may be a function of his ability, but it may also be a function of the training and leadership provided by the organization in which he resides. In this case, universe-score vari-
ance might include, in addition to systematic variation among individuals, systematic variation among higher units in which the individual is embedded (see the next section; also Kahan et al., 1985).
Perhaps most importantly for military applications, the principle of symmetry provides one possible means for estimating the generalizability of unit performance, a topic beyond the scope of the Services' concerns at this point, but something that certainly should be on a future measurement agenda. For this reason, this paper on G theory has been subtitled, “I. Individual Performance.” An example of the application of G theory to unit performance measurements is given in the next section.
ILLUSTRATIVE APPLICATIONS OF GENERALIZABILITY THEORY
To this point, generalizability theory has been applied to military performance measurements using hypothetical data. In this section, two published G studies are presented. These studies were selected because they illustrate the concepts and procedures described in previous sections. One is a study of the generalizability of general educational development ratings based on job descriptions found in the Dictionary of Occupational Titles (Shavelson and Webb, 1981; Webb and Shavelson, 1981; Webb et al., 1981). The other is a study of the generalizability of a tank-crew performance measurements (Kahan et al., 1985).
Generalizability of General Educational Development Ratings
The U.S. Department of Labor (1972) developed the General Educational Development scale to rate the amount of reasoning, mathematics, and language abilities needed to perform various jobs. General educational developmental ratings are used in several employment and training situations. For example, they provide the basis for: (1) estimates of time required to learn job skills; (2) state employment agencies ' decisions to refer persons to specific employers, job training programs, or remedial education programs; and (3) equating jobs that have similar educational requirements.
G-Study Design
In this study, job analysts were given written descriptions of jobs, published in the Dictionary of Occupational Titles, and were asked to rate the jobs on three components of the general educational development scale: reasoning development, mathematics development, and language development. Each component was measured on a 6-point scale. Each of 71 raters
from 11 geographic field centers across the United States evaluated the three components of a sample of jobs on two occasions. Different centers had different numbers of job analysts, ranging from 2 to 12. Hence, the Gstudy design was a partially nested, unbalanced design with different numbers of raters nested within centers. To illustrate G theory in its basic form, a random sample of two raters from each center was taken to form a balanced design. (The unbalanced design is discussed below.) Because concern attaches to estimating the general educational development required to perform each job, jobs is the object of measurement and the variance component for jobs (![]() ) is interpreted as the universe-score variance. All other variance components were considered measurement error in this study since absolute decisions are made regarding general educational development requirements for each job. These include the components for raters nested within center, center, occasion, and all interactions.
) is interpreted as the universe-score variance. All other variance components were considered measurement error in this study since absolute decisions are made regarding general educational development requirements for each job. These include the components for raters nested within center, center, occasion, and all interactions.
Univariate G Analysis
For the univariate G study, a random effects analysis of variance was used to estimate the variance components contributing to the observed variation in job ratings. A separate analysis was performed for each component of the general educational development scale. The results are presented in Table 12.
Since the analysis focuses on absolute decisions, the error variance, ![]() , reflects not only disagreements about the ordering of jobs but also mean differences in ratings. It is important to know, for example, whether raters use essentially the same mean level of the rating scale as well as whether they rank order jobs similarly.
, reflects not only disagreements about the ordering of jobs but also mean differences in ratings. It is important to know, for example, whether raters use essentially the same mean level of the rating scale as well as whether they rank order jobs similarly.
The estimated variance components for jobs differ across general educational development ratings. They suggest that jobs can be distinguished more on their demands for language than on their demands for mathematics and reasoning. The patterns of variance components' contribution to error were consistent: raters' ratings accounted for most of the error variation and occasions and centers accounted for little. This pattern suggested that, by taking the average rating of four raters, measurement error can be reduced by about 75 percent (![]() ) in Table 12) and the G coefficients (ρ2) correspondingly increased to .87 for reasoning, .79 for mathematics, and .85 for language.
) in Table 12) and the G coefficients (ρ2) correspondingly increased to .87 for reasoning, .79 for mathematics, and .85 for language.
The consistent pattern of results for the ability components was not unexpected since their correlations were as follows: for reasoning and mathematics, r = .73; for reasoning and language, r = .84; and for mathematics and language, r = .73. The magnitude of these correlations suggests that all three general educational development ratings share a common, underlying factor and that a multivariate G coefficient would be appropriate.
TABLE 12 Univariate Generalizability Study of General Educational Development Ratings
|
Estimated Variance Component |
Estimated Variance Component with nr = 4, no = 1, and nc = 1 |
|||||
|
Source of Variation |
Reasoning |
Math |
Language |
Reasoning |
Math |
Language |
|
Jobs(J) |
0.74 |
0.63 |
1.01 |
0.74 |
0.63 |
1.01 |
|
Occasions(O) |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
|
Centers(C) |
0.00 |
0.02 |
0.05 |
0.00 |
0.02 |
0.05 |
|
Raters:C (R:C) |
0.06 |
0.02 |
0.00 |
0.02 |
0.00 |
0.00 |
|
JO |
0.00 |
0.01 |
0.01 |
0.00 |
0.01 |
0.01 |
|
JC |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
|
JR:C |
0.13 |
0.16 |
0.14 |
0.03 |
0.04 |
0.04 |
|
OC |
0.01 |
0.00 |
0.00 |
0.00 |
0.00 |
0.00 |
|
OR:C |
0.00 |
0.09 |
0.07 |
0.00 |
0.02 |
0.02 |
|
JOC |
0.00 |
0.02 |
0.01 |
0.00 |
0.02 |
0.01 |
|
JOR:C |
0.22 |
0.25 |
0.22 |
0.06 |
0.06 |
0.05 |
|
|
0.42 |
0.57 |
0.50 |
0.11 |
0.17 |
0.18 |
|
|
0.64 |
0.53 |
0.67 |
0.87 |
0.79 |
0.85 |
|
NOTE: The design is raters nested within centers crossed with jobs and occasions. From Webb, Shavelson, Shea, and Morello (1981:190). |
||||||
Multivariate G Analysis
For the multivariate generalizability study, a random effects MANOVA was run using the reasoning, mathematics, and language ratings as a vector of scores. Due to the limited capacity of computer programs available to perform the multivariate analysis and because geographic center contributed little to variability among job ratings, geographic center was excluded from the multivariate analysis. The design, then, was raters crossed with jobs and occasions with three ability scores.
For each source of variation in the design, variance and covariance component matrices were computed from the mean product matrices. Hence, one matrix, for example, contained estimated universe-score variances and covariances. All matrices with negative estimated variance components (diagonal values) were set equal to 0 in further estimation. For this analysis, the matrices of variance components, coefficients of generalizability, and canonical weights corresponding to each coefficient of generalizability were computed.
The estimated variance and covariance component matrices are presented in Table 13. Only the components for one rater and one occasion are
TABLE 13 Estimated Variance and Covariance Components for Multivariate Generalizability Study of General Educational Development Ratings (nr=1, no=1)
|
Source of Variation |
Reasoning |
Mathematics |
Language |
|
Jobs (J) |
0.75 |
||
|
0.64 |
0.66 |
||
|
0.88 |
0.74 |
1.09 |
|
|
Occasions (O) |
0.00 |
||
|
0.00 |
0.00 |
||
|
0.00 |
0.00 |
0.00 |
|
|
Raters (R) |
0.03 |
||
|
0.03 |
0.09 |
||
|
0.03 |
0.05 |
0.05 |
|
|
JO |
0.00 |
||
|
0.00 |
0.00 |
||
|
0.00 |
0.00 |
0.00 |
|
|
JR |
0.12 |
||
|
0.11 |
0.13 |
||
|
0.09 |
0.07 |
0.11 |
|
|
OR |
0.00 |
||
|
0.01 |
0.01 |
||
|
0.00 |
0.00 |
0.01 |
|
|
JRO,e (residual) |
0.21 |
||
|
0.07 |
0.29 |
||
|
0.11 |
0.10 |
0.26 |
|
|
NOTE: The design is raters crossed with jobs and occasions with scores on reasoning, mathematics, and language. From Shavelson and Webb (1981:18). |
|||
included. To obtain results for four raters, the components corresponding to the rater effect and rater interactions need only to be divided by four.
As a consequence of the calculation procedure, the variance components in Table 13 are the same as those produced by the univariate analysis. The components of covariance, however, provide new information. The large components for jobs reflects the underlying correlations among the general educational development components. Jobs that require high reasoning ability are seen by raters to require high mathematics and language ability. Whereas the nonzero components of variance for raters indicate that some raters give higher ratings than others, the positive components of covari-
ance indicate that the raters who give higher ratings on one general educational development component are likely to give higher ratings on the other general educational development components. The positive components for the job × rater interaction suggest that not only do raters disagree about which jobs require more ability but their disagreement is consistent across general educational development components. The nonzero components for error suggest that the unexplained factors that contribute to the variation of ratings also contribute to the covariation between ratings. As expected, the components of covariance due to the occasion main effect and interactions are negligible.
Composites of general educational development that have maximum generalizability are presented in Table 14. When multivariate generalizability was estimated for one rater and one occasion, one dimension with a coefficient exceeding .50 emerged. This dimension is a verbal composite of reasoning and language. The analysis with four raters and one occasion produced two dimensions with coefficients over .50. One composite was defined by reasoning and language (coefficients .74 and .92 for one and four raters, respectively); the other by a mathematics-language contrast with a G coefficient of .62 for four raters and one occasion.
Unbalanced Designs
The original G-study design was unbalanced with a different number of raters nested within geographic centers. The results of the unbalanced design were compared with those of two balanced designs: (1) raters randomly sampled from each of 5 randomly sampled centers, and (2) two raters randomly selected from each of the 11 centers. The estimates of variance com-
TABLE 14 Canonical Variates for Multivariate Generalizability Study of General Educational Development Ratings
|
Canonical Coefficients |
|||
|
General Educational Development Component |
nr=1, no=1 |
nr=4, no=1 |
|
|
I |
I |
II |
|
|
Reasoning |
0.34 |
0.38 |
0.05 |
|
Mathematics |
0.06 |
0.06 |
−1.95 |
|
Language |
0.51 |
0.57 |
1.33 |
|
Coefficient of generalizability |
0.74 |
0.92 |
0.62 |
|
NOTE: The design is raters crossed with jobs and occasions. |
|||
ponents in the unbalanced design were obtained with a modification of Rao's MIVQUE procedure suggested by Hartley et al. (1978; see Shavelson and Webb, 1981).
The magnitudes and pattern of estimated variance components from the three analyses were very similar. The generalizability coefficients ranged from .65 (unbalanced design) to .63 (two raters, five centers). These findings are consistent with those of Bell (1985). Random deletion of conditions to create a balanced design appears not to distort G-study findings.
Generalizability of Unit-Performance Measurements
This G study of tank crews illustrates the application of multilevel G theory (Cronbach, 1976) and the principle of symmetry (see the earlier discussion) to hierarchical populations, a characteristic of military performance measurements. Tank-crew performance data were collected in the spring of 1971 during the annual qualification firing exercises at the Seventh Army Training Center, Grafenwohr, Germany. The tank crews performed the Table VIII mission—deliberate attack (live fire)—based on the Army Training and Evaluation Program for Mechanized Infantry Tank Force (ARTEP 71-2, 1978). The tank crews represented three companies, with each company comprised of three platoons of five tank crews each. The performance of the 45 tank crews was scored on two occasions, once when they carried out the mission in daytime and once at night. A single observer scored the performance of each crew according to the detailed ARTEP guidelines. Scores for the sample ranged from a low of 210 to a high of 1150. These scores will be referred to as Table VIII data.
Design of the G Study
Admittedly, the designers of the Table VIII data collection did not have generalizability theory in mind. As a consequence, the universe of generalization resolved itself into observation occasions which were confounded with days, time of day, and observer. The full design, taking into account the hierarchical structure in which crews were nested, is a Company (C) × Platoon:Company (P:C) × Crew:Platoon:Company (Cr:P:C) × Occasion (O) partially nested design. In words, crews (5) were nested within platoons, and platoons (3) were nested within each company (3); performance was measured on two different occasions (day and night).
Classical Reliability Approach
In classical theory, the best estimate of reliability is the correlation between tank crew scores obtained on two occasions. For a performance score
averaged over the two occasions and ignoring the effect of platoon and company, the reliability is .64.
Clearly, this reliability coefficient is influenced by leniency of different observers, the difficulty of the terrain or terrains on which the missions were conducted, the differences between missions, the time of day (day or night), the day that the performance was observed, and so forth. However, the importance of these possible sources of measurement error cannot be estimated using classical theory, even if the measurement facets had been systematically identified. Furthermore, performance might be influenced by the policies and leadership skills within particular companies or platoons. Classical reliability is mute on how to treat these hierarchical data.
Generalizability Theory Approach
The generalizability analysis proceeded along the lines suggested by symmetry:
-
Choose the facets of measurement and compute mean squares.
-
Estimate variance components.
-
Specify the facet (or combination of facets) that is the focus of measurement, and specify the sources of error.
-
Examine alternative D-study designs.
Steps 1 and 2 are shown in Table 15 for the Company (C) × Platoon: Company (P:C) × Crew:Platoon:Company (Cr:P:C) × Occasion (O) partially nested design.
Interpretation of Variance Components In theory, a variance component cannot be negative, yet a negative estimate occurred (as indicated in
TABLE 15 Variance Components for the Study of TankCrew Performance Measurement a
|
Source of Variation |
Mean Squares |
Estimated Variance Component |
|
Companies (C) |
55461 |
0b |
|
Platoons:C (P:C) |
78636 |
1607.19 |
|
Crews:P:C (Cr:P:C) |
45383 |
15967.50 |
|
Occasions (O) |
244505 |
3573.21 |
|
C × |
83711 |
3538.79 |
|
P:C × O |
30629 |
3436.17 |
|
Cr:P:C × O |
31448 |
13448.20 |
|
aThe design is crews nested in platoons nested in companies crossed with occasions. bNegative variance component set to 0. |
||
Table 15). With sample Table VIII data, a negative variance component can arise either due to sampling error or misspecification of the measurement model. If the former, the most widely accepted practice is to set the variance coefficient to 0, as was done in Table 15. If the latter, the model should be respecified and variance components estimated with the new model. The rationale for setting the company variance component to 0 was the following. First, the difference in the mean performance of the three companies was small: 770.90, 763.33, and 692.93. Variation among company means accounted for only 0.3 percent of the total variation in the data. The best estimate of the variance due to companies, then, was 0. (See the concluding section for additional discussion on estimating variance components.)
The largest variance component in Table 15 is for crews: the universescore variance. Crew performance differs systematically, and the measurement procedure reflects this variation. The next largest component is associated with the residual, indicating that error is introduced due to inconsistency in tank-crew performance from one occasion to the next, and other unidentified sources of error (e.g., inconsistency due to time of day, observer, terrain, and the like). The remaining variance components are roughly onefourth the size of the residual, with the exception of the component for companies. Since the variance component for companies is 0 and the variance component for platoons is the smallest one remaining, neither sufficiently influences variation in performance enough to have an important influence if they are considered part of the universe-score variance.
Generalizability Coefficients. Since decision makers are interested in the generalizability of unit performance, one possible method for calculating the G coefficient for crews is:
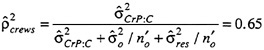
The generalizability of tank crew performance, averaged over the two observation occasions, is .65. If, however, the decision maker is interested in the generalizability of the score of a single tank crew selected randomly and observed on a single occasion, the coefficient drops to .48 due to the large residual variance component.
The principle of symmetry states that the universe-score variance is comprised of all components that give rise to systematic variation among crews. In this case, variation due to companies and platoons, as well as variation due to crews, must be considered universe-score variation. Characteristics of companies and platoons, such as leadership ability, contribute to systematic variation among crews. Following symmetry, the G coefficient for crews, averaged over two occasions, is:
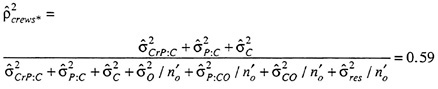
We write ![]() to distinguish this coefficient from the one above.
to distinguish this coefficient from the one above.
Surprisingly, by increasing universe-score variance, the G-coefficient decreased, for two reasons. The increase in universe-score variance by incorporating systematic variation due to companies was negligible:
And the additional error introduced (![]() ) by considering variation due to companies and platoons as universe-score variance, while not large relative to other sources of variation (e.g.,
) by considering variation due to companies and platoons as universe-score variance, while not large relative to other sources of variation (e.g., ![]() ), were large relative to the systematic variability of companies and platoons.
), were large relative to the systematic variability of companies and platoons.
Finally, if the decision maker is interested in the dependability of platoon performance, the generalizability of the measurement was estimated (aggregating over crews within platoons and occasions) as follows:
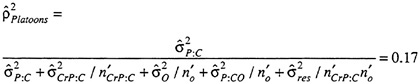
Notice here that crews is considered a source of error; variability in crews introduces uncertainty in estimating the performance of the entire platoon— the average of the performance of a platoon's individual crews. The low generalizability coefficient, then, reflects the fact that there was greater variability among crews within a platoon than among platoons.
CONCLUDING COMMENTS ON GENERALIZABILITY THEORY: ISSUES AND LIMITATIONS
In the preceding sections, I argued that generalizability theory was the most appropriate behavioral measurement theory for treating military performance measures and showed how the theory could be used to model and improve performance measures. Even the best of theories have limitations in their applications, and generalizability theory is no exception. In concluding, I address the following topics: negative estimated variance components; assump-
tion of constant universe scores; and dichotomous data (for a more extensive treatment, see Shavelson and Webb, 1981; Shavelson et al., 1985).
Small Samples and Negative Estimated Variance Components
Two major contributions of generalizability theory are its emphasis on multiple sources of measurement error and its deemphasis of the role played by summary reliability or generalizability coefficients. Estimated variance components are the basis for indexing the relative contribution of each source of error and the undependability of a measurement. Yet Cronbach et al. (1972) warned that variance-component estimates are unstable with usual sample sizes of, for example, a couple of occasions and observers. While variance-component estimation poses a problem for G theory, it also afflicts all sampling theories. One virtue of G theory is that it brings estimation problems to the fore and puts them up for examination.
Small Samples and Variability of Estimated Variance Components
The problem of fallible estimates can be illustrated by expressing an expected mean square as a sum of population variances. In a two-facet, crossed (p × i × j), random model design, the variance of the estimated variance component for persons—of the estimated universe-score variance—is
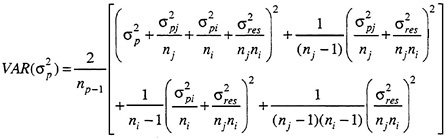
With all of the components entering the variance of the estimated universescore variance, the fallibility of such an estimate is quite apparent, especially if n(i) and n(j) are quite modest. In contrast, the variance of the estimated residual variance has only one variance component,
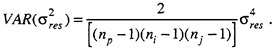
In a crossed design, then, the number of components and hence the variance of the estimator increase from the highest-order interaction component to the main effect components. Consequently, sample estimates of the universe-score variance—estimates of crucial importance to the dependability of a measurement—may reasonably be expected to be less stable than estimates of components of error variance.
Negative Estimates of Variance Components
Negative estimates of variance components can arise because of sampling errors or because of model misspecification (Hill, 1970; see also previous discussion). With respect to sampling error, the one-way ANOVA illustrates how negative estimates can arise. The expected mean squares are:
and
where E MSWithin is the expected value of the mean square within groups and E MSBetween is the expected value of the mean square between groups. Estimation of the variance components is accomplished by equating the observed mean squares with their expected values and solving the linear equations. If MSWithin is larger than MSBetween, the estimate of ![]() will be negative.
will be negative.
Realizing this problem in G theory, Cronbach et al. (1972:57) suggested that
a plausible solution is to substitute zero for the negative estimate, and carry this zero forward as the estimate of the component when it enters any equation higher in the table of mean squares.
Notice that by setting negative estimates to 0, the researcher is implicitly saying that a reduced model provides an adequate representation of the data, thereby admitting that the original model was misspecified. Although solutions such as Cronbach et al.'s are reasonable, the sampling distribution of the (once negative) variance component as well as those variance components whose calculation includes this component is more complicated and the modified estimates are biased. Brennan (e.g., 1983) provides an alternative algorithm that sets all negative variance components to 0. Each variance component, then, “is expressed as a function of mean squares and sample sizes, and these do not change when some other estimated variance component is negative” (Brennan, 1983:47). Brennan's procedure produces unbiased estimated-variance components, except for negative components set to 0.
Bayesian methods provide a solution to the problem of negative variance-component estimates (e.g., Box and Tiao, 1973; Davis, 1974; Fyans, 1977; Shavelson and Webb, 1981). Consider a design with two sources of variation: within groups and between groups. The Bayesian approach includes the constraint that MS(between groups) is greater than or equal to MS (within groups) so that the between-groups variance component cannot be negative. Unfortunately, the computational complexities involved and the distributional-form assumptions make these procedures all but inaccessible to practitioners.
An attractive alternative that produces nonnegative estimates of variance components is maximum likelihood (Dempster et al., 1981). Maximum likelihood estimators are functions of every sufficient statistic and are consistent and asymptotically normal and efficient (Harville, 1977). Although these estimates are derived under the assumption of a normal distribution, estimators so derived may be suitable even with an unspecified distribution (Harville, 1977). Maximum likelihood estimates have not been used extensively in practice because they are not readily available in popular statistical packages. However, researchers at the University of California, Los Angeles, (Marcoulides, Shavelson, and Webb) are examining a restricted maximum likelihood approach that, in simulations so far, appears to offer considerable promise in dealing with the negative variance component problem.
Assumption of Constant Universe Scores
Nearly all behavioral measurement theories assume that the behavior being studied remains constant over observations; this is the steady-state assumption made by both classical theory and G theory. Assessment of stability is much more complex when the behavior changes over time. Among those investigating time-dependent phenomena are Bock (1975), Bryk and colleagues (Bryk and Weisberg, 1977; Bryk et al., 1980), Rogosa and colleagues (Rogosa, 1980; Rogosa et al., 1982, 1984).
Rogosa et al. (1984) consider generalizability theory as one method for assessing the stability of behavior over time. Their approach is to formulate two basic questions about stability of behavior: (1) Is the behavior of an individual consistent over time? (2) Are individual differences among individuals consistent over time?
For individual behavior, consistency is defined as absolutely invariant behavior over time. They characterized inconsistency in behavior in several ways: unsystematic scatter around a flat line, a linear trend (with and without unsystematic scatter), and a nonlinear trend (with or without scatter). Changing behavior over time has important implications in generalizability theory for the estimation of universe scores. When behavior changes systematically over time, the universe-score estimate will be time dependent.
The second, and more common, question about stability is the consistency of individual differences among individuals. Perfect consistency occurs whenever the trends for different individuals are parallel, whether the individuals' trends are flat, linear, or nonlinear.
A generalizability analysis with occasions as a facet is described by Rogosa et al. (1984) as one method for assessing the consistency of individual differences over time. The variance component that reflects the stability of individual differences over time is the interaction between individuals and occasions. A small component for the interaction (compared to the variance component for universe scores) suggests that individuals are rank-ordered similarly across occasions; that is, their trends are parallel. It says nothing about whether individual behavior is changing over time. As described above, the behavior of all individuals could be changing over time in the same way (a nonzero main effect for occasions). A relatively large value of the component for the individuals × occasion interaction (compared to the universe-score variance component) shows that individuals are ranked differently across occasions. This could be the result of unsystematic fluctuations in individual behavior over time, the usual interpretation made in G theory under the steady-state assumption. But it could also reflect differences in systematic trends over time for different individuals. The behavior of some individuals might systematically improve over time, while that of others might not. Furthermore, the systematic changes could be linear or nonlinear.
Clearly, it is necessary to specify the process by which individual military performance changes in order to model this change. Rogosa et al. provide excellent steps in that direction by describing analytic methods for assessing the consistency of behavior of individuals and the consistency of differences among individuals. At the least, their exposition is valuable for clarifying the limited ability of G theory to distinguish between real changes in behavior over time and random fluctuations over time that should be considered error.
Although the analytic models for investigating time-dependent changes in behavior are important, they do not alleviate the investigator 's responsibility to define the appropriate time interval for observation. In studying the dependability of a measurement, it is necessary to restrict the time interval so that the observations of behavior can reasonably be expected to represent the same phenomenon.
There are other developments in the field that examine changing behavior over time, such as models of change based on Markov processes (e.g., Plewis, 1981). However, since these developments do not follow our philosophy of isolating multiple sources of measurement error, and do not provide much information about how measurement error might be characterized or estimated, they are not discussed here.
Dichotomous Data
Analysis of variance approaches to reliability, including G theory, assume that the scores being analyzed represent continuous random variables. When the scores are dichotomous, as they were in the earlier example with observers' “go-no go” scores for soldiers' performance on the revolver task, analysis of variance methods produce inaccurate estimates of variance components and reliability (Cronbach et al., 1972; Brennan, 1980). In analyses of achievement test data with dichotomously scored items, L. Muth én (1983) found that the ANOVA approach for estimating variance components tended to overestimate error components and underestimate reliability. She found that a covariance structure analysis model (see B. Muth én, 1978, 1983; Jöreskog, 1974), specifically designed to treat dichotomous data as a manifestation of an underlying continuum (B. Muthén, 1983), produced estimates of variance components and generalizability coefficients that were closer to the true values than those from the ANOVA.
Concluding Comment
Used wisely, none of the foregoing limitations invalidates G theory. They simply point to the care needed in designing and interpreting the results of G studies.
In spite of its limitations, generalizability theory does what those seeking to determine the dependability of performance measures want a theory of behavioral measurement to do. G theory:
-
models the sources of error likely to enter into a performance measurement,
-
models the ways in which these errors are sampled,
-
provides information on where the major source of measurement error lies,
-
provides estimates of how the measurement would improve under alternative plans for sampling and thereby controlling sources of error variance, and
-
indicates when the measurement problem cannot be overcome by sampling, so that alternative revisions of the measurement (e.g., modifications in administration, training of observers, or both) might be considered.
REFERENCES
Bell, J.F. 1985 Generalizability theory: the software problem. Journal of Educational Statistics 10:19-30.
Bock, D. 1975 Multivariate Statistical Methods in Behavioral Research. New York: McGraw-Hill.
Box, G.E.P., and G.C. Tiao 1973 Bayesian Inference in Statistical Analysis. Reading, Mass.: Addison-Wesley.
Brennan, R.L. 1980 Applications of generalizability theory. In R.A. Berk, ed., Criterion-Referenced Measurement: The State of the Art. Baltimore, Md.: The Johns Hopkins University Press.
1983 Elements of Generalizability Theory. Iowa City, Iowa: American College Testing Publications.
Bryk, A.S., and H.I. Weisberg 1977 Use of the nonequivalent control group design when subjects are growing Psychological Bulletin 84:950-962.
Bryk, A.S., J.F. Strenio, and H.I. Weisberg 1980 A method for estimating treatment effects when individuals are growing Journal of Educational Statistics 5:5-34.
Cardinet, J., and L. Allal 1983 Estimation of generalizability parameters. Pp. 17-48 in L.J. Fyans, Jr., ed., Generalizability Theory: Inferences and Practical Applications. San Francisco: Jossey-Bass.
Cardinet, J., and Y. Tourneur 1974 The Facets of Differentiation [sic] and Generalization in Test Theory Paper presented at the 18th congress of the International Association of Applied Psychology,
Montreal, July-August. 1977 Le Calcul de Marges d'Erreurs dans la Theorie de la Generalizabilite. Neuchatel, Switzerland: Institut Romand de Recherches et de Documentation Pedagogiques.
Cardinet, J.Y. Tourneur, and L. Allal 1976a The generalizability of surveys of educational outcomes. Pp. 185-198 in D.N.M. DeGruijter and L.J. Th. van der Kamp, eds., Advances in Psychological and Educational Measurement. New York: Wiley.
1976b The symmetry of generalizability theory: applications to educational measurement. Journal of Educational Measurement 13:119-135.
1981 Extension of generalizability theory and its applications in educational measurement. Journal of Educational Measurement 18:183-204.
Cronbach, L.J. 1976 Research on Classrooms and Schools: Formulation of Questions, Design, and Analysis. Occasional paper, Stanford Evaluation Consortium. Stanford University (July).
Cronbach, L.J., G.C. Gleser, A.N. Nanda, and N. Rajaratnam 1972 The Dependability of Behavioral Measurements: Theory of Generalizability for Scores and Profiles. New York: Wiley.
Davis, C.E. 1974 Bayesian Inference in Two-way Analysis of Variance Models: An Approach to Generalizability. Unpublished doctoral dissertation. University of Iowa.
Dempster, A.P., D.B. Rubin, and R.K. Tsutakawa 1981 Estimation in covariance components models. Journal of the American Statistical Association 76:341-353.
Erlich, O., and R.J. Shavelson 1976 The Application of Generalizability Theory to the Study of Teaching Technical Report 76-9-1, Beginning Teacher Evaluation Study. Far West Laboratory, San Francisco.
Fyans, L.J. 1977 A New Multi-Level Approach for Cross-Cultural Psychological Research Unpublished doctoral dissertation. University of Illinois at Urbana-Champagne.
Hartley, H.O., J.N.K. Rao, and L. LaMotte 1978 A simple synthesis-based method of variance component estimation. Biometrics 34:233-242.
Harville, D.A. 1977 Maximum likelihood approaches to variance component estimation and to related problems. Journal of the American Statistical Association 72:320-340.
Hill, B.M. 1970 Some contrasts between Bayesian and classical influence in the analysis of variance and in the testing of models. Pp. 29-36 in D.L. Meyer and R.O. Collier, Jr., eds., Bayesian Statistics. Itasca, Ill.: F.E. Peacock.
Jöreskog, K.G. 1974 Analyzing psychological data by structural analysis of covariance matrices. In D.H. Krantz, R.C. Atkinson, R.D. Luce, and P. Suppes, eds., Contemporary Developments in Mathematical Psychology, Vol. II. San Francisco: W.H. Freeman & Company.
Kahan, J.P., N.M. Webb, R.J. Shavelson, and R.M. Stolzenberg 1985 Individual Characteristics and Unit Performance: A Review of Research and Methods. R-3194-MIL. Santa Monica, Calif.: The Rand Corporation.
Muthén, B. 1978 Contributions to factor analysis of dichotomous variables. Psychometrika 43:551-560.
1983 Latent variable structural equation modeling with categorical data Journal of Econometrics 22:43-65.
Muthén, L. 1983 The Estimation of Variance Components for the Dichotomous Dependent Variables: Applications to Test Theory. Unpublished doctoral dissertation, University of California, Los Angeles.
Office of the Assistant Secretary of Defense (Manpower, Reserve Affairs, and Logistics) 1983 Second Annual Report to the Congress on Joint-Service Efforts to Link Standards for Enlistment to On-the-Job Performance. A report to the House Committee on Appropriations. U.S. Department of Defense, Washington, D.C.
Plewis, I. 1981 Using longitudinal data to model teachers' ratings of classroom behavior as a dynamic process. Journal of Education Statistics 6:237-255.
Rogosa, D. 1980 Comparisons of some procedures for analyzing longitudinal panel data Journal of Economics and Business 32:136-151.
Rogosa, D., D. Brandt, and M. Zimowski 1982 A growth curve approach to the measurement of change. Psychological Bulletin 90:726-748.
Rogosa, D., R. Floden, and J.B. Willett 1984 Assessing the stability of teacher behavior. Journal of Educational Psychology 76:1000-1027.
Rubin, D.B., reviewer 1974 The dependability of behavioral measurements: theory of generalizability for scores and profiles. Journal of the American Statistical Association 69:1050.
Shavelson, R.J. 1985 Evaluation of Nonformal Education Programs: The Applicability and Utility of the Criterion-Sampling Approach. Oxford, England: Pergamon Press.
Shavelson, R.J., and N.M. Webb 1981 Generalizability theory: 1973-1980. British Journal of Mathematical and Statistical Psychology 34:133-166.
Shavelson, R.J., N.M. Webb, and, L. Burstein 1985 The measurement of teaching. In M.C. Wittrock, ed., Handbook of Research on Teaching, 3rd ed. New York: Macmillan.
Tourneur, Y. 1978 Les Objectifs du Domaine Cognitif. 2me Partie: Theorie des Tests. Ministere de l'Education Nationale et de la Culture Francaise, Universite de l'Etat a Mons, Faculte des Sciences Psycho-Pedagogiques.
Tourneur, Y., and J. Cardinet 1979 Analyse de Variance et Theorie de la Generalizabilite: Guide pour la Realization des Calculs. Doc. 790.803/CT/9. Universite de l'Etat a Mons, France.
U.S. Department of Labor 1972 Handbook for Analyzing Jobs. Washington, D.C.: U.S. Department of Labor.
Webb, N.M., and R.J. Shavelson 1981 Multivariate generalizability of general educational development ratings. Journal of Educational Measurement 18:13-22.
Webb, N.M., R.J. Shavelson, J. Shea, and E. Morello 1981 Generalizability of general educational development ratings of jobs in the U.S. Journal of Applied Psychology 66:186-191.
Webb, N.M., R.J. Shavelson, and E. Maddahian 1983 Multivariate generalizability theory. Pp. 67-82 in L. J. Fyans, Jr., ed., Generalizability Theory: Inferences and Practical Applications. San Francisco: Jossey-Bass.
Wittman, W.W. 1985 Multivariate reliability theory: principles of symmetry and successful validation strategies. Pp. 1-104 in R.B. Cattell and J.R. Nesselroade, eds., Handbook of Multivariate Experimental Psychology, 2nd ed. New York: Plenum Press.