13
NONLINEAR DYNAMICS OF MULTIPARTICLE SYSTEMS
There exist numerous systems of scientific and engineering interest, such as bulk granular solids and particulate suspensions, which involve large numbers of mechanically interacting solid particles. The need to understand better their rheological behavior and their interaction with processing equipment has long been recognized, but progress in the field is hampered by the difficulty of comprehensive experimental measurement. Advances in the basic science could provide significant economic benefits to a wide variety of energy and mineral recovery industries and other technologies utilizing or producing solid materials.
Recent years have seen a vigorous growth of activity in computer simulation of multiparticle systems by direct solution of the underlying equations of motion that, because of the inherent nonlinearity and numerous degrees of freedom, are otherwise mathematically intractable. Much of the current work involves the mechanics of soils, granular materials, and fluid-particulate suspensions.
In many respects, particulate simulations can be viewed as an outgrowth of similar work in the fields of the statistical physics, statistical mechanics, and kinetic theory of molecular solids and fluids, where such nonequilibrium molecular dynamics (NEMD) simulations represent a well-established, continually evolving, computational science.10
In contrast to the conservative Hamiltonian structure of most molecular systems, many particulate systems of engineering interest are highly irreversible due to frictional forces operating at the particulate level, which not only makes for additional mathematical complexity but also raises new and interesting scientific questions about the statistical mechanics
of strongly dissipative systems. Among these questions is the extent to which certain well-established molecular concepts carry over to particulate systems, where one can discern phenomena such as granular "temperature," particle diffusion, and viscoelasticity of granular flow.11
Despite the obvious differences from molecular statistical mechanics, one can nevertheless exploit a now generally accepted paradigm in that field based on the triad of continuum modeling, computer simulation, and experimental testing.12 Computational simulations on idealized particle systems offer a relatively direct method to test, improve, or reject continuum models before undertaking much more costly and difficult experimental measurements on real systems. Also, with computer simulation many detailed properties of idealized systems can be "observed" that are virtually inaccessible to direct experimental measurement. Apart from the practical utility, this may serve to spawn scientific questions and ideas that would otherwise be slow to emerge. Following is a summary of a few important research efforts now under way in the simulation of multiparticle systems.
DISCRETE PARTICLE SIMULATION OF GRANULAR MATERIALS
Three methodologies to model the mechanical behavior of deforming or flowing systems comprising many distinct granules can be discerned. First and most well established is a continuum description based on suitable phenomenological constitutive relations that, with the advent of high-speed computation, can now be supplemented by discrete models of the type to be discussed briefly here.
The Particle Dynamics Method
Numerical techniques from NEMD, which have already served to elucidate transport phenomena in molecular systems, are now being adapted to systems of macroscopic particles.
Among these techniques are trajectory-tracking algorithms that allow the motion of individual particles to be followed as they interact with inelastic frictional contact forces and gravity. In molecular-dynamics-type calculations, the Particle Dynamics Method (PDM),13 the Newtonian equations of motion are solved for a large number of interacting grains (typically a few thousand). In the quasi-static limit appropriate to certain problems in soil and rock mechanics, one recovers the so-called Distinct Element Method of Cundall14 and others. Displacements, linear and angular velocities, and forces on individual particles are all computable, and the temporal and spatial averaging of these quantities allows direct computation of densities, flow speeds, strains, and stresses in a granular material. Figure 13.1 illustrates the kind of complex flow that can be treated by current simulations.
While numerous quantities may be computed directly, one may also attempt to extract continuum constitutive relations and then switch to a continuum description for actual applications. This approach, often desirable because of the relatively small number of particles that can be monitored by direct integration of the Newtonian equations, has led to new continuum models for granular materials based on concepts from dense-gas kinetic theory. However, the inelasticity of microscopic collisions and local energy loss is found to have dramatic effects on the distribution of microscopic velocity fluctuations and the resulting non-Newtonian fluid behavior.
By means of periodic-cell models, numerical simulations with samples as small as a few hundred particles have been able to provide valuable new information on bulk material properties. Figure 13.2 shows a periodic-cell computation involving 512 particles per cell. Application of these same methods to quasi-static deformation of inelastic frictional particle assemblies reveal long-range spatial correlations reflected in the formation of stress networks ("bridges or arches") extending over many particle diameters, somewhat reminiscent of critical-point phenomena in molecular systems. The meaningful simulation of bulk material properties in such situations may require large numbers of particles in order to span the typical "arch" or coherence length (perhaps as high as
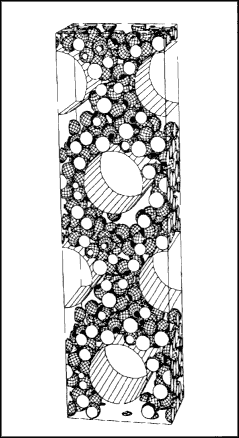
Figure 13.1 Perspective view of spherical particles in a simulation of glass beads falling through a chute with cylindrical obstacles, in a configuration similar to proposed design of burner and cooler for a commercial oil-shale retort. Open circles show intersection of particles with periodic boundary parallel to plane of figure. Source: After O. Walton, 1988, Energy and Technology Review, Lawrence Livermore National Laboratory, Report UCRL-52000-88-9, Livermore, CA). Reprinted with Permission.
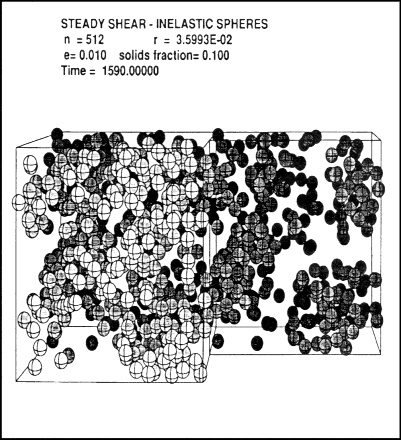
Figure 13.2 Computer-generated snapshot of 512 particles in one and one-half neighboring periodic cells, from a discrete particle simulation of steady shearing flow of a dry granular medium. Periodic-image cells above the primary cell move from left to right and those below from right to left at constant velocity to stimulate the shear. Source: After O. Walton, 1988, Energy and Technology Review, Lawrence Livermore National Laboratory, Report UCRL-52000-88-9, Livermore, CA). Reprinted with Permission.
thousands of particles for three-dimensional simulations). Modern supercomputers coupled with vectorized coding of simulation algorithms are just beginning to achieve adequate sample sizes in sufficiently short times to make such simulations practicable. Very little simulation work with such large sample sizes has actually been done to date since most researchers are still concentrating on the refinement of interparticle-force models and methods for efficiently calculating the response of frictional and irregularly shaped particles. The advent of a new, fast, and inexpensive generation of massively parallel computers could have a significant impact on the scale of problems accessible to direct simulation, with dramatic improvements in both the quantity and quality of results. In the future we can expect to see such simulation of granular materials become more and more commonplace, as the computing power of widely available workstations continues to increase and other hardware and software developments allow for the treatment of ever more realistic and larger systems.
Lattice-Gas (Cellular-Automata) Models
To overcome some of the current computational limitations of PDM, an alternative, inspired by the Lattice-Gas Model (LGM) or Cellular-Automata Model of statistical mechanics, the Lattice Grain Model (LGrM), has recently been introduced 15 to allow for explicit tracking of the trajectories of millions of grains. For such particle-tracking methods, neither complex geometric boundaries nor explicit time dependence of flow poses great difficulty in the calculation, in contrast to the numerical solution of the corresponding continuum partial differential equations (when those are known).
The LGrM trades off particle complexity against particle number. While in many PDM applications a fairly realistic contact force is employed, the LGrM description of particle interactions usually entails only momentum conservation, together perhaps with a one-parameter ("coefficient of restitution") model of energy loss. Thus, the update of particle states due to collisions can be performed much more quickly than in the PDM. Because particles are tied to the lattice, the problem of contact detection, a significant computational burden in the
PDM, is highly simplified with the result that the LGrM can follow the motion of vastly larger numbers of particles.
In the LGrM, energy is not conserved, and the corresponding continuum limit of the automata motion is not as well understood as the Navier-Stokes limit of the LGM. Nevertheless, LGrM calculations involving approximately 16,000 particles on an NCUBE parallel computer show encouraging agreement with experiments on time-dependent granular flows in highly complex geometries.16 LGrM simulations like these are highly suited to parallel computation because of the local nature of motion and collision on the lattice. Other parallelized simulations involving upwards of 106 particles in granular Couette and Poiseuille flows have been reported.
NUMERICAL MODELING OF PARTICULATE SUSPENSIONS
The flow of suspensions and slurries is complex and unpredictable, especially near solid walls. A major cause of this complexity are the hydrodynamic forces between solid particles transmitted by the fluid, which, together with aggregation of the particles, lead to many interesting effects, such as dramatically large viscosity. Unfortunately, no simple pairwise additive force rules are adequate to describe these interactions when the solid concentrations exceed more than a few volume percent, so there is an urgent need for novel computational methods.
Stokesian Dynamics
For particles suspended in viscous fluids at zero Reynolds number (Stokes) flow, a new numerical method called Stokesian Dynamics (SD) 17 is currently under development. The method entails solution of the fluid equations throughout the space between particles and determination of the induced forces on the surfaces of the suspended particles.
The crux of the technique is the computation of the induced forces which for spheroidal particles can be done numerically to any desired accuracy by multipolar expansions of particle-surface force distributions.
SD calculations of the theological properties of suspensions have been shown to give excellent agreement with analytical theories for the limiting case of regular arrays as well as with high-frequency experimental viscosity measurements on random dispersions. Such simulations can provide accurate benchmark computations of theological properties, for both small clusters of spheres and large random assemblages. These computations serve as valuable limiting cases for the theory development and testing of various numerical simulations of full (inertial) dynamics behavior of suspensions. The SD method is computationally intensive, especially for simulations of high solids packing.
The computational efficiency of SD has been systematically improved over the past couple of years, and periodic cells containing upwards of a hundred particles can now be treated. To improve efficiency, the method has been modified to include the effects of short-range lubrication forces between nearest-neighbor particles as separate, pairwise forces, significantly reducing computational effort in the high-concentration regime. This method has now been applied to such problems as determining the transport properties of random sphere assemblies, including viscosity, permeability, sedimentation velocity, and diffusion coefficient at various concentrations. With current computer limitations the inherent N2 dependence of the method precludes its application to systems of more than a few hundred particles.
Lattice-Gas Suspension Models
The Lattice-Gas Model discussed above also provides an alternative approach to the simulation of a molecular fluid containing supramolecular suspended particles.18 For a sufficiently large number of particles, this model presumably reproduces the Navier-Stokes equations for the suspending fluid, but with the significant advantage that thermal (Brownian) fluctuations for colloidal-sized particles can also be included. One goal of current lattice-gas suspension modeling is to understand the relationship between the theological pro-
perties of suspensions and their microstructure under shear. The nonequilibrium structures that arise from complex hydrodynamic interaction, possibly competing with Brownian effects, can be very different from those at rest.
While the earliest three-dimensional LGMs were not strictly isotropic, newer models (based on the projection of a face-centered four-dimensional hypercube onto a three-dimensional cubic array) can now eliminate artifacts such as anisotropic viscosity. New local "microrules" have also recently been developed to simulate no-slip fluid-particle boundary conditions. Initial tests of the newly developed simulations show that hydrodynamic interactions between particles are quantitatively reproduced by the LGM, even when the particles are almost touching. The significant improvements in efficiency and realism of these new LGM fluid simulations and their inherent applicability to a much wider range of problems suggest that much future effort should be concentrated on further development and application to particulate suspensions.
One exciting aspect of the lattice-gas approach is the prospect of simulating suspensions with about the same computational effort as that now used for dry granular solids by means of special very large-scale integrated (VLSI) chips, which are particularly well suited to simple cellular automata. It is estimated that the massively parallel computer hardware necessary to update a lattice-gas cellular automata at Cray supercomputer speeds could be produced for about $10,000. Prototype machines for such calculations are now under development in the Netherlands.
Such hardware developments hold promise for the scientific and engineering aspects of suspension dynamics, and possible future applications include studies of anisotropic molecular shapes, colloidal forces, and polydisperse-size effects. Such modeling need not be limited to periodic-cell models. A variety of realistic geometries to consider are pipes, chutes, and nozzles.









