Research Directions in Computational Mechanics (1991)

As a first step, virtually all modeling procedures in use in computational mechanics involve a process of discretization in which continuum models of nature are transformed into discrete or digital forms manageable by digital computers. This discretization process is critical to the overall computer simulation and governs its accuracy, efficiency, and general effectiveness.

Most discretization procedures involve the construction of a mesh or grid overlaid on the volume of matter to be studied; quantities of interest within gridcells or quantities defined at gridpoints are evaluated computationally. Other techniques model the so-called spectral content of continua with finite but high-order spectral representations. Collectively, these grid parameters characterize the discretization. Indeed, the accuracy with which the discrete model can represent the continuum usually depends on parameters such as the grid space (mesh size), density of gridpoints, and order of the representation.

It is clear that in this necessary first step of the computational process, the discretization, an error is always made, because a discrete model cannot possibly capture all of the information embodied in continuum models of gaseous, fluid, or solid materials. This inherent error has been a subject of concern and a topic of research for many decades and remains a source of many open questions—how can the error be measured, controlled, and effectively minimized? These issues will be among the most important topics of research in computational mechanics for the next decade and are at the heart of the reliability of computer simulations of nature. If the mathematical models of mechanics were perfect representations of mechanical events (which, of course, they are not), their utility in simulating events would be solely dependent on the discretization process used in computations and the errors it produces.

The subject concerned with measuring or estimating the discretization error that prevails in a computed simulation is called a posteriori error estimation. If it were possible to measure the discretization error with some level of mathematical precision, the reliability of the computed simulation could, at least partially, be assessed. Moreover, the entire discretization process could conceivably be modified or controlled to minimize and control the error.

The subject of a posteriori error estimation is in the early stages of development, although significant progress has been made in recent years for linear elliptic problems. Typically, finite element methods, finite difference methods, or boundary element methods are used in the discretization process, and the error is measured by error indicators that express the error in a single element or gridcell in an appropriate norm. Numerical experiments are generally performed on benchmark problems for which the exact error can be calculated, and the effectiveness of the error estimate can be assessed by computing effectively indices defined by

Today, most of the a posteriori error estimation theory pertains to linear elliptic problems and employs energy-norm estimates in some cases. Estimates for which 0.8 ξ 1.2 can be achieved. However for more general problems, particularly time-dependent or nonlinear problems, the theory is much less developed. There is also an urgent need to develop methods of error estimation in other norms since different classes of problems need different measures of error.

Nonlinear problems present special challenges in error estimation. The discretization process can introduce spurious solutions that have little bearing on the true behavior of the system under study. In addition, the theory of a posteriori error estimation for bifurcation problems, hyperbolic conservation laws, problems with multiple scales, and problems with resonance is in its infancy and deserves detailed study in the future. Work on methods of error estimation and control for the Navier-Stokes equations of fluid dynamics has mainly been a subject of ad hoc experimentation; no mathematical analysis of methods for this important class of problems exists.

Undoubtedly, this subject will be the focus of much research during the next decade.

Most existing methods of error estimation pertain to finite element methods of discretization. Additional work is needed on error estimation procedures for boundary element methods, finite difference methods, spectral and spectral element schemes, and other related techniques. For the short term, research will continue to focus on models characterized by linear elliptic equations, but research on the important areas of time-dependent and nonlinear problems will be vital to future developments in adaptive methods throughout the next decade.

Again, if one can estimate even roughly the error induced in the discretization process, it is then possible to adjust the discretization parameters (e.g., mesh size, order of the approximation, density of gridpoints, even the solution algorithm) to control the computation (the error, stability, overall performance of methods used in the analysis of the model). Methods of discretization and numerical analysis that automatically adjust these parameters are called adaptive methods. Their goal is the optimal control of the computational process to produce the best results for the least effort. Differences in various adaptive schemes hinge on how this optimum is defined, how control parameters are selected and measured, and how the effort is defined. The control parameter is usually the discretization error in each gridcell. Some strategies exist in which numerical stability is also a factor, so that the time step, for example, is also controlled to maintain stability at minimum computational cost.

The best adaptive procedures function independently of the user, who merely prescribes a level of error that he/she can tolerate or a dollar value (cost) that he/she is willing to endure to complete a simulation. Thereafter, the adaptive code makes the decisions necessary to produce solutions within the user-specified limits. Once the control parameters (the gridcell, element errors, or some reasonable approximation of them) are available, the adaptive code attempts to adjust them to meet control objectives—to minimize the error. Typically, error control is achieved by refining the mesh in areas of the solution domain where errors are too large and coarsening the mesh (using larger elements) where the error is small, or relocating nodes to increase nodal densities near regions of high error. Also, one could increase the order of

approximation and expect the accuracy of the approximation to be increased. Thus, in adaptive finite element methods, several broad types of adaptivity can be used in the control process:

1. h-methods: The mesh size h is used to control error. Error is reduced by refining the mesh or regenerating a new finer mesh. To obtain an optimal h-mesh (one with the least error possible for a fixed number of refinements), provisions for also coarsening a mesh must be included in the adaptive strategy.

2. r-methods: A fixed number of elements of a given order are used in a mesh, but nodes are relocated to reduce error in certain regions. The r-methods are thus moving grid methods in which the number of degrees of freedom is fixed, but the node locations are adapted to control error.

3. p-methods: The spectral order p of the approximation is raised or lowered to control error. In finite element methods or boundary element methods, the order p corresponds to the degree of the polynomial shape function used over an element.

4. Combined methods: Combinations of h-, r-, and/or p-adaptivity are used.

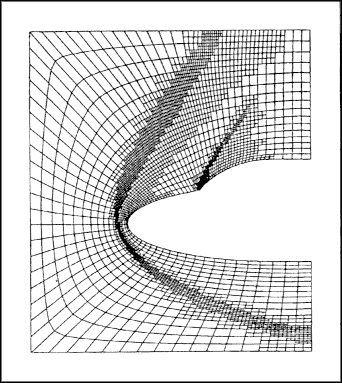
Figures 1.1a and 1.1b show a mesh modeling supersonic flow around a space shuttle in which h-method adaptivity has been employed to optimize the mesh structure to produce accurate simulation of flow features important in assessing the performance of the design—such as the profiles of pressure distribution shown.

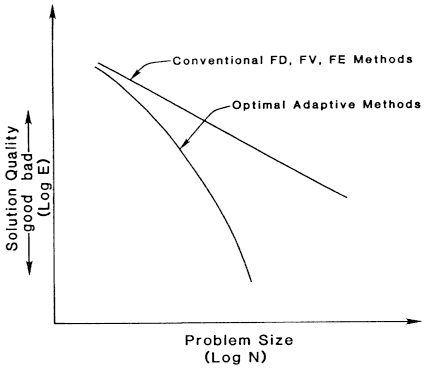
The potential advantages of adaptive methods over conventional methods of computational mechanics are enormous. For example, for many typical problems in two dimensions uniform mesh and degree distribution would lead to 100,000 or more equations, whereas adaptive approaches involving only 700 to 1,000 equations give results with comparable accuracy. Theoretically, in many cases adaptive procedures can lead to exponential convergence rates compared to algebraic convergence of classical low-order nonadaptive approaches. The potential impact on computational mechanics of exponentially convergent computational schemes may be one of the most important factors affecting research in this area for the next decade. Figure 1.2 illustrates the performance of exponentially convergent finite difference, finite

volume, or finite element schemes. The significance of the curves in this figure is that no matter what the capacity of the computer on hand to solve large-scale problems in computational mechanics, a level of accuracy can always be specified that cannot be attained by conventional methodologies. Such specified accuracies may be attained using superalgebraic convergent schemes (e.g., adaptive methods) since these can deliver results of a specified accuracy with many orders of magnitude fewer unknowns than conventional methods.

To date, certain p-version adaptive finite element methods, combined hp adaptive finite element methods, and spectral, pseudospectral, and spectral element methods have attained exponential convergence rates. Further research on adaptive strategies that produce optimal distributions of discretization parameters and exponential rates of convergence is urgently needed and should be a principal topic of research during the next decade.

Several other research issues on adaptive methods require additional study. Adaptive procedures should reflect various special aims of the computation, such as stress intensity, velocity, contact pressure, and vorticity. There is need for flexible adaptive principles that will focus on these specific quantities. Very little has been done in this direction. In time-dependent problems, successful approaches based on r-methods (relocating mesh points in time) combined with h-methods (refinement and coarsening) have been developed recently. Further research on these types of discretization is needed. In finite difference methods, some success has been achieved with moving overlapping meshes for hyperbolic problems and other types of time-dependent problems. In nonlinear solid mechanics, much remains to be done in the development of effective adaptive schemes. be enriched by the appearance of adaptive methods.

The successful implementation of adaptive methods often leads to nonsparse systems of equations that are not readily handled by conventional linear equation solvers. Research on the development of special techniques for solving the algebraic equations arising from adaptive methods is needed. These may include domain decomposition methods for multiprocessor computation, multigrid techniques, preconditioned iterative techniques, and related methods.

Postprocessing. A topic somewhat related to error estimation is referred to as (mathematical) postprocessing of numerical solutions to produce results for enhanced accuracy and utility. Postprocessing techniques extract extra information present in computed results to obtain even better simulations. For example, these schemes may exploit supercon-

vergence properties of finite element methods or employ extrapolation techniques that use data from sequences of meshes obtained in adaptive processes, or they may use so-called extraction schemes that use Green's formulas to ''extract'' superaccurate properties of solutions at points in the domain where high accuracy is sought. The basic goal is to extract maximum information and precision from computed simulations. To date, the subject has been developed only for model linear elliptic problems. Much research is needed to extend these postprocessing ideas to more general classes of problems.

In summary, the major research directions in the general areas of adaptive methods and error estimation are to:

• develop reliable a posteriori error estimation of computed data of interest with the effectivity index of order 0.9 < ξ < 1.1.

• develop a posteriori error estimation techniques for nonlinear problems in solid mechanics;

• develop a posteriori error estimation techniques in fluid mechanics for both compressible and incompressible flow;

• explore and develop a posteriori estimates and adaptive methods for space-time approximations; determine optimal techniques for h-, p-, and r-adaptive schemes;

• develop a modeling reliability theory, including possible expert system development and bracketing theory;

• devise postprocessing techniques for enhancement of solution accuracy; and

• develop adaptive modeling in which criteria for changes of models are incorporated in the adaptive process.