4
ARTIFICIAL INTELLIGENCE IN MATHEMATICAL MODELING
ARTIFICIAL INTELLIGENCE AND KNOWLEDGE-BASED SYSTEMS
Artificial intelligence (AI) is as much a branch of computer science as are its other branches, which include numerical methods, language theory, programming systems, and hardware systems. While computational mechanics has benefited from, and closely interacted with, the latter branches of computer science, the interaction between computational mechanics and AI is still in its infancy. Artificial intelligence encompasses several distinct areas of research each with its own specific interests, research techniques, and terminology. These sub-areas include search technologies, knowledge representation, vision, natural language processing, robotics, machine learning, and others.
A host of ideas and techniques from AI have the potential to impact the practice of mathematical modeling. In particular, knowledge-based systems and environments can provide representations and associated problem-solving methods that can be used to encode domain knowledge and domain-specific strategies for a variety of ill-structured problems in model generation and result interpretation. Advanced AI programming languages and methodologies can provide high-level mechanisms for implementing numerical models and solutions, resulting in cleaner, easier to write, and more adaptable computational mechanics codes. A variety of algorithms for heuristic search, planning, and geometric reasoning can provide effective and rigorous mechanisms for addressing problems such as shape description and transformation, and constraint-based model representation. Before discussing the applications of AI in mathematical modeling, we briefly review knowledge-based expert systems and problem-solving techniques.
Knowledge-Based Expert Systems
A good standard definition of knowledge-based expert systems (KBES) is the following: knowledge-based expert systems are interactive computer programs incorporating judgment, experience, rules of thumb, intuition, and other expertise to provide knowledgeable advice about a variety of tasks.
Many computer-aided engineering professionals initially react to this definition with boredom and impatience. After all, conventional computer programs for engineering applications have become increasingly interactive. They have always incorporated expertise in the form of limitations, assumptions, and approximations, as discussed above, and their output has long ago been accepted as advice, not as ''the answer'' to a problem.
There is a need, therefore, to add an operational definition to distinguish the new wave of KBES from conventional algorithmic programs that incorporate substantial amounts of heuristics about a particular application area. The distinction should not be based on implementation languages or on the absolute separation between domain-dependent knowledge and generic inference engine. The principal distinction lies in the use of knowledge. A traditional algorithmic application is organized into two parts: data and program. An expert system separates the program into an explicit knowledge base describing the problem-solving knowledge and a control program or inference engine that manipulates the knowledge base. The data portion or context describes the problem and the current state of the solution process. Such an approach is denoted as knowledge based.
Knowledge-based systems, as a distinctly separate AI research area, are about a decade old. This decade of research has seen many changes in the importance placed on various elements of the methodology. The most characteristic change is methodological; the focus has shifted from application areas and implementation tools to architectures and unifying principles underlying a variety of problem-solving tasks.
In the early days of knowledge-based systems, the presentation and analysis were at two levels: 1) the primitive representation mechanisms (rules, frames, etc.) and their associated primitive inferencing mechanisms (forward and backward chaining, inheritance, demon firing, etc.), and 2) the problem description. Unfortunately, it turned out that the former descriptions are too low level and do not describe the kind of problem that is being solved, while the latter descriptions are necessarily domain specific and often incomprehen-
sible and uninteresting for people outside the specific area of expertise.
A description level is needed that adequately describes what heuristic programs do and know—a computational characterization of their competence that is independent of both task domain and programming language implementation. Several characterizations of generic tasks that arise in a multitude of domains have been presented recently in the literature. Generic tasks are described by the kind of knowledge on which they rely and their control of problem solving. Generic tasks constitute higher-level building blocks for expert systems design. Their characterizations form the basis for analyzing the contents of a knowledge base (for completeness, consistency, etc.) to describe the operation and limitations of systems and to build specialized knowledge acquisition tools.
Problem Solving
Many problem-solving tasks can be formulated as a search in a state space. A state space consists of all the states of the domain and a set of operators that change one state into another. The states can best be thought of as nodes in a connected graph and the operators as edges. Certain nodes are designated as goal nodes, and a problem is said to be solved when a path from an initial state to a goal state has been found. State spaces can get very large, and various search methods to control the search efficiency are appropriate.
-
Search reduction. This technique involves showing that problem's answer cannot depend on searching a certain node. There are several reasons this could be true: (a) No solution can be in the subtree of this node. This technique has been called "constraint satisfaction" and involves noting that the conditions that can be attained in the subtree below a node are insufficient to produce some minimum requirement for a solution. (b) A solution in another path is superior to any possible solution in the subtree below this node. (c) The node has already been examined elsewhere in the search. This is the familiar dynamic programming technique in operations research.
-
Problem reduction. This technique involves transforming the problem space to make searching easier. Examples of problem reduction include: (a) planning with macro operators in an abstract space before getting down to the details of actual operators; (b) means-end analysis, which attempts to reason backward from a known goal; and (c) sub-goaling,
-
which breaks down difficult goals into simpler ones until easily solved ones are reached.
-
Adaptive search techniques. These techniques use evaluation functions to expand the "next best" node. Some algorithms (A*) will expand the node most likely to contain the optimal solution. Others (B*) will expand the node that is most likely to contribute the most information to the solution process.
-
Using domain knowledge. One way to control the search is to add additional information to nongoal nodes. This information could take the form of a distance from a hypothetical goal, operators that may be usefully applied to it, possible backtracking locations, similarity to other nodes that could be used to prune the search, or some general goodness in formation.
APPLICATIONS IN MATHEMATICAL MODELING
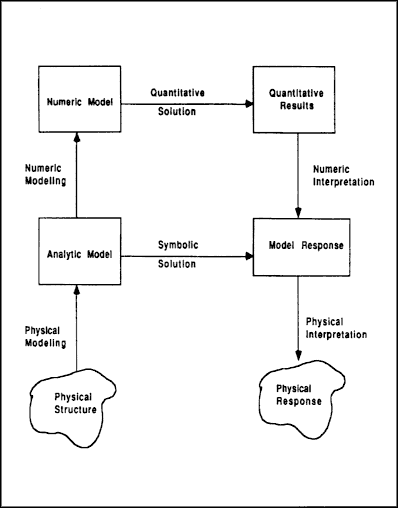
Mathematical modeling is the activity devoted to the study of the simulation of physical phenomena by computational processes. The goal of the simulation is to predict the behavior of some artifact within its environment. Mathematical modeling subsumes a number of activities, as illustrated by Figure 4.1.
The following sections discuss the applications and potential impacts of AI technology on various mathematical modeling activities. The mathematical modeling activities presented include model generation, interpretation of numerical results, and development and control of numerical algorithms. Note that these activities are not independent, and this organization is used primarily to assist in the exposition of ideas.
Model Generation
The term model generation is used to encompass all activities that result in the generation of models of physical systems suitable as input for a computational mechanics program. The generation of mathematical models from physical descriptions of systems is a problem of great practical importance. In all disciplines that use computational mechanics—aerospace, nuclear, marine, civil, and mechanics—there is a need to model an increasingly wider range of phenomena in all stages of system design from the earliest conceptual studies to the most detailed component performance evaluation. In addition, there is an urgent need for much
closer integration of computational mechanics evaluations into computer-aided design (CAD) and to extend analyses to computer-aided manufacturing where there is a great interest in analyzing not just the finished components, structures, or systems but also the manufacturing processes themselves, such as casting, forging, or extrusion.
With the availability of literally hundreds of computational mechanics codes, including a large number of general-purpose finite element programs with a broad range of capabilities, model generation has become the primary activity of the analyst. However, in the current state of the art, the preparation of input data is a tedious, error-prone, and time-consuming process. Analysts are forced to interact with programs at a level much lower than the conceptual level at which they make decisions. Hence, there is a need for higher-level program interfaces that will free analysts from details, allowing them to generate models in terms of high-level behavioral descriptions, thereby increasing their productivity and improving the quality and reliability of their analyses.
Moreover, because of the very small number of experienced modelers who can confidently and reliably model physical problems and the increasing need for modeling expertise, it has also become increasingly important to capture and organize the modeling knowledge of experienced analysts and transfer it to the less experienced novice analysts. The methodology of AI and knowledge-based systems promises to provide an opportunity to respond to the needs identified above.
Model generation tools can be discussed at three levels of increasing abstraction.
-
Intelligent help systems. Intelligent help systems address the issue of providing consulting advice to nonexpert engineers. The subject of help could be either how to use a particular analysis program or what model parameters and procedures are appropriate for particular physical systems. Help systems are not connected to analysis programs and are not meant to provide complete solutions to modeling problems. They simply guide the user—typically the novice user—in conducting some modeling tasks.
Typically, help systems act as interactive passive consultants. They query the user on some key aspects of the problem and, based on the key problem features, inform the user on the appropriate sequence of commands, program options to select, analysis strategies to invoke, numerical parameters to assign, etc. The interaction is often through a question-and-answer session and custom menus. These help systems can be readily built using simple shells that provide
-
forward and/or backward chaining capabilities. With the advent of powerful personal computer software that can write and organize knowledge and communicate with the user through standard interfaces (HyperCard, HyperX), systems can be properly integrated in a variety of analysis and design environments.
-
Customized preprocessors. Customized preprocessors are knowledge-based programs that are integrated into the environment in which they operate. Customized preprocessors extract relevant features from a data base that describes the physical object to be modeled (often a simple geometric model). These features play the role of higher-level, symbolic descriptions that provide semantics to geometric entities. Features are used to classify various components and match them to corresponding analysis methods and parameters (e.g., finite element mesh density). These parameters are then used to derive special-purpose interfaces to produce input files for the appropriate analysis programs of the environment.
The advantage of customized systems is that the user intervention in the modeling process is minimal. Essentially, the user is only required to enter some description of the physical object to be modeled. The preprocessors rely on the fact that the object can be adequately described in terms of a predetermined set of features encoded in the knowledge base and that a set of rules for modeling, analyzing, and evaluating these features exists. The structure of this class of knowledge-based systems can be analyzed in terms of three primitive tasks: (1) data abstraction (definitional, qualitative, or generalization abstractions); (2) heuristic associations between the abstracted features that characterize the object and the categories of known models; and (3) refinement that specializes a chosen model category to the particular problem at hand.
Unfortunately, customized preprocessors are typically limited to narrow domains. This is due to the fact that they rely on structuring the objects of the domain in very specific ways: to fit the templates of a set of a priori chosen features. The ways in which models can be used must be anticipated and fixed when the system is designed. As the domain expands, significant knowledge engineering effort is required to find, organize, and encode the myriad pieces of knowledge needed to extract all the relevant features and analyze their potential interactions. The combinatorial explosion of rules needed to cover very large domains can become prohibitive.
-
High-level model generation tools. High-level model generation tools incorporate techniques that are more flexible than the heuristic classification approaches used by the systems discussed above. In particular, the goal of these tools
-
is to put at the analyst's disposal a set of powerful representations and reasoning mechanisms that can be invoked as needed and that serve as a means of high-level specification of modeling operations.
A representation of modeling knowledge that can provide effective modeling assistance is an explicit representation of the assumptions that can generate various model fragments. Assumptions are the basic entities from which models are constructed, evaluated, and judged as adequate. Analysts often refer to and distinguish from various models by the assumptions they incorporate. The vocabulary of assumptions corresponds more closely to how analysts describe and assess the limitations of proposed models. Hence, the explicit representation and use of modeling assumptions in a modeling assistant can make the modeling operations correspond more closely to analyst's methods and could make it easier to organize and build a knowledge base. Assumptions encode a larger chunk of knowledge than rules and hence can provide a conceptual structure that is clearer and easier to manage than the typical knowledge-based or rule-based systems.
Turkiyyah and Fenves provide an example of how assumptions can be represented in a modeling assistant for their Generation and Interpretation of Finite Element Models in a Knowledge Based Environment5. In this representation, assumptions are modular units that, besides a prescription of how they affect the model, incorporate declarative knowledge about the scope of their applicability and their relevance for various modeling contexts, as well as their (heuristic) a priori and (definitional) a posteriori validity conditions. Assumptions can be used either directly by the analyst or indirectly through analysis objectives. When an analysis objective is posted, a planning algorithm selects an appropriate set of assumptions that can satisfy the modeling objective. These assumptions can then be applied automatically to generate a model that can be input into a finite element program.
Geometric reasoning techniques also provide the basis for high-level model generation tools. For example, geometric abstractions such as the skeleton can capture significant spatial object characteristics. Effectively, the skeleton is a symbolic representation of shape that corresponds to the way in which analysts visualize and describe shape and shape information, namely in terms of axis and width for elongated subdomains, center and radii for rounded subdomains, bisec-
tor and angle for pointed subdomains, etc. Because such abstractions are domain independent and hence general purpose, they can be used to suggest simplifications to the model (e.g., replace certain elongated two-dimensional regions by one-dimensional beam elements). They can also be used to subdivide a spatial domain into subregions of simple structure that can then be meshed directly by mapping or other mesh generation techniques.
MODEL INTERPRETATION
This section describes the AI potential to assist in postanalysis operations. Postanalysis operations are generically referred to as interpretation, although they involve distinctly different types of processes, including model validation, response abstraction, response evaluation, and redesign suggestions.
MODEL VALIDATION
Model validation determines if the mathematical model's numerical results accurately reflect the modeled system's real behavior. Knowledge-based techniques provide practical mechanisms to represent and characterize one important class of possible errors—idealization errors. Recently, a framework to validate idealized models has been proposed such that if the system model is methodically generated through the application of a set of assumptions any idealization error can be traced to one or more of those generative assumptions. Furthermore, each assumption encodes the conditions under which it is valid; hence, model validation involves checking the validity conditions of individual assumptions. There are many ways of verifying assumptions ranging in complexity from the evaluation of simple algebraic expressions to analysis of a model that is more detailed than the original one.
ABSTRACTION OF NUMERICAL RESULTS
Response abstraction is the task of generating some abstract description of the raw numerical results obtained from the analysis program. This description is presented in terms of high-level aggregate quantities representing key response parameters or behavior patterns.
Response abstractions can be classified in two types. The first, functional response abstractions, depends on the role that various subsystems or components play outside the model proper, that is, the meaningful aggregate quantities that are generated depend on knowledge of characteristics beyond the geometric and material properties of the system. The ability to generate the function-dependent response abstraction depends on the ability to represent the functional information that underlies the object modeled.
The second type of response abstraction is function independent. One seeks to recognize patterns, regularities, and interesting aspects and generate qualitative descriptions (e.g., stress paths) of the numerical results, independent of the functional nature of the object being modeled. Techniques from computer vision and range data analysis can be used to generate these interpretations. Well-developed vision techniques such as aggregation, segmentation, clustering classification, and recognition can be applied to the task. One interesting use of response abstractions assists the user in checking the "physical reasonableness" of numerical results by comparing the response abstractions between more refined models and simpler models.
CONFORMANCE EVALUATION
Conformance evaluation is the task of verifying that the computed results satisfy design specifications and functional criteria such as stress levels, ductility requirements, or deflection limitations. Conformance evaluation is largely a diagnostic problem, and the well-developed techniques for diagnosis can be applied to the task. Conformance evaluation requires heuristics on what are the (1) possible failure modes, (2) applicable code and standard provisions, (3) response quantities (stresses, deflections, etc.) affected by the provisions, and 4) approximations of the provisions and responses necessary.
A major issue in developing expert systems for conformance evaluation is the representation of code and standard provisions in a form suitable for evaluation yet amenable to modification when standards change or an organization wishes to use its own interpretations. One technique suitable for this purpose is to represent standards provisions by networks of decision tables.6
INTEGRATION IN DESIGN
Analysis is rarely, if ever, an end in itself. The overwhelming use of analysis is to guide and confirm design decisions. One important application of AI techniques is to provide redesign recommendations when the analyzed system's response is not satisfactory. One problem that has to be addressed is the nature of the knowledge base that can generate redesign recommendations. Should it be separate and independent, or should it use the same modeling knowledge responsible for generating and interpreting models? The second approach formulates redesign as a goal-oriented problem: Given some deficiencies uncovered by an analysis, what modifications to the design object are required so that a model whose response satisfies the design specifications can be generated?
Another problem that has to be addressed if computational methods are to be adequately incorporated in CAD is the general capability to provide analysis interpretations and design evaluations compatible with the progress of the design process from the initial conceptual sketch to a fully detailed description. Evaluations should occur at increasingly higher degrees of refinement throughout the design process. Early simple models can provide early feedback to the designer (or design system) on the global adequacy of the design, while evolved models, paralleling the evolving design, help to guide the designer in the detailed design stages. An important issue in developing general mechanisms for hierarchical modeling is how to generate and represent various kinds of geometric abstractions.
NUMERICAL MODEL FORMULATION
The term formulation denotes the process of producing a computational mechanics capability—a set of numerical routines—from a representation of a physical phenomenon. It is well known that the development of a computational mechanics program is time consuming, expensive, and error prone. Processes that can help in the quick development of reliable numerical software can be of great practical benefit. Ideas from AI can contribute significantly to various aspects of the formulation process: performing symbolic computations, expressing subroutines in a form that makes them reus-
able, designing large systems with appropriate data abstractions, assisting in the synthesis of computational mechanics programs, and integrating heuristics and knowledge-based methods into numerical solutions. These aspects are examined in turn.
SYMBOLIC PROCESSING
One aspect of program development that is particularly time consuming and error prone is the transition from a continuum model involving operations of differentiation and integration to a computational model involving algebraic and matrix operations. A branch of AI deals with symbolic computations, culminating in symbolic computation programs such as MACSYMA and Mathematica. Programs in this class operate on symbolic expressions, including operations of differentiation and integration, producing resulting expressions in symbolic form. A particularly attractive practical feature of these programs is that the output expressions can be displayed in Fortran source code format.
The potential role of symbolic processing has been investigated by several researchers. Studies indicate that symbolic processing can significantly assist the generation of computational model components to be incorporated in the source code. Symbolic generation of source code for clement stiffness and load matrices can eliminate the tedious and error-prone operations involved in going from a differential algebraic representation to a discrete procedural representation. Additional run-time efficiency improvements are possible through functionally optimized code and the use of exact integrations. Finally, conceptual improvements are possible, such as symbolically condensing out energy terms that contribute to shear and membrane locking.
REUSABLE SUBROUTINES
Numerical subroutines that perform function evaluations, domain and boundary integrations, linear and nonlinear equation solving, etc., abound in computational mechanics codes. However, the typical implementation of these subroutines bears little resemblance to our mathematical knowledge of the operations they perform. They are written as a sequence of concrete arithmetic operations that include many mysterious numerical constants and are tailored to specific machines. Because these routines do not exhibit the structure
of the ideas from which they are formed, their structure is monolithic, handcrafted for the particular application, rather than constructed from a set of interchangeable parts that represent the decompositions corresponding to the elemental concepts that underly the routine. Often numerical routines are difficult to write and even more difficult to read.
The idea of expressing mathematical routines constructively is widely applicable. Even the simplest routines that are of ten thought of as ''atomic''—such as sin(x)—can be constructed from their primitive constituent mathematical operations, that is, periodicity and symmetry of the sine function and a truncated Taylor expansion. Abelson et al.7 shows how Romberg's quadrature can be built by combining a primitive trapezoidal integrator with an accelerator that speeds the convergence of a sequence by Richardson extrapolation. The idea is that instead of writing a subroutine that computes the value of a function, one writes code to construct the subroutine that computes a value.
Such a formulation separates the ideas into several independent pieces that can be used interchangeably to facilitate attacking new problems. The advantages are obvious. First, clever ideas need to be coded once in a context independent of the particular application, thus enhancing the reliability of the software. Second, the code is closer to the mathematical basis of the function and is expressed in terms of the vocabulary of numerical analysis. Third, the code is adaptable to various usages and precisions because the routine's accuracy is an integral part of the code rather than a comment that the programmer adds; just changing the number that specifies the accuracy will generate the single, double, and quadruple precision versions of a subroutine.
Writing subroutines in this style requires the support of a programming language that provides higher-order procedures, streams, and other powerful abstraction mechanisms available in functional languages. The run-time efficiency does not necessarily suffer. The extra work of manipulating the function's construction need be done only once. The actual function calls are not encumbered. Moreover, because functional programs have no side effects, they have no required order of execution. This makes it exceptionally easy to execute them in parallel.
PROGRAMMING WITH DATA ABSTRACTIONS
The current generation of computational mechanics software is based on programming concepts and languages that are two or three decades old. As attention turns to the development of the next generation of software, it is important that the new tools, concepts, and languages that have emerged in the interim be properly evaluated and that the software be built using the best appropriate tools.
Designs for finite element systems based on object-oriented concepts have begun to emerge in the literature. As these designs show, object-oriented programming, an offshoot of AI research, can have a major impact on computational mechanics software development. It is possible to raise the level of abstraction present in large-scale scientific programs (i.e., allowing finite element programmers to deal directly with concepts such as elements and nodes) by identifying and separating levels of concern. Programs designed in this manner allow developers to reason about program fragments in terms of abstract behavior instead of implementation. These program fragments are referred to as objects or data abstractions, their abstract quality being derived from precise specifications of their behavior that are separate and independent of implementation and internal representation details.
MODEL SYNTHESIS ASSISTANCE
While the bulk of today's computational mechanics production work is done by means of large comprehensive programs, there is a great deal of exploratory work requiring the development of "one-shot" ad hoc custom-built programs. Developers of such ad hoc programs may have access to subroutine libraries for common modules or "building blocks" but not much else. These developers frequently have to reimplement major segments of complete programs in order to "exercise" the few custom components of their intended program.
One potential application of AI methodology is an expert system to assist in synthesizing computational programs tailored to particular problems, on the fly. The system would require some specifications of the program goal; the constraints (e.g., language, hardware environment, performance); and the description of custom components (e.g., a new equation solver, a new element, a new constitutive equation for a standard element) as input. The system's knowledge base would contain descriptions of program components with their attributes (lan-
guage, environment, limitations, interface descriptions, etc.) and knowledge about combining program components, which might include the knowledge to write interface programs between incompatible program segments. The expert system would have to use both backward and forward chaining components—the former to break down the goal into the program structure and the latter to select program components to "drive" the low-level custom components.
MONITORING NUMERICAL SOLUTIONS
Combining numerical techniques with ideas from symbolic computation and with methods incorporating knowledge of the underlying physical phenomena can lead to a new category of intelligent computational tools for use in analysis. Systems that have knowledge of the numerical processes embedded within them and that can reason about the application of these processes can control the invocation and evolution of numerical solutions. They can "see what not to compute" (Abelson 1989) and take advantage of known characteristics of the problem and structure of the solution to suggest data representations and appropriate solution algorithms.
The coupling of symbolic (knowledge-based) and numerical computing is particularly appropriate in situations where the application of pure numerical approaches does not provide the capabilities needed for a particular application. For example, numerical function minimization methods can be coupled with constraint-based reasoning methods from AI technology to successfully attack large nonlinear problem spaces where numerical optimization methods are too weak to find global minima. To derive a solution to the problem, domain-specific knowledge about problem solving in terms of symbolic constraints guides the application of techniques such as problem decomposition, constraint propagation, relaxation, and refinement.
COMPREHENSIVE MODELING ENVIRONMENTS
As higher level modeling tools are built and larger modeling knowledge bases are constructed, issues such as integration, coordination, cooperative development, and customization become critical. A framework for a general finite element modeling assistant has also been proposed recently in the literature. The framework is intended to permit a
cooperative development effort involving many organizations. The key feature of the framework is that the system consists of a set of core knowledge sources for the various aspects of modeling and model interpretation that use stored resources for the problem-dependent aspects of the task. In this fashion, new problem types, as well as individual organizations' approaches to modeling, only involve expansion of the resources without affecting the knowledge sources.
In the comprehensive framework envisaged, the core knowledge sources would perform the function of model generation and interpretation and program selection (with possible customization and synthesis) and invocation. The three major resources used by these knowledge sources are as follows:
-
Physical class taxonomies. These represent an extended taxonomy or semantic network of the various classes of physical systems amenable to finite element modeling and the assumptions appropriate for each class. Their purpose is to provide pattern matching capabilities to the knowledge sources so that the definition of problem class and key problem parameters can be used by the knowledge sources in their tasks at each level of abstraction. The major design objective in developing these taxonomies will not be to avoid exhaustive enumeration of individual problems to be encountered, but rather to build a multilevel classification of problem types based on their functionality, applicable assumptions, behavior, failure modes, analysis strategies, and spatial decompositions. It is also expected that a large part of knowledge acquisition can be isolated into modifying these taxonomies either by specialization (customization to individual organization) or generalization (merging or pooling knowledge of separate organizations).
-
Program capability taxonomies. In a manner similar to the above, these taxonomies represent the capabilities, advantages, and limitations of analysis programs. The taxonomy must be rich enough so that the knowledge source invoking the programs can make recommendations on the appropriate program(s) to use based on the high-level abstractions generated by the other knowledge sources or, if a particular program is not available in the integrated system, to make recommendations on alternate modeling strategies so that the available program(s) can be effectively and efficiently used. As with the previous taxonomy, the program capability taxonomy needs to be designed so that knowledge acquisition about additional programs can be largely isolated to the expansion of the taxonomy data base.
-
Analysis programs. The programs, including translators to and from neutral files as needed, are isolated in the design to serve only as resources to solve the model. The issues in this interconnection are largely ones of implementation in coupling numerical and knowledge-based programs. Modern computing environments make such coupling relatively seamless.
Research Issues
This section discusses briefly two important problems that must be addressed before reliable modeling environments, such as the one discussed above, can be built. The first problem is the need to provide more flexibility to knowledge-based systems, and the second is the need to compile a core of modeling assumptions.
FLEXIBLE KNOWLEDGE-BASED SYSTEMS
The present generation of knowledge-based systems has been justly criticized on three grounds: they are brittle, idiosyncratic, and static.
Present knowledge-based systems are brittle—in the sense used in computer science as a contrast to "rugged" systems—in that they work in a very limited domain and fail to recognize, much less solve, problems falling outside of their knowledge base. In other words, these systems do not have an explicit representation of the boundaries of their expertise. Therefore, there is no way for them to recognize a problem for which their knowledge base is insufficient or inappropriate. Rather than exhibiting "common sense reasoning" or "graceful degradation," the systems will blindly attempt to ''solve" the problem with their current knowledge, producing predictably erroneous results. Current research on reasoning from first principles will help overcome this problem. Combining first principles with specialized rules will allow a system to resort to sound reasoning when few or no specialized items in its knowledge base cover a situation. First principles can also be used to check the plausibility of conclusions reached by using specialized knowledge.
A KBES developed using the present methodology is idiosyncratic in the sense that its knowledge base represents the expertise of a single human domain expert or, at best, that of a small group of domain experts. The system thus reproduces only the heuristics, assumptions, and even style of
problem solving of the expert or experts consulted. The nature of expertise and heuristics is such that another, equally competent expert in the domain may have different, or even conflicting, expertise. However, it is worth pointing out that a KBES is useful to an organization only if it reliably reproduces the expertise of that organization. At present, there appear to be no usable formal methods for resolving the idiosyncratic nature of KBESs. There are some techniques for checking the consistency of knowledge bases, but these techniques are largely syntactic. One practical approach is to build a domain-specific metashell that contains a common knowledge base of the domain and excellent knowledge acquisition facilities for expansion and customization by a wide range of practitioners.
Present KBESs are static in two senses. First, the KBES reasons on the basis of the current contents of its knowledge base; a separate component, the knowledge acquisition facility, is used to add to or modify the knowledge base. Second, at the end of the consultation session with a KBES, the context is cleared so that there is no provision for retaining the "memory" of the session (e.g., the assumptions and recommendations made). Research on machine learning is maturing to the point where knowledge-based systems will be able to learn by analyzing their failed or successful performance—an approach called explanation-based learning.
COMPILATION OF MODELING KNOWLEDGE
One task of great practical payoff is the development of a knowledge base of modeling assumptions that contains what is believed to be the shared knowledge of analysts. Such a core knowledge base will be beneficial in two important ways. First, it could be used as a starting point to build a variety of related expert systems, hence making the development cycle shorter. Second, such a knowledge base could become the "corporate memory" of the discipline and, hence, could give insights into the nature of the various aspects of modeling knowledge. One starting point to build such a knowledge base is to "reverse engineer" existing models to recognize and extract their assumptions.
Two useful precedents from other domains offer guidance. Cyc is a large-scale knowledge base intended to encode knowledge spanning human consensus reality down to some reasonable level of depth—knowledge that is assumed to be shared between people communicating in everyday situations. Cyc is a 10-year effort that started in 1984.
Progress to date indicates that the already very-large knowledge base (millions of assertions) is not diverging in its semantics and already can operate in some common situations.
Knowledge-based Emacs (KBEmacs) is a programmer's apprentice. KBEmacs extends the well-known text editor Emacs with facilities to support programming activities interactively. The knowledge base of KBEmacs consists of a number of abstract programs (cliches) ranging from very simple abstract data types such as lists to abstract notions such as synchronization and complex subsystems such as peripheral device drivers. The fundamental idea is that the knowledge base of cliches encode the knowledge that is believed to be shared by programmers. KBEmacs has been used successfully to build medium-sized programs in Lisp and Ada.
SUMMARY
The objective of this appendix was to present some of the concepts and methodologies of AI and examine some of their potential applications in various aspects of computational mechanics. The methodologies sketched herein are maturing rapidly, and many new applications in computational mechanics are likely to be found. Undoubtedly, AI methodologies will eventually become a natural and integral component of the set of computer-based engineering tools to the same extent as present-day "traditional" algorithmic tools. These tools will then significantly elevate the role of computers in engineering from the present-day emphasis on calculation to the much broader area of reasoning.