6
MATERIALS RESEARCH: NUMERICAL MODELING OF NEW MATERIALS
Computational mechanics is an essential tool in the quest to engineer materials for specific purposes. Many of the manufacturing and performance-limiting issues of these materials are appropriately addressed within a continuum mechanics framework. The numerical solution of continuum mechanics problems is used to (1) analyze microscale deformation modes in order to design materials and processes, (2) develop macro-scale constitutive and damage laws, and (3) design machines and structures that fully utilize the capabilities of these new materials.
The performance of a material in service is controlled by a large set of properties. One purpose of computational mechanics studies is to link properties as measured in standard tests to performance under service conditions. For example, standard test procedures exist to measure a material's resistance to crack growth. Computational mechanics analyses are used to correlate performance in such a test with crack growth behavior under service conditions and relate the property measured in this test to material microstructure. Another purpose is to relate properties to measurable and controllable features of the material's microstructure such as the orientation of crystal structure, the configuration of phases, and the morphology and distribution of second-phase particles.
Much of the computational mechanics of materials is finite element based and therefore, to a large extent, is an unanticipated outgrowth of development in computational structural mechanics. Formulations and algorithms developed in the structural mechanics context for problems involving both geometrical and material nonlinearities have provided the foundation to develop a powerful capability to analyze and predict material behavior. Although the foundations have been laid, much remains to be done to make this capability an engineering design tool in the same sense as computational structural mechanics. The potential payoff is enormous.
One can envision real-time calculations being used to control processes in order to maximize throughput and ensure
desirable product properties, even tailoring product properties in real time for different applications. For example, the mechanical properties and formability of metal sheet depend on the crystallographic texture (the orientation of the crystal axes of the microscopic grains that make up a polycrystalline structural metal). In turn, the texture of the metal sheet coming out of a rolling mill depends on the mill settings. At present, calculation of texture under complex loading histories is itself a subject of much research. The ability to compute texture development quickly and accurately would permit cheap and efficient tailoring of sheet products for specific applications. This capability will undoubtedly be developed. The only question is when and by whom.
Off-line analyses permit ''what if" studies of the implications of alternative manufacturing options and alternative material microstructures. The design of composite materials involves considering a very large number of possibilities, even presuming that the basic matrix and reinforcing material are given. What are the optimal volume fraction and second-phase size and shape distributions necessary to achieve specified performance goals at reasonable cost? If the shape of the reinforcement phase can be changed, does improvement in performance justify the extra effort and cost? How strong should the interface bond be? Too strong a bond can reduce energy dissipation in certain failure modes, which makes the composite brittle and unsafe in certain applications. Too weak a bond can reduce stiff ness and degrade other mechanical properties to the point where the composite is unsuitable for the intended application.
The following examples illustrate some current computational capabilities on issues related to new material design and performance assessment.
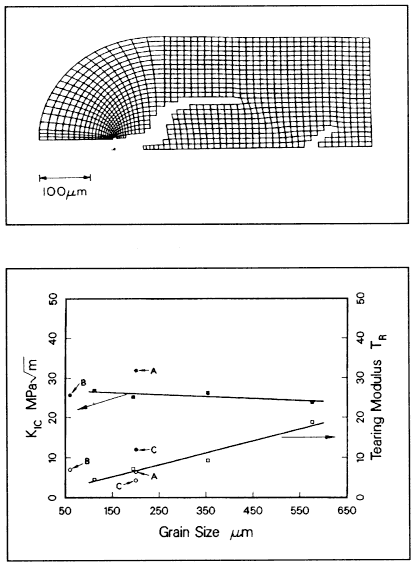
Figure 6.1 shows some results for an aluminum-lithium alloy that fails by grain boundary cavitation at room temperature. A complete compact tension specimen was analyzed, but Figure 6.1 shows the mode of crack propagation in the region just ahead of the crack. The material is described by a porous plastic constitutive relation that allows for creation of a new free surface, and the elements in which there has been a complete loss of stress-carrying capacity are deleted from the mesh plot. The model is a highly idealized one; nevertheless, there are no adjustable parameters. All material parameters input into the analysis were independently measured or inferred. The quantitative agreement between the model predictions and the experimentally measured values was quite good. The predicted critical stress intensity values were within a factor of two of the experimental values, while the
predicted and observed values of the tearing modulus (a measure of material resistance to crack growth) were typically within 50 percent of each other.
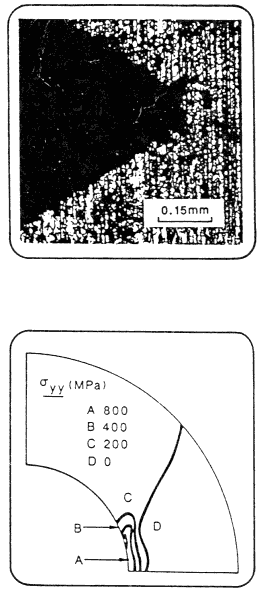
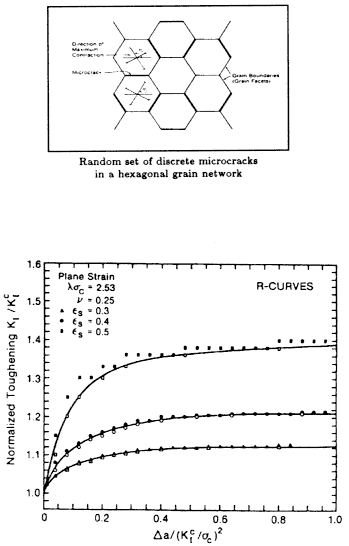
A possible method for improving the toughness of ceramics is to use materials, such as zirconia partially stabilized with magnesia, that undergo a stress-induced phase transformation. Constitutive models have been developed that represent the shear strains and volume change accompanying the phase transformation. Finite element analyses based on these models have successfully predicted toughness enhancements and the mode of fatigue crack growth at notches. Figure 6.2 shows that the direction of crack growth follows the predicted shape of the residual tensile stress contours near a notch tip growth from a notch tip and predicted contours of constant normal stress at the notch tip. Another key issue is to understand the role of microcracks on toughness to improve the performance of ceramic materials. Figure 6.3 shows a picture of a random array of microcracks in a model of a polycrystalline ceramic and computed crack growth resistance curves. The resistance to the extension of a macroscopic crack builds up as a result of the wake of microcracked material left behind by the advancing large crack. This gives an increase in toughness of up to 40 percent for mode I conditions (tensile crack loading). However, subsequent work showed that there is no appreciable gain in toughness due to microcracking when the crack loading contains a significant shear component. This has important implications for the design of ceramics tough enough for a broad range of structural applications.
Structural steel is a complex multiphase material. The development of high-strength steels, with properties optimized for specific applications, poses a considerable challenge. In high-purity, high-strength steels, for an important range of loading conditions, the ductility and toughness-limiting event is void nucleation by debonding of grain-refining particles. Figure 6.4 shows the predictions of a continuum model for the debonding strain as a function of grain-refining particle size, with the volume fraction for each size adjusted to attain a constant grain size. The prediction is that substantial improvements in toughness can be obtained by decreasing the grain-refining dispersion particle size. Whether or not such performance actually occurs remains to be seen.
Convergence of calculation procedures is an important issue. The phenomena computed must be reliable characteristics of the problem formulation and not of the spatial or temporal discretization. For material modeling problems that may involve large deformations, path-dependent material response, instabilities, and the creation of new free surface, essentially
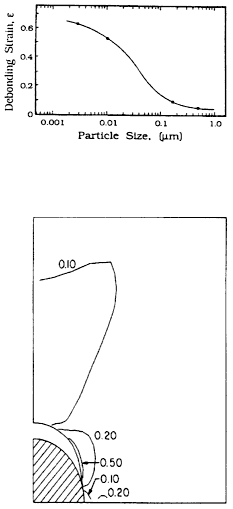
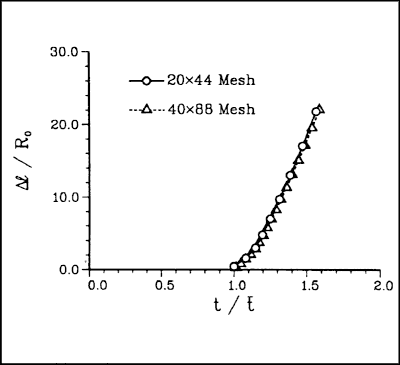
Figure 6.4 Debonding process and predicted particle debonding strain versus particle diameter. Source: G.B. Olson, ''Overview: Science of Steel," in Innovations in Ultrahigh-Strength Steel Technology, Proceedings of the 34th Sagamore Army Materials Research Conference, ed. by G.B. Olson, M. Azrin and E.S. Wright, pp. 3–66. Reprinted with permission. Creep crack growth versus time for two meshes. Source: F.Z. Li, A. Needleman, and C.F. Shih, 1988, International Journal of Fractures, Vol. 36, pp. 163–186.
nothing is known on a fundamental mathematical basis about the convergence behavior of the algorithms used. Numerical experimentation has given some feeling for which features are mesh sensitive and which are not and how this sensitivity depends on apparently subtle features of the problem formulation. Figure 6.5 shows results from a finite element calculation of creep crack growth using a micromechanically based constitutive relation that allows for the loss of stress-carrying capacity due to grain boundary cavitation. The finer mesh is obtained by halving the grid spacing in each spatial direction. There is clearly very little mesh dependence for the crack growth rate. The features of the problem formulation and the numerical procedure that permit such mesh-independent results to be obtained need to be understood better. (The highly viscous nature of creep response is one such feature.)
It is worth noting that these computational models have two spatial dimensions while the actual phenomena are three-dimensional. The reason is simply that the computer time and storage required for fully three-dimensional analyses would preclude, or at least severely limit, the parameter studies that the investigations require. Clearly, such studies would benefit from improved algorithms for path-dependent material response that are flexible enough to accommodate physically based constitutive descriptions, instabilities, and progressive creation of new free surface. In order to transform these types of computations from research projects into engineering tools, significant advances in computational capability and understanding are required.
Brief descriptions are given below of areas where improved computational mechanics capabilities appear likely to have a real impact on the design, processing, and performance evaluation of new materials. The focus is on issues that are especially material related, and in this area computational and modeling issues often are not readily decoupled; an accurate predictive capability depends on an accurate physical model. Although purely modeling issues will not be discussed, a key need for further progress is the development of accurate constitutive models for large strain inelastic deformation that are suitable for use in computations. Also, general computational issues, while important, are not highlighted.
THE LOCALIZATION OF DEFORMATION
When ductile solids are deformed sufficiently far into the plastic range, it is frequently observed that a smoothly
varying deformation pattern gives way to one involving highly localized bands of deformation. This phenomenon of flow localization occurs in a wide variety of solids: ductile single crystals, polycrystalline structural metals, polymers, granular materials, and concrete. Such localizations are often termed shear bands because the deformation mode in the localized band is primarily one of shear. Shear bands have a dual significance: as a precursor to fracture and as a mechanism for further deformation. The ability to predict their onset, evolution, and subsequent failure is essential for efficient control of a variety of manufacturing processes and design of material microstructures.
Problems involving shear localization present special complications for numerical methods in general and finite element methods in particular. For rate-independent solids, a shear band is associated with a change in the character of the governing equations. Under quasi-static loading conditions, the equations governing incremental equilibrium lose ellipticity, while under dynamic loading conditions, wave speeds become imaginary. Since the governing equations have no natural length scale, the width of the shear band is arbitrary. Hence, numerical solutions to localization problems can exhibit an inherent mesh dependence because in a grid-based numerical solution the minimum width of the band of localized deformation is set by the mesh spacing. Furthermore, global quantities such as the overall stiffness characteristics of the body depend on the mesh size used to resolve the band of localized deformations.
Pathological mesh dependence can be eliminated by a "regularization" of the governing equations. This regularization can take a variety of forms, including accounting for material rate sensitivity or introducing a nonclassical strain gradient modification to the constitutive relation. The regularization needs to be understood and justified on physical grounds. Different regularizations present different numerical challenges, and the implications of these for numerical accuracy, efficiency, and stability need to be understood. There are also important mathematical questions concerning the existence, regularity, and stability of solutions to localization problems. A more complete understanding of physically appropriate and computationally convenient regularizations is needed.
However, regardless of the formulation, the mesh sets the minimum band width at one grid spacing. Conventional displacement finite element methods can only resolve bands of concentrated deformation when the band interfaces follow element boundaries. Unless special care is used to align
element boundaries along band directions, the mesh introduces a shear band broadening that can control the course of strain localization and mask the effects of physical response mechanisms on localization. At present, the onset of localization and the orientation of localization bands can be predicted accurately if an adequate constitutive model is available for the material. In certain circumstances, including a restriction to one or two spatial dimensions, strain localization development and failure modes can be computed that are in qualitative and, in some cases, quantitative agreement with the experiment. Current computational capabilities need to be extended in order to predict reliably general localization and failure phenomena. Recently, much progress has been made on developing enhanced and enriched element formulations that permit resolution of sharp gradients oriented arbitrarily with respect to the mesh. These methods open up the possibility of analyzing shear band development in general three-dimensional problems.
Since shear band widths are generally much smaller than the overall body size and develop at locations that are not always known a priori , localization problems are ideally suited to benefit from adaptive mesh methods and, perhaps, combined adaptive-enrichment strategies. This has not happened yet, but the potential benefits are great.
PROGRESSIVE CREATION OF NEW FREE SURFACE
Fracture involves the creation of new free surface. In traditional approaches to fracture analysis, the presence of a single dominant flaw is presumed, and the key issue is whether that flaw will grow under the given loading conditions. This question can be addressed by solving a boundary value problem for the flawed body and then imposing an appropriate failure criterion. However, in order to investigate the relation of ductility and strength to material microstructure or to analyze fracture in circumstances where there is no single dominant flaw, an approach is needed where the material's constitutive relation embodies a physically appropriate model of the failure process. In such boundary value problem formulations, failure—the creation of new free surface—is an outcome of the solution procedure. The creation of new free surface is also a desired outcome in many shaping and forming operations. The aim in this type of application is to develop the capability to predict and control how the free surface evolves as process parameters are varied. It is important to note that because of the progressive nature of the separation process the formula-
tion must be fully coupled, that is, it must contain a description of the failure mechanism and predict its evolution. An uncoupled calculation where a stress analysis is carried out and then a failure criterion imposed is inadequate for the task.
Several methods can be used to analyze problems involving the creation of new free surface—for example, an ''element vanish" technique and a critical energy release rate fracture criterion have been used for ductile and brittle solids, respectively. The critical energy release rate formulation has enabled fundamental questions concerned with the micro-mechanical origin of toughness in ceramics to be addressed by computational modeling. The element vanish technique is applicable when the material constitutive relation allows for a complete loss of stress-carrying capacity and has been used successfully in a wide variety of circumstances where the failure mechanism is ductile void growth. However, other ductile separation mechanisms occur; for example, in machining operations, shear band-type localizations can occur and, the large strains within a band of localized deformation subsequently lead to the creation of new free surface. Quantifying this process is important to understanding when localized deformation leads to separation.
The development of accurate models for the creation of new free surface by a variety of physical mechanisms, and of algorithms for the efficient and reliable implementation of these models is an important need for safety assessment and process modeling for broad classes of materials.
SURFACES, INTERFACES, AND MATERIAL-DEPENDENT LENGTH SCALES
Identification of appropriate material length scales is an issue that arises in a variety of guises. Predictions of fracture necessarily, from dimensional considerations, involve a material length scale. Predicting shear band widths also involves a material length scale. Whenever phenomena are governed by both surface and volume effects, the ratio of material volume to surface area introduces a length scale. In coupled field problems, phenomena such as heat conduction and diffusion introduce length scales. In multiphase materials, it is well known that the absolute size, as well as the volume fraction of the second-phase constituent, plays an important role in determining performance.
There are many important situations where phenomena at surfaces and interfaces play a dominant role. For example, the ductility and toughness of composite materials are often
governed by the bonding between the constituents. Surface quality in machine products and wear under service conditions depend on surface rather than bulk properties. The incorporation of surface characterizations into the formulation often introduces a material length scale as well as allowing for surface-specific phenomena (e.g., slip-stick instabilities).
However, most of what is known about continuum formulations and their numerical implementation pertains to circumstances independent of size scale. An improved understanding is needed of the implications of material length scales for the convergence and efficiency of numerical algorithms.
COUPLED FIELD PROBLEMS
Computational approaches are extremely important in nontraditional areas of application where coupled processes occur between mechanical, chemical, thermal, and electronic phenomena. Examples include hydrogen embrittlement and stress corrosion resistance of materials. Creep at high temperatures typically involves mass diffusion as well as dislocation creep. Thermal variations encountered in material processing can significantly affect properties and performance. In this regard it is worth emphasizing that an understanding of the effects of thermomechanical processing on materials is important even when the ultimate application is not mechanical. Mechanical effects on nonmechanical behavior will undoubtedly become an increasing concern. For example, an important problem in microelectronics, where significant advances have been made by finite element analyses, concerns the prediction of piezoelectrically induced threshold voltage shifts in gallium arsenide metal semiconductor field effect transistors. The development of efficient and robust computational procedures for complex coupled field problems is an area of potentially great impact.
PHYSICALLY BASED INELASTIC CONSTITUTIVE LAWS
Computational mechanics has an important role to play in the development of constitutive laws for new materials through an analysis of the deformation behavior of material microstructures. Modern developments in averaging methods for polycrystalline metals are giving predictions of deformation-induced texture development that are accurate enough to have an impact on industrial processes. Unit cell model studies of composites and solids with various forms of
microdamage (i.e., microvoids and microcracks) are elucidating key features of material deformation and failure modes.
Available phenomenological inelastic constitutive models for composite materials are almost all based on a characterization of the distribution in terms of a single parameter, the volume fraction. Computational studies of irregular distributions are being used to assess the extent to which the overall response of such materials does admit a one-parameter characterization. Recent studies have shown important circumstances where the details of the distribution have a profound effect on overall response. The appropriate characterization of distributions that go beyond the one-parameter volume fraction description for the nonlinear behavior of hetereogeneous materials is an open issue. It seems clear that computational studies will play a major role in identifying appropriate characterization parameters and will be a key ingredient in a yet-to-be-developed extension of current approaches to homogenization for inelastic solids.