4
The Influence of Orography
INTRODUCTION AND BASIC PARAMETERS
The transition from a nearly flat ocean to land in the coastal zone is often accompanied by major changes in elevation. Flow over and around such changes in orography in a rotating stratified fluid represents one of the classic problems in meteorology and oceanography. For a far-field wind perpendicular to a barrier, the horizontal extent and magnitude of upstream modification of the flow pattern in response to the barrier should be determined. There is also a downwind modification of the flow, which is not, in general, symmetric with the upwind influence.
Low-level air flow is generally blocked by a mountain when the parameter known as the Froude number is less than unity (Smith, 1979, 1989). The Froude number provides a measure of the relative importance of potential and kinetic energy in flow around and over obstacles. It is defined by:
(1)
where N is the static stability and is equal to (-g∂zθ/θo)1/2, U is the speed of the free air stream, hm is the height of the ridge, θo is the constant mean potential temperature, and g is gravity. For typical atmospheric stratification of N ≅ 10-1 to 10-2, an elevation of only 100 m is often sufficient to cause ''blocking" of the onshore flow at low levels. Such blocking occurs along the west and east coasts of the United States; along the east coast, it is often referred to as cold air damming. Leeside effects can be important for flow directed offshore; for island wakes; in regions where the coastline
curves, such as Southern California; or where there are inland marine regions, such as Puget Sound, San Francisco Bay, and southeast Alaska.
In the coastal zone it is not necessary to have an upstream velocity directed toward the mountains for the orography to influence coastal winds. If a localized region of high or low pressure is generated in the coastal zone, it will, under certain conditions, be trapped and propagate along the coastline within the coastal zone. This is a common phenomenon, for example, along the coasts of California and Australia.
The Froude number considers the relative importance of vertical displacement of isentropic surfaces in flow around and over obstacles. A second factor is the influence of the earth's rotation on upstream flow deceleration (Queney, 1948). One can consider the influence of rotation through a Rossby number:
(2)
where U is the upstream velocity, f the Coriolis force, and lm is the half-width of the ridge; little flow deceleration is found when Rm is less than unity. Numerical simulations by Pierrehumbert and Wyman (1985) and trajectory analyses by Chen and Smith (1987) suggest that in the region of steep topography the deceleration zone will grow upstream to a width of:
(3)
This parameter lR is known as the radius of deformation. Steep topography is defined by the nondimensional slope, (hm/lm)(N/f), being greater than 1. For the coastal case, lR is often on the order of 50 to 150 km and lR >> lm; this contrasts with broad mountain ranges such as the Rockies with lm on the order of 500 km. In the broad mountain case, lm >> lR, the flow stays quasi-geostrophic with Rm < 1 (i.e., wind blows perpendicular to the pressure gradient as it flows over the topography, with little upstream influence). The coastal region, however, is often in the knife-edge mountain case, lR >> lm, where Rm >> 1. Here one expects the coastal mountains to represent a wall, and the momentum balance in the along-shore direction near the wall is not expected to be geostrophic. The smoothed topographies in current-generation numerical weather prediction (NWP) models do not even qualitatively represent knife-edge slopes and thus do not correctly include coastal phenomena.
To further delineate the influence of orography on coastal meteorology, let L be the scale for motion in the along-coast (y) direction, and l be the scale in the cross-shore direction (-x), where
(4)
We can nondimensionalize the equations of motion in the following manner. The cross-shore wind component, u, and along-shore wind component, v, are scaled by UL/l, time by l/U, vertical distances by D = fl/N , and
pressure p by PoflU. The equations of motion for such a shallow system become (Overland, 1984):
(5)
and
(6)
where Rl = U/fl = V/fL is a coastal Rossby number, CD' = CD(U + V)/D is a coastal drag coefficient that indicates the relative importance of surface friction, and Po is a synoptic-scale pressure imposed on the coastal layer. The term ![]() Po/
Po/![]() y on the right-hand side of Eq. (6) nondimensionally equals unity and represents the along-shore pressure gradient associated with the incident geostrophic wind, U. For many coastal problems, the left-hand side of Eq. (5) is small, even though Rl is on the order of Eq. (2); the flow in the along-shore direction is in geostrophic balance. The left-hand side of Eq. (6), however, is on the order of Eq. (2), and v can exhibit accelerations in response to the imposed along-shore pressure gradient. Small l/L and Rl ~ 1 are the heart of the coastal zone semigeostrophic approximation. The only remaining free parameter is the nondimensional mountain height
y on the right-hand side of Eq. (6) nondimensionally equals unity and represents the along-shore pressure gradient associated with the incident geostrophic wind, U. For many coastal problems, the left-hand side of Eq. (5) is small, even though Rl is on the order of Eq. (2); the flow in the along-shore direction is in geostrophic balance. The left-hand side of Eq. (6), however, is on the order of Eq. (2), and v can exhibit accelerations in response to the imposed along-shore pressure gradient. Small l/L and Rl ~ 1 are the heart of the coastal zone semigeostrophic approximation. The only remaining free parameter is the nondimensional mountain height
(7)
This may also be written as Rl/Fr. Thus, the coastal mountain problem can be specified in terms of Rl and Fr, a Rossby number and a Froude number. Note that for hm/D = 1 (i.e., steep topography), the offshore length scale is defined by l = lR, the Rossby radius of deformation, which scales coastal influence offshore of mountainous coasts to be 10 to 100 km.
The foregoing discussion suggests that mesoscale meteorological features (10 to 100 km) are generated in the vicinity of coastal orography, and that ageostrophic motions are anticipated in the along-shore direction. However, the upstream flow is seldom stationary and uniform; vertical stratification is seldom constant. While theoretical considerations define the scales and processes important to the coastal zone, they are less successful in fully explaining particular case studies (Walter and Overland, 1982; Mass and Ferber, 1990).
LOW FROUDE NUMBER FLOW: TRAPPED PHENOMENA
Isolated Response: Kelvin Wave and Gravity Current
Along subtropical mountainous coastlines such as California and Australia, subsidence in the subtropical high pressure often develops a strong marine inversion structure below the height of the coastal topography. This case is the most studied of orographic coastal phenomena. In this case the
stability scale can be replaced by the difference in temperature, θ2–θ1, across the inversion occurring at height hi. The coastal zone semigeostrophic equations, (5) and (6), admit Kelvin wave solutions
(8)
where G is an arbitrary function. The solution is trapped to a unit distance from the coast (i.e., a Rossby radius) and propagates at a unit speed that in dimensional terms has the phase speed c = flR. On the other hand, if the equations are initialized with a density front, a nonlinear gravity current, with some Kelvin-like aspects, can form. Along-shore disturbances can also be forced by an along-shore pressure gradient ![]() Po/
Po/![]() y imposed by the synoptic-scale pressure field above the coastal layer. The existence of this class of mesoscale coastal features has been documented in California (Beardsley et al., 1987; Dorman, 1985, 1987; Mass and Albright, 1987; Winant et al., 1988; Zemba and Friehe, 1987) and Australia (Holland and Leslie, 1986). Figure 4.1 shows a typical summer trapped feature along the west coast of the United States. The GOES visible imagery (Figure 4.1a) shows a wedge like feature that propagates northward from central California to British Columbia in about 2 days. Note that in the sea-level pressure analysis (Figure 4.1b) the wind shifts from northerly to southerly with the passage of
y imposed by the synoptic-scale pressure field above the coastal layer. The existence of this class of mesoscale coastal features has been documented in California (Beardsley et al., 1987; Dorman, 1985, 1987; Mass and Albright, 1987; Winant et al., 1988; Zemba and Friehe, 1987) and Australia (Holland and Leslie, 1986). Figure 4.1 shows a typical summer trapped feature along the west coast of the United States. The GOES visible imagery (Figure 4.1a) shows a wedge like feature that propagates northward from central California to British Columbia in about 2 days. Note that in the sea-level pressure analysis (Figure 4.1b) the wind shifts from northerly to southerly with the passage of
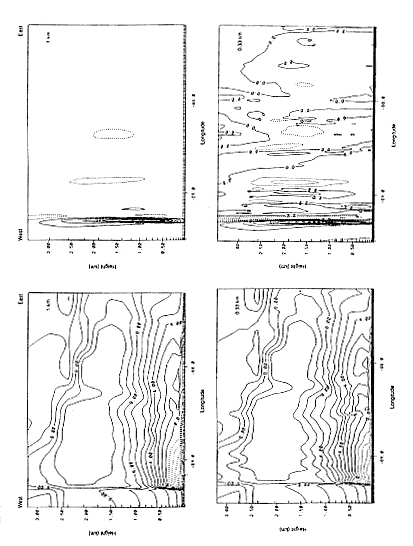
Figure 4.1 Typical summertime northward surge of marine air trapped to the west coast: (a) GOES visible image 1800 GMT, May 27, 1983; (b) observed wind and subjective sea-level pressure analysis for the same time based on satellite images and available surface synoptic data. Note that there is wind shift in the coastal zone as the surge propagates northward (after Mass et al., 1986).
the feature. The case for South Africa (Bannon, 1981; Gill, 1977; Reason and Jury, 1990) is quite distinct from the Australia and California cases (Reason and Steyn, 1990) (see Table 4.1). Calculation of the Rossby number based on half the mountain width yields 0.1, so dynamics lie within the quasi-geostrophic regime (i.e., small mountain slope) and blocking of an incipient flow will not persist (Pierrehumbert and Wyman, 1985).
While these isolated wave/frontal features are perhaps the most obvious of coastal phenomena, understanding their source mechanisms and composite nature (density flow versus propagating wave) is uncertain in any particular realization. These isolated trapped phenomena are generally initiated by changes in the synoptic-scale flow. The climatology of such changes is not well documented and is an area for further research. There is also a need to understand all factors that contribute to the depth and spatial variability of coastal marine stratus and fog as a result of interactions among wave dynamics, radiation, and cloud processes.
Damming
The case of damming refers to blocked winds on the windward side of a mountain for uniform onshore flow or modification of a frontal feature by coastal orography. This phenomenon is less well documented for coastal regions than for other mountain regions. The balance of the wind and pressure (mass) fields within the storm is disrupted at the coast. As a result, the path of the storm can change abruptly, and, in certain instances, barrier jets and enhanced surface winds can develop in the coastal zone. Mass and Ferber (1990) show the development of ridging along the coast of western Washington state with the approach of a cold frontal system (Figure 4.2). When this orographically induced pressure field is added to the synoptic-scale pressure field, it produces large along-shore pressure gradients, which the momentum field responds to by producing an along-shore wind jet that is stronger than the winds in the weather system farther off-shore. Similar super-geostrophic winds have been observed at coastal stations along Alaska (Businger and Walter, 1988; Reynolds, 1983). What is not known for these cases is how the storm system itself is modified by the presence of a coastline and orography. This interaction of storms and orography to produce coastal jets is a major area for research.
A related phenomenon along the east coast of the United States is Appalachian cold air damming (Bell and Bosart, 1988; Xu, 1990). These episodes arise when there is high pressure over New England and onshore flow toward the Appalachians with an estimated Froude number of 0.3 to 0.4. A semigeostrophic system is set up on the eastern slopes with a low-level wind maximum parallel to the ridge. This wind maximum is fed by a pool of cold air from the north, which creates a cold dome along the eastern slopes. In the Bell and Bosart (1988) study, over-water winds were not
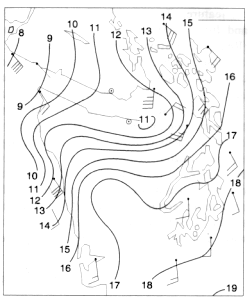
Figure 4.2 Sea-level pressure analysis and surface winds for Washington state, 2100 GMT, March 5, 1988. Note the coastal wind jet, which developed as an ageostrophic response to the increased along-shore pressure gradient (after Mass and Ferber, 1991).
directly considered; however, it is clear from their analyses that the cold air damming region extended to coastal weather stations.
Results from research on inland mountain systems may be relevant to damming, particularly the Alpine experiment (Chen and Smith, 1987; Davies and Pichler, 1990; Schuman, 1987, for example), which considers blocking and synoptic weather system/orographic interaction in the Alps. Another case is along the Sierra Nevada Mountains (Parish, 1982). One difficulty is that these cases may have more gentle slopes than those at coastlines and thus more of a quasi-geostrophic than semigeostrophic response. A summary of Rm and Fr for several cases is presented in Table 4.1. Poor verification of coastal weather forecasts is often attributed to the formation of mesoscale systems by the interaction of storms with coastal orography and to the feedback of these features on storm intensity within the coastal zone (±100 km), yet even basic documentation of this interaction and feedback is lacking (Bane et al., 1990).
Gap Winds
A special case of trapped phenomena is a sea-level channel between two mountainous coastlines where the width of the strait is on the order of the Rossby radius or less. This establishes a semigeostrophic system in the strait with winds accelerating down the strait in response to the synoptic-scale along-strait pressure gradient (Overland and Walter, 1981) (Figure 4.3). In a case
TABLE 4.1 Rossby (Rm) and Froude (Fr) Numbers, Coastal Mountain Half-Width lm, Inversion Thickness hi, and Reduced Gravity g' for Coastally Trapped Disturbances in Southern Africa, Southeastern Australia, California, and the Alps (noncoastal)
|
|
Southern Africa |
Southeastern Australia |
California |
Alps |
|
Rm |
0.1 |
0.8 |
1.3 |
2.0 |
|
Fr |
0.33 |
0.18 |
0.21 |
0.4 |
|
RmFr |
0.30 |
4.44 |
6.19 |
5 |
|
lm (km) |
600 |
75 |
50 |
50 |
|
hm (m) |
450 |
800 |
700 |
2500 |
|
g' (m/s2) |
0.11 |
0.60 |
0.41 |
N = 0.01a |
|
aN is the Brunt-Vaiasala frequency. SOURCE: After Reason and Steyn (1990) and Pierrehumbert and Wyman (1985). |
||||
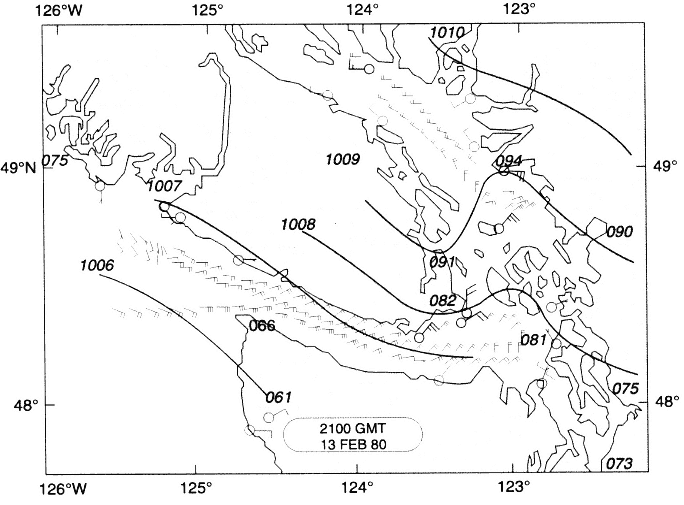
Figure 4.3 Sea-level pressure analysis for a gap wind event in the Strait of Juan de Fuca. Flow accelerates along the strait, and there is an abrupt transition in wind speed and direction beyond the exit of the strait. Small wind arrows are from aircraftderived estimates; large wind arrows are coastal stations (after Overland and Walter, 1981).
study of an event in Shelikof Strait (Lackmann and Overland, 1989), it was entrainment of slower-velocity air from above the strait that provided the principal retarding effect opposing the along-strait pressure gradient. A feature of both these studies is a geostrophic adjustment process that occurs seaward of the exit to both straits, with front-like characteristics, rather than a smooth transition to the flow along the open coast.
MODERATE FROUDE NUMBER FLOW
For inland sounds and offshore flow, there can be a mesoscale response in the lee of coastal mountains (Dempsey and Rotunno, 1988). In general, this response is not symmetric with the windward response. Reed (1980), Smith (1981), Mass and Ferber (1990), Ferber and Mass (1990), and Walter and Overland (1982) discuss the response of flow in the lee of the Olympic Mountains in Washington (see Figure 4.2). Only a couple of times a winter will the incident flow (Froude number) be great enough to create an orographically induced mesoscale low-pressure center of significant amplitude in the lee of the mountains. During such an event, winds in Puget Sound will accelerate ageostrophically toward mesoscale low pressure, giving localized marine winds of 20 to 40 m/sec.
The Catalina eddy feature occurs south of where the California coastline changes from a north-south to an east-west orientation (Figure 4.4). A consensus (Bosart, 1983; Mass, 1989) is that under northerly flow the Santa Ynez Mountains north of Santa Barbara favor a lee eddy feature. Similar to the Puget Sound case, the induced mesoscale low creates an along-shore pressure gradient that can initiate northward propagation of trapped phenomena from the south (Dorman, 1987) and modify the position and magnitude of the lee eddy. However, a lee eddy is not a prerequisite, according to Mass (1989), for the formation of a Catalina eddy. An alternate explanation (Clark and Dembek, 1991) is that the eddies form just south of Santa Barbara and move southward. Sea breeze circulation often masks the structure of the Catalina eddy during the daytime.
Upwind and lee-side effects also influence coastal regions of islands and peninsulas. Nickerson and Dias (1981) and Smolarkiewicz et al. (1988) investigated the downwind regime of the Hawaiian Islands for very small Froude numbers (0.1 to 0.5). A pair of vertically oriented vortices form on the lee side of the island of Hawaii. These vortices form as a result of the tilting of horizontally oriented vorticity, produced baroclinically as isentropes deform in response to flow around the obstacle, rather than as a consequence of viscous boundary layer separation (Smolarkiewicz and Rotunno, 1989). Gaps in mountain chains can produce strong jets when there is a major cold reservoir on one side of the mountains (Macklin, 1988). Macklin et al. (1990) discuss one such jet that forms across the Alaskan
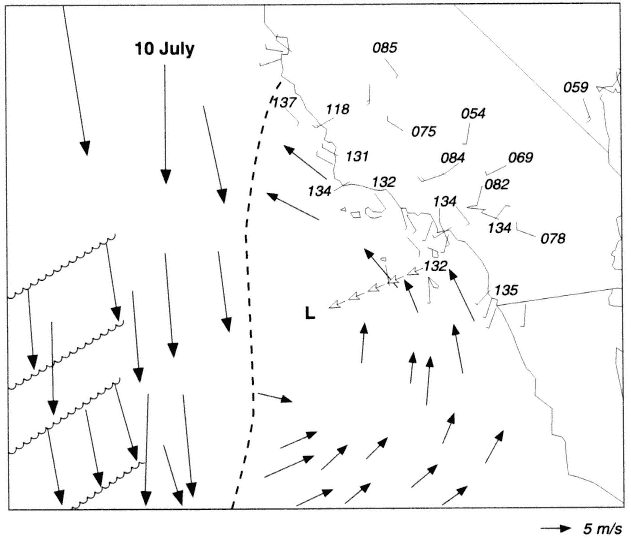
Figure 4.4 Cloud track wind estimates based on GOES visible imagery for a Catalina eddy case, July 10, 1987. L marks the position of the circulation center, with arrows showing the migration of the center from its formation location near Santa Barbara (after Clark and Dembek, 1991).
peninsula and continues across lower Cook Inlet with winds >>20 m/sec. Bond and Macklin (1992) noted that, when the Froude number was greater than 1 for northerly winds incident on the Alaskan peninsula, there were mountain waves above the boundary layer and strong winds up to 34 m/sec along the south side of the peninsula. In a low Froude number case, strong winds were confined to regions downwind of low-level passes. Such lee-eddy features should be amenable to numerical modeling given sufficient vertical and horizontal resolution; models can include simplified cloud processes.
KATABATIC AND OTHER LOCAL WINDS
So far we have discussed phenomena with spatial scales of the order of the Rossby radius (50 to 150 km). However, there are smaller inlets and mountain passes, often perpendicular to the coastline, that can produce locally strong marine winds. If there is a cold reservoir of air inland, this air
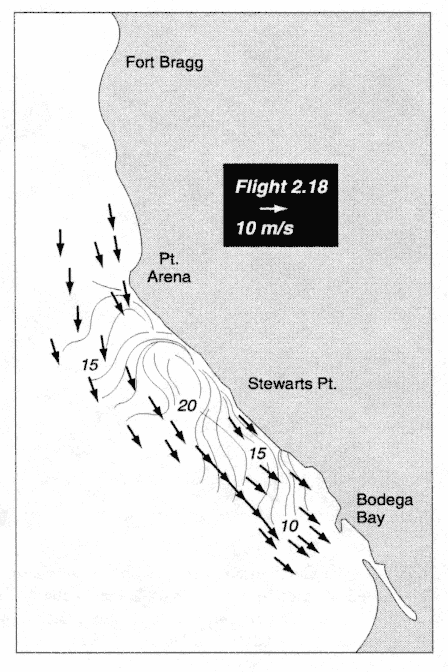
Figure 4.5 Isotachs observed July 14, 1982, off central California from aircraft. The increase in winds from ~15 m/sec to 20 m/sec is attributed to a decrease in inversion height from 300 to 50 m, which counters the deceleration associated with the change in coastline orientation. The decrease from ~20 m/sec to 10 m/sec is associated with a hydraulic jump with the inversion base quickly increasing to 200 m (after Winant et al., 1988).
can accelerate down the mountain slope into a fjord and continue over the ocean. Changes in the orientation of the coastline can produce eddies, such as those near Cape Mendocino (Dorman, 1985; Reason and Steyn, 1990) or local changes in inversion height (Figure 4.5) with a local wind maximum on the scale of 30 km, such as those south of Point Arena (Samuelsen, 1992; Winant et al., 1988).
The katabatic wind is a drainage wind current caused by the gravitational flow of cold air off high ground, whose direction is controlled almost entirely by orographical features. The strongest and most frequent katabatic winds occur in high latitudes, most notably Antarctica (see Bromwich, 1989; Ohata et al., 1985; Parish and Bromwich, 1989). Other high-and midlatitude katabatic winds have been reported in Greenland by Gryning and Lyck (1983); in Brugge, Belgium, by Dawe (1982); and in coastal Alaska by Reynolds (1983) and Macklin et al. (1988). Katabatic winds in low latitudes (Veracruz, Mexico) have been described by Fitzjarrald (1986).
Ackerman (1982) has summarized observations in Poona, India, in Mauna Loa, Hawaii, and in Cato, South Africa. Lopez and Howell (1967) have described katabatic winds in the equatorial Andes.
Coastal katabatic winds prevent fog formation, or when fog is present, they may clear it. Although katabatic winds typically dissipate within a few kilometers downstream of the forcing, Bromwich and Kurtz (1984) found that katabatic winds inland of Terra Nova Bay, Antarctica, are present some 25 km beyond the end of the main slope; this is also seen for southeastern Alaska in Figure 4.6. The physical processes important in the development of katabatic winds are radiative cooling, development of a sloped pressure gradient force, adiabatic warming of downward moving air, friction, and entrainment (Gutman, 1983; Manins and Sawford, 1979; Nappo and Rao, 1987; Parish, 1984; Parish and Waight, 1987).
The forcing of katabatic winds can be traced to the strong cooling of air adjacent to the surface. The net long-wave radiation is initially the dominant forcing term, acting to cool the surface of the slope. According to
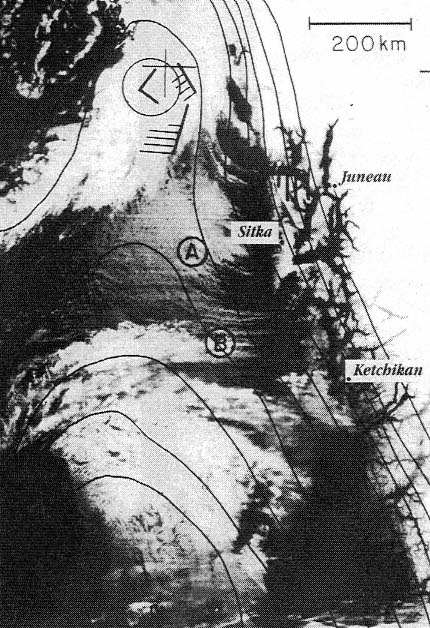
Figure 4.6 Satellite photograph of the Gulf of Alaska in winter. As a low-pressure system approaches the coast, strong, cold ageostrophic winds exit the fjords and continue across the continental shelf, as indicated by the low-level cloud streets. These winds merge with the synoptic flow either gradually, as in this case, or with a frontal feature. Such coastal wind systems influence coastal-ocean circulation through increased wind stress and wind stress curl (from Gray and Overland, 1986).
Lettau and Schwerdtfeger (1967), one serious limitation on the continued occurrence of katabatic winds in a region is the supply of cold air upslope. Persistent katabatic flow requires replenishment of cold air either by convergence of drainage currents upwind or by continued localized intense cooling. As katabatic winds develop, the mixing processes become enhanced, and the turbulent heat flux to the surface increases. This efficient removal of heat from the lowest levels of the atmosphere produces the sloped-inversion pressure gradient force and leads to further enhancement of katabatic winds.
The depth of the katabatic layer is on the order of 100 m, although depths as great as 1000 m may be found on the Antarctic coast. The coastal katabatic winds effectively mix a deeper atmospheric column, thereby spreading the diabatic cooling throughout the boundary layer. As a result of this mixing, air in the free atmosphere must be entrained into the katabatic layer. This entrainment process acts as a retarding mechanism on the katabatic flow by warming the katabatic layer and by acting as a drag on it.
Although a reasonable understanding of katabatic winds has been obtained, gaps in our understanding still remain. Two areas of uncertainty are the mechanisms of radiative cooling and turbulence in sloping flow, including entrainment. According to Manins and Sawford (1979), direct computation shows that the divergence of radiation responsible for cooling the air is much smaller than the surface radiation flux used in models of katabatic winds. This raises the issues of how deep the cooling layer is and whether water hazes or fogs play a role in radiative cooling. During rapid nocturnal cooling, condensation may occur, affecting radiative transfer. Particularly in polar regions, formation of low-level ice crystals in the cooling air appears to be the rule rather than the exception (see, e.g., Bromwich, 1988; Curry, 1983; Curry et al., 1990; Overland and Guest, 1991), and their presence has the potential to substantially perturb the radiation balance. Also, the radiative effect of low-level clouds within the katabatic layer has not been investigated; cloud-top radiative cooling from low-level clouds may enhance inversion-slope pressure gradients in the katabatic layer even though actual surface cooling may be reduced, while higher clouds will simply retard surface cooling and not contribute to the pressure gradient. Improved observations are required to elucidate the fine-scale structure of the katabatic flow.
To date, the modeling of katabatic winds has focused on understanding the physical mechanisms rather than actually predicting their occurrence and strength. Prediction of katabatic winds will require that consideration be given to the entire katabatic setting, including the dynamic and thermodynamic processes occurring upslope.
SUMMARY AND CONCLUSIONS
The major feature of the interaction of synoptic-scale flow with coastal topography is that mesoscale features are formed that have the scale of the half-width of broad coastal mountains or, more typically, for steep mountains have the scale of the Rossby radius based on mountain height. These scales of 50 to 150 km are smaller than observing networks, especially over water. Their dynamics are qualitatively known, and local orographic forcing is known by specifying the fine-scale topography. In principle, it should be possible to forecast coastal winds by using a regional numerical model driven by the larger synoptic-scale flow and the coastal orography. Inadequately studied areas limit current understanding of orographically dominated coastal meteorology. To address these limitations the panel recommends the following:
-
Case studies that include the low-level wind regime should be undertaken to explain the modification of the structure and path of storm systems by coastal orography.
-
A climatology should be developed of the synoptic-scale regimes that initiate or terminate coastal-trapped phenomena and the type of feature, wave-like or front-like, that evolves from each regime.
-
Research to improve the resolution of numerical weather forecasting models must be conducted to focus on scales distinguishing important coastal processes.
-
Studies should be conducted to determine the predictability of smallscale hydrodynamic features, such as hydraulic jumps, eddies, wind maxima, and katabatic flows.
-
Long-term measurement programs should be supported to determine the low-frequency climatology of winds in the coastal zone. Ideally, observing system operations should be coordinated with mesoscale atmospheric models running on a continuous basis.














