2
Boundary Layer Processes
The atmospheric boundary layer (ABL) is the part of the lower troposphere that interacts directly with the earth's surface through turbulent transport processes. A coast separates two drastically different surfaces, and a coastal region has an inhomogeneous boundary layer. ABL processes are important in determining the evolution of atmospheric structure. The boundary layer is also a buffer zone that interacts both with the ''free'' tropospheric flow at its upper interface (through entrainment processes) and with the surface (through surface exchange processes).
Past studies of the ABL have emphasized certain idealized, near-equilibrium, and horizontally homogeneous boundary layer regimes (Wyngaard, 1988). For example, Stull's (1988) comprehensive reference on boundary layer meteorology devotes only about 5 percent of its discussion to geographic effects. In fact, many common ABL conditions are still poorly understood even for homogeneous surfaces. The horizontally inhomogeneous and rapid temporal forcing conditions typical of coastal regions dictate consideration of problems that have rarely been investigated. Furthermore, even those aspects of the physical processes that are generally regarded as being well understood (e.g., bulk parameterization of surface fluxes) must be reevaluated before applying them to coastal environments.
In this chapter, current understanding of boundary layer processes is examined, and some important deficiencies are identified. Following introductory material on boundary layers, generic problems in boundary layer processes are examined. Then, special coastal problems are considered that involve surface fluxes, internal boundary layer growth, baroclinicity, and a
variety of phenomena that are either inherently inhomogeneous or are associated with inhomogeneous forcing.
CURRENT UNDERSTANDING AND CHALLENGES
The ABL has been investigated extensively. Certain aspects are considered to be well understood. This understanding has developed from a combination of sources: laboratory models (e.g., Deardorff and Willis, 1982; Willis and Deardorff, 1974); three-dimensional primitive equation large-eddy simulations (e.g., Deardorff, 1974, 1980; Moeng, 1984a, b); and atmospheric measurements with aircraft and tethered balloons (e.g., Brost et al., 1982; Kaimal et al., 1976; Lenschow, 1973; Lenschow et al., 1980; Nicholls, 1984).
A variety of ABL models are now available. Because a model represents the reduction of a problem to its important components, it not only is a useful tool but also an expression of our understanding of the physics. Linear regression and crude parameterizations often imply little or no understanding. Today, a hierarchy of complexity is available in atmospheric models. Similarity models are the simplest but typically are applicable only to idealized situations. One index of understanding is in simplified conceptual models and useful scaling laws. By this measure, the cloud-free convective ABL is clearly the best-understood regime.
Numerical solutions to systems of physical equations form the basis of the more sophisticated models commonly used in meteorology. Two approaches are used, depending on whether solutions are sought for the ensemble average or for the volume average atmospheric budget and state equations. Ensemble average models are often referred to as higher-order closure models. Grid-volume average models are usually referred to as large eddy simulation (LES) models. These approaches are fundamentally different; an LES model produces an explicit simulation of a single realization of a three-dimensional, time-dependent atmospheric structure. An ensemble average model predicts or describes relationships between the moments of the atmospheric variables (the first moments are averages of the variables and the second moments are variances and fluxes). LES models are currently used strictly for research (such as developing parameterizations); ensemble average models have a variety of practical as well as research applications.
The Generic Atmospheric Boundary Layer
Scaling theories have their origins in dimensional analysis; important variables of the problem are selected, and other properties are calculated from dimensionally consistent combinations of those variables. Modern
ABL similarity theories are now based on arguments about the relative variability and magnitude of the terms in the mean and turbulent budget equations. In the ABL the similarity regimes are broken down by the vertical scale, assuming that the horizontal fields are statistically homogeneous. Historically, this process has proceeded from the ground up. Figure 2.1 depicts schematically the idealized mean structure of the ABL under convective, well-mixed, cloud-free, horizontally homogeneous conditions in a synoptic regime that has sufficient subsidence to ensure the presence of a capping inversion. Compared to the ABL, the overlying free troposphere can be considered essentially nonturbulent.
Surface layer similarity theory is based on scaling parameters obtained from the surface fluxes (Wyngaard, 1973). The theory is considered valid in the region near the surface where various terms (particularly the gradients) in the turbulent kinetic energy and scalar variance budget equations are considerably more dependent on height than are the fluxes. Thus, the assumptions on which the theory is based are generally valid in the lowest 10 percent of the ABL. For the convective ABL, we also have mixed layer similarity (Moeng and Wyngaard, 1989) and inversion region similarity (Wyngaard and LeMone, 1980). For the stable ABL, no mixed layer exists. Instead, there is a gradual transition from the surface layer to the inversion layer. A local similarity theory (Nieuwstadt, 1984) has been proposed for a
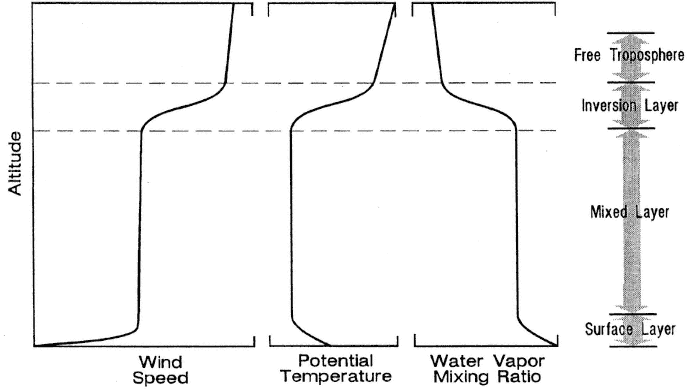
Figure 2.1 Idealized profiles of wind speed, potential temperature, and water vapor mixing ratio for the convectively mixed, cloud-free atmospheric boundary layer (after Fairall et al., 1982).
stable ABL in steady-state or slowly evolving conditions. This theory has, however, exhibited shortcomings in general application.
In terms of simple models, the present state of understanding of the generic ABL can be described crudely as follows. It is natural to classify conditions of the ABL by dynamical regimes of increasing complexity: cloud-free, convective; cloud-free and shear-driven; baroclinic; stable; stratocumulus; tradewind cumulus; and broken clouds. Coastal meteorology encompasses all seven of these regimes. Cloud-modified and stable boundary layers remain essentially unsolved problems. A general similarity theory that can handle all possible cloud regimes does not exist. Higher-order closure models have yet to demonstrate detailed agreement for even the simplest cases (Holt and Raman, 1988), and recent LES studies (Moeng and Wyngaard, 1989) have called into question the transport and dissipation closures used in most second-order models. Transport and dispersion properties of the ABL are strongly dependent on the characteristics of coherent structures and the higher-order moments (Weil, 1990). These properties have only recently been studied for the homogeneous convective ABL (Moeng and Rotunno, 1990; Moeng and Wyngaard, 1989). Although some understanding of the idealized ABL (Figure 1.1) exists, actual coastal ABL structure is often significantly different. For example, Figure 2.2 shows a stable
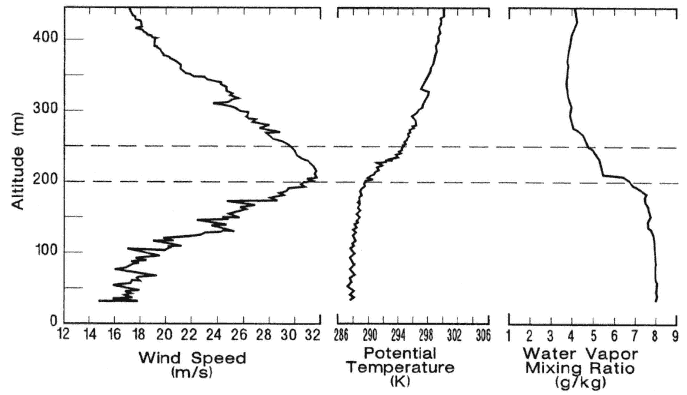
Figure 2.2
Vertical profiles of wind speed, potential temperature, and water vapor mixing ratio along the north coast of California (after Winant et al., 1988). Note the strong low-level inversion in potential temperature at approximately 250 m altitude, coincident with the maximum in wind speed. Contrast these profiles with the simple mixed layer structure depicted in Figure 2.1.
ABL with a baroclinically induced jet but a well-mixed humidity. Thus, there is a need both to improve our understanding of the idealized case and to study cases that exhibit stable boundary layers as well as those with strong baroclinicity.
Surface Interactions
Surface fluxes can be measured in homogeneous and moderately inhomogeneous terrain using the eddy correlation technique (Businger, 1986; McMillen, 1988; Wyngaard, 1988), which is considered to be the measurement standard. In numerical models (or when the direct method is not available or applicable), bulk transfer coefficients and surface layer similarity parameterizations are used to relate the fluxes to the near-surface mean meteorological variables and the surface properties. This approach is often quite successful over the open ocean but cannot be straightforwardly applied over land; terrain, soil, and plant canopy interactions greatly complicate the physics (Priestly and Taylor, 1972; Sellers et al., 1986). This is the situation for local coastal climatology where the intensity of the land-sea breeze circulation is relatively much stronger with dry, lightly vegetated coastal lands (Segal et al., 1988).
Inhomogeneous surfaces cause special problems because it is difficult to relate the point measurements used to characterize the surface to the larger-scale mean fluxes (Schuepp et al., 1990). Also, the bulk expressions are intended to relate the average flux to the average bulk variables. Since ABL-scale eddy turnover time is about 15 minutes, it takes about an hour to average ABL variability to obtain a representative sample. In that hour a parcel of air in the ABL can easily travel horizontally about 20 km. This calls into question whether one can rely on surface similarity expressions that are obtained from 1-hour averages of field measurements over homogeneous terrain in models with 1-minute time steps applied over 10 × 10 km horizontal grids. For example, Beljaars and Holtslag (1991) found that characterization of momentum transfer on horizontal scales of a few kilometers required an "effective" roughness length considerably greater than the local value. The situation for moisture and sensible heat transfer is even more difficult. To quote Beljaars and Holtslag (1991), "More complicated land surface schemes are certainly available to describe the physics in more detail. . . . [H]owever, it is not clear whether all the parameters that specify the land surface in such models can easily be determined." There is also a distinction between a patchy surface that is statistically homogeneous and a "nonstationary'' situation where the average properties vary with position and time. The applicability of surface layer similarity and the implications for the bulk transfer coefficients for these conditions are virtually unexplored.
On the ocean side of a coastal region, special problems arise in interfacial transfer. For the open ocean, a reasonable set of bulk transfer coefficients (e.g., Smith, 1988) is available that appears adequate for many applications. These coefficients represent air-sea transfer processes for average surface wave conditions as a function of mean wind speed. Wind speed, wave spectrum, and bulk transfer coefficients have been related theoretically (Geernaert et al., 1986; Huang et al., 1986), but field measurements in coastal regions (e.g., Geernaert et al., 1987; Smith et al., 1990a, b) have demonstrated greatly increased drag coefficients in shallow water (Figure 2.3).
It is clear that fetch and shallow water effects upset the normal equilibrium wind-wave relationships. Fetch is primarily an issue for offshore wind conditions, but distortion of the open ocean directional wave spectrum in coastal shallow regions is important regardless of wind regime; it becomes increasingly important as wind speeds increase. Sounds and estuaries add complexities, often with irregular coastlines, river deltas, and islands. Effects on heat and gas fluxes also are unknown. (See Chapter 6 for further discussion and Geernaert (1990) for a comprehensive review of these con-
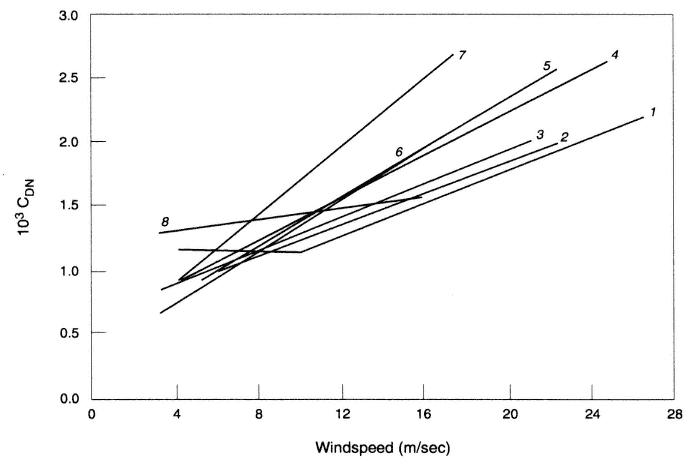
Figure 2.3 Distribution of neutral drag coefficient, CDN, with wind speed: (1) over deep open ocean, (2) over deep coastal ocean, (3) over deep water, (4) North Sea depth of 30 m, (5) North Sea depth of 16 m, (6) Lough Neagh depth of 15 m, (7) Lake Ontario depth of 10 m, (8) Lake Geneva depth of 3 m (from Geernaert, 1990).
cepts.) The evolving wave field is influenced by the wind stress, but the stress vector produced by a given wind field is dependent on the directional wave field. Thus, predictions of wind and wave fields on the continental shelves are strongly coupled. Significant and unexplained differences between the mean wind direction and the mean stress direction have been observed in coastal regions (Geernaert, 1990). Substantial hydrostatic stability modulation of stress and surface wind fields has also been observed in association with sea surface temperature variations typical of coastal regions. A comprehensive theoretical and experimental study of wind-wave-stress-scalar flux relationships on the continental shelves should be an important component of a coastal meteorology research program.
Internal Boundary Layers
Air that is modified by flow over an abrupt change in surface properties is said to be confined to an internal boundary layer (IBL). Here we are concerned with the effects of a boundary between two different but individually homogeneous surfaces, as opposed to the boundary layer effects of more general forms of inhomogeneity discussed below. When the surface heat flux changes at such a boundary, a thermal IBL (Garratt, 1987; Lyons, 1975) is formed on the downwind side. Growth in the depth of the IBL is usually parameterized in terms of the downwind distance from the interface. Typically, the form is that of a power law, but many different formulas are available. Convective conditions promote rapid growth; thus, the IBL depth quickly reaches the existing capping inversion. In this case IBL considerations are important only close to the transition. Stable, convection-suppressing conditions downwind of the transition result in slow IBL growth, and the tendency is to form a permanent surface-based inversion (Mulhearn, 1981). The situation is similar to the afternoon-evening transition for the overland convective ABL (Zeman and Lumley, 1979). In this case any turbulence above the new surface-based inversion can be cut off from the surface source of energy and, in the absence of other sources, begin to decay. In an LES study of the decay of convective turbulence, Nieuwstadt and Brost (1986) found that the ABL depth, divided by the convective mixing velocity, formed a characteristic decay time scale, but the behavior of various turbulent variables was not easily parameterized.
Currently, the standard approach to describing near-surface meteorological profiles is to use surface similarity expressions with one set of scaling parameters for the IBL and a second set for the old ABL above and the constraint that the profiles must match continuously at the IBL interface. This approach assumes that the dynamics above the IBL are unaffected by its formation. This approximation can be valid only fairly close to the transition region. More sophisticated model studies (e.g., Claussen,
1987) have shown that substantial mean vertical motions are also induced by the transition, even outside the IBL. Because the IBL exists for such a short distance in convective conditions, the formation and growth of the stable IBL are more critical. Here a key issue is the physics of the entrainment processes at the top of the IBL and the associated induced vertical velocity fields.
The Inhomogeneous Atmospheric Boundary Layer
Understanding ABL development and evolution in regions of abrupt or gradual changes of surface properties (coastal zones, ice-to-water surface transitions, ocean surface temperature fronts, etc.) involves consideration of horizontal advection, baroclinic forcing, nonequilibrium turbulence effects (for instance, the time derivative of the turbulent kinetic energy is not negligible), the special influence of local clouds, and fully three-dimensional dynamical processes.
A simple way to view this three-dimensional problem is to break it down into a conceptual model: a surface grid with each surface point occupied by a mean and turbulence profile, governed by one-dimensional turbulent mixing processes. Adjacent grid points are coupled in the normal manner through horizontal advection and horizontal pressure gradients. This approach has enjoyed some success with mixed layer models (Overland et al., 1983; Reynolds, 1984; Stage and Businger, 1980; Steyn and Oke, 1982) and higher-order closure models (Bennet and Hunkins, 1986; Tjernstrom, 1990; Wai and Stage, 1990). However, decoupling of the turbulence dynamics from the horizontal structure is a simplifying assumption that has never been tested. Clearly, similarity approaches (e.g., mixed layer models) that are tuned to quasi-equilibrium conditions are of limited applicability in inhomogeneous conditions. However, these limits have not been established. It may be that the techniques used in highly inhomogeneous urban boundary layer models (e.g., Uno et al., 1989) are adaptable to coastal problems.
Both land-sea breeze cycles and cold air outbreaks have been examined with models, but a comprehensive and extensive program to compare model results with measurements has not been attempted. Baroclinic effects associated with a sloping inversion (Brost et al., 1982; Overland et al., 1983) are known to be substantial, especially in west coast regimes, but they too are virtually unstudied.
The relative lack of experimental studies of boundary layer physics in coastal zones is not the only reason to question present-day boundary layer models. A recent LES study (Moeng and Wyngaard, 1989) of second-order closure parameterizations suggests that their rather modest successes in homogeneous conditions (e.g., Holt and Raman, 1988) are not expected to
carry over to the coastal regime because homogeneous conditions do not severely test the parameterizations. To quote Moeng and Wyngaard (1989, italics added for emphasis), "Most observational and model studies show that in the absence of abrupt changes in boundary conditions , the heat flux profile is indeed essentially linear in the mixed layer. Thus, given the proper boundary conditions, second-order models will tend to have the correct vertical profile of buoyant production rates within the mixed layer, regardless of the fidelity of their closure parameterizations." Moeng and Wyngaard also point out that under homogeneous conditions the mean value of the rate of dissipation of turbulent kinetic energy in the mixed layer is also nearly independent of closure approximations.
The importance of local coherent wind circulations generated by heterogeneous surfaces also must be assessed. Existing work (e.g., André et al., 1990; Hadfield et al., 1991, 1992; Pielke et al., 1991; Walko et al., 1992) suggests that, if the spatial scale of the inhomogeneity is sufficiently large, a well-defined atmospheric circulation can develop. Development of such coherent circulations is also dependent on the large-scale wind speed, with stronger winds inhibiting their development. Claussen (1991) has introduced the concept of a blending height that could be applied when coherent wind circulations are likely to occur. This height is correlated with the horizontal scale of variability and the aerodynamic roughness of the land-scape. When this height nears the height of the boundary layer, adjacent boundary layers are not significantly homogenized, and the resultant horizontal gradient in boundary layer heating can produce a well-defined local flow. When this height is much less than the planetary boundary layer height, however, the horizontal mixing of the boundary layer precludes coherent circulations. We need to understand the conditions under which horizontal inhomogeneities in surface heating and cooling generate coherent wind circulations.
Boundary Layer Clouds
Clouds within the ABL greatly complicate the physical processes because they represent a form of vertical and horizontal inhomogeneities, significantly affect the dynamics, and couple strongly with atmospheric radiation. For example, radiative heating effects of marine stratocumulus clouds can cause stress divergence to vary within the lower part of the ABL. During the day, if the cloud layer warms faster than the subcloud layer, the cloud may become decoupled, with a corresponding increase in wind stress and heat flux divergence between the top of the subcloud layer and the surface (e.g., Hignett, 1991; Rogers and Koracin, 1992).
Stratiform clouds are persistent features of cool upwelling coastal regions, such as the west coast of the United States, and cool climate regions
such as the Arctic. Recent studies of the global radiation budget have highlighted the possible role of stratiform clouds as an ameliorating influence on the warming of the atmosphere by high-altitude clouds (Ramanathan et al., 1989). Although a number of experiments provide considerable insight into the processes that control the development and dissipation of stratiform clouds (Randall et al., 1984), the effect of variability of the coastal ocean, topography, and the marine ABL on these clouds has received much less attention. The effect of coastally trapped waves on the depth of the marine layer may also play an important role in the persistence of these clouds; the effect of the sea breeze on subsidence and the mesoscale pressure gradients may also be an important mesoscale process that controls the life cycle and fractional coverage of coastal stratus. In turn, the stratus clouds can substantially modulate the sea breeze cycle by moving ashore and reducing inland solar-induced convection. Skupniewicz et al. (1991) have presented the only measurement and model examination of the diurnal evolution of the coastal stratocumulus cloud edge and its dramatic effect on sea breeze front dynamics.
SUMMARY AND CONCLUSIONS
Understanding of coastal boundary layer processes will be improved by general advances in boundary layer science. However, some problems specific to the coastal regime require immediate study. Theoretical developments, modeling studies, and field measurement programs are required to explain key unknown properties and processes involving the ABL. The panel recommends the following:
-
Studies should be conducted to determine the properties for inhomogeneous and nonequilibrium conditions, including suitable surface flux and mixed layer similarity parameterizations, and the general relationships of the ensemble average first-and higher-order turbulence variables.
-
Further research on the fundamental relationships among the ocean wave spectrum, surface fluxes, and bulk ABL properties should be conducted.
-
Studies should be carried out to determine the physical process of the growth of the top of the stable IBL, including entrainment and induced mean vertical velocity effects, and the decay processes of turbulence above a newly formed IBL.
-
Investigations to clarify coastal marine stratocumulus and overland fair weather cumulus cloud regimes and their influence on land-sea breeze cycles should be conducted.
-
Studies should be undertaken to determine the spatial scale at which horizontal inhomogeneities in surface heating and cooling become large enough to generate coherent wind circulations.










