3
NEMS ARCHITECTURE
OVERVIEW
Chapter 2 described expected uses and desirable inputs and outputs of a National Energy Modeling System (NEMS). In this chapter a general architecture is proposed for the NEMS.
The proposed NEMS should be designed for simulations and analysis relating to the mid-term time horizon, up to about 25 years in the future. While such a modeling system could be used in principle for both shorter and longer term modeling, these kinds of modeling typically have special analytical requirements. For this reason, the committee recommends that EIA not attempt to use a single model for the three kinds of analysis (that is, for short-term analysis, that of up to about 2 years), medium-term analysis, up to roughly 25 years), and long-term analysis, beyond 25 years). In particular, the Department of Energy (DOE) should not select the mid-term model to be used based on the desire to carry out long-term analysis within the same framework.
For short-term modeling, it is usually important to consider supply and demand fluctuations over the course of an annual cycle. Effects of random events--severe weather, strikes, international hostilities--may be of particular interest. Considering adjustments to projected supply and demand disequilibria (based on forecasted starting point derived from the mid-term model) may also be important, for example, when modeling our vulnerability to energy supply disruptions. This report will not consider in greater depth modeling for the short-term time horizons.
For long-term modeling, modeling structures should be much simpler, because in projecting the longer term there are many more unknowns. Long-term modeling systems stress uncertainty about possible outcomes and allow the uncertainty itself to be easily examined. Issues of interest for long-term energy modeling include fuel substitution, physical limitations of natural resources, technological evolution, lifestyle changes, and effects of population growth. Basic concepts for long-term analysis were discussed briefly in Chapter 2, and these also will not be pursued further here.
The proposed modeling system for the medium term would consist of modules linked together in a larger analytical system. It should be possible to run these models separately, all together, or in combinations, depending on the analytical needs.
This modeling system should be designed primarily to simulate or project energy futures based on assumptions about policies and other driving variables. NEMS should also be useful for some kinds of planning and optimization. In optimization, possible future patterns are compared to objectives encoded in the model. For example, patterns of energy use the modeler deems optimal can be compared with observations about actual rates of energy use and production under various conditions. In what follows, it is assumed that NEMS models will be used mostly for simulations rather than optimizations.
NEMS should be structured to project supply and demand equilibria in U.S. energy markets. Prices, which guide the energy system toward a supply-and-demand equilibrium, should be explicitly accommodated in both supply and demand modules (for discussion of general equilibrium analysis, see Ballard and Goulder, 1985; Roger and Goulder, 1984). The modeling system should be able to analyze the impacts of policy options and other variables on the economy, the environment, and the security of energy supplies. Existing regulatory impacts should be represented in the individual modules and the system should allow analysis of contemplated regulatory regimes. In addition, supply and demand modules should allow the examination of non-policy factors (e.g., demographic trends) that, in addition to prices, shape supply and demand.
Individual modules would include energy supply and demand models and an interindustry economic growth model brought together in one “integrating system,” and auxiliary models that would generally use outputs from the integrating system once its solution were found. Figure 3-1 provides a simple illustration of the proposed NEMS architecture.
The interindustry growth model would take prices of energy and supply and demand-side investments as inputs and project the economic activities resulting from those inputs. Each energy demand model in the integrating system would take as inputs the prices of energy (P) and levels of economic activity (A), and would produce as outputs the quantities of energy utilized (Q) and the demand-side investments associated with that energy use (I). The integrating system's supply and conversion modules would take as inputs the quantities of energy demanded in this system and provide as outputs the prices at which those quantities of energy would be made available. In addition, the supply and conversion models would provide the levels of investments associated with those energy quantities.
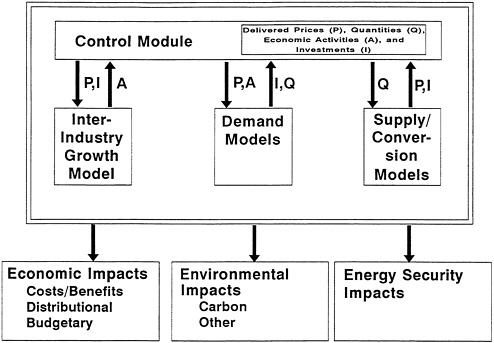
Figure 3-1 Simple representation of proposed NEMS architecture.
The models within the integrating system would interact with one another through common data files, which would provide information to models and accept it from them, as appropriate. The modules would run sequentially under the guidance of a control module that would seek convergence to an equilibrium. The control module would take as outputs from the other modules values for prices, energy quantities, and investments, and would store them in the common data files. These values would then be passed by the control module back to the individual modules for the next iteration. The control module would include criteria to determine when the system had come sufficiently close to equilibrium.
The integrating system would be run iteratively until a solution was found. For any iteration, the integrating system would begin with an initial set of prices and investments over the entire time horizon and would predict demand-side investments and energy quantities demanded over that horizon. These values for energy demand would then be passed to the supply and conversion models, which would in turn provide prices and investments as outputs, which would likely not be consistent with the assumed initial set. The control module would include an algorithm to successively adjust the trajectory of prices and investments to converge toward an equilibrium. Equilibrium would be obtained
when a fixed point was found, that is, a set of price and investment values such that input and output values were identical for each fuel, region, and time.
Once an equilibrium solution is found for the integrating system, then outputs from each of its modules could be used in the three auxiliary models, those examining the economic, environmental, and energy security impacts of the given equilibrium.
The rationale and for more detail about this proposed NEMS architecture are provided below.
MODULAR ARCHITECTURE
The proposed NEMS system is described as modular. Modularity in modeling, however, is a relative concept: all modeling systems can be viewed as modular in that equations can be removed and other equations substituted and the model can be run. The modular system intended here refers to a group of modules that, each taking the limited set of inputs from the control module, could be run separately from one another. As the committee envisions it, the defining characteristic of a modular system is the ability to run the modules within a system separately. These modules should have common data files, from which they take inputs to perform calculations and to which their outputs flow. The system should be able to run any individual module without any of the other modules being loaded into the computer. A modular system would allow users to replace modules with alternative versions conferring great flexibility to address highly varied analysis requirements.
To implement such a modular system, the EIA must clearly define what data will be passed among the various modules. All such data would be passed through common data files; none would go directly between the component modules, except between the control module and others. EIA must carefully define input and output variables so that they have the same precise definition in all of the modules. Once attention is paid to the interfaces between the modules and the common data files, the internal structure (and possibly even the software) of any module can be independent of any other.
Modularity is not a new concept to EIA modeling, as was noted in Chapter 2. Some modularity characterized even the earliest modeling systems of the EIA and Federal Energy Administration. For example, the Project Independence Evaluation System (PIES) and International Energy Evaluation System (IEES) permitted different demand models to be used to calibrate a constant elasticity demand representation and different oil supply curves to be used in the linear programming representation. The current EIA integrated model--the Intermediate Future Forecasting System (IFFS)--is a modular system.
The NEMS system that the committee proposes would be a logical extension of the IFFS. There would be no need to develop the NEMS from scratch. Initially it could rely strongly on existing models, adapting them to the new configuration.
The EIA now stresses modularity as an important goal. EIA papers assessing existing and desired modeling systems have emphasized the importance of the modular approach (EIA, 1990a). The committee strongly endorses this emphasis.
Advantages of Modular Systems
Modular architecture facilitates the decentralized development and maintenance of modeling system components, the modules (Hogan and Weyant, 1983; Cowing and MacFadden, 1984). Thus, once NEMS model inputs, outputs, and module interfaces are well defined, development of NEMS modules could proceed in a decentralized manner under EIA supervision.
The ability to substitute one component for another in a modular system allows, among other things, running any combination of modules without running the others (e.g., by using “null modules,” that do nothing and do not change the output values stored in the data files, in place of the full modules).
An important related advantage of modular systems is the ability to create and use reduced-form versions of the modules. Reduced-form versions approximate the more detailed modules in translating input variables (e.g., prices for demand or quantities for supply) to output variables (e.g., quantities and investments for demand and prices and investment for supply). Reduced-form versions can be easily substituted for the full modules. They would not be independent models, but simple mathematical structures estimated from the original modules to approximate these modules' full responses.
Such reduced-form versions would allow great flexibility in the use of the NEMS. When outputs from particular full modules of the system were not important, these components could be replaced by their reduced-form versions. If many such substitutions were made, the NEMS could be quickly run. Frequent fast runs would be particularly valuable when NEMS were being used for probabilistic analysis. In addition, when many reduced-form versions were used, users could routinely conduct in-depth analyses using the full module of interest without being burdened by the computational costs of running all the full modules. The committee believes that the NEMS could represent crucial relationships in the overall energy system using reduced-form modules, with little deviation in projections from those of the full modular system. Because these simplifications can introduce further error, work needs to be done to assure that the increased variability attributable to the use of reduced-form modules is held to acceptable levels.
Modular structure could allow the testing of uncertainty, including that associated with the structure of alternative modules. Simply removing one model and replacing it with another of a different structure would allow testing the uncertainty associated with alternative beliefs about various components of the energy system. Similarly, modularity would allow NEMS to integrate results from external models whenever this were desirable.
The committee below recommends that NEMS be developed to run on personal computers if the resulting configuration would not significantly sacrifice the NEMS models'
content. Modular architecture could make this goal easier to achieve inasmuch as only some parts of the entire system would need to be in computer memory at a given time.
Disadvantages of Modular Systems.
Modular architecture can create coding difficulties not seen in single integrated models that run with one kind of software. The modular structure proposed for the NEMS would rely instead on a control module to guide the operation of the other modules. Off-the-shelf software may not be available and EIA will probably need to develop such a control module.
Decentralized development of the NEMS could well lead to few (if any) people understanding the entire model. Thus, few may be capable of interpreting and assessing it as a whole. This is a legitimate concern. The committee believes that EIA should explicitly structure its efforts to avoid this difficulty. In particular, one or more EIA analysts should be charged with overall knowledge of all modules, even those not developed in EIA.
Time and effort should also be devoted to ensure that the model as a whole--or larger aspects of it--are understood by those with an appropriate range of strong expertise in modeling and energy-related matters, but not necessarily strong modeling backgrounds. It should also be noted that a modular design places a heavy burden on the architects of the system to think through and specify the requirements of individual modules, and to interact with module-builders in a continuing process of validation and modification.
Decentralized development could lead to significant quality control problems in both model development and model maintenance. EIA must take responsibility for maintaining high quality, even for modules developed outside of EIA and for making sure that EIA personnel fully understand them.
INTEGRATING MODEL OPERATION
The integrating system would take a set of inputs--for example, world oil price, U.S. population growth, and policy and other assumptions--and run the modules until the system converged to an equilibrium. Results from the integrating framework would then be used as inputs to run satellite modules.
The solution of the integrating model would typically represent market clearing, that is, supply being equal to demand, for every energy commodity, in every region, at each time. To find a solution, the modules would take as inputs price, quantity, and investment, or some other limited number of vectors from common data files. Once these modules were run, outputs--values for price, quantity, and investment, or other vectors--would be passed back to the common data files. These vectors would be indexed by energy commodity, region, and time. Environmental impact vectors could also be passed to and from the modules in finding a solution.
Figure 3-2 illustrates one convergence to an equilibrium, for energy price and energy quantity. The demand module response is represented by the downward sloping curve, which projects the energy quantity demanded at each energy price. The supply module response is represented by the upward sloping curve, which projects energy supply price for each energy quantity supplied. Equilibrium is represented by the values for price and quantity at which the two curves cross.
In Figure 3-2, an initial price is chosen as P0 (for illustration, P0 is chosen far away from the equilibrium price). The price P0 would be read from the common data files by the demand module. The demand module would then project Q0, a value for energy quantity that would be fed into the common data files.
The supply module would then read the quantity Q0 from the files and provide a supply price of P'0, which would be sent back to the common data files. The integrating system would be at a solution if P'0 were close enough to P0. If not, the next iteration would use both these prices to calculate a new price estimate, possibly a weighted average of the input and output prices. This new starting point is represented by P1. The process is repeated, giving an output price of P'1. And so the process would continue until input and output price values were sufficiently close.
Figure 3-2 illustrates an adjustment process such that energy prices and energy quantities converge to the equilibrium. Yet in other modeled adjustment processes, no equilibrium may be reached, but instead proposed solutions oscillate around the equilibrium point. For example, if the starting point of each iteration were set equal to the output price from the last iteration, the proposed solution could oscillate and would always oscillate for some shapes of the supply-and-demand curve. Additionally, when the number of prices and quantities is greater than those in Figure 3-2, the process of convergence to the equilibrium may be more complex. This complexity may slow the process of convergence or may prevent convergence from being reached.
To avoid such problems, EIA should adopt or develop appropriate algorithms for NEMS. For example, by choosing an appropriately weighted average of the initial prices (P0) and the output prices from a given iteration (P'0), convergence can be guaranteed for most supply and demand curves. The appropriate choice of weights also generally greatly decreases the time to convergence. EIA should devote some attention to adapting or developing algorithms to ensure efficient convergence to equilibrium.
In Figure 3-2 only a unique equilibrium, or single equilibrium, point exists. Because the supply module response is upward sloping and the demand module response is downward sloping, these two curves can cross only once: the equilibrium is unique. However, if there were many prices and quantities, there might well be more than one equilibrium.
If there are multiple equilibria, policy analysis and forecasting becomes especially difficult. With multiple equilibria, the model typically provides no indication which of the several possible system equilibria would be obtained. Therefore, unless the analyst can
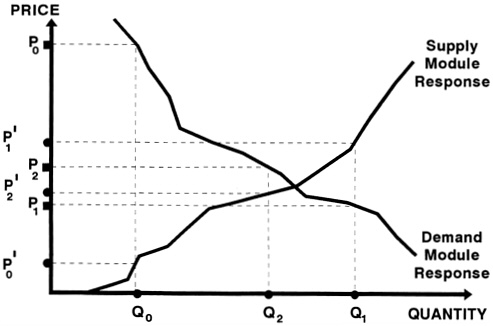
Figure 3-2 Illustration of the convergence of price to a supply-demand equilibrium.
assess which of the equilibria is most likely to occur, the projections would remain ambiguous.
In addition, policy analysis is hampered when multiple equilibria exist. Unless each equilibrium point is examined, the projected impacts of policy measures can be extremely misleading. Figure 3-3 abstractly illustrates the difficulty for the situation in which two outcomes, labeled “Variable 1” and “Variable 2” are being examined.
In Figure 3-3, for the first policy measures, the group of points labeled “equilibrium set” could all be equilibria, while for the second policy measures, the group of points labeled “equilibrium set B” could all be equilibria. Note that equilibrium set B is translated downwards and to the left from equilibrium set A. The interpretation is that, whatever
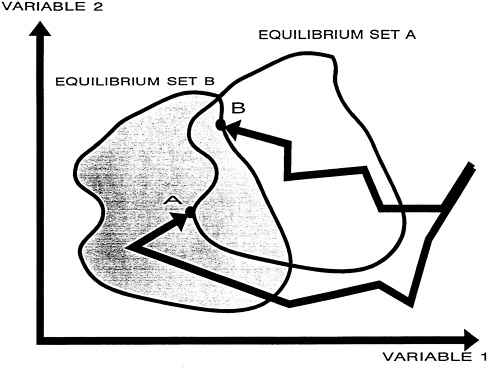
Figure 3-3 Illustration of multiple equilibria.
equilibrium point in fact occurs, changing to the second policies will decrease the values of both variables.
But a model run does not trace out all the equilibrium points. Rather, in a given run, variables are sequentially calculated until one equilibrium point is found. This process is represented by the crooked lines converging to points A and B. The points A and B would then typically be interpreted as the outcomes occurring with the first and the second policies, respectively. The difference between points A and B would typically be interpreted as the impacts of the policy choices.
Notice that point B lies upward and to the right of point A. Thus, if these two points were the only ones that had been determined using the model, it would be natural to conclude that changing to the second policy would increase the values of both variables.
This estimate of policy impacts would be incorrect, as indicated by the shifting of the equilibrium sets.
When multiple equilibria exist, therefore, modelers must trace out the set of equilibrium points and examine how the set of points change in response to policy measures. It does not suffice to find only one solution for each configuration of policies. We do not know whether the NEMS will have a unique equilibrium or multiple equilibria. However, EIA personnel must determine which is the case.
There are theoretical results that suggest the NEMS might have a unique equilibrium. These results depend upon mathematical properties of the matrices of supply-and-demand derivatives. However, we do not anticipate that all of the assumptions required to prove uniqueness will in fact be valid for the model. For that reason, EIA must explore the model, searching for multiple equilibria, until it is determined that multiple equilibria do exist or until confidence is gained in the idea that the equilibrium is unique.
In developing the model, careful attention should also be paid to the hardware to be used in running the model. The committee believes that NEMS should be configured to run on personal computers if such a configuration would not sacrifice the content of the model.1 Modular architecture could make such a configuration easier to achieve. The control module could be designed so to load the modules sequentially into personal computer memory. The control module itself would always remain in memory, while other modules and data files would reside on the hard disk, with only one module at a time in random access memory (RAM). As long as each module were small to be run alone (in conjunction with the control module), then the entire system could be run on a personal computer. For personal computers with sufficient memory, the control module could keep several or all component modules in RAM, running them sequentially, and not expending time or frequent disk swaps.
If the NEMS model cannot be adequately structured for use with a personal computer, then it should be configured to operate on a workstation using current software that allows transportability among computers.
If the system could be run on personal computers, it could be made widely available, increasing the number of analysts who understood, used, and tested it. Configuring NEMS for workstations would reduce the breadth of its use outside DOE and EIA, but it would still be more accessible than if designed for use only on mainframe computers. The committee believes that such model transportability is important for allowing non-EIA users to understand, critique, and offer ideas for model improvement. For this reason, the committee recommends that NEMS be developed to run on widely available computers unless the resulting configuration would significantly sacrifice the NEMS models' content.
PROPOSED MODULES
Figure 3-4 shows the general proposed structure of the NEMS in more detail. Modules shown in double frames indicate models that, to the committee's knowledge, do not exist now within EIA.
Separate regionally disaggregated modules would represent various energy-consuming sectors (residential, commercial, industrial, and transportation). These modules would provide as outputs the quantities of the various energy forms demanded for the input delivered prices of energy.
Separate modules would also represent various energy supplies (gas, oil, coal, and renewables). These modules would additionally represent U.S. regional transportation of energy, so that supply modules would provide as outputs delivered prices. Single-fuel conversion processes (e.g., refining of crude oil into products) would be represented within the corresponding energy supply model (e.g., the model for oil). These supply modules would take as inputs regional demand and provide as outputs regional prices over time by energy form.
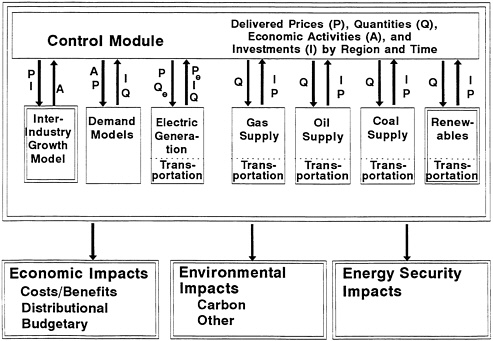
Figure 3-4 Proposed NEMS architecture in greater detail.
Electricity generation would be modeled taking as inputs the prices of the fuels used to generate electricity (oil, coal, nuclear, natural gas, and biomass) and the quantities of electricity demanded, and providing as outputs the prices of electricity and the quantities of the various fuels used.
A relatively simple aggregate model of the world energy system should also be developed, to estimate its interactions with the U.S. energy system.
The Control Module
The control module would include switches that would allow alternative versions of the modules to be used. It is envisioned that each module would routinely have three versions: the full model, a null model, and a reduced-form version of the full model. The user would choose which module version to use, and the control module would use this information in iterating to a solution. Such switches could be controlled with input data files or with more easily used menus.
Again, the control module would guide the sequential exercising of other modules. If the system could run on personal computers, the control module would guide the swapping of various modules into and out of RAM. It would choose the initial prices for each iteration based on the initial and output prices from the preceding iteration. It would also test for whether convergence had been obtained.
The control module would also include the user interface. The more “user friendly” this interface, the more readily the model could be transferred to users outside EIA and the more readily EIA personnel could learn to use the system. However, it is more important that the system have good content than that it have a user-friendly interface.
Fossil Fuel Supply Modules
The EIA now has fossil-fuel models for IFFS and other modeling systems. Additional work is ongoing. Because so much information is available about such modules, they are discussed here only with regard to a few points in medium-term forecasting.
The main concept behind current modules of energy supply is cost minimization, the obtaining of a given supply of a particular energy form at minimal cost. Analyzing and forecasting such activities often involves optimization models. For such models, delivered prices are represented by “shadow prices” or dual variables resulting from the constraint that fixed demands must be met.2 Wellhead or mine-mouth prices are delivered prices minus the marginal transportation prices to the point of delivery.
Such a representation implicitly assumes that the industry examined is reasonably competitive and that the information available is nearly perfect. It also assumes that replacement cost pricing is a prerequisite for new investment and that entrance and exit from the industry are relatively frictionless. However, if these assumptions are not valid, for example, if the industry does not minimize costs or if prices differ from marginal costs, then optimization approaches cannot be used directly without some adjustment. In particular, the optimization approach may ignore many important regulatory issues associated with the bulk transmission of electricity and transportation of natural gas. Particular attention should be devoted in NEMS modeling to such transportation issues. The approach to be used must be designed case by case.
Although oil and gas supply models have been used extensively for many years,3 they may have substantial shortcomings (Huntington and Schuler, 1990; Bohi and Toman, 1984).4 Current U.S. energy supply data bases and technology evolution models, particularly for oil and gas, are inadequate for all but relatively short-term analysis (not as great as 20 years). Oil and gas resources are presumed to be fixed and finite; technology is presumed to not respond to changing conditions. Overcoming these inherent problems in current long-term oil and gas supply modeling will require a two-part effort. First, the oil and gas resource base and supply models need to include the very large volumes of unconventional oil and gas that exist in low permeability formations, fractured reservoirs, coal seams and heavy oil and tar sand deposits. These resources already make a substantial contribution to energy supplies and will become even more important in the future. Second, the oil and gas models need to better capture the evolution of advances in oil and gas extraction technology. The general effect of these technology advances has been to improve the recovery efficiency of hydrocarbons and to decrease their extraction costs.
Similarly, the effects of improvements in oil, gas and coal extraction and conversion technologies are poorly captured by models. For example, continuing efficiency gains in coal mining, particularly through the now widely used long-wall mining technology, have steadily decreased the mine-mouth costs of coal and thus fuel prices for electric utilities below values forecast by EIA and other coal models. Also, technology advances in oil and gas extraction, including 3-D seismic exploration, horizontal drilling, well stimulation, sophisticated reservoir simulation and new drill bits, have all reduce costs and improved the efficiency of recovering new reserves. As a result, the supplies of oil and gas have been larger, as well as the costs to find and recover them lower than predicted.
While oil and gas are ultimately finite and depletable resources, when and how such depletion occurs thus becomes of critical interest to energy outlook and policy. The data base on long-term oil and gas resources appears to have major limitations (NRC, 1991b).
|
3 |
In Figure 3-4 the oil and gas models have been shown as closely linked. Oil and supply models probably should be closely integrated because their economics are closely related. Oil and gas may both be produced from a single well or from different wells in the same field. Drilling equipment for the two is to a great extent interchangeable. Oil may be the target of drilling but gas may be found or vice versa. |
|
4 |
Current oil and gas models have even greater shortcomings for longer term energy projections, those beyond the year 2010. |
In addition, the committee believes that changes in energy extraction technology and production costs will be important for understanding the potential of the very large unconventional oil and gas resources that are already making an impact on U.S. supplies.
Explicit modeling of such technology uses and implications and technologies' environmental effects will provide a stronger base for analyzing longer term energy supplies. The NEMS must recognize limitations in current oil and gas supply data bases for long-term energy studies and it should take steps to improve the oil and gas resource data that are essential inputs to such studies. Similarly, it will be important to differentiate policies that expand the available resource base from those that simply make it faster or less expensive to extract. In particular, considerations for NEMS should include adding the large in-place volumes of unconventional oil and gas resources into its resource assessments and supply models, and develop the capability to estimate the effects of continuing evolution in extraction technology and production costs.
The current EIA coal model is extremely detailed, far more so than would be appropriate for NEMS. One priority for NEMS development would be a great simplification of this model to use in general modeling, forecasting, and analysis. The simple model would then be used in NEMS. Detailed analyses of coal issues should probably be conducted outside the NEMS.
Energy Conversion Modules
The electricity generation model would be a hybrid of demand and supply models, taking as inputs the prices of possible fuels and the quantity of electricity demand (Qe), and producing as outputs the price of electricity (Pe), investments, and quantities of fuels used to generate electricity. Other energy conversion activities involving more than one energy form in a substantial way (e.g., synthetic fuel conversion) would also be represented by hybrids of demand and supply models. However, such other modules will not be addressed here.
Output prices from the electricity generation model should not be represented as marginal costs of electricity generation and transmission. Most utilities are still regulated based on average cost plus a regulated rate of return on invested capital. For such sectors, a cost-minimizing approach could still be used but dual variables cannot be directly used for price determination. Rather, average costs should be calculated based on utility accounting conventions and used as estimates of delivered costs. Thus, the financial accounting information should remain in the electricity generation model.
The effects of utility-financed energy conservation investments should be considered when calculating average costs for electricity generation. Some such investments are simply expenses by the utilities while others are capitalized into the rate base and thus earn a return over time. A smaller number are paid for over time by the utility customer. Judgments must be made about the fraction of investments to be treated in each of the three ways. Investments either expensed or capitalized by the utility will increase the average price of electricity charged by the utility.
Modeling the electricity generation sector will present other special challenges for EIA. EIA should also give explicit attention to the changing structure of the industry. Demand-side investments by electric utilities and others should be addressed. Renewable sources and nonutility electricity generators who sell to utilities are growing in importance and present an additional modeling challenge. Financial transfers and utility incentives to end users should likewise be incorporated. Such structural changes in the sector imply that its behavior in the future may be very different from that observed in the past.
EIA's current electric utility model has a vast amount of detail about conventional fossil fuel inputs to electricity generation. EIA should simplify the representation of these inputs and otherwise streamline the existing model for the NEMS. For nuclear power, EIA currently estimates generation capacity and financial information offline, which serve as input to its current electric utility module. Additionally, the current model has little or no detail about renewable energy sources. In the following section, some approaches to modeling renewable energy conversion are addressed.
Renewable Energy Conversion Modules
Data requirements and acceptable model structures for renewable energy are different from those for fossil energy. For purposes of this discussion on how DOE models treat renewables, renewables are divided into two categories: biomass energy, for which ongoing fuel expenses are a significant fraction of total costs; and nonbiomass renewables like hydroelectric, solar, wind and geothermal energy, for which there is near total substitution of capital for ongoing fuel expenses. The latter type of renewables will be discussed first.
“Screening curves” are used in large-scale energy models to simulate electric utility choices of conventional primary energy sources: estimates of fixed costs are considered along with a measure of conversion efficiency and fuel prices to project end-use cost. For example, most electricity supply models specify a technology by capital cost in units of dollars per kilowatt ($/kW); fixed operating and maintenance (O&M) costs in units of dollars per kilowatt per year ($/kW-yr); variable O&M costs in cents per kilowatt-hour (¢/kWh); and efficiency or “heat rate” in units of British thermal units per kilowatt-hour (Btu/kWh). These factors are combined with fuel prices in units of dollars per British thermal unit ($/Btu) and a depreciation factor expressed as a “fixed charge rate” (the percentage of capital costs to be recovered each year). The output of this analysis is a screening curve with production costs in cents per kilowatt-hour (¢/kWh) on the Y-axis and “capacity factor,” or percentage of design output over time (usually annually), on the X-axis. These screening curves and electricity demand functions are input to production cost models to simulate utility decisions about the use of existing resources (“dispatch”) and thus fuel mix, and choice of new resources. Uncertainties in the screening curves and demand functions are treated parametrically over multiple model runs.
Conventional screening curves are inadequate to simulate choices of nonbiomass renewables, for three reasons, especially when these curves are aggregated over a generic resource base. First, because almost all production costs are fixed, a curve relating production costs to capacity factor conveys less information than the capital cost estimate itself. The shape of the screening curve makes the utility's acquisition choices appear to
be very sensitive to demand function uncertainty. In reality, the opposite is true because the individual plant size for a renewable resource is usually small. Second, because there is no single market-clearing price for the primary resource (falling water, blowing wind, shining sun, etc.) and the resource spatial density distribution is highly variable, an average capital cost in dollars per kilowatt ($/kW) is almost useless as a production cost model input. For example, the output of a wind turbine is proportional to the square of the wind speed, and average wind speed varies by an order of magnitude or more over very short distances. Thus, production cost is very site-specific and highly dependent on the resource energy-density. In contrast, market-clearing prices smooth out production cost variance for natural gas and allow a combined-cycle gas turbine to be accurately modeled with a simple screening curve. Also, gas energy-density, transportation costs, and location-specific fixed costs are widely known and easily modeled. Third and finally, diurnal or seasonal variations in the renewable resource complicate the use of capacity factor as an independent variable.
Using traditional screening curves to model utility choices about the use of renewable resources induces several problems. Near-term utilization would tend to be underestimated because low-cost or high-value applications would not be captured in traditional screening curves that are based on average cost and value, even though they would be seen by the utility.
Such a modeling approach would also tend to overemphasize the importance of R&D for initial market penetration for the same reason. Barriers to commercialization would appear to be much larger than they really are. Such models would tend to show policies such as tax credits or capital cost subsidies to be less effective (subsidies would appear to lead to less incremental production than would actually be the case). Since many new technology penetration models imply that adoptions in one year positively influence adoptions in the next year, if early adoption were underestimated the error would be compounded over a long horizon.
Economies of scale could be misrepresented as increasing unit equipment size instead of increasing equipment production rate: cost reduction does not take place in the laboratory, but in the factory and the field. At the same time, such simulations would tend to overstate renewables' long-term contribution to energy supply because of inadequate representation of daily and annual cycles of energy production, low energy-density in the marginal resource base, and overly optimistic projections about R&D results.
These problems can be minimized by properly modeling capacity additions as a supply curve, recognizing low costs where resource energy-density is high and the value of niche markets where special characteristics confer high value. These high-value markets would support early high-cost production leading to lower costs as experience is gained.
Data requirements for renewables are therefore significantly different from those for fossil fuels. More attention must be paid to near-term markets and low-cost pockets of the primary resource. Energy production cannot be represented as a simple capacity factor for most renewables. More site-specific and technology-specific representations must be generated in a format that can be input into a production cost model. The model needs to be chronological rather than driven by summary representations of load shape. Because
equipment unit production volumes for dispersed renewables like wind and solar energy are very high, learning curves and factory operations research methodology need to be considered rather than one-shot construction economies of scale in modeling cost reductions.
Biomass energy creates special modeling problems. Conversion facilities are like lignite plants in that both use solid feedstocks with low energy-density. Lower pollution control costs for biomass are balanced by this lower energy-density. Adequate representation of feedstock costs is the crucial problem. Low energy-density implies that collection and transportation costs are relatively high. Agricultural processing wastes and forest product residues represent one class of feedstock. Costs for these byproducts are very low and net energy balance is unimportant because the growing, collection, and transportation costs are absorbed by higher-valued products such as food, lumber and paper pulp. However, the biomass resource in such cases is limited.
Once the leap is made to growing biomass specifically for energy production, net energy balance becomes a key consideration. The costs associated with low energy-density drive biomass energy programs to high yields per unit land area. High yields drive the process toward high input agriculture. For these reasons, useful models and data are generally found outside the energy sector. Uncertainty within such models may be particularly high because the difference between energy input and energy output is the small difference between two large numbers.
In addition to the engineering and economic issues discussed above, there are significant policy issues that must be addressed. For example, the adoption of most renewables is shaped by widely varying state regulatory policies. The success of renewable energy development has depended on regulatory decisions to require utilities to purchase independently generated power for a fixed, relatively high price. In the future, such decisions could be made on an environmental basis in addition to an economic one.
The discussion above suggests that models to simulate renewable energy conversion will require a high degree of geographical and temporal detail. Such detail would lead to a model far more complex than is appropriate for direct integration with the NEMS. For this reason, EIA should develop smaller, simpler modules (but modules larger than reduced-form versions) that simulate the operations of the more complex renewable energy conversion modules. These smaller modules would be integrated with NEMS.
The difficulties of modeling renewable energy conversion suggest that the endeavor requires creative research, modeling, and data development. Significant intellectual resources, from EIA, other DOE offices, and outside DOE should be applied.
The International Energy Module
The price of oil in the United States is primarily determined by the world oil market, the availability of natural gas is influenced by Canadian natural gas exports, methanol prices in the United States are greatly influenced by world methanol prices, and the world price of oil and other energy forms is influenced by U.S. supply and demand: for these and
similar reasons, a relatively simple aggregate model of the world energy system should also be developed, to estimate interactions between the U.S. and world energy systems (see, e.g. Manne et al., 1985).5
In particular, U.S. energy exports (e.g., coal) and imports (e.g., oil, Canadian and Mexican gas and electricity and methanol) should be included. It would also be useful to estimate energy supplies imported from and produced in the most unstable regions of the world. The goal would be to examine prices and quantities of U.S. energy imports and exports and to assess variables particularly important for energy security. The immediate goal in NEMS development would not be detailed examination of world energy markets but only the examination of their features most important to inform U.S. policy analysis.
Endogenous (determined internally by the model) determination of world energy prices and U.S. import and export quantities depends partly on reasonable representations of the impact of U.S. imports and exports on world prices. But if such representations exist, they could be incorporated in the integrating system of the NEMS model.
The international model of U.S. energy imports (oil, natural gas, methanol and electricity) would resemble other supply models, with world energy prices as outputs and U.S. demands for imports for the various energy forms as the inputs. The international model of U.S. energy exports (coal) would resemble other demand models, with export coal demands as outputs and the prices of exported coal as inputs.
Such representations would allow the assessment of policies expected to change the world price of oil or of other energy forms. For example, if increased U.S. oil imports led to increased world oil price, then from the U.S. perspective, the incremental cost to the United States of additional imports is greater than the price paid by the users of oil. This difference between incremental cost and price reflects the terms-of-trade costs to the United States of increased import prices associated with increases in the import quantity. There is disagreement among analysts about the degree to which terms-of-trade changes should be included in welfare assessments of policy actions. However, if one could adequately model the forces determining world oil prices, then such terms-of-trade impacts could be consistently quantified if the representation of world oil price determination were incorporated in the NEMS' integrating module.
It is more complex to model the influence of U.S. regulatory policies on the technologies that shape energy supply and demand abroad (for example, when U.S. standards for automobiles or appliances are applied internationally to these commodities). Yet if the impacts of such policies on world energy supply-demand patterns could be assessed, then such a representation could be used to estimate other similar policy impacts on world energy prices.
A key difficulty in developing such an international module is understanding the nature of the relationships between U.S. actions and international conditions. This problem may be especially acute for the world oil market, because it is uncertain whether increases in oil imports raise world oil price, decrease it, or leave it virtually unchanged (Sweeney, 1981). The uncertainty stems from different perspectives about the workings of the Organization of Petroleum Exporting Countries (OPEC). For example, many economic models of OPEC suggest that the greater the demand for OPEC oil, the greater the increase in OPEC price. A significant decrease in demand would thus reduce price. However, OPEC might also be seen as an imperfect cartel that is more cohesive when oil prices are high. When oil prices are low, revenues to member countries are low and they may be less willing to reduce production. This model would imply that the higher the price, the lower the OPEC supply of oil, the reverse of the common assumption. For such reasons, it is difficult to have confidence in projected U.S. policy effects on world oil prices.
The modeling of natural gas, electricity, and coal imports and exports will probably be less difficult. The demand for U.S. coal exports can be expected to be negatively related to export price: higher prices decrease export demands. Imports of natural gas from Canada to the United States will be positively related to price: the higher the price, the greater the natural gas imports to the United States. Such relationships could be estimated for NEMS use based on more detailed models of the world coal market and Canadian natural gas market, even though the more detailed models themselves would not be incorporated in NEMS.
The Interindustry Growth Model
As far as the committee is aware, the EIA has not included interindustry, economic growth models in their modeling system, but has used macroeconomic models, such as the Data Resources, Inc. (DRI), quarterly macroeconomic model. Such quarterly macroeconomic models emphasize the aggregate demand for goods and services rather than the supply side of the economy. They are most appropriate, therefore, for relatively short time horizons. But for modeling over the roughly 10 to 25 period, analysis that emphasizes the ability of the economy to produce and considers the economy-wide structure of industry is more appropriate. Such models have already been developed and are broadly used (Jorgenson and Wilcoxen, 1990). For this reason, NEMS should probably acquire and incorporate an interindustry growth model rather than develop its own estimates of energy system interactions with the economy.
The interindustry economic growth model should incorporate the idea that economic activities both influence and are influenced by energy sector outcomes. For example, energy demand in the industrial sector varies significantly with the balance between heavy and light industry. Thus, the model should consider appropriate economic activities as driving variables for demand sectors. Economic growth rates will be influenced by the magnitude and type of capital investment required for energy supply development or in end-use technologies. In addition, energy prices will influence the relative sizes of economic sectors, the overall savings rate, and the patterns of capital investment. These relationships should be represented by the model.
Integrating an interindustry growth model into NEMS would require careful analysis of the linkages between that model and the rest of the system. For example, a typical interindustry growth model would include many of the energy industries that NEMS would be modeling in greater detail than would the interindustry model. An interindustry growth model such as the Jorgenson-Wilcoxen model would already have a full structure for determining energy demand. It is not clear that a full structure of econometrically estimated demand equations could be reconciled with bottom-up models of industrial energy use. At the minimum, major problems of logical consistency can be expected when the process of integration is started. In addition, the problems that will arise in matching the industry classification adopted in the interindustry growth model with the energy accounts within NEMS can be expected to be very difficult if not intractable.
Significant intellectual effort will be needed to correctly integrate an interindustry growth model into NEMS. And such an integration may ultimately not be possible at all and will not be possible within the next year. However, we believe that intensive modeling and research efforts could lead to a successful integration. EIA should structure a process that would bring the requisite intellectual talent to bear on this problem in the expectation that some integration can be achieved.
Energy Demand Modules.
Two broad approaches are feasible in developing energy demand forecasting models: “top down” and “bottom up.” Top-down models rely on aggregate relationships between energy consumption and economic, demographic, regulatory, and other forces (Hogan, 1989). They primarily use statistical techniques to estimate historical relationships between underlying forces and observed consumption (for a comparison of different models of this type see Bohi, 1981). Bottom-up models construct estimates by adding up the amounts of energy used in different energy-consuming activities (McMahan, 1986; EEA, 1982). They rely primarily on forecasts about future activities expected to use energy: the nature of such activities, their extent, the technologies available and likely to be adopted for these activities, and the behavioral rules that govern the evolution of these factors.
Current energy demand forecasting often combines the two approaches (e.g., Difiglio et al., 1990). For example, in estimating gasoline demand, an econometric model might be used to project vehicle miles traveled. Efficiency of cars can be projected based on technological feasibility and regulatory constraints, such as the corporate average fuel economy (CAFE) standards, as well as empirically based estimates of new car sales for each year. Estimates of vehicle miles traveled and fuel efficiency are combined to project gasoline demand for automobiles. The committee expects and encourages EIA to use such hybrid forecasting for much of its energy demand modeling.
Current EIA energy demand models are disaggregated by consuming sector rather than by fuel. Disaggregation by consumer sector is appropriate for several reasons. First, there is too much difference in energy use among the consumer sectors to aggregate them meaningfully in one model for many purposes. Second, interfuel substitution is an important factor: the price of one energy form can influence the demand for other energy
forms within a single consuming sector. For this reason, it would be less useful for NEMS to build separate models for each energy form.
Current EIA demand forecasting models stress the response of energy consumers to energy prices and other economic and noneconomic driving variables. These models have been developed to be consistent with historically observed behavior. EIA energy demand models vary in their reliance on top-down estimates of observed energy consumption and bottom-up calculations of consumption. But all currently have very little technological detail.
Both bottom-up and top-down models begin with the observation that energy is typically not desired as an end in itself; rather, it is employed along with appliances and other machines to generate energy services (e.g., warm or cold air, lighting, and power applications). The demand for energy therefore depends on the stock of energy-using equipment, the energy efficiency of this equipment stock, and its rate of use.
One important implication is that, once energy-using equipment is in place, short-term variations in energy demand owe primarily to changing rates of use, whereas over the medium-term, both equipment stock and equipment energy-efficiency may change. Thus, when modeling energy demand, it is imperative that short-term dynamics be distinguished from medium-term dynamics. This distinction must be recognized in both bottom up and top down modeling.
Bottom-up demand modeling typically estimates energy consumption as the product of an activity times an energy-intensity, for each sector. The challenge to the modeler is to project the activities and energy-intensities. Both should be modeled as functions of energy prices, regulations, economic growth, and other forces. Bottom-up forecasting requires specific technology projections and projections about the underlying activities, such as construction of housing units, industrial production, and travel. Such analysis also requires analysis of the rates of technology adoption, conditional on the underlying forces.
Optimization as well as forecasting models can be used to analyze energy consumption. For example, some members of the committee believe that the energy-intensity of most equipment in use today, both new and existing equipment, is higher than “optimal” given the consumer's cost of energy and the cost of capital. Thus, one interesting kind of policy analysis might address whether private decision makers are using technologies in a manner inconsistent with their own self interests or whether the analysts have come to mistaken conclusions (perhaps by ignoring important subjective costs and benefits of energy-using activities or by an overly optimistic view of the technologies they are assessing).
If real-world market forces lead individuals to use too much energy, then models could be used to assess the economic, energy, and environmental effects of reducing the differences between actual and “optimal” levels of energy-intensity. To conduct such technology-and activity-specific analyses would require the characterization of a vast array of technologies. Many of these technologies would only become available at higher energy prices.
The bottom-up modeler needs extensive data, projections, and information:
-
Data on energy use and projections of activities by sector, energy form, time, region, and other key characteristics for each possible energy price scenario.
-
Data and projections about characteristics of energy-using technologies, such as their applicability, costs, performance, and environmental impacts, including operational variations and energy-efficiency add-ons, for both existing and prospective technologies.
-
Data on, behavioral information about, and models of decision makers and decision making in the acquisition of energy technologies, including such factors as institutional setting, financing issues, response to reliability, and technical sophistication, as well as price. Such information should cover not only the current institutional setting, but also plausible future settings, including the availability of financial assistance and information to improve efficiency.
EIA is familiar with the conventional data requirements in these areas and is working to collect more current data, for example, for commercial buildings and especially industry, where the heterogeneity of energy-related activities makes good analysis complicated. Depending on the type of analysis, highly disaggregated data of the first two types above may be needed. Such data are receiving attention in other agencies and EIA can use this work, although the data surveys are limited, especially for the industrial sector. However, EIA would need to verify the quality of these data, since field measurements are inadequate for some of the data collection activities (e.g., no one has verified the accuracy with which census energy-consumption forms are filled out. Since there are many different types of units there may be a serious problem.).
Top-down, dynamic modeling of energy demand can itself be addressed in at least two ways. One body of literature, beginning with the classic study by Fisher and Kaysen (1962), explicitly introduces measures of the energy-using capacity of the capital stock, and then models factors affecting the use of this stock. A second approach, also considered by Fisher and Kaysen, has been further developed by D. McFadden (1983), Dubin (1985) and McFadden and Dubin (1984).
The discussion here focuses on aggregate sectoral models for areas in which it is impractical to obtain detailed data on a vast variety of energy-using capital goods, that is, on models incorporating the effects of the capital stock indirectly. Taylor et al. (1984) call these models “flow-adjustment models,” since changes in the flow of energy depend on the speed with which capital stocks are adjusted through investment.
According to flow-adjustment models, consumers form expectations concerning future prices and incomes, and based on these expectations and other exogenous (external) variables, they choose desired or preferred levels of energy consumption. At any point in time, consumers' actual purchases of energy may differ from their desired consumption, in part because of psychological, institutional, and technological factors that make instantaneous adjustment costly.
To use a flow-adjustment approach in a top-down model, therefore, requires that several issues be addressed:
-
The factors affecting desired levels of energy consumption must be specified explicitly, including the way in which consumers' expectations of future prices and incomes are formed.
-
The adjustment process from actual to desired consumption must also be formulated.
The second issue is typically approached through the partial adjustment model, in which current energy consumption depends on past energy consumption and other exogenous variables.
As for the first, desired energy consumption can plausibly be argued to depend on expected real energy prices and expected real income (or economic output), particularly because energy is used in conjunction with long-lived durables, demand for which in turn depends on expectations of several explanatory variables. Since expectations of these variables are usually unobserved, the challenge is to specify a working representation incorporating nonstatic expectations, and in terms of observed variables. This is the “adaptive expectations” approach discussed in most econometrics textbooks, but it can be expanded to include optimal or rational expectation predictors of real energy price and real income or output (see Nelson and Peck [1985] for an example of such estimation, and Pindyck and Rottenberg [1983]).
The most modern demand models constructed by Daniel McFadden and his research associates employ engineering-economic models, sophisticated econometric and statistical procedures, and extensive data bases on individual U.S. households for the residential demand for electricity (Goett and McFadden, 1984; Berndt, 1991; the following discussion derives from Berndt). These models are based on the conceptual framework of Houthakker (1951) and Fisher and Kaysen (1962). This engineering-econometric model employs data from the 1977–79 U.S. Department of Housing and Urban Development Housing Surveys, an annual survey based on over 70,000 households. These surveys include information on household's appliance stocks and sufficient geographic information to construct normal weather condition variables and the marginal price schedules facing these households. Other microdata from the U.S. Department of Labor Consumer Expenditure Survey, as well as engineering and construction sources, were also used in this collection of models referred to as the Residential End-Use energy Planning System (REEPS). Such use of microdata can allow a detailed understanding of the variables affecting appliance choice that cannot be discerned using aggregate or average data.
One module in REEPS represents appliance choice decisions based on household socioeconomic characteristics, appliance holdings and attributes, type and size of residence, and geographic and economic characteristics associated with the household location. This appliance choice framework was modeled separately for each energy-related function such as space heating, water heating, or refrigeration. The model captures weighing of capital and operating costs in making household appliance decisions. The econometric technique
involves a discrete choice framework known as the multinomial logit model and its generalization.
The second major modeling effort in REEPS involves households' choice of utilization rates with specified short-run, nonlinear demand equations that include explanatory variables such as appliance operating efficiencies, marginal energy prices, and demographic and geographic variables; equation estimation was accomplished using nonlinear least squares procedures.
Simulation of the REEPS models were conducted under a wide variety of alternative assumptions with the results used to summarize the sensitivity in the short and long run to changes in economic, regulatory and demographic variables. Elasticity estimates are derived from the simulations.
Behavioral Information Requirements
Both top-down and bottom-up models include behavioral information. However, bottom-up models require specific formulations of behavioral rules, while top-down models implicitly make behavioral assumptions through aggregate estimated relationships. The explicit assumptions of bottom-up models allow easy interpretation of the model results, but may not correspond to actual behavior observed. The implicit assumptions of top-down models may correspond in the aggregate to consumption behavior, but may prove misleading in forecasting the future, for example, if behavior changes, because of policy changes not reflected in price. In addition, when prices are the only relevant policy variables incorporated in such models, it is difficult to use these models to examine policy options that do not involve (implicit or explicit) price changes.
One kind of behavioral information concerns investment choices among types of equipment with different energy-efficiencies. Unfortunately, there are major gaps in our knowledge about such decisions. Some analysts assert that implicit annual real discount rates of 30 percent, and higher, characterize markets for energy-efficient equipment (Ruderman et al., 1987; Hausman, 1979). They believe that consumers give energy-efficiency much lower priority than simple economic analysis would suggest, and that producers and sellers often do not market products with energy-efficiency benefits. In a bottom-up forecasting model explicit assumptions must be made about whether these assertions are correct. If such assumptions are made, the modeler should understand quantitatively and in detail the forces that lead to the assumed implicit discount rates. With top-down models this issue is not addressed explicitly.
For example, a fundamental concept in bottom-up demand analysis is “energy service,” a particular “good” in which energy consumption plays an important role. If the passenger transportation energy service is assumed to be mobility, then passenger-miles for different transportation modes constitute the activity and energy demand is the sum of energy demands for each mode. Unfortunately, the issue of what constitutes the fundamental service is difficult yet crucial for longer range modeling. People may not simply substitute one mode for another, for example, a mile of travel on a bus for a mile of travel by car. The fundamental service in daily travel may actually be access to various amenities. The
suitability of different travel modes and trip lengths depends on the nature of the community in which one lives and works. The need for travel also depends on alternative forms of access, such as electronic access to information. A useful prediction of demand over several decades should thus raise fundamental issues associated with the amount of daily travel. Daily travel must be related to such factors as land use practices, public transportation investments, population densities in metropolitan areas, and alternative technologies for meeting access requirements. It is not realistic for all such information to be captured in NEMS and the committee is not recommending such an approach. However, a model that fails to address the most important of these issues will not answer crucial questions about transportation energy policy.
What are needed are the identification of key variables, insight about their behavior, and some lively debate about the ways modelers may improve their assumptions. EIA does not have to conduct or sponsor all the research needed. But it is essential that EIA allocate sufficient human resources to determine the principal behavioral information needs for effective medium-term demand modeling, and to determine what relevant information exists and what kinds of information require new surveys or, more generally, research. Where behavioral information is inadequate, EIA should help generate interest in the issue and follow through by soliciting research or stimulating another agency to sponsor research. Where funding is needed to spur essential research, EIA should have the resources to participate.
Sectoral Information Needs
Residential and Commercial Sectors. Top-down econometric studies have shown that residential demand for energy depends on a combination of economic, demographic, technological, weather, and seasonal factors.
Detailed technology-characterization of the residential sector has already been carried at Lawrence Berkeley Laboratory and the Electric Power Research Institute. Most energy services can be defined straightforwardly, and data can be collected on alternative ways to satisfy the energy service at different levels of technology and investment. Each technology, both commercially available and new technologies, have associated costs and energy savings. (The cost and performance of not-yet-available technologies are, of course, speculative.)
Using such analysis, a supply-curve (which may be quite uncertain) for space heating is constructed. The supply curve describes the rate of energy consumption as it depends on the level of investment in space-heating efficiency equipment. The level of investment can be related in turn to energy prices and decision making behavior. Such supply curves have been incorporated into bottom-up models.
A critical need for the bottom-up approach in analysis of the residential sector is in modeling of the aggregate behavior of contractors who build residences. Information on the actual implicit discount rates characterizing the householder market is also needed.
Energy demand of the commercial sector has traditionally proved more difficult to model econometrically than that of the residential sector. One reason for the difficulty is that the commercial sector is extremely diverse, ranging from hospitals to retail stores to
churches and offices. In addition, decision makers for investments in energy-using equipment are a highly heterogeneous group, ranging from speculative builders, who will not own or operate the buildings they build, to builders who will be owner-occupiers. This heterogeneity should be collapsed in the form of one aggregate relationship whichever modeling approach is used.
Industrial Sector. Industrial sector energy demand is greatly affected by the level of regional economic activity. Although the ratio of energy use to gross national product is important, it is not fixed, and it is now widely known that this important ratio varies with changes in real energy prices and other factors. Such changes, however, tend to take time and are often larger over the long than short run, as in the residential sector.
Energy demand in the industrial sector differs from that in residential and commercial sectors in a number of ways (Halvorson, 1978). In the industrial sector fuel substitutions, among electricity, gas, oil, and biomass, are more readily made. Substitution possibilities vary considerably among the various industries. In a top-down model it is thus important to estimate empirically the interfuel substitutions by including all energy prices as regressors in the industrial energy sales equations. Like the commercial sector, the industrial sector is very diverse, with different industries having sharply different energy consumption patterns. Aggregate industrial sector models are essentially confined to employing an average energy price; but marginal energy price for the “representative” industrial customer is a concept that does not make much sense.
For bottom-up modeling, the industrial sector presents a strong contrast to the residential sector. While rather extensive energy and activity time-series data are available for the manufacturing sector, these data are extremely limited given the heterogeneity of the industrial sector. It is not feasible to model industrial energy use reasonably in terms of generic energy services as it is in the case of the residential sector. A good analysis requires examining the different production processes and the potential for changing them, in energy and material terms. To model all production processes of interest would be too costly.
However, not only does considerable process detail still need to be described, technological and economic futures for each subsector need to be characterized. One approach to the challenge may be to model a small number of subsectors in some detail, selecting them for their importance and representativeness. For longer term modeling, the selected subsectors should not be confined to energy-intensive industries, but include industries that are likely to experience major growth. The analysis of even a few subsectors would require major data gathering and analysis including engineering case studies in the field for each subsector to establish a baseline for analysis, and wide-ranging efforts to identify and characterize potential process changes. Moreover, this information should be informed by a sophisticated appreciation of the likely economic future of any subsector, the evolution of its products and competitive climate (Boyd et al., 1986; Squitier, 1984; Doblin, 1984; Ross, 1984).
Table 3-1 indicates the nature of available data and information on the industrial sector. Some energy consumption and activity data are regularly developed by EIA and
TABLE 3-1 Available Data and Information, Industrial Energy Demand
|
Category |
Data/Information Availability |
|
Energy consumption Electricity Fuels |
Four-digit manufacturing, annual Two-digit manufacturing, three-year; Some four-digit manufacturing, three-year |
|
Production activity |
At the four-digit level, manufacturing output available in nominal dollars annually; deflated output available after further delay; physical measures (tons) of production of selected materials available on a timely basis at least annually |
|
Technology Characteristics Basic process Existing |
Extensive anecdotal but little survey information on technology type and technology type and performance. few data on extent of technologies and trends in use; |
|
Prospective Conservation add-ons |
Little information Extensive information on technology types, but not on costs and adoption. |
in the Department of Commerce's Annual Survey of Manufactures at the four-digit Standard Industrial Classification (SIC) level of manufacturing, except that fuel consumption is not sampled extensively enough to disaggregate well by sector. If adequate data were collected for disaggregation at the four-digit level, this would be satisfactory in most cases. There is potentially valuable data by four-digit SIC section and by geographic location from the National Acid Precipitation Analysis Program (NAPAP) and from Dun & Bradstreet data bases for the mid-1980s. Considerable effort would be needed to bring these data into useful form, however. Energy consumption data for nonmanufacturing areas (agriculture, mining, and construction) are very poor. Moreover, while there is much information on the claimed performance of major industrial process technology, there is little survey data on actual performance. Cost information on potential energy-efficiency improvements and on the extent of adoption of efficiency technologies are largely lacking in a form that could be used by modelers. The process of adopting energy-conservation technology is poorly
understood, although there is anecdotal information on the role of high implicit discount rates in this process.
Analysts disagree substantially about even the most basic industrial sector modeling issues, including about how much price trends determine the creation and introduction of new technology, and about the proper way to measure production activity. EIA needs to develop a new industrial model and the modular structure proposed for NEMS proposed will allow EIA to change industrial sector models as they evolve and improve.
Transportation Sector. The transportation sector presents perhaps the greatest challenges of any sector for mid-and long-term modeling. Again, the type of community in which people live has a major impact on the extent and types of travel. Fundamental transportation fuel choices also face us in the coming decades. Petroleum supply, congestion, and emission crises may lead to relatively rapid and profound changes in policy and behavior and in turn to major unexpected changes in transportation technology and activity. Such dramatic changes also confront modelers in some areas of energy supply. But for the transportation sector, little relevant data and information are available and modeling approaches largely remain undeveloped. Present models are, naturally, based on past activities and technologies and past trends.
A good start has been made in analyzing past changes in the use of transportation fuels (Sperling, 1988) and the costs of a few new automotive fuel choices (U.S. DOE, 1988; NRC, 1990). The impact of gasoline prices on vehicle miles traveled has been estimated by many researchers. Much less is known about the effects on daily travel of type of community and land use public-transportation, and transportation management policies (e.g., parking charges, high occupancy vehicle lanes, and road pricing). Even in traditional areas of data gathering, knowledge is far from adequate. The sudden increase in vehicle miles traveled per driver in the late 1980s is not understood. It could be due to metropolitan area growth, changing employment patterns (with more outsourcing of services and part-time work), or increased income in high-income brackets. The effects of income itself are poorly understood, often being confounded with household size and employment effects.
There are data and information needs in all these areas. Current acquisition of data, for example, in the Department of Transportation's Nationwide Personal Transportation Studies, is slow and somewhat limited in its usefulness. The EIA's Residential Energy Consumption Survey (RECS) data series Consumption Patterns of the Household Vehicles is even more limited in its usefulness to the modeler, now that it no longer provides a reliable estimate of in-use vehicle fuel economy. EIA needs to develop more detailed transportation models that can better respond to modeling policy options.
Utility Demand-Side Programs. Promising opportunities for energy conservation are seen in policies that encourage investment by regulated utilities to increase customers' energy-efficiency. These policies bring utilities' financial criteria and expertise to bear on demand-side as well as supply-side investment. Several states, representing roughly 20 percent of the U.S. population, have already committed themselves to such policies through their utility commissions.
The effort has brought into focus the lack of information available to analysts about demand as compared to supply (Hirst, 1989). Electricity supply data are collected in great detail and with great frequency. EIA has annual electric utility reports relating to many aspects of generation, but none specifically on the recently developed demand-side programs. EIA publishes three surveys with highly limited information on end use, one for each major demand sector, every three years. However, the infrequent survey schedule and long delays in publication are less an impediment to demand analysis than is the paucity of detail.
It is likely that the energy use reductions created by demand-side programs can account for a substantial share of new electrical capacity requirements. For example, California has adopted as a goal that 75 percent of its projected energy growth be satisfied by demand-side programs. Analysis of this potential requires substantial data. A variety of data are beginning to be collected at the state level. Improved definitions and standardization of information collected and national collection of selected information are all needed (Hirst, 1990).
Information Needs for Policy Analysis
In addition to ongoing data and information, demand analysis requires specific information on the efficacy and other characteristics of selected public policies. For example, the effectiveness of different policies in encouraging investment in more efficient energy-using equipment needs to be understood. Specific policies include investment tax credits and regulatory mechanisms to reward utilities for investing on the consumer's side of the meter. The way such policies work is complex. For instance, detailed field studies show that the effects of the energy conservation tax credit in the early 1980s were much more limited than might be assumed in a typical model of investment decision making (Alliance to Save Energy, 1983). Similarly, utility demand-side programs need to be understood through research before such policies can be adequately modeled. Such programs vary from state to state and utility to utility.
The evaluation of federal policies appears to be an awkward research area for federal agencies to support, but means should be sought to foster this activity. Evaluations of the many energy-demand policies tried in the late 1970s and early 1980s, as well as those undertaken recently, would be especially valuable.
Quality and Timeliness of Data and Information
The value of data is obviously limited if they are not accurate or not available when really needed. On the other hand, because increased precision or speed of data collection entails increased costs, accuracy and timeliness must be understood relative to the eventual data use. Most statistical agencies specify the nature of data quality by providing details on how data are collected, measures of sampling variability, questionnaires used, validation methods (if any), and characteristics of sources.
Because energy issues and problems are sometimes urgent, preliminary estimates (with measures of uncertainties) that are available quickly can sometimes have greater value than
more precise data available several years later. Such timely energy data are largely lacking for most areas of demand, except at the most aggregate level.
Data are available from organizations outside EIA, including industry sources, such as the American Petroleum Institute and American Gas Association, state and local government sources, such as the Northwest Regional Power Planning Council and California Energy Commission, and others. Use of data from such sources could greatly improve EIA analysis.
Reduced-Form Modules
As discussed above, EIA should routinely estimate reduced-form versions for each of the major components of the integrating system. Reduced-form versions would provide estimated response surfaces of the full modules. Relatively simple functional forms could be chosen to approximate the more complete models in translating from the input variables (e.g., prices for demand and quantities for supply) to the output variables (e.g., quantities and investments for demand and prices and investments for supply). A reasonably accurate approximation of this translation from inputs to outputs is necessary to capture the essential information captured by the complete model.
However, it is neither necessary nor possible that reduced-form versions exactly represent the full modules. How much variation between the two is acceptable depends on the modeling needs. For example, a reduced-form energy consumption module for a sector in a given region might include a base-case projection of energy consumption along with a constant elasticity (own-elasticity and cross-elasticity) approximation for the impacts of energy prices on consumption of different energy forms over time.
Reduced-form versions would be estimated for each region in the integrating system. Regional estimates would not be collapsed into one national estimate. Such a collapsing could be expected to significantly modify the nature of the feedbacks in the overall system in response to changes in one component of the system. Thus, collapsing several regions into one geographically aggregated reduced-form version could be expected to lead to significantly different projections than those resulting when a regional structure is used. However, the magnitude of the error associated with such regional aggregation cannot be estimated at this time.
Reduced-form versions should be periodically recalibrated (refitted) to pseudodata generated by running the full model. Recalibration would consist of fitting the parameters of the reduced-form version based on a structured set of runs from the full modules. The process is essentially a statistical procedure and statistical concepts can be used to guide it. However, to ensure that such recalibration can be carried out routinely, EIA must develop the software to facilitate the process. Such software probably does not exist, although research in this area has been conducted (Griffin, 1971, 1978, 1982). In addition, the statistical approaches to such reduced-form representations must be carefully understood.
In NEMS operation, reduced-form versions would typically be used for many or all sectors except those being analyzed. The full module would typically be used for the sector
analyzed. Reduced-form versions would allow close approximations to the operation of the entire energy system with significantly decreased computational time and costs.
Satellite Modules
NEMS Satellite modules would examine the impacts of the energy system on economic, environmental, and security concerns. Many economic impacts would be evident directly from the outputs of the interindustry growth model. For example, overall rates of growth in gross national product (GNP) and the distribution of that growth among industries would be projected by the interindustry growth model. Other economic estimates, such as the income and regional impacts of energy policies, short-run macroeconomic effects, and effects on federal financial variables, such as the federal deficit budget, would be estimated through the use of satellite models.
Energy Security
Energy security problems are based upon the adjustment difficulty facing the U.S. and other economies in times of rapid changes, particularly rises, in the world oil price (Hickman et al., 1987; Toman, 1991). Rapid increases in oil price lead to unemployment (of people and capital equipment), GNP losses, inflation, and sharp jumps in costs of imports. Energy security, then, is measured by the likelihood and severity of economic losses associated with energy disruptions.
The severity of economic losses during energy disruptions is in proportion to the increase in the average U.S. energy price, which in turn is influenced by the fraction of the world oil (or energy) market that is disrupted. Therefore, security estimates will depend upon projections of oil production or production of close oil substitutes within unstable world regions, relative to worldwide production.
The severity of economic losses during energy disruptions also increases with the economic value of the energy (as a fraction of GNP) whose price suddenly increases. Thus the modeling system should be able to represent the dollar quantities of the various energy forms used in the United States as fractions of GNP. Short run economic analysis, most likely outside of the NEMS, must be performed to examine the linkage between world oil price changes during disruptions and changes in the prices of the various energy forms. Short run macroeconomic analysis, also probably outside of NEMS, must be conducted to examine the linakages between energy price changes and economic consequences.
The Environmental Module
The environmental implications of energy policy are of major and growing social and political concern, and they require significant attention in designing the NEMS. The integrating systems currently employed by DOE and EIA for national energy analyses do not contain an environmental component. However, some of the satellite models used by DOE for specific energy sectors (e.g., electric utilities) do reflect environmental factors and could serve as building blocks for a more systematic treatment of environmental issues.
Some of the basic requirements for a NEMS environmental module are sketched below, along with a strategy for developing NEMS capability in environmental analysis.
There is no single answer to the question of what environmental issues the NEMS should address. However, the committee believes that NEMS cannot be used appropriately to model highly site-specific environmental impacts nor those associated with unusual accidents. The system would be more appropriately used to estimate chronic environmental impacts associated with the energy system. For example, the model could be useful for estimating emissions of greenhouse gases, acid rain precursors, and the various ingredients of air pollution (volatile organic compounds, nitrogen oxides, and air toxics) outlined earlier in Table 2-1.
Such emissions are of concern because of their potential effects on natural ecosystems and human health. In most cases, however, robust measures of these effects are not readily available. Indeed, there are still significant uncertainties in most estimates of the environmental effects of energy production and use. The issues that the environmental model could address would not be comprehensive. Other environmental concerns--many in the context of local or regional issues, such as wastewater discharges, land-use issues, site-specific impacts--also are associated with energy projects. NEMS should be structured to examine the environmental issues that are expected to have a major influence in the development of U.S. energy policy in the next decade and beyond.
How, then, should the NEMS incorporate environmental concerns? The committee believes that the NEMS component models should have sufficient technological detail to estimate the total emissions of primary pollutants associated with component areas. A subsequent goal would be to develop auxiliary measures that relate emissions to effects at the global, national, and (where appropriate) regional levels. The last effort would involve experts and models largely outside EIA to characterize environmental effects and associated uncertainties.
The committee believes that all such environmental analyses should ultimately help provide the empirical basis for pursuing a policy goal of full social cost pricing, in which all the environmental “externalities” of energy production and use are valued in some appropriate way (whether using monetary or nonmonetary measures). Recognizing the difficulty of empirical work toward supporting this goal, however, the committee recommends an initial effort focused on quantifying the direct and indirect emissions associated with various environmental, health, and safety issues. This analysis would still allow interested individuals and organizations some insight into the environmental consequences of energy system changes (Edmonds, 1991; Edmonds and Barnes, 1990; Hogan and Jorgenson, 1991; Manne et al., 1990).
The approach envisioned would begin by characterizing the direct air emissions of primary pollutants for major energy supply, transport, conversion, and end-use activities. For example, emissions of carbon dioxide, sulfur dioxide, oxides of nitrogen, and trace species from coal-fired power plants, petroleum refineries, and other energy conversion sources could be characterized in terms of coefficients applicable to energy quantities
calculated by NEMS for a particular scenario. This approach would yield an estimate of aggregate national emissions. Similarly, emissions from automobile use, residential heating, and other end-use activities can be estimated. This approach was used in some energy modeling in the early 1970s and has been updated in more recent linear programming models used in the United States and Europe. Appropriate data should be available through other organizations such as the Environmental Protection Agency (EPA); EIA need not develop the primary data itself.
A related, but more ambitious, effort would employ data available for major industrial processes to estimate the secondary or indirect emissions associated with energy-related activities. For example, in comparing solar photovoltaics to fossil fuels for power generation, one might want a more complete picture of environmental implications, including emissions from the mining and refining of materials for solar cells and other plant components and similar information about fossil fuel plants. These broader analyses would require something akin to an environmental input-output model of the U.S. economy--something not currently available at DOE or EIA. Yet sufficient information is available to begin constructing this type of model for use in conjunction with future energy analyses.
Inventories of direct and indirect emissions provide a starting point for quantitatively assessing the environmental implications of alternative energy scenarios (Reister, 1984). In the longer run, additional measures and models will be needed to assess the effects of different scenarios of projected emissions. In this area, again, the committee envisions NEMS drawing on other work in the public and private sectors to find answers, such as cooperation with the Environmental Protection Agency. For the short term, estimates of the national emissions implications of energy scenarios will add significantly to the analytical capability of NEMS.
It may well be that EIA cannot devote sufficient resources to the ambitious tasks described above. In that case, it is recommended that EIA initially focus attention on the greenhouse gas emissions associated with the extraction, transportation, and use of energy. This area will probably continue to command attention in the years to come. Experience in this area may then provide EIA with sufficient expertise to move to the more complete analysis outlined above.
Report Writers.
The NEMS system should include well-designed graphics and report writers to provide routine graphical and numerical outputs of the types normally found to be helpful for analytical purposes. The outputs would take the form of standard projections of variables associated with energy security, the economy, and the environment. The system should also allow custom graphics to be generated easily. In addition, report writers should make runs self-documenting, by providing information such as the date of run, the settings for the various switches, and the model user.
NEMS COMPARED TO CURRENT DOE MODELING
Since the mid-1970s, several large-scale integrated modeling systems of energy supply and demand have been developed at EIA and later in the Office of Policy, Planning and Analysis, for use in recurring publications of energy forecasts and for policy analysis. The modeling systems include the Project Independence Evaluation System (PIES), later renamed the Mid-term Energy Forecasting System (MEFS), the Intermediate Future Forecasting System (IFFS), the Long-Term Energy Analysis Program (LEAP), the Short-Term Integrated Forecasting System (STIFS), and Fossil2 (see Appendix E).
One trend exhibited in these models has been for increased modularity and decomposition. Another related trend has been the increased diversity of modeling methodologies employed in the modeling systems. These trends have evolved as system coverage and the complexity of energy issues treated have both increased.
The model structure proposed in this report resembles current EIA modeling systems, particularly the IFFS, which is a modular system. The proposed NEMS would represent a logical continuation of EIA model development. NEMS would draw heavily on current EIA approaches and could use revised versions of many current EIA models.
There would be some notable differences, however, between NEMS and the IFFS. Reduced-form versions of full modules have not been constructed. The IFFS system cannot run as a complete system on a personal computer, although parts of it can. NEMS would also require some entirely new models, in particular, the interindustry economic growth model and an environmental impacts model. In addition, current models of economic and energy security impacts are not adequate for the proposed system. Finally, IFFS calculations currently clears markets one year at a time, thereby precluding any representation of rational expectations or other “look-ahead” behavior.
The Fossil2 model of the Office of Policy, Planning and Analysis, which was used as the integrating framework for the first NES, is constructed using a different strategy. It is not modular. Rather, it includes all supply, demand, and market-clearing equations in one comprehensive dynamic simulation model. Each sector is represented by a set of differential and integral equations that relate the stocks (energy production, transformation, and consumption facilities and entities) and the flows (energy quantities, prices, and information). It would be very difficult, if not impossible, to substitute alternative component modules in Fossil2.
For the NES, the various component parts of Fossil2 were calibrated to mimic the EIA Annual Energy Outlook (AEO) reference case to the year 2010. Fossil2 parameters describing sectoral behavior were changed so that projections (at baseline prices) corresponded to the projections in the AEO base case. However, the response of supplies and demands to prices in general was not calibrated to the external models, such as those at EIA.
This use of Fossil2 would be quite similar to the proposed NEMS with all (only) reduced-form versions, if Fossil2 were calibrated so that the responses of outputs to inputs
(for example, quantities to prices) were chosen to correspond to the external models. The key difference, however, is that Fossil2 components may well be more complex than NEMS reduced-form versions. Such greater complexity would provide greater richness of detail and more policy “handles” for analysts, but would make calibration more difficult for the NEMS. Nevertheless, NEMS reduced-form versions could be exactly like the components of Fossil2, if Fossil2 components were deemed the best reduced-form versions of the external models. Fossil2 components then could be used in NEMS if it were possible to separate them in the form of component modules.
The Fossil2 model differs from the proposed NEMS in that its structure is explicitly calculated on an annual basis: one year is calculated, then the next, and so on. Given such a structure it is easy to incorporate myopic expectations and adaptive expectations. However, to incorporate rational expectations, the entire model must be run over and over, using the output prices from any run as input prices for the next run. While in principle such an approach is feasible, in practice it would be very time consuming and probably not routinely pursued.
The Fossil2 model also differs from the proposed NEMS in its market-clearing mechanism. Prices move over time in response to differences between supply and demand, so that in any given year prices might not cause markets to clear. To minimize the modeling difficulties such nonclearing might cause, Fossil2 is recalculated four times for each year. While four interactions is probably sufficient to bring each year's supply and demand into close approximation, it cannot be guaranteed that markets would clear.
NEMS TREATMENT OF CONCEPTUAL ISSUES
NEMS architecture should incorporate conceptual issues that are significant to debates about energy market operations. This section considers how the proposed NEMS could address such conceptual issues.
Market Disequilibrium
NEMS architecture should be based on the idea that energy markets will clear: energy prices will take values such that supply is equal to demand for each energy form (Weyant, 1985). One question is the time it takes markets to clear, given whatever regulatory or other rules exist. The concept of equilibrium is less useful if markets do not clear within the time period modeled, for example, one year.
The equilibrium price model assumes that instantaneous adjustments occur; it does not consider the actual time it may take real markets to clear. In some cases, market clearing occurs over a long period as when there are government-imposed price controls and nonmarket allocations of energy forms. Government interventions can create market disequilibria that last for years, if not decades.
The NEMS modeling system could be used in a simple way to examine non-market-clearing associated with price controls. Rather than require the price-controlled market to converge to equilibrium, the model user could set product price-say retail price
for gasoline--to the government controlled price. The test for convergence could be modified to allow the price-controlled product market to remain out of equilibrium while other markets converged to supply-demand equilibria (equilibria likely to differ in many markets from those that would obtain without the price controls).
Another important question is the market-clearing mechanism. Do markets clear based on fluctuations in price? With other clearing mechanisms (fluctuations in production, for example) the economy still has competitive markets that clear, but these markets have different characteristics and outcomes. Instead of moving to the equilibrium point given by conventional supply-and-demand curves, the markets may clear by shifts in the curves themselves. For example, when there are government imposed price controls on gasoline, the length of the gasoline lines could be expected to adjust to clear markets. In an aggregate model, such adjustments in waiting times could be seen as shifts in the demand functions for gasoline. Such adjustments could be incorporated in the modeling system if it were known what shifts might occur.
The success of the equilibrium price-model in predicting politically feasible outcomes depends on relatively large responses on either the supply or the demand side of the market to changes in price. If the responses (elasticities) are both very small, price increases (e.g., in oil) may cause large real-income changes (people cannot reduce their oil bills by buying less), and the public is politically unlikely to let the market work. Thus, the model user must consider political infeasibility of some possible equilibria.
Uncertainty
As discussed previously, forecasting and policy analysis require understanding the degree of uncertainty in model outputs. As discussed in Chapter 2, careful analysis of uncertainty requires a large number of model runs, using not only the standard modules, but also various combinations of alternative modules. Unless some method is used to shorten the time this analysis required, it is so time-consuming in practice that it is seldom conducted.
One requirement for the NEMS, therefore, to analyze uncertainty, is the ability to run the model very quickly. One method of doing so relies on the use of reduced-form versions that can each be run quickly, to rapid system convergence to an equilibrium.
Such analysis would be conducted in two stages. In stage one, the uncertainties associated with each individual module would be characterized by exercizing that module. Two elements of uncertainty are particularly important for projections: uncertainty about the projections based on a particular set of inputs, and uncertainty about actual values of the input variables. These uncertainties could be used to construct a stochastic version of the reduced-form version for a given sector. This simplification could be achieved by imposing a probability distribution on the parameters used in the reduced-form version to correspond with the probability distribution associated with the full module.
Once the stochastic reduced-form versions were developed, the overall system could be configured to run based entirely on reduced-form versions. Monte Carlo simulation techniques could be used to randomly select combinations of the various parameter values
for each of the reduced-form versions. Then the entire model could be run until it converged to an equilibrium. This process of randomly selecting parameters and running the overall model could be reiterated until sufficient data were obtained.
The advantage of using reduced-form versions for such a process is primarily that of speed. The greatly reduced turnaround time that the use of reduced-form modules permits may bring such Monte Carlo simulations to manageable proportions. In addition, the use of reduced-form versions may make it easier to incorporate purely subjective probability distributions for the underlying parameters. This ability might encourage researchers to avoid underestimating the uncertainty associated with the underlying models and therefore to avoid underestimating the uncertainty associated with the system as a whole.
Contingent Strategies
As discussed previously, many private and public policies cannot be regarded as predetermined, but rather should be seen as responsive to the immediate, externally imposed situation. For example, were it not for the rapid oil price increases in 1973–74, Presidents Ford and Carter probably would not have initiated the energy policy proposals of that period nor would Congress have passed legislation such as that imposing corporate average fuel economy (CAFE) for new cars. Thus, energy demand and supply functions for energy were themselves shaped by unexpected events. Similarly, the U.S. Synthetic Fuels Corporation could be seen as having pursued contingent strategies in attempting to create energy technologies that could be more rapidly developed by the private or public sector, in case changing energy situations created the need. As it turned out, evidence mounted that energy prices would not rise as rapidly as previously expected and that the costs of synthetic fuels would be higher than some had expected, and the entire effort was disbanded.
Such contingent strategies are conceptually important in modeling the uncertainty in the energy system. In a deterministic forecast, contingent strategies can be treated exactly like deterministic policy choices: they are adopted or not. Thus, for deterministic modeling there is nothing special about contingent strategies.
The essence of contingent strategies is that policy rules themselves may depend on features of the energy system. For example, if energy prices go above a particular point, then energy conservation rules may be imposed. If energy prices remain below another level, or are projected to continue below some level, then such policies may be repealed. In a stochastic modeling environment, contingent strategies will be governed by one set of rules in one state of the world and by another in a different world state.
Projecting such endogenous policy changes is particularly difficult and not always relevant. However, if they can be predicted with some probability, then such contingent strategies can be encoded into NEMS. Within the relevant modules, there would simply be logical statements that test whether the state of the system is such that new rules would be triggered or old rules eliminated. If so, then the relevant equations in the modules would be adjusted. Thus, the conceptual difficulty with analysis of contingent strategies is their clear specification in the first place.
There would also be practical difficulties in addressing contingent strategies. It will be much more difficult, if not impossible, to use reduced-form versions of modules that accommodated contingent strategies. However, reduced-form versions could still be used for other modules. Clearly, the analysis and computing time, but especially computing time, for examining contingent strategies may be extremely large.
The Formation of Expectations
Yet another question, related to that of disequilibrium, is how models should represent expectations of future prices (Muth, 1981a, b; Lucas and Sargent, 1981). Several alternative assumptions are possible. The simplest is “myopic expectations,” that individuals in the market assume future prices will remain the same as current prices (Muth, 1981a, b; Lucas and Sargent, 1981). In a stochastic setting, “myopic expectations” are calculated using the random-walk model that has been highly successful in forecasting financial markets.
Alternatively, the “extrapolative expectations” hypothesis assumes that individuals extrapolate recent trends in prices to forecast future prices. Individuals do adjust, but not instantly, to changing information, and a random walk characterizes the trend lines of energy variables.
Finally, individuals assumed to have “rational” expectations forecast prices and other economic conditions consistently with the model. When economic actors behave “rationally,” rather than “adaptively” they do not gradually change their behavior in response to new information or different circumstances but adopt new decision rules as information or circumstances change. Decision makers are also assumed to look to the future-- to their expectations-- rather than just to the past--their experiences-- when making decisions. Assuming rational expectations, if the model is deterministic, then individuals forecast prices correctly; if the model is probabilistic, then individuals forecast prices using the same probability distribution about future prices that results from the model.
The assumption of rational expectations emphasizes the important point that people learn from their pasts and try not to repeat mistakes. It reflects the observation that behavior sometimes does change quickly and discontinuously. Because expectations about the future are strongly conditioned by our experience, the real question becomes the extent to which our behavior is rational or adaptive. Learning theory researchers have found that people often make systematic mistakes and that they take time to move from one mode of behavior to another. Thus neither theory perfectly predicts actual human behavior.
There is a further conceptual distinction between rational expectations and adaptive expectations approaches when incorporated into policy relevant models. Rational expectations, or self-consistent expectations, when incorporated in models, embodies the basic concept that government policymakers cannot know the future better than private actors. Use of rational expectations concepts in NEMS would be consistent with a belief that policymakers cannot be assumed to have such privileged access to information about the future. The use of adaptive or myopic expectations implies that government planning can always improve on private decision, because the government can be assumed to know the future better than private actors.
It is currently an open debate as to which assumptions about expectations most accurately, or most inaccurately, describe the world. And a number of energy policy debates turn on disagreements as to whether governmental regulation can improve on private decision-making from the perspective of the individual actors. Thus the appropriate description of expectations will not be easily resolved. For that reason it is important that the modeling system be capable of addressing each of the assumptions about expectations formation.
These assumptions can influence model projections including assessments of particular policy options. Unless the process of expectation formation is considered explicitly by NEMS, it will be difficult to assess the system-wide consequences of programs designed to educate people about energy issues or of behavior shifts occasioned by changes in beliefs. If people systematically underestimated future energy prices and therefore systematically bought more energy-intensive capital equipment than they would otherwise, this belief, if identified, might lead to a policy of advertising that energy prices are likely to increase. In a world of myopic expectations, such a strategy might significantly change behavior. In a world of rational expectations, such a strategy would have little or no effect on behavior, since the assumption of rational expectations is contrary to people systematically understating future conditions.
A less obvious example illustrates the feedbacks that may depend on expectation formation. Assume that incentives are proposed to increase the efficiency of newly purchased cars beginning in five years. Such a policy might significantly reduce consumption five or ten years from its implementation. But the consumption reduction might reduce the price of gasoline and thus make it more cost-effective for consumers to buy less fuel-efficient cars in the first few years. If we assume rational expectations, then the model will show that consumers will buy less efficient cars in early years and will therefore consume more gasoline during the first few years the policy is in place. Even over a longer period, the earlier purchases of inefficient cars would increase gasoline use compared to the case if there were no such anticipation of a price drop. If the model assumed myopic or extrapolative expectations, then it would show consumers in the first few years as not anticipating the price reduction and thus not changing their automobile purchases. These models would show that in all years the policy would reduce gasoline use or leave it unchanged. Thus, assumptions about expectations formation can change the magnitude and even the direction of overall impacts of some policy impacts.
If either myopic or extrapolative expectations are believed to best describe world, then NEMS can be run on a year-by-year basis and price data can be based on either the current price or the current and previous prices. However, if rational expectations formation is assumed and a deterministic model used, then NEMS must be solved for all years simultaneously, since supplies in any year will depend on prices projected for future years as well as current and past prices. In principle, iteration based upon all prices would be similar to iteration based upon only the current prices. However, the greater dimensionality of the problem could be expected to increase the time until convergence is obtained, perhaps greatly. In such a case, it would be important to devote attention to computationally efficient algorithms.
For a probabilistic model, however, the process would involve an immensely more complex, time-consuming endeavor. In principle, one would start with a probability distribution of prices, associated with the full range of uncertainty. This distribution would lead to one vector of actual prices for each possible outcome. Finding this one vector would require the iterative processes discussed above, and the process would have to be repeated for each resolution of the uncertainty. The result would be a probability distribution of prices over time. If this distribution were consistent with the starting distribution of prices, then the solution would be a “rational expectations” equilibrium. However, if the distributions were not consistent, then the starting distribution would be adjusted and the process repeated. This sequence would be continued until convergence were reached.
While in principle rational expectations equilibria could be found in this way for a probabilistic model, in practice the process would be so time-consuming as to be entirely impractical unless better algorithms are developed and computer speeds increased above those currently available. Thus, the NEMS will not be used routinely to examine probabilistic rational expectations equilibria, even though rational expectations concepts are logically most consistent only in a stochastic environment. Yet it is important that the model capture as well as possible the effects on behavior of changing information, particularly information changing as a result of contemplated policy actions.
Environmental Constraints
The NEMS is likely to be used to examine the economic, environmental, and security implications of various types of environmental constraints. Historically, the instruments for environmental regulation were primarily technology-specific requirements relating to the use of so-called “best available control technology.” Such rules set limitations on the technologies that could be adopted in the regulated sectors. Simulations of the effects of such restrictions could readily be incorporated into the proposed system by modifying descriptions of technologies underlying the various supply and conversion models.
More recently, however, more market-related policies have been adopted, such as the marketable-permit system for acid rain precursors. Such regulations impose system-wide or sector-wide constraints on the amount of residuals emitted. System-wide or sector-wide constraints can also be incorporated into NEMS, by bringing some parts of the environmental impacts module into the integrating system. A per-unit emissions price (e.g., a price per ton of airborne sulfur) could be associated with discharge of the measured residual. Total discharge could be calculated at each iteration based on the economic incentives associated with the estimated emission price. Equilibrium would obtain when the total emissions “supplied” by the system are identical to the maximum emissions allowed. When these two quantities differ, the emission price could be adjusted from iteration to iteration in the same way other prices are adjusted.
Figure 3-5, illustrates the convergence process for system-wide environmental constraints. This figure is similar to Figure 3-2, but in place of the demand module response is the maximum total emission, set by the regulations. The emission “supply” response is represented by the downward sloping curve, which projects total emission supply
price for each possible total emission level. This supply price would be based on the estimated behavior of the industries modeled. Equilibrium would be represented by the emission price and emission quantity at which the two lines cross.
In Figure 3-5, an initial price is chosen, P0, far from the equilibrium price. The maximum total emission remains at QMax. The modules projecting emissions would then read the price P0 and provide an emission estimate of Q0. The integrating system would be at a solution if Q0 were close enough to QMax. If Q0 exceeded QMax, the next iteration would be based on a higher price, and conversely, if Q0 were smaller than QMax, the next iteration would be based on a lower emission price. This new starting point is represented in Figure 3-5 by P1. The process is repeated until projected and maximum emission are sufficiently close.
OPERATIONAL ISSUES FOR NEMS DEVELOPMENT
Several operational issues should be given careful attention in constructing a modular system. Such attention should be given to the tradeoffs among model detail, needs for data to support the model, computing hardware, and software requirements. It is useful for each module to be scaled to about the same size and detail, so that no single module dominates the choice of computer hardware and limits the usability of the overall system. However, the EIA models include at least one--the coal model--that is far more detailed and larger than useful for the NEMS. Such models will need to be greatly streamlined and simplified. Other models may need expansion to provide the detail appropriate for the system.
Although a modular system could be developed through decentralized teams, in practice full decentralization is not feasible. Rather, constraints should be imposed beyond those implied by the interfaces. For example, the NEMS office may specify that a given module must not require more than a certain amount of comuter memory, to allow the entire system to be operated on a personal computer. EIA personnel could be expected to examine models for quality assurance. Particular coordination would be required to assure that modules all use common data bases, common economic assumptions, and regional, product, and time definitions, as appropriate.
The time sequence of efforts will be important, because it would be unrealistic to expect all NEMS modules to be developed during the first year of NEMS efforts. Perhaps construction of the integrating framework and the control module should be given the highest priority. Early attention could be paid to reducing the size of any unnecessarily large model that would be included within the integrating system. The EIA should build the integrating framework and control module from scratch, after determining the appropriate regional, temporal, and product definitions. However, development of the other modules probably should initially rely heavily upon models already in existence in EIA or elsewhere. Such development might involve bridge or conversion systems to link existing modules into the new integrating framework. It might involve recalibration of modules to the new regional, temporal, and product structure. Or it might involve redevelopment of existing models, using existing conceptual structures, empirical evidence,
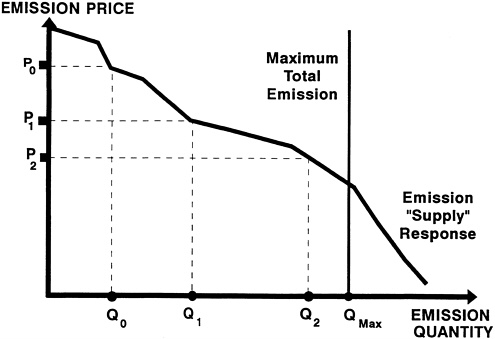
Figure 3-5 Modeling a system-wide environmental constraint.
and data, but entirely new computer code. Over time, it is envisioned that new modules would be developed and would supplant these modules.
Several issues are particularly important for redeveloping existing modules. EIA should incorporate the capability of projecting key system-wide environmental impacts into each of the models as they are redeveloped. In particular, emissions of various air pollutants should be estimated for each of the modules within the system.
While modules are being constructed, EIA should give attention to building in to the modules explicit representation of factors that might be modified by specific policy actions. Examples of policy actions that the committee believes to be important include those associated with taxes, environmental constraints, conservation incentives and regulations, and new technology development.
To use reduced-form versions, EIA would have to develop the appropriate methodologies and software for estimating response surfaces. While other researchers have developed methods, EIA personnel or contractors would need to further develop these approaches or to contract for their further development. Because reduced-form versions would greatly facilitate NEMS use for quick-turnaround analyses, the development of the methods and software to estimate response surfaces should be given fairly high priority.
RECOMMENDATIONS.
-
The NEMS should be designed to be modular in structure, so to be flexible in its use and to readily accommodate the substitution of alternative models (modules) in the system.
-
A single model should not be used for short-term, medium-term, and long-term analysis. Similarly, the DOE should not select the model to be used for medium-term analysis based on the desire to conduct long-run analysis through the same framework.
-
The EIA should attempt to acquire an existing interindustry growth model and should not attempt to develop one itself.
-
Development of the NEMS can rely extensively on existing models. However, several new models should be developed or acquired from external sources: beyond the interindustry economic growth model, these should include an environmental impacts model and a renewable energy supply and conversion model. Demand models need to be modified to enable a broader range of policy analysis than is possible with the current EIA models.
-
A reduced-form version of each module should be developed and integrated in to the NEMS. Such versions should approximate the response surface of the full modules. For typical policy analyses, the full module would be used for the sector examined and reduced-form versions would be used for other sectors. Reduced-form versions could also be used in uncertainty analyses, tests of the integrated set of modules, and quick-turnaround policy analyses.
-
The NEMS should be configured to run on personal computers or workstations, unless such hardware constraints would entail significant loss of the capabilities envisioned for NEMS.
-
One or more EIA analysts should be charged with the general knowledge of all modules, even those not developed at EIA.
-
In developing the environmental module, initial efforts should be focused on quantifying direct and indirect air emissions. If resources are not sufficient for this
-
task, then EIA should focus attention first on the greenhouse gas emissions associated with the extraction, production, transportation, and use of energy.
-
The NEMS should capture the effects on behavior of changing information, particularly information changing as a result of contemplated policy actions. Model users should be able to include alternative assumptions about the formation of expectations, including those defined theoretically as myopic, adaptive, and rational expectations.
-
The NEMS should provide carefully envisioned graphics and report writers to provide routine graphical and numerical outputs of the types normally found helpful for analytical purposes.
-
A major effort is needed to collect more extensive data and information on the U.S. energy system, especially on end use. In such an effort, DOE and EIA should consider the following points:
-
Essential to bottom-up demand modeling is knowledge of underlying activities: housing, commercial buildings, industrial production, and transportation. To obtain such information, EIA needs to improve its link to other data-gathering entities.
-
Where behavioral information is inadequate, EIA or other DOE offices should help generate interest in obtaining it, by soliciting research, holding workshops, or stimulating other agencies to sponsor research. EIA should devote some resources to sponsoring research in ayuiathis area.
-












































