5
Could a Nearby Earthquake Cause Flooding of the Proposed Repository?
INTRODUCTION
Contemporary Crustal Motions
Understanding contemporary crustal motions in the Yucca Mountain area is fundamental to estimating recurrence rates and magnitudes of earthquakes that might be expected, and hence to the problem of assessing tectonically induced hydrologic effects on Yucca Mountain. Theoretical models to date, as discussed later in this chapter, suggest that both interseismic (between earthquakes) and coseismic (during earthquakes) strain are unlikely to cause flooding of the repository for a broad range of crustal strain rates. Nonetheless, the contemporary strain field is one of the few parameters in most models of tectonically induced water table fluctuations that can be measured, and both the number and size of potential excursions of the water table from its present level induced by earthquakes over the next 10 ka are dependent in part on contemporary crustal motions. The lower the contemporary displacements, the lower the chances of tectonically induced flooding, and vice versa.
As was suggested in Chapter 2, both rapid and slow tectonic extension has affected the Yucca Mountain area over the last 20 Ma. Here it is important to distinguish between rapid extension and slow extension rates in the region. The Great Basin in general is currently extending slowly and fairly diffusely, at a total rate of 5-10 mm/yr. However, at various times in the past, rapid extension (10-30 mm/
yr) developed locally in narrow domains embedded in various places in the province. Slow extension appears to be associated with the formation of the modern basins and ranges in the northern Great Basin, and largely post-dates the early rapid extension. The Death Valley extensional fault system is the youngest of these rapid-extension domains. Much of the basin-range topography in the region is a reflection of rapid extension over the last 10 Ma (especially south of Yucca Mountain in the Death Valley region), but slow extension faults that post-date rapid extension appear to control much of the topography in the Yucca Mountain area (e.g., the Bare Mountain fault). While relatively rapid extension may still be active in the Death Valley/ Owens Valley region, the Yucca Mountain area has not experienced rapid extension in the last 10 million years. Thus while rapid rates may have approached 30 mm/yr in mid-Miocene time (15-10 Ma), the average extension rate across the entire basin and range since then is probably on the order of 10 mm/yr, currently concentrated in areas to the west of Yucca Mountain (see, e.g., Eddington et al., 1987; Wernicke et al., 1988).
Several independent means of determining contemporary motions have been employed, emphasizing varying scales of deformation. Calculations of contemporary plate motions for the last 2 Ma combined with the movement history on the San Andreas fault indicated a discrepancy between the inferred net plate motion between the North American and Pacific plates and the measured slip on the fault. Reconciling the difference in movement estimates requires including WNW extension across the Basin and Range of about 8-11 mm/yr (Minster and Jordan, 1987). This rate is corroborated by very long baseline interferometry (VLBI), a technique that measures distances on the earth's surface by the use of radio waves, and can measure small changes in those distances over time. The changes in distance measured suggest contemporary extension of not more than 12 mm/yr in the region east of the San Andreas fault (Minster and Jordan, 1987).
Seismic analysis, although covering only a brief segment of the recent past, suggests similar values. Adding up the fault slip and averaging it into an extension rate across the southern Great Basin yields approximately 3.5 mm/yr total. This calculation excludes the 1872 Owens Valley earthquake which had a magnitude of approximately 8 (M ≈ 8) on the western edge of the basin. The rate increases to 29.2 mm/yr if that event is included (Eddington et al., 1987). The northern Basin and Range yields values on the order of 8-10 mm/yr. These values are in broad agreement with local geodetic studies (e.g. Savage, 1983) and estimates from slip rates on Quaternary faults (summarized in Eddington et al., 1987).
There are few data on the nature and rate of contemporary motions in the Yucca Mountain area because of the low seismicity there. On the basis of a summary of geologic information related to Quaternary vertical offsets on faults on Yucca Mountain, Scott (1990) estimated the present extension rate to be less than 0.01 mm/yr. There is, however, considerable uncertainty associated with that estimate.
Elevation surveys in Nevada along a line from Tonopah to Las Vegas that crosses the southern part of Crater Flat and Yucca Mountain suggest 25.5 ±3.5 cm of subsidence of Crater Flat relative to Bare Mountain and Yucca Mountain over the last 75 years, based on three surveys from 1910 to 1984 (Gilmore and Carr, unpublished data). These data indicate a subsidence rate of over 3 mm/yr. Such subsidence could occur as a result of slip on dipping normal faults and hence would require extension rates at least two orders of magnitude greater than the accumulated slip rates on Quaternary faults on Yucca Mountain estimated by Scott (1990). The greater rate, 3 mm/yr, is consistent with the rate determined for the southern Great Basin excluding the Owens Valley event. Unfortunately, no detailed geodetic information across Yucca Mountain has been published that could be the basis for evaluating the difference in rates.
Additional uncertainty about the total strain of the region results from unknown relative contributions of strike-slip and normal dipslip movement on faults of the region. The 0.01 mm/yr Quaternary extension rate reported by Scott (1990) was based only on the easily observable vertical components of fault offset in alluvium. Often small lateral offsets on young faults are much more difficult to detect and measure. Contemporary analysis of fault motion from seismic data (focal mechanisms) of small to moderate earthquakes in the southern Nevada region indicate the dominance of strike-slip motion (Harmsen and Rogers, 1986). This dominantly strike-slip mode of deformation is observed in focal mechanisms in a 100-150 km wide zone along the Northern Basin and Range-Sierra Nevada border zone (Zoback, 1989). Large historic earthquakes with surface rupture in this zone all show primarily strike-slip offsets (Beanland and Clark, 1992; Bellier and Zoback, 1991; dePolo et al., 1987; Saunders and Slemmons, 1979).
Thus, the focal mechanisms in the southern Nevada area and regional relations all suggest that a future large magnitude earthquake in the Yucca Mountain area would be strike-slip, not dominantly dipslip as has been assumed in the past. Consideration must be given to potential strike-slip fault zones such as a possible fault up Yucca Wash. Furthermore, extension rates calculated from vertical fault offsets may be poor indicators of the total contemporary strain in the Yucca Mountain region.
Recommendation
Another means of measuring changes in crustal dimensions is the Global Positioning System (GPS). The advent of GPS satellites in the last five years provides the capacity to measure crustal positions accurately to within approximately 3 mm for 10 km baselines, without need for line-of-sight procedures between stations (Hager et al., 1991). In addition, GPS yields vector motions (changes in lengths and angles) between points, rather than simply angles or absolute distances, and does so with easily deployable receivers. Thus GPS offers the potential to constrain the contemporary displacements in the Yucca Mountain area. With this rapidly developing technology, it is expected that in the near future GPS surveys will be able to distinguish baselines extending at <0.3 mm/yr or greater. Although the impact of this information on increased understanding of the hydrologic conditions around Yucca Mountain is uncertain, knowledge of the rate of crustal strain is clearly important to nearly any seismic risk assessment related to the proposed repository site. In the panel's view, this information used as an accessory to, or confirmatory of, more standard information on rates of crustal deformation, can provide additional confidence in the prediction of future tectonic behavior and the probabilities of seismic events in the area.
The panel recommends that a combined GPS and leveling program be carried out across the Yucca Mountain region. GPS is more accurate for horizontal motions than vertical, but with relatively short baselines and atmospheric corrections it is also capable of precision at the millimeter scale in the vertical. Leveling surveys and local GPS surveys across Quaternary faults have been initiated by the USGS (G. Perasso, pers. comm., 1991), but longer baseline studies that offer valuable information for evaluating risk should also be included.
HYDROLOGIC RESPONSES TO EARTHQUAKES
Assessing how ground water in a specific locale will respond to a nearby earthquake involves several diverse considerations, including the hydrologic character of the region, the type of crustal rocks and their response to stresses, the tectonics of the region and likely type of faulting, historical seismicity (to evaluate the possibilities), and the probability that earthquakes of a particular size will occur. These considerations involve knowledge of a variety of disciplines and the application of several techniques. Besides hydrology and seismology, geology is needed to define the location, geometry, and potential
of seismic sources; geophysics is required to identify the elastic properties of materials at depth; and historical seismicity must be considered to provide the experiences of past earthquake history; mathematics, especially the statistical/probabilistic subdiscipline, and modeling, or computations of likely behavior and responses, are necessary for evaluating the possible response of a system to earthquake wave disturbances, whether it is natural, like the hydrologic system, or engineered (see, e.g., Reiter, 1990). The likelihood (or probability) of the occurrence of an earthquake of a given size in a specific location is an important part of that evaluation.
Thus, in evaluating the range of possible responses of the water table to an earthquake that could reasonably be expected to occur in the Yucca Mountain vicinity, the panel has considered some examples from the historical record of water table responses to significant recent earthquakes; some modeling results, with the data and assumptions used in the calculations; and the probabilities of significant earthquakes occurring in the area.
There are two distinct responses of the ground-water system to an earthquake: (1) the dynamic response accompanying the passage of earthquake waves that follow the earth's surface, and (2) the response that accompanies the resulting permanent change (volume strain) in the rocks of the crust after the earthquake waves have passed through.
The dynamic water-well response is usually associated with dynamic changes in rock volume that accompany the type of surface wave called the Rayleigh wave. This response can occur at great distances from the earthquake epicenter. For example, the water level in a well in Florida fluctuated approximately 10 meters in response to the Alaskan earthquake of 1964 (Waller, 1968a). This dynamic response of ground water is a short-lived phenomenon known as a transient, and therefore is not relevant to the long-term behavior of the crust in the vicinity of a proposed repository.
The response of the ground-water system to the permanent post-earthquake changes in both strain and permeability of the rocks is of concern because either or both types of change may produce long-term changes in the level of the water table. The observed long-term responses appear to be related to either of two phenomena: (1) a change in pore fluid pressure resulting from the dilatation produced by the permanent volume strain, or (2) an increase in permeability produced by the dynamic ground motion. The two phenomena may be difficult to distinguish from one another.
HISTORICAL EVIDENCE
The hydrologic changes associated with moderate and large earthquakes have been known for some time (Carnegie Institution, 1908; La Rocque, 1941). As suggested above, many of the observed phenomena are associated with the dynamic response (Eaton and Takasaki, 1959; Cooper et al., 1965; Liu et al., 1989). As examples, post-seismic changes in both spring flow and stream flow were documented in response to: (1) the 1952 Arvin-Tehachapi earthquake—M=7.1 (Briggs and Troxel, 1955), (2) the 1959 Hebgen Lake earthquake—M=7.3 (Stermitz, 1964), (3) the 1968 Matsushiro earthquake swarm (Nur, 1974), (4) the 1983 Borah Peak—M=7.0 (Whitehead et al., 1985; Wood et al., 1985; Wood, 1991), and (5) the 1989 Loma Prieta earthquake—M=7.0 (Rojstaczer and Wolf, 1991, 1992). The stream flow was observed to increase following the earthquake in all of these instances. Post-seismic changes in ground-water levels have also been observed in (1) a series of Los Angeles basin earthquakes from 1933 to 1940 (La Rocque, 1941), (2) the Dixie Valley-Fairview Peak, Nevada earthquakes of 1954 (Bell and Katzer, 1987), (3) the Arvin-Tehachapi earthquake (Davis et al., 1955), (4) the Good Friday earthquake in Alaska, 1964 — M=8.6 (Waller, 1968a; Waller, 1968b), (5) the Borah Peak earthquake (Wood et al., 1986; Wood, 1991), and (6) the Loma Prieta earthquake (Rojstaczer and Wolf, 1991, 1992). This is not a comprehensive list of previous observations in this area.
Several mechanisms have been postulated to explain the observed long term changes. As suggested above, the mechanisms fall into two classes: (1) a change in pore pressure associated with volume strain produced by the earthquake, and (2) an increase in permeability caused by dynamic ground motion. The best documented of hydrologic responses are for the Alaskan Good Friday earthquake; the Loma Prieta earthquake; and the Borah Peak earthquake.
In some instances it is difficult to distinguish between the hydrologic effects produced by volume strain and those produced by an increase in permeability. If the steep gradient north of Yucca Mountain (discussed in Chapter 3 of this report) is the result of a permeability barrier, dynamic shaking could increase the permeability of the barrier. The results of a study modeling this scenario, also described in Chapter 3, suggest a modest rise of the water table, about 40 meters, beneath Yucca Mountain.
Loma Prieta, California
The Loma Prieta earthquake (M=7.0) of 1989, which was in the San Francisco area, caused a tenfold or more increase in the amount of water flowing in streams of the nearby Santa Cruz Mountains. The most dramatic increases were measured in a 30-40 km2 area north of the end of the ruptured part of the fault that caused the earthquake. This phenomenon was well documented by a number of stream gages in the area that measured the increase in stream flow (Rojstaczer and Wolf, 1991, 1992). The best explanation of these observations appears to be that the ground motion, which was amplified along Skyline Ridge as the surface wave passed through, increased the permeability of the shallow aquifers. The increase in permeability caused the water table to drop as the ground water drained downward through the rocks and discharged to the streams. Numerous water wells at higher elevations along Skyline Ridge dried up, suggesting that the mechanism described was the likely cause. As yet, no analysis of the magnitude of the increase in permeability has been made. This hydrologic response to the Loma Prieta earthquake is the best documented example of this phenomenon. The increases in streamflow persisted for 6 to 12 months.
Anchorage, Alaska
Wells in the Anchorage area near the epicenter of the Good Friday, 1964 earthquake (M=8.6) had changes in water levels that are clearly associated with that event (Waller, 1968a; Waller, 1968b). This earthquake is the largest in North America in historic time. It involved thrust faulting (denoting compressed crustal rocks) along a 1000 km section of the Alaskan subduction zone. As in the Loma Prieta event, in most cases the ground-water levels declined by amounts ranging up to approximately 5 meters. Most of the observed lowered water levels were in quite shallow wells.
Borah Peak, Idaho
The hydrologic responses associated with the Borah Peak earthquake of 1983 (M=7.0) are well documented (Wood et al., 1985; Wood, 1991). The Borah Peak earthquake involved movement on a normal fault (denoting extended crustal rocks) along the western front of the Lost River Mountain Range in Idaho. Many springs in the area in-
creased their flow. The baseflow, or ground-water discharge, to local streams also increased. The stream flow effects resemble those for Loma Prieta, but smaller; in the Borah Peak area stream flow increased by a factor of only two or three. Unlike Loma Prieta, however, there was a 5-35 m increase in water levels in the vicinity of the epicenter attributed to an increase in ground-water pressure (Wood et al., 1985; Wood, 1991); in one area of cavernous carbonate aquifers, unconfined fountaining of jets of ground water to 5 m in the air occurred for several minutes, about 2 km west of the fault trace.
The largest observed effect of increased water pressure resulting from the Borah Peak event occurred in the Clayton Silver Mine, about 50 km west of the epicenter, where the seepage into the mine following the earthquake could not be controlled, as it had been before the earthquake, by the 930 gallons per minute (gpm) pump previously installed to keep the mine dry. Due to post-earthquake changes, an increase in ground-water flow caused the water level in the mine to rise approximately 60 m in a matter of 10 days. Two weeks later a 2000 gpm pump was installed and the water was lowered back to the mining level. Increased flow into the mine could have resulted from either an increase in permeability or a rise in pore pressure. The data are insufficient to determine which was the cause.
The mechanisms responsible for the hydrologic changes resulting from the Borah Peak earthquake are not easy to interpret. Wood (1991) observed that the major increase in hydraulic head (elevation to which water rises because of ground-water pressure) occurred on the down-dropped fault block. This suggested to him that a compressive volume strain within the block caused the rise in water level.
RECOMMENDATION
The information included here by no means reflects an exhaustive search of the water level changes associated with earthquakes. The panel recommends that DOE conduct a detailed literature search to determine the hydrologic effects of other historic earthquakes, local and worldwide, to evaluate the potential for significantly large water table rises by the coupling of the seismic and hydrologic systems. Such information as earthquake magnitudes, type of faulting, rupture length of the fault, depth to the pre-earthquake water table, and details of the hydrologic system and its response should be obtained for comparisons and analysis of possible natural analogs to Yucca Mountain.
EARTHQUAKE MODELS
Introduction
Two approaches have been used to evaluate the impacts of a nearby earthquake on the water table. One models the strain in the traditional way, using dislocation theory, which examines the effect of the fault movement associated with an earthquake on the surrounding rocks. The difficulty with the dislocation model is that it does not yield a regional change in the state of stress. The mathematical procedure integrating the change in stress across the fault, in effect, balances the resultant extension on one side of the fault following an earthquake caused by movement on that fault with the compression on the other side of the fault. The change in stress thus sums to zero. This suggests that the increase in pore-water pressure on the compressed side of the fault will dissipate as the water is driven towards the opened pores on the extended side of the fault and equalize. A rise in the water level is thus unlikely.
The second approach is to model the change in the regional stress caused by a normal-fault earthquake in a region of extension, where the earth's crust is pulling apart, such as the Basin and Range. In that case the earthquake has the effect of removing the horizontal tension. Release of the horizontal tension is roughly equivalent to increasing the horizontal compressive stress. This then compresses the rocks at depth, squeezing out ground water, which now can only move upward. This mechanism could raise the water table.
Both modeling approaches (the dislocation and the regional stress change), have been used to analyze the effects of an earthquake on the water table level. Carrigan and King (1991) used the dislocation model and focused on a relatively shallow depth, approximately 1 km below the surface. A subsequent analysis (Carrigan et al., 1991) included depths to 8 km and high-magnitude earthquakes. Cook and Kemeny (1991) used the regional stress change model. Bredehoeft analyzed the problem (unpublished, Appendix D) using a three-dimensional dislocation analysis similar to that of Carrigan and King (1991). The panel also did an analysis using the regional stress change model.
Dislocation Models
Dislocation model analyses suggest that a small disturbance of the water table, generally a rise of less than 10 m would result from a M=6.5-6.8 normal fault earthquake (Carrigan et al., 1991; Bredehoeft,
Appendix D). Looked at in the larger context, zones of extension on one side of the fault are balanced by nearby zones of compression across the fault. Unless the fault is exceptionally impermeable, local ground water flow will quickly flow across it to equalize initial changes in pore-water pressure. Thus, the ground water tends to move horizontally, inhibiting vertical excursions (Carrigan et al., 1991). One has to invoke an improbable permeability distribution with this model to produce a large water table rise.
Regional Stress Change Models
Cook and Kemeny (1991), and the panel did very similar analyses for the regional change in stress in the deep crustal rocks that accompanies a nearby earthquake. Both analyses assumed a 100 bar (=100 atmospheres=1500 psi) drop in the shear stress that accompanies an earthquake. Both used a simple poro-elastic analysis based primarily on the elastic properties of the rocks in question. Cook and Kemeny (1991) obtained the porosity, rock density, and elastic constants used in their model from seismic refraction data. The panel used rock properties derived from the tidal and barometric analysis of Yucca Mountain water wells (Galloway and Rojstaczer, 1988).
Parameter values for the model used for analysis by the panel were obtained from Galloway and Rojstaczer (1988). These values indicated that the Paleozoic carbonate is extremely stiff, with very low porosity. In a very stiff rock a significant part of the strain is taken up by the solids in the rock, rather than by the pore space. However, the parameter values for the Paleozoic carbonate are based on a single drill core from that unit, and therefore may not be reliable.
In evaluating the effect of stress on pore pressure, the ratio of the change in mean stress to change in pore pressure (known as Skempton's B coefficient) can be derived if one knows certain elastic properties of the whole rock and of the individual minerals that make up the rock. These properties are known as the rock bulk modulus (incompressibility), K, and the bulk modulus of the minerals (solids) that make up the rock, Ks. The assumptions and parameters used to compute the changes in pore pressure are outlined in Box 5.1.
To illustrate the effect on the water table of the difference in compressibility between the mineral grains and the whole rock, the panel made calculations for rocks with the same properties as the lower tuffs (Galloway and Rojstaczer, 1988), a rock type with elastic properties that seem typical of crustal rocks. For the lower tuff Galloway and Rojstaczer's parameters suggest K/Ks is 0.66, which yields a rise of 22 meters.
|
BOX 5.1 Assumptions for Determining Changes in Water Level The calculations that yielded the results in Table 5.1 are based on the following assumed parameters:
The results depend upon the ratio of the mineral grain compressibility (1/Ks) to whole rock compressibility (1/K), or K/Ks. |
Table 5.1 indicates that as the rock becomes much more compressible than the individual grains (the K/Ks ratio decreases), much of the volume strain is taken up in the pore space causing the spaces to close and the water to be squeezed upward. The table shows that the results can approach a water level rise of 100 m or more only if the compressibilies of the whole rock is considerably greater than that of the individual minerals. As the compressibilities of the rock and the grains approach each other (a ratio closer to 1.0), the volume strain is distributed in both the solids and the pores, and the amount of the water level rise diminishes. Although direct data are not available, the general tendency of bulk rock compressibility is to decrease with depth, so that pore strain at or below 3-4 km or so should be quite low (K/Ks = 0.7-0.9). This suggests that the water table rise will be less than 40 meters (see Table 5.1).
Table 5.1 also indicates that knowledge of the properties of the carbonate rocks at depth at Yucca Mountain is essential to predicting water table behavior in response to changes in the regional crustal stresses produced by earthquakes. The panel recommends that more data on the elastic and hydrologic properties of the deep carbonate aquifer be obtained so that credible models can be developed.
Cook and Kemeny (1991) calculated a water table rise of approximately 10 m. Their calculation is based upon the assumption of
Table 5.1 Effects of Ratio of Mineral Compressibility to Rock Compressibility on Rise in Water Table Level Resulting from a Seismic Event
|
K/Ks |
Water Table Rise |
|
0.1 |
330 meters |
|
0.3 |
150 meters |
|
0.5 |
78 meters |
|
0.7 |
36 meters |
|
0.85 |
16 meters |
seven percent unsaturated porosity. The panel calculated a potential rise of approximately 20 m, using a one percent unsaturated porosity and a K/Ks equal to 0.66. Had Cook and Kemeny used one percent unsaturated porosity their calculated rise would have been approximately 70 m. Their value is this high because the parameters they used resulted in a K/Ks close to 0.3 which the panel considers unlikely at the depths of the carbonate aquifer. In addition, one percent unsaturated porosity is probably a conservative assumption.
The analyses of both the panel and Cook and Kemeny indicate that the calculated water table rise in the regional stress change model is especially sensitive to: (1) the amount of the stress change, (2) the compressibility of the whole rock versus the compressibility of the individual minerals that make up the rock, and (3) the moisture content above the water table.
The water table rise associated with a regional drop in shear stress, which accompanies an earthquake, is a transient imposed on the system. It is equivalent to adding an instantaneous slug of recharge to the water table over a large area. This will gradually dissipate. The panel did not attempt to analyze the life of this transient.
Sources of Information on In Situ Physical Properties
A summary of the information on in situ physical properties of the rocks applicable to earthquake modeling in the Yucca Mountain region suggests how inadequate the available data is.
Information on the characteristic stress drop following a seismic event in the Basin and Range, which is on the order of 100 bars, was
determined by analysis of earthquakes (Kanamori and Anderson, 1978; Scholz et al., 1986). The data on the compressibility of the deep carbonate rocks beneath Yucca Mountain is based on analyses from a single well (Galloway and Rojstaczer, 1988) and on the seismic refraction data used by Cook and Kemeny (1991). These data suggest stiff rock of low permeability at depth.
Approximately 100 unsaturated samples of cores from above the water table at Yucca Mountain have been analyzed for porosity and saturation (Montazer and Wilson, 1984). The results show wide scatter. The deeper tuff units, closer to the water table, indicate two or four percent unsaturated porosity; some of the unwelded tuff is nearly saturated.
This sums up most of the data that are available for developing poro-elastic models to predict the behavior of the crust and the resulting hydrologic responses. This severe limitation of the data base produces large uncertainties in any analytical results.
CONCLUSIONS BASED ON RESULTS OF MODELING TO DATE
The models suggest that regardless of which approach is taken, only a modest rise in the water table of less than 50 m is likely to occur as the result of a nearby earthquake. Although the models are based on very limited data, the panel concludes that stress/strain changes resulting from an earthquake are inadequate to cause more than a few tens of meters rise in the water table based on the convergence of the results by a variety of models and assumptions, especially if the deep carbonate aquifer is as incompressible as the limited data suggest.
A Possible Alternate Modeling Approach: Discontinuum Analysis of Ground-Water Motion
Another approach to prediction of seismically induced ground-water motion is based on explicit recognition of the discontinuous state of a seismically active rock mass. Cundall and Strack (1979) introduce the essential concepts for analysis of the discontinuum mechanics of a saturated rock mass. In principle, the geometry of a rock mass can be described in terms of the spatial arrangement of the set of faults, joints and other fractures distributed through the rock body. Each feature is a potential pathway for fluid movement under the hydrostatic potential field (pressurized water) that may be generated by change in the stress distribution in the rock. The volume of fluid mobilized by an incremental change in the normal stress is deter-
mined by the storativity of the fracture aperture, i.e. the degree to which open fractures can store ground water, under the prevailing state of stress. Furthermore, each fracture is a potential conduit for fluid flow because it can open if properly orientated relative to the prevailing normal stress.
An obvious question concerning fractures in an otherwise low-porosity rock mass is whether the specific fluid storage capacity (storativity) of fractures at depth can provide sufficient fluid which, on subsequent displacement, can have a substantial effect on the water table in the near-subsurface. The states of stress in the shallower part of the crust are typically low, resulting in open fractures, and consequent high storativity.
It is well known that the hydraulic conductivity of fractures in rock is highly sensitive to change in fracture aperture, and therefore to change in the state of effective normal stress on the fracture. In principle, if a sufficient volume of water were mobilized by an earthquake, a network of fractures could provide a highly conductive channel to transfer water from domains of high pressure at depth to higher elevations in the host rock. Such a mechanism is implied in the hypothesis of seismic pumping (Sibson et al., 1975). The hypothesis suggests that an analysis based on discontinuous deformation of the rock mass may lead to a better understanding of the hydrologic response by focusing on the flow of fluid through fissures, or open fractures.
The Distinct Element Method is a comparatively well developed technique for discontinuous analysis of fractured rock masses. The principles of the method were presented initially by Cundall (1971). A rock mass is considered an assembly of rock blocks generated by the system of fractures transgressing the medium. The individual blocks may be considered to be continuous and elastic and to interact with their neighbors through a deformable joint contact. The description of the deformation behavior of the contact can account for the mechanical behavior of both the solid rock and the fluid in response to changes in the stress field.
Several examples demonstrate the application of discontinuum analysis of coupled solid deformation and fluid flow in a jointed, saturated rock mass (Pine and Batchelor, 1984; Lemos, 1988). These studies illustrate the utility of the Distinct Element Method for analysis of coupled rock deformation and ground-water flow. In particular, it is possible to account for the storativity of joints, joint and rock mass dilation during shear displacement, the stress dependence of joint and rock mass permeability, and the effect of the time history of motion on rock displacements.
These factors suggest that scoping studies with the Distinct Element method would contribute substantially to establishing possible modes of rock and ground-water response to seismic events at Yucca Mountain. The studies should be based on cross-section models of the Yucca Mountain setting, representing the general features rather than the details of the structural geology and hydrogeology. The model may be used to determine changes in ground-water conditions for stress changes within the range of values that may occur during a major seismic event. Furthermore, the model may be exercised to determine the site and seismic conditions that could induce substantial upward flow of ground water. It may then be possible to determine if physically reasonable conditions consistent with an hypothesis of seismically-driven flooding of the repository horizon would develop at the site.
RECOMMENDATION
The panel recommends that additional modeling be done to aid in the understanding and prediction of the likely behavior of the water table at Yucca Mountain in response to earthquakes. However, the models must be better constrained by data. Additional data are needed on the hydrologic and elastic properties of the deeper carbonate rocks and the chemical and isotopic composition of fluids in the saturated zone below the water table that underlies the proposed repository site.
As the panel's independent analysis indicates, data are needed on rock compressibility, porosity, and permeability of the deep aquifer. Several deep core holes should be drilled well into the Paleozoic carbonates to obtain this information.
Moreover, the dependence of the results on the unsaturated porosity of the vadose (unsaturated) zone requires that more knowledge of the properties, character and history of the unsaturated zone be obtained.
The panel is confident that this information will reduce the large uncertainty presently associated with all coupled processes models of the Yucca Mountain area.
EARTHQUAKE PROBABILITY
All of the modeled seismic/hydrologic effects are conditional upon the occurrence of an earthquake that releases extensional stress, causing dilatational changes in crustal rocks. A separate but important question is the likelihood of such earthquakes occurring in the vicinity of the repository. The panel has applied a preliminary eval-
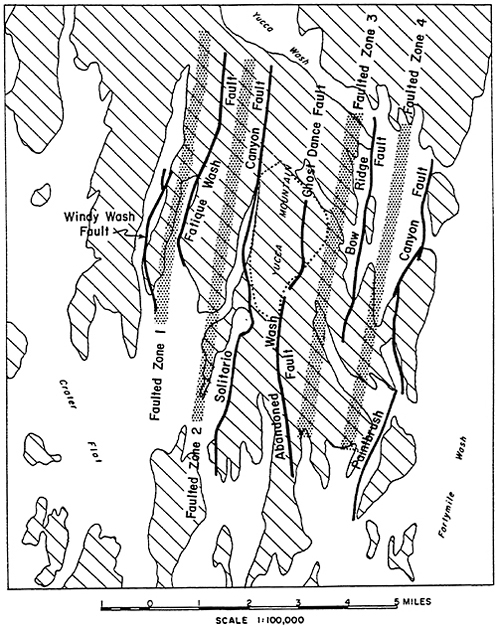
uation of earthquake probabilities to Yucca Mountain (see Appendix E), using estimated slip rates for identified and suspected active normal or normal-oblique faults in the region (Figure 5.1 and Table 5.2).
Slip rates for the late Quaternary determined from field measurements on most of these faults are not available. One exception is the Windy Wash fault, for which a vertical offset of 40 cm on a 270 ka gravel is documented (Whitney et al, 1984), yielding a vertical slip rate of 0.0015 mm/yr. Movement on this fault is probably oblique, given its orientation with respect to the regional principal stresses. Assuming equal amounts of vertical and strike-slip movement, the total current slip rate on this fault is estimated as 0.0021 mm/yr.
In order to make estimates of slip rate on other faults and faulted zones close to Yucca Mountain, the panel has made several assumptions about the responses of these faults to the tectonic processes currently active in the area:
-
On average, all faults and faulted zones have a slip rate equal to that observed on the Windy Wash fault.
-
The current slip rate is proportional to the total displacement observed on the Topopah Spring member of the Paintbrush Tuff, as represented by Scott and Bonk (1984). (This unit is approximately 13 million years old and is not a reliable indicator of the current slip rate, but is used to estimate relative rates of current deformation.)
-
All moderate earthquakes (magnitude 5 to 7) that might affect crustal stress conditions and the water table near Yucca Mountain will occur on one of the identified faults or faulted zones.
The most critical of these assumptions is the first; it says that the slip rate on the Windy Wash fault is typical of slip rates on other faults in the region. The resulting estimated slip rates are in fact comparable to those estimated by other investigators, as is noted below.
The maximum magnitudes allowed on the ten faults in Table 5.2 range from 6.5 to 7, depending on the hypothesis considered in the next section. These values may be conservative in that the length of faulting mapped on Figure 5.1 may not support such large events. On the other hand, there is no conclusive evidence that these faults do not extend farther north or south, nor is there evidence that they are not structurally connected with other mapped faults to the north or south.
Table 5.2 shows, for each fault and faulted zone, the length of the fault, the offset of the Topopah Spring unit, and the slip rate estimated as described above. For this table, and for computations, the Ghost Dance and Abandoned Wash faults have been assumed to be one continuous fault. By way of comparison, Coppersmith and Youngs
(1990) estimated slip rates between 0.002 and 0.006 mm/yr for the six named faults, and a total slip rate of 0.0275 mm/yr. All tectonic activity was ascribed to the named faults by Coppersmith and Youngs, with other movement being secondary faulting subsequent to the main rupture. The total rate of 0.0275 mm/yr is of the same order as the total of 0.0212 mm/yr shown in Table 5.2. Again, the purpose here is to make reasonable estimates of slip rates that are not low or high by an order of magnitude. If alternative slip rates are preferred, their effects on the probabilities reported here would be proportional, at least at the lower probability levels. That is, if slip rates were doubled, the lowest probabilities reported in Box 5.2 would approximately double. It should be noted that in Chapter 4 of this report, a slip rate of 0.01 mm/yr was used to calculate effects of a basaltic dike intrusion. The panel does not consider this inconsistent because it is within the range of uncertainty in the estimates of slip rates.
In calculating current slip rates it is reasonable to consider that the offset of 270 ka geologic units is most relevant, and that only earthquakes in the immediate vicinity of Yucca Mountain (within several km) will affect ground-water levels for long time periods. Under these assumptions, the probability of an earthquake is 3 to 15 percent over 10 ka (see Box 5.2). The validity of alternative assumptions cannot be completely ruled out, however, and these might lead to
Table 5.2 Faults and Parameters Used In Analyses of Slip Rates
|
Fault |
Length, km |
Offset of Topopah Spring Unit m * |
Slip rate, ** mm/yr |
|
Windy Wash |
4.6 |
400 |
0.0021 |
|
Faulted Zone 1 |
10.0 |
70 |
0.00090 |
|
Fatigue Wash |
7.1 |
60 |
0.00077 |
|
Faulted Zone 2 |
10.0 |
225 |
0.0029 |
|
Solitario Canyon |
13.7 |
205 |
0.0027 |
|
Ghost Dance-Abandoned Wash |
9.2 |
50 |
0.00064 |
|
Faulted Zone 3 |
10.0 |
338 |
0.0043 |
|
Bow Ridge |
7.4 |
196 |
0.0025 |
|
Faulted Zone 4 |
10.0 |
130 |
0.0017 |
|
Paintbrush Canyon |
12.0 |
206 |
0.0027 |
|
Total |
0.0212 |
||
|
* Taken from Scott and Bonk (1984) for all faults except Windy Wash, which was taken from Carr (1984). ** Estimated over the last 270 ka, based on slip rate for Windy Wash fault. |
|||
|
BOX 5.2 Considerations in Calculating Earthquake Probabilities Important questions relevant to the calculation of earthquake probabilities within the Yucca Mountain area are:
These issues and their effects on earthquake probability calculations are discussed in Appendix E. Assuming all slip on faults occurs seismically, the results can be summarized as follows: SUMMARY OF PROBABILITIES OF EARTHQUAKE OCCURRENCE OVER 10,000 YEARS
|
probabilities approaching 100 percent if a much larger area is included for the occurrence of an earthquake.
It should be noted that apparent slip rates over the past 13 Ma are an order of magnitude larger than those described above. This can be concluded from two independent interpretations. First, the vertical offsets of the Topopah Spring Member shown on Table 5.2 total 1880 m; dividing this by the 13 Ma age of this unit gives a total vertical slip rate for the faults in Figure 5.1 of about 0.15 mm/yr. Assuming oblique slip with equal components of horizontal and vertical movement gives a total slip rate of 0.21 mm/yr.
A second, independent estimate of total slip rate can be obtained from paleomagnetic declination data in the region. These data (from Rosenbaum et al., 1991) indicate that the southern portion of Yucca Mountain has rotated 20° to 30° clockwise about a vertical axis since the emplacement of the 13 Ma Tiva Canyon tuff. Assuming that this rotation was accommodated by block rotations and strike-slip on faults between the blocks and assuming some average distance between the active faults, one can estimate the long-term average fault slip rate. For rotations of 20° and 30°, and faults spaced 5 km apart, average strike-slip rates (left-lateral) are in the range of 0.25 to 0.35 mm/yr. Assuming equal components of normal and strike-slip movement would yield a total slip rate of 0.35 to 0.49 mm/yr over a 5 km width.
If these high slip rates apply to the present and are assumed to be entirely seismic, it would imply that three to five earthquakes with a total oblique slip of 1 m could occur over the 5 km faulted zone within 10 ka. However, as previously discussed, the rate of extension of the region has undergone a documented decrease over the last 5-10 Ma, especially in the Yucca Mountain area, suggesting that the more recent slower rate of extension is a more relevant measure to apply to average slip rates.
An additional complication is that fault movement may be primarily strike-slip, as discussed earlier in this chapter, in which the north-trending faults (Figure 5.1) respond to WNW-ESE extension. If this is so, vertical offsets are not reliable as indicators of current total slip rates, and rates of activity may be higher than those discussed here. We have no data with which to estimate the possible rates of strikeslip faulting suggested by the focal mechanisms of small magnitude earthquakes in the Yucca Mountain area.
All of this points to the large uncertainties in estimating fault slip rate, given current information. These uncertainties undoubtedly can be reduced with further site-specific fault investigations. For perspective on rates of earthquake occurrence, the panel used the slip rates estimated over the past 270 ka (as shown in Table 5.2), with the understanding that further fault-specific site investigations are likely to improve or refine those estimates.
CONCLUSIONS
A range of uncertainties necessarily accompany any current assessment of the effects of earthquakes on the water table in the Yucca Mountain area, because of the absence of sufficient data to constrain the models, to determine slip rates, and to predict earthquake magnitudes.
There are uncertainties in the changes in the water table that could be induced by earthquakes. Based on modeling by the panel and others of which we are aware, and the historical record, these changes likely are small; but larger changes cannot be ruled out, given current uncertainties on rock properties at the site. Additional investigations are required to resolve these uncertainties, especially those regarding properties of the Paleozoic carbonate aquifer.
Furthermore, the likelihood of an earthquake close enough to induce significant stress changes in the vicinty of the proposed repository depends strongly on how large an area might be affected by earthquake-induced stress changes. If changes are limited to several kilometers around a fault, the probability of such an event occurring at the proposed repository is several percent in 10 ka (with large uncertainties). If changes occur over distances of several tens of km, then the probability is nearly unity that a moderate earthquake will occur within that distance of the proposed repository over 10 ka, even using the low slip rates derived from offsets of young gravels on the Windy Wash fault. All of these conclusions have significant uncertainty as a result of the uncertainties in fault slip rates.
Therefore, while there are uncertainties in current interpretations because specific site data are not available, the panel concludes that there is nevertheless sufficient confidence in the aseismicity of the site and in the inability of earthquakes to generate large water table changes at the site, based on the historical evidence and modeling results, to warrant further characterization of the site to determine its suitability for a MGDS. That is, while current uncertainties exist, the panel supports further characterization to resolve those uncertainties and to assess the safety potential of Yucca Mountain as the high level radioactive waste repository.
RECOMMENDATIONS
The panel is aware that fault studies are in the site characterization plan. Considering the large uncertainties in fault slip rates, lengths of faults, and ages of offsets, the panel strongly endorses studies to obtain the data necessary to reduce the uncertainties in the probability estimates.
REFERENCES
Beanland, S., and M. M. Clark. 1992. The Owens Valley fault zone, eastern California, and surface rupture associated with the 1872 earthquake U.S. Geological Survey Bulletin 1982 In press.
Bell, J. W., and T. Katzer. 1987. Surficial geology, hydrology, and late Quaternary tectonics of the IXL Canyon area, Nevada, as related to the 1954 Dixie Valley earthquake Nev. Bureau of Mines and Geology Bulletin 102, pp. 1-52.
Bellier, O., and M. L. Zoback. 1991. Implications of young strike-slip and normal slip on subparallel faults in the W. Basin and Range province EOS (Trans. American Geophysical Union) 72: 461.
Bredehoeft, J. B. 1991. Response of the ground-water system at Yucca Mountain to an earthquake: An elastic continuum model, in this report: Unpublished Appendix D.
Briggs, R. C., and H. C. Troxel. 1955. Effects of the Arvin-Tehachapi earthquake on spring and stream flows In Earthquakes in Kern County, California, During 1952 G. B. Oakeshott, ed. California Division of Mines and Geology Bulletin 171: 81-97.
Carnegie Institution of Washington. 1908. The California earthquake of April 18, 1906 In Report of the State Earthquake Investigation Commission. Washington, D.C. Carnegie Institution, pp. 402-409.
Carr, W. J. 1984. Regional Structural Setting of Yucca Mountain, Southwestern Nevada, and Late Cenozoic Rates of Tectonic Activity in Part of the Southwestern Great Basin, Nevada and California U.S. Geological Survey Open-File Report. 84-854.
Carrigan, C., and P. King. 1991. Models of water table excursions induced by seismic and volcanic events at Yucca Mountain, Nevada (abs.) EOS 72: 116.
Carrigan, C., G. P. King, G. E. Barr, and N. E. Bixler. 1991. Potential for water table excursions induced by seismic events at Yucca Mountain, Nevada Geology 19: 1157-1160.
Cook, W., and J. M. Kemeny. 1991. A mechanical estimate for water level change due to a normal faulting earthquake (abs.) EOS 71: 116.
Cooper, H. J., Jr., J. D. Bredehoeft, I. S. Papadopulos, and R. R. Bennett. 1965. The response of well-aquifer systems to seismic waves. Journal of Geophysical Research 70: 3915-3926.
Coppersmith, K. J., and R. R. Youngs. 1990. Earthquakes and tectonics calculations. In Demonstration of a Risk-Based Approach to High-Level Waste Repository Evaluation, prep. by Risk Engineering, Inc. Electric Power Research Institute, Report. NP-7057 Palo Alto, October.
Cundall, P. A. 1971. A computer model for simulating progressive large scale movements in blocky rock systems In Rock Fracture, Proc. Int. Symp. Rock Fracture, Nancy. Paper 2-8
Cundall, P. A. and O. D. L. Strack. 1979. A discrete numerical model for granular assemblies Geotechnique 29: 47-65.
Davis, G. H., G. F. Worts, Jr., and H. D. Wilson. 1955. Water-level fluctuations in wells In Earthquakes in Kern County, California, During 1952. G. B., Oakeshott, ed. California Division of Mines and Geology Bulletin 171: 99-106.
dePolo, C. M., J. W. Bell, and A. R. Ramelli. 1987. Geometry of strike-slip faulting related to the 1932 Cedar Mountain earthquake, central Nevada Geological Society of America Abstracts with Programs 19: 371.
Eaton, J. P., and K. J. Takasaki. 1959. Seismological interpretation of earthquake-induced water level fluctuations in wells Seismological Society of America Bulletin 49: 227-245.
Eddington, P. K., R. B. Smith, and C. Renggli. 1987. Kinematics of Basin and Range intraplate extension In Continental Extension Tectonics, M. P. Coward, J. F. Dewey and P. L. Hancock, eds. Geological Society Special Publication 28, Blackwell, Oxford, pp. 371-392.
Galloway, D., and S. Rojstaczer. 1988. Analysis of the frequency response of water wells to earth tides and atmospheric loading In Proceedings of the Fourth Canadian/American Conference on Hydrology —Fluid Flow, Heat Transfer and Mass Transport in Fractured Rocks National Water Well Association, pp. 100-113.
Hager, B. H., R. W. King, and M. H. Murray. 1991. Measurement of crustal deformation using the Global Positioning System Annual Reviews of Earth and Planetary Science 19: 351-382.
Harmsen, S. C., and A. M. Rogers. 1986. Inferences about the local stress field from focal mechanisms: applications to earthquakes in the southern Great Basin of Nevada Bulletin of the Seismological Society of America 76: 1560-1572.
Kanamori, H., and D. L. Anderson. 1978. Theoretical basis of some empirical relations in seismology Bulletin of the Seismological Society of America 65: 1073-1095.
La Rocque, C. A., Jr. 1941. Fluctuations of water level in wells in the Los Angeles basin, California, during five strong earthquakes, 1933-1940 American Geophysical Union Transactions 22: 374-386.
Lemos, J. A. 1987. A Distinct Element Model for Dynamic Analysis of Jointed Rock with Application to Dam Foundations and Fault Motion Ph.D. thesis, University of Minnesota.
Liu, L. B., E. Roeloffs, and X. Y. Zheng. 1989. Seismically induced water level fluctuations in the Wali well, Beijing, China Journal of Geophysical Research 94: 9453-9462.
Lorig, L. J., and B. E. Hobbs. 1990. Numerical modeling of slip instability using the distinct element method with state variable friction laws International Journal of Rock Mechanics Mining Science & Geomechanics Abs 27: 525-534.
Minister, J. B., and T. H. Jordan. 1987. Vector constraints on western U.S. deformation from space geodesy, neotectonics, and plate motions Journal of Geophysical Research 92: 4798-4804.
Montazer, P., and W. E. Wilson. 1984. Conceptual hydrologic model of flow in the unsaturated zone, Yucca Mountain, Nevada U.S. Geological Survey Water Resources Invest. Report 84-4345 55 pp.
Nur, A. 1974. Matsushiro, Japan earthquake swarm: Confirmation of the dilatancyfluid diffusion model Geology 2: 217-221.
Pine, R. J. and A. S. Bachelor. 1984. Downward migration of shearing in jointed rock during hydraulic injections (abs.) International Journal of Rock Mechanics Mining Science & Geomechanics 21: 249-63.
Reiter, L. 1990. Earthquake Hazard Analysis: Issues and Insights. Columbia University Press, N. Y. 254 pp.
Rojstaczer, S., and S. Wolf. 1991. Hydrologic changes associated with the Loma Prieta earthquake in the San Lorenzo and Pescadero drainage basins U. S. Geological Survey Open-File Report 91-567. 21 pp.
Rojstaczer, S., and S. Wolf. 1992. Permeability changes associated with large earthquakes: an example from Loma Prieta, California Geology, in press.
Rosenbaum, J. G., M. R. Hudson, and R. B. Scott. 1991. Paleomagnetic constraints on the geometry and timing of deformation at Yucca Mountain, Nevada Journal of Geophysical Research 96: 1963-1979.
Sanders, C. O., and D. B. Slemmons. 1979. Recent crustal movements in the central Sierra Nevada-Walker Lane region of California-Nevada—Part III The Olinghouse fault zone. Tectonophysics 52: 585-597.
Savage, J. C. 1983. Strain accumulation in the western United States. Annual Reviews of Earth and Planetary Science 11: 11-43.
Scholz, C. H., C. A. Aviles, and S. G. Wesnousky. 1986. Scaling differences between large interplate and intraplate earthquakes Bulletin of the Seismological Society of America 76: 65-70.
Scott, R. B. 1990. Tectonic setting of Yucca Mountain, southwest Nevada. In B. P. Wernicke, ed., Basin and Range extensional tectonics near the latitude of Las Vegas, Nevada Geological Society of America Memoir 176: 251-282.
Scott, R. B. and H. Bonk. 1984. Geologic Map of Yucca Mountain, Nye County, Nevada, with Cross-Sections U.S. Geological Survey Open-File Report 84-494.
Sibson, R. H., J. McM. Moore and A. H. Rankin. 1975. Seismic pumping—a hydro thermal fluid transport mechanism Journal of the Geological Society (London) 131: 653-59.
Stermitz, F. 1964. Effects of the Hebgen Lake earthquake on surface water. U. S. Geological Survey Prof. Paper 435-L, pp. 139-150.
Waller, R. M. 1968a. Hydrologic effects in South Central Alaska. In The Great Alaska Earthquake of 1964—Hydrology, Part A. National Research Council Report, Washington, D.C., pp. 12-39.
Waller, R. M. 1968b. Hydrologic effects in the Anchorage Area. In The Great Alaska Earthquake of 1964—Hydrology, Part A. National Research Council Report, Washington, D.C., pp. 82-96.
Wells, D. L., K. J. Coppersmith, D. B. Slemmons, and X. Zhang. 1990. Earthquake source parameters: Updated empirical relationships among magnitude, rupture length, rupture area, and surface displacement Manuscript in preparation.
Wernicke, B., G. J. Axen, and J. K. Snow. 1988. Basin and Range extensional tectonics at the latitude of Las Vegas, Nevada Geological Society of America Bulletin 100: 1738-1757.
Whitehead, R. L., R. W. Harper, and H. G. Sisco. 1985. Hydrologic changes associated with the October 28, 1983, Idaho earthquake Pure and Applied Geophysics 122: 280-293.
Whitney, J. W., R. R. Shroba, F. W. Simonds, and S. T. Harding. 1984. Recurrent Quaternary movement on the Windy Wash Fault, Nye County, Nevada (abs.) Geological Society of America Annual Meeting Abstracts with Program San Antonio, p. 787.
Wood, S. H. 1991. Observations and subsequent history of spectacular ground water flows and aquifer pressure increases: 1083 Borah Peak and 1957 Hebgen Lake earthquakes (abs.) EOS 72: (17)115
Wood, S. H., C. Wurts, T. Lane, N. Ballenger, M. Shaleen, and D. Totorica. 1985. The Borah Peak, Idaho earthquake of October 28, 1983—hydrologic effects Earthquake Spectra 2: 127-150.
Zoback, M. L. 1989. State of stress and modern deformation of the northern Basin and Range province Journal of Geophysical Research 94: 7105-7128.