Appendix D
Response of the Ground-Water System at Yucca Mountain to an Earthquake
J.D. Bredehoeft
U.S. Geological Survey
Menlo Park, California
Revised February 12, 1992
ABSTRACT
The volume strain produced by a normal fault earthquake, of approximate magnitude 6, is computed using dislocation theory. The head change produced by the change in volume strain associated with the earthquake is also computed. Using the head change as an initial condition the three dimensional ground water flow is modeled.
Flow is found to occur from areas where the rock is compressed to areas where the rock was put into tension. In the dislocation calculations the volume put into compression equals the volume put into tension. The calculations suggest that the head change produced by the earthquake is quickly dissipated by local flow (in approximately 1 day). The water table is relatively unaffected in these calculations.
INTRODUCTION
The question has been asked: what would be the effect of an earthquake on the water table beneath Yucca Mountain? One hypothesis is that such an event could raise the water table dramatically causing a potential hazard for the proposed nuclear repository. As currently designed, the repository at one point is approximately 200 meters above the water table; the depths will range from 200 to 390 meters.
The purpose of this report is to examine the impact of an earthquake on the ground-water system at Yucca Mountain. A set of calculations is presented; the purpose of these calculations is to examine the order of magnitude of potential effects. These results are not intended to predict exactly the effects beneath Yucca Mountain; they are an attempt to investigate if there is a potential problem.
There are two models for the deformation that would accompany a nearby earthquake: (1) a strain produced by a regional change in the state of stress caused by the earthquake, and (2) a dislocation strain model for the earthquake. In this paper I will examine the implications of the dislocation model. If one integrates the change in stress, or the strain, produced by the dislocation model over a sufficiently large volume of rock, it sums to zero. In other words, the usual dislocation calculation does not produce a regional change in either the stress or the strain. In the dislocation model local changes in both the positive and negative directions balance each other.
Rocks at Yucca Mountain are continually loaded by changes in the barometric pressure and are continually strained by the earth tide. Both conventional hydrologic tests and the effects of barometric loading and earth tide strain have been analyzed in 4 drill holes. This provides one reasonably complete set of data from which one can estimate the response to both stress and strain. We will attempt to put these data in perspective before attempting an analysis.
EARTH TIDES AND ATMOSPHERIC LOADS
Near the earth's surface rocks are subjected to earth tide strain and changes in atmospheric pressure. The response of the groundwater system to these effects can be used to investigate both the elastic and the hydrologic parameters of rocks in the area. In the case of earth tides, the disturbance has such a long wave length that the response is determined by material properties deep into the mantle. Near-surface crustal rocks are along for the ride. In analyzing the tidal response of water wells the best assumption is that horizontal strains are imposed (Bredehoeft, 1967; Hsieh et al., 1988). Analysis of
the tidal and atmospheric effects indicate how the groundwater system responds to both imposed stresses and strains.
ELASTIC AND HYDROLOGIC PARAMETERS
Galloway and Rojstaczer (1988) analyzed the response of 4 water wells at Yucca Mountain to both atmospheric loading and earth tides. Figure 1, taken from Galloway and Rojstaczer (1988), shows schematically the stratigraphic section open to each well. A summary of the
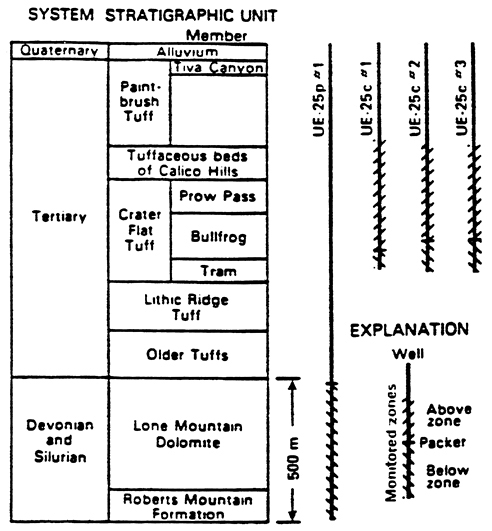
Figure 1 Schematic stratigraphic section of the rocks penetrated at the UE-25 drill site (after Galloway and Rojstaczer, 1988).
necessary elastic and hydrologic parameters is presented in Table 1; much of the information is taken directly from Galloway and Rojstaczer (1988).
A few comments are in order regarding the data in Table 1. The carbonate aquifer has a high sensitivity to volume strain: approximately two meters change in head (pore pressure) per microstrain. The specific storage for the carbonate aquifer is also low.
Galloway and Rojstaczer point out that this low value indicates a stiff rock with low porosity; they estimate the porosity at 6 × 10 −4 or less. The permeability of the carbonates is high, approximately an order of magnitude or more higher than that of permeable tuff. These data are consistent with a fractured, permeable carbonate aquifer.
Galloway and Rojstaczer use a well sensitivity to tidal strain, A s, that is a sensitivity to only the horizontal strain. It is more useful in this analysis to have the sensitivity to strain expressed in terms of the total strain. One can show that for an undrained Poisson's ratio of 0.33 the sensitivity to total strain, At, will be twice the sensitivity to the horizontal strain: At = 2 As. Galloway and Rojstaczer's analysis also indicates a tight confining layer overlying the carbonate aquifer. This unit is approximately 4 orders of magnitude less permeable than the overlying tuffs. The unit makes a significant difference in the hydraulic response of the system.
One other important question is: what are the conditions just above the water table? Data from Montazer and Wilson (1984) indicate that the unsaturated pore space maybe approximately 5 percent. However, many tuffaceous rocks above the water table have moisture contents near 100 percent saturation; this is especially true of the less welded units. For this analysis, I assume that the rock just above the water table has 1 percent porosity that is unsaturated with moisture. Assuming 1 percent is a conservative assumption. A larger unsaturated porosity reduces the response of the water table; conversely a smaller unsaturated porosity would increase the response.
The stratigraphy of the volcanic sequence at the Yucca Mountain site is well known (see Figure 1). However, the deeper stratigraphy below 1.5 kilometers is not well known. The UE-25p#1 hole penetrates 500 m. of the Paleozoic carbonate rock. I will assume that 500 meters of saturated tuffaceous rock overlies Paleozoic carbonate rocks that extend to a depth of 17 kilometers. The properties of these rocks are described in Table 1. As discussed above, this appears to be a conservative assumption useful for purposes of computing the order of magnitude of expected changes in the water table.
Table 1 Elastic and hydrologic properties of the Yucca Mountain site.
|
Matrix * Compressibility B × 10−12 (cm2/dyne) |
Strain * Sensitivity At × 10−9 (cm/strain) |
Vertical * Hydraulic Diffusivity Kv/Ss (cm2/sec) |
Specific * Storage Ss × 10−9 (cm−1) |
Vertical * Hydraulic Conductivity Kv × 10−6 cm/sec) |
Horizontal Hydraulic Conductivity K × 10−6 (cm/sec) |
|
|
Water Table |
[.01] ** |
|||||
|
Upper Tuffs |
5.7-5.9 |
.026-.060 |
330-420 |
14-15 |
4.6-6.3 |
[5] † |
|
Lower Tuffs |
2.9-3.7 |
.058-.072 |
180-390 |
4.9-9.6 |
0.9-3.7 |
|
|
Confining Layer |
18 |
[.037] |
0.0007 |
|||
|
Carbonate Aquifer |
1.6-1.7 |
.24-.26 |
.037 |
[50] † |
50 ‡ |
|
|
[ ]Brackets indicate estimates. * Data from Galloway and Rojstaczer, 1988. ** The unsaturated zone is assumed to have 1% unsaturated porosity. † The permeability is assumed to be isotropic in both the tuff and the carbonate aquifer. ‡ Data from Craig and Robison, 1984. |
||||||
FAULT DISLOCATION
Most geophysicists consider an earthquake to be a more-or-less instantaneous displacement on a finite fault plane. One classic model of this process is a slip on the finite plane in an elastic half-space. The displacement on the rupture plane causes the half-space to deform to accommodate the slip. Several investigators have used this formulation to calculate strains and tilts accompanying earthquakes (Chinnery, 1961; Chinnery, 1963; Maruyama, 1964; Press, 1965).
One justification for an elastic analysis is that seismic waves propagate outward from the hypocenter of an earthquake. One also observes permanent co-seismic deformation which accompanies the earthquake. This permanent deformation can often be fit, at least to a first approximation, by an elastic deformation model (Roeloffs and Bredehoeft, 1984; Roeloffs and Quilty, 1989)
In the analysis presented here an elastic model is used to calculate the volume strain accompanying a magnitude 6+ earthquake. The volume strain causes an increase in pore pressure in the deformed zone near the fault. A three dimensional flow model is then used to investigate the propagation of the pore pressure transient created by the earthquake. We are especially interested in a potential rise in the water table.
For the purposes of analysis I assume a simple geologic model. The model chosen consists of a section of tuff approximately 1 kilometer thick underlain by carbonates to a depth of 17 kilometers. Because I have chosen to use grid cells 2 × 2 × 2 kilometers, I have arbitrarily made the thickness of each rock layer a minimum of 2 kilometers. This restriction is arbitrary and can be removed should it seem desirable. I also assume both the overlying tuff and the underlying carbonate to have isotropic permeability. As discussed above, Galloway and Rojstaczer's (1988) analysis suggests that there is a low-permeability confining layer overlying the carbonate aquifer (see Table 1); this confining layer is included in the hydrologic model.
Given a compressibility and a Poisson's ratio one can calculate the volume strain associated with a given fault displacement. For this calculation we have used a normal displacement of 1 meter along a 30 kilometer fault plane, dipping 60° to the vertical, and extending to a depth of 10 kilometers. Such a fault displacement is comparable in size to the sequence of Parkfield earthquakes, a magnitude 6+ earthquake. A cross-section normal to the strike of the fault is shown in Figure 2. For these calculations we have taken the bulk compressibil-
ity of the entire rock section as, B = 5 × 10−12 cm2 / dyne, and Poisson's ratio, v = 0.25.
The maximum volume strains occur near the lower tip of the fault plane. Regions of negative volume change (compression) balance zones of positive volume change (extension) on opposite sides of the fault. The maximum volume strains are about 100 microstrain units (10−4 ). One can imagine this hypothetical fault oriented more-or-less north-south along the east side of Yucca Mountain, dipping to the west below the mountain.
One also can estimate the change in the average stress associated with the displacement. At depths of 5 kilometers and more, the volume strain ranges from −5 to −10 microstrain units (in the convention used here a − sign indicates compression). This suggests a change in mean stress (octahedral stress) of approximately 3 to 6 bars; if this change was produced by a change in only one principal stress, the total stress change would be three times as large.
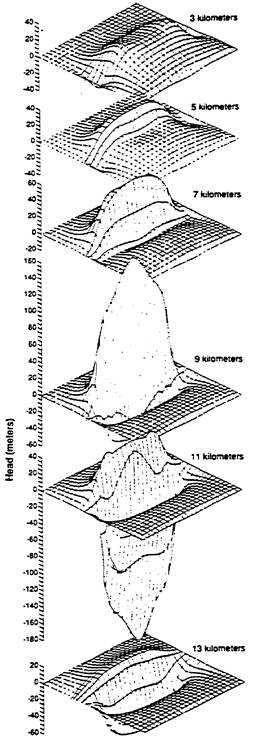
Using the strain sensitivities determined by Galloway and Rojstaczer, At, I calculate the fluid pressure changes that will be produced by the dislocation. These pressure changes are plotted as changes in hydraulic head in Figure 3. Again, increases in head are balanced locally by the decreases.
Starting with the initial condition, as shown in Figure 3, one can simulate the change in head following the earthquake. I make the calculations using a 3 dimensional flow simulation model, which has 9 layers with grid blocks of 2 × 2 × 2 kilometers. The region modeled
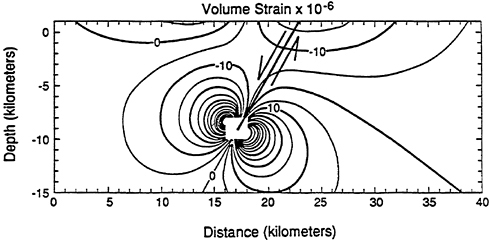
Figure 2 Cross-section normal to the strike of the fault indicating the volume strain. The volume strain is in units of microstrain ( ×10−6). A negative value indicates compression.
extends out to 20 kilometers both east and west of the fault and 5 kilometers beyond both the north and south tip of the fault. The model grid is also plotted on Figure 3. The bottom of the region simulated is at a depth of 17 kilometers. All the flow calculations are done on a 286 personal computer (PC) using a code developed by Bredehoeft (1990).
In the flow modeling there was no attempt to make the hydraulic conductivity a function of the pore pressure change. In the model I assume the fault plane to have the same hydraulic conductivity as the surrounding rocks. Both the upper tuff layer and the lower carbonate rocks have isotropic hydraulic conductivity.
In the base case simulation the tight confining layer is not included. The decay of the hydraulic head is shown in Figure 4. The head
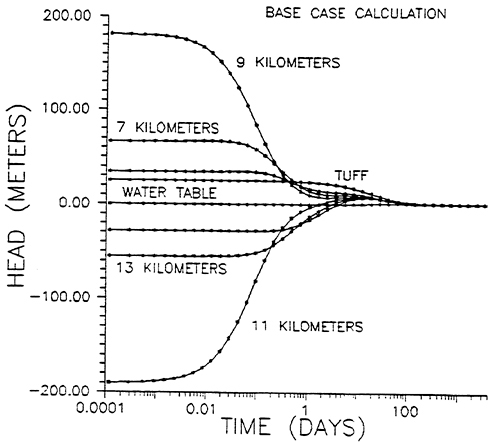
Figure 4 Transient head plotted as a function of time at various depths in the system (base case). The points of observation are taken at points of maximum initial head change in each model layer.
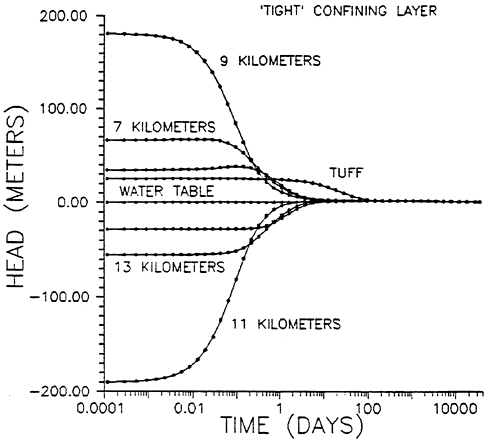
Figure 5 Transient head plotted as a function of time for the dislocation model in which the tight confining layer is included.
produced by the volume strain decays rapidly from the system. The decay is rapid because the specific storage indicated for the deeper system is small (Table 1). (The storage coefficient plays an analogous role in ground-water problems as the specific heat in heat-flow problems. With a small storage coefficient very little water is stored for a given change in head). The rise in the water table in what we designate the base case, is of the order of 1 meter.
I also simulated the effect of the tight confining layer; this result is shown in Figure 5. Because of the tight confining layer the deeper carbonate aquifer is insulated from the overlying tuff and the water table. Compressive regions balance regions of tension. The system quickly comes back to its initial state through local flow. The tuff unit, because of its larger specific storage and lower permeability, takes longer to reach equilibrium. Again the response of the water table is of the order of 1 meter.
CONCLUSION
A rise in the water table of approximately 200 meters is required to endanger the repository. The Dislocation Model indicates a small rise in the water table caused by a magnitude 6+ earthquake near the repository—of the order of 1 m.. The approach taken here is one of an elastic continuum. It seems unlikely that a more sophisticated model would produce water table changes an order of magnitude larger.
ACKNOWLEDGMENT
I thank Bob Simpson, USGS, Menlo Park, for calculating the volume strain for the dislocation model; and Bill Brace and Amos Nur for their discussions of the role of a regional change in stress following an earthquake.
REFERENCES
Bredehoeft, J.D. 1967. The response of the well-aquifer system to earth tides. Jour. Geophys. Res. 72: 3057-3087.
Bredehoeft, J.D. 1990. Microcomputer codes for simulating transient ground water flow in two and three space dimensions U.S. Geol. Survey Open-File Report 90-559, 106p.
Chinnery, M.A. 1961. The deformation of the ground around surface faults. Bull. Seismol. Soc. Am. 51: 355-372.
Chinnery, M.A. 1963. The stress changes that accompany strike-slip faulting. Bull. Seismol. Soc. Am. 53: 921-932.
Craig, R.W. and J.H. Robinson. 1984. Geohydrology of the rocks penetrated by well UE-25p#1, Yucca Mountain area, Nye County, Nevada U.S. Geol. Survey Water Res. Inv. Report 84-4248 57p.
Galloway, D. and S. Rojstaczer. 1988. Analysis of the frequency response of water wells to earth tides and atmospheric loading: proceedings 4th Canadian/American Conference on Hydrogeology edited by B. Hitchon and S. Bachu. Nat'l Water Well Assoc., Dublin, OH. 100-113.
Hsieh, P.A., J.D. Bredehoeft, and S.A. Rojstaczer, 1988. Response of the well-aquifer system to earth tides: problem revisited Water Resources Res. 23: 1824-1832.
Maruyama, T., 1964. Statical elastic dislocations in an infinite and semi-infinite medium Bull. Earthquake Res. Institute Tokyo Univ. 42: 289-368.
Montazer, Parvis and W.E. Wilson. 1984. Conceptual model of flow in the unsaturated zone, Yucca Mountain, Nevada U.S. Geol. Survey Water Res. Inv. Report 84-4345. 55p.
Press, F., 1965. Displacements, strains, and tilts at teleseismic distances. Jour. Geophysical Res. 70: 2395-2412.
Roeloffs, E. and J.D. Bredehoeft. 1984. Coseismic response of water wells near Parkfield, California to the August 4, 1985 Kettleman Hills earthquake (abstract) EOS. 66: 986.
Roeloffs, E. and E. Quilty. 1989. Groundwater level changes near Parkfield, California, before the August 4, 1985 Kettleman Hills earthquake (abstract) EOS. 70: 1230.