8.
Probability and Problems in Euclidean Combinatorial Optimization
J. Michael Steele,1
University of Pennsylvania
ABSTRACT
This chapter summarizes the current status of several streams of research that deal with the probability theory of problems of combinatorial optimization. There is a particular emphasis on functionals of finite point sets. The most famous example of such functionals is the length associated with the Euclidean traveling salesman problem (TSP), but closely related problems include the minimal spanning tree problem, minimal matching problems, and others. Progress is also surveyed on (1) the approximation and determination of constants whose existence is known by subadditive methods, (2) the central limit problems for several functionals closely related to Euclidean functionals, and (3) analogies in the asymptotic behavior between worst-case and expected-case behavior of Euclidean problems.
No attempt has been made in this survey to cover the many important applications of probability to linear programming, arrangement searching, or other problems that focus on lines or planes.
8.1 Introduction
Almost all of the results surveyed here owe a debt of one sort or another to the classic theorem of Beardwood, Halton, and Hammersley that lays out the basic behavior of the length of the shortest tour through a random sample from a general distribution in Rd:
Theorem 8.1 (Beardwood et al., 1959) If Xi, ![]() are independently and identically distributed random variables with bounded support in Rd, then the length Ln under the usual Euclidean metric of the shortest path through the points {X1, X2, ... , Xn} satisfies
are independently and identically distributed random variables with bounded support in Rd, then the length Ln under the usual Euclidean metric of the shortest path through the points {X1, X2, ... , Xn} satisfies
Here, f(x) is the density of the absolutely continuous part of the distribution of the Xi, and βTSP, d is a positive constant that depends on d but not on the distribution of the Xi.
The Beardwood, Halton, and Hammersley (BHH) theorem has led to developments of several different types. The first developments that we review concern generalizations of the BHH theorem that aim to provide insight into larger classes of processes. It turns out that the essential geometric features of the TSP are present in many of the problems that have been investigated in the theory of combinatorial optimization, and there is also a close connection between these properties and the notions of subadditivity. These subadditivity-driven generalizations of the BHH are addressed primarily in §8.2.
The second type of problem considered looks at the BHH theorem from the perspective of precision, rather than generality. It turns out that Ln, the length of the shortest tour through an n-sample, is highly concentrated about its mean. The main result of this development, the theorem of Rhee and Talagrand, is spelled out in §8.3. It tells us that the tails of the TSP functional Ln decay as rapidly as those of the normal distribution. This remarkable result has evolved through several intermediate stages, each of which offered new tools for the analysis of functionals of finite point sets in the plane.
Section 8.4 is the last to focus explicitly on the theory of the TSP, and, though we start to strain the notion of a Euclidean problem, the development casts light on problems like those just described. The main purpose of §8.4 is
to introduce the connection between Euclidean optimization problems and self-similar sets of fractional dimension; the principal result reviewed is a theorem by S. Lalley on the TSP. This is an intriguing result that suggests a rich connection between the rapidly developing theory of sets of fractals and many classical problems.
In §§8.5 and 8.6 the set of problems studied is widened. We first consider the theory of the minimal spanning tree (MST) and review how one can construct an infinite analog to the MST that leads to answers of a number of classical questions. One of the best reasons for introducing any new mathematical structure is that it simplifies and strengthens earlier results, and this is exactly what occurs in this development of an "infinite MST." The new structure permits one to make many deductions that are apparently difficult (or perhaps impossible) to address without such a tool.
Section 8.6 gives a brief survey of some of the new developments in the theory of matching. This subject began with the theorem of Ajtai, Komlós, and Tusnády on the two-sample matching problem, but it has developed rapidly because of its rich connections to such topics as bin packing, scheduling, and the theory of empirical processes. There are many engaging special results in this active area, and it is not possible to offer much more than a taste. We particularly want to call attention to a new theory of majorizing measure initiated by M. Talagrand. This theory unifies and deepens many earlier results and also suggests many new concrete problems.
In the last three sections the pace is quickened, but the work that is surveyed represents many recent developments that can be expected to lead to much further research. In §8.7, recent progress is reviewed in the calculations of the constants that appear in results such as the BHH theorem. Section 8.8 then considers the very recent progress on the central limit problem for some geometric problems closely related to Euclidean functionals. Finally, in §8.9 we see some tight analogies between the probabilistic analysis of Euclidean functionals and their worst-case behavior. The concluding section mainly focuses on the omissions that have been occasioned by our focus on functionals on points rather than on the full range of Euclidean structures.
The Connection to Algorithms. Before going to the survey just outlined, there is one top-level observation about the BHH theorem that should be made. It is likely that this remarkable 1959 result would have remained relatively undeveloped if it had not been for the striking use of the BHH
theorem in the polynomial-time probabilistic TSP algorithm of Karp (1976, 1977). The TSP was among the first of the traditional problems of geometric optimization to be proved to be NP-hard, and it is also a problem of genuine practical interest, so it is not surprising that considerable excitement was generated when Karp showed that the TSP is perfectly tractable under the plausible stochastic assumption that the sites to be visited by the tour can be modeled as a random uniform sample. In this context, Karp showed that, given any ![]() , there is a (simple!) polynomial time algorithm that produces a tour of length no more than
, there is a (simple!) polynomial time algorithm that produces a tour of length no more than ![]() times the optimal tour length with probability that converges to one as the size of the problem is increased. This discovery launched an important branch of the field of probabilistic algorithms. Moreover, it generated powerful interest in the BHH theorem, its generalizations, and sharpenings that are at the center of this survey.
times the optimal tour length with probability that converges to one as the size of the problem is increased. This discovery launched an important branch of the field of probabilistic algorithms. Moreover, it generated powerful interest in the BHH theorem, its generalizations, and sharpenings that are at the center of this survey.
8.2 Subadditive Euclidean Functionals
By abstracting from the traveling salesman tour just a few of its basic properties, it is possible to suggest a very general result that provides information comparable to that given by the BHH theorem for a large number of problems of combinatorial optimization in Euclidean space.
Let L be a function that associates a real number to each finite subset ![]() . To spell out the most innocent properties of L that mimic the behavior of the TSP, we first note that for the TSP, L exhibits homogeneity and translation invariance; i.e.,
. To spell out the most innocent properties of L that mimic the behavior of the TSP, we first note that for the TSP, L exhibits homogeneity and translation invariance; i.e.,
and
The TSP's length also has some strong smoothness and regularity properties, but these turn out not to be too important for most purposes. All that is needed is that L be Borel measurable when viewed as a function from Rnd to R. This condition is almost always trivial to obtain, but still one has to have it to be able to talk honestly about probabilities involving L.
Functions on the finite subsets of Rd that are measurable in the sense just described and that are homogeneous of order one and translation invariant are called Euclidean functionals. These three properties are commonplace
but bland. One should not expect to be able to prove much in such a limited context, but, with the addition of just a couple of other structural features, a rich and useful theory emerges.
The first additional property of the TSP functional that we consider is that it is monotone in the sense that
The final feature of the TSP functional that we abstract is the most substantial one. It expresses both the geometry of the underlying space and the fundamental suboptimality of one of the most natural TSP heuristics, the partitioning heuristic. If ![]() is a partition of [0, t]d into smaller cubes of edge length t/m, the subadditive property says there exists a constant B independent of m and t such that
is a partition of [0, t]d into smaller cubes of edge length t/m, the subadditive property says there exists a constant B independent of m and t such that
for all integers ![]() and real
and real ![]() .
.
Euclidean functionals that satisfy equations (8.3) and (8.4) will be called monotone subadditive Euclidean functionals. This class of processes seems to abstract the most essential features of the TSP that are needed for an effective asymptotic analysis of the functional applied to finite samples of independent random variables with values in Rd.
To see how subadditive Euclidean functionals arise (and to see how some problems just barely elude the framework), it is useful to consider two additional examples.
The first is the Steiner minimum tree. For any finite set of n points, ![]() , a Steiner minimum tree for S is a tree T whose vertex set contains S such that the sum of the lengths of the edges in T is minimal over all such trees. Note that the vertex set of T may contain points not in S; these are called Steiner points. If LST(x1, x2, ... , xn ) is the length of a Steiner tree of x1, x2, ... , xn and if we let |e| be the length of an edge e, another way of defining LST is just
, a Steiner minimum tree for S is a tree T whose vertex set contains S such that the sum of the lengths of the edges in T is minimal over all such trees. Note that the vertex set of T may contain points not in S; these are called Steiner points. If LST(x1, x2, ... , xn ) is the length of a Steiner tree of x1, x2, ... , xn and if we let |e| be the length of an edge e, another way of defining LST is just
The second example is closely related, yet it points out that the innocuous monotonicity property of the TSP can fail even in natural problems. The example we have in mind is the minimum spanning tree . For
![]() , let
, let ![]() , where the minimum is over all connected graphs T with vertex set {x1, x2, ... , xn}. It is an easy matter to check that any minimizing graph must indeed be a spanning tree.
, where the minimum is over all connected graphs T with vertex set {x1, x2, ... , xn}. It is an easy matter to check that any minimizing graph must indeed be a spanning tree.
The functional LMST is easily seen to be homogeneous, translation-invariant, and measurable. One can also check without much trouble that it is subadditive in the sense required above. Still, many simple examples such as the sets S = {(0,0), (0,2), (2,0), (2,2)} and ![]() } will show that LMST fails to be monotone. One should suspect that this failure is of an exceptional sort that would not have great influence on asymptotic behavior, and this suspicion is well justified. Still, the example puts us on warning that non-monotone functionals can require delicate considerations that axe not needed in cases that mimic the TSP more closely.
} will show that LMST fails to be monotone. One should suspect that this failure is of an exceptional sort that would not have great influence on asymptotic behavior, and this suspicion is well justified. Still, the example puts us on warning that non-monotone functionals can require delicate considerations that axe not needed in cases that mimic the TSP more closely.
The main theorem of this section shows that the properties (8.1) through (8.4), together with a modest moment condition, are sufficient to determine the asymptotic behavior of L(X1, X2,..., Xn) when the Xi are independent and identically distributed:
Theorem 8.2 (Steele, 1981b) Let L be a monotone subadditive Euclidean functional. If {Xi}, i=1, 2, ... , are independent random variables with the uniform distribution on [0, 1]d, and Var ![]() for each
for each ![]() , then as
, then as ![]()
with probability one, where ![]() is a constant depending only on L and d.
is a constant depending only on L and d.
The restrictions that this theorem imposes on a Euclidean functional are as few as one can reasonably expect to yield a generally useful limit theorem, and because of this generality the restriction to uniformly distributed random variables is palatable. Moreover, since many of the probabilistic models studied in operations research and computer science also focus on the uniformly distributed case, the theorem has immediate applications. Still, one cannot be long content with a theory confined to uniformly distributed random variables. Fortunately, with the addition of just a couple of additional constraints, the limit theory of subadditive Euclidean functionals can be extended to quite generally distributed variables.
To get to the essence of the extension, we first consider the case of random variables with a singular component, i.e., variables such that there
is a measurable set ![]() with Lebesgue measure zero such that
with Lebesgue measure zero such that ![]() . Random variables with a singular component provide a kind of geometrical worst case and hence provide a useful test case.
. Random variables with a singular component provide a kind of geometrical worst case and hence provide a useful test case.
To deal with such random variables, we need to draw out three additional properties shared by many subadditive Euclidean functionals. The first of these, called scale-boundedness, holds provided there is a constant C such that
for all ![]() . The second property, called simple subadditivity, holds provided there is a constant D such that
. The second property, called simple subadditivity, holds provided there is a constant D such that
for any finite subsets A1 and A2 contained in [0, t]d.
These two properties hold for many natural examples, and in particular they are easily checked for the TSP. The key benefit of scale-boundedness and simple subadditivity comes from their showing that the singular component of a distribution makes a contribution that is of lower order than that of the absolutely continuous component.
Lemma 1 Let L be a monotone subadditive Euclidean functional that is scale-bounded (8.5) and simply subadditive (8.6). If {Xi} are independent identically distributed (i.i.d.) random variables and E is any bounded set of Lebesgue measure zero, then as ![]()
with probability one.
The last property we will require for the extension of this theorem to general distributions calls on a type of restricted converse of simple sub-additivity. A Euclidean functional L is called upper-linear provided we have the following: For every finite collection of cubes Qj, where ![]() and the edges of the Qj are parallel to the axes, and for every infinite sequence xi, where
and the edges of the Qj are parallel to the axes, and for every infinite sequence xi, where ![]() and
and ![]() , we have
, we have
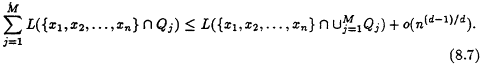
8.3 Tail Probabilities
The theory just outlined has a number of extensions and refinements. The first of these that we consider is the work of Rhee and Talagrand (1989) on the behavior of the tail probabilities of the TSP and related functionals under the model of independent uniformly distributed random variables in the unit d-cube. In Steele (1981a), it was observed that in dimension 2 Var (Ln) is bounded independently of n. This somewhat surprising result motivated the search for a more detailed understanding of the tail probabilities ![]() , and, in particular, it opened the question of determining if these probabilities might decay at the Gaussian rate exp(-ct2/2).
, and, in particular, it opened the question of determining if these probabilities might decay at the Gaussian rate exp(-ct2/2).
After introducing several methods from martingale theory and interpolation theory that led to interesting intermediate results, Rhee and Talagrand (1989) finally provided a remarkable proof that in d = 2 the TSP (and many related functionals) do indeed have Gaussian tail bounds.
Theorem 8.3 (Rhee and Talagrand, 1989) Suppose f is a Borel measurable function that assigns to each finite subset ![]() a real value f(F) such that
a real value f(F) such that
There is then a constant K = Kf such that if Xi are independent and uniformly distributed in [0, 1]2, then the random variables defined by Un = f ({ X1, X2, ... , Xn }) satisfy
The proof of this result rests on the systematic exploitation of the martingale versions of the Hoeffding and Prokhorov large-deviation inequalities together with a powerful bare-hands construction that helps articulate technical features of a random sample being well spread out.
8.4 The TSP in Fractal Spaces
The BHH theorem may seem like a result that is wedded to Rd; certainly the growth rate n(d-1)/d emerges as a natural characteristic of the dimension. Lalley (1990) has provided a set of results that cast new light on the role of dimension in problems like the TSP by developing limit results for TSP tours in fractal spaces. Lalley considered finite random samples chosen uniformly
(in an appropriate sense) from self-similar subsets of R2 that have Hausdorff dimension strictly less than two. Lalley obtained an almost-sure limit law for the length Ln of the shortest tour through {X1, X2, ... , Xn}, but now the normalizing denominator is no longer ![]() but a power of n that depends on the structure of the self-similar set.
but a power of n that depends on the structure of the self-similar set.
To give the flavor of the results obtained by Lalley, we will consider one specific example. A compact set K is said to be a strongly self-similar subset of R2 provided that there is a finite collection of transformations ![]() so that
so that
where each h Ti is a transformation that can be written as a strict affine contraction (with contraction factor ri < 1) followed by a rigid motion. The strong self-similarity of K requires moreover that the intersections ![]() , where
, where ![]() , be small in a technical sense that we will not detail.
, be small in a technical sense that we will not detail.
Theorem 8.4 (Lalley, 1990) If Xi, ![]() , are independent random variables with the ''uniform distribution'' on a strongly self-similar set If that has representation
, are independent random variables with the ''uniform distribution'' on a strongly self-similar set If that has representation
where ![]() , then the length Ln of the shortest tour through the point set
, then the length Ln of the shortest tour through the point set ![]() satisfies
satisfies
with probability one, where CK > 0 and ![]() is a constant uniquely determined by the similarity ratios ri.
is a constant uniquely determined by the similarity ratios ri.
8.5 Minimal Spanning Trees
If x = {x1, ... , xn} is a finite set of points in Rd for ![]() , a minimal spanning tree (MST) t of x is a connected graph with vertex set x such that the sum of the edge lengths of t is minimal; i.e.,
, a minimal spanning tree (MST) t of x is a connected graph with vertex set x such that the sum of the edge lengths of t is minimal; i.e.,
where |e| = |xi-xj| is the Euclidean length of the edge e = (xi, xj) and the minimum is over all connected graphs G.
Minimal spanning trees are among the most studied objects in combinatorial optimization, and even the probability theory of MST is rather well developed. For example, in Steele (1989) one finds results that cover the basic almost-sure asymptotic behavior of the MST that parallels the BHH theorem and even deals with edge weights that are more complicated than those given by the basic edge lengths. In particular, it is shown that if Xi are i.i.d. with compactly supported density f and 0 < α < d, then
where c(α, d) depends only on α and d.
One peculiar aspect of this result is that it fails to cover the extreme case α = d. This failure was particularly intriguing since the case α = d for d = 2 had been the source of an interesting conjecture by R. Bland, who by direct computational experience had been led to believe that if one takes the sum of the squares of the edges of the MST of a sample of points chosen randomly from the unit square, then as ![]() the sum converges to a constant. This result is hinted at by the limit cited above, but the specifically desired result fell just outside of its domain.
the sum converges to a constant. This result is hinted at by the limit cited above, but the specifically desired result fell just outside of its domain.
In Aldous and Steele (1992) an approach to such limit problems was taken that differs completely from the subadditivity-based analyses such as that mentioned in §8.2 or the more ad hoc method used in Steele (1989). The new approach is based on the study of an analog of the MST for an infinite set of points, in particular the points of a Poisson process on all Rd. The basic philosophy that guided the analysis is that because the empirical distributions of any independent uniform sequences look locally like a realization of the Poisson process, one should be able to relate the MST of a uniform sample to the MST of the (unbounded) Poisson process. Though this sounds a little like the "Poissonization" trick that goes back even as fax as Beardwood, Halton, and Hammersley, it is really radically different in concept and detail. To give a forward hint of that difference, note that we have no idea how to apply the method to the TSP. To sketch the basic idea, let x = (xi) be a finite or countably infinite subset of Rd, ![]() . We call x nice if (1) x is locally finite, i.e., has only finitely many elements in bounded subsets of Rd, and (2) the interpoint distances (|xj-xi|, i < j) are all distinct. Now, given a pair (x, x) with x nice and
. We call x nice if (1) x is locally finite, i.e., has only finitely many elements in bounded subsets of Rd, and (2) the interpoint distances (|xj-xi|, i < j) are all distinct. Now, given a pair (x, x) with x nice and ![]() , we can define trees tm(x, x) with vertices from x as follows: Let ξ1 = x, and let t1
, we can define trees tm(x, x) with vertices from x as follows: Let ξ1 = x, and let t1
be the single vertex ξ1. Let t2 be the tree consisting of the vertex ξ1 and the vertex ![]() that is closest to ξ1 in Euclidean distance, together with the edge (straight line segment) connecting ξ1 and ξ2. We then proceed inductively in a greedy fashion and define tm = tm(x, x) to be tm-1 together with a new edge (ξm, ξm), where
that is closest to ξ1 in Euclidean distance, together with the edge (straight line segment) connecting ξ1 and ξ2. We then proceed inductively in a greedy fashion and define tm = tm(x, x) to be tm-1 together with a new edge (ξm, ξm), where ![]() and
and ![]() are chosen so that the edge length |ξm-ξjm| is minimal (over all possible edges connecting tm-1 to x \ tm-1.) In the finite case where
are chosen so that the edge length |ξm-ξjm| is minimal (over all possible edges connecting tm-1 to x \ tm-1.) In the finite case where ![]() , this procedure terminates with the tree tn(x, x), and in that circumstance the tree obtained does not depend on the choice of the starting vertex x.
, this procedure terminates with the tree tn(x, x), and in that circumstance the tree obtained does not depend on the choice of the starting vertex x.
When x is infinite, the situation is more complex. We write ![]() for the set
for the set ![]() , but some work is required to obtain useful structural information about this graph. In fact, it turns out to be technically useful to look at a different but related graph, described in the next lemma.
, but some work is required to obtain useful structural information about this graph. In fact, it turns out to be technically useful to look at a different but related graph, described in the next lemma.
Lemma 2 Let g = g(x) be the graph on an infinite nice vertex set x defined by taking (x1, x2) as an edge in g if it is an edge in either ![]() or
or ![]() . Then the graph g is a forest and each component of g is an infinite tree.
. Then the graph g is a forest and each component of g is an infinite tree.
The main object of Aldous and Steele (1992) is the random tree ![]() constructed by taking a Poisson point process
constructed by taking a Poisson point process ![]() of rate 1 in Rd, letting
of rate 1 in Rd, letting ![]() . Let
. Let ![]() be the forest constructed as in the lemma, and finally take the connected graph
be the forest constructed as in the lemma, and finally take the connected graph ![]() to be the largest tree containing 0.
to be the largest tree containing 0.
It is natural to conjecture that ![]() is itself a tree with probability 1, but this possibility seems to be related to deep issues in continuum percolation, and the introduction of
is itself a tree with probability 1, but this possibility seems to be related to deep issues in continuum percolation, and the introduction of ![]() permits one to finesse that subtle issue.
permits one to finesse that subtle issue.
Lemma 3 Let D be the degree of vertex 0 in ![]() and let L1, ... , LD be the lengths of the edges of
and let L1, ... , LD be the lengths of the edges of ![]() incident to 0. We then have
incident to 0. We then have
-
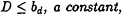
-
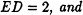
-
 .
.
Now let ![]() denote the point process consisting of n points
denote the point process consisting of n points ![]() that are independent and uniformly distributed on the unit cube [0, 1]d. With probability 1,
that are independent and uniformly distributed on the unit cube [0, 1]d. With probability 1, ![]() is a nice subset of Rd. Let
is a nice subset of Rd. Let ![]() be the minimal spanning tree of these n vertices. It is intuitive that
be the minimal spanning tree of these n vertices. It is intuitive that ![]() , after a suitable rescaling, should converge locally to
, after a suitable rescaling, should converge locally to ![]() .
.
Theorem 8.5 (Aldous and Steele, 1992) (a) If {|ei|} denotes the set of lengths of the edges of ![]() , then
, then
(b) If Δn,i denotes the proportion of vertices of ![]() with degree i, then for each i,
with degree i, then for each i,
The existence of limits in (b) was proved by different methods in Steele et al. (1987), where one also finds a proof of almost sure convergence. The analogous question in the model in which the cost assigned to each edge is independent and identically distributed is solved in Aldous (1990) using "limit process" arguments such as those reviewed above.
8.6 Matching Problems
The problem of determining the least weight matching in a graph (G, E) for which there is a function that assigns a real value to the edges of G is a central problem of combinatorial optimization. The matching problem is intermediate in complexity between the MST problem and the TSP. The minimal matching problem cannot be solved by a naive greedy algorithm such as that used for the MST, but there is still a polynomial-time algorithm that does solve the problem—in contrast to the TSP.
There are two natural Euclidean versions of the matching problem. The simplest version considers 2n points in Rd and asks for the perfect matching of the set for which the total edge length is minimum. This matching problem has a theory that is almost perfectly parallel to the theory of the MST.
A more subtle set of issues arise when one instead considers two distinguished subsets {x1, x2, ... , xn} and {y1, y2, ... ,yn}. Here the probability theory becomes much trickier, and new phenomena arise. A first taste of the new behavior is given by the results of Ajtai, Komlós, and Tusnády, one of which we note below:
Theorem 8.6 (Ajtai et al., 1984) If Xi and Yi are independent and uniformly distributed in R2for ![]() , then there are constants K1and K2
, then there are constants K1and K2
such that
with probability that approaches one as ![]() .
.
The ![]() term in this result adds a new spin to the theory of Euclidean functionals for several reasons. First, it shows that the scaling arguments and self-similarity ideas that were useful for the TSP and the MST are no longer accurate enough to lead to the right orders. Still, the basic motivation remains substantially intact, and for
term in this result adds a new spin to the theory of Euclidean functionals for several reasons. First, it shows that the scaling arguments and self-similarity ideas that were useful for the TSP and the MST are no longer accurate enough to lead to the right orders. Still, the basic motivation remains substantially intact, and for ![]() one again finds the characteristic growth rates of n(d-1)/d.
one again finds the characteristic growth rates of n(d-1)/d.
As an added impetus to the theory of Euclidean matching, there are some powerful connections with other parts of combinatorial optimization. It was through their work on bin packing and scheduling that Leighton and Shor were led to the investigation of the maximum length that must exist in a two-sample matching. The following example from their work again exhibits a curious logarithmic term:
Theorem 8.7 (Leighton and Shor, 1989) If Xi and Yi are independent and uniformly distributed in [0, 1]2for ![]() , then there is a constant K such that
, then there is a constant K such that
with probability that approaches one as ![]() .
.
In one of the most recent and most sweeping studies reviewed for this survey, Talagrand (1991) has unified the two preceding results as well as many others. The details of that development are too substantial to review here, but it is possible to indicate some of the sources of the new power.
Begin by noting that there is a basic relation between the behavior of the two sample matching problems and the theory of empirical discrepancy. We recall that if ![]() is any class of functions from [0, 1] to [0, 1], the empirical discrepancy associated with
is any class of functions from [0, 1] to [0, 1], the empirical discrepancy associated with ![]() is defined by
is defined by
where the Xi are i.i.d. random variables with density f. Even before the work of Ajtai, Komlós, and Tusnády, it was well understood that there was
a close connection between Mn and Dn when ![]() is taken to be the class of Lipschitz functions. It was also known that the theory associated with Dn was closely linked to the epsilon entropy of the class
is taken to be the class of Lipschitz functions. It was also known that the theory associated with Dn was closely linked to the epsilon entropy of the class ![]() , and finally people were beginning to understand that the issues addressed by epsilon entropy could in some cases be more effectively addressed by an emerging method of majorizing measures.
, and finally people were beginning to understand that the issues addressed by epsilon entropy could in some cases be more effectively addressed by an emerging method of majorizing measures.
Unfortunately, even defining all these terms would take us rather far afield, but hopefully it is meaningful to say that epsilon entropy is a tool for measuring the complexity of a class of functions by counting the number of epsilon balls that are needed to cover certain compact subsets, whereas the method of majorizing measures refines the theory of epsilon entropy to deal more effectively with aspects of inhomogeneity in ![]() . The substantial achievement of Talagrand (1991) was to develop the concrete tools of the theory of majorizing measures that make it directly useful in the theory of Mn and Dn and then to show how those tools could be used to deepen and unify the investigations initiated by Ajtai, Komlós, and Tusnády and broadened by Leighton and Shor.
. The substantial achievement of Talagrand (1991) was to develop the concrete tools of the theory of majorizing measures that make it directly useful in the theory of Mn and Dn and then to show how those tools could be used to deepen and unify the investigations initiated by Ajtai, Komlós, and Tusnády and broadened by Leighton and Shor.
8.7 The Values of the Constants
There is a long history of effort devoted to the determination of the limiting constraints in results like the BHH theorem. There is also a substantial literature that addresses the constraints associated with worst-case upper bounds.
Work by Supowit et al. (1983), Moran (1984), and Goldstein and Rein-gold (1987) provide recent progress on the worst-case bounds and provide surveys of the older literature. Two particularly noteworthy contributions for the TSP are those of Goddyn (1990) and Karloff (1987). The latter broke the ![]() barrier in dimension 2 by showing that
barrier in dimension 2 by showing that ![]() , whereas Goddyn (1990) obtained the best bounds in general dimension by means of a powerful technique that uses an infinite number of translations of quantizers other than cubical cylinders.
, whereas Goddyn (1990) obtained the best bounds in general dimension by means of a powerful technique that uses an infinite number of translations of quantizers other than cubical cylinders.
After the constraints on the TSP, the best-studied value is αRST, d , the constant associated with the worst-case length of a rectilinear Steiner minimum tree in the unit d-cube. Chung and Graham (1981) proved that αRST, 2 = 1, which is significant in that it is the only nontrivial worst-case constant for which we have an exact expression. The problem of determining αRST, d in higher dimensions is still open, the bounds being
![]() for
for ![]() (cf. Snyder, 1990, 1991; Salowe, 1991).
(cf. Snyder, 1990, 1991; Salowe, 1991).
Other than these bounds, little progress concerning the βL, d was made until Bertsimas and van Ryzin (1990) developed exact expressions for the probabilistic minimum spanning tree and matching constants as d gets large. Specifically, they showed that ![]() and
and ![]() as
as ![]() .
.
The crowning achievement concerning the probabilistic constants was the determination of an exact expression for βMST, d for all ![]() by Avram and Bertsimas (1992). The expression for βMST, d is a series expansion, each term of which requires a rather difficult integration. Still, the first few terms of the series in dimension 2 have been computed to yield a numerical lower bound of
by Avram and Bertsimas (1992). The expression for βMST, d is a series expansion, each term of which requires a rather difficult integration. Still, the first few terms of the series in dimension 2 have been computed to yield a numerical lower bound of ![]() , which agrees well with experimental data. We note that the proof employed by Avram and Bertsimas relies strongly on the fact that a greedy construction is guaranteed to yield an MST. Unfortunately, such a construction fails for many objects of interest, including the TSP. It is therefore evident that entirely new methods probably will be required to develop exact expressions for constants such as βTSP, d that arise from NP-hard problems.
, which agrees well with experimental data. We note that the proof employed by Avram and Bertsimas relies strongly on the fact that a greedy construction is guaranteed to yield an MST. Unfortunately, such a construction fails for many objects of interest, including the TSP. It is therefore evident that entirely new methods probably will be required to develop exact expressions for constants such as βTSP, d that arise from NP-hard problems.
As a final note, we return to the rectilinear Steiner minimum tree problem. Bern (1988) showed that, for a Poisson process with intensity N on the unit square, the value of the rectilinear MST constant is at least that of the rectilinear Steiner tree constant plus 0.0014. This separation of the constants was increased by Hwang and Yao (1990), who also extended the result to include points uniformly distributed in the unit square.
8.8 The Central Limit Problem
The recent work of Avram and Bertsimas (1992) provides enticing progress on the important and long-standing problem of providing a central limit theory (CLT) for Euclidean functionals. Their method falls short of providing a CLT for the MST problem or the TSP, but it provides very useful CLTs for somewhat easier problems, including the kth nearest neighbor problem, the Delaunay triangulation, and the length of the Voronoi diagram.
There axe two keys to the approach used by Avram and Bertsimas. The first is the observation of the applicability of the relatively recent CLT for dependent random variables due to Baldi and Rinott (1989). This new CLT deals with the dependence relations within a collection of random vari-
ables through the structure of a dependency graph Gn and offers an explicit Berry-Essen type bound where the maximal degree DnGn plays a critical role. The second key observation is that one achieves a considerable simplification of the CLT problem by first conditioning on the event An that in the subdivision of [0, 1] into subcubes of approximate size n/log n each subcube contains at least one and at most e log n of the sample points. The specifics of the problems handled by the Avram-Bertsimas method are such that once one conditions on An, one finds a problem that is within range of the Baldi-Rinott CLT. Any given problem has a number of details that must be directly resolved.
8.9 Worst-Case Growth Rates
One engaging aspect of the asymptotic theory of combinatorial optimization of point functionals is the persistent similarity between the probabilistic rates of growth that have been reviewed and the behavior of the corresponding functionals in worst-case settings.
As a primary example of a worst-case growth rate, consider the worst-case length of an optimal traveling salesman tour in the unit d-cube:
In words, ρTSP(n) is the maximum length over all n point sets in [0, 1]d that an optimal traveling salesman tour can attain. There is absolutely no probability theory here, for the point sets and tours are deterministic, yet there is a theory for this function that parallels the BHH theorem as closely as one could hope.
Theorem 8.8 (Steele and Snyder, 1989) As ![]() ,
,
where αTSP,d > 0 is a constant depending only on the dimension d.
The proof of this theorem and several related results all call on the subadditivity and smoothness properties of the underlying functional. The following elementary lemma often helps focus one's investigation of these problems by putting a finger on one clear set of sufficient conditions.
Lemma 4 If ρ(1) = 0 and there exists a constant ![]() such that for all integers
such that for all integers ![]() and
and ![]() , we have
, we have
-
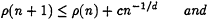
-
 ,
,
where ![]() as
as ![]() , then as
, then as ![]() ,
,
for a positive constant α.
For the analysis of any particular problem, there is almost always serious work to be done to make the problem amenable to this lemma or its variant. Still, the lemma has already proved its effectiveness in a number of problems, including minimum matchings (Snyder, 1987), minimum spanning trees (Steele and Snyder, 1989), greedy matchings (Snyder and Steele, 1990), and rectilinear Steiner minimum trees (Snyder, 1991).
8.10 Concluding Remarks
In the areas in which this survey has been forced to make the most substantial omissions, there are good sources to which one can turn. One important class of results that we have touched upon concerns the study of discrepancies of sequences that are more general than random samples. This subject goes under the name of irregularity of distribution, and it is closely allied in many technical ways with the work surveyed here. The volume by Beck and Chen (1987) gives one a view of the subject that it would be wrong to try to reprise, though it would have been interesting to make more explicit some of the relationships to questions such as the MST and Steiner trees.
Another huge area of related problems that have not been engaged here fails in the domain of the recent book Intersection and Decomposition Algorithms for Planar Arrangements, by F.K. Agarwal (1991). The work of K. Clarkson, D. Dobkin, H. Edelsbrunner, L. Guibas, E. Welzl and many others is surveyed there, and the volume offers a compelling view of the power that emerges from a detailed understanding of the way a set of lines cut up the plane. Duality is one of the powerful tools of that subject, so the restriction that is made here to focus on problems involving only "sets of points" and not "sets of lines" would not show up as a valid distinction
in the context of that theory. Still, a division had to be drawn, and there can be practical differences even where there are formal isomorphisms.
A third class of related results that have only been touched on here concern bin packing and its relation to scheduling. This topic is surveyed in Chapter 7 of this volume as well as in the beautiful recent book by Coffman and Lueker (1991) that is devoted to the topic.
Galileo is supposed to have said, "To study science, one must speak the language of science, and the language of science is written in circles, lines, and squares." With luck, this survey reveals that there is something a priori appropriate about the probability theory of combinatorial optimization. The subject has not strayed far from motivations that would have had meaning for Galileo. Still, the development has been extensive, and the methods have become powerful and diverse.
Acknowledgment. Sections 8.7 and 8.9 of this chapter are based in part on the geometrical portions of the article "Probability Theory of Network Optimization," written jointly with T.L. Snyder, which will appear in a multivolume series, The Handbook of Operations Research , coming from North-Holland Publishers. The author also thanks D. Aldous, D.F. Avram, D. Bertsimas, A.S. Golstein, L. Goddyn, E.M. Reingold, T.L. Snyder, J.S. Salowe, and M. Talagrand for making available prepublication copies of their work.
References
Agarwal, F.K. (1991), Intersection and Decomposition Algorithms for Planar Arrangements, Cambridge University Press, New York.
Ajtai, M., J. Komlós, and G. Tusnády (1984), On optimal matchings, Combinatorica 4, 259-264.
Aldous, D.J. (1990), A random tree model associated with random graphs, Rand. Struct. Alg. 1, 383-402.
Aldous, D.J., and J.M. Steele (1992), Asymptotics of Euclidean minimal spanning trees on random samples, to appear in Probability and Related Fields.
Avram, F., and D. Bertsimas (1992), The minimum spanning tree constant in geometrical probability and under the independent model: A unified approach, Ann. Appl. Probab. 2, 113-130.
Baldi, P., and Y. Rinott (1989), On normal approximations of distributions in terms of dependency graphs, Ann. Probab. 17, 1646-1650.
Beardwood, J., J.H. Halton, and J. Hammersley (1959), The shortest path through many points, Proc. Cambridge Philos. Soc. 55, 299-327.
Beck, J., and W.W.L. Chen (1987), Irregularities of Distribution, Cambridge University Press, New York.
Bern, M.W. (1988), Two probabilistic results on rectilinear Steiner trees, Algorithmica 3, 191-204.
Bertsimas, D., and G. van Ryzin (1990), An asymptotic determination of the minimum spanning tree and minimum matching constants in geometric probability, Oper. Res. Lett. 9, 223-231.
Chung, F.R.K., and R.L. Graham (1981), On Steiner trees for bounded point sets, Geom. Dedic. 11, 353-361.
Coffman, E.G., Jr., and G.S. Lueker (1991), Probabilistic Analysis of Packing and Partitioning Algorithms, John Wiley & Sons, New York.
Goddyn, L. (1990), Quantizers and the worst-case Euclidean traveling salesman problem, J. Comb. Theory B, 50, 65-81.
Goldstein, A.S., and E.M. Reingold (1987), Improved bounds on the traveling salesman problem in the unit cube, Technical Report, Department of Computer Science, University of Illinois, Urbana-Champaign, Ill.
Hwang, F.K., and Y.C. Yao (1990), Comments on Bern's probabilistic results on rectilinear Steiner trees, Algorithmica 5, 591-598.
Karloff, H.J. (1987), How long can a Euclidean traveling salesman tour be?, Technical Report 87-20, Department of Computer Science, University of Chicago, Chicago, Ill.
Karp, R.M. (1976), The probabilistic analysis of some combinatorial search algorithms, in Algorithms and Complexity: New Directions and Recent Results, J.F. Traub, ed., Academic Press, New York, 1-19.
Karp, R.M. (1977), Probabilistic analysis of partitioning algorithms for the traveling salesman problem in the plane, Math. Oper. Res. 2, 209-224.
Lalley, S.P. (1990), Traveling salesman with a self-similar itinerary, Probab. Eng. Inform. Sci. 4, 1-18.
Leighton, T., and P.W. Shor (1989), Tight bounds for minimax grid matching with applications to the average case analysis of algorithms, Combinatorica 9, 161-187.
Moran, S. (1984), On the length of optimal TSP circuits in sets of bounded diameter, J. Comb. Theory B, 37, 113-141.
Rhee, W.T., and M. Talagrand (1989), A sharp deviation inequality for the stochastic traveling salesman problem, Ann. Probab. 17, 1-8.
Salowe, J.S. (1991), A note on lower bounds for rectilinear Steiner trees, Technical Report, Department of Computer Science, University of Virginia, Charlottesville, Va.
Snyder, T.L. (1990), On minimal rectilinear Steiner trees in all dimensions, in Proc. 6th Annual ACM Symposium on Computational Geometry , ACM Press, New York, 311-320.
Snyder, T.L. (1991), Lower bounds for rectilinear Steiner trees in bounded space, Inform. Process. Lett. 37, 71-74.
Snyder, T.L., and J.M. Steele (1990), Worst-case greedy matchings in the unit d-cube, Networks 20, 779-800.
Steele, J.M. (1981a), Complete convergence of short paths and Karp's algo
rithm for the TSP, Math. Oper. Res. 6, 374-378.
Steele, J.M. (1981b), Subadditive Euclidean functionals and non-linear growth in geometric probability, Ann. Probab. 9, 365-376.
Steele, J.M. (1989), Efficacy of spacefilling heuristics in Euclidean combinatorial optimization, Oper. Res. Lett. 8, 237-239.
Steele, J.M., and T.L. Snyder (1989), Worst-case growth rates of some problems from combinatorial optimization, SIAM J. Comput. 18, 278-287.
Steele, J.M., L.A. Shepp, and W.F. Eddy (1987), On the number of leaves of a Euclidean minimal spanning tree, J. Appl. Probab. 24, 809-826.
Supowit, K.J., E.M. Reingold, and D.A. Plaisted (1983), The traveling salesman problem and minimum matchings in the unit square, SIAM J. Comput. 12, 144-156.
Talagrand, M. (1991), Matching theorem and empirical discrepancy computations using majorizing measures, Technical Report, Department of Mathematics, Ohio State University, Columbus, Ohio.






















