10.
Randomization in Parallel Algorithms
Vijaya Ramachandran1
University of Texas at Austin
ABSTRACT
A randomized algorithm is one that uses random numbers or bits during the runtime of the algorithm. Such algorithms, when properly designed, can ensure a correct solution on every input with high probability. For many problems, randomized algorithms have been designed that are simpler or more efficient than the best deterministic algorithms known for the problems. In this chapter, we define a natural randomized parallel complexity class, RNC, and give a survey of randomized algorithms for problems in this class.
10.1 Introduction
In recent years, there has been an explosive growth in the availability and diversity of parallel processors for computation. For the purpose of parallel algorithm design, it is convenient to work with an abstract, simplified machine model, known as the Parallel Random Access Machine (PRAM). The PRAM incorporates the basic elements of a parallel machine and has the property that an algorithm designed for it will perform without significant degradation on most commonly available parallel machines, including
shared-memory multiprocessors and fixed interconnection networks. For a survey of PRAM algorithms, both deterministic and randomized, see Karp and Ramachandran (1990).
The PRAM consists of a collection of independent sequential machines, each of which is called a processor, that communicate with one another through a global memory. This is a synchronous model, and a step of a PRAM consists of a read cycle in which each processor can read a global memory cell, a computing cycle in which each processor can perform a unit-time sequential computation, and a write cycle in which each processor can write into a global memory cell. There are many variants of this model, differing in whether a read conflict or a write conflict is allowed and, in the latter case, differing by the method used to resolve a write conflict. Because efficient simulations of the various models are known, we shall not elaborate on these variants.
Parallel algorithms have been designed on the PRAM for a large number of important problems. This has been a rich and exciting area of research in recent years, and many new techniques and paradigms have been developed. However, in spite of impressive gains, some problems have proved to be resistant to attempts to design highly parallel algorithms for their solution. For some other problems, parallel algorithms with good performance have come at the expense of extremely complex and intricate algorithms. In this context, several researchers have turned to randomization in an attempt to obtain better algorithms for these problems.
A randomized parallel algorithm is an algorithm in which each processor has access to a random number generator. The goal is to use this capacity to generate random numbers to come up with an algorithm that solves a problem quickly and with high probability on every input. The requirement that the algorithm achieves its performance guarantee on every input is much stronger than that of demanding good average-case performance and is a highly desirable property in an algorithm that uses randomization. Correspondingly, such algorithms are more difficult to design. Fortunately, there have been a number of successes in the design of such algorithms for parallel machines.
10.2 Quality Measures for Randomized Parallel Algorithms
For the purpose of this exposition, it is convenient to consider a problem as a binary relation s(x, y), where x is the input to the problem and y is a possible output for x. The value of s(x, y) will be true if and only if y is a
solution on input x. An algorithm for the problem should, on input x, either output some y such that s(x, y) is true, or output the fact that no such y exists. A Monte Carlo (or one-sided error) randomized algorithm is one that returns a y such that s(x, y) is true with probability at least 1/2 if such a y exists; if no such y exists, the algorithm always reports failure. Other types of randomized algorithms can be defined, but Monte Carlo algorithms are the ones used most commonly.
Given a Monte Carlo algorithm for a problem, we can improve our confidence in the result supplied by the algorithm from 1/2 to (1-1/2k) by performing k independent runs of the algorithm. Hence, given any ![]() , we can obtain a confidence level greater than
, we can obtain a confidence level greater than ![]() by performing
by performing ![]() independent runs of the algorithm.
independent runs of the algorithm.
The notion of a Monte Carlo algorithm applies to algorithms in any model—sequential, parallel, or distributed. In the following sections, we will address the issue of obtaining Monte Carlo algorithms that execute quickly on a PRAM.
10.3 The Randomized Parallel Complexity Class RNC
In the design and analysis of highly parallel algorithms for various problems, it has been observed that some problems have simple highly parallel algorithms using a relatively small number of processors whereas others have resisted all attempts so far to obtain any algorithm with a significant amount of parallelism. In this context, researchers have identified a natural parallel complexity class NC. The class NC consists of those problems that have PRAM algorithms that run in polylog time, i.e., time polynomial in the logarithm of the input size, with a polynomial number of processors. This class is robust in the sense that the collection of problems it contains does not vary with the machine model used, whether it is a shared-memory machine or a low-diameter interconnection network. It is also the smallest nontrivial class with this property. Although several important problems have been shown to be in NC, many others have not. The latter problems are of two types (for our purposes): one type consists of those problems that are either provably not in NC by virtue of the fact that they are provably not in P (polynomial time), or are highly unlikely to be in NC by virtue of the fact that they are complete problems for a larger class (such as P); for these problems, we currently know of no technique, randomized or otherwise, to come up with algorithms that run in polylog time with a polynomial number of processors. The other type of problems are those for which no one
has come up with either an algorithm to place the problem in NC or a completeness result to make it highly unlikely to be placed in NC. This latter type includes several important problems such as finding a maximum matching or a depth-first search tree (an important type of spanning tree) in a graph. For these problems, randomization has proved to be a valuable tool in coming up with fast parallel algorithms. For more on parallel complexity classes, see Cook (1981, 1985) and Karp and Ramachandran (1990).
The class RNC is the class of problems that can be solved by a Monte Carlo randomized algorithm that runs in polylog time with a polynomial number of processors. Thus, RNC is the randomized counterpart of NC.
10.4 Some Important Problems in RNC
10.4.1 Testing if a Multivariate Polynomial is not Identically Zero
Let Q (x0, . . ., xn-1) be a multivariate polynomial over a field. Consider the problem of determining if this polynomial is not identically zero. It is not known if this problem can be solved deterministically in polynomial time sequentially. However, if we allow randomization, we can come up with a simple Monte Carlo algorithm for the problem, as shown below.
The randomized algorithm is based on the following lemma, which is fairly straightforward to prove by induction on the number of variables n (note that the base case n = 1 follows from the fact that any single variable polynomial of degree n has at most n zeros).
Lemma 1 Let Q(x0, . . . , xn-1) be a polynomial of degree d with coefficients over a field F. For any set ![]() , the number of zeros of Q in
, the number of zeros of Q in ![]() .
.
The above lemma gives us the following Monte Carlo algorithm to determine if Q is not identically zero (Schwartz, 1980):
-
Choose any set
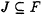 containing 2d elements.
containing 2d elements. -
Pick a random element
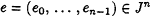 and evaluate Q(e).
and evaluate Q(e). -
If
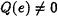 , then report
, then report 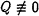 , else report failure.
, else report failure.
The probability of success in the case in which Q is not identically zero can be enhanced to 1-1/2k by repeating steps 2 and 3 k times. This algorithm is easily implemented on a PRAM with n processors by having the ith processor generate ei. Then, provided Q(e) can be determined quickly
given e, we have a fast algorithm to test if ![]() . In particular, if evaluating Q (e) is in NC, then determining if
. In particular, if evaluating Q (e) is in NC, then determining if ![]() is in RNC.
is in RNC.
10.4.2 Finding a Maximum Matching in a Graph
A matching in an undirected graph is a subset of edges, no two of which share a vertex. A perfect matching is a matching that contains all vertices of the graph. An RNC algorithm for the problem of determining if a graph has a perfect matching can be obtained using a theorem of Tutte (1947) that shows that the determinant of a certain matrix of multivariate polynomials becomes identically zero if and only if the graph does not have a perfect matching. This matrix is easily constructed from a description of the input graph. Because computing the determinant of an integer matrix is in NC, the problem of determining the existence of a perfect matching is in RNC by virtue of the above result on determining if a multivariate polynomial is not identically zero. This result can be extended to place the problem of determining the cardinality of a matching of maximum size, and that of finding a matching with this cardinality, in RNC (see Karp et al., 1986; Mulmuley et al., 1987).
The problem of finding a maximum matching in a graph is an important one and one that has received extensive attention in the context of sequential algorithm design. Although the problem is not known to be in NC, the above result allows us to find a maximum matching quickly and with high confidence. RNC algorithms for several other problems have been obtained in recent years; e.g., Aggarwal and Anderson (1987), Aggarwal et al. (1989), Babai (1986), Gibbons et al. (1988), Karloff (1986), and Ramachandran (1988).
10.5 Randomization Leads to Simple Parallel Algorithms
In practice, the number of processors available for solving a problem is typically much smaller than the problem size. Although massive parallelism may become a reality in the future, it is still of importance to address the issues that arise when the amount of parallelism available is small in comparison to the size of the input. In such a case the efficiency of a parallel algorithm becomes important. This refers to the speedup provided by the
parallel algorithm using a fixed number of processors over the best currently known sequential algorithm. A parallel algorithm is considered efficient if the product of its running time and the number of processors it uses is within a polylog factor of the running time of the current best sequential algorithm; it is considered optimal if this product is within a constant factor of the running time of the best sequential algorithm. A parallel algorithm that is efficient (or optimal) when run using a certain number of processors win remain an efficient (or optimal) parallel algorithm when implemented on a smaller number of processors while running proportionately slower. Hence it is of interest to construct efficient parallel algorithms that run very fast, regardless of the number of processors available.
There are a few problems, such as computing a depth-first or breadth-first search tree in a dense graph or performing Gaussian elimination, for which parallel algorithms with very efficient speedups are known even though NC algorithms are either not known or highly inefficient. However, most problems for which efficient parallel algorithms are known are in NC. Thus, placing a problem in NC is generally a first step to obtaining an efficient parallel algorithm for it.
Randomization has proved useful in the design of efficient and optimal parallel algorithms. It has also been useful in developing algorithms that are simpler than the best deterministic parallel algorithm known for the problem. Randomization has been applied to achieve these goals for a wide range of problems in graph theory (e.g., Alon et al., 1986; Gazit, 1986; Gibbons et al., 1988; Karp and Wigderson, 1985; and Luby, 1986), sorting (Hagerup, 1991; Rajasekharan and Reif, 1989; Reif and Valiant, 1987), list processing (Vishkin, 1984), computational geometry (Reif and Sen, 1989), string matching (Karl) and Rabin, 1987), linear algebra (Borodin et al., 1982, 1983), and load balancing (Gil, 1991; Gil et al., 1991). The last is a subroutine used in many efficient parallel algorithms to ensure that all of the processors perform about the same amount of work. We illustrate this simplifying potential of randomization with a problem that has received much attention in this context, the maximal independent set problem (Alon et al., 1986; Karp and Wigderson, 1985; Luby, 1986).
The problem of finding a maximal independent set in a graph has been studied extensively in the context of parallel algorithm design. One reason for this is the fact that this problem arises quite frequently in the design of parallel graph algorithms. Another reason is that this problem is a very easy one to solve by a sequential algorithm, but designing a good parallel algorithm for it places quite a few challenges.
Given an undirected graph, a set of vertices is independent if no pair is connected by an edge. The maximal independent set problem is the problem of finding an independent set in an input graph with the property that the set cannot be enlarged into a larger independent set that contains it. This problem has a simple sequential algorithm: Fix an ordering of the vertices and examine them in order, adding the examined vertex to the independent set if it contains no edge to a vertex in the set, and discarding the vertex otherwise. Unfortunately, this sequential algorithm does not seem to lend itself to parallelization. Although fast, efficient deterministic parallel algorithms have been developed for this problem, these algorithms tend to be fairly complicated. On the other hand, the following simple randomized algorithm gives a fast parallel algorithm for the problem and is more efficient than any of the deterministic NC algorithms known for it.
The randomized algorithm examines each vertex v independently in parallel and assigns the vertex to the independent set with probability 1/(2δ(v)), where δ(v) is the degree of v in the graph. Because this assignment is made simultaneously over all vertices, it is possible that the set constructed is not independent. The algorithm corrects this by examining each edge in the graph, and if the edge has both endpoints in the set, it throws out the vertex with smaller degree (breaking ties randomly). The resulting-set is clearly independent. The algorithm then deletes all neighbors of all vertices in the set from the graph and repeats the procedure with the new, smaller graph. It can be shown that the expected number of edges in the new graph is no more than 7/8 the original number of edges. Hence a logarithmic number of stages of this algorithm suffices to construct an independent set that is maximal in the original graph. This gives an efficient randomized algorithm that runs in O (log2n) time using a linear number of processors.
10.6 Eliminating Randomization
In some applications, it is desirable or necessary to have a deterministic algorithm. It turns out that some randomized algorithms can be derandomized provided only a limited amount of independence is required. This strategy is applicable to the algorithm described above for the maximal independent set problem. An analysis of that algorithm shows that only pairwise independence is required in the random trials. Hence the algorithm can be made deterministic by searching the entire space in parallel using a quadratic number of processors (Luby, 1986).
An alternate strategy that preserves the number of processors is to compute conditional probabilities while fixing one bit of the output at a time. If k-wise independence suffices for the randomized algorithm, for some constant k, then this gives a deterministic strategy that uses the same number of processors but increases the parallel time by a logarithmic factor. This technique has proved to be a powerful one and has resulted in efficient deterministic NC algorithms for several problems using the technique of first constructing an efficient randomized parallel algorithm with limited independence and then transforming the randomized algorithm into a deterministic one (Berger and Rompel, 1989; Luby, 1988; Motwani et al., 1989).
10.7 Conclusion
This chapter has described some of the most significant applications of randomization in parallel algorithm design. Randomization has led to fast parallel algorithms and to algorithms that are simple and efficient. These parallel algorithms provide correct solutions with high probability on every input. For most applications, such a performance is almost as satisfactory as a foolproof guarantee. Hence it is not surprising that randomization is a major trend in parallel algorithm design and applications, and we expect the field of randomized parallel algorithms to continue to be a thriving and productive area of research.
References
Aggarwal, A., and R.J. Anderson (1987), A random NC algorithm for depth first search, in Proc. 19th Annual A CM Symposium on Theory of Computing, ACM Press, New York, 325-334.
Aggarwal, A., R.J. Anderson, and M. Kao (1989), Parallel depth-first search in general directed graphs, in Proc. 21st Annual ACM Symposium on Theory of Computing, ACM Press, New York, 297-308.
Alon, N., L. Babai, and A. Itai (1986), A fast and simple randomized parallel algorithm for the maximal independent set problem, J. Algorithms 7, 567-583.
Babai, L. (1986), A Las Vegas-NC algorithm for isomorphism of graphs with bounded multiplicity of eigenvalues, in Proc. 27th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 303-312.
Berger, B., and J. Rompel (1989), Simulating logsupcn-wise independence in NC, in Proc. 30th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 2-7.
Borodin, A., S.A. Cook, and N. Pippenger (1983), Parallel computation for well-endowed rings and space-bounded probabilistic machines, Inform. Contr. 58, 113-136.
Borodin, A., J. von zur Gathen, and J.E. Hopcroft (1982), Fast parallel matrix and GCD computations, in Proc. 23d Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 65-71.
Cook, S.A. (1981), Towards a complexity theory of synchronous parallel computation, Enseign. Math. 27, 99-124.
Cook, S.A. (1985), A taxonomy of problems with fast parallel algorithms, Inform. Contr. 64, 2-22.
Gazit, H. (1986), An optimal randomized parallel algorithm for finding connected components in a graph, in Proc. 27th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 492-501.
Gibbons, P., R.M. Karp, G. Miller, and D. Soroker (1988), Subtree isomorphism is in Random NC, in Proc. 3rd Aegean Workshop on Computing , Springer-Verlag, New York, 43-52.
Gil, J. (1991), Fast load balancing on a PRAM, in Proc. 3rd IEEE Symposium on Parallel and Distributed Processing, IEEE Computer Society Press,
Los Alamitos, Calif., 10-17.
Gil, J., Y. Matias, and U. Vishkin (1991), Towards a theory of nearly constant time parallel algorithms, in Proc. 32nd Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 698-710.
Hagerup, T. (1991), Constant-time parallel integer sorting, in Proc. 23rd Annual ACM Symposium on Theory of Computing, ACM Press, New York, 299-306.
Karloff, H.J. (1986), A Las Vegas RNC algorithm for maximum matching, Combinatorica 6, 387-392.
Karp, R.M., and M.O. Rabin (1987), Efficient randomized pattern-matching algorithms, IBM J. Res. Develop. 31, 249-260.
Karp R.M., and V. Ramachandran (1990), Parallel algorithms for shared-memory machines, in Handbook of Theoretical Computer Science, vol. A, J. van Leeuwen, ed., Elsevier, New York, 869-941.
Karp, R.M., and A. Wigderson (1985), A fast parallel algorithm for the maximal independent set problem, J. Assoc. Comput. Mach. 32, 762-773.
Karp, R.M., E. Upfal, and A. Wigderson (1986), Constructing a perfect matching is in random NC, Combinatorica 6, 35-48.
Luby, M. (1986), A simple parallel algorithm for the maximal independent set problem, SIAM J. Comput. 15, 1036-1053.
Luby, M. (1988), Removing randomness in parallel computation without a processor penalty, in Proc. 29th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 162-173.
Motwani, R., J. Naor, and M. Naor (1989), The probabilistic method yields deterministic parallel algorithms, in Proc. 30th Annual IEEE Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 8-13.
Mulmuley, K., U.V. Vazirani, and V.V. Vazirani (1987), Matching is as easy as matrix inversion , in Proc. 19th Annual ACM Symposium on Theory of Computing, ACM Press, New York, 345-354.
Rajasekharan, S., and J.H. Reif (1989), Optimal and sublogarithmic time randomized parallel algorithms, SIAM J. Comput. 18, 594-607.
Ramachandran, V. (1988), Fast parallel algorithms for reducible flow graphs, in Concurrent Computations: Algorithms, Architecture, and Technology, S.K. Tewksbury, B.W. Dickinson, and S.C. Schwartz, eds., Plenum Press, New York, 117-138.
Reif, J., and S. Sen (1989), Polling: A new randomized sampling technique for computational geometry, in Proc. 21st Annual ACM Symposium on Theory of Computing, ACM Press, New York, 394-404.
Reif, J.H., and L.G. Valiant (1987), A logarithmic time sort for linear size networks, J. Assoc. Comput. Sci. 34, 60-76.
Schwartz, J.T. (1980), Fast probabilistic algorithms for verification of polynomial identities, J. Assoc. Comput. Sci. 27, 701-717.
Tutte, W.T. (1947), The factorization of linear graphs, J. London Math. Soc. 22, 107-111.
Vishkin, U. (1984), Randomized speed-ups in parallel computation, in Proc. 16th Annual ACM Symposium on Theory of Computing, ACM Press, New York, 230-239.












