11.
Randomly Wired Multistage Networks
Bruce M. Maggs
NEC Research Institute
ABSTRACT
Randomly wired multistage networks have recently been shown to outperform traditional multistage networks in three respects. First, they have fast deterministic packet-switching and circuit-switching algorithms for routing permutations. Second, they are nonblocking, and there are on-line algorithms for establishing new connections in them, even if many requests for connections axe made simultaneously. Finally, and perhaps most importantly, they are highly fault tolerant.
11.1 Introduction
Networks derived from hypercubes form the architectural basis of most parallel computers, including machines such as the BBN Butterfly, the Connection Machine, the IBM RP3 and GF11, the iPSC, and the NCUBE. The butterfly, in particular, is quite popular, and has been demonstrated to perform reasonably well in practice. An example of an N-input butterfly (N = 8) with depth log N = 3 is shown in Figure 11.1. The nodes in this graph represent switches, and the edges represent wires. Messages are typically sent from the switches on level 0, called the inputs, to those on level log N, called the outputs.
The message-routing algorithm for a butterfly is quite simple. Each message simply follows the unique path of length log N from its source input
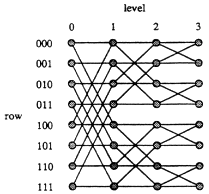
FIGURE 11.1: An 8-input butterfly network. Reprinted, with permission, from Arora et al. (1990). Copyright © 1990 by ACM Press.
to its destination output. One problem with this algorithm (and hence the network) is that if some switch or edge along the unique path from input i to output j (say) becomes congested or fails, then communication between input i and output j will be disrupted.
11.1.1 Dilated Butterflies
Because message congestion is a common occurrence in real networks, the wires in butterfly networks are typically dilated, so that each wire is replaced by a channel consisting of two or more wires. In a d-dilated butterfly, each channel consists of d wires. Because it is harder to congest a channel than it is to congest a single wire in a butterfly, dilated butterflies are better routing networks than simple butterflies (e.g., Koch, 1988; Kruskal and Snir, 1983; Rettberg et al., 1990).
11.1.2 Delta Networks
Butterfly and dilated butterfly networks belong to a larger class of networks called delta networks (see, e.g., Kruskal and Snir, 1986). The switches on each level of a delta network can be partitioned into blocks. All of the switches on level 0 belong to the same block. On level 1, there axe two blocks, one consisting of the switches that are in the upper N/2 rows and the other consisting of the switches that are in the lower N/2 rows. In general, the switches in a block B of size M on level l have neighbors in two blocks, Bu, and Bl, on level l + 1. The upper block, Bu, contains the switches on level l + 1 that are in the same rows as the upper M/2 switches

FIGURE 11.2: The logical path from any input to output 011. Reprinted, with permission, from Lisinski et al. (1990). Copyright © 1990 by IEEE.
of B. The lower block, Bl, consists of the switches that are in the same rows as the lower M/2 switches of B. The edges from B to Bu are called the ''up-edges,'' and those from B to Bl are called the "down-edges." The three blocks, B, Bu, and Bl, and the edges between them are collectively called a splitter. The switches in B are called the splitter inputs, and those in Bu and Bl are called the splitter outputs.
In a delta network, each input and output are connected by a single logical (up-down) path through the blocks of the network. For example, Figure 11.2 shows the logical path from any input to output 011. In a butterfly, this logical path specifies a unique path through the network, since only one up-edge and one down-edge emanate from each switch. In general, however, each switch may have several up-and down-edges, say d of each, and each step of the logical path can be taken on any one of d edges.
11.1.3 Multibutterflies
A d-dilated butterfly can be thought of as d butterflies that are merged together by merging switches that have the same row and level numbers. In a recent paper, Upfal (1989) proposed a more general way to merge butterfly networks. The idea is to permute the order of the switches within each block before merging the networks. Thus, given two N-input butterflies G1 and G2 and a collection of permutations Π = <π0, π1, . . ., πlog N> where ![]() , a 2-butterfly is formed by first permuting all of the switches in each block on level l according to πl, for
, a 2-butterfly is formed by first permuting all of the switches in each block on level l according to πl, for ![]() , and then merging switches with the same row and level numbers. The result, as
, and then merging switches with the same row and level numbers. The result, as
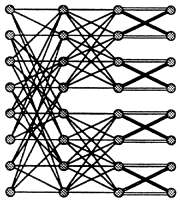
FIGURE 11.3: An 8-input 2-butterfly network. Reprinted, with permission, from Leighton and Maggs (1989). Copyright © 1989 by IEEE.
shown in Figure 11.3, is an N-input graph with depth log N in which each switch has four input edges and four output edges. Of the four output edges at a switch, two are up-edges and two are down-edges (with one up-edge and one down-edge coming from each butterfly). Multibutterflies (i.e., d-butterflies) are composed from d butterflies in a similar fashion using d -1 sets of permutations, Π(1),..., Π( d-1), resulting in a depth log N network with 2d × 2d switches.
11.1.4 Expansion
Dilated butterflies have remained the network of choice for many parallel machines. Recent work, however, suggests that this may be about to change. In fact, it now appears as though randomly wired multibutterfly networks (i.e., multibutterfly networks where the permutations Π(1),..., Π(d-1) are chosen at random) are superior to dilated butterflies for many message-routing applications. The crucial property that these networks possess is known as expansion . In particular, an M-input splitter is said to have (α, β)-expansion if any set of ![]() inputs is connected to at least βk up-outputs and βk down-outputs, where β > 1, ab < 1/2, and α and β are fixed constants. Figure 11.4 shows a splitter with expansion (α, β). Splitters with expansion β > 1 are known to exist for any
inputs is connected to at least βk up-outputs and βk down-outputs, where β > 1, ab < 1/2, and α and β are fixed constants. Figure 11.4 shows a splitter with expansion (α, β). Splitters with expansion β > 1 are known to exist for any ![]() , and they can be constructed deterministically in polynomial time (e.g., Kahale, 1991; Lubotzky et al., 1988; Upfal, 1989), but randomized wirings typically provide the best possible expansion. In fact, the expansion β of a randomly wired splitter will be close to d-1 with probability close to 1, provided
, and they can be constructed deterministically in polynomial time (e.g., Kahale, 1991; Lubotzky et al., 1988; Upfal, 1989), but randomized wirings typically provide the best possible expansion. In fact, the expansion β of a randomly wired splitter will be close to d-1 with probability close to 1, provided
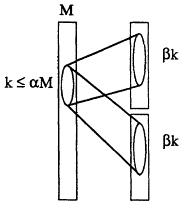
FIGURE 11.4: An M-input splitter with expansion property (α, β). Reprinted, with permission, from Arora et al. (1990). Copyright © 1990 by ACM Press.
that α is a sufficiently small constant. (For a discussion of the trade-offs between α and β in randomly wired splitters, see Leighton et al. (1991) and Upfal (1989).) Furthermore, the constructions in §§11.3 through 11.5 require β > d/2, but, at present, there are no known deterministic algorithms for constructing splitters with this much expansion in polynomial time.
Splitters with expansion are good for routing because one must block βk splitter outputs in order to block k splitter inputs. In classical networks such as the butterfly, the reverse is true: it is possible to block 2k inputs by blocking only k outputs. When this effect is compounded over several levels, the effect is dramatic. In classical networks such as the butterfly, a single fault can block 2l switches l levels back, whereas in a multibutterfly, it takes βl faults to block a single switch l levels back. Splitters with expansion can be const11:22 AM 1/2/04ted deterministically, but for ![]() , randomized wirings typically provide the best possible expansion.
, randomized wirings typically provide the best possible expansion.
11.1.5 History
Randomly wired multibutterfly networks have been discovered several times. Bassalygo and Pinsker (1974) used random multibutterfly-like networks to construct the first nonblocking network with size of O(NlogN) and depth of O(logN). Fahlman (1980) proposed a related randomly wired network called the Hashnet. More recently, Upfal (1989) coined the term multibutterfly and provided a simple deterministic algorithm for routing any permutation of N messages in O(log N) steps on an N-input multibutterfly network.
(In fact, Upfal's algorithm can be pipelined to route log N permutations in O(log N) steps.) Leighton and Maggs (1989) proved that a randomly wired multibutterfly is an efficient routing network even when many of the switches are faulty. Later, Arora et al. (1990) developed a circuit-switching algorithm for the multi-Benes network and showed that it can be used to establish connections in a nonblocking fashion. Most recently, DeHon et al. (1991) designed a 64-processor switching network using a randomly wired delta network for processor-to-memory communications.
11.1.6 Outline
The remainder of this chapter is organized as follows. Section 11.2 describes Upfal's algorithm for packet switching on multibutterfly networks. Next, §11.3 presents a multibutterfly algorithm for circuit switching. Section 11.4 describes a strategy for tolerating faults. Finally, §11.5 sketches an algorithm for establishing connections in a randomly wired nonblocking network.
11.2 Packet Switching
In a one-to-one packet-routing problem, each input sends a packet to a distinct output. The goal of the routing algorithm is to deliver the packets to their destinations as quickly as possible, subject to the constraint that at each time step each edge can transmit at most one packet. There may also be restrictions on the number of packets that can be queued at any one switch.
Upfal (1989) proved that an N-input d-butterfly with expansion (α, β) can solve any one-to-one packet-routing problem in O(log N) steps using a simple greedy algorithm. Moreover, he showed that by using pipelining, O(log N) problems can also be routed in O(log N) steps. The result is important because the only other known deterministic on-line linear-hardware O(log N)-step packet-routing algorithm (Leighton, 1985) requires the use of the AKS sorting circuit (Ajtai et al., 1983), which is more complicated and has larger constant factors.
Upfal's algorithm starts by partitioning the packets into "waves" so that at most one packet in each wave is destined for any set of L contiguous outputs. One way to do this is to group packets into the same wave if they are in the same permutation and their destinations are congruent modulo L. If there are P permutations to be routed, this results in the formation of at most PL waves. In general, we will set L = 1/(2α) because then we win be guaranteed that at most M/(2L) = αM packets in any wave will
ever pass through the up-(or down-) edges of any M-input splitter of the multibutterfly (for any M). This will allow us to apply the (α, β) expansion property to the set of inputs of any splitter occupied by the packets of a single wave at any time. (E.g., if k inputs of a splitter contain packets of a single wave that want to traverse up-edges, then these inputs are connected to at least βk up-outputs.) This is because packets going through the M/2 up (or M/2 clown) splitter outputs can only be destined for the descendant set of M/2 contiguous multibutterfly outputs.
The routing of the packets proceeds in stages, each stage consisting of an even and odd phase, and each phase consisting of 2d steps. In even phases, packets axe sent from even levels to the next (odd) level, and in odd phases, packets axe sent from the odd levels to the next (even) level. The edges connecting levels axe colored in 2d colors so that each node is incident to one edge of each color. In each phase, we process the colors in sequence, one step per color. For each color, we move a packet forward along an edge with that color if there is a packet in the switch at the tail of the edge that wants to go in that direction (up or down) and if there is no packet in the switch at the head of the edge. Alternatively, if there is a packet in the switch at the head of the edge and if it is in a later wave than the packet at the tail of the edge, then the two packets axe swapped, so that the packet in the earlier wave moves forward. Note that every switch processes and/or contains at most one packet at any step.
The following theorem summarizes the performance of Upfal's algorithm.
Theorem 11.1 (Leighton and Maggs, 1989; Upfal, 1989) On an N-input multibutterfly with expansion (α, β), Upfal's algorithm routes P permutations in O(P + log N) steps.
11.3 Circuit Switching
In a one-to-one circuit-switching problem, each input wishes to establish a connection (path) to a distinct output. The connections must not intersect at any switch or edge. The goal of the circuit-switching algorithm is to find the connections as quickly as possible.
Arora et al. (1990) present an O(log N)-bit-step algorithm for circuit switching on multibutterfly networks. The only previously known O(log N)-bit-step algorithms for circuit switching relied on the AKS sorting circuit (Ajtai et al., 1983)or used randomness on the hypercube (Aiello et al., 1990). (Recently, Leighton and Plaxton (1990) have developed an O(log N)-bit-step randomized sorting algorithm for the butterfly.)
11.3.1 Unique Neighbors
The circuit-switching algorithm requires the splitters in the multibutterfly to have a special unique neighbor property. An M-input splitter is said to have the (α, δ) unique neighbor property if in every subset X of ![]() inputs, there are δk nodes in X that have an up-output neighbor that is not adjacent to any other node in X, and there axe δk nodes in X that have a down-output neighbor that is not adjacent to any other node in X. It is relatively easy to prove (see Arora et al., 1990) that any splitter with (α,β) expansion has the (α, δ) unique neighbor property where δ = 2β/d -1, provided that α > d/2. Randomly wired multibutterflies are known to have expansion (α, β) where β d/2 (Leighton and Maggs, 1989; Upfal, 1989). Explicit constructions of such splitters are not known, however.
inputs, there are δk nodes in X that have an up-output neighbor that is not adjacent to any other node in X, and there axe δk nodes in X that have a down-output neighbor that is not adjacent to any other node in X. It is relatively easy to prove (see Arora et al., 1990) that any splitter with (α,β) expansion has the (α, δ) unique neighbor property where δ = 2β/d -1, provided that α > d/2. Randomly wired multibutterflies are known to have expansion (α, β) where β d/2 (Leighton and Maggs, 1989; Upfal, 1989). Explicit constructions of such splitters are not known, however.
11.3.2 The Algorithm
In order for the algorithm to succeed, the number of paths passing through each M-input splitter must be at most αM. Thus, in an N-input network, we make connections between the N/L inputs and outputs only in rows that are multiples of L, where L is some fixed constant greater than 1/α.
There is a simple algorithm for extending paths from one level to the next in an M-input splitter with the (α, δ) unique neighbor property. The basic idea is that those paths at switches with unique neighbors can be extended without worrying about blocking any of the other paths. Paths are extended by repeating steps of the following type. First, every unextended path sends out a proposal to his neighbors among the splitter outputs in the desired direction (up or down). Next, every output that receives precisely one proposal sends back its acceptance to that proposal. Finally, every unextended path that receives an acceptance advances to one of its accepting outputs. In each step, the fraction of unextended paths drops by a factor of (1 -δ). Thus, after O(log M) phases, all of the paths are extended. By applying this algorithm one level at a time, it is possible to establish paths from the inputs to the outputs of an N-input multibutterfly with the (α, δ) unique neighbor property in O(log2N) bit-steps.
A more sophisticated algorithm is needed to construct the paths in O(log N) bit-steps. Given a set of paths that need to be extended at an M-input splitter, the algorithm does not wait O(log M) time for every path to be extended before it begins the extension at the next level. Instead, it executes path extension steps until the number of unextended paths falls to some fraction ρ of its original value, where ρ is a fixed constant that depends on d. Then the path extension process can start at the next level.
The danger is that the paths left behind may find themselves blocked by the time they reach the next level. To ensure that this does not happen, stalled paths send out "placeholders" to all of their neighbors at the next level, and henceforth the neighbors with placeholders participate in path extension at the next level, as if they were paths. Of course, the neighbors holding placeholders must in general extend in both the upper and the lower output portions of the splitter, because they do not yet know which path will ultimately use them. Notice that a placeholder not only reserves a spot that may be used by a path at a future time but also helps to chart out the path by continuing to extend ahead.
In order to prevent placeholders from multiplying too rapidly and clogging the system—because if the fraction of inputs of a splitter that are trying to extend rises above α, the path extension algorithm ceases to work—we need to ensure that as stalled paths get extended, they send cancellation signals to the placeholding nodes ahead of them to tell them they are not needed anymore. When a placeholding node gets cancellations from all the nodes that had requested it to hold their place, it ceases its attempts to extend. It also sends cancellations to any nodes ahead of it that may be holding a place for it.
The O(log N)-bit-step algorithm alternates between two types of phases. First, path extension steps are executed until the fraction of unextended paths in each splitter drops by a factor of ρ. In this phase, each path is restricted to extending forward by at most one level. We refer to the first wave of paths and placeholders to arrive at a level as the wavefront. The wavefront moves forward by one level during each phase. If a path or placeholder in the wavefront is not extended, then at the end of the phase it sends placeholders to all of its neighbors. In the second phase, cancellations are passed through the network. They travel a distance of C, where C is some fixed constant that depends on ρ and d.
The performance of the circuit-switching algorithm is summarized in the theorem below.
Theorem 11.2 (Arora et al., 1990) On an N-input multibutterfly with expansion (α, β), β d/2, the algorithm solves any one-to-one circuit-switching problem in O(log N) bit-steps.
11.4 Fault Tolerance
Leighton and Maggs (1989) showed that multibutterfly networks are highly fault tolerant. In particular, they proved that no matter how an adversary
chooses k switches to fail, there will be at least N-O(k) inputs and N-O(k) outputs between which permutations can be routed in O(log N) steps. Note that this is the best that could be hoped for in general, because the adversary can choose to make Ω(k) inputs and Ω(k) outputs faulty. Thus, the multibutterfly is the first bounded-degree network known to be able to sustain large numbers of faults with minimal degradation in performance.
The strategy for tolerating faults consists of two stages: erasure of outputs and fault propagation.
Each splitter in the multibutterfly is examined in the erasure stage. If more than an ε fraction of the splitter inputs are faulty, where ε = 2α(β'-1) and ![]() , then the splitter, as well as all descendant switches and outputs, is erased from the network. The erasure of an M-input splitter causes the removal of M multibutterfly outputs and accounts for at least εM faults. Hence, at most k/ε = (kL) / (β'-1) = O(k) multibutterfly outputs are removed by this process.
, then the splitter, as well as all descendant switches and outputs, is erased from the network. The erasure of an M-input splitter causes the removal of M multibutterfly outputs and accounts for at least εM faults. Hence, at most k/ε = (kL) / (β'-1) = O(k) multibutterfly outputs are removed by this process.
Next, working from level log N back to level 0, each switch is examined in the fault propagation stage to see if at least half of its upper outputs lead to faulty switches that have not been erased or if at least half of its lower outputs lead to faulty switches that have not been erased. If so, then the switch is declared faulty (but not erased). It is not difficult to prove (see Leighton and Maggs, 1989) that at most k / (α'-1) additional switches are declared faulty at each level by this process. Hence, at most O(k) multibutterfly inputs will be faulty (declared or otherwise).
We now erase all the remaining faulty switches. This leaves a network with N-O(k) inputs and N-O(k) outputs. Moreover, every input in every splitter is linked to ![]() functioning upper outputs (if the descendant multibutterfly outputs exist) and
functioning upper outputs (if the descendant multibutterfly outputs exist) and ![]() functioning lower outputs (if the corresponding multibutterfly outputs exist). Hence every splitter has an (α,β') expansion property. Thus, we can apply theorems 11.1 and 11.2 with β replaced by β' to show that the network can solve packet-switching and circuit-switching problems on the working inputs and outputs in O(log N) steps.
functioning lower outputs (if the corresponding multibutterfly outputs exist). Hence every splitter has an (α,β') expansion property. Thus, we can apply theorems 11.1 and 11.2 with β replaced by β' to show that the network can solve packet-switching and circuit-switching problems on the working inputs and outputs in O(log N) steps.
11.5 Nonblocking Networks
In a nonblocking network, inputs are connected to outputs with node-disjoint paths, as they were in §11.3. The inputs, however, are not all required to make their requests for connections at the same time. Inputs may wait to make their requests and may later break connections and request new ones. The main invariant obeyed by a nonblocking network is that
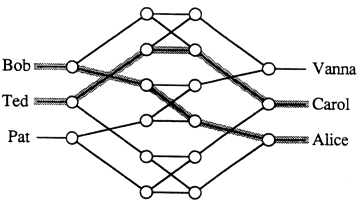
FIGURE 11.5: A nonblocking network with 3 inputs and 3 outputs. Reprinted, with permission, from Arora et al. (1990). Copyright © 1990 by ACM Press.
any unused input-output pair can be connected by a path through unused switches, no matter what paths have previously been established. The 6-terminal graph shown in Figure 11.5 is an example of a nonblocking network. In particular, if Bob is talking to Alice and Ted is talking to Carol, then Pat can still call Vanna.
The existence of a bounded-degree strict-sense nonblocking network with size O(N log N) and depth O(log N) was first proved by Bassalygo and Pinsker (1974). Unfortunately, there has not been much progress on the problem of setting the switches so as to realize the connection paths since then. Until recently, no algorithm was known that could cope with simultaneous requests for connections in any O(N log N)-size nonblocking network.
Arora et al. (1990) discovered an O(N log N)-switch nonblocking network for which each path connection can be made on-line in O(log N) bit-steps. The algorithms work even if many calls are made at once—every call still gets through in O(log N) bit-steps, no matter what calls were made previously and no matter what calls are currently active, provided that no two inputs try to access the same output at the same time.
The nonblocking network is called a multi-Benes network. A multi-Benes network is constructed by combining expanders and the Benes network in much the same way that expanders and butterflies are combined to fore a multibutterfly. As shown in Figure 11.6, a multi-Benes network is essentially a reversed multibutterfly followed by a multibutterfly.
As in the circuit-switching algorithm, the network must be lightly loaded by some fixed constant factor L, where L > 1/α. Since the other inputs and
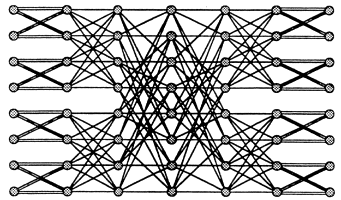
FIGURE 11.6: An 8-input 2-multi-Benes network.
outputs are not used, the first and last log2L. levels of the network can be removed, and the N/L, inputs and outputs can each be connected directly to their L descendants and ancestors on levels log2L and 2log2N-log2L, respectively.
The basic idea is to treat the switches through which paths have already been established as if they were faulty and to apply the fault propagation techniques from §11.4 to the network. In particular, we define a node to be "busy" if there is a path currently routing through it, and we recursively define a node to be "blocked" according to the following rule. Working backwards from level 2log2N-log2L-1 to level log2N, a switch is declared blocked if more than 2β-d-1 of its up (or down) neighbors on level l+1 are busy or blocked. From level log2N-1 to level log2L, a switch is declared blocked if more than 4β-d-2 of its 2d neighbors on level l+1 are busy or blocked. A switch that is neither busy nor blocked is said to be ''working."
Two important properties can be proved about the network switches. First, for β > 2d/3+2/3 and L > 1/2α(3β-2d-2), at most a 2α fraction of the switches in any block are declared to be blocked. Thus, all of the unused inputs are working. As a consequence, no matter what paths have already been established, any unused input can reach any unused output. Second, for β > d/2, the network of working switches has a (α, 1/d) unique neighbor property. As a consequence, the circuit-switching algorithm from §11.3 can be used to establish new paths, even if many requests for connections are made simultaneously.
References
Aiello, W., T. Leighton, B. Maggs, and M. Newman (1990), Fast algorithms for bit-serial routing on a hypercube, in Proc. 1990 ACM Symposium on Parallel Algorithms and Architectures, ACM Press, New York, 55-64.
Ajtai, M., J. Komlos, and E. Szemeredi (1983), Sorting in clog n parallel steps, Combinatorica 3, 1-19.
Arora, S., T. Leighton, and B. Maggs (1990), On-line algorithms for path selection in a non-blocking network, in Proc. 22nd Annual ACM Symposium on Theory of Computing, ACM Press, New York, 149-158.
Bassalygo, L.A., and M.S. Pinsker (1974), Complexity of optimum non-blocking switching network without reconnections, Probl. Inform. Transm. 9, 64-66.
DeHon, A., T. Knight, and H. Minsky (1991), Fault-tolerant design for multistage routing networks, in Proc. International Symposium on Shared Memory Multiprocessing, Information Processing Society of Japan.
Fahlman, S.E. (1980), The Hashnet interconnection scheme, Technical Report CMU-CS-80-125, Department of Computer Science, Carnegie Mellon University, Pittsburgh, Pa.
Kahale, N. (1991), Better expansion for Ramanujan graphs, in Proc. 32nd Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 398-404.
Koch, R.R. (1988), Increasing the size of a network by a constant factor can increase performance by more than a constant factor, in Proc. 29th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 221-230.
Kruskal, C.P., and M. Snir (1983), The performance of multistage interconnection networks for multiprocessors, IEEE Trans. Comput. C-32, 1091-1098.
Kruskal, C.P., and M. Snir (1986), A unified theory of interconnection network structure, Theor. Comput. Sci. 48, 75-94.
Leighton, F.T. (1985), Tight bounds on the complexity of parallel sorting, IEEE Trans. Comput. C-34, 344-354.
Leighton, T., and B. Maggs (1989), Expanders might be practical: Fast algorithms for routing around faults in multibutterflies, in Proc. 30th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif, 384-389.
Leighton, T., and G. Plaxton (1990), A (fairly) simple circuit that (usually) sorts, in Proc. 31st Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 264-274.
Leighton, T., C.L. Leiserson, and M. Klugerman (1991), Theory of parallel and VLSI computation, Research Seminar Series Report MIT/LCS/RSS 10, Laboratory for Computer Science, Massachusetts Institute of Technology, Cambridge.
Lisinski, D., T. Leighton, and B. Maggs (1990), Empirical evaluation of randomly-wired multistage networks, in Proc. 1990 International Conference on Computer Design, IEEE Computer Society Press, Los Alamitos, Calif., 380-385.
Lubotzky, A., R. Phillips, and P. Sarnak (1988), Ramanujan graphs, Combinatorica 8, 261-277.
Rettberg, R.D., W.R. Crowther, P.P. Carvey, and R.S. Tomlinson (1990), The monarch parallel processor hardware design, Computer 23, 18-30.
Upfal, E. (1989), An O(log N) deterministic packet routing scheme, in Proc. 21st Annual ACM Symposium on Theory of Computing, ACM Press, New York, 241-250.














