2.
Simulated Annealing
Dimitris Bertsimas and John Tsitsiklis
Massachusetts Institute of Technology
ABSTRACT
Simulated annealing is a probabilistic method proposed in Kirkpatrick et al. (1983) and Cerny (1985) for finding the global minimum of a cost function that may possess several local minima. It works by emulating the physical process whereby a solid is slowly cooled so that when eventually its structure is "frozen," it happens at a minimum energy configuration.
We restrict ourselves to the case of a cost function defined on a finite set. Extensions of simulated annealing to the case of functions defined on continuous sets have also been introduced in the literature (e.g., Gidas, 1985a; Geman and Hwang, 1986; Kushner, 1985; Holley et al., 1989; Jeng and Woods, 1990). Our goal in this review is to describe the method, its convergence, and its behavior in applications.
2.1 The Method
The basic elements of simulated annealing (SA) are the following:
-
A finite set S.
-
A real-valued cost function J defined on S. Let
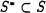 be the set of global minima of the function J, assumed to be a proper subset of S.
be the set of global minima of the function J, assumed to be a proper subset of S. -
For each
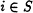 , a set
, a set 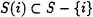 , called the set of neighbors of i.
, called the set of neighbors of i.
-
For every i, a collection of positive coefficients qij,
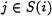 , such that
, such that 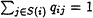 . It is assumed that
. It is assumed that 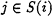 if and only if
if and only if  .
. -
A nonincreasing function
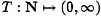 , called the cooling schedule. Here N is the set of positive integers, and T(t) is called the temperature at time t.
, called the cooling schedule. Here N is the set of positive integers, and T(t) is called the temperature at time t. -
An initial "state"
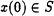 .
.
Given the above elements, the simulated annealing algorithm consists of a discrete-time inhomogeneous Markov chain x(t), whose evolution we now describe. If the current state x(t) is equal to i, choose a neighbor j of i at random; the probability that any particular ![]() is selected is equal to qij. Once j is chosen, the next state x(t +1) is determined as follows:
is selected is equal to qij. Once j is chosen, the next state x(t +1) is determined as follows:
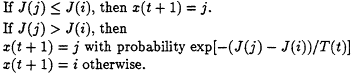
Formally,
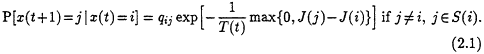
If ![]() and
and ![]() , then P[x(t+1) = j | x(t) = i] = 0.
, then P[x(t+1) = j | x(t) = i] = 0.
The rationale behind the SA algorithm is best understood by considering a homogeneous Markov chain xT(t) in which the temperature T(t) is held at a constant value T. Let us assume that the Markov chain xT (t) is irreducible and aperiodic and that qij = qji for all i, j. Then xT(t) is a reversible Markov chain, and its invariant probability distribution is given by
where ZT is a normalizing constant. (This is easily shown by verifying that the detailed balance equations hold.) It is then evident that as ![]() , the probability distribution πT is concentrated on the set S* of global minima of J. This latter property remains valid if the condition qij = qji is relaxed (Faigle and Kern, 1989).
, the probability distribution πT is concentrated on the set S* of global minima of J. This latter property remains valid if the condition qij = qji is relaxed (Faigle and Kern, 1989).
The probability distribution (2.2), known as the Gibbs distribution, plays an important role in statistical mechanics. In fact, statistical physicists have been interested in generating a sample element of S, drawn according to the probability distribution πT. This is accomplished by simulating the Markov chain xT(t) until it reaches equilibrium, and this method is known as the Metropolis algorithm (Metropolis et al., 1953). In the optimization context, we can generate an optimal element of S with high probability if we produce a random sample according to the distribution ζT, with T very small. One difficulty with this approach is that when T is very small, the time it takes for the Markov chain xT(t) to reach equilibrium can be excessive. The SA algorithm tries to remedy this drawback by using a slowly decreasing "cooling schedule" T(t).
The SA algorithm can also be viewed as a local search algorithm in which (unlike the usual deterministic local search algorithms) there are occasional "upward" moves that lead to a cost increase. One hopes that such upward moves will help escape from local minima.
2.2 Convergence Analysis
2.2.1 Basic Results
Having defined the algorithm, we now address its performance. The main questions are:
-
Does x(t) "converge" to the optimal set S*?
-
How fast does the convergence to S* take place?
The first question has been more or less completely answered, and we will now survey the main results. Much less is known about the second, as we will discuss later.
From now on, we assume that for some fixed T (and therefore for all T) the Markov chain xT(t) is irreducible and aperiodic. We say that the SA algorithm converges if ![]() . (Note that this is convergence in probability, rather than almost sure convergence.) A fair amount of work has been concerned with finding necessary and sufficient conditions for convergence, in the above sense. The main result, due to Hajek, is presented next, following some definitions.
. (Note that this is convergence in probability, rather than almost sure convergence.) A fair amount of work has been concerned with finding necessary and sufficient conditions for convergence, in the above sense. The main result, due to Hajek, is presented next, following some definitions.
Theorem 2.1 (Hajek, 1988) We say that state i communicates with S* at height h if there exists a path in S (with each element of the path being a
neighbor of the preceding element) that starts at i and ends at some element of S*, and such that the largest value of J along the path is J(i) + h. Let d* be the smallest number such that every ![]() communicates with S* at height d*. Then, the SA algorithm converges if and only if
communicates with S* at height d*. Then, the SA algorithm converges if and only if ![]() and
and
The most popular cooling schedules (in theory, at least) are of the form
where d is some positive constant. Theorem 2.1 states that SA converges if and only if ![]() .
.
The constant d* is a measure of the difficulty for x(t) to escape from a local minimum and go from a nonoptimal state to S*. We axe primarily interested in problems where d* > 0, which will be assumed from now on. Such problems have local minima that are not optimal. Some understanding of theorem 2.1 is provided by the following argument. Consider a local minimum whose "depth" is d*. The SA makes an infinite number of trials to escape from it, and the probability of success at each trial is of the order of exp[-d*/T(t)]. Then condition (2.3) amounts (by the Borel-Cantelli lemma) to saying that an infinite number of these trials will be successful. Indeed, the proof in Hajek (1988) proceeds by estimating the statistics of the exit times from certain neighborhoods of local minima.
Let ζ(i; t) = P[x(t) = i]. If T(t) decreases very slowly, as is the case in (2.4), then x(t) behaves, over fairly long time intervals, like a homogeneous Markov chain, and it can be reasonably expected that the difference between ζT(t)(i) and π(i; t) is small at all times. Indeed, one of the very first convergence proofs (Geman and Geman, 1984) was based on this idea, although the results therein were less sharp than theorem 2.1.
In order to acquire more intuition about the interpretation of theorem 2.1, we will carry the connection between SA and the corresponding family of homogeneous Markov chains further. For this goal we consider the cooling schedule T(t) = d/log t. In general, the statistics of the Markov chain x(t) under a slowly varying cooling schedule T(t) remain pretty much unchanged if a related cooling schedule is used in which the temperature is held constant for fairly long time periods. In our case, the schedule T(t) = d/log t can be approximated as follows. Let t1 = 1 and tk+1 = tk + exp(kd). Then
let ![]() , for
, for ![]() . Consider the kth segment [tk, tk+1] of the piecewise constant schedule
. Consider the kth segment [tk, tk+1] of the piecewise constant schedule ![]() . We are dealing with the reversible homogeneous chain x1/ k(t), and we will now investigate how fast it reaches steady state.
. We are dealing with the reversible homogeneous chain x1/ k(t), and we will now investigate how fast it reaches steady state.
We want to study the convergence of the chain x1/k(t). The eigenvalues of its transition-probability matrix are real. Its relaxation time is determined by its second-largest eigenvalue λ2 for which good estimates are available, at least in the limit as ![]() (see, e.g., Ventcel, 1972; Chiang and Chow, 1988; and Holley and Stroock, 1988). In particular, if the cost function J has a unique global minimum, the relaxation time |log(1 -λ2)| is well approximated by exp(kd*). Interestingly enough, this is the same as constant d* defined in theorem 2.1, something that is far from obvious. This yields another interpretation of the convergence condition
(see, e.g., Ventcel, 1972; Chiang and Chow, 1988; and Holley and Stroock, 1988). In particular, if the cost function J has a unique global minimum, the relaxation time |log(1 -λ2)| is well approximated by exp(kd*). Interestingly enough, this is the same as constant d* defined in theorem 2.1, something that is far from obvious. This yields another interpretation of the convergence condition ![]() for the schedule
for the schedule ![]() . If d < d*, then at each temperature 1/k we are running x1/k(t) for a negligible fraction of its relaxation time, and this is not enough for π(i; t) to stay close to πT(i). On the other hand, if d > d*, then the interval [t k, tk+1] corresponds to exp[k(d*-d)] relaxation times of x1/k(t), which implies that π(i; tk+1) is very close to π1/k(i), as
. If d < d*, then at each temperature 1/k we are running x1/k(t) for a negligible fraction of its relaxation time, and this is not enough for π(i; t) to stay close to πT(i). On the other hand, if d > d*, then the interval [t k, tk+1] corresponds to exp[k(d*-d)] relaxation times of x1/k(t), which implies that π(i; tk+1) is very close to π1/k(i), as ![]() .
.
One can also pursue this approximation by piecewise constant schedules directly, without introducing eigenvalue estimates. The main idea is that, at low temperatures, the statistics of a homogeneous chain can be accurately bounded by viewing it as a singularly perturbed Markov chain and using rather crude large-deviation bounds (Tsitsiklis, 1988, 1989). For other convergence proofs, see Connors and Kumar (1988), Gidas (1985b), Mitra et al. (1986), and Honey and Stroock (1988).
The convergence of SA (in the sense defined earlier in this section) is a reassuring property, but it is fax from enough for SA to be a useful algorithm. We also need to know the speed of convergence. It can be shown that for any schedule T(t) = d/log t, and for all t,
where A and a are positive constants depending on the function J and the neighborhood structure. If we wish x(t) to be outside S* with probability less than ![]() , we need
, we need ![]() .
.
We now turn our attention to the practical relevance of some of the convergence results. From a more practical perspective, while the algorithm is being run, one should keep track of the best state i encountered so fax and its associated cost J(i). If the algorithm is to be run for t* time steps, we are
not really interested in the value of ![]() . Rather, we are interested in the probability that no state in S* is visited during the execution of the algorithm. Given a cooling schedule of the form T(t) = d/log t, with d > d*, it can be shown that this probability is at most A/(t*)a, for some positive constants A and a. It vanishes as
. Rather, we are interested in the probability that no state in S* is visited during the execution of the algorithm. Given a cooling schedule of the form T(t) = d/log t, with d > d*, it can be shown that this probability is at most A/(t*)a, for some positive constants A and a. It vanishes as ![]() , which might seem encouraging. On the other hand, if the temperature is fixed at any positive value (or even at infinity, corresponding to a random walk), the probability that no state in S* is visited in t* time units is at most
, which might seem encouraging. On the other hand, if the temperature is fixed at any positive value (or even at infinity, corresponding to a random walk), the probability that no state in S* is visited in t* time units is at most ![]() , for suitable positive constants B and b. So, for very large times, the performance of a random walk would seem to be better than the performance guarantees of simulated annealing. The key point is that the above analyses, based on time asymptotics, involve extremely large constants and are largely irrelevant. Indeed the constants in the above estimates are often much larger than the cardinality of the state space S. In particular, the above analysis cannot even establish that simulated annealing is preferable to exhaustive search.
, for suitable positive constants B and b. So, for very large times, the performance of a random walk would seem to be better than the performance guarantees of simulated annealing. The key point is that the above analyses, based on time asymptotics, involve extremely large constants and are largely irrelevant. Indeed the constants in the above estimates are often much larger than the cardinality of the state space S. In particular, the above analysis cannot even establish that simulated annealing is preferable to exhaustive search.
2.2.2 Taking the Instance Size into Account
One can trace the inadequacy of the analytical methods mentioned so far to the fact that they deal with one instance at a time. A more realistic approach would be to consider a family of instances, together with a notion of instance size, and then study the statistics of the first hitting time of the set S* as a function of the instance size. (We refer to such results as complexity results.) This would then provide a meaningful yardstick for comparing simulated annealing to alternative methods. As an extension, if we are only interested in approximately optimal solutions to a given problem, we can define a set S* of approximately optimal solutions and study the statistics of the first hitting time of S*. Unfortunately, such results have proved very difficult to derive. We review briefly some of the progress that has been made along this direction.
All available positive complexity results we are aware of use a schedule T(t) in which the temperature is held constant in time, although it may depend on the instance size. The only nontrivial combinatorial problem for which SA has been rigorously analyzed is the maximum matching problem. It has been shown by Sasaki and Hajek (1988) that, for bounded-degree graphs with n nodes, the expected time until SA hits an optimal configuration is O(n5). This is slower than other available algorithms, but the result is encouraging. On the other hand, no algorithm of the simulated annealing type (even with time-varying temperature) can solve the matching problem
in polynomial expected time when the degree bound is relaxed (see Sasaki and Hajek, 1988).
Hajek (1985)studied an example in which the state space is S = {1, 2, 3}N and the cost of a typical state s = (s1, ... , sN) is equal to ![]() . This corresponds to a minimization in N identical uncoupled problems, and the optimal solution is evident. It is argued that if the temperature is suitably chosen as a function of N, the expected first hitting time of the global minimum grows polynomially with N. This is better than exhaustive search, because the cardinality of S is 3N. It is also better than the "local search with multistart" method, whereby a state in S is chosen repeatedly at random and each time a local search (pure descent) algorithm is run until a local minimum is reached (Hajek, 1985). Of course, in this example a much more efficient algorithm exists. What is encouraging is that SA does not really use the information that the cost is separable, i.e., that there is no coupling between si and sj. For this reason, one may hope that simulated annealing would run in polynomial time even if the problem was perturbed by introducing some sufficiently weak coupling between components. No such extensions are currently available.
. This corresponds to a minimization in N identical uncoupled problems, and the optimal solution is evident. It is argued that if the temperature is suitably chosen as a function of N, the expected first hitting time of the global minimum grows polynomially with N. This is better than exhaustive search, because the cardinality of S is 3N. It is also better than the "local search with multistart" method, whereby a state in S is chosen repeatedly at random and each time a local search (pure descent) algorithm is run until a local minimum is reached (Hajek, 1985). Of course, in this example a much more efficient algorithm exists. What is encouraging is that SA does not really use the information that the cost is separable, i.e., that there is no coupling between si and sj. For this reason, one may hope that simulated annealing would run in polynomial time even if the problem was perturbed by introducing some sufficiently weak coupling between components. No such extensions are currently available.
One reason why SA works well in the preceding example is that if a given state is far from optimal, then there exists a large number of paths that lead to another state with lower cost. The probability that the state x(t) escapes from a local minimum of depth d along any particular path, and in a single trial, is at most exp(-d/T). On the other hand, if the number of candidate paths is very large, the probability of escape is substantial. It is here that the combinatorial structure of the state space S and its neighborhood system should become significant.
In interesting combinatorial settings the state space is usually exponential in the instance size. So constant-temperature SA would work in polynomial time if the relaxation time were polylogarithmic in the size of the state space ("rapid mixing"). There are a number of available positive results on rapid mixing in Markov chains, but they deal mostly with the case where ![]() , corresponding to a random walk. (This is a much simpler special case, because the cost function J has no effect.) Unfortunately, simulated annealing becomes interesting at the opposite end, when T is very small. Proving rapid mixing for large SA Markov chains at small temperatures is a challenging task.
, corresponding to a random walk. (This is a much simpler special case, because the cost function J has no effect.) Unfortunately, simulated annealing becomes interesting at the opposite end, when T is very small. Proving rapid mixing for large SA Markov chains at small temperatures is a challenging task.
One class of problems for which there is some hope of obtaining positive complexity results arises in the context of image processing. Here, we have an N × N grid. To each gridpoint (i, j), we associate a variable sij taking
values in a finite set A. We thus obtain a configuration space ![]() . Many image processing and pattern recognition problems lead to a cost function
. Many image processing and pattern recognition problems lead to a cost function ![]() of the form
of the form
where ![]() is identically zero unless (i, j) and
is identically zero unless (i, j) and ![]() are neighboring grid-points. Starting with Geman and Geman (1984), simulated annealing has become a very popular method for such problems. Here one defines two states (configurations) to be neighbors if they differ only at a single grid-point. Note that when a configuration change is contemplated (that is, a change of some sij), the cost difference (which determines the probability of accepting the change) depends only on the gridpoints neighboring (i, j). For this reason, the evolution of the configuration can be viewed as the time evolution of a Markov random field. The relaxation times of Markov random fields have been extensively studied (see, e.g., Liggett, 1988), but under rather special assumptions on the functions fij and
are neighboring grid-points. Starting with Geman and Geman (1984), simulated annealing has become a very popular method for such problems. Here one defines two states (configurations) to be neighbors if they differ only at a single grid-point. Note that when a configuration change is contemplated (that is, a change of some sij), the cost difference (which determines the probability of accepting the change) depends only on the gridpoints neighboring (i, j). For this reason, the evolution of the configuration can be viewed as the time evolution of a Markov random field. The relaxation times of Markov random fields have been extensively studied (see, e.g., Liggett, 1988), but under rather special assumptions on the functions fij and ![]() . Thus, the available results are not yet applicable to the cost functions that arise in image processing.
. Thus, the available results are not yet applicable to the cost functions that arise in image processing.
As far as theory is concerned, there is at present a definite lack of rigorous results justifying the use of simulated annealing. Even if SA is accepted, there are no convincing theoretical arguments favoring the use of time-varying (decreasing) cooling schedules, as opposed to the use of a constant temperature. (This latter question is partially addressed in Hajek and Sasaki (1989).)
2.3 Behavior in Practice
Despite the lack of a rigorous theoretical justification of its speed of convergence, researchers have used SA extensively in the last decade. There are numerous papers discussing applications of SA to various problems. We have already mentioned that SA is extensively used in image processing. In order to give an indication of its performance, we will review some of the work concerning the application of SA to combinatorial optimization problems.
In a comprehensive study of SA, Johnson et al. (1990, 1991, 1992) discuss the performance of SA on four problems: the traveling salesman problem (TSP), graph partitioning problem (GPP), graph coloring problem (GCP),
and number partitioning problem (NPP). Johnson et al. apply SA to these NP-hard problems using a cooling schedule in which the temperature decreases geometrically; i.e., T(t + 1) = rT(t). In general, the performance of SA was mixed: in some problems, it outperformed the best known heuristics for these problems, and, in other cases, specialized heuristics performed better. More specifically:
-
In the graph partitioning problem, a graph G = (V, E) is given, and we are asked to partition the set of vertices V into two subsets V1 and V2 so as to minimize
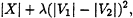
where X is the set of edges joining a node in V1 with a node in V2 , and λ is a weighting factor. For the GPP, SA obtains final solutions that are at best some 5 percent better than those obtained by the best of the more traditional algorithms (e.g., the Kernighan and Lin (1970) heuristic) if the latter are allowed the same amount of computation time as SA. For sparse graphs, SA was better than repeated applications of the Kernighan-Lin heuristic, which is based on ideas of local optimization, whereas for some structured graphs the Kernighan-Lin heuristic was better.
-
In the graph coloring problem, a graph G = (V, E) is given, and we are asked to partition the set of vertices into a minimal number of subsets, such that no edge has both endpoints in the same subset. For the graph coloring problem, SA produces final solutions that are competitive with those obtained by a tailored heuristic (the one by Johri and Matula (1982)), which is considered the best one for this problem. However, computation times for SA are considerably longer than those of the specialized heuristic.
-
For the traveling salesman problem, SA consistently outperforms solutions found by repeated application of iterative improvement, based on 2-opt or 3-opt transitions, but it is a consistent loser when compared with the well-known algorithm of Lin and Kernighan (1973). The latter is based on k-opt transitions, and at each iteration it decides dynamically the value of k.
Another interesting point is that the choice of the cooling schedule influences the quality of solution obtained. In Laarhoven and Aarts (1987)
the authors compare three different cooling schedules for the graph partitioning problem, and they observe that the quality of the solution found by the different cooling schedules can differ as much as 10 percent. Another observation is that the computation times can be excessive for some problems.
In addition to the above mentioned developments in image processing, SA and various alternative versions based roughly on it have been used in statistical applications. Bohachevsky et al. (1986) proposed a ''generalized'' SA procedure for continuous optimization problems and applied their method to an optimal design problem. Many researchers have considered SA as a tool in the development of optimal experimental designs. Recent examples include Currin et al. (1991), Meyer and Nachtsheim (1988), and Sacks and Schiller (1988). Variants of SA based on Bayesian ideas have been proposed by Laud et al. (1989) and van Laarhoven et al. (1989).
Overall, SA is a generally applicable and easy-to-implement probabilistic approximation algorithm that is able to produce good solutions for an optimization problem, even if we do not understand the structure of the problem well. We believe, however, that more research, both theoretical and experimental, is needed to assess further the potential of the method.
References
Bohachevsky, I., M.E. Johnson, and M.L. Stein (1986), Generalized simulated annealing for function optimization, Technometrics 28, 209-217.
Cerny, V. (1985), A thermodynamic approach to the traveling salesman problem: An efficient simulation, J. Optim. Theory Appl. 45, 41-51.
Chiang, T.-S., and Y. Chow (1988), On eigenvalues and optimal annealing rate, Math. Oper. Res. 13, 508-511.
Connors, D.P., and P.R. Kumar (1988), Balance of recurrence order in time-inhomogeneous Markov chains with applications to simulated annealing,
Prob. Eng. Inform. Sci. 2, 157-184.
Currin, C., T. Mitchell, M. Morris, and D. Ylvisaker (1991), Bayesian prediction of deterministic functions, with applications to the design and analysis of computer experiments, J. Amer. Star. Assoc. 86, 953-963.
Faigle, U., and W. Kern (1989), Note on the Convergence of Simulated Annealing Algorithms, Memorandum 774, University of Twente, Enschede, Netherlands.
Geman, S., and D. Geman (1984), Stochastic relaxation, Gibbs' distribution and the Bayesian restoration of images, IEEE Trans. Pattern Anal. Mach. Intell. 6, 721-741.
Geman, S., and C.-R. Hwang (1986), Diffusions for global optimization, SIAM J. Contr. Optim. 24, 1031-1043.
Gidas, B. (1985a), Global optimization via the Langevin equation, in Proc. 24th IEEE Conference on Decision and Control, IEEE, New York, 774-778.
Gidas, B. (1985b), Nonstationary Markov chains and convergence of the annealing algorithm, J. Stat. Phys. 39, 73-131.
Hajek, B. (1985), A tutorial survey of theory and applications of simulated annealing, in Proc. 24th IEEE Conference on Decision and Control, IEEE, New York, 755-760.
Hajek, B. (1988), Cooling schedules for optimal annealing, Math. Oper. Res. 13, 311-329.
Hajek, B., and G. Sasaki (1989), Simulated annealing—to cool or not, Syst. Contr. Lett. 12, 443-447.
Holley, R.A., and D.W. Stroock (1988), Simulated annealing via Sobolev inequalities, Commun. Math. Phys. 115, 553-569.
Holley, R.A., S. Kusuoka, and D.W. Stroock (1989), Asymptotics of the spectral gap with applications to the theory of simulated annealing, J. Funct. Anal. 83, 333-347.
Jeng, F.-C., and J.W. Woods (1990), Simulated annealing in compound Gaussian random fields, IEEE Trans. Inform. Theory 36, 94-107.
Johnson, D., C. Aragon, L. McGeoch, and C. Schevon (1990), Optimization by simulated annealing: An experimental evaluation, Part I: Graph partitioning, Oper. Res. 37, 865-892.
Johnson, D., C. Aragon, L. McGeoch, and C. Schevon (1991), Optimization by simulated annealing: An experimental evaluation, Part II: Graph coloring and number partitioning , Oper. Res. 39, 378-406.
Johnson, D., C. Aragon, L. McGeoch, and C. Schevon (1992), Optimization by simulated annealing: An experimental evaluation, Part III: The traveling salesman problem, in preparation.
Johri, A., and D. Matula (1982), Probabilistic bounds and heuristic algorithms for coloring large random graphs, Technical Report 82-CSE-6, Department of Computer Science and Engineering, Southern Methodist University, Dallas, Tex.
Kernighan, B., and S. Lin (1970), An efficient heuristic procedure for partioning graphs, Bell Syst. Tech. J. 49, 291-307.
Kirkpatrick, S., C.D. Gelett, and M.P. Vecchi (1983), Optimization by simulated annealing, Science 220, 621-630.
Kushner, H.J. (1985), Asymptotic global behavior for stochastic approximations and diffusions with slowly decreasing noise effects: Global minimization via Monte Carlo, Technical Report LCDS 85-7, Brown University, Providence, R.I.
Laud, P., L.M. Berliner, and P.K. Goel (1989), A stochastic probing algorithm for global optimization, in Proc. 21st Symposium on the Interface between Computer Science and Statistics. Revised version to appear in J. Stoch. Opt. (1992).
Liggett, T. (1988), Interacting Particle Systems, Springer-Verlag, New York.
Lin, S., and B. Kernighan (1973), An effective heuristic algorithm for the
traveling salesman problem, Oper. Res. 21, 498-516.
Metropolis, N., A.W. Rosenbluth, M.N. Rosenbluth, A.H. Teller, and E. Teller (1953), Equation of state calculations by fast computing machines, J. Chem. Phys. 21, 1087-1092.
Meyer, R.K., and C.J. Nachtsheim (1988), Constructing exact D-optimal experimental designs by simulated annealing, Amer. J. Math. Manage. Sci. 8, 329-359.
Mitra, D., F. Romeo, and A. Sangiovanni-Vincentellim (1986), Convergence and finite-time behaviour of simulated annealing, Adv. Appl. Probab . 18, 747-771.
Sacks, J., and S. Schiller (1988), Spatial designs, in Fourth Purdue Symposium on Statistical Decision Theory and Related Topics , S.S. Gupta, ed., Academic Press, New York.
Sasaki, G., and B. Hajek (1988), The time complexity of maximum matching by simulated annealing, J. Assoc. Comput. Mach. 35, 387-403.
Tsitsiklis, J.N. (1988), A survey of large time asymptotics of simulated annealing algorithms, in Stochastic Differential Systems, Stochastic Control Theory and Applications, W. Fleming and P.L. Lions, eds., Springer-Verlag, 583-599.
Tsitsiklis, J.N. (1989), Markov chains with rare transitions and simulated annealing, Math. Oper. Res. 14, 70-90.
van Laarhoven, P., and E. Aarts (1987), Simulated Annealing: Theory and Applications, D. Reidel, Dordrecht, Netherlands.
van Laarhoven, P., C. Boender, E. Aarts, and A. Rinnooy Kan (1989), A Bayesian approach to simulated annealing, Probab. Eng. Inform. Sci. 3, 453-475.
Ventcel, A.D. (1972), On the asymptotics of eigenvalues of matrices with elements of order ![]() , Dokl. Akad. Nauk SSSR 202, 65-68.
, Dokl. Akad. Nauk SSSR 202, 65-68.














