4.
Probabilistic Algorithms for Speedup
Joan Feigenbaum and Jeffrey C. Lagarias
AT&T Bell Laboratories
ABSTRACT
This chapter surveys situations in which probabilistic algorithms offer speedup over what is possible using deterministic algorithms, either in practice or in principle.
4.1 Introduction
One of the most compelling reasons to use randomized algorithms is that they permit certain problems to be solved faster than is possible by deterministic methods.
One pays a price for such speedup, which is the possibility of occasional very long computations or of occasional errors in the computation. The amount of possible speedup may depend on whether the algorithm is required to give either a correct answer or no answer, or whether it is permitted to give incorrect answers.
Section 4.2 describes a formal version of such questions from the viewpoint of computational complexity theory, in terms of probabilistic complexity classes. The question of whether probabilistic algorithms can give a superpolynomial speedup over deterministic algorithms is restated there as the unsolved problem, does ![]() ? Thus it is unresolved whether or
? Thus it is unresolved whether or
not speedup exists, and settling this question is likely to be as hard as the notorious ![]() ? problem of complexity theory.
? problem of complexity theory.
There is a weaker sense in which probabilistic algorithms currently offer advantages over deterministic ones. There exist problems for which the fastest known algorithm is probabilistic and problems for which at present the fastest fully analyzable algorithm is probabilistic. Here the situation reflects the current limitations on our knowledge. Section 4.3 describes examples of such problems from number theory, i.e., primality testing and factorization. In both cases, at present, the best fully analyzed algorithms are probabilistic ones.
Probabilistic algorithms give a demonstrable speedup in the exchange of information among several people, each having partial information to begin with. This is the subject matter of communication complexity. It plays an important role in distributed computing, in which exchange of information among the processors is an important part of the computational task. Communication complexity results are described in §4.4.
4.2 Probabilistic Complexity Classes
The theoretical possibility of speedup has been formalized in computational complexity theory with the notion of probabilistic complexity classes; these classify computational problems according to the running times and types of error allowed by probabilistic algorithms. Here we define several of these complexity classes.
The model of computation used is a probabilistic Turing machine. This is a Turing machine that has an extra "random" tape containing a random string of zeros and ones that can be read as necessary. A probabilistic polynomial-time Turing machine (PPTM) is such a machine equipped with a clock that, when given an input of n bits, always halts after p(n) steps, where p is a fixed polynomial. The performance of such machines is averaged over the uniform distribution of all random bits read by the machine. (At most, p(n) random bits are read during the computation on an n-bit input.) The computational problems considered are those of recognizing a language ![]() , where {0, 1}* denotes the set of all finite strings of zeros and ones. For example,
, where {0, 1}* denotes the set of all finite strings of zeros and ones. For example, ![]() might consist of all prime numbers, expressed using their binary representations.
might consist of all prime numbers, expressed using their binary representations.
We say that ![]() is in the complexity class BPP (bounded-error-probability polynomial time) if there is a PPTM that, given
is in the complexity class BPP (bounded-error-probability polynomial time) if there is a PPTM that, given ![]() , outputs
, outputs
![]() with probability at least 3/4, averaged over all random tapes for the fixed input x, and given
with probability at least 3/4, averaged over all random tapes for the fixed input x, and given ![]() outputs
outputs ![]() with probability at least 3/4 similarly. In this complexity class, two-sided classification errors are allowed: The machine may output
with probability at least 3/4 similarly. In this complexity class, two-sided classification errors are allowed: The machine may output ![]() when in fact
when in fact ![]() , and vice versa. Note that any problem in BPP is solvable by a PPTM for which the error probability is exponentially small. The new PPTM repeats the test for
, and vice versa. Note that any problem in BPP is solvable by a PPTM for which the error probability is exponentially small. The new PPTM repeats the test for ![]() on the old PPTM n times using independent random bits each time, and then takes a majority vote on the n outputs to decide whether
on the old PPTM n times using independent random bits each time, and then takes a majority vote on the n outputs to decide whether ![]() ; the error probability for the new PPTM is less than (3/4) n/2.
; the error probability for the new PPTM is less than (3/4) n/2.
We say that ![]() is in the complexity class RP (random polynomial time) if there is a PPTM that, when given an input
is in the complexity class RP (random polynomial time) if there is a PPTM that, when given an input ![]() , outputs
, outputs ![]() at least 3/4 of the time and, when given an input
at least 3/4 of the time and, when given an input ![]() , always outputs
, always outputs ![]() . That is, only one-sided error is allowed. We say that
. That is, only one-sided error is allowed. We say that ![]() is in the complementary complexity class co-RP (co-random polynomial time) if there is a PPTM that, when given an input
is in the complementary complexity class co-RP (co-random polynomial time) if there is a PPTM that, when given an input ![]() , outputs
, outputs ![]() at least 3/4 of the time and, when given an input
at least 3/4 of the time and, when given an input ![]() , always outputs
, always outputs ![]()
Finally, we say ![]() is in ZPP (zero-error-probability polynomial time) if
is in ZPP (zero-error-probability polynomial time) if ![]() is in both RP and co-RP. In this case, when the PPTM outputs either
is in both RP and co-RP. In this case, when the PPTM outputs either ![]() or
or ![]() , it is correct, but it is allowed to give no output for a small fraction of random tapes.
, it is correct, but it is allowed to give no output for a small fraction of random tapes.
The complexity class BPP is closed under complementation, and we have the following inclusions shown in Figure 4.1, where P denotes the set of (deterministic) polynomial-time recognizable languages.
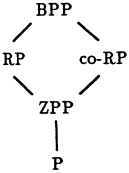
FIGURE 4.1: Relationships between complexity classes.
In this framework, it is unknown whether probabilistic algorithms ever give a superpolynomial speedup, i.e., whether there are any languages in
BPP that are not in P. Yao (1982) announced a converse result suggesting that at most a subexponential speedup is possible:
Theorem 4.1 (Yao, 1982) If there exists a uniform secure polynomial pseudorandom bit generator, then
A proof of this result appears in Boppana and Hirschfeld (1989). Several researchers, most recently Babai et al. (1991), have since improved the result by showing that the same conclusion follows from weaker hypotheses.
A detailed discussion of probabilistic complexity classes is given in Johnson (1990) and Zachos (1988).
4.3 Probabilistic Algorithms in Number Theory: Factoring and Primality Testing
The primality testing problem is that of determining whether an integer N is prime or composite, and the factoring problem is that of finding all the prime factors of N. These are two of the most basic computational problems in number theory.
The primality testing and factoring problems have the added practical significance of playing complementary roles in the RSA cryptosystem, which is the current best candidate for public key cryptography and for digital signatures. The practicality of constructing RSA ciphers depends on primality testing's being easy to do, whereas the security of the cipher depends on the apparent difficulty of factoring large numbers.
At present, the fastest known fully analyzed algorithms for both primality testing and factoring are probabilistic.
Theoretical and practical progress in primality testing has been rapid since 1977. Analysis of various primality testing algorithms led to study of the complexity classes described in §4.2.
Most methods of primality testing are based on variants of Fermat's little theorem, which asserts that if N is prime, then
if N does not divide a. Most composite numbers have many residues a (mod N) for which ![]() (mod N); hence a test for probable primality
(mod N); hence a test for probable primality
is to test whether ![]() (mod N) for many random a. Unfortunately, there exist composite numbers N for which
(mod N) for many random a. Unfortunately, there exist composite numbers N for which ![]() (mod N) if (a, N) = 1; these are called pseudoprimes. Refinements of the condition (4.1) can be used to rule out pseudoprimes, either probabilistically or deterministically.
(mod N) if (a, N) = 1; these are called pseudoprimes. Refinements of the condition (4.1) can be used to rule out pseudoprimes, either probabilistically or deterministically.
The primality testing problem is believed by many to be solvable in polynomial time. In fact, Miller (1976) proposed a deterministic algorithm believed to have this property:
Miller's Primality Test
Given ![]() (mod 2) find the largest 2k exactly dividing N - 1.
(mod 2) find the largest 2k exactly dividing N - 1.
For ![]() (log N)2do:
(log N)2do:
Is ![]() (mod N)? If not, output "N composite."
(mod N)? If not, output "N composite."
For ![]() do
do
Is ![]() (mod N)? If so, output "N composite."
(mod N)? If so, output "N composite."
Is ![]() (mod N)? If so, exit loop.
(mod N)? If so, exit loop.
od
od.
Output "N prime."
Note that aN-1 (mod N) may be computed in polynomial time by expanding N in binary and computing ![]() (mod N) by repeated squaring and reduction (mod N), so this is a polynomial-time algorithm. Miller proved that this algorithm is always correct when it outputs "N composite" and that, assuming the truth of the extended Riemann hypothesis (ERH), it is correct when it outputs "N prime." However, because the ERH is unproven, it is currently not actually known to be a primality test.
(mod N) by repeated squaring and reduction (mod N), so this is a polynomial-time algorithm. Miller proved that this algorithm is always correct when it outputs "N composite" and that, assuming the truth of the extended Riemann hypothesis (ERH), it is correct when it outputs "N prime." However, because the ERH is unproven, it is currently not actually known to be a primality test.
Probabilistic analogs of this algorithm were developed by Solovay and Strassen (1977) and Rabin (1980):
Solovay-Strassen Primality Test
Given ![]() (mod 2) find the largest 2k exactly dividing N - 1.
(mod 2) find the largest 2k exactly dividing N - 1.
Draw a at random from [1, N - 1]
Is ![]() (mod N) ? If not, output "N composite".
(mod N) ? If not, output "N composite".
For ![]() do
do
Is ![]() (mod N)? If so, output "N composite."
(mod N)? If so, output "N composite."
Is ![]() (mod N)? If so, exit loop.
(mod N)? If so, exit loop.
od.
Output "N prime".
They proved that, if N is composite, this test outputs "N is composite" with probability at least 3/4 and, if N is prime, it always outputs "N is prime." This shows that ![]() . By repeating the test (log N)2 times, the probability of error can be made exponentially small.
. By repeating the test (log N)2 times, the probability of error can be made exponentially small.
The drawback of the Solovay-Strassen test is that it does not guarantee that N is prime when it outputs "N prime"; i.e., it provides no proof of primality.
This situation was partially remedied by Goldwasser and Kilian (1986). They gave a probabilistic algorithm that counts points on "random" elliptic curves (mod N), and they proved that for almost all primes p it finds in probabilistic polynomial time a proof that p is prime. However, they could not rule out the possibility of the existence of a small set of "exceptional" p for which there was no proof of the kind they searched for. Recently, Adleman and Huang (1987) announced a proof that ![]() . Their result is technically difficult and proceeds by counting points on ''random'' Abelian varieties (mod p) of certain types. Taken together with the Solovay-Strassen result, it shows that
. Their result is technically difficult and proceeds by counting points on ''random'' Abelian varieties (mod p) of certain types. Taken together with the Solovay-Strassen result, it shows that ![]() .
.
In contrast, the fastest fully analyzed deterministic primality testing algorithm is due to Adleman et al. (1983). It tests N for primality in time ![]() for a certain positive constant c0.
for a certain positive constant c0.
For the factoring problem, all known algorithms, whether probabilistic or deterministic, require superpolynomial time. The fastest fully analyzed deterministic algorithm for factoring N, due to Pollard (1974), has the exponential running-time bound ![]() .
.
The algorithms used in practice for factoring large numbers are probabilistic in nature. The basic approach of most of them is to find solutions to ![]() (mod N) and hope that (X + Y, N) is a nontrivial factor of N. This is done by generating probabilistically many pairs (Xi, ai) with
(mod N) and hope that (X + Y, N) is a nontrivial factor of N. This is done by generating probabilistically many pairs (Xi, ai) with ![]() (mod N) where the ai's are not squares, and then finding a product of the ai's that is a square by an auxiliary method. The basic approach is to consider only ai's having all prime factors less than a bound y; such numbers are called y-smooth. Those ai's that do not have this property are discarded. Then the y-smooth ai's are factored
(mod N) where the ai's are not squares, and then finding a product of the ai's that is a square by an auxiliary method. The basic approach is to consider only ai's having all prime factors less than a bound y; such numbers are called y-smooth. Those ai's that do not have this property are discarded. Then the y-smooth ai's are factored
Now if sufficiently many such ai's are known, the matrix [eij] considered over GF(2) must have a linear dependency. The product of the ai's corresponding to this linear dependency is the desired square Y2, where X2 is the product
of the corresponding ![]() . This approach was first described in the Morrison and Brillhart (1975) continued fraction method. Dixon (1981) gave a fully analyzable version of the method. Let L = exp[(log n loglog n)1/2]. The Dixon algorithm uses y-smooth numbers with y = Lβ, for a small constant
. This approach was first described in the Morrison and Brillhart (1975) continued fraction method. Dixon (1981) gave a fully analyzable version of the method. Let L = exp[(log n loglog n)1/2]. The Dixon algorithm uses y-smooth numbers with y = Lβ, for a small constant
Dixon's Random Squares Factoring Algorithm
-
Test N for primality. If N is not prime, continue.
-
Randomly pick Xi and compute the least positive residue ai of
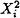 (mod N).
(mod N). -
Trial divide ai by all primes pj < Lβ. If ai completely factors as
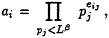
add (Xi, ai, eij) to a list. Continue until the list has Lβ -elements .
-
The matrix [eij] is now linearly dependent over GF(2). Compute a linear dependency, i.e., a set S of rows with
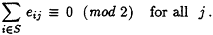
-
Set
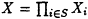 and
and 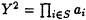 . Then
. Then 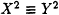 (mod N). Test whether (X + Y, N) is a nontrivial factor of N. If so, halt. If not, go to step 2 and repeat.
(mod N). Test whether (X + Y, N) is a nontrivial factor of N. If so, halt. If not, go to step 2 and repeat.
Here a dependency in the matrix [eij] is found using Gaussian elimination over GF(2)). Dixon (1981) showed that the probability of finding a factor of a composite N in one pass through this algorithm is at least 1/2.
The key to analysis of the algorithm is that the probability that a random integer in [1, N] is Lβ-smooth is about L-1/2β. Dixon showed that a similar probability estimate holds for ai that are random quadratic residues ![]() . Hence the expected time needed to generate the matrix [eij] is
. Hence the expected time needed to generate the matrix [eij] is ![]() , and the time needed to Gaussian reduce the matrix [eij] is about L3β. This is minimized for β = 1/2, and the algorithm takes time
, and the time needed to Gaussian reduce the matrix [eij] is about L3β. This is minimized for β = 1/2, and the algorithm takes time ![]() and space
and space ![]() bits. This is Dixon's result.
bits. This is Dixon's result.
Note that this expected running time bound,
is subexponential in N; i.e., it represents a superpolynomial speedup of the currently best fully analyzed deterministic factoring algorithm.
Pomerance (1987) gives a refined variant of this probabilistic algorithm that is rigorously proven to run in expected time ![]() . There are several other factoring algorithms of a similar nature that are believed to run in expected time
. There are several other factoring algorithms of a similar nature that are believed to run in expected time ![]() (see Pomerance, 1982, and Lenstra and Lenstra, 1990) and one such algorithm for which the bound
(see Pomerance, 1982, and Lenstra and Lenstra, 1990) and one such algorithm for which the bound ![]() can be proven rigorously (see Lenstra and Pomerance, 1992).
can be proven rigorously (see Lenstra and Pomerance, 1992).
More recently, a new factoring algorithm, the number field sieve, has been found that incorporates probabilistic ideas and uses arithmetic in an auxiliary algebraic number field to generate ![]() (mod N). It appears to have running time
(mod N). It appears to have running time ![]() but is likely not to be fully analyzable. It is particularly efficient for factoring numbers of special form, such as xn +2, and has already been used in practice to factor a 158-digit number; a preliminary description appears in Lenstra et al. (1990).
but is likely not to be fully analyzable. It is particularly efficient for factoring numbers of special form, such as xn +2, and has already been used in practice to factor a 158-digit number; a preliminary description appears in Lenstra et al. (1990).
4.4 Communication Complexity
Communication complexity studies variants of the following problem:
Problem 1 A Boolean function f is defined on a finite set X × Y. Two persons, PX knowing ![]() and PY knowing
and PY knowing ![]() , both want to know f(x, y). How many bits of information do they need to exchange to do this?
, both want to know f(x, y). How many bits of information do they need to exchange to do this?
This problem was proposed by Yao (1979). It is a basic problem in distributed computation, where the "persons" are processors, each possessing partial information about the current state of the computation.
The worst-case (deterministic) communication complexity ![]() is defined as follows. Let Φ be a deterministic protocol describing a sequence of bit exchanges between PX and PY that always computes f correctly. Let lΦ(x, y) denote the number of bits exchanged using Φ when PX knows x and PY knows y. The worst-case communication complexity for the protocol Φ is
is defined as follows. Let Φ be a deterministic protocol describing a sequence of bit exchanges between PX and PY that always computes f correctly. Let lΦ(x, y) denote the number of bits exchanged using Φ when PX knows x and PY knows y. The worst-case communication complexity for the protocol Φ is
and the worst-case deterministic communication complexity for f is
Randomized algorithms offer provable speedups for some problems in communication complexity. Here one allows protocols Φ in which PX and PY each have access to different sources of independent random bits. Let Φ be a protocol computing f(x, y) with probability of error at most ![]() for all (x, y). Let
for all (x, y). Let ![]() denote the expected number of bits needed by Φ when PX knows x and PY knows y, and define
denote the expected number of bits needed by Φ when PX knows x and PY knows y, and define
The ![]() randomized communication complexity is
randomized communication complexity is
where the infimum is computed over all protocols with error probability at most ![]() . We single out the zero-error randomized communication complexity
. We single out the zero-error randomized communication complexity ![]() .
.
We describe two specific functions for which probabilistic computations give speedups. The first is the equality function equ. Here X = Y = {1, 2, ..., n}, and
Yao (1979) showed that ![]() . In fact,
. In fact, ![]() is exactly [log(n)] + 1. A protocol attaining this bound is as follows: PX transmits x to PY and PY transmits back the value f(x,y). Yao (1979) also gave a randomized protocol Φ with error probability at most
is exactly [log(n)] + 1. A protocol attaining this bound is as follows: PX transmits x to PY and PY transmits back the value f(x,y). Yao (1979) also gave a randomized protocol Φ with error probability at most ![]() and showed that
and showed that
thus demonstrating a speedup. To describe this protocol, let ![]() :
:
Randomized Prime Protocol
-
PY picks a random prime p in the interval
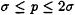 . He transmits p and y (mod p).
. He transmits p and y (mod p). -
PX transmits 1 if
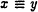 (mod p) and 0 otherwise.
(mod p) and 0 otherwise. -
PX and PY both take the bit transmitted to be the value equ(x,y ).
If this algorithm outputs equ(x,y) = 0, this answer is correct, but when it outputs equ(x,y) = 1, this answer may be incorrect, with probability at most ![]() . For the function equ, no speedup exists using a zero-error randomized algorithm (see Orlitsky and El Gamal, 1990).
. For the function equ, no speedup exists using a zero-error randomized algorithm (see Orlitsky and El Gamal, 1990).
Next we consider the function componentwise-equal (c.e.), which has ![]() . Write x = (x1,..., xn) with each
. Write x = (x1,..., xn) with each ![]() and similarly for y. Then
and similarly for y. Then
Mehlhorn and Schmidt (1982) showed that ![]() . They exhibited a zero-error randomized protocol Φ such that
. They exhibited a zero-error randomized protocol Φ such that
The protocol is as follows:
Repeated Equality Protocol
-
For
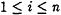 ,
,
-
PX and PY determine equ(xi, yi) using the randomized prime protocol with
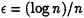 .
. -
If they conclude that
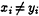 , they move to step (a) and next i. If they conclude xi = yi, they exchange xi and yi and check whether they are actually equal. If so, they output 1 and halt. If not, they move back to step 1.
, they move to step (a) and next i. If they conclude xi = yi, they exchange xi and yi and check whether they are actually equal. If so, they output 1 and halt. If not, they move back to step 1.
-
Output 0 if all i are scanned and no xi = yi are exchanged.
This protocol is zero-error because it checks directly whether xi = yi on indices i where the randomized prime protocol might have made a mistake. Fürer (1987) further improved the zero-error bound for this function to
for a constant c0.
Aho et al. (1983) demonstrated that at most a quadratic speedup is possible for zero-error randomized communication complexity relative to worst-case communication complexity; i.e.,
The second example above shows that this bound is essentially sharp.
Finally, we mention a recent result of Ahlswede and Dueck (1989) that any object among ![]() objects can be identified in blocklength n using a discrete memoryless channel of rate R with arbitrarily small error probability via an encoding procedure that uses randomization.
objects can be identified in blocklength n using a discrete memoryless channel of rate R with arbitrarily small error probability via an encoding procedure that uses randomization.
Orlitsky and El Gamal (1988) give a general survey of communication complexity, and Halstenberg and Reischuk (1990) state the best currently known results about relationships among communication complexity classes.
References
Adleman, L., and M.D. Huang (1987), Recognizing primes in random polynomial time, in Proc. 19th Annual Symposium on Theory of Computing , ACM Press, New York, 462-469.
Adleman, L., C. Pomerance, and R. Rumely (1983), On distinguishing prime numbers from composite numbers, Ann. Math. 117, 173-206.
Ahlswede, R., and G. Dueck (1989), Identification via channels, IEEE Trans. Inform. Theory 35, 15-29.
Aho, A., J.D. Ullman, and M. Yannakakis (1983), On notions of information transfer in VLSI circuits, in Proc. 15th Annual Symposium on Theory of Computing, ACM Press, New York, 133-139.
Babai, L., L. Fortnow, N. Nisan, and A. Wigderson (1991), BPP has subexponential-time simulations unless EXP has publishable proofs, in Proc. 6th Annual Structure in Complexity Theory Conference, IEEE Computer Society Press, Los Alamitos, Calif., 213-219.
Boppana, R., and R. Hirschfeld (1989), Pseudorandom generators and complexity classes, in Randomness and Computation, S. Micali, ed., Advances in Computing Research, vol. 5, JAI Press, Greenwich, Conn., 1-26.
Dixon, J. (1981), Asymptotically fast factorization of integers, Math. Comp. 36, 255-260.
Füter, M. (1987), The power of randomness for communication complexity, in Proc. 19th Annual Symposium on Theory of Computing, ACM Press, New York, 178-181.
Goldwasser, S., and J. Kilian (1986), Almost all primes can be quickly certified, in Proc. 18th Annual Symposium on Theory of Computing, ACM Press, New York, 316-329.
Halstenberg, B., and R. Reischuk (1990), Relationships between communication complexity classes, J. Comput. Syst. Sci. 41, 402-429.
Johnson, D.S. (1990), A catalog of complexity classes, in Handbook of Theoretical Computer Science, vol. A, J. von Leeuwen et al., eds., North-Holland, New York.
Lenstra, A.K., and H.W. Lenstra, Jr. (1990), Algorithms in number theory, in Handbook of Theoretical Computer Science, vol. A, J. von Leeuwen et al., eds., North-Holland, New York.
Lenstra, A.K., H.W. Lenstra, Jr., M.S. Manasse, and J. Pollard (1990), The number field sieve, in Proc. 22nd Annual Symposium on Theory of Computing, ACM Press, New York, 564-572.
Lenstra, H.W., and C. Pomerance (1992), A rigorous time bound for factoring integers, J. Amer. Math. Soc., to appear.
Lutz, J. (1990), Pseudorandom sources for BPP, J. Comput. Syst. Sci . 41, 307-320.
Mehlhorn, K., and E.M. Schmidt (1982), Las Vegas is better than determinism in VLSI and distributed computing (extended abstract), in Proc. 14th Annual Symposium on Theory of Computing, ACM Press, New York, 330-337.
Miller, G. (1976), Riemann's hypothesis and tests for primality, J. Comput. Syst. Sci. 13, 300-317.
Morrison, M., and J. Brillhart (1975), A method of factoring and the factorization of F7, Math. Comp. 29, 183-205.
Orlitsky, A., and A. E1 Gamal (1988), Communication complexity, in Complexity in Information Theory, Y.S. Abu-Mostafa, ed., Springer-Verlag, New York, 16-61.
Orlitsky, A., and A. E1 Gamal (1990), Average and randomized communication complexity, IEEE Trans. Inform. Theory 36, 3-16.
Pollard, J.M. (1974), Theorems on factorization and primality testing, Proc. Cambridge Philos. Soc. 76, 521-528.
Pomerance, C. (1982), Analysis and comparison of some integer factoring algorithms, in Computational Methods in Number Theory, H.W. Lenstra, Jr. and R. Tijdeman, eds., Math. Centre Tract 144, University of Amsterdam, 89-139.
Pomerance, C. (1987), Fast rigorous factorization and discrete logarithm algorithms, in Discrete Algorithms and Complexity, D.S. Johnson, T. Nishizeki, A. Nozaki, and H. Wilf, eds., Academic Press, Boston, 119-144.
Rabin, M.O. (1980), Probabilistic algorithms for testing primality, J. Number Theory 12, 128-138.
Solovay, R., and V. Strassen (1977), A fast Monte-Carlo test for primality, SIAM J. Comput. 6, 84-85; erratum 7, 118.
Yao, A. (1979), Some complexity questions related to distributed computing (extended abstract), in Proc. 11th Annual Symposium on Theory of Computing, ACM Press, New York, 209-213.
Yao, A. (1982), Theory and applications of trapdoor functions (extended abstract), in Proc. 23rd Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 80-91.
Zachos, S. (1988), Probabilistic quantifiers and games, J. Comput. Syst. Sci. 36, 433-451.














