5.
Probabilistic Algorithms for Defeating Adversaries
Joan Feigenbaum
AT&T Bell Laboratories
ABSTRACT
Randomization appears to be an essential ingredient in algorithms for maintaining some form of privacy. This chapter discusses probabilistic algorithms for authenticating a user and for allowing the private use of shared resources.
5.1 Introduction
We consider two types of adversarial computation in which randomness is used in an essential way.
The first type of scenario concerns authentication: Player A makes a claim that player B may not believe. So there is a need for a protocol in which A "proves" to B that the claim is correct (or at least provides overwhelming statistical evidence of correctness). Scenarios of this type include:
-
A is a bank customer, and B is an automatic teller machine (ATM). Here, A's "claim" is that he is the legitimate owner of the smart card that he inserts in the ATM.
-
A is a computing workstation, and B is a file server. If there is no direct hardware connection between A and B, A may send its requests
-
for files over a telephone line. Of course, anyone can dial the phone number of the file server; A's claim is that it is legitimately entitled to access the files.
-
A is a television owner, and B is a cable company. A's claim is that he is a paying customer and that the broadcast should be descrambled for him.
These are really three examples of the same thing. Player A must be able to authenticate himself (or prove his identity) to B. Any potential impersonator A* must have only a negligible probability of convincing B that he is A.
Goldwasser et al. (1989) and Babai and Moran (1988) initiated a complexity-theoretic study of such problems. They defined the class of sets with interactive proof systems and suggested that this definition correctly captures the notion of a set in which membership of an element can be verified efficiently. A proof system for a set ![]() is an interactive protocol between a prover A (with unlimited computing power) and a verifier B (limited to probabilistic polynomial-time computation). If
is an interactive protocol between a prover A (with unlimited computing power) and a verifier B (limited to probabilistic polynomial-time computation). If ![]() , then A is able to convince B to accept x with high probability. If
, then A is able to convince B to accept x with high probability. If ![]() , then no player A*, even if he deviates from the legitimate behavior of A, should be able to convince B to accept x with more than negligible probability. The more general notion of a multiprover interactive proof system was put forth by Ben-Or et al. (1988); in these protocols, the role of the prover is played by several machines A1,..., Am, each with unlimited computing power. Two ingredients of proof systems are absolutely vital in making the theory interesting: interaction (i.e., the fact that prover(s) and verifier can exchange polynomially many rounds of messages before the verifier decides whether or not to accept), and randomness (i.e., the fact that the verifier can toss coins at any point in the protocol and that cheating provers do not know the outcomes of these tosses at the start of the protocol).
, then no player A*, even if he deviates from the legitimate behavior of A, should be able to convince B to accept x with more than negligible probability. The more general notion of a multiprover interactive proof system was put forth by Ben-Or et al. (1988); in these protocols, the role of the prover is played by several machines A1,..., Am, each with unlimited computing power. Two ingredients of proof systems are absolutely vital in making the theory interesting: interaction (i.e., the fact that prover(s) and verifier can exchange polynomially many rounds of messages before the verifier decides whether or not to accept), and randomness (i.e., the fact that the verifier can toss coins at any point in the protocol and that cheating provers do not know the outcomes of these tosses at the start of the protocol).
Consider the previous examples, in which A is required to prove his identity to B. Suppose we use a trivial protocol in which B is given a table of users and passwords, A is given only his own password, and to prove his identity, A simply reveals the password to B. (Note the absence of interaction and randomness.) In this scheme, A transfers full knowledge of his identity proof to B. An eavesdropper (or even B himself) can turn around and claim to be A by presenting the same proof. Is there a proof system that achieves the same goal but transfers no knowledge to B except
the one bit that A is who he claims to be? Goldwasser et al. (1989) define the notion of a zero-knowledge proof system formally and propose it as the right way to capture the intuitive requirements of an authentication scheme. Basically, an interactive proof system for the set T is zero-knowledge if, for any ![]() , anything that a (potentially cheating) verifier B* can compute given the transcript of his interaction with A, he can also compute given only the one bit of information ''x is in T.'' Zero-knowledge is defined analogously for multiprover interactive proof systems.
, anything that a (potentially cheating) verifier B* can compute given the transcript of his interaction with A, he can also compute given only the one bit of information ''x is in T.'' Zero-knowledge is defined analogously for multiprover interactive proof systems.
The second type of scenario concerns private use of shared resources . A community of users shares a valuable computing resource, and each member of the community would like to use the resource without revealing his private data. Scenarios of this type include the following:
-
The users are scientists, and the resource is a government supercomputer.
-
The users are pairs of computers or telephones, and the shared resource is a communication line.
-
The users are potential customers, and the resource is the vendor's proprietary software.
-
The users are investors, and the resource is a service that analyzes financial markets.
Abadi et al. (1989) formalized this scenario as follows. There is a function f that is intractable for the user A to compute, because A has limited computing power. The shared resource B is a program or device that computes f. (More generally, B can compute some function g that is closely related to f.) A has a private input x; he would like to use this resource to find out f(x) without revealing x to B.
An instance-hiding scheme for the function f is a pair of functions E and D with the following properties. The inputs to E are A's private data x and some random bits r. A computes y = E(x, r) and sends it to B, who sends back f(y). Then A computes D(x,r,f(y)), which is the desired answer f(x). B should not be able to deduce x from y. A, on the other hand, can deduce f(x) from f(y), because he has the random bits r that were used to compute y from x. (More generally, B could send back g(y), and A could use it to compute f(x).) Note that such a scheme makes sense only if the functions E and D are easier to compute than the function f.
Randomness plays an essential role here, just as it does in zero-knowledge. The input y that is sent to B is a random variable. If x1 and x2 are both possibilities, from B's point of view, for A's private input, and R is uniformly distributed over all bit-strings of the appropriate length, then Y1 = E(x1, R) and Y2 = E(x2, R) should be identically distributed. Hence B learns nothing about x when he receives a random query.
In the next section, we give examples of zero-knowledge proof systems and instance-hiding schemes. In §5.3, we state some of the major known results on both types of schemes. Section 5.3 also contains some suggestions for further work.
5.2 Examples
5.2.1 Authentication
Feige et al. (1988) developed the following protocol to allow a community of users to authenticate themselves to each other. For each user, there is a pair (I, S). The public information I can be interpreted as the user's identity and the private information S as his secret key. The goal of the authentication scheme is to allow a user with identity I to convince another user that he "knows" the corresponding key S without revealing anything about S beyond the fact that he knows it. (In the language of cryptography theory, user I provides a zero-knowledge proof of knowledge of the key S.) The effectiveness of the scheme is based on the assumption that it is computationally infeasible to compute square roots modulo a large composite integer with unknown factorization; this is provably equivalent to the assumption that factoring large integers is difficult.
Modulus Generation. A trusted center generates two large primes, each congruent to 3 mod 4. The product m of these primes is published, but the primes are not.
Note that -1 is a quadratic nonresidue modulo m: that is, there is no a such that a2 = -1 mod m. In what follows, ![]() denotes the set of integers between 1 and m that are relatively prime to m and have Jacobi symbol +1 with respect to m.
denotes the set of integers between 1 and m that are relatively prime to m and have Jacobi symbol +1 with respect to m.
Key Generation. Each user chooses t1 random numbers ![]() in
in ![]() and t1 random bits
and t1 random bits ![]() . He sets Ij equal to
. He sets Ij equal to ![]() mod m,
mod m,
for ![]() . This user's identity, which he publishes, is
. This user's identity, which he publishes, is ![]() , and his secret key, which he keeps private, is
, and his secret key, which he keeps private, is ![]() .
.
Proofs of Identity. User A authenticates himself to user B as follows: Let I be A's published identity and S his secret key. A and B repeat the following four steps t2 times:
-
A picks a random R in
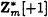 and a random bit c and sends X = (-1)cR2 mod m to B.
and a random bit c and sends X = (-1)cR2 mod m to B. -
B sends a random vector of bits
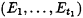 to A.
to A. -
A sends
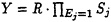 mod m to B.
mod m to B. -
B verifies that
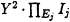 mod m is equal to ±X.
mod m is equal to ±X.
B believes that A is who he claims he is if the verification in step (4) succeeds in each of the t2 trials.
Feige et al. (1988) show that this scheme works correctly for the values t1 = O(log log m) and t2 = Θ(log m). The most important feature of the scheme is that there is no need for the prover to have significant computational power. These identity proofs require only a few modular multiplications and can be implemented on smart cards.
5.2.2 Computing with Encrypted Data
In our first example of computation with encrypted data, the hard-to-compute function is the discrete logarithm modulo primes. Let p be a large prime and g be a generator for the multiplicative group ![]() . If x = ge mod p, where e is an element of {1,..., p-1}, then e is called the discrete logarithm of x (with respect to g and p). There is an efficient algorithm to compute x given e that is based on repeated squaring modulo p. However, there is no efficient algorithm known to compute e given x. There are many cryptographic protocols that try to exploit the presumed intractability of the discrete logarithm problem. For example, Diffie and Hellman (1976) give a protocol for secret key exchange that is based on the difficulty of discrete logarithms.
. If x = ge mod p, where e is an element of {1,..., p-1}, then e is called the discrete logarithm of x (with respect to g and p). There is an efficient algorithm to compute x given e that is based on repeated squaring modulo p. However, there is no efficient algorithm known to compute e given x. There are many cryptographic protocols that try to exploit the presumed intractability of the discrete logarithm problem. For example, Diffie and Hellman (1976) give a protocol for secret key exchange that is based on the difficulty of discrete logarithms.
Suppose that we have a box B that computes discrete logarithms. In complexity theoretic terms, B is an oracle—we can ask it questions, but we do not know how it works and cannot compute what it computes on
our own. In real applications, B may be a piece of proprietary software or hardware, or it may be a large table that was computed at great expense. In any case, a discrete logarithm box would be a valuable resource, and many mutually suspicious users would want access to it.
Abadi et al. (1989) give a simple scheme by which A can get the discrete logarithm of x without revealing x. First, A chooses an element r uniformly at random from {1,..., p-1} and computes y = x· gr mod p. Next, A sends y to B, and B sends back the discrete logarithm of y; that is, B sends e' such that y = ge' mod p. Finally, A computes e = e'-r mod p-1. This exponent e is the discrete logarithm of x. Because r was chosen uniformly at random, y is also a uniformly distributed random element of {1,..., p-1}. Hence, no one else who has access to the box B and overhears A's query gets any information about A's private input x.
In our second example, the hard function is a multivariate polynomial ![]() , where K is a finite field. Such a polynomial may be hard to compute, because the number of terms may be exponential in n. Let d be the degree of h. Assume that |K| > d + 1 and that α1,..., αd+1 are distinct nonzero elements of K. The following scheme, in which user A obtains h(x1,..., xn) without revealing x = (x1,..., xn), was devised by Beaver and Feigenbaum (1990) and Lipton (1991).
, where K is a finite field. Such a polynomial may be hard to compute, because the number of terms may be exponential in n. Let d be the degree of h. Assume that |K| > d + 1 and that α1,..., αd+1 are distinct nonzero elements of K. The following scheme, in which user A obtains h(x1,..., xn) without revealing x = (x1,..., xn), was devised by Beaver and Feigenbaum (1990) and Lipton (1991).
Once again, let B be a box that computes h. For this example, we must have d + 1 copies, say B1,..., Bd+1, of B; furthermore, for ![]() , the communication between A and Bi cannot be overheard by Bj. Think of the Bi's as distinct physical boxes that are kept in d + 1 different locations.
, the communication between A and Bi cannot be overheard by Bj. Think of the Bi's as distinct physical boxes that are kept in d + 1 different locations.
Let c = (c1,..., cn) be an n-tuple of elements of K, and let Z be an indeterminate that is distinct from each of X1, ..., Xn. Consider the univariate polynomial
Note that H has degree at most d and that
To compute h(x) privately, A first chooses c uniformly at random from Kn. Next, A computes y1, ..., yd+1, where
For ![]() , A sends the query yj to Bj and gets back h(yj). Note that h(yj) = H(αj). Thus, after receiving these answers, A has d+1 distinct
, A sends the query yj to Bj and gets back h(yj). Note that h(yj) = H(αj). Thus, after receiving these answers, A has d+1 distinct
points {(αj, H(αj))} on the degree-d univariate polynomial H. Using these points, A can recover H by interpolation; the desired answer h(x) is just the constant term of H.
Each query yj is a uniformly distributed random element of Kn. Of course, yi and yj are correlated; if Bi and Bj could communicate, they could recover x. In isolation, however, Bj and its other users learn nothing about A's private input x from the random query yj.
5.3 Zero-Knowledge Proof Systems and Instance-Hiding Schemes
In this section, we give a brief, informal summary of the known results on zero-knowledge proof systems and instance-hiding schemes. More extensive summaries, as well as more precise formulations of the concepts, are given by Feigenbaum (1992) and Brassard (1990).
The first basic problem is to characterize the sets that have interactive proof systems. A complete characterization was achieved in a sequence of papers culminating in the work of Lund et al. (1990) and Shamir (1990).
Theorem 5.1 The sets with interactive proof systems are exactly those that are recognizable in polynomial space.
The second basic question is whether every set that has an interactive proof system in fact has one that is zero-knowledge. Recall that a function is one-way if it is easy to compute but hard to invert. The next result follows from the work of Impagliazzo and Yung (1988) and Naor (1991).
Theorem 5.2 Assume that one-way functions exist. Then every set that has an interactive proof system has one that is zero-knowledge.
In a forthcoming paper, Ostrovsky and Wigderson (1992) show that if there is a zero-knowledge proof system for any set that is hard on average, then there is a one-way function.
The set-recognition power of multiprover interactive proof systems has also been completely characterized; this result is due to Babai et al. (1991). The question of zero-knowledge also is settled completely for multiprover interactive proof systems; see Ben-Or et al. (1988).
Theorem 5.3 The sets with multiprover interactive proof systems are exactly those recognizable in nondeterministic exponential time. Furthermore, all of these sets have multiprover systems that are zero-knowledge.
In the instance-hiding scheme for the discrete logarithm function that is given in §5.2.2, player A queries only one box B. This is an example of a one-oracle instance-hiding scheme. The scheme for the multivariate polynomial is an example of a multi-oracle instance-hiding scheme.
The first basic question here is to determine exactly which sets have instance-hiding schemes that leak no information about x to the oracles. Actually, it impossible to find schemes that leak absolutely no information—A must leak to B at least the length of x if the function computed by B is nontrivial. (This is stated and proven precisely in Abadi et al., 1989.) Thus, the real question is which sets have instance-hiding schemes that leak at most the length of x.
For one-oracle schemes, Abadi et al. (1989) obtained the following conditional negative result:
Theorem 5.4 No NP-hard set has a one-oracle instance-hiding scheme that leaks at most the length of x, unless the polynomial-time hierarchy collapses at the third level.1
Beaver and Feigenbaum (1990) used the low-degree polynomial trick given in §5.2.2 to obtain a universal construction of multi-oracle instance-hiding schemes:
Theorem 5.5 Every Boolean function of n bits has an (n + 1)-oracle instance-hiding scheme that leaks at most the length of x to each oracle.
Interestingly, this low-degree polynomial trick, which was devised in order to construct instance-hiding schemes, became a crucial ingredient in the characterization of the set-recognition power of interactive proof systems, both one-prover and multiprover. A thorough explanation of this connection appears in Brassard (1990).
Finally, we remark that it is natural to consider zero-knowledge, instance-hiding proof systems. These are proof systems in which the verifier does not learn the proof, and the prover does not learn what he is proving! Beaver et al. (1991) formalize this notion and prove the following positive result:
Theorem 5.6 Every set recognizable in nondeterministic exponential time has a multiprover interactive proof system that is both instance-hiding and zero-knowledge.
One theoretical open question remaining concerns the power needed by a prover; for example, how powerful must the prover be in a proof system for a co-NP-complete set? For a list of other open theoretical questions, see Feigenbaum (1992).
There are many open questions concerning the applicability of this theory to practical computing. The authentication protocol of §5.2.1 forms the basis of a working, commercial system that is in wide use today. We do not know any other examples of working systems that use the theory. This immediately suggests two questions.
First, the proof system of Feige et al. (1988) is based on a highly structured, number-theoretic problem that does not have interesting complexity-theoretic properties. None of the elegant general results stated above are relevant to this one known example of a practical proof system. Can the general results of the theory be applied in practice? For example, can zero-knowledge proof systems for NP-complete problems be used for authentication?
Second, what other practical applications exist for zero-knowledge proof systems? Many ambitious proposals have been made; see, for example, the work of Goldreich et al. (1987). These proposals have enhanced the theoretical literature in cryptography and probably can be put to use in real systems; so far, however, we know of no such uses.
Most of the existing work on instance-hiding is currently not practical. What is the right application domain in which one can make practical use of these ideas?
References
Abadi, M., J. Feigenbaum, and J. Kilian (1989), On hiding information from an oracle, J. Comput. Syst. Sci. 39, 21-50.
Babai, L., and S. Moran (1988), Arthur-Merlin games: A randomized proof system and a hierarchy of complexity classes, J. Comput. Syst. Sci. 36, 254-276.
Babai, L., L. Fortnow, and C. Lund (1991), Nondeterministic exponential time has two-prover interactive protocols, Comput. Complexity 1, 3-40.
Beaver, D., and J. Feigenbaum (1990), Hiding instances in multioracle queries, in Proc. 7th Annual Symposium on Theoretical Aspects of Computer Science, Lecture Notes in Computer Science no. 415, Springer-Verlag, New York, 37-48.
Beaver, D., J. Feigenbaum, and V. Shoup (1991), Hiding instances in zero-knowledge proof systems, in Proc. 10th CRYPTO, Lecture Notes in Computer Science no. 537, Springer-Verlag, New York, 326-338.
Ben-Or, M., S. Goldwasser, J. Kilian, and A. Wigderson (1988), Multiprover interactive proof systems: How to remove intractability assumptions, in Proc. 20th Annual Symposium on Theory of Computing, ACM Press, New York, 113-131.
Brassard, G. (1990), Cryptology Column #4: Hiding information from oracles, SIGACT News 21, Spring issue, Association for Computing Machinery, 5-11.
Diffie, W., and M. Hellman (1976), New directions in cryptography, IEEE Trans. Inform. Theory 22, 644-654.
Feige, U., A. Fiat, and A. Shamir (1988), Zero knowledge proofs of identity, J. Cryptology 1, 77-94.
Feigenbaum, J. (1992), Overview of interactive proof systems and zero-
knowledge, in Contemporary Cryptology: The Science of Information Integrity, G. Simmons, ed., IEEE Press, New York, 423-440.
Goldreich, O., S. Micali, and A. Wigderson (1987), How to play ANY mental game, in Proc. 19th Annual Symposium on Theory of Computing , ACM Press, New York, 218-229.
Goldwasser, S., S. Micali, and C. Rackoff (1989), The knowledge complexity of interactive proof systems, SIAM J. Comput. 18, 186-208.
Impagliazzo, R., and M. Yung (1988), Direct minimum-knowledge computations, in Proc. 7th CRYPTO, Lecture Notes in Computer Science no. 293, Springer-Verlag, New York, 40-51.
Lipton, R. (1991), New directions in testing, in Distributed Computing and Cryptography, DIMACS Series on Discrete Mathematics and Theoretical Computer Science, vol. 2, American Mathematical Society, Providence, R.I., 191-202.
Lurid, C., L. Fortnow, H. Karloff, and N. Nisan (1990), Algebraic methods for interactive proof systems, in Proc. 31st Annual Symposium on Foundations of Computer Science, IEEE Computer Science Press, Los Alamitos, Calif., 2-10.
Naor, M. (1991), Bit commitment using pseudo-randomness, J. Cryptology 4, 151-158.
Ostrovsky, R., and A. Wigderson (1992), One-way functions are essential for non-trivial zero-knowledge, submitted to 33rd Annual Symposium on Foundations of Computer Science (IEEE).
Shamir, A. (1990), IP = PSPACE, in Proc. 31st Annual Symposium on Foundations of Computer Science, IEEE Computer Science Press, Los Alamitos, Calif., 11-15.












