6.
Pseudorandom Numbers
Jeffrey C. Lagarias
AT&T Bell Laboratories
ABSTRACT
This chapter surveys the problem of generating pseudorandom numbers. It lists many of the known constructions of pseudorandom bits. It outlines the subject of computational information theory. In this theory the fundamental object is a secure pseudorandom bit generator. Such generators are not theoretically proved to exist, although functions are known that appear to possess the required properties. In any case, pseudorandom number generators are known that work reasonably well in practice.
6.1 Introduction
A basic ingredient needed in any algorithm using randomization is a source of "random" bits. In practice, in probabilistic algorithms or Monte Carlo simulations, one uses instead "random-looking" bits. A pseudorandom bit generator is a deterministic method to produce from a small set of ''random" bits called the seed a larger set of random-looking bits called pseudorandom bits.
There are several reasons for using pseudorandom bits. First, truly random bits are hard to come by. Physical sources of supposedly random bits, which rely on chaotic, dissipative processes such as varactor diodes, typically produce correlated bits rather than independent sequences of bits. Such sources also produce bits rather slowly (see Schuster, 1988). Hence
one would like to conserve the number of random bits needed in a computation. Second, the deterministic character of pseudorandom bit sequences permits the easy reproducibility of computations. A third reason arises from cryptography: the existence of secure pseudorandom bit generators is essentially equivalent to the existence of secure private-key cryptosystems.
For Monte Carlo simulations, one often wants pseudorandom numbers, which are numbers simulating either independent draws from a fixed probability distribution on the real line R, or more generally numbers simulating samples from a stationary random process. It is possible to simulate samples of any reasonable distribution using as input a sequence of i.i.d. 0-1 valued random variables (see Devroye, 1986, and Knuth and Yao, 1976). Hence the problem of constructing pseudorandom numbers is in principle reducible to that of constructing pseudorandom bits.
Section 6.2 describes explicitly some pseudorandom bit generators, as well as some general principles for constructing pseudorandom bit generators. Most of these generators have underlying group-theoretic or number-theoretic structure.
Section 6.3 describes the subject of computational information theory and indicates its connection to cryptography. The basic object in this theory is the concept of a secure pseudorandom bit generator, which was proposed by Blum and Micali (1982) and Yao (1982). The basic properties characterizing a secure pseudorandom bit generator are ''randomness-increasing" and "computationally unpredictable." Recently obtained results are that if one of the following objects exist then they all exist:
-
a secure pseudorandom bit generator,
-
a one-way function, and
-
a secure (block-type) private-key cryptosystem.
The central unsolved question is whether any of these objects exist. However, good candidates are known for one-way functions. A major difficulty in settling the existence problem for this theory is summarized in the following heuristic:
Unpredictability Paradox. If a deterministic function is unpredictable, then it is difficult to prove anything about it; in particular, it is difficult to prove that it is unpredictable.
Section 6.4 surveys results on the statistical performance of various known pseudorandom number generators. In particular, a pseudorandom bit generator called the RSA generator produces secure pseudorandom bits (in the sense of §6.2) if the problem of factoring certain integers is computationally difficult. A good general reference for pseudorandom number generators is Knuth (1981, Chapter 3).
6.2 Explicit Constructions of Pseudorandom Bit Generators
Where might pseudorandom number generators come from? There are several general principles useful in constructing deterministic sequences exhibiting quasi-random behavior: expansiveness, nonlinearity, and computational complexity.
Expansiveness is a concept arising from dynamical systems. A flow ft on a metric space is expansive (or hyperbolic) at a point ![]() if nearby trajectories diverge (locally) at an exponential rate from each other, i.e.,
if nearby trajectories diverge (locally) at an exponential rate from each other, i.e., ![]() provided |x-y| < δ, where λ > 1 and for
provided |x-y| < δ, where λ > 1 and for ![]() . Such flows exhibit sensitive dependence on initial conditions and are numerically unstable to compute. A discrete version of this phenomenon for maps on the interval I = [0, 1] is a map
. Such flows exhibit sensitive dependence on initial conditions and are numerically unstable to compute. A discrete version of this phenomenon for maps on the interval I = [0, 1] is a map ![]() such that |T'(x)| > 1 for almost all
such that |T'(x)| > 1 for almost all ![]() ; e.g., T(x) = Θx (mod 1), where Θ > 1. In particular, it requires knowledge of at least the first O(n) bits of T(n)(x) to determine if
; e.g., T(x) = Θx (mod 1), where Θ > 1. In particular, it requires knowledge of at least the first O(n) bits of T(n)(x) to determine if ![]() or
or ![]() as
as ![]() .
.
Nonlinearity provides a second source of deterministic randomness. Functional compositions of linear maps are themselves linear, but nonlinear polynomial maps, when composed, can yield exponentially growing nonlinearity; e.g., if f(x) = x2 and f(j)= f(f(j-1)(x)), then ![]() . Even the simple nonlinear map f(x) = ax(1 -x) for
. Even the simple nonlinear map f(x) = ax(1 -x) for ![]() , which maps [0,1] into [0,1], exhibits extremely complicated dynamics under iteration (see Collet and Eckmann, 1980).
, which maps [0,1] into [0,1], exhibits extremely complicated dynamics under iteration (see Collet and Eckmann, 1980).
Computational complexity is a third source of deterministic randomness. Kolmogorov (1965), Chaitin (1966), and Martin-Lof (1966) defined a finite string A = a1 ... ak of bits to be Kolmogorov-random if the length of the shortest input to a fixed universal Turing machine ![]() that halts and outputs A is of length greater than or equal to kc0 for a constant c0. This notion of randomness is that of computational incompressibility. Unfortunately, it is an undecidable problem to tell whether a given string A is Kolmogorov-
that halts and outputs A is of length greater than or equal to kc0 for a constant c0. This notion of randomness is that of computational incompressibility. Unfortunately, it is an undecidable problem to tell whether a given string A is Kolmogorov-
random. However, one obtains weaker notions of computational incompressibility by restricting the amount of computation allowed in attempting to compress the string A. For example, given a nondecreasing time-counting function T such as T(x) = 5x3, a string A is T-incompressible if the shortest input to ![]() that halts in T(|A|) steps and outputs A has length greater than |A|. This notion of incompressibility is effectively computable. One can similarly define incompressibility of ensembles of strings S with respect to time complexity classes such as PTIME. In fact, the accepting function for membership in a "hard" set in a time-complexity class
that halts in T(|A|) steps and outputs A has length greater than |A|. This notion of incompressibility is effectively computable. One can similarly define incompressibility of ensembles of strings S with respect to time complexity classes such as PTIME. In fact, the accepting function for membership in a "hard" set in a time-complexity class ![]() behaves "randomly" when viewed as input to a Turing machine that has a more restricted amount of time available. This idea goes back at least to Meyer and McCreight (1971).
behaves "randomly" when viewed as input to a Turing machine that has a more restricted amount of time available. This idea goes back at least to Meyer and McCreight (1971).
The three principles all involve some notion of functional composition or of iteration of a function. Indeed, running a computation of a Turing machine can be viewed as a kind of functional composition with feedback. The first two principles directly lead to candidates for number-theoretic pseudorandom number generators (see below). The computational complexity principle leads to pseudorandom number generators having provably good properties with respect to some level of computational resources, but most of these are not of use in practice because one must use more than the allowed bound on computation to find them in the first place. Finally, we note that there are very close relations between expansiveness properties of mappings and the Kolmogorov-complexity of descriptions of their trajectories (see Brudno, 1982).
A variety of functions have been proposed for use in pseudorandom bit generators. We give several examples below. Most of these functions are number-theoretic, and nearly all of them have an underlying group structure.
Example 1 (Multiplicative Congruential Generator). The generator is defined by
where ![]() . Here (a, b, M) are the parameters describing the generator and x0 is the seed. This was one of the first proposed pseudorandom number generators. Generators of this form are widely used in practice in Monte Carlo methods, taking xi/M to simulate uniform draws on [0,1] (see Knuth, 1981; Rubinstein, 1982; and Marsaglia, 1968). More generally, one can consider polynomial recurrences (mod N).
. Here (a, b, M) are the parameters describing the generator and x0 is the seed. This was one of the first proposed pseudorandom number generators. Generators of this form are widely used in practice in Monte Carlo methods, taking xi/M to simulate uniform draws on [0,1] (see Knuth, 1981; Rubinstein, 1982; and Marsaglia, 1968). More generally, one can consider polynomial recurrences (mod N).
Example 2 (Power Generator). The generator is defined by
Here (d, N) are parameters describing the generator and x0 is the seed.
An important special case of the power generator occurs when N = p1p2 is a product of two distinct odd primes. The first case occurs when (d,Φ(N)) = 1, where
is Euler's totient function that counts the number of multiplicatively invertible elements (mod N). Then the map ![]() (mod N) is one-to-one on (Z/NZ)*, and this operation is the encryption operation of the RSA public-key cryptosystem (see Rivest et al., 1978), where (d, N) are publicly known. We call this special case an RSA generator.
(mod N) is one-to-one on (Z/NZ)*, and this operation is the encryption operation of the RSA public-key cryptosystem (see Rivest et al., 1978), where (d, N) are publicly known. We call this special case an RSA generator.
Example 3 (Discrete Exponential Generator). The generator is defined by
Here (g, N) are parameters describing the generator and x0 is the seed.
A special case of importance occurs when N is an odd prime p and g is a primitive root (mod p). Then the problem of recovering xn given (xn+1, g, P) is the discrete logarithm problem, an apparently hard number-theoretic problem (see Odlyzko, 1985). The discrete exponentiation operation (mod p) was suggested for cryptographic use in the key exchange scheme of Diffie and Hellman (1976). A key exchange scheme is a method for two parties to agree on a secret key using an insecure channel. Blum and Micali (1982) gave a method for generating a set of pseudorandom bits whose security rests on the difficulty of solving the discrete logarithm problem.
Example 4 (Kneading Map). Consider a bivariate transformation
where f is a fixed bivariate function, usually taken to be nonlinear. The function f(·,·) determines the generator, and (x0, y0) and the family {zn}
constitute the seed. One often takes zn := K for all integers n, for a fixed K. This mapping has the feature that it is one-to-one, with inverse
One can generalize this construction to take x, y, and f(·, ·) to be vector-valued. The data encryption standard (DES) cryptosystem is composed of 16 iterations of (vector-valued) maps of this type, where (x0, y0) are the data to be encrypted, all zi = K compose to key, and f is a specific nonlinear function representable as a polynomial in several variables.
Other examples include the 1/P-generator and the square generator studied in Blum et al. (1986) and cellular automata generators proposed by Wolfram (1956).
In addition to these examples, more complicated pseudorandom number generators can be built out of them using the following two mixing constructions:
Construction 1 (Hashing). If {xn} are binary strings of k bits and ![]() with l < k is a fixed function, called in this context a hash function, then define {zn} by
with l < k is a fixed function, called in this context a hash function, then define {zn} by
The traditional role of hash functions is for data compression, in which case l is taken much smaller than k. Sets of good hash functions play an important role in the theory of pseudorandom generators, where they are used to convert highly nonuniform probability distributions on k inputs into nearly uniform distributions on l inputs; see, for instance, Goldreich et al. (1988).
A very special case of this construction is the truncation operator
which extracts from a k-bit string x the substring of l bits starting j bits from its right end. In its most extreme form, ![]() (mod 2) extracts the least significant bit. The truncation operation was originally suggested by Knuth to be applied to linear congruential generators to cut off half their bits (saving the high-order bits) as a way of increasing apparent randomness. This idea was used in a number of schemes for encrypting passwords to computer systems. However, it is insecure. Reeds (1979) successfully
(mod 2) extracts the least significant bit. The truncation operation was originally suggested by Knuth to be applied to linear congruential generators to cut off half their bits (saving the high-order bits) as a way of increasing apparent randomness. This idea was used in a number of schemes for encrypting passwords to computer systems. However, it is insecure. Reeds (1979) successfully
cryptanalyzed one such system.
Construction 2 (Composition). Let {xn} and {yn} be sequences of k-bit strings, let ![]() be a binary operation, and set
be a binary operation, and set
The simplest case occurs with k = 1, where * is the XOR operation:
where zn, xn, and yn are viewed as k-dimensional vectors over GF(2) . More generally, whenever the operation table of * on {0,1)k×{0,1} k forms a Latin square (but is not necessarily either commutative or associative), then the * operation has certain randomness-increasing properties when the elements {xn}and {yn}are independent draws from fixed distributions Q and Q on {0, 1}k (see Marsaglia, 1985).
There is a constant search for new and better practical pseudorandom number generators. Recently, Marsaglia and Zaman (1991) proposed some simple generators that have extremely long periods; whether they have good statistical properties remains to be determined.
6.3 Computational Information Theory and Cryptography
In the last few years, there has been extensive development of a theoretical basis of secure pseudorandom number generators. This area is called computational information theory.
Computational information theory represents a blending of information theory and computational complexity theory (see Yao, 1988). The basic notion taken from information theory is entropy, a measure of information. Here, "information" equals "randomness." Information theory was developed by Shannon in the 1940s, and a relationship between computational complexity and information theory was first observed by Kolmogorov. Both Shannon and Kolmogorov assumed in defining ''amount of information" that unbounded computational resources were available to extract that information from the data. Computational information theory assumes that the amount of computational resources is bounded by a polynomial in the size of the input data.
Here we indicate the ideas behind the theory, assuming some familiarity with the basic concepts of computational complexity theory for uniform models of computation (Turing machines) and for nonuniform models of computation (Boolean circuits). Turing machines and polynomial-time computability are discussed in Garey and Johnson (1979), and circuit complexity is described in Savage (1976) and Karp and Lipton (1982).
What is a pseudorandom number generator? The basic idea of pseudo-randomness is to take a small amount of randomness described by a seed drawn from a given source probability distribution and to produce deterministically from the seed a larger number of apparently random bits that simulate a sample drawn from another target probability distribution on a range space. That is, it is randomness-increasing.
The amount of randomness in a probability distribution is measured by its binary entropy (or information), which for a discrete probability distribution P is
where x runs over the atoms of P. In particular
i.e., "k coin flips give k bits of information." The notion of randomness-increasing is impossible in classical information theory because any deterministic mapping G applied to a discrete probability distribution P never increases entropy; i.e.,
However, this may be possible when computing power is limited. Indeed, what may happen is that G(P) may approximate a target distribution Q having a much higher entropy so well that, within the limits of computing power available, one cannot tell the distributions G(P) and Q apart. If H(Q) is much larger than H(P), then we can say G is computationally randomness-increasing.
The fundamental principle is a definition of pseudorandom numbers is always relative to the use to which the pseudorandom numbers are to be put. This use is to simulate the target probability distribution to within a specified degree of approximation.
We measure the degree of approximation using statistical tests. Let P be the source probability distribution, G(P) the probability distribution generated by the pseudorandom number generator G, and Q the target
probability distribution to be approximated by G(P). A statistic is any deterministic function σ(x) of a sample x drawn from a distribution, and a statistical test σ consists of computation of a statistic σ drawn from G(P). We say that distributions P1 and P2 on the same sample space ![]() are
are ![]() using the statistic σ on
using the statistic σ on ![]() provided that the expected values of σ(x) drawn from P1 and P2, respectively, agree to within the tolerance level
provided that the expected values of σ(x) drawn from P1 and P2, respectively, agree to within the tolerance level ![]() ; i.e.,
; i.e.,
Given a collection ![]() of statistical tests σi with corresponding tolerance levels
of statistical tests σi with corresponding tolerance levels ![]() , we say that G is a
, we say that G is a ![]() number generator from source P to target Q provided that G(P) is
number generator from source P to target Q provided that G(P) is ![]() from Q for all the statistical tests σi drawn from
from Q for all the statistical tests σi drawn from ![]() .
.
To make these ideas clearer, we allow as source distribution the uniform distribution Uk on the set {0, 1}k of binary strings of length k, and for target distributions we allow either ![]() for some
for some ![]() , or else
, or else ![]() , which is the distribution of
, which is the distribution of ![]() independent draws from the uniform distribution on [0, 1].
independent draws from the uniform distribution on [0, 1].
As an example, consider the linear congruential generator ![]() (mod M) with M = 2k -1, where the seed x0 is drawn from
(mod M) with M = 2k -1, where the seed x0 is drawn from ![]() and is viewed as an element of {0, 1}k drawn with distribution Uk. We use this generator to produce a vector of
and is viewed as an element of {0, 1}k drawn with distribution Uk. We use this generator to produce a vector of ![]() iterates,
iterates, ![]() , and view G(Uk) as approximating the distribution
, and view G(Uk) as approximating the distribution ![]() . Various statistics that one might consider for
. Various statistics that one might consider for ![]() in the sample space
in the sample space ![]() are
are
|
1. Average: |
|
|
2. Maximum: |
|
|
3. Maximal run: |
|
|
4. mth autocorrelation: |
|
It is now a purely mathematical problem to decide what ![]() level can be achieved for each of these statistics, viewing G(Uk) as approximating
level can be achieved for each of these statistics, viewing G(Uk) as approximating ![]() . Various results for such statistics for linear congruential generators can be found in Niederreiter (1978).
. Various results for such statistics for linear congruential generators can be found in Niederreiter (1978).
The statistical tests applied to pseudorandom number generators for use in Monte Carlo simulations are generally simple; for cryptographic applications, pseudorandom number generators must pass a far more stringent battery of statistical tests.
Now we are ready to give a precise definition of a secure pseudorandom bit generator. To achieve insensitivity to the computational model, this definition, due to Yao (1982), is an asymptotic one. Instead of a single generator G of fixed size, we consider an ensemble ![]() of generators, with
of generators, with
that have the property of being polynomial length-increasing; i.e.,
for some fixed integer ![]() . We say that
. We say that ![]() is a nonuniform secure pseudorandom bit generator (abbreviated N-PRG) if
is a nonuniform secure pseudorandom bit generator (abbreviated N-PRG) if
-
There is a (deterministic) polynomial-time algorithm that computes all Gk(x), given (k, x) as input with
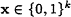 , and
, and -
For any PSIZE family
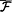 of Boolean circuit statistical tests, Gk( Uk) is polynomially indistinguishable by
of Boolean circuit statistical tests, Gk( Uk) is polynomially indistinguishable by 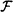 from Uf(k); i.e., for all
from Uf(k); i.e., for all 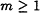 the distribution Gk(Uk) is k-m-indistinguishable by
the distribution Gk(Uk) is k-m-indistinguishable by 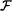 from Uf(k) for all sufficiently large k.
from Uf(k) for all sufficiently large k.
Condition 1 says that ![]() is easy to compute. Condition 2 requires more explanation. A Boolean circuit
is easy to compute. Condition 2 requires more explanation. A Boolean circuit ![]() is made of and, or, and not gates, having
is made of and, or, and not gates, having ![]() inputs, and computes a Boolean function
inputs, and computes a Boolean function ![]() . A family
. A family ![]() of Boolean circuits is of polynomial size (abbreviated
of Boolean circuits is of polynomial size (abbreviated ![]() ) if there is some fixed m such that the number of gates in Ck is
) if there is some fixed m such that the number of gates in Ck is ![]() , for all m. The Boolean function
, for all m. The Boolean function ![]() computed by
computed by ![]() with
with ![]() provides a statistical test for comparing Gk(Uk) and
provides a statistical test for comparing Gk(Uk) and ![]() . Then condition 2 asserts that
. Then condition 2 asserts that
The PSIZE measure of computational complexity is nonuniform in that no relation between the circuits Ck for different k is required. In particular, the family ![]() might be noncomputable (nonrecursive). Condition 2 may be colloquially rephrased as, "
might be noncomputable (nonrecursive). Condition 2 may be colloquially rephrased as, "![]() passes all polynomial size statistical tests."
passes all polynomial size statistical tests."
This definition implies that N-PRGs must have a one-way property: Given the output ![]() , one cannot recover the string
, one cannot recover the string ![]() using a PSIZE family of circuits for a fraction of the inputs exceeding 1/(km+m), for any fixed m. Otherwise, it would fail the statistical test, "Is there a seed x such that Gk(x) = y?"
using a PSIZE family of circuits for a fraction of the inputs exceeding 1/(km+m), for any fixed m. Otherwise, it would fail the statistical test, "Is there a seed x such that Gk(x) = y?"
We also consider the weaker notion of uniform secure pseudorandom bit generator (U-PRG) in which PSIZE in condition 2 is replaced by PTIME, where a family ![]() of circuits is in PTIME if there is a polynomial-time algorithm for computing Ck, given 1k as input. This condition may be rephrased as, "
of circuits is in PTIME if there is a polynomial-time algorithm for computing Ck, given 1k as input. This condition may be rephrased as, "![]() passes all polynomial time statistical tests." Since
passes all polynomial time statistical tests." Since ![]() , an N-PRG is always a U-PRG.
, an N-PRG is always a U-PRG.
These definitions of N-PRG and U-PRG form the basis of a nice theory, whose purpose is to reduce the existence question for apparently very complicated objects (N-PRGs) to the existence question for simpler, more plausible objects. As an example, we have
Theorem 6.1 If there exists an N-PRG with f(x) = k + 1, then there exists an N-PRG with f(k) = xm + m for each ![]() . (Similarly for U-PRGs.)
. (Similarly for U-PRGs.)
That is, if there is an PRG that can inflate k random bits to k + 1 pseudorandom bits, this is already sufficient to construct a PRG that inflates k random bits to any polynomial number of pseudorandom bits. A proof appears in Boppana and Hirschfeld (1989).
One disadvantage of these definitions (N-PRG, etc.) at present is that no such generators have been proved to exist. In fact, proving that they exist is at least as hard a problem as settling the famous ![]() question of theoretical computer science. On the positive side, however, theorem 6.4 below suggests that the RSA generator may well be a U-PRG.
question of theoretical computer science. On the positive side, however, theorem 6.4 below suggests that the RSA generator may well be a U-PRG.
Yao (1982) provided the basic insight that the nature of secure pseudo-randomness (N-PRG) is the computational unpredictability of successive bits produced by a pseudorandom bit generator. The notion of computational unpredictability is captured by the concept of a nonuniform next-bit test, as follows. Let ![]() be a collection of mappings
be a collection of mappings ![]() , where f(k) is polynomial in k. A predicting collection is a doubly-indexed family of Boolean circuits
, where f(k) is polynomial in k. A predicting collection is a doubly-indexed family of Boolean circuits ![]() computing functions
computing functions ![]() , where the circuit Ci,k is viewed as predicting the (i + 1)st bit of a sequence in {0,1} f(k) given the first i bits. The predicting collection is polynomial size if there is some
, where the circuit Ci,k is viewed as predicting the (i + 1)st bit of a sequence in {0,1} f(k) given the first i bits. The predicting collection is polynomial size if there is some ![]() such that each Ci,k has at most km + m gates. Let
such that each Ci,k has at most km + m gates. Let ![]() denote the probability that the output of
denote the probability that the output of ![]() applied to a bit sequence (x1, ... ,xi) drawn from Gk(Uk) is xi+1. We say that
applied to a bit sequence (x1, ... ,xi) drawn from Gk(Uk) is xi+1. We say that ![]() passes the nonuniform next-bit test if for each polynomial-size predicting collection
passes the nonuniform next-bit test if for each polynomial-size predicting collection ![]() and each
and each ![]() , for all sufficiently large k,
, for all sufficiently large k,
holds for ![]() . This test says that xi+1 cannot be accurately guessed using PSIZE circuit families with x1, ..., xi as input.
. This test says that xi+1 cannot be accurately guessed using PSIZE circuit families with x1, ..., xi as input.
Theorem 6.2 (Yao, 1982) The following are equivalent:
-
A collection
 passes the nonuniform next-bit test.
passes the nonuniform next-bit test. -
A collection
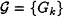 passes all polynomial-size statistical tests.
passes all polynomial-size statistical tests.
In this theorem, there is no restriction on the sizes of circuits needed to compute the functions Gk; e.g., they could be of exponential size in k. The direction ![]() is fairly easy to prove because the next-bit test is essentially a family of PSIZE statistical tests. The direction
is fairly easy to prove because the next-bit test is essentially a family of PSIZE statistical tests. The direction ![]() is harder. A proof of this result is given in Boppana and Hirschfeld (1989).
is harder. A proof of this result is given in Boppana and Hirschfeld (1989).
Corollary 1 A polynomial-time computable collection ![]() that passes the nonuniform next-bit test is an N-PRG.
that passes the nonuniform next-bit test is an N-PRG.
Pseudorandom bit generators must have a very strong one-way property: from the output of such a generator, it must be computationally infeasible to extract any information at all about its input, for essentially all inputs. One-way functions are required only to satisfy a weaker one-way property: they are easy to compute but difficult to invert on a nonnegligible fraction of their instances.
A formal definition of one-way function is as follows: A nonuniform one-way collection {fk} consists of a family of functions ![]() , where
, where ![]() for some fixed m, such that
for some fixed m, such that
-
The ensemble {fk} is uniformly polynomial-time computable, and
-
For each PSIZE circuit family {Ck} with
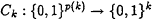 , the functions {fk} are hard to invert on a nonnegligible fraction 1/(kc + c) of their inputs, where c is a fixed positive constant depending on {Ck}. That is, for x drawn from the uniform distribution on {0, 1}k,
, the functions {fk} are hard to invert on a nonnegligible fraction 1/(kc + c) of their inputs, where c is a fixed positive constant depending on {Ck}. That is, for x drawn from the uniform distribution on {0, 1}k,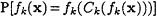
is at most 1 -(kc + c)-1 for all large enough k (depending on {Ck}).
The one-way property embodied in this definition is weaker than that required of an N-PRG in several ways: a function fk can have an extremely nonuniform probability distribution on its range {0, 1} p(k), it is required to
be hard to invert only on a possibly small fraction 1/(kc + c) of its inputs, and even on those inputs where it is hard to invert, some partial information about its inverse may be easy to obtain.
Impagliazzo et al. (1989) showed that one can bootstrap a nonuniform one-way collection into an N-PRG:
Theorem 6.3 The following are equivalent:
-
There exists a nonuniform polynomial pseudorandom bit generator (N-PRG).
-
There exists a nonuniform one-way collection {fk} of functions.
The implication ![]() is easy, because an N-PRG
is easy, because an N-PRG ![]() is a one-way collection. To prove
is a one-way collection. To prove ![]() , it suffices by theorem 6.1 to enlarge a set of
, it suffices by theorem 6.1 to enlarge a set of ![]() random bits to obtain
random bits to obtain ![]() pseudorandom bits, for an infinite set of
pseudorandom bits, for an infinite set of ![]() . We may reduce to the case that the function fk is length-preserving by padding its input bits if necessary. The first key idea, due to Goldreich and Levin (1989), is that the Boolean inner product
. We may reduce to the case that the function fk is length-preserving by padding its input bits if necessary. The first key idea, due to Goldreich and Levin (1989), is that the Boolean inner product
is a hard-core predicate for all length-preserving one-way families ![]() . That is, the probability distribution of the (2k+1)-bit strings (f(x), r, B(x, r)) for (x, r) drawn uniformly from {0, 1}2k is polynomially indistinguishable from (f(x), r , β), where β is a truly random bit drawn independent of x and r. We are now done if f is a permutation, because then (f(x), r, β) would be uniformly distributed on 2k + 1 bits. The difficult case occurs when f is not one-to-one, in which case the set Sx = {y: f(y) = f(x)} may be large. In this case, f(x) contains only about k-log2 |Sx| bits of information, and so the entropy of (f(x), r, β) may be smaller than 2k, and we gain no computational entropy. The key idea of Impagliazzo et al. (1989) was to add in log2 |Sx| extra bits of information from x by hashing x with a random hash function
. That is, the probability distribution of the (2k+1)-bit strings (f(x), r, B(x, r)) for (x, r) drawn uniformly from {0, 1}2k is polynomially indistinguishable from (f(x), r , β), where β is a truly random bit drawn independent of x and r. We are now done if f is a permutation, because then (f(x), r, β) would be uniformly distributed on 2k + 1 bits. The difficult case occurs when f is not one-to-one, in which case the set Sx = {y: f(y) = f(x)} may be large. In this case, f(x) contains only about k-log2 |Sx| bits of information, and so the entropy of (f(x), r, β) may be smaller than 2k, and we gain no computational entropy. The key idea of Impagliazzo et al. (1989) was to add in log2 |Sx| extra bits of information from x by hashing x with a random hash function ![]() . If one can do this, then the distribution of (f(x), r, h, h(x), B(x, r)) will be polynomially indistinguishable from (f(x), r, h, h(x), β) and one extra pseudorandom bit will have been created. The nonuniform model of computation is used in determining the number log2 |Sx| of bits to hash in the hash function for x.
. If one can do this, then the distribution of (f(x), r, h, h(x), B(x, r)) will be polynomially indistinguishable from (f(x), r, h, h(x), β) and one extra pseudorandom bit will have been created. The nonuniform model of computation is used in determining the number log2 |Sx| of bits to hash in the hash function for x.
Hastad (1990) proved that a uniform version of theorem 6.3 holds; i.e., one may replace ''nonuniform" by "uniform" in (1) and (2).
Finally, secure PRGs can be used to construct secure private-key cryptosystems and vice versa. A private-key cryptosystem uses a (private) key exchanged by some secure means between two users, the possession of which enables them both to encrypt and decrypt messages sent between them. Encrypted messages should be unreadable to anyone else. They should appear random to any unauthorized receiver, and ideally no statistical information at all should be extractable from the encrypted message. This is seldom achieved in actual cryptosystems, and statistical methods are one of the staples of cryptanalysis. Absolute security can always be achieved by using a key of the same length as the totality of encrypted messages to be exchanged (the "one time pad"). How much security is possible when the key is to be shorter than the messages to be encrypted? An analogy between pseudorandom number generation and private-key cryptosystems is apparent: the key supplies absolutely random bits from which pseudorandom bits (the encrypted message) are created. This analogy can be made precise. For a statement of the result, see Lagarias (1990, §6); some related results appear in Impagliazzo and Luby (1989).
Rompel (1990) showed how to construct a secure authentication scheme based on a one-way function.
Finally, we mention that probabilistic algorithms play a fundamental role in the theoretical foundations of modern cryptography, as indicated in Goldwasser and Micali (1984).
6.4 Performance of Certain Pseudorandom Bit Generators
We now turn to results on the performance of various generators; see Knuth (1981) for general background.
Linear congruential pseudorandom number generators have been extensively studied, and many of their statistical properties carefully analyzed. With proper choice of parameters, they can produce sequences {xk} such that ![]() is close to uniformly distributed on [1, M]. Marsaglia (1968) was the first to notice that these generators have certain undesirable correlation properties among several consecutive iterates (xn, xn+1, ..., xn+k). Extensive analysis is given in Niederreiter (1978). These generators are apparently unsuitable for cryptographic uses (see Frieze
is close to uniformly distributed on [1, M]. Marsaglia (1968) was the first to notice that these generators have certain undesirable correlation properties among several consecutive iterates (xn, xn+1, ..., xn+k). Extensive analysis is given in Niederreiter (1978). These generators are apparently unsuitable for cryptographic uses (see Frieze
et al., 1988).
The group-theoretic structure of certain other generators can be used to prove "almost-everywhere hardness" results for such generators, including the following one:
RSA Bit Generator. Given ![]() and
and ![]() , select odd primes p1and p2uniformly from the range
, select odd primes p1and p2uniformly from the range ![]() and form N = p1p2. Select e uniformly from [1, N] subject to (e, Φ(N)) = 1. Set
and form N = p1p2. Select e uniformly from [1, N] subject to (e, Φ(N)) = 1. Set
and let the bit zn+1be given by
Then ![]() are the pseudorandom bits generated from the seed x0of length 2k bits.
are the pseudorandom bits generated from the seed x0of length 2k bits.
We consider the problem of predicting the next bit zn+1 of the RSA generator, given {z1, ..., zn}. Alexi et al. (1988) showed that getting any information at all about zn+1 is as hard as the (apparently difficult) problem of factoring N. Their argument shows how an oracle that guesses the next bit with a probability slightly greater than 1/2 can be used in an explicit fashion to construct an inversion algorithm.
Theorem 6.4 Let (e, N) be a fixed pair, where (e, Φ(N)) = 1 and N = p1p2is odd, with the associated power generator
Suppose one is given a 0-1 valued oracle function O(x) for which
holds for ![]() N of all inputs
N of all inputs ![]() , where k = log2N Then there is a probabilistic polynomial time algorithm that makes
, where k = log2N Then there is a probabilistic polynomial time algorithm that makes ![]() oracle calls, uses
oracle calls, uses ![]() "random" bits, halts in
"random" bits, halts in ![]() steps, and for any x finds y with probability
steps, and for any x finds y with probability ![]() , where the probability is taken over all sequences of "random" bits.
, where the probability is taken over all sequences of "random" bits.
This algorithm involves several clever ideas. The first of these is due to Ben-Or et al. (1983), using the fact that the encryption function E(·) respects the group law on (Z/NZ)*; i.e.,
They suppose that one is given an oracle OI that perfectly recognizes membership in an interval ![]() for fixed positive
for fixed positive ![]() ; i.e.,
; i.e.,
Define [x]N to be the least nonnegative residue (mod N) and define absN(x) to be the distance of the least (positive or negative) residue from 0 so that
Let parN(x) be the parity of absN(x). The clever idea is to generate "random" a, b and attempt to compute the gcd of [ay]N and [by]N using a modified binary gcd algorithm due to Brent and Kung (1983) and Purdy (1983). This algorithm computes the greatest common divisor (r, s) by noting that it is equal to ![]() if r, s both even, to (
if r, s both even, to (![]() s) or (r,
s) or (r, ![]() ) if one is even, and to
) if one is even, and to ![]() otherwise. It is easy to check that max(|r|, |s|) is nonincreasing at each iteration and that it decreases by a factor of 3/4 over every two iterations, so this algorithm halts in at most 2log4/3N iterations. The Ben-Or et al. algorithm draws pairs (a, b) of "random" numbers uniformly on [0, N]. Such a pair will be called "good" (for the unknown y) if [ay]N and [by]N both fall in I. For a good pair the oracle OI can be used to determine correctly the parity of [ay]N and [by]N, even though y is unknown. We use the fact that if
otherwise. It is easy to check that max(|r|, |s|) is nonincreasing at each iteration and that it decreases by a factor of 3/4 over every two iterations, so this algorithm halts in at most 2log4/3N iterations. The Ben-Or et al. algorithm draws pairs (a, b) of "random" numbers uniformly on [0, N]. Such a pair will be called "good" (for the unknown y) if [ay]N and [by]N both fall in I. For a good pair the oracle OI can be used to determine correctly the parity of [ay]N and [by]N, even though y is unknown. We use the fact that if ![]() is even then
is even then ![]() , whereas if it is odd then
, whereas if it is odd then ![]() . Hence for a good pair, one has
. Hence for a good pair, one has ![]() if [ay]N is even and
if [ay]N is even and ![]() if [ay]N is odd. This holds similarly for [by]N. Thus using the group law
if [ay]N is odd. This holds similarly for [by]N. Thus using the group law
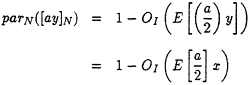
is calculable. Consequently, one can compute one step of the modified binary gcd algorithm to ([ay]N, [by]N) and obtain new values ([a'y ]N, [b'y]N), with (a', b') known. Now (a', b') is still a good pair, so we can continue to follow the modified binary gcd algorithm perfectly and eventually determine [ly]N = gcd ([ay]N, [by]N), where l is known. We say that the algorithm succeeds if [ly]N = 1, because in that case ![]() (mod N) is found. We verify success in this case by checking that E[l-1] = x. In all other cases, when (a, b) is not good or when it is good and the gcd is not 1, we carry out the above procedure for 2log4/3N iterations and check the final iterate l to see whether E[l-1] = x.
(mod N) is found. We verify success in this case by checking that E[l-1] = x. In all other cases, when (a, b) is not good or when it is good and the gcd is not 1, we carry out the above procedure for 2log4/3N iterations and check the final iterate l to see whether E[l-1] = x.
This procedure is a probabilistic polynomial-time algorithm. The pair (a, b) is good with probability at least σ2. Also, because the distributions of [ay]N, [by]N are uniform on ![]() and because the probability that gcd(r, s) = 1 for such draws approaches
and because the probability that gcd(r, s) = 1 for such draws approaches ![]() , it exceeds a positive constant α for all values of {|I|}. Thus the success probability for any draw (a, b) is
, it exceeds a positive constant α for all values of {|I|}. Thus the success probability for any draw (a, b) is ![]() , and the expected time until the algorithm succeeds is polynomial in log N.
, and the expected time until the algorithm succeeds is polynomial in log N.
One immediately sees that this algorithm still works if the oracle OI is not perfect but is accurate with probability of error less than (4log4/3N)-1.
Subsequent work of several authors showed how an oracle having a 1/2 + 1/(log N)k advantage in guessing parity of the smallest RSA bit can be used to simulate a much more accurate oracle and then to simulate an oracle such as OI above with sufficient accuracy to obtain theorem 6.4 (see Alexi et al., 1988).
Theorem 6.4 shows that if the factoring problem is difficult, then recovering any information at all about zn+1 given {z1, ..., zn} is hard. In particular, the bits {zk} would then be computationally indistinguishable from i.i.d. coin flips.
One can extract several pseudorandom bits from each of the iterates xn of the RSA generator. The strongest result to date on this problem can be found in Schrift and Shamir (1990).
The use of the group structure on (Z/NZ)* to ''randomize" is an example of the concept of an instance-hiding scheme discussed in Chapter 5.
Acknowledgment. This chapter is an abridged and revised version of Lagarias (1990), published by the American Mathematical Society.
References
Alexi, W., B. Chor, O. Goldreich, and C.P. Schnorr (1988), RSA and Rabin functions: Certain parts are as hard as the whole, SIAM J. Comput. 17, 194-209.
Ben-Or, M., B. Chor, and A. Shamir (1983), On the cryptographic security of single RSA bits, in Proc. 15th Annual Symposium on Theory of Computing , ACM Press, New York, 421-430.
Blum, L., M. Blum, and M. Shub (1986), A simple unpredictable pseudorandom number operator, SIAM J. Comput. 15, 364-383. (Preliminary version: CRYPTO '82.)
Blum, M., and S. Micali (1982), How to generate cryptographically strong versions of pseudorandom bits, in Proc. 22nd Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 112-117. (Final version: SIAM J. Comput. 13 (1984), 850-864.)
Boppana, R., and R. Hirschfeld (1989), Pseudorandom generators and complexity classes, in Randomness and Computation, S. Micali, ed., Advances in Computing Research, vol. 5, JAI Press, Greenwich, Conn., 1-26.
Brent, R.P., and H.T. Kung (1983), Systolic VLSI arrays for linear time gcd computations, in VLSI 83, IFIP, F. Anceau and D.J. Aas, eds., Elsevier Science Publishers, New York, 145-154.
Brudno, A.A. (1982), Entropy and the complexity of the trajectories of a dynamical system, Trans. Moscow Math. Soc. 44, 127-151.
Chaitin, G.J. (1966), On the length of programs for computing finite binary sequences, J. Assoc. Comput. Mach. 13, 547-569.
Collet, P., and J.-P. Eckmann (1980), Iterated Maps on the Interval as Dynamical Systems, Birkhäuser, Boston.
Devroye, L. (1986), Nonuniform Random Variate Generation, Springer-Verlag, New York.
Diffie, W., and M. Hellman (1976), New directions in cryptography, IEEE Trans. Inform. Theory 22, 644-654.
Frieze, A, J. Hastad *, R. Kannan, J.C. Lagarias, and A. Shamir (1988), Reconstructing truncated integer variables satisfying linear congruences, SIAM J. Comput. 17, 262-280.
Garey, M., and D. Johnson (1979), Computers and Intractability: A Guide to the Theory of NP-Completeness, W.H. Freeman, San Francisco.
Goldreich, O., and L. Levin (1989), A hard-core predicate for all one-way functions, in Proc. 21st Annual Symposium on Theory of Computing , ACM Press, New York, 25-32.
Goldreich, O, H. Krawczyk, and M. Luby (1988), On the existence of pseudorandom generators, in Proc. 29th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 12-24.
Goldwasser, S, and S. Micali (1984), Probabilistic encryption, J. Comput. Syst. Sci. 28, 270-299. (Preliminary version: Proc. 14th Annual Symposium on Theory of Computing (1982), ACM Press, New York, 364-377.)
Hastad*, J. (1990), Pseudo-random generators under uniform assumptions, in Proc. 22nd Annual Symposium on Theory of Computing, ACM Press, New York, 395-404.
Impagliazzo, R., and M. Luby (1989), One-way functions are essential for complexity-based cryptography, in Proc. 30th Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 230-235.
Impagliazzo, R., L. Levin, and M. Luby (1989), Pseudorandom number generation from one-way functions, in Proc. 21st Annual Symposium on Theory of Computing, ACM Press, New York, 12-24.
Karp, R., and R. Lipton (1982), Turing machines that take advice, L'En-seignement Math. 28, 191-209. (Preliminary version: Some connections between nonuniform and uniform complexity classes, in Proc. 12th Annual
Symposium on Theory of Computing (1980)
, ACM Press, New York, 302-309.)Knuth, D. (1981), The Art of Computer Programming, vol. 2: Seminumerical Algorithms (second ed.), Addison-Wesley, Reading, Mass.
Knuth, D., and A.C. Yao (1976), The complexity of nonuniform random number generation, in Algorithms and Complexity, J.F. Traub, ed., Academic Press, New York, 357-428.
Kolmogorov, A.N. (1965), Three approaches to the concept of "the amount of information," Probl. Inform. Transm. 1, 3-13.
Lagarias, J.C. (1990), Pseudorandom number generators in number theory and cryptography, in Cryptology and Computational Number Theory, C. Pomerance, ed., Proc. Syrup. Appl. Math. No. 42, American Mathematical Society, Providence, R.I., 115-143.
Marsaglia, G. (1968), Random numbers fall mainly in the planes, Proc. Nat. Acad. Sci. USA 61, 25-28.
Marsaglia, G. (1985), A current view of random number generators, in Computer Science and Statistics: Sixteenth Symposium on the Interface, L. Billard, ed., North-Holland, New York, 3-11.
Marsaglia, G., and A. Zaman (1991), A new class of random number generators, Ann. Appl. Probab. 1, 462-480.
Martin-Lof, P. (1966), The definition of random sequences, Inform. Contr. 9, 619-682.
Meyer, A.R., and E.M. McCreight (1971), Computationally complex and pseudorandom zero-one valued functions, in Theory of Machines and Computations, Z. Kohlavi and A. Paz, eds., Academic Press, New York, 19-42.
Niederreiter, H. (1978), Quasi-Monte Carlo methods and pseudorandom numbers, Bull. Amer. Math. Soc. 84, 957-1041.
Odlyzko, A.M. (1985), Discrete logarithms in finite fields and their cryp-
tographic significance, in Advances in Cryptology: Eurocrypt '84, Lecture Notes in Computer Science no. 209, Springer-Verlag, New York, 224-316.
Purdy, G.B. (1983), A carry-free algorithm for finding the greatest common divisor of two integers, Comput. Math. Appl. 9, 311-316.
Reeds, J. (1979), Cracking a multiplicative congruential encryption algorithm, in Information Linkage Between Applied Mathematics and Industry, P.C. Wong, ed., Academic Press, New York, 467-472.
Rivest, R., A. Shamir, and L. Adleman (1978), On digital signatures and public key cryptosystems, Commun. ACM 21, 120-126.
Rompel, J. (1990), One-way functions are necessary and sufficient for secure signatures, in Proc. 22nd Annual Symposium on Theory of Computing, ACM Press, New York, 387-394.
Rubinstein, R.Y. (1982), Simulation and the Monte Carlo Method, John Wiley & Sons, New York.
Savage, J. (1976), The Complexity of Computing, John Wiley & Sons, New York.
Schrift, A., and A. Shamir (1990), The discrete log is very discreet, in Proc. 22nd Annual Symposium on Theory of Computing, ACM Press, New York, 405-415.
Schuster, H.G. (1988), Deterministic Chaos, VCH Verlagsgeselleschaft mbH, Weinheim, Germany.
Wolfram, S. (1986), Random sequence generation by cellular automata, Adv. Appl. Math. 7, 123-169.
Yao, A. (1982), Theory and applications of trap door functions (extended abstract), in Proc. 23rd Annual Symposium on Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, Calif., 80-91.
Yao, A. (1988), Computational information theory, in Complexity in Information Theory, Y. Abu-Mostafa, ed., Springer-Verlag, New York, 1-15.






















