3
Approaches to Vulnerability Assessments
INTRODUCTION
Numerous approaches have been used or proposed for assessing ground water vulnerability. They range from sophisticated models of the physical, chemical, and biological processes occurring in the vadose zone and ground water regime, to models that weight critical factors affecting vulnerability through either statistical methods or expert judgment. Each of these categories of techniques are reviewed in this chapter, with particular emphasis on their strengths and limitations.
A fundamental characteristic of all approaches to vulnerability assessment is uncertainty, either in the method itself or in the data it uses. These uncertainties are discussed, and ways to analyze and minimize them are presented. Possibilities for testing and evaluating models are discussed for both field-scale and regional-scale assessments. At the conclusion of this chapter, geographic information systems (GIS) are presented as a commonly used computing environment for executing some types of assessments and for displaying the results of virtually all types of assessments.
The potential for contaminants to leach to ground water depends on many factors, including the composition of the soils and geologic materials in the unsaturated zone, the depth to the water table, the recharge rate, and environmental influences on the potential for biodegradation. The composition of the unsaturated zone can greatly influence transformations and reactions. For example, high organic matter or clay content increases sorption
and thus lessens the potential for contamination. The depth to the water table can be important because short flow paths decrease the opportunity for sorption and biodegradation and thus increase the potential for contamination. Conversely, longer flow paths from land surface to the water table can lessen the potential for contamination by chemicals that sorb or degrade along the flowpath. The recharge rate is important because it affects the extent and rate of transport of contaminants through the unsaturated zone. Finally, environmental factors, such as temperature and water content, can significantly influence the loss of contaminants by microbial transformations.
Some general geologic and hydrologic factors that influence an aquifer's vulnerability to contamination are shown in Table 3.1, along with examples of features that lead to low or high vulnerability. Although these factors may seem quite simple at first inspection, many of them interact in the
TABLE 3.1 Principal Geologic and Hydrologic Features that Influence an Aquifer's Vulnerability to Contamination (After Johnston 1988)
|
Feature Determining Aquifer Vulnerability to Contamination |
Low Vulnerability |
High Vulnerability |
|
A. Hydrogeologic Framework |
||
|
Unsaturated Zone |
Thick unsaturated zone, with high levels of clay and organic materials. |
Thin unsaturated zone, with high levels of sand, gravel, limestone, or basalt of high permeability. |
|
Confining Unit |
Thick confining unit of clay or shale above aquifer. |
No confining unit. |
|
Aquifer Properties |
Silty sandstone or shaley limestone of low permeability. |
Cavernous limestone, sand and gravel, gravel, or basalt of high permeability. |
|
B. Ground Water Flow System |
||
|
Recharge Rate |
Negligible recharge rate, as in arid regions. |
Large recharge rate, as in humid regions. |
|
Location within flow system (proximity to recharge or discharge area) |
Located in the deep, sluggish part of a regional flow system. |
Located within a recharge area or within the cone of depression of a pumped well. |
TABLE 3.2 A Listing of Some Key Parameters in Models of Pesticide Transport in Soils (Adapted from Wagenet and Rao 1990. Reprinted, by permission, from the Soil Science Society of America, 1990.)
|
Pesticide Parameters Organic carbon-normalized sorption coefficient (Koc) Distribution coefficient (Kd) Aqueous solubility Henry's constant Saturated vapor density Gas phase diffusion coefficient Biological half-life Hydrolysis half-life Oxidation half-life Foliar decay rate Soil Parameters Dispersion coefficient Saturated water content Field-capacity water content (θFC) Wilting-point water content Hydraulic properties Bulk density (ρb) Organic carbon content (foc) pH Cation exchange capacity Heat flow parameters Crop Parameters Root density distribution Maximum rooting depth Pesticide uptake rates Climatological Parameters Rainfall or irrigation rates Pan evaporation rates Daily maximum and minimum temperature Snow melt Hours of sunlight Management Parameters Pesticide application rate and timing Pesticide application method and formulation Crop production-system variables Soil-management variables |
environment to create more complex and subtle distinctions in vulnerability than the extreme situations in Table 3.1. Furthermore, many of these factors affecting vulnerability are highly variable and difficult to characterize over any given area. One set of characterizations is shown in Table 3.2, which lists some of the key parameters often used in modeling one aspect of ground water contamination potential, pesticide transport and transformation in soils.
REVIEW OF CURRENT APPROACHES
Combinations of some or all of the factors noted above are included in the various approaches used to assess ground water vulnerability. These approaches range in complexity from a subjective evaluation of available map data to the application of complex contaminant transport models. The U.S. Environmental Protection Agency (EPA 1992a) evaluated the methods
currently available for assessing aquifer sensitivity or ground water vulnerability to pesticide contamination. Their categorization includes three broad classes of approaches depending on the factors included in the assessment method. Each class is broken down further into specific types of approaches, such as aquifer sensitivity assessment methods which consider only hydrogeologic factors; hybrid methods, which consider hydrogeologic and pesticide factors; and ground water vulnerability assessment methods, which consider hydrogeologic, pesticide, and agronomic factors. Statistical tools are also noted for their usefulness in validating methods or providing hydrogeologic setting information.
Our alternative classification scheme places assessment methods in three general categories: (1) overlay and index methods, (2) methods employing process-based simulation models, and (3) statistical methods.
Assessment methods in the first category, overlay and index methods, are based on combining maps of various physiographic attributes (e.g., geology, soils, depth to water table) of the region by assigning a numerical index or score to each attribute. In the simplest of these methods, all attributes are assigned equal weights, with no judgment being made on their relative importance. Thus, areas where simple confluence of the specified attributes occurs (e.g., sandy soils and shallow ground water) are deemed vulnerable. Such methods were the earliest to be used and are still favored by many state and local regulatory and planning agencies. Overlay and index methods that attempt to be more quantitative assign different numerical scores and weights to the attributes in developing a range of vulnerability classes, which are then displayed on a map. Popularization of GIS technology has made it increasingly easy to adopt map overlay and index methods.
The assessment methods in the second category, methods employing process-based simulation models, require analytical or numerical solutions to mathematical equations that represent coupled processes governing contaminant transport. Methods in this category range from indices based on simple transport models to analytical solutions for one-dimensional transport of contaminants through the unsaturated zone to coupled, unsaturated-saturated, multiple phase, two- or three-dimensional models.
Statistical methods having a contaminant concentration or a probability of contamination as the dependent variable form the basis for the third category. These methods incorporate data on known areal contaminant distributions and provide characterizations of contamination potential for the specific geographic area from which data were drawn. Statistical methods are sometimes used by regulatory agencies that have the regional databases on ground water contamination needed to develop models.
Some characteristics of selected vulnerability assessment methods used in the United States are listed in Table 3.3. Comparative details on these
TABLE 3.3 Selected Methods Used in the United States to Evaluate Ground Water Vulnerability to Contamination
|
Method |
Reference |
Map Scale1 |
Reference Location |
Intrinsic and/or Specific |
|
Overlay and Index Methods |
||||
|
Kansas Leachability Index |
Kissel et al. 1982 |
Small |
Soil |
Intrinsic |
|
DRASTIC |
Aller et al. 1985, 1987 |
Variable |
Ground Water |
Intrinsic |
|
California Hotspots |
Cohen et al. 1986 |
Large |
Water Table |
Intrinsic and Specific |
|
Washington Map Overlay Vulnerability |
Sacha et al. 1987 |
Small |
Ground Water |
Intrinsic and Specific |
|
SEEPPAGE |
Moore 1988 |
Variable |
Ground Water |
Intrinsic |
|
Iowa Ground Water Vulnerability |
Hoyer and Hallberg 1991 |
Small |
Ground Water |
Intrinsic |
|
EPA/UIC |
Pettyjohn et al. 1991 |
Small |
Ground Water |
Intrinsic |
and other methods were published recently by EPA (1992a). Inspection of Table 3.3 reveals some general similarities within the broad classes of methods. Overlay and index methods tend to be applied at small map scales (large study areas), typically greater than 1:50,000, whereas most current process-based models apply to problems at much larger map scales (smaller study areas). Most overlay and index methods and most statistical methods refer to the saturated zone (the ground water resource) or water table as the reference location. In contrast, most process-based models have a floating reference location depending on the extent to which contamination is investigated through the vadose zone (for example, the reference location may be the bottom of the crop root zone for agricultural scenarios). Most overlay and index methods are designed to evaluate intrinsic vulnerability or have mixed specific and intrinsic utility. In contrast, most process-based models and statistical methods are designed for specific classes of contaminants such as pesticides or nitrate.
Overlay and Index Methods
Overlay and index methods rely primarily on qualitative or semiquantitative compilations and interpretations of mapped data. Selected overlay and index methods are listed in Table 3.4 together with the parameters used in their application. Additional methods are summarized by the U.S. Environmental Protection Agency (1992a). Variables used in the overlay and index methods typically include approximate depth to the water table, ground water recharge rate, and soil and aquifer material properties.
Depth to Ground Water
The shorter the distance to ground water, the less soil and underlying unsaturated zone material is there to act as a filter or adsorbent. Depth to ground water also affects the transit time available for various abiotic and biotic processes to degrade the chemical. Depth to ground water corresponds to the depth to water table in unconfined aquifers or to the depth to the bottom of a confining geologic unit when the uppermost aquifer is confined. Varying degrees of confinement over an area are common. Overlay and index methods use a single depth to ground water at each location. However, large seasonal fluctuations in water levels in unconfined aquifers can complicate the estimate of single representative values. Seasonally high water table depths may be used to provide conservative estimates. Information on the depth to ground water is available from many sources, including well logs, federal and state agency computer files, and water-level maps published by federal and state agencies, universities, and consulting firms.
TABLE 3.4 Parameters Used in Selected Overlay and Index Methods for Vulnerability Assessments
|
Parameters Related to |
|||||
|
Method |
Author(s) |
Depth to Ground Water |
Recharge |
Unsaturated Zone and Aquifer Material |
Other |
|
DRASTIC |
Aller et al. 1985 Aller et al. 1987 |
Depth to water table |
Net recharge |
Soil media Vadose zone media Aquifer media Hydraulic conductivity |
Slope |
|
Wisconsin Ground Water Contamination Susceptibility |
Wisconsin Department of Natural Resources, Wisconsin Geological and Natural History Survey 1987 |
Depth to water table |
— |
Soil characteristics (4 classes based on texture) surficial deposits Depth to bedrock Bedrock type |
— |
|
Potential for Contamination of Shallow Aquifers in Illinois by Agricultural Chemicals |
Berg and Kempton 1988; McKenna and Keefer 1991 |
— |
— |
Soils and geologic materials differentiated by thickness, texture, permeability, and stratigraphic position |
— |
|
Ground Water Vulnerability Regions of Iowa |
Hoyer and Hallberg 1991 |
Depth to private well water sources |
— |
Aquifer type (alluvial, bedrock, glacial drift) and thickness of confinement by low permeability drift or shale |
Locations of sinkholes and agricultural drainage wells |
|
State-by-State Assessment of Aquifer Vulnerability and Sensitivity for the Conterminous U.S. |
Pettyjohn et al. 1991 |
— |
— |
Geologically based classification of surficial and relatively shallow aquifers |
— |
Recharge
Estimates of ground water recharge used in vulnerability assessments should account for all inputs (e.g., rainfall, irrigation, artificial recharge, and wastewater applications) and losses (e.g., runoff, evapotranspiration) of water. Typically, average annual values of recharge are used, and recharge is assumed to be uniform over large areas. In reality, recharge is commonly quite variable in time, both seasonally and annually, and it can be highly variable over a region.
The identification of recharge and discharge zones may be particularly useful in assessing the potential for contaminants introduced at the water table to move deeper into the ground water system. Evaluating recharge and discharge zones can be difficult in hydrogeologic systems where ground water flow systems occur at different scales. For instance, a given area may have local flow systems with discharge zones within hundreds of meters of the recharge zones, intermediate-scale systems of one or a few kilometers that encompass two or more local flow systems, and regional-scale flow systems many kilometers long that begin at the major ground water system divide and traverse the entire regional system to the major drain. The extent to which flow systems of different spatial scales can be defined as parts of regional assessments of ground water vulnerability is subject to significant limitations. Nonetheless, the identification of recharge and discharge zones may be one of the more important elements of a vulnerability assessment.
Properties of the Unsaturated Zone and Aquifer Material
Many different properties of the unsaturated zone and aquifer material may be incorporated into overlay and index methods. Ideally, one might consider properties of the unsaturated zone to indicate the potential for vertical transport of contaminants to ground water, while properties of the aquifer indicate the potential for lateral transport. Because the aquifer material commonly is also part of the unsaturated zone, such a clear distinction does not always exist in application of overlay and index methods. In fact, for many overlay and index methods, it is not always obvious whether the reference location is the water table or some unspecified location within the ground water flow system.
Properties of the unsaturated zone and aquifer material listed in Table 3.4 illustrate considerable diversity among vulnerability assessment methods. Many of the methods consider geology, but neglect soils, others focus on soils, but ignore geology. Some indexing methods, like DRASTIC, attempt to be universally applicable and incorporate parameters that should be available to some degree virtually everywhere; other methods are adjusted
to the setting and data bases available in a particular area. An advantage of the latter approach is that geologic and geographic features unique to a particular area can be taken into account. For example, the Illinois method (Berg and Kempton 1988, McKenna and Keefer 1991) involved an intensive examination of stratigraphy and the identification of low and high permeability units in a three-dimensional context throughout the state.
Finally, in addition to the foregoing factors related to hydrology, geology, and soils, some overlay and index methods have combined use of these factors with surrogate data on contaminant loading. For example, Moreau and Danielson (1990) used DRASTIC scores in combination with estimated pesticide use rates to produce vulnerability maps for selected pesticides for the state of North Carolina.
Major sources of data used in overlay and index methods include: 1) soil maps generated by the Soil Conservation Service (SCS) in conjunction with state and local agencies, 2) topographic maps produced by the U.S. Geological Survey (USGS), 3) geologic maps published by the USGS, state geological surveys, and other sources, and 4) regional and local land-use planning maps.
Discussion
A simple overlay-type vulnerability map is prepared by superposing a series of maps showing the areal distributions of attributes considered important in characterizing the potential for ground water contamination (e.g., soil types, depth to ground water, recharge rate). Each attribute is given equal weight, and areas with different vulnerability ratings are defined by the patterns or ranges of attribute values that overlap in the area. Typically, the product is a single map depicting areas of differing vulnerability, designated by a score, pattern, or color. In some instances, overlay methods identify areas with different expected ground water vulnerabilities, but no attempt is made to rank the areas from most to least vulnerable.
Perhaps the simplest overlay method is that used by Pettyjohn et al. (1991) for evaluating the potential for ground water contamination in the contiguous United States on a state-by-state basis. They developed their method specifically for the U.S. EPA's Underground Injection Control Program, but indicated that "the products are equally valuable to assess the potential for ground water contamination from other surface or near surface sources." Their vulnerability assessment is based solely on a geologic classification of surficial and relatively shallow aquifers. Pettyjohn et al. (1991) also evaluated aquifer sensitivity in which they included population density as an additional factor.
Overlay methods are commonly used for vulnerability assessments at
the state level. For example, Illinois (Berg and Kempton 1988, McKenna and Keefer 1991) and Iowa (Hoyer and Hallberg 1991) have developed GIS-based maps using overlay methods with an emphasis on geology as the key attribute for assessing vulnerability. An overlay map for the state of Wisconsin considers depth to water, geology, and soils information (Wisconsin Department of Natural Resources and Wisconsin Geological and Natural History Survey 1987).
In contrast to simple overlay methods, index methods assign a numerical value to each attribute based on its magnitude or qualitative ranking. Each attribute, in turn, is assigned a relative importance or weight compared to the other attributes. A consensus of experts may be solicited (the Delphi approach) to determine the relative weights assigned to different attributes and the numerical values assigned to different levels of each attribute. The weighted-attribute ratings are summed to obtain an overall numerical score for ground water vulnerability. These numerical scores are used to group similar areas into classes or categories of vulnerability (e.g., low, medium, and high) that are then displayed on a map. Some methods multiply the numerical scores or values assigned to the attributes together rather than adding them (c.f., Back et al. 1984).
Several types of indices have been developed for ground water vulnerability assessments. The DRASTIC index (Aller et al. 1987) is perhaps the best known of these methods. Some state regulatory agencies have developed index assessment methods similar to DRASTIC (cf., Rupert et al. 1991). Using information about pesticide leaching abilities, Kellogg et al. (1992) developed the GWVIP and GWVIN indices to generate national-scale vulnerability maps for pesticides and nitrates, respectively (see Chapter 5).
Overlay and index methods have often been developed with the availability of information keenly in mind. These methods are driven largely by data availability and expert judgment, with less emphasis on processes controlling ground water contamination. One can argue whether the factors included in the methods are the relevant ones for vulnerability assessment and whether the factor ratings are appropriate. For example, Banton and Villeneuve (1989) questioned the basis for the numerical weighting scheme used by Agricultural DRASTIC after comparing its results with those from a process-based modeling approach (PRZM). Further, Holden et al. (1992) concluded that "the complex weighting and coding procedures used in the DRASTIC scoring are self defeating," and that in the short-term, "simpler classification schemes, focusing on only a few major vulnerability factors, look to be more useful than DRASTIC." There are no quantitative criteria for evaluating the scientific basis of these methods.
Many overlay and index methods address intrinsic vulnerability, although some of them address what might be called pseudospecific vulnerability.
The latter methods (e.g., Agricultural DRASTIC) were developed with a particular type of contamination in mind, but generally lack any real specificity among the contaminants considered. For example, a method that lumps all agricultural contaminants clearly lacks specificity, given the wide range of properties among pesticides and other agricultural chemicals.
Process-Based Simulation Models
Everything must be made as simple as possible, but not simpler.
—Albert Einstein
Process-based simulation models are distinguished from all other methods because many of them attempt to predict contaminant transport in both space and time. For example, simulations of one-dimensional transport in the unsaturated soil zone may predict contaminant concentrations with depth at discrete time intervals during and after the time the contaminant is applied to the land surface. Similarly, the computer algorithms available for contaminant transport in the saturated and unsaturated zones (NRC 1990) predict the vertical and areal extent of contamination with time and mathematically incorporate many of the physical, chemical, and microbial processes in the unsaturated and saturated zones.
Process-based models can be used in both regional and site-specific studies and have been developed and applied primarily by research scientists rather than by regulators. The complex simulation models for solving coupled and/or multiphase contaminant transport in two or three dimensions have been used almost exclusively to evaluate physical, biological, and chemical controls in hypothetical settings or well-evaluated local incidences of contamination (NRC 1990). Such complex models have not been used to evaluate ground water vulnerability on a regional scale; therefore, this discussion will focus on simpler process-based models of one-dimensional transport through the vadose zone.
Table 3.5 indicates the various process representations used in several simulation models that have been used to predict pesticide behavior in the unsaturated zone. Outputs from three of these models are detailed in Table 3.6. These tables are included for illustrative purposes; more recent versions of these models include enhancements in areas of process representation, input parameter estimation, and output capabilities. The models listed in these tables differ in complexity. LEACHM is the most complex in terms of the number of processes included and the most sophisticated in terms of process description. Models such as LEACHM have large data requirements, but they offer the flexibility of being applicable to more diverse scenarios and provide detailed outputs (see Table 3.6). Models such as GLEAMS and PRZM are designed to assist in management decisions;
TABLE 3.5 A Comparison of Process Conceptualization in Five Models Used to Predict Pesticide Behavior in the Vadose Zone (Adapted from Pennell et al. 1990. Copyright by the American Geophysical Union.)
|
Process |
Simulation Model |
|
|
|
CMLS (Ver. 4.0, 1987)1 |
GLEAMS (Ver. 1.8, 54, 1989)2 |
|
Water Flow |
Piston displacement of water. Instantaneous redistribution between field capacity and wilting point. |
Predicts water flow between soil layers based on a storage similar to the "tipping bucket" method. |
|
Runoff |
Runoff not considered. |
Runoff based on SCS curve-number method. Erosion calculated using overland, channel, and impoundment elements, and soil particle characteristics. |
|
Solute Transport |
Piston displacement of solute. |
Convection transport of solute using water flow between soil layers. Solute can move upward by capillary flow. |
|
Solute Dispersion |
Tracks a nondispersive solute point. |
Numerical dispersion, from convective transport equation, used to simulate actual solute dispersion. |
|
Sorption |
Input solute Koc. Input organic carbon by soil horizon or enter Kd by soil horizon. |
Input Kocs for up to ten solutes and metabolites. Input organic matter by soil horizon. |
|
Degradation |
Input solute half-life by soil horizon. |
Input half-life for each solute or metabolite by horizon. Input one coefficient of transformation for each component. |
|
Evapotranspiration |
Input daily PET. Water removed from wettest soil horizons in the root zone first. |
Potential evaporation calculated from solar radiation and air temperature. Actual ET is then calculated using leaf area index and soil-water content. |
|
Roots |
Input maximum rooting depth. Root biomass constant. |
Input maximum rooting depth. Water use is a function of depth based on an exponentially decreasing function. |
|
1Nofziger and Hornsby 1986 2Knisel et al. 1989 3Wagenet and Hutson 1987 4Carsel et al. 1984
|
||
|
Simulation Model |
|
|
LEACHM (Ver. 1.0, 1987)3 |
PRZM (Release 1, 1985)4 |
|
Solves Richards' equation. Requires moisture release curve data which must be fit to a modified Campbell's function. |
Water flow based on "tipping bucket" method. Operates between field capacity and wilting point. Instantaneous or time dependent water redistribution. |
|
Runoff not considered. |
Runoff based on SCS curve-number method. Erosion based on the Universal Soil Loss Equation. |
|
Solves the convective-dispersive transport equation. |
Convective transport of solute based on water flow between soil increments. |
|
Calculated hydrodynamic dispersion. |
Numerical dispersion, from convective transport equation, used to simulate actual dispersion. |
|
Input Koc for solute and two metabolites. Input organic carbon by soil increment. |
Input solute Kd by soil horizon. |
|
Input five degradation rate coefficients for three components by soil increment. |
Input solute degradation rate coefficients by soil horizon. |
|
Input weekly PET total. Water removal based on root distribution, root resistance, and soil-water potential. |
Input daily ET and crop ET coefficient. Water removal based on root distribution and soil-water content. |
|
Root biomass can be constant or increasing. For constant root biomass, input relative root fraction by soil increment. |
Root biomass can be constant or increasing. Root distribution decrease linearly to maximum rooting depth. |
|
1Nofziger and Hornsby 1986 2Knisel et al. 1989 3Wagenet and Hutson 1987 4Carsel et al. 1984 |
|
TABLE 3.6 Major Outputs of Four Types of Pesticide Simulation Models (Adapted from Wagenet and Rao 1990. Reprinted, by permission, from the Soil Science Society of America, 1990.)
|
Output1 |
Type of Model |
|
|
|
|
|
LEACHM (Ver. 1.0, 1987) |
GLEAMS (Ver. 1.8, 54, 1989) |
PRZM (Release 1, 1985) |
CMLS (ver. 4.0, 1987) |
|
Pore-water solute concentration |
+ |
+ |
+ |
- |
|
Depth of maximum solute concentration |
+ |
+ |
+ |
+ |
|
Maximum depth of solute penetration |
+ |
+ |
+ |
- |
|
Soil-water flux |
+ |
+ |
- |
- |
|
Soil-water content |
+ |
+ |
+ |
- |
|
Phase partitioning of solute mass |
+ |
+ |
+ |
- |
|
Temperature |
* |
* |
- |
- |
|
Water uptake |
+ |
+ |
+ |
- |
|
Pesticide uptake |
* |
+ |
* |
- |
|
Volatile losses |
+ |
- |
- |
- |
|
Runoff |
- |
+ |
+ |
- |
|
1 A plus sign indicates that the output parameter values are provided, and a minus sign indicates that the parameter values are not provided. An asterisk indicates that the parameter can be considered, but usually is not because of insufficient data. |
||||
they are constructed to include most of the major processes, but some or many of the processes are represented in a less sophisticated manner. A loss of scientific rigor and conceptual detail is usually accompanied by a reduction in computational time and greater ease of use. Management and screening models usually require less data, but also provide commensurately less detailed prediction of system behavior. Finally, models designed
primarily for instructional purposes (e.g., CMLS) are based on simplified representations of fewer processes and so require the least data.
The models listed in Tables 3.5 and 3.6, and others like them, are similar in that they are deterministic, with model parameters assumed to have no variability. Thus, given a specific set of parameters (usually the mean or modal values), these models generate a set of unique outputs (not necessarily the mean values). Stochastic models, in contrast, are formulated with the premise that all input parameters, or even the processes included in the model, are inherently variable; they provide outputs in terms of means (expected values), the associated variances, and in some cases probability distributions. In practice, the lack of realistic probabilistic information from deterministic models can be overcome by employing Monte Carlo simulation techniques, which require assumptions about the probability density functions representing the spatial or temporal variability of the input parameters in the simulation models. Model outputs from multiple runs of a deterministic model, each run using a randomly chosen set of input parameters, are then represented as probability density functions of the prediction of certain likely outcomes (e.g., concentration in excess of a certain value). Such stochastic extensions of otherwise deterministic models have been presented by Jones et al. (1983), Villeneuve et al. (1987), Carsel et al. (1988a, b), and Laskowski et al. (1990) (see Box 3.2).
Discussion
It must be recognized that sophisticated models may not necessarily provide more reliable outputs, especially for regional-scale, and even for field-scale applications. Since data for many of the required input parameters for sophisticated models are not always available, their values have to be estimated by indirect means using surrogate parameters or extrapolated from data collected at other locations. Errors and uncertainties associated with such estimates or extrapolations can be large and may negate the advantages gained from a more rigorous process description in the simulation model.
After comparing measured data on pesticide leaching in a 1.6 hectare citrus grove with outputs from simulation models listed in Table 3.5, Pennell et al. (1990) concluded that deterministic pesticide simulation models should not be expected to predict observed solute concentration distributions accurately because the measured concentration distributions themselves are subject to considerable error. If the observed concentrations have a large measurement error then one would want the model to predict the most likely distribution rather than the observed distribution. One major source of error in measured pesticide concentrations cited is variability introduced by the method used to apply pesticide at the ground surface. Such variability
is neither characterized in most field studies nor accounted for in any of the current models. Pennell et al. (1990) also concluded that the pesticide simulation models they evaluated were able to predict the location of the solute center of mass and the solute mass remaining in the soil profile within plus or minus 50 percent of the actual values. Measured values for these two parameters were found to be much less variable than the measured concentration profiles. Thus, the parameters that a more sophisticated model (LEACHM) is designed to predict cannot be measured with certainty, while the outputs of the simpler models (CMLS) appear to be subject to less variability. These findings suggest that models based on simplified process representation may be more useful for certain types of vulnerability assessments. The convective-dispersive solute transport approach employed in LEACHM and other models predicts the asymptotic behavior and is least likely to be valid when used for shallow depths. This problem can be circumvented by calibrating the model parameters using experimental data from the zone of interest (i.e., near soil surface), but extrapolation to much greater depths in the vadose zone can lead to significant errors.
All of the simulation models discussed here suffer from another major limitation, arising from the spatial scales over which the process conceptualization is valid. None of the models included in Tables 3.5 and 3.6 has the ability to simulate water flow and solute transport in cases where preferential flow exists. An increasing number of scientists argue convincingly that such bypass flow may be the rule rather than the exception for field situations (Bowman and Rice 1986, Germann 1988, Butters et al. 1989, Jury and Ghodrati 1989, Beven 1991, Jury and Flüher 1992).
Preferential flow can be the dominant transport phenomenon under certain circumstances, even in soils that exhibit no identifiable macrostructure (Ghodrati and Jury 1990, Roth et al. 1991). Even the most sophisticated model, LEACHM, cannot handle the complexities in flow and transport at finer spatial scales than those for which the model was formulated. Nicholls et al. (1982a, b) compared measured leaching and transformations of pesticides in field plots with predictions of two simulation models, one similar to LEACHM, and the other an empirical model, CALF, that considers preferential flow and transport in structured soils. They concluded that both models provided adequate predictions, and preferred the use of the simpler model CALF for management purposes since herbicide leaching was described as accurately by the CALF model as the more complex model and the CALF model required much less input data. Complex models that explicitly account for certain types of preferential flow in structured soil are available, but the required information on spatial distribution of preferential flow paths is practically impossible to determine using existing soils databases (Beven 1991) and models remain virtually untested in any practical sense. Conceptual qualitative explanations have been presented describing
transport in soils with no macrostructural features. Models may be calibrated to produce agreement between predictions and field observations, however, the fitted parameter values have no physical basis and their values cannot be estimated based on measured soil properties (Roth et al. 1991). Most process models are based on the assumption of local sorption equilibrium, which likely is not achieved under natural conditions. However, transport nonequilibrium arising from preferential flow likely is more significant than sorption nonequilibrium.
In applying these models at various spatial scales, it has been assumed that the area of interest can be represented as a patchwork of homogeneous polygons, and that the model adequately represents the processes within each of these subareas. Thus, regional scale behavior is assumed to be predicted by the composite representation of local-scale behavior simulated in each polygon. Such an approach does not consider the possibility that other processes or factors might be significant at the regional-scale, necessitating formulation of new models appropriate for larger areas. For example, surface and subsurface water flow focused toward the bottom of a hill slope can lead to greater solute leaching compared to that at the top of the hill. The importance of such regional-scale features often is not represented by simply aggregating outputs of models designed to represent processes at local spatial scales.
An analogous situation exists in watershed modeling, where field-scale models are used to calculate runoff and contaminant loadings, which are then used in stream or river models to calculate flow and water quality for the entire watershed. Typically, field-scale models are calibrated on one or more small sites within the watershed, and these results are aggregated to the watershed scale through a network of channel sections simulated by the river model. These procedures have been shown to be realistic as long as the field-scale models and sites include all the processes that are important over larger areas (Donigian et al. 1983, Imhoff et al. 1983). For example, the field-scale model will need to represent both surface and subsurface flow components (and contaminant loadings), since both components are important at the watershed scale. If the model represents only field-size areas (e.g., 5 to 20 hectares) where only surface contributions are modeled, the regional watershed cannot be adequately modeled through aggregation of the individual field areas since subsurface contributions are not included. The problem is significantly greater for ground water, partly because of the difficulties in defining multidimensional subsurface flow and transport processes.
The foregoing discussion suggests that a principal limitation of simulation models currently used to make vulnerability assessments may be their failure to account for flow and transport processes at spatial scales either smaller or larger than those for which the models were developed. Although
this situation can be remedied by use of other simulation models, the data needed to estimate many of the needed model parameters are not available currently, and the effort and cost of gathering such information for regional-scale assessments may be prohibitively large.
Statistical Techniques for Vulnerability Assessment
While statistical approaches for assessing ground water vulnerability have not received as much attention as overlay, index, and simulation modeling techniques, they have interesting potential applications to vulnerability assessment. Statistical methods can be used to evaluate, determine, and quantify the association between measures of vulnerability and various types of information that are thought to be related to vulnerability. Statistical methods are based on the concept of uncertainty which is described in terms of probability distributions for the variables of interest.
Since ground water vulnerability is a probabilistic notion, statistical methods should have more application in vulnerability assessments than they have had to date. Statistical methods can more easily deal with differences in scale than other methods that are based on the description of physical relationships. Also, the variety of statistical techniques available for treating assorted types of data makes statistical approaches inherently flexible. They include methods designed to deal with qualitative, quantitative, or mixed data sets, as well as truncated or censored data (e.g., data exhibiting detection or reporting limit effects). Examples of statistical methods include simple and multiple regression for single and multivariate variables, analysis of variance, discriminant and cluster analyses, geostatistical analyses (including kriging), and time series. The uncertainty methods applied to process models that are described in the previous section are based on statistical and probabilistic methods.
Typical of many statistical applications to ground water vulnerability is the goal of describing in mathematical terms (function or model) a relationship between water quality and natural and/or human-generated features in a discrete area or region through the use of surrogate or independent variables. In general, no a priori decisions are made about the subset of candidate variables to be included in the model, nor do the results purport to identify or define cause-effect relationships. Parameters from simple process-based indices (e.g., travel time, retardation factor) can be used as variables in a statistical analysis. To our knowledge such a hybrid approach has not yet been attempted for assessing ground water vulnerability.
Two possible applications of statistical techniques in vulnerability assessments described here are: (1) regionalization, and (2) assessment of vulnerability with probability models.
Regionalization
Delineation and description of an assessment area is of interest to managers and scientists alike. Agencies involved in land use planning and management have demonstrated needs for employing regionalization concepts. Regions delineated by natural drainage basins are convenient management tools. However, the applicability of regionalization schemes based on drainage systems to ground water management has been questioned, since aquifer boundaries do not necessarily coincide with drainage boundaries and are not themselves readily distinguished and measured.
Regionalization based on statistical analyses of hydrologic, geologic, and human activity data have been useful in differentiating ground water regions. Several examples appear in the literature, and a few are examined below. Seyhan et al. (1985) found that hydrochemical data from a dolomitic reef aquifer subjected to multivariate cluster analysis supported earlier conclusions that hydrogeological partitioning existed within the aquifer. The original partitioning study that was confirmed by Seyhan et al. used more traditional hydrogeological techniques to define aquifer compartments. Pedroli (1990) identified 16 classes of shallow ground water within a 20 km2 area using cluster and discriminant analyses of hydrochemical data. Pedroli associated the variations in water quality with ecohydrological patterns, including landscape features, infiltrating and discharging water components and fertilizer pollutants resulting from farming practices. A study with immediate impacts on the hydrologic study unit (HSU) concept was conducted by Riley et al. (1990) in the vicinity of the Hanford Reservation in Washington. In an application of exploratory and confirmatory statistical analysis of existing hydrochemical data, Riley et al. (1990) quantitatively determined by multivariate cluster analysis (later confirmed through a combination of MANOVA, canonical, and discriminant analyses) that ground waters taken from opposing sides of the Columbia River were distinctly different. Such cases bring into question the logic of using surface water drainage basins as regions for conducting vulnerability assessments. The statistically-based regionalization schemes considered here do not depend on pollutant databases, but require adequate and largely routine water quality data.
Vulnerability Assessment
The integrity of and confidence in vulnerability assessment can be bolstered by statistical analyses. Statistical methods such as principal components analysis, discriminant analysis, cluster analysis, time series and regression analyses and an assortment of other parametric and nonparametric techniques are used in ground water studies to estimate the likelihood that a
pollutant will contaminate an experimental unit or subset of a region. Riley et al. (1990) and many others have observed that ''water quality is a multivariate concept… [that is] not defined by any single constituent." Thus multivariate statistical techniques may be well suited to analysis of water quality data and other regional data, which can include soils and geologic information, vegetal coverage and land management practices. Vulnerability assessments that use overlay/indexing techniques are an eyeballed form of multivariate discriminant analyses that lack probability estimates.
Interpretations of statistical applications vary in difficulty, and depend on the method used, the researcher(s') experience, and the amount and quality of the data investigated. Simple linear regression models using single independent and dependent variables (Y = a + b1X1) are not commonly applied to complex issues of ground water quality. More complex models, like multiple regression, can accommodate additional independent variables (Y = a + b1X1 + b2X2 + …). For example, Chen and Druliner (1988) used multiple regression to describe the relationship of nine variables to observations of triazine concentrations in ground water in Nebraska. The variables included data that can be practically collected (well characteristics, nitrate concentrations) or that have some demonstrated effect on pollutant transport (hydraulic gradient and conductivity). The best-fit model suggested a strong relationship (R2 = 84 percent) between specific discharge (well characteristic), the surrogate nitrate pollutant concentrations, and the dependent triazine concentrations.
Statistical procedures such as discriminant analysis are more complex. Discriminant analysis is a tool for assigning observations described by multiple independent variables (X1, X2, …) to multiple discrete classes. Teso et al. (1988) used discriminant analysis to describe relationships between soil mapping unit data from 1 square mile areas (sections) and areas vulnerable to DBCP contamination in California. The discriminant model developed proved to be useful in delineating the DBCP contamination status of sections in a different county whose center of contamination was 100 kilometers from the model development region.
In addition to the methods discussed above, nonparametric statistical techniques are also used in vulnerability assessment. Berryman et al. (1988) has reviewed these techniques for their application to the detection of trends in water quality time series. A more general discussion of nonparametric approaches to environmental impact assessment is offered by Hipel (1988).
Geostatistical methods describe the spatial distribution of process parameters that affect vulnerability. Spatial statistical simulation methods then can be used to link nearby polygons through the continuity of the underlying processes. Such simulations do not show the discontinuities in the results between individual polygons. As with other techniques, one
must pay attention to the uncertainty associated with the apparent gradations in vulnerability.
All statistical techniques require data. Some place more stringent requirements on data quality than others. As with most other forms of vulnerability assessment there is no replacement for high quality data. Since ground water data are used in developing statistical models, these methods are best applied to areas having adequate monitoring programs and/or a good hydrogeologic database coverage. In some cases, statistical models can be applied to regions outside the region of model development. The extent to which this is possible is limited to areas where available or obtainable data are similar to those used in model development. Application should also be guided by review of the assumptions and presuppositions made in data collection and model development. In general, the more complex approaches require greater expertise for interpretation and are best used in a team effort, where the team is composed of a statistician and other experts familiar with available data and their sources.
UNCERTAINTY IN VULNERABILITY ASSESSMENT METHODS
To be absolutely certain about something, one must know everything or nothing about it.
—Olin Miller
Uncertainties inherent in all approaches to ground water vulnerability assessments may be derived from: (1) model related errors, which include uncertainty resulting from inadequate or incomplete representation of the system processes, and (2) data related errors, which include uncertainty resulting from errors in input data, even if the model used is correct (Loague and Green 1991). Thus, uncertainties are likely even when the model(s) or data are perfect. Imperfect model(s) and data are the norm rather than the exception.
Sources of Errors
Numerous reviews of errors and sampling methodology appear in the literature. Several reviews pertinent to ground water vulnerability assessment include those by Burrough (1986), who describes many important sources of error that result from inappropriate use of GIS systems, and by Kempthorne and Allmaras (1986), who review sampling errors as they relate to soil sampling. Statistical procedures for identifying extreme values that are indicative of error are described by Dixon (1986).
In Table 3.7, sources of error are grouped into six classes, which, in
TABLE 3.7 Sources of Errors in Ground Water Vulnerability Assessment (Adapted from Burrough 1986. Principles of Geographical Information Systems for Land Resource Assessment. Reprinted by permission of Oxford University Press.)
|
I. |
Errors in Obtaining Data |
|
|
|
1. |
Accuracy in locating sites |
|
|
2. |
Sample collection and handling |
|
|
3. |
Laboratory preparation and analysis |
|
|
4. |
Interpretation |
|
II. |
Errors Due to Natural Spatial and Temporal Variability |
|
|
|
1. |
Random sampling error |
|
|
2. |
Bias |
|
|
3. |
Regionalization, extrapolation, interpolation |
|
|
4. |
Scale effects, changes in variance due to averaging |
|
|
5. |
Interpretation |
|
III. |
Errors in Computerization (Digitizing) and Storage of Data |
|
|
|
1. |
Data entry |
|
|
2. |
Data age |
|
|
3. |
Changes in storage format |
|
|
4. |
Errors in programs to access data |
|
|
5. |
Use of surrogate data and procedures |
|
|
6. |
Adjustments in scale |
|
|
7. |
Determining boundaries |
|
|
8. |
Changes in representation of data |
|
|
9. |
Interpretation |
|
IV. |
Data Processing Errors |
|
|
|
1. |
Numerical, truncation, and round-off errors |
|
|
2. |
Discretization errors |
|
|
3. |
Problems in solution convergence |
|
|
4. |
Interpretation |
|
V. |
Modeling and Conceptual Errors |
|
|
|
1. |
Process representation and coupling |
|
|
2. |
Parameter identification |
|
|
3. |
Scale effects |
|
|
4. |
Interpretation |
|
VI. |
Output and Visualization Errors |
|
|
|
1. |
Determination of boundaries |
|
|
2. |
Classification into vulnerability categories |
|
|
3. |
Interpretation |
effect, represent the various stages involved in developing a vulnerability assessment. Although a list of possible errors is very long, the following discussion will be directed toward these six general classes. The first three classes are related to data errors and the final three to model errors. Because each step in a vulnerability assessment requires some degree of interpretation, Table 3.7 lists interpretation as one source of error in each class.
Errors in Obtaining Data
A large number of errors can be made in obtaining data. These include errors in the methods used to collect, transport, handle, and analyze field data, and errors introduced by laboratory or other methods used to determine the property of interest.
Errors Due to Natural Spatial and Temporal Variability
Many, if not most, of the data used in vulnerability assessments display significant spatial and temporal variability. Thus, large sampling errors can occur because different estimates of attributes or model parameters will be obtained from different samples at different locations or time periods. Bias may also be present because the sites selected for data collection may not truly represent the area or volume they are intended to characterize, or the timing of data collection may not account for seasonal effects on measured values. In fact, the concept of a representative value for processes that vary continuously in time or space is difficult to justify in theory. For practical purposes, however, it is necessary to assume representative values, particularly when data are limited.
Consequently, at any given spatial and temporal scale of interest, the model parameters should represent effective values at the appropriate scale. Any method to obtain averages will not eliminate uncertainty due to variability occurring at smaller scales. Large scale average values have reduced variance compared to values obtained over the same spatial and temporal domain but at a smaller scale, thus increasing the uncertainty of localized behavior. Appropriate averaging schemes and the magnitude of the associated uncertainty are model and problem specific and depend on the spatial and temporal structure of the variability. For example, areas of missing information in the mapped region should be found and data obtained as needed to create as complete a database as possible. Where empirical data are not available, estimates can be made by conditional simulations, interpolation, or extrapolation. One simple method is to assign the nearest data series available to a nearby map cell and assume that the value is constant over each cell. Alternatively, collected data can be used to develop estimates for the data at locations where data are missing. This process may involve a geostatistical technique such as kriging in which a model of the spatial correlation is developed from existing data and used to estimate an unknown value and the estimation variance. Statistical time series methods may be used for data exhibiting temporal variability. In any event, these or any other methods of interpolation or extrapolation will introduce additional sources of error and/or uncertainty.
Errors in Computerization (Digitizing) and Storage of Data
Computerization and storage errors are associated with preparing, entering, and processing data into a computer storage medium, such as GIS. Many such errors can be minimized by suitable quality control procedures. The uncertainty associated with many of the factors in Table 3.7, including surrogate data, density of observations, and the determination of boundaries, may be difficult, if not impossible, to determine quantitatively.
Data Processing Errors
Data processing errors include inaccuracies in the computational scheme used to obtain numerical values from a model or other quantitative measures of ground water vulnerability. These errors can include numerical dispersion errors, discretization errors, round-off errors, precision errors, possible solution convergence, and uniqueness errors. If the computational algorithm used is appropriate for the application, these errors will be a relatively minor part of the overall error.
Models and Conceptualizations
Modeling and conceptual errors result from lack of understanding of the spatial and temporal nature of transport processes, especially at a regional scale. No model currently available provides a completely accurate simulation of the flow of water and transport processes at the field scale, let alone at the regional scale. This shortcoming introduces some model error into every simulation. Model error is very difficult to measure quantitatively. The task would require a perfectly known system, which is never possible.
Conceptual errors are due to our view of a given part of the transport process. For example, if the transport of a chemical is subject to degradation, this process must be conceptualized before developing a model of the degradation process. The model developer chooses whether to describe the process using a first-order decay equation or some other formulation. The formulation the modeler uses, however, may only approximate the true process. Conceptual errors can also be caused by using a model that is not appropriate for the system considered. These errors may include errors in the approach used to describe the governing process, initial and/or boundary conditions, processes included in the models, and how these processes are coupled.
Output and Visualization Errors
The completed ground water vulnerability assessment results in a map or some other output. Errors at this stage include determination of the boundaries between areas, the classification of vulnerability levels into categories, and the misinterpretation of displays caused by indistinguishable colors or patterns.
The output reflects the ideas, conditions, and biases of its creator. However, the user may not clearly understand the assumptions, limitations, and restrictions that were built into the output (i.e., map). These errors may be obvious to the mapmaker, but not to the user. Errors associated with presentation using GIS are discussed later in the section on Geographic Information Systems.
Uncertainty Analyses
In these matters, the only certainty is that there is nothing certain.
—Pliny the Elder
Vulnerability assessments using a specific method usually generate a map of the region depicting various polygons or cells; the distinctions between levels of vulnerability, however, are arbitrary. The vulnerability assigned to a particular point or polygon is uncertain because of model and data errors and is subject to spatial variability. Therefore, confidence intervals associated with the numerical values assigned to neighboring cells or polygons may overlap to the point that subtle distinctions made between vulnerability classes in adjacent cells are not defensible; hence, the boundaries delineating vulnerability classes are indeterminate because of both model and data errors. This inability to distinguish differences between adjacent cells with differing vulnerability scores increases with increasing magnitude of the relevant model and data uncertainties.
Few published vulnerability assessments account for uncertainties from either model or data errors. More is usually implied about the apparent certainty in vulnerability assessments than is stated about the underlying uncertainties. Little attention has been paid to the problem of errors in GIS databases and propagation of such errors where these databases are used for generating thematic maps (Mead 1982, Chrisman 1984, Burrough 1986, Goodchild and Dubuc 1987, Goodchild and Min-hua 1988).
Uncertainty analyses are used to evaluate the spatial and temporal variability and the propagation of errors in model calculations (i.e., variance in model outputs and the sufficiency of existing spatial databases) (Eisenberg et al. 1989). Such techniques have been used extensively in development of criteria for site selection and for designing radioactive waste-disposal facilities
(Buxton 1989), but not for vulnerability assessments. Methods for evaluating uncertainty associated with data errors can be grouped into the following five categories (Brandstetter and Buxton 1989):
-
Classical statistical variance component analysis, which can be used to partition the total observed variance in the output to contributing factors.
-
First-order uncertainty analysis (FOUA) based on Taylor series expansion of the function (model) to evaluate variance of the output as a function of the variance in input parameters.
-
Statistical sampling methods that utilize a range of likely values for input parameters to assess the probable range of output parameters. Examples are Monte Carlo simulation, Latin hypercube sampling, discrete-event simulation, and boot-strapping methods.
-
Stochastic modeling approaches that directly incorporate the parameter or process uncertainties into the model itself and provide direct uncertainty estimates of model outputs.
-
Bayesian methods when uncertainties in input parameters can be specified by either expert judgment, or estimated from existing databases from which input parameter values have been determined.
Of these techniques, only FOUAs statistical sampling methods, and stochastic modeling techniques have been applied to vulnerability assessments. A description of the FOUA technique is presented in Box 3.1 and an example of the use of Monte Carlo methods in Box 3.2. Recent examples of first-order uncertainty analysis applied to a process-based index of vulnerability are reviewed below. Small and Mular (1987) and Jury and Gruber (1989) present examples of the applications of stochastic modeling approaches to evaluate uncertainty associated with climatic and soil variability in assessments of ground water vulnerability.
Applications of FOUA to Vulnerability Assessment
The earliest attempt to utilize spatial modeling techniques for regional-scale assessment of pesticide leaching potential was reported by Khan et al. (1986) and Khan and Liang (1989). They used two simple indices—the Retardation Factor (RF) and the Attenuation Factor (AF) developed by Rao et al. (1985)—as measures of leaching potential, and a GIS database—the Hawaii Natural Resource Information System (HNRIS) developed by Liang and Khan (1986)—in conducting an assessment for the Hawaiian island of Oahu. An example of the vulnerability maps generated by Khan and Liang (1989) is shown in Figure 3.3. The RF index is a measure of the relative time needed for a pesticide pulse to leach past some specified depth when compared to a nonsorbed tracer, whereas the AF index is the fraction of the
|
Box 3.1 First-Order Uncertainty Analysis First-order uncertainty analysis (FOUA) is a well-known method for evaluating error propagation when mathematical operations are performed to calculate values of some parameter of interest, referred to as the dependent or derived variable, given the values for a set of other variables, referred to as the independent variables. The objective is to estimate the uncertainty, such as variance, in the derived parameter given the error in the independent variables. Here, we will briefly examine the basis for FOUA approximation method and its application in estimating the uncertainty in numerical measures of ground water vulnerability calculated by simple methods. Consider some dependent variable, U, which is calculated as some function, f(X1, X2,…,Xk), of independent variables, X1, X2, … ,Xk. Given that  In case 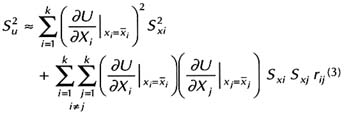 Usually in practice, if any of the independent variables is not distributed normally, some sort of transformation (usually, taking logarithms) will be necessary such that the transformed variable (say, log X) follows a normal frequency distribution. The FOUA technique is recommended when U can be specified by a differentiable and well-behaved function of the independent variables. Burrough (1986) and Heuvelink et al. (1989) presented examples of the application of the FOUA technique to a GIS-based spatial analysis. Loague et al. (1989, 1990) presented the first examples of the application of FOUA in regional assessments of ground water vulnerability. |
|
Box 3.2 Uncertainty in Pesticide Leaching Assessments The movement of pesticides to ground water is the end result of complex interactions involving physical, chemical, and biological processes which are further impacted by meteorologic conditions, soil and chemical characteristics, and agricultural practices. Movement within ground water (i.e., the saturated zone) is further affected by hydrogeological characteristics and conditions, in addition to the chemical characteristics of the pesticide. Most scientists recognize the uncertainty in attempting to quantify this complex system, yet attempts to quantify the uncertainty itself have been rare. The simulation models discussed in this chapter are primarily deterministic models that attempt to simulate the soil system without considering the inherent uncertainty in both the soil processes and system characteristics. Several attempts have been made to integrate the application of Monte Carlo techniques with simulation models for predicting pesticide leaching and migration processes within a framework that allows consideration of uncertainty in both process and soil and ground water system characterization. Carsel et al. (1988a) describe use of the Pesticide Root Zone Model (PRZM) (Carsel et al. 1984) in conjunction with probability distributions of soil characteristics in a simple screening procedure to assess pesticide leaching potential. National statistical distributions of selected soil parameters required by the model were generated from information on almost 3000 soil series in 40 states obtained from the U.S. Soil Conservation Service. Monte Carlo techniques were then used to generate randomized parameter sets, including SCS soil hydrologic group, weather data, pesticide degradation rate, and correlated values for field capacity, wilting point, and organic matter for each soil layer. The results of the 2,000 runs, for aldicarb application to corn in Ohio, were analyzed in a variety of ways, including cumulative distribution of aldicarb leached below selected depths in the soil as shown in Figure 3.1. This type of information indicates that, for the simulated conditions, in 97 percent of the simulations the model predicted that aldicarb residues of less than 0.1 kg/ha would leach below 1.5 m, and 99 percent of the simulations showed movement of less than 0.1 kg/ha below 3.0 m. Laskowski et al. (1990) described a procedure they called probability modeling for assessing the regional variations expected in pesticide-use impacts on ground water quality. Their scheme is similar to that used by Carsel et al. (1988a) and involves the use of a simulation model (PRZM) for predicting pesticide behavior in the soil. The regional variations in rainfall and temperature distribution patterns are represented by the outputs of a weather generator model, and the SCS soil survey database is used to generate soil property distributions. |
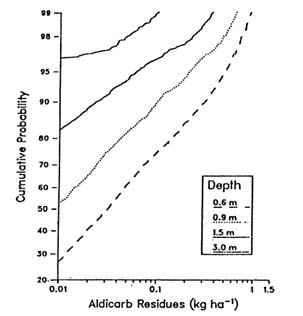
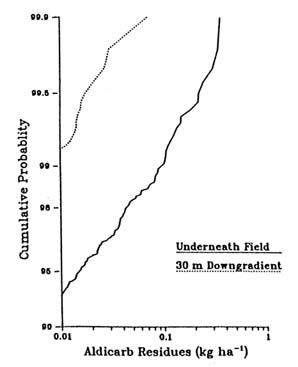 FIGURE 3.2 Cumulative probability distribution for aldicarb loadings underneath source area and 30 m downgradient for peanut production in North Carolina. (Carsel et al. 1988b. Reprinted, by permission, from Elsevier Science Publishers B.V., 1988.) were analyzed to compare residue remaining both beneath the field site and 30 m downgradient in the shallow surface aquifer, as shown in Figure 3.2. These results show that the residues 30 m downgradient were generally an order of magnitude less than they were beneath the field, and the downgradient values exceeded 0.01 kg/ha in less than 1 percent of the simulations. The output probability distributions produced by the integration of simulation modeling and Monte Carlo techniques allow consideration of uncertainties in soils properties, pesticide characteristics, meteorology, and hydrogeologic conditions of pesticide migration to and within ground water systems. This type of information will help managers make the types of decisions needed to protect vulnerable ground water regions with scarce resources. |
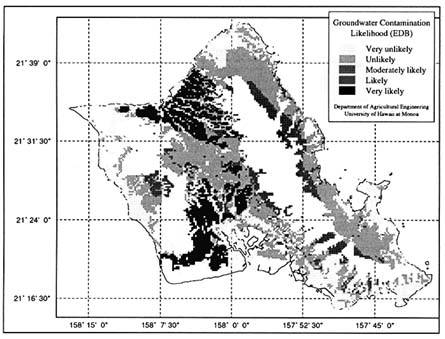
FIGURE 3.3 Map for Island of Oahu, Hawaii depicting relative vulnerability to ground water contamination with the pesticide ethylenedibromide (EDB). Vulnerability ratings are based on the values of retardation factor (RF), which is used as an index of pesticide leaching through soils. (Khan and Liang 1989. Reprinted, by permission, from Springer-Verlag, 1989.)
applied pesticide mass that is likely to leach past the depth of interest. Equations used for calculating RF and AF are shown in Table 3.8. The scales used to group contaminants on the basis of RF and AF indices in Figure 3.3 are entirely arbitrary.
Two principal assumptions made in deriving RF and AF indices must be noted: (1) water is assumed to move through the soil under steady, unsaturated conditions, with net ground water recharge rate (q) representing the steady flux, and (2) the soil profile is assumed to be homogeneous, where the soil property values used are depth-weighted averages. Computational schemes to eliminate both restrictions can be waived, as discussed by Rao et al. (1985). Model errors resulting from the use of these simple indices may be partially evaluated by comparing the ranking of the leaching potentials of several pesticides as determined from RF and AF with rankings from more rigorous model simulations. Of particular interest are evaluation of: (1) errors introduced by using annual recharge rate neglecting temporal
TABLE 3.8 Equations used to calculate the Retardation Factor (RF) and the Attenuation Factor (AF)
|
 |
variations in soil water and solute fluxes resulting from episodes of rainfall and irrigation, and (2) errors arising from use of depth-averaged soil properties in place of depth-varying values. Rao et al. (1985) and Kleveno et al. (1992) performed such evaluations and reached similar conclusions on the utility of the AF index for vulnerability assessments. Their results suggest that the relative order in which the pesticides were ranked in terms of their leaching potentials was not significantly different, whether the AF index or a more rigorous simulation model (e.g., CMLS, PRZM) was used. Thus, indices, such as AF, derived from simplified models may be adequate for vulnerability assessments because model errors are likely to be acceptable, in this case for relative rankings of contamination potentials.
Data errors, and their effects on uncertainty in vulnerability assessments, have been examined in some detail for the AF and RF indices. In particular, Loague and coworkers (Loague et al. 1989, 1990, Loague 1991, Kleveno et al. 1992) have used first-order uncertainty analysis (FOUA) to
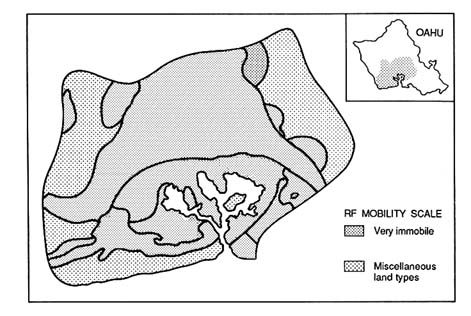
FIGURE 3.4a Map depicting the potential for ground water contamination with diuron herbicide at the Pearl Harbor basin. The relative vulnerability ratings are based on RF values, which is used as an index for pesticide mobility in soils. (Loague et al. 1990. Reprinted, by permission, from Elsevier Science Publishers B.V., 1990.)
illustrate the need for recognizing the uncertainties associated with delineating areas of different levels of vulnerability using these indices. An example of such uncertainty is shown by comparing Figures 3.4.a and 3.4.b. Figure 3.4a shows vulnerability ratings, developed using the RF index, for the herbicide diuron in the Pearl Harbor Basin of Hawaii. Figure 3.4.b is a rating map with one standard deviation subtracted from the RF. Estimates of uncertainty were determined by first-order uncertainty analysis of the pesticide parameter Koc and soil parameters (e.g., ![]() b, foc, and
b, foc, and ![]() FC). Note the large change in the RF map rating classes, largely resulting from uncertainty in foc and Koc.
FC). Note the large change in the RF map rating classes, largely resulting from uncertainty in foc and Koc.
The large change in vulnerability ratings shown in Figure 3.4b, caused simply by accounting for a single standard deviation due to data errors, suggests the need for considerable caution in making regulatory decisions that distinguish between vulnerabilities in adjacent cells. Such uncertainties, and the likely changes in vulnerability classification of a subregion, clearly have considerable impacts on regulatory policy or land use management. Deterministically derived pesticide rating maps can be attractive to
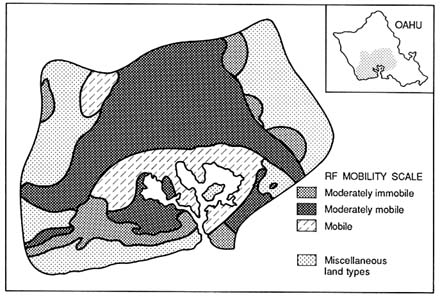
FIGURE 3.4b Uncertainty in vulnerability maps shown in Figure 3.4a is represented by the rating maps produced with one standard deviation subtracted from average RF values. (Loague et al. 1990. Reprinted, by permission, from Elsevier Science Publishers B.V., 1990.)
decision makers because they provide sharp boundaries that lead to definitive interpretations of relative vulnerability. However, pesticide rating maps that incorporate existing knowledge of data uncertainty are preferable to those that do not because they give decision makers additional information.
The practical significance of uncertainty analyses in providing reliable and cost-effective vulnerability assessments for resource managers and regulatory officials can be summarized as follows (Heuvelink et al. 1989):
-
Identification of spatial attributes that need to be measured more accurately to reduce uncertainty of the outputs to a specified level.
-
Identification of spatial attributes that are known too precisely (i.e., model outputs are insensitive to this input), so that fewer measurements need be made in future data collection efforts. Cost savings can be redirected to measurement of more sensitive attributes.
-
Determination of whether a simpler or a more sophisticated model is needed for reliable vulnerability assessment. Data requirements for complex models may be such that the variability in required input parameters is
-
large, or available data are unreliable, or the error propagation through the model greatly magnifies errors in the input data.
Uncertainty of Uncertainty Analyses
Uncertainty analyses require information on the statistical properties of the attributes used in vulnerability assessments. For example, to use FOUA it is necessary to know the mean values for the input parameters, their variances, and the correlations among them. Information on statistical frequency distributions of the input parameters is needed to implement Monte Carlo simulation techniques to assess uncertainties in model outputs. Other, more sophisticated stochastic techniques may require knowledge of the spatial structure of parameter variance and covariance.
In most practical situations, two types of problems are encountered in attempts to perform uncertainty analyses: (1) no information is available on uncertainty of the spatial attributes or model coefficients, and (2) uncertainty information extrapolated from other sources is often of questionable quality. Thus, in many cases uncertainty analyses cannot be performed or themselves contain uncertainty. Despite these limitations, uncertainty analyses should be done to the extent practicable when conducting vulnerability assessments and can be useful in determining the impact of different levels of uncertainty on the results of the vulnerability assessment. Uncertainty information should be presented as a part of the results.
TESTING AND EVALUATION OF VULNERABILITY ASSESSMENTS
Evaluation of a vulnerability assessment must address at least two questions:
-
Is the vulnerability rating assigned to a given subarea (a polygon or a cell) valid?
-
Are the values assigned to neighboring subareas sufficiently different?
Issues of data quality and the scientific basis for the method play dominant roles in answering these questions. The vulnerability index assigned to a polygon or a cell may be incorrect because the model is inappropriate or because the input data used are unreliable. Even if a model is valid locally, it is not necessarily reliable for regional-scale simulations. As noted earlier, since the confidence intervals associated with the vulnerability index assigned to a cell or a polygon can often be large (because of data and
model errors), we may not be able to distinguish differences in vulnerabilities of neighboring subareas.
General considerations in model testing and evaluation at the field scale are discussed in Box 3.3. Note that the term model, as used throughout this section, corresponds most directly to process-based assessment methods, but some of the concepts are also relevant to index or overlay methods.
One must be careful in extrapolating the experiences and results from field-scale testing of models to inferences of their applicability to regional scale assessments. One limitation is that the sites where a model has been tested may not be representative of the conditions throughout a region. Second, it is likely that the available data will be much more detailed at the field scale than at the regional scale. For comprehensive evaluation of a regional vulnerability assessment model, the application at the field-plot scale should be based on the same type and detail of data as exists at the regional-scale to the greatest extent possible.
Model validation and testing is more a process than an absolute yes or no result. According to Hern et al. (1986), ''… model development and subsequent validation is an evolutionary process by its very nature." It involves multiple assessments of the model's abilities to represent observed data under a range of conditions. Each time new data are observed to agree with the predictions of a model, confidence in that model is increased.
|
Box 3.3 Field-Scale Model Testing and Validation Models of contaminant transport through the vadose zone have received limited testing in real-world situations even at the field scale. Model testing and evaluation at the field scale is considered in greater detail by U.S. EPA (1982, 1989), Smith et al. (1988), and Donigian and Rao (1990). The field testing of models can be viewed as a systematic analysis of errors, including most of the uncertainties discussed earlier. In any model testing effort, the user is continually faced with the need to analyze and explain differences between observations and model predictions. This requires assessments of the accuracy and validity of observed model input data, parameter values, system representation, and observed output data. Model testing and evaluation against field data ideally should include three steps: calibration, validation, and postaudit. We say ideally because in many applications existing data will not support performance of all steps. In chemical-fate modeling, measured data |
|
for validation are often lacking and postaudit analyses are rare for any type of modeling exercise. Confusion surrounds model testing because of the different meanings that have been attached to the terms calibration, validation, etc. Here, we adopt the standardized concepts developed by the American Society for Testing and Materials (ASTM 1984). Calibration is probably the most misunderstood of all the model testing components. Calibration is the process of adjusting selected model parameters within an expected range until the differences between model predictions and field observations are within selected criteria for performance. For all operational deterministic models (or portions thereof), calibration is usually needed and highly recommended. Validation is the complement of calibration; model predictions are compared to field observations that were not used in model development or calibration. This is usually the second half of split-sample testing procedures, where the universe of data is divided (either in space or time), with a portion of the data used for calibration and the remainder used for validation. In essence, validation is an independent test of how well the model (with its calibrated parameters) is representing the important processes occurring in the natural system. Split-sample testing is common for surface-water models, but independent data sets may be difficult or impossible to obtain for ground water systems owing to the slowness of response times (NRC 1990, Konikow and Bredehoeft 1992). Verification and validation have been used interchangeably by many investigators, but the ASTM definition of verification is restricted to verifying the operation of the numerical procedures in the code. Postaudit Analyses are the ultimate tests of a model's predictive capabilities. Model predictions for a proposed alternative are compared to field observations following implementation of the alternative. The degree to which agreement is obtained, given the acceptance criteria, reflects both the model capabilities and the assumptions made by the user to represent the proposed alternative. However, postaudit analyses have been performed in only a few situations (Alley and Emery 1986, Konikow and Bredehoeft 1992). The recent U.S. EPA resolution (through its Science Advisory Board) on the use of models recognizes and advocates this view of model performance testing, as indicated in their quotation below: "The stepwise procedure of checking the numerical consistency (i.e., code verification) of a model, followed by field calibration, validation, and a posterior (postaudit) evaluation should be an established protocol for environmental quality models in all media, recognizing that the particular implementation of this may differ for surface water, air and ground water quality models" (EPA 1989) (Note: Parenthetical text added by authors). |
However, many investigators (e.g., Popper 1959) consider that a scientific hypothesis, such as a model, cannot be validated, but only invalidated. They argue that a good match between observations and model predictions does not prove the validity of the model. The match may be fortuitous owing to compensating errors in the model or erroneous observations. Conversely, a poor match does not necessarily mean the model is wrong or invalid. In reality, uncertainties and variabilities in measurements of the natural environment also limit the extent to which a model can be adequately tested to assess its validity, especially in the ground water arena.
The term validation itself may be part of the problem; inherently it implies a positive result—the model is valid for the conditions simulated. However, results showing lack of agreement between model and observed data are just as valuable, if not more valuable, because they help to demonstrate the bounds of applicability, or limitations, of the model. Ultimately, the purposes of model testing and evaluation are to identify the level of confidence in the form and structure of the model and to provide statements on the appropriate use of the model and its outputs.
Regional-Scale Testing and Evaluation
Ideally, regional vulnerability assessments could be tested against field observations of vulnerability to lead to improved methods and a better understanding of the factors affecting aquifer vulnerability to contamination. However, it is not possible to test regional vulnerability assessments in the same way that a field-scale simulation model can be tested, nor is it possible to make definitive statements about the predictive accuracy of one method compared to another at the regional scale. One difficulty is that a vulnerability assessment method may yield an index value or a probability, rather than a concentration. Thus, vulnerability, as treated in many methods, is not a property that can be directly measured in the field. A second difficulty is that to compare predicted values of vulnerability with observed constituent concentrations meaningfully one must either know the history of contaminant loading to the subsurface or assume that the contaminant loading has been spatially and temporally uniform. Neither situation is likely, except perhaps with a very small, well controlled field-plot study.
Despite these difficulties, and others noted below, inferences about the validity of a regional vulnerability assessment can be made through several lines of inquiry. Testing and evaluating vulnerability assessments may involve a hierarchical approach that evolves through several stages. In fact, the most sensible applications of vulnerability assessments may include explicit plans to test, review, and refine the assessment over time, perhaps over many years.
One approach to evaluating an assessment method is to compare the
concentrations or the percent detections of one or more contaminants among different vulnerability classes predicted by the method. An example is provided by Meeks and Dean (1990), who compared the frequency of detections of DBCP to a vulnerability index applied to part of the San Joaquin Valley in California (see Box 3.4).
The use of ground water quality data to examine differences among vulnerability classes should be done with considerable caution for a number of reasons. Some of these are:
-
The production zone of the well may be quite different from the reference location of the vulnerability method.
-
Differences in ground water quality observed among vulnerability classes may be an artifact of spatial and temporal variations in chemical loadings.
-
Short-circuiting of natural flow paths by movement down wells or their annuli can cause misleading results.
-
Contaminants introduced at or near the land surface may have had sufficient time to reach the water table but may do so at a future date if they are sufficiently persistent and mobile.
-
Information on well construction features, condition of the well, and location of the sampling point relative to water distribution, storage, or treatment are needed to evaluate the suitability of the well for sampling the constituents of concern. This information is incomplete for many wells. Information on the location of open interval(s) and the hydrogeologic unit(s) to which the well is open also may be lacking for many wells.
-
Temporal variations in water quality may be a complicating factor, particularly for wells in shallow aquifers or with significant variations in pumping.
-
Limitations in the protocols used for water quality monitoring may cause considerable uncertainty in the measured concentrations of constituents that are to be compared to model predictions.
As an example, some comparisons of ground water quality data with DRASTIC scores have been made using data from two national monitoring programs—the National Pesticide Survey (EPA 1992b) and the National Alachlor Well Water Survey (Holden et al. 1992). In both studies, little association between contamination by agricultural chemicals and DRASTIC scores was found, indicating that individual DRASTIC parameters were poorly correlated with contamination. The lack of association between contamination and the DRASTIC scores (or individual parameters) in these studies may reflect significant limitations in DRASTIC as a vulnerability assessment method. Conversely, the lack of association may be related to the problems listed above in relating ground water quality to vulnerability
|
Box 3.4 Evaluation of Regional Vulnerability Assessment Meeks and Dean (1990) have proposed an index, the Leaching Potential Index (LPI), defined as follows: LPI = [(103v / (R The utility of the LPI index for making regional-scale vulnerability assessments was evaluated by Meeks and Dean (1990) for a 381 square mile (975 km2) study area in Stockton East Water District in the San Joaquin Valley of central California. The study area was discretized into 381 township and range sections, and for each section  FIGURE 3.5 Geographic distribution of LPI ranks. (Meeks and Dean. 1990. Evaluating ground-water vulnerability to pesticides. Journal of Water Resources Planning and Management. Reprinted, by permission, from American Society of Civil Engineers, 1990.) |
|
the LPI value was calculated. The calculated LPI values ranged from 2 to 133 (a mean LPI value of 19.3), with a strongly skewed frequency distribution. This finding suggests that a vast majority of the sections have a small leaching potential, with only a few sections having high vulnerability rating. The sections were then ranked by the LPI index and grouped into areas of similar leaching potential. A map showing the geographic distribution of the vulnerability classes is shown in Figure 3.5. Note that sections rated very high and high are clustered in a three-mile wide (4.84 km wide) band corresponding to an area of sandy soils, high recharge rates, and shallow water tables. The next step in the Meeks and Dean (1990) assessment involved comparison of ground water quality monitoring data with the vulnerability ratings based on LPI values. The results from analyses of DBCP pesticide in ground water samples from wells throughout the study area were compiled; of the total 272 analyses, 202 were nondetects, while 70 were positive detections. The distribution of the negative and positive detects for the wells within each of the five areas grouped by vulnerability (plus urban areas, which were not rated) is shown in Table 3.9. The greatest percentage of positive detects was in areas rated as having very high or high vulnerability (45 and 50 percent, respectively), with progressively smaller percentage of positive detects for wells in areas with lower vulnerability. Despite this evidence of the validity of the vulnerability assessment, the areas identified as very high and high are perhaps the trivial cases, and in the absence of uncertainty information, further subdivision of the study area may not be defensible. |
TABLE 3.9 Percentage of Wells Tested with Detectable DBCP Categorized by Leaching Potential Index (Adapted from Meeks and Dean 1990. Evaluating ground-water vulnerability to pesticides. Journal of Water Resources Planning and Management. Reprinted, by permission, from American Society of Civil Engineers, 1990.)
|
Leaching Potential Category |
Number of Wells in which DBCP was Detected |
Number of Wells Tested |
Percentage of Tested Wells in which DBCP was Detected |
|
Very High |
17 |
38 |
45 |
|
High |
38 |
71 |
54 |
|
Moderate |
11 |
56 |
20 |
|
Low |
2 |
46 |
4 |
|
Very Low |
2 |
47 |
4 |
|
Urban |
0 |
16 |
0 |
|
Total |
70 |
272 |
26 |
indices. For example, the screened intervals for the wells in the studies are at a wide range of depths from the water table, and many of the wells, particularly the community water system wells in the National Pesticide Survey, are from deeper, confined aquifers. Note, however, that in the National Alachlor Well Water Survey, a simple measure of vulnerability (based on the most likely aquifer tapped) is associated with pesticide contamination despite a less than clear relationship between the well-specific DRASTIC score and pesticide occurrence.
In addition to evidence from ground water observations of chemicals introduced by humans, various types of geochemical data may be useful in evaluating a vulnerability assessment, particularly the intrinsic vulnerability of an aquifer system. The types of ions in solution and their concentrations result from chemical processes responding to the lithology and hydrologic flow pattern of a particular hydrologic system (Freeze and Cherry 1979). Thus, the ionic composition of water in different locations may be an important indicator of flow paths of water through the subsurface and, in some instances, of the sources of water. For example, in a study of part of the coastal plain in Maryland and Delaware, Hamilton and Denver (1990) found that areas affected by agricultural chemicals could be identified by a distinct chemical signature of major inorganic constituents. Furthermore, measurements of isotopic data may be useful in the evaluation process. For example, elevated levels of tritium (a hydrogen isotope associated with the atmospheric testing of nuclear weapons) indicate that at least part of the ground water withdrawn from a well originally recharged the system after the early 1950s and hence helps distinguish young water from older water. The use of environmental isotopes and selected other chemicals as indicators of young ground water is reviewed in Plummer et al. (1993).
Limitations of Ground Water Quality Sampling
Vulnerability approaches are calibrated and validated using measured concentrations of contaminants in samples of ground water. In addition to analytical errors, the accuracy of the water quality data is constrained by how ground water samples are taken (Nelson and Dowdy 1990). The methods for obtaining representative ground water samples are relatively controversial, and errors can occur when: (1) samples are inappropriately handled, preserved, or stored, (2) ground water chemistry is stratified with depth below the water table, (3) and different pumping and purging methods are used. In addition, errors related to inappropriate sample processing occur when air is accidentally introduced to the sample (changing the redox status, which affects solubility of dissolved metals) and when samples are not preserved for later analysis (bioactivity may affect nutrients, organic compounds,
and dissolved metals). Three further examples of limitations in obtaining representative ground water samples are briefly noted below.
Difficulties in Characterizing the Mobile Fraction of Contaminants
Many ground water samples have excess turbidity caused by clay and silt entrained in the water column during sampling. The suspended solids are difficult to remove without filtering the sample, and digestion of the suspended solids routinely results in anomalously high concentrations of metals and other solutes that may not be transported naturally in the flow field. Nevertheless, some federal and state environmental regulations stipulate that samples must not be prefiltered before analysis of the "mobile fraction (particularly metals)" because of the possibility of removing contaminants sorbed onto colloid-sized particles that otherwise might be ingested (e.g., Puls and Barcelona 1989a, b). To remove clays and other solids entrained during sampling, it is recommended that wells be screened with narrower slits and that finer grained material be packed around the exterior of the screened interval (Puls and Barcelona 1989a, b). In this case, samples are still filtered, but in situ, at the well screen rather than during or after sampling.
A balance must be reached between the ideal sampling protocol and the realities of monitoring numerous locations in heterogeneous soils. For example, Ryan and Gschwend (1990) recently used the combination of field light scattering methods, sampling and storage under anoxic conditions, and pumping rates lower than 100 ml/minute to evaluate the amount of trace metal transport associated with colloids in a sand aquifer. Research reported by Kearl et al. (1992) and Puls and Powell (1992) similarly suggests that ambient water without artifactual turbidity can be obtained when low pumping rates are used to sample monitoring wells. However, until such methods are more widely used, analyses for total concentrations of many substances of interest may be suspect.
Sampling Near the Water Table
The elevation of the water table rises and falls on a seasonal basis in many areas. To ensure that some water always enters water table monitoring wells, well screens are usually positioned partly above and partly below the water table. Thus when water levels are low, only a small water column will be in the screened portion of the monitoring well. When water levels are high, the water table will still be in the screen, although there will be a larger column of water in the well (Driscoll 1986). In many contamination cases, however, solute concentrations below the water table are not uniform,
but rather decrease or increase quick with depth below the water table. Therefore, measured contaminant concentrations will be affected by dilution, depending on how much of the water column below the water table is sampled and how the sample is obtained. Sampling error caused by screen placement relative to the water table has been evaluated by Robbins (1989), Robbins et. al. (1989), and Robbins and Martin-Hayden (1991). Robbins and colleagues conclude that concentrations of contaminants in water sampled from partially submerged well screens may be in error by orders of magnitude. To avoid these sampling problems, piezometers near the water table must be closer spaced vertically and have smaller screened intervals (e.g., Cherry 1983).
Purging and Pumping
Compounding the sampling problem is the process by which three to five casing volumes of water are purged from monitoring wells before a representative sample of ground water is collected. Empirical studies show that different pumping methods during purging produce different concentrations of contaminants (e.g., Gibb et al. 1981, Robin and Gillham 1987). Robbins and Martin-Hayden (1991) have used mass continuity models of monitoring well purging to show that the number of casing volumes cannot be set a priori without information on the degree of contaminant stratification in the aquifer. Given all the uncertainties of sampling, standard monitoring wells may in fact provide only relative qualitative information on the concentrations of many contaminants.
COMPUTING ENVIRONMENTS FOR VULNERABILITY ASSESSMENTS
Regardless of the approach chosen, a large quantity of data (attribute and geographic) are required to conduct a ground water vulnerability assessment. In addition, suitable analytical tools are needed to prepare, combine, study, and display the various components of the assessment. Numerous techniques have been used to perform these tasks, normally following advances in the allied fields of computer, graphic, and statistical sciences.
The earliest assessments were produced manually by compiling known information into an overall impression of the vulnerability of a certain area. Contaminated areas were studied and their site-specific environmental characteristics analyzed. Other areas with similar characteristics were then depicted as potential problem areas. Weighting of the various factors and regional differences were not generally included in these assessments.
More sophisticated assessments became possible with the advent of the
computer. More factors could be simultaneously compared to determine relative risk. Environmental conditions could be codified into models of vulnerability. Many of the original forms of this type of assessment used grid-cell based models partly to standardize data collection and partly owing to the technical requirements of the computer in the days of punch-card data entry. This form of assessment, still used by many researchers, offers a more systematic approach and is relatively easy to create. However, these grid-cell models are inflexible to data of varying resolutions and accuracies, cannot be applied to various scales, and generally oversimplify complex, real world situations.
Recently, a computer model has been developed that uses geography to relate data layers, thereby allowing simultaneous use of data of varying scales, accuracies, and extents. A geographic information system (GIS) combines spatial information (geographic coordinates) with attributes to more accurately depict natural or man-made phenomena. GIS may also provide a wide array of functions to access, manage, manipulate, and display data. Further description of GIS systems is provided in Box 3.5.
Use of GIS has been growing in recent years. Specifically, GIS have been useful in ground water analysis and other spatial applications by federal, state, and local governments and private organizations. Generally, GIS have been used to create digital geographic databases, to manipulate and prepare data as input for various model parameters, and to graphically display model output. Primarily these functions have supported overlay or index approaches, but new GIS functions that are available or under development could further support the analytical requirements of process-based approaches.
Building and Making Databases Available for Assessment Approaches
Ground water vulnerability assessments require the input of data into an assessment approach where they are manipulated or analyzed to produce a measure of vulnerability. The large volumes of data often needed have led to a growing demand for computerized data sets and the development of computerized databases.
Most GISs have significant geographic database building capabilities. Map digitizing, map scanning, database editing, and data importing and exporting are standard GIS database development features. GISs can apply spatial estimation and smoothing techniques to convert line area data (vector polygons) to cell data (rasters). For example, point data, such as weather station data, can be converted into area surface data through surface generation algorithms and then accessed as cell input parameters.
|
Box 3.5 Geographic Information Systems GIS is an integrating information technology that includes aspects of geography, surveying, mapping, cartography, photogrammetry, remote sensing, landscape architecture, and computer science. GIS technology links the characteristics of a place, a resource, or a feature with its spatial location. This linkage between the cartographic aspects of spatial information with characteristics or attributes of a resource or place creates an expanded database management system that could lead to new uses of emerging insights into the interrelationship between the environment and human activities. Geographic information systems are commonly described by the functions they perform; they collect, manage, analyze, and display spatially-referenced data and their associated attributes. These functions and their relationships in a GIS are illustrated in Figure 3.6. While each function is important to the operation of a system, the figure does not adequately capture their interaction in the technology. More useful may be a definition of the system—GIS is the computer hardware, specialized spatial database software, database management system, spatial and attribute databases, and applications software that is interfaced or integrated with the GIS software, the data, and the people necessary to operate the system. This definition is illustrated in Figure 3.7. GIS provides a computing environment for scientific investigation and for information management and utilization that is particularly conducive to data display and spatial data stratification. A wide selection of GIS software is available for either personal computers (PCs) or mainframes; the current computer preference is a workstation running some form of UNIX operating system. Software prices can range from $1,000 to $100,000, with a concomitant range 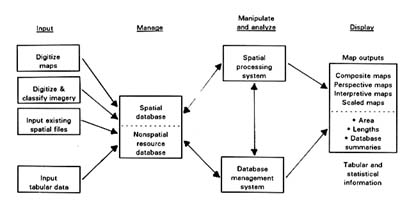 FIGURE 3.6 GIS functions and their relationships. |
Since GISs also manage nonspatial attribute databases that are linked to the spatial data, information such as soil characteristics can be made available to each spatial location (each cell) or other desired spatial model input parameter. Thus, numerous data sets on a variety of characteristics can be combined into a coordinated, georeferenced database. GISs can be used to derive additional data layers from original source materials. Functions are available that can combine two or more data files, either spatially or by recomputing attributes.
This concept of derived data simply reflects the fact that required parameters often have not been measured for a specific site or region, are not at the scale of the assessment, or are not identified as specific data parameters. These parameters must be estimated from derived database(s), or other measurements or interpolated and/or extrapolated from data points. Most process-based approaches include some parameters that are difficult or impossible to measure directly and so must be calculated or estimated by other means. Among the reasons:
-
It may be physically impossible to measure the parameter (e.g., diffusion coefficient).
-
Limited resources may preclude obtaining the number of measurements needed for the scale and/or time period of interest.
-
Point measurements may not have sufficient coverage for regional assessments, considering issues of spatial variability.
A number of automated procedures are available for estimating specific model parameters from existing databases. The most commonly used procedures estimate soil parameters from existing soil databases; examples are DBAPE, SOILPROP, and GRASS Waterworks. Data Base Analyzer and Parameter Estimator (DBAPE) (Imhoff et al. 1990), an U.S. Environmental Protection Agency product, is an interactive system designed to allow users to estimate soil parameters and develop meteorologic input for the EPA PRZM (Carsel et al. 1984) and RUSTIC (Dean et al. 1989) models using soils and meteorological databases. The soils database is a selected subset of the SCS national archival data system, NSSAD/SIRS (USDA 1985), that focuses only on agricultural soils. County soils information is included for almost 8,000 soil series with information on soil layering, soil texture class, percent sand, percent clay, bulk density, percent organic matter, available water, hydrologic soil group, and potential crops. From these basic data extracted from NSSAD/SIRS, DBAPE provides procedures for calculating model parameters for wilting point, water content at field capacity (0.1 and 0.33 bar tension), residual water content, saturated hydraulic conductivity, and soil water retention parameters from correlations developed by van Genuchten (1978), Rawls and Brakensiek (1985), and others.
The meteorologic data in DBAPE include a 25-year record of daily precipitation, air temperature, and wind speed for more than 200 NOAA weather stations across the country. Procedures are provided to calculate pan evaporation and solar radiation from these data for use by process-based simulation models.
SOILPROP is a proprietary program distributed by Scientific Software Group of Washington, D.C., that provides an interactive capability to estimate saturated hydraulic conductivity, soil water retention parameters, and associated uncertainty from particle size distribution information. The estimation procedures are similar to those used by DBAPE, but in addition covariances of parameter values are estimated using first-order error analysis. Input data must be supplied by the user since no database is associated with SOILPROP.
GRASS Waterworks (Vieux and Kang 1990) is GIS application software that performs analyses of spatial input parameters for hydrologic and water quality models. The program encompasses a generic set of analyses for hydrologic models, using spatial data sets and the GRASS GIS developed by the U.S. Army Corps of Engineers (U.S. Army Corps of Engineers 1988). GRASS Waterworks currently allows users to generate slope and aspect maps, delineate watershed boundaries and outlets, calculate land surface parameters (flow path length, average channel slope, watershed slope) from digital elevation data and do hydrologic modeling with the SCS TR-55 watershed model (USDA 1986). Although it is currently limited to surface parameters, linkages to other models and estimation of soil and vegetation parameters are planned in ongoing development efforts.
These three procedures—DBAPE, SOILPROP, and GRASS Waterworks—are examples of efforts to offset the lack of data for vulnerability assessments by using computerized databases and GIS technology to derive needed parameter values. These parameter derivation procedures are limited by the scale, accuracy, and validity of the basic data in the databases from which the parameters are calculated. More importantly, since the calculated values are simply estimates based on available information, they may introduce additional data errors into the vulnerability assessment. As discussed in the section on Uncertainty in Vulnerability Assessment Methods, such errors may substantially increase the uncertainty of the vulnerability assessment.
Geographical Display of Assessment Results
In most ground water vulnerability assessments, the results are portrayed on a map of the study area, typically in the form of polygons shaded or colored to depict the levels of vulnerability for all locations on the map. Too often, these maps oversimplify the results of the assessment or include
too much information and so confuse or mislead the viewer. Ineffective maps are due to a combination of poor definition of the purpose of the map, poor assessment of the viewers' knowledge, and poor cartographic skills. Attention to each of these factors and tests of alternative methods can lead to maps that more effectively portray the results of the assessment. GIS technology is a useful tool for creating vulnerability maps and for quick and simple testing of methods of display.
Vulnerability assessment maps typically have not conveyed the uncertainty arising from errors in data and assessment methods. With GIS, for example, a very poor assessment (in terms of errors) can be mapped in a manner that, though very sophisticated, misrepresents the quality of the assessment. Thus, ways should be developed to assist in displaying uncertainty as well as results.
GIS technology presently offers excellent capabilities for displaying vulnerability assessment results on maps. With improvements in assessment methods and uncertainty analyses, GIS may also prove useful for depicting associated uncertainties on these same maps. These improvements will require the collection of better information on data quality, development of techniques for visualizing component and net uncertainty of individual data layers, development of models of the propagation of error through the assessment process, and production of maps depicting these factors.
One way of depicting uncertainty is the case of a two-color vulnerability map showing areas of comparatively high and low vulnerabilities in red and green, respectively. Uncertainty could be indicated by variations in the intensity of the basic colors. A pale green could indicate high uncertainty for a low vulnerability area; intense green could indicate high confidence. As each of the two basic colors becomes paler, they could bleed into a white area representing high uncertainty. These white areas are expected in the zone separating a vulnerable region from a less vulnerable one. The uncertainty associated with the color intensities should be included on the map legend.
Analytical Functions
GIS technology can support ground water vulnerability assessments in the analysis and modeling of spatial and physical relationships of critical environmental elements. Functions such as map overlay, reclassification, and query assist in analyzing these conditions. Many simple models for surface water applications have been developed by federal, state, and local water authorities using only basic GIS tools.
One example is the use of GIS to compute soil loss using SCS's Universal Soil Loss Equation (USLE). USLE estimates average annual soil
loss in tons per acre as a product of factors representing climate (R), soil erodibility (K), topography (LS), vegetative cover (C), and supporting conservation practices (P). Actual soil loss (A) can be computed by the equation:
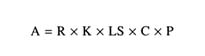
For each of these factors, an intermediate map layer is generated using GIS. Some of these maps are created by simply regrouping the classes on another map (e.g., soil mapping units on a soils map are regrouped into classes of erodibility to create an erodibility factor map). Maps for other factors are created by applying mathematical formulae between map layers. For example, the topography factor (LS) is computed from the steepness of slope (S) and the length of the slope (L), with the formula:
where, ![]() = slope length in feet;
= slope length in feet; ![]() = angle of slope; and m = 0.5 if the percent slope is 5 or more, 0.4 on slopes of 3.5 to 4.5 percent, 0.3 on slopes of 1 to 3 percent, and 0.2 on uniform gradients of less than 1 percent.
= angle of slope; and m = 0.5 if the percent slope is 5 or more, 0.4 on slopes of 3.5 to 4.5 percent, 0.3 on slopes of 1 to 3 percent, and 0.2 on uniform gradients of less than 1 percent.
Such equations can be solved with generic GIS tools, using the map layers to supply the variables. Likewise, to create a map of soil loss using GIS, the intermediate maps representing the five USLE factors are simply multiplied together, resulting in a map of estimated soil loss as well as the associated statistical data.
In these examples, the computations are applied across the map, with the equations applied independently for each point on the map. Although the concept of adding two maps or multiplying several maps may seem unusual, this is a routine capability of GIS technology and is duplicated in most non-GIS based approaches that attempt to deal with the spatial distribution of simple models like USLE.
New GIS functions and developments in related technologies have resulted in the ability to model environmental factors in a more sophisticated manner. Examples of these functions are:
-
Diffusion functions can be used to depict the migration of entities across surfaces based on attributes of those surfaces.
-
N-dimensional queries allow the user to interrogate the database for attribute information from multiple data layers at the same time, which is very useful in data visualization and model validation.
-
Neighborhood analysis develops information on the adjacency, size, and geometry of physical features to further model them and their relationship to other features.
-
Direct linkages between databases and software facilitate transfer of
-
up-to-date information among applications, which promotes collaboration rather than duplication of efforts among supporting technologies.
-
Software programs can transform an arduous set of commands into a simple procedure, thus providing sophisticated analyses to GIS novices.
Many GIS environments, however, still lack some of the basic analytical capabilities needed by modelers. For example, GIS analytical functions use static information and are run on demand. The dynamic nature of environmental phenomena is lost by these static models. Additionally, most GIS techniques today work only in two dimensions, which makes it difficult to visualize the relationships among surface and subsurface features. Some of these problems may be solved by software developments and should be reevaluated over time.
GIS technology can be used beneficially in ground water vulnerability assessments by supplying tools for encoding and producing geographic and attribute data, by computing spatial and attribute relationships, and by graphically portraying these relationships and model output. The technology can also be particularly useful to overlay and index methods by allowing various data layers to be integrated and/or weighted. Since GIS technology is designed to be adaptable to different technical and procedural requirements of vulnerability assessments, developments in the field can be expected to strengthen the support GIS can offer other assessment approaches.
SUMMARY
The methods used to assess ground water vulnerability range from simple overlay and index methods to more complicated process-based simulation models. Each method has advantages and limitations, and none is best for all situations.
Process-based models at the appropriate scale would be ideal in a perfect world, since they attempt to capture the true physical, chemical, and biological reactions that occur from the surface through the ground water regime. Process-based models, however, have not been demonstrated to be more effective than other techniques. The limitations of process-based models derive from model structure (i.e., lack of knowledge of how to formulate processes mathematically) and, more significantly, from limitations in data availability and quality. Furthermore, limited field experimentation with pesticide simulation models suggests that models based on simplified process representation may be more useful for many vulnerability assessments than more complicated models.
Most approaches for ground water vulnerability assessment assume undisturbed surficial deposits with spatially uniform percolation. Preferential flow paths, such as roots and worm holes, cracks, joints, and solution channels,
are ignored. Yet these may well be the fundamental pathways affecting vulnerability, providing more direct and rapid paths for contaminants to reach ground water than they would otherwise have. Recent literature suggests that under certain circumstances preferential flow can be a dominant phenomenon (cf., Roth et al. 1991), that it can occur in soils with no apparent structure (cf., Ghodrati and Jury 1990), and that it can channel virtually all of the water and chemical flux through a small portion of the matrix in highly permeable soils that have subsurface lenses in them (cf., Kung 1990a, b).
Statistical methods incorporate uncertainty and attempt to explicitly minimize error, but require observations of surrogates for vulnerability (e.g., ground water samples from shallow wells). Using these surrogates, the methods directly derive parameter coefficients instead of assigning weights to attributes based on expert judgment as is done in overlay and index methods. Parameters from simple process-based indices (e.g., travel times) could be used in statistical methods, making for a sort of hybrid approach. However, the results of these methods can only be applied to the geographic areas in which the data were collected to regions where similar factors are associated with the likelihood of ground water contamination.
Overlay and index methods have been developed because of limitations in process-based models and because of a lack of monitoring data required for statistical methods. Overlay and index methods are based on assumptions that a few major factors largely control ground water vulnerability and that these factors are known and can be weighted (explicitly in index methods or implicitly in overlay methods). These assumptions have not been demonstrated, particularly with respect to assigning weights to different factors.
In reviewing vulnerability assessment methods, it is useful to distinguish between (1) the ability to explain the factors and processes leading to potential contamination of ground water, and (2) the ability to predict likely contamination of ground water at the desired spatial scale. Research over the past two to three decades has contributed significantly to our knowledge and enables us to offer explanations of contamination of ground water. However, our ability to translate this understanding into reliable predictive models is not as sound. Although we can identify many of the factors leading to ground water contamination and construct process-based models that incorporate these parameters, our ability to apply these models in real-world situations is significantly limited.
The foregoing remarks suggest that predictions of ground water vulnerability are probabilistic—that is, we may be able to forecast the probability of ground water contamination over a given area, but the level of confidence in such forecasts for any particular location is quite low. Furthermore,
it is difficult, if not impossible, to test the validity of these predictions.
The challenge of vulnerability assessments resembles the problem of weather forecasting. For example, a forecast of a 70 percent chance of thunder showers in a specific location might be equated to identification of areas with high vulnerability. According to the National Weather Service, such a forecast does not predict rain at any given location or over the entire region, but only a 70 percent probability of rain somewhere (locations unspecified) in the region.
It can be argued that vulnerability assessments predict ground water contamination in a relative, not an absolute sense. That is, an assessment only identifies some areas in the region as more or less vulnerable than other areas. Uncertainty is pervasive in both spatial databases and computational schemes; as a result, all vulnerability assessments are inherently uncertain. It may be fairly easy to identify areas where ground water contamination is highly probable but not areas where it is highly improbable. For example, it is relatively easy to determine that ground water in a mature karst aquifer system or in a shallow sand and gravel alluvial aquifer is highly vulnerable to contamination. However, it may be much more difficult to demonstrate that ground water underlying a clay-rich unsaturated zone indeed has low vulnerability to contamination, because many factors difficult to quantify, such as preferential flow paths, may complicate the situation. Moreover, differentiation of areas that are not highly vulnerable to ground water contamination into more subtle distinctions in vulnerability is very difficult. This conclusion may be summarized as the Third Law of Ground Water Vulnerability:
The obvious may be obscured and the subtle indistinguishable.
Uncertainty in vulnerability assessments needs to be better recognized and revealed in the outputs. Assessment methods coupled with GIS and other sophisticated presentations can suggest greater knowledge than truly exists. Ways in which uncertainty could be better integrated into presentations include identifying the data sites used, developing companion uncertainty maps based on uncertainty analysis of data errors (these maps could be further broken down to show uncertainty associated with different parameters), and presentation of vulnerability maps generated by different methods. Maps produced by different methods, however, should be interpreted with caution as indicators of error because different methods use many of the same data and hence are not independent tests.
Vulnerability assessment is an interactive process that should be continually modified and improved using new information. Although assessment methods cannot be validated in the traditional sense, efforts to develop multiple lines of evidence for evaluating these assessments are encouraged.
Ground water quality data, however, should be used with considerable caution to examine differences among vulnerability classes, for a number of reasons. These include uncertainty in the reference location of the production zone of the well used to obtain the sample, uncertainty about the spatial and temporal variations in chemical loadings at the land surface, possible short-circuiting of natural flow paths by wells, and limitations in obtaining representative ground water samples from wells.
Several approaches for vulnerability assessments are available, and each has its own strengths, and limitations. All approaches combine uncertainty and should explicitly capture or reflect that uncertainty. Testing and evaluating these approaches is critical to producing a more justifiable, useful, and reasonable assessment.
REFERENCES
Aller, L., T. Bennett, J.H. Lehr, and R.J. Petty. 1985. DRASTIC: A Standardized System for Evaluating Ground Water Pollution Potential Using Hydrogeologic Settings. Ada, Oklahoma: U.S. Environmental Protection Agency.
Aller, L., T. Bennett, J.H. Lehr, R.J. Petty, and G. Hackett. 1987. DRASTIC: A Standardized System for Evaluating Ground Water Pollution Potential Using Hydrogeologic Settings. EPA-600/2-87-035. Ada, Oklahoma: U.S. Environmental Protection Agency.
Alley, W.M., and P.A. Emery. 1986. Ground water model of the Blue River basin, Nebraska—Twenty years Later. Journal of Hydrology 85:225-249.
American Society for Testing and Materials (ASTM). 1984. Standard Practice for Evaluating Environmental Fate Models of Chemicals, 1978-84. Philadelphia, Pennsylvania: American Society for Testing and Materials.
Back, R.C., R.R. Romine, and J.L. Hansen. 1984. Rating system for predicting the appearance of temik aldicarb residues in potable water. Environmental Toxicology and Chemistry 3:589-597.
Banton, O., and J.P. Villeneuve. 1989. Evaluation of ground water vulnerability to pesticides: A comparison between the quantities. Journal of Contaminant Hydrology 4:285-296.
Berg, R.C., and J.P. Kempton. 1988. Stack-Unit Mapping of Geologic Materials in Illinois to a Depth of 15 Meters. Champaign: Illinois State Geological Survey Circular 542.
Berryman, D., B. Bobée, D. Cluis, and J. Haemmerli. 1988. Nonparametric approaches for trend detection in water quality time series. Water Resources Bulletin 24(3):545-556.
Beven, K. 1991. Modeling preferential Flow: An uncertain future? In Preferential Flow, T.J. Gish and A. Shirmohammadi, eds. Proceedings National Symposium, December 16-17, 1991. St. Joseph, Michigan: American Society of Agricultural Engineers.
Bowman, R.S., and R.C. Rice. 1986. Accelerated herbicide leaching resulting from preferential flow phenomenon and its implications for ground water contamination. In Proceedings of the Conference on Southwestern Ground Water Issues, Pheonix, Arizona, October 20-22, 1986. Dublin, Ohio: National Water-Well Association.
Brandstetter, A., and B.E. Buxton. 1989. The role of geostatistical, sensitivity and uncertainty analysis in performance assessment. Pp. 89-220 in Geostatistical, Sensitivity, and Uncertainty Methods for Ground Water Flow and Radionuclide Transport Modeling, B.E. Buxton, ed. Conf-870971, Columbus, Ohio: Battelle Press.
Burrough, P.A. 1986. Principles of Geographical Information Systems for Land Resource Assessment. Monographs on Soil and Resources Survey No. 12. Oxford, U.K.: Oxford Science Publications, Clarendon Press.
Butters, G.L., W.A. Jury, and F.F. Ernst. 1989. Fieldscale transport of bromide in an unsaturated soil: I. Experimental methodology and results. Water Resources Research 25:1575-1582.
Buxton, B.E., ed. 1989. Geostatistical, Sensitivity, and Uncertainty Methods for Ground-Water Flow and Radionuclide Transport Modeling. Conf-870971. Columbus, Ohio: Battelle Press.
Carsel, R.F., C.N. Smith, L.A. Mulkey, J.D. Dean, and P. Jowise. 1984. User's Manual for the Pesticide Root Zone Model (PRZM): Release 1. Athens, Georgia: U.S. Environmental Protection Agency, Environmental Research Laboratory.
Carsel, R.F., R.S. Parrish, R.L. Jones, J.L. Hansen, and R.L. Lamb. 1988a. Characterizing the uncertainty of pesticide leaching in agricultural soils. Journal of Contaminant Hydrology 2:111-124.
Carsel, R.F., R.L. Jones, J.L. Hansen, R.L. Lamb, and M.P. Anderson. 1988b. A simulation procedure for ground water quality assessments of pesticides. Journal of Contaminant Hydrology 2(2):125-138.
Chen, H., and A.D. Druliner. 1988. Agricultural Chemical Contamination of Ground Water in Six Areas of the High Plains Aquifer, Nebraska. National Water Summary 1986—Hydrologic Events and Ground-Water Quality . Water-Supply Paper 2325. Reston, Virginia: U.S. Geological Survey.
Cherry, J.A. 1983. Piezometers and other permanently installed devices for ground water quality monitoring. Pp. IV-1 to IV-39 in Proc.: Petroleum Association for Conservation of the Canadian Environment, Seminar on Ground water and Petroleum Hydrocarbons Protection, Detection, Restoration. Ottawa.
Chrisman, N.R. 1984. The role of quality information in long-term functioning of geographical information systems. Cartographica 21:79-87.
Cohen, D.B., C. Fisher, and M.L. Reid. 1986. Ground-water contamination by toxic substances: A California assessment. Pp. 499-529 in Evaluation of Pesticides in Ground Water, W.Y. Garner, R.C. Honeycutt, and H.N. Nigg, eds. ACS Symp. Series 315, Washington, D.C.: American Chemical Society.
Dean, J.D., P.S. Huyakorn, A.S. Donigian, Jr., K.A. Voos, R.W. Schanz, Y.J. Meeks, and R.F. Carsel. 1989. Risk of Unsaturated/Saturated Transport and Transformation of Chemical Concentrations (RUSTIC). Volumes I and II. EPA/600/3-89/048a. Athens, Georgia: U.S. Environmental Protection Agency.
Dixon, W.J. 1986. Extraneous values. Pp. 83-90 in Methods of Soil Analysis, Part I, Physical and Mineralogical Properties, Second Edition, A. Klute, ed. Agronomy Servies No. 9. Madison, Wisconsin: American Society of Agronomy.
Donigian, A.S., Jr., and P.S.C. Rao. 1990. Selection, application, and validation of environmental models. Pp. 577-600 in Proceedings of the International Symposium on Water Quality Modeling of Agricultural Nonpoint Sources, Part 2. ARS-81. Washington, D.C.: USDA Agricultural Research Service.
Donigian, A.S., Jr., J.C. Imhoff, and B.R. Bicknell. 1983. Modeling Water Quality and the Effects of Agricultural Best Management Practices in Four Mile Creek, Iowa. Athens, Georgia: U.S. Environmental Protection Agency.
Driscoll, F.G. 1986. Ground water and Wells. St. Paul, Minnesota: Johnson Division, UOP.
Eisenberg, N.A., L.D. Richerstein, and C. Voss. 1989. Performance assessment, site characterization, and sensitivity and uncertainty methods: Their necessary association for licensing. Pp. 9-38 in Proceedings of the Conference on Geostatistical, Sensitivity, and Uncertainty Methods for Ground-Water Flow and Radionuclide Transport Modeling, B.E. Buxton, ed. Conf-870971. Columbus, Ohio: Battelle Press.
Enfield, C.G., R.F. Carsel, S.Z. Cohen, T. Phan, and D.M. Walters. 1982. Approximating pollutant transport to ground water. Ground Water 20(6):711-722.
Freeze, R.A., and J.A. Cherry. 1979. Ground water. Englewood Cliffs, New Jersey: Prentice-Hall.
Germann, P.F., ed. 1988. Rapid and far-reaching hydrologic processes in the vadose zone. Journal of Contaminant Hydrology 3:115-380.
Ghodrati, M., and W.A. Jury. 1990. A field study using dyes to characterize preferential flow of water. Soil Science Society of America Journal 54:1558-1563.
Gibb, J.P., R.M. Schuller, and R.A. Griffin. 1981. Procedures for the Collection of Representative Water Quality Data from Monitoring Wells, Cooperative Ground Water Report 7. Champaign: Illinois State Water Survey.
Goodchild, M.F., and O. Dubuc. 1987. A model of error for choroplett maps, with applications to geographic information systems. Pp. 165-172 in Proc. Auto-Carto 8. Falls Church, Virginia: Amer. Congress of Surveying and Mapping.
Goodchild, M.F., and W. Min-hua. 1988. Modeling error in raster-based spatial data. Pp. 97-106 in Proc. Third Internal. Symp. Spatial Data Handling. Sydney, Australia.
Hamilton, P.A., and J.M. Denver. 1990. Effects of land use and ground-water flow on shallow ground-water quality, Delmarva Peninsula, Delaware, Maryland, and Virginia. Ground Water 28(5):789.
Hern, S.C., S.M. Melancon, and J.E. Pollard. 1986. Generic steps on the field validation of vadose zone fate and transport models. In Vadose Zone Modeling of Organic Pollutants, S.C. Hern and S.M. Melancon, eds. Chelsea, Michigan: Lewis Publishers, Inc.
Heuvelink, G.B.M., P.A. Burrough, and A. Stein. 1989. Propagation of errors in spatial modeling with GIS. Int. Jour. Geographical Information Systems 3(4):303-322.
Hipel, K.W. 1988. Nonparametric approaches to environmental impact assessment. Water Resources Bulletin 24(3):487-492.
Holden, L.R., J.A. Graham, R.W. Whitmore, W.J. Alexander, R.W. Pratt, S.F. Liddle, L.L. Piper. 1992. Results of the national alachlor well water survey. Environmental Science and Technology 26(5):935-43.
Hoyer, B.E., and G.R. Hallberg. 1991. Ground water Vulnerability Regions of Iowa, Special Map 11. Iowa City: Iowa Department of Natural Resources.
Imhoff, J.C., B.R. Bicknell, and A.S. Donigian, Jr. 1983. Preliminary Application of HSPF to the Iowa River Basin to Model Water Quality and the Effects of Agricultural Best Management Practices. EPA Contract No. 68-03-2895. Athens, Georgia: U.S. Environmental Protection Agency.
Imhoff, J.C., R.F. Carsel, J.L. Kittle, Jr., and P.R. Hummel. 1990. Data Base Analyzer and Parameter Estimator, DBAPE (User's Manual). EPA/600-3-89-083. Athens, Georgia: Environmental Research Laboratory, U.S. Environmental Protection Agency.
Johnston, R.H. 1988. Factors Affecting Ground-Water Quality. National Water Summary 1986: Hydrologic Events and Ground-Water Quality. Water-Supply Paper 2325. Reston, Virginia: U.S. Geological Survey.
Jones, R.L., P.S.C. Rao, and A.G. Hornsby. 1983. Fate of aldicarb in florida citrus soils: 2. Model evaluation. Pp. 959-978 in Proceedings of a Conference of Characterization and Monitoring in the Vadose (Unsaturated) Zone, D.M. Nielson, and M. Curl, eds. Dublin, Ohio: National Water Well Association.
Jury, W.A., and H. Flüher. 1992. Transport of chemicals through soil: Mechanisms, models, and field applications . Advances in Agronomy 47:141-201.
Jury, W.A., and M. Ghodrati. 1989. Overview of organic chemical environmental fate and transport modeling approaches. Pp. 271-304 in Reactions and Movement of Organic Chemicals in Soils, B.L. Sawhney, and K. Brown, eds. Special Publication No. 22. Madison, Wisconsin: Soil Science Society of America.
Jury, W.A., and J. Gruber. 1989. A stochastic analysis of the influence of soil and climatic variability on the estimate of pesticide ground water pollution potential. Water Resources Research 25(12):2465-2474.
Jury, W.A., W.F. Spencer, and W.J. Farmer. 1983. Behavior assessment model for trace organics in soil: I. Description of model. Journal of Environmental Quality 12:558-564.
Kearl, P.M., N.E. Korte, and T.A. Cronk. 1992. Suggested modifications to ground water sampling procedures based on observations from the colloidal baroscope. Ground Water Monitor Review 12:155-161.
Kellogg, R.L., M.S. Maizel, and D.W. Goss. 1992. Agricultural Chemical Use and Ground Water Quality: Where Are the Potential Problems? Washington, D.C. : U.S. Department of Agriculture, Soil Conservation Service.
Kempthorne, O., and R.R. Allmaras. 1986. Errors and variability of observations. Pp. 1-32 in Methods of Soil Analysis, Part 1. Physical and Mineralogical Methods, Agron. Monograph, No. 9 (2nd edition). Madison, Wisconsin: American Society of Agronomy.
Khan, M.A., and T. Liang. 1989. Mapping pesticide contamination potential. Environmental Management 13(2):233-242.
Khan, M.A., T. Liang, P.S.C. Rao, R.E. Green. 1986. Use of an interactive computer graphics and mapping system to assess the potential for ground water contamination with pesticides. EOS 67(16):278.
Kissel, D.E., O.W. Bidwell, and J.F. Kientz. 1982. Leaching Classes in Kansas Soils. Bulletin No. 641. Manhatten, Kansas: Kansas State University.
Kleveno, J.J., K. Loague, and R.E. Green. 1992. Evaluation of a pesticide mobility index: Impact of recharge variation and soil profile heterogeneity. Journal of Contaminant Hydrology 11(1-2):83-99.
Knisel, W.G., R.A. Leonard, and F.M. Davis. 1989. GLEAMS User Manual. Tifton, Georgia: Southeast Watershed Research Laboratory.
Konikow, L.F., and J.D. Bredehoeft. 1992. Ground-water models cannot be validated. Advances in Water Resources 15:75-83.
Kung, K.S. 1990a. Preferential flow in a sandy vadose zone: 1. Field observations. Geoderma 46:51-58.
Kung, K.S. 1990b. Preferential flow in a sandy vadose zone: 2. Mechanism and implications. Geoderma 46:59-71.
Laskowski, D.A., P.M. Tillotson, D.D. Fontaine, and E.J. Martin. 1990. Probability Modelling. London: Phil. Trans. Royal Society B329:383-389.
Leonard, R.A., W.G. Knisel, and D.A. Still. 1987. GLEAMS: Ground water loading effects of agricultural management systems. Trans. Amer. Soc. Agric. Eng. 30:1403-1418.
Liang, T., and M.A. Khan. 1986. A natural resource information system for agriculture. Agricultural Systems 21:81-105.
Loague, K. 1991. The impact of land use on estimates of pesticide leaching potential: Assessments and uncertainties. Journal of Contaminant Hydrology 8:157-175.
Loague, K., and R.E. Green. 1991. Statistical and graphical methods for evaluating solute transport models: Overview and application. Journal of Contaminant Hydrology 7:51-73.
Loague, K.M., R.S. Yost, R.E. Green, and T.C. Liang. 1989. Uncertainty in a pesticide leaching assessment for Hawaii. Journal of Contaminant Hydrology 4:139-161.
Loague, K., R.E. Green, T.W. Giambelluca, T.C. Liang, and R.S. Yost. 1990. Impact of uncertainty in soil, climatic, and chemical information in a pesticide leaching assessment. Journal of Contaminant Hydrology 5:171-194.
McKenna, D.P., and D.A. Keefer. 1991. Potential for Agricultural Chemical Contamination of Aquifers in Illinois. Open File 1991-7R. Champaign: Illinois State Water Survey.
McLean, J.E., R.C. Sims, W.J. Doucette, C.R. Caupp, and W.J. Girenney. 1988. Evolution of mobility of pesticides in soil using U.S. EPA methodology. ASCE. Journal of Environmental Engineering 114(3):689-703.
Mead, D.A. 1982. Assessing data quality in geographic information systems. Pp. 51-62 in
Remote Sensing for Resource Management, C.J. Johansen, and J.L. Sanders, eds. Ankeny, Iowa: Soil Conservation Society of America.
Meeks, Y.J., and J.D. Dean. 1990. Evaluating ground-water vulnerability to pesticides. Journal of Water Resources Planning and Management 116(5):693-707.
Moore, J.S. 1988. SEEPPAGE: A System for Early Evaluation of Pollution Potential of Agricultural Ground Water Environments. Geology Technical Note 5 (Revision 1). Washington, D.C.: U.S. Department of Agriculture, Soil Conservation Service.
Moreau, D.H., and L.E. Danielson. 1990. Agricultural Pesticides and Ground Water in North Carolina: Identification of the Most Vulnerable Areas. North Carolina: Water Resources Research Institute of the University of North Carolina, North Carolina State University.
National Research Council (NRC). 1990. Ground Water Models: Scientific and Regulatory Applications. Washington, D.C.: National Academy Press.
Nelson, D.W., and R.H. Dowdy, eds. 1990. Methods for ground water quality studies. In Proc. National Workshop, Arlington, VA, November 1-3 , 1989. Lincoln, Nebraska: University of Nebraska—Lincoln Press.
Nicholls, P.H., R.H. Bromilow, and T.A. Addiscott. 1982a. Measured and simulated behavior of fluometuron, aldoxycarb, and chloride ion in a fallow structured soil. Pesticide Science 12:475-483.
Nicholls, P.H., A. Walker, and R.J. Baker. 1982b. Measurement and simulation of the movement and degradation of atrazine and metribuzin in a fallow soil. Pesticide Science 12:484-494.
Nofziger, D.L., and A.G. Hornsby. 1986. A microcomputer-based management tool for chemical movement. Soil. App. Agr. Res. 1:50-56.
Pedroli, B. 1990. Classification of Shallow ground water types in a dutch covers and landscape. Journal of Hydrology 115:361-375.
Pennell, K.D., A.G. Hornsby, R.E. Jessup, and P.S.C. Rao. 1990. Evaluation of five simulation models for predicting aldicarb and bromide behavior under field conditions. Water Resources Research 26(11):2679-2693.
Pettyjohn, W.A., M. Savoca, and D. Self. 1991. Regional Assessment of Aquifer Vulnerability and Sensitivity in the Conterminous United States . Report EPA-600/2-91/043. Ada, Oklahoma: U.S. Environmental Protection Agency.
Plummer, L.N., R.L. Michel, E.M. Thurman, and P.D. Glynn. 1993. Environmental tracers for age-dating young ground water. Pp. 255-294 in Regional Ground-Water Quality, W.M. Alley, ed. New York: Van Nostrand Reinhold.
Popper, K. 1959. The Logic of Scientific Discovery. New York: Harper and Row.
Puls, R. W., and M.J. Barcelona. 1989a. Filtration of ground water samples for metals analysis. Hazardous Waste & Hazardous Materials 6(4):385-393.
Puls, R.W., and M.J. Barcelona. 1989b. Ground Water Sampling for Metals Analysis. Superfund Ground Water issue. U.S. Environmental Protection Agency.
Puls, R.W., and R.M. Powell. 1992. Acquisition of representative ground water quality samples for metals. Ground Water Monitoring Reviews 12:167-176.
Rao, P.S.C., A.G. Hornsby, and R.E. Jessup. 1985. Indices for Ranking the Potential for Pesticide Contamination of Ground water . Soil Crop Science Society Florida Proceedings 44:1-8.
Rawls, W.J., and D.L. Brakensiek. 1985. Prediction of Soil Water Properties for Hydrological Modeling. In Proc. Symposium of Committee of Watershed Management, Irrigation and Drainage Div., ASCE Convention, Denver, CO.
Riley, J.A., R.K. Steinhorst, G.V. Winter, and R.E. Williams. 1990. Statistical analysis of the hydrochemistry of ground waters in Columbia River basalts. Journal of Hydrology 119:245-262.
Robbins, G.A. 1989. Influence of using purged and partially penetrating monitoring wells on contaminant detection, mapping, and modeling. Ground Water 27(2):155-162.
Robbins, G.A., and J.M. Martin-Hayden. 1991. Mass balance evaluation of monitoring well purging: I. Theoretical models and implications for representative sampling. Journal of Contaminant Hydrology 8:203-24.
Robbins, G.A., R.D. Bristol, J.M. Hayden, and J.D. Stuart. 1989. Mass continuity and distribution implications for collection of representative ground water samples from monitoring wells. Pp. 125-140 in Proceedings of the Conference on Petroleum Hydrocarbons and Organic Chemicals in Ground Water: Prevention, Detection, and Restoration. Dublin, Ohio: National Water Well Association.
Robin, M.J.L., and R.W. Gillham. 1987. Field evaluation of well purging procedures. Ground Water Monitoring Review 7:85-93.
Roth, K., W.A. Jury, H. Flüher, and W. Attinger. 1991. Transport of chloride through an unsaturated field soil. Water Resources Research 27(10):2533-2541.
Rupert, M., T. Dace, M. Maupin, and B. Wicherski. 1991. Ground Water Vulnerability Assessment: Snake River Plain, Southern Idaho. Boise: Idaho Department of Health and Welfare.
Ryan, J.N., and P.M. Gschwend. 1990. Colloid mobilization in two Atlantic coastal plain aquifers: Field studies. Water Resources Research 26:307-322.
Sacha, L., D. Fleming, and H. Wysocki. 1987. Survey of Pesticides in Selected Areas Having Vulnerable Ground Waters in Washington State. EPA/910/9-87/169. Seattle, Washington: U.S. Environmental Protection Agency, Region X.
Seyhan, E., A.A. van de Griend, and G.B. Engelen. 1985. Multivariate analysis and interpretation of the Hydrochemistry of a Dolomitic Reef Aquifer, Northern Italy. Water Resources Research 21(7):1010-1024.
Small, M.J., and J.R. Mular. 1987. Long-term pollutant degradation in the unsaturated zone with stochastic rainfall infiltration. Water Resources Research 23:2246-2256.
Smith C.N., R.S. Parrish, R.F. Carsel, A.S. Donigian, Jr., and J.M. Cheplick. 1988. Validation Status of Pesticide Leaching and Ground water Transport Model. Athens, Georgia: U.S. Environmental Protection Agency, Environmental Research Laboratory.
Steenhuis, T.S., S. Pacenka, and K.S. Porter. 1987. MOUSE: A management model for evaluation ground water contamination from diffuse surface sources aided by computer graphics. Appl. Agr. Res. 2:277-289.
Teso, R.R., T. Younglove, M.R. Peterson, D.L. Sheeks, III, and R.E. Gallavan. 1988. Soil taxonomy and surveys: Classification of areal sensitivity to pesticide contamination of ground water. Journal of Soil and Water Conservation 43(4):348-352.
U.S. Army Corps of Engineers. 1988. GRASS, Geographic Resource Analysis Support System Version 3.0. Champaign, Illinois: Construction Engineering Research Laboratory.
U.S. Department of Agriculture (USDA). 1985. User Manual for Interactive Soils Data Bases: National Soil Survey Area Data Base, Soil Interpretations Record Data Base and Plant Name Data Base. Fort Collins, Colorado: USDA, Soil Conservation Service.
U.S. Department of Agriculture (USDA). 1986. Urban Hydrology for Small Watersheds, TR-55. USDA, Soil Conservation Service.
U.S. Environmental Protection Agency (EPA). 1982. Exposure modeling committee report: Testing for the field applicability of chemical exposure models. In Proc. Workshop on Field Applicability Testing. Athens, Georgia: U.S. EPA.
U.S. Environmental Protection Agency (EPA). 1989. Resolution on Use of Mathematical Models by EPA for Regulatory Assessment and Decision-Making. Prepared by the Environmental Engineering Committee of the Science Advisory Board. EPA-SAB-EEC-89012. Washington, D.C.: U.S. Environmental Protection Agency.
U.S. Environmental Protection Agency (EPA). 1992a. A Review of Methods for Assessing
Aquifer Sensitivity and Ground-Water Vulnerability to Pesticides. Contract No. 68-C0-0083. Raleigh, North Carolina: Geraghty & Miller, Inc.
U.S. Environmental Protection Agency (EPA). 1992b. Another Look: National Survey of Pesticides in Drinking Water Wells Phase II Report. Washington, D.C.: U.S. Environmental Protection Agency.
van Genuchten, M.T. 1978. Calculating the Unsaturated Hydraulic Conductivity with a New Closed-Form Analytical Model. 78-WR-08. Princeton, New Jersey: Water Resources Program, Department of Civil Engineering, Princeton University.
Vieux, B.E., and Y.T. Kang. 1990. GRASS Waterworks: A GIS Toolbox for Watershed Hydrologic Modeling. Proceedings of Application of GIS, Simulation Models, and Knowledge-Based Systems for Land Use Management. November 12-14, 1990. Blacksburg: Virginia Polytechnic and State University.
Villeneuve, J., O. Banton, P. Lafrance, and P.G.C. Cambell. 1987. A new model for the evaluation of ground water vulnerability to non-point contamination by pesticides. Pp. 1097-1109 in Vulnerability of Soil and Ground water to Pollutants, W. van Duijvenbooden and H.G. van Waegeningh, eds. The Hague, Netherlands: TNO Committee on Hydrological Research., National Institute of Public Health and Environmental Hygiene.
Wagenet, R.J., and J.L. Hutson. 1987. LEACHM: A Finite-Difference Model for Simulating Water, Salt, and Pesticide Movement in the Plant Root Zone, Continuum 2. Ithaca: New York State Resources Institute, Cornell University.
Wagenet, R.J., and P.S.C. Rao. 1990. Modeling pesticide fate in soil. Pp. 357-399 in Pesticides in the Soil Environment, SSSA Book Series No. 2, H.H. Cheng, ed. Madison, Wisconsin: Soil Science Society of America.
Wisconsin Department of Natural Resources, and Wisconsin Geological and Natural History Survey. 1987. Ground water Contamination Susceptibility in Wisconsin. Madison: Wisconsin Geological and Natural History Survey.