The Taxman
|
Develop strategies based on systematic analysis Present convincing arguments Use uniform introduction for all classes Generalize from specific cases |
Suggested time allotment
One class period
Student social organization
Working alone or in pairs, following a videotaped introduction
Task
Assumed background: This task assumes that children are familiar with the concept of factors of whole numbers and, in particular, with prime numbers. It also assumes that they have had some experience in developing multi-step strategies and in articulating those strategies coherently.
Presenting the task: The problem is to analyze a game that we assume is unfamiliar to the children. Hence the first task for the teacher is to introduce the rules of the game. One way of doing this is to show a videotape in which a teacher shows a small group of

children how the game of Taxman is played. The script for such a videotape is given below. (If a tape is not available, the classroom teacher can use the script as a guide to introducing the game.)
The scene opens in a classroom setting, with a teacher and a group of six students. There is a chalkboard on one wall.
Teacher: Today I'm going to show you how to play a new number game, called Taxman. The game is played with a list of numbers starting with the number one. For example, the Taxman game with six numbers would start with this list: [Teacher writes list on chalkboard]
There are two players, You and the Taxman. Every time it is your turn, you can take any number in the list, as long as at least some factors of that number are also in the list. You get your number, and the Taxman gets all of the factors of that number that are in the list. For example, if you take 4, …
Student A: … then the Taxman would get 2!
Teacher: Why?
Student A: Because 2 is a factor of 4.
Student B: The Taxman'd get 1, too.
Student C: Oh, yeah, because 1's a factor of 4.
Teacher: So if you took 4, then the list would look like this: [writes]
Now you have 4 points …
Student D: … and the Taxman has 3 points. [Teacher writes]

Teacher: So, the first rule of the Taxman game is:
|
1. |
The Taxman must get something every time. |
|
That means you can't choose if there aren't any factors of that number still in the list. The only other rule is this: |
|
|
2. |
When none of the numbers in the list has any factors left in the list, then the game is over, and the Taxman gets all the numbers that are left in the list. |
Student E: I don't get the second rule.
Teacher: Let's play a game together to see what this second rule means. We'll use the same list:
What would you like to start with?
Student F: 6. [Teacher gives chalk to Student F, who crosses off the "6" and records 6 points for You.]
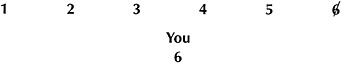
Student A: So the Taxman gets 3 and 2 [crosses them off the list] …
Student B: … and 1 [crosses off 1 and updates the score].

Student F: So now you could take 5.
Student E: No you can't! 5 doesn't have any factors that are left on the list.
Student F: Oh, OK. The 1's not there any more. How about 4?
Student D: That won't work either. The factors of 4 are 1 and 2, and they're both gone already.
Student F: Oh, I see. So the game is over?
Teacher: Right. At this point, the only the numbers left are 4 and 5. Neither of these has any factors that are still in the list. So the game is over, and the Taxman gets both the 4 and the 5: [writes]

Student C: So You lost — 6 to 15.
Student B: I bet we can do better than that.
Teacher: Well, let's see. We'll start with our list again: [writes]
Student F: How about if we start with 5 this time? [Student F crosses off the 5]
Student B: Hah! The Taxman only gets 1. [Crosses off 1 and records scores]

Student A: Now take 6.
Student D: No, wait a minute. If you do that, the Taxman'll get 3 and 2.
Student E: And then you won't be able to take the 4 …
Student D: … 'cause the 2 and 1'll be gone.
Student A: So take the 4 now.
Student C: Yeah, that'd be better. Then the Taxman'll get only the 2.
Student F: And you'll still be able to take the 6.
Teacher: Wait a second. I don't follow you. So what do you want to do now?
Student B: Take the 4, so the Taxman gets the 2. [Crosses off and records scores.]

Student E: And now you can choose the 6 because the 3 is still left for the Taxman. [Crosses off and records scores.]
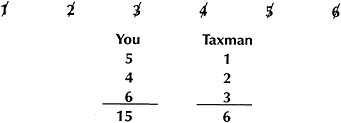
Student D: So this time, You won, 15 to 6!
Teacher: Do you think you could ever do better, starting with the list from 1 to 6?
Student A: I don't think so. …
Student C: I'm positive there's no way to do any better than that.
Teacher: How do you know?
Student C: Well, look. Every time you play, the Taxman has to get something, right? So that means …
(Fade to black)
Following the viewing of the videotape, let students play a game of Taxman using more than six numbers. In small groups they can play Taxman-8:
Together the group should choose the numbers to claim for You; then one student removes that number and updates the score, while another member of the group removes the factors and updates the Taxman's score. Remind the students that the Taxman must always get something.
Student assessment activity: See the following pages. A Spanish translation is provided after the English version.
Name ________________________________________ Date _____________
Play several games of Taxman with these ten numbers:
Make a record of your best game. Be sure to show which numbers you took and the order in which you took them, not just the final score.
Then answer the following questions:
|
1. |
Did you beat the Taxman? ________ |
|
2. |
What number did you choose first? ________ Why? |
|
3. |
Do you think anyone could ever play a better game than your best game? ________ Explain why or why not. |
|
4. |
Suppose you were going to play Taxman with the whole numbers from 1 to 95. What number would you choose first? ________ Why? |
Nombre ________________________________________ Fecha _____________
Juega varios partidos de el Cobrador de Impuestos con estos diez números:
Mantín un registro de tu mejor partido. Asegúrate de escribir los números que escogiste y en el orden en que los escogiste, y no solamente tu puntuación final.
A medida que investigas el juego de el Cobrador de Impuestos con los diez números, contesta las siguientes preguntas:
|
1. |
¿Puedes ganarle al cobrador de impuestos? ________ |
|
2. |
¿Qué número escogerías primero? ________ ¿Por qué? |
|
3. |
¿Crees que alguien pudiera jugar un partido mejor que el tuyo? Explica por qué sí o por qué no. |
|
4. |
Imaginate que vas a jugar al Cobrador de Impuestos con los números del 1 al 95. ¿Qué número escogerías primero? ________ ¿Por qué? |
Rationale for the mathematics education community
The Taxman task provides a good example of a mathematical situation in which systematic analysis involving several steps is critical, an important characteristic of mathematical power. The task also presents an opportunity for children to generalize what they have learned beyond the particular instance; e.g. analyzing Taxman-10 to describe a strategy for Taxman-95. At the same time, the task asks students to construct convincing arguments about their strategy. These steps are all essential facets of mathematical proofs.
Moreover, the task is a situation in which reasoning with prime numbers, composites, and factors plays a vital role; it is up to the children, however, to determine how these ideas should be applied to analyzing the game.
It is worth noting that the Taxman game has no pretense of applications to the ''real world" in the usual sense; it is a purely abstract, without grounding in some physical context. But games are a significant aspect of a fourth grader's real world and can be motivational in and of themselves.
To ensure that children from different classrooms will get exactly the same introduction to the game, the use of a videotaped introduction is recommended. Uniformity of presentation is important if the results of one classroom are to be compared fairly with results from another. The widespread availability of videocassette recorders in classrooms now makes it feasible to introduce problem settings that would previously have been too complex to replicate reliably from one classroom to another.
Certain features of the Taxman task — and other potential assessment tasks — make a uniform introduction even more important. With a videotape, everyone will have the same experiences in exploring optimal and non-optimal choices. A teacher who introduces the games in his or her classroom without the videotape might never consider an opening move of 6, for example, simply because no one in the class happened to offer it as a choice during the explanation.
Task design considerations: A few points about the construction of this task should be made:
First, the choice of the number 95 for the last question was made very carefully. One would expect even a fairly unsophisticated child to recognize that 95 is a multiple of 5, and therefore not prime; it is also straightforward to recognize 93 as being composite — a multiple of 3. It's harder to see that 91 is also not a prime, and that in fact the largest available prime (and therefore one's best first move) is 89. Hence the choice of Taxman-95 can yield information about the child's conceptions of primes and factors that other games would not necessarily reveal. (Suppose instead that the task had been to choose the best first number in Taxman-101. If a child (correctly) chose 101 one could not determine whether she chose it because it was a large prime, a large odd number, or just large.)
Related to this point, in a pilot, an earlier version of this task asked, "Did you find any strategies that might be useful if you were playing Taxman with some other set of numbers? If you did, please explain." Clearly this is much more openended than the current version. Since the point was to see if the child understands the role of prime numbers in Taxman, the last question was narrowed down so that it addressed more specifically the strategy for finding an optimal first move.
Second, the instruction to "Play several games of Taxman …." is similar to instructions in some of the other prototypes (see, for example, the Hog Game task). The wording is intermediate between specifying exactly how many games should be played, on the one hand, and, on the other, not saying anything at all about playing the game. It is left up to the child to determine (a) how many games to play, (b) how (if at all) to record them. Knowing how much experimentation is needed or when enough data is available are important features of mathematical power. Clearly a decision about how much direction to provide through the instructions is a matter of judgment for the task designer. Presumably older students would be in a better position to determine if they need to play any games at all.
Note also the wording near the beginning of the task: "Make a record of your best game," rather than "Make a record
of each game." The latter instruction tells students what to do, while the former lets them decide for themselves what they need to do. The NCTM Standards call for students who can make cogent decisions in the problem-solving process.
Third, question 3 is phrased "Do you think anyone could play a better game …?" rather than "Do you think you could play a better game …?" to encourage children to create a proof. In effect, the student is being asked to complete the argument that Student C started as the videotape fades out: According to the rules, the Taxman must get at least one number for every number that You claims. So if there are 10 numbers in all, the Taxman must get at least 5 of them. Further, it is possible to play the game (by You choosing 7, 9, 6, 8, and 10, in that order) so that the Taxman gets only five numbers, and they are the smallest five. Hence there is no better game. Question 4 also calls for a short proof: The Taxman is going to get the number 1 as the result of the first move (no matter what it is), and hence no prime number can be chosen after the first move. Therefore, one might as well choose a prime on the first move, and, in fact, the largest prime available. Since 89 is the largest prime less than 95, 89 is the best first move.
A related point: One should be aware that there may be cultural or personality effects operating in question 3. Some children will think that it is generally unseemly or boastful to claim that anything they do is "best." Others may think that it is important to put up a front of asserting that whatever they do is "best." Or perhaps prior personal experiences have convinced the child that nothing he or she does could be "best." Thus the answers given to question 3 may depend on factors other than those that are really relevant to the mathematics. Part of the point of developing one's reasoning abilities, however, is to become better able to distinguish between "the best possible" from ''the best that I personally can do."
Note that Taxman with larger numbers is much harder to analyze when one gets beyond the first few moves.
The general points about the translation into Spanish that appear in the discussion of the Checkers Tournament task apply here as well.
Variants and extensions: One natural variant of the task is to use different sets of numbers — from 1 through 15, for example, or 1 through 20. (One should keep in mind the earlier caveat that complete analyses of the games become considerably harder as the numbers increase.)
Another variation of the same kind is to replace 95 (in question 4) with a smaller number, keeping in mind the points made above about how 95 was chosen.
Of course the numbers do not have to be consecutive whole numbers starting with 1. What happens if the numbers are the odd numbers from 1 through 19, or the even numbers from 2 through 20?
Another possibility is to concentrate more on the number theoretical ideas than the sequencing of moves, by looking at the score after only one move. Consider Taxman-65, for example (starting with the set of whole numbers from 1 through 65). A starting move of 62 means that You leads, 62 to 34 (which is 31 + 2 + 1). A starting move of 60, on the other hand would put You behind, 60 to 108 (which is the sum of all the other factors of 60). An opening move of 6 would result in a tie, 6 to 6. The following questions would be of interest: "Which opening moves result in You leading, which result in the Taxman leading, and which result in a tie? Are there opening moves that result in scores for You and the Taxman that differ by just one point? What are the underlying patterns here?"
Protorubric
Characteristics of the high response:

The high-level response is one that demonstrates an optimal game, communicates it effectively, and, generally shows an understanding of choosing the largest available prime as the best first move.
In response to the questions about Taxman-10, the pair of students present a winning game with
the optimal score, in a form that can be followed clearly. For example, this table is given:
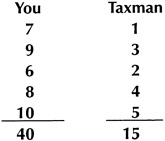
The first number chosen, 7, is justified on the basis that it is the largest prime on the list, or on a basis that amounts to a complete analysis of the game (e.g., "I chose the 7 first because if I chose the 10, then …; and if I chose the 9, then …; and if I chose the 8, then .…").
No better game is possible because "You" has captured the five largest numbers on the list, while giving the Taxman the five smallest numbers.
For the game of Taxman-95, 89 is chosen as the first move. The justification asserts that if any prime is to be chosen at any point in the game, it must be on the first turn. Since 89 is the largest prime number in the list, it's the best first move.
A somewhat less advanced response is simply that 89 is the largest number on the list that has only one factor on the list.
An even less satisfactory response is to declare that the largest prime is the optimal opening move, but then to misidentify 91, 93, or 95 as a prime.
Characteristics of the medium response:

A winning game is described, although it need not be an optimal one.
The first number chosen is justified simply on the basis that it works out to be a winning first move.
A correct answer, with some justification, is given to Question 3. (Of course, this response will have
to depend on the best game that the students can find. If a less-than-optimal game is described, then an answer of "Yes" is correct here.)
Some number other than 89 is suggested as the first move, with a rationale that includes some reference to the number's factors. For example, "95, because it's big, and the Taxman would get only 5, 19, and 1."
Characteristics of the low response:

Some game is described, but sketchily and perhaps ambiguously (that is, it may not be possible to tell in what order the numbers were selected).
No justification is provided for the first number chosen, or the justification does not take into account the factors of the number.
In question 4, no reference is made to factors of the number selected as the first move. For example: "95, because it is the biggest number you can get."














