Hexarights
|
Apply familiar concepts in unfamiliar settings Apply mathematical definitions and explore their subtleties Choose tools to help in problem-solving |
Suggested time allotment
One class period
Student social organization
Students working alone or in pairs
Task
Assumed background: This task assumes that the children are familiar with area and perimeter of plane figures and with perpendicular lines. In particular, the children should have had some experience in
-
measuring lengths of line segments and in drawing right angles (using an L-square or similar tool)
-
drawing objects (like rectangles) that meet predetermined criteria — for example with given areas or perimeters.

It is also assumed that the students have had some experience in dealing with newly defined geometric objects. The assessment activity does not, however, assume any familiarity with hexarights. Indeed, part of what is being assessed is children's abilities to grapple with a concept that is new to them.
Presenting the task: The teacher should first be sure that everyone recalls that a hexagon is a 6-sided plane figure, and that adjacent sides are sides that touch. Then he or she should distribute copies of the student sheet and read through the first item to ensure that everyone has a beginning understanding of what a hexaright is. As always, tools for drawing should be available for children to use as they see the need. The tools should include rulers, L-squares (which provide an easy way to draw right angles), centimeter tiles, and centimeter graph paper. An L-square is provided on the back cover of this book.
Student assessment activity: See the following pages. Note: the student work pages have been drawn to fit the 7'' × 10" page of this volume. Reproduction of these pages for student use may affect the scale of the centimeter graph paper in questions 2 and 3 and the hexaright in question 4. The teacher may choose to redraw these diagrams to achieve proper scale.
Name _________________________________________ Date _____________
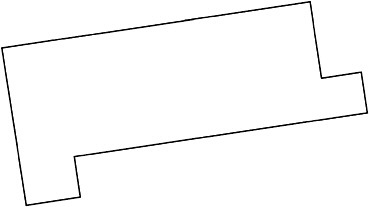
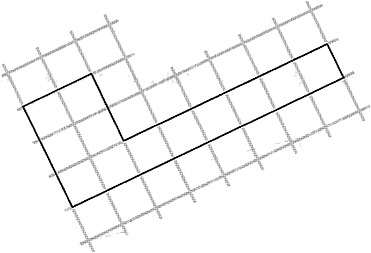
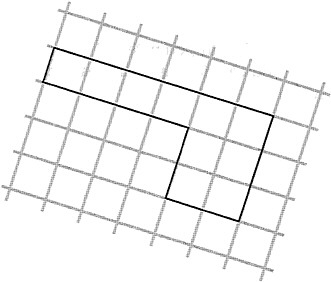
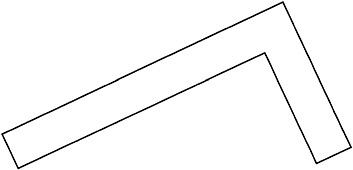
We made up a new kind of shape and made up a name for it: hexaright. Here's the definition: A hexaright is a hexagon in which each pair of adjacent sides is perpendicular.
Here are some examples of hexarights:
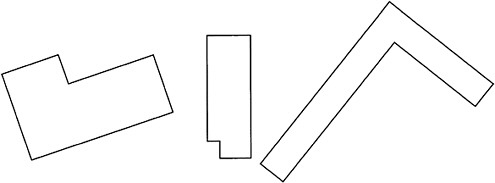
This is not a hexaright because not all pairs of adjacent sides are perpendicular.
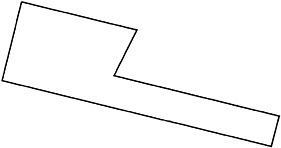
5. There are lots of different hexarights with a perimeter of 24 cm. On a separate piece of paper, draw two different hexarights, each one with a perimeter of 24 cm. (Be sure to put your name on the paper!)
6. Draw one more hexaright with perimeter 24 cm, and make the area as large as you can. You can draw it in the space below or on another piece of paper.
What is the area of the hexaright you just drew? _______
7. What did you find out about the areas of hexarights with a perimeter of 24 cm?
Rationale for the mathematics education community
An important feature of this task is that it incorporates basic ideas from geometry and measurement — perpendicularity, line segments, area, perimeter — to define a new geometric figure previously unknown to students — hexarights. It is not, however, hexarights in and of themselves that are important. Rather, it is the ability of students to use some familiar mathematical ideas to define and explore a new class of mathematical objects.
The purpose of the task is to assess how well students can deal with this new concept, in the sense of (a) being able to distinguish what fits the definition and what does not and (b) constructing examples that fulfill given constraints.
The ideas suggested by hexarights are particularly rich from a mathematical standpoint. The task provides an opportunity for students to explore the idea of maximizing one property — area in this case — while keeping other properties — perimeter here — fixed. Again, it is neither hexarights nor area and perimeter that make the task noteworthy; it is the mathematical investigation of interrelated properties that is an important part of mathematical power. Similarly, the task asks students to think about what hexarights are not. The point is that the little "bite" that makes the figure a hexaright (rather than a rectangle) can be made as small as one wishes; but once the bite disappears, so too does the hexaright! Hence, while the area can be arbitrarily close to 36 cm2, it cannot equal 36 cm2.
Still another important reason for including this task is that the students are given the opportunity to select the tools that they need or want to use to do the drawings. Some children will prefer to use paper ruled in centimeters (which in fact may limit their drawings to hexarights with integral sides); others will use a centimeter L-square, which is a very appropriate tool in this case. It is important for teachers and texts to leave the selection of tools for particular tasks to the students, particularly by the time they reach fourth grade. The selection of the proper tool from several possibilities is a vital part of problem-solving because each tool may have its own advantages and disadvantages in a given setting.
Task design considerations: Several features of this task deserve highlighting:
Note that hexarights are formally defined in words, as opposed to being implicitly "defined" solely through lots of examples and non-examples. (Of course it may well be that some children of this age will form the "hexaright" concept through the pictures rather than through the words. If the task were used with older children, it might be appropriate to convey the concept without the pictures. The students would then be expected to generate whatever pictures they would need to solidify the concept in their own minds.) Note also that the shape was intentionally given a name that suggests its meaning, rather than an invented nonsense word (as is typical of some materials that aim at concept formation through examples and non-examples).
All the pictures of hexarights are drawn so their sides are not parallel with the edges of the paper. This is in an effort to combat one of the most prevalent misconceptions about geometry: that the properties of being a rectangle or square, or (more generally) the relations of parallel and perpendicular have something to do with the orientation of the lines with respect to the edges of the page or the chalkboard. Even in the cases of questions 2 and 3, the pieces of centimeter graph paper are shown as if they had been torn from a larger sheet and placed obliquely with respect to the edges of the page.
Question 5 deliberately does not leave sufficient space to answer the question, and instead calls for the student to use a separate piece of paper. The purpose of this is to force the child to decide what kind of paper to use. Centimeter graph paper will be helpful to some students and a distraction for others.
Similarly, in question 7, no lines are provided for the student to write on. Some children will want to describe their findings in words, while others will want to explain via pictures. No method is best a priori. (Students should be encouraged to use a sheet of lined paper, however, if they ask to do so.) Filling the page with lines to write on might convey the message that pictures are not appropriate.
A note on the definition of "hexaright": Although three technical words are involved in the definition — "hexagon," "adjacent,'' and "perpendicular" — they are all useful in a variety of settings, mathematical and non-mathematical. In any case, teachers are asked to make sure everyone understands these terms.
Notice also the introductory sentence that says that "hexaright" is a made-up term. One would also not want teachers or other adults to think that a hexaright is some concept from high school geometry that they have forgotten!
An alternative would have been to define the hexaright as a hexagon all of whose angles are right angles. Some may object to this form of the definition, thinking that "angle" connotes "interior angle." Since the measure of one interior angle of a hexaright is 270°, confusion might result.
Variants and extensions: The difficulty of the task can be varied by asking intermediate questions. For example, even before question 1, the student might be asked to draw some hexarights (without size conditions) or to describe in their own words what hexarights look like.
One variant of the task is to use numbers that are not integers for the areas or perimeters of the figures. This might help some children to see that there is no largest hexaright with a perimeter of 24 cm; for others, however, the task would become more difficult.
A natural extension of the task is to consider octarights (or, more generally, polyrights) and their areas and perimeters. Interestingly, octarights occur in three basic shapes (as opposed to hexarights' single basic L-shape).
An extension in another direction is to consider the 3-dimensional analog of a hexaright. If a rectangular box in 3 dimensions is the analog of a rectangle in 2 dimensions, what does the 3-dimensional analog of a hexaright look like? What are the corresponding roles of volume and surface area?
Protorubric
Characteristics of the high response:
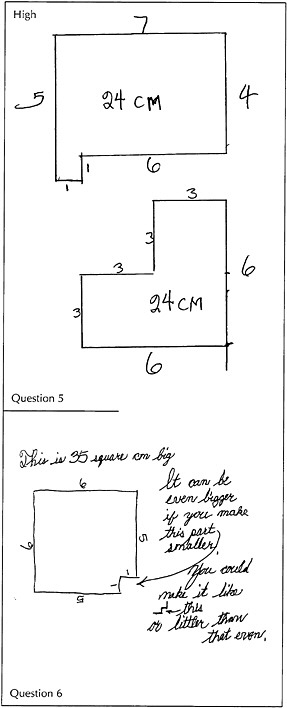
The high-level response is one that demonstrates an overall facility for dealing with the newly-defined hexaright, and that shows some understanding of the complementary roles of perimeter and area in the task — that is, that there are hexarights with perimeter 24 cm and areas that are very close (but not equal) to 36 square centimeters.
The student's responses to questions 1 through 4 are correct, although the indications of "cm" and "square cm" (or "cm2") may be missing.
The hexarights drawn for questions 5 and 6 are close to being completely accurate, with virtually right angles and side lengths within 0.5 cm of being correct. (An alternative, which in some ways is more sophisticated, is a sketch, drawn without a straightedge, that indicates clearly the dimensions.) The area of the hexaright for question 6 is accurate, is at least 34 square cm, and is as large as the ones in question 5.
The highest level response to question 7 says something to the effect that there is no hexaright with perimeter 24 cm and area 36 cm2. (No fourth grader should be expected to justify this fact completely.) Full credit should be
given to any response that refers to a square of perimeter 24 cm, or that says there are hexarights of perimeter 24 cm and area arbitrarily close to 36 cm2. Somewhat less is assigned to a response that simply refers to some (finite) sequence of hexarights of perimeter 24 cm and increasing area.
Characteristics of the medium response:

The responses to questions 1-4 show an understanding of what a hexaright is and what the perimeter and area are. There may be a flaw in one of the calculations. The responses to question 5 provides supporting evidence of understanding, if there are any miscalculations.
The figures drawn in questions 5 and 6 are hexarights, although the lengths of the sides may be up to a centimeter wrong in either direction, the angles may not be accurately drawn right angles, and the perimeter may not be exactly 24 cm. (Of course the nature of the errors will depend on the kinds of tools, including type of paper, that the student selects.)
In question 6, the partial understanding that is typical of the medium-level response can be shown in a variety of ways. For example, the student could draw a hexaright with a relatively small area (perhaps 30 cm 2), but report the area accurately (within perhaps 1 cm2 of the correct area). Alternatively, an appropriate hexaright could be drawn very well, but the area misidentified as 23 cm2 rather than 35 cm2.
The response to question 7 is something that is true (for example, that there are lots of hexarights of different areas, for a fixed perimeter) but that does not address any connections between or among hexarights with perimeter 24 cm.
Characteristics of the low response:
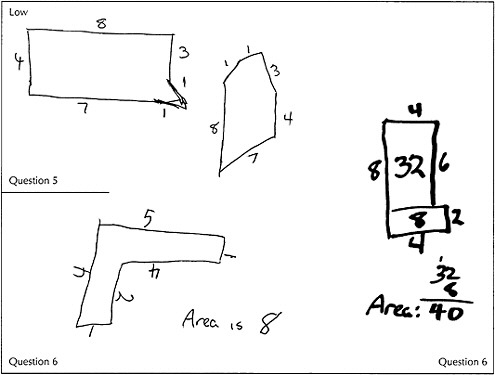
Little understanding evinced of what a hexaright is, and of what area and perimeter are. The drawings are done without regard to accuracy, either in making straight line segments or in making right angles. Moreover, the student's response to question 7 is not related to the problem in a low response.