How Many Buttons?
|
Use approximation and estimation Use calculators appropriately Link assessment and instruction |
Suggested time allotment
A total of two or three class periods (one class period of introductory work plus one or two class periods of student work)
Student social organization
Students working in groups of two or three
Task
Assumed background: This task assumes that the children have had experience in gathering data and making estimates in relatively complex situations.

Presenting the task: This assessment is embedded in a context-setting activity introduced by the teacher to the whole class. The context-setting activity takes one class period, and the paired work—the assessment task itself—requires a second class period, possibly spilling over into part of a third.
The following is written as directions to the teacher:
Introduce the activity by telling the students they will be working on estimating the number of buttons in their class today.
Ask students for their estimates of the number of buttons in the class. Give students a few minutes to look around—at their own buttons, at the number of buttons that students near them have—and to discuss their estimates with students near them. Collect some of their estimates and list them on the board.
As students are estimating, some questions and issues will probably arise. Encourage students to talk about any questions that occur to them (for example, ''What about buttons on sweaters or coats hanging in the closet?" "Were there buttons that they didn't notice or forgot about because they were not in obvious places?" "Should the teacher's buttons be included?" The answers to these questions, which can be decided jointly by you and your students, will depend on your particular situation. For instance, if students' outerwear is stored in an inconvenient location you might decide not to include it.)
Now each student should carefully count the number of buttons that he or she has. They might work in pairs or threes to help each other count carefully. Record their data on a line plot so that everyone in the class can see it. For example:
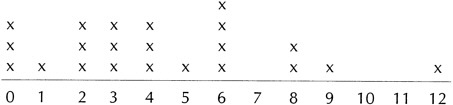
Encourage students to describe these data by asking: "What would you say about the number of buttons in our class?" Students may comment on the range of the data, where data are clumped, for
which values there are no people with exactly that number of buttons, and what (if anything) seems typical of their class.
Student assessment activity: The assessment should be done on the day after the activity just described. You will need the class data from the previous day, and pencil and paper for each student. Of course, they should have access to calculators.
Tell students they will be working in small groups to estimate the number of buttons there are in the whole school. They can refer to the class data from the previous session. Suggest that they may want to consider questions such as: "Is it likely that other classes in the school will have a similar number of buttons?" "Do younger students have fewer or more buttons?" "What about older students?" "How should teachers or other adults in the school be included in the estimate?'' These questions should be written on the board. They can contribute greatly to the depth and sophistication of the children's responses, so students should have equal access to them.
Each pair of students then works together to solve this problem, as described above. They should be encouraged to record their strategies, including the numbers they chose and why they chose them.
Rationale for the mathematics education community
This item pushes the curriculum to include work with large numbers and with a complex situation in which estimation is a legitimate mathematical process—not simply a prelude to finding the "real" answer. Further, it connects a range of mathematical ideas—multiplicative relationships (e.g., an average of about 6 buttons per student, with 22 students per classroom), estimation, averages ("I decided there are about 22 students in each classroom."), and beginning ideas about sampling. Use of the calculator is incorporated in a natural way.
The problem is accessible: Almost any child can arrive at some solution, but the possible solutions span a broad spectrum of depth and complexity. The problem provides all students with the opportunity to think about and discuss which factors to take into account — whether or not to include adults' buttons or clothes in the closet, and so forth. One strength of a task like this is that its context is immediate and tangible.
Many estimation tasks arise in some setting that provides a "real-life" motivation and a criterion for judging how precise an estimate should be. One must remember, however, that fourth graders are not as concerned as adults are with the "real" reasons for doing something. In this case, classroom trials have suggested that just the allure of the large numbers, of finding out something that no one has ever known before, and of getting the best possible estimate, are plenty of motivation.
The mode of presentation embeds the assessment task as an integral part of a piece of curriculum. Indeed, teachers might want to move from the assessment task back into curriculum by continuing the investigation with the whole class—comparing the students' individual estimates, gathering additional information, and refining these estimates. (See the Variants and extensions section below.)
Finally, it offers a problem on which students work in pairs. Working together to pool information and expertise to come to a solution are essential problem-solving skills for today's students.
Task design considerations: The protorubric for this task is phrased in terms of the factors that the child's response takes into account. Nonetheless, careful consideration must be given to the specific details of the task if it is to be used to make comparisons among, or to draw conclusions about, different kinds of schools in different geographical areas of the country. Depending on the season, a child in a colder climate is likely to wear more clothes, with more buttons, than one from a warmer climate. A school that contains 25 classrooms is a very different setting from one that has five classrooms. Because of such potential variations in complexity, the task would be inappropriate to use universally for comparative purposes.
Variants and extensions: Objects other than buttons can be used in this sort of activity — for example, books that the student happens to have in his or her desk. In fact, this might alleviate (but not eliminate) some of the geographical differences noted above.
Using the task as the basis for extended classroom discussion might be particularly valuable. One can continue the investigation by considering how many buttons there might be
in all the schools in the town or city, or even all the schools in the state. This would involve the use of almanacs or atlases to find out the appropriate numbers to use, depending on the question. Similarly, students might explore how the number of buttons that people wear varies from one section of the country to another. Thus, the students would want to communicate with at least one other school of the same size in some other region and compare data.
Protorubric
Characteristics of the high response:

The response appropriately takes into consideration the following aspects of the problem: (a) the data collected from the day before; (b) some estimate of the number of children per classroom; (c) the number of classes in the school; (d) variation of buttons among children of various ages; and (e) adults' buttons (which the pair may choose to disregard entirely).
Reasonable justifications are given for how each numerical value was chosen or calculated.
The numerical values are put together with appropriate arithmetic processes. (For example, if the students decided there were an average of 90 buttons in each of the 12 upper grade classrooms and an average of 60 buttons in each of the 8 lower grade classrooms, they would calculate with these values so that their result would be (90 × 12) + (60 × 8), not in some invalid way, such as adding 90 and 60, then multiplying by the total number of classrooms.)
The final report on the solution clearly details the steps the students went through to solve the problem so that a reader can easily follow their solution strategy.
Characteristics of the medium response:

The response takes into consideration the results of the previous day's work. Further, it uses a reasonable estimate for the number of students per class (if needed for the solution) and the number of classrooms in the school, with appropriate justifications for the values chosen.
Consideration of factors like variation of button numbers by age of child or adults' buttons is lacking.
The arithmetic processes are appropriate.
The final report on the solution clearly explains some (but not all) aspects of the student's strategy.
Characteristics of the low response:

Some reference is made to the previous day's work, and some other values may be chosen reasonably.
Either some values (e.g., the number of students per class or the number of classes) are chosen inappropriately, or the way in which the arithmetic processes are used is incorrect.
The explanation and justification of the student's reasoning is incomplete or unclear.
Reference
"Investigations in Number, Data, and Space" project of TERC, Cambridge, MA.






