Issues in Risk Assessment (1993)

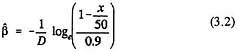
of ß. We will consider tumor counts in the range 10 = x = 49, the lower limit being the smallest value of x which is significantly greater (p < 0.05) than the assumed background incidences of 10%, and the upper limit being the largest value of x which leads to a meaningful estimate of ß. (Since 100% tumor incidence is rarely observed, this truncated upper limit has little practical significance.) Under these conditions, we have 0.118/D = ß = 3.807/D, so that ß could vary by about 32-fold. It follows from (2.3) that the corresponding estimate of carcinogenic potency varies by the same amount. Bernstein et al. (1985) assert that this result also tends to hold for more general experimental designs involving two or three exposed groups in addition to an unexposed control. It follows that since cancer potency values are constrained to lie within a narrow range determined by the MTD, the wide variation in MTDs for chemical carcinogens necessarily induces a high correlation between cancer potency and the MTD.

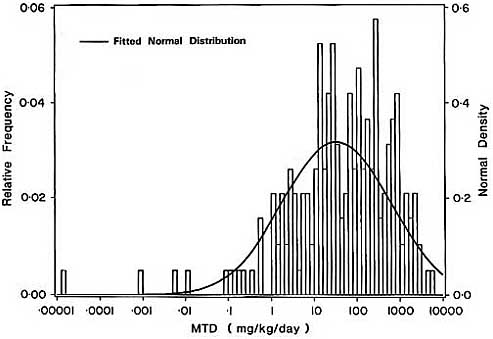
The correlation between the MTD and the TD₅₀ may be also be established using analytical arguments, details of which are provided in annex D. Suppose first that the MTD for a population of carcinogens follows a log-normal distribution as suggested by Bernstein et al. (1985). This assumption is supported by the approximate normality of the log₁₀TD₅₀ values for the 191 chemicals discussed in section 3.1 (see Figure 3). (The normality assumption is actually not essential here since the correlation depends only on the variance of this distribution.) Suppose further that the TD₅₀ is uniformly distributed about the MTD within the limits calculated the methods of by Bernstein et al. (1985). To the extent that these limits are greater than would be observed in practice, this assumption would tend to reduce the value of the correlation coefficient to be calculated by this argument. Under these assumptions, the correlation between log₁₀(TD₅₀) and log₁₀(MTD) is 0.965 for a sample of size n = 50 animals in the exposed group.