THE MATHEMATICAL MICROSCOPE
Waves, Wavelets, and Beyond
by Barbara Burke
Mathematician Michael Frazier of Michigan State University was educated in the tradition that maintains that "real" mathematics by "real" mathematicians is and should be useless. "I never expected to do any applications—I was brought up to believe I should be proud of that," he says. ''You did pure harmonic analysis for its own sake, and anything besides that was impure, by definition." But in the summers of 1990 and 1991 he found himself using a mathematical construction to pick out the pop of a submarine hull from surrounding ocean noise.
In St. Louis, Victor Wickerhauser was using the same mathematics to help the Federal Bureau of Investigation store fingerprints more economically, while at Yale University Ronald Coifman used it to coax a battered, indecipherable recording of Brahms playing the piano into yielding its secrets. In France, Yves Meyer of the University of Paris-Dauphine found himself talking to astronomers about how they might use these new techniques to study the large-scale structure of the universe.
Over the past decade a number of mathematicians accustomed to the abstractions of pure research have been dirtying their hands—with great enthusiasm—on a surprising range of practical projects. What these tasks have in common is a new mathematical language, its alphabet consisting of identical squiggles called wavelets, appropriately stretched, squeezed, or moved about.
A whole range of information—your voice, your fingerprints, a snapshot, x-rays ordered by your doctor, radio signals from outer space, seismic waves—can be translated into this new language, which emerged independently in a number of different fields, and in fact was only recently understood to be a single language. In many cases this transformation into wavelets makes it easier to transmit, compress, and analyze information or to extract information from surrounding "noise"—even to do faster calculations.
In their initial excitement some researchers thought wavelets might virtually supplant the much older and very powerful mathematical language of Fourier analysis, which you use every time you talk on the telephone or turn on a television. But now they see the two as complementary and are exploring ways to combine them or even to create more languages "beyond wavelets."
Different languages have different strengths and weaknesses, points out Meyer, one of the founders of the field: "French is effective for analyzing things, for precision, but bad for poetry and conveying emotion—perhaps that's why the French like mathematics so much. I'm told by friends who speak Hebrew that it is much more expressive of poetic images. So if we have information, we need to think, is it best expressed in French? Hebrew? English? The Lapps have 15 different words for snow, so if you wanted to talk about snow, that would be a good choice."
Some information processing is best done in the language of Fourier; other with wavelets; and yet other tasks might require new languages. For the first time in a great many years—almost two centuries, if one goes back to the very birth of Fourier analysis—there is a choice.
A MATHEMATICAL POEM
Although wavelets represent a departure from Fourier analysis, they are also a natural extension of it: the two languages clearly belong to the
same family. The history of wavelets thus begins with the history of Fourier analysis. In turn the roots of Fourier analysis predate Fourier himself (and much of what is now called Fourier analysis is due to his successors). But Fourier is a logical starting point; his influence on mathematics, science, and our daily lives has been incalculable, if to many people invisible. Yet he was not a professional mathematician or scientist; he fit these contributions into an otherwise very busy life.
His father's twelfth child, and his mother's ninth, Joseph Fourier was born in 1768 in Auxerre, a town roughly halfway between Paris and Dijon. His mother died when he was nine and his father the following year. Although two younger siblings were abandoned to a foundling hospital after their mother's death, Fourier continued school and in 1780 entered the Royal Military Academy of Auxerre, where at age 13 he became fascinated by mathematics and took to creeping down at night to a classroom where he studied by candlelight.
Fourier's academic success won the favor of the local bishop. But when at the end of his studies his application to join the artillery or the army engineers was rejected, he entered the abbey of St. Benoît-sur-Loire. (The popular story that he was rejected by the army because he was not of noble birth—and therefore ineligible "even if he were a second Newton"—is questioned by at least two of Fourier's contemporaries.)
The French Revolution erupted before Fourier took his vows. At first indifferent, he became increasingly committed to the cause of establishing "a free government exempt from kings and priests"1 and in 1793 joined the revolutionary committee of Auxerre.
Twice he was arrested, once in the bloody days shortly before the fall of Robespierre and again the following year, on charges of terrorism. In defending himself Fourier pointed out that during the Terror no one in Auxerre was condemned to death; a friend related that once, to prevent a man he believed to be innocent from arrest and the guillotine, Fourier invited the agent charged with the arrest to lunch at an inn and, "having exhausted every means of retaining his guest voluntarily," left the room on a pretext, locked the door, and ran to warn the suspect, returning later with excuses.
After several years teaching in Paris, Fourier next accompanied Napoleon to Egypt, serving as permanent secretary of the Institute of Egypt that Napoleon had set up, in part to study Egypt's past and natural history. Upon Fourier's return to France, Napoleon appointed him prefect of the department of Isère. He served as prefect, living in Grenoble, for 14 years, earning a reputation as an able administrator; he was responsible for the draining of some 20,000 acres of swamps that
|
Mathematical Analysis … mathematical analysis … defines all observable relationships, measures time, space, force, temperature. This difficult science grows slowly but once ground has been gained it is never relinquished. … Analysis brings together the most disparate phenomena and discovers the hidden analogies which unify them. If material escapes us like air or light because of its extreme fineness, if bodies are placed far from us in the immensity of space, if man desires to know the aspect of the heavens for times separated by many centuries, if the effects of gravity and temperature occur in the interior of the solid earth at depths which will remain forever inaccessible, yet mathematical analysis can still grasp the laws governing the phenomena. Analysis makes them actual and measurable and seems to be a faculty of human reason meant to compensate for the brevity of life and the imperfection of our senses. … —Joseph Fourier, La Théorie Analytique de la Chaleur |
had caused annual epidemics of fever. After Waterloo, denied a government pension because he had served under Napoleon, he found a safe haven in the Bureau of Statistics in Paris, and in 1817 (after an initial rebuff by King Louis XVIII) he was elected to the Academy of Sciences.
Despite his administrative duties—and his isolation from Paris for many years—Fourier managed to pursue his scientific and mathematical interests. Victor Hugo called him a man "whom posterity has forgotten,"2 but Fourier's name is as familiar to countless scientists, mathematicians, and engineers as the names of their own children. This fame rests on ideas he set forth in a memoir in 1807 and published in 1822 in his book, La Théorie Analytique de la Chaleur (The Analytic Theory of Heat).
Physicist James Clark Maxwell called Fourier's book "a great mathematical poem," but the description does not begin to give an idea of its influence. In the seventeenth century Isaac Newton had a new insight: that forces are simpler than the motions they cause, and the way to understand the natural world is to use differential and partial differential equations to describe these forces—gravity, for example.
Newton's differential equation showing how the gravitational pull between two objects is determined by their mass and the distance between them replaced countless observations, and predictive science became possible. Theoretically possible, at least. Solving differential equations—actually predicting where we will be taken by forces that
themselves depend at each moment on our changing position—is not easy. As Fourier himself wrote in La Théorie Analytique de la Chaleur , although the equations that describe the propagation of heat have a very simple form, "existing methods do not give any general way to integrate them; as a result it is impossible to determine the values of the temperature after a given period of time. This numerical interpretation … is nevertheless essential. … As long as we cannot achieve it … the truth that we wish to discover is as thoroughly hidden in the formulas of analysis as in the physical question itself."3
Some 150 years after Newton, Fourier provided a practical way to solve numerically a whole class of such equations, linear partial differential equations. His ideas dominated mathematical analysis for 100 years and had surprising ramifications even for number theory and probability. Outside mathematics their influence is difficult to exaggerate. Virtually every time scientists or engineers model systems or make predictions, they use Fourier analysis. Fourier's ideas have also found applications in linear programming, in crystallography, and in countless devices from telephones to radios and hospital x-ray machines; they are, in mathematician T. W. Körner's words, "built into the commonsense of our society."
A RABBLE OF FUNCTIONS
There are two parts to Fourier's contribution: first, a mathematical statement (actually proved later by Dirichlet), and, second, showing why this statement is useful.
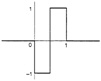
The mathematical statement is that any periodic (repeating) function can be represented as a sum of sines and cosines (see Figure 7.1). Roughly what this means is that any periodic curve, no matter how irregular (the output of an electrocardiogram, for example), can be expressed as the sum, or superposition, of a series of perfectly regular sine and cosine curves, of different frequencies. The irregular curve and the sum of sines and cosines are two different representations of the same object in different "languages."
Even a jagged line can be represented as a Fourier series. The trick is to multiply the sines and cosines by a coefficient to change their amplitude (the height of their waves) and to shift them so that they either add or cancel (changing the phase). One can also treat nonperiodic functions this way, using the Fourier transform (see Box on p. 202).
Fourier himself found this statement "quite extraordinary," and it met with some hostility. Mathematicians were used to functions that when graphed took the form of regular curves; the function f(x) = x2, for
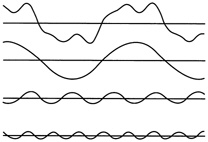
FIGURE 7.1 In 1807 Fourier showed that any function (even an irregular one) can be expressed as the sum of a series of sines and/or cosines. The function at the top is a combination of the three functions below: sin (x), 0.3 sin (3x) and 0.2 cos (5x).
example, produces a well-behaved, symmetrical parabola. (A function gives a rule of changing an arbitrary number into something else; f(x) = x2 says to square any number x; if x = 2, then f(x) = 4.)
The idea that any arbitrary curve could be expressed as a series of sines and cosines and thus treated as a function came as a shock and contributed to a profound and sometimes disturbing change in mathematics; mathematicians spent much of the nineteenth century coming to terms with just what a function was.
"We have seen a rabble of functions arise whose only job, it seems, is to look as little as possible like decent and useful functions," wrote French mathematician Henri Poincaré in 1889. "No more continuity, or perhaps continuity but no derivatives. … Yesterday, if a new function was invented it was to serve some practical end; today they are specially invented only to show up the arguments of our fathers, and they will never have any other use."4
Ironically, Poincaré himself was ultimately responsible for showing that seemingly "pathological" functions are essential in describing nature (leading to such fields as chaos and fractals), and this new direction for mathematics proved enormously fruitful, giving new vigor to a discipline that some had found increasingly anemic, if not moribund. In 1810 the French astronomer Jean-Baptiste Delambre had issued a report on mathematics expressing the fear that "the power of our methods is almost exhausted,"5 and some 30 years earlier Lagrange, comparing mathematics to a mine whose riches had all been exploited, wrote that it was ''not impossible that the mathematical positions in the academies will one day become what the university chairs in Arabic are now."6
"Looking back," writes Körner in his book Fourier Analysis, we can see Fourier's memoir "as heralding the surge of new mathematical methods and results which were to mark the new century."
THE EXPLANATION OF NATURAL PHENOMENA
The German mathematician Carl Jacobi wrote that Fourier believed the chief goal of mathematics to be "the public good and the explanation
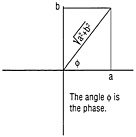
FIGURE 7.2
|
The Fourier Transform The Fourier transform is the mathematical procedure by which a function is split into its different frequencies, like a prism breaking light into its component colors. But the Fourier transform goes further and tells both how much of each frequency the function contains (the amplitude of the frequency) and the phase of the signal at each frequency (the extent to which it is shifted with respect to a chosen origin). The term also describes the result of that operation: the Fourier transform of a particular function (that varies with time) is a new function (that varies with frequency). A Fourier series is a special case of Fourier transform, representing a periodic, or repeating, function. For functions that vary with time, such as sound recorded as changes in air pressure, or fluctuations in the stock market, frequency is generally measured in hertz or cycles per second. For functions that vary with space, "frequency" is often related to the inverse of a distance. For instance, the Fourier transform of a fingerprint will have large values near the "frequency" 15 ridges per centimeter. The Fourier series of a periodic function of period 2π is given by the formula The Fourier coefficients, an and bn, tell how much a signal contains of each frequency n: its amplitude at frequency n is the square root of Calculating coefficients of the Fourier series of a function f(x) involves integral calculus: (This means that you multiply the function f(x) by the appropriate sine or cosine and integrate, measuring the area enclosed by the resulting curve; the result is divided by π. To multiply the function by a sine or cosine, the value of each point on the function is multiplied by the value of the corresponding point on the sine or cosine.) The phase can, in principle, be calculated from the coefficients. If you plot the point an, bn on a coordinate system, the amplitude is the length of the line from the origin to that point, while the phase is the angle formed by that line and the positive x axis (Figure 7.2). The function can be reconstructed from the coefficient using formula (1) above; the sine or cosine at each frequency is multiplied by its coefficient, and the resulting functions are added together, point by point; the first term is divided by 2. |
of natural phenomena," and Fourier showed how his mathematical statement could be used to study natural phenomena such as heat diffusion, by turning a difficult differential equation into a series of simple equations.
Suppose, for example, we want to predict the temperature at time t of each point along a metal bar that has been briefly heated at one end. We start by establishing the initial temperature, at time zero, which we consider a function of distance along the bar. (This is why Fourier needed a technique that would work with all functions, even irregular or discontinuous ones: he couldn't expect the initial temperature to be so obliging as to take the form of a regular curve.)
When that function is translated into a Fourier series a remarkable thing happens: the intractable differential equation describing the evolution of the temperature decouples, becoming a series of independent differential equations, one for the coefficient of each sine or cosine making up the function. These equations tell how each Fourier coefficient varies as a function of time. The equations, moreover, are very simple—the same as the equation that gives the value of a bank account earning compound interest (negative interest in this case).
One by one, we simply plug in the coefficients describing the temperature at time zero and crank out the answers; these are the Fourier coefficients of the temperature at time t, which can be translated back into a new function giving the new temperature at each point on the bar. The procedure is no harder than the one banks use to compute the balance in their clients' accounts each month.
Essentially we have made a little detour in Fourier space, where our calculations are immensely easier—as if, faced with the problem of multiplying the Roman numerals LXXXVI and XLI, we translated them into Arabic numerals to calculate 86 × 41 = 3526, and then translated the answer back into Roman numerals: LXXXVI × XLI = MMMDXXVI.
The techniques Fourier invented have of course had an impact well beyond studies of heat or even solutions to differential equations. Real data tend to be very irregular: consider an electrocardiogram or the readings of a seismograph. Such signals often look like "complicated arabesques," to use Yves Meyer's expression—tantalizing curves that contain all the information of the signal but that hide it from our comprehension. Fourier analysis translates these signals into a form that makes sense.
In addition, in many cases the sines and cosines making up a Fourier series are not simply a mathematical trick to make calculations easier; they correspond to the frequencies of the actual physical waves
making up the signal. When we listen to music or conversation, we hear changes in air pressure caused by sound waves—high sounds having high frequency and low sounds having lower frequency. (In fact, a piano can perform a kind of Fourier analysis: a loud sound near a piano with the damper off will cause certain strings to vibrate, corresponding to the different frequencies making up the sound.)
Similarly—although this was not known in Fourier's time—radio waves, microwaves, infrared, visible light, and x-rays are all electromagnetic waves differing only in frequency. Being able to break down sound waves and electromagnetic waves into frequencies has myriad uses, from tuning a radio to your favorite station to interpreting radiation from distant galaxies, using ultrasound to check the health of a developing fetus, and making cheap long-distance telephone calls.
With the discovery of quantum mechanics, it became clear that Fourier analysis is the language of nature itself. On the "physical space" side of the Fourier transform, one can talk about an elementary particle's position; on the other side, in "Fourier space" or "momentum space," one can talk about its momentum or think of it as a wave. The modern realization that matter at very small scales behaves differently from matter on a human scale—that at small scales we cannot have precise knowledge of both sides of the transform at once, we cannot know simultaneously both the position and momentum of an elementary particle—is a natural consequence of Fourier analysis.
BEING ACADEMIC OR BEING REAL
While irregular functions can be expressed as the sum of sines and cosines, those sums usually are infinite. Why translate a complex signal into an endless arithmetic problem, calculating an infinite number of coefficients, and summing an infinite number of waves? Fortunately, a small number of coefficients is often adequate. From the heat diffusion equation, for example, it is clear that the Fourier coefficients of high-frequency sines and cosines rapidly get exceedingly close to zero, and so all but the first few frequencies can safely be ignored. In other cases engineers may assume that a limited number of calculations give a sufficient approximation until proved otherwise.
In addition, engineers and scientists using Fourier analysis often don't bother to add up the sines and cosines to reconstruct the signal—they "read" Fourier coefficients (at least the amplitudes; phases are more difficult) to get the information they want, rather the way some musicians can hear music silently, by reading the notes. They may spend
hours on end working quite happily in this "Fourier space," rarely emerging into "physical space."
But the time it takes to calculate Fourier coefficients is a problem. In fact, the development of fast computers and fast algorithms has been crucial to the pervasive, if quasi-invisible, use of Fourier analysis in our daily lives in connection with today's digital technology.
The basis for digital technology was given by Claude Shannon, a mathematician at Bell Laboratories whose Mathematical Theory of Communications was published in 1948; while he is not well known among the general public, he has been called a "hero to all communicators."7 Among his many contributions to information theory was the sampling theorem (discovered independently by Harry Nyquist and others). This theorem proved that if the range of frequencies of a signal measured in hertz (cycles per second) is n the signal can be represented with complete accuracy by measuring its amplitude 2n times a second.
This result, a direct consequence of Fourier analysis, is simple to state and not very difficult to prove, but it has had enormous implications for the transmission and processing of information. It is not necessary to reproduce an entire signal; a limited number of samples is enough.
Since the range of frequencies transmitted by a telephone line is about 4000 hertz, 8000 samples per second are sufficient to reconstitute your voice when you talk on the telephone; when music is recorded on a compact disc, about 44,000 samples a second are used. Measuring the amplitude more often, or trying to reproduce it continuously, as with old-fashioned records, does not gain anything.
Another consequence is that, in terms of octaves, more samples are needed in high frequencies than in low frequencies, since the frequency doubles each time you go up an octave: the range of frequency between the two lowest As on a piano is only 28 hertz, while the range of frequency between the two highest As is 1760 hertz. Encoding a piece of music played in the highest octave would require 3520 samples a second; in the lowest octave, 56 would be enough.
The sampling theorem opened the door to digital technology: a sampled signal can be expressed as a series of digits and transmitted as a series of on-and-off electrical pulses (creating, on the other hand, round-off errors). Your voice can even be shifted temporarily into different frequencies so that it can share the same telephone line with many other voices, contributing to enormous savings. (In 1915 a 3-minute call from coast to coast cost more than $260 in today's dollars). In 1948 Shannon and his colleagues Bernard Oliver and John Pierce expected digital
|
The Fast Fourier Transform An algorithm is a recipe for doing computations. When schoolchildren learn to "carry," "borrow," or multiply two-digit numbers without a calculator, they are learning algorithms. Fast algorithms are mathematical shortcuts for dealing with large computations. The fast Fourier transform, published by J. W. Cooley and T. W. Tukey in 1965, is a prime example. It cuts the number of computations from n2 in standard Fourier analysis to n log n. When n is big, this makes a substantial difference: if n = 1,000,000, then n2 = 1,000,000,000,000, but n log n = 6,000,000 (log 1,000,000 is 6 since 106 = 1,000,000). The logarithm is roughly the number of digits, so it grows slowly. The larger n is, the more impressive the difference becomes. If n is a billion and a computer can complete a billion calculations a second, this cuts computing time from approximately 32 years to 9 seconds. With the FFT one can computer π to a billion digits in about 45 minutes; without it the job would take almost 10,000 years. |
transmission to "sweep the field of communications;"8 the revolution came, if later than they had expected.
Fueling this revolution was the fast Fourier transform (see Box on this page), a mathematical trick that catapulted the calculation of Fourier coefficients out of horse-and-buggy days into supersonic travel. With it, calculations could be done in seconds that previously were too costly to do at all. "It's the difference," Michael Frazier says, "between being academic and being real."
This fast algorithm, known as the FFT, requires computers in order to be useful. "Once the method was established it became clear that it had a long and interesting prehistory going back as far as Gauss," Körner writes. "But until the advent of computing machines it was a solution looking for a problem." On the other hand, the gain in speed from the FFT is greater than the gain in speed from better computers; indeed, significant gains in computer speed have come from such fast algorithms built into computer hardware.
DRIVING A CAR HALF A BLOCK
It could be argued that the fast Fourier transform was too successful. "Because the FFT is very effective, people have used it in problems
where it is not useful—the way Americans use cars to go half a block," says Yves Meyer. "Cars are very useful, but that's a misuse of the car. So the FFT has been misused, because it's so practical."
The problem is that Fourier analysis does not work equally well for all kinds of signals or for all kinds of problems. In some cases, scientists using it are like the man looking for a dropped coin under a lamppost, not because that is where he dropped it but because that's where the light is.
Fourier analysis works with linear problems. Nonlinear problems tend to be much harder, and the behavior of nonlinear systems is much less predictable: a small change in input can cause a big change in output. The law of gravity is nonlinear and using it to predict the very long term behavior of even three bodies in space is wildly difficult, perhaps impossible; the system is too unstable. (Engineers make clever use of this instability when sending space probes to distant planets: NASA's Pioneer and Voyager spacecraft were both aimed at Jupiter in such a way that Jupiter's gravity accelerated the probes and bent their paths, sending them on to Saturn.)
"It is sometimes said," quips Körner, "that the great discovery of the nineteenth century was that the equations of nature were linear, and the great discovery of the twentieth century is that they are not."
Engineers faced with a nonlinear problem often resort to the rough-and-ready expedient of treating it like a linear problem and hoping the answer won't be too far off. For example, the engineers charged with defending Venice from the high waves that flood it every year, forcing Venetians to make their way across the Piazza San Marco on sidewalks set on stilts, want to predict the flood waters far enough in advance so that eventually they could raise inflatable dikes to protect the city. Since they can't solve the nonlinear partial differential equation that determines the behavior of the waves (an equation involving winds, position of the moon, atmosphere pressure, and so on), they simply reduce it to a linear equation and solve it with Fourier analysis. Despite some progress, they are still taken by surprise by sudden rises in water level of up to a meter.
In information processing Fourier analysis has other limits as well: it is poorly suited to very brief signals or to signals that change suddenly and unpredictably. A Fourier transform makes it easy to see how much of each frequency a signal contains but very much harder to figure out when the various frequencies were emitted or for how long. It pretends, so to speak, that any given instant of the signal is identical to any other, even if the signal is as complex as a Bach prelude or changes as dramatically as the electrocardiogram of a fatal heart attack.
Mathematically this is correct. The same sines and cosines can represent very different moments in a signal because they are shifted in phase so that they amplify or cancel each other. A B-flat that appears, from the Fourier transform, to be omnipresent in a prelude may in fact appear only intermittently; the rest of the time it is part of an elaborate juggling act. But as physicist J. Ville wrote in 1948, "If there is in this concept a dexterity that does honor to mathematical analysis, one can't hide the fact that it also distorts reality."9 One moment of a prelude does not sound like another; the flat line of an electrocardiogram that announces death is not the same as the agitated lines produced by a beating heart.
The time information is not destroyed by the Fourier transform, just well hidden, in the phases. But the fact that information about any point in a signal is spread out over the entire transform—contained in all the frequencies—is a serious drawback in analyzing signals or functions. Brief changes often carry the most interesting information in a signal; in medical tests, for example, being able to detect them could make the difference between a correct or an incorrect diagnosis. In theory, the phases containing this time information can be calculated from the Fourier coefficients; in practice, calculating them with adequate precision is virtually impossible.
In addition, the lack of time information makes Fourier transforms vulnerable to errors. "If when you record an hour-long signal you have an error in the last five minutes, the error will corrupt the whole Fourier transform," Meyer points out. And phase errors are disastrous; if you make the least error in phase, you can end up with something that has nothing to do with your original signal.
To get around this problem, the windowed Fourier transform was created in the 1940s. The idea is to analyze the frequencies of a signal segment by segment; that way, one can at least say that whatever is happening is happening somewhere in a given segment. So while the Fourier transform uses sines and cosines to analyze a signal, windowed Fourier uses a little piece of a curve. This curve serves as the "window," which remains fixed in size for a given analysis; inside it one puts oscillations of varying frequency.
But these rigid windows force painful compromises. The smaller your window, the better you can locate sudden changes, such as a peak or discontinuities, but the blinder you become to the lower-frequency components of your signal. (These lower frequencies won't fit into the little window.) If you choose a bigger window, you can see more of the low frequencies but the worse you do at "localizing in time."
So Yves Meyer, who as a harmonic analyst was well aware of the power and limitations of Fourier analysis, was interested when he first heard of a new way to break down signals, or functions, into little waves—ondelettes in French—that made it possible to see fleeting changes in a signal without losing track of frequencies.
TALKING TO HEATHENS
"I got involved almost by accident," recalls Meyer. "I was a professor at the Ecole Polytechnique, where we shared the same photocopy machine with the department of theoretical physics. The department chairman liked to read everything, know everything; he was constantly making photocopies. Instead of being exasperated when I had to wait, I would chat with him while he made his copies.
"One day in the spring of 1985 he showed me an article by a physicist colleague of his, Alex Grossmann in Marseille, and asked whether it interested me. It involved signal processing, using a mathematical technique I was familiar with. I took the train to Marseille and started working with Grossmann."
Often pure math "trickles down" to applications, but this was not the case for wavelets, Meyer added. "This is not something imposed by the mathematicians; it came from engineering. I recognized familiar mathematics, but the scientific movement was from application to theory. The mathematicians did a little cleaning, gave it more structure, more order."
Structure and order were needed; the predecessors of today's wavelets had grown in a topsy-turvy fashion, to the extent that in the early days wavelet researchers often found themselves unwittingly recreating work of the past. "I have found at least 15 distinct roots of the theory, some going back to the 1930s," Meyer said. "David Marr, who worked on artificial vision and robotics at MIT, had similar ideas. The physics community was intuitively aware of wavelets dating back to a paper on renormalization by Kenneth Wilson, the Nobel prize winner, in 1971."
But all these people in mathematics, physics, vision, and information processing didn't realize they were speaking the same language, partly for the simple reason that they rarely spoke to one another but also partly because the early work existed in such disparate forms. (Grossmann had in fact spoken about wavelets to other people in Meyer's field, but they "didn't make the connection," he said. "With Yves it was immediate, he realized what was happening.")
Wavelet researchers sometimes joke that the main benefit of wavelets is to allow them to have wavelet conferences. Behind that joke lies the reality that the modern coherent language of wavelets has provided an unusual opportunity for people from different fields to speak and work together, to everyone's benefit.
"Under normal circumstances the fields are pretty much water-tight one to the other," Grossmann said. "So one of the main reasons that many people find this field very interesting is that they have found themselves outside of their usual universe, talking to heathens of various kinds. Anybody who is not in one's little village is a heathen by definition, and people are always surprised to see—'look, they have two ears and a single nose, just like us!' That has been a very pleasant experience for everyone."
"THIS MUST BE WRONG.…"
Tracing the history of wavelets is almost a job for an archeologist, but let's take as a starting point Jean Morlet, who developed them independently in prospecting for oil for the French oil company Elf-Aquitaine. (It was he who baptized the field, originally using the term "wavelets of constant shape" to distinguish them from other "wavelets" in geophysics.) A standard way to look for underground oil is to send vibrations into the earth and analyze the echoes that return. Doing this, Morlet became increasingly dissatisfied with the limits of Fourier analysis; he wanted to be able to analyze brief changes in signals. To do this he figured out both a way to decompose a signal into wavelets and a way to reconstruct the original signal.
"The thing that is surprising is how very far Jean went all by himself, with no formal baggage. He had a lot of intuition to make it work without knowing why it worked," says Marie Farge of the Ecole Normale Supérieure in Paris, who uses wavelets to study turbulence.
But when Morlet started showing his results to others in the field, he was told that "this must be wrong, because if it were right, it would be known." Convinced that his wavelets were important—and aware that he didn't understand why they worked—Morlet spoke to a physicist at the Ecole Polytechnique who sent him, in 1981, to see Alex Grossmann in Marseille.
"Jean was sent to me because I work in phase space quantum mechanics," Grossmann said. "Both in quantum mechanics and in signal processing you use the Fourier transform all the time—but then somehow you have to keep in mind what happens on both sides of the transform.
When Jean arrived, he had a recipe, and the recipe worked. But whether these numerical things were true in general, whether they were approximations, under what conditions they held, none of this was clear.''
The two spent a year answering those questions. Their approach was to show mathematically that when wavelets represent a signal, the amount of "energy" of the signal (a measure of its size) is unchanged. This means that one can transform a signal into wavelet form and then get exactly the same signal back again—a crucial condition. It also means that a small change in the wavelet representation produces a correspondingly small change in the signal; a little error or change will not be blown out of proportion.
The work involved a lot of experimenting on personal computers. "One of the many reasons why the whole thing didn't come out earlier is that just about this time it became possible for people who didn't spend their lives in computing to get a little personal computer and play with it," Grossmann says. "Jean did most of his work on a personal computer. Of course, he could also handle huge computers, that's his profession, but it's a completely different way of working. And I don't think I could have done anything if I hadn't had a little computer and some graphics output."
A MATHEMATICAL MICROSCOPE
Wavelets can be seen as an extension of Fourier analysis. As with the Fourier transform, the point of wavelets is not the wavelets themselves; they are a means to an end. The goal is to turn the information of a signal into numbers—coefficients—that can be manipulated, stored, transmitted, analyzed, or used to reconstruct the original signal (see Box on p. 212; Figure 7.3).
The basic approach is the same. The coefficients tell in what way the analyzing function (sines and cosines, a Fourier window or wavelets) needs to be modified in order to reconstruct the original signal. The idea underlying the calculation of coefficients is the same (although in practice the mathematical details vary). For his wavelets Morlet even used the Gaussian, or bell-shaped, function often used in windowed Fourier analysis. But he used it in a fundamentally different way. Instead of filling a rigid window with oscillations of different frequencies, he did the reverse. He kept the number of oscillations in the window constant and varied the width of the window, stretching or compressing it like an accordion or a child's slinky (see Figure 7.4). When he stretched the wavelet, the oscillations inside were stretched,
|
The Wavelet Transform The wavelet transform decomposes a signal into wavelet coefficients. Each wavelet is multiplied by the corresponding section of the signal. Then one integrates (measures the area enclosed by the resulting curve). The result is the coefficient for that particular wavelet. Essentially, the coefficient measures the correlation, or agreement, between the wavelet (with its peaks and valleys) and the corresponding segment of the signal. "With wavelets, you play with the width of the wavelet in order to catch the rhythm of the signal," Meter says. "Strong correlation means that there is a little piece of the signal that looks like the wavelet." Constant stretches give wavelet coefficients with the value zero. (By definition, a wavelet has an integral of zero—half the area enclosed by the curve of the wavelet is above zero and half is below. Multiplying a wavelet by a constant changes both the positive and the negative components equally, so the integral remains zero.) Wavelets can also be made that give coefficients of zero when they meet linear and quadratic stretches and even higher polynomials. The more zero coefficients, the greater the compression of the signal, which makes it cheaper to store or transmit, and can simplify calculations. A typical signal may have about 100,000 values, but only 10,000 wavelets are needed to express it; parts of the signal that give coefficients of zero are automatically disregarded. Using wavelets that are "blind" to linear and quadratic stretches, and higher polynomials, also makes it easier to detect very irregular changes in a signal. Such wavelets react violently to irregular changes, giving big coefficients that stand out against the background of very small coefficients and zero coefficients indicating regular changes. |
decreasing their frequency; when he squeezed the wavelet, the oscillations inside were squeezed, resulting in higher frequencies.
As a result, wavelets adapt automatically to the different components of a signal, using a big "window" to look at long-lived components of low frequency and progressively smaller windows to look at short-lived components of high frequency. The procedure is called multiresolution; the signal is studied at a coarse resolution to get an overall picture and at higher and higher resolutions to see increasingly fine details. Wavelets have in fact been called a "mathematical microscope";
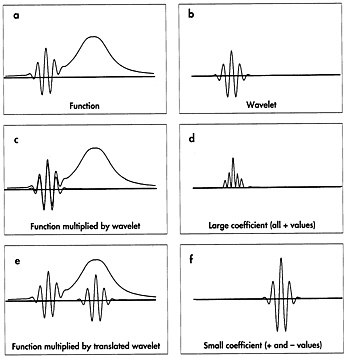
FIGURE 7.3 In the wavelet transform a wavelet is compared successively to different sections of a function. The product of the section and the wavelet is itself a curve; the area under that curve is the wavelet coefficient. Sections of the function that look like the wavelet give big coefficients, as seen in panels c and d. (Two negative functions multiplied together give a positive function.) Slowly changing sections produce small coefficients, as seen in panels e and f. (Courtesy of John Hubbard, Cornell University.)
compressing wavelets increases the magnification of this microscope, enabling one to take a closer and closer look at small details in the signal.
And unlike a Fourier transform, which treats all parts of a signal equally, wavelets only encode changes in a function. That is, unchanging stretches of a signal give coefficients with the value zero, which can be ignored. This makes them good for "seeing" changes—peaks in a signal, for example, or edges in a picture—and also means that they can be effective for compressing information.
"Wavelet analysis is a way of saying that one is sensitive to changes," Meyer says. "It's like the way we respond to speed." We don't feel the speed of a train as long as the speed is constant, but we notice when it speeds up or slows down.
MOTHER OR AMOEBA?
In wavelet analysis a function is represented by a family of little waves: what the French call a "mother" wavelet, a "father," and a great many babies of various sizes. But the French terminology "shows a scandalous misunderstanding of human reproduction," objects Cornell mathematician Robert Strichartz. "In fact the generation of wavelets more closely resembles the reproductive life style of an amoeba.''
To make baby wavelets one clones la mère and then either stretches or compresses the new wavelets; in mathematical jargon they are "dilated." These new wavelets can then be shifted about or "translated."
But the father function plays an important role. If you were looking at changes in temperature, you might be interested in broad changes over millions of years (the ice ages, for example), fluctuations over the past hundred years, or changes between day and night. If your real interest were the effect of climate on wheat production in the nineteenth century, you might look at temperatures on the scale of a year, a decade, or possibly a century; you wouldn't bother with changes on the scale of a
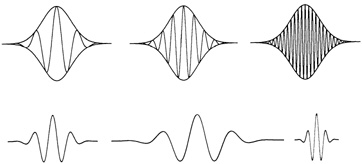
FIGURE 7.4 Top row: In windowed Fourier analysis the size of the window is fixed and the number of oscillations varies. A small window will be "blind" to low frequencies, which are too large to fit into the window. If a large window is used, information about a brief change will be submerged in the information about the entire section of the signal corresponding to the window. Bottom row: In wavelet analysis, a "mother wavelet" (left) is stretched or compressed to change the window size, making it possible to analyze a signal at different scales. The wavelet transform has been called a "mathematical microscope": wide wavelets give an overall picture,while smaller and smaller wavelets are used to "zoom in" on small details. (Courtesy of John Hubbard, Cornell University.)
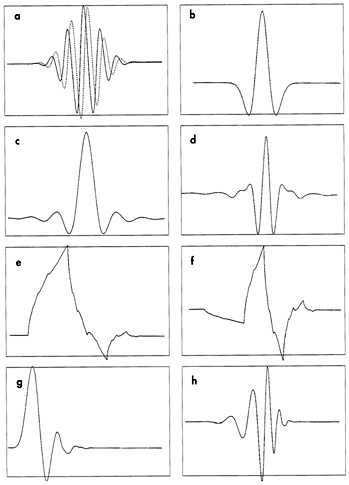
FIGURE 7.5 A small sample of wavelets and scaling functions (father functions). Wavelets shown in panels a and b are used in continuous representations; no father function is needed. The Morlet wavelet in panel a is complex valued; the dotted line gives the imaginary part. The "Mexican hat" shown in panel b is the second derivative of a Gaussian function (bell curve). The other wavelets are orthogonal, and are associated with a scaling function: c, Battle-Lemarié scaling function; d, Battle-Lemarié wavelet corresponding to c; e, Daubechies scaling function, order 2; f, Daubechies wavelet, order 2; g, Daubechies scaling function, order 7; h, Daubechies wavelet, order 7. The "order" of a wavelet is a measure of its regularity or smoothness; the Daubechies wavelet in panel h is more regular than the one in panel f. (Courtesy of Marie Farge and Eric Goirand.)
thousand years, much less a million. The father function (now more often referred to as the "scaling function") gives the starting point (see Figure 7.5).
To do this, you construct a very rough approximation of your signal, using only father functions. Imagine covering your signal with a row of
identical father functions. You then multiply each one by the corresponding section of the signal and integrate (measure the space under the resulting curve). The resulting numbers, or coefficients, give the information you would need to reconstitute a very rough picture of your function.
Wavelets are then used to express the details that you would have to add to that first rough picture in order to reconstitute the original signal. At the coarsest resolution, perhaps a hundred fat wavelets are lined up next to each other on top of the signal. The wavelet transform (see Box on p. 212) assigns to each one a coefficient that tells how much of the function has the same frequency as the fat wavelets.
At the next resolution the next generation of wavelets—twice as many, half as wide, and with twice the frequency—is put on top of the signal, and the process is repeated. Each step gives more details; at each step the frequency doubles and the wavelets are half as wide. (Typically, up to five different resolutions are used.)
If the procedure is compared to expressing the number 78/7 in decimal form (11.142857142 …), then the number 11 corresponds to the information given by the father functions, and the first set of wavelets would encode the details 0.1; the next, skinnier wavelets would encode 0.04, the next wavelets 0.002, the next wavelets 0.0008, and so on. The farther you go in layers of detail the more accurate the approximation will be, and each time you will be using a tool of the appropriate size. At the end, your signal has been neatly divided into different-frequency components—but unlike Fourier analysis, which gives you global amounts of different frequencies for the whole signal, wavelets give you a different frequency breakdown for different times on your signal.
To reconstruct the signal, you add the original rough picture of the function and all the details, by multiplying each coefficient by its wavelet or father function and adding them all together, just as to reconstruct the number 78/7 you add the number 11 given by the father and all the details: 0.1, 0.04, 0.002, and so on. Of course, the number will still be in decimal form; in contrast, when you reconstruct a signal from a father function, wavelets, and wavelet coefficients, you switch back to the original form of representation, out of "wavelet space."
AVOIDING REDUNDANCY
When Meyer took the train to Marseille to see Grossmann in 1985 the idea of multiresolution existed—it originated with Jean Morlet—but wavelets were limited and sometimes difficult to use, compared with the
choices available today (which are still changing rapidly). For one thing computing wavelet coefficients was rather slow. For another the wavelet transforms that existed then were all continuous. Imagine a wavelet slowly gliding along the signal, new wavelet coefficients being computed as it moves. (The process is repeated at all possible frequencies or scales; instead of brutally changing the size of the wavelets by a factor of 2, you stretch or compress it gently to get all the intermediate frequencies.)
In such a continuous representation, there is a lot of repetition, or redundancy, in the way information is encoded in the coefficients. (The number of coefficients is in fact infinite, but in practice "infinite may mean 10,000, which is not so bad," Grossmann says.) This can make it easier to analyze data, or recognize patterns. A continuous representation is shift invariant: exactly where on the signal one starts the encoding doesn't matter; shifting over a little doesn't change the coefficients. Nor is it necessary to know the coefficients with precision.
"It's like drawing a map," says Ingrid Daubechies, professor of mathematics at Princeton and a member of the technical staff at AT&T Bell Laboratories, who has worked with wavelets since 1985. "Many men draw these little lines and if you miss one detail you can't find your way. Most women tend to put lots of detail—a gas station here, a grocery store there, lots and lots of redundancy. Suppose you took a bad photocopy of that map, if you had all that redundancy you still could use it. You might not be able to read the brand of gasoline on the third corner but it would still have enough information. In that sense you can exploit redundancy: with less precision on everything you know, you still have exact, precise reconstruction."
But if the goal is to compress information in order to store or transmit it more cheaply, redundancy can be a problem. For those purposes it is better to have a different kind of wavelet, in an orthogonal transform, in which each coefficient encodes only the information in its own particular part of the signal; no information is shared among coefficients (see Box on p. 218).
At the time, though, Meyer wasn't thinking in terms of compressing information; he was immersed in the mathematics of wavelets. A few years before it had been proved that it is impossible to have an orthogonal representation with standard windowed Fourier analysis; Meyer was convinced that orthogonal wavelets did not exist either (more precisely, infinitely differentiable orthogonal wavelets that soon get close to zero on either side). He set out to prove it—and failed, in the summer of 1985, by constructing precisely the kind of wavelet he had thought didn't exist.
UNIFICATION
The following year, in the fall of 1986, while Meyer was giving a course on wavelets at the University of Illinois at Urbana, he received several telephone calls from a persistent 23-year-old graduate student in computer vision at the University of Pennsylvania in Philadelphia.
Stéphane Mallat (now at the Courant Institute of Mathematical Sciences in New York) is French and had been a student at the Ecole Polytechnique, one of France's prestigious grandes écoles, when Meyer taught there, but the two hadn't met. "The system at Ecole Polytechnique is very rigid and very elitist, the students have a rank when they graduate," Meyer said. "According to their rank they are directed to this or that profession. Mallat had found this system absurd and had decided that he would do what he wanted." So after graduating he did something that, from a French perspective, was extraordinary: abandoning the social and professional advantages of being a polytechnician (the first 150 in each graduating class are even guaranteed a salary for life), he left France for the United States.
"Working in the United States, for Stéphane Mallat, was starting over from zero," Meyer said. "No one there knows what Ecole Polytechnique is, they couldn't care less, he was in the same situation as a student from Iran, for example. … He's completely original, in his behavior, his way of thinking, his way of progressing in his career."
Mallat had heard about Meyer's work on wavelets from a friend in the summer of 1986 while he was vacationing in St. Tropez; to him it sounded suspiciously familiar. So on returning to the United States, he called Meyer, who agreed to meet him at the University of Chicago. The two spent 3 days holed up in a borrowed office ("I kept telling Mallat that he absolutely had to go to the Art Institute in Chicago, but we never had time," Meyer says) while Mallat explained that the multiresolution Meyer and others were doing with wavelets was the same thing that electrical engineers and people in image processing were doing under other names.
"This was a completely new idea," Meyer said. "The mathematicians were in their corner, the electrical engineers were in theirs, the people in vision research like David Marr were in another corner, and the fact that a young man who was then 23 years old was capable of saying, you are all doing the same thing, you have to look at that from a broader perspective—you expect that from someone older."
In 3 days the two worked out the mathematical details; since Meyer was already a full professor, at his insistence the resulting paper,
"Multiresolution Approximation and Wavelets," appeared under Mallat's name alone. The paper made it clear that work that existed in many different guises and under many different names—the pyramid algorithms used in image processing, the quadrature mirror filters of digital speech processing, zero-crossings, wavelets—were at heart all the same. For using wavelets to look at a signal at different resolutions can be seen as applying a succession of filters: first filtering out everything but low frequencies, then filtering out everything but frequencies twice as high, and so on. (And, in accordance with Shannon's sampling theorem, wavelets automatically "sample" high frequencies more often than low frequencies, since as the frequency doubles the number of wavelets doubles.)
The realization benefited everyone. A whole mathematical literature on wavelets existed by 1986, some of it developed before the word wavelet was even coined; this mathematics could now be applied to other fields.
"All those existing techniques were tricks that had been cobbled together; they had been made to work in particular cases," says Marie Farge. "Mallat helped people in the quadrature mirror filters community, for example, to realize that what they were doing was much more profound and much more general, that you had theorems, and could do a lot of sophisticated mathematics."
Wavelets got a big boost because Mallat also showed how to apply to wavelet multiresolution fast algorithms that had been developed for other fields, making the calculation of wavelet coefficients fast and automatic—essential if they were to become really useful. And he paved the way for the development by Daubechies of a new kind of regular orthogonal wavelet that was easier and faster to use: wavelets with "compact support." Such wavelets have the value zero everywhere outside a certain interval (between -2 and 2, for example).
EVADING INFINITY
Daubechies, who is Belgian, was trained as a mathematical physicist; she had worked with Grossmann in France on her Ph.D. research and then spent 2 years in the United States working on quantum mechanics. She is the recipient of a 5-year MacArthur fellowship.
"Ingrid's role has been crucial," Grossmann said. "Not only has she made very important contributions, but she has made them in a form that was legible, and usable, to various communities. She is able to speak to engineers, to mathematicians; she is trained as a physicist and one sees her training in quantum mechanics."
Daubechies had heard about Meyer and Mallat's multiresolution work very early on. "Yves Meyer had told me about it at a meeting. I had been thinking about some of these issues, and I got very interested," she said. The orthogonal wavelets Meyer had constructed trial off at the sides, never actually ending; this meant that calculating a single wavelet coefficient was a lot of work.
"I said why can't we just start from the fact that we want those numbers and that we want a scheme that has these properties [and] proceed from there," Daubechies said. "That's what I did. … I was extremely excited; it was a very intense period. I didn't know Yves Meyer so very well at the time. When I had the first construction, he had gotten very excited, and somebody told me he had given a seminar on it. I knew he was a very strong mathematician and I thought, oh my God, he's probably figuring out things much faster than I can. … Now I know that even if that had been true, he would not have taken credit for it, but it put a very strong urgency on it; I was working very hard. By the end of March 1987 I had all the results."
Together, multiresolution and wavelets with compact support formed the wavelet equivalent of the fast Fourier transform: again, not just doing calculations a little faster, but doing calculations that otherwise very likely wouldn't be done at all.
HEISENBERG
Multiresolution and Daubechies's wavelets also made it possible to analyze the behavior of a signal in both time and frequency with unprecedented ease and accuracy, in particular, to zoom in on very brief intervals of a signal without becoming blind to the larger picture.
But although one mathematician hearing Daubechies lecture objected that she seemed "to be beating the uncertainty principle," the Heisenberg uncertainty principle still holds. You cannot have perfect knowledge of both time and frequency. Just as you cannot know simultaneously both the position and momentum of an elementary particle (if you could hold an electron still long enough to figure out where it was, you would no longer know how fast it would have been going if you hadn't stopped it). The product of the two uncertainties (or spreads of possible values) is always at least a certain minimum number.
One must always make a compromise; knowledge gained about time is paid for in frequency, and vice versa. "At low frequencies I have wide wavelets, and I localize very well in frequency but very badly in time. At very high frequency I have very narrow wavelets, and I localize very well in time but not so well in frequency," Daubechies said.
This imprecision about frequency results from the increasing range of frequencies at high frequencies: as we have seen, frequency doubles each time one goes up an octave. This widening spread of frequencies can be seen as a barrier to precision, but it's also an opportunity that engineers have learned to exploit. It is the reason why the telephone company shifts voices up into higher frequencies, not down to lower ones, when it wants to fit a lot of voices on one line: there's a lot more room up there. It also explains the advantage of fiber optics, which carry high-frequency light signals, over conventional telephone wires.
PUTTING WAVELETS TO WORK
Wavelets appear unlikely to have the revolutionary impact on pure mathematics that Fourier analysis has had. "With wavelets it is possible to write much simpler proofs of some theorems," Daubechies said. "But I know of only a couple of theorems that have been proved with wavelets, that had not been proved before." But the characteristic features of wavelets make them suited for a wide range of applications.
Because wavelets respond to change and can narrow in on particular parts of a signal, researchers at the Institute du Globe in Paris are using them to study the minuscule effect on the speed of the earth's rotation of the El Niño ocean current that flows along the coast of Peru. British scientists are using wavelets to study ocean currents around the Antarctic, and researchers and mechanics are exploring their use in detecting faults in gears by analyzing vibrations.
Multiresolution lends itself to a variety of applications in image processing. One can imagine transmitting pictures electronically quickly and cheaply by sending only a coarse picture, calling up a more detailed picture only when needed. Mathematician Dennis Healy, Jr., and radiologist John Weaver of Dartmouth College are exploring the use of wavelets for "adaptive" magnetic resonance imaging, in which higher resolutions would be used selectively, depending on the results already found at coarser scales. (Since a half-hour magnetic resonance imaging exam costs $500 to $1000 or more, anything that reduces the time spent is of obvious interest.)
Multiresolution is also useful in studying the large-scale distribution of matter in the universe, which for years was thought to be random but which is now seen to have a complicated structure, including "voids" and "bubbles."10 Wavelets have enabled astronomers at the Observatoire de la Côte d'Azur in Nice to identify a subcluster at the center of the Coma supercluster, a cluster of about 1400 galaxies. Subsequently,
that subcluster was identified as an x-ray source. "Wavelets were like a telescope pointing to the right place," Meyer said. And at the Centre de Recherche Paul Pascal in Pessac (near Bordeaux), Alain Arnéodo and colleagues have exploited "the fascinating ability of the wavelet transform to reveal the construction rule of fractals"11.
In addition, it can be instructive to compare wavelet coefficients at different resolutions. Zero coefficients, which indicate no change, can be ignored, but nonzero coefficients indicate that something is going on—whether an abrupt change in the signal, an error, or noise (an unwanted signal that obscures the real message). If coefficients appear only at fine scales, they generally indicate the slight but rapid variations characteristic of noise. "The very fine scale wavelets will try to follow the noise," Daubechies explains, while wavelets at coarser resolutions are too approximate to pick up such slight variations.
But coefficients that appear at the same part of the signal at all scales indicate something real. If the coefficients at different scales are the same size, it indicates a jump in the signal; if they decrease, it indicates a singularity—an abrupt, fleeting change. It is even possible to use scaling to sharpen a blurred signal. If the coefficients at coarse and medium scales suggest there is a singularity, but at high frequencies noise overwhelms the signal, one can project the singularity into high frequencies by restoring the missing coefficients—and end up with something better than the original.
CUT THE WEEDS AND SPARE THE DAISIES
Wavelets also made possible a revolutionary method for extricating signals from pervasive white noise ("all-color," or all-frequency, noise), a method that Meyer calls a "spectacular application" with great potential in many fields, including medical scanning and molecular spectroscopy.
An obvious problem in separating noise from a signal is knowing which is which. If you know that a signal is smooth—changing slowly—and that the noise is fluctuating rapidly, you can filter out noise by averaging adjacent data to kill fluctuations while preserving the trend. Noise can also be reduced by filtering out high frequencies. For smooth signals, which change relatively slowly and therefore are mostly lower frequency, this will not blur the signal too much.
But many interesting signals (the results of medical tests, for example) are not smooth; they contain high-frequency peaks. Killing all high frequencies mutilates the message—"cutting the daisies along with the weeds," in the words of Victor Wickerhauser of Washington University in St. Louis.
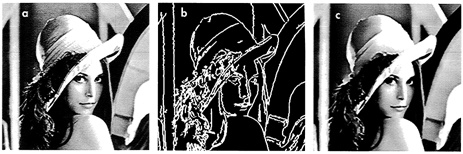
FIGURE 7.6 The wavelet transform can detect the edges of an image at several scales. Among all edges of panel a, a computer program has selected the ''important" ones. Panel b displays these edges at a fine scale. Panel c is reconstructed from edges selected at different scales, with an algorithm developed by Mallat and Zhifeng Zhang. The edge selection removes the noise and small irregular structures. The skin is now smoother.
A simple way to avoid this blind slaughter has been found by a group of statisticians. David Donoho of Stanford University and the University of California at Berkeley and his colleague Iain Johnstone of Stanford had proved mathematically that if a certain kind of orthogonal basis existed, it would do the best possible job of extracting a signal from white noise. (A basis is something with which you can represent any possible function in a given space; each mother wavelet provides a different basis, for example, since any function can be represented by it and its translates and dilates.)
This result was interesting but academic since Donoho and Johnstone did not know whether such a basis existed. But in the summer of 1990, when Donoho was in St. Flour, in France's Massif Central, to teach a course in probability, he heard Dominique Picard of the University of Paris-Jussieu give a talk on the possibility of using wavelets in statistics. After discussing it with her and with Gérard Kerkyacharian of the University of Picardy in Amiens, "I realized it was what we had been searching for a long time," Donoho recalled. "We knew that if we used wavelets right, they couldn't be beaten."
The method is simplicity itself: you apply the wavelet transform to your signal, throw out all coefficients below a certain size, at all frequencies or resolutions, and then reconstruct the signal. It is fast (because the wavelet transform is so fast), and it works for a variety of kinds of signals. The astonishing thing is that it requires no assumptions about the signal. The traditional view is that one has to know, or assume, something about the signal one wants to extract from noise—that, as Grossmann put it, "if there is absolutely no a priori assumption you can make about your signal, you may as well go to sleep. On the other hand, you don't want to put your wishes into your algorithm and then be surprised that your wishes come out."
The wavelet method stands this traditional wisdom on its head. Making no assumptions about the signal, Donoho says, "you do as well as someone who makes correct assumptions, and much better than someone who makes wrong assumptions." (Furthermore, if you do know something about the signal, you can adjust the coefficient threshold and get even better results.)
The trick is that an orthogonal wavelet transform makes a signal look very different while leaving noise alone. "Noise in the signal becomes noise in the wavelet transform and it has about the same size at every resolution and location," Donoho says. (That all orthogonal representations leave noise unchanged has been known since the 1930s.) So while noise masks the signal in "physical space," the two become disentangled in "wavelet space."
In fact, Donoho said, a number of researchers—at the Massachusetts Institute of Technology, Dartmouth, the University of South Carolina, and elsewhere—independently discovered that thresholding wavelet coefficients is a good way to kill noise. "We came to it by mathematical decision theory, others simply by working with wavelet transforms and noticing what happened," he said.
Among those was Mallat, who uses a somewhat different approach. Donoho's method works for a whole range of functions but isn't necessarily optimal for each. When it is applied to blurred images, for example, it damages some of the edges; the elimination of small coefficients creates ripples that can be annoying. Mallat and graduate student Wen Liang Hwang developed a way to avoid this by computing the wavelet transform of the signal and selecting the points where the correlation between the curve and the wavelet is greatest, compared to nearby points. These maximum values, or wavelet maxima, are kept if the points are thought to belong to a real edge and discarded if they are thought to correspond to noise. (That decision is made automatically, but it requires more calculations than Donoho's method; it is based on the existence and size of maxima at different resolutions.)
WAVELETS DON'T EXIST …
Although Donoho and Johnstone's technique is simple and automatic, wavelets aren't always foolproof. With orthogonal wavelets it can matter where one starts encoding the signal: shifting over a little can change the coefficients completely, making pattern analysis hazardous. This danger does not exist with continuous wavelets, but they have their own pitfalls; what looks like a correlation of coefficients (different coefficients "seeing" the same part on the signal) may sometimes be an
artifact introduced by the wavelets themselves. "It's the kind of thing where you can shoot yourself in the foot without half trying," Grossmann said.
Generally, using wavelets takes practice. "With a Fourier transform, you know what you get," Meyer says. "With a wavelet transform you need some training in order to know what you get. I have a report from EDF [Electricité de France] giving conclusions of engineers about wavelets—they say they have trouble with interpretation." Part of that difficulty may be fear of trying something new; Gregory Beylkin of the University of Colorado at Boulder reports that one student, who learned to use wavelets before he knew Fourier analysis, experienced no difficulty. Farge has had similar experiences, but Meyer thinks the problem is real.
Because Fourier analysis has existed for so long, and most physicists and engineers have had years of training with Fourier transforms, interpreting Fourier coefficients is second nature to them. In addition, Meyer points out, Fourier transforms aren't just a mathematical abstraction: they have a physical meaning. "These things aren't just concepts, they are as physical, as real, as this table. But wavelets don't exist in nature; that's why it is harder to interpret wavelet coefficients," he said.
Curiously, though, both our ears and our eyes appear to use wavelet techniques in the first stages of processing information. The work on "wavelets" and hearing goes back to the 1930s, Daubechies said. "They didn't talk about wavelets—they talked about constant q filtering, in which the higher the frequency, the better resolution you have in time." This is unlikely to lead to new insights about hearing or vision, she said, but it could make wavelets effective in compressing information. "If our ear uses a certain technique to analyze a signal, then if you use that same mathematical technique, you will be doing something like our ear. You might miss important things, but you would miss things that our ear would miss too."
COMPRESSING INFORMATION
One way to cope with an ever-increasing volume of signals is to widen the electronic highways—for example, by moving to higher frequencies. Another, which also reduces storage and computational costs, is to compress the signal temporarily, restoring it to its original form when needed.
In fact, only a small number of all possible "signals" are capable of being compressed, as the Russian mathematician Andrei Kolmogorov pointed out in the 1950s. A compressible signal can by definition be expressed
by something shorter than itself: one sequence of digits (the signal) is encoded by a shorter sequence of digits (e.g., a computer program).
It is easy to see that, using any given language (such as the computer language Pascal), the number of short sequences is much smaller than the number of long sequences: most long sequences cannot be encoded by anything shorter than themselves. (Even a highly efficient encoding scheme like a library card catalog cannot cope with an infinite number of books; eventually, the only way to distinguish one book from another would be to print the entire book in the card catalog.) Like Heisenberg with his uncertainty principle, Kolmogorov has set an absolute limit that mathematicians and scientists cannot overcome, however clever they are. Accepting some loss of information makes more compression possible, but a limit still remains.
In practice, however, many signals people want to compress have a structure that lends itself to compression; they are not random. For instance, any point in such a signal might be likely to be similar to points near it. (In a picture of a white house with a blue door, a blue point is likely to be surrounded by other blue points, a white point by other white points.) Wavelets lend themselves to such compression; because wavelet coefficients indicate only changes, areas with no change (or very small change) are automatically ignored, reducing the number of figures that have to be kept to encode the information.
So far, Daubechies says, image compression factors of about 35 or 40 have been achieved with wavelets with little loss. That is, the information content of the compressed image is about 1/35th or 1/40th the information content of the original. But wavelets alone cannot achieve those compression factors; an even more important role is played by clever quantization methods, mathematical ways of giving more weight in the encoding to information that is important for human perception (edges, for example) than information that is less so.
"If you just buy a commercially available image compressor you can get a factor of 10 to 12, so we're doing better than that," Daubechies said. "However, people in research groups who fine-tune the Fourier transform techniques in commercial image compressors claim they can also do something on the order of 35. So it's not really clear that we can beat the existing techniques. I do not think that image compression—for instance, television image compression—is really the place where wavelets will have the greatest impact."
But the fact that wavelets concentrate the information of a signal in relatively few coefficients makes them good at detecting edges in images, which may result in improved medical tests. Healy and Weaver have
found that with wavelets they can use magnetic resonance imaging to track the edge of the heart as it beats by sampling only a few coefficients. And wavelet compression is valuable in speeding some calculations. In the submarine detection work that Frazier and colleague Jay Epperson did for Daniel H. Wagner Associates, they were able to compress the original data by a factor of 16 with good results.
Ways to compress huge matrices (square or rectangular arrays of numbers) have been developed by Beylkin, working with Ronald Coifman and Vladimir rokhlin at Yale. The matrix is treated as a picture to be compressed; when it is translated into wavelets, "every part of the matrix that could be well represented by low-degree polynomials will have very small coefficients—it more or less disappears," Beylkin says. Normally, if a matrix has n2 entries, then almost any computation requires at least n2 calculations and sometimes as many as n3. With wavelets one can get by with n calculations—a very big difference when n is large.
Talking about numbers "more or less" disappearing, or treating very small coefficients as zero, may sound sloppy but it is "very powerful, very important"—and must be done very carefully, Grossmann says. It works only for a particular large class of matrices: "If you have no a priori knowledge about your matrix, if you just blindly use one of those things, you can expect complete catastrophe."
Just how important these techniques will prove to be is still up in the air. Daubechies predicts that "5, certainly 10 years from now you'll be able to buy software packages that use wavelets for doing big computations, in simulations, in solving partial differential equations."
Meyer is more guarded. "I'm not saying that algorithmic compression by wavelets is a dead end; on the contrary, I think it's a very important subject. But so far there is very little progress; it's just starting." Of the matrices used in turbulence, he said, only one in 10 belongs to the class for which Beylkin's algorithm works. "In fact, Rokhlin has abandoned wavelet techniques in favor of methods adapted to the particular problem; he thinks that every problem requires an ad hoc solution. If he is right, then Ingrid Daubechies is wrong, because there won't be 'prefabricated' software that can be applied to a whole range of problems, the way prefabricated doors or windows are used in housing construction."
TURBULENCE AND WAVELETS
Rokhlin works on turbulent flows in connection with aerodynamics; Marie Farge in Paris, who works in turbulence in connection with
weather prediction, remains confident that wavelets will prove to be an effective tool. She was working on her doctoral thesis when she heard about wavelets from Alex Grossmann in 1984.
"I was very much excited—in turbulence we have needed a tool like wavelets for a long time," she said. (Much later she learned that some turbulence researchers in the former Soviet Union, in Perm, had been working with similar techniques completely independently since 1976.)
"When you look at turbulence in Fourier space," Farge explains, "you see cascades of energy, where energy is transferred from one wavenumber [frequency] to another. But you don't see how those cascades relate to what is happening in physical space; we had no tool that let us see both sides at once, so we could say, voilà , this cascade corresponds to this interaction. So when Alex showed me that wavelets were objects that allowed one to unfold the representation both in physical space and in scale, I said to myself, this is it, now we're going to get somewhere.
"I invited him to speak in a seminar and told everyone in the turbulence community in Paris to come. I was shocked by their reaction to his talk. 'Don't waste your time on that,' they told me. Now some of the people who were the most skeptical are completely infatuated and insist that everyone should use wavelets. It's just as ridiculous. It's a new tool, and one cannot force it into problems as shapeless as turbulence if it isn't calibrated first on academic signals that we know very well. We have to do a lot of experiments, get a lot of practice, develop methods, develop representations."
She uses orthogonal wavelets, or related wavelet packets, for compression but continuous wavelets for analysis: "I would never read the coefficients themselves in an orthogonal basis; they are too hard to read." With continuous wavelets she can take a one-dimensional signal that varies in space, put it into wavelet space, and get a two-dimensional function that varies with space and scale: she can actually see, on a computer screen or a printout what is happening at different scales at any given point.
Orthogonal wavelets also give time-scale information, of course (although in a rougher form, since one doubles the scale each time, ignoring intermediate scales). The difference is largely one of legibility. Once, Meyer says, Jean Jacques Rousseau invented a musical notation based on numbers rather than notes on a staff, only to be told that it would never catch on, that musicians wanted to see the shape and movement of music on the page, to see the patterns formed by notes.
The coefficients of orthogonal wavelets correspond to Rousseau's music by numbers; continuous wavelets to the musical notation we know.
Farge compares the current state of turbulence research to "prescientific zoology." Many observations are needed, she says, to see what structures in turbulence are dynamically important and to try to recreate the theory in terms of their interactions. Possible candidates are ill-defined creatures called "coherent structures" (a tornado, for example, or the vortex that forms when you drain the bath). She uses wavelets to isolate them and to see how many exist at different scales or whether a single structure exists at a whole range of scales.
Identifying the dynamically important structures would tell researchers "where we should invest lots of calculations and where we can skimp," Farge said. For studying turbulence requires calculations that defy the most powerful computers. The Reynolds number for interactions of the atmosphere—a measure of its turbulence—ranges from 109 to 1012; direct computer simulations of turbulence can now handle Reynolds numbers on the order of 102 or 103.
But so far the results have been disappointing, Meyer says: "There should be something between turbulence and wavelets, everyone thinks so, but so far no one has a real scientific fact to offer." Certainly wavelets do not offer an easy trick for solving nonlinear equations (such as the Navier-Stokes equation used to describe turbulent flows), in the way that Fourier turned many linear equations into cookbook problems.
"Wavelets are structurally a little better adapted to nonlinear situations," such as those found in turbulence, Meyer said. "But is something that is better in principle actually better in practice?" He is disturbed that when wavelets are used in nonlinear problems they "are used in a neutral way; they are always the same wavelets—they aren't adapted to the problem. … It is in this sense that there is perhaps a doubt about using wavelets to solve nonlinear problems. What can one hope for from methods that don't take the particular problem into account? At the same time, there are general methods in science. So one can give a different answer depending on one's personality."
FINGERPRINTS AND HUNGARIAN DANCES
One contribution of wavelets, Farge says, is that they have "forced people to think about what the Fourier transform is, forced them to think that when they choose a type of analysis they are in fact mixing the signal and the function used for the analysis. Often when people use the same technique for several scientific generations, they become blind to it."
As work with wavelets progressed, it became clear that if Fourier analysis had limitations, wavelet analysis did also. As David Marr wrote in Vision, "Any particular representation makes certain information explicit at the expense of information that is pushed into the background and may be quite hard to recover." Very regular, periodic signals are more easily recognized, and more efficiently encoded, by a Fourier transform than by wavelets, for example.
So Coifman, Meyer, and Wickerhauser developed an information-compression scheme to take advantage of the strengths of both Fourier and wavelet methods: the "Best Basis" algorithm.
In Best Basis a signal enters a computer like a train entering a switchyard in a train station. The computer analyzes the signal and decides what basis could encode it most efficiently, with the smallest possible amount of information. At one extreme it might send the signal to Fourier analysis (for signals that resemble music, with repeating patterns). At the other extreme it might send it to a wavelet transform (irregular signals, fractals, signals with small but important details). Signals that don't fall clearly into either group are represented by "wavelet packets" that combine features of both Fourier analysis and wavelets.
Loosely speaking, a wavelet packet is the product of a wavelet by a wiggle, an oscillating function. The wavelet itself can then react to abrupt changes, while the wiggle inside can react to regular oscillations. "The idea is that you are introducing a new freedom," Meyer said. Since the choice of wiggles is infinite, "it gives a family that is very rich."
Working with the FBI, Wickerhauser and Coifman applied Best Basis to the problem of fingerprint compression, and in a test conducted by the FBI's Systems Technology Unit it outperformed other methods. (Because Best Basis was being patented, Wickerhauser said, the FBI did not adopt it but instead custom-made a similar technique.) So far, the wavelet technique is intended only to compress fingerprints for storage or transmission, reconstructing them before identification by people or machines. But the FBI plans to hold a competition for automatic identification systems. "Those who understand how to use wavelet coefficients to identify will probably win, on speed alone if nothing else, because the amount of data is so much less," Wickerhauser said.
In studies with military helicopters, Best Basis has been used to simplify the calculations needed to decide, from radar signals, whether a possible target is a tank or perhaps just a boulder. In trials the Best Basis algorithm could compress the 64 original numbers produced by the radar system to 16 and still give "identical or better results than the original 64, especially in the presence of noise," Wickerhauser said.
But probably the most unusual use of Best Basis has been in removing noise from a battered recording of Brahms playing his own work, recorded in 1889 on Thomas Edison's original phonograph machine, which used tinfoil and wax cylinders to record sound. The Yale School of Music had entrusted it to Coifman after all else had failed.
"Brahms was recorded playing his music for Edison," Wickerhauser said. "It was played on the radio sometime in the 1920s—possibly using a wooden needle, and was recorded off the radio. Then it was converted to a 78 record. That was the condition in which Yale had it—beaten to death."
Coifman's approach was to say that noise can be defined as everything that is not well structured and that "well structured" means easily expressed, with very few terms, with something like the Best Basis algorithm. So the idea is to use Best Basis to decompose the signal and to remove anything that is left over. The result was not musical—no one hoped for that, from a recording that contained perhaps 30 times as much noise as signal—but they were able to identify the music as variations on Hungarian dances. The project, with Jonathan Berger of the Yale School of Music, is still going on. "We don't know yet how far we can restore it," Coifman said.
BEYOND WAVELETS
For some purposes, however, Best Basis is not ideal. Because it treats the signal as a whole, it has trouble dealing with highly nonstationary signals—signals that change unpredictably. To deal with such signals Stéphane Mallat and Zhifeng Zhang have produced a more flexible system, called Matching Pursuits, which finds the best match for each section of the signal, out of "dictionaries" of waveforms.
"Instead of trying to globally optimize the match for the signal, we're trying to find the right waveform for each feature," Mallat said. "It's as if we're trying to find the best match for each 'word' in the signal, while Best Basis is finding the best match for the whole sentence."
Depending on the signal, Matching Pursuits uses one of two "dictionaries": one that contains wavelet packets and wavelets, another that contains wavelets and modified "windowed Fourier" waveforms. (While in standard windowed Fourier the size of the window is fixed and the number of oscillations within the window varies, in Matching Pursuits the size of the window is also allowed to vary.) First, the appropriate dictionary is scanned and the "word" chosen that best matches the signal; then that "word'' is subtracted out, and the best match is chosen for the remaining part of the signal, and so on. (To some
extent, the dictionaries can produce words on command, modifying waveforms to provide a better fit.)
Because the waveforms used are not orthogonal to each other, the system is slower than Best Basis: n2 calculations compared to n log n for Best Basis. On the other hand, the lack of orthogonality means that it doesn't matter where on the signal you start encoding. This makes it better suited for pattern recognition, for encoding contours and textures, for example.
But the quest for new ways to encode information is far from over. "When you speak, you have a huge dictionary of words and you pick the right words so that you can express yourself in a few words. If your dictionary is too small, you'll need a lot of words to express one idea," Mallat said. "I think the challenge we are facing right now is, when you have a problem, how are you going to learn the right representation? The Fourier transform is a tool, and the wavelet transform is another tool, but very often when you have complex signals like speech, you want some kind of hybrid scheme. How can we mathematically formalize this problem?"
In some cases the task goes beyond mathematics; the ultimate judge of effective compression of a picture, or of speech, is the human eye or ear, and developing the right mathematical representation is often intimately linked to human perception. Information is not all equal. Even a young child can draw a recognizable outline of a cat, for example, while the very notion of a drawing without edges is perplexing, like the Cheshire cat who vanished, leaving only his smile. Other differences are less well understood. People have no trouble differentiating textures, for example, while "after 20 years of research on texture, we still don't really know what it is mathematically," Mallat said.
Wavelets may help with this, especially since some wavelet-like techniques are used in human vision and hearing, but any illusions researchers may have had that wavelets will solve all problems unsuited to Fourier analysis have long since vanished; the field has become wide open.
"Wavelets have gone off in many directions; it becomes a little bit of a scholastic question, what you call wavelets," Grossmann says. "Some of the most interesting very recent things would technically not be called wavelets, the scale is introduced in a somewhat different way—but who cares?"
It may not be the least of the contributions made by wavelets that they have inspired both a closer and a broader look at mathematical languages for expressing information: a more judicious look at Fourier analysis, which was often used reflexively ("The first thing any engineer
does when he gets hold of a function is to Fourier transform it—it's an automatic reaction," one mathematician said) and a more free-ranging look at what else might be possible.
"When you have only one way of expressing yourself, you have limits that you don't appreciate," Donoho says. "When you get a new way to express yourself, it teaches you that there could be a third or a fourth way. It opens up your eyes to a much broader universe."
NOTES
REFERENCES
Cousin, V. 1831. Notes biographiques pour faire suite à l'éloge de M. Fourier (Biographical notes to follow praise of Mr. Fourier), Fourier file AdS, archives, Académie des Sciences, Institut de France, Paris.
Delambre, Jean-Baptiste. 1810. Rapport historique sur le progrès des sciences mathématiques depuis 1789 (Historical report on the progress of mathematical sciences since 1789), part of Rapport à l'Empereur sur le progrès des sciences, des lettres et des arts depuis 1789, published by Belin, Paris, 1989.
Encyclopedia Britannica, 11th ed. 1972. Harmonic analysis. Vol. 11, pp. 106–107.
Farge, M., J.C.R. Hunt and J.C. Vassilicos (eds). 1993. Wavelets, Fractals, and Fourier Transforms . Clarendon Press, Oxford.
Fourier, J. 1822. Théorie analytique de la chaleur (published in Oeuvres de Fourier, Vol. 1, Gauthier-Villars et fils, Paris 1888).
Healy, D., Jr., and J. B. Weaver. 1992. Two Applications of Wavelets Transforms in Magnetic Resonance Imaging. IEEE Transactions on Information Theory, Vol. 38, No. 2, March 1992.
Herivel, J. 1975. Joseph Fourier — the Man and the Physicist. Clarendon Press, Oxford.
Körner, T.W. 1988. Fourier Analysis. Cambridge University Press, Cambridge.
Lagrange, J.-L. Oeuvres de Lagrange, Gauthier-Villars, Paris, 1867–1892.
Marr, D. 1982. Vision. W. H. Freeman, New York.
Meyer, Y. (ed). 1992. Wavelets and Applications: Proceedings of the International Conference, Marseille, France. Masson and Springer-Verlag.
Meyer, Y. 1993. Wavelets: algorithms & applications. Society for Industrial and Applied Mathematics, Philadelphia. (This is an English translation of Les Ondelettes Algorithmes et Applications, Meyer, Y., Armond Colin, Paris, 1992.)
Pierce, J. R., and A. M. Noll. 1990. Signals — The science of telecommunications. Scientific American Library, New York.
Poincaré, H. 1956. Oeuvres de Henri Poincaré, vol. 11, Gauthier-Villars, Paris.
Strichartz, R. 1993. How to make wavelets, American Mathematical Monthly, Vol. 100, no. 6, June-July 1993, pp. 539–556.
Strömberg, J.-O. 1981. A modified Franklin system and higher-order spline systems on Rn as unconditional bases for Hardy spaces. Conference on Harmonic Analysis in Honor of Antoni Zygmund, vol. II, pp. 475–494; W. Beckner, A. Caldéron, R. Fefferman, and P. Jones, eds. University of Chicago, 1983.
RECOMMENDED READING
Books Accessible to the General Public
Gratten-Guinness, I., and J.R. Ravetz. 1972. Joseph Fourier, 1768–1830. MIT Press, Cambridge, Mass.
Herivel, John. 1975. Joseph Fourier—The Man and the Physicist. Clarendon Press, Oxford.
Körner, T.W. 1988. Fourier Analysis. Cambridge University Press, Cambridge.
(This is a book for mathematicians, but it includes delightful sections that require no mathematical background, such as the description of the laying of transatlantic cables, where "half a million pounds was being staked on the correctness of the solution of a partial differential equation." )
Pierce, John R., and A. Michael Noll. 1990. Signals—The Science of Telecommunications. Scientific American Library, New York.
A Sampling Of Technical Books
Benedetto, J., and M. Frazier (eds.) 1993. Wavelets: Mathematics and Applications. CRC Press, Boca Raton.
Chui, C.K. (ed.). 1992. Wavelets-A Tutorial in Theory and Applications. Academic Press, Boston.
Daubechies, I. 1992. Ten Lectures on Wavelets. Society for Industrial and Applied Mathematics, Philadelphia.
Farge, M., J.C.R. Hunt, and J.C. Vassilicos (eds.). 1993. Wavelets, Fractals, and Fourier Transforms. Clarendon Press, Oxford.
Körner, T.W. 1988. Fourier Analysis. Cambridge University Press, Cambridge.
Meyer, Y. 1990. Ondelettes et Opérateurs. Three volumes. Hermann, Paris. (English translation published by Cambridge University Press in 1992.)
Meyer, Y. 1992 Wavelets and Operators, Cambridge University Press, Cambridge and New York. (This is a translation of Ondelettes et Operateurs, Hermann, Paris, 1990.)
Meyer, Y. 1993. Wavelets: algorithms & applications. Society for Industrial and Applied Mathematics, Philadelphia.
Ruskai, B. (ed.) 1992. Wavelets and Their Applications. Jones and Bartlett, Boston.