8
Estimating the Risks
THE PRECEDING CHAPTERS have demonstrated that infants and children may have special sensitivities to certain toxic insults. Children also consume notably more of certain foods relative to their body weight than do adults. Thus, their ingestion of pesticide residues on these foods may be proportionately higher than that of adults. For certain chronic toxic effects such as cancer, exposures occurring early in life may pose greater risks than those occurring later in life. For these reasons, risk assessment methods that have traditionally been used for adults may require modification when applied to infants and children.
To evaluate the potential risks from dietary intake of pesticide residues by infants and children, some familiarity with basic toxicological approaches to risk assessment is required. In the first part of this chapter, the committee reviews principles of toxicological risk assessment, including interspecies extrapolation, forms of toxicity, mathematical models for assessing cancer risk, low-dose linearity, and multiple exposures. Special characteristics of infants and young children that must be considered when assessing their risks from dietary exposures to pesticides are then discussed.
The fundamental purpose of regulatory toxicology is the determination of risks (including zero risk) at various possible levels of human exposure to toxicants present in the environment. For risk assessment applications, it is useful to distinguish between toxic processes that are either stochastic or nonstochastic in nature. Stochastic processes such as carcinogenesis result from the random occurrence of one or more biological events in specific individuals. Thus, whether or not a particular individual will develop a cancerous lesion under specified conditions or exposure cannot
be predicted with certainty. Nonstochastic events such as enzyme inhibition following exposure to a certain toxicant are more predictable. Nonstochastic effects may not be seen if lifetime exposures are below a certain threshold concentration, whereas stochastic effects such as carcinogenesis may have no threshold. Different approaches to risk assessment are usually used for these two categories of response.
Information on health risks may be obtained directly from epidemiological and other studies of humans or indirectly through toxicological experiments conducted in animal models. Although results of laboratory studies are applicable to humans only indirectly, they can be used to predict potential health hazards in advance of actual human exposure and thus continue to be used widely to identify substances with potential toxicity.
Three major problems are inherent in the translation of results of animal tests to humans:
-
Laboratory tests are conducted at relatively high doses to induce measurable rates of response in a small sample of animals. These results must often extrapolated to lower doses that correspond to anticipated human exposure levels.
-
Interspecies differences must be considered when extrapolating between the animal model and humans.
-
It may be necessary to extrapolate from a route of exposure chosen for experimental practicality to a different but more likely route of human exposure.
General Principles of Risk Assessment
Toxicological Risk Assessment
Classical methods in toxicological risk assessment are applicable with nonstochastic toxic effects. For many kinds of agents and end points, toxicity is manifest only after the depletion of a physiological reserve. In addition, the biological repair capacity of many tissues can accommodate a certain degree of damage by reversible toxic processes (Aldridge, 1986; Klaassen, 1986). Above this threshold, however, the compensatory mechanisms that maintain normal biological function may be overwhelmed, leading to organ dysfunction. The objective of classical toxicological risk assessment, which has focused on nonstochastic end points, has been to establish a threshold dose below which adverse health effects were expected to be rare or absent.
Historically, the threshold concept was introduced by Lehman and Fitzhugh (1954), who proposed that an acceptable daily intake (ADI) could be calculated for chemical contaminants in human food. This concept was
endorsed by the Joint FAO/WHO Expert Committee on Food Additives (JECFA) in 1961 and subsequently adopted by the Joint FAO/WHO Meeting of Experts on Pesticide Residues (JMPR) in 1962 (Lu, 1988). Formally, the ADI was defined as:
ADI = NOEL/SF,
where the NOEL is the no-observed-effect level in toxicity studies, usually in the most sensitive species, and SF is the safety factor. Weight loss, reduction in weight gain, alteration in organ weight, and inhibition of cholinesterase activity are indicative of specific adverse effects that may be considered when establishing the NOEL (Babich and Davis, 1981). The safety factor makes allowances for the type of effect, the severity or reversibility of the effect, and variability among and within species (NRC, 1970).
In 1977, the National Research Council's Safe Drinking Water Committee reviewed the methods that had evolved for establishing ADIs and made several important recommendations. First, the committee proposed that the NOEL be expressed in mg/kg of body weight rather than mg/kg of diet to adjust for differences in dietary consumption patterns. Since children consume proportionally more food relative to body weight than do adults, ADIs established on a body weight basis would be more protective of children than would ADIs established as dietary concentrations. Second, the committee explicitly supported the use of only a 10-fold safety factor (now called uncertainty factor) in the presence of adequate dose-response data derived from human studies. And third, the committee proposed an additional 10-fold safety factor in the absence of adequate toxicity data, for an overall safety factor of 100. The use of these factors was later supported in a report by the Safe Drinking Water Committee in a reexamination of the earlier risk assessment practices (NRC, 1986). For carcinogenesis, that committee proposed the following definitions for two levels of safety factors:
-
10: When studies in humans involving prolonged ingestion have been conducted with no indication of carcinogenicity.
-
100: When chronic toxicity studies have been conducted in one or more species with no indication of carcinogenicity. Data on humans are either unavailable or scanty.
With cholinesterase inhibitors, an uncertainty factor of 10 is applied, since toxicity in humans and animals has been shown to be similar, and because the effect is generally reversible. An uncertainty factor of 100 is more commonly used for compounds with other toxic end points, assuming that humans are 10 times more sensitive than the most sensitive test animal and that the most sensitive humans are 10 times more sensitive
than the average human. The interspecies uncertainty factor is based on studies in adult laboratory animals and, therefore, is applicable to adult human beings, but studies in adult laboratory animals are not necessarily good for predicting the response of human infants and children. The other 10-fold intraspecies uncertainty factor is meant to cover variations within human populations, including genetic predisposition, poor nutrition, disease status, and age (Babich and Davis, 1981). A factor of 10 for intraspecies variation in susceptibility may be sufficient for any one element of interpersonal difference but may not be sufficient for multiple elements. Thus, as presently determined, an uncertainty factor of 100 may not be sufficient to account for the potential increased sensitivity of infants and children.
When insufficient toxicity data are available, an uncertainty factor of 1,000 may be applied. The ADI is then converted to the maximal permitted intake (MPI), which is the product of the ADI and the average body weight of an adult, considered to be 60 kg, or sometimes 70 kg, by the U.S. Environmental Protection Agency (EPA) and 70 kg by the Food and Drug Administration (FDA) (Babich and Davis, 1981).
Uncertainty factors used in toxicological risk assessment have some widely recognized limitations. Since the ADI is based on an estimate of the population threshold or true no-effect level (NEL), it does not provide absolute assurance of safety (Crump, 1984b). Larger and better studies can demonstrate effects at lower doses, but the size of the uncertainty factor is not directly related to sample size. Therefore, smaller and poorer experiments tend to lead to larger ADIs (Schneiderman and Mantel, 1973). Although a factor of 10 is used to accommodate variation in sensitivity among species, and another factor of 10 is used for variation within a species, it cannot be guaranteed that a combined uncertainty factor of 100 will afford adequate protection in all cases. Nor are these factors of 10 based on validated biological models. There is additional uncertainty, usually small, about whether some observed biological responses are adverse effects or innocuous. Thus, the ADI is not intended to have a high degree of mathematical precision. Rather, it is a guide to human exposure levels that are not expected to present serious health risks.
The EPA has recommended using the term uncertainty factor (UF) rather than safety factor in recognition of the fact that the ADI does not guarantee absolute safety consistent with more recent recommendations of the Safe Drinking Water Committee (NRC, 1986). The agency has also adopted the reference dose (RfD) as a replacement for the ADI (Barnes and Dourson, 1988; EPA, 1988). In addition, EPA introduced the concept of a modifying factor (MF) to be applied to the UF in recognition of the possible special circumstances surrounding the establishment of a specific RfD. The RfD
is determined by use of the equation:
RfD = NOAEL/(UF x MF),
where the NOAEL (no-observed-adverse-effect level) is the highest dose at which there is no statistically significant adverse effect in the test animals beyond that exhibited by a control group, and the UF accommodates uncertainties in the extrapolation of dose-threshold data to humans. The MF is applied when scientific uncertainties in the study are not accommodated by the UF. When the data do not demonstrate a NOAEL, a LOAEL (lowest-observed-adverse-effect level) may be used. This is the lowest dose at which a statistically significant adverse effect is observed.
The NOAEL and the LOAEL depend on the design of the study, particularly on the selection of the experimental dose groups. If the dose groups are far apart, then the LOAEL may be significantly higher than the true concentration at which adverse effects occur and the NOAEL may be much lower than the minimum concentration producing an adverse effect. In the present context, the term adverse effect is defined as any effect that results in a functional impairment or pathological lesion that may affect the performance of the whole organism, or that reduces the ability of the organism to respond to additional challenges (Dourson, 1986).
By definition, a UF is a number that reflects the degree of uncertainty that must be considered when experimental data are extrapolated to humans (Dourson and Stara, 1983; Barnes and Dourson, 1988). When the critical study (the one with the best available dose-response data) is selected for calculation of the reference dose, five factors may contribute to the composite uncertainty factor:
-
the need to extrapolate from animal data to humans when human exposure data are unavailable or inadequate;
-
the need to accommodate human response variability to include sensitive subgroups;
-
the nature, severity, and chronicity of the effect;
-
the need to accommodate the necessity of using LOAEL rather than NOAEL data; and
-
the need to extrapolate from a data base that is inadequate or incomplete.
The overall UF may vary from 1 to 10,000, depending on the combination of these individual factors, but usually does not exceed 100. An MF between 1 and 10 may be used to account for scientific uncertainties, either in the study or in the data base, that are not explicitly taken into consideration in any of the five factors listed above (Barnes and Dourson,
1988). For example, application of the MF may be regarded as a professional judgment that each test group contained too few animals.
Cancer Risk Estimation
The quantitative estimation of risks associated with low levels of exposure to carcinogens present in the environment is an important part of the regulatory process. At present, risk estimation methods are usually based on the assumption that the dose-response curve for carcinogenesis is linear in the low-dose region. This position is reflected in the principles proposed by the Office of Science and Technology Policy (1986), which stated:
When data and information are limited … and when much uncertainty exists regarding the mechanism of carcinogenic action, models or procedures which incorporate low-dose linearity are preferred. (OSTP, 1986)
This position is also reflected in the EPA's (1986) Carcinogen Risk Assessment Guidelines.
Although the Guidelines emphasize risk estimates derived using some form of linear extrapolation, they are based on the assumption that such estimates may be more appropriately viewed as plausible upper limits on risk and that the lower limit may well be effectively zero. The Guidelines also state that procedures for obtaining a best estimate lying somewhere between these two extremes generally do not exist at present, but that it may be possible to move away from a linearized extrapolation to obtain an upper limit in some circumstances and instead, use a threshold approach. For example, the EPA has recently taken a step in this direction by considering the possibility of a threshold for the induction of thyroid tumors (Paynter et al., 1988).
The EPA now uses the linearized multistage model for low-dose cancer risk estimation. The most important aspect of this practice is not the choice of the multistage model itself for risk estimation purposes but, rather, the linearized form of the model. Because the model is constrained to be linear at low doses, it is expected to yield risk estimates comparable to those based on other linear extrapolation procedures, including those proposed by Gaylor et al. (1987) and Krewski et al. (1990).
Additivity to Background and Low-Dose Linearity
Additivity to background is often cited in support of the assumption of low-dose linearity in carcinogenic risk assessment. In the additive background model proposed by Crump et al. (1976) and Peto (1978),
spontaneous tumors are associated with an effective background dose, to which exposure from environmental carcinogens is added. According to Crump and colleagues:
If carcinogenesis by an external agent acts additively with an already ongoing process, then under almost any model the response will be linear at low doses. (Crump et al., 1976)
Hoel (1980) subsequently demonstrated that this result also holds for partial additivity. This is expressed as follows in the current Guidelines:
If a carcinogenic agent acts by accelerating the same carcinogenic process that leads to the background occurrence of cancer, the added effect of the carcinogenic process at low doses is expected to be virtually linear. (EPA, 1986)
The basic idea behind the additive background model is illustrated in Table 8-1. Here the spontaneous response rate is considered to arise as a consequence of a background dose d, and the effects of the test chemical administered at dose d are additive in a dosewise fashion. The linearity of the excess risk over background P(d + d) - P(d) at low doses follows from the fact that the secant between doses of d and (d + d) converges to the tangent to the dose-response curve as the dosed of the test compound becomes small.
Within the framework of this model, the only condition required for this result to hold is that the probability of tumor occurrence be a smooth, strictly increasing function of dose. No further assumptions are required concerning either the mathematical form of the dose-response relationship or the toxicological mechanism by which tumors are induced.
The low-dose linearity implied by this model refers to the slope of
TABLE 8-1 Effect of Background Rate on Accuracy of Additivity Approximation Under the Assumption of the Multistage Modela
the dose-response curve at an applied dose of zero. Without additional assumptions, no further general statements can be made about the magnitude of this slope or about the range of low doses over which this linear approximation will be sustained reasonably well. The linear approximation in the multistage model holds well, even at doses that double the background tumor rate if that rate is not trivially small (Crump et al., 1976). When attempting to fit curves in the average regulatory setting, however, the lowest dose tested under usual experimental conditions is often one-quarter or a smaller fraction of the MTD (NRC, 1993). Compared to actual dietary concentrations, one-quarter of the MTD will often be very high, and linear interpolation between a tumor response at one-quarter or less of the MTD and the tumor response of the controls may still overestimate the response at the (low) regulatory dose and the low dose to which it is anticipated that humans will be exposed.
Nonlinearity at High Doses
Linearity at low doses does not imply that the dose-response curve will also be linear at high doses. In particular, curvature at high doses can result from factors such as saturation of absorption or elimination pathways or the alteration of pharmacokinetic processes involved in metabolic activation (Hoel et al., 1983). Nonlinearity at high doses can also be attributable to saturation of DNA repair systems or the induction of cellular proliferation. Dose-response curves for chemicals that can both cause DNA damage and induce cellular proliferation can be subject to a high degree of upward curvature, as with the hockey-stick-shaped dose-response curves for tumors of the urinary bladder induced by 2-acetylaminofluorene (2-AAF) (Cohen and Ellwein, 1990). Similarly, secondary carcinogens may act only at relatively high doses.
Nonlinearity due to saturation of elimination pathways results in upward curvature (as with methylene chloride), whereas saturation of activation processes leads to downward curvature (as with vinyl chloride). For processes that saturate in accordance with Michaelis-Menten kinetics, however, the amount of the proximate carcinogen formed at low doses will be directly proportional to the administered dose, since such processes are essentially first order at low doses (Murdoch et al., 1987). But again there is no way to estimate the shape or the range of the linearity.
If the pharmacokinetic model governing metabolic activation is known, dose-response may be assessed in terms of the dose delivered to the target tissue (NRC, 1987a). This may result in a more nearly linear dose-response curve, which greatly facilitates statistical extrapolation to low doses (Hoel et al., 1983; Krewski et al., 1986). To estimate delivered dose, however, it is important to consider the uncertainty associated with the parameters
used in the pharmacokinetic model (Portier and Kaplan, 1989). Several additional parameters introduced in the modeling when pharmacokinetics is considered will introduce more uncertainty.
Molecular Dosimetry
Different chemicals may induce different kinds of DNA lesions involving anywhere from two to 13 sites on molecular DNA (NRC, 1989). At the same time, there is evidence that spontaneously occurring DNA lesions (i.e., those with no known cause) can differ from those caused by exposure to alkylating agents. This suggests that fingerprinting of DNA damage in exposed and unexposed individuals may provide a practical means for distinguishing between additive and independent backgrounds.
The dose-response curve for tumor induction can be linear or nonlinear for a genotoxic agent that acts completely independently of background. If neoplastic conversion can result from a single mutagenic DNA lesion, the linearity of adduct formation at low doses implies linearity with respect to tumor induction (Lutz et al., 1990). If two or more mutagenic lesions are required to create a malignant cancer cell, however, the dose-response curve will be nonlinear with an effective threshold at low doses. This is essentially a multihit, independent background model in which the response is proportional to dose raised to a power equal to the number of DNA lesions required for neoplastic conversion.
Mathematical Modeling of Cancer Risk
Mathematical modeling has been a dominant feature of the quantitation of cancer risk. However, no model has been adequately validated in practice, and none account for all possible situations. Following are brief general descriptions of the more important risk assessment models that have been proposed and used over the years as background for the assessment of the risk to children from dietary exposures to pesticides.
Linear Extrapolation Approaches. In the absence of evidence to the contrary, existing arguments support the adoption of low-dose linearity for cancer risk assessment. Various methods for low-dose linear extrapolation have been proposed by several investigators. Gross et al. (1970) suggested discarding data starting at the highest dose until a linear model provided an adequate description of the remaining data. Van Ryzin (1980) proposed the use of any dose-response model that fits the data reasonably well to estimate the dose producing an excess risk of 1% followed by simple linear extrapolation to lower doses. Gaylor and Kodell (1980) suggested fitting a dose-response model to obtain an upper confidence
limit on the probability of tumor incidence at the lowest experimental dose and then using linear extrapolation at doses between zero and that dose. Since estimates at low doses might be unduly influenced by the choice of the dose-response model, Farmer et al. (1982) recommended linear extrapolation below the lowest experimental dose, or from the dose corresponding to an excess risk of 1%, whichever is larger.
Krewski et al. (1984) proposed what is called a model-free procedure using a linear interpolation from the response at the lowest dose showing any increase, down to the response at zero dose (i.e., control response). This approach is simple, but is not strictly model free, since the use of a linear interpolation implies a model of response directly proportional to the dose or exposure. Krewski et al. (1986) modified this procedure to consider the upper confidence limits of the low-dose slopes for each dose showing no statistically significant increase in tumor incidence above background. The shallowest slope was then selected for low-dose risk estimation.
Gaylor (1987) recommended using the smallest upper confidence limit where there is evidence to believe that the lowest dose is in a portion of the dose-response curve that is likely to lie between linearity and some upward curvature. Only rarely is it known with any exactness where this region is located, and often it is not certain that it exists at all.
Because of the difficulties in specifying and implementing a fully biologically based model of carcinogenesis for purposes of risk assessment (NRC, 1993), simple model-free approaches to low-dose risk estimation are attractive, especially when little is known about the process of tumor induction. Krewski et al. (1991) compared the behavior of the upper confidence limits of the slopes obtained from the model-free extrapolation (MFX) procedure with the upper confidence limit of the low-dose slope estimate obtained from the linearized multistage (LMS) procedure of Crump (1984a), as described below in the section on ''Estimates of Carcinogenic Potency." Comparisons were obtained for 572 bioassays taken from a compilation in the Carcinogenic Potency Database by Gold et al. (1984). Bioassays were restricted to rodent experiments exhibiting definite carcinogenicity. The median of the ratio of the upper 95% confidence limits on low-dose slopes for MFX: LMS was 1.3. In 433 of the 572 bioassays, the MFX estimate was within a factor of two of the LMS estimate. In eight cases, the MFX estimate exceeded the LMS estimate by a factor of 10. In these cases, there was a leveling off or decrease in the slope of the dose-response curve at higher doses, which tended to reduce the LMS values.
Biologically Based Cancer Models. The multistage model has a long history of use in theoretical descriptions of carcinogenesis (Whittemore and Keller, 1978; Brown and Koziol, 1983; Armitage, 1985). As described
by Armitage and Doll (1961), a stem cell must sustain a series of mutations in order to give rise to a malignant cancer cell. This model predicts that the age-specific cancer incidence rates should increase in proportion to age raised to a power related to the number of stages in the model, and provides a good description of many forms of human cancer by allowing for two to six stages.
The biological basis for the multistage model is incomplete in that it does not incorporate tissue growth or cell kinetics. Furthermore, as many as six stages may be required to describe dose-response curves with high upward curvatures, raising questions of biological interpretation. For these reasons, dose-response models that do reflect certain biological processes (e.g., cell deaths, cell turnover) have received considerable attention in recent years. Perhaps most widely discussed is the two-stage mutation-birth-death model, which was developed by Moolgavkar, Venzen, and Knudson and is therefore known as the MVK model (Moolgavkar, 1968a,b).
The MVK model is a biologically motivated model of carcinogenesis based on the hypothesis that a tumor may be initiated following genetic damage in one or more cells in the target tissue as a result of exposure to a compound called an initiator (Moolgavkar, 1986a,b; Thorslund et al., 1987). The initiated cells may then undergo a further transformation to give rise to a cancerous lesion. The rate at which such lesions occur may be increased by subsequent exposure to a promoter, which increases the pool of initiated cells through clonal expansion. Mathematical formulations of this process have been developed by Greenfield et al. (1984) and Moolgavkar et al. (1988).
The MVK model assumes that two mutations are necessary for a normal cell to become malignant. Initiating activity may be quantified in terms of the rate of occurrence of the first mutation. The rate of occurrence of the second mutation quantifies progression to a fully differentiated cancerous lesion. Promotional activity is measured by the difference in the birth and death rates of initiated cells. In the absence of promotional effects and variability in the pool of normal cells, the two-stage mutation-birth-death model reduces to a classic two-stage model.
The MVK model provides a convenient context for the quantitative description of the initiation/promotion mechanisms of carcinogenesis (Moolgavkar, 1986a). As described above, initiator increases the rate of occurrence of the first mutation, whereas a promoter increases the pool of initiated cells. Thus, the term progressor is used to describe an agent that increases the rate of occurrence of the second mutation, resulting in malignant transformation to a cancerous cell (EPA, 1987). It is possible that the same agent could play two or even all three of these roles (initiator, promoter, progressor), thereby enhancing both initiation and progression.
This model was applied by Thorslund and Charnley (1988) in estimating cancer risks associated with exposure to dioxin and chlordane, two putative tumor-promoting agents. The model provided a good fit to laboratory bioassay data on these two compounds, thereby facilitating a quantitative description of the mechanism of carcinogenic action within the framework of the MVK model. Using either a simple exponential (one-hit) or logistic model to describe the dose-response relationship for promotion, these investigators developed estimates of risk that were appreciably lower than those based on the linearized multistage model. Before this model can be recommended for routine application, however, its statistical properties require further study, especially with respect to predictions of risk at low doses (Portier, 1987).
Because the MVK model can be used to describe a variety of dose-response curves, it may not always provide an adequate description of the most important events involved in tumor induction. In certain cases, more than two mutations may be required for neoplastic conversion. Similarly, nongenotoxic factors may be required to foster development of a malignant tissue mass. As additional components are incorporated, the model rapidly becomes more complex and its tractability will be reduced (NRC, 1993).
Despite this potential for further elaboration, the MVK model is viewed as biologically more meaningful than the Armitage-Doll multistage model (Armitage, 1985). To apply this model, however, it will be necessary to have data on tissue growth and cell kinetics as well as bioassay data on tumor occurrence. Attempts to estimate all the parameters involved in the model without such supplementary data may result in unstable estimates (Portier, 1987). Separate estimates of the parameters governing the two mutation rates characterizing the genotoxic process in the model will also require more elaborate bioassay protocols than those currently in use (EPA), 1987). Nonetheless, explorations of the MVK model should be encouraged in order to learn more about its utility (NRC, 1993).
Estimates of Carcinogenic Potency. Several numerical indices have been proposed to describe the potency of chemical carcinogens (Barr, 1985). This concept derives from early work by Twort and Twort (1933) and Iball (1939). Gold et al. (1984) used the results of laboratory studies of carcinogenicity to tabulate the TD50 for a large number of chemical carcinogens, thereby popularizing the TD50 index. The TD50 for carcinogenesis is defined as the dose that reduces the proportion of tumor-free animals by 50% (Peto et al., 1984; Sawyer et al., 1984).
Some correlation has been noted between the TD50 and the LD50 used to measure acute toxicity (Zeise et al., 1984, 1986), although the correlation is not high (Metzger et al., 1989). The TD50 is also highly correlated with
the maximum tolerated dose (MTD), which is often used as the high dose in carcinogenicity bioassays (Bernstein et al., 1985). Little correlation between the TD50 and biological indicators of tumor pathology is apparent (Gold et al., 1986), however, indicating the impossibility of summarizing the characteristics of a chemical carcinogen in a single index (Wartenberg and Gallo, 1990).
Correlations between the TD10, LD50, and MTD need to be interpreted with care (Crouch et al., 1987). Since the range of possible values of the TD50 is limited by the choice of the MTD, the wide variation in the carcinogenic potency of different chemicals could produce a correlation between these two indices (Bernstein et al., 1985). In this regard, Rieth and Starr (1989) noted that little correlation exists between the TD50 and MTD after normalizing the TD50 values relative to the MTD. These investigators also suggest that the correlation between the LD50 and the TD50 may increase in part because an observed TD50 could be larger than the LD50.
The TD50 may be of some use in representing the overall strength of carcinogenic substances, but it does not necessarily indicate the level of risk posed at low exposure levels (Wartenberg and Gallo, 1990). As discussed previously, assessment of risk at low doses is generally accomplished by extrapolating results obtained at higher doses approaching the TD50.
As noted above, the EPA (1986) uses the linearized multistage model to estimate risk at low doses. A risk assessment analysis based on the LMS uses q1* (a quantitative carcinogenic potency factor) (Crump, 1984a), which is the estimated slope of the dose-response curve from animal tests yielding a positive carcinogenic response. The q1* value represents the estimated tumor incidence (the number of tumors per milligrams of pesticide per kilogram of body weight per day) at the relatively low concentrations of pesticides found in the human diet. It is based on a mathematical extrapolation of tumor incidence observed at the high doses used in tests in laboratory animals. High and low q1* values indicate strong and weak carcinogenic responses, respectively. For example, q1* values are 9.4 x 10-1 for chlordimeform, 2.3 x 10-3 for captan, and 5.9 x 10-5 for glyphosate (NRC, 1987b). Chlordimeform is thus considered a more potent carcinogen than captan (roughly 30-fold) or glyphosate (roughly 200-fold).
The q1* values among pesticides can vary by orders of magnitude (NRC, 1986, 1987b). The estimated q1* depends on whether a surface area or body weight correction is made in extrapolating risks from rodents to human beings, whether malignant and benign tumors are combined, and the extrapolation model used. The EPA uses surface area, whereas FDA uses body weight.
The EPA follows a policy in setting q1* values that minimizes the chance of underestimating cancer risks. As a result, EPA's estimates derived by using the q1* are believed by many to lead to an overestimate of the cancer risk. Use of the upper 95% confidence limit of the slope of the dose-response curve attempts to allow for variability in response among the laboratory animals and statistical stability in the estimate, and thus possibly errs on the side of caution when extrapolating risk to humans. However, the approach makes no allowance for variability among humans, such as the possible existence of highly susceptible persons, or other sources of uncertainty.
The value of q1* is the slope of the fitted dose-response curve in the low-dose region. It estimates the risk associated with a standard dose (such as 1 mg/kg/day). EPA uses the upper confidence limit on this slope both to introduce caution into its estimates and to provide a more stable measure of risk than would come about if the maximum likelihood (ML) estimate of the slope were used. The ML estimate is highly unstable, and the addition or removal of one or two tumor-bearing animals leads to large swings in the slope estimate and, hence, the risk estimate. The value of q1* derived is negatively correlated with the TD50 (Krewski et al., 1989, 1993). Thus, compounds with a low TD50 will tend to be associated with higher levels of estimated risk at low doses than will compounds with high TD50s.
EPA uses a time-independent model that estimates the lifetime risk of cancer and assumes that the risk from a given dose is the same at all ages. EPA's model assumes, for example, that the excess risk from exposure at age 5 is the same as the risk from the same exposure at age 70. However, because high levels of exposure to carcinogenic pesticides may occur during childhood and because decades may pass before the cancer resulting from that exposure is manifested, the use of EPA's methodology may substantially underestimate the lifetime cancer risk at young ages of exposure.
As noted in Chapter 4 (Methods for Toxicity Testing), the toxicity data base used in either the time-independent or time-dependent models for cancer risk assessment derives from carcinogenicity studies in young adult or adult laboratory animals whose responses may not be representative of those in neonates and weanlings. Newborn animals are often found to be more sensitive to certain carcinogens than are older animals (Rice, 1979). Thus, carcinogenicity studies in young adult animals, as recommended by EPA, may underestimate risks from exposures incurred during infancy or childhood—whether the time-dependent or time-independent models are used.
Species Conversion
In the absence of direct information on the carcinogenic potential of a particular agent in humans, toxicity studies in animals are often used as the basis for carcinogenic risk assessment (Rall et al., 1987). At present, all known human carcinogens have also been shown to be carcinogenic in one or more animal species (IARC, 1987). Although this does not necessarily imply that all compounds that are clearly carcinogenic in animals will also be carcinogenic in humans, it is considered prudent to regard them as such. Empirical support for this position may be derived from the high concordance in results reported as positive and negative (74% when effects in both sexes are considered) between rats and mice exposed to 266 different chemicals tested for carcinogenicity in the U.S. National Toxicology Program (NTP) (Haseman and Huff, 1987). True concordance may be higher but observed only in small samples with imperfect laboratory methods. These same data were used by Chen and Gaylor (1987) to demonstrate good agreement between the values of q1* for rats and mice among chemicals that tested positive for carcinogenicity in both species. Gaylor and Chen (1986) noted a similar association for the TD50.
Ideally, quantitative extrapolation of carcinogenic risks across species should take into account known species differences that might affect responses. Traditionally, dose equivalency across species has usually been estimated from average body weight. However, many physiological constants (e.g., consumption of water and food) have been shown to vary as a power function of body weight (Linstedt, 1987). Dourson and Stara (1983) noted that the metabolic rate and the toxicity of many compounds may be more accurately related to body surface area, which approximates body weight to the 2/3 power, than to body weight (Pinkel, 1958; Freireich et al., 1966). The activity of drugs in human infants and newborns has also been related to body surface area (Wagner, 1971; Homan, 1972). On the basis of an empirical study of the carcinogenic potency of chemotherapeutic agents, Travis and White (1988) recommended an intermediate scaling factor based on body weight to the ¾ power.
In an attempt to directly address the question of species conversion for carcinogens, Allen et al. (1988) examined the relationship between the TD25 estimated from human and animal data and the TD25 expressed on both a body-weight and a surface-area basis. A correlation coefficient exceeding 70% carcinogenic potency in animals and humans was obtained by using both scales of measurement. The correlation was slightly higher when the dose was expressed in relation to body weight.
Bernstein et al. (1985) suggested that the apparent interspecies correlation
in carcinogenic potency is due to the high correlation between the MTDs for rats and mice. Other investigators argued that while the correlation in carcinogenic potency between rats and mice may be due in part to the correlation between the corresponding MTDs, at least part of the correlation is not artifactual (Crouch et al., 1987; Shlyakhter et al., 1992). In a recent review of the use of the MTD in animal cancer tests, the NRC (1993) concluded that the implications of the MTD for quantitative risk assessment were unclear.
Benchmark Dose
The concept of the benchmark dose approach was proposed by Crump (1984b) as an alternative to other existing quantitative risk assessment techniques. In 1991, the EPA proposed using this approach in its recent guidelines for developmental toxicity risk assessment (EPA, 1991). A benchmark dose is defined as the lower confidence limit for the dose corresponding to a specific increase in the response rate over the background rate. The dose is estimated using a dose-response model fit to experimental data, typically with a 5 to 10 percent response. Crump (1984b) suggests using a likelihood (statistical) approach to estimating the lower confidence limit.
The advantages of using the benchmark dose approach over the NOAEL approach have been discussed by Crump (1984b) and more recently by Kimmel et al. (1991). The benchmark dose approach takes into consideration the dose-response model, which utilizes all the data available in the experiment. The NOAEL approach ignores the shape of the dose-response curve and focuses only on the experimental dose group, which was estimated to be the NOAEL. Thus, the true NOAEL could be anywhere between the estimated NOAEL and the first dose group at which adverse effects are observed. Moreover, smaller and poorly designed studies could result in larger NOAELs due to insufficient statistical power. Thus, the benchmark dose approach provides a consistent basis for calculating the RfD.
Two limitations of the benchmark dose approach are that the computations are more laborious than the NOAEL and that a dose-response model may not readily fit the data. The NOAEL approach also allows for the identification of the LOAEL.
Benchmark doses provide an integrated approach for risk assessment for both carcinogenic and noncarcinogenic health effects. Rather than using two different methods of estimating risk (e.g., the NOAEL approach for threshold toxicants and low dose extrapolation for nonthreshold toxicants), the method can be applied in a similar manner to both.
Risk Assessment for Infants and Children
Pharmacokinetics
Carcinogens may require some form of metabolic activation to exert their effects, whereas others are often deactivated. Pharmacokinetic models may be used to describe such processes as well as the uptake, absorption, distribution, and elimination of compounds that enter the body (O'Flaherty, 1981). This may in turn permit estimation of the amount of the reactive metabolite reaching the target tissue. Tissue dosimetry is important for risk assessment purposes when one or more steps in the process of metabolic activation and biological action are saturable, since this can lead to a relationship between the dose of the parent compound administered to the test subjects and the dose of the reactive metabolite reaching the target tissue (Hoel et al., 1983), which is not directly proportional.
Compartmental pharmacokinetic models have often been used to describe biological systems in terms of a small number of conceptual compartments (Godfrey, 1983). More recently, physiologically based pharmacokinetic (PBPK) models that imply a larger number of physiologically meaningful compartments have been used to accommodate metabolic activation (Menzel, 1987). The application of PBPK models requires extensive information on the anatomy and physiology of the test animals, the solubility of the test chemical in various organs and tissues, and biochemical parameters governing metabolism (Andersen et al., 1987).
If metabolic activation can be adequately characterized in terms of a suitable pharmacokinetic model, the dose delivered to the target tissue may be used in place of the administered dose for purposes of dose-response modeling. This may sometimes lead to more accurate predictions of cancer risk (Krewski et al., 1987), but accuracy may be reduced when the uncertainty associated with the many parameters involved in a PBPK model is taken into account (Portier and Kaplan, 1989).
Pregnancy, Lactation, and Nursing
Many changes that occur during pregnancy can have a significant impact on the toxicodynamics of a particular chemical. For example, the changes in body weight, total body water, plasma proteins, body fat, and cardiac output will alter the distribution of many xenobiotic compounds (Hytten and Chamberlain, 1980; Mattison, 1986; Mattison et al., 1991).
PBPK models have been used to describe the kinetics and disposition of the drugs tetracycline, morphine, and methadone (Olanoff and Anderson, 1980; Gabrielsson et al., 1983; Gabrielsson et al., 1985a,b). Two recent
reports described the pharmacokinetics and disposition of trichloroethylene and its principal metabolite, trichloroacetic acid, in the pregnant rat as well as in the lactating rat and nursing pup. A PBPK model, consisting of eight compartments for trichloroethylene in the pregnant rat and nine compartments for trichloroacetic acid, was used (Fisher et al., 1989). Both models accommodated multiple routes of exposure and repeated dosing. The model provided for a variable litter size from 1 to 12 pups per rat as well as placental growth.
Values of the maximum rate of metabolic removal velocity (Vmax) (rate at which a chemical is removed from the organism) in unmated and pregnant rats were 10.98 and 9.18 mg/kg/hr, respectively. This reduction is significant, and has been related to a decrease in the cytochrome P-450 monooxygenase activity due to altered steroid hormones. A high substrate affinity was demonstrated for metabolism and elimination of chemical substances. Although the value of the Michaelis constant (Km) was low (0.25 mg/liter), it was similar in both groups of rats. Fetal exposure to trichloroethylene was estimated to range from 67 to 76% of the maternal exposure; fetal exposure to the trichloroacetic acid metabolite was 63 to 64% of that of the dam.
The model fitted data obtained after exposure by inhalation, oral gavage, or via drinking water. Other kinetic parameters predicted by the model (such as the relative volumes of distribution, the peak blood concentration following oral gavage, fetal concentrations following inhalation exposure, absorption and elimination rates) agreed well with data previously reported in the literature. These results demonstrated that fetal exposure to both the parent compound and its principal metabolite was significantly elevated in relation to the maternal exposure.
Fisher et al. (1990) examined the transfer of trichloroethylene and trichloroacetic acid nursing pups from lactating dams exposed to trichloroethylene by inhalation of 610 ppm 4 hours per day, 5 days per week from days 3 to 14 of lactation. A further study involved exposure of the lactating dam to 333 µg/ml of trichloroethylene in drinking water from days 3 to 21 of lactation. The pups were exposed to trichloroethylene solely from ingested maternal milk; however, their exposure to trichloroacetic acid came from maternal milk and from metabolism of ingested trichloroethylene. The model provided for different published values for compartmental volumes, blood flows, and milk yield during lactation. Metabolic and other kinetic parameters were determined experimentally.
The value of Vmax = 9.26 mg/kg/hr in the lactating rat was similar to that in the pregnant rat. However, the value of Vmax = 12.94 mg/kg/hr obtained for male and female pups indicated that the ability of the pups to metabolize trichloroethylene was greater than that in the adult. The plasma half-life (16.5 hr) of trichloroacetic acid in the pups was also
substantially greater than that in the mature rat. Unlike most other physiological distribution processes that are flow limited, the distribution of trichloroacetic acid to mammary tissue is diffusion limited. The exposure of the pups to trichloroethylene from maternal milk was small, representing only about 2% of the exposure of the dam. Pup plasma levels of trichloroacetic acid, however, were as high as 30 and 15% of the maternal exposure for drinking water and inhalation exposures, respectively.
Neurotoxicity
Two classes of insecticides, the organophosphates and the carbamates, are acetylcholinesterase inhibitors, which interfere with nerve transmission. Chemically induced functional alterations of the nervous system are often assessed with neurobehavioral tests. However, it has been very difficult to integrate observations of behavior with other aspects of neurotoxicological testing (NRC, 1992). This has been especially true for assessing neurodevelopmental effects in young animals. For example, some studies in laboratory animals have shown that exposure to organophosphates and carbamates before or immediately after birth may alter neurological development and cause subtle and long-lasting neurobehavioral impairments. (See Chapter 4 for a discussion of neurotoxicity testing.) Therefore, additional laboratory animal data are needed to evaluate the effects of low-level chronic exposures on subtle neurotoxicities, including alterations of behavior. The recent NRC report Environmental Neurotoxicology (NRC, 1992) describes in detail the research necessary to improve the neurotoxicological testing of chemical substances, including pesticides. There is currently no validated testing system that satisfies all the necessary requirements for a screening program to detect the neurotoxic potential of chemical substances (NRC, 1992).
Multiple Exposures
Because humans are exposed to multiple chemicals simultaneously, the potential risks associated with joint exposures require consideration (Krewski and Thomas, 1992). Factorial experiments with pairs of chemicals have demonstrated both synergistic and antagonistic effects as well as a lack of interaction, depending on the pair of agents used, the tissues in which the cancers appear, and the time of appearance of different primary site tumors (Elashoff et al., 1987; Fears et al., 1988, 1989). Epidemiological studies have also demonstrated the existence of synergism between two agents, such as tobacco and asbestos (NRC, 1988). Brown and Chu (1989) demonstrated that the multistage model can lead to a spectrum of effects, ranging from additive to multiplicative age-specific relative risks, depending
on the patterns of joint exposure to the two agents of interest. Kodell et al. (1991) reported similar findings for the two-stage clinical expansion model of carcinogenesis, including the possibility of supra-multiplicative relative risks in the case of joint exposure to two promoters.
The existence of synergism at low levels of exposure cannot be assessed directly. It must be inferred by other means. For example, the multistage model predicts additivity of excess risks at low doses, even in the presence of interactive effects (NRC, 1988). Similarly, the multiplicative relative risk model leads to additivity of excess risks at low doses (Krewski et al., 1989). Although these models imply that interactions will be negligible at low levels of exposure under certain conditions, the possibility of synergy at low doses under other conditions cannot be ruled out. It is conceivable, for example, that two compounds, innocuous by themselves, might interact chemically even at low doses to form a new substance that is toxic.
Since more than one pesticide may be applied during the growing season of some crops, multiple pesticide residues are possible. Those pesticides can interact synergistically to increase the total toxic potential. For example, synergistic effects between malathion and O-ethyl O-p -nitrophenylphosphonothioate (EPN) have been noted since 1957 (NRC, 1977). Nevertheless, 33 of the 35 crops with tolerances for EPN also have tolerances for malathion (AOR, 1988).
Inert Ingredients
A pesticide product is generally formulated by combining one or more active ingredients with one or more inert ingredients. The active ingredients are selected because their potency can achieve the intended pesticidal action; the inert ingredients are designed not to kill the target pest but to provide bulk to the pesticide formulation and to improve its spreading or sticking ability. Inert ingredients are not regulated, and although many of them are innocuous, others are themselves potent toxicants and may cause adverse health effects. Examples of the latter include asbestos fibers, benzene, epichlorohydrin, methylene chloride, 2-methoxyethanol, pentachlorophenol, formaldehyde, and vinyl chloride. Dietary exposure to these compounds may be significant, since they usually appear in pesticide formulations in much greater quantity than the active ingredients. Furthermore, EPA does not require registrants to submit analytic methods to detect inert ingredients in foods (AOR, 1988).
In 1987, EPA divided the 1,200 inert ingredients currently contained in pesticide products into four toxicity categories based on available hazard information: ingredients of toxicological concern (57); substances that are potentially toxic and have a high priority for testing (67); ingredients
whose potential for toxicity is unknown (800); and those considered to be innocuous (300) (Peach, 1987). In an attempt to encourage the use of less toxic inert ingredients, EPA gave pesticide registrants until October 20, 1988, to replace ingredients in the first category with compounds that do not appear in the first two classifications. After that deadline, any compounds in the first category still present in pesticide products had to be identified on the product label and were subject to data call-in for chronic health effects (AOR, 1988).
Considerations Specific to Children
Certain populations of children may be more sensitive to the effects of pesticides because of physiological and biochemical factors such as genetic predisposition, chronic medical conditions, interactions (or additive effects) of pesticides with medications, and general health status. Other factors that may make certain children more susceptible include increased exposure through farm work or parental occupational exposure and low socioeconomic status.
Exposure and Low Socioeconomic Status
Children living in poverty may constitute an additional sensitive population. Illness, when it occurs, is more severe among children of poor families (Starfield, 1982). For example, common childhood conditions such as asthma tend to be more severe in these children (Mitchell and Dawson, 1973). Furthermore, children of poor families are 2 to 3 times more likely to contract illnesses such as rheumatic fever, twice as likely to contract illnesses such as bacterial meningitis, 9 times more likely to have elevated levels of lead in their blood, and 2 to 3 times as likely to have iron-deficiency anemia (Starfield and Budetti, 1985). In the poor, rural agricultural community of McFarland, California, studied because of a childhood cancer cluster, 23.8% of children from 1 to 12 years of age were anemic. In the 1to 4-year-old age group, 30.6% were anemic (McFarland Child Health Screening Project, 1991).
One factor contributing to compromised health status is poor nutrition. Preschool children of low socioeconomic status have been found to have lower dietary intakes, lower biochemical indices, and smaller physical size for their age than children of higher socioeconomic status (Owen and Frankle, 1986).
Because of compromised health status, poor children are probably more susceptible to any toxic insult, including pesticide exposure. Children of poor families are more likely to live in highly polluted neighborhoods and thus to have greater exposure to environmental toxicants. In the Los
Angeles area, many immigrant poor may be fishing in contaminated waters to supplement their source of protein.
The combined effect of poorer health status and of likely higher exposure to environmental toxicants suggests that the further burden of pesticide exposure could lead to toxic effects at levels that do not produce effects in other children. Therefore one might expect that adverse effects of pesticides, whether acute or chronic, might be magnified in this subpopulation.
Age-Dependent Toxicity
Traditional risk assessment methods generally do not make specific allowances for any unique features of infants and children. Species conversion of dietary intakes per unit of body weight are normally based on adult body weights and food consumption data (McColl, 1989).
Infants and children are unique in a number of ways (see Chapters 2 and 3). Babich and Davis (1981) noted that children may be hypersusceptible to food toxicants, especially heavy metals and pesticides. The realization that the process of atherosclerosis begins in childhood has led to recommendations that total fat intake of children over 2 years of age not exceed 30% of calories and that cholesterol intake not exceed 300 mg daily (American Health Foundation, 1989). Gaines and Linder (1986) estimated the LD50s for 57 pesticides in adult and weanling rats and found four cases (leptophos, methidathion, pyrazon, and sulfoxide) in which the weanlings were more sensitive than the adults several in which they were less sensitive.
Infants and children may be more or less susceptible to exposure to toxic chemicals than adults (see Chapters 2 and 3). Drugs such as amikacin and the aminoglycosides are less toxic to children than adults, whereas children seem to be more sensitive to salicylates than adults (Mendelson and Grisolia, 1975; Brown et al., 1982; Faden et al., 1982). Comparative analyses of the acute lethality of drugs (Goldenthal, 1971), chemotherapeutic agents (Glaubiger et al., 1982), insecticides acting through cholinesterase inhibition (Brodeur and DuBois, 1963), and pesticides (Gaines and Linder, 1986) indicate that infants and children may exhibit a higher or lower LD50 than adults.
Collectively, these data provide information on the magnitude of the effects of age on susceptibility to toxic chemicals. Specifically, Brodeur and Dubois (1963) observed that the LD50s for adult rats were 2 to 4 times greater than the corresponding LD50s for weanling rats for 15 of 16 insecticides examined.
Potential carcinogenic risks may depend on the unique physiological sensitivities of infants and children as well as the specific age at which
exposure occurs. In a study of the carcinogenic effects of N-nitroso compounds in the diets of rats conducted by the British Industrial Biological Research Association, for example, different tumor response rates were observed in animals exposed throughout their lives beginning at 3, 6, or 12 weeks of age (Peto et al., 1986). Other investigators have identified perinatal exposure as a critical factor in neoplastic development. During the 1970s, three independent two-generation cancer bioassays involving in utero exposure showed a clear increase in the incidence of malignant tumors in the urinary bladders of male rats, whereas this effect was not observed in single generation studies in which exposure began at the time of weaning (Arnold et al., 1983). These results confirm an important role of in utero exposure in bladder tumor induction. In a study conducted by the International Research and Development Corporation (IRDC), animals were exposed only from birth onward (Food and Chemical Toxicology, 1985). Tumor yields were similar to those observed in the two-generation studies. Although this association seems not to have been studied directly, these data are consistent with the view that perinatal exposure can be a critical determinant in the initiation and extent of carcinogenic response.
Recently, both the multistage and two-stage models have been extended to accommodate the age at which exposure occurs (Kodell et al., 1987; Chen et al., 1988; Gaylor, 1988; Murdoch and Krewski, 1988; Murdoch et al., 1992). These results indicate that when an early stage of carcinogenesis is dose dependent, early exposures will be of greater concern than later exposures. In this case, equivalent exposures will present greater risks to infants and children than to adults. Estimates of the size of this excess risk in infants and children depend on the particular assumptions made concerning the mechanism of carcinogenesis. In the classical interpretation of the multistage model, the increase cannot exceed a factor of k, the number of stages in the biological system under study. With the two-stage model, however, the increased risk can be substantial when the chemical greatly increases the proliferation rate of the initiated cell population.
Genetic Susceptibility
Polymorphism in Metabolism
In recent years a number of genetic polymorphisms of metabolic enzymes have been identified in humans. Several cytochrome P-450 polymorphisms have been established (Guengerich et al., 1986). Polymorphisms of N-acetyltransferase (Weber, 1987), glutathione-S-transferase (Board, 1990), and paraoxonase (Ortigoza-Ferado et al., 1984) have also
been documented. High biological activity of an enzyme(s) that catalyzes the activation of a pesticide or low activity of an enzyme that mediates deactivation may increase the sensitivity of an individual to pesticide exposure.
Parathion is activated to paraoxon by mixed-function oxygenase enzymes. Hydrolysis (and deactivation of the active paraoxon) is mediated by plasma paraoxonase (arylesterase). The activity of this arylesterase is polymorphic with respect to paraoxon (La Du and Eckerson, 1984). There are two, possibly three, paraoxonase phenotypes with activity toward paraoxon varying by 11-fold (Furlong et al., 1988). Low arylesterase activity could potentiate the cholinergic effects of this pesticide; thus, children with the low activity phenotype would be at greater risk of adverse health effects because of a decreased ability to hydrolyze paraoxon.
The specificity of this arylesterase toward most other aromatic organophosphate esters is not clear. Activity toward chlorpyrifos, however, has been studied. Arylesterase activity toward chlorpyrifos is not polymorphic but follows a Gaussian distribution with a four- to fivefold variation. Even though polymorphism was not observed, individuals with the lowest paraoxonase activity also had the lowest chlorpyrifos-oxonase levels (Furlong et al., 1988). Other arylester organophosphates that may be substrates for arylesterase include guthion, EPN, and diazinon.
Fish-eye (Tangier's) disease, a rare genetic disorder characterized by severe corneal opacities and abnormal plasma lipoproteins, has been associated with decreased paraoxonase activity. Mackness et al. (1987) reported that the mean value of paraoxonase activity in two patients with this disease was only 11 percent of the mean value for 55 control subjects. One could expect children with this disorder to be more prone to adverse health effects if exposed to parathion or other organophosphates that are substrates for this arylesterase.
A toxic encephalopathy has been associated with exposure to N,N-diethyl-m-toluamide (Deet) (Gryboski et al., 1961; Zadikoff et al., 1979; Heick et al., 1980). At least four cases of Deet-induced toxicity have been documented after heavy but routine use of Deet-containing products (Edwards and Johnson, 1987). All cases involved young girls. The most recent report linked the toxicity with ornithine carbamoyltransferase (OCT) deficiency (Heick et al., 1980)—a sex-linked disorder that is fatal in males during the neonatal period. In females, severity varies. There are certain characteristic syndromes common with OCT deficiency, such as feeding problems during infancy and hepatic syndromes including hyperammonia, oroticaciduria, and increased serum glutamine. OCT deficiency is extremely rare and may go undetected. If these cases are identified, then parents and other adults concerned can be notified of the possible toxic effects that may be encountered with Deet exposure.
Increased Sensitivity of Unknown Origin. A case of acrodynia, a form of mercury poisoning that occurs in infants and young children, was recently reported after exposure to latex paint containing the fungicide phenylmercuric acetate (Agocs et al., 1990). Mercury exposure occurs when vapor is released from painted surfaces after the paint has dried. Although EPA now forbids the addition of phenylmercuric acetate to interior latex paint (as of August 20, 1990), mercury-containing paint manufactured before this date may still be sold.
There is wide interindividual variability in susceptibility to acrodynia. In 1980 in Buenos Aires, Argentina, three cases of acrodynia were reported when up to 12,000 infants were exposed to a phenylmercuric fungicide used by a commercial diaper service (Gotelli et al., 1985). The reason why particular children are more sensitive than others is unknown.
Chronic Medical Conditions
Exposure to pesticides could exacerbate common childhood conditions. For instance, the increased cholinergic response induced by organophosphates may increase contraction of bronchial muscles and stimulation of bronchial glands. Therefore, asthmatic children might be affected more easily and more severely than normal children.
Interactions with Medication
Children taking medication may be at increased risk from pesticide exposure. Many drugs compromise nutritional status, and this in itself may increase sensitivity to pesticides. In addition, acetylcholinestrase (AChE) inhibitors, antiepileptic drugs, other drugs that act on the central nervous system (centrally acting drugs), propranolol and digoxin, and drugs that alter hepatic blood flow might be of concern.
Acetylcholinesterase Inhibitors
Any child taking AChE inhibitors would be at increased risk from organophosphate exposure. For instance, increased levels of organophosphates would increase the cholinergic effects observed during the use of the cholinesterase inhibitor phospholine iodide (echothiophate) for glaucoma patients.
Antiepileptic Pharmaceuticals
Phenobarbital and phenytoin induce cytochrome P-450 isozymes. Phenobarbital is also known to induce a number of other hepatic drug metabolizing
enzymes. With regard to pesticide exposures, these drugs might induce a cytochrome P-450-dependent isozyme involved in bioactivation of a pesticide, while the deactivation pathways (that is, hydrolysis or conjugation) may be induced to a lesser degree or not induced at all.
Alterations in the activation/deactivation ratio depend on the pesticide as well as the inducing agent. For example, pretreatment with phenobarbital induced both cytochrome P-450-mediated activation of malathion and carboxylesterase-linked hydrolysis in mice (Ketterman et al., 1987). In this case, phenobarbital did not affect the toxicity of malathion. In studies with parathion, on the other hand, pretreatment with phenobarbital decreased acute toxicity in mice (Sultatos, 1986). Phenobarbital pretreatment did increase the toxicity of diazinon in calves (Abdelsalam and Ford, 1986). The effect of chronic phenobarbital or phenytoin treatment on the activation and deactivation of any of these pesticides in humans is unknown.
Other Pharmaceuticals
Fenyvesi et al. (1985) reported that the fungicide thiram potentiated the effects of promethazine in behavioral studies in rats. Promethazine is an H1 (type 1 histaminergic receptor) antagonist. Two H1 antagonists commonly given to children are diphenhydramine (Benadryl®) and dimenhydrinate (Dramamine®).
Because of structural similarities, thiram may act similarly to its ethyl analog, disulfiram, a well-studied drug. Disulfiram inhibits hepatic microsomal, drug-metabolizing enzymes and interferes with the metabolism of many drugs, including phenytoin (Gillman and Sandyk, 1985). In addition, disulfiram has been found to greatly increase the cancer-causing effects of the pesticide ethylene dibromide. Whether low levels of thiram would have any of the above effects is not known.
Disulfiram has also been found to interact with centrally acting drugs including amphetamine (Sharkawi et al., 1978). In this regard, a potential interaction between thiram exposure and methylphenidate (Ritalin®), a drug with pharmacological properties similar to those of amphetamine, might be worth investigating. Although thiram residues in food are likely to be low, the potential susceptibility for children taking methylphenidate should be of concern.
Children taking medication for heart disease might also be at increased risk. Propranolol, a ß-adrenergic blocker, decreases the heart rate, a response that could be magnified by pesticides that increase cholinergic activity. Digoxin is another medication commonly given to children with heart disease. Pesticides that increase cholinergic activity might potentiate digoxin-induced bradycardia and depressed conduction at the sinoatrial
and arterioventricular nodes. One toxic effect of digoxin is complete arterioventricular blockage. There may also be a cholinergic response. Therefore, pharmacological actions induced by pesticides may reduce the margin of safety of these drugs.
Many drugs alter hepatic blood flow and consequently may alter biotransformation or excretion of xenobiotic compounds that are readily cleared by the liver. For example, propranolol decreases hepatic blood flow. This may be an advantage in exposures to pesticides activated by metabolism, but it could cause greater toxicity in cases of exposure to pesticides that are deactivated by metabolism. Phenobarbital, on the other hand, increases liver blood flow and, therefore, speeds up delivery of pesticides to the liver. For pesticides that are extracted by the liver, extraction would be increased. Thus, for a pesticide that is bioactivated by liver enzymes, activation would increase.
The effects of altered blood flow would not be significant for orally absorbed pesticides. However, altered blood flow would have an effect on pesticides absorbed dermally. Theoretically, then, children taking medication that alters hepatic blood flow would be more affected than other children. In addition, if these children had damaged skin (such as cuts and scrapes), the increased absorption could potentiate the effects of increased (or decreased) hepatic blood flow.
Carcinogenesis
Factors That Might Increase Risk of Cancer Among Infants and Children
When subjected to the same low levels of pesticide residues in food measured as parts per million (ppm), infants and children may be at greater cancer risk than adults for several reasons. First, exposures to an early-stage carcinogen early in life can be more effective than exposures to the same carcinogen in later years (Day and Brown, 1980; Kaldor and Day, 1987). A multistage model of carcinogenesis shows that completion of the first stages of neoplastic transformation of normal cells early in life increases chances that subsequent stages will be completed within a normal lifespan. Early exposures are not always associated with increased risk, however, since exposures to late-stage carcinogens are more effective in later years.
Second, tissues undergoing rapid growth and development may be more susceptible than mature tissues to the effects of chemical carcinogens, but empirical evidence to support this is mixed. In studies of the LD50s of pesticides in rats, weanlings were found to be more sensitive than adults to some carcinogens but less sensitive to others (Gaines and
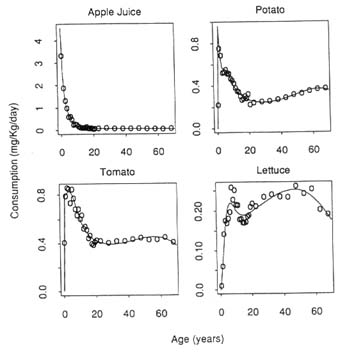
Figure 8-1 Consumption rates for apple juice, potato, tomato, and lettuce by age.
SOURCE: Murdoch et al., 1992.
Linder, 1986). Drew et al. (1983) demonstrated that rats, mice, and hamsters are more sensitive to the carcinogenic effects of vinyl chloride when exposure occurs early in life, compared to later exposures of the same duration. And as noted in the preceding section, Peto et al. (1986) reported that the incidence of liver tumors decreased appreciably with advanced age among rats exposed to nitrosodimethylamine (NDMA) beginning at 3, 6, and 12 weeks of age. Perinatal exposure has also been shown to be necessary for the induction of urinary bladder tumors in male rats exposed to saccharin in the diet. In utero exposure to ethylenethiourea has recently been found to increase the incidence of malignant thyroid tumors (NTP, 1991).
Third, infants and children may be at greater risk than adults because of their greater consumption (on a kilogram of body weight basis) of certain foods. As shown in Chapter 5, children consume fewer foods than do adults but many of these are consumed at much higher levels when expressed on a body weight basis. To illustrate, Figure 8-1 shows the
consumption of apple juice as reported in the 1977–1978 Nationwide Food Consumption Survey (NFCS) (Murdoch et al., 1992). The average intake of apple juice for survey respondents is indicated by open circles; the solid lines represent smooth curves fitted to the raw data. On a body weight basis, 1 year-old children consume more than 30 times as much apple juice per day as adults.
The data for the three other foods depicted in Figure 8-1 reflect different consumption patterns with age. These particular foods were chosen to illustrate a variety of food consumption patterns. The maximum consumption of potatoes and tomatoes occurs among children 1 to 6 years of age. The consumption of lettuce increases throughout childhood and is higher among adults than among children.
These consumption data have important implications for assessing the risk of carcinogenesis in infants and children. In laboratory studies of carcinogenicity in which the dose is expressed relative to body weight (in mg/kg bw/day), the dose is generally held constant throughout the study. Such studies are used to estimate carcinogenic potency in terms of a unit risk factor (q1*). Multiplication of the anticipated level of exposure by the unit risk factor leads to an estimate of cancer risk.
Effects of Age-Dependent Exposures
Methods for estimating lifetime cancer risk when the level exposure varies over time have been investigated by Crump and Howe (1984) and Kodell et al. (1987). One simple approach is to calculate a lifetime average daily dose (LADD) by distributing the cumulative lifetime dose equally over a lifetime. This amortization of total lifetime exposure is suggested by the EPA (1986) in the absence of evidence of dose-rate effects. This method is especially appealing when considering carcinogens that remain in the body permanently or have very long half lives, such as some fat-soluble organic compounds and heavy metals.
Murdoch and Krewski (1988) showed that except in very special cases, the use of the LADD will not lead to the same lifetime risk as the actual time-dependent exposure pattern. These authors defined a lifetime equivalent constant dose (LECD) in terms of the relative effectiveness of dosing at different ages, which leads to the same lifetime risk as the time-dependent dosing pattern. (The LECD is a weighted average of the time-dependent dose; weights are proportional to the relative effectiveness of dosing at each point.) The ratio C = LECD/LADD then provides a measure of error of risk estimates based on the LADD.
Murdoch et al. (1992) used this measure to investigate the extent risk estimates based on average adult levels of exposure may underestimate the risks for infants and children as a consequence of their higher exposures on
a body weight basis. This analysis relies on the recent interpretations of the classical Armitage-Doll multistage model of carcinogenesis (Armitage, 1985) and the MVK two-stage mutation-birth-death model (Moolgavkar and Luebeck, 1990).
Application of the approximate form of the two-stage model requires specification of the number of cells at risk N(t) in the target tissue at time t as well as the net birthrate d(t) of initiated cells that have sustained the first mutation as a function of time t. Application of the exact form of the two-stage model, which is necessary when the lifetime probability of tumor formation is high (Moolgavkar et al., 1993), further requires specification of the birth rate a(t) and death rate ß(t) of initiated cells, rather than just the difference d (t) = a(t)- ß(t).
In some applications of the two-stage model, it has been assumed that N(t) and d (t) are constant over time. The assumption that N( t) is constant is also implicit in most applications of the multistage model. Assumptions of the constancy of N(t) and d (t) expedite the mathematical analysis of the two-stage model, but are oversimplifications of reality. For example, Enesco and Leblond (1962) found that the number of cells in most rat tissues increase with age up to approximately 34 to 48 days after birth, well past weaning in these species, at which point tissue size starts to stabilize.
Tissue growth can result from an increase in either cell size (hypertrophy) or in cell number (hyperplasia). Hyperplasia is the dominant feature in initial tissue growth, but the rate of cell division decreases with age (Brasel and Gruen, 1978) and reaches zero at maturity in tissues that are not self-renewing. Some tissues such as the brain are fully developed in early childhood, whereas others such as the skeletal system do not achieve maturity until after adolescence.
Growth in cell mass is sometimes assessed by comparing tissue weight to DNA content (Brasel and Gruen, 1978). However, this approach to distinguishing between increases in cell number and cell size is difficult to apply in mammalian liver because of the formation of multinucleate cells and cells with single nuclei, but with diploid or tetraploid amounts of DNA (polyploidy).
The interpretation of N(t) as the number of normal stem cells may also be an oversimplification. Moolgavkar and Luebeck (1990) noted that this is inconsistent with the assumption that mutation occurs during cell division, because the mitotic index (the per-cell rate of cell division) varies with age. For example, Ellwein and Cohen (1988) report that mitotic indices in stem cells in 1-week-old rats are approximately 100 times higher than in rats 8 weeks of age. The estimation of mitotic rates based on DNA incorporation of tritiated thymidine during cell division is discussed by Moolgavkar and Luebeck (1992).
In general, little information is available about the net birth rate d(t) of initiated cells and even less about a(t) and ß(t) separately. Initiation/promotion assays may provide some direct information on the birth and death rates of initiated cells. In the mouse liver system described by Pitot and Dragan (1991), foci believed to correspond to clones of premalignant initiated cells can be identified histologically and interpreted in terms of numbers of initiated cells. Such assays have been used to study cancers of the liver, urinary bladder, and skin, but are not yet well developed for other tissues. Moolgavkar et al. (1990) and Luebeck et al. (1991) discussed the statistical use of data on the kinetics of initiated cells in a two-stage model.
Murdoch and Krewski (1988) explored the results obtained by assuming a constant rate of proliferation of intermediate cells, independent of age, while Krewski and Murdoch (1990) assumed that the net birth rate was a constant multiple of the birth rate of normal cells. Murdoch et al. (1992) considered an intermediate approach:
d(t) = dN(t) + d,
where dN(t) is the net birth rate of normal cells at time t calculated on the assumption that all changes in tissue weight are due to changes in cell number rather than cell size, and the constant d is the excess net birth rate of intermediate cells. This model implies that intermediates cells respond to their microenvironment in essentially the same way as normal cells do, but may be slightly more (d>0) or less (d<0) successful at proliferation.
When specific information on N(t) is unavailable, a rough surrogate for the number of stem cells in the target tissue is gross organ weight. This latter indicator has the advantage of being readily available in humans, but does not take into account hypertrophic effects or changes in mitotic indices over time. For example, Murdoch et al. (1992) assumed that N(t) is proportional to human liver weight (Snyder et al., 1974).
Murdoch et al. (1992) calculated the values of C = LECD/LADD for apple juice, potatoes, tomatoes, and lettuce, assuming that exposure is characterized by the amount of food consumed. The values of C shown in Tables 8-2 and 8-3 for the multistage and two-stage models, respectively, indicate the degree to which the use of adult exposure data may underestimate or overestimate the actual risks, taking into account the greater levels of food consumption by infants and children. Consider, for example, the value of C = 3.74 for a six-stage model in which only the first stage is dose-dependent, based on the actual levels of apple juice consumed. This implies that the actual lifetime cancer risk due to the presence of residues of a pesticide found in apple juice will be more than 3 times that calculated on the basis of a LADD obtained by amortization of the cumulative lifetime exposure. Assuming a constant daily lifetime exposure
TABLE 8-2 Values of the Ratio C = LECD/LADD for the Multistage Model for Pesticide Residues in Apple Juice, Potatoes, Tomatoes, and Lettucea
equal to that of adults would lead to a slight underestimation of risk.
Examination of Tables 8-2 and 8-3 reveals several important findings. First, the largest correction factors C increase with the number of stages k in the multistage model and the cumulative net birth rate of initiated cells in the two-stage model. The values of C also increase as the stage affected r decreases. Values of C less than unity correspond to cases in which the use of the LADD will overestimate rather than underestimate risk.
The largest values of C encountered under the conditions considered in Tables 8-2 and 8-3 range from 3- to 4-fold for apple juice. Since apple juice was selected to show the wide differences between childhood and adult food consumption patterns, it is not unreasonable to suggest that the use of adult exposure levels will not underestimate actual lifetime.
TABLE 8-3 Values of the Ratio C = LECD/LADD for the Two-Stage Mutation-Birth-Death Model for the Pesticide Residues in Apple Juice, Potatoes, Tomatoes, and Lettucea
cancer risks more than 5-fold, taking into account the increased consumption of these foods by infants and children.
Percent Contribution to Lifetime Risk. The contribution to lifetime risk made by exposures at different ages can be characterized by applying the methods developed by Murdoch et al. (1992) and described above. The percent contribution to lifetime risk (PCLR) made by exposure at age t can be written as:
PCLRt = [(dtrtf)/LECD] × 100%,
where dt is exposure at age t, rt denotes the effectiveness of exposure at age t, and LECD (effectively the sum or integral of dtrt over t) is a normalizing factor. Here, f is the fraction of the lifespan composed by the tth time interval. (For example, f is 1/70 for yearly age groups with an expected lifespan of 70 years.) In this example, exposure depends on both food consumption patterns and pesticide residue levels, whereas relative effectiveness is determined by the model of carcinogenesis used.
For illustration purposes, if one assumes that pesticide applications produce constant levels of residues in food over time, then the only factors that affect exposure levels are changes in food consumption. Such changes could involve changes in the sources of food (e.g., more imported foods with different levels of residues than domestically grown foods) as well as changes in quantities consumed. However, this is an unlikely scenario since the amount of pesticide residues in food is affected by change in regulations, climate, and application practices.
Figure 8-2 shows the percent contribution to lifetime risk from a hypothetical
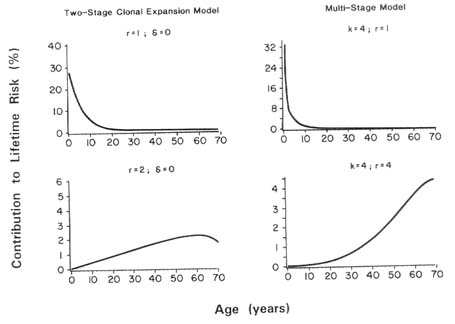
FIGURE 8-2 Annualized contributions to lifetime risk from the consumption of apple juice.
SOURCE: Murdoch and Krewski, 1988.
pesticide residue in apple juice by using a two-stage model with no proliferation of initiated cells (δ = 0). When only the first stage is dose dependent, the PCLR is highest early in life. Specifically, more than 27% of the lifetime risk accrues during the first year of life. This increases to more than 81% by age 10. This occurs because both the highest exposures and the greatest relative effectiveness occur early in life. Calculations (not shown) for δ ≠ 0 indicate that the PCLR early in life increases when δ > 0 and decreases when δ < 0. Even for tδ = -10, however, the PCLR up to age 10 exceeds 56%. (The parameter tδ represents the cumulative net birth rate of initiated cells up to t = 70 years of age, and provides a convenient indicator of the rate of proliferation of initiated cells.)
When the second stage is affected, the relative effectiveness of dosing is low early in life, and only about 5% of the lifetime risk accrues by age 10. After age 40, more than 60% of the lifetime risk accrues. The PCLR up to age 10 decreases when δ > 0 and increases when δ < 0. For tδ = -10, the PCLR up to age 10 is only about 18%.
The PCLR for pesticide residues in lettuce (not shown) are notably different from those for apple juice (Figure 8-2). Because children consume less lettuce than do adults, the PCLR for up to age 10 is comparatively lower. However, with a first-stage carcinogen and a high net birth rate of initiated cells (td = 10), the PCLR up to age 10 is nearly 70%.
These results indicate that the PCLR depends strongly on the form of the underlying two-stage model of carcinogenesis. Which of the two mutation rates is dose dependent appears to be a more critical factor than the proliferation rate d of initiated cells. Similar calculations (see Figure 8-2) for the multistage model with k = 4 stages indicate that assumptions about which stage or stages in the model are dose dependent have a marked effect on the PCLR, since earlier dose-dependent stages lead to a higher PCLR from exposures experienced early in life.
Age-Specific Risks. The preceding analysis of the relative contribution to lifetime risk indicates only the percentage of lifetime risk that accrues each year—not the actual lifetime risk. The lifetime risk (LR) can be expressed as follows:
where LRt = (dtrtP) /70 denotes the contribution to the lifetime risk at t years of age and P is a measure of carcinogenic potency such as the unit risk factor q1* based on the linearized multistage model. The weights rt defined by the relative effectiveness function represent age-specific multipliers that can be used to estimate the risk LRt due to exposure dt at t years of age.
The age-specific multipliers for the two-stage model with d = 0 and the multistage model with k = 4 stages are shown in Figure 8-3. When the last stage is dose dependent, the age-specific multipliers decrease with age, reflecting the fact that earlier exposures are more effective than later exposures (Murdoch and Krewski, 1988). When only the second stage is dose dependent, the age-specific multipliers increase with age.
Consumption and Exposure Data
The data on food consumption and pesticide residues were extremely limited, as described in Chapters 5 and 6, and the limitations were especially severe for infants and children. Furthermore, when determining the acceptability of a food tolerance, EPA compared the theoretical maximum residue contribution (TMRC; see Chapter 6) and anticipated residues to
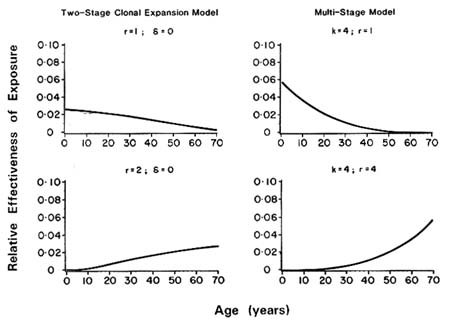
FIGURE 8-3 Multipliers used to obtain annualized contribution to lifetime risk.
SOURCE: Murdoch and Krewski, 1988.
the RfD and if the values were less than the RfD, it was assumed that no adverse health effects would result. However, the TMRC methodology is limited to pesticide exposures from residues in food alone. Thus, although the TMRC values may be less than the RfD, an individual may also be exposed to nondietary sources of that particular pesticide, so that the total exposure exceeds an RfD and is detrimental to health. Although such nondietary exposures of both children and adults are of concern, children may experience greater exposures because of their tendency to ingest foreign objects (a practice called pica). Furthermore, breastfeed infants may be expected to be exposed to low levels of lipophilic pesticides (Babich and Davis, 1981). Lactating women may be, or may have been, exposed to lipophilic pesticides from various sources, including air, food, water, cosmetics, and occupational and household environments, and they may have substantial stores of some that can be mobilized during lactation. Within a few months of birth, the concentration of halocarbons in the body fat of the breastfeed infant may be equivalent to that in the fat of the lactating mother. Although the period of breastfeeding is short compared to the total life span, the lipophilic chemicals accumulated in
the body during these early months may be retained for years (WHO, 1986).
Another source of exposure to pesticides is groundwater (Russell et al., 1987), which supplies drinking water to 97% of rural Americans and 53% of all Americans (USGS, 1988). Water intake should be considered, although an EPA survey of groundwater (EPA, 1990, 1992) indicates that in most cases this will be an insignificant source of pesticide exposure. Neither nondietary exposures nor exposures in drinking water were considered in setting food tolerances using the ''food factor" system. Because of this limitation, total exposures of infants and children may be underestimated.
Conclusions and Recommendations
The evaluation of potential risks to infants and children due to pesticide residues present in the diet requires consideration of a number of factors. In particular, the level of risk depends on individual food consumption patterns, levels of pesticide residues in foods as consumed by infants and children, and the toxicological potency of the pesticide. A comprehensive analysis of the potential risks to infants and children exposed to pesticides in their diets requires consideration of all these factors, as well as any unique characteristics of infants and children relative to adults. The conclusion and recommendations presented here address each of these components of risk assessment.
Conclusions
-
The health risks experienced by infants and children as a result of their exposure to pesticide residues in the diet may differ from those experienced by adults both in nature and severity.
-
Infants and children may exhibit unique susceptibility to the toxic effects of pesticides because they are undergoing rapid tissue growth and development, but empirical evidence to support this is mixed.
-
For some pesticides, infants and children are at greater risk than adults. For others they may exhibit less risk.
-
Infants and children consume much greater quantities of certain foods than do adults on a body weight basis and may thus be subjected to higher levels of exposure to certain pesticides than adults.
-
Exposures occurring earlier in life can lead to greater or lower risk of chronic toxic effects such as cancer than exposures occurring later in life.
-
Traditional approaches to toxicological risk assessment may not always adequately protect infants and children.
Although current uncertainty factors used to extrapolate toxicological data to humans provide for 10-fold variations between species and within the human population, additional protection for developmental toxicity may be required, depending on the toxicant of interest and the amount of testing that has been conducted.
-
It is known that socioeconomic, nutritional, and health status factors influence the vulnerability of human infants and children to environmental toxicants. The committee acknowledges that these are adequately protected by the existing 10-fold uncertainty factor for intraspecies variability.
-
An additional uncertainty factor of up to 10-fold is currently used when prenatal developmental effects are observed.
As a result of its consideration of toxicity to organs that may be particularly susceptible to developmental effects—such as the central nervous system, immune surveillance system, and endocrine system—the committee encourages the development and validation of animal test systems to evaluate toxicity to these organ systems.
-
There is a need for validated animal models for predicting the risks to infants and children.
-
There exist only limited data on the food consumption patterns of infants and children that are appropriate for use in risk assessment.
The data used by the committee to evaluate food consumption patterns of infants and children were derived primarily from the 1977–1978 NFCS. This survey involved relatively small numbers of people in the younger age categories and may not reflect current food consumption patterns.
Recommendations
-
Additional data on the food consumption patterns of infants and children are needed.
Current data indicate that infants and children consume much more of certain foods on a body weight basis than do adults. Because such higher exposures can lead to higher risks, it is important to have accurate data on the food consumption patterns of infants and children. The available data are based on relatively small samples and may not reflect current trends in food consumption by infants and children.
-
All sources of exposures to pesticides—dietary and nondietary—need to be considered when evaluating the potential risks to infants and children.
Since many pesticides are applied to more than one crop, residues of a particular pesticide may be found on different foods. The total intake from all foods on which residue may be present should be calculated when estimating exposure of infants and children. Pesticides may also be present in drinking water due to contamination of groundwater. Nondietary environmental sources, including air, dirt, surfaces, lawns, and pets, should also be considered.
-
Physiological and biochemical characteristics of infants and children that influence metabolism and disposition need to be considered in risk assessment.
Physiological parameters such as tissue growth rates and biochemical parameters such as enzyme induction may affect the response of infants and children to pesticide residues in food.
-
Pharmacokinetic models that provide for the unique physiologic characteristics of infants and children should be developed.
Physiologically based pharmacokinetic models can be used to estimate the dose of toxic metabolites reaching target tissues. Such models can be extended to allow for such factors as lactation and development that are unique to infants and children.
-
Three 10-fold uncertainty factors are now applied to the NOEL to develop the RfD: 10 to account for interspecies differences, 10 to account for intraspecies difference, and 10 when there is evidence of developmental effects as demonstrated by toxicological testing and metabolic/disposition studies. Thus, a 10-fold factor has been applied by the EPA whenever toxicity studies have shown fetal developmental effects. Because of specific periods of vulnerability that exist during development, the committee recommends that an uncertainty factor up to the 10-fold factor traditionally used for fetal developmental toxicity should also be considered for postnatal developmental toxicity and when data from toxicity testing are incomplete. The committee wishes to emphasize that this is not a new, additional uncertainty factor but, rather, an extended application of a uncertainty factor now routinely used by the EPA for a narrower purpose.
Data on anticancer agents and other drugs, insecticides, and pesticides have indicated that infants and children may be more susceptible or less susceptible to the effects of these agents than adults. Additional data are required to better quantify the magnitude of the differences in susceptibility between infants and children and adults, especially with agents causing, neurological or immunological disorders. Systematic studies of age-dependent toxicity are needed to define the magnitude of such differences more precisely.
-
The committee recommends development and validation of animal test systems to evaluate toxicity to developing organ systems.
These tests should be designed to evaluate the unique developmental waypoints of infants and children, including assessment of the central nervous system, immune system, endocrine system, and reproductive system.
-
Estimates of cancer risk should take into account both the higher exposures of infants and children to certain pesticides and the earlier age at which these exposures occur in comparison to adults.
These factors can be taken into account using cancer risk estimation methods that allow for time-dependent exposure patterns and toxicological testing paradigms that include early exposures.
-
The use of biologically based models of carcinogenesis that take into account the special physiological characteristics of infants and children should be developed.
Biologically based models such as the two-stage clonal expansion model of carcinogenesis provide a realistic approach to cancer risk estimation. If the rate of clonal expansion of initiated cells could be determined as a function of age, this information could be used in developing biologically based models of carcinogenesis for use in risk estimation.
-
The use of the benchmark dose for risk assessment applications involving infants and children should be explored.
Although not yet widely applied in risk assessment, the benchmark dose approach offers certain advantages over the NOEL. In particular, this approach uses all the available dose-response data, better reflects the slope of the dose-response curve, and provides an explicit indication of risk at doses at or below the benchmark dose. The benchmark dose may also be used as a means of integrating toxicological and carcinogenic risk assessment methodologies.
-
The use of risk distributions rather than a point estimate such as a mean, median, or outer bound should be used where possible to provide a more complete characterization of risk.
In this report, the notion of combining distributions of individual food consumption levels with distributions of pesticide residue levels in food to obtain a distribution of exposure levels was used extensively and is illustrated by the examples presented in Chapter 7. Data on the potency of a particular pesticide (expressed either in terms of a reference dose or measure of carcinogenic potency) can then combined with data on the distribution of exposures to estimate a distribution of risks across a population of infants and children. Successful application of this method will
require more elaborate food consumption survey data than are currently available. To avoid serious bias in estimates of upper and lower percentiles of distributions of individual daily intakes, repeated observations of food consumption on several different days will be required.
REFERENCES
Abdelsalam, E.B., and E.J. Ford. 1986. Effect of pretreatment with hepatic microsomal enzyme inducers on the toxicity of diazinon in calves. Res. Vet. Sci. 41:336–339.
Agocs, M.M., R.A. Etzel, R.G. Parrish, D.C. Paschal, P.R. Campagna, D.S. Cohen, E.M. Kilbourne, and J.L. Hesse. 1990. Mercury exposure from interior latex paint. New Engl. J. Med. 323:1096–1101.
Aldridge, W.N. 1986. The biological basis and measurement of thresholds. Annu. Rev. Pharmacol. Toxicol. 26:39–58.
Allen, B.C., K.S. Crump, and A.M. Shipp. 1988. Correlation between carcinogenic potency of chemicals in animals and humans. Risk Anal. 8:531–544.
American Health Foundation. 1989. Coronary artery disease prevention: Cholesterol, a pediatric perspective. Prev. Med. 18:323–409.
Andersen, M.E., H.J. Clewell III, M.L. Gargas, F.A. Smith,and R.H. Reitz. 1987. Physiologically based pharmacokinetics and the risk assessment process for methylene chloride. Toxicol. Appl. Pharmacol. 87:185–205.
AOR (Assembly Office of Research). 1988. Pp. 35–36 in The Invisible Diet. Sacramento: Joint Publications Office, State of California.
Armitage, P. 1985. Multistage models of carcinogenesis. Environ. Health Perspect. 63:195–201.
Armitage, P., and R. Doll. 1961. Stochastic models for carcinogenesis. Pp. 19–38 in Fourth Berkeley Symposium on Mathematical Statistics and Probability. Berkeley Calif.: University of California Press.
Arnold, D.L., D. Krewski, and I.C. Munro. 1983. Saccharin: A toxicological and historical perspective. Toxicology 27:179–256.
Babich, H., and D.L. Davis. 1981. Food tolerances and action levels: Do they adequately protect children? BioScience 31:429–438.
Barnes, D.G., and M.L. Dourson. 1988. Reference dose (RfD): Description and use in health risk assessments. Regul. Toxicol. Pharmacol. 8:471–486.
Barr, J.T. 1985. The calculation and use of carcinogenic potency: A review. Regul. Toxicol. Pharmacol. 5:432–459.
Bernstein, L., L.S. Gold, B.N. Ames, M.C. Pike, and D.G. Hoel. 1985. Some tautologous aspects of the comparison of carcinogenic potency in rats and mice. Fundam. Appl. Toxicol. 5:79–86.
Board, P. 1990. Genetic polymorphisms of glutathione S-transferase in man. Pp. 232–241 in Glutathione S-Transferase and Drug Resistance, J.D. Hayes et al., eds. London: Taylor and Frances.
Brasel, J.A., and R.K. Gruen 1978. Cellular growth: Brain, liver, muscle, and lung. Pp. 3–19 in Human Growth: Postnatal Growth, Vol. 2, F. Falkner and J.M. Tanner, eds. New York: Plenum Press.
Brodeur, J., and K.P. DuBois. 1963. Comparison of acute toxicity of anticholinesterase insecticides to weanling and adult male rats. Proc. Soc. Exp. Biol. Med. 114:509–511.
Brown, A.E., O. Quesada, and D. Armstrong. 1982. Minimal nephrotoxicity with cephalosporin-aminoglycoside combinations in patients with neoplastic disease. Antimicrob. Agents Chemother. 21:592–594.
Brown, C.C., and K.C. Chu. 1989. Additive and multiplicative models and multistage carcinogenesis theory. Risk Anal. 9:99–105.
Brown, C.C., and J.A. Koziol. 1983. Statistical aspects of the estimation of human risk from suspected environmental carcinogens. SIAM Rev. 25:151–181.
Chen, J.J., and D.W. Gaylor. 1987. Carcinogenic risk assessment: Comparison of estimated safe doses for rats and mice. Environ. Health Perspect. 72:305–309.
Chen, J.J., R.L. Kodell, and D. Gaylor. 1988. Using the biological two-stage model to assess risk from short-term exposures. Risk Anal. 8:223–230.
Cohen, S.M., and L.B. Ellwein. 1990. Proliferative and genotoxic cellular effects in 2-acetylaminofluorene bladder and liver carcinogenesis: Biological modeling of the ED01 study. Toxicol. Appl. Pharm. 104:79–93.
Crouch, E., R. Wilson, and L. Zeise. 1987. Tautology or not tautology? J. Toxicol. Environ. Health 20:1–10.
Crump, K.S. 1984a. An improved procedure for low-dose carcinogenic risk assessment from animal data. J. Environ. Pathol. Toxicol. Oncol. 6:339–348.
Crump, K.S. 1984b. A new method for determining allowable daily intakes. Fundam. Appl. Toxicol. 4:854–871.
Crump, K.S., and R.B. Howe. 1984. The multistage model with a time-dependent dose pattern: Applications to carcinogenic risk assessment. Risk Anal. 4:163–167.
Crump, K.S., D.G. Hoel, C.H. Langley, and R. Peto. 1976. Fundamental carcinogenic processes and their implications for low dose risk assessment. Cancer Res. 36:2973–2979.
Day, N.E., and C.C. Brown. 1980. Multistage models and primary prevention of cancer. J. Natl. Cancer Inst. 64:977–989.
Dourson, M.L. 1986. New approaches in the derivation of acceptable daily intake (ADI). Comments Toxicol. 1:35–48.
Dourson, M.L., and J.F. Stara. 1983. Regulatory history and experimental support of uncertainty (safety) factors. Regul. Toxicol. Pharmacol. 3:224–238.
Drew, R.T., G.A. Boorman, J.K. Haseman, E.E. McConnell, W.M. Busey, and J.A. Moore. 1983. The effect of age and exposure duration on cancer induction by a known carcinogen in rats, mice and hamsters. Toxicol. Appl. Pharmacol. 68:120–130.
Edwards, D.L., and C.E. Johnson. 1987. Insect-repellent-induced toxic encephalopathy in a child. Clin. Pharm. 6:496–498.
Elashoff, R.M., T.R. Fears, and M.A. Schneiderman. 1987. Statistical analysis of a carcinogen mixture experiment. I. Liver carcinogens. J. Natl. Cancer Inst. 79:509–526.
Ellwein, L.B., and S.M. Cohen. 1988. A cellular dynamics model of experimental bladder cancer. Analysis of the effect of sodium saccharin in the rat. Risk Anal. 8:215–221.
Enesco, M., and C.P. Leblond. 1962. Increase in cell number as a factor in the growth of the organs and tissues of the young male rat. J. Embryol. Exp. Morphol. 10:530–562.
EPA (U.S. Environmental Protection Agency). 1986. Guidelines for carcinogen risk assessment. Fed. Regist. 51:33992–34003.
EPA (U.S. Environmental Protection Agency). 1987. Report of the EPA Workshop on the Development of Risk Assessment Methodologies for Tumor Promoters. EPA/600/9–87/03. Washington, D.C.: U.S. Environmental Protection Agency.
EPA (U.S. Environmental Protection Agency). 1988. Reference Dose (RfD): Description and Use in Health Risk Assessment. Integrated Risk Information System (IRIS). Online. Office of Health and Environmental Assessment, Environmental Criteria and Assessment Office. Cincinnati, Ohio: U.S. Environmental Protection Agency.
EPA (U.S. Environmental Protection Agency). 1990. National Survey of Pesticides in Drinking Water Wells. Phase I. NTIS Doc. No. PB-91-125765. Springfield, Va.: National Technical Information Service.
EPA (U.S. Environmental Protection Agency). 1991. Guidelines for developmental toxicity risk assessment: Notice. Fed. Regist. 56:63798–63826.
EPA (U.S. Environmental Protection Agency). 1992. Another Look: National Survey of Pesticides in Drinking Water Wells - Phase II Report. Office of Pesticides and Toxic Substances. EPA 579/09-91-020. Washington, D.C.: U.S. Environmental Protection Agency.
Faden, H., G. Deshpande, and M. Grossi. 1982. Renal and auditory toxic effects of amikacin in children with cancer. Am. J. Dis. Child. 136:223–225.
Farmer, J.H., R.L. Kodell, and D.W. Gaylor. 1982. Estimation and extrapolation of tumor probabilities from a mouse bioassay with survival/sacrifice components . Risk Anal. 2:27–34.
Fears, T.R., R.M. Elashoff, and M.A. Schneiderman. 1988. The statistical analysis of a carcinogen mixture experiment. II. Carcinogens with different target organs, N-methyl-N'-nitro-N-nitrosoguanidine, N-butyl-n(4-hydroxybutyl) nitrosamine, dipentylnitrosamine and nitrilotriacetic acid. Toxicol. Ind. Health 4:221–255.
Fears, T.R., R.M. Elashoff, and M.A. Schneiderman. 1989. The statistical analysis of a carcinogen mixture experiment. III. Carcinogens with different target systems, aflatoxin B1, N-butyl-n (4-hydroxybuty 1) nitrosamine, lead acetate, and thiouracil. Toxicol. Ind. Health 5:1–23.
Fenyvesi, G., M. Botos, and J. Iván. 1985. Pesticide-drug interaction in rats. Arch. Toxicol. (Suppl.) 8:269–271.
Fisher, J.W., T.A. Whittaker, D.H. Taylor, H.J. Clewell III, and M.E. Andersen. 1989. Physiologically based pharmacokinetic modeling of the pregnant rat: A multiroute exposure model for trichloroethylene and its metabolite, trichloroacetic acid. Toxicol. Appl. Pharmacol. 99:395–414.
Fisher, J.W., T.A. Whittaker, D.H. Taylor, H.J. Clewell III, and M.E. Anderson. 1990. Physiologically based pharmacokinetic modeling of the lactating rat and nursing pup: A multiroute exposure model for trichloroethylene and its metabolite, trichloroacetic acid. Toxicol. Appl. Pharmacol. 102:497–513.
Food and Chemical Toxicology. 1985, Saccharin-Current status. Food Chem. Toxicol. 23:543–546.
Freireich, E.J., E.A. Gehan, D.P. Rall, L.H. Schmidt, and H.E. Skipper. 1966. Quantitative comparison of anticancer agents in mouse, rat, hamster, dog, monkey and man. Cancer Chem. Rep. 50:219–248.
Furlong, C., R. Richter, S. Seidel, and A. Motulsky. 1988. Role of genetic polymorphism
of human plasma paraoxonase/arylesterase in hydrolysis of the insecticide metabolites chlorpyrifos oxon and paraoxon. Am. J. Hum. Genet. 43:230–238.
Gabrielsson, J.L., and L.K. Paalzow. 1983. A physiological pharmacokinetic model for morphine disposition in the pregnant rat. J. Pharmacokinet. Biopharm. 11:147–163.
Gabrielsson, J.L., P. Johansson, U. Bondesson, and L.K. Paalzow. 1985a. Analysis of methadone disposition in the pregnant rat by means of a physiological flow model. J. Pharmacokinet. Biopharm. 13:355–372.
Gabrielsson, J.L. Paalzow, S. Larsson, and I. Blomkvist. 1985b. Constant rate of infusion-improvement of tests for teratogenicity and embryotoxicity. Life Sci. 37:2275–2282.
Gaines, T.B., and R.E. Linder. 1986. Acute toxicity of pesticides in adult and weanling rats. Fundam. Appl. Toxicol. 7:299–308.
Gaylor, D.W. 1987. Linear-nonparametric upper limits for low dose extrapolation. Pp. 63–66 in Proceedings of the Biopharmaceutical Section of the American Statistical Association. Alexandria, Va.: American Statistical Association.
Gaylor, D.W. 1988. Risk Assessment: Short-term exposure at various ages. In Phenotypic Variation in Populations: Relevance to Risk Assessment, A.D. Woodhead, M.A. Bender, and R.C. Leonard, eds. New York: Plenum.
Gaylor, D.W., and J.J. Chen. 1986. Relative potency of chemical carcinogens in rodents. Risk Anal. 6:283–290.
Gaylor, D.W., and R.L. Kodell. 1980. Linear interpolation algorithm for low dose risk assessment of toxic substances. J. Environ. Pathol. Toxicol. 4:305–312.
Gillman, M.A., and R. Sandyk. 1985. Phenytoin toxicity and co-trimoxazole. Ann. Intern. Med. 102:559.
Glaubiger, D.L., D.D. von Hoff, J.S. Holcenberg, B, Kamen, C. Pratt. and R.S. Ungerleider. 1982. The relative tolerance of children and adults to anticancer drugs. Front. Radiat. Ther. Oncol. 16:42–49.
Godfrey, K. 1983. Compartmental Models and Their Application. London: Academic Press.
Gold, L.S., C.B. Sawyer, R. Magaw, G.M. Backman, M. deVeciana, R. Levinson, N.K. Hooper, W.R. Havender, L. Bernstein, R. Peto, M.C. Pike, and B.N. Ames. 1984. A carcinogenic potency database of the standardized results of animal bioassays. Environ. Health Perspect. 58:9–19.
Gold, L.S., J.M. Ward, L. Bernstein, and B. Stern. 1986. Association between carcinogenic potency and tumor pathology in rodent carcinogenesis bioassays . Fundam. Appl. Toxicol. 6:677–690.
Goldenthal, E.I. 1971. A compilation of LD50 values in newborn and adult animals. Toxicol. Appl. Pharmacol. 18:185–207.
Gotelli, C.A., E. Astolfi, C. Cox, E. Cernichiari, and T.W. Clarkson. 1985. Early biochemical effects of an organic mercury fungicide on infants: "Dose makes the poison." Science 227:638–640.
Greenfield, R.E., L.B. Ellwein, and S.M. Cohen. 1984. A general probabilistic model of carcinogenesis: Analysis of experimental urinary bladder cancer. Carcinogenesis 5:437–445.
Gross, M.A., O.G. Fitzhigh, and N. Mantel. 1970. Evaluation of safety for food additives: An illustration involving the influence of methyl salicylate on rat reproduction. Biometrics 26:181–194.
Gryboski, J., D. Weinstein, and N.K. Ordway. 1961. Toxic encephalopathy apparently related to the use of an insect repellant. New Engl. J. Med. 264:289–291.
Guengerich, F.P., L.M. Distlerath, P.E. Reilly, T. Wolff, T. Shimada, D.R. Umbenhauer, and M.V. Martin. 1986. Human liver cytochromes P-450 involved in polymorphisms of drug oxidation. Xenobiotica 16:367–378.
Haseman, J.K., and J.E. Huff. 1987. Species correlation in long-term carcinogenicity studies. Cancer Lett. 37:125–132.
Heick, H., M. Shipman, M. Norman, and W. James. 1980. Brief clinical and laboratory observations: Reye-like syndrome associated with use of insect repellent in a presumed heterozygote for ornithine carbamoyltransferase deficiency. J. Pediatr. 97:471–473.
Hoel, D.G. 1980. Incorporation of background in dose-response models. Fed. Proc. 39:73–75.
Hoel, D.G., N.L. Kaplan, and M.W. Anderson. 1983. Implication of nonlinear kinetics on risk estimation in carcinogenesis. Science 219:1032–1037.
Homan, E.R. 1972. Quantitative relationships between toxic doses of anti-tumor chemotherapeutic agents in animals and man. Cancer Chemother. Rep. (3):13–19
Hytten, F.E., and G. Chamberlain. 1980. Clinical Physiology in Obstetrics. Oxford: Blackwell.
IARC (International Agency for Research on Cancer). 1987. IARC Monographs on the Evaluation of Carcinogenic Risks to Humans. Overall Evaluations of Carcinogenicity: An Updating of IARC Monographs, Vols. 1–42, Supplement 7. Lyon, France: International Agency for Research on Cancer.
Iball, J. 1939. The relative potency of carcinogenic compounds. Am. J. Cancer 35:188–190.
Kaldor, J.M., and N.E. Day. 1987. Interpretation of epidemiological studies in the context of the multistage model of carcinogenesis. Pp. 21–57 in Mechanisms of Environmental Carcinogenesis: Vol. II—Multistep Models of Carcinogenesis, J.D. Barrett, ed. Boca Raton, Fla.: CRC Press.
Ketterman A.J., S.M. Pond, and C.E. Becker. 1987. The effects of differential induction of cytochrome P-450, carboxylesterase and glutathione S-transferase activities on malathion toxicity in mice. Toxicol. Appl. Pharmacol. 87:389–392.
Kimmel, C.A., B.C. Allen, R.J. Kavlock, and E.M. Faustman. 1991. Alternatives to the NOAEL/UF approach for calculating reference dose. Unpublished.
Klaassen, C.D. 1986. Principles of toxicology. Pp. 11–32 in Casarett and Doull's Toxicology: The Basic Science of Poisons, 3rd ed. C.D. Klaassen, M.O. Amdur, and J. Doull, eds. New York: Macmillan. 974 pp.
Kodell, R.L., D.W. Gaylor, and J.J. Chen. 1987. Using average lifetime dose rate for intermittent exposures to carcinogens. Risk Anal. 7:339–345.
Kodell, R.L., D. Krewski, and J.M. Zielinski. 1991. Additive and multiplicative relative risk in the two-stage clonal expansion model of carcinogenesis. Risk Anal. 11:483–490.
Krewski, D., and D.J. Murdoch. 1990. Cancer modeling with intermittent exposures. Pp. 196–214 in Scientific Issues in Quantitative Cancer Risk Assessment, S.H. Moolgavkar, eds. Cambridge, Mass.: Birkhauser.
Krewski, D., and R.D. Thomas. 1992. Carcinogenic mixtures. Risk Anal. 12:105–113.
Krewski, D., S. Brown, and D. Murdoch. 1984. Determining "safe" levels of exposure: Safety factors or mathematical models? Fundam. Appl. Toxicol. 4:S383–S394.
Krewski, D., D. Murdoch, and A. Dewanji. 1986. Statistical modeling and extrapolation of carcinogenesis data. Pp. 259–282 in Modern Statistical Methods in Chronic Disease Epidemiology, S.H. Moolgavkar and R.L. Prentice, eds. New York: John Wiley and Sons.
Krewski, D., D.J. Murdoch, and J.R. Withey. 1987. The application of pharmacokinetic data in carcinogenic risk assessment. Pp. 1–468 in Drinking Water and Health, Vol. 8: Pharmacokinetics and Risk Assessment. Washington, D.C.: National Academy Press.
Krewski, D., T. Thorslund, and J. Withey. 1989. Carcinogenic risk assessment of complex mixtures. Toxicol. Ind. Health 5:851–867;
Krewski, D., D.W. Gaylor, and M. Szyszkowicz. 1991. A model-free approach to low dose extrapolation. Environ. Health Perspect. 90:279–285.
Krewski, D., D.W. Gaylor, A.P. Soms, and M. Szyszkowicz. 1993. Correlation between carcinogenic potency and the maximum tolerated dose: Implications for risk assessment. Pp. 111–171 in Issues in Risk Assessment. Washington, D.C.: National Academy Press.
La Du, B.N., and H.W. Eckerson, 1984. The polymorphic paraoxonase arylesterase isozymes of human serum. Fed. Proc. 43:2338–2341.
Lehman, A.J., and O.G. Fitzhugh. 1954. 100-fold margin of safety. Assoc. Food Drug Off. Q. Bull. 18:33–35.
Lindstedt, S.L. 1987. Allometry: Body size constraints in animal design. Pp. 65–79 in Drinking Water and Health, Vol. 8: Pharmacokinetics in Risk Assessment. Washington, D.C.: National Academy Press.
Lu, F.C. 1988. Acceptable daily intake: Inception, evolution, and application. Regul. Toxicol. Pharmacol. 8:45–60.
Luebeck, E.G., S.H. Moolgavkar, A Buchmann, and M. Schwartz. 1991. Effects of polychlorinated biphenyls in rat liver: Quantitative analysis of enzyme-altered foci. Toxicol. Appl. Pharmacol. 111:469–484.
Lutz, W.K., P. Buss, A. Baertsch, and M. Caviezel. 1990. Evaluation of DNA binding in vivo for low dose extrapolation in chemical carcinogenesis. In Genetic Toxicology of Complex Mixtures, M.D. Waters, S. Nesnow, J. Lewtas, N.M. Moore, and F.B. Daniels, eds. New York: Plenum.
Mackness, M., C. Walker, and L. Carlson. 1987. Low A-esterase activity in serum of patients with fish-eye disease. Clin. Chem. 33:587–588.
Mattison, D.R. 1986. Drug and Chemical Action in Pregnancy, S. Fabro and A.R. Scialli, eds. New York: Marcel Dekker.
Mattison, D.R., E. Blann, and A. Malek. 1991. Symposium: Pharmacokinetics in Developmental Toxicity. Physiological alterations during pregnancy: Impact on toxicokinetics. Fundam. Appl. Toxicol. 16:215–218.
McColl, S., 1989. Biological Safety Factors in Toxicological Risk Assessment. Ottawa: Health & Welfare Canada.
McFarland Child Health Screening Project. 1991. McFarland Child Health Screening Project: 1989. Environmental Epidemiology and Toxicology Branch, California Department of Health Services, Emeryville, Calif.
Mendelson, J., and S. Grisolia. 1975. Age-dependent sensitivity to salicylate. Lancet 2(7942):974.
Menzel, D.B. 1987. Physiological pharmacokinetic modeling. Environ. Sci. Technol. 21:944–950.
Metzger, B., E. Crouch, and R. Wilson. 1989. On the relationship between carcinogenicity and acute toxicity. Risk Anal. 9:169–177.
Mitchell, R., and B. Dawson. 1973. Educational and social characteristics of children with asthma. Arch. Dis. Child 48:467–471.
Moolgavkar, S.H. 1986a. Carcinogenesis modeling from molecular biology to epidemiology. Annu. Rev. Public Health 7:151–169.
Moolgavkar, S.H. 1986b. Hormones and multistage carcinogenesis. Cancer Surv. 5:635–648.
Moolgavkar, S.H., and E.G. Luebeck. 1990. Two-event model for carcinogenesis: Biological, mathematical, and statistical considerations. Risk Anal. 10:323–341.
Moolgavkar, S,H., and E.G. Luebeck. 1992. Interpretation of Labeling indices in the presence of cell death. Carcinogenesis 13:1007–1010.
Moolgavkar, S.H., A. Dewanji, and D.J. Venzon. 1988. A stochastic two-stage model for cancer risk assessment. I. The hazard function and the probability of tumor. Risk Anal. 8:383–392.
Moolgavkar, S.H., E.G. Leubeck, M. de Gunst, R.E. Port, and M. Schwarz. 1990. Quantitative analysis of enzyme-altered foci in rat hepatocarcinogenesis experiments-I. Single agent regimen. Carcinogenesis 11:1271–1278.
Moolgavkar, S.H., E.G. Luebeck, D. Krewski, and J.M. Zielinski. 1993. Radon, cigarette smoke and lung cancer: A reanalysis of the Colorado plateau uranium miners' data. Epidemiology 4:204–217.
Murdoch, D.J., and D. Krewski. 1988. Carcinogenic risk assessment with time-dependent exposure patterns. Risk Anal. 8:521–530.
Murdoch, D.J., D.R. Krewski, and K.S. Crump. 1987. Quantitative theories of carcinogenesis. Pp. 61–89 in Cancer Modeling, J.R. Thompson and B. W. Brown, eds. New York: Marcel Dekker.
Murdoch, D.J., D. Krewski, and J. Wargo. 1992. Cancer risk assessment with intermittent exposure. Risk Anal. 12:569–577.
NRC (National Research Council). 1970. Evaluating the Safety of Food Chemicals. Washington, D.C.: National Academy of Sciences.
NRC (National Research Council). 1977. Drinking Water and Health. Washington, D.C.: National Academy Press.
NRC (National Research Council). 1986. Drinking Water and Health, Vol. 6. Washington, D.C.: National Academy Press.
NRC (National Research Council). 1987a. Drinking water and Health, Vol. 8: Pharmacokinetics in Risk Assessment. Washington, D.C.: National Academy Press.
NRC (National Research Council). 1987b. Regulating Pesticides in Food: The Delaney Paradox. Washington, D.C.: National Academy Press.
NRC (National Research Council). 1988. Complex Mixtures: Methods for In Vivo Toxicity Testing. Washington, D.C.: National Academy Press.
NRC (National Research Council). 1989. Diet and Health: Implications for Reducing Chronic Disease Risk. Washington, D.C.: National Academy of Sciences.
NRC (National Research Council). 1992. Environmental Neurotoxicology. Washington, D.C.: National Academy Press.
NRC (National Research Council). 1993. Issues in Risk Assessment. Washington, D.C.: National Academy Press.
NTP (National Toxicology Program). 1992. NTP Technical Report on the Perinatal Toxicity and Carcinogenicity Studies of Ethylene Thiourea in F/344 rats and B6C3F1 mice (Feed Studies). NTP Technical Report 388. Research Triangle Park, N.C.: National Toxicology Program.
O'Flaherty, E.J. 1981. Toxicants and Drugs: Kinetics and Dynamics. New York: John Wiley and Sons.
Olanoff, L.S., and J.M. Anderson. 1980. Controlled release of tetracyline III: A physiologically pharmacokinetic model of the pregnant rat. J. Pharmacokinet. Biopharm. 8:599–620.
Ortigoza-Ferado, J., R. Richter, C. Furlong, and A.G. Motulsky. 1984. Biochemical genetics of paraoxonase. Pp. 177–188 in Banbury Report No. 16: Genetic Variability in Responses to Chemical Exposure, G.S. Omenn and H.V. Gelboin, eds. New York: Cold Spring Harbor Laboratory.
OSTP (Office of Science and Technology Policy). 1986. Chemical carcinogenesis, A review of the science and its associated principles. Environ. Health Perspect. 67:201–282.
Owen, Y., and R. Frankle. 1986. Nutrition and the Community, 2nd ed. St. Louis, Mo.: Times Mirror/Mosby College Publishing.
Paynter, O.E., G.J. Burin, R.B. Jaeger, and C.A. Gregorio. 1988. Goitrogens and thyroid follicular cell neoplasia: Evidence for a threshold process. Regul. Toxicol. Pharmacol. 8:102–119.
Peach, J.D. 1987. Statement of J. Dexter Peach, General Accounting Office. Pp. 14–43 in Pesticides in Food. Hearing before the Subcommittee on Oversight and Investigations of the Committee on Energy and Commerce, House of Representatives, April 30, Serial No. 100-17. Washington, D.C.: U.S. Government Printing Office.
Peto, R. 1978. Carcinogenic effects of chronic exposure to very low levels of toxic substances. Environ. Health Perspect. 22:155–159.
Peto, R., M.C. Pike, L. Bernstein, L.S. Gold, and B.N. Ames. 1984. The TD50: A proposed general convention for the numerical description of the carcinogenic potency of chemicals in chronic-exposure animal experiments. Environ. Health Perspect. 58:18.
Peto, R., R. Gray, P. Brantom, and P. Grasso. 1986. Nitrosamine carcinogenesis in 5120 rodents: Chronic administration of sixteen different concentrations of NDEA, NDMA, NPYR and NPIP in the water of 4440 inbred rats, with parallel studies on NDEA alone of the effect of age of starting (3, 6 or 20 weeks) and of species (rats, mice or hamsters). Pp. 627–665 in N-Nitroso compounds: Occurrence, Biological Effects and Relevance to Human Cancer, I.K. O'Neill, R.C. Von Borstel, C.T Miller, J.I. Long, and H. Bartsch, eds. IARC Scientific Publication No. 57. Lyon, France: International Agency for Research on Cancer.
Pinkel, D. 1958. The use of body surface area as a criterion on drug dosage in cancer chemotherapy. Cancer Res. 18:853–860.
Pitot, H.C., and Y.P. Dragan. 1991. Facts and theories concerning the mechanisms of carcinogenesis. FASEB J. 5:2280–2286.
Portier, C.J. 1987. Statistical properties of a two-stage model of carcinogenesis. Environ. Health Perspect. 76:125–131.
Portier, C.J., and N.L. Kaplan. 1989. Variability of safe dose estimates when using complicated models of the carcinogenic process. A case study: Methylene chloride. Fundam. Appl. Toxicol. 13:533–544.
Rall, D.P., M.D. Hogan, J.E. Huff, B.A. Schwetz, and R.W. Tenant. 1987. Alternatives to using human experience in assessing health risks. Annu. Rev. Public Health 8:355–385.
Rice, J.M. 1979. Perinatal period and pregnancy: Intervals of high risk for chemical carcinogens. Environ. Health Perspect. 29:23–27.
Rieth, J.P., and T.B. Starr. 1989. Chronic bioassays: Relevance to quantitative risk assessment of carcinogens. Regul. Toxicol. Pharmacol. 10:160–173.
Russell, H.H., R.J. Jackson, D.P. Spath, and S.A. Bock. 1987. Chemical contamination of California drinking water. West. J. Med. 147:615–622.
Saunders, D.S. 1987. Briefing Paper on the Tolerance Assessment System (TAS) for Presentation to the FIFRA Science Advisory Panel, Hazard Evaluation Division. Washington, D.C.: Environmental Protection Agency, Office of Pesticide Programs.
Sawyer, C., R. Peto, L. Bernstein, and M.C. Pike. 1984. Calculation of carcinogenic potency from long-term animal carcinogenesis experiments. Biometrics 40:27–40.
Schneiderman, M.A., and N. Mantel. 1973. The Delaney Clause and a scheme for rewarding good experimentation. Prev. Med. 2:165–170.
Sharkawi, M., D. Cianflone, and A. El-Hawari. 1978. Toxic interactions between disulfiram and some centrally acting drugs in rats. J. Pharmaceut. Pharmacol. 30:63.
Shlyakhter, A., G. Goodman, and R. Wilson. 1992. Monte Carlo simulation of rodent carcinogenicity bioassays. Risk Anal. 12:73–82.
Snyder, W.S., M.J. Cook, E.S. Nasset, L. R. Karhausen, G.P. Howells, and I.H. Tiptar. 1974. Report of the Task Group on Reference Man. Oxford: Pergamon.
Starfield, B. 1982. Family income, ill health, and medical care of U.S. Children. J. Public Health Policy 3:244–259.
Starfield, B., and P.P. Budetti. 1985. Child health status and risk factors. Health Serv. Res. 19:817–886.
Sultatos, L.G. 1986. The effects of phenobarbital pretreatment on the metabolism and acute toxicity of the pesticide parathion in the mouse. Toxicol. Appl. Pharmacol. 86:105–111.
Thorslund, T., and G. Charnley. 1988. Quantitative dose-response models for tumor promoting agents. Pp. 245–255 in Banbury Report No. 31: Carcinogen Risk Assessment: New Directions in the Qualitative and Quantitative Aspects, R.W. Hart and F.D. Hoerger, eds. New York: Cold Spring Harbor Laboratory.
Thorslund, T., C.C. Brown, and G. Charnley. 1987. Biologically motivated cancer risk models. Risk Anal. 7:109–119.
Travis, C.C., and R.K. White. 1988. Interspecies and scaling of toxicity data. Risk Anal. 8:119–125.
Twort, C.C., and J.M. Twort. 1933. Suggested methods for the standardization of the carcinogenic activity of different agents for the skin of mice. Am. J. Cancer 17:293–320.
USGS (U.S. Geological Survey). 1988. National Water Summary 1986: Hydrologic Events and Ground-water Quality. U.S. Geological Survey Water Supply Paper 2325. Denver, Colo.: U.S. Government Printing Office.
Van Ryzin, J. 1980. Quantitative risk assessment. J. Occup. Med. 22:321–326.
Wagner, J.G. 1971. Biopharmaceutics and Relevant Pharmacokinetics, Chapter 4. Hamilton, Ill.: Drug Intelligence Publications.
Wartenburg, D., and M.A. Gallo. 1990. The fallacy of ranking possible carcinogenic hazards using the TD50. Risk Anal. 10:609–613.
Weber, W.W. 1987. The Acetylator Genes and Drug Response. New York: Oxford University Press.
Whittemore, A., and J.B. Keller. 1978. Quantitative theories of carcinogenesis. SIAM Rev. 20:1–30.
WHO (World Health Organization). 1986. Environmental Health Criteria 59. Principles for Evaluating Health Risks from Chemicals during Infancy and Early Childhood. The Need for a Special Approach. Geneva: World Health Organization.
Zadikoff, C.M. 1979. Toxic encephalopathy associated with use of insect repellant. J. Pediatr. 95:140–142.
Zeise, L., E.A.C. Crouch, and R. Wilson. 1984. Use of acute toxicity to estimate carcinogenic risk. Risk Anal. 4:187–199.
Zeise, L., E.A.C. Crouch, and R. Wilson. 1986. A possible relationship between toxicity and carcinogenicity. J. Am. Coll. Toxicol. 5:137–152.


















































