9
Models of the Demographic Effect of AIDS
Michael A.Stoto
INTRODUCTION
With the increasingly high prevalence of the human immunodeficiency virus (HIV) infection, the devastating nature of HIV disease, and the possibility of heterosexual and perinatal transmission, acquired immunodeficiency syndrome (AIDS) seems to have the potential, especially in less developed countries, for major demographic and social effects. The disease obviously affects mortality, and it could indirectly affect fertility through behavioral changes such as condom use, number of partners, and so on, or by causing the death of men and women of childbearing age. Patterns of rural-urban migration could also change if the epidemic’s effect is different in urban and rural areas. To help understand the potential effects of this epidemic, several different computer-based epidemic models have been developed. They have been used for both developed and less developed countries (LDCs), especially African countries. These modeling efforts have the potential to help health policymakers understand the dynamics of the epidemic, to forecast the burden of illness in the future, and to evaluate potential interventions.
An exchange in the popular press in 1992 illustrates the results and
Michael A.Stoto is director of the Division of Health Promotion and Disease Prevention, Institute of Medicine, National Academy of Sciences.
policy uses (and perhaps misuses) of HIV/AIDS models. In June, a number of newspapers and magazines reported on projections made by Roy Anderson and colleagues at Imperial College in London. The New York Times article opened with the statement that “populations in the worst-afflicted African countries will within 20 years switch over from their present high rate of increase to an actual decrease in numbers” (Perlez, 1992). The report noted that these projections were “far gloomier than those of other mathematical modelers at the World Bank, the World Health Organization …, and the Population Council in New York” and also said that the findings were controversial because they rely on sexual behavior for which there are still only imprecise data. In support, however, the article noted recent (but as of then not published) pessimistic projections from the Harvard School of Public Health (Altman, 1992). Anderson was quoted as saying that he hoped his projections would awaken policymakers in the West and in Africa to the gravity of the situation, which he called “the most serious threat to humankind in modern times,” and he added that “the situation calls for massive investment to find a vaccine.” He also mentioned that the projections were useful for assessing how best to curb the rate of infection and called for methods to change behavior soon but suggested that it was already too late for sexually active people in hard hit areas. In response, an unnamed senior official at the U.S. State Department was quoted suggesting that investment in African family planning programs was no longer necessary because “the population is about to be decimated.”
In July, two officials from the Rockefeller Foundation wrote in response that even if the projections were accurate, it was wrong to “abandon hopes for millions of people” who were not already infected (Berkley and Hughes, 1992). They added that Anderson’s pessimistic assumptions that there would be no change in sexual behavior in Africa might be wrong and that it was unfair to single Africa out in this way. Furthermore, they suggested that fertility rates could possibly increase to offset the loss of young children to AIDS and, despite the State Department official’s comment, suggested that family planning is essential where HIV infection is high in order to empower women to manage their own fertility. In addition to the policy issues that this letter raises, the interchange also suggests that we must consider how to validate or otherwise assess the quality of model results, especially when they are necessarily based on many assumptions.
This chapter describes the currently available models of the HIV/AIDS epidemic and summarizes what these models say about the potential future demographic effects of AIDS in Africa. It is not a comprehensive review of the epidemiology of HIV/AIDS or of all modeling efforts. The chapter begins with a brief introduction to the epidemiology of AIDS in Africa, with a focus on aspects of the epidemic that must be incorporated in the models. It then describes the main features of epidemic models developed
to date. Some quantitative and qualitative results of these models for the African situation are described, and the major sources of uncertainty are addressed.
This analysis is based, in large part, on a United Nations/World Health Organization (UN/WHO) publication entitled The AIDS Epidemic and its Demographic Consequences (United Nations, 1991). The UN/WHO report is the proceedings of a workshop that these two organizations sponsored in late 1989 on modeling the demographic effect of the AIDS epidemic in countries in which HIV transmission is primarily heterosexual or perinatal. The report summarizes the efforts of eight modeling teams to apply their models with a common set of assumptions and compares the results. Reports of more recent modeling efforts are also referred to.
EPIDEMIOLOGY OF AIDS IN SUB-SAHARAN AFRICA1
AIDS represents the late clinical stage of infection with HIV. HIV causes severe damage to the immune system, and the course of HIV disease usually spans several years. Some individuals develop an acute illness resembling mononucleosis several weeks or months after infection, but most infected persons have no other clinical signs or symptoms for years. The first clinical symptoms are often nonspecific; they could include chronic diarrhea, weight loss, fever, and fatigue. As the immune system fails, however, the body becomes increasingly susceptible to potentially fatal conditions such as Kaposi’s sarcoma and opportunistic infections. The clinical manifestations of AIDS in developing countries can be very different from those in developed countries because the background microbiological flora are different.
The proportion of HIV-infected persons who ultimately develop AIDS is not known precisely because no cohorts have been followed for much more than a decade, but the proportion is usually assumed to be 100 percent. Cohort studies of HIV-infected adults in the United States suggest that about 15 to 20 percent develop AIDS within five years and about 50 percent develop it within ten years. The data for Africa are limited, and the incubation period may be similar or shorter because Africans are typically exposed more frequently to a larger range of infectious agents.
HIV is transmitted in a number of ways, but primarily through sexual intercourse with infected partners, through injections with contaminated needles or syringes, through the administration of infected blood or blood products, perinatally from mother to child, and possibly through breastfeeding. Estimates of the probability that HIV will be transmitted through any of these
routes and of the efficiency of transmission vary substantially. In Africa, the high prevalence of sexually transmitted diseases (STDs) with genital ulcers and the otherwise high infectious disease burden are thought to increase the efficiency of HIV transmission. Individuals become infectious after they are themselves infected and remain so for the course of the disease. Some evidence suggests, however, that individuals have an initial burst of infectiousness soon after they are themselves infected, the level of infectiousness subsides, and then it gradually increases as the concentration of HIV increases in the blood.
The World Health Organization has described three distinct epidemiological patterns of HIV/AIDS, and the countries of sub-Saharan Africa are known as “pattern II” countries: HIV infection and AIDS are found primarily in sexually active heterosexuals. By the end of the 1980s, the HIV/ AIDS epidemic appeared to be most severe in middle and eastern Africa, extending into several adjacent countries. Most of the cases in these areas are infected with HIV-1, the form of the virus most prevalent in much of the world. An apparently less pathogenetic form of the virus, HIV-2, has been found in western Africa, but at lower prevalence levels.
The HIV epidemic seems to be concentrated in the cities of Africa; as many as 5 to 10 percent of infants born in these areas, on average, are HIV positive. Chin (1991) estimates that HIV seroprevalence among sexually active adults in urban areas is 20 to 30 percent, about 10 times that in rural areas. Rural areas along heavily traveled roads, however, tend to have higher rates. All told, the World Health Organization (1992) estimates that 8 million people in sub-Saharan Africa are infected with HIV.
PURPOSES AND TYPES OF HIV/AIDS MODELS: GENERAL CONSIDERATIONS
HIV/AIDS models have been developed for several purposes, and these purposes have determined the models’ structure and capabilities. The primary purpose of some models is to forecast the effect of the epidemic in order to plan a response or perhaps to warn policymakers of the consequences of inaction. The forecasts could be either short term (a few years) or long term (a few decades or more). Other models have as their primary purpose the assessment of possible interventions and their implications for policy. Such models explore, for instance, the relative effect of changing sexual behaviors such as number and choice of partners, the use of condoms, and the screening of blood. A third group of models aims at understanding the epidemic’s dynamics for the purposes of interpreting epidemiological data, understanding biological aspects of HIV disease and transmission, and making policy recommendations for disease control.
Reflecting the disciplines of the modelers as well as the different rea-
sons for constructing the models, a wide variety of approaches have been taken. In order to compare these approaches, it is helpful to characterize the models in terms of their “state variables” and “dynamics.”
State variables summarize the state of the epidemic at any instant. They usually represent the number of people (and sometimes couples) in certain groups who are uninfected, have HIV infection, or have AIDS. These groups are usually chosen to increase the homogeneity with regard to risk of HIV infection within groups and to maximize differences with regard to risk across groups. In the HIV/AIDS models, the categories are generally defined by combinations of age and sex; risk-related practices such as sexual patterns, intravenous (IV) drug use, and so on; rural-urban residence; presence of STDs; and other variables.
The models’ dynamics are the mathematical rules that determine how the state variables change over time. Some of these rules relate to the infection process and the natural history of the disease, and others relate to changes in the risk-related behaviors and to population dynamics unrelated to AIDS. A model’s dynamics are usually specified through mathematical equations. The form of these equations defines the structure of the model, and the constants in these equations—the model’s parameters—adapt it to a given population.
In developing HIV/AIDS models, several choices must be made. Perhaps the most important is the degree to which the model uses statistical extrapolation or attempts to construct a realistic representation of the biological and behavioral patterns that underlie the epidemic.
Statistical models are based on mathematical extrapolations—perhaps complex—of trends in HIV or AIDS incidence. These models have a relatively small number of state variables, and these variables usually correspond to the categories in which HIV/AIDS cases are reported in surveillance systems. Their dynamics are specified mathematically with reference to historical trends, rather than reflecting epidemiological or behavioral functions. Statistical models tend to be simple, and (subject to data quality constraints) one can easily assess how well the model has worked in the past. There is never assurance, however, that historical trends will continue in the future. Furthermore, these models offer no possibility for evaluating behavioral interventions.
Epidemic models, on the other hand, specify biologically and behaviorally realistic dynamics and, therefore, must employ a relatively large number of state variables to reflect differences in behavior and disease status in the population. The dynamics of these models reflect the epidemic process; for instance, the number of new HIV infections in a given period is commonly a function of both the number of infectious individuals (based on past infections, the natural history of HIV disease, and other biological and
behavioral assumptions) and the number of susceptible individuals (based on demographic trends and behavioral assumptions).
Because of their more realistic dynamics, epidemic models can be used to explore the effect of the HIV/AIDS epidemic in finer detail than statistical extrapolation models. They can also be used to evaluate possible behavioral and other interventions. Epidemic models, however, make formidable demands on the available data. The modeler must make a large number of assumptions about the parameters that specify the model’s dynamics. Initial values are needed for the number of people in a large and complex set of groups. As a result of the complexity of epidemic models, it is often difficult to validate the form of model or its results, or to estimate the parameters needed to adapt a model to a given country’s situation.
Modelers face a number of other choices in constructing HIV/AIDS models. The unit of analysis, for instance, can be the entire population (for extrapolation models), subgroups within it (with differing degrees of disaggregation), couples, or individuals.
Models differ in terms of their degree of disaggregation by demographic factors, risk groups, geography, and so forth, and in the inclusion of biological, behavioral, and policy variables. More disaggregation is thought to make the models more realistic, and permits the evaluation of more complex and targeted interventions. Disaggregation, however, tends to increase data demands for parameter estimation in an almost geometric fashion.
Models also can be specified as deterministic or stochastic. In deterministic models, the state variables are continuous variables representing the number of individuals in each population category. The model dynamics consist of equations that describe how the number of individuals in each category changes over time, given the model parameters. The state variables in stochastic or microsimulation models describe the demographic characteristics, risk-related behavioral characteristics, and infection/disease status of each of a finite number of discrete individuals. The dynamics are expressed in probability statements about the possible changes in any individual’s characteristics. Microsimulation models can offer more flexibility in specifying complex behavioral patterns and interventions, but they are frequently more computer intensive and the results can be more difficult to interpret.
EXISTING HIV/AIDS MODELS
As already noted, a wide variety of HIV/AIDS models have been developed. Although they differ on a number of dimensions, they can be categorized in three major groups: statistical extrapolation and “back-calculation” models, models that represent the biological nature of the epidemic, and demographic/behavioral models.
Statistical Extrapolation and Back-Calculation Models
Some of the more prominent AIDS modeling efforts in the United States and other developed countries are based on statistical extrapolation of the number of AIDS cases reported to surveillance systems. The earliest projection of AIDS in the United States published by the Centers for Disease Control (CDC), for instance, was based on polynomial extrapolation of AIDS cases reported to the CDC’s surveillance system (Morgan and Curran, 1986). Similar projections, relying on a more complex mathematical form, were published by Hyman and Stanley (1988).
The method known as back-calculation, developed by Brookmeyer and Gail (1988), uses the same AIDS case data but brings in additional information on the latency distribution—the time between infection with HIV and onset of the full clinical manifestations of AIDS. It is based on the relationship among the cumulative number of new infections at time t, I(t); the cumulative number of new AIDS cases at time t, A(t); and the incubation distribution of duration from infection to AIDS, g(x). The relationship is given by the following equation:
(1)
By using surveillance estimates of A(t) and estimates of g(x) based on epidemiological studies, this equation can be solved for the unknown I(t) to yield estimates of the number of people infected with HIV in the past. With additional assumptions the model can yield estimates of future HIV prevalence and AIDS incidence.
The strengths of this approach are that additional biomedical information on the latency distribution is used and that a more biologically realistic model is developed. Using the back-calculation model, for instance, Brookmeyer (1991) and others have shown that the number of new HIV infections in the United States peaked in the mid-1980s, but that the number of AIDS cases will not peak until the mid-1990s. Another analysis using this model has looked at the possible effect that AZT has had on AIDS mortality (Gail et al., 1990). Despite the additional complexity, however, the back-calculation model does not generally provide for estimates of the effect of future behavioral interventions.
In the United States and Europe, extrapolation and back-calculation methods have been used to project the epidemic in the population as a whole and in subgroups that correspond to the standard groupings in the CDC AIDS surveillance system: homosexual men, IV drug users, and so on. They are generally not suited for less developed countries, however, because they rely heavily on complete and accurate AIDS case reporting, which few LDCs have (Chin and Lwanga, 1991).
Epidemic Models
Epidemic models employ a more realistic representation of the natural history of HIV disease and its modes of transmission, but have relatively few behavioral variables.
Brouard (1991), for instance, has developed a renewal model analogous to a stable population model in demography. This model can be expressed in terms of three variables. The state variable I(t) is the number of new HIV infections in the population at time t. In stable population theory, this is analogous to the population born in year t. Brouard defines S(d) as the probability of surviving without developing AIDS for d years after HIV infection. This is analogous to the life table survival function l(d). Finally, f(d)Δd is defined as the number of infections that occur in the time interval [d, d+Δ] that are attributable to a person who has been infected for d years (in the limit as Δ goes to zero). This is similar to an age-specific fertility rate. The dynamics of the model are specified by the equation
(2)
When combined with a similar renewal model for the entire population, the model provides a full representation of an HIV/AIDS epidemic. One benefit of this model is that it provides mathematical expressions for critical relationships in the epidemic. For instance, it can be shown that the net reproductive rate of the HIV-infected population is
(3)
With various simplifying assumptions, Brouard is also able to describe the initial growth rate of the epidemic and its long-run behavior when it comes to equilibrium with the base population.
Artzrouni (1988) has developed a more elaborate version of this model by distinguishing three mutually exclusive states: healthy, infected and asymptomatic, and symptomatic. In his model, the flows among these three states are dependent on assumptions about the incubation period, survival rates, and probabilities that an infected person will infect others (like f(d) in the Brouard model).
The major weakness of both of these models is in the definition of f(d). The time invariance of f(d) seems untenable unless the number of susceptibles is not appreciably diminished by the epidemic. Furthermore, although all behavioral aspects of the epidemic and the effect of possible interventions are incorporated in the f(d) function, there is no clear representation of how specific behavioral or biological changes affect f(d).
Both models are also difficult to fit to empirical data. First, data on the distribution of the incubation period S(d) and on mortality rates of people with AIDS are supplied exogenously, based on the experience of study populations. The results, however, are highly dependent on the values chosen, and the data on American or European populations may not be appropriate to describe AIDS in Africa. Furthermore, no information is available on the pattern of I(t) over time, and it must be estimated by determining which values of the model’s initial values and parameters best reproduce the observed number of AIDS cases. As a result, applying the model in LDCs with poor AIDS surveillance is problematical.
A related model has been developed by Chin and Lwanga (1991) for the WHO Global Programme on AIDS (GPA). Rather than past values of I(t) being estimated endogenously by the model, they are estimated directly by analysts from epidemiological surveys. Once this estimation has been done for rough age groups and various points in time, it is possible to calculate future AIDS cases by applying the incubation distribution to the estimated numbers infected. This approach is thought to be superior for LDCs, which typically have poor AIDS surveillance data but numerous HIV surveillance studies. The model is very dependent, however, on the estimates of I(t) as well as on the assumed incubation distribution.
Demographic/Behavioral Models
The distinguishing characteristic of demographic/behavioral models is their explicit representation of the behavioral assumptions underlying the generation of new cases as well as a representation of the epidemic as in the previous category. Within this major category, three subcategories can be distinguished: demographic models, sexual behavior simulation models, and analytic models.
The critical elements of all of these models can be represented in terms of differential equations describing the evolution of three subsets (healthy, Hi(t); infected and asymptomatic, Ii(t); and symptomatic, Ai(t)) of risk-related population groups indexed with subscript i.
First, the rate of change in the population of healthy, noninfected individuals Hi(t) in group i is
dHi(t)/dt=Σjbi,jHj(t)–Hi(t)Σjci,jPj(t)–μiHi(t). (4)
The first term in this equation describes the recruitment of new individuals according to a set of “recruitment rates” bi,j from group j into group i. When j=i, this term is a birthrate. The second term describes the number of new infections in group i as proportional to the number of individuals currently in group i multiplied by a factor for each group with which they come in contact. The factor for group j is the proportion of individuals in
group j who are infectious Pj(t), times a constant ci,j that expresses the rate of infection per contact and per unit time for those in i with those in j. The proportion Pj(t) is usually defined as (Ij(t)+Aj(t))/Nj(t), where Nj(t) is the total population, but the Aj(t) term can be deleted if it is assumed that symptomatic individuals are no longer sexually active. The third term is the non-AIDS mortality, expressed at a mortality rate μi times the population.
The rate of change in the population of infected individuals Ii(t) in group i is
dIi(t)/dt=Σjb′i,jIj(t)+Hi(t)Σjci,jPj(t)–πiIi(t)–αiIi(t). (5)
The first term in this equation represents recruitment from group j into group i. The “recruitment rates” b′i,j are not necessarily the same as those for the noninfected population. The second term represents the number of new infections in group i. It is the negation of the second term of equation (4). The third term is the mortality in the HIV-infected but asymptomatic population (at a rate πi). The fourth term is the number of transformations from asymptomatic to symptomatic cases (at a rate αi).
The rate of change in the population of symptomatic individuals Ai(t) in group i is
dAi(t)/dt=Σjb″i,jAj(t). (6)
The first term in this equation represents recruitment from group j into group i. The recruitment rates b″i,j are not necessarily the same as those for the noninfected or the infected but asymptomatic population. The second term is the number of transformations from asymptomatic to symptomatic cases (at a rate αi). It is the negation of the fourth term of equation (5). The third term is the mortality in the symptomatic population (at a rate τi).
The main distinctions among the specific models to be discussed below are the definitions of the groups, the treatment of heterogeneity, and the mathematical/computer operationalization of the differential equations above. In the simple formulation above, neither age nor duration of infection is taken into account, although most models do so by adding more population groups and appropriate transition terms. Terms to represent infected and noninfected babies born to infected mothers can also be added, as well as terms explicitly representing IV drug use as well as sexual contact, transfusion-related infections, and so forth.
Demographic Models
Most of the models of the AIDS epidemic are essentially extensions of the models commonly used in demographic projections. These include the models developed by Bulatao (1991), Palloni and Lamas (1991), Bongaarts
(1989), and John (1991). The Interagency Working Group (IWG) model (Stanley et al., 1991) has the same basic structure, but uses more sophisticated mathematical techniques to deal with heterogeneity in risk factors.
The basic structure of these models is determined by the definition of the groups in the differential equations above. The groups are usually some combination of age, sex, urban-rural residence, and social status, as well as groups defined by marital status and sexual practices (including monogamous, contacts with prostitutes and/or others, use of condoms, and so on), and STD status. The models’ state variables are the number of people in each group, and computers are used to update these numbers each year (or other unit of time).
Changes in the sizes of the groups, determined by the bi,j, b′i,j, and b″i parameters, reflect demographic processes and behavioral changes. Modelers often rely on available demographic data to choose representative age-specific fertility, mortality, and migration rates for particular countries of sub-Saharan Africa as a whole. Behavioral change parameters are chosen to reflect “typical values” and are usually less empirically based.
Infection rates, determined by the ci,j parameters, are based on assumptions about the number of sexual contacts between people in different groups per unit time and the probability of infection per contact. Most models define contact as a single act of intercourse, and the probability of infection per act is used. Other models define contact in terms of new sexual partners, and the probability of infection per partner is used. Estimates of numbers of contacts and probability of infection per contact are based on empirical studies, data from other countries such as the United States, and educated guesses.
HIV-related mortality rates and rates of transition between stages of HIV infection are determined by epidemiological studies. The existing models differ most markedly in the assumptions they make about the distribution of time from infection to the appearance of symptoms of AIDS. Some use a constant rate of progression (implying an exponential distribution); others use a more complex probability distribution such as a Gamma or a Weibull. There are also substantial differences in the assumed mean of this distribution.
The IWG model (Stanley et al., 1991) differs from the others in the way it handles heterogeneity. Unlike the other models that assume homogeneity within each group, the IWG model allows for heterogeneity within groups with respect to risk factors such as the partner acquisition rate. Within each group it is assumed that there is a joint distribution that describes the number of people with the following characteristics: partner acquisition rate, infection duration, circular migration status, condom use frequency, presence of STDs, and transmissibility of the virus. All of these, other than migration and STD status, are continuous variables. For simplicity, some,
but not all, of these characteristics are assumed independent of the others. To deal with this heterogeneity, the differential equations expressing changes in the number in each group over time are replaced by equations expressing changes in the distribution over time.
The strength of the demographic approach is that these models provide results for a wide range of demographic outcomes that are difficult to obtain from other approaches. The models can show, for instance, the effect of the epidemic on the rate of population growth, life expectancy, age distribution and dependency ratios, interregional population distributions, and distribution of the population by disease state. They also permit the evaluation and comparison of interventions targeted to particular groups or behaviors. The weaknesses are the large number of parameter values that have to be assumed and the difficulty of empirically verifying the model.
Sexual Behavior Simulation Models
Two of the existing models focus on detailed descriptions of sexual behavior. One of these models uses a microsimulation approach; the other uses macrosimulation.
Auvert (1991) has developed a microsimulation model that permits the study of complex decision rules about sexual behavior. Unlike most other HIV/AIDS models that have been developed, the unit of analysis of this study is the individual, not a population group. Each individual in the model has attributes corresponding to those that define the population groups in the deterministic approach: age, sex, region of residence, marital status, sexual behavior variables, and so on. Individuals can also be classified as having HIV infections, AIDS, and so on, and pairings of particular individuals are tracked. In Auvert’s model, rules analogous to the differential equations above are stipulated that govern the way in which an individual’s attributes change over time. These rules are implemented as probability statements in a computer simulation for a finite population, and are repeated a number of times to reduce the effect of stochastic variation.
Dietz (1988, 1989, 1991) has developed a deterministic model in which partner selection is a major factor. Through careful selection of the groups in the differential equations above, this model distinguishes between male and female populations according to the number of sexual partners and IV drug use, and allows various degrees of contact and flows between groups.
The population groups in Dietz’s model are (1) monogamous males, (2) nonmonogamous males who have relations with nonprostitutes, (3) nonmonogamous males who have contacts with prostitutes, (4) monogamous females, (5) nonmonogamous females who are not prostitutes, and (6) female prostitutes. The populations are also divided into 10 five-year age
groups for each sex, and a probability distribution of male preferences for the age of their partners is specified.
An algorithm in the model creates pairings between 225 types of partnerships (three subgroups for each sex times five HIV infection states) and 150 possible combinations of partner ages. The computer keeps track of people in (and movements among) 33,750 types of partnerships.
The major strength of these models is that more complex specifications of sexual behavior can be used. In Dietz’s model, moreover, couple formation and marital dissolution are explicitly modeled so that unrealistic assumptions about random mating within a homogeneous population do not have to be made. Dietz shows, for instance, that models that do not include couples can overestimate the effects of the epidemic. As with the demographic models, however, the weakness is the large number of parameters to be estimated.
Analytic Models
Anderson and his colleagues (1988, 1991a,b) have developed a series of formal models based on their experience in population biology. The simplest of these models has a single closed population (e.g., homosexual men) that assumes homogeneous mixing patterns for sexual contacts between susceptible and infectious groups. More complex versions include heterogeneity in sexual behavior via a probability distribution for preferred number of partners. They also include heterosexual transmission, age patterns, and age-sex preference matrices for sexual pairing, and so on.
Much of the attention in these models is focused on the quantity R0, the reproduction rate of infected persons. This quantity, analogous to the net reproduction rate in stable population theory, expresses the number of secondary cases generated by one primary case in a susceptible population. If R0 is greater than 1.0, the epidemic grows; if R0 is less than 1.0, the epidemic dies out. In the simplest model, for instance, Anderson and his colleagues (1988) show that if D is the duration of the incubation period (assumed constant), b is the probability of infection per partner, and c is the average number of new sexual partners per unit time, R0=Dbc. One implication of this formulation is that the rate of acquisition of new partners and the probability of infection per partner are the critical behavioral and epidemiological parameters that determine the epidemic’s effect.
For heterosexual transmission, they show that R0=D(β1β2c1c2)1/2, where β1 is the probability of female-to-male transmission, β2 is the probability of male-to-female transmission, c1 is the average number of new male sexual partners for females per unit time, and c2 is the average number of new female sexual partners for males per unit time. More complex models are
also characterized by R0, but it is not always possible to arrive at a closed-form representation of it.
These models illustrate several important aspects of the HIV/AIDS epidemic. They show, for instance, that where there is more heterogeneity in the number of new sexual partners per year, the epidemic is smaller (May and Anderson, 1987). The major difficulty with these models is finding data to estimate the model parameters.
Model Results
Because the existing HIV/AIDS models have been developed with different purposes in mind, it is difficult to compare their results. For example, the possible demographic effect of the epidemic—the focus of this chapter—is not the primary issue addressed by some of the models. The UN/GPA workshop held in 1989, however, was an attempt to have modelers address the demographic effects of the epidemic. Moreover, a strong effort was made to coordinate the nature of the model input and the form of the output so that the results would be as comparable as possible. To take advantage of the UN/GPA efforts, this section begins with a summary of the comparative results of the modeling workshop. The section concludes with a discussion of important results that are more recent or are related to topics that were not the primary focus of the workshop.
UN/GPA Workshop Results
The goal of the UN/GPA workshop (United Nations, 1991) was to evaluate model differences by comparing the outputs from a series of different HIV/ AIDS models by using a standard set of demographic and epidemiological variables. A working group prepared standard input values, and six modeling groups used these inputs to produce an agreed-upon set of demographic outputs over a 25-year period beginning in 1985. The models included in the exercise included one epidemic model (Brouard), three demographic models (Bulatao, IWG, Palloni), and two sexual behavior simulation models (Auvert, Dietz).
Input Values
A single value was set for most parameters; high and low values were given for some parameters about which there is substantial uncertainty. Details of the standard inputs can be found in the UN/GPA report (United Nations, 1991: Chs. I, II).
The input values specified an initial population structure, fertility and marriage rates, and mortality levels and trends typical of African countries
in which the AIDS epidemic is at an advanced stage. The initial mortality rates followed a Coale and Demeny (1966) North model life table with life expectancies of 53 years for women and 50 years for men, and were assumed to change over time consistent with the most recent medium-variant population projections of the United Nations (United Nations, 1989). In the last five years of the projection period, 2005 to 2010, life expectancies were thus assumed to be 63 years for women and 60 years for men. Initial fertility rates were calculated to be consistent with a stable population crude birthrate and an age pattern of fertility corresponding to a mean childbearing age of 29 years. The total fertility rate was assumed to change over the projection period from 7.3 to 5.3. The intrinsic growth rate implied by the initial assumptions was 3.5 percent per year, and it would decline to 3.0 percent per year in the absence of AIDS. Marriage patterns by age were based on the Coale marriage model (Coale, 1971) as incorporated in the Coale and Trussell (1974) fertility model, with parameters consistent with information collected by the World Fertility Survey for the countries in question: that is, it was assumed that the median age of marriage for women is 17 years; 95 percent of all women marry, and women marry men 5 years older than themselves.
The hypothetical population was assumed to be 25 percent urban. The age-specific HIV prevalence rates for urban and rural population were based on HIV serological surveys conducted in several African countries, as estimated by Chin and Lwanga (1991). Age-specific HIV prevalence peaks for urban residents at about 25 percent at ages 30 to 45, and for rural residents at about 24 percent at ages 30 to 34.
The working group found little systematic, quantitative information upon which to estimate parameters describing sexual activity. Using qualitative information, the working group assumed parameter values such as the following: 30 percent of married men were nonmonogamous; each year these men had, on average, 104 sexual contacts with their wives and either 12 or 36 with prostitutes. The working group also assumed that condoms were used in either 2 or 20 percent of all sexual acts and that condoms were 80 percent effective in preventing the transmission of HIV.
Finally, the working group made a set of assumptions about epidemiological parameters. The probability of transmission from an infected person in a single unprotected sexual act was assumed to be .003 to .1 from male to female and .001 to .1 from female to male. The assumed incubation distribution was based on data from large cohorts of U.S. males; 50 percent of those infected with HIV were assumed to become symptomatic with 10 years of infection.
The specification of these input values was somewhat problematical. First, it was impossible for the working group to develop assumptions that were equally applicable to all models. Some modeling groups had to ignore
parts of the standard input values; some had to specify values for parameters not covered in the standard set. Attempts were made to assign parameters that were consistent with the assumed values, but this was not always possible. Second, there were problems of internal consistency. For instance, in some models the epidemic is initiated by introducing a few infected persons into a population. For some of the standard values, these models were not able to produce a starting set of HIV prevalence figures consistent with the other parameters.
Results
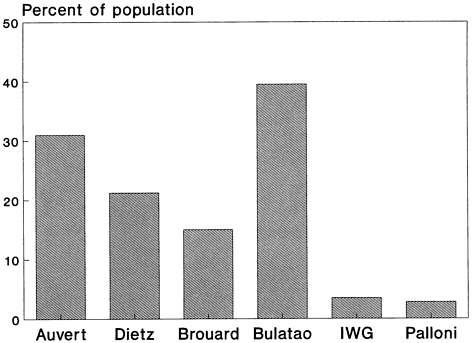
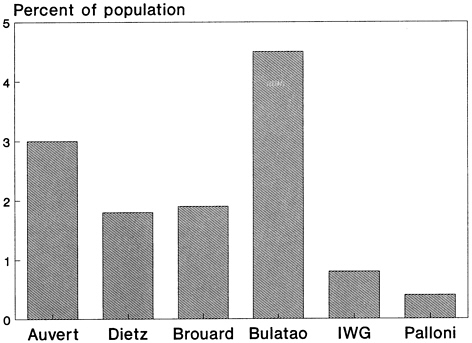
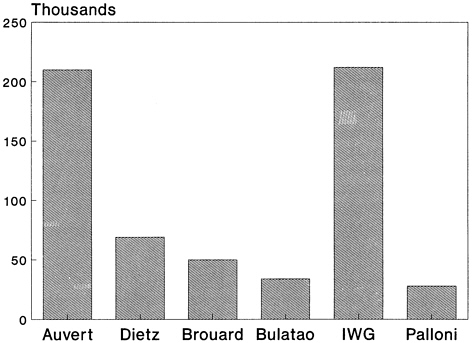
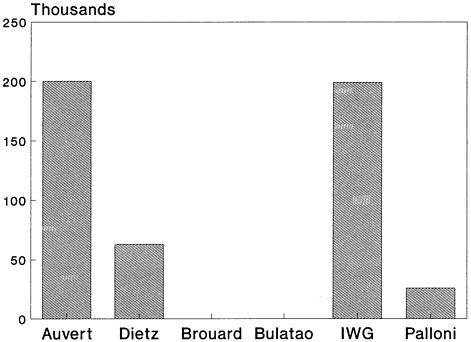
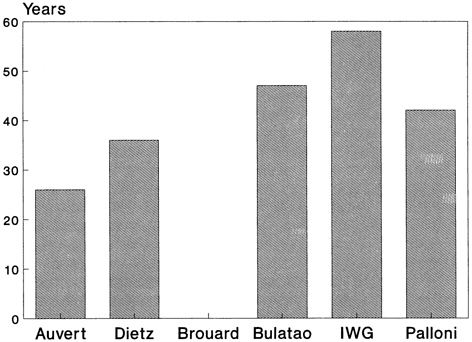
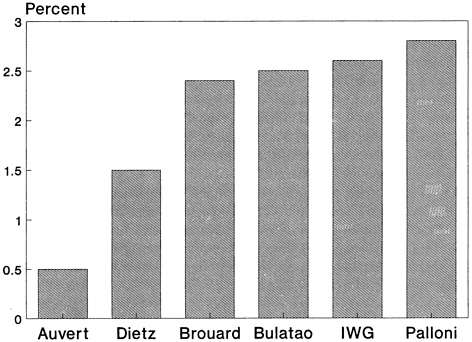
Results were available from six models under three scenarios corresponding to the best, intermediate, and worst values of three variables: the probability of infection per sexual contact, the number of sexual contacts between males and prostitutes, and the proportion of sexual contacts with condom use. For the intermediate scenario, these variables were set equal to the average of the upper and the lower extremes. The probability of infection was the dominant factor. Summary results on the state of the population and the epidemic after 25 years—in 2010—are shown in Table 9–1, which is based on the UN/GPA report (United Nations, 1991).
The models essentially agree under the “best” scenario (first panel of Table 9–1), the epidemic is not sustained, and there is almost no demographic trace of it in 2010. This scenario was the one for which some of the models were not able to produce starting HIV prevalence rates consistent with the assumed values. Because many African countries already have substantial HIV prevalence rates, it appears as if the combination of assumptions in this scenario is not reasonable, at least for Africa.
In the worst-case scenario (third panel of Table 9–1), there was only modest agreement among the models: HIV prevalence ranges from 30.3 to 57.5 percent; life expectancy at birth ranges from 16 to 45 years. In four of the six models, the intrinsic growth rate is negative after 25 years. The qualitative results, however, are starkly consistent: The HIV/AIDS epidemic has a major demographic effect, especially on mortality rates. The key assumption driving these results, the rate of infectivity, seems high. In this scenario it is assumed to be 10 percent per act of sexual intercourse from male to female and from female to male. Although there is little precise empirical information available, workshop participants agreed that the best values to use were 3 percent for male-to-female transmission and 1 percent for female-to-male transmission.
Discrepancies were largest for the intermediate scenario (second panel of Table 9–1). Although the patterns are somewhat erratic (see Figures 9–1 through 9–7), it appears as if the demographic models (Bulatao, IWG, and Palloni) were more similar to one another than to the others. The two
TABLE 9–1 UN/CPA Modeling Workshop Results—Summary of Selected Outcomes from Selected Models After 25 Years of Projection for Three Scenarios
|
|
Models |
|||||
|
Best, Intermediate, and Worst Case Scenarios |
Auvert |
Dietz |
Brouard |
Bulataoa |
IWG |
Palloni |
|
Best Scenario |
|
|||||
|
HIV prevalence (%) |
0.0 |
0.0 |
0.2 |
0.3 |
0.0 |
0.1 |
|
AIDS prevalence (%) |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
0.0 |
|
Cumulative AIDS cases (thousands) |
0 |
0 |
7 |
2 |
7 |
0 |
|
Cumulative AIDS deaths (thousands) |
0 |
0 |
– |
– |
7 |
0 |
|
Life expectancy at birth (years) |
60 |
61 |
– |
61 |
65 |
60 |
|
Rate of natural increase |
3.0 |
3.2 |
3.3 |
3.0 |
2.9 |
3.1 |
|
Population (thousands) |
464 |
470 |
467 |
449 |
392 |
446 |
|
Intermediate Scenario |
|
|||||
|
HIV prevalence (%) |
31.0 |
21.2 |
15.0 |
39.5 |
3.5 |
2.8 |
|
AIDS prevalence (%) |
3.0 |
1.8 |
1.9 |
4.5 |
0.8 |
0.4 |
|
Cumulative AIDS cases (thousands) |
210 |
69 |
50 |
34 |
212 |
28 |
|
Cumulative AIDS deaths (thousands) |
200 |
63 |
– |
– |
199 |
26 |
|
Life expectancy at birth (years) |
26 |
36 |
– |
47 |
5842 |
|
|
Rate of natural increase |
0.5 |
1.5 |
2.4 |
2.5 |
2.6 |
2.8 |
|
Population (thousands) |
236 |
355 |
426 |
409 |
378 |
427 |
|
Worst Scenario |
|
|||||
|
HIV prevalence (%) |
55.0 |
43.9 |
55.0 |
57.5 |
42.4 |
30.3 |
|
AIDS prevalence (%) |
5.8 |
4.7 |
7.0 |
4.4 |
12.0 |
5.2 |
|
Cumulative AIDS cases (thousands) |
230 |
172 |
138 |
500 |
213 |
166 |
|
Cumulative AIDS deaths (thousands) |
220 |
174 |
– |
– |
214 |
154 |
|
Life expectancy at birth (years) |
16 |
24 |
– |
45 |
28 |
22 |
|
Rate of natural increase |
–2.0 |
–0.7 |
0.16 |
2.4 |
–2.5 |
–0.0 |
|
Population (thousands) |
146 |
120 |
344 |
382 |
245 |
260 |
|
NOTE: —: data unavailable. aValues correspond to the interval 20–25 years after the beginning of the projection. |
||||||
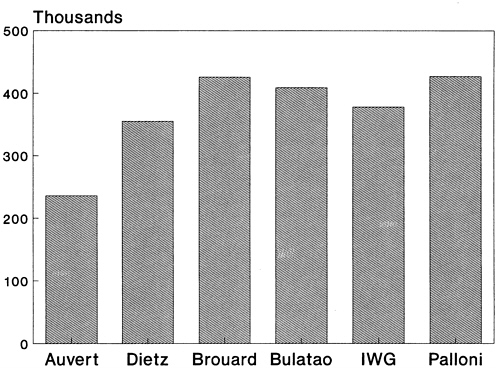
FIGURE 9–7 Size of a hypothetical population after 25 years as projected by six models.
models that followed couples rather than individuals (Auvert and Dietz) also have somewhat similar results. These similarities are more apparent for life expectancy (Figure 9–5), the intrinsic growth rate (Figure 9–6), and the final population (Figure 9–7) than they are for the other outputs. This pattern may indicate the importance of model assumptions about couple formation. Among the demographic models, the Bulatao model predicts substantially higher HIV and AIDS prevalence rates in the final period than all of the other models, and the IWG model predicts substantially higher cumulative AIDS cases and deaths.
The intermediate scenario seems to be the most realistic of the three UN/GPA workshop scenarios, but the numerical results are widely divergent. Even so, the results are informative. Models of more than one type predict large numerical effects on epidemiological parameters such as HIV/ AIDS cases and deaths, and on demographic parameters such as life expectancy and the rate of natural increase.
Other Model Results
Beyond the results of the UN/GPA modeling workshop, a number of other aspects of the demographic effects of AIDS have been explored.
The latest report from the Interagency Working Group (Way and Stanecki, 1991), for instance, reaches a number of important conclusions about the demographic effects of AIDS in a 25-year projection that uses data typical of sub-Saharan Africa:
-
HIV seroprevalance increases from 4 to 16 percent in urban areas and from 1 to 5 percent in rural areas;
-
the number of people infected with HIV in sub-Saharan Africa increases to more than 70 million, and the number infected in rural areas is greater than in urban areas;
-
the annual number of deaths in sub-Saharan Africa increases to 13.8 million, of which 4.6 million are due to AIDS; life expectancy in urban areas is 18 years less than expected without AIDS;
-
infant mortality levels in urban areas increase by more than 20 percent; urban mortality under the age of 5 increases by nearly 50 percent; and
-
mortality rates among those aged 30 to 49 increase to six or seven times the normal level.
These are major demographic changes. Although the precise results depend on a large number of unverifiable model assumptions, it is clear that major demographic effects are possible.
The IWG model predicts one important “noneffect,” and this result is supported by other models of various types: The AIDS/HIV epidemic has very little effect on the population age distribution or on dependency ratios. Because AIDS affects childhood as well as adult mortality (and across a relatively wide age range), 25 years into the epidemic the dependency ratio (the ratio of persons under age 15 or 65 and over per 100 persons 15 to 64 years of age) changes only from 76.5 to 77.5. Other models have come to similar conclusions.
Models have also shown the effects of possible policy interventions on the epidemic. Anderson and colleagues (1991b) point to the importance of changes in sexual behavior (especially partner choice) and the use of condoms. Both of these would be more effective if targeted to high-risk groups. Given the growing body of evidence that links other STDs and genital ulcers to increased likelihood of HIV transmission, Anderson and colleagues (1991b) also suggest that treatment and control of STDs could have an important effect on the HIV/AIDS epidemic. Bulatao and Bos (1988) have investigated the effect of various control measures on the spread of HIV infection in African countries, and concluded that encouraging the use of condoms would have a major effect on the HIV/AIDS epidemic. Reducing STDs and genital ulcers, providing clean needles, and screening the blood supply have only minor effects. Using the IWG model, Way and Stanecki (1991) obtain similar results about condom use and blood screening, but find relatively
large declines associated with a decrease in the duration of STDs. The difference between the results of Bulatao and Bos with regard to genital ulcers and those of Way and Stanecki with regard to STDs could be due to uncertainty about the prevalence of the problems in question and about their effects on infectivity.
Efforts are being made to understand why some HIV/AIDS models yield the divergent results seen in the UN/GPA workshop. In a recent working session, for instance, developers of the Auvert microsimulation model and the IWG demographic model met and agreed on a set of parameter specifications that had the same meaning for both models. Apparently, this agreement has brought the results of the two models closer (Culotta, 1991).
The IWG model itself continues to be further developed and used, but no complete description of its modeling assumptions or results had been published as of August 1993. Way and Over (1992) have added an economic component to the IWG model and explored the possible macroeconomic effect of the HIV/AIDS epidemic. For a typical African country they find that total gross domestic product (GDP) would continue to grow, but could be reduced by as much as 22 percent relative to the non-AIDS scenario. Per capita GDP would also be reduced (relative to the non-AIDS projection), but by a lesser amount due to the parallel reduction in population size.
Model Uncertainties
Sensitivity analyses using the models have also indicated some of the critical uncertainties. Palloni and Glicklich (1991) identify the following six variables or issues as ones that have a large effect on model results.
Heterogeneity with Regard to Sexual and IV Drug Behavior
The models that include heterogeneity uniformly show that it has an effect on development of the epidemic, yet few behavioral data are available to estimate the details of variations across individuals, time, and location with regard to sexual practices or IV drug use.
Communicability of Groups with Regard to Sexual and IV Drug Behavior
To estimate the parameters of epidemiological and demographic/behavioral models, data are needed to specify the degree of contact between population groups defined by demographic variables and risk behaviors. There is reason to believe that these patterns vary substantially across country and region, but few systematic data are available to describe them.
Probability of Transmission by Sexual Contact
Experience with the models has shown that this parameter is crucial, but there is little direct evidence on its value, and most of what does exist comes from countries not in Africa. The probability is likely to depend on sexual practices and thus to vary across population groups. The probability of transmission also depends on whether sexual contact is defined as a single sexual act or a partnership. Although most models use a fixed probability per sexual act, available evidence suggests that the probability of transmission per partnership is independent of the number of sexual acts between partners (Palloni and Glicklich, 1991).
Cofactors
Cofactors such as the presence of STDs apparently increase infectivity in a given sexual contact, but it is not clear which cofactors or what quantitative effect they have. Data on the prevalence of most potential cofactors are also lacking.
Distribution of the Incubation Period
Each of the models reviewed by Palloni and Glicklich (1991) uses a different functional form to specify the distribution of the incubation period, reflecting the lack of precise epidemiological information, especially for African populations. Whether the mean or the functional form of the incubation period depends on cofactors is not known. There is evidence that antiviral drugs such as AZT can lengthen the incubation period as well as the symptomatic period, but this increase is unlikely to be relevant for African countries in the near future.
Duration-Dependent Infectivity
Some evidence suggests that an infected individual’s infectivity may follow a bimodal pattern, with one peak immediately following the initial infection and the second about the time that the symptoms of AIDS appear. May and colleagues (1988) have shown that such patterns can effect HIV and AIDS trends, and complicate the interpretation of data from the past.
There are, in fact, uncertainties about most elements of the models. Estimates of the probability of transmission from mother to child, for instance, range from 13 to 39 percent (Anderson et al., 1991b), which can have a large effect on the results of demographic/behavioral models.
It is important to note that these uncertainties result from lack of knowledge about behavioral patterns and biological realities. Some information on
these variables is available for developed countries, but it is often not clear whether behavioral and biological facts are transferable. Much less information is available for Africa.
As the interchange in the New York Times discussed at the beginning of this chapter illustrates, one of the more contentious open questions is whether the HIV/AIDS epidemic in Africa is such that the intrinsic rate of growth will become negative. Under the IWG model, population growth continues in both rural and urban areas, but the total population in the region is reduced by 5 percent by 2015, more than fifty million people, from the non-AIDS projected population (Way and Stanecki, 1991). When they choose their own input values, most of the other AIDS modelers find similar results: large relative decreases but still nonnegative intrinsic growth rates.
The two major exceptions to this result are the UN/GPA worst-case scenario and the Anderson results. The UN/GPA worst-case results are driven by a infection probability of .1 from male to female and from female to male. This probability is substantially higher than the current range of estimates. These rates are comparable to the current best estimates per partnership (Anderson et al., 1991b) but are used in the models to express the probability of transmission in one sexual act. Thus, the negative growth rates found in the UN/GPA workshop results may not be realistic.
In a recent review article, Anderson and his colleagues (1991b:588) comment:
Simple models based on random mixing in age classes suggest that, with realistic assumptions concerning the major epidemiological and demographic parameters…, AIDS is able to reverse the sign of population growth rates over timescales of a few to many decades. The added refinements of age-dependent changes in sexual behavior, men having sexual contact with women younger than themselves and not infrequent male contact with a small proportion of women with high rates of sexual-partner change, all serve to accentuate the predicted demographic impact, with the only significant uncertainty being whether AIDS induced mortality will decrease population size over a few or many decades.
Note that this statement in a scientific journal is less extreme than the news reports mentioned earlier. In particular, it suggests that part of the differences among the modelers on the question of growth rate might be a matter of time scale. As Anderson and colleagues note in their scientific article, the uncertainty is whether the sign change will take “a few or many decades.” Most of the other modeling efforts make projections for only a few decades, whereas Anderson’s models run for many decades. Given the possibilities for behavioral change and eventual medical interventions, projections that go beyond a few decades are questionable.
May and Stover (1992) have explored these issues using a relatively simple HIV/AIDS model that is essentially an ordinary cohort component
demographic projection model with additional exogenous assumptions about adult HIV prevalence rates. Using data and assumptions for Uganda and Rwanda, including assumptions that adult HIV prevalence increases to a plateau of 15 percent in Uganda and 6–12 percent in Rwanda, they find that growth rates fall but do not become negative. Most of the decrease in growth rates, however, is due to large projected decreases in fertility rates.
Because of assumptions about behavioral change not related to AIDS that result in decreasing birthrates, most projections for sub-Saharan Africa show decreasing but not negative growth rates for some decades into the future. Most of the current AIDS models indicate that growth rates will fall, but Anderson and colleagues are generally alone in predicting negative rates. Although these results have not been shown to be incorrect, they have not been replicated by others and should be interpreted with caution.
SUMMARY AND CONCLUSIONS
A wide variety of approaches have been used to model the HIV/AIDS epidemic in less developed countries, and the possible long-range demographic effects predicted by these models vary from minor to substantial. Based on the available demographic, behavioral, and epidemiological information, and on judgments about the appropriateness of different modeling approaches, it is difficult to say that any one of these models is correct or incorrect, or to choose the most accurate among them. The available data do not unambiguously determine the appropriate parameter values of any model, nor do they permit in-depth empirical verification of any model’s goodness of fit or predictive ability.
Faced with this uncertainty, it may be best to interpret the variability in the available results as an indicator of the state of current knowledge about the HIV/AIDS epidemic. The variability reflects choice of analytical model as well as the biological and behavioral parameters that are assumed. The large variability evident in the results of models attempting to use similar assumptions suggests that these models (perhaps because of data availability) are not yet capable of accurate numerical projections of the HIV/AIDS epidemic for individual countries.
Despite this variability, the UN/GPA workshop results show that there are plausible scenarios in which AIDS can have large demographic effects. The largest effect would be on mortality rates for children age 0 to 5 years and for young adults, and the changes could reverse mortality gains of the last few decades. Changes of this magnitude would substantially decrease population growth rates, but it is not clear whether negative growth rates would obtain, at least in the next few decades. Despite the effect on mortality rates, however, there is not likely to be a major effect on population age structure or dependency ratios. The most pessimistic projections of Ander-
son and colleagues (especially those reported in the popular press) have not been replicated by other modelers and are questionable. The range of results from other models, such as those presented at the UN/GPA workshop, however, is sufficient to warn policymakers that the HIV/AIDS epidemic is a major demographic threat in Africa.
Another result of the modeling efforts so far is an understanding of the dynamics of the HIV/AIDS epidemic and the necessary outlines of prevention policies. In particular, the importance of targeting interventions to the groups at highest risk is clear. In further modeling efforts, it might be possible to identify policy choices that are relatively robust to model uncertainties, that is, to identify polices that are appropriate under a broad range of model parameters.
In contrast to these qualitative results, much remains to be learned before HIV/AIDS models can provide reliable numerical estimates of demographic effects. There is little hard information on many of the critical biological parameters that describe the infectious process and the natural history of HIV disease. Even as more information becomes available from developed countries, its relevance for Africa will remain questionable. Similarly, little is known in a systematic way about important aspects of sexual behavior in Africa, especially about the number and choice of sexual partners. Whatever the current patterns, they may change in the future as a result of control strategies or other factors.
Most of the relevant parameters are likely to vary substantially among the different countries of Africa; thus the HIV/AIDS epidemic could take very different forms in different countries. Except for currently available HIV prevalence data, there is little evidence now available to characterize intercountry variability in future HIV/AIDS trends. Major regional, urban-rural, and other differences within countries are also likely.
Current modeling efforts have concentrated on gross demographic variables; little is known about the potential effects of the epidemic on family structure, orphanhood, and so on (Hunter, 1990). Given that HIV is transmitted both horizontally and vertically within families, there could be major effects on family structure. Although there has been some anthropological research on the current effect of AIDS in Africa, as well as the patterns and determinants of sexual behavior (Ahonsi, 1991), the potential future social effect of the HIV/AIDS epidemic in less developed countries has not been explored systematically.
To address the uncertainty in currently available results, it would also be useful to organize more modeling workshops such as the one sponsored by the United Nations and the WHO Global Programme on AIDS. As the results discussed above indicate, this type of activity can identify consistent qualitative or quantitative results that are thus presumably reliable, help clarify the reasons for differences among the existing models and the policy
implications of these differences, and suggest areas in which further epidemiological and social/behavioral research in needed. Workshops of this sort provide a mechanism for sensitivity analyses among models. This comparison should not preclude sensitivity analyses within models, nor should it be a substitute for peer review of the individual models. The key idea is that because so much about the modeling assumptions is uncertain, sensitivity analysis should be carried out at the level of the models (or the modelers). As the UN/GPA experience indicated, deciding which assumptions to fix and which to leave up to the modelers is a difficult question that needs serious attention. It is likely, however, that a better set of assumptions could be developed in a series of workshops. Given the state of the art and of knowledge, this approach is likely to yield information not available through the uncoordinated efforts of modelers.
REFERENCES
Ahonsi, B. 1991 Seminar on anthropological studies relevant to the sexual transmission of HIV. Newsletter of the International Union for the Scientific Study of Population No. 41 (January-April).
Altman, L.K. 1992 Researchers report much grimmer AIDS outlook. New York Times (June 4).
Anderson, R.M., R.M.May, and A.R.McLean 1988 Possible demographic consequences of AIDS in developing countries. Nature 332:228–234.
Anderson, R.M., W.Ng, J.T.Rowley, and A.R.McLean 1991a The Anderson approach: Potential demographic impact of AIDS—Uncertainties in prediction. Pp. 63–76 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Anderson, R.M., R.M.May, M.C.Boily, G.P.Garnett, and J.T.Rowley 1991b The spread of HIV-1 in Africa: Sexual contact patterns and the predicted demographic impact of AIDS. Nature 352:581–589.
Artzrouni, M. 1988 A two-stage structured model for the spread of human immunodeficiency virus and the acquired immune deficiency syndrome in the United States. Paper presented at the annual meeting of the Population Association of America, New Orleans, April.
Auvert, B. 1991 The Auvert approach: A stochastic model for the heterosexual spread of the human immunodeficiency virus. Pp. 77–83 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Berkley, S., and J.Hughes 1992 We must not abandon Africa to AIDS (letter). New York Times (July 8).
Bongaarts, J. 1989 A model of the spread of HIV infection and the demographic impact of AIDS. Statistics in Medicine 8(1):103–120.
Brookmeyer, R. 1991 Reconstruction and future trends of the AIDS epidemic in the United States. Science 253:37–42.
Brookmeyer, R., and M.H.Gail 1988 A method for obtaining short-term projections and lower bounds on the size of the AIDS epidemic. Journal of the American Statistical Association 83(402):301–308.
Brouard, N. 1991 The Brouard approach: Forecasting the AIDS epidemic in an African population. Pp. 84–89 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Bulatao, R. 1991 The Bulatao approach: Projecting the demographic impact of the HIV epidemic using standard parameters. Pp. 90–104 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Bulatao, R., and E.Bos 1988 Implications of control measures for the spread of HIV infection. Paper presented at the annual meeting of the Population Association of America, New Orleans, April.
Chin, J. 1991 The epidemiology and projected mortality of AIDS. Pp. 203–213 in R.G.Feacham and D.T.Jamison, eds., Diseases and Mortality in Sub-Saharan Africa. Oxford: Oxford University Press for The World Bank.
Chin, J., and S.Lwanga 1991 The World Heath Organization approach: Projection of non-paediatric HIV infection and AIDS in pattern II areas. Pp. 137–140 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Coale, A.J. 1971 Age patterns of marriage. Population Studies 25:193–214.
Coale, A.J., and P.Demeny 1966 Regional Model Life Tables and Stable Populations. Princeton, N.J.: Princeton University Press.
Coale, A.J., and T.J.Trussell 1974 Model fertility schedules: Variations in the age structure of childbearing in human populations. Population Index 40(2):185–258.
Culotta, E. 1991 Forecasting the global AIDS epidemic. Science 253:852–854.
Dietz, K. 1988 On the transmission dynamics of HIV. Mathematical Biosciences 90(1,2):297– 414.
1989 The role of pair formation in the transmission of HIV. In Sesquicentennial Invited Paper Sessions. Alexandria, Va.: American Statistical Association.
1991 The Dietz approach: Modelling the demographic impact of the AIDS epidemic. Pp. 105–107 in The AIDS Epidemic and Its Demographic Consequences. New York : United Nations.
Gail, M.H., P.S.Rosenberg, and J.J.Goedert 1990 Therapy may explain recent deficits in AIDS incidence. AIDS 3(6):296.
Hunter, S.S. 1990 Orphans as a window on the AIDS epidemic in sub-Saharan Africa: Initial results and implications of a study in Uganda. Social Science and Medicine 31(6):681– 690.
Hyman, J.M., and E.A.Stanley 1988 Using mathematical models to understand the AIDS epidemic. Mathematical Biosciences 90(1,2):415–473.
John, M. 1991 A model of HIV-1 transmission for urban areas of Africa. Theoretical Population Biology 39(2):148–169.
May, J.F., and J.Stover 1992 The impact of HIV/AIDS on population growth in Central Africa: The cases of Uganda and Rwanda. Paper presented at the annual meeting of the Population Association of America, Denver, April.
May, R.M., and R.M.Anderson 1987 Transmission dynamics of HIV infection. Nature 326(6109):137–142.
May, R.M., R.M.Anderson, and A.M.Johnson 1988 The influence of temporal variation in the infectiousness of infected individuals on the transmission dynamics of HIV. Lecture Notes in Biomathematics. New York: Springer-Verlag.
Morgan, W.M., and J.W.Curran 1986 Acquired immunodeficiency syndrome: Current and future trends. Public Health Reports 101(5):459–465.
Palloni, A., and M.Glicklich 1991 Review of approaches to modelling the demographic impact of the AIDS epidemic. Pp. 20–50 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Palloni, A., and L.Lamas 1991 The Palloni approach: A duration-dependent model of the spread of HIV/AIDS in Africa. Pp. 109–118 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Perlez, J. 1992 Briton sees AIDS halting Africa population rise. New York Times (June 22).
Stanley, E.A., S.T.Seitz, P.O.Way, P.D.Johnson, and T.F.Curry 1991 The United States Interagency Working Group approach: The IWG model for the heterosexual spread of HIV and the demographic impact of the AIDS epidemic. Pp. 119–136 in The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
United Nations 1989 World Population Prospects. New York: United Nations.
1991 The AIDS Epidemic and Its Demographic Consequences. New York: United Nations.
Way, P.O., and M.Over 1992 The projected economic impact of an African AIDS epidemic. Paper presented at the annual meeting of the Population Association of America, Denver, April.
Way, P.O., and K.Stanecki 1991 The demographic impact of an AIDS epidemic on an African country: Application of the IWG AIDS model. CIR Staff Paper No. 58. Washington, D.C.: U.S. Bureau of the Census.
World Health Organization 1992 Current and Future Dimensions of the HIV/AIDS Pandemic: A Capsule Summary. Geneva: United Nations.