Health Indices as a Guide to Health Sector Planning: A Demographic Critique
Samuel H.Preston
Cruel choices have got to be made, and it seems to me utterly irresponsible in a public official to make these choices without tracing their consequences to the fullest extent possible.
Milton Russell (1990)
INTRODUCTION
This paper examines, from a demographic perspective, the index of healthy years of life saved by health interventions. This index has been widely applied to summarize the expected gains from health programs in developing countries. The paper attempts to identify the demographic circumstances under which this index does and does not provide reliable information. It compares existing practices to the demographic accounting identities that describe how populations change over time. Problems that are revealed in using the index as a planning instrument include imprecision about the time sequence and age pattern of health program effects; inconsistency of assumptions; failure to incorporate interactions among disease processes; and failure to make explicit potentially valuable information. These problems are averted by the use of population projection to demonstrate the expected effects of health programs.
Samuel H.Preston is at the Population Studies Center, University of Pennsylvania.
BACKGROUND
In 1981, a useful and very detailed analysis of diseases in Ghana developed a measure of the years of healthy life lost to various diseases (Ghana Health Assessment Project Team, 1981). Although similar measures had been proposed earlier, the careful and imaginative application of this measure to a concrete situation drew attention to the procedure as a possible device for health planning. It was quickly recognized that what was needed for planning purposes was not an index of the total burden of a disease but that portion of the burden that could be eliminated by a health program. It was also recognized that the healthy years saved by a program would have to be related to the cost of the program. The measure of healthy years of life saved became the numerator of a cost-effectiveness calculation that permitted comparisons across various kinds of health programs (e.g., Prost and Prescott, 1984; Barnum, 1987).
These and other analyses have elaborated on this measure and considered whether to treat all healthy years lost to a disease (i.e., potentially saved through health interventions) equally (Murray, 1990; Mooney and Creese, 1990). The main issues here are:
-
whether to discount years saved beyond the initial year by a social discount rate, which has become a conventional procedure in assessing many government programs;
-
whether to count years saved in the “productive” age interval (typically, 15–60 or 15–65) in the same fashion as years saved outside this interval;
-
whether disabled or unhealthy years of life should be treated in the same way as years lost to premature death (some have argued that disability actually exacts a higher social cost than death and should be given greater negative weight (Prost and Prescott, 1984), whereas most other analysts would take the point of view of the potential victim and apply a lower weight to disabled years than to years lost to death); and
-
whether to recognize different degrees of disability, morbidity, and quality of life in arriving at a single index. A great deal of attention has been devoted to the development of health status indicators in developed countries (for recent reviews, see Patrick and Deyo, 1989; Loomes and McKenzie, 1989).
One way of dealing with these issues is to present different measures embodying the distinctions raised above and allow health planners to choose among them. Such an elaboration proved unwieldy in the World Bank’s massive Health Sector Priority Review. This valuable assessment of 48 types of health interventions in developing countries settled on an index of
the cost-effectiveness of discounted years of healthy life for making interprogram comparisons. That is, the questions identified above were resolved in favor of discounting future years (a discount rate of .03 was recommended); treating years inside and outside the productive range equally; treating years lost to disability and death equally; and ignoring distinctions among degrees of disability (Jamison and Mosley, 1991: Chapter 1). Individual chapters in the review often use a wider variety of indicators.
These choices inevitably affect the relative value of interventions targeted at children and those targeted at adults. The decision to discount increases the relative cost-effectiveness of adult interventions, because the years of healthy life gained by children lie further in the future, on average, than those gained by adults. The choice of a low discount rate, however, makes this tilt less consequential. The decision not to give higher weight to years saved in the productive age span clearly promotes the relative cost-effectiveness of interventions aimed at children. This decision seems more vulnerable to criticism than others. Neonatal deaths (nearly half of childhood deaths in developing countries) are often “replaced” by additional births that would not otherwise have occurred. Such replacement is clearly not possible among adults. Furthermore, an infant’s net contribution to other members of a society is obviously less than that of older children and adults.
The consequences of some of these choices for the relative importance of programs aimed at children and those aimed at a wider spectrum of ages are illustrated nicely by Prost and Prescott (1984). Table 1 reproduces their comparison of a measles control program and a program of onchocerciasis control in the Côte d’Ivoire. If an index of discounted years of productive life is used, as advocated by the authors, onchocerciasis control is more cost-effective than measles immunization. For any of the three remaining versions of the index, measles immunization is more cost-effective.
The purpose of this paper is not to express views on the set of choices required in constructing an index of years saved by health programs. Nor does it assess the different means available to place a value on the years of life gained (e.g., Torrance, 1986; Mishan, 1988), an operation that is ultimately required if the benefits of health programs are to be compared to those of other government programs. Rather, it examines the demographic adequacy of existing health indices as guides to evaluating the potential effects of programs (i.e., in measuring what they purport to measure). By using the same information and data that are required to construct such an index, population projections can generally supply more accurate and detailed information with little added effort on the analyst’s part. Under certain circumstances, the information provided by this approach can be collapsed into one of the health indices now in common use.
TABLE 1 Cost-Effectiveness of Onchocerciasis Control and Measles Immunization in the Côte d’Ivoire Under Various Procedures Regarding Discounting and Weighting of Productive Years
|
Index of Cost per |
Cost of Onchocerciasis Control ($) |
Cost of Measles Immunization ($) |
|
Year of healthy life added |
20 |
10 |
|
Productive year of healthy life addeda |
20 |
15 |
|
Discounted year of healthy life addedb |
150 |
49 |
|
150 |
190 |
|
|
SOURCE: Prost and Prescott (1984: Table 7). aThe age range 15–59 is considered productive. No distinctions are made among ages within this range. bA discount rate of .10 is used. |
||
EVALUATING THE EFFECTIVENESS OF HEALTH INTERVENTIONS
The information required to evaluate the effectiveness of a health program includes the following elements:
-
How many more years of life will be lived as a result of this program?
-
How many of those years of life will be lived in a healthy state?
-
How many of those years will be lived in an unhealthy state?
-
At what ages will those additional years of total, healthy, and unhealthy life be lived?
-
How will those added years be distributed over time?
Item 4 is needed if different ages are to be weighted differently, and item 5 is needed if time discounting is to be used. Even if neither of these conditions prevails, the information in items 4 and 5 may still help planners understand the full implications of undertaking a program.
To answer these questions explicitly, population projection is necessary. The elements required for population projection are the following:
|
N(a,0) |
= |
number of people aged a at time 0, when the health program is initiated, |
|
npa |
= |
probability that a person aged a will survive n years in the absence of the health program, |
|
np′a |
= |
probability that a person aged a will survive n years in the presence of the health program, |
|
h(a) |
= |
probability that someone aged a is healthy in the absence of the health program, |
|
h′(a) |
= |
probability that a person aged a is healthy in the presence of the health program. |
These same data are required to construct one of the indices in common use, although various simplifications have been made to reduce the age detail required. For the time being, we set aside the important question of whether the effects on those unborn at the time the health program is initiated are to be included among its effects and assume that we are counting only the years of life added among the population alive at time 0.
Table 2 shows the formulas for projecting the population alive at time 0 forward in the presence and absence of the health program. They are presented in the form of summations across all age groups, but detail is required on each age group in order to produce the sum. Although the formulas can be expressed more compactly by using calculus, nothing more than simple algebra is required to apply them. Many applications of the procedures to alternative mortality scenarios have been made (e.g., United Nations, 1991; Preston, 1976).
Let us see how standard health indices relate to these procedures. In so doing, we rely mainly on the description by the Ghana Health Assessment Project Team (1981), which provides the most extensive exposition of this method and which appears to have been followed by subsequent analysts. First, we focus on mortality alone. In Ghana, 70 percent of the healthy years of life added by the array of interventions studied were a product of life extension rather than of morbidity reduction (Ghana Health Assessment Project Team, 1981).
Health Programs That Operate for One Year
We first show that the conventionally defined total years of life added by a health program can be derived from these procedures by making the assumption that the entire effect of the health program on mortality is realized in the program’s first year. Under this condition, death rates change by Δμ(a) during the first year and then revert to their previous levels. The new probability of survival for one year is
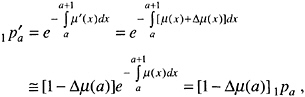
where μ(x) is the death rate (deaths divided by person-years of exposure) at age x. If all of the effect of a program is realized in the first year, then all survival probabilities beyond the first year are unaltered. Therefore,
The total years of life added by the health program (the summation over time of the top right-hand column in Table 2) is therefore
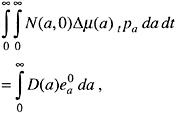
where D(a) is the number of deaths averted in the first year of the program by the mortality reduction at age a and ![]() is life expectancy at age a in the absence of the program. This formula embodies the standard procedure for calculating the total years of life added by a health program: simply estimate the number of deaths that would be averted by the program and multiply them by life expectancy at each age. Clearly, this procedure assumes that the health program operates for only one year and that those “saved” by the program revert to the average level of mortality in the population (as embodied in the set of npa’s) thereafter.
is life expectancy at age a in the absence of the program. This formula embodies the standard procedure for calculating the total years of life added by a health program: simply estimate the number of deaths that would be averted by the program and multiply them by life expectancy at each age. Clearly, this procedure assumes that the health program operates for only one year and that those “saved” by the program revert to the average level of mortality in the population (as embodied in the set of npa’s) thereafter.
We have shown that the conventional procedure produces a reliable estimate of undiscounted years of life saved for programs that operate for only one year. When discounting is used, however, this approach introduces an unnecessary flaw. Many analysts have recognized that the time effect of a health program in terms of years of life saved is not uniform and that gains will diminish for the population alive at time 0. The conventional assumption is that those “saved” by the program at age a in year 0 will subsequently live ![]() years and that all will die at an age of
years and that all will die at an age of ![]() . Although this formulation is correct as an undiscounted average, it provides misleading information when the years of life saved are to be discounted. In reality, some of those saved will die before age
. Although this formulation is correct as an undiscounted average, it provides misleading information when the years of life saved are to be discounted. In reality, some of those saved will die before age ![]() , whereas others will die at an older age. Because of discounting, however, the years lost before
, whereas others will die at an older age. Because of discounting, however, the years lost before ![]() by people who die before that age have a higher present value than the years gained after that age by those who live beyond it. A procedure that assigns
by people who die before that age have a higher present value than the years gained after that age by those who live beyond it. A procedure that assigns ![]() additional years to all those saved thus overstates the gains from the health program.
additional years to all those saved thus overstates the gains from the health program.
To illustrate what error the assumption can introduce, let us assume that those “saved” are subject thereafter to an annual age-specific death rate of .03. Thus, their life expectancy is 33.33 years and their probability of surviving n years beyond the start of the program is e-.03n. We will assume
a discount rate of 10 percent. The present value of a life saved by the program is
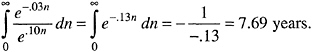
If we assume erroneously that all of those saved die at their life expectancy, i.e., the probability of surviving n additional years is one, then the present value of a life saved is
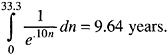
The conventional procedure overestimates the present value of years of life saved in this example by 25 percent. The bias will typically be smaller than this amount because mortality rates among those saved will not be constant but will rise with age. Nevertheless, an upward bias will result and it will vary across programs. The bias is obviously unnecessary because population projection provides an explicit indication of the time sequence of program effects.
Multiyear Health Programs
Although mass immunization campaigns or campaigns to screen for cervical cancer may operate in only one year, most health programs do not. Is it reasonable to assume that the gains from extending the program to later years will more or less replicate those of the first year? This assumption is required to use some measure of life years gained as a guide to implementing a multiyear or permanent program. Unfortunately, the index of years of life saved does not automatically provide reliable estimates for later years. The population alive at time 0 diminishes over time until all members are dead; any health program with constant features (in terms of Δμ(a)) will eventually save many fewer lives among the population alive at time 0 and even fewer years of future life. The index of years of life gained will, in general, overstate the gains for future years unless those unborn at time 0 are admitted to the calculus.
Let us assume for the moment that they are not admitted and that health decisions are to be made on behalf of the population alive at the time a program is implemented. Then the conventional approach produces a major distortion in its assessment of the relative merits of interventions aimed at adults and those aimed at children. Age distributions in developing countries are typically very youthful. There are many more people aged 5, for example, than people aged 30. The assumption that the health program lasts for only one year means that there are many more potential beneficia-
ries at young ages than at older ages. However, if the program is permanent, then 30 birth cohorts of the existing population will benefit from a mortality improvement at age 30, and only 5 will benefit from an improvement at age 5 (by maintaining the assumption that we care only about the population alive at time 0). The fact that the benefits to younger cohorts of health improvements at older ages are not counted in the “years of life added” calculation can create a serious bias tilting calculations in favor of health interventions directed at children. It would not be a “bias” if programs lasted only one year, but few do.
To illustrate the bias against adult interventions under conventional procedures, let us perform two thought experiments:
-
Assume that a health intervention succeeds in permanently reducing death rates at age 5 in developing countries by .001.
-
Assume that a health intervention succeeds in permanently reducing death rates at age 30 in developing countries by .001.
In projecting the population forward to demonstrate the effects of these changes, we use the estimated age distribution of developing countries in 1990 (United Nations, 1989) and a life table with a life expectancy at birth of 63.1 years.1 We assume that the benefits (i.e., added years of life) are to be registered only for the population alive at the initiation of the program. We then calculate the present value of years of life added without discounting and with discounting at a rate of .03. Results are shown in Table 3.
The relative gains in years of life are radically different according to the different methods. By the conventional measure, the number of years added by the mortality reduction at age 5 is 2.5 times greater than the number added by the reduction at age 30. This difference reflects the fact that there are more 5-year-olds than 30-year-olds, as well as the longer life expectancy at age 5 than at age 30. However, if the reduction in death rates is permanent (i.e., lasts 30 years), then the reduction at age 30 produces 2.7–3.0 times as many years of added life as the reduction at age 5, depending on whether discounting is used. The reason is that there are many more potential beneficiaries of the reduction at age 30.
If a population chooses its health programs on the basis of the interests of those alive at the time choices are made (including children whose interests may be represented by adults), then the conventional index will provide misleading information about relative gains from different programs. It is reasonable to suppose that social decisions are made by the living popula-
TABLE 3 Comparisons of Total Years of Life Added by Permanent Health Programs That Reduce Death Rates by One per Thousand at Ages 5 and 30: Less Developed Countries, 1990
|
|
Years Added (thousands) |
||
|
Total Years Added by |
Reduction at Age 5 (1) |
Reduction at Age 30 (2) |
Ratio, (2)/(1) |
|
Conventional methoda |
6,454 |
2,579 |
0.40 |
|
Projection of living population forward |
|
|
|
|
Undiscountedb |
33,854 |
101,853 |
3.01 |
|
Discounted at 3% |
13,637 |
36,086 |
2.70 |
|
aYears added as a result of mortality reduction at age bYears added as a result of mortality reduction at age |
|||
tion primarily on behalf of the living population. Only if unborn generations have equal status—that is, they are given equal weight in social decisions—to those currently alive would the conventional approach embody a roughly appropriate representation of social decision making.
Useful information about how people actually value saving lives at different dates has emerged from three U.S. surveys (Cropper et al., 1992). Respondents were asked to choose between programs that would save, for example, 100 lives now or 1,000 lives 50 years from now. The length of time and the number of future lives saved were varied randomly among respondents. Basic results are presented in Table 4.
The table shows that attitudes toward the saving of lives are highly present oriented. For example, a life saved a decade hence is only one-third as valuable as a life saved in the present. The authors report that the implicit discount rates did not vary significantly with income or education, so the figures in the table may also be reasonable approximations to values in developing countries.
These results show that the saving of lives is discounted at a much higher rate than the 3 percent figure used by the World Bank in its Health Sector Priority Review. The discount rate is 17 percent during the first 5 years, 11 percent for the first 10 years, and diminishes thereafter. While the results do not bear directly on the issue of whether the unborn at time 0 are to be treated differently from those alive at time 0, it is reasonable to suppose that the high discount rate partially reflects the fact that they are not given a weight equal to those currently alive. If they are not, then the
TABLE 4 Average Value to Respondents of Lives Saved—Future Versus Present: United States
|
Years Since Program Initiation (t) |
Value of Life Saved at Time t, Relative to Value of Life Saved in Present |
|
0 |
1.00 |
|
5 |
.43 |
|
10 |
.33 |
|
25 |
.16 |
|
50 |
.09 |
|
100 |
.02 |
|
SOURCE: Adapted from Cropper et al. (1992: Table 1). |
|
conventional approach is distorted away from adult and toward children’s programs.
What if those unborn at the time of program initiation are in fact to be considered equal beneficiaries of health programs? That is to say, whatever discount rate is used, it is applied equally to all cohorts regardless of whether or not they were alive at the time program implementation decisions were made. Does the conventional index provide a fair representation of the relative benefits of different multiyear programs under this circumstance?
Under one circumstance, the index of years of life saved would be almost exactly correct: if the reduction in mortality induced by the program were constant with respect to age (Δμ(a)=K), then it would induce no change in the population’s age distribution (Keyfitz, 1968). If, in addition, the population to which the mortality change is applied is demographically “stable”—with constant fertility, mortality, and migration rates leading to a constant age distribution—then the age distribution of deaths averted by the program (D(a)) would not change over time. The only error in the index under this circumstance is that the preprogram p(a) function is used to estimate ![]() instead of the postprogram p′(a) function.
instead of the postprogram p′(a) function.
These conditions are, of course, highly restrictive. The most serious distortion that they introduce results from the assumption that age distributions are constant. Largely as a result of declining fertility, age distributions are growing older in nearly all developing countries, and the aging process will almost certainly continue (United Nations, 1989). Given a particular change in age-specific death rates, the deaths-averted function (D(a)) at baseline is thus younger than it would be in future years. The conventional index is thus biased toward health interventions at young ages in aging populations.
The amount of bias is directly proportional to impending changes in the age distribution. Table 5 displays the changes projected by the United
TABLE 5 Age Bias in Conventional Measures of Years of Lite Saved by Health Programs: Less Developed Countries
|
|
Projected Ratio of Population in Age Interval to Population 0–4 |
Bias in 1990 Measure of Years of Lite Saved by Health Programs Targeted at Particular Ages, Relative to Age 0–4 (%) |
|||||
|
Age |
1990 |
2000 |
2010 |
2020 |
2000 |
2010 |
2020 |
|
0–4 |
1.000 |
1.000 |
1.000 |
1.000 |
0 |
0 |
0 |
|
30–34 |
.533 |
.644 |
.680 |
.834 |
21 |
27 |
56 |
|
50–54 |
.265 |
.309 |
.434 |
.603 |
17 |
63 |
128 |
|
70–74 |
.096 |
.119 |
.154 |
.213 |
24 |
60 |
122 |
|
SOURCE: Compiled from United Nations (1989:8). |
|||||||
Nations. The assumption that the age distribution at baseline will not change, which is built into the conventional approach, produces large biases in favor of programs targeted at young ages, even during the first decade. Relative to health interventions targeted at ages 0–4, those directed at ages 50–54 or 70–74 would produce 17–24 percent more years of life saved in 2000 than would be indicated by the index computed for 1990. This bias grows rapidly to 60–63 percent in 2010 and to 122–128 percent in 2020.
It is widely recognized that age distributions in developing countries are growing older and that more attention should be paid to adult health issues. It is not so apparent that the index of years of life saved takes no account of these changes when applied to multiyear programs. The result of embedding the initial age distribution in concrete is to bias calculations in favor of youthful and against adult interventions. The only solution is to use population projection to provide a more reliable estimate of the age and time effects of various programs.
Adding Health to Years of Life
An additional problem with conventional procedures is their treatment of disability. Let us assume that we can agree on a definition of disability and that years of life added in the disabled state do not count toward the gain in “healthy” years of life. The correct formulas for calculating years of healthy life added are presented in the lower portion of Table 2.
Unfortunately, conventional practice deviates markedly from these formulas. The years of healthy life gained are calculated as the sum of two components, one resulting from the morbidity reduction and the other from the mortality reduction. In computing the latter component, the years of life saved by a health intervention (Equation (1) of Table 2) are all assigned
to the healthy state (cf. Ghana Health Assessment Project Team, 1981:74, 80). Even if the intervention had no effect on age-specific disability rates (h'(a) =h(a)), some of the years of life added by a program would be disabled years, simply because many disease processes that produce disability will not be affected by the intervention. The conventional procedure clearly overestimates years of healthy life gained. If disability rates are 20 percent at each age, then the gain in healthy years of life from the mortality reduction—the bulk of the total gain in years of healthy life—will be overestimated by this amount. In general, the conventional procedure will overestimate the value of interventions targeted at older ages more than those targeted at younger ages because rates of disability rise with age.
A second, less critical, problem with the treatment of ill-health in the Ghana team’s procedures is that it concentrates the morbidity associated with a disease at one age, typically a youthful age (Barnum, 1987). This tactic means that the gains from morbidity reduction are too heavily concentrated in the first year of the program and are underrepresented in later years. The relative distortion in index values across diseases will, as a result, vary with the discount rate that is employed.
Program Interactions
The conventional procedure does not incorporate interactions among disease processes or programs (Barnum, 1987). Many such interactions are possible. The simplest situation arises when two potential programs would act “independently” to reduce mortality rates. Suppose that program 1 would reduce mortality rates by Δμ1(a) and program 2 would reduce mortality rates by Δμ2(a). Then the gain in years of life from introducing both programs will exceed the sum of gains from introducing each of them individually, unless they both operate at one and the same age. The reason is that those “saved” from death by one program will live more years as a result of implementation of the other program. Thus, the gains from the two programs are synergistic rather than additive. Synergy is particularly likely to involve programs spanning a variety of adult ages. Only if the two programs operate at exactly the same age—and early childhood is the most likely target of multiple programs—would this property be absent. To incorporate these interactions in population projection, it is only necessary to introduce both sets of effects into the np′a function, which is a straightforward operation.2
More complex interactions are, of course, likely. These would typically involve not only mortality but morbidity. Mosley and Becker (1991) provide a lucid account of how changes in the intensity of one disease process
can affect other processes. They note that, in general, interventions that alter the incidence of a disease would be expected to add more years of life than those that alter case-fatality rates, even though the initial effect on age-specific death rates may be equivalent. The reason is that alterations in case-fatality rates are more likely to raise levels of morbidity and hence leave the survivors more vulnerable to other disease processes. The problem is one not only of modeling the proper effects of interventions h'(a) but also of predicting their effects on np′a. These are unquestionably important issues that bedevil not only a projection approach to planning but also the computation of conventional indices. The problems are, in fact, identical in the two cases. More complex models of disease and death processes involving disease interactions have been used to study health issues in developed countries (e.g., Manton and Stallard, 1984; Rogers et al., 1989), but Mosley and Becker’s approach is better suited to yielding practical guidelines for developing country health programs.
How Should Births Added by Health Programs be Treated?
We have noted that the family of conventional measures of years of life gained assumes that a program lasts only one year. The measures work as crude approximations to the effects of a permanent program if those unborn at the time of program initiation are included among the beneficiaries. To make the approximation more exact, it would be necessary to use the new (i.e., postprogram) set of npa’s and h(a)'s and to project the number of births that will occur in the future. Meeting these requirements involves nothing more or less than performing a population projection.
In a projection framework, births will increase as a result of a successful health program that improves survivorship at any age less than 45 or 50. The question is not simply whether to allow the unborn to count as beneficiaries of the program but also how to count the births that would be added as a result of the program. Do their entire lives count toward years of life added by the program? If so, the most cost-effective health intervention would be a restriction of contraceptive availability, which would both save money and add years of life. Not surprisingly, advocates of contraceptive programs have used other indices and procedures.
The question is far from trivial because most of the years of life eventually added by most health programs will be lived by people who would not have been born in the program’s absence. The huge expansion of the human population since 1940 is primarily a result of successful health programs; most of the years of life added represent births that would not otherwise have occurred, rather than longer lives for people who would have been born in any event. Put more concretely, saving the life of a 20-year-old woman in a typical developing country will lead to approximately four
more births in the next two decades. The issue is not readily swept under the rug, as critics of expanded health programs are quick to point out (e.g., King, 1990).
This issue is contentious because of the presumed economic burden of additional births in poor countries. Although this burden may not be as great as once believed (National Research Council, 1986), it is unquestionably true that the “extra” births will not become productive citizens for 15 years or so, by which time their productive contribution will be heavily discounted under most accounting procedures. It is also true that most of these births will be “wanted” by their parents and will help to fulfill the aspirations of those whose lives may have been spared by health interventions. Most of the costs of raising children through their dependent years will be borne not by society at large but by the parents who voluntarily bore them.
When economic issues are introduced, it is appropriate—if not always politically expedient—to make them explicit. Once again, population projections are the most direct and straightforward means of making the underlying considerations operational. For example, by using the age distribution of projected populations at future dates together with age profiles of consumption and production, it is a simple matter to take a first cut at identifying the effects of a health program on the relative balance of the two and on per capita income. The effects are not likely to be large, although the short-term and long-term consequence of most mortality declines has been to increase the fraction of the population outside labor force age (Coale, 1972). The most complete consideration of the effects of health programs on a wide array of economic processes in a population projection framework remains Barlow’s (1968) analysis of antimalarial programs in Sri Lanka.
The point, however, is not to make the comparative assessment of health programs so complex as to be impractical. The indices of years of life gained have achieved great currency because they provide relatively simple measures that allow cross-program comparisons. We have tried to show more precisely what assumptions are necessary in interpreting these indices. In so doing, we have identified certain problems, inconsistencies, and interpretive difficulties to which the measures are subject. These difficulties can be removed—without adding any data requirements—by the use of population projections. Such projections also serve as a solid and trustworthy vehicle for answering more complex questions if those are pertinent to the planning process.
DISCUSSION
The conventional measure of years of healthy life gained functions best as a guide to evaluating health interventions lasting one year. Can the
measure simply be reapplied each year to evaluate whether a program should continue? There are two obvious difficulties with this approach. One is that most interventions involve both start-up costs and continuing costs. In order to properly evaluate whether start-up costs should be invested, an assessment is needed that stretches over the full life of a program. The second problem is that as a practical matter, government agencies do not engage in continuous self-reflection. Planning is sporadic, and careful evaluation of existing programs is impeded by the constituencies that develop around them. It is realistic to suppose that careful health planning by using quantitative measures of expected program effects will occur infrequently in developing countries. When it does occur, it is best that the methods used take full advantage of the information available.
SUMMARY
The conventional calculation of the years of healthy life gained through a health intervention functions best as a health planning device when a one-year intervention is being considered. Its principal problems in this case are
-
its assumption that all the years of life saved will be healthy years, and
-
its assumption that all of those saved by the intervention will die at their life expectancy.
Both of these procedures produce an upward bias in estimating years of healthy life gained; the latter bias occurs only when discounting is used.3
Most health interventions stretch over periods longer than one year. The index is a poorer planning instrument in these cases. If the aim is to represent the effects of a program on the population alive at the time the program is initiated, then the index produces a severe bias against interventions directed primarily at adults. Health improvements among adults will add healthy years for many cohorts, whereas those directed at children will benefit few. This feature is not represented in the index.
If those unborn at program initiation are to be given equal weight as beneficiaries, then this bias may be largely averted. However, the index typically will still give misleading information about the effects of long-term programs because its values are entirely dependent on the initial age distribution. Because age distributions in most developing countries (apart from Africa) are changing rapidly, important biases can result. In particu-
lar, the index will be biased toward interventions at youthful ages in aging populations.
All of these problems, whether applicable to one-year or multiyear interventions, can be avoided through the use of population projection. Projections also provide a straightforward means of incorporating other dimensions, such as the total gain in production, changes in the balance between production and consumption, or changes in per capita income.
REFERENCES
Barlow, R. 1968 The Economic Effects of Malaria Eradication. Economic Research Series No. 15. Ann Arbor: University of Michigan School of Public Health.
Barnum, H. 1987 Evaluating healthy days of life gained from health projects. Social Science and Medicine 24(10):833–841.
Coale, A.J. 1972 The Growth and Structure of Human Populations. Princeton, N.J.: Princeton University Press.
Coale, A.J., and P.Demeny 1983 Regional Model Life Tables and Stable Populations. New York: Academic Press.
Cropper, M.L., S.K.Aydede, and P.R.Portney 1992 Rates of time preference for saving lives. American Economic Review 82(2):469–472.
Ghana Health Assessment Project Team 1981 A quantitative method of assessing the health impact of different diseases in less developed countries. International Journal of Epidemiology 10(1):73–80.
Jamison, D.T., and W.H.Mosley 1991 Disease control priorities in developing countries. Manuscript, Population, Health, and Nutrition Division, World Bank, Washington, D.C.
Keyfitz, N. 1968 Introduction to the Mathematics of Population. Reading, Mass.: Addison-Wesley.
King, M. 1990 Health is a sustainable state. Lancet 336:664–667.
Loomes, G., and L.McKenzie 1989 The use of QALY’s in health care decision making. Social Science and Medicine 28(4):299–308.
Manton, K.G., and E.Stallard 1984 Recent Trends in Mortality Analysis. New York: Academic Press.
Mishan, E.J. 1988 Cost-Benefit Analysis, 4th ed. London: University Hyman.
Mooney, G., and A.Creese 1990 Cost and cost-effectiveness analysis of health interventions. Health Sector Priorities Review Paper HSPR-23. Population, Health, and Nutrition Division, World Bank, Washington, D.C.
Mosley, W.H., and S.Becker 1991 Demographic models for child survival and implications for health intervention programs. Health Policy and Planning 6(3):218–233.
Murray, C.J.L. 1990 Rational approaches to priority setting in international health. Journal of Tropical Medicine and Hygiene 93:303–311.
National Research Council 1986 Population Growth and Economic Development: Policy Questions. Washington, D.C.: National Academy Press.
Patrick, D.L., and R.A.Deyo 1989 Generic and disease-specific measures in assessing health status and quality of life. Medical Care 27(3) supplement: S217-S232.
Preston, S.H. 1976 Mortality Patterns in National Populations. New York: Academic Press.
Prost, A., and N.Prescott 1984 Cost-effectiveness of blindness prevention by the Onchocerciasis Control Programme in Upper Volta. Bulletin of the World Health Organization 62:795–802.
Rogers, A., R.Rogers, and L.Branch 1989 A multistate analysis of active life expectancy. Public Health Reports 104(3):222–226.
Russell, M. 1990 The making of cruel choices. Pp. 15–22 in P.B.Hammond and R.Coppock, eds., Valuing Health Risks, Costs, and Benefits for Environmental Decision Making. Washington, D.C.: National Academy Press.
Torrance, G.W. 1986 Measurement of health state utilities for economic appraisal. Journal of Health Economics 1–30.
United Nations 1989 Global Estimates and Projections of Population by Sex and Age: The 1988 Revision. Population Study No. 93. New York: United Nations.
1991 World Population Prospects: 1990. Population Study No. 120. New York: United Nations.



















