6
EVALUATING MATHEMATICS ASSESSMENTS
Whether a mathematics assessment comprises a system of examinations or only a single task, it should be evaluated against the educational principles of content, learning, and equity. At first glance, these educational principles may seem to be at odds with traditional technical and practical principles that have been used to evaluate the merits of tests and other assessments. In recent years, however, the measurement community has been moving toward a view of assessment that is not antithetical to the positions espoused in this volume. Rather than view the principles of content, learning, and equity as a radical break from past psychometric tradition, it is more accurate to view them as gradually evolving from earlier ideas.
Issues of how to evaluate educational assessments have often been discussed under the heading of "validity theory." Validity has been characterized as "an integrated evaluative judgment of the degree to which empirical evidence and theoretical rationales support the adequacy and appropriateness of inferences and actions based on test scores or other modes of assessment."1 In other words, an assessment is not valid in and of itself; its validity depends on how it is interpreted and used. Validity is a judgment based on evidence from the assessment and on some rationale for making decisions using that evidence.
Validity is the keystone in the evaluation of an assessment. Unfortunately, it has sometimes been swept aside by other technical matters, such as reliability and objectivity. Often it has been thought of in narrow terms ("Does this assessment rank students in the same way as another one that people consider accurate?"). Today, validity is being reconceived more broadly and given greater emphasis in discussions of assessment.2 Under this broader conception,
validity theory can provide much of the technical machinery for determining whether the educational principles are met by a mathematics assessment. One can create a rough correspondence between the content principle and content validity,3 between the learning principle and consequential or systemic validity,4 and between the equity principle and criteria of fairness and accessibility that have been addressed by Silver and Lane.5
Although every mathematics assessment should meet the three principles of content, learning, and equity, that alone cannot guarantee a high-quality assessment. Technical considerations, including generalizability, evidence, and costs, still have a place. The educational principles are primary and essential but they are not sufficient.
THE CONTENT PRINCIPLE
|
The contexts in which assessment tasks are administered and the interpretations students make of them are critical in judging the significance of the content. |
Key Questions
What is the mathematical content of the assessment?
What mathematical processes are involved in responding?
Applying the content principle to a mathematics assessment means judging how well it reflects the mathematics that is most important for students to learn. The judgments are similar to early notions of content validity that were limited to asking about the representativeness and relevance of test content. The difference lies in a greater concern today for the quality of the mathematics reflected in the assessment tasks and in the responses to them.
Procedures for evaluating the appropriateness of assessment content are well developed and widely used. Most rely heavily on expert judgment. Judges are asked how well the design of the assessment as a whole captures the content to be measured and how well the individual tasks reflect the design. The two sets of judgments determine whether the tasks sufficiently represent the intended content.
New issues arise when the content principle is applied:
-
the nature of the important mathematics content leads to some types of tasks that have not been common in educational assessment,
-
the emphasis on thinking processes leads to new forms of student performance, and
-
the characteristics of today's important mathematics lead to a broader view of curricular relevance.
CONTENT OF TASKS
Because mathematics has been stereotyped as cut and dried, some assessment designers have assumed that creating high-quality mathematics tasks is simple and straightforward. That assumption is false. Because mathematics relies on precise reasoning, errors easily creep into the words, figures, and symbols in which assessment tasks are expressed.
Open-ended tasks can be especially difficult to design and administer because there are so many ways in which they can misrepresent what students know and can do with mathematics.6 Students may give a minimal response that is correct but that fails to show the depth of their mathematical knowledge. They may be confused about what constitutes an adequate answer, or they may simply be reluctant to produce more than a single answer when multiple answers are called for. In an internal assessment constructed by a teacher, the administration and scoring can be adapted to take account of misunderstanding and confusion. In an external assessment, such adjustments are more difficult to make. The contexts in which assessment tasks are administered and the interpretations students are making of them are critical in judging the significance of the content.
|
The Ironing Board 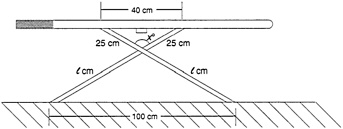 The diagram shows the side of an ironing board. The two legs cross at x°
|
Difficulties arise when attempts are made to put mathematics into realistic settings. The setting may be so unfamiliar that students cannot see mathematics in it. Or, the designer of the task may have strained too hard to make the mathematics applicable, ending up with an artificial reality, as in the example above.7 As a practical matter, the angle between
the legs of the ironing board is not nearly so important as the height of the board. As Swan notes,8 the mathematical content is not incorrect, but mathematics is being misused in this task. A task designer who wants to claim the situation is realistic should pose a genuine question: Where should the stops be put under the board so that it will be convenient for people of different heights?
|
The thinking processes students are expected to use are as important as the content of the assessment tasks. |
The thinking processes students are expected to use in an assessment are as important as the content of the tasks. The process dimension of mathematics has not merited sufficient attention in evaluations of traditional multiple-choice tests. The key issue is whether the assessment tasks actually call for students to use the kind of intellectual processes required to demonstrate mathematical power: reasoning, problem solving, communicating, making connections, and so on. This kind of judgment becomes especially important as interesting tasks are developed that may have the veneer of mathematics but can be completed without students' ever engaging in serious mathematical thinking.
To judge the adequacy of the thinking processes used in an assessment requires methods of analyzing tasks to reflect the steps that contribute to successful performance. Researchers at the Learning Research and Development Center (LRDC) at the University of Pittsburgh and the Center for Research, Evaluation, Standards, and Student Testing (CRESST) at the University of California at Los Angeles are beginning to explore techniques for identifying the cognitive requirements of performance tasks and other kinds of open-ended assessments in hands-on science and in history.9
|
Mixing Paint To paint a bathroom, a painter needs 2 gallons of light blue paint mixed in a proportion of 4 parts white to 3 parts blue. From a previous job, she has I gallon of a darker blue paint mixed in the proportion of I part white to 2 parts blue. How many quarts of white paint and how many quarts of blue paint (I gallon = 4 quarts) must the painter buy to be able to mix the old and the new paint together to achieve the desired shade? How much white paint must be added and how much blue paint? Discuss in detail how to model this problem, and then use your model to solve it. |
The analysis of task demands, however, is not sufficient. The question of what processes students actually use in tackling the tasks must also be addressed. For example, could a particular problem designed to assess proportional reasoning be solved satisfactorily by using less sophisticated operations and knowledge? A problem on mixing paint, described at left, was written by a mathematics teacher to get at high-level understanding of proportions and to be approachable in a variety of ways. Does it measure what was intended?
Such questions can be answered by having experts in mathematics education and in cognitive science review tasks and evaluate student responses to provide information about the cognitive processes used. (In the mixing paint example, there are solutions to the problem that involve computation with complicated fractions more than proportional reasoning, so that a student who finds a solution has not necessarily used the cognitive processes that were intended by the task developer.) Students' responses to the task, including what they say when they think aloud as they work, can suggest what those processes might be. Students can be given part of a task to work on, and their reactions can be used to construct a picture of their thinking on the task. Students also can be interviewed after an assessment to detect what they were thinking as they worked on it. Their written work and videotapes of their activity can be used to prompt their recollections.
None of these approaches alone can convey a complete picture of the student's internal processes, but together they can help clarify the extent to which an assessment taps the kinds of mathematical thinking that designers have targeted with various tasks. Researchers are beginning to examine the structure of complex performance assessments in mathematics, but few studies have appeared so far in which labor-intensive tasks such as projects and investigations are used. Researchers at LRDC, CRESST, and elsewhere are working to develop guidelines for gauging whether appropriate cognitive skills are being engaged by an assessment task.
Innovative assessment tasks are often assumed to make greater cognitive demands on students than traditional test items do. Because possibilities for responses to alternative assessment tasks may be broader than those of traditional items, developers must work harder to specify the type of response they want to evoke from the task. For example, the QUASAR project has developed a scheme for classifying tasks that involves four dimensions: (1) cognitive processes (such as understanding and representing problems, discerning mathematical relationships, organizing information, justifying procedures, etc.); (2) mathematical content (which is in the form of categories that span the curriculum); (3) mode of representation (words, tables, graphs, symbols, etc.); and (4) task content (realistic or nonrealistic). By classifying tasks along four dimensions, the QUASAR researchers can capture much of the richness and complexity of high-level mathematical performance.
The QUASAR project has also developed a Cognitive Assessment Instrument (QCAI)10 to gather information about the program itself and not individual students. The QCAI is a paper-and-pencil instrument for large-group administration to individual students. At each school site, several dozen tasks might be administered, but each student might receive only 8 or 9 of them. A sample task developed for use with sixth grade students is at left.11
|
Sample QUASAR Task The table shows the cost for different bus fares. BUSY BUS COMPANY FARES One Way $1.00 Weekly Pass $9.00 Yvonne is trying to decide whether she should buy a weekly bus pass. On Monday, Wednesday and Friday she rides the bus to and from work. On Tuesday and Thursday she rides the bus to work, but gets a ride home with her friends. Should Yvonne buy a weekly bus pass? Explain your answer. |
The open-ended tasks used in the QCAI are in various formats. Some ask students to justify their answers; others ask students to show how they found their answers or to describe data presented to them. The tasks are tried out with samples of students and the responses are analyzed. Tasks are given internal and external reviews.12
Internal reviews are iterative, so that tasks can be reviewed and modified before and after they are tried out. Tasks are reviewed to see whether the mathematics assessed is important, the wording is clear and concise, and various sources of bias are absent. Data from pilot administrations, as well as interviews with students thinking aloud or explaining their responses, contribute to the internal review. Multiple variants of a task are pilot tested as a further means of making the task statement clear and unbiased.
External reviews consist of examinations of the tasks by mathematics educators, psychometricians, and cognitive psychologists. They look at the content and processes measured, clarity and precision of language in the task and the directions, and fairness. They also look at how well the assessment as a whole represents the domain of mathematics.
The scoring rubrics are both analytic and holistic. A general scoring rubric (similar to that used in the California Assessment Program) was developed that reflected the scheme used for classifying tasks. Criteria for each of the three interrelated components of
the scheme were developed at each of the five score levels from 0 to 4. A specific rubric is developed for each task, using the general scoring rubric for guidance. The process of developing the specific rubric is also iterative, with students' responses and the reactions of reviewers guiding its refinement.
Each year, before the QCAI is administered for program assessment, teachers are sent sample tasks, sample scored responses, and criteria for assigning scores that they use in discussing the assessment with their students. This helps ensure an equitable distribution of task familiarity across sites and gives students access to the performance criteria they need for an adequate demonstration of their knowledge and understanding.
CURRICULAR RELEVANCE
The mathematics in an assessment may be of high quality, but it may not be taught in school or it may touch on only a minor part of the curriculum. For some purposes that may be acceptable. An external assessment might be designed to see how students approach a novel piece of mathematics. A teacher might design an assessment to diagnose students' misconceptions about a single concept. Questions of relevance may be easy to answer.
|
The term alignment is often used to characterize the congruence that must exist between an assessment and the curriculum. |
Other purposes, however, may call for an assessment to sample the entire breadth of a mathematics curriculum, whether of a course or a student's school career. Such purposes require an evaluation of how adequately the assessment treats the depth and range of curriculum content at which it was aimed. Is each important aspect of content given the same weight in the assessment that it receives in the curriculum? Is the full extent of the curriculum content reflected in the assessment?
The term alignment is often used to characterize the congruence that must exist between an assessment and the curriculum. Alignment should be looked at over time and across instruments. Although a single assessment may not be well aligned with the curriculum because it is too narrowly focused, it may be part of a more comprehensive collection of assessments.
The question of alignment is complicated by the multidimensional nature of the curriculum. There is the curriculum as it exists
in official documents, sometimes termed the intended curriculum; there is the curriculum as it is developed in the classroom by teachers through instruction, sometimes termed the implemented curriculum; and there is the curriculum as it is experienced by students, sometimes termed the achieved curriculum. Depending on the purpose of the assessment, one of these dimensions may be more important than the others in determining alignment.
Consider, for example, a curriculum domain consisting of a long list of specific, self-contained mathematical facts and skills. Consider, in addition, an assessment made up of five complex open-ended mathematics problems to which students provide multi-page answers. Each problem might be scored by a quasi-holistic rubric on each of four themes emphasized in the NCTM Standards: reasoning, problem solving, connections, and communication. The assessment might be linked to an assessment framework that focused primarily on those four themes.
|
Better methods are needed to judge the alignment of new assessments new curricula. |
An evaluator interested in the intended curriculum might examine whether and with what frequency students actually use the specific content and skills from the curriculum framework list in responding to the five problems. This examination would no doubt require a reanalysis of the students' responses because the needed information would not appear in the scoring. The assessment and the intended curriculum would appear to be fundamentally misaligned. An evaluator interested in the implemented curriculum, however, might be content with the four themes. To determine alignment, the evaluator might examine how well those themes had been reflected in the instruction and compare the emphasis they received in instruction with the students' scores.
The counting and matching procedures commonly used for checking alignment work best when both domains consist of lists or simple matrices and when the match of the lists or arrays can be counted as the proportion of items in common. Curriculum frameworks that reflect important mathematics content and skills (e.g., the NCTM Standards or the California Mathematics Framework) do not fit this list or matrix mode. Better methods are needed to judge the alignment of new assessments with new characterizations of curriculum.
THE LEARNING PRINCIPLE
Key Questions
How are enhanced learning and good instruction supported by the assessment?
What are its social and educational consequences?
Mathematics assessments should be judged as to how well they reflect the learning principle, with particular attention to two goals that the principle seeks to promote—improved learning and better instruction—and to its resulting goal of a high-quality educational system.
IMPROVED LEARNING
|
Student engagement in assessment tasks should be judged through various types of evidence, including teacher reports, student reports, and observations. |
Assessments might enhance student learning in a variety of ways. Each needs careful investigation before a considered judgment is reached on the efficacy of specific assessment features. For example, a common claim is that assessment can and should raise both students' and teachers' expectations of performance, which will result in greater learning. Research on new assessments should seek to document this assertion.
Students are also presumed to need more active engagement in mathematics learning. Assessments support student learning to the extent that they succeed in engaging even those students with limited mathematical proficiency in solving meaningful problems. This support often involves activities about which students have some knowledge and interest or that otherwise motivate engagement. However, if challenging assessments are so far beyond the grasp of students whose knowledge lags behind the goals of reform, and such students are closed off from demonstrating what they do know, the assessments may well have negative effects on these students' learning. This question, like many others, deserves further investigation. In any case, student engagement in assessment tasks should be judged through various types of evidence, including teacher reports, student reports, and observations.
Learning to guide one's own learning and to evaluate one's own work is well recognized as important for developing the
capability to continue learning. Some new forms of assessment make scoring rubrics and sample responses available to students so they can learn to evaluate for themselves how they are doing. There are indications that attention to this evaluative function in work with teachers and students has desirable effects. More research is needed to determine how best to design and use rubrics to help students' assess their own work. This is another avenue that might be explored to help assessors evaluate an assessment's potential to improve mathematics learning.
|
Changes in student learning can be assessed directly through changes in performance over time. |
Finally, changes in student learning can be assessed directly through changes in performance over time. The nature of the assessment used to reflect change is critical. For example, should one use an assessment for which there is historical evidence, even if that assessment cannot capture changes in the mathematics considered most important for students to learn? Or should one use a new assessment reflecting the new goals but for which there is no historical evidence for comparison? The difficulty with the first situation is that it compromises the content principle. For a short time, however, it may be desirable to make limited use of assessments for which there is historical evidence and to implement, as quickly as possible, measures that better reflect new goals in a systematic way.
BETTER INSTRUCTION
Attempts to investigate the consequences of an assessment program on instruction should include attention to changes in classroom activities and instructional methods in the assignments given, in the classroom assessments used, and in the beliefs about important mathematics. Studies of the effects of standardized tests have made this point quite clearly. For example, a survey of eighth-grade teachers' perceptions of the impact of their state or district mandated testing program revealed an increased use of direct instruction and a decreased emphasis on project work and on the use of calculator or computer activities.13 Some studies have suggested that the instructional effects of mandated testing programs on instruction have been rather limited when the stakes are low,14 but these effects appear to increase as stakes are raised.15 Teachers may see the effects on their instruction as positive even when those effects are directed away from the reform vision of mathematics instruction.16
Assessments fashioned in keeping with the learning principle should result in changes more in line with that vision. New methods
of assessing writing have shown how changes in instructional methods and activities can follow from reform in assessment. The change from multiple-choice tests to directed writing assessments seem to have refocused classroom instruction in California schools. A recent study showed that 90% of California teachers now assign more writing and more varied kinds of writing (e.g., narrative, persuasive).17
Evaluating instructional changes in mathematics requires evidence about how teachers spend their instructional time, the types of classroom activities they initiate, and how they have changed what they see as most important for instruction. Shortly after the 1989 publication of the NCTM Standards, a study of teachers who were familiar with the document and with its notions about important mathematics showed that they continued to teach much as they had always taught. The topics and themes recommended in the Standards had not been fully integrated into instruction, and traditional teaching practices continued to dominate.18 As assessment practice changes under the guidance of the learning principle, more teaching should be in line with the reform vision, even for teachers who are not well acquainted with the Standards documents.
|
The importance of sustained attention to the professional development of teachers is critical to the sucess of reform. |
Some evidence of this change can be seen in schools where teachers are experimenting with new, more powerful forms of assessment. Early observations also raise warnings about superficial changes and about lip service paid to views that teachers have not yet internalized. Teachers weak in mathematics often have difficulty making critical judgments about the mathematics reflected in student work. They cannot differentiate confidently between correct and incorrect alternatives presented by students with novel ideas about a problem. They do not always recognize when a powerful but misconceived idea underlies an incorrect answer.19 These observations point once again to the importance of sustained attention to the professional development of teachers. As new assessments take hold and necessary changes in curriculum and teacher development are made, the instructional effects of assessments will need to be continuously monitored and evaluated to see whether these difficulties have been overcome.
EFFECTSON THE EDUCATIONAL SYSTEM
Recent proposals for assessment reform and for some type of national examination system contend that new forms of assess
ment will promote improvements in American education. The report Raising Standards for American Education claims that high national standards and a system of assessment are needed because "in the absence of well-defined and demanding standards, education in the United States has gravitated toward de facto national minimum expectations."20 The argument asserts that assessments can clarify expectations and motivate greater effort on the part of students, parents, teachers, and others involved in the educational enterprise. Evaluative questions regarding the impact of assessment on the system should concern not only the degree to which the assessments have these intended, beneficial consequences, but also the nature and size of possible unintended consequences whether positive or negative (e.g., dropout rates or tracking students).
|
The intended and the unintended effects of an assessment on how teachers and students use their time and conceive of their goals should be studied. |
Questions about the effects of assessment on the educational system as a whole have received increased attention in the past decade. The growing concern in measurement circles with consequential21 and systemic22 validity have helped guide the discourse. Consequential validity refers to the social consequences that the use of an assessment can have. For example, teachers may adjust their instruction to reflect assessment content. They may spend class time using practice materials that match the assessment. Evidence needs to be collected on the intended and the unintended effects of an assessment on how teachers and students use their time and conceive of their goals.23 Systemic validity refers to the curricular and instructional changes induced in the educational system by an assessment. Evaluating systemic effects thoroughly is a massive undertaking, and there are few extant examples in assessment practice. Even so, it is important to keep a systemic orientation in mind, for the potential impact of assessment on instruction and learning can not be separated from broader educational considerations.
Curricular Effects A comprehensive evaluation of the consequences of any assessment system would include evidence about the impact of the assessments on the curriculum. Influences on curriculum include changes in the way instructional time is allocated and in the nature of the assignments given students. Evidence of curriculum changes can be obtained through questionnaires given to teachers or students, logs kept by teachers on actual class activities, or observations of classrooms. Most of the research on curriculum changes as a consequence of mandated testing programs has made use of teacher questionnaires.24
Outside Effects Assessments such as the Scholastic Assessment Test (SAT) and the Advanced Placement (AP) test are undergoing fundamental change with widespread impact. The use of calculators on the calculus AP exam, for example, is having a profound effect on many high school teachers and way they use technology in their classrooms.25
Another aspect of system effects sought in many reform efforts is to change the attitudes of parents, policymakers, and other citizens about the nature of mathematics students need to learn and to bring each group into a closer and more supportive role with the efforts of the school. Although there is little evidence to date on these systemic effects, it will be important to evaluate any change in such attitudes and actions which may evolve with changes in assessment.
THE EQUITY PRINCIPLE
Key Questions
Does the assessment favor one group over others for reasons irrelevant to what it is intended to measure?
How justifiable are comparisons with a standard or with the performance of others?
Are the tasks accessible to these students?
Several aspects of the principle require examination and evaluation. The first aspect involves the usual issues associated with equity of assessment: traditional questions of fairness and of comparability across groups, scores, tasks, and situations. The second aspect involves questions of whether students have the opportunity to learn important mathematics (whether they have been taught the important mathematics being assessed). The third aspect is newer and is associated with pedagogy that requires that all students find assessment tasks accessible if the tasks are to have the needed positive impact on their learning.
FAIRNESS AND COMPARABILITY
Traditional concerns with fair assessment are amplified or take on different importance in the context of new forms of mathematics assessment. For example, when an assessment includes a few complex tasks, often set in contexts not equally familiar to all students, any systematic disparity in the way tasks are devised or
chosen becomes magnified. These disparities become critical if group differences in performance are due primarily to differences in familiarity with the contexts rather than to the underlying mathematical skills and concepts. Systematic differences in scorers' judgments may exacerbate the problem.
Equity challenges are raised by new emphases in mathematics assessments on types of student performance, such as communication, that once were considered quite separate from mathematics. As researchers using a variety of assessment formats are learning, tasks that require explanation, justification, and written reflection may leave unclear the extent to which student performance reflects different knowledge of mathematics and different language and communication skills.26 Even though both are important, inferences about groups may be misleading if distinctions between these different skills are not made.27
|
Different learning opportunities at home and at school can be a major factor in students' performance on educational assessments. |
Assessors need to know how far they are justified in comparing mathematics performance across sites (e.g., school to school, state to state) and across levels (e.g., school to district, student to state or national norm). Comparisons also need to be justified if they are going to be made from year to year. Such comparisons can be examined either statistically or by a judgmental-linking process.28 In either case, the adequacy of the comparison for different groups of students should be demonstrated.
OPPORTUNITY TO LEARN
Students have different learning opportunities at home and at school, and such opportunities can be a major factor in their performance on educational assessments. Differences in educational experiences between groups have, for example, been a major explanatory variable in studies of group differences. However, in an educational setting designed to provide all students the opportunity to learn important mathematics, such differences may take on other implications. For reasons of equity, all students need to have experienced the important mathematics being assessed. Thus, studies of the congruence of assessments with the instructional experiences of all students are needed.
When the assessments have high-stakes implications for students, demonstrating opportunity to learn is essential. For example, in court cases involving state assessments required for high school graduation, it has been incumbent on the state to demonstrate that the skills tested are a part of the curriculum of all students, that students had an opportunity to learn the material tested. When educational reformers propose high-stakes assessment of important subject matter as a basis for key school-leaving certifications, similar opportunity-to-learn questions are raised.
|
The role assessments play in giving students the sense that mathematics is something they can successfully learn is largely unexplored territory. |
ACCESS
Assessors need to know whether an assessment has offered all students the opportunity to engage in mathematical thinking. Today's vision of mathematics instruction requires a pedagogy that helps students learn mathematics that is accessible to them and relevant to their lives. This requirement affects assessment as well. If students are to find mathematics approachable, assessments must provide ways for every student to begin work on problems even if they cannot complete them as fully or as well as we would wish. Assessments can be evaluated according to how well they provide such access.
Traditionally, it has been recognized that assessment as a whole must be in the range of what a target group can do, or little information about the group tested is gained from the assessment. Consequently a range of difficulty is built into most assessments with the expectation that the majority of students will be able to complete the easiest tasks and only a few the most difficult ones. Typically, the target level of difficulty for tests has been set so that the test will seem fairly difficult to students, with slightly more than 50 percent of the questions answered correctly on average.
When the tasks are more complex and there are fewer of them, perceived difficulty of tasks takes on greater significance. If the goal is to help support students' opportunity to learn important mathematics, perceived difficulty must be taken into account along with other aspects of accessibility. The role assessments play in giving students the sense that mathematics is something they can successfully learn is largely
unexplored territory. That territory needs to be explored if mathematics assessments are to be evaluated with respect to the equity principle.
GENERALIZATION
Key Questions
What generalizations can be made about student performance?
How far are they justified?
A major issue in using alternative assessments concerns the inferences that can be drawn from them. To what extent can an assessor generalize from a student's score on this particular set of tasks to other tasks, on the format of tasks to other formats, on the occasion of assessment to other occasions, on the particular scorers to other scorers? Accumulating evidence suggests that in the areas explored most extensively to date (writing and hands-on science assessment), relatively good reliability of the assessment process can be obtained by systematically training the raters, generating performance tasks systematically, using explicit criteria for scoring responses, and using well-chosen sample responses to serve as anchors or exemplars in assigning performance levels.29 Although few innovative mathematics assessments have been in place long enough to provide a solid base from which to draw conclusions, recent research suggests that acceptable levels of consistency across raters may be achievable in mathematics as well.30
|
A broad variety of tasks are needed to measure the facets of proficiency and performance that make up mathematical competence. |
A second aspect of generalizability reflects whether the alternative assessment measures the particular set of skills and abilities of interest within a domain. This aspect may represent a special challenge in mathematics, particularly as assessments strive to meet broader goals.31 As researchers using a variety of assessment formats are discovering, tasks that require explanation, justification, and written reflection leave unclear the extent to which student performance reflects knowledge of mathematics rather than language and communication skills.32
A third aspect of generalizability rests on the consistency of scores over different tasks which can be thought of as task comparability. High levels of task generalizability are required to draw broad inferences about a learner's mathematical development or compe-
tence from performance on a specific set of tasks. Research in mathematics is beginning to replicate the central finding from investigations of performance assessments in other content areas: The more direct methods of assessing complex performance do not typically generalize from one task to another.33 It may be necessary to administer a broad variety of tasks to measure the many facets of proficiency and performance that make up mathematical competence. It will be essential to continue evaluating evidence on generalizability as new forms of assessment are widely used.
EVIDENCE
Key Questions
What evidence does the assessment provide?
What is the value of that evidence?
|
The nature, weight, and coverage of information an assessment provides for a given purpose determines its value as evidence of student learning. |
Current interest in broadening the range of mathematics assessment tasks reflects a desire that students engage in important mathematical thinking: creative, motivated, associative thinking that is a goal of mathematics education. Whereas traditional item-writing procedures and test theory focus attention on the measurement properties of an assessment, the content, learning, and equity principles recognize the educational value of assessment tasks. However, if inferences and decisions are to be made about school systems or individual students, educational values cannot be the only ones present in the analysis. Especially as stakes increase, the assessor must ensure that the evidence an assessment evokes and the way it is interpreted can be justified, possibly in a court of law. The nature, weight, and coverage of information an assessment provides for a given purpose determines its value as evidence of student learning.
Assessment data, such as right or wrong responses, methods of solution, or explanations of approach, are not inherently evidence in and of themselves. They become evidence only in relation to various inferences made.34 Moreover, a given observation can provide direct evidence about certain inferences and indirect evidence about others. It may provide conclusive evidence about some inferences, moderate evidence about others, and none whatsoever about still others. The central question, then, is Evidence about what? Until it has been answered, How much evidence? cannot
even be posed. The best guideline is more of a metaguideline: First determine what information is needed, and then gauge the effectiveness and efficiency of an assessment in providing such information.
|
Determine what information is needed and then gauge the effectiveness and efficiency of an assessment in providing such information. |
Different kinds and amounts of evidence must be gathered to suit different purposes. For example
-
Do inferences concern a student's comparative standing in a group of students, that is, are they norm-referenced, or do they gauge the student's competencies in terms of particular levels of skills or performance, that is, are they criterion referenced? A norm-referenced assessment assembles tasks to focus evidence for questions such as, Is one student more or less skilled than another? Accuracy of comparisons is of interest, which is reflected by traditional reliability coefficients. A criterion-referenced assessment in the same subject area might have tasks that were similar but selected to focus evidence for questions such as, What levels of skills has this student attained? Reliability coefficients are irrelevant for this purpose; what matters is the weight of evidence for the inference, to be established by investigating how such inferences vary with more or fewer tasks of various types.
-
Will important decisions be based on the results, that is, is it a high-stakes assessment? A quiz to help students decide what to work on today is a low-stakes assessment; a poor choice is easily remedied. An assessment to determine whether they should graduate from eighth grade is high stakes at the level of the individual. An assessment to distribute state funds among schools is high stakes at the level of the school. Any assessment that supports decisions of consequence must provide commensurately dependable evidence. For high-stakes decisions about individuals, for example, several tasks may be necessary to establish the range and level of each student's proficiency.
-
What is the relationship between tasks and the instructional backgrounds of students? When the purpose of assessment is to examine students' competence with the concepts they have been studying, an assessment is built around tasks that are relevant to those concepts in various ways. Because the students have been provided requisite instruction, extended and focused tasks can be quite informative. If the assessment is designed to survey a broad range of proficiency across the state, it is unconscionable for students whose classroom experience has left them unprepared to spend two days on a task that is inaccessible to them.
-
Do inferences concern the competencies of individual students, as with medical certification examinations, or the distributions of competencies in groups of students, as with the National Assessment of Educational Progress (NAEP)? When the focus is on the individual, enough evidence must be gathered about each student to support inferences about the student specifically. On the other hand, a bit of information about each of several students—too little to say much about any of them as individuals—can suffice in the aggregate to monitor the level of performance in a school or a state. In these applications, classical reliability coefficients can be abysmal but that is not relevant. The pertinent question is whether accuracy for group characteristics is satisfactory.
-
To what degree can and should contextual information be taken into account in interpreting assessment results? Mathematics assessment tasks can be made more valid if they broadly reflect the range of mathematical activities people carry out in the real world. This includes features not traditionally seen in assessments: collaborative work, variable amounts of time, or resources such as spreadsheets or outside help. The classroom teacher is in a position to evaluate how these factors influence performance and effectively take it into account in inferences about the students' accomplishments and capabilities. It is not so easy for the state director of assessment or the chief state school officer who must deal with results from a quarter million students to appreciate when students' responses reflect more or less advantaged circumstances.
Just looking at an assessment task or a collection of tasks cannot indicate whether the assessment will serve well for a given
purpose. The tasks provide an opportunity to gather evidence; whether it is acceptable for a given use depends critically on what that use will be. High-stakes decisions for individuals are most demanding in the sense that they require strong enough evidence about each and every individual about whom decisions are being made to justify those decisions: to the student, to the parent, and, increasingly often, to the court. The same amount of time on the same tasks found inadequate for a high-stakes decision about individual students, however, may be quite satisfactory for high-stakes decisions about schools or for low-stakes instructional feedback to individual students.
COSTS AND BENEFITS
Key Questions
What are the costs of the assessment?
What are the benefits?
In traditional educational testing, the guidelines for evaluation of assessment tasks concerned almost exclusively how consistently and how well they ordered individual students along a scale. This view shaped the evolution of testing to favor multiple-choice tasks because they were the most economical, within a traditional cost/benefits framework. However, if one is interested in a expanded range of inferences about student learning, or if one takes a broader view of the potential values of assessment tasks, then the cost/benefits equation is changed. Whenever decisions of consequence are to be made from assessment results, it is incumbent on the assessor to characterize the evidence from the assessment tasks on which the decision is based.
Assessments must be feasible. They need to be practical and affordable, credible to the profession, and acceptable to the public. The following estimates have been offered for the development, administration, and scoring costs of different assessments in use today:35
-
Commercial standardized test: $2 to $5 per student
-
NAEP (I hour, machine scorable): $100 per student
-
European experience (essay exams of four to six questions): $135 per student
-
AP exams: $65 per subject or $325 per student for the five-battery test proposed by the National Council on Education Standards and Testing
-
Estimated total cost for AP-type exam, three grade levels per year: $3 billion annually
|
Assessments need to be practical and affordable, credible to the profession, and acceptable to the public. |
A recent study by the General Accounting Office (GAO)36 of costs of a national examination yielded much lower estimates for performance assessments:
-
Systemwide multiple-choice tests in four or five subjects (including staff time): $15 per student
-
Systemwide performance-based tests used in some states (including staff time): $33 per student
-
Estimated total cost for a national test modeled on systemwide multiple-choice tests: $160 million annually
-
Estimated total cost for a national test modeled on systemwide performance-based tests: $330 million annually.
Although the earlier estimate of $325 per student annually was undoubtedly inflated because it did not take into account some of the savings that might be realized in a national examination if it were not based on the AP model, the GAO estimate of $33 seems very low.37 The GAO survey oversampled seven states that were using performance-based formats in state-mandated testing. Two states that were experimenting with portfolio assessments, Arizona and Vermont, felt that portfolio assessments were not "tests," and, as a result, did not complete that portion of the survey.38 Something closer to the European figure of $135 per student may be more plausible than $33.
Whatever the estimate, performance assessment in mathematics is clearly going to be more expensive than standardized multiple-choice tests have been. Standardized tests have costs that are clearly defined. Such tests may be very costly to develop, but the costs can be amortized over millions of students taking the test over several years. Performance assessment brings high development costs together with additional costs of training teachers to
administer the assessment and paying for scoring. These costs are often hard to detect because local districts pay the cost of substitutes for the teachers who are being trained or doing scoring.39
Performance assessments can take time that might be used for other instruction. By one estimate,40 the Standard Assessment Tasks recently introduced in Great Britain and scheduled to take 3 weeks were estimated by local administrators to require closer to 6 weeks. In Frederick County, Maryland, classes in some grades lost a whole week of instruction completing performance assessments in mathematics and language arts.41
|
Time spent on high-quality mathematics assessment is time well spent because such assessment contributes directly to the learning process. |
These estimates of direct costs may understate the benefits of performance assessments because innovative assessments contribute to instruction and teacher development. Thus, significant portions of assessment could be "charged" to other accounts.42 As noted elsewhere in this report, the benefits of good assessments are many. Time spent on high-quality mathematics assessment is time well spent because such assessment contributes directly to the learning process.
Assessment, even performance assessment, can be made relatively affordable, as experience with new examinations in various European countries suggests. The problem may be that when the same assessment is used for instructional purposes and accountability purposes, the price gets inflated. If assessment contributes to teaching and learning, then a major cost (administration time) can be attributed to instruction,43 since time spent looking at students' work or listening to their reports is time the teacher may need to spend as part of instruction anyway. It is the external markers, the monitoring schemes, and the policing of teacher judgments that impose the true added costs.
Educators appreciate the need for a broad view of the goals of assessment and for what constitutes good evidence that the goals are being met. Assessors need more evidence on matters such as the effects of administering one assessment rather than another. More importantly from the mathematics teacher's point of view, if the mathematics assessed is not good mathematics that relates to the student's learning, all the validity coefficients in the world will be of little value.
POSTSCRIPT
The three principles proposed here—content, learning, and equity—function as a gyroscope for reform of mathematics assessment, one that will help keep mathematics reform on course to new assessments that reflect important mathematics, support good instruction, and promote every student's opportunity to learn.
The guidance system of this gyroscope provides a powerful tool in the journey toward assessment reform. However, it is only a tool, not in itself sufficient to the task. Equally important is the worthiness of the vessel for the voyage, a crew capable of making necessary midcourse corrections, and a detailed navigation chart showing the desired port.
The vessel of reform is the nationwide focus on systemic change: a coordinated response of all major components of the educational system (curriculum, teaching, assessment, governance, teacher education, school organization, etc.). In mathematics, the vessel is particularly sturdy and well launched on its journey. Already available are descriptions of the challenge (Everybody Counts), goals for what students should learn (Curriculum and Evaluation Standards), and teaching methods needed in support of that learning (Professional Standards for Teaching Mathematics). NCTM is now developing a third in its series of standards volumes, this one on assessment. Scheduled for release in spring 1995, this volume will lay out standards for assessments that serve a range of purposes from classroom instruction to policy, program evaluation, planning, and student placement. The three components of standards—curriculum, pedagogy, and assessment—provide a basis for renewing teacher education, rethinking school organization, enhancing implementation of reform, and promoting dialogue about systemic change among the many stakeholders in mathematics education.
Provisions for the voyage are supplied by material resources that stimulate wide-spread participation in assessment reform. These resources provide a rich array of examples of high-quality assessment consonant with the vision of mathematics and mathematics education expressed in the Standards. Some provide specific examples to exemplify overarching ideas (e.g., Mathematics Assess-
ment: Myths, Models, Good Questions, and Practical Suggestions44and Measuring Up). Others rely on specific examples that emerge from large-scale projects with schools nationwide, such as the New Standards Project, QUASAR, and the materials that will emerge from projects supported by the National Science Foundation and other funding sources. Measuring What Counts enhances this suite of resources by providing a conceptual guide to move states, districts, and individuals ahead in their thinking about assessment reform.
Individuals from all parts of the educational system bring different talents and insights to their role as crew on the voyage of assessment reform. Teachers are the captains, charged with the front-line responsibility of providing high-quality mathematics education to all students. Many in the measurement community are exploring new paradigms consonant with principles of validity, reliability, generalizability, and other psychometric constructs. Teacher educators see in innovative assessment the opportunity and necessity to enrich both teacher preparation and professional development. New assessments encapsulate what is valued in mathematics education and often provide the basis for creating a shared vocabulary about the needed changes among faculty. Content specialists are exploring the use of assessment as a lever to create significant curricular and pedagogical change, making "teaching to the test" a positive force for change. Researchers in mathematics education are examining many unresolved questions about how cognitive, affective, and social factors relate to students' performance on assessments. Assessment researchers are rethinking basic measurement constructs and refining their tools to be appropriate both to the kinds of assessments now favored by educators and to the new functions that assessment is expected to serve, as a guidance system for educational reform.45 Policymakers are speaking out on behalf of systemic change, with a deep understanding of the potential for new assessments to move the entire enterprise forward.
|
All educational actions must support students' learning of more and better mathematics; assessment is no exception. |
Many organizations are emerging on local, state, and national levels to broaden the recruitment of new members. Networks and alliances such as State Coalitions for Mathematics and Science Education, the Alliance to Improve Mathematics for Minorities, the State Systemic Initiatives, and the Math Connection are defining their mission to promote reform in mathematics education, including assessment that meets the content, learning, and equity principles.
Through these organizations, people are finding new ways to communicate and to explore new ideas. For example, an emerging network linking measurement and mathematics content experts will help promote development of high-quality assessment instruments. This rich flow of information helps keep reform on course as more is learned about potential trouble spots and potential solutions become quickly and widely disseminated.
The destination for the voyage of reform is well-known: every student must learn more mathematics. All educational actions must support this goal, and assessment is no exception. Although there are many unanswered questions that will require continuing research, the best way for assessment to support the goal is to adhere to the content, learning, and equity principles.






























