5
ASSESSING TO SUPPORT EQUITY AND OPPORTUNITY IN MATHEMATICS LEARNING
High-quality mathematics assessments must focus on equity concerns to ensure that all students are well served by assessment practices. This fundamental concept is embodied in the third educational principle
THE EQUITY PRINCIPLE
Assessment should support every student's opportunity to learn important mathematics.
The tendency in education has been to think about equity in terms of groups of children who by some definition are not well served by educational institutions. Quite often in these discussions the focus has been on groups that are defined in terms of status variables such as sex, ethnicity, native language, and socioeconomic indicators, because these factors influence access, expectations, and the systems of rewards. Increasingly, however, educators have recognized that although status characteristics of learners may be important, they are far less important than functional characteristics are in the design of instructional strategies.1 Reforms in mathematics and other areas of schooling must aim to ensure that each student, regardless of achievement level or demographic characteristics, has the opportunity to study challenging subject matter. The example on the following page, a policy statement adopted by the National Council of Teachers of Mathematics (NCTM) in April 1990,2 reflects this perspective on equity.
Some proponents of educational reform maintain that use of more flexible assessment methods and more performance-oriented
|
Mathematics for All Students In April 001990, the NCTM Board of Directors endorsed the following statement: As a professional organization and as individuals within that organization, the Board of Directors sees the comprehensive mathematics education of every child as its most compelling goal. By every child we mean specificallly
|
tasks can produce fairer measures of all students' intellectual development.3 Others have cautioned that new assessment content and methods alone can not assure equity:
The call for performance assessment did not derive from concerns for fairness or equal access… Well designed assessment systems might act as a lens to more clearly reveal existing and ongoing inequalities, and to inform policy and practice… but only if explicitly designed to do so in all its parts.4
Designing for equity requires conscientious rethinking of not just what we assess and how we do it, but how different individuals and groups are affected by assessment design and procedures. It also requires conscientious attention to how we use assessment results to make decisions about individual children and the schools they attend.
DEVELOPING ASSESSMENTS TO INCREASE EQUITY
To meet the equity principle, tasks must be designed to give children a sense of accomplishment, to challenge the upper reaches of each child's mathematical understanding, and to provide a window on each student's mathematical thinking. Just as good instruction accommodates differences in the ways learners construct knowledge, good assessments accommodate differences in the ways that students think about mathematics and display mathematical understanding. Although all students are to be assessed on important mathematical concepts and skills, in accord with the content and learning principles, the equity principle implies that assessments must be sufficiently flexible to allow all students to show what they know and can do.
DESIGN FEATURES
|
Just as good instruction accommodates differences in the ways learners construct knowledge, good assessments accommodate differences in the ways that students think about and display mathematical understanding. |
Some ways of accommodating differences among learners include permitting multiple entry and exit points in an assessment and allowing students to respond in ways that reflect different levels of mathematical knowledge or sophistication. These design characteristics are critical to assessment equity just as they are critical to the content and learning principles.
Consider the two apparently parallel problems illustrated below and on the following page.5 Close inspection indicates that the first problem may be less accessible to many students. In the first mosaic there is no indication of how the colored tiles are arranged to form the picture. Therefore, to find how many of the different colored tiles would be needed for the enlarged picture, one must already known the general proposition that doubling the length of a figure quadruples its area. On the other hand, the figure in the second problem, with its explicit specification of the color of each part, opens alternative avenues for approaching the task. For example, the student might draw a sketch
|
Pythagoras—A Mosaic Problem Your school's math club has designed a fancy mosaic in honor of Pythagoras, whose work united algebra and geometry. The mosaic includes a picture of the Pythagorean Theorem and its algebraic statement, as indicated below. The figure appears inside a square. 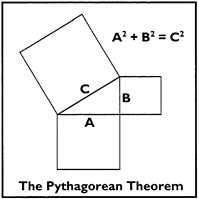 You have constructed a 2' × 2' scale model of the mosaic, which used 120 red mosaic pieces, 200 blue mosaic pieces, and 150 yellow pieces
|
|
Tri-Tex Logo—A Mosaic Problem Tri-Tex Corporation has the following logo. It's going to put a large-scale mosaic of the logo on the side of its corporate headquarters building. 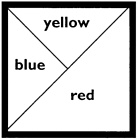 A 2' × 2' scale model of the logo uses: 144 yellow tile pieces 144 blue tile pieces 288 red tile pieces When the logo is placed on the side of the building it will also have a border that consists of a single band of long black tiles. It takes 40 of the black tiles to make a border for the 2' × 2' scale model.
|
of the enlarged figure and discover how many congruent copies of the original figure will be needed to cover it. In fact, by using an informal, experimental approach to the task, the student has the opportunity to gain insight into the relation between length and area, thus potentially learning some important mathematics in the process of doing the task.
As the preceding illustration suggests, assessments designed with multiple entry and exit points permit each student—even those who had mastered only the most elementary knowledge and skills tapped by a problem—to experience some success. However, this goal is not always easily accomplished. Consider the response on the following page of a Ute Indian student to an assessment task.6 Rather than focusing on the mathematical question asked, the student responded to the hypothetical nature of its premise.
Children who live in harsh environments in the inner cities and in remote rural areas often respond to hypothetical problems in much the same way. Hypothetical situations representing options that do not exist in their daily lives may be treated as meaningless or nonsensical. Therefore, their responses may reveal little about their-
|
A Cultural Convention An elementary school student from the Northern Ute Indian reservation in Utah was interviewed as he solved some word problems. He was asked to determine how much his brother would have to spend on gasoline if he wanted to drive his truck from the reservation to Salt Lake City. Instead of estimating (or generalizing) a response, or attempting to calculate an answer based on the information presented in the request, the student responded quite simply: "My brother does not have a pickup." He was assessing the truth value of the conditions presented by the problem. Such assessments are a common part of everyday life of this reservation. Decisions regarding personal conduct as well as innovations and changes affecting tribal membership as a whole are made only if the proposed line of action seems consistent with recognized cultural convention. Proposals that conflict with the way things are may be briefly considered, then set aside for action at some later time, or may simply be given no serious discussion at all. |
understanding of the mathematical problem posed or the mathematical knowledge and skills required by the problem.
As assessments become more complex and more connected to real-world tasks, there is a greater chance that the underlying assumptions and views may not apply equally to all students, particularly when differences in background and instructional histories are involved. In such instances special care will be needed to determine whether differences in performance stem from differences in unrelated characteristics or genuinely reflect differences in mathematical development.
|
The evolving agenda for research on assessment must reflect as much concern for equity as for content, learning, and technical issues. |
SUPPORTING STRATEGIES
When assessments are administered by the teacher in a classroom setting to gauge student progress or diagnose a particular difficulty, differences in students' backgrounds that might affect results are likely to be known. In such cases skillful probing can be used to clarify the basis of the students' responses. Questions can be reframed in ways that better reflect students' understanding of the mathematics required.
In many assessment settings, particularly those used for accountability, it is less possible to accommodate differences in students' ways of understanding and responding to a task. To help overcome this difficulty, it is important that varied perspectives be represented at every phase of assessment development and use. The teams that create the intellectual frameworks from which specific tasks are generated should include experts with different views and life experiences. Broad-based representation is also vital on the research teams that pose study
questions, devise data collection protocols and strategies, and oversee analyses and reporting of results. It is equally important in pilot research: sites should be selected to provide realistic variation among students, teachers, and schools. The raters who evaluate student responses should also represent varied backgrounds.7
The evolving agenda for research on assessment must reflect explicit concern for equity as well. Several projects of major national significance have taken steps in this direction. The New Standards Project (NSP), for example, has created special equity initiatives to ensure that the standards and tasks adopted reflect the experiences and aspirations of varied groups. NSP has conducted focus groups with local and national advocacy representatives to gain broad perspectives on how equity concerns might be addressed. It has also established advisory groups of scholars and practitioners with expertise in culture, gender, and language issues to advise the project on development of assessment tasks and procedures. In addition, a special advisory group was created to address issues involved in administering appropriate assessment tasks and procedures for students who are not native speakers of English.8
The Center for Research, Evaluation, and Student Testing (CRESST) at the University of California at Los Angeles also has special equity initiatives. CRESST created a task force of consultants and scholars to investigate the equity challenges confronting the assessment community. The task force has a broad agenda, encompassing very practical issues as well as a range of theoretical issues and basic research problems:
-
What dimensions of diversity have relevance for education and the assessment of educational achievement?
-
How do group identity and status influence learning of varied cultural groups and their responses to assessment probes?
-
How can problems of reliability, validity, and calibration posed by cultural diversity be addressed?
-
How can procedures and criteria be developed so that appropriate and inappropriate responses are defined that are sensitive to differences among the groups being assessed?
-
On what kinds of tasks do specific groups tend to excel or have difficulty?9
INTERPRETING ASSESSMENT RESULTS
Despite efforts such as those described above and the hopes of the educational reform community that new assessments will be fairer to every student than traditional forms of testing were, preliminary research does not confirm the corollary expectation that group differences in achievement will disappear. Surely, there are many anecdotal reports from classroom teachers and researchers of some students who perform quite poorly on traditional tests exhibiting advanced reasoning and mathematical understanding on more flexible assessments. However, several studies suggest that differences in average group performance are essentially unchanged with the switch from multiple-choice to open-ended assessments. Still other research suggests that group differences might be magnified when performance assessment tasks are used.10 Although the results may vary depending on the content area assessed, the nature of the specific tasks used, and whether group or individual performance is the focus of comparisons, it seems clear that reformers' hopes must be balanced by a spirit of empiricism: there is much more to be learned about how changes in assessment will affect long-standing group differences, one facet of equity concerns.
|
Equity implies a commitment to seek and explore the sources of any systematic performance differences that may be observed on new assessments. |
In any event, equity implies a commitment to seek and explore the sources of any systematic performance differences that may be observed on new assessments. It is important to know whether observed differences among groups reflect genuine differences in mathematical development or can be attributed to factors such as those identified in earlier chapters as special challenges for assessment design:
-
The context in which a task is presented can influence mathematics performance.11 The words and concepts used, the expressions of knowledge required or permitted, will always reflect some particular set of values or life experiences. Not all children will be equally familiar with any given context. Use of genuinely novel contexts or pre-assessment experience with a given context will allow students to enter on an equitable footing.
-
Language can be a potent factor in mathematics assessments.12 Better readers may more easily grasp what they are being asked to do on an assessment task. Better writers may more often present their ideas well, even when of marginal mathematical quality. Because communication is a legitimate facet of mathematical power, some balance must be sought in determining how to weigh students' general command of language in evaluating their expressions of mathematical ideas.
-
Open-ended assessment procedures may exacerbate the influence of resource inequities that exist in the real world. If parents or teachers participate in rather than support students' work, assessments may overestimate the student's mathematical fluency.
-
Rater influences may distort judgments of performance on more open-ended tasks. Many factors can come into play: the rater's expertise and knowledge of the specific mathematics content of the task, the rater's interpretation of task requirements and scoring criteria, or even similarities or differences in the backgrounds of the rater and the student being evaluated.13
When any of these factors contribute to systematic differences among definable groups, assessment results have meanings or implications that are different for some groups than for others. Inferences based on results from such an assessment are said to be biased, that is, not equally valid for all groups.14
|
Solid documentation on the students assessed, the schools they attend, and the instruction they have received makes it possible to identify inequities in opportunity. |
Solid documentation on the students assessed, the schools they attend, and the instruction they have received makes it possible to identify inequities in opportunity. Pilot testing provides an opportunity to ferret out biases and to try out potential remedies. Thorough documentation also is important when assessments are fully implemented so that appropriate cautions and conditions can be applied to interpretations and uses of the results.15 Remedies for group differences depend on the source of the difference. Not all differences will be due to bias. Some, in fact, may be due to systematic differences in the quality of mathematics instruction provided. The following example outlines some of the kinds of information needed to form inferences about individuals and schools.16
|
Equity of Opportunity Indices CRESST has identified the kinds of process information that will be needed about the quality of students' educational experiences to ensure that clear inferences can be drawn from assessment results:
|
USING ASSESSMENTS TO COMMUNICATE NEW EXPECTATIONS
Assessments represent an unparalleled tool for communicating the goals and substance of mathematics education reform to various stakeholders. Teachers, students, parents, policymakers, and the general public will need to understand clearly where mathematics reform will take America's children and why they should support the effort. Assessments can be enormously helpful in this reeducation campaign.
|
Public dialogue is an important strategy for ensuring that assessments are designed and used equitably. |
PROMOTING PUBLIC INVOLVEMENT
Increasingly, public dialogue is seen as an important strategy for ensuring that assessments are designed and used equitably.17 The Urban District Assessment Coalition (UDAC), a joint effort of Boston College and the American Federation of Teachers, organized a series of conversations about assessment reform among various groups before designing a new assessment system for the Boston schools. Over several months, parents, teachers, administrators, and members of the business community worked to arrive at a
consensus on the values, goals, and information needs the system would serve. Representatives of each group have been involved in all stages of the development process, from planning to scoring responses during the first round of pilot tests. That process is being replicated in other UDAC sites.18 Another strategy for increasing public engagement involves making assessment blueprints public. CRESST has proposed that the public be given quite extensive information in blueprints,19 as indicated in the example below.
|
Assessment Blueprints CRESST views public reporting of assessment blueprints as an equity remedy for assessment design. They have recommended that the following questions be addressed in such blueprints.
|
PROMOTING COMMUNITY UNDERSTANDING OF ASSESSMENT REFORM
For mathematics education reform to reach each child, parents and other community members will need to understand the new vision of school mathematics. Their involvement is needed to support the efforts of the teachers, school administrators, and others who, with them, share responsibility for the education of their children. Because many students are "doing well" or "showing improvement" in mathematics achievement as measured by many of
the tests in use today, members of each school community will need to be assured that new assessments and the standards they reinforce are not arbitrary. They need to understand that "doing better" by old standards is no longer good enough to secure children's futures. Assessment tasks and their corresponding scoring criteria can be used to make this point quite convincingly. They illustrate that the knowledge and proficiency that students are being asked to demonstrate are of value of all students.
|
Parents and community members need to understand that doing well by old standards is no longer good enough to secure children's future. |
Supervisors in the San Francisco Unified School District have reported that working with assessments in PTA meetings helped parents in one community see exactly how the mathematics that their children will need differs from the mathematics the parents learned.21 These sessions helped assure parents that much of the mathematics that they value (e.g., numbers and computation) remains important but that it is being learned and assessed as a part of meaningful problem solving and reasoning. After preliminary discussion of the kinds of mathematics students would need in the future and an overview of K–12 program content, parents met in small groups to discuss the mathematics required by several problems. One of the more challenging problems is shown below.22 Scoring rubrics and sample responses were also made available to the small groups.
The program coordinator reported several interesting reactions from parents. Many were awed by the kinds of problems that students are now expected to do and the sophisticated mathematical problem solving and reasoning required. Most believed it important for their children to develop the kinds of skills the problem tapped. Most also believed their children could do the kind of work required but stressed the importance of students getting an early start in primary grades. Many parents asked questions about the quality of mathematics instruction at the school and sought reassurance that their children were getting the right kind of teaching. Most significantly, perhaps, no parent asked why children were not drilling on multiplication facts, a rare
|
Multiplication Task Used in Parent Workshop 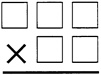 The five digits—1, 2, 3, 4, and 5—are placed in the boxes above to form a multiplication problem. If they are placed to give a maximum product, the product will fall between:
|
outcome at meetings that focus on curriculum content, according to the mathematics and science supervisor.
|
Working with assessments challenges teachers' expectations about who can learn important mathematics. |
CHALLENGING TEACHERS' EXPECTATIONS
Working with assessments and scoring criteria helps teachers crystallize their understanding of what content and teaching standards in mathematics and new performance expectations imply about what should be taught and how. Working with assessments also challenges teachers' expectations about who can learn important mathematics. Teachers sometimes discover that students who rarely make a good showing when tested in traditional ways truly shine on tasks that are more flexible and more engaging.
For example, teachers working with researchers at the Educational Testing Service have been surprised at which students do well and which do poorly on complex tasks. One of the tasks required students to explain how to set up an activity similar to a game of darts, although it involved tossing compact discs rather than darts.23 As indicated in the example below, students were to write a description that included information on how the game would be set up, chances of winning, and expected profits.
|
The Compact Disc Tossing Game For a popular carnival game, a player tosses a coin onto a game board that looks like a checker board. If the coin touches a line on the game board the player loses. If not, the player wins. Players get three throws for a dollar! 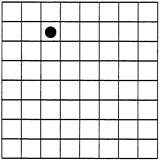 You've been asked to design a similar game for a fund-raising carnival at your school. For prizes, a local record store will sell up to 100 compact discs (CDs) to your class for $5 per disc. You can choose any CDs you want as long as the regular price of the CD is less than $20. To make the game more fun, you've decided to let players throw old scratched CDs rather than coins. Two sizes of CDs can be used (3-inch discs and 5-inch discs). So, the cost of three throws can depend on which size a player chooses to throw. All plans for games must be approved by the carnival planning committee. You want to make as large a profit as possible, but if too few people win, people won't want to play the game. Write a plan to submit to the carnival planning committee that includes details about the size of the game board, the cost of throws, the chances of winning, and an estimate of the expected profits. |
When low-performing middle school students were given an hour or more to work on the problem using physical models, several came up with solutions that were similar to, though less formal than, answers given by college-level mathematicians who spent 5 to 10 minutes on the task. The example below traces the conversation of three students' efforts to think through the problem. The boys began by drawing a game board on a large sheet of paper and cutting out several cardboard disks that were used to act out the game. They worked in this way for about 15 minutes before noticing that the size of the disk made a difference. Their conversation from that point follows.24
|
Dialogue of Three Students Working on the CD Tossing Game Jamal: Mine [small] is better. Yours never works [too large]. [Five minutes passes as the boys tried several more disks, gradually making them smaller and smaller (so they could win more often).]  Bart: This would be easy if this thing [disk] was a dart. Carl: Yah, but it's not a dart. Bart: But what if it was. Look! Look at this. [Bart draws lots of little squares inside the original game board squares as shown in the figure below.] I win if my dart lands in here [referring to his disk as a dart, and pointing to the shaded squares in the diagram shown below.] And, I lose if the dart lands out here [pointing to the unshaded squares]. I've got this many chances to win, and this many to lose. Jamal: Let's count 'em. [He counts, but not very carefully.] There are 300 here [pointing to the unshaded squares.] And 100 here [pointing to the shaded squares]. Bart: So I've got a 100 to 300 chance to win. Carl: Yah, but what if you was Michael Jordan? He'd throw it like this [down the center of one row of squares]. He wouldn't throw it like this [from corner to corner]. Jamal: That's right! And, Tina, my sister, she's so dumb, she'd miss the whole thing. |
Both the boys' solution and the mathematicians' solution were modeled in terms of the position of the discs' center relative to the "win" area of the game board. However, the university professors produced solutions based on the (generally false) assumption that the tosses were random but still good enough to hit the game board. In several important respects, however, the three students come up with a more elegant solution, as their letter to the carnival committee makes clear. Reproduced verbatim, it says:
This is a good game. Don't make the squares on the board too big. Make it about this size (a drawing is given). If your like Tina Jackson, your chances to lose are about 100 to 1. If your like Michael Jordan, your chances are about 50/50. Most people will be about 1 to 8. 500 people will come. About half will be like Tina. They won't play much. Only a few guys will be like Michael Jordan. They like to play a lot. So, make them quit after they win once. There are about 20 of these guys. They will all win sometimes. Most people who play aren't like Tina or Jordan. About 200 will play. You should charge I dollar to play the game.25
The boys' solution reflected understanding of conditional probabilities and identified the factors that would determine success and profits. The boys who produced this solution also demonstrated exceptional mathematics capability when assessed on other problems that rewarded their use of real-life knowledge and skills. Although not all students with histories of low academic performance produced elegant solutions in response to challenging tasks, it was not unusual to discover at least two or three such students in a typical-size classroom. It also was not unusual to find cases in which high achievers, based on traditional measures, exhibited poorer performance on such problems.26
|
Fairness requires that students understand what they are expected to do and what criteria will be used to judge their performance. |
HELPING STUDENTS UNDERSTANDAND MEET NEW EXPECTATIONS
The equity principle requires that students be prepared for more challenging assessments. Fairness requires that students understand what they are expected to do and what criteria will be used to judge their performance. As noted earlier assessment tasks and scoring criteria provide good targets to teach to and good models of the kinds of mathematical thinking expected of all students, especially to those who, in the past, have been held to a lower standard.
USING ASSESSMENT RESULTS TO SUPPORT OPPORTUNITY
Although it is important to consider how differences in opportunity can affect assessment results, it is equally important to be aware of how assessment results can affect students' opportunities to learn important mathematics. The equity principle implies that uses of assessment results be scrutinized for their impact on both students' opportunities to learn and schools' capacities to
provide instruction consonant with the vision of mathematics education.
RETHINKING ASSESSMENT USE FOR SORTING AND GROUPING
Assessment has always been looked to as much for how it could improve educational opportunity as for how it might be used to sort and select. For every Galton who looked for quantitative differences between groups, there has been a Binet who wanted to help children in need of special education and who resisted attempts to reify intelligence and rank children accordingly. When inadequate attention has been paid to the policy context into which testing programs are introduced, however, many negative, unintended consequences have followed. Binet could never have anticipated that his mental tests would be used to support an American hereditarian theory of intelligence and its tragic aftermath.27
More recently, states and school districts introduced minimum competency tests to ensure that each student who was graduated or promoted learned essential subjects. Some of the anticipated benefits of these policies are being realized. One clear benefit was that differences in the achievement of African American and white students began to decline,28 but there were unanticipated negative effects as well. When these programs were implemented along with sanctions for schools, many had punitive effects on low-achieving students and schools serving large numbers of those students. For example, in some cases, low-achieving students were retained in grade or identified for special education services and thus exempted from assessment. Low-performing schools had difficulty attracting and keeping good teachers with the threat of sanctions in force.29 Another negative outcome was minimum standards and expectations, which resulted in schools emphasizing basic skills at the expense of the kinds of higher-order skills that students need to function in a technologically advanced society.30
|
For assessments to help children and to promote better instruction rational policies must be developed for using assessment results. |
A growing consensus among policymakers, assessment developers, and educators is that if assessments continue to be used to sort learners rather than to promote learning and to punish schools and teachers rather than to support them, new assessments will have the same effects as the old ones.31 For assessments to help children rather than harm them and to promote better instruction
rather than to manipulate test scores, rational policies must be developed for using assessments. Policies that promote equity may challenge well-entrenched school practice and the educational philosophies upon which it rests. Clearly, teachers' evaluations play a strong role in grouping and tracking decisions, but the sorting would not take place without shared beliefs to sustain it. The practice of sorting rests on a general societal preoccupation with individual differences in ability, particularly in ability to learn and achieve in mathematics. Assessment also plays a role in perpetuating the practice. The scientific mystique that surrounds tests and testing procedures helps to convince teachers, parents, the public, and students themselves that this sorting is both rational and efficient.
|
Assessments should not be used to channel students into dead-end mathematics courses. |
Assessments should not be used to channel students into dead-end mathematics courses that will leave them ill prepared to meet the challenges of the twenty-first century. The lessons of Chapter I remedial programs make this point clearly. Chapter I of Title I of the Elementary and Secondary Education Act provides funds for programs to improve the achievement of low-income students who are functioning below grade level in mathematics and reading. Eligibility for Chapter I services is determined by scores on standardized achievement tests that do not target higher-order skills. Program effectiveness is judged by performance gains on those same tests. Although the basic skills gap separating Chapter I students from other students has declined in the past 15 years, critics have charged that "A continued focus on remediation denies the richness of learning to those who need more, not less, of what makes education engaging and exciting."32 In mathematics, many of the children who begin remediation in third grade never catch up to their peers. By ninth grade many are so far behind that they opt out of more challenging mathematics courses if given a choice. Others are programmed out of such courses by teachers and counselors who judge them poorly prepared for gateway subjects, such as algebra and geometry.
Many of the proposals for improving Chapter I programs focus on assessment, because Chapter I eligibility is based on students' performance on tests that reflect very low standards, and on students' relative standing. The tests typically used provide no information on how students measure up to standards of what they need to know to function in the adult world. Although proposals differ, most recommend the use of assessments consonant with the
ideas embedded in the content and learning principles. Most also recommend that assessment results not be used for individual placements that deny children access to powerful and engaging learning experiences.33
PROVIDING SAFEGUARDS FOR STUDENTS
The equity principle requires that opportunity to learn be considered whenever assessment results are reported or used. Obviously, students who have had opportunities to reflect on the mathematics they are learning, to present and defend their ideas, or to organize, execute, and report on a complex piece of work will have an advantage when called upon to do so in an assessment situation. There is a legal basis for this requirement as well. The courts have held, in several landmark cases, that schools are obligated to see that all students have a chance to learn content that is assessed for high-stakes purposes.
|
The courts have held that schools are obligated to provide all students a chance to learn content for high-stakes assessments. |
In Florida, for example, the state legislature imposed a testing program to guarantee that all students would graduate with the minimum skills needed to function in society. To be granted a high school diploma, students had to pass functional literacy examinations in reading, writing, and mathematics in addition to completing all required courses. Average test performance was poor across the board when the program began, but minority students failed the test at disproportionately high rates. This practice was successfully opposed in the case of Debra P. v. Turlington, where the court ruled that the state "may not constitutionally so deprive its students [of a high school diploma based upon test performance] unless it has submitted proof of the curricular validity of the test which the court defined as 'a fair test of that which was taught.'" The ruling in that case and several others that dealt with high-stakes use of tests for placement established two important guidelines for fairness in educational assessment. First, assessments used to allocate different instructional treatments must be demonstrably fair tests of what students have been taught. Second, schools must show that they have taken affirmative steps to remove the effects of any past discrimination that might influence the results of the assessments.34
These rulings have been construed to mean that when assessments are used to make high-stakes decisions on matters such as graduation and promotion, certain basic safeguards must be built
into the system for students. Social compacts, school delivery standards, and a variety of other mechanisms have been proposed to provide the needed safeguards. The National Council on Educational Standards and Testing recommended that schools be held to standards of instructional quality (termed school delivery standards) to ensure that students have a fair chance to develop the knowledge and skills targeted by the more challenging assessments now being proposed.35 The council was formed to advise the Congress, the Secretary of Education, and the National Education Goals Panel on the desirability and feasibility of instituting a national testing system. Other groups, while not endorsing a specific proposal for school delivery standards, have endorsed the notion that opportunity to learn must be taken into account in interpreting and making decisions based on assessment results.36
|
NSP Social Compact We pledge to do everything in our power to ensure all students a fair shot at reaching the new performance standards, and to prevent students' performance on the new assessments from being used as the basis for awarding a diploma or any other form of credential unless all students in the jurisdiction awarding the credential have had an opportunity to prepare themselves well. This means that they will be taught a curriculum that will prepare them for the assessments, their teachers will have the preparation to enable them to teach it well, and there will be an equitable distribution of the resources the students and their teachers need to succeed. |
The NSP requires the states and school districts working with them to enter into a social compact (see left) designed to address issues of fairness in accountability.37
Social compacts and school delivery standards are straightforward enough in conception. Both attempt to ensure that all students have a chance to learn the mathematics that is assessed. Neither proposal has found universal support among educators and policymakers, however. Challenges have been raised on technical grounds mainly related to the difficulty of developing and validating appropriate indicators and cutoff scores. Opposition has also been forthcoming on policy grounds: the burdens delivery standards might impose on states, unresolved consequences for schools that fail to satisfy standards, and unresolved questions about consequences for individual rights in high-stakes contexts when schools fail to meet delivery standards. Some of the strongest opposition to delivery standards, however, rests on the observation that remedies designed to improve schools in the past often failed precisely because the emphasis was placed on the resources schools should provide rather than the outcomes that schools should achieve.38 The equity principle requires that due consideration be given to the consequences of assessments for individual students.
PROVIDING SAFEGUARDS FOR SCHOOLS
The equity principle also requires some consideration of assessment consequences for schools. This implies, first of all, that fair comparisons can be made of what schools are accomplishing only when assessment data include information on the nature of the students served and the adequacy of resources. Second, the principle implies that assessment results must be compiled and reported in ways that support efforts to achieve greater equity among schools. Schools educating large numbers of poor and minority students have further to go and have fewer discretionary resources with which to pursue reform than do more affluent schools. Those schools that have more to do need greater resources.
Without equity in resources—not the same as numerical equality—there can be no equity in assessment or any other sphere of education.39 This does not absolve schools of their responsibility to educate students to the level of new standards. Rather, it obligates educational reformers and the general public to take quite strong measures to ensure that every school has the resources needed to educate its students well. Such efforts are under way in a number of states, as evidenced by recent litigation and legislative proposals in Alabama, Texas, and Massachusetts aimed at reducing disparities in the funding of poor and more affluent schools.40
|
Without equity in resources there can be no equity in assessment. |
HOLDING ALL STUDENTSTO HIGH EXPECTATIONS
Assessments can contribute to students' opportunities to learn important mathematics only if they reflect and are reinforced by high expectations for every student. Performance standards communicate expectations for achievement. They provide concrete examples and explicit definitions of what students must do to demonstrate that they have learned required content, process, and skills to a satisfactory level.41 If we want excellence from every student, performance standards must be set high enough so that, with effort and good instruction, every student will learn important mathematics. Some students may take longer than others to master the mathematics that they will need throughout their lives. Some may require different kinds of instructional support to meet performance standards, but there can be no equity in assessment as long as excellence is not demanded of every student.
Performance standards must be high enough to ensure that doing well on an assessment means that the student has learned enough of the right kinds of mathematics to function as an informed citizen. Meeting performance standards should mean that students have an adequate foundation on which to build, regardless of their eventual chosen career.
|
There can be no equity in assessment as long as excellence is not demanded of every student. |
We have much to learn about how to ensure that performance standards are uniformly high for everyone while also ensuring that students are adequately prepared to pursue their chosen field. We also have much to learn about how to maintain uniformly high performance standards while allowing for assessment approaches that are tailored to varied backgrounds. Consistent application of standards to a varied set of tasks and responses poses an enormous challenge that we do not yet know how to meet fairly and effectively. Nonetheless, the challenge is surely worth accepting.
To meet this challenge, equity must be viewed in the broadest terms possible. Equity considerations must be a part of every decision affecting the development, interpretation, and use of assessments. This view is expressed quite forcefully in a statement of equity principles adopted by a number of educational leaders, reproduced here on the following page.42
|
Leadership Statement of Nine Principles on Equity and Educational Testing and Assessment March 12, 1993 The following statement was developed by a group of educational leaders seeking to ensure that concerns for equity would be reflected in all efforts at assessment reform. Since the statement was articulated, it has been signed by educational policymakers, measurement scientists, educational researchers, school administrators, and experts on equity and diversity who represent a variety of perspectives and expertise. Although these leaders have not always agreed on the particulars of assessment reform, they have unanimously supported the need to address equity and excellence in tandem as assessment reform moves forward. As policymakers move forward to develop new standards and assessments, they should consider including the following principles, which will help to ensure that both equity and quality are dominant themes:
|


























