4
Enabling Science
Enabling science describes the fundamental work that makes possible the development of technological applications. This work includes synthesis, characterization, and theory.
POLYMER SYNTHESIS
Synthesis provides the underpinnings for all advances in the science and engineering of polymeric materials. The past decade has produced many notable synthetic advances: the extension of living polymerization methods to new classes of reactive intermediates and new classes of monomers, the appearance of hyperbranched polymers, the controlled preparation of inorganic polymers and organic-inorganic hybrids, the development of efficient biological polymerization strategies, and many others.
This section considers the objectives of synthetic polymer chemistry, both fundamental and practical. The most important issues examined below include:
-
Control of chain architecture,
-
Synthesis of polymers of controlled end-group structure,
-
Design and synthesis of polymers with outstanding thermal stability or useful electronic properties,
-
Modification of polymer surfaces,
-
Development of new polymerization methods,
-
Challenges in reactive processing, and
-
Interplay of organic, inorganic, and biological chemistry in producing novel macromolecular materials.
Some of the key synthetic advances of the last 10 years are noted, and unsolved problems and important research directions are identified.
Control of Chain Architecture
Topology
Chain topology controls many critical properties (e.g., crystallization, solubility, and rheological behavior) of polymeric systems. The development of linear polyethylene via the Ziegler and Phillips processes in the 1950s provides the most important example, wherein "straightening of the chain" resulted in a rise in Tm of ~30°C and significant improvements in strength and toughness. Control of topology in this case led directly to a new class of materials now sold in quantities of millions of tons per year.
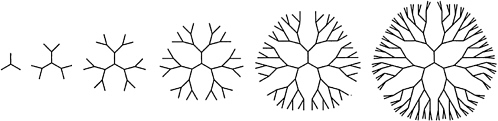
Current synthetic methodology affords a high level of control of chain structure, and syntheses of linear and branched chains, stars, rings, and combs have been achieved. A striking recent advance has been the preparation of hyperbranched—or dendritic—macromolecules, in which iterative branching steps lead to structures in which segment density grows rapidly as one proceeds radially from the molecular "core" (Figure 4.1). Dendritic polymers of narrow molecular weight distribution have been prepared by laborious stepwise synthesis, while "one-pot" methods have been developed for polydisperse samples. In some instances, remarkable improvements in solubility (in comparison with linear analogues) have been reported for hyperbranched chains, and there has been plausible speculation that dendritic polymers may have useful sequestration and reactivity properties. Commercial applications for these materials have not emerged as of this writing.
Polymeric rotaxanes, in which the chain backbone is threaded through a series of macrocycles, have also been reported recently. In this arrangement, the macrocyclic "rotors" are not covalently attached to the "axle" but instead are constrained by bulky end groups from topological dethreading. It has been suggested that controlled, reversible switching of rotor positions on the axle might provide a basis for functional molecular devices (Figure 4.2).
Even given these advances, there is no shortage of intriguing and important topological issues yet to be addressed, and it appears likely that attention will shift to molecules of even greater complexity. Preliminary reports of two-dimensional ribbonlike polymers have appeared, as have descriptions of synthetic DNAs with the topological character of a cube. Particularly intriguing is the prospect of exploiting both covalent and non-covalent interactions, to provide control not only of topology, but also of the molecular geometry over large length scales in real space.
FIGURE 4.2 A polymeric rotaxane with an aromatic polyamide "axle" and macrocyclic polyether "rotors." SOURCE: Reprinted with permission from Gibson et al. (1992). Copyright© 1992 by the American Chemical Society.
Length
Many desirable properties of polymers, such as mechanical strength, thermal behavior, processibility, diffusion, miscibility, and adsorption at interfaces, are dependent to a large extent on the molecular weight. Hence, synthetic polymer chemists have directed attention to development of methods appropriate for molecular weight control. Great strides have been made, especially in the area of living polymerizations. Over the past decade, besides improvement in living anionic techniques, several new methods have been devised and/or improved. Notable among these are group transfer polymerization (GTP) for polymerization of (meth)acrylates (Figure 4.3), ring-opening metathesis polymerization for cyclic hydrocarbons (ROMP), Lewis base-mediated cationic polymerization for vinyl ethers, and immortal (metalloporphyrin-catalyzed) polymerization for heterocyclic monomers. All of these methods are capable of controlling not only the average chain length but also the molecular weight distribution.
However, chain length control is still statistical. One can argue that one of the current major challenges facing the polymer chemist is the preparation of polymers of absolutely uniform chain length for a wide range of polymers. There are indications that this may be met through the use of genetic techniques and solid-phase synthesis. How properties will be affected and which properties will be influenced by the truly monodisperse materials are two questions to be explored. Another challenge is in condensation polymerization, where chain length control is not precise. The use of the cyclic oligomer method recently developed shows promise, but there is a need for further studies. A thorough mechanistic
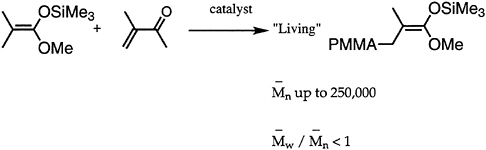
FIGURE 4.3 Group transfer polymerization (GTP).
study to delineate the factors affecting chain termination and chain transfer, events that adversely affect chain length control, is also needed if one is to solve completely the problem of molecular weight control.
Sequence
Control of monomer unit sequence in copolymers is the most difficult of the fundamental problems facing polymer synthesis. Whereas nature prepares macromolecules of precisely defined length and sequence, synthetic polymers are mixtures of chains characterized by substantial heterogeneity. As described in the preceding section, considerable progress has been made in the development of polymers with narrow distributions of chain length. By comparison, the control of sequence that can be exercised is primitive and is limited essentially to the preparation of statistical, alternating, and block copolymers.
Three approaches to the synthesis of copolymers of controlled sequence are available, but all suffer from significant limitations. Solid-phase methods, developed in the 1960s for peptide synthesis, remain slow and costly. Genetic engineering techniques are more rapid and efficient, but are for the foreseeable future restricted to the preparation of polypeptides. The third method, now in its infancy, consists of the controlled, portionwise addition of monomers to living chain ends. While this method is unlikely ever to lead to precise control of sequence at the monomer level, the preparation of complex architectures comprising many short monomer blocks appears to be feasible. One might expect such controlled-sequence copolymers to exhibit unique and interesting behavior in self-assembly, at interfaces, or in optical or electronic applications.
Isomerism
The geometrical, stereochemical, and regioisomeric structures of the constituent chains have major influences on the transition behavior, morphology,
thermal stability, and so on, of polymeric materials. Geometrical isomers can be most easily illustrated by pointing out the possible microstructures available in polydienes, such as polyisoprene and polybutadiene. Microstructures of polybutadiene are shown in Figure 4.4.
Polybutadiene can exist in the cis or trans arrangements or in vinyl or 1,2-structures. Furthermore, the 1,2-microstructure can exist in highly isotactic or syndiotactic configurations or in a mixture of the two, which one describes normally as atactic. The importance of these various isomers varies widely. The cis structure has a remarkably low glass transition temperature and is widely used in tires and other important elastomeric applications. By contrast, the trans structure is highly crystalline and currently has no important applications, even though various biomedical uses (e.g., casts) have been proposed in the past. Both highly isotactic and syndiotactic semicrystalline 1,2-polybutadiene materials have been prepared by coordination catalysis; however, at this time neither has found significant application. Atactic 1,2-polybutadiene is accessible by anionic polymerization and has been considered as a potential hydrophobic, moderate-cost starting material for low dielectric thermosetting networks. However, significant applications of this material have not been developed.
The current state of the art in these areas utilizes principally free radical, anionic, and coordination catalysis. Free radical polymerization of butadiene in emulsion is practiced and produces a mixed cis-trans structure with about 20 percent of the 1,2-microstructure. The ratio of cis to trans units is polymerization temperature dependent. Current practices produce approximately 50 to 60 percent trans, ~20 percent 1,2-microstructure, and the remainder cis 1,4-microstructure. Anionic polymerization in hydrocarbon solvents is industrially important and produces 90 percent 1,4-microstructure with short sequences of cis and trans arrangements predominating. About 10 percent of the chains are atactic 1,2-units. This material is used in a variety of applications and displays a glass transition temperature of about -90°C. Coordination catalysis can generate rather high isomeric purity in all of these systems.
Regioisomerism can include variations on the usual head-to-tail enchainment that is observed in most chain polymerization of vinyl monomers. In general, both electronic and steric driving forces produce largely head-to-tail enchainment. However, it is well known that small amounts of the abnormal head-to-head and tail-to-tail structures are found in a variety of materials, including poly(vinylidene fluoride), poly(vinyl chloride), and to some extent, poly(vinyl acetate). Minor imperfections of this type can influence critical performance or processing parameters, such as piezoelectricity or thermal stability in the melt. This has been a problem in poly(vinylidene fluoride), where variation in polymerization conditions can result in a proportion of head-to-head structures as high as 20 to 30 percent. These structures are inevitably less thermally stable and, in general, are undesirable. Exceptions certainly are possible, particularly where controlled instability is desired, as in some resist materials.
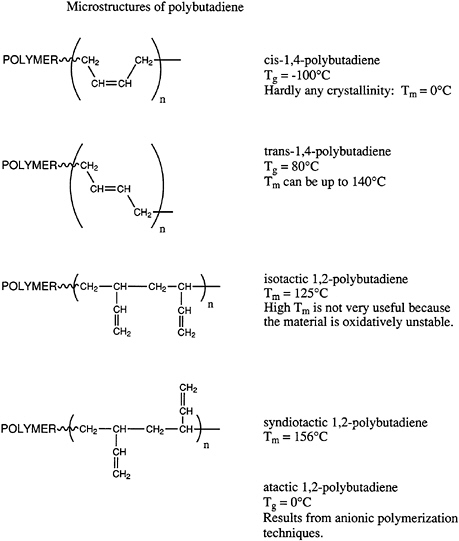
FIGURE 4.4 Microstructures of polybutadiene.
The tacticity of vinyl polymers is critical to the control of the crystallinity and thermal transition behavior of these materials. Free radical polymerization produces mostly atactic structures, with the temperature being one important parameter, which can modestly control placement. In general, ionic polymerization, and especially coordination catalysis, is required to produce either highly isotactic or highly syndiotactic materials. A limited number of possibilities exist with anionic polymerization, for example, with certain methacrylates and with cationic polymerization in, for example, vinyl alkyl ethers. Recent advances in this area concern the preparation of syndiotactic polystyrene with titanium-aluminum
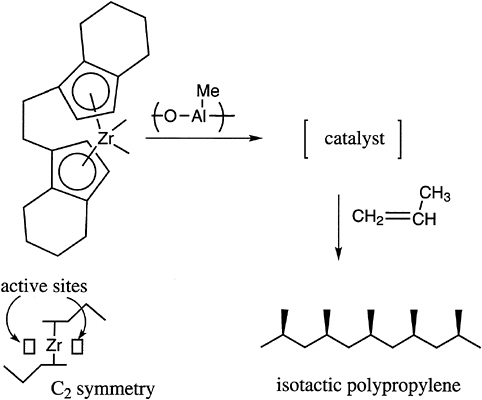
FIGURE 4.5 Chiral complex for the control of tacticity of polypropylene.
catalysts and the production of stereoblock polypropylenes with soluble metallocene catalysts (Figure 4.5).
Control of macromolecular asymmetry has also been achieved within the last decade, such that optically active materials can now be prepared on the basis of a controlled helix sense, that is, a predominance of left-or right-handed helices in the solid polymer. Such materials have found application as media for chromatographic resolution of enantiomers.
Advances in catalysis that could produce better understanding of polymerization mechanisms are needed to further refine the microstructure and to produce improved materials.
Synthesis of Polymers of Controlled End-Group Structure
An increasingly important class of polymers are telechelic polymers, which contain reactive end groups that can be used to further increase the molecular weight of a polymer during processing or to generate block copolymers. Perhaps the most widely used materials of this type are the polyols or polyglycols.
These nominally difunctional materials are used in a wide variety of applications in which they are reacted with isocyanates to prepare segmented polyurethanes and polyureas (Figure 4.6). Polyols can be prepared by either ring-opening or step-growth polymerization. In the latter case, the end-group functionality will be defined by the component that is present in molar excess, and the molecular
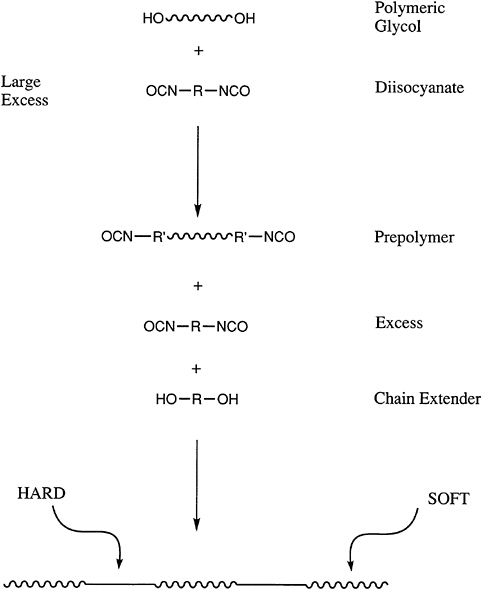
FIGURE 4.6 Reactive end groups in the synthesis of segmented polyurethanes.
weight can be controlled by the stoichiometry. Thus, the same chemistry that allows end-group control also can produce other, more sophisticated block or segmented copolymers. The success of the polyglycols, such as polypropylene glycol and polytetramethylene glycol and their copolymers, demonstrates the value of this approach. For example, urethane foams for automobile seats are generated from the polypropylene glycols. Thermoplastic polyurethanes, which are important in a variety of applications, are synthesized from the polyether systems, as well as polyester polyols.
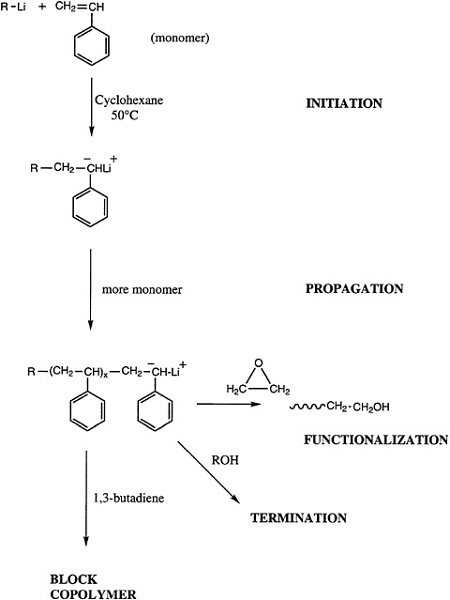
Telechelic polymers can also be produced by living polymerization, and either a functionalized initiator or a terminator can be used to introduce the reactive groups of interest (Figure 4.7). Alternatively, a difunctional initiator can be used, and the reactive ends can be functionalized. Both approaches have been demonstrated for anionic and group transfer polymerization, and an analogous technology for cationic polymerizations is beginning to emerge.
In cases in which the reaction is not living and cannot be controlled to be living, chain transfer with a functionalized agent is the only solution for the preparation of telechelic polymers. Some success has been realized using this technique for radical polymerizations, and recent advances have been made in the preparation of telechelic polymers using difunctional acyclic olefins as chain transfer agents in ring-opening metathesis polymerization. This system is particularly suited to this approach owing to the near identity of the reactivity of the acyclic chain transfer agent and the cyclic olefin monomer.
In spite of this progress, telechelic polymers synthesized by chain processes remain difficult to prepare on a large scale and with a high degree of end-group functionality. New techniques and methods are essential to prepare such materials. For example, there are no straightforward routes for the preparation of telechelic polyethylene and polypropylene.
Major advances will come from the development of new techniques to control the molecular weight and molecular weight distribution of step growth polymers and the synthesis of chain growth polymers that have precise end-group structures.
Design and Synthesis of Thermally Stable Polymers
Thermal stability has been defined as the capacity of a material to retain useful properties for a required period of time under well-defined environmental conditions. Many factors contribute to heat resistance, including primary bond strength, secondary bonding forces (hydrogen bonding, dipolar interactions), and resonance stabilization (in aromatic structures). The mechanism of bond cleavage (particularly with respect to whether the broken chains can be combined or further unzipped) must also be considered. For example, α–methyl-substituted macromolecular materials often will regenerate sizable amounts of monomer, whereas highly aromatic condensation polymers and even vinyl polymers with
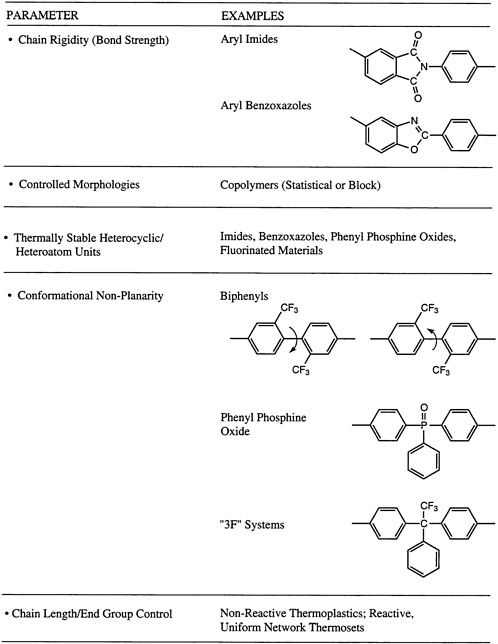
tertiary hydrogens will often prefer to recombine. Of course, molecular weight and molecular weight distribution can play a role, along with molecular symmetry. This latter parameter influences whether or not ordered morphologies, such as a semicrystalline structure, can be generated. The possibility of cross-linking, either randomly or via a terminal unit, to produce networks may be significant, along with the overall ''purity" of the system. This last point includes the retention of catalyst fragments utilized for the polymerization. Concepts used in the molecular design of processible macromolecular materials with exceptional thermo-oxidative stability are summarized in Figure 4.8, where a number of the parameters described above are illustrated in the context of two of the major thermo-oxidatively stable materials systems, the poly(aryl imides) and the poly(aryl benzoxazoles).
Synthesis of Conjugated Polymers
Conjugated polymers show considerable promise in electrical and optical applications. However, the synthesis and use of these materials have presented a variety of formidable problems. In general, these materials by their very nature are difficult to process. The parent systems are rigid and flat and exhibit very strong interchain interactions. Consequently, they are insoluble and difficult to fabricate. Two major approaches have been used to allow these materials to be fabricated: (1) the development of precursors and (2) the use of solubilizing side groups.
Precursor routes to conjugated polymers can be as simple as the deprotonation of a heterocyclic polymer or as complex as a major carbon skeleton rearrangement. The fabrication of polyaniline is an example of the former, and the conversion of polybenzvalene to polyacetylene is an example of a major carbon backbone rearrangement.
Major advances have been made in solubilizing conjugated polymers by attaching side chains. For example, polythiophene is insoluble, whereas poly(nhexylthiophene) is processible by spin casting and by the use of other solvent-based fabrication techniques. A similar approach has been used to solubilize poly(paraphenylene)s and poly(phenylene vinylene)s (PPVs; Figure 4.9).
Problems are associated with each approach. The precursor approach requires that chemistry be performed on the polymer. In many cases, this leaves defects and voids. The substituent approach results in defects in the polymer chains and diminishes interchain interactions that are important to some desired properties. Given the real and potential advances in the use of conjugated polymers in device applications, a vigorous synthetic attack on such problems is badly needed.
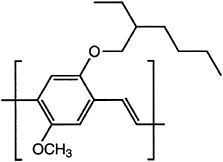
FIGURE 4.9 Poly(2-methoxy-5-(2-ethylhexyloxy)-1,4-phenylene vinylene), a soluble form of poly(phenylene vinylene).
Modification of Polymer Surfaces
Chemical surface modification of solid organic polymers is generally carried out to change chemical or physical surface properties of preformed objects (e.g., film, fibers, and bottles) when alteration of the polymer bulk properties is not desired. This type of modification alters only a small fraction of the sample material (typically the outermost 10 Å to 1 mm). This is in contrast to solid polymer modification reactions such as vulcanization of diene elastomers to prepare cross-linked rubbers or sulfonation of cross-linked polystyrene beads to prepare ion exchange resins, in which the modifications occur throughout the sample. Surface modifications proceed "on" polymers (normally at the solid-solution interface) as opposed to "in" polymers.
Surface modification of polymers is a topic of considerable current interest and will continue to advance technology and various research fields in the future. As a field, chemistry at polymer surfaces is becoming scientifically interwoven with the research fields and technologies of chemical, biological, and physical sensors, protective layers, adhesion, membranes, electrodes, information storage, and optical devices and will, in the future, have an impact in these areas.
The classical methods for surface modification (i.e., plasma modification, surface graft polymerization, and chemical reaction) are crude and were developed to treat high-volume (high-surface-area) commercial polymers. Plasma modification techniques are widespread and versatile. Although surface chemistry can be changed to effect the desired properties, the method is brutal, and cascades of reactions involving homolytic bond scission, fragmentation, and cross-linking occur. Little control is possible. Surface graft polymerization is also common, but the polymer-polymer interface structure and graft density and location have generally not been controllable. The classical chemical methods are likewise crude. Oxidations of hydrocarbon polymers, reductions of fluoropolymers,
halogenations, dehydrohalogenations, and hydrolyses are important modification reactions but are most often corrosive and not controllable.
The difficulties of performing specific organic chemistry at the solution-solid interface have become appreciated over the past 10 years, and strategies to perform organic chemistry in a controlled fashion in this milieu have been developed. The structure of the solution-solid interface in a modification reaction is extremely system dependent, and a large variety of situations can be envisioned. The mobility of polymer chains in contact with the solution depends on the polymer morphology (degree of crystallinity) and structure (glass transition temperatures span 400°C for common polymers) as well as the solution—to what extent it wets or swells the solid. There is no generic picture of a solid polymer-solution interface. The fact that the interface structure changes upon reaction further complicates the possibilities. Surface modifications have been reported that are either "autoinhibitive" or corrosive. In the former type of modification the solution interacts with the product surface to a lesser extent than it does with the starting polymer, and the reaction stops when a thick layer of modified material forms and acts as a barrier to further reaction. In the latter type of modification the solution interacts more strongly with the product surface than it does with the starting polymer, and the reaction proceeds to a greater depth, or the product dissolves as it forms. This "interfacial free energy" component of surface modification reactions that controls the three-dimensional structure of the product has no counterpart in solution chemistry. Other unique considerations are the two-dimensional uniformity of reaction products and the uniformity of reaction as a function of depth into the solid.
The surface functionalization of unreactive polymers has advanced significantly in recent years. Fluoropolymers have been modified to incorporate discrete reactive functional groups (e.g., alcohols, amines, and carboxylic acids) into the outer few tens of angstroms of the solid samples. Polyethylene and polypropylene have been modified by selective oxidation, sulfonation, hydrogen abstraction/radical addition reactions, and "entrapment functionalization," in which functional groups are introduced to the surface by blending low-molecular-weight functionalized oligomers with the "host" polymer. The functional group chemistry of these modified polymers has been studied, and the control of surface properties, particularly wettability, with functional group manipulation has been assessed.
Reactive polymers that have been functionalized and the products well-characterized include poly(ether ether ketone) (the carbonyl chemistry was developed), polyimide (hydrolysis renders carboxylic acids), poly(phenylene terephthalamide) (metalation of the amide and subsequent alkylation), and polysulfone (metalation and carbonylation).
That the surface-modified materials are kinetic and not thermodynamic products is now recognized, and the thermal reconstructions of several functionalized polyolefin and fluoropolymer surfaces have been reported. The reconstructions
typically involve movement of polar functional groups from the surface to greater depths and are driven by a decrease in surface energy. The functional groups do not migrate far and in some cases can be forced to return to the surface by contact with a polar medium. This mobility can effect desired surface properties and likely plays an important role in further chemistry of these surfaces.
Certainly significant advances have been made in this field in the past decade, but with respect to the highly evolved disciplines of organic polymer synthesis and synthetic organic chemistry, the field is in its infancy in terms of elegance and versatility. Few modified polymer surface systems have been studied with any degree of detail, and there is not currently a model system that can be used for comparisons. Key questions concern the applicability of the tenets of solution organic chemistry to surfaces, the utility of functionalized surfaces, correlations between surface structure and properties, and the new types of materials that can be prepared with surface synthetic techniques.
Biocatalysis in Polymer Synthesis
Organisms carry out an astonishing array of complex chemical transformations via coupled enzymatic reactions. The fact that enzymes operate selectively and under mild conditions of temperature, pressure, and solvent has generated justifiable interest in the use of enzymes in polymer synthesis. Work to date has addressed three issues: (1) in vitro use of isolated enzymes to catalyze polycondensations, (2) use of organisms (either wild type or genetically altered) to produce monomers that are subsequently converted to polymers by conventional methods, and (3) use of organisms to produce polymers directly.
The in vitro use of enzymes to catalyze polycondensations has been shown to offer several advantages. Enantioselective polymerizations have been reported, and polymerizations of monomers containing reactive functional groups (e.g., epoxy diesters) have been accomplished without destruction of the reactive functionality. Limitations of the method arise in part from the fact that many of the polymerizations of interest are best run in solvents for which the enzyme is poorly suited (i.e., in nonaqueous systems). As a result of this—and perhaps other—factors, molecular weights of the polymers prepared in this way are modest—generally Mn < 15,000. Recent developments in nonaqueous enzymology, including the use of protein engineering to improve enzymatic activity in organic solvents, offer promise for a solution to this problem.
Several intriguing reports have discussed the use of microorganisms to produce polymer intermediates. For example, 4,4'-dihydroxybiphenyl, an intermediate in the manufacture of engineering thermoplastics, has been produced in yields of greater than 95 percent in a one-step fermentation process. Microbial syntheses of long-chain dicarboxylic acids (useful in the production of polyamides and polyesters), and of 5,6-dihydroxy-1,3-cyclohexadiene (an intermediate in the preparation of polyparaphenylene) have also been reported. The opportunities
for further development of this approach appear to be significant. Environmental considerations here are complex but will almost surely play a key role in defining the impact of biocatalysis in this area.
The direct production of polymers in bacteria and in higher plants is also under active investigation. Commercial development of biodegradable materials based on plant-derived polysaccharides has begun, and fermentation is being used to produce biodegradable polyesters for packaging applications. Recent reports of production of similar materials in higher plants suggest that agricultural routes to these polymers may ultimately prove viable.
A recent development has been the use of genetic engineering to produce polymeric materials. In some cases, this has taken the form of cloning and expression of the genes for natural structural proteins (e.g., spider silk); in others, amino acid copolymers have been designed de novo, encoded into artificial genes, and produced in bacterial hosts via fermentation. This approach offers significant advantages, in that it leads to uniform chain populations of controlled chain length, sequence, and stereochemistry, all the important structural components in polymer synthesis. In addition, the factors that control the secondary structure of proteins can be used to impose three-dimensional structure on the synthetic polymers made by this technique. This approach offers unique possibilities for tailoring the structure of synthetic polymers. The preparation of polymers with useful biological properties is particularly straightforward by this method, and there are promising indications that the scope of the method will be extended beyond the 20 naturally occurring amino acids. This area of research is an excellent point for the interface of the areas of biochemistry and traditional polymer chemistry.
Development of New Polymerization Methods
Even given the synthetic advances described in the preceding sections, there remains an urgent need for the development of new synthetic routes to polymeric materials. To illustrate, one need only consider the striking contrast between the synthetic methods used in the laboratory and in industry on the one hand and in nature on the other. In each case, the process begins with simple feedstocks, that is, with simple carbon compounds derived either from petroleum or from biomass. In industry, such compounds are isolated and then subjected to a series of separate chemical transformations leading to the monomer structure of interest. After rigorous purification to "polymerization grade" material, the monomer is converted in still another step, often at high temperature and pressure, to the polymer. Nature works differently. From mixed feedstocks, nature converts simple carbon compounds to complex polymers directly, without isolation of intermediates and without the assistance of harsh reaction conditions. Until industrial polymer chemistry works with the same degree of process integration and efficiency, there will be room for advances in synthetic methodology.
This analogy also serves to highlight the special value of synthetic methods that can make direct use of simple, inexpensive feedstocks for the synthesis of new polymers. An example of such an advance is the development of palladium-catalyzed copolymerizations of ethylene and carbon monoxide. As low-cost monomers, ethylene and carbon monoxide are difficult to beat. Early developments using radical polymerization techniques resulted in copolymers that were highly branched, with random monomer enchainment. Subsequent research demonstrated that palladium catalysts could be used to produce linear copolymers. These materials contained multiple ethylene insertion segments that resulted in a lack of photostability. Recent developments, derived from a better understanding of the basic chemistry of the catalysts, have resulted in a copolymer of ethylene and carbon monoxide that is perfectly alternating. The regular structure provides a crystalline material with excellent mechanical properties and enhanced photostability. To facilitate processing, the commercial product is a terpolymer of ethylene, carbon monoxide, and a few percent of propylene. This material is projected to capture some of the market that has been held by traditional polymers. The processes used to manufacture this polymer consume 1 gram (g) of palladium for every 106 g of polymer, resulting in a catalyst cost of $0.50 per ton. The commercial catalyst produces 3 × 104 g of polymer per gram of palladium per hour. A second example is provided by palladium-catalyzed carboalkoxylation and amidation reactions, which have been used to convert aryl halides to aromatic polymers in a single step, starting from carbon monoxide and the appropriate bisphenols or aryl diamines, respectively. New developments in catalysis and in organometallic chemistry will be critical to such discoveries and should be accorded high priority in exploratory research programs in polymer synthesis.
Exploring the Periodic Table: Inorganic Polymers
Although most current polymeric materials are based on the chemistry of carbon, the remainder of the periodic table is accessible through the synthesis of inorganic polymers and networks or hybrid organic-inorganic systems often composed of interpenetrating organic and inorganic polymers. Because the compositional and structural diversity of such nontraditional polymers is immense, only a few examples of synthesis strategies and challenges are presented here.
Inorganic and Organometallic Polymers
Inorganic and organometallic oligomers and polymers are macromolecules in which a metal or metalloid is part of the main-chain backbone or pendant to it. Familiar examples are those involving main-group elements: polyphosphazenes [–RR'P=N–]x, polysiloxanes (silicones) [–RR'SiO–]x, and polysilanes (polysilylenes) [–RR'Si–]x (Figure 4.10).
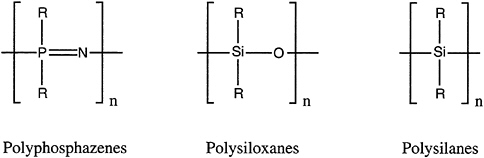
FIGURE 4.10 Three important classes of inorganic polymers; from left, the polyphosphazenes, the polysiloxanes, and the polysilanes.
The polyphosphazenes comprise a large and versatile class of inorganic macromolecules. Perhaps the most important feature of polyphosphazene chemistry is the method of synthesis that allows the R and R' groups to be varied over a very wide range: organic, organometallic, or inorganic units, imparting diverse properties to the resulting polymers. In the macromolecular substitution method, hexachlorocyclotriphosphazene is heated to induce polymerization. Solutions of poly(dichlorophosphazene) in organic solvent are then reacted with nucleophiles such as alkali metal alkoxides, amines, or organometallics such as Grignard reagents to yield the derivative polymers plus the chlorides as by-products. Inherent to this synthesis procedure is the possibility that two or more different pendant groups can be introduced either simultaneously or sequentially. Organic or organometallic side groups can also be introduced at the cyclic trimer level, followed by ring-opening polymerization of the cyclic polymer to the high polymer. Because the substitutive method does not allow sufficient control over the stereoregularity of mixed-substituent polymers, microcrystallinity of polyphosphazenes occurs only when one type of side group is present.
Polysilanes and, analogously, polygermanes are usually made by dehalogenation of diorganodichlorosilanes with sodium metal in an inert diluent. Because cyclic oligomers are the exclusive products at equilibrium, high polymers are formed only when the reaction is kinetically controlled. At present, the reaction mechanisms are not well understood but probably involve the ion pair [RR'SiCl]- Na+, which in the rate-determining step reacts with dichlorosilane, adding one silicon unit and producing a chlorine-ended chain. Under ultrasound irradiation, at low temperature, high molecular weights and monomodal molecular weight distributions are obtained. Alternatively, dehydrogenation could be brought about catalytically by transition metals. Once formed, polysilanes may be chemically modified, or protected functional groups resistant to sodium metal may be used in the standard synthesis to introduce further compositional and structural diversity. A few copolymers have been synthesized. Silylene-olefin block copolymers can be made by the addition of styrene to anionically terminated
polysilanes, followed by anionic polymerization of the olefin. Random polysilane-polygermane copolymers have been synthesized simply by co-condensation of dichlorosilanes and dichlorogermanes with elimination of sodium chloride.
The familiar polysiloxanes were first synthesized by hydrolysis of dichlorosilanes R2SiCl2, but this process has been largely replaced by ring-opening polymerization of cyclic oligomers, such as hexamethylcyclotrisiloxane, most often using anionic initiators. Initiation and propagation involve nucleophilic attack on the monomer, opening the ring, followed by chain extension. Polymerization of nonsymmetrical cyclic siloxanes gives polymers [–SiRR'O–] that are analogous to vinyl polymers. In principle, it should be possible to prepare them in stereoregular forms (isotactic and syndiotactic). This has not yet been accomplished.
There are of course many examples of less common inorganic polymers. Polymeric sulfur and selenium are synthesized by free radical polymerization of cyclic molecules. Stannoxane polymers with [–Sn–O–R'–] backbones are prepared by interfacial polymerization between diorganotin dihalides and difunctional organic molecules, while novel "drum" and "ladder" tin polymers are synthesized by the reaction of stannoic acid with a carboxylic acid. Addition or condensation polymerization can be used to prepare metal coordination polymers in which coordination occurs between an organic group in the polymer and a metal atom.
Network-forming Inorganic Polymers
Network-forming polymers incorporate branch points in the polymer backbone or on pendant groups. So-called "sol-gel" processing utilizing simple salts or metal organic precursors such as alkoxides [M(OR) n] has made much of the periodic table accessible to the synthetic inorganic chemist, although the distinction between polymer and ceramic now has become blurred. Sol-gel synthesis involves nucleophilic substitution reactions often represented as
where X can be H (hydrolysis), M (condensation), or L (complexation). The chemical reactivity of a metal alkoxide toward hydrolysis and condensation increases with the positive charge of the metal and its ability to increase its coordination number. In general, the reactivity increases when going down a column of the periodic table (Ti < Zr < Ce). Because the preferred coordination numbers of most metals are much greater than two, the formation of polymeric networks (rather than precipitates) often requires complexation of the metal with slowly hydrolyzing multidentate ligands such as carboxylic acids, β-diketones, or alcohol amines to reduce the effective functionality. Polymer size and structure
are controlled by the L/M and H2O/M ratios. Heterometallic alkoxides or oxoalkoxides are useful precursors to multicomponent polymers analogous to random copolymers and block copolymers. Recently, attempts have been made to synthesize well-defined oligomeric oxoalkoxides such as Ti16O16(OEt)32 for use as "molecular building blocks" to assemble networks with intermediate range order.
Hybrid Organic-Inorganic Polymers and Networks
Structural features of traditional organic polymers are married with those of nontraditional inorganic polymers in hybrid materials. Polycarbosilanes [–SiRR'–CH2–], polysilazanes [–SiRR'–NR"–], and polyborazines [–BR–NR'–], precursors to silicon carbide, silicon nitride, and boron nitride, also fall in this category. A common synthetic route to the formation of hybrid materials is the hydrolysis of organoalkoxysilanes R'xSi(OR)4x in a sol-gel process. If R' is a nonreactive group such as an alkyl, it will serve to modify the inorganic network. If R' is itself polymerizable (e.g., epoxy or vinyl), interpenetrating organic and inorganic networks can form. Depending on the choice of catalyst and the uniformity of the hydrolysis process, the reaction can be designed so that the organic and inorganic networks form simultaneously or sequentially. Other interesting hybrid materials result from the dispersion of an inorganic phase within an organic matrix or vice versa. For example, the swelling of polydimethylsiloxane with tetraethoxysilane followed by in situ hydrolysis yields a silicon-dioxide-filled composite. The addition of appropriate organic molecules or enzymes to sol-gel matrices results in optically active or bioactive materials.
Opportunities and Challenges
With most of the elements of the periodic table available, the opportunities for chemists to synthesize new inorganic polymers and networks with unique properties are clearly unlimited. However, the greater chemical and structural diversity represented by this class of materials compared to traditional organic polymers provides daunting synthetic challenges. In general, the ability to tailor chain (or network) architecture (e.g., topology, sequence, molecular weight, and stereochemistry) has not been widely demonstrated, especially for heterometallic systems. Future directions of research should focus not only on new materials but also on strategies to control the architectures of existing polymers and networks. Along these lines, some chemists are looking to nature, where there exist numerous examples of low-temperature routes to high-strength, high-toughness inorganic materials such as abalone shells and novel magnetic and nonlinear optical materials and processes such as magnetotactic growth of Fe3O4 in bacteria and cadmium sulfide particles formed by yeast. Biological systems rely on the organic matrix to control morphology and crystal nucleation sites, on interactive
proteins to modulate crystal growth, and on ion transport systems (ion pumps) to provide localized supersaturated solutions. Other strategies that might provide more control over polymerization include nonhydrolytic processes, small molecule elimination reactions, polymerization within micelles and vesicles, and sonochemical syntheses.
Reactive Processing
The production of new materials depends not only on successful molecular design and construction, but also on effective control of processing steps. In many applications, coupled synthesis and processing schemes provide advantages.
Reaction injection molding (RIM) provides an example. RIM processes were introduced in the late 1960s and early 1970s and are widely used in the manufacture of polyurethane elastomers and foams. On a smaller scale, polyesters, epoxy resins, nylons, and dicyclopentadiene materials are produced in this way. The RIM technique involves rapid impingement of reactive monomers prior to injection into a mold where polymerization takes place, and the high rate of reaction between aromatic isocyanates and alcohols has made this chemistry particularly suitable for RIM technology. The challenge to the synthetic chemist is to develop new chemistries that occur at adequate rates in the absence of solvent and that are tolerant of the phase changes and temperature excursions that characterize the RIM process.
Reactive processing is also used to prepare a variety of toughened polymer blends. These processes use maleic anhydride-modified polyolefins or oxidized poly(phenylene oxide)s as reactive targets for covalent linkage with nylons. As in RIM, the chemistry must occur on the time scale of the processing step, and interesting challenges are posed by the interplay of chemical and physical factors (e.g., phase boundaries and thermal transitions) in determining the course of reaction and the properties of the product. New chemistries, both for preparation of reactive precursor polymers and for the interpolymer coupling step, are needed.
Supramolecular Chemistry
Polymer science and engineering have traditionally been concerned with the preparation and properties of chain molecules constructed via the formation of covalent bonds. Most often, such preparations involve reactions of organic monomers in isotropic phases such as solutions, suspensions, or emulsions. Over the last decade, there has emerged a broader appreciation of the role of non-covalent interactions in the synthesis of polymeric materials, and polymerizations in monolayers, bilayers, crystals, and liquid crystals have become a popular area of investigation. This work has been motivated by interest in (1) preorganization of the monomer as a strategy for controlling polymer structure and (2) use of polymerization to stabilize, or to alter the properties of, anisotropic phases.
Substantial successes have been achieved in these areas, but many aspects of polymerization in organized media remain poorly understood. It has been suggested that confinement of functional groups to a lattice or in two-dimensional arrays may either enhance or reduce reactivity, but the evidence for such effects is, with few exceptions, anecdotal. As materials science seeks control of structure and properties on shorter and shorter length scales, polymerization in anisotropic phases is sure to take on increasing importance.
A related area of investigation concerns polymeric structures held together by non-covalent forces, for example, by hydrogen bonds. Although they are significantly weaker than covalent bonds, hydrogen bonds exhibit directional character and are therefore useful in controlling both the size and the shape of molecular aggregates of dimensions comparable to those of polymer chains. Penetrating studies of molecular recognition processes in organic chemistry are providing new strategies for the assembly of large-scale structures, and it is clear that a broad view of polymer synthesis, a view that embraces both covalent and non-covalent bond-forming steps, should be encouraged.
Conclusions
-
The last decade has witnessed advances in the control of macromolecular architecture. Nevertheless, important challenges remain, particularly with respect to the control of chain sequence. New synthetic approaches to controlled architecture, including the use of biological methods, should be vigorously pursued.
-
Polymer synthesis, both on the laboratory scale and in manufacturing, is still largely a series of stepwise conversions, from feedstocks, to monomers, to polymers, to products. The development of more highly coupled, integrated syntheses, in which advanced materials are derived efficiently from simple feed-stocks, will depend in large part on research on new catalysts and new catalytic reactions.
-
The demands of new technologies will continue to place a premium on the synthesis of high-performance polymers, that is, on polymers of unprecedented thermal or mechanical properties. Continued efforts to design, prepare, and evaluate such materials must be accorded high priority.
-
Polymer science in general—and polymer synthesis in particular—must embrace a broader view of the field, in which both covalent and non-covalent interactions are exploited to maximum advantage. This view will create lively exchanges of information and ideas between practitioners of polymer science and workers in related areas of organic and inorganic chemistry, biology, physics, engineering, and materials science. Work at these disciplinary interfaces should be supported and pursued.
-
Environmental issues in polymer synthesis, as in other areas of polymer science, will continue to grow. Environmentally sound synthetic methods, strategies
-
for biomass conversion, and design for disposal all offer the synthetic chemist intriguing challenges as well as opportunities to contribute solutions to some of the nation's most urgent problems.
POLYMER CHARACTERIZATION
Significant advances in characterization techniques have paralleled the development of new polymeric materials. Identification of the unique properties and structure is necessary for further technological development and applications of the material. Sophisticated techniques now available to characterize various properties of polymers have dramatically improved our understanding of the mechanisms and principles governing polymer function. Using many techniques now developed for polymer characterization, individual molecules as well as molecular assemblies (i.e., melts and solids) and polymer surfaces and interfaces may be studied.
Rather than discuss all the techniques that have been introduced, many of which can be applied to characterize polymers in a wide variety of states, this section concentrates on recent breakthroughs and potential breakthroughs, where new capabilities should have major impact. A sampling of recent breakthroughs is given in Table 4.1, and potential breakthroughs are listed in Table 4.2. There are five main areas of application:
-
Molecular characterization of the architecture of isolated polymer chains;
-
Characterization of solutions, melts, and elastomers, especially the dynamics of polymer chains;
-
Characterization of polymer solid-state structure and properties, wherein new microscopies can offer major advances;
-
Characterization of polymer surfaces and interfaces, especially with new depth profiling techniques; and
-
Characterization of biopolymers to provide information for development of biotechnology.
Molecular Characterization
Molecular characterization plays a critical role in understanding polymeric materials. New polymeric materials must be characterized to understand how their structure determines their properties; such information illuminates fundamental scientific questions and enables potential commercial applications.
Challenges are presented by synthetic homopolymers because they are generally polydisperse, not only in terms of molecular weight, but also in branching, tacticity, and microstructure. Copolymers may have all these polydispersities as well as additional ones in composition and sequence. Because physical properties
TABLE 4.1 Recent Breakthroughs in Characterization of Polymers
|
1. |
Molecular Characterization |
|
|
• Size exclusion chromatography, combined with light scattering and viscosity detectors |
|
|
• Multidimensional nuclear magnetic resonance methods for determining chain architecture |
|
|
• Millisecond time-resolved ultraviolet/visible, Fourier transform infrared, and Raman spectroscopies |
|
2. |
Solutions, Melts, and Elastomers |
|
|
• Many new techniques for measuring diffusion |
|
|
• Simultaneous rheological and optical/X-ray/neutron measurements |
|
|
• New nuclear magnetic resonance and optical techniques for measuring local polymer dynamics and tertiary structure of biopolymers |
|
|
• Neutron spin-echo techniques for measuring intermediate-scale polymer motion |
|
|
• Neutron-scattering methods for determining the thermodynamics of polymer blends |
|
3. |
Solid-State Structure and Properties |
|
|
• Environmental scanning electron microscopy |
|
|
• Near-field optical microscopy |
|
|
• Simultaneous X-ray and calorimetry measurements |
|
|
• Solid-state nuclear magnetic resonance techniques |
|
|
• Molecular imaging with transmission electron microscopy |
|
|
• Confocal optical microscopy |
|
|
• Transmission electron microscope image-processing techniques |
|
|
• Techniques using synchrotron radiation sources for solution of the phase problem in solving the structure of large biomolecules |
|
4. |
Surfaces and Interfaces |
|
|
• Many new deuterium depth-profiling techniques with complementary depth resolutions |
|
|
• Surface forces apparatus to characterize the forces between adsorbed polymer layers |
|
|
• Atomic force microscopy of surface topology |
|
|
• Neutron reflectometry of surfaces and interfaces |
|
5. |
Biopolymers |
|
|
• Improved separation and purification methods and capillary zone electrophoresis for separating small amounts of biopolymers |
|
|
• Polymerase chain reaction technique for amplifying very small quantities of DNA |
|
|
• Multidimensional nuclear magnetic resonance methods for obtaining high-resolution structures in solution |
|
|
• Mass spectroscopy that quickly sequences biomolecules |
|
|
• Computer database technology for comparing informational macromolecules |
of polymers can depend not only on the averages, but also on the polydispersities of the attributes just mentioned, it is necessary to characterize all of these. Methods for determining average molecular weights of soluble polymers and some of the other average properties are well known, but characterization methods for the distribution of these properties, especially for more than one of these properties at a time, are in short supply.
TABLE 4.2 Potential Breakthroughs in Characterization of Polymers
|
1. |
Molecular Characterization |
|
|
• Ways to find molecular weight distributions for insoluble polymers |
|
|
• Better ways to determine branch content and sequence information |
|
|
• Better ways of measuring how branch content and monomer composition are distributed over range of molecular weights |
|
2. |
Solutions, Melts, and Elastomers |
|
|
• Better ways to measure the distribution of molecular lengths between cross-links |
|
|
• More intense sources of long-wavelength neutrons to make possible time-resolved experiments |
|
|
• Better techniques for the preparation of isotopically labeled biomaterials |
|
3. |
Solid-State Structure and Properties |
|
|
• Energy-filtered soft X-ray microscopy |
|
|
• Electron tomography |
|
|
• New techniques for reducing electron radiation damage |
|
|
• Chemical-imaging transmission electron microscopy |
|
|
• Ways to measure plastic deformation and fracture properties of small samples |
|
|
• Methods to probe mechanism of shear yielding in glassy polymers |
|
|
• Methods to characterize the microscopic deformation of rubber-modified polymers at impact strain rates |
|
|
• New techniques for the solution of the phase problem in biomolecules |
|
|
• Computational techniques for the solution of nonglobular virus structures such as the AIDS virus and complex structures such as those of molecular motors |
|
4. |
Surfaces and Interfaces |
|
|
• Analysis techniques that can characterize curved interfaces |
|
|
• Interface analysis techniques with both good depth resolution and good lateral resolution |
|
|
• Ways to use atomic force microscopy to characterize local mechanical properties |
|
5. |
Biopolymers |
|
|
• Scanning tunneling microscopy to read out biopolymer sequences |
|
|
• Rapid sequencing methods |
|
|
• Computer algorithms to predict biomolecular structures from sequences |
|
|
• Higher-resolution electrophoretic methods for separating large biopolymers |
|
|
• Time-resolved Laue diffraction methods for X-ray crystal structure determination |
|
|
• Hydrogen exchange nuclear magnetic resonance for local motions and internal structure of biopolymers |
The number and average molecular weight of soluble polymers can be obtained by numerous methods, including colligative property measurements, scattering, and ultracentrifugation. Viscosity measurements, which are sensitive to molecular weight, size, and polydispersity, are also useful. Size exclusion chromatography (SEC), which is sensitive to molecular size rather than weight, now may be equipped with light scattering and viscosity detectors so that absolute molecular weights can be obtained directly. Further research is needed, however,
to improve the material used to pack the SEC columns. Better columns are needed both for the analysis of high-molecular-weight samples (>107) and for use at high temperatures. Methods for obtaining molecular weight distributions of insoluble polymers are, however, in their infancy; one example involves mass spectroscopy, which has recently been used for molecules with molecular weights as high as 100,000. Methods for studying higher-molecular-weight molecules are needed.
There are few methods for studying more than one polydispersity at a time. Among the few existing methods is orthogonal chromatography, in which the output of a SEC-yielding separation by molecular size is injected into a second SEC or a high-performance liquid chromatograph operated so as to separate by composition. Routine methods for providing such analysis need to be developed.
All instrumental methods are benefiting from the advances in electronics and data-handling techniques that have occurred over the last three decades, and this progress continues apace. The improved sensitivity has led to shorter sampling times, allowing study of kinetic properties, and higher spatial resolution, which should enable the development of new forms of microscopy and imaging.
Nuclear magnetic resonance (NMR) spectroscopy is still the premier tool for investigating the architecture of the polymer chain, that is, monomer sequence, stereochemistry and tacticity, monomer orientation, and branch content. The power of NMR arises because the signals for the different hydrogen, carbon, and other atoms along the main chain and side chains of polymers can be resolved, and the NMR parameters (chemical shifts, coupling constants, and relaxation times) are determined by the local environment. Recent advances in NMR are higher-field magnets leading to increased sensitivity and resolution and the development of new methods to study solid polymers. The introduction of multidimensional NMR (NMR experiments with more than one frequency dimension) has been a particularly important development. Prior to the development of such methods, it was not possible to study the interactions between many pairs of carbons or protons because of spectral overlap. These interactions can be visualized using two-dimensional NMR because the spectra are dispersed into a two-dimensional plane rather than along a single-dimensional axis. Similar multidimensional NMR techniques have been discovered that make it possible to investigate polymer chain and side group motions in much more detail than in the past. The use of solid-state NMR allows one to analyze bulk polymers and films, as well as insoluble materials. NMR can also be used to study the local organization in semicrystalline materials and the domain size in phase-separated materials.
While NMR techniques have made it possible to routinely determine the average tacticity, microstructure, and composition in polymers, NMR methods for studying the monomer sequence and branching still can yield only a partial
description of these. It is currently much too difficult to obtain information on the distribution of these attributes in a sample by NMR or otherwise.
We are all familiar with the wonders that three-dimensional NMR imaging has wrought for medical diagnosis; such imaging has great potential for polymer science as well. At the 1- to 0.1-millimeter (mm) level already achieved in medical instruments, NMR imaging can potentially play a role in characterizing polymer processes such as injection molding, mixing, and extrusion. While at the moment three-dimensional NMR imaging even at the scale of an optical microscope (10 to 1 micrometer [µm]) seems far in the future because of sensitivity problems, one-and two-dimensional NMR microscopies may be imminent. Such microscopies, with their sensitivity to details of chemical bonding and isotopic composition, will find relevant applications in characterizing diffusion, reaction, and structures in polymer solutions, melts, and solids.
Other spectroscopic methods of importance to polymer researchers are ultraviolet/visible (UV/Vis), Fourier transform infrared (FTIR), and Raman spectroscopies. These spectroscopies, in common with NMR, are nondestructive; no changes in the chemical bonding, conformational order, crystalline structure, or morphology of the polymer are caused during the interrogation of the sample.
UV/Vis spectroscopy provides information on the electronic states of the polymer backbone in both crystalline and amorphous polymer phases. It has played a major role in unraveling the mechanism of conduction and nonlinear optical response in π-conjugated polymers while providing new insights into thermo-and piezochromic behavior in β-conjugated systems. Recent advances allow UV/Vis spectra to be obtained in less than 100 milliseconds (ms). Future advancements will focus on high-sensitivity diode array detectors and even faster data acquisition times providing UV/Vis spectra ''on the fly" so as to follow reaction kinetics and phase transitions.
Probably the most revolutionary optical spectroscopic advance in the polymer area in the last decade has been the ability of Raman spectroscopy to provide important conformational and morphological information about polymers. Not only have the detectors used in conventional Raman spectrometers been improved significantly from the former single-element photomultiplier to a multipixel array charge-coupled detector (CCD), but their range of sensitivity has also extended to the near infrared with the introduction of an entirely new set of solid-state lasers. This development has provided new pathways for the investigation of polymers that contain intrinsic chromophores as part of their structure, and following the introduction of Fourier transform spectroscopy, structural polymers containing fluorescent impurities can still be investigated using Raman spectroscopy without the fluorescence overwhelming the much weaker inelastically scattered Raman signal. At an incident wavelength of 1,064 nanometers (nm), no fluorescence can be excited because the incident photon energy is too low, and hence good-quality Raman data can be routinely collected. With significant improvement in detectors on the horizon, Fourier transform-Raman
and conventional Raman (using visible excitation) will mount a formidable challenge to FTIR spectroscopy in the area of sensitivity.
Characterization of Solutions, Melts, and Elastomers
The past decade has brought major advances in methods for characterizing solutions and melts, particularly techniques for investigating "molecular rheology," the relation between the molecular structure of a polymer and its flow characteristics. This area is particularly important because the main polymer-processing methods, including injection molding, fiber spinning, and extrusion, involve flow of melts or solutions. Many new techniques for studying diffusion have been invented, and diffusion measurements have become a major probe of molecular rheology. Some of these techniques, such as fluorescence recovery after photobleaching or forced Rayleigh scattering, involve polymers labeled with fluorescent molecules that can be bleached or chemically altered with an optical interference pattern; analysis of the time dependence of the disappearance of the bleached pattern yields a diffusion coefficient. Other techniques rely on labeling of the diffusing polymers with isotopes, usually deuterium. The concentration profile of the deuterium-labeled polymer diffusing in a protonated polymer melt can be determined directly by infrared microdensitometry or by any of a number of depth-profiling methods, as discussed below.
Rheological characterization capabilities have also expanded greatly. Particularly promising are rheometers that allow optical techniques (e.g., infrared dichroism and light scattering) that probe the deformation of polymer molecules and phases in melts and solutions to be carried out under well-defined stress and strain rate conditions. Recent studies of light scattering from sheared solutions and blends, for example, have demonstrated the effect of shear on fluctuations and phase stability. These can be expected to be critical in defining processing conditions to produce desired phase structures. Other developments of note have included the use of synchrotron X-ray beams to probe the rheological state of liquid crystalline melts and solutions. The high intensity of such beams makes possible characterization not only of the steady-state structure of the system under flow but also of transient structures. Major advances in this area await the development of fast area detectors for X-rays that can be read and recorded on a time scale of seconds or even milliseconds.
Neutron scattering has become an indispensable tool in the characterization of polymer melts and elastomeric networks. Neutrons of wavelengths from 0.2 to 2.5 nm available from modern neutron sources permit studies of the dimensions of single polymer molecules as well as the chain conformation over much shorter length scales.
Neutron scattering can take great advantage of deuterium-labeled polymers in which deuterium has been substituted for hydrogen. Because of the great difference in neutron scattering length between these isotopes, appreciable contrast
between hydrogen-and deuterium-containing molecules may be achieved. While little chemical or thermodynamic perturbation is produced by the replacement of hydrogen by deuterium, the effect is important in some situations. The contrast permits the measurement of the geometry of single molecules in concentrated solutions and melts, of the topology of molecules folded within crystals or interconnecting them, and of the connectivity of microdomains in block copolymers. Selective substitution in parts of molecules allows for the determination of their arrangement in superstructures. Portions of structural units, such as those of shell-core structures and micelles, may be labeled as an aid to their structural determination. The extension of single molecules in sheared melts and stretched networks can be measured, permitting critical tests of deformation theories. However, better methods are needed to characterize the distribution of molecular lengths between cross-links in networks produced under polymer-processing conditions typical of industrial practice.
Through use of methods such as neutron spin-echo spectrometry (Mesei, 1980), experiments have provided the most thorough test to date of whether the details of the reptation model are correct (Richter et al., 1990; Butera et al., 1991). Quasi-elastic neutron scattering has extended the range of dynamic studies achievable by light scattering to smaller dimensions, utilizing the advantages of isotopic labeling. These advantages are somewhat offset by the low neutron fluxes available, leading to long data acquisition times.
The neutron scattering from polymer mixtures depends on fluctuations from uniformity. Such concentration fluctuations require work against osmotic forces, and so their size relates to the osmotic compressibility. Thus, neutron-scattering measurements can provide thermodynamic information. While such techniques have long been applied to the molecular characterization of dilute polymer solutions, recent developments in neutron scattering using deuterium-labeled molecules have permitted their extension to concentrated solutions, amorphous blends, and melts. These have provided values of interaction parameters (Flory χ values) in such concentrated systems. The excess scattering occurring as phase separation is approached serves to characterize critical phenomena and has proved useful for studying spinodal decomposition of polymer mixtures.
Scattering techniques have grown in use because of developments of intense radiation sources (lasers, synchrotrons), of efficient area detectors (optical multi-channel analyzers, CCDs), and the employment of computers for rapid data analysis. Faster X-ray detectors are needed for efficient use of the high fluxes available with synchrotrons. Currently, available neutron fluxes are too low to permit dynamic studies, so that the prospect of a high-flux advanced neutron source is a welcome possibility. The case for an advanced neutron source is reinforced by the emergence of neutron reflectometry as a primary tool for characterizing polymer surfaces and interfaces (see below), because our aging reactor neutron sources are nearing the end of the time when they can be operated safely to give even-current fluxes of neutrons. Synchrotron X-ray and neutron-scattering techniques
require experimentation at a central facility, and therefore the development of user-oriented centers to permit measurements by users other than the experts in these fields is highly desirable so as to encourage more general use of these important techniques.
Characterization of Polymer Solid-State Structure and Properties
Structural characterization of the polymer solid state has advanced rapidly, driven partly by the need to understand the complicated structures present in semicrystalline polymers and partly by the desire to characterize the morphology of multiphase polymer blends. Traditional thermal analysis techniques, such as differential scanning calorimetry, have been combined with powerful synchrotron X-ray sources to allow simultaneous structure and calorimetric measurements in a time-resolved fashion. The structural transformation giving rise to a thermal effect thus can be unambiguously determined.
Many new microscopy techniques, developed in the last decade, are just beginning to be exploited by polymer scientists. For example, it is difficult to observe thick specimens owing to the limited depth of field of conventional optical microscopes. By focusing a laser beam on a particular point on the sample and scanning, an "in focus" three-dimensional image can be constructed and an image of a section at a given depth can be generated. Resolution can be enhanced by using fluorescent dyes that require a two-photon process for emission.
Near-field scanning optical microscopy (NSOM) is another new technique that has found important applications in biology and that could be very useful for high-resolution optical microscopy of polymers. An evanescent optical wave field from the tip of an optical fiber, as small as 12 nm in diameter and much smaller than the wavelength of the light, is coupled to the surface of the sample, exciting fluorescence or scattering. As the tip is scanned over the surface of the sample, the image thus produced has a resolution much better than that of conventional optical microscopes, but without the problems (such as radiation damage and vacuum) associated with electron microscopies.
New environmental scanning electron microscopes (SEMs), which can operate in a partial pressure of water vapor, can eliminate the necessity for coating samples with metal to prevent charging artifacts, thus achieving superior resolution. Solvent as well as water effects on the mechanical properties can be studied in situ.
For the ultimate in resolution, the transmission electron microscope (TEM) is necessary, but until recently TEM images of polymers were restricted to relatively low magnification because of radiation damage effects. Recently, however, imaging of molecular structures in radiation-resistant polymers has been demonstrated by using TEM image-processing methods. Biologists have made use of electron tomography (the electron equivalent of the X-ray CAT scan) to reconstruct
three-dimensional images of structures within the cell. A number of polymer problems would benefit from a similar approach.
The ability to generate high-resolution chemical maps of the polymer structure in blends would be a breakthrough. Current scanning transmission electron microscopic methods, which employ energy-dispersive X-ray analysis or electron energy loss spectroscopy, are not suitable for most polymers. New chemical imaging electron microscopes, which permit recording of images created with electrons with a well-defined energy loss, may revolutionize this field. By digitally subtracting two images, one just below and one just above the absorption edge of a particular element, one can generate a chemical map of that element, while minimizing radiation damage.
A related technique for chemical mapping is soft X-ray microscopy. By tuning the X-ray energy to a strong absorption characteristic of a particular moiety, say, the π-plasmon associated with a phenyl group on one of the components of the blend, and scanning the focused X-ray beam, one can map the distribution of that moiety over the sample. Tunable soft X-ray sources are available at synchrotron radiation facilities, and the necessary focusing X-ray optics are now becoming available; already, spatial resolutions of approximately 50 nm have been demonstrated.
For most of the applications of solid polymers, mechanical properties are of primary importance. While there have been advances in characterizing and understanding these properties, there are many areas where improvements can be made. Techniques to characterize the mechanical properties of small samples of polymers are needed. Most conventional mechanical testing requires very large samples, for example, compact tension samples for fracture toughness measurements, tensile "dogbone" bars, and so on. To evaluate a new polymer or polymer blend, one would like to use 10-gram (g) batches synthesized by a polymer chemist rather than scaling up to produce 10 kilograms (kg) in a pilot plant. It is now possible to test polymer films that are as thin as 1 µm; the principal difficulty is that thickness has well-known and severe effects on the mechanics of the plastic deformation of polymers. Nevertheless, with experience it is possible to extrapolate from measurements on films to bulk samples. Thin film testing has the natural advantage that samples can be examined by both optical microscopy and transmission electron microscopy. Another area where improvements can be made rapidly is in fracture testing. The fracture behavior of interfaces and thin polymer layers embedded between two tough, transparent polymer slabs may be measured by using nothing more than a razor blade and an optical microscope. Further development to allow opaque polymers to be tested would be of great benefit.
While there has been considerable progress in the past several decades in our fundamental understanding of the deformation and fracture of solid polymers, particularly in the area of crazing and fracture, much more improvement is possible. The microscopic mechanisms of shear deformation are little known,
yet these mechanisms are responsible for the toughness of the toughest polymers, such as polycarbonate. The addition of rubber particles is the usual way of producing tough polymeric materials, yet the microscopic fundamentals of rubber toughening are not yet fully understood. Experimental techniques to probe the microscopic nature of the deformation and fracture of such systems, preferably in a time-resolved fashion at typical impact strain rates, are needed.
Characterization of Polymer Surfaces and Interfaces
Surfaces and interfaces present challenges that are distinctly different from those presented by bulk, three-dimensional polymeric materials. The surface or interface introduces new characteristics unique to its quasi-two-dimensional character. They require special techniques that sample only the layer of interest near the top surface or at the buried interface.
New depth-profiling techniques, which measure some attribute of the polymer as a function of depth from the outer surface, are advancing this field rapidly. While some well-established techniques, such as angle-resolved X-ray photoelectron spectrometry (XPS), can sense the local chemistry near the surface, others, such as the ion spectrometries, forward recoil spectrometry (FRES), nuclear reaction analysis (NRA), and secondary ion mass spectrometry (SIMS), as well as neutron reflectivity (NR) and attenuated total reflection FTIR (Fourier transform infrared) spectroscopy, can find the depth profile of deuterium-labeled polymers, with depth resolutions usually well below 100 nm. These depth-profiling techniques have been used recently to characterize short-range diffusion of polymers across interfaces, the enrichment at the surface of one component in a miscible polymer blend, the depletion of polymers near a solution-solid interface, and the segregation of block copolymer surfactants to the interface between two immiscible polymers, to name only a few applications. It should be realized that the techniques have complementary capabilities, with some, such as NR, providing the best resolution of sharp features of the profile and others, such as FRES, enabling a better picture to be drawn of their long-range and integrated features.
While depth profiling is discovering aspects of the structure of polymer surfaces and interfaces never before accessible, it is also likely to have a major impact on our understanding of polymer fracture. Depth profiling the two surfaces produced by fracture has made it possible to determine the locus of fracture precisely with respect to particular deuterium-labeled polymers (a deuterium-labeled block of a diblock copolymer) and to derive great insight with regard to mechanism of fracture from this information.
Such depth-profiling measurements, however, usually require flat samples, which are stratified in depth; making such measurements on samples with geometries such as cylinders (fibers) and spheres (particles) is normally not possible. In addition, all of these techniques have much more limited resolution laterally,
that is, in directions in the plane of the interface. These lateral resolutions range from centimeters to, at best, micrometers. There is a need for interface analysis techniques that have both good depth and good lateral resolution and that can analyze curved interfaces.
Because the different depth-profiling techniques have complementary capabilities and no one technique is usually adequate to provide the level of resolution, sensitivity, and quantitation desired, it is important that researchers in this field have access to a wide variety of depth-profiling instrumentation. Facilities for SIMS and ion beam analysis, while common in semiconductor research, are not widely available to researchers interested in polymers. Some effort, perhaps on a regional basis and involving both universities and industry, should be made to ensure that this instrumentation is accessible to polymer scientists.
The characterization of interfacial properties has also advanced dramatically in the past decade. The surface forces apparatus (SFA) has become a standard method for measuring the (normal) forces between layers of polymer adsorbed in solution on solid substrates. Such measurements are important for understanding the steric stabilization of colloidal suspensions by polymers as well as for determining the thermodynamics of polymer adsorption from solution. For example, such measurements have led to an understanding of the stretching of polymer chains normal to interfaces between a solid and the solution as a function of their areal density. While the original SFA required the use of cleaved mica surfaces, recent workers have lifted this restriction, and a much wider variety of solid surfaces is now available. Shear forces between surfaces, as well as normal forces, can now be measured by some SFA devices, enabling the study of the fundamentals of polymer effects on lubrication. The SFA remains an apparatus that demands considerable skill and experience on the part of the experimenter, however; efforts to simplify the apparatus by improving the drive and mechanisms for detecting distance are under way and should be encouraged.
The SFA has also been used in the last few years to measure interfacial energies and adhesion; by measuring the area of contact between the polymer-coated mica cylinders as a function of the applied normal force, one can determine the reversible work of adhesion. An elegant variant of this method has been developed recently using a elastomer sphere pressed into contact with a elastomer flat. The surface of the elastomer can be modified—for example, one can form a thin silicon dioxide layer on a siloxane elastomer by treatment with an oxygen plasma—and highly organized organic films can be self-assembled on such modified surfaces. The work of adhesion between a wide variety of surfaces can thus be measured with little more than an optical microscope and an analytical balance.
More conventional ways of measuring surface properties include the determination of contact angles of fluids on polymer surfaces and the measurement of the shapes of polymer melt and solution droplets, under conditions where these shapes are modified by the action of gravity or centrifugal force. Here the major
difficulties are caused by the highly viscous nature of polymer melts, which makes it hard to know whether the equilibrium shape has been obtained. It is particularly difficult to measure the interfacial tension between phases in a polymer melt. One promising approach involves measuring the retraction and break-up into droplets of a fiber of one phase in a matrix of another, but more attention should be devoted to this problem because the interfacial tension helps determine the morphology of melt-processed polymer multiphase blends.
The atomic force microscope (AFM) has already had an impact on the measurement of the surface topology of polymers. It seems likely, however, that the AFM can be suitably modified to allow measurement of very local surface properties as well as mechanical properties of polymers. One example is the lateral force microscope (LFM), an AFM modified so it can measure lateral forces as well as normal forces. With the LFM, it is possible to reveal the morphology of a phase-separated blend of hydrocarbon elastomers simply by scanning a microtomed surface. Another, more speculative, possibility would be the chemically sensitive AFM. In such an instrument, the tip would be modified to expose an outer surface of hydrogen bonding groups. By operating such an AFM in a "tapping" mode, it might be possible to distinguish hydrogen bonding regions of the surface from nonhydrogen bonding ones. Such further developments of the AFM and related instruments should have a large payoff in polymer surface research.
Characterization of Biopolymers
Biopolymers require many techniques other than those used for synthetic polymers. To characterize a biopolymer, the first steps are to purify and produce the material in quantity and learn its molecular sequence. The main methods for sequencing and purification include chromatography, gel electrophoresis, centrifugation, and dialysis. They will continue to play important roles. There are also new methods that promise to revolutionize how we obtain, purify, and understand the message encoded in biopolymer sequences. Capillary zone electrophoresis separates materials with very high resolution and works with extremely small volumes of material (in some cases, even the volume of a single biological cell!). Mass spectrometry, particularly in conjunction with electrospray and matrix-assisted laser desorption methods, can determine the sequences of informational polymers very rapidly and can detect subtle aspects of biologically important sequences. At present, there are limitations on the sizes of molecules that can be studied in this way, but the maximum size is growing as the technology evolves. Polymerase chain reaction (PCR) is a method for amplifying very small quantities of DNA. Because most molecules in the cell are in limited supply, this technology now opens the possibility of fishing out even the rarest of molecules and producing the appropriate DNA, RNA, or protein sequence in
sufficient quantity to study them. Major advances in identifying and characterizing new proteins and nucleic acids will result from new electrophoretic techniques with enhanced resolution and reproducibility. Having determined the sequence of a biopolymer, computer database search methods now make it possible to search through the enormous number of known sequences and structures to make educated guesses about the biopolymer's possible structure and function. Because sequencing and purification methods are developing rapidly, the sizes of the databases are growing exponentially. The sophistication of computer search methods is keeping pace with this information explosion.
Structure Determination
Once a sufficient quantity of a pure biopolymer is available, the next step is to learn its atomic structure. The main methods for determining biopolymer structures are X-ray crystallography, NMR spectroscopic methods, electron microscopy, and scanning tunneling microscopy. The highest-resolution structures have been obtained by X-ray crystallography. Because crystallography requires that the molecules be crystallized, which is a poorly understood process, obtaining new structures by crystallography can be slow. A further bottleneck in obtaining crystal structures is the so-called "phase problem," which results from the unavoidable loss of information in recording X-ray intensities rather than amplitudes and makes it difficult to reconstruct the molecular structure from the diffraction data. While this problem is most severe for the large molecules typical of biopolymers, new approaches and solutions continue to emerge. Multiple wavelength anomalous diffraction, a technique requiring a synchrotron source, provides one solution to the phase problem. A most exciting new technology is the Laue diffraction method for time-resolved X-ray crystallography. Preliminary successes indicate that this technique may allow us to watch the dynamic processes, step-by-step, in chemical reactions and physical changes in biomolecules.
Another major development has been the emergence of multidimensional NMR for obtaining high-resolution structures of biomolecules in solution. An advantage over crystallography is that the NMR experiment does not involve crystallization or the phase problem. However, NMR is currently limited to studying smaller molecules than X-ray crystallography, although this situation is rapidly improving. NMR imaging of supermolecular biopolymer structures would offer a tool with almost limitless possibilities. Major advances could result from the ability to label biomolecules cheaply. Carbon-13 NMR spectroscopy of proteins is extremely powerful. However, its use is limited owing to the present expense of preparing the required carbon-13-enriched samples. Scanning tunneling microscopy is another new technology with preliminary successes and much promise for biomolecular structures.
The Folding Problem
How do biopolymer structures arise from interatomic forces? A major goal in characterization is to explain biomolecular structure using fundamental chemical principles. The "folding problem" is to understand how the monomer sequence encodes the conformation of the biopolymer. The fact that molecular "chaperones" are needed to obtain the correct folded structure for some proteins complicates the issue even further. Major efforts are going into developing theoretical models and methods of computational chemistry and statistical mechanics to allow one to predict the folding. The two main problems are the need for better interatomic and intermolecular potential functions, particularly for modeling aqueous solutions, and faster conformational search strategies, which will also rely on new developments in massively parallel computer hardware and software, in order to find conformations of low free energy. Experimental advances have been occurring rapidly in several areas. Mutation experiments replace one or more monomers, often through genetic engineering, and explore the consequences of the small changes on structure or function of a biopolymer. Unnatural monomers are synthesized chemically to create mimics of biomolecules or monomer replacements. Hydrogen exchange NMR methods have recently begun to allow unprecedented access to information about the local motions and internal structure. Small-molecule models and high-resolution calorimetry are helping to understand the driving forces. Direct synthesis and redesign of proteins are now becoming feasible, for increased stability and new applications of proteins as catalysts, and in information and energy transduction and storage.
Conclusions
-
National facilities are important for polymer characterization. These facilities, producing neutron and synchrotron radiation, are employed for diverse purposes, and continuing support and improvement must be based on the sum of the benefits and costs.
-
Improved characterization methods for structures between the monomeric and macroscopic levels are needed, for solutions, surfaces, solid-state polymers, and insoluble polymeric materials. Methods and instrumentation need to be developed.
-
Polymer characterization has prospered from the collaborative interaction of various disciplines with the common goal of developing characterization tools. While many techniques have been specially developed for polymers, many were imported into polymer science after being developed for other purposes. Given the extent to which polymer characterization has been advanced by techniques developed first in other fields, the education of polymer scientists and engineers must be broad enough that they will be able to capitalize on similar
-
outside developments in the future. At the same time, increased contact between polymer workers and those in outside fields will ensure that new techniques developed within polymers will be rapidly exploited in those outside fields where they are useful.
THEORY, MODELING, AND SIMULATION
Enormous opportunities and new needs for polymeric materials exist in the rapidly expanding and internationally competitive high-technology areas, such as the information industry, aerospace industry, and biotechnology. Realizing these opportunities and meeting the needs for novel materials, however, depend on a much deeper understanding of polymeric materials than has been necessary for developing commodity polymers in the traditional chemical industry.
Theory and computations can help provide this deeper understanding. They reduce large collections of experimental observations to working knowledge, rules, patterns, models, and general understanding. They explain experimental observations; they correlate data from different materials and phenomena; and, in general, they quantify and unify our knowledge. More importantly, theory provides new predictive capabilities to guide the development of new ideas and to direct experimental efforts in exploring new chemical structures, processes, and physical properties.
In favorable cases, theory and simulation can reduce the amount of experimental work required or even eliminate it entirely. For example, one of the classical theoretical problems is to predict ''phase diagrams," diagrams that describe the resulting states of matter and the conditions when polymers and solvents are mixed together. This is a central problem in the design of new materials. Modern polymeric materials often involve mixtures of several different types of polymers, of different molecular weights, and in complex solvents at different temperatures and pressures. They involve many variables. Such variables determine the difference between achieving a successful material with appropriate optical, thermal, mechanical, and chemical stability properties or producing a useless mixture. To find optimal conditions could require exploring 5 or 10 variables in detail, which could require tens of person-years of experiments. Instead, theoretical or computational models often permit the exploration of many different variables quickly, and thus they reduce the amount of time to develop new materials by an enormous factor.
Another example of the use of theory and simulation is in the area of polymer processing. Many companies currently model (1) kinetics of polymerization reactions and (2) fabrication, combining phenomenological rheological and heat transfer characterization of the polymer, to assess a proposed design before cutting a mold or die. Extensive efforts have been devoted to modeling fabrication operations such as extrusion, mixing, and molding operations. Once a process configuration has been selected, computer-based models are generally able to
predict temperature, pressure, and conversion profiles in time or space. More sophisticated versions are able to predict certain product qualities, such as molecular weight averages, copolymer composition, and branching frequencies. They can sometimes also evaluate questions of process safety. (Additional modeling information is given in Chapter 3 in the section "Polymer Processing.")
While even rudimentary theories are often important sources of guidance, the ultimate power of theoretical and computational models depends on reducing their assumptions and approximations by building deeper and more fundamental models.
Theory and computer modeling will play increasingly valuable roles in the development of new advanced materials. The strong interdependence of experiment and theory in polymer science is well illustrated by the Nobel Prizes in polymer theory awarded in 1974 to Paul J. Flory (in chemistry) and in 1991 to Pierre-Gilles de Gennes (in physics). In certain areas of polymer theory, there has been enormous progress in the 1970s and 1980s. Some topics have been so thoroughly explored that they are currently receiving little attention, while other areas have moved to the forefront of theoretical activity. Further shifts in the centers of interest will undoubtedly be propelled by advances in theoretical methods, experimental developments, societal needs, and the phenomenal increase in computer performance and algorithm development.
Theory and computation have developed into two separate disciplines, although they are often intertwined to varying degrees. Theory is associated with the construction of physical and mathematical models of the system, with attempts to solve basic equations describing the properties of the system, and with predictions for the outcomes of experiments, including those that have not yet been done. Computation represents an application of theory, often with the aid of large-scale computers, either to compute the desired properties for a system of interest or to simulate the behavior of the system at a level of detail unavailable experimentally. These simulations are designed for furthering our understanding to test current theories or to provide data necessary for developing new and improved theories.
Great advances in theory and in computational resources have resulted in the development of a scientific computation industry, which constructs large-scale computer codes that are increasingly being used by scientists and engineers in industry and universities, in addition to the home-grown codes, which are in a constant state of renewal and development. It must be stressed, however, that these computer packages are no better than their underlying theories and the input data employed. Thus, advances in theoretical methodologies, computer technology, and the acquisition and codification of relevant experimental data will play essential roles in improving the capabilities of these computer packages.
Theory and computation are applied on several levels, ranging from the microscopic level, involving a detailed description of the molecular constituents, to a macroscopic level, involving continuum mechanics or thermodynamics, to
describe the bulk properties of matter. Intermediate between the microscopic and macroscopic descriptions lies the mesoscopic world characterized by lengths long on a microscopic scale but short on a macroscopic one. Each level generates its own conceptual, theoretical, and computational challenges, but perhaps the most significant challenge lies in providing a bridge between the different levels. Thus, a goal of the complete molecular modeling of materials involves use of molecular theories to compute the property information necessary to describe the processing or performance behavior of the new bulk materials.
States of Matter
Polymer Solutions
Because many theories of polymers in concentrated solutions and bulk rely on single-chain concepts developed and tested in dilute solutions, the understanding of dilute polymer solutions has repercussions throughout polymer science. Hence, dilute solutions of flexible polymers have received much attention in the past 50 years, and as a result many aspects of the average conformation of an isolated polymer molecule are now well understood. Nevertheless, many problems remain, especially for solutions of stiff polymers and their hydrodynamic properties. As the solution concentration increases, these theoretical problems become even more complex, and these properties are less well understood.
Amorphous Polymers
Flexible polymer molecules in the undiluted amorphous state generally assume unperturbed random-coil configurations. This fundamental conclusion is derived from both theoretical and experimental studies on very flexible and non-polar polymers. However, many technologically important polymers normally contain considerable numbers of polar atoms or groups and exhibit considerably reduced chain flexibility. Because sufficient chain stiffness and/or orientation-dependent polar interatomic interactions produce anisotropic ordered phases, the embryonic structure of such order is present in amorphous polymers, which are not very flexible or which contain polar groups, as indicated by recent computer simulations. Simulations and theoretical studies are needed, therefore, of the local correlations among such molecules in the amorphous state to guide and interpret suitable experimental studies. An amorphous polymer is a glass below its glass transition temperature, Tg. Such glasses are never in thermodynamic equilibrium, and consequently their properties depend on their thermal and mechanical histories. Although significant efforts have been made recently in both theoretical and simulation studies of the glass transition, and new computational advances have opened the way to simulation of the properties of the glassy state, much more effort is needed to explain the underlying cause of the glass transition,
how it depends on the chemical structure of a polymer, and the specific characteristics of glasses that emerge from polymers. Above Tg, thermal energy produces long-range molecular motions whose rate increases rapidly with the temperature. At sufficiently high temperatures, a polymer is either an elastic fluid or an elastomer, depending on whether or not it is cross-linked into a three-dimensional network structure. When the elastomer chains are sufficiently long, its elastic behavior is explained on a single-chain molecular level. However, our understanding of the role played by trapped entanglements and the swelling behavior of networks due to solvent remains limited.
Crystalline Polymers
Crystallinity reinforces and stiffens an otherwise compliant amorphous polymer so that when oriented in fibers and films, semicrystalline polymers can exhibit outstanding physical properties. For example, highly oriented crystalline polyethylene fibers exhibit tensile properties nearly equivalent to those of carbon fibers, whereas the noncrystalline ethylene-propylene copolymers are soft, rubbery materials. Over the past 40 years, the semicrystalline state of (flexible) polymers has been the subject of many investigations, and some theoretical understanding has been generated concerning the thermodynamics and kinetics of crystallization. However, this area still has many unanswered questions. For example, the structures and properties of the crystal-amorphous interphase and their dependence on chemical structures need more attention in light of their technological importance for high-performance materials. Also needed is a better understanding of chain topology, such as entanglements and tie-chains interconnecting crystals, in the intercrystalline region, its variation with crystallization conditions, and its influence on bulk properties. Theoretical and simulation studies will aid greatly in further improving the properties of numerous synthetic fibers and films.
Liquid Crystalline Polymers
Rodlike polymers, and many semiflexible polymers with limited flexibility, are now known to exhibit liquid crystalline, or mesomorphic, order in solutions, in melts (the liquid state), and in the solid state. The spontaneous ordering of these polymers provides a unique means of aligning polymer chains to obtain materials having exceptional strength, rigidity, and toughness. Fibers spun from many of these polymers (Kevlar®, for example) exhibit mechanical properties that are almost equal to those of carbon fibers. Therefore, the fabrication of these polymers into fibers, films, and molded parts promises many new opportunities that have not been fully exploited because of a lack of understanding of the relationship of molecular structure to the properties of the liquid crystalline state. Theoretical advances will be key to establishing this badly needed understanding.
They include describing the basic thermodynamics and kinetics of formation of the mesomorphic phase, the nature of defects (disclinations), the chain conformations and intermolecular packing in mesomorphic states, the dependence on processing history, and heterogeneities at large spatial scales. In particular, molecular descriptions are required that can explain and predict the influence of monomer structure, copolymer sequence, and interactions between chains.
Polymer Blends
Multicomponent polymer systems, such as polymer mixtures (blends), provide a new approach to the development of novel materials. These materials enable properties to be tailored, without resorting to costly new synthetic routes and also without the problems of proof of environmental and health safety entailed in new syntheses. Many important polymer properties, such as toughness, impact strength, heat and solvent resistance, and fatigue, have thus been improved significantly by blending polymers with different properties, and this has enabled many new commercial applications. Despite these advances, questions remain unanswered concerning predictions of miscibility and phase separation, control of morphology, and the structures of the interfaces between domains of different phases. Unlike small molecules, the mixing of two polymers is accompanied by only a small gain in entropy, and hence miscibility is more the exception than the rule. Because many of these materials must be processed in the liquid state, it is important to understand those features governing the phase diagrams of polymer liquid mixtures, that is, those factors determining whether the system is homogeneous or phase separated at a given temperature, pressure, composition, and so on. Traditionally, theories of this phase behavior have been based on simple models, but such models have not been fully satisfactory in relating the thermodynamic behavior of liquid polymer mixtures to the detailed chemical structures and interactions of their constituents; this is necessary for the molecular design of novel composite materials.
Newly emerging theories are establishing the much-needed link between phase behavior and molecular driving forces, through generalization of the classic lattice model of polymer solutions and through generalization, to polymers, of integral equation methods that have traditionally been applied to small-molecule liquids. A growing body of theoretical and experimental information suggests an alteration of chain dimensions in polymer blends, and further investigation is desirable. More difficult problems are those dealing with composite systems with mixtures of different phases, such as mixtures of crystalline with amorphous, liquid crystalline (stiff chains) with amorphous (flexible chains), and so on. For example, a challenging problem occurs when both amorphous phase separation and crystallization occur in the same system. There is coupling of the kinetics of the two processes, whereby the resulting morphology and
consequent properties depend critically on thermal history. Similar problems exist to formulate molecular-level composites as mixtures of stiff and flexible chains. Very little theoretical work is available for addressing these problems and guiding critical experimental work.
Block Copolymers
To achieve a well-defined phase-separated morphology, in the process of designing materials with optimal properties, an important approach is to connect the two polymers of different chemical structures by covalent bonds, thereby producing block copolymers. Many prominent examples include thermoplastic elastomers used in commerce and biomedical technology. Block copolymers also have other uses, such as compatibilizing immiscible polymers, which arise from their ability to form micelles and self-assembled structures. Theories have begun to describe the morphologies of the self-assembled structures but are still unable to explain some observed structures. Further theoretical advances are needed to understand the features of their complex phase diagrams, such as the influence of chain architecture. Improved processing of materials containing block copolymers would benefit from theoretical guidance on the behavior of these systems in shear flows, in external fields, and under pressure, all of which are used as means for controlling morphology.
Polymer Interfaces
An increasing number of new composite materials are materials that have different phases dispersed throughout. The strengths of such materials are often determined by the strengths and morphologies of the interfaces between the phases. Adhesion is of intense interest: in some cases, such as for paints and bonding agents, adhesion should be high; in other cases, such as for lubricants, it should be low. Hence the need arises to understand the interfacial characteristics between different polymers and to understand the morphologies of compatibilizing agents, typically block or graft copolymers, that join two or more dissimilar components. Only recently have investigations considered the behavior of homopolymers and copolymers at interfaces and the nature of interfacial energies between polymers. There has been much progress in understanding properties of polymer interfaces, but we do not yet have a satisfactory understanding, at the molecular level, of the factors involved in strength and failure. In addition, the viability of certain polymeric materials is affected by the segregation of their components at the interfaces, so the properties of these interfaces are likewise of interest, especially in systems containing block copolymers. Theoretical and computational work will aid greatly in developing novel multicomponent polymer systems, where progress, although remarkable so far, still has a long way to go.
Polymer Surfaces and Thin Films
A number of surface properties of polymers, such as friction, wear, lubrication, adhesion, and sorption of surface species, have been investigated for many years because of their technological importance. But these studies have tended to be macroscopic and empirical, and thus little is known at the molecular level. It is observed that surface enrichment occurs where species preferentially concentrate at the surface according to composition and molecular weight. Surface segregation and phase separations near surfaces are not well understood. Nor is much known about the interactions between polymer surfaces and other materials such as liquid crystals, for example, in flat panel displays. Experimental methods to study the structures and properties of polymers on the 10- to 100-Å thickness scales are limited. Theoretical and computational efforts are critically needed to fill in details from the limited available experiments, which are often difficult and costly to perform.
Biopolymers
Biopolymers are another important class among polymeric states of matter. Biomolecules adopt an extremely wide variety of structures, spanning a large range of different types of organization and hierarchical complexity. Biology has control over specific monomer sequences, a power that is not yet available in synthetic polymer chemistry. It is the sequences, for example of proteins, RNA, and DNA, that control molecular architectures, and they do so with a high degree of precision. Force-field simulations for polymers were mainly developed first in the biomolecules area, and they continue to be of major importance in understanding biomolecule properties. More synergy is desirable between the polymer and biopolymer communities, because many of the needs and problems for theories and simulations are the same. Major needs in this area are for (1) theories and simulations that can couple and bridge a wide range of time and spatial scales and (2) better understanding of the complex interactions, such as electrostatic, hydrophobic, and hydrogen bond forces, that are important for biomolecules and other polymers in water.
Dynamics and Properties
Local Motions in Polymers
Localized motions in polymers include the same vibrational and torsional movements that are characteristic of motions in small molecules. However, the connectivity of a polymer chain introduces additional scales of "local motion," which can range from side-group rotations to cooperative movements involving segment sizes with tens of repeat units. It is these localized segmental motions
that underlie variations in physical properties of polymers as a function of temperature and that influence mechanical and other properties of polymer materials. Theoretical descriptions of local motions lag far behind the experimental advances made in the last decade. Experimental advances have derived from tools such as NMR, fluorescence, electron spin resonance (ESR), and dielectric, rheo-optical, and dynamic mechanical instruments. Theoretical and simulation efforts are badly needed to provide a focus for producing a unified picture of chain dynamics with predictive capabilities based on fundamental principles. Also, currently available theoretical techniques have not yet linked the microscopic details of local motions to the long time relaxation behavior that is central to understanding mechanical, viscoelastic, and aging properties of materials. It is thus necessary to develop more molecular treatments of long time dynamics. Nowhere is this problem more apparent than in work on protein dynamics and folding, the separations of biomolecules according to their mobility under electric fields in polymer gels, and the rheology of entangled polymers. Important steps are being made in understanding how small molecules, such as gases and diffusants, affect local motions of polymeric chains, in order to diffuse through them. Such studies are necessary for developing better polymeric membranes for gas separations technology and better polymeric packaging materials for electronic circuitry, soft drink containers, and so on.
Rheology of Liquid Polymers
Molecular rheology has received considerable attention in the last 15 years. Substantial advances have been made by using the simple idea that the transport kinetics of polymers in dense media can be described in terms of the "reptating" motion of one chain within a medium of other chains by snakelike motions of the chain through a "tube" created by entangled neighboring chains. Much work remains to be done because current theories are still mainly of the single-chain type. New insights are required to better describe the nature of entanglement phenomena of the surrounding chains and to incorporate the relaxation of the surroundings and other motions on the rheological properties.
Advances in this area will also benefit from increased studies on copolymers in solvents, and on systems with complex topologies, such as stars and rings, and well-defined molecular weight distributions. We do not yet have a good theoretical understanding of the influence of chemical structure on rheology, because these effects are currently described by simple empirical monomer friction coefficients. Advances are likewise desirable in treating thermodynamics and phase behavior of polymers under the strong flows typical of processing conditions used to fabricate commercial materials. The molecular rheology of stiff chains, with its relationship to the nature of liquid crystalline order and their domain boundaries or disclinations, is another area that requires much more effort. An increased use of continuum rheological models to solve realistic polymer-processing
flow problems has been spurred by the recent expansion in computing power. Further increases in computing power will enable workers to tackle more complex flows and to use the more sophisticated nonlinear models available. Instabilities in fibers, jets, wakes, and inlets will need continuing attention in this regard. Furthermore, a better connection between continuum and molecular rheology is necessary. Continuum rheology describes phenomena in terms of coefficients whose molecular significance is not clear. The rheology of multiphase systems is currently an active research area. This work considers the rheology due to assemblies of continuum phases with small dimensions. Examples are rigid fibers or more symmetrical ones in polymer fluids, phase-separated block or graft copolymers, and phase-separated polymer liquid crystals. Questions associated with polymer interfaces will be prominent in this area, because the wetting and bonding of the heterophases are important in these systems.
Mechanical Properties
There has recently been considerable improvement in molecular descriptions for the crazing and failure mechanisms of single-phase glassy polymers in terms of entanglements and chain breakage. The use of multiphase polymers, particularly block copolymers and polymer blends, has increased substantially in the last 10 years, but the deformation and toughening mechanisms of these systems are little understood. In general, a molecular-level description for mechanical properties of glassy polymers, such as toughness and fatigue, is still at a primitive stage, although computer simulation studies have recently shown promising results in understanding mechanical modulus and certain plastic flow processes.
Mechanical properties, such as adhesion, at polymer interfaces have recently received considerable theoretical attention, because they are critical to many technological problems. Present theoretical models that are based on simple single-chain-level pull-out and breakage need improvements in view of recent carefully designed experimental tests. All the highly oriented polymer fibers, such as Kevlar®, that exhibit outstanding tensile moduli and strength unfortunately show poor compressive strength, thus complicating their applications. Molecular-level description of compressive properties of oriented polymers is sorely needed in order to overcome this fundamental weakness in understanding high-strength polymers.
There is a continuing use of macroscopic nonlinear viscoelasticity models to describe polymer deformations, but the problems of uniqueness and physical significance of the representations are by no means solved. Fracture mechanics has proved useful in describing the failure of brittle materials and is now being extended to tougher materials. More work is required for the description of the failure process and its relation to other mechanical properties, especially for polymer matrix composites. Again, it is important to establish bridges between
these continuum descriptions of fracture processes and molecular mechanisms involving stress concentrations on chemical bonds and the relationship to molecular topology.
Electro-active Properties
Conducting polymers have been an active research area during the last 15 years, but there are still fundamental problems in understanding the conduction processes. This understanding is critical to decreasing the bandgap of a conducting polymer to find an intrinsic conductor without any stability problems, to shifting the optical transitions out of the visible region in order to produce a transparent conductor, and to boosting the conductivity to obtain a truly metal-like conductor. Relatively little is known about the nature of conduction carriers for many of the polymers that are being investigated for this purpose. The mechanism of charge transport needs greater study, particularly with regard to the jumping of charge carriers between chains. Many unsolved problems persist concerning fabrication and stability of these materials, and theory could be very helpful in this regard.
Nonlinear optical properties of polymers, both second-and third-order non-linearities, present enormous potential applications for future electro-optic devices, such as high-speed communications, data storage, and optical computing. Hence, the nonlinear optical properties exhibited by a large number of chromophore structures and polymer architectures have been investigated in the last several years. Despite the impressive amount of experimental work so far, advances in device applications are hampered by the lack of predictive capabilities for the optical absorption, linear optical, and nonlinear optical characteristics of chromophore structures, and chromophore-polymer interactions. Semiempirical computational methods, with the parameters optimized by using available experimental data, do provide reasonable trends within a given class of materials, but they are not reliably transferable to different types of chromophores. More theory is needed to relate these semiempirical methods to first-principle ab initio approaches to guide the improvement of the former methods. We need new theory dealing with methods for correlating many electrons.
Polymers have become an integral part of the current flat panel liquid crystal display technologies, where polymers form the aligning layers to give the liquid crystals the desired tilt angles. Moreover, polymer-dispersed liquid crystal systems show great promise for improved display applications. There is not yet theory for polymer-liquid crystal systems and their dynamics under electric fields. This is required to understand their display characteristics.
Computational Methods
As noted above, the growth in computing capabilities has enabled the modeling of polymer properties through computer simulations, often called computer
experiments. Computer experiments are useful to address a wide range of questions and to model systems at the level of atomic interactions and in other situations at the macroscopic level. However, the simulation of equilibrium and dynamical polymer properties is complicated by the huge variations in processes that occur on disparate time and length scales.
Local small motions and small deformations occur on short time scales of picoseconds to nanoseconds while diffusion of entangled polymers and protein folding occur on time scales of milliseconds to seconds. Many other polymer processes occur on intermediate scales or over wide ranges of scales from the microscopic to the macroscopic. Different simulation methods (and theories) are needed for the different time and length scales.
Force-Field Simulation
One important computational tool is high-resolution force-field computer simulation. It is based on the interatomic forces, appropriately parameterized from either experiments on simple systems or ab initio quantum mechanical methods. Molecular dynamics (MD) methods, for example, use these forces to continually solve Newton's laws of motions for successive steps in time. A typical time step is about 1 femtosecond, at which the positions and velocities of the particles are recomputed. As the system evolves in time, the computer monitors the internal structures, the motions of molecules, and related properties. Given current capabilities, it is now possible to simulate systems having about 10,000 atoms to hundreds of picoseconds. These simulations are instructive for learning about the behavior of polymers and biopolymers and for capturing our understanding of them in underlying physical force laws on atomistic scales and in terms of the repeat chemical structure of polymers. However, the power of MD simulations is currently limited by the practically achievable time scales and physical sizes and the uncertainties in the force-field parameterization.
Figure 4.11 shows the power and limitations of force-field methods. The second line of the figure shows many processes of biopolymers, and the first line gives the time scale on which they occur. The third line shows processes of synthetic polymers. The power of force-field methods is the wide range of phenomena to which they can be applied, because all physical processes are ultimately derivable from the underlying forces. The main limitation of the method is that computer power is not currently great enough to explore many properties. The fourth line shows projections for the year in which various properties are expected to be accessible by simulations. This time line is based on estimated developments in parallel-processing computing. The maximum run length for a small protein in water in 1992 was about 500 picoseconds (ps), which requires a few hundred hours on a supercomputer. But a single run does not yield an understanding of a process. In 500 ps, we can observe about 10 occurrences of a process that has a 50-ps relaxation time. If we need 10 different samples of the computer experiment in order to understand the statistical errors,
FIGURE 4.11 Time scales for various motions within biopolymers and nonbiological polymers. The year scale at the bottom shows estimates of when each such process might be accessible to force-field simulation on supercomputers, assuming that parallel processing capability on supercomputers increases at about the rate of 103 every 10 years and neglecting new approaches or breakthroughs. At current capabilities, a given allotment of computer time can be used for one run performed over a few hundred picoseconds for a small protein in a few thousand water molecules, or for 1,000 runs to explore 1,000 processes that have relaxation times of hundreds of femtoseconds; this range is indicated by the error bar below the year scale. SOURCE: Reprinted with permission from Chan and Dill (1993), p. 29. Copyright © 1993 by the American Physical Society.
then our ''understanding" of processes could be said to be only in the tens of picoseconds range at the present time. By these estimates, it will be tens of years until many processes such as protein folding, glass transition, shear thinning, and creep and aging in polymers will be fully understood by force-field simulation.
Nevertheless, important steps are already being made. For example, it is expected that advances in algorithms that exploit newer techniques to integrate Newton's equations of motion for the system will be developed to effectively increase the size of the time step. Among these methods are united-atom algorithms, Monte Carlo sampling of configuration space coupled with MD, Brownian dynamics, and the stiff-equation methods. By these means, times into the nanosecond real-time domain will become accessible. One of the most important aspects of MD simulation is the fact that the algorithms are well suited to vectorization and parallelization. With the development of teraflop machines, MD codes will be among the first to be developed for massively parallel computers. The machines will be approximately 1,000 times faster than the current fast single processors, and the time domains that can be reached will then be on the order of microseconds of real time. While this is not yet into the very long times of seconds to years that characterize the longer relaxation times in polymers, the dynamical range that will be covered with the new technology could span 9 orders of magnitude (from femtoseconds to microseconds).
Continued progress will also require improvements and stringent testing in force-field potentials and parameters. Advances in computational capabilities will allow the ab initio quantum mechanical calculations of geometries and force-field energies to be carried out on appropriate chain segment scales with adequate basis functions and rudimentary electron correlation effects. However, limitations on treating electron correlation put the reliable accuracy in these potentials as optimistically no better than about 0.3 kilocalories per mole, nearly comparable to RT (where R is the gas constant and T is the temperature). Hence, the results of quantum mechanical calculations will provide a good guide to force-field parameterization, but the parameters must be adjusted further and tested against experiments.
Coarse-grained Simulations
An alternative to solving Newton's laws for the dynamics of molecules is the use of statistical sampling methods, referred to as Monte Carlo, or complete enumeration of polymer or biopolymer conformations. These approaches are often used with lower-resolution representations of chain molecules (e.g., where chains are represented as strings of "beads," rather than in atomic detail). The advantage over high-resolution simulations is the ability to explore more conformations and thereby represent more accurately some physical properties. Exhaustive simulations are the most complete in this regard, but they suffer either a power-law or exponential dependence of computer time on chain length and are
therefore not practical for long chains. Nevertheless, exhaustive simulations and Monte Carlo methods have been important for testing physical principles, for testing underlying assumptions in other simple models of polymer behavior, and for motivating some of the theoretical developments described below.
Among the most exciting new developments are the Gibbs ensemble Monte Carlo and configurational bias Monte Carlo techniques. They permit computation of phase diagrams from force-field simulations, and chemical potentials for insertion of polymer chains, even into high-density media.
More advances in sampling methods and in algorithms are needed, especially to take advantage of massively parallel computer architectures. Such advances would be particularly valuable for improving our abilities to simulate dense polymer systems and thereby guide further experiments and theoretical developments.
A lower-resolution alternative to force-field simulation for dynamic properties is known as the Brownian dynamics simulation. This method usually models the polymer chain as beads interconnected by elastic springs and moving in a viscous medium. While this method allows the probing of much longer time scales, the spring and viscous damping constants are not directly derivable from atomic quantities, and the model itself becomes problematic for dense polymer systems. Better algorithms and models are required, as well as statistical mechanical methods that will link the parameters in the Brownian dynamics method to molecular-level potentials available in the force-field simulations.
Impressive advances are also being made in the atomistic modeling of glassy polymers. In this approach, the model system is a cube with periodic boundaries, filled with polymer segments. An initial configuration is generated and then relaxed by potential energy minimization. The resulting "equilibrium" structure is examined for predictive and interpretive information. In this way, it is possible to obtain estimates of cohesive energy densities, Hildebrand solubility parameters, degree of randomization of the "amorphous" chains, elastic constants, thermal expansion coefficients, and structural changes brought about by shear and tension deformations. One of the current directions in which these simulations are being extended is to predictions of chain dispositions in the vicinity of a bounding surface. Another is the diffusion of small molecules through polymer films, which is relevant to the understanding of gas-separation membranes and the design of materials of improved permeability and selectivity. Calculations such as these are proving to be quite successful in predicting and interpreting polymer properties and should be extended to other applications.
Another centerpiece of polymer science is the rotational isomeric state (RIS) theory developed in Russia, Japan, Israel, and the United States in the 1950s. For certain conditions, it predicts a wide range of polymer properties from the known chemical constitution of the monomer units. Its premise is that skeletal bonds are in one or another of a few favored conformations. Its power comes from its separation of the computation of a polymer conformation into local and
nonlocal aspects. Computer resources can be used efficiently because the main computational effort is directed only toward extracting information about two-bond or three-bond units, rather than being expended inefficiently in exploring conformations of a long chain. The statistical mechanical machinery then uses that information efficiently to predict the properties of long chains. The RIS theory is a paradigm for combining molecular simulations with statistical mechanics in a way that makes most effective use of both methodologies. Applications to date have focused on isolated chains, and most involve the calculation of equilibrium properties such as chain dimensions, but recent work addresses applications to dynamic properties as well.
Mathematical Methods
With the tremendous increase in computing capability, it will become feasible to solve many fundamental statistical mechanical equations by numerical integrodifferential methods. Recent advances in ab initio quantum mechanical methods, for example, have been made by advanced numerical methodologies that take advantage of the processing power of present supercomputers or advanced workstations. Similar advances in mathematical methodologies will turn out to be as useful for many polymer problems.
Conclusions
-
Theoretical and computational methods play a fundamental role in developing new properties and polymeric materials. Explosive developments in computer technology have fueled the growth of computational experiments and simulations. But computational studies should not overshadow the development of deeper and more rigorous theory, because theory is a powerful wellspring of major paradigm changes. Unique insights will come from theorists and physicists, who should be encouraged to explore polymers and biomolecules.
-
Computational and theoretical methods are often limited to treating narrow ranges of time and spatial scales. But polymers and biomolecules have behaviors that can range over tens of orders of magnitude in time and space within a single system. An important area of future development is methods that can bridge broadly from the fast and microscopic scales to the slow and macroscopic scales. We need to relate continuum fracture mechanics models to atomic levels of bonding, semiempirical predictions of optical properties to ab initio quantum mechanics, picosecond atomic motions of proteins to tens-of-seconds folding processes, atomic bond rotations and interactions to macroscopic glass transitions, and so on. Totally new modeling approaches are needed to bridge these gaps.
-
Force-field simulations and experiments have grown enormously. Further developments will rely not only on increasing computer power and increased
-
access to supercomputers and to fast networks, but also on improved force fields, deeper connections to quantum mechanics, and better treatments of the environment of surrounding and entangled chains or solvents. Better quantum mechanical methods are needed to treat large numbers of electrons and atoms.
-
Practical challenges include applying theory and computation to polymer behaviors in complex media—polymer blends, liquid crystalline polymers, semicrystalline materials, composites, block copolymers, interfaces, the rheology of mixtures, branched molecules, soft matter, and so on.
REFERENCES
Butera, R., L.J. Fetters, J.S. Huang, D. Richter, W. Pyckout-Hinzen, A. Zirkel, B. Farago, and B. Ewen. 1991. "Microscopic and Macroscopic Evaluation of Fundamental Facets of the Entanglement Concept." Physical Review Letters 66:2088.
Chan, H.S., and K.A. Dill. 1993. "The Protein Folding Problem." Physics Today 46(2):24-32.
Gibson, H.W., C. Wu, Y.X. Shen, M. Bheda, A. Prasad, H. Marand, E. Marand, and D. Keith. 1992. "Synthesis, Thermal and Phase-Behavior of Polyester, Polyurethane and Polyamide Rotaxanes." Polymer Preprints 33(1):235.
Mesei, F. 1980. Lecture Notes on Physics. Vol. 122. Berlin: Springer Verlag.
Richter, D., B. Farago, L.J. Fetters, J.S. Huang, B. Ewen, and C. Lartique . 1990. "Direct Microscopic Observation of the Entanglement Distance in a Polymer Melt." Physical Review Letters 64:1389.
Tomalia, D.A., D.R. Swanson, and D.M. Hedstrand. 1992. "Comb-burst Dendrimers—A New Macromolecular Architecture." Polymer Preprints 33(1):180.