Page 199
Training and Search Methods for Speech Recognition
SUMMARY
Speech recognition involves three processes: extraction of acoustic indices from the speech signal, estimation of the probability that the observed index string was caused by a hypothesized utterance segment, and determination of the recognized utterance via a search among hypothesized alternatives. This paper is not concerned with the first process.
Estimation of the probability of an index string involves a model of index production by any given utterance segment (e.g., a word). Hidden Markov models (HMMs) are used for this purpose (Makhoul and Schwartz, this volume). Their parameters are state transition probabilities and output probability distributions associated with the transitions. The Baum algorithm that obtains the values of these parameters from speech data via their successive reestimation will be described in this paper.
The recognizer wishes to find the most probable utterance that could have caused the observed acoustic index string. That probability is the product of two factors: the probability that the utterance will produce the string and the probability that the speaker will wish to produce the utterance (the language model probability).
Even if the vocabulary size is moderate, it is impossible to search for the utterance exhaustively. One practical algorithm is described (Viterbi) that, given the index string, has a high likelihood of finding the most probable utterance.
Page 200
INTRODUCTION
It was pointed out by Makhoul and Schwartz (this volume) that the problem of speech recognition can be formulated most effectively as follows:
Given observed acoustic data A, find the word sequence W that was the most likely cause of A.
The corresponding mathematical formula is:
W = arg max P(A I W)P(W) (1)
W
P(W) is the a priori probability that the user will wish to utter the word sequence W = wl, w2, . . . wn (wi denotes the individual words belonging to some vocabulary V). P(A ï W) is the probability that if W is uttered, data A = al, a2,. . . ak will be observed (Bahl et al., 1983).
In this simplified presentation the elements ai are assumed to be symbols from some finite alphabet A of size êAú. Methods of transforming the air pressure process (speech) into the sequence A are of fundamental interest to speech recognition but not to this paper. From my point of view, the transformation is determined and we live with its consequences.
It has been pointed out elsewhere that the probabilities P(A ô W) are computed on the basis of a hidden Markov model (HMM) of speech production that, in principle, operates as follows: to each word 1 of vocabulary V, there corresponds an HMM of speech production. A concrete example of its structure is given in Figure 1. The model of speech production of a sequence of words W is a concatenation of models of individual words wi making up the sequence W (see Figure 2).
We recall that the HMM of Figure 1 starts its operation in the initial state SI and ends it when the final state SF is reached. A transi-

FIGURE 1 Structure of a hidden Markov model for a word.
Page 201
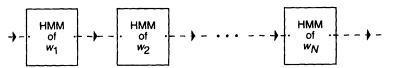
FIGURE 2 Schematic diagram of a hidden Markov model for a sequence of words.
tion out of state s into a next state is either performed in a fixed unit of time along a solid arc and results in an output a from the alphabet A, or is performed instantaneously along an interrupted arc (a null transition) and results in no output.
It is assumed that the different HMMs corresponding to various words v have the same transition structure (e.g., that of Figure 1) and that they differ from each other in the number of states they have, in the values of the probabilities p(t) of the interstate transitions, and in the distributions q(a ô t) of generating output a when the (nonnull) transition t is taken.
The first task, discussed in the second and third sections of this paper, is to show how the values of the parameters p(t) and q(a ô t) may be estimated from speech data, once the structure of the models (including the number of states) is selected by the system designer.
Returning to formula (1), we are next interested in modeling P(W). We will assume that

where f(wl ,w2, . . . wi-1) denotes the equivalence class (for the purpose of predicting the next word wi ) to which the history wl, w2, . . . wi-1 belongs. Essentially without loss of generality we will consider only a finite alphabet f of equivalence classes, so that

A popular classifier example is:

(the bigram model) or

(the trigram model). In this paper it is assumed that the equivalence
Page 202
classifier f was selected by the designer, who also estimated the language model probabilities P(v ÷ f) for all words v e V and classes f e F (Such estimation is usually carried out by processing a large amount of appropriately selected text.)
The second task of this article, addressed in the third and fourth sections, is to show one possible way to search for the recognizer sequence W that maximizes the product P(A ÷ W) P(W) [see formula (1)].
This tutorial paper is not intended to be a survey of available training and search methods. So-called Viterbi training (Rabiner and Juang, 1993) is useful in special circumstances. As to search, various generalizations of the Stack algorithm (Jelinek, 1969) are very efficient and have, in addition, optimality properties that the beam search presented here does not possess. However, these methods (Bahl et al., 1993; Paul, 1992;) are quite difficult to explain and so are not presented here.
ESTIMATION OF STATISTICAL PARAMETERS OF HMMs
We will arrive at the required algorithm (known in the literature variously as the Baum, or Baum-Welch, or Forward-Backward algorithm) by intuitive reasoning. Proofs of its convergence, optimality, or other characteristics can be found in many references (e.g., Baum, 1972) and will be omitted here.
It is best to gain the appropriate feeling for the situation by means of a simple example that involves the basic phenomenon we wish to treat. We will consider the HMM of Figure 3 that produces binary sequences. There are three states and six transitions, t3 being a null transition. The transition probabilities satisfy constraints
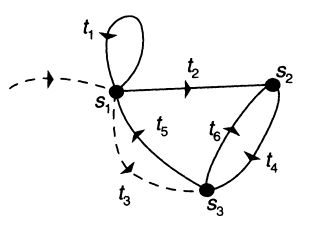
FIGURE 3 Sample three-state hidden Markov model.
Page 203
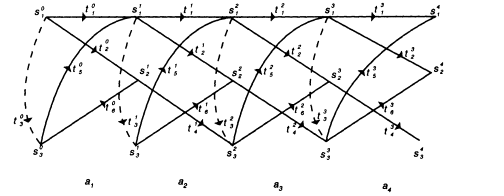
FIGURE 4 Trellis for the hidden Markov model of Figure 3.
![]()
We will wish to estimate the probabilities p(ti) and q(a ÷ ti), where a e {0,1) and i e{1, . . . , 6}. We will designate s1 as the starting state. There is no natural final state.
Suppose we knew that the HMM produced the (long) sequence al, a2. . . ak. How would we estimate the required parameters?
A good way to see the possible operation of the HMM is to develop it in time by means of a lattice, such as the one in Figure 4, corresponding to the production of al, a2, a3, a4 by the HMM of Figure 3. The lattice has stages, one for each time unit, each stage containing all states of the basic HMM. The states of successive stages are connected by the nonnull transitions of the HMM because they take a unit of time to complete. The states within a stage are connected by the null transitions because these are accomplished instantaneously. The starting, Oth stage contains only the starting state (s1) and those states that can be reached from it instantaneously (s3, connected to s1 by a null transition). In Figure 4 superscripts have been added to the transitions and states to indicate the stage from which the transitions originate where the states are located.
We now see that the output sequence can be produced by any path leading from s1 in the 0th stage to any of the states in the final stage.
Suppose we knew the actual transition sequence T = tl, t2, ... tn (n£k, because some transitions may be null transitions and k outputs were generated) that caused the observed output. Then the so-called maximum likelihood parameter estimate could be obtained by counting. Define the indicator function,
Page 204
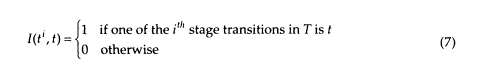
and using it,

for all transitions t, as well as
![]()
for nonnull transitions t' . In Equation (9), d ( , ) denotes the Kronecker delta function. c(t) is then the number of times the process went through transition t, and c(a,t) is the number of times the process went through t and produced the output a.
The ''natural" estimates of the probablity parameters then would be
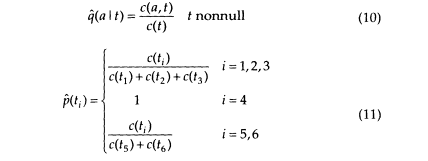
Of course, the idea of us knowing the transition sequence tl, t2, . . . tn, is absurd. But what if we knew the probabilities P{ti = t} that transition t was taken out of the ith stage of the process? Then it would seem intuitively reasonable to define the "counts" by (t' is restricted to nonnull transitions)
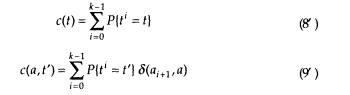
and use these in the estimation formulas (10) and (11).
Since the production of each output ai corresponds to some nonnull
Page 205
transition from stage i - 1 to stage i, then SP{ti = t" } = 1, where the sum is over all nonnull transitions t". Thus, while in case (8), the counter of exactly one of the nonnull transitions is increased by 1 for each output, this same contribution is simply distributed by (8') among the various counters belonging to nonnull transitions.
The estimates arising from (8') and (9') will be convenient only if it proves to be practically sensible to compute the probabilities P {ti = t). To derive the appropriate method, we need a more precise notation:
| L (t) | the initial state of transition t [e.g., L(t6) = S3] |
| R (t) | the final state of transition t [e.g., R(t6) = s2] |
| P{ti = t} | the probability that al, a2, . . . akwas produced and the transition out of the ithstage was t |
| P{si= s} | the probability that al, a2 . . . ai was produced and |
| the state reached at the ithstage was s | |
| P{restïsi= s } | the probability that ai+1, ai+2 . . . akwas produced when the state at the ith stage was s |
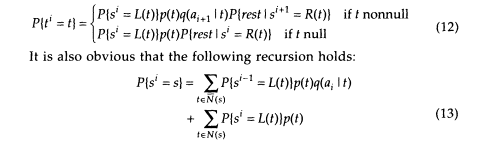
Here N(s) is the set of all null transitions ending in s, and N (s) is the set of all nonnull transitions ending s. That is,
![]()
Even though Equation (13) involves quantities P{si = s} on both sides of the equation, it can easily be evaluated whenever null transitions do not form a loop (as is the case in the example HMM), because in such a case the states can be appropriately ordered. We can also obtain a backward recursion:
Page 206
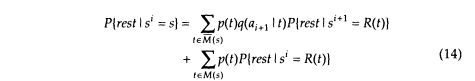
where M(s) and M (s) are the sets of null and nonnull transitions leaving s, respectively:
![]()
Recursions (13) and (14) then lead directly to an algorithm computing the desired quantities P{ti = t} via formula (12):
1. The Forward Pass
Setting P{s0 = sI}= 1 (in our HMM, sI = sl), use (13) to compute P{si = s} for all s, starting with i = 0 and ending with i = k.
2. The Backward Pass
Setting P{restïsk = s} = 1 for all s, use (14) to compute P{restïsi = s}, starting with i = k - 1 and ending with i = 0.
3. Transition Probability Evaluation
Using formula (12), evaluate probabilities P{ ti = t} for all t and i = 0, 1, . . . , k - 1.
4. Parameter Estimation
Use the counts (8') and (9') to get the parameter estimates
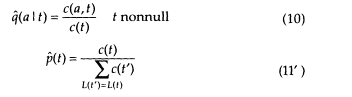
There is only one flaw, seemingly a fatal one, to our procedure: formulas (12), (13), and (14) use the values of the parameters p(t) and q(a ï t) that we are trying to estimate! Fortunately, there is a good way out: we put the above algorithm into a loop, starting with a guess at p(t) and q(a ï t), obtaining a better estimate (this can be proved!) with (10) and (11' ), plugging these back in for p(t) and q(a ï t), obtaining an even better estimate, etc.
Page 207
REMARKS ON THE ESTIMATION PROCEDURE
The heuristic derivation of the HMM parameter estimation algorithm of the previous section proceeded from the assumption that the observed data were actually produced by the HMM in question. Actually, the following maximum likelihood properties are valid regardless of how the data were produced:
Let Pl(A) denote the probability that the HMM defined by parameters l produced the observed output A. If l' denotes the parameter values determined by (10) and (11') when parameters l were used in (12), (13), and (14), then Pl,(A) > Pl(A).
The previous section showed how to estimate HMM parameters from data. We did not, however, discuss the specific application to speech word models. We do this now.
First, it must be realized that the word models mentioned in the first section (e.g., see Figure 1) should be built from a relatively small number of building blocks that are used in many words of the vocabulary. Otherwise, training could only be accomplished using separate speech data for each and every word in the vocabulary. For instance, in the so-called fenonic case (Bahl et al., 1988), there is an alphabet of 200 elementary HMMs (see Figure 5), and a word model is specified by a string of symbols from that alphabet. The word HMM is then built out of a concatenation of the elementary HMMs corresponding to the elements of the defining string. The training data A = al, a2, . . . ak is produced by the user, who is told to read an extended text (which, however, contains a small minority of words in the vocabulary). The corresponding HMM to be trained is a concatenation of models of words making up the text. As long as the text HMM contains a sufficient number of each of the elementary HMMs, the resulting estimation of the p(t) and q(a ï t) parameters will be successful, and the HMMs
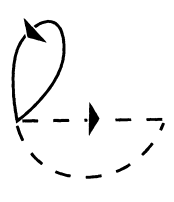
FIGURE 5 Elementary hidden Markov model for the fenonic case.
Page 208
corresponding to all the words of the entire vocabulary can then be specified, since they are made up of the same elementary HMMs as those that were trained.
FINDING THE MOST LIKELY PATH
Our second task is to find the most likely word string W given the observed data A. There are many methods to do this, but all are based on one of two fundamental methods: the Viterbi algorithm or the Stack algorithm (A* search). In this paper the first method is used.
Consider the following basic problem:
Given a fully specified HMM, find the sequence of transitions that were the most likely "cause" of given observed data A.
To solve the problem, we again use the trellis representation of the HMM output process (see Figure 4). Let p be the desired most likely path through the trellis, that is, the one that is the most probable cause of A. Suppose p passes through some state sij, and let p' be the initial segment of p ending in sij, and p* the final segment starting in sij. Then p' is the most likely of all paths ending in sij, because if p" were more likely, then p"p* would be more likely than p = p'p*, contradicting our assumption that p is the most likely path.
The direct consequence of this observation is that, if there are multiple paths leading into sij, only the most probable of them may be the initial segment of the most likely total path. Hence, at each stage of the trellis, we need to maintain only the most probable path into each of the states of a stage; none of the remaining paths can be the initial segment of the most probable complete path.
Let Pm{si = s} be the probability of the most likely path ending in state s at stage i. We have the following recursion:
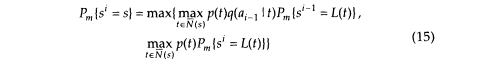
where the transition sets N(s) and N (s) were defined in (13').
The desired Viterbi algorithm (Viterbi, 1967) then is:
1. Setting Pm{s0 = s1} = 1 , use (15) to compute Pm{ si = s} for all s, starting with i = 0 and ending with i = k. For each state s at stage i keep a pointer to the previous state along that transition in formula (15) that realized the maximum.
Page 209
2. Find (k is the length of the output data)
![]()
3. The trace-back from s along the pointers saved in 1 above defines the most likely path.
DECODING: FINDING THE MOST LIKELY WORD SEQUENCE
We are now ready to describe the method of search for the most likely word sequence W to have caused the observed acoustic sequence A. This method, like all the others for large vocabulary sizes N, will be approximate. However, it gives very good results from the practical point of view [i.e., it is very rare that the sequence IW defined by Equation (1) is the one actually spoken and will not be found by our search method].
First, consider the simplest kind of a language model, one in which all histories are equivalent [see Eq. (2)]. Then
![]()
It is immediately obvious that in this case finding W amounts to searching for the most likely path through the graph of Figure 6. This statement must be interpreted literally-we do not care what happens inside the HMM boxes.
The slightly more complicated bigram language model [see Eq. (4)] results in
![]()
and W is defined by the most likely path through the graph of Figure 7. Note that while Figure 7 is somewhat more complicated than Figure 6, the number of states is the same in both. It is proportional to the vocabulary size N. Thus, except in cases where estimates P(vi ï vj) cannot be obtained, one would always search Figure 7 rather than Figure 6.
For a trigram language model [see Eq. (5)],
![]()
the graph is considerably more complex-the number of states is proportional to N2 . The situation for N = 2 is illustrated in Figure 8.
Page 210
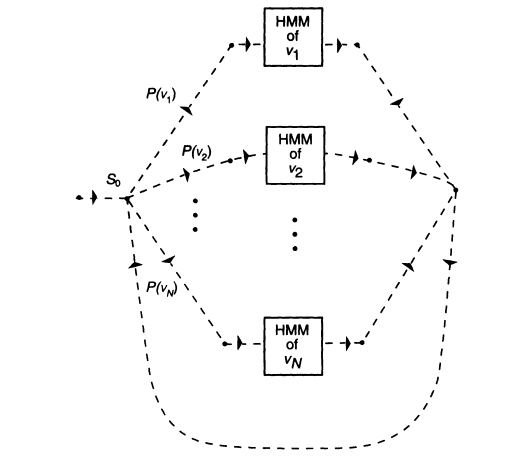
FIGURE 6 Schematic structure of the hidden Markov model for a unigram language model.
In general, similar graphs can be derived for any equivalence classifier f, as long as the number of equivalence classes is finite.
How do we find the most likely paths through these graphs? There exist no practical algorithms finding the exact solution. However, if we replace the boxes in Figures 6 through 8 with the corresponding HMM models, all the figures simply represent (huge) HMMs in their own right. The most likely path through an HMM is found by the Viterbi algorithm described in the previous section!
The only problem is that for practical vocabularies (e.g., N = 20,000) even the HMM of Figure 7 has too many states. One solution is the so-called beam search (Lowerre, 1976). The idea is simple. Imagine the
Page 211
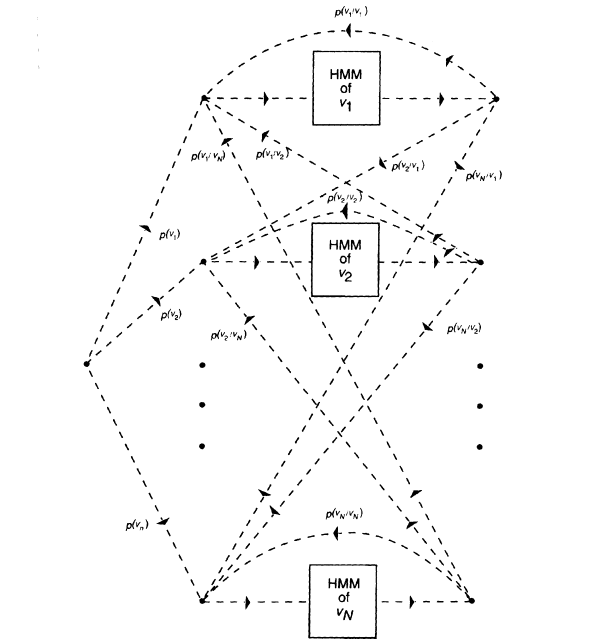
FIGURE 7 Schematic structure of the hidden Markov model for a bigram language model.
Page 212
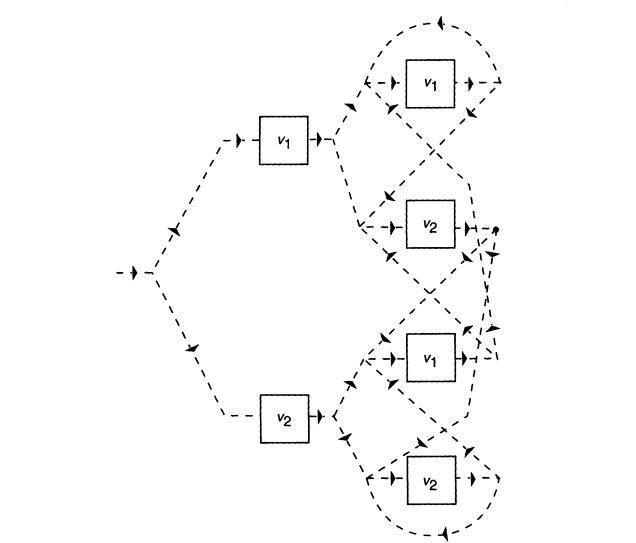
FIGURE 8 Schematic structure of the hidden Markov model for a trigram language model corresponding to a two-word vocabulary.
trellis (see the third section of this paper) corresponding to Figure 7. Before carrying out the Viterbi purge (15) at stage i, we determine the maximal probability Pmi-1 of the states at stage i - 1.

Page 213
We then establish a dynamic threshold
![]()
where K is a suitably chosen number. Finally, we eliminate from the trellis all states s on level i - 1 such that
![]()
This procedure is capable of drastically reducing the number of states entering the comparison implied by the max function in (15), without significantly affecting the values Pm {si = s} and makes the Viterbi algorithm a practical one, at least for the case of bigram language models.
Is there any expedient way to implement the search for W for a trigram language model? One ingenious method has recently been suggested by researchers at SRI (Murveit et al., 1993). I will describe the main idea.
The HMMs for each word in the vocabulary have a final state (see the right-most column of states in Figure 7). Final states of words therefore occur at various stages of the trellis. As the beam search proceeds, some of these states will be killed by the thresholding (21). Consider now those final states in the trellis that remain alive. The trace-back (see fourth section) from any of these final states, say, of word v at stage j, will lead to the initial state of the same word model, say at stage i. The pair (i,j) then identifies a time interval during which it is reasonable to admit the hypothesis that the word v was spoken. To each word v there will then correspond a set of time intervals: {[i1(v),j1(v)], [i2(v),j2(v)], . . . [im(v),jm(v)]}. We can now hypothesize that word v' could conceivably follow word v if and only if there exist intervals [ik(v),jk(v)] and [it(v'),jt (v')] such that ik(v) < it(v'), jk(v) > it(v'), and jk(v) < jt (v'). We can, therefore, construct a directed graph whose intermediate states correspond to words ve V that will have two properties: (1) Any path from the initial to the final state of the graph will pass through states corresponding to a word sequence w1,w2, . . . wn, such that wi is permitted to follow wi-1 by the word interval sets. (2) Arcs leading to a state corresponding to a word v' emanate only from states corresponding to one and the same word v. (Figure 8 has this property if its boxes are interpreted as states).
To the arcs of this graph we can then attach trigram probabilities P(wi ï wi-2wi-1), and we can expand its states by replacing them with the HMMs of the corresponding word. We can then construct a trellis for the resulting overall trigram HMM that will have only a small
Page 214
fraction of states of the trellis constructed directly for the trigram language model (cf. Figure 8).
Consequently, to find W we conduct two beam searches. The first, on the bigram HMM, results in word presence time intervals. These give rise to a trigram HMM over which the second beam search is conducted for the final W.
REFERENCES
Bahl, L. R., F. Jelinek, and R. L. Mercer, ''A maximum likelihood approach to continuous speech recognition," IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. PAMI-5, pp. 179-190, March 1983.
Bahl, L., P. Brown, P. de Souza, R. Mercer, and M. Picheny, "Acoustic Markov Models used in the Tangora speech recognition system," in Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing, New York, April 1988.
Bahl, L. R., P. S. Gopalakrishnan, and R. L. Mercer, "Search Issues in Large Vocabulary Speech Recognition," Proceedings of the IEEE Workshop on Automatic Speech Recognition, Snowbird, Utah, 1993.
Baum, L., "An inequality and associated maximization technique in statistical estimation of probabilistic functions of a Markov process," Inequalities, vol. 3, pp. 1-8, 1972.
Jelinek, F., "A fast sequential decoding algorithm using a stack," IBM Journal of Research Development, vol. 13, pp. 675-685, Nov. 1969.
Lowerre, B. T., "The Harpy Speech Recognition System," Ph.D. Dissertation, Department of Computer Science, Carnegie-Mellon University, Pittsburgh, Pa., 1976.
Murveit, H., J. Butzberger, V. Digalakis, and M. Weintraub, "Large-Vocabulary Dictation Using SRI's Decipher Speech Recognition System: Progressive Search Techniques," Spoken Language Systems Technology Workshop, Massachusetts Institute of Technology, Cambridge, Mass., January 1993.
Paul, D. B., "An Essential A* Stack Decoder Algorithm for Continuous Speech Recognition with a Stochastic Language Model," 1992 International Conference on Acoustics, Speech, and Signal Processing, San Francisco, March 1992.
Rabiner, L. R., and B. H. Juang, Fundamentals of Speech Recognition, Prentice-Hall, Englewood Cliffs, N.J., 1993, pp. 378-384.
Viterbi, A. J., "Error bounds for convolutional codes and an asymmetrically optimum decoding algorithm," IEEE Transactions on Information Theory, vol. IT-13, pp. 260-267, 1967.
















