2
The Formal Demography of Population Aging, Transfers, and the Economic Life Cycle
Ronald D. Lee
INTRODUCTION
The human life-cycle has two stages of dependency—childhood and old age—separated by a long stage of surplus production. Dependent age groups are sustained by flows of resources upwards and downwards by age from the more productive stage in the middle. These resource flows occur through three institutional channels: the family, the public sector, and financial markets. Through each channel, resource reallocation takes one of three forms: capital formation, credit transactions, and interage transfers. As fertility and mortality decline, the population age distribution shifts toward older ages, which changes the terms on which these resource flows take place. The public sector, through which some of the transfer flows are channeled, is particularly sensitive to the consequences of these age distribution changes. The governments of many industrial nations are concerned that transfers to the elderly, which are already costly, will be raised rapidly by population aging in the early twentieth century. Many Third World nations, preoccupied in the past with the costs of their young populations'
The author is grateful to Robert Willis for many helpful discussions and for the extensive use made of his earlier work, and to Michael Anderson for excellent research assistance. James Poterba and Samuel Preston provided helpful comments on an earlier draft. Research support from the Institute for International Studies of the University of California at Berkeley is gratefully acknowledged.
high child dependency burden, are now beginning to worry instead about the costs of impending population aging.
This chapter develops an accounting framework for evaluating systems of interage transfers, and examines how such systems are affected by changing population age distributions. To understand the role of transfers in achieving a desirable allocation of consumption over the life-cycle, it is necessary to consider them in relation to the other forms of reallocation: credit and capital. There is a rich and controversial literature on the relation between transfer systems and capital accumulation: Does life-cycle saving account for the capital stock of industrial nations (Modigliani, 1988; Tobin, 1967)? Or is the desire to leave bequests responsible (Kotlikoff and Summers, 1981, 1988)? Do public sector pension systems undermine private saving (Feldstein, 1974)? Or do elderly parents simply increase their familial transfers to their children to offset the pensions (Barro, 1974)? Transfers may be used to achieve efficient allocations over the life-cycle that are unattainable via competitive market mechanisms (Samuelson, 1958), and if transfers upwards or downwards by age are needed to achieve efficient allocations, that fact tells us that the population growth rate is less than or more than the optimal rate (Samuelson, 1975, 1976; Willis, 1988; Lee, in press, b). These are issues that a coherent accounting framework may help to clarify.
The theoretical basis for a comprehensive framework for studying the reallocation of resources across age in general, and transfers in particular, has been laid by economic and demographic research over the past 35 years. Macroeconomic models with "overlapping generations" sprang from the seminal work of Samuelson (1958) and, later, Diamond (1965). The literature has developed to the point that there is now a textbook that teaches macroeconomic theory entirely from the point of view of a simple model of economies with overlapping generations (McCandless, 1991). The models have been used to explore such diverse topics as the existence of money, the rate of interest, aggregate savings rates, the Ricardian equivalence theorem, optimal population growth rates, economic fluctuations, and so on. These important developments in economic theory pave the way for a deeper integration of demography and macroeconomics than has yet proven possible. However, perhaps because of the wish to examine nonsteady-state situations, the demographic models used by most mainline economists are very simplistic: the life-cycle typically consists of two broad age groups, workers and retirees, or young and old, with perfect survival until the end of the second. Childhood is often ignored, and life really begins at labor market entry. This life-cycle incorporates only one period of dependency rather than two. In such a demographic world (used all the way through the McCandless textbook), some of the most basic questions cannot be properly posed or will receive misleading answers. This is true of most questions
concerning aging, such as the effect of mortality change on saving behavior or capital accumulation, or the effect of slower growth due to lower fertility, which will alter the share of life-cycle resources devoted to children and alter saving behavior in complex ways (see Mason, 1987). Many interesting empirical questions are also overlooked, including those that involve the interaction of age distribution with institutional context.
Largely ignored by mainline economists, a few economic demographers have begun to explore the interface of richer demographic models and the overlapping generation models of economists. Arthur and McNicoll (1978) published a brief but seminal comment on a paper by Samuelson (1975). Willis (1988), building on Gale (1973), published an important paper incorporating familial and public transfer systems into an accounting framework that related flows to stocks, and on which the work proposed here leans heavily. Lee (1980, in press, a) and Lee and Lapkoff (1988) also contributed analytic and empirical studies and developed early versions of the approach proposed here. On the more demographic side, Keyfitz (1985, 1988) and Bourgeois-Pichat (1978) developed formal analyses of the demography of funded and unfunded pension systems, and Preston (1982) developed and applied analytic tools relating the distribution of characteristics over the individual life-cycle to the distribution of characteristics in a stable population, and showed how these distributions are affected by changes in fertility and mortality.
This chapter develops a conceptual and accounting framework that builds on these two approaches and seeks to bridge the gap between them. Parts are heavily influenced by Willis (1988). The past literature in both demography and economics has paid insufficient attention to mortality change, and this chapter also offers some advances in that direction. At the same time, the analysis here is limited to comparative steady states and mainly to the special case of steady states with optimal saving and investment. These are serious limitations in the United States since recent decades have been marked by major changes in mortality, rates of inflation, real interest rates, regulations governing Social Security and private pensions, rates of real wage growth, rates of appreciation of housing, and so on.
SOME ANALYTICS OF AGING IN STABLE POPULATIONS
In a closed population, population aging can occur due either to decline in fertility or to decline in mortality, and these have quite different effects. Nonetheless, the distinction between the effects of changing fertility and changing mortality is not the most helpful one.
Let p(x) be the probability of survival from birth to age x, let B(t) be the number of births at t (actually, the number between t and t + dt), and let n be the growth rate of the stable population. Then the stable population age
distribution at time t is N(x,t) = B(t)e-nxp(x). We can divide by population size to find the proportional age distribution, be-nxp(x), where b is the crude birth rate; b is simply a scaling factor here, the same for every age. The natural decomposition, therefore, is into a "rate of growth" effect, due to n, and a "life-cycle" effect or "individual aging" effect, due to the survival schedule, p(x).
When fertility changes, this affects the rate of growth, n, but not p(x). Therefore fertility has only a rate of growth effect. Higher fertility raises n, which increases the size of more recently born cohorts relative to older ones and therefore makes the population younger.
A mortality decline is of course reflected in p(x), which leads to individual aging, tending to make the population older. However, lower mortality also raises the population growth rate, n, since more women survive to childbearing age. In this way, lower mortality tends to make the population younger. The net effect of mortality decline is therefore ambiguous, and can in fact make the population either younger or older, depending on the pattern of mortality change, which in turn depends on the initial level of mortality. Figure 2-1 depicts this decomposition.
The Rate of Growth Effect
Fertility Change
Let us consider more formally the way that fertility and mortality affect the population age distribution through the rate of growth and individual
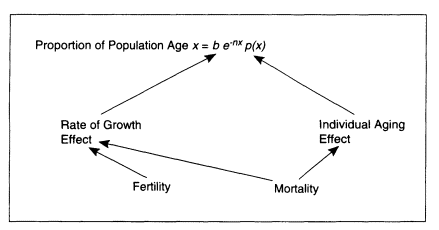
Figure 2-1 Fertility, mortality, and stable age distributions.
aging. Let F be the total fertility rate, let sr be the proportion of births that is female, and let Af be the mean age of childbearing in the stationary population; p(Af) is then the proportion of female births surviving to the mean age of childbearing. To a linear approximation, the population growth rate is given by1
The effect on n of a change in F is found by differentiating this expression for n
Note that while the effect of fertility change depends on its initial level, it is independent of the level of mortality, to a first approximation.
Mortality Change
Let i be some index of the level of mortality, such that the survival probabilities vary with i. For any level of i there will be some corresponding level of life expectancy at birth, e0. The scaling of index i is arbitrary. It will be convenient to choose a scale such that in the neighborhood of any given level of life expectancy, a one-unit change in i corresponds to a change of 1 year in life expectancy; that is, d(e0)/di = 1.
The effect on n of a change in mortality, indexed by i, is given by
The effect of mortality decline on the population growth rate is independent of the level of fertility, to a first approximation. Note that p(Af) is bounded above by unity, so that once mortality is already very low, further declines in mortality can have very little effect on the population growth rate. Figure 2-2 plots ∂n/∂i as calculated from Coale-Demeny model life tables, where i is scaled so that a unit change corresponds to a gain in e0 by one year. Figure 2-2 shows how ∂n/∂i changes, depending on the initial level of life expectancy, for life expectancy from 20 to 80 years. When mortality is initially very high, a 1-year gain from a life expectancy of 20 years to a life expectancy of 21 years leads to an increase in the population growth rate by 0.16 percent per year. When mortality is very low, a 1-year gain in life expectancy from 79 years to 80 years would raise the population growth rate by less than 0.01 percent per year, a tiny amount.
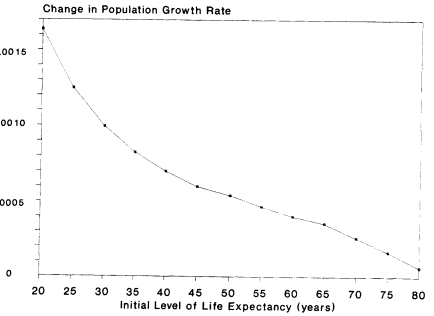
Figure 2-2 The effect of a 1-year gain in life expectancy on the population growth rate, from differing initial levels of life expectancy (∂n/∂i). SOURCE: Calculated from Coale-Demeny (1983) model life tables (west females).
The Life-Cycle Effect, or Individual Aging
The shape of the individual life-cycle is described, from a demographic point of view, by the distribution of expected person years lived by age. Ex post, every individual simply lives until death, which is a discrete event. But in prospect, the individual faces a series of probabilities of survival, p(x), which change with age. We can also think of p(x) as describing the density of expected person-years lived at age x for an individual at birth. Expectation of life at birth, e0, is simply the integral over all ages of p(x); put differently, it is the sum over all ages of the expected person-years lived.
The shape of the demographic life-cycle depends on the severity of the mortality regime: under high mortality, the proportion of the life-cycle lived in the third stage, old age, is relatively small, and under very low mortality it is relatively high. Figure 2-3 plots the number of person-years lived in each of the three stylized life-cycle stages for different mortality regimes indexed by e0, life expectancy at birth.2 When life expectancy is
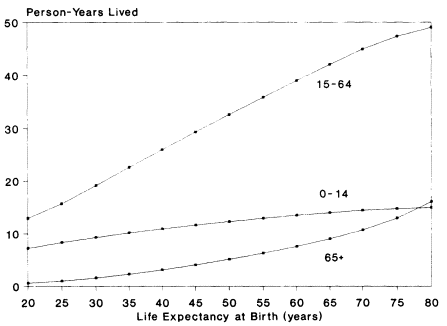
Figure 2-3 Person-years lived in each life-cycle stage, by life expectancy. SOURCE: Calculated from Coale-Demeny (1983) model life tables (west females).
20, only 0.6 of a person-year is lived at age 65 and above; when life expectancy is 80, 16 years are. This is a 27-fold increase. Person-years lived in childhood increase from 7.2 to 14.9, just more than doubling. Person-years lived in the working ages rise from 12.2 to 49.0, quadrupling. This is a different pattern than most of us would expect, since it is well known that, historically, mortality has declined most rapidly in childhood and least rapidly at the older ages.3
Figure 2-4 shows how the proportion of the life-cycle spent in each stage changes as we pass from the high-mortality regime to a low-mortality regime. The proportion of the life-cycle spent in the working years changes little; the proportion spent in childhood declines markedly; and the proportion spent in old age increases dramatically.
Recall that life expectancy is the sum over all ages of p(x). If life
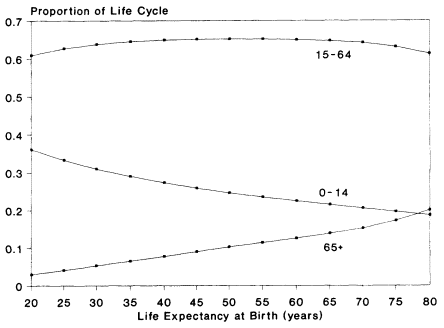
Figure 2-4 Proportion of life cycle lived in life-cycle stage, by life expectancy. SOURCE: Calculated from Coale-Demeny (1983) model life tables (west females).
expectancy increases by 1 year, then the sum of p(x) must also increase by 1 year. Put differently, the plot of the changes in p(x) when life expectancy changes by 1 year gives us an additive decomposition of that 1 year into gains in person-years lived at the various ages. Figure 2-5 plots dp(x)/di for various initial levels of life expectancy, showing how these gains in person-years are distributed across the three life-cycle stages, and how that distribution varies from initially low to initially high levels of life expectancy.4 For example, by starting at a life expectancy of 20, if life expectancy were
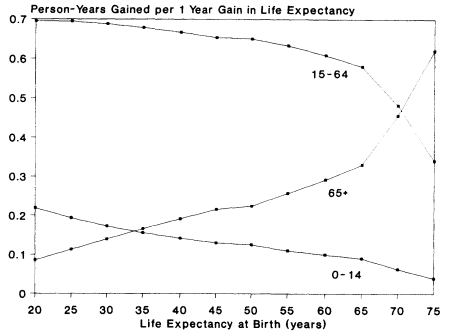
Figure 2-5 Person-years gained in each life-cycle stage when life expectancy increases by 1 year, by initial level of life expectancy. SOURCE: Calculated from Coale-Demeny (1983) model life tables (west females).
to increase to 21 then, according to the Coale-Demeny life-table system, this would consist of 0.22 year for children, 0.70 year for the working ages, and 0.08 year for the elderly. When initial life expectancy is 75, however, as it is now in the United States, then a gain of 1 year in life expectancy would be distributed as only 0.04 year to children, only 0.34 year to the working ages, and 0.62 year to the elderly.
We have now considered the effects of fertility and mortality on the population age distribution through the rate of growth effect and the life-cycle effect. While I have described the sign and magnitude of each effect, I have not combined them all in an appropriately weighted combination to find their net effect on population aging. I am not doing this here, in part because it is not useful for the analysis later in this chapter, and, in part, because it has been done elsewhere (see, for example, Coale, 1972). Suffice it to say here that fertility decline unambiguously causes population aging. Mortality decline starting from very high mortality actually makes populations younger, as the rate of growth effect overwhelms the individual aging effect. However, when starting from lower levels of mortality, the
individual aging effect outweighs the rate of growth effect, and the population becomes older.
THE ECONOMIC LIFE-CYCLE AND AGGREGATE CONSTRAINTS
We now turn from the formal demography of aging to the economics of population age distributions. We can carry out our analysis at the level of either the individual or the household. Individuals live in households, and consumption in households is subject to resource pooling, scale economies, and public goods. Furthermore, children are not responsible for financing or choosing their own level of consumption; instead, this is done by their parents. For these reasons, the household accounting framework is appealing. However, the household framework also presents serious analytic difficulties: the dissolution and reconstitution of households over the life-cycle, the presence of multiple adults of different ages in the household, and covariation of household headship propensities with earnings or wealth of individuals. Because of these difficulties with the household framework, I employ the individual accounting framework predominantly here, despite its occasional artificiality in dealing with children. For a household-based analysis, see Lee (in press, b). Some technical details on the household accounting framework are provided in the appendix to this chapter.
The Economic life-cycle
The human life-cycle begins and ends with stages of dependency, in the sense that consumption exceeds labor earnings. This generalization applies on average to age groups, but not necessarily to individuals so far as old age is concerned. The average shape appears to be universal, although ages and extent of dependency may vary widely from population to population. It arises from the combined influence of physiology, culture, institutions, and economic choice, in ways that we take as given.5
Figure 2-6 shows profiles of labor earning and consumption for U.S. households by age of respondent for 1987. Earnings are before taxes and include employers' contributions to Social Security, as well as fringe benefits. Quinn and Burkhauser, in this volume, discuss some of the economic and social factors shaping this age profile and the way it has changed over time. If labor markets are competitive, then this age profile reflects the
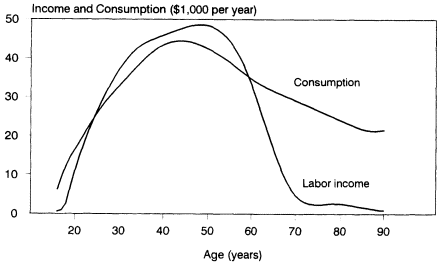
Figure 2-6 Labor income and consumption by age of household respondent. SOURCE: Calculated from 1987 U.S. Consumer Expenditure Survey.
efficiency of labor at each age, as well as the hours of labor supplied, for surviving individuals at each age, averaged across sex. Consequently this age profile can be used to calculate the aggregate quantity of labor in efficiency units as a weighted sum of the population age distribution. When the population age distribution changes, for example as a result of population aging, this age profile permits assessment of the consequences for aggregate production. Consumption includes in-kind public sector transfers (health, education, food stamps, housing benefits) and the imputed value of services from owner-occupied housing, automobiles, and consumer durables (for details, see Lee, in press, b).
Reallocation Across Age and Time
The household age profiles in Figure 2-6 indicate that old households are able, on average, to consume far more than they produce through their own labor, whereas young households consume slightly more than they produce. Evidently there has been a reallocation of output from more productive to less productive age groups. Such reallocations take one of three forms: credit, capital accumulation, or transfers. The defining feature of transfers is that unlike borrowing or lending, they involve no quid pro quo.6
TABLE 2-1 Resource Reallocation Across Age and Time
|
|
Institution |
||
|
Form |
Family |
Market |
Public Sector |
|
Capital |
House |
Factories |
Social |
|
|
Car |
Inventories |
infrastructure |
|
|
Consumer durables |
Farms |
(hospitals, roads |
|
|
Inventories |
|
airports, government |
|
|
Education |
|
buildings) |
|
Transfers |
Child rearing |
Government debt |
Public education |
|
|
College costs |
|
Medicaid, Medicare |
|
|
Gifts |
|
Social Security |
|
|
Bequests |
|
Food stamps |
|
|
Help to elderly |
|
Aid for dependent children |
|
Borrowing/lending |
Familial loans "Transfers" with a quid pro quo |
Credit markets (mortgages, credit cards, bond issues) |
Government loans |
Each of these three forms of reallocation can take place through each of three kinds of institutions: the family, the public sector, or the market.7Table 2-1 provides examples of each form of reallocation as achieved through each institution.
Net worth, which includes debt or credit plus the value of physical assets and other financial assets, is a familiar concept. Estimates of average net worth for age groups are available. For our purposes, it is helpful to extend this familiar concept of age-specific net worth or wealth to include transfer debt or transfer wealth for an age group. This is defined as the present value of expected transfers to be received in the future, minus the expected value of transfers to be made in the future. Under steady-state conditions, patterns of transfers will be repeated generation after generation, so these average expectations for age groups are well defined, even though no particular individual is obligated to leave a particular size bequest, for example.
Using the data shown in Figure 2-6, we can calculate the life-cycle wealth or debt accumulated by a cohort up to each age x, per original member of the cohort (equations are derived later). Results of such a calculation are shown in Figure 2-7. This figure looks very different from
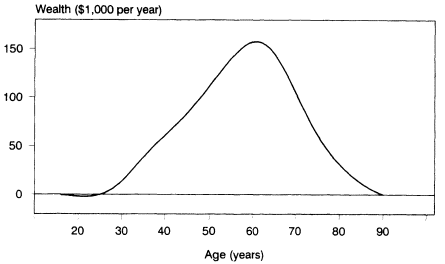
Figure 2-7 Total wealth per original birth cohort member, by current age of cohort (r = n = 0). SOURCE: Calculated from 1987 U.S. Consumer Expenditure Survey.
most plots of wealth by age, for several reasons. First, it is plotted per original member of the birth cohort rather than per surviving member. Second, it includes Social Security and Medicare wealth, which decline steeply with age after the early 60s, as remaining person-years of life decline. Third, under the golden rule assumption, the average person dies with zero wealth, and the constituent age profiles have been adjusted to ensure this. Fourth, it only includes wealth held for purposes of spreading consumption over the life-cycle, not wealth held for purposes of leaving bequests or making other transfers. Furthermore, it assumes that the consumption-spreading motive is actuarially derived, and if people actually hold extra wealth beyond that necessary to consume for the average length of life, that extra wealth is not counted here.
Social Security wealth is one important portion of total life-cycle wealth; it is plotted in Figure 2-8. At age 60, it accounts for about 45 percent of total life-cycle wealth. Note that it starts at 0 at labor market entry, then rises smoothly to about $65,000 in the early 60s. It then falls to 0 in step with declining remaining person-years to be lived by the cohort.
With this generalization of the concept of wealth or debt, we can say that the age profiles of labor earnings and consumption give rise to a demand for a certain amount of wealth at each age in terms of ex ante plans, or entail a certain age profile of wealth ex post. If we sum these age-
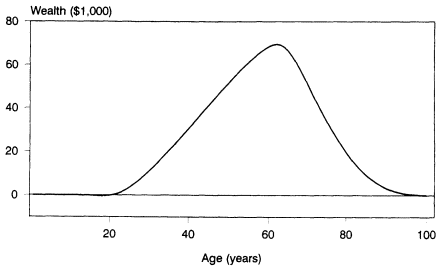
Figure 2-8 Social Security wealth per original birth cohort member, by age of cohort (r = n = 0). SOURCE: Calculated from 1987 U.S. Consumer Expenditure Survey.
specific wealth functions weighted by the entire population age distribution, then we find the aggregate demand for wealth in the population.8 Populations in which child dependency dominates tend to consume, on average, before they produce and therefore have a negative aggregate demand for wealth, that is, a demand for debt. Populations in which old-age dependency dominates tend to consume, on average, after they have produced and therefore have a positive aggregate demand for wealth. I show that in any case, this aggregate demand for wealth per person, W, must equal the value of the aggregate capital stock, K, plus the value of transfer wealth, T. The aggregate value of credit, M, must, of its nature, be zero (with government debt and foreign participation in credit markets ignored). Thus society as a whole cannot use credit to satisfy its aggregate demand for positive or negative wealth. For this reason, there are some average life-cycle consumption paths that cannot be attained through competitive markets if physical accumulation is not possible, as Samuelson (1958) pointed out. These ideas are developed more formally below.
The Economic Demography of Age Accounts
Consider a closed stable population in which age profiles of labor earning, y1(x), and consumption, c(x), are fixed. The economy, which is closed, is on a golden rule steady-state growth path, so that the interest rate, r, equals the population growth rate, n, plus the rate of labor-augmenting technical progress, λ, and aggregate consumption equals aggregate labor earnings. Labor earnings depend on physical capital per efficiency unit of labor, k, and in a more complete analysis would depend on the education of each age group as well. Capital is homogeneous and indestructible. The earnings profile and the cross-sectional consumption profile both shift upward proportionately at the exponential rate λ. In the analysis below, λ is taken to be zero, but it is easily shown that all the results continue to hold more generally, except that per capita averages have an exponential trend when λ≠0, which does not affect the results of interest. It should be kept in mind that when, in the following, I say that r = n = 0, the results also hold for r = n+ λ, which, based on historical experience, might be about 0.02 per year.
Transfer patterns are taken as fixed and exogenous, for the most part. Bequests are treated as if they were inter vivos transfers, without loss of generality as long as mortality is held constant. All public sector transfer budgets are taken by definition of transfers to be balanced; the partially funded portion of Social Security is viewed as government saving, rather than as a transfer. Money as a store of value does not exist. The public sector provides no goods and services except as transfers.
Consumption and Labor Earnings
Let c(x) be per capita consumption at age x. Total consumption by the population in some year can be found by multiplying the population at age x by c(x) and integrating over all ages. Dividing this by total population, we get per capita consumption, c. If we instead divide total consumption by the number of births, B(t), then in a stable population we will get
In both cases, the quantity is invariant over time in a stable population with λ = 0. The variable C can be seen to be the present value of expected life-cycle consumption with a discount rate of n. That is, if we interpret p(x) as the probability of being alive at age x, then p(x)c(x) is expected consumption at age x as viewed from age 0, and e-nx is the discount factor. (The interpretation for a household is more complicated; see the appendix
to this chapter.) Evidently per capita consumption, c, is related to the present value of life-cycle consumption (with discount rate n) by C = c/b. Per capita labor income in a stable population, denoted y1, is defined similarly. The present value of expected life-cycle labor earnings, discounted at n, is denoted Y1. This equals y1/b and is given by
In a golden rule population, C = Y1 (or equivalently, c = y1).
It is easily shown that ∂c/∂n = -k across golden rule steady states, so population growth unambiguously reduces per capita consumption in neoclassical growth models of this type.9 However, this need not be true for life-cycle consumption, C: even while per capita consumption, c, is falling with more rapid growth, the present value of expected life-cycle consumption could be rising—or could be falling even more rapidly than c. This possibility is at the heart of concerns about the consequences of aging due to slowing population growth. Transfers, as we see later, play a central role in determining the outcome.
Transfers
Assume that a system of transfers is established by some combination of legislation, social norms, and individual choices, such that on average an individual age x makes transfers to others in the amount τ-(x), and receives transfers from others in the amount τ+(x), for a net gain or loss of τ(x) = τ+(x)-τ-(x). These are averages for age groups and need not hold for individuals. It is clear that the societal total of all transfers among age groups at any instant must sum to zero, because every transfer given is also a transfer received. For present purposes, I assume that all public sector transfers are also strictly pay-as-you-go (PAYGO); that is, current program expenditures are exactly balanced by current program taxes, with no deficit and no surplus.10
In a stable population with a strictly PAYGO system of transfers, the following social budget constraint must hold, whether or not the economy is golden rule:
This cross-sectional budget constraint can also be given a life-cycle interpretation: the present value of net transfers over the life-cycle, discounted by the population growth rate, is 0, so the implicit rate of return earned through the transfer system is n, the population growth rate (or n + λ if there is labor-augmenting technical progress). This result is well known for the Social Security system but holds more generally for every PAYGO transfer subsystem, including bequests and other familial transfers.
Government Debt
Suppose that government debt is held by individuals in the form of bonds, which appreciate in value at rate n, and may be bought or sold at any time. Let d-(x) be purchases of government bonds by individuals age x, and let d+(x) be sales of bonds, so that d(x), their difference, is net sales of bonds and represents an inflow of funds to the individual's budget. In golden rule steady state, the aggregate value of outstanding government debt must grow at rate n, which is exactly the rate at which the value of the existing bonds at any moment grows. Therefore the government issues no new bonds, and all bond transactions are between individuals. It follows that their value must sum to zero across all individuals, so that
In fact, government debt is, in some important respects, similar to government transfers: the young buy bonds that, in later years when they are older, are sold once again to young households. They differ in that there is no compulsion to buy bonds and in that the bonds are salable and bequeathable unlike other transfer wealth. It is convenient in what follows to group government debt with other transfers, denoting it with a superscript D, as in τD and TD.
Credit
Assume that the age group aged x borrows an amount m+(x) and loans an amount m-(x) for a net amount borrowed equal to their sum, m(x). Such loans take place through the family, the market, and possibly the public sector. We have already treated government debt separately. Under the assumption that the economy is closed to foreign participation in credit markets, and by treating the borrowing and lending of the private nonhousehold sector as adhering to the individuals holding equity in these firms, it must be the case that the flows of borrowing and lending add to zero across the population at all times, so that
Investment in Capital
Let i(x) = i-(x)-i+(x) be net investment in capital, K, by individuals at age x. This is defined such that positive i indicates a net flow of funds out of the individual's budget to purchase K, in contrast to the other variables, which indicate inflows (an arbitrary decision). If we integrate this over all ages, we should get the aggregate flow of investment per individual in the population. In a golden rule economy, this must equal income earned by capital, nK:
Budget Constraint for Flows
We can now gather together all these different flows into and out of the individual budget and relate them one to the other in an aggregate age-specific constraint on the flows:
where K(x) and M(x) are stocks of capital and credit held by individuals at age x expressed per member of the original birth cohort, rather than per surviving member of the cohort.
Aggregate Wealth Accounting
Now note that the accumulation of assets in the form of capital, K, and credit, M, is governed by the following differential equations: dK(x)/dx = p(x)i(x) and dM(x)/dx = -p(x)m(x), where the negative sign in the latter results from having defined m as net flows into the budget.
Grouping these assets together and substituting for i(x)-m(x), we have
From this it follows that
Consider the bracketed terms in the integral. Recall that transfer wealth at some age is just the present value of the expected difference between transfers to be received and made in the future. This is simply the negative of the integral shown, as follows from the fact that transfer flows integrate to zero over the population (see above). Thus one component of the integral is simply -T(x). The other component can be seen to be the quantity of life-cycle wealth accumulated up to age x per original member of the cohort, where a surplus (or deficit) of labor earnings over consumption at age a is cumulated up to age x, earning interest at the rate n. Thus the other component of the integral is W(x). We then have
Life-cycle wealth at age x can be held as capital, transfer wealth (including government debt), or credit.
We can now integrate over all age groups, weighted by initial birth cohort size, B(t)e-nx. If we divide this by the size of the population, or alternatively weight by be-nx, then we get wealth per capita. For example
In this way, we find W = K+T, recalling that M must be zero.
In principle, this integral should cover all cohorts that ever existed, because wealth accumulated by distant cohorts may have survived their lifetimes and may continue to exist and earn interest at time t. In the golden rule case, however, each cohort must leave neither wealth nor debt, since C = Y1, and net transfers and credit must always integrate to zero for the population, so the integral can be taken to ω.
The aggregate wealth equations can be reexpressed in a suggestive way by going back to their original defining integrals. This is done for W; the calculations for T are similar:
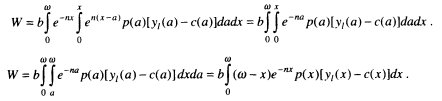
The second line is obtained by changing the order of integration. Inspection of the last expression on the right shows that bω is multiplied by (Y1- C), which under the golden rule assumption must be zero. The integrals involving the factor x can be seen to be the numerators of average ages, for which Y1 or C would be the denominator. These observations lead to the appealingly simple result
Here, Ac and Ay1 are the ages at which the average dollar is consumed and earned in the stable population—conveniently referred to as the average ages of consuming and earning. This fundamental result is closely related to a similar result in Willis (1988) for a population with discrete age distribution and no intra-life span mortality.
The equation has an intuitive interpretation: Consider the case n = 0, and suppose that all earnings over the life-cycle, amounting to Y1, were received at the average age of earning, Ay1. Similarly suppose that all life-cycle consumption, amounting to C = Y1, occurs at age Ac. If Ac> Ay1, then every person in the population between age Ay1 and Ac will hold an amount of wealth C = Y1. Everyone else will have no wealth at all. The proportion of the population holding wealth will be
Therefore the wealth held by the average person will be
If Ac< Ay1, then a similar argument shows that this expression gives the average negative wealth, or debt. An alternative interpretation can be given in terms of the length of time the average dollar earned is held before being spent.
As for transfer wealth, note that because the present value of transfers must integrate to zero over the expected life-cycle, transfer wealth at age x is just the negative of the weighted integral of t(a) up to age x. Let t+ = t- be the average gross flow of transfers to or from individuals in the population. Then by a similar derivation, the per capita value of transfer wealth is given by
Although the flows of transfers made and received at any instant must sum to zero, transfer wealth is not generally zero, which distinguishes transfers sharply from private sector loans. Transfer wealth can be nonzero because society can obligate the as yet unborn to make (or receive) future transfers—transfers that show up only in the expected payments or receipts of current members of the population, but not correspondingly in the expectations of the unborn since they do not enter the integral.
Combining these results, we have
The Accounting Framework: Economic Hypotheses and Interpretations
These results provide a coherent and comprehensive framework that can be used to express hypotheses in the economics literature pertaining to various aspects of age-distributed economic behavior. This is illustrated very briefly with a few examples.
Starret (1972:283) writes about models of this general sort: ''Investment does not require waiting! ... since it is possible to distribute consumption so that everyone consumes before he earns, the effect of increased roundaboutness on increased waiting is eliminated. It is this peculiar divorce of investment from waiting that really lies behind the 'biological theory of interest.'" The basic identity W = K + T expresses this peculiar divorce. Even if W is negative, indicating that "everyone consumes before he earns," so that there is no waiting, there may still be a positive K, provided only that T is sufficiently negative, that is, that output is sufficiently strongly reallocated to younger ages. I believe that this constellation was actually the typical case in high-mortality traditional societies.
Let TF denote transfer wealth arising from familial transfers, TG denote transfer wealth arising from public sector transfers, and TD denote government debt. Then the identity derived above becomes
K = W- TF- TG- TD.
Many economists, and most notably Modigliani (e.g., 1988), argue that the life-cycle saving motive, principally to provide for retirement, is the most important explanation for aggregate capital accumulation. In my notation, Modigliani argues that the magnitude of W largely accounts for the magnitude of K, in some sense. Other economists, most notably Kotlikoff and Summers (e.g., 1981 and 1988), argue that the desire to make transfers to children, and in particular the desire to make bequests, is the most important explanation for the level of K. In my notation, they argue that -TF largely accounts for K. In practice, this debate has sometimes taken the form of evaluating the ratio -TF/K which is taken to measure the importance of the intergenerational transfer motive, or the ratio (W- TG- TD)/K, which is taken to measure the importance of the life-cycle saving motive.11K
sometimes is taken to be solely non-household sector, non-government sector capital, and at other times only government capital is excluded.
Calculating (W - TG- TD)/K, Kotlikoff and Summers (1981) find that it is perhaps as low as 0.2, leading them to conclude that familial intergenerational transfers must provide the main motive for capital accumulation in the United States. This is not inconsistent with my own calculations if K is restricted to the production sector and excludes household capital and public sector capital. However, that formulation obscures the relative magnitudes of the various components. For example, I find W to be nearly three times as large as -TF. Indeed, since the life-cycle demand for wealth is met in good measure by holdings of public sector transfer wealth, TG, which is nearly twice the size of -TF, the comparison of -TF to K seems to me not to be very informative. An alternative comparison would be of -TF and W to K + TG + TD. In this comparison, W would appear to be three times as important as -TF. However, as seems to be generally acknowledged, what is really relevant is the elasticity of K with respect to -TF, for which these accounting identities provide no information.
Generational accounts (Auerbach et al., 1991; Kotlikoff, 1992) are calculations of age-specific public sector wealth, TG(x), excluding educational transfers, with particular attention to the implications of the changing form of taxation. Generational accounting does not generally assume the steady state, and indeed much of its interest derives from its ability to tell us who gains and who loses in transitional situations.
Another important issue is the effect of public sector transfer wealth, TG, on K. Feldstein has argued that TG is a close substitute for K and that therefore δK/δTG is a large negative number, perhaps -1 in the extreme case. If Social Security and Medicare, the most important components of TG, were primarily a remedy for the improvidence of a population that failed to save in such a way as to achieve an optimal allocation of consumption over the life-cycle, then TG might lead to more consumption at older ages and thereby raise W rather than diminishing saving earlier in life. In the extreme case, this would lead to ∂K/∂TG= 0. Another possibility, raised by Barro (1974), is that parents recognize that Social Security will require higher taxes from their children while delivering more income to them later in life. They may respond by making larger inter vivos transfers, or leaving larger bequests, so that K is unaffected and familial transfers change to offset governmental transfers. In the extreme case, ∂K/∂TG= 0 and ∂TF/∂TG = -1. The accounting framework can be used to pose the hypotheses, but cannot say which is correct.
ECONOMIC CONSEQUENCES OF POPULATION AGING DUE TO SLOW GROWTH
Now that we have sketched the way in which various mechanisms are used to reallocate resources across age and/or time over the life-cycle, it is time to consider how changes in the population age distribution interact with these mechanisms to generate economic consequences. What are the costs of population aging? Is it possible that more rapid population growth, while reducing per capita consumption due to capital dilution, might nonetheless lead to higher life-cycle consumption? Here, I consider how the change in the population growth rate affects the present value of life-cycle consumption across golden rule steady states by differentiating the budget constraints developed above.
The Economic Rate of Growth Effect
When the growth rate, n, and interest rate, r = n, change across golden rule steady states, the relative weighting of dependents and earners in the population will change, and therefore the amount consumed at some or all ages must change or, alternatively, the amount worked at some or all ages must change. The changes at age x that are made to maintain the accounting identities when population growth rates change may be denoted ∂c(x)/∂n and ∂y1(x)/∂n.12 The integral over all ages, x, of these changes must be such that they preserve the equality of C and Y1 across golden rule steady states. Differentiating the golden rule identity with respect to n = r, while holding p(x) fixed (and ignoring for the moment the effect on capital per worker) but letting the age profiles of earning and consumption vary as discussed above, we find
if K is held fixed.
But the changed growth rate will also alter the amount of capital per worker, which will change the productivity of labor, and thereby change the earnings function and require additional adjustments. When this model is embedded in a Solow growth model13 (Arthur and McNicoll, 1978; Lee,
1980; Willis, 1988), an additional term reflecting the effects of capital dilution across golden rule paths is added to the derivative:
where K is the average amount of capital (or real wealth) per person. (This derivative, by ignoring the effect of population growth rate on the age distribution of capital stock, and hence on the rate of depreciation, may considerably overstate the role of capital dilution; see Blanchet, 1988.) But this is just (W - K)/b, or T/b, the per capita level of transfer wealth divided by the birth rate (see also Willis, 1988):
This result may be interpreted as follows. Consider two stable populations with different total fertility rates of two and three children, and the same life expectancy of 75. Their annual growth rates will differ by 0.0142. In the one with higher fertility, individuals may consume more over their life-cycles, or work less, such that the present value of all the expected changes equals 0.0142 x T/(1/75) = 1.065 x T, which could be positive or negative.14 The specific changes in consumption and earnings at each age are not determined without additional behavioral assumptions—or, put differently, the result is very general and must hold across many different institutional contexts and preference functions. Consumption could be reduced by increased life-cycle savings, increased Social Security taxes, or increased familial transfers to the elderly. Labor earnings could be increased by additional hours of work each week or by postponing the age of retirement. The precise size of each such adjustment could be calculated by using this expression.
There are a number of points to make about this result. First, note that if parents plan to leave bequests to their children, this should be treated as a component of the net cost of children and included in the augmented expression just described. If, however, bequests are an accidental by-product of life-cycle saving and the uncertainty of age at death, then the analysis presented above is correct without additional modification. Although be-
quests were notationally finessed by viewing them as inter vivos transfers, the substance of the Modigliani-Kotlikoff/Summers debate has an important effect on the calculated effects of population aging.
If we wished to give a welfare interpretation to these calculations, we would have to take into account the utility parents receive from having the incremental children when n increases. For optimizing parents, the marginal utility from a child will equal the value of all the familial transfers that they plan to make to it, that is, TF. Therefore, only the effects of changed age distribution on public sector transfers, TG, will affect welfare (Lee and Lapkoff, 1988). Put differently, TG, translated into per child units, constitutes an externality to childbearing.
From the point of view of the individual, these changes are responses to the changed interest rate, n, and to whatever changes in tax and transfer policies are made in order to keep the economy on the golden rule path when n changes. For example, to raise capital formation, the government could increase downward transfers by increasing funding of higher education and raising taxes accordingly. To reduce capital formation, the government could increase public sector pensions, while raising taxes accordingly. These actions would reduce T and raise T, respectively.
From the macro point of view, they are changes in response to the changed population age distribution. In order for the golden rule accounting identity to remain true, this quantity must equal the difference between the average ages of consumption and earning, less the capital/consumption ratio. For example, if the third life-cycle stage is very long and consumption is relatively high in old age relative to childhood, as is the case in most contemporary industrial populations, then Ac - Ay1 will be positive, since the average age of consuming will be high. In this case, there are beneficial effects of a declining dependency burden that will tend to offset the negative effects of capital dilution if the population growth rate is higher. By contrast, if the mortality is very high and old age is seldom attained, then Ac - Ay1 may be negative, with a young average age of consuming. In this case, both the dependency effect and the capital dilution effect work in the same direction.
In fact, it appears that in the United States in the 1980s, Ac -Ay1 was about +4 years, on a household basis (Lee and Lapkoff, 1988), and similar results have been found for Japan and England (Ermisch, 1989). Evidently, the average household needs to hold positive wealth equal to about four times its average consumption or earnings in order to achieve the desired reallocation of income from younger to older ages.
Using the Mueller (1976) age profiles of consumption and earnings for a Third World agricultural population, together with a Coale-Demeny life table for a life expectancy of 20 years, and taking n = 0, we can also calculate Ac - Ay1 for a hypothetical high-mortality traditional society. In
contrast to the gap of +4 years for the United States, this calculation yields a gap of -5 years, indicating strong downward transfers from older to younger people. This is not surprising, given that old age occupies only 3 percent of the average life-cycle, while childhood occupies 36 percent. In such a society, there is aggregate life-cycle debt rather than wealth because the average member of the population has received transfers from his or her parents that have not yet been repaid by making equivalent transfers to their own children.
If we made some assumptions about the specific forms of life-cycle utility function governing the choice of consumption at each age and labor supply at each age, the functional dependence of y1(x) and c(x) on the population growth rate could be calculated explicitly. But the characterization of the necessary adjustments to consumption and earnings given above is very general and must hold for any behavioral assumptions we might choose to add to this model.
Samuelson (1975) suggested that because more rapid growth lowered life-cycle consumption through capital dilution, but also raised it by reducing the old age dependency burden, there might be an optimal rate of population growth at which the two effects were just offsetting. He called such an optimal rate of population growth for an economy with optimal saving, the "goldenest golden rule path." From the analysis above, we can conclude that when T = 0 on a golden rule path so that individuals willingly hold exactly the amount of capital that is socially optimal in the golden rule sense, then the population growth rate is optimal and the path is the goldenest golden rule.
Samuelson (1975) was initially mistaken about second-order conditions, and under his assumption the optimal growth rate was actually infinitely slow or infinitely rapid (Deardorff, 1976; Samuelson, 1976). Kim and Willis (1982) consider the more general case in which the life-cycle incorporates both old age and childhood dependency stages. They note that consumption will have higher variance across age than earnings, since earnings are all in the middle age group, whereas consumption is spread out across all ages. This fact, and some other weak conditions, are sufficient to guarantee that some finite growth rate will be optimal. Arthur and McNicoll (1978) also made an important contribution to this controversy.
The Impact of Aging Due to Slow Growth on Transfer Systems
Regardless of whether the economy is golden rule or follows some other steady-state path with r different from n, a change in the population growth rate will entail adjustments in all transfer systems, as indicated by the following equation:
This equation applies to the aggregate of all transfer systems, but it also applies to each one individually. The interpretation is by now familiar: if, on average, payments are made into the system before benefits are received, then a more rapidly growing, younger population will be able either to increase the benefits at some or all ages or to reduce the payments.
For example, consider total governmental transfers in the United States, including state, local, and federal. About 3.8 dollars is spent on each elderly person for each dollar spent per child (O'Higgins, 1988). Furthermore, the steady-state age distribution based on current rates (replacement level fertility, and a life expectancy of 75 years) will be quite old. Consequently, based on 1987 Consumer Expenditure Survey data (Lee, in press, b),
where the G indicates governmental transfers (the observational unit is households by age of respondent, but the age gap from individual data is similar). The average annual inflow per household was $6,800, which is about $2,600 per capita. Governmental transfer wealth per capita, therefore, was about 12(2,600) = $31,200 in 1987. If population growth were 1 percent per year more rapid, transfer payments could be greater by $312 per year, or taxes could be less by this amount, per person; $312 is roughly 2.5 percent of per capita consumption in 1987. The annual flow of $312 can be converted to a life-cycle total by multiplying by 1 divided by the household equivalent of the crude birth rate—in this case, multiplying by 28.5, which is the expected years of household headship in the stationary population.
One should not think, however, that more rapid population growth always relaxes governmental transfer system budget constraints. The results just given for the United States are probably fairly typical for modern industrial countries, but they are quite different from those for most Third World countries. Figure 2-9, for example, shows the age profiles of government taxes and transfers for India in 1981 (see Lee, 1991), weighted by the stable population age distribution. For India,
turns out to be -11 years, so that transfers flow downwards in India about as much as they flow upwards in the United States. This result is typical of the seven Third World countries I have studied, the only apparent exception being the rare Third World countries with strong public sector pension programs, such as Brazil (Lee and Miller, 1990).
It is also interesting to look in more detail at the way in which slower
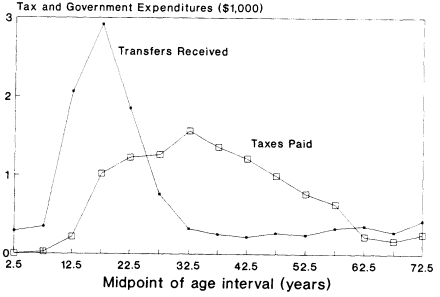
Figure 2-9 Indian public expenditures on health, education and pensions, and tax payments, 1981, weighted by stable population. SOURCE: Based on data in Lee (1991).
population growth would affect different transfer subsystems in the United States. Table 2-2 shows such a breakdown, based on the household accounting framework.
The effects shown in the second to last column are calculated on a per household per year basis. To convert these into lifetime costs or gains per individual, the last column shows them multiplied by the expected number of years of household headship per individual, which is about 28.5. Bequests are treated here as if they are simply another cost of children, an aspect of expenditure on child "quality." But it is also possible that they are the unintended by-product of unexpectedly early death or of saving more than is on average necessary for retirement. In this case, the saving on bequests attributed in the table to slower growth is spurious.
Overall, it appears that on an individual accounting basis, the upward transfers through the public sector roughly offset the downward transfers within the family, so the net effect of slower growth is small. However, strong pressures obviously emerge in federal transfer programs, where households must either pay about $1,000 more per year in taxes ($690 + $350), receive correspondingly less annually in benefits, or some combination of the two.
TABLE 2-2 Annual Costs or Gains per Household of 0.01 per Year Slower Population Growth, Arising Through Transfer Subsystems in the United States
|
Transfer Channel |
At+, Average Age of Receiving Transfer (years) |
At-, Average Age of Making Transfer (years) |
t+, Average Annual Inflow per Household (dollars) |
T, Average Transfer Wealth Held in this Form (dollars) |
Average Annual Cost per Household of dn = 0.01 or of 0.5 Lower TFR (dollars) |
Lifetime Cost or Gain for an Individual (dollars); (28.5 times previous column) |
|
Social Security |
71.7 |
41.2 |
2,270 |
69,000 |
690 |
19,700 |
|
AFDC |
36 |
45 |
91 |
800 |
-8 |
230 |
|
Education |
39.3 |
46.7 |
2,342 |
-17,000 |
-170 |
-4,800 |
|
Total health |
61.6 |
42.8 |
1,862 |
35,000 |
350 |
10,000 |
|
Inter vivos gifts |
38 |
53 |
370 |
-5,500 |
-55 |
-1,600 |
|
Bequests |
52 |
77 |
1,750 |
-44,000 |
-440 |
-12,500 |
|
Child rearinga |
10.6 |
39.3 |
2,820 |
-81,000 |
-405 |
-11,542 |
|
College costsa |
20 |
48 |
215 |
-6,000 |
-30 |
-855 |
ECONOMIC CONSEQUENCES OF POPULATION AGING DUE TO LOW MORTALITY
Mortality Change and Life-Cycle Planning
''Individual aging" refers, in common language, to the increasing age of some person. Here, however, I use it to refer to the changing shape of the average life-cycle, when life expectancy rises so that the expected number of person-years lived at older ages increases, as shown in the figures earlier. When individual aging occurs, the life-cycle budget constraint above will no longer hold for the initial age profiles of earning, consumption, and transfers. In particular, if the expected numbers of person-years lived in the elderly life-cycle stage increases relative to the number of person-years lived in the working ages, then either consumption will have to be reduced at some or all ages, or earnings will have to be increased. For this reason, we can view the age profiles of earning and consumption as functions, at every age, of the general level of mortality, indexed by i as above, just as we have viewed them earlier as functions of n.
Mortality Decline, Consumption, and Earning: The Economic Life-Cycle Effect
The basic strategy is to differentiate the golden rule life-cycle budget constraint with respect to the mortality level and set the derivative equal to zero. For the present, we hold n constant and assume that labor productivity is unaffected by changes in the amount of capital per worker; later we allow these to vary with i.
In the golden rule case, we have
holding n fixed.
The integral on the right is the discounted sum, over all ages, of the changes in person-years lived at each age multiplied by the surplus or deficit of earnings over consumption at each age. Evidently, if person-years lived increase at an age in which more is earned than is produced, the life-cycle budget constraint will be relaxed; if person-years lived increase at an age in which more is consumed than is produced, such as childhood or old age, then the budget constraint will be tightened. The integral gives the net effect of all these surpluses and deficits and may be positive or negative. This integral is the present value, at birth, of all the adjustments that must be made when life expectancy rises by 1 year.
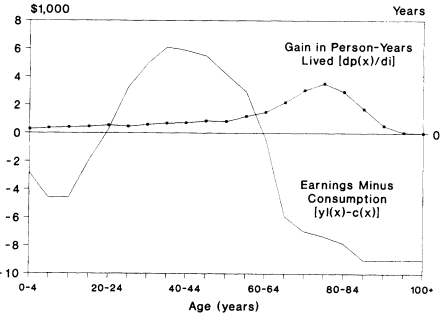
Figure 2-10 Person-years of life gained for 1-year increase in life expectancy versus labor earnings minus consumption, U.S. data, 1985. SOURCE: The distribution of person-years gained is based on recent Swedish life tables. The data on earnings minus consumption are taken from Lee and Lapkoff (1988), based on the 1985 Consumer Expenditure Survey.
It is instructive to plot ∂p(x)/∂i against y1(x) -c(x) for actual data. Figure 2-10 does this for U.S. data. It is striking that the greater part of the gains in person-years lived occurs at ages for which consumption vastly exceeds earning. Indeed, 66 percent of the gains occur at age 65 or over.15 Computing the population-weighted integral as described by the right side of the equation, and dividing by the present value of life-cycle consumption so that both sides are expressed as proportions, yields a value of -0.009, or nearly -1 percent. The interpretation is that a 1-year increase in life expectancy requires adjustments to life-cycle consumption or labor earnings equal to 0.9 percent of their present value at birth. These adjustments could take the form of a 0.9 percent reduction in consumption at every age; an increase in labor supply by 0.9 percent at every age, say from 40 hours per week to 40.36 hours per week; or a postponement of retirement by five months from
age 65 (if the productivity at age 65 is assumed to equal the life-cycle average, and the rate of population growth is zero; if productivity is below average, or the growth rate is positive, then retirement would have to be postponed longer).16
I call this the life-cycle effect, or individual aging effect, of declining mortality because it reflects the simple need to provide for more years of life, in this case life lived in retirement.
One should not think, however, that mortality decline is necessarily costly in this way. A similar calculation can be carried out for a hypothetical high-mortality population with initial life expectancy of 20 years, and earning and consumption profiles as reported in Mueller (1976), intended to be representative of Third World agricultural populations. In this case, the life-cycle effect is actually positive! Person-years of life gained are predominantly in the working ages, as can be confirmed by reference to Figure 2-5, which shows that at a life expectancy of 20, 69 percent of the gain accrues to the ages 15-64.
Mortality Decline and Transfers
There is a corresponding equation constraining adjustments to the transfer system, which holds not only for the golden rule case, but for the general case as well:
for fixed n.
Figure 2-11 shows the information needed to make this calculation for Social Security. The integral equals about $3,200 over an individual life-cycle. To put this on an annual per capita basis, we can simply multiply by b, which yields $43 per year. The interpretation is similar to previous ones. When person-years are gained at ages that, on net, receive transfers, this is costly. The integral of gains and losses on the right must be balanced by adjustments to age-specific transfer flows on the left.
The effect of mortality change on health costs cannot be treated this simply, however. An appropriate analysis must treat separately the health costs of those who survive and the health costs of those who die. Those who die impose the heavy costs of a terminal illness. When mortality
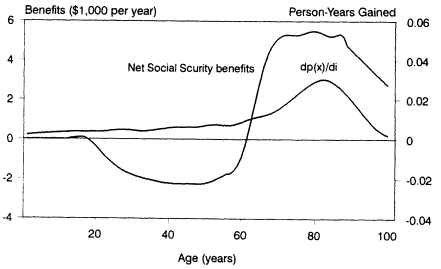
Figure 2-11 Annual net Social Security benefits and person-years of life gained (for a gain of 1 year in life expectancy) by age of individual. SOURCE: Tax and benefit data calculated from 1987 U.S. Consumer Expenditure Survey. Mortality data calculated from recent Swedish life tables.
changes, the distribution of deaths by age changes, and hence the age profiles of health costs themselves change. This can all be handled in a straightforward way, but is not done here.
Mortality Decline and the Rate of Growth Effect
The derivatives above hold the population growth rate fixed. In practice, as discussed earlier, mortality decline leads to more rapid population growth, because more female births survive to the reproductive ages. The full derivative is as follows:
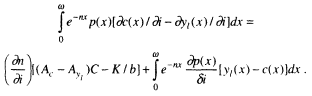
What is added here is the factor ∂n/∂i which is multiplied by the rate of growth effect discussed earlier and has been shown to equal transfer wealth, T/b. We have seen earlier that ∂n/∂i is close to zero in low-mortality populations, but that it is substantial in high-mortality settings. In low-mortality settings such as the United States, therefore, the effect of mortality decline is essentially equal to the life-cycle, or individual aging, effect: people live longer, and their additional years are years of leisure. They must either consume less at each age or work longer in order to pay for the gift of longer life. We have seen that each additional year of life expectancy requires a reduction in consumption, or an increase in labor supply, of about 1 percent.
In high-mortality settings, ∂n/∂i is substantial, so that mortality decline makes populations younger. Because transfers are downwards in such populations, a younger population is costly. However, because there is little capital in such societies, capital dilution is presumably relatively unimportant. (Increased pressure on fixed resources probably is important, but is not included in this analysis.) Finally, the life-cycle effect is relatively small and positive, since mortality decline adds years of life mainly during the working years. The net effect is that mortality decline in both high-mortality and low-mortality settings has similar consequences, but for very different reasons: a 1-year gain in life expectancy entails a 1- percent reduction in the present value of consumption or a corresponding increase in earnings.
We see, then, that when mortality declines in high-mortality settings, the rate of growth effect dominates. Higher rates of return are earned on life-cycle wealth, which is held mainly in the form of transfer wealth. But since net allocational flows are downwards by age, such populations hold net transfer debt, and a higher rate of return is therefore costly and leads to reduced life-cycle consumption. When mortality declines in low-mortality settings, however, there is very little effect on the rate of growth, so the life-cycle effect dominates. The rate of return to life-cycle wealth is unchanged, but individuals must provide for more years of retirement, which is costly in terms of forgone consumption or leisure earlier in the life-cycle. In the special and historically inaccurate case of a neutral mortality decline, in which the absolute decline in the force of mortality at every age is equal, the rate of growth effect on the age distribution exactly offsets the life-cycle effect. Longer years of retirement could be paid for exactly by the increased rate of return on life-cycle wealth, requiring no readjustment of life-cycle consumption or earning profiles—if we ignore the effect of capital dilution.
The results of this section can be compared to those of Kotlikoff (1989:359),
who reaches an apparently very different conclusion: "... increasing the length of life, including productive life, appears to permit a higher level of consumption in every year that an individual is alive." The principal difference, I believe, lies in Kotlikoff's assumption that labor supply increases at some ages over the life-cycle; I treat this as a costly reduction in leisure.
CONCLUSION: RESEARCH DIRECTIONS
This chapter has developed an economic-demographic age accounting framework with strong links to formal demography, as well as links to various models and themes in economics. These economic links include overlapping generations, optimal population growth, life-cycle saving, the bequest motive, generational accounting, and private responses to public transfer programs. I believe that further development of this interface of formal demography and macroeconomics holds promise for theory, measurement, empirical work, and policy-oriented research. Research needs can be divided into empirical applications of the basic framework, on the one hand, and further development of the accounting and analytic framework, on the other.
Empirical Applications
The framework described here can be used to organize, summarize, and interpret data on transfer systems and the life-cycle. As long as we use synthetic cohort methods, which assume that cohort profiles can be constructed from cross sections, the data necessary to implement the framework appear to be widely available in both developed and Third World populations. Because the analysis requires only aggregate age profiles rather than individual data, information can be drawn from differing sources and pooled, with a basic household expenditure survey providing much of what is needed. Data on bequests are an important exception, and for Third World populations, it may be necessary to develop measures of within-household transfers. More experience with application of the framework will indicate whether currently available data are adequate. If we abandon the synthetic cohort assumption, data requirements become very severe, because it is then necessary to reconstruct the life histories of each cohort. Some of the work by Kotlikoff and his collaborators makes only partial synthetic cohort, steady-state assumptions (Kotlikoff and Summers, 1981; Auerbach et al., 1991).17
One particularly promising use of the framework would be to shape and inform the development of age-based national accounts, continuing the work begun by generational accounting (Auerbach et al., 1991). Comparative cross-cultural and historical estimation also appears possible and should provide an interesting view of the transition from familial to public transfer systems as the welfare state develops, and perhaps also afford some insights into how the growth of public sector transfers affects life-cycle consumption profiles and capital accumulation. Some aspects of the resource flows from one ethnic group to another can be investigated within this framework; for example, do transfers flow from younger nonwhite populations to older white populations in the United States? It would also be very interesting to incorporate immigration, because the transfer patterns of subpopulations arriving as young adults would be quite different. There is a literature on the effect of migration on population age distribution (e.g. Schmertmann, 1992). Similarly, it may be possible to address gender issues. To do so properly would require introducing time use into the accounts, so as to treat explicitly the productive use of home time. Most of these extensions would require further methodological research.
Methodological Research
Although the basic framework is quite general, its implementation here is confined to a doubly special case: first, to steady states, and second, to golden rule economies with r = n. For calculations of the various forms of wealth, it is a simple matter to relax the golden rule assumption. However, to analyze the comparative statics of aging without the golden rule assumption would require making additional behavioral assumptions in order to determine ∂r/∂n, for example, by specifying a life-cycle utility function as in Tobin (1967). Serious policy-oriented work requires relaxation of the steady-state assumption, so that transitional phases can be considered. There are two distinct aspects of the steady-state assumption. The first is the assumption that age profiles are changing only at a constant exponential rate, so that synthetic cohort estimation of the profiles is possible from a single cross section. Relaxing this assumption would impose very heavy demands for detailed longitudinal data over many decades. The second is that the population and economy are in steady state; this assumption is difficult to relax analytically, but it can in principle be handled by appropriate macrosimulation, elaborating on the methods used by Auerbach and Kotlikoff (1987).
There are a number of other issues that need to be resolved, some straightforward and some more difficult. Both the individual life-cycle framework and the household life-cycle framework require attention to conceptual as well as measurement issues. Education should be incorporated as
a form of capital formation. Mortality change should be modeled in such a way that morbidity and labor efficiency change at the same time. Bequests and terminal illnesses should be made to depend not on age-group membership, but rather on age at death.
Behavioral Theory
This chapter has primarily addressed questions of accounting and has paid scant attention to behavioral issues. But there are important related research literatures on why people make familial transfers, on the rationale for public sector transfer systems (Becker and Murphy, 1988), and on the relations between public sector and familial transfers, as discussed earlier. There is also an important literature on the relation of familial and public transfer systems to fertility behavior (Caldwell, 1982; Willis, 1980, 1987). Advances in the conceptualization and description of transfer systems may also inform and stimulate further work on these important issues.
Although a great deal of work evidently remains to be done, the time is ripe for a synthesis of work carried out over the past three decades by formal demographers, economic demographers, and economists working on age-distributed macroeconomic models.
APPENDIX: HOUSEHOLDS
As shown earlier, in a stable population the proportion of people age x is be-nxp(x). Let h(x) be the household headship rate at age x. The age distribution of household heads will then be bhe-nxp(x)h(x), where bh is the birth rate for households, given by
This could be viewed as 1 divided by the discounted expected years of household headship over the life-cycle. The undiscounted expected number of years of headship is simply
which for the United States in 1987 was about 28.5 years. The average headship rate, h, is given by the integral over all ages of the stable age distribution for individuals in the population, weighted by h(x).
Adult individuals often move through a succession of households as they age over the life-cycle. This does not cause problems for the accounting of budgetary flows. It does cause problems, however, for the account-
ing of stocks. The approach taken here is to use household headship rates to translate the household level flows into average pseudoindividual flows by multiplying by headship rates. Then these pseudoindividual flows are cumulated to get stocks, calculated per original member of the birth cohort. These stocks can then be reexpressed on a per household basis, if desired, or left at the individual level. For example, by letting the superscripts h and i denote household and individual flows, the equation for cumulation of life-cycle wealth would be
To find W we would weight this by the size of individual birth cohorts as in the main text. Then if desired we could calculate the aggregate life-cycle wealth per household by dividing this individual measure by the aggregate household headship rate.
Unfortunately, these analytic expressions gloss over two serious complications. First, not all adults in the household need be the same age. When adults of very different ages are grouped together in households, as is sometimes the case, the age profiles for households will be far less informative about the life-cycle profiles of individuals—and it is ultimately individuals in whom we are interested. In many data sets, women will rarely be designated head if a male is present, so female ages will be systematically misrepresented by these procedures. The kind of flipping back and forth between accounts for households and for individuals that was just done for wealth accounting may then be incorrect and give misleading results. This problem will be particularly acute in Third World settings. Second, household headship is typically not distributed randomly across individuals of a given age. Instead, it may be that household headship is associated with economic variables of interest, such as labor earnings, consumption, or receipt of transfers. In this case, observing the economic flows into and out of households headed by a fraction of the population at some age, and then implicitly allocating a share of those flows to all people at that age, will be misleading.
One way to lessen the distortions arising in these ways is to take the ages of all adults in the household into account. A simple way to do this would be to randomly choose one of the adult household members to designated the head, or better, the household reference person. A more efficient way would be to allocate a share of the household resources to each adult, keeping track of their individual ages. Such procedures can eliminate much of the bias in working at the household level.
REFERENCES
Arthur, B.W., and G. McNicoll 1978 Samuelson, population and intergenerational transfers. International Economic Review 19(1):241-246.
Auerbach, A.J., and L.J. Kotlikoff 1987 Dynamic Fiscal Policy. Cambridge: Cambridge University Press.
Auerbach, A.J., J. Gokhale, and L.J. Kotlikoff 1991 Generational accounts: A meaningful alternative to deficit accounting. Pp. 55-110 in D. Bradford, ed., Tax Policy and the Economy. Cambridge, Mass.: MIT Press for the National Bureau of Economic Research.
Barro, R.J. 1974 Are government bonds net wealth? Journal of Political Economy 28(6):1095- 1117.
Becker, G., and K. Murphy 1988 The family and the state. Journal of Law and Economics 31 (April):1-18.
Blanchet, D. 1988 Age structure and capital dilution effects in neo-classical growth models. Journal of Population Economics 1(3):183-194.
Bledsoe, C.H., and B. Cohen, eds. 1993 Social Dynamics of Adolescent Fertility in Sub-Saharan Africa . Committee on Population, Commission on Behavioral and Social Sciences and Education, National Research Council. Washington, D.C.: National Academy Press .
Bourgeois-Pichat, J. 1978 Le financement des retraites par capitalisation. Population 6:1115-1136.
Bureau of Labor Statistics 1987 Consumer Expenditure Survey. Washington, D.C.
Bureau of the Census 1990 Statistical Abstract of the United States: 1990, 110th ed. Washington, D.C.: U.S. Department of Commerce.
Caldwell, J.C. 1982 Theory of Fertility Decline. New York: Academic Press.
Coale, A. 1972 The Growth and Structure of Human Populations. A Mathematical Investigation. Princeton, N.J.: Princeton University Press.
Coale, A., and P. Demeny 1983 Regional Model Life Tables and Stable Populations. New York: Academic Press.
Deardorff, A.V. 1976 The growth rate for population: Comment. International Economic Review 17(2):510-515.
Diamond, P.A. 1965 National debt in a neoclassical growth model. American Economic Review 55:1126-1150.
Ermisch, J. 1989 Intergenerational transfers in industrialized countries: Effects of age distribution and economic institutions. Journal of Population Economics 1:269-284.
Feldstein, M. 1974 Social security, induced retirement, and aggregate capital formation. Journal of Political Economy 82(5):905-927.
Gale, D. 1973 Pure exchange equilibrium of dynamic economic models. Journal of Economic Theory 6:12-36.
Hurd, M. 1990 Research on the elderly: Economic status, retirement, and consumption and saving. Journal of Economic Literature 28(2):565-637.
Keyfitz, N. 1985 The demographics of unfunded pensions. European Journal of Population 1:5-30.
1988 Some demographic properties of transfer schemes: How to achieve equity between the generations. Pp. 92-105 in R.D. Lee, W.B. Arthur, and G. Rodgers, eds., Economics of Changing Age Distributions in Developed Countries. Oxford: Oxford University Press.
Kim, O., and R. Willis 1982 The Growth of Population in Overlapping Generation Models. Unpublished manuscript, Economic Research Center/National Opinion Research Center, University of Chicago.
Kotlikoff, L.J. 1989 What Determines Savings? Cambridge, Mass.: MIT Press.
1992 Generational Accounting. New York: Macmillan, The Free Press.
Kotlikoff, L.J., and L.H. Summers 1981 The role of intergenerational transfers in aggregate capital accumulation. Journal of Political Economy 89:706-732.
1988 The contribution of intergenerational transfers to total wealth: A reply. Pp. 53-67 in D. Kessler and A. Masson, eds., Modeling the Accumulation and Distribution of Wealth. Oxford: Clarendon Press.
Lazear, E.P., and R.T. Michael 1988 Allocation of Income Within the Household. Chicago: University of Chicago Press.
Lee, R.D. 1980 Age structure, intergenerational transfers and economic growth: An overview. Revue Economique 31(6):1129-1156.
1988 Induced population growth and induced technological progress: Their interaction in the accelerating phase. Mathematical Population Studies 1(3):265-288.
1991 Evaluating externalities to childbearing in developing countries: The case of India. Pp. 297-342 in G. Tapinos, D. Blanchet, and D.E. Horlacher, eds., Consequences of Rapid Population Growth in Developing Countries. New York: Taylor and Francis.
In press a Fertility, mortality and intergenerational transfers: Comparisons across steady states. In J. Ermisch, ed., The Family, The Market and The State. Oxford: Oxford University Press.
In press b Population age structure, intergenerational transfers, and wealth: A new approach, with applications to the United States. Journal of Human Resources.
Lee, R.D., and S. Lapkoff 1988 Intergenerational flows of time and goods: Consequences of slowing population growth. Journal of Political Economy 96(31):618-651.
Lee, R.D., and T. Miller 1990 Population growth, externalities to childbearing, and fertility policy in the third world. Proceedings of the World Bank Annual Conference on Development Economics, 1990. Supplement to the World Bank Economic Review and to the World Bank Research Observer 275-304.
Mason, A. 1987 National savings rates and population growth: A new model and new evidence. Pp. 523-560 in D.G. Johnson and R.D. Lee, eds., Population Growth and Economic Development: Issues and Evidence. Madison: University of Wisconsin Press.
McCandless, Jr., G.T., with N. Wallace 1991 Introduction to Dynamic Macroeconomic Theory: An Overlapping Generations Approach. Cambridge, Mass.: Harvard University Press.
Modigliani, F. 1988 Measuring the contribution of intergenerational transfers to total wealth: Conceptual issues and empirical findings. Pp. 21-52 in D. Kessler and A. Masson, eds., Modeling the Accumulation and Distribution of Wealth. Oxford: Clarendon Press.
Mueller, E. 1976 The economic value of children in peasant agriculture. Pp. 98-153 in R. Ridker, ed., Population and Development: The Search for Interventions . Baltimore: Johns Hopkins Press.
O'Higgins, M. 1988 The allocation of public resources to children and the elderly in OECD countries. Pp. 201-228 in J.L. Palmer, T. Smeeding, and B.B. Torrey, eds., The Vulnerable. Washington, D.C.: The Urban Institute Press.
Preston, S. 1982 Relations between individual life-cycles and population characteristics. American Sociological Review 7(2):253-264.
Romer, P. 1990 Endogenous technological change. Journal of Political Economy 98(5):S71-S102.
Sahlins, M. 1972 Stone Age Economics. Chicago: Aldine-Atherton.
Samuelson, P. 1958 An exact consumption-loan model of interest with or without the social contrivance of money. Journal of Political Economy 66(6):467-482.
1975 The optimum growth rate for population. International Economic Review 16(3):531-538.
1976 The optimum growth rate for population: Agreement and evaluations. International Economic Review 17(2):516-525.
Schmertmann, C.P. 1992 Immigrants' ages and the structure of stationary populations with below-replacement fertility. Demography 29(4):595-612.
Solow, R. 1956 A contribution to the theory of economic growth. Quarterly Journal of Economics 70:65-94.
Starret, D. 1972 On golden rules, the ''biological rate of interest," and competitive efficiency. Journal of Political Economy 80:276-291.
Tobin, J. 1967 life-cycle saving and balanced economic growth. Pp. 231-256 in W. Fellner et al., eds., Ten Economic Studies in the Tradition of Irving Fisher. New York: John Wiley & Sons.
Willis, R. 1980 The old age security hypothesis and population growth. In T.K. Burch, ed., Demographic Behavior: Interdisciplinary Perspectives on Decision Making. Boulder, Colo.: Westview Press.
1987 Externalities and population. Pp. 661-702 in D.G. Johnson and R.D. Lee, eds., Population Growth and Economic Development: Issues and Evidence. Madison: University of Wisconsin Press.
1988 life-cycles, institutions and population growth: A theory of the equilibrium interest rate in an overlapping-generations model. Pp. 106-138 in R.D. Lee, W.B. Arthur, and G. Rodgers, eds., Economics of Changing Age Distributions in Developed Countries. Oxford: Clarendon Press.










































